Abstract
Intrinsically disordered proteins (IDPs) have received increasing attention in recent studies due to their structural heterogeneity and critical biological functions. To fully understand the structural properties and determine accurate ensembles of IDPs, molecular dynamics (MD) simulation was widely used to sample diverse conformations and reveal the structural dynamics. However, the classical state-of-the-art force fields perform well for folded proteins while being unsatisfactory for the simulations of disordered proteins reported in many previous studies. Thus, improved force fields were developed to precisely describe both folded proteins and disordered proteins. Preliminary tests show that our newly developed CHARMM36IDPSFF (C36IDPSFF) force field can well reproduce the experimental observables of several disordered proteins, but more tests on different types of proteins are needed to further evaluate the performance of C36IDPSFF. Here, we extensively simulate short peptides, disordered proteins, and fast-folding proteins as well as folded proteins, and compare the simulated results with the experimental observables. The simulation results show that C36IDPSFF could substantially reproduce the experimental observables for most of the tested proteins but some limitations are also found in the radius of gyration of large disordered proteins and the stability of fast-folding proteins. This force field will facilitate large scale studies of protein structural dynamics and functions using MD simulations.
1. Introduction
Intrinsically disordered proteins (IDPs) and proteins with intrinsically disordered regions (IDRs) have received increasing attention recently.1,2 IDPs or IDRs carry out many important biological functions in eukaryotes3,4 and have a close association with variant human diseases.5–7 A full understanding of the structural properties of IDPs is crucial to reveal the mechanism of their variant functions and to treat complex human diseases. Different from folded proteins, IDPs lack a well-defined three-dimensional structure while sampling a heterogeneous ensemble with diverse conformations that interconvert with each other.8 Therefore, sampling accurate conformational ensembles of IDPs become the main goal of many recent studies.9–11
Molecular dynamics (MD) simulation is one of the effective methods to determine the ensembles of IDPs based on a set of empirical physics-based parameters, which is usually called the force field. The accuracy of the force field plays a key role in the precise description of IDP ensembles in MD simulations.8 However, the classical force fields perform better in simulations of folded proteins with stable structures12–14 than those in the IDPs with a large conformational fluctuation. These force fields are usually unsatisfactory in simulations of IDPs and they always overestimate the compactness of IDPs when compared with the experimental measurements.15–17
Efforts to improve the accuracy of force fields make great progress in well reproducing the IDP characteristics using MD simulations. Some IDP-specific force fields were developed by the modifications of the classical force fields to better describe IDPs, such as ff99IDPs,18 ff14IDPs,19 ff14IDPSFF.15 In preliminary tests, these force fields could sample more diverse conformations and the simulated NMR observables agree well with the experimental measurements for the tested IDPs by hundreds of nanosecond simulations. Based on the methods of previous studies, we developed an IDP-specific force field CHARMM36IDPSFF (C36IDPSFF) originating from the CHARMM36m (C36m) force field20 with modifications of the backbone dihedral correlation map (CMAP) parameters for all 20 amino acids.21 We reduced the energy barrier between PPII and the right-handed a-helix region in the Ramachandran plot of the previous C36m. This will facilitate conformational conversion and will save a lot of computing resources in achieving enough sampling of IDPs. In previous preliminary tests, we found that C36IDPSFF could well predict the experimental observables of the tested short peptides and disordered proteins in hundreds of nanosecond simulations. This suggests that the C36IDPSFF force field could accurately simulate the IDPs, but extensive tests are needed to further evaluate the performance of C36IDPSFF for other disordered peptides and proteins, and also for the folded proteins which are not our initial optimized targets. In this study, we tested two short peptides, six disordered proteins, and four fast-folding proteins as well as six folded proteins, and compared the simulated results with abundant experimental data. We found that the simulated results of C36IDPSFF agree well with most of the experimental data for both disordered and folded proteins, which could be beneficial for the wide-spread applications of C36IDPSFF in future studies on protein structural dynamics and functions using MD simulations. C36IDPFF also performs well when compared with the recently developed a99SB-disp force field which provides the accurate and balanced description for both disordered and folded proteins. In addition, we also found that C36IDPSFF has the character of compatibility for different initial structures, and whether the simulations were from a compact conformation or an extended conformation, similar results were generated. However, some limitations of C36IDPSFF were also found in reproducing the radius of gyration of large disordered proteins and the stability of some fast-folding proteins. We hope that this work would illuminate the strengths and limitations of C36IDPSFF as far as possible and provide some suggestions for further improvement of our force field as well as other force fields. Furthermore, we believe that C36IDPSFF could be helpful to study the structural mechanism and functions of proteins, especially for the IDPs, and establish a disorder-function paradigm.
2. Materials and methods
2.1. MD simulations
All MD simulations were run using GROMACS version 5.0.4.22 The detailed simulation conditions are listed in Table 1. The initial structure was solvated in a water box with counterions to neutralize the systems. Energy minimizations were conducted with the steepest descent algorithm up to 50 000 steps. The LINCS algorithm23 was used to constrain the covalent bonds with hydrogen atoms. Lennard-Jones interactions were truncated at 12 Å with a potential switching function from 10 to 12 Å. The electrostatic interactions were calculated using the particle mesh Ewald method with a cutoff of 12 Å on an approximately 1 Å grid with a fourth-order spline.24 Temperature coupling was controlled using a velocity rescaling25 thermostat and pressure coupling was controlled using a Parrinello–Rahman algorithm.26 The systems were heated and equilibrated both for 100 ps in an NVT ensemble and an NPT ensemble, respectively. The integration time step was set to 2 fs and the coordinates were saved every 5 ps. For folded proteins, one 1 ms simulation was run, while for disordered peptides and proteins, five independent 1 ms simulations were run to reduce random error and sample enough conformations. For fast-folding peptides and proteins, 36 replicas were spaced from 278 to 390 K and each replica was run for 500 ns in replica exchange simulations.
Table 1.
Simulation conditions of all tested peptides and proteins. The default water models of C36IDPSFF is CHARMM modified TIP3P, the “disp-water” model from a99SB-disp is also used in some simulations
| Systems | Length | Initial structure | Ions | Waters | Temperature (K) | Simulation time | Force fields/water models |
|---|---|---|---|---|---|---|---|
| ala5 | 5 aa | Extended | 0 | 2703 | 300 | 1 μs × 5 | C36IDPSFF |
| ala7 | 7 aa | Extended | 0 | 2271 | 300 | 1 μs × 5 | C36IDPSFF |
| Aβ40 | 40 aa | PDB 1Z0Qa34 | 3 Na+ | 8439 | 273 | 1 μs × 5 | C36IDPSFF |
| 8371 | C36IDPSFF/disp-water | ||||||
| Extended | 11 Na+ 8 Cl− | 8629 | 300 | C36IDPSFF | |||
| Aβ42 | 42 aa | PDB 1Z0Q34 | 3 Na+ | 8347 | 273 | 1 μs × 5 | C36IDPSFF |
| ACTR | 71 aa | PDB 1KBHb35 | 17 Na+ 9 Cl− | 9472 | 304 | 1 μs × 5 | C36IDPSFF |
| 9519 | C36IDPSFF/disp-water | ||||||
| drkN SH3 | 59 aa | pE-DB 8AAC-136 | 16 Na+ 10 Cl− | 10 677 | 304 | 1 μs × 5 | C36IDPSFF |
| 10686 | C36IDPSFF/disp-water | ||||||
| hIAPP | 37 aa | PDB 5MGQ37 | 2 Cl− | 4791 | 278 | 1 μs × 5 | C36IDPSFF |
| Histatin-5 | 24 aa | Extended | 50 Na+ 55 Cl− | 17 746 | 300 | 1 μs × 5 | C36IDPSFF |
| BPTI | 58 aa | PDB 5PTI38 | 6 Cl− | 4518 | 273 | 1 μs × 1 | C36IDPSFF |
| GB3 | 56 aa | PDB 1P7E39 | 6 Na+ 4 Cl− | 3783 | 298 | 1 μs × 1 | C36IDPSFF |
| HEWL | 129 aa | PDB 6LYZ40 | 8 Cl− | 6679 | 273 | 1 μs × 1 | C36IDPSFF |
| 2JPU | 129 aa | PDB 2JPU41 | 19 Na+ 18 Cl− | 8954 | 298 | 1 μs × 1 | C36IDPSFF |
| 2JQN | 116 aa | PDB 2JQN42 | 19 Na+ 11 Cl− | 5186 | 293 | 1 μs × 1 | C36IDPSFF |
| 2KL6 | 108 aa | PDB 2KL643 | 45 Na+ 38 Cl− | 9463 | 298 | 1 μs × 1 | C36IDPSFF |
| (aaqaa)3 | 15 aa | Extended | 11 Na+ 11 Cl− | 3776 | REMDc | 0.5 μs × 36 replica | C36IDPSFF |
| Villin | 36 aa | PDB 1VII44 | 9 Na+ 11 Cl− | 3014 | REMDc | 0.5 μs × 36 replica | C36IDPSFF |
| CLN025 | 10 aa | Extended | 15 Na+ 13 Cl− | 4418 | REMDc | 0.5 μs × 36 replica | C36IDPSFF |
| GB1 | 16 aa | Extended | 15 Na+ 12 Cl− | 4128 | REMDc | 0.5 μs × 36 replica | C36IDPSFF |
The last two residues were removed from the PDB structure.34
Homology modeling was performed based on the PDB structure35 to match the length of the experimental NMR measurements.
The temperatures used in replica exchange MD simulations are 278.00, 280.82, 283.67, 286.54, 289.43, 292.34, 295.28, 298.24, 301.22, 304.23, 307.26, 310.31, 313.39, 316.49, 319.68, 322.83, 326.00, 329.20, 332.43, 335.55, 338.83, 342.13, 345.45, 348.80, 352.18, 355.59, 359.02, 362.48, 365.96, 369.48, 373.02, 376.59, 380.18, 383.87, 387.52, and 391.21, units in K.
2.2. Analysis of simulations
For time-dependent results, entire simulation trajectories were used for the analysis; for ensemble averaged results, the first 200 ns of each trajectory was discarded and the remaining 800 ns was used for the analysis. All the calculation errors were estimated with block analysis by dividing the MD trajectories into 8 blocks (100 ns for one block). In RMED simulations, the first 100 ns of the replicas were discarded and the remaining 400 ns replicas were analyzed in 4 blocks.
The gmx rms and gmx gyrate modules embedded in GROMACS were used for the analysis of the root-mean-square deviation (RMSD) and the radius of gyration (Rg), respectively. The DSSP algorithm27 was used to calculate the secondary structure fraction. Chemical shifts were calculated by SHIFTX228 and scalar couplings were calculated using the Karplus equations listed in Table S1 (ESI†). To compare with the previous results of a99SB-disp, the chemical shifts were calculated using the SPARTA+29 software for several tested proteins. Residual dipolar couplings (RDCs) were calculated using the PALES software30 using an alignment window of 15 residues. Amide S2 order parameters were calculated using the MOP S2 software.31,32 Conformational clustering was conducted using the kclust software in MMTSB toolset33 for two cycles. The conformations were clustered based on the 361 backbone dihedral angle (φ) in the first cycle and then the representative conformations were clustered based on the RMSD in 4 Å in the second cycle. In addition, in order to verify the convergence of simulations of disordered peptides and proteins, time-dependent number of conformational clusters and time-dependent RMS errors between the experimental data and the simulated NMR observables are calculated.
3. Results and discussion
3.1. Convergence of simulations for IDPs
Convergence should be first of all considered for the MD simulations, as it will ensure the adequacy of the simulation time and the validity of the simulation analysis. Different from ordered proteins, the analysis of structural stability, such as the root-mean-square deviation (RMSD), is not feasible to assess the convergence of simulations for disordered proteins, as they have heterogeneous ensembles of interconverting conformations. Although the conformations of disordered proteins are converting during the simulation, we believe that the conformational clusters and the ensemble-averaged NMR observables will converge if the sampling is enough. Therefore, we use the time-dependent changes of conformational clusters as well as simulated NMR observables to testify the simulation convergence in this work, which could provide information of both the structure and NMR properties of the simulated ensembles.
We calculated the time-dependent cumulative numbers of conformational clusters and the time-dependent differences between the experimental data and cumulative-averaged NMR observables from MD simulations for all disordered peptides and proteins. The time-dependent numbers of clusters which occupy 70% of total conformational ensembles for Aβ40 and Aβ42 are shown in Fig. 1. As the initial structures of Aβ40 and Aβ42 are retrieved from PDB structures, the numbers of clusters increase at the early period of simulation due to the conformational rearrangements of these two proteins, but these numbers are finally converged at the last 200 ns of 1 μs simulations. The numbers of clusters for all disordered peptides and proteins are shown in Fig. S1 (ESI†). All systems are converged according to the results of conformational clustering. In addition, we also testify the convergence of the simulated NMR observables. The time-dependent root-mean-square (RMS) errors between the experimental data and simulated chemical shifts and scalar couplings for Ab40 and Ab42 are shown in Fig. 2. The initial structures of simulations were retrieved from PDB structures, which are quite different from the realistic conformational ensembles of Aβ40 and Aβ42. Thus, large initial RMS errors are observed between the experimental data and the calculated chemical shifts of Cα and Cβ atoms and 3JHNHa scalar couplings. These errors show a large decrease at the first 200 ns and finally converge to low values within 1 μs simulations. The time-dependent RMS errors for other disordered peptides and proteins were also calculated and are shown in Fig. S2 and S3 (ESI†). According to the time-dependent analysis, we found that even when more conformers are involved after 200 ns, the ensemble averages of the simulated NMR observables are almost converged. These results suggest that 1 μs is enough for the simulations of these disordered peptides and proteins and these simulations are suitable for further analysis.
Fig. 1.
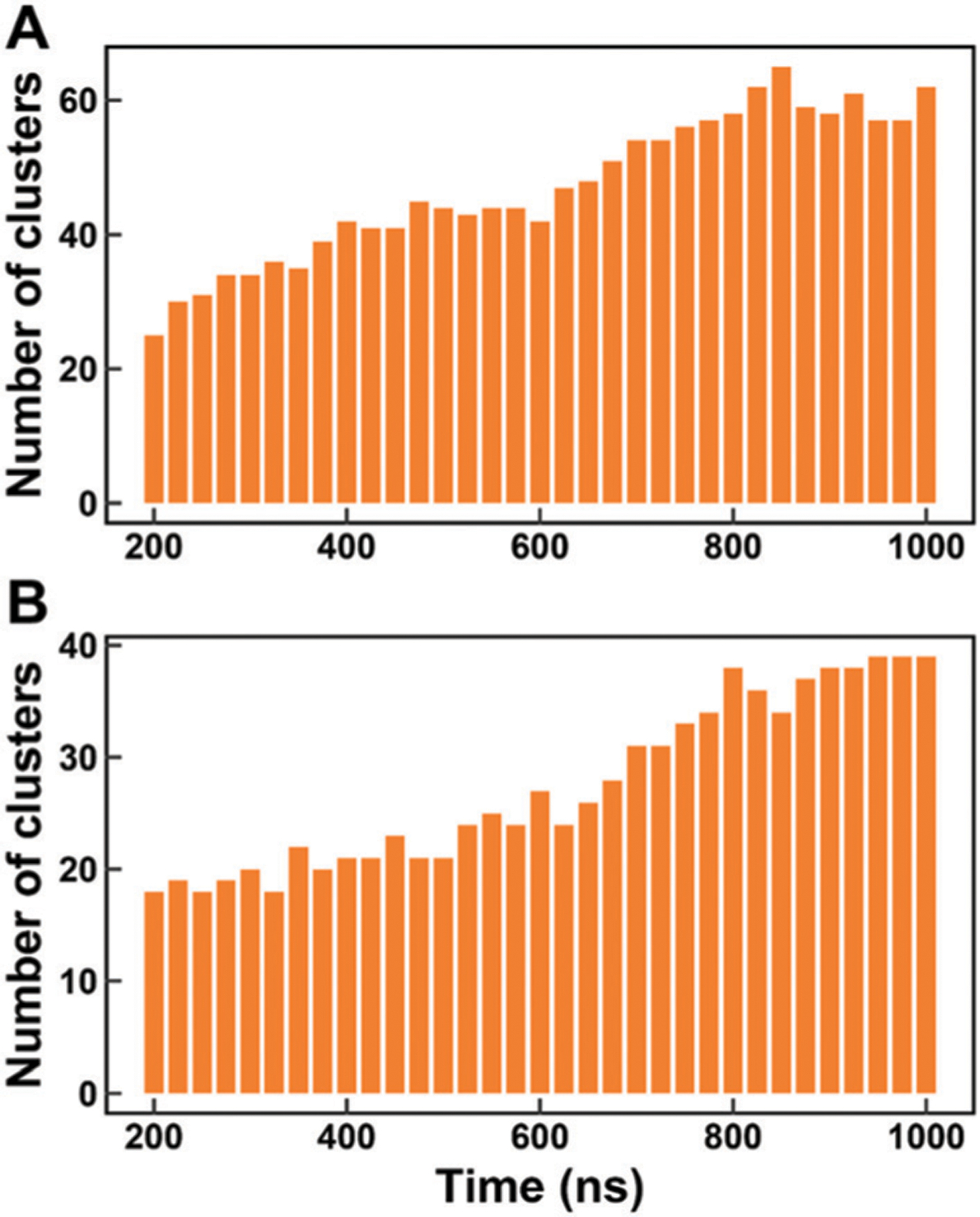
Time-dependent cumulative numbers of conformational clusters. (A) Ab40. (B) Ab42. The number of conformational clusters at a certain time is calculated with the simulated ensembles from 0 ns to this certain time.
Fig. 2.
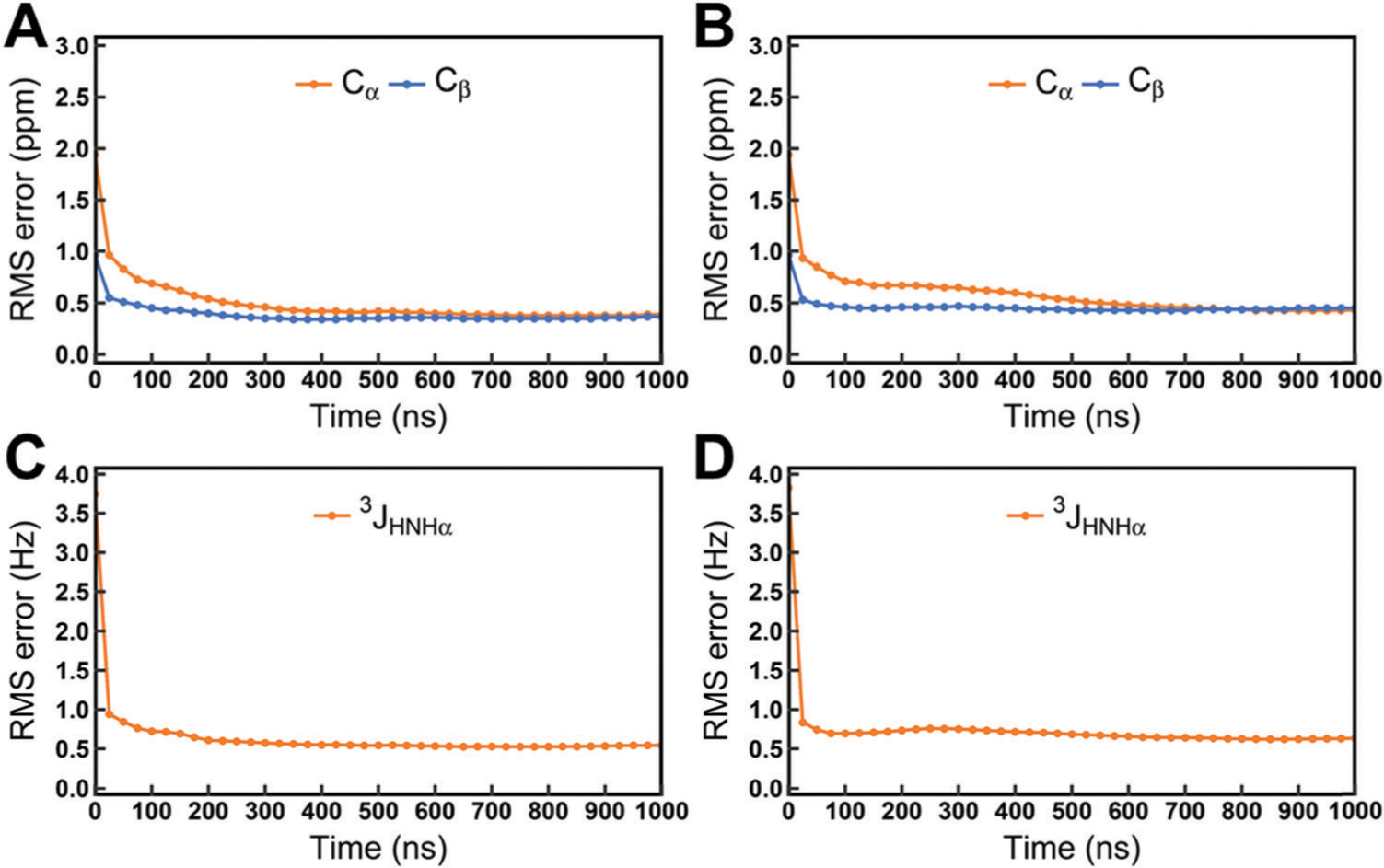
Time-dependent RMS errors between the experimental data and cumulative-averaged NMR observables. (A) Chemical shifts of Cα and Cβ atoms for Aβ40. (B) Chemical shifts of Cα and Cβ atoms for Aβ40. (C) 3JHNHa couplings for Aβ40. (D) 3JHNHa couplings for Aβ42. The chemical shifts are reported in ppm, J-couplings are in Hz.
3.2. Accuracy of simulations
3.2.1. Comparison with NMR observables.
NMR is an important method to measure the IDPs by providing site-specific information, such as chemical shifts and scalar couplings. It is crucial to compare the simulated and measured NMR observables to evaluate the performance of the force field.
ALA5 and ALA7.
The simulated chemical shifts and scalar couplings of ALA5 and ALA7 compared with the experimental data45 are shown in Fig. 3. The RMS errors of the Cα chemical shifts are 0.16 ppm and 0.09 ppm for ALA5 and ALA7 respectively, and the RMS errors of three backbone scalar couplings are 0.11 Hz and 0.15 Hz for ALA5 and ALA7, respectively. In addition, other chemical shifts and scalar couplings of ALA5 and ALA7 are calculated. The chemical shifts of all atoms and backbone scalar couplings are shown in Fig. S4 and S5 (ESI†). The RMS errors are listed in Tables S2 and S3 (ESI†). These results suggest that the calculated NMR data in the simulations of these two short peptides with the C36IDPSFF force field are in quantitative agreement with the experimental data.
Fig. 3.
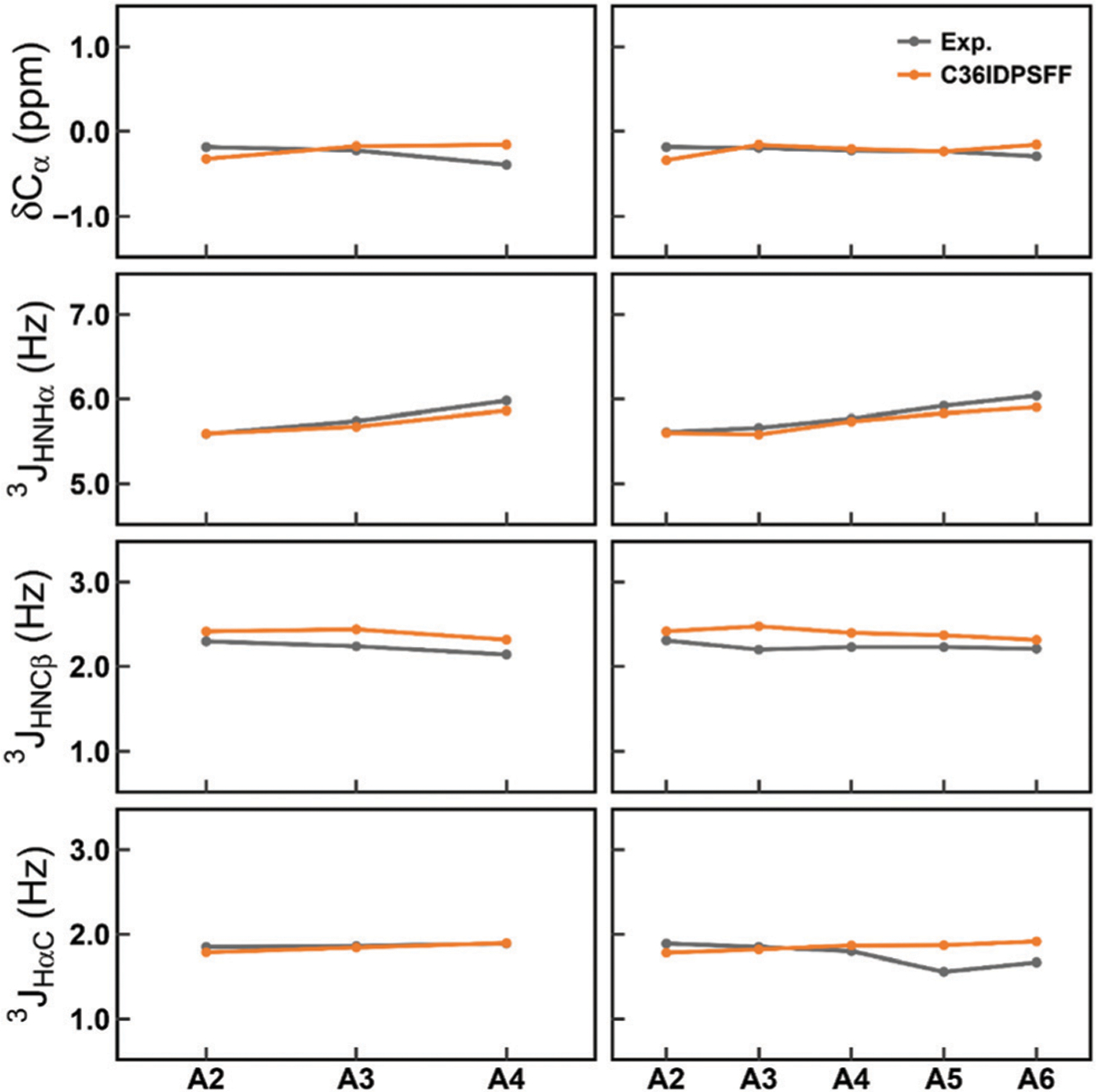
Comparison of the simulated and measured NMR observables for ALA5 and ALA7. The left panels stand for ALA5 and the right panels stand for ALA7. The top panels stand for Ca chemical shifts and the other panels stand for three backbone scalar couplings, 3JHNHα JHNCβ, and JHaC. The standard errors of the mean of residual chemical shifts and scalar couplings are very small and are not shown for the sake of clarity of the figures.
Disordered proteins.
In previous work, we simulated several disordered proteins with C36IDPSFF and the results proved the effectiveness of this force field for IDPs.21 To further evaluate the force field, six typical disordered proteins were tested in this study, including Amyloid β(1–40)46 (Aβ40), Amyloid β(1–42)46 (Aβ42), activator for thyroid hormone and retinoid receptors47 (ACTR), the N-terminal Src homology 3 (SH3) domain of Drosophila drk48 (drkN SH3), the human islet amyloid polypeptide49 (hIAPP), and Histatin-5.50
Fig. 4 shows the Cα chemical shifts and 3JHNHa scalar couplings of Aβ40 and Aβ42. The RMS errors of Cα chemical shifts are 0.39 ppm and 0.57 ppm for Aβ40 and Aβ42 respectively and the RMS errors of 3JHNHa couplings are 0.44 Hz and 0.68 Hz. The calculated values with the C36IDPSFF force field are consistent with the experimental data.51–53 More chemical shifts and scalar couplings of Aβ40 and Aβ42 are shown in Fig. S6–S8 (ESI†), and the corresponding RMS errors are listed in Tables S2 and S3 (ESI†).
Fig. 4.

Comparison of simulated and measured NMR observables for Aβ40 and Aβ42. (A) Cα chemical shifts of Aβ40. (B) 3JHNHa scalar couplings of Aβ40. (C) Ca chemical shifts of Aβ42. (D) 3JHNHa scalar couplings of Aβ42. The standard errors of the mean of the residual chemical shifts and scalar couplings are very small and are not shown for the sake of clarity of the figures.
We also calculated the chemical shifts and scalar couplings for other disordered proteins. The results are shown in Fig. S9–S12 (ESI†) and the RMS errors are listed in Tables S2 and S3 (ESI†). The calculated NMR observables from simulations with the C36IDPSFF force field, especially the Cα chemical shifts and 3JHNHa scalar couplings, agree well with the experimental measurements. In addition, backbone N–H RDCs are calculated and Q factors of RDCs are shown in Fig. S13 (ESI†). All of the results show that the C36IDPSFF force field can well reproduce the experimental NMR observables for IDPs.
Folded proteins.
Interestingly, we found that the C36IDPSFF force field also performs well for folded proteins in the previous simulation with ubiquitin even though the initial optimized targets are not the folded proteins.21 In this study, we tested three typical folded proteins from the benchmark set in the previous work by Paul Robustelli et al.,54 including the bovine pancreatic trypsin inhibitor (BPTI), the third IgG-binding domain of protein G (GB3), and hen egg white lysozyme (HEWL), and another three folded proteins (PDB IDs: 2JPU, 2JQN and 2KL6) with more than 100 residues from the set by Mao et al.55
Fig. 5 shows the results of simulations for three typical folded proteins. Backbone RMSDs with respect to the initial PDB structure are lower than 2 Å within 1 μs MD simulation and the Rg values are very stable. This indicated that the C36IDPSFF force field could well maintain the conformation of folded proteins. The calculated Cα chemical shifts show good agreement with the experimental data. The chemical shifts of all six folded proteins are shown in Fig. S14–S19 (ESI†), and most of the calculated values are also close to the experimental measurements. In addition, we calculated several backbone scalar couplings for BPTI and GB3 (Fig. S20, ESI†) and order parameters S2 for GB3 and HEWL (Fig. S21, ESI†) for the available experimental data.56–59 The calculated values agree well with the experimental data except for the order parameters in K19–D22 of GB3 due to the structural fluctuation in this loop region. These results all indicate that the C36IDPSFF force field also shows a good performance on folded proteins.
Fig. 5.
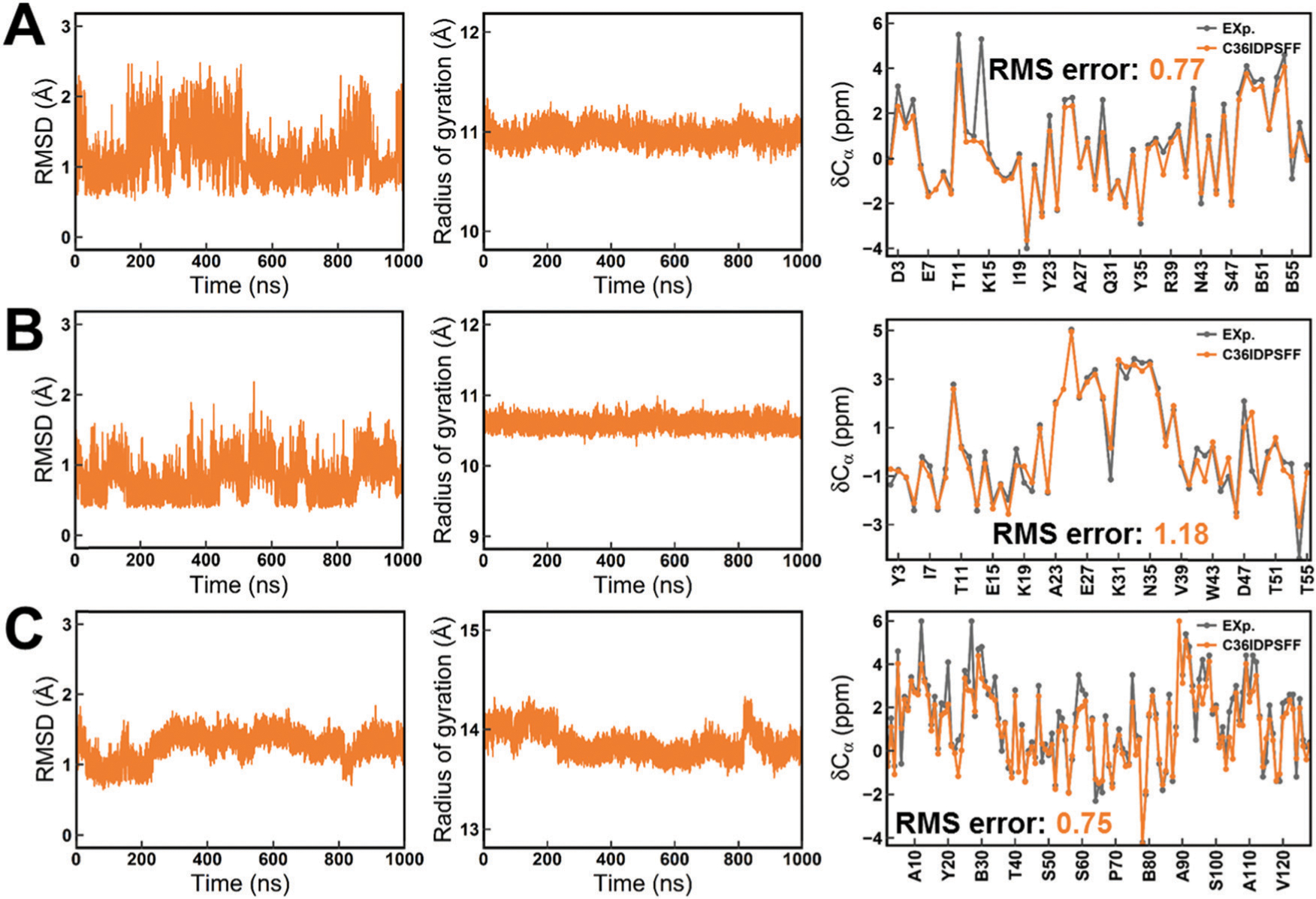
Structure stability and Ca chemical shifts of folded proteins in simulations with the C36IDPSFF force field. (A) BPTI. (B) GB3. (C) HEWL. The left panels stand for the RMSD, the middle panels stand for Rg and the right panels stand for Cα secondary chemical shifts. The residue name abbreviated “B” indicates the cysteine residue which forms a disulfide bond with another cysteine residue. The standard errors of the mean of the residual chemical shifts are very small and are not shown for the sake of clarity of the figures.
3.2.2. Distribution of the radius of gyration.
Overestimation of the compactness for the IDP ensembles is a common problem for classical force fields, which is found in our previous studies15,17 and the other studies of force field evaluation.20 Ensemble-averaged Rg is an effective parameter to describe the compactness of ensembles in MD simulations and its variation is greatly affected by water models. In this work, we calculated the average Rg values of simulations with C36IDPSFF for several IDPs with the experimental data available. All the average simulated Rg values with the experimental values are listed in Table 2 and the distributions of the Rg values are shown in Fig. S22 (ESI†). The Rg value of Aβ40 is very close to the experimental values, while the Rg value of ACTR, drkN SH3, and Histatin-5 is smaller than the corresponding experimental value, respectively. In particular for ACTR, the calculated Rg is almost half of the experimental value. We believe that water models might be the most important reason, because the Rg values of simulations with TIP3P or CHARMM modified TIP3P(we refer to mTIP3P), ranging from 11.63 Å to 18.62 Å, are also lower than the experimental values in the previous work by Paul Robustelli et al., while the Rg values are close to the experimental values when using a TIP4P-D or a99SB-disp water model (small modification of TIP4P-D, we refer to disp-water here).54 As the default water model is mTIP3P inherited from the C36m force field, C36IDPSFF may underestimate the Rg values of large disordered proteins with more than 60 amino acids in the same way as C36m which is also described in a previous study.54
Table 2.
Comparison between the calculated Rg values from simulations with C36IDPSFF and the experimental data. The standard errors of the mean are provided using the block analysis described in the Methods section
3.2.3. Secondary structure propensity.
Accurate secondary structure sampling is also an evaluating indicator of the force field. In this study, we calculated the residual secondary structure propensity for disordered proteins. The fraction of the helix for drkN SH3 is shown in Fig. 6. The result indicates that the simulated results agree well with both the predicted values from the experimental NMR chemical shifts using the d2d software64 and the experimental estimates from the ensemble models.36 In addition, the previous study has reported that the conformational rearrangement from helix and coil to β-sheet is important for Ab assembling into protofibrils and fibrils.65 The circular dichroism (CD) experiments show that the fraction of β-sheet increases after Aβ structures are cross-linked.65 We also observe this trend in simulations of Aβ40 and Aβ42 with the C36IDPSFF force field shown in Fig. 7 and Fig. S23 (ESI†). Because the initial structure of Aβ40 and Aβ42 in MD simulations was retrieved from the PDB structure (Fig. 7) with helical fragments, we discarded the first 200 ns trajectories and then divided the remaining 800 ns trajectories into two parts according to the increase of the β-sheet fraction. The average fractions of α-helix, β-sheet, and coil in 200–800 ns simulations are 4.9%, 12.5%, and 82.6% respectively. The fractions are close to the uncross-linked CD experimental values65 (3% α-helix, 13% β-sheet and 84% coil). In 800–1000 ns simulations, the fractions of α-helix, β-sheet, and coil became 5.2%, 20.6% and 74.2%, which are close to the cross-linked CD experimental values65 (6% α-helix, 20% β-sheet and 74% coil). Similar to Aβ40, the fractions of α-helix, β-sheet and coil for Aβ42 are 3.8%, 14.6% and 81.6% respectively in 200–600 ns simulations and are 2.3%, 21.4% and 76.3 respectively in 800–1000 ns simulations, which agree well with the CD experimental values65 (3% α-helix, 18% β-sheet and 79% coil in the uncross-linked state and 7% α-helix, 24% β-sheet and 69% coil in the cross-linked state).
Fig. 6.
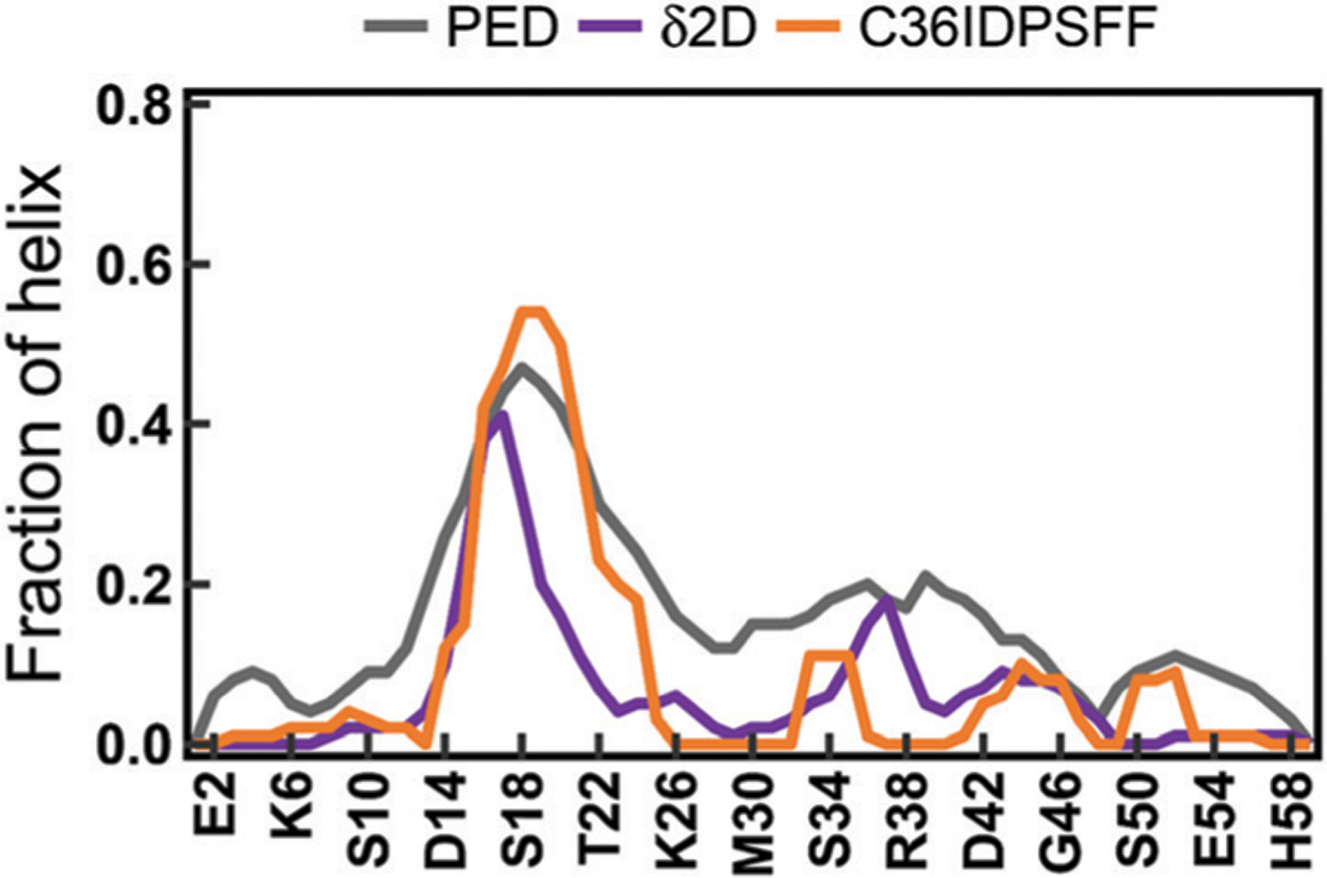
The fraction of helical structures of drkN SH3. The PED results were calculated from an ensemble with 1700 structures retrieved from the protein ensemble database66 (PED). The ᵟ2D results were calculated from the chemical shifts of drkN SH3 using the ᵟ2D software.64 The simulated results were calculated using the DSSP software.27
Fig. 7.
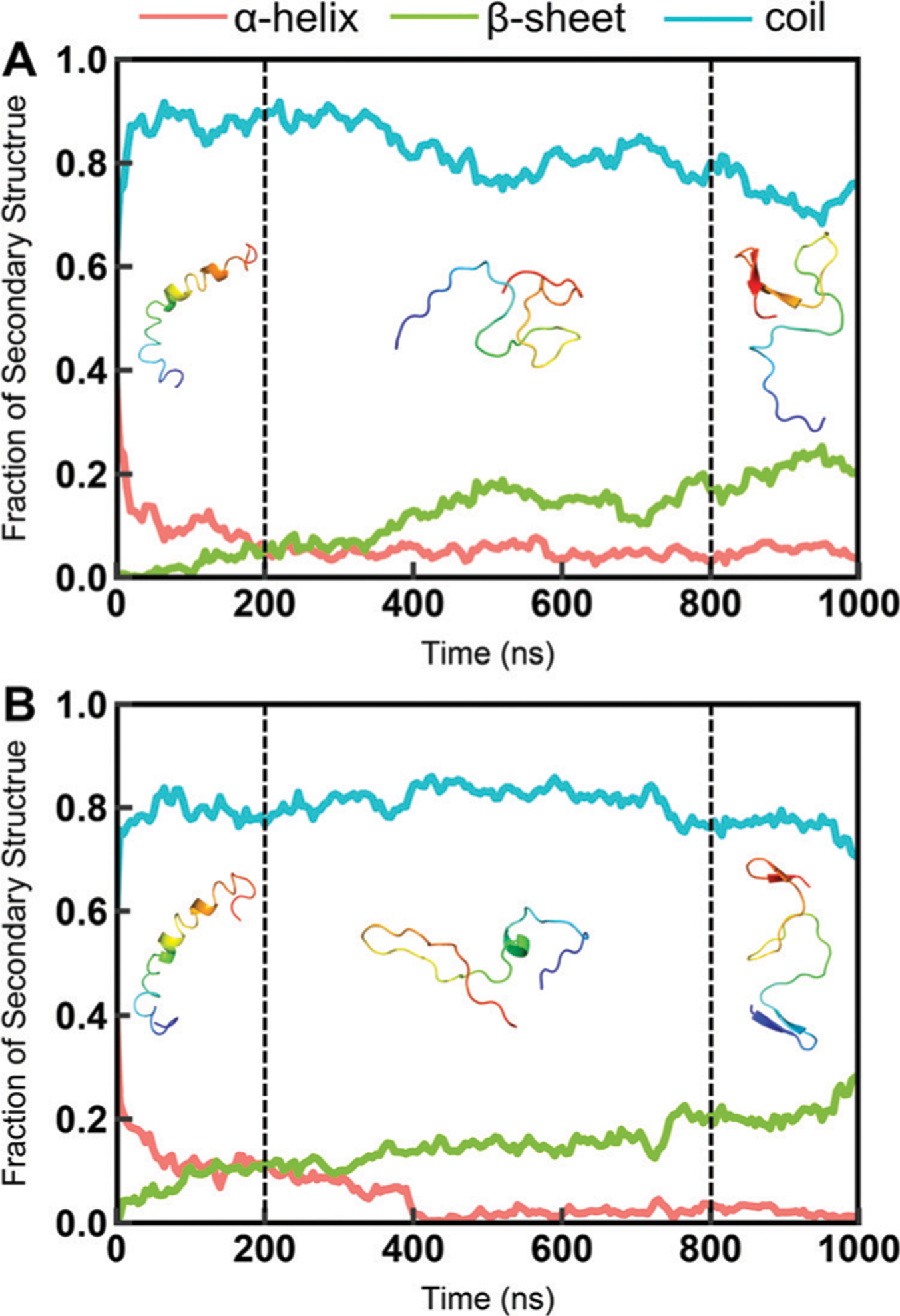
The fraction of the secondary structures of Ab40 and Ab42 during the simulation. (A) Aβ40. (B) Aβ42. The simulation was divided into three parts. The first 200 ns of simulation trajectories were discarded because the initial structures of Aβ40 and Aβ42 are from PDB structures shown in the 0–200 ns simulations. The representative structures of the largest conformational cluster from 200–800 ns and 800–100 ns simulations are shown here. The fractions of the secondary structure were calculated using the DSSP software.27 In this calculation, DSSP codes “H”, “G” and “I” are considered as the “helix”; “B” and “E” are considered as the “sheet”; “T”, “S” and blanks are considered as the “coil”.
Furthermore, we analyzed the conformational clusters for Aβ40 and Aβ42 in these two periods of simulations. The representative structures of the largest conformational cluster are shown in Fig. 7 and the detailed conformational cluster results are shown in Fig. S24 (ESI†). As shown in Fig. 7, the dominated conformations are coil conformations in 200–800 ns simulations, while in 800–1000 ns β-sheet conformations are found in both Aβ40 and Aβ42 simulations. In addition, the ensembles of Aβ42 have more β-sheet conformations than those of Aβ40 in these two periods (shown in Fig. S24, ESI†), which is consistent with the previous CD experiment for Aβ42 with a higher fraction of β-sheet in both the uncross-linked and cross-linked state. These results show that simulations with the C36IDPSFF force field could well reproduce the conformational rearrangement process of assembly of Aβ, which will be beneficial for the future study of neuronal diseases related to Aβ.
3.2.4. Stability of fast-folding peptides and proteins.
To reproduce the protein folding for the C36IDPSFF force field, typical fast-folding peptides and proteins were simulated by replica exchange simulations (REMD). We chose four fast-folding peptides and proteins, including (AAQAA)3 and the villin headpiece subdomain (we refer to villin) with the helical propensity and CLN025 and the GB1 hairpin with the b-sheet propensity. As shown in Fig. 8A, a full helical structure of (AAQAA)3 was captured, and villin, CLN025, and the GB1 hairpin were successfully folded with a low backbone RMSD in simulations with the C36IDPSFF force field. When compared with the experimental melting curves, C36IDPSFF underestimated the stability of (AAQAA)3 in the same way as several tested force fields in the previous work by Paul Robustelli et al.,54 such as C36m and a99SB-disp. Also, C36IDPSFF overestimated the stability of CLN025, suggesting that the C36IDPSFF may have the preference of the β-sheet structure over the helical structure in simulations of fast-folding proteins.
Fig. 8.
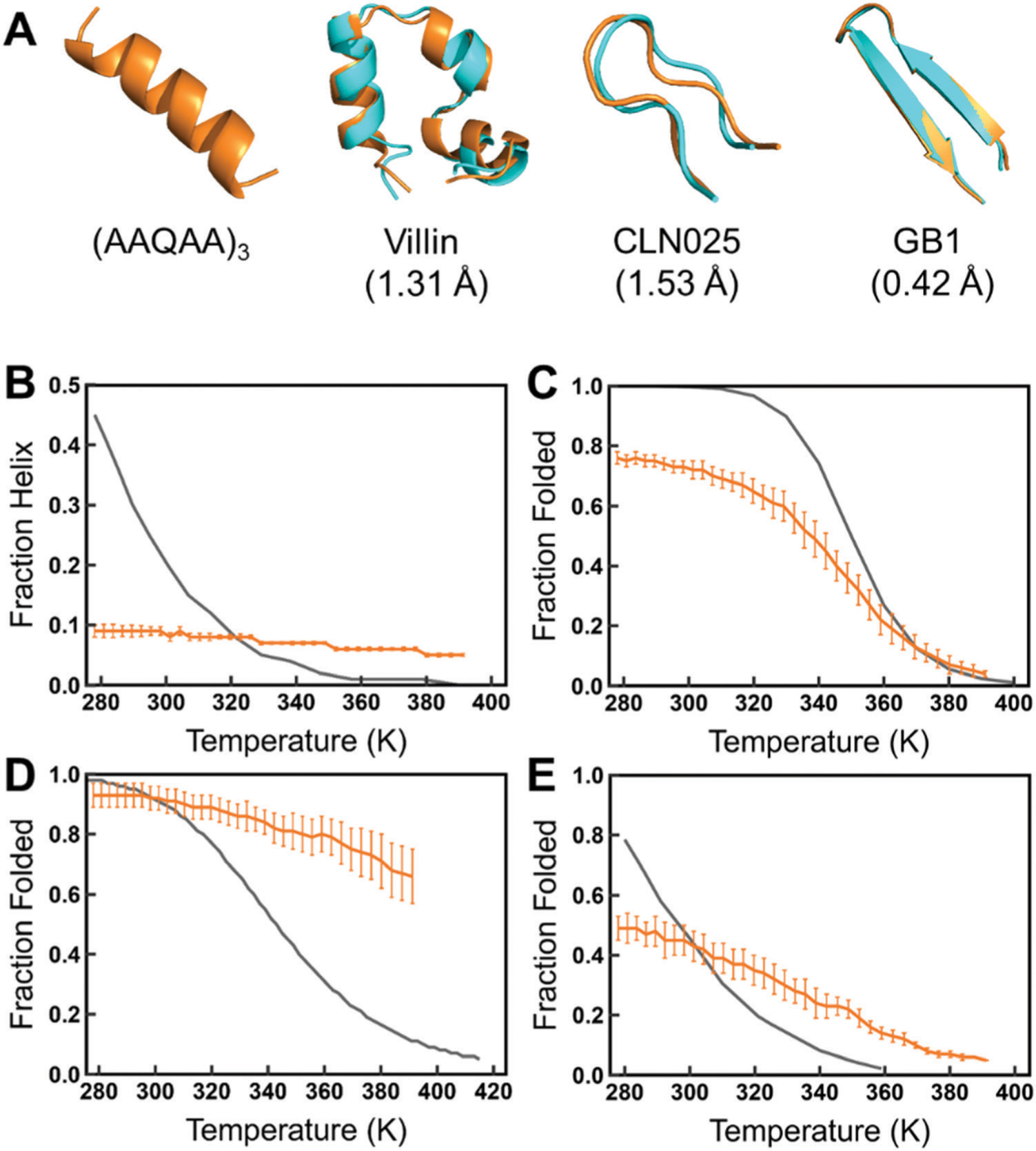
Temperature replica exchange simulations of the fast-folding peptides and proteins. (A) The helical structure of (AAQAA)3 and the superposition of the folded structures (orange) of villin, CLN025, and the GB1 hairpin from simulations and the corresponding PDB structures44,67,68 (cyan). The melting curves of (AAQAA)3 (B), villin (C), CLN025 (D), and the GB1 hairpin (E) are compared with the experimental data.67,69–71 The folded state is defined as RMSD which is less than 2.0, 2.5, and 3.0 Å for CLN025, the GB1 hairpin, and villin according to the length of each protein, respectively.
3.3. Influence of water models in simulations of disordered proteins
Based on the previous Rg results, we applied disp-water in simulations of Aβ40, ACTR, and drkN SH3 to test the influence of different water models. As shown in Fig. 9, the average Rg values of disp-water are always larger than those of mTIP3P, indicating that simulation with disp-water can generate more disordered conformations and reduce the over compactness of IDP ensembles. However, simulations with disp-water overestimated the Rg values for two small IDPs, AB40 and drkN SH3, while provided a Rg value extremely close to the experimental measurement for relatively larger ACTR. This result indicates that the disp-water is just suitable for the simulation of larger IDPs with C36IDPFF and can help to solve the over compactness problem caused by the mTIP3P water model.
Fig. 9.
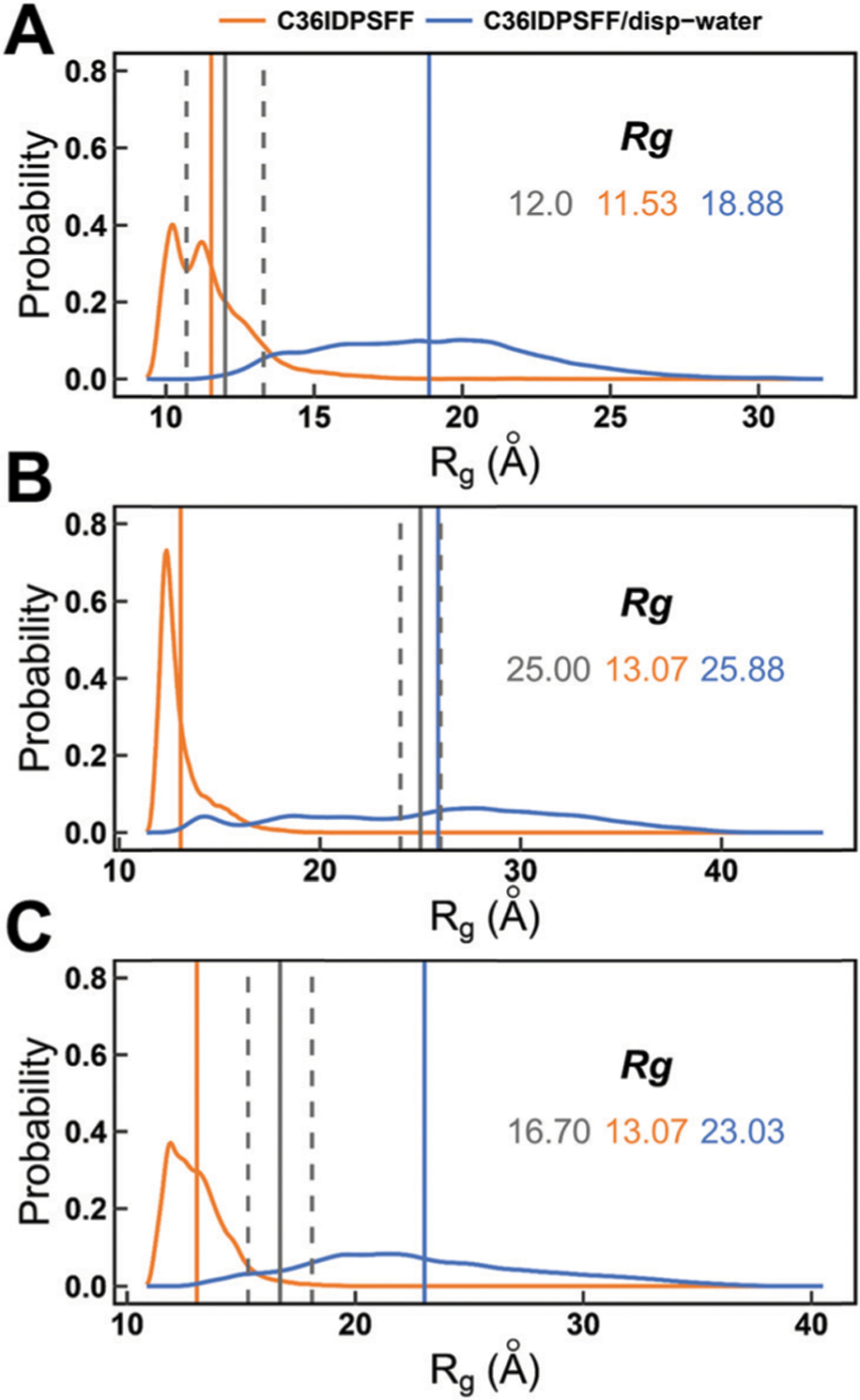
Probability distributions of the radii of gyration for disordered proteins simulated with mTIP3P and disp-water water models. (A) Aβ40. (B) ACTR. (C) drkN SH3. The averaged Rg values of simulations with mTIP3P and disp-water are marked by vertical solid lines in orange and blue, respectively. The experimental values are marked by vertical solid lines in gray and the errors are marked by two vertical dash lines in gray. The simulated and experimental Rg values are also labeled with the corresponding colors.
Thus, we compared the conformations of ACTR in simulations with these two different water models. This difference of the Rg values between two water models is consistent with the difference of conformational clustering results. We analyzed the conformational clusters for ACTR in 200–1000 ns simulations using these two water models and they are shown in Fig. 10A. It is obvious that simulations with disp-water sampled more disordered conformations than that of mTIP3P, suggesting that the disp-water is beneficial for the extension of conformations even though the initial structure of ACTR is quite helical.
Fig. 10.
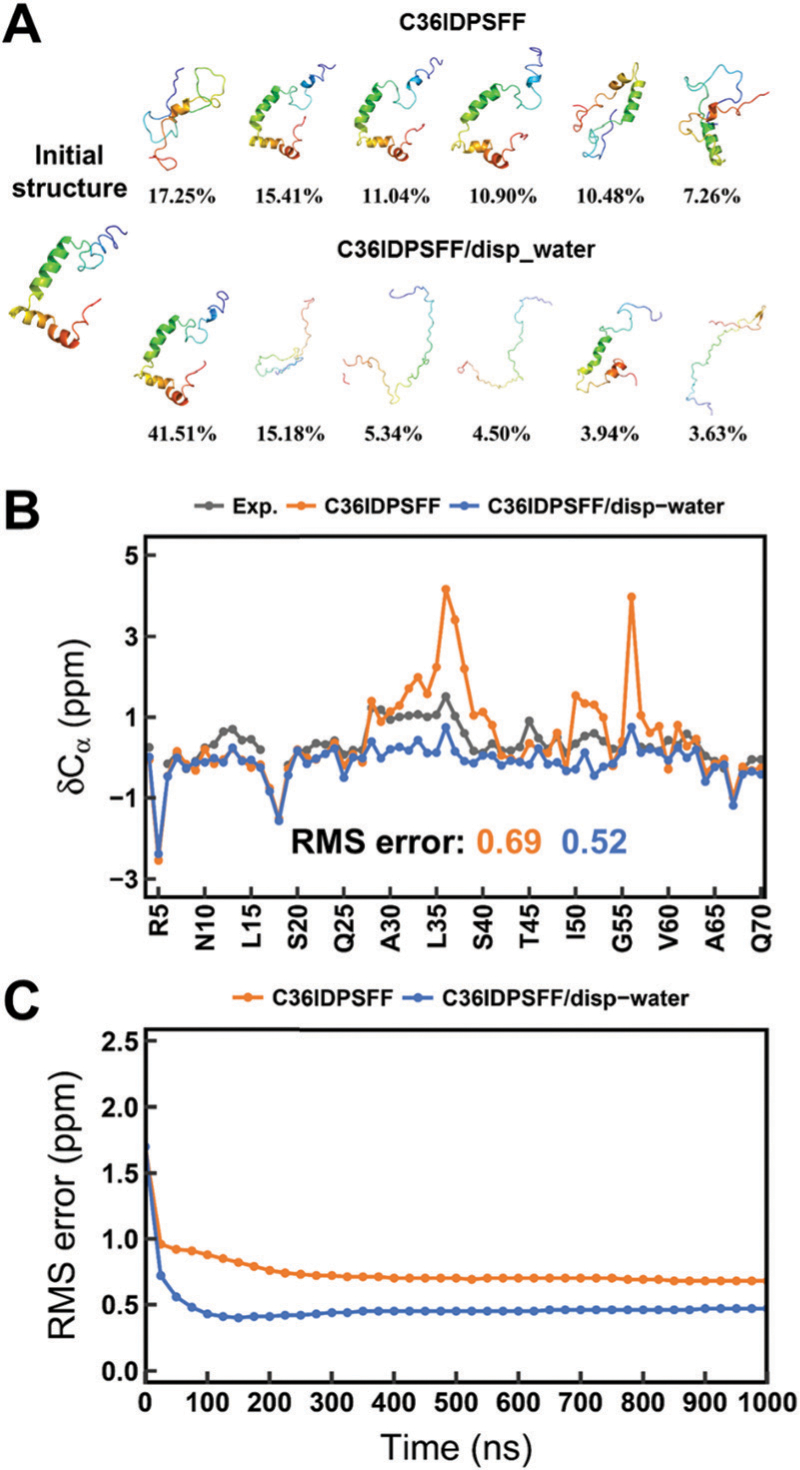
Simulation results of ACTR using the C36IDPSFF force field with mTIP3P and disp-water water models. (A) Conformational clusters. (B) Cα chemical shifts. (C) Time-dependent RMS errors of Cα chemical shifts. The standard errors of the mean of the residual chemical shifts and scalar couplings are very small and are not shown for the sake of clarity of the figures.
In addition, we compared the chemical shifts of ACTR in simulations with these two different water models. In Fig. 10B, the higher chemical shift values of Cα atoms are found for several residues (near H36 and I56) in the a-helix regions of the initial structure of ACTR when the mTIP3P water model was used in simulations. These chemical shifts became much lower when disp-water is applied and the values are even lower than the experimental data. These results are consistent with the previous results of conformational clusters that more helical conformations exist in the conformational ensembles of simulation with mTIP3P, while more disorder conformations are found in the conformational ensembles of simulation with disp-water. The RMS errors between the experimental and simulated chemical shifts in simulations with disp-water are slightly lower than those of the mTIP3P water model, and the time-dependent RMS errors (Fig. 10C) show that the simulations with both mTIP3P and disp-water are converged within 1 μs.
These results show the mTIP3P water model in C36IDPSFF is suitable for the small IDPs but still has deficiency in simulation of the larger disordered proteins. Even though converged results can be achieved in the simulations, the simulated NMR observables may not agree well with the experimental data due to the compactness of conformational ensembles. Therefore, the TIP4P-D or disp-water water model might be better in simulations of larger disordered proteins.
3.4. Influence of initial structures
The initial structure is also a crucial factor in MD simulations of proteins, especially for IDPs. A suitable initial structure will be beneficial for conformational transitions of the disordered proteins. So extended conformers are usually used as initial structures for IDP simulations in previous work.20,54 Otherwise, if a simulation started with a highly folded structure, it usually takes a long time to unfold this structure and then to sample an accurate conformational ensemble. However, we found that reasonable simulation results can be obtained with a set of modified force field parameters even though the initial structures are much different from the experimental measurements. In simulations of Aβ40 with the C36IDPSFF force field, we obtained reasonable simulation results within a simulation time of 1 μs even though we started with a structure with several helical fragments which have higher RMS errors compared with experimental observables. This suggests that the C36IDPSFF force field may have high compatibility of the initial structure in simulations of IDPs which usually have high heterogeneous ensembles of conformations.
Thus, in this study, we launched extra simulations of Aβ40 starting with the extended conformations using C36IDPSFF and compared the NMR observables with previous simulations starting from a PDB structure. Fig. 11 shows the comparison of the simulated and experimental NMR observables. The RMS errors of Cα chemical shifts are 0.39 ppm and 0.37 ppm and the RMS errors of 3JHNHa scalar couplings are 0.56 Hz and 1.09 Hz for simulations of Aβ40 with mTIP3P and disp-water, respectively. The detailed values are listed in Tables S4 and S5 (ESI†). The C36IDPSFF force field exhibits a similar performance for Ab40 starting from two different initial structures. Time-dependent RMS errors (shown in Fig. 11b and d) also confirm this similarity and convergence of two simulations of Aβ40. In addition, we compared other NMR observables in simulations of Aβ40 with the C36IDPSFF force field from two different initial structures and the results are shown in Fig. S25–S27 (ESI†). The differences in the chemical shifts and scalar couplings between two simulations of Aβ40 are invisible. These results indicate that the C36IDPSFF force field could reproduce similar simulated NMR observables for IDPs from different initial structures within 1 μs.
Fig. 11.
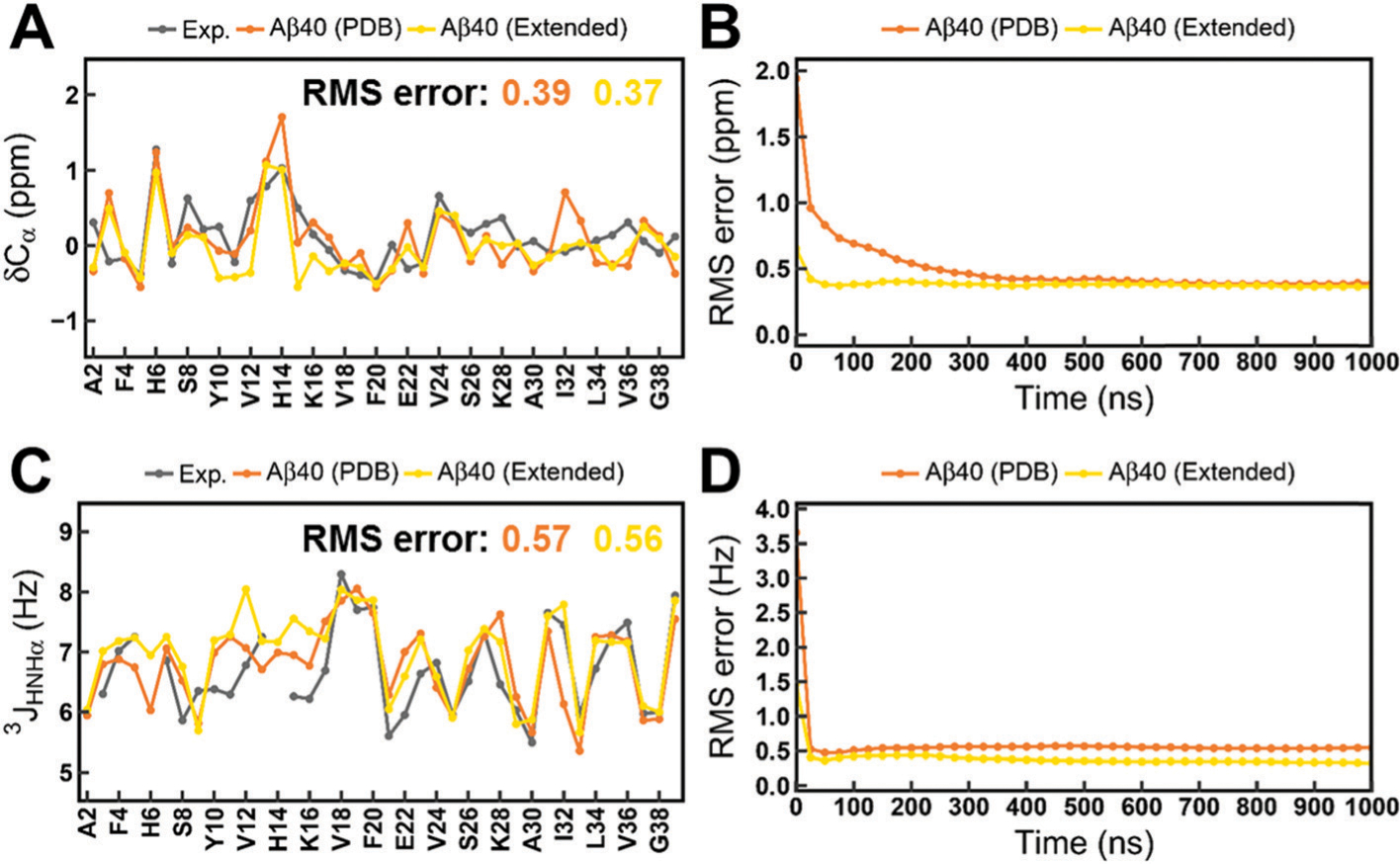
Calculated NMR observables in simulations of Aβ40 starting from the PDB structure and the extended structure. (A) Cα chemical shifts. (B) Time-dependent RMS error of Cα chemical shifts. (C) 3JHNHa scalar couplings. (D) Time-dependent RMS error of 3JHNHa scalar couplings. The standard errors of the mean of the residual chemical shifts and scalar couplings are very small and are not shown for the sake of clarity of the figures.
3.5. Comparison with the a99SB-disp force field
Recently, Paul Robustelli and coworkers developed a well balanced force field a99SB-disp for both disordered and folded proteins starting from the a99SB-ILDN force field and the TIP4P-D water model. The a99SB-disp force field was evaluated by a large benchmark set of proteins and extremely long-time simulations. The simulation results indicated that the a99SB-disp force field substantially improves the accuracy for simulations of disordered proteins while maintaining accuracy for folded proteins, thus broadening the range of biological systems amenable to MD simulations.
In this work, the simulation time is relatively shorter than that of a99SB-disp in previous work, so it will be helpful for comparing our simulation results with the long-time simulation results for further evaluation of the C36IDPSFF force field. Also, we wonder if the short-time simulation using the C36IDPSFF force field is capable of accurately reproducing the experimental measurements as a99SB-disp. If the results are still reasonable in short-time simulations, it will save a lot of computing resources and facilitate large-scale applications for the MD simulation study of proteins. Thus, we chose several disordered and folded proteins, which were tested both in our simulations and previous simulations of a99SB-disp, and compared our simulation results directly with previously reported results of a99SB-disp.
In order to make the comparison more reasonable, the same experimental data and calculation methods were used, especially the chemical shifts which were calculated again using the SPARTA+ software. The difference between the simulated and experimental observables is shown in Fig. 12 and the detailed values are listed in Table S6 (ESI†). In general, the C36IDPSFF could achieve similar accuracy to a99SB-disp, while some deficiencies were also observed. As discussed above, simulations with mTIP3P water models are not fine enough to accurately describe the structural properties of ACTR. The Rg results of ACTR from simulation of a99SB-disp are closer to the experimental data. In addition, the a99SB-disp also performs better in reproducing the chemical shifts of Cβ in both the simulation of disordered and folded proteins. Despite the deficiencies mentioned above, we believe that the C36IDPSFF force field could substantially well reproduce the experimental measurements with the reasonable choice of water models for some large disordered proteins.
Fig. 12.
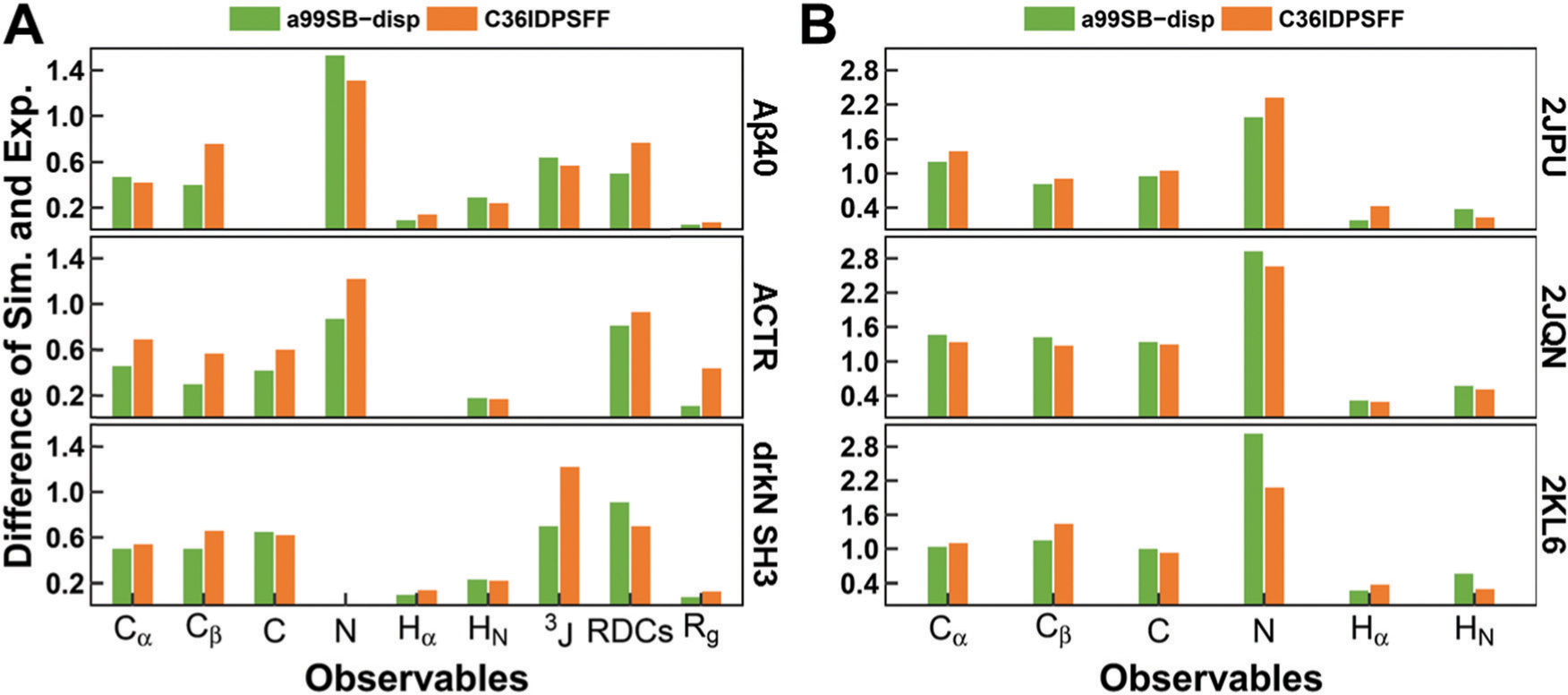
Difference between the experimental data and the simulated observables from C36IDPSFF in this study and a99SB-disp in previous work. (A) Disordered proteins, including Aβ40, ACTR, and drkN SH3. (B) Folded proteins, including 2JPU, 2JQN, and 2KL6. The differences of chemical shifts and J-couplings were estimated by RMS errors, and the differences of RDCs were estimated by Q factors. The differences of Rg were estimated by RgPenalty same as previous work. The 3JHNHa couplings were compared and referred to as 3J here. The missing values mean that the corresponding experimental data are not available.
4. Conclusion
MD simulation is an efficient method to study disordered proteins and folded proteins as it can provide atomic-level information of protein structural dynamics. The performance of simulations strongly depends on the accuracy of the force field used, especially in simulations of disordered proteins with high conformational heterogeneity. Thus, improved force fields in MD simulations are needed to well describe both folded and disordered proteins.
In this study, we extensively assessed the accuracy of our previously developed residue-specific C36IDPSFF force field for IDPs by simulations with several disordered peptides and proteins, fast-folding proteins and folded proteins. Based on the convergence of the simulations, a comparison between the simulated and experimental data, such as NMR observables, Rg values and residual secondary structures, shows that C36IDPSFF could substantially reproduce the available experimental measurements and provide accurate descriptions of both disordered and folded proteins. The comparison between our simulation results and long-time simulation results of a99SB-disp also indicates the good performance of the C36IDPSFF force field in relatively short-time simulations.
However, the limitations of the C36IDPSFF force field are also found in this study. Because the default water model used in C36IDPSFF is mTIP3P, the radii of gyration of large disordered proteins are underestimated, such as ACTR. This is also found in the simulation of ACTR with the mTIP3P water model in a previous study. The combination of C36IDPSFF with TIP4P-D or disp-water would be a better choice. In addition, the helical structures seem not very stable in simulations with (AAQAA)3, which is also described in our previous work. The CMAP energy terms in the right-handed a-helix are slightly high so that the helical structures are sometimes not well maintained. This could be further revised by a small modification of the CMAP parameters in this region.
Supplementary Material
Acknowledgements
This work was supported by the Center for HPC at Shanghai Jiao Tong University, the National Natural Science Foundation of China (31770771, 21977068, and 31620103901), the National Key Research and Development Program of China (2018YFC0310803 and 2017YFE0103300), and the Medical Engineering Cross Fund of Shanghai Jiao Tong University (YG2017MS08). We kindly thank Stefano Piana-Agostinetti for providing the a99SB-disp force field files in GROMACS and the experimental data in the benchmark set used in the development of the a99SB-disp force field.
Footnotes
Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp03434j
Conflicts of interest
The authors declare that there is no conflict of interest.
References
- 1.Ozenne V, Schneider R, Yao MX, Huang JR, Salmon L, Zweckstetter M, Jensen MR and Blackledge M, Mapping the Potential Energy Landscape of Intrinsically Disordered Proteins at Amino Acid Resolution, J. Am. Chem. Soc, 2012, 134, 15138–15148. [DOI] [PubMed] [Google Scholar]
- 2.Fong JH, Shoemaker BA and Panchenko AR, Intrinsic protein disorder in human pathways, Mol. BioSyst, 2012, 8, 320–326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Dyson HJ and Wright PE, Intrinsically unstructured proteins and their functions, Nat. Rev. Mol. Cell Biol, 2005, 6, 197–208. [DOI] [PubMed] [Google Scholar]
- 4.Wright PE and Dyson HJ, Intrinsically disordered proteins in cellular signalling and regulation, Nat. Rev. Mol. Cell Biol, 2015, 16, 18–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Skrabana R, Skrabanova-Khuebachova M, Kontsek P and Novak M, Alzheimer’s-disease-associated conformation of intrinsically disordered tau protein studied by intrinsically disordered protein liquid-phase competitive enzyme-linked immunosorbent assay, Anal. Biochem, 2006, 359, 230–237. [DOI] [PubMed] [Google Scholar]
- 6.Joerger AC and Fersht AR, Structure-function-rescue: the diverse nature of common p53 cancer mutants, Oncogene, 2007, 26, 2226–2242. [DOI] [PubMed] [Google Scholar]
- 7.Wells M, Tidow H, Rutherford TJ, Markwick P, Jensen MR, Mylonas E, Svergun DI, Blackledge M and Fersht AR, Structure of tumor suppressor p53 and its intrinsically disordered N-terminal transactivation domain, Proc. Natl. Acad. Sci. U. S. A, 2008, 105, 5762–5767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Rauscher S, Gapsys V, Gajda MJ, Zweckstetter M, de Groot BL and Grubmuller H, Structural Ensembles of Intrinsically Disordered Proteins Depend Strongly on Force Field: A Comparison to Experiment, J. Chem. Theory Comput, 2015, 11, 5513–5524. [DOI] [PubMed] [Google Scholar]
- 9.Jensen MR, Zweckstetter M, Huang JR and Backledge M, Exploring Free-Energy Landscapes of Intrinsically Disordered Proteins at Atomic Resolution Using NMR Spectroscopy, Chem. Rev, 2014, 114, 6632–6660. [DOI] [PubMed] [Google Scholar]
- 10.Rauscher S and Pomes R, Molecular simulations of protein disorder, Biochem. Cell Biol, 2010, 88, 269–290. [DOI] [PubMed] [Google Scholar]
- 11.Cordeiro TN, Herranz-Trillo F, Urbanek A, Estana A, Cortes J, Sibille N and Bernado P, Small-angle scattering studies of intrinsically disordered proteins and their complexes, Curr. Opin. Struct. Biol, 2017, 42, 15–23. [DOI] [PubMed] [Google Scholar]
- 12.Lange OF, van der Spoel D and de Groot BL, Scrutinizing Molecular Mechanics Force Fields on the Submicrosecond Timescale with NMR Data, Biophys. J, 2010, 99, 647–655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lindorff-Larsen K, Maragakis P, Piana S, Eastwood MP, Dror RO and Shaw DE, Systematic validation of protein force fields against experimental data, PLoS One, 2012, 7, e32131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Beauchamp KA, Lin YS, Das R and Pande VS, Are Protein Force Fields Getting Better? A Systematic Benchmark on 524 Diverse NMR Measurements, J. Chem. Theory Comput, 2012, 8, 1409–1414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Song D, Luo R and Chen HF, The IDP-Specific Force Field ff14IDPSFF Improves the Conformer Sampling of Intrinsically Disordered Proteins, J. Chem. Inf. Model, 2017, 57, 1166–1178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Piana S, Donchev AG, Robustelli P and Shaw DE, Water Dispersion Interactions Strongly Influence Simulated Structural Properties of Disordered Protein States, J. Phys. Chem. B, 2015, 119, 5113–5123. [DOI] [PubMed] [Google Scholar]
- 17.Ye W, Ji DJ, Wang W, Luo R and Chen HF, Test and Evaluation of ff99IDPs Force Field for Intrinsically Disordered Proteins, J. Chem. Inf. Model, 2015, 55, 1021–1029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wang W, Ye W, Jiang C, Luo R and Chen HF, New Force Field on Modeling Intrinsically Disordered Proteins, Chem. Biol. Drug Des, 2014, 84, 253–269. [DOI] [PubMed] [Google Scholar]
- 19.Song D, Wang W, Ye W, Ji D, Luo R and Chen H-F, ff14IDPs force field improving the conformation sampling of intrinsically disordered proteins, Chem. Biol. Drug Des, 2017, 89, 5–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Huang J, Rauscher S, Nawrocki G, Ran T, Feig M, de Groot BL, Grubmuller H and MacKerell AD Jr., CHARMM36m: an improved force field for folded and intrinsically disordered proteins, Nat. Methods, 2017, 14, 71–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Liu H, Song D, Lu H, Luo R and Chen HF, Intrinsically disordered protein-specific force field CHARMM36IDPSFF, Chem. Biol. Drug Des, 2018, 92, 1722–1735. [DOI] [PubMed] [Google Scholar]
- 22.Abraham MJ, Murtola T, Schulz R, Páll S, Smith JC, Hess B and Lindahl E, GROMACS: high performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1–2, 19–25. [Google Scholar]
- 23.Hess B, Kutzner C, van der Spoel D and Lindahl E, GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation, J. Chem. Theory Comput, 2008, 4, 435–447. [DOI] [PubMed] [Google Scholar]
- 24.Essmann U, Perera L, Berkowitz ML, Darden T, Lee H and Pedersen LG, A smooth particle mesh Ewald method, J. Chem. Phys, 1995, 103, 8577–8593. [Google Scholar]
- 25.Bussi G, Donadio D and Parrinello M, Canonical sampling through velocity rescaling, J. Chem. Phys, 2007, 126, 014101. [DOI] [PubMed] [Google Scholar]
- 26.Parrinello M and Rahman A, Polymorphic transitions in single crystals: a new molecular dynamics method, J. Appl. Phys, 1981, 52, 7182–7190. [Google Scholar]
- 27.Kabsch W and Sander C, Dictionary of protein secondary structure: pattern recognition of hydrogen-bonded and geometrical features, Biopolymers, 1983, 22, 2577–2637. [DOI] [PubMed] [Google Scholar]
- 28.Han B, Liu YF, Ginzinger SW and Wishart DS, SHIFTX2: significantly improved protein chemical shift prediction, J. Biomol. NMR, 2011, 50, 43–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Shen Y and Bax A, SPARTA plus: a modest improvement in empirical NMR chemical shift prediction by means of an artificial neural network, J. Biomol. NMR, 2010, 48, 13–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zweckstetter M and Bax A, Prediction of sterically induced alignment in a dilute liquid crystalline phase: aid to protein structure determination by NMR, J. Am. Chem. Soc, 2000, 122, 3791–3792. [Google Scholar]
- 31.Trbovic N, Kim B, Friesner RA and Palmer AG, Structural analysis of protein dynamics by MD simulations and NMR spin-relaxation, Proteins: Struct., Funct., Bioinf, 2008, 71, 684–694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mockel C, Kubiak J, Schillinger O, Kuhnemuth R, Della Corte D, Schroder GF, Willbold D, Strodel B, Seidel CAM and Neudecker P, Integrated NMR, Fluorescence, and Molecular Dynamics Benchmark Study of Protein Mechanics and Hydrodynamics, J. Phys. Chem. B, 2019, 123, 1453–1480. [DOI] [PubMed] [Google Scholar]
- 33.Feig M, Karanicolas J and Brooks CL, MMTSB Tool Set: enhanced sampling and multiscale modeling methods for applications in structural biology, J. Mol. Graphics Modell, 2004, 22, 377–395. [DOI] [PubMed] [Google Scholar]
- 34.Tomaselli S, Esposito V, Vangone P, van Nuland NA, Bonvin AM, Guerrini R, Tancredi T, Temussi PA and Picone D, The alpha-to-beta conformational transition of Alzheimer’s Abeta-(1–42) peptide in aqueous media is reversible: a step by step conformational analysis suggests the location of beta conformation seeding, ChemBioChem, 2006, 7, 257–267. [DOI] [PubMed] [Google Scholar]
- 35.Demarest SJ, Martinez-Yamout M, Chung J, Chen H, Xu W, Dyson HJ, Evans RM and Wright PE, Mutual synergistic folding in recruitment of CBP/p300 by p160 nuclear receptor coactivators, Nature, 2002, 415, 549–553. [DOI] [PubMed] [Google Scholar]
- 36.Marsh JA and Forman-Kay JD, Structure and Disorder in an Unfolded State under Nondenaturing Conditions from Ensemble Models Consistent with a Large Number of Experimental Restraints, J. Mol. Biol, 2009, 391, 359–374. [DOI] [PubMed] [Google Scholar]
- 37.Rodriguez Camargo DC, Tripsianes K, Buday K, Franko A, Gobl C, Hartlmuller C, Sarkar R, Aichler M, Mettenleiter G, Schulz M, Boddrich A, Erck C, Martens H, Walch AK, Madl T, Wanker EE, Conrad M, de Angelis MH and Reif B, The redox environment triggers conformational changes and aggregation of hIAPP in Type II Diabetes, Sci. Rep, 2017, 7, 44041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wlodawer A, Walter J, Huber R and Sjolin L, Structure of bovine pancreatic trypsin inhibitor. Results of joint neutron and X-ray refinement of crystal form II, J. Mol. Biol, 1984, 180, 301–329. [DOI] [PubMed] [Google Scholar]
- 39.Ulmer TS, Ramirez BE, Delaglio F and Bax A, Evaluation of backbone proton positions and dynamics in a small protein by liquid crystal NMR spectroscopy, J. Am. Chem. Soc, 2003, 125, 9179–9191. [DOI] [PubMed] [Google Scholar]
- 40.Diamond R, Real-space refinement of the structure of hen egg-white lysozyme, J. Mol. Biol, 1974, 82, 371–391. [DOI] [PubMed] [Google Scholar]
- 41.Wu Y, Singarapu KK, Zhang Q, Eletski A, Xu D, Sukumaran D, Parish D, Wang D, Jiang M, Cunningham K, Maglaqui M, Owens L, Xiao R, Liu J, Baran M, Swapna GVT, Acton T, Rost B, Montelione G and Szyperski T, Solution structure of NESG target SsR10, Orf c02003 protein, Northeast Structural Genomics Consortium, 2008. [Google Scholar]
- 42.Aramini JM, Rossi P, Moseley HNB, Wang D, Nwosu C, Cunningham K, Ma L, Xiao R, Liu J, Baran MC, Swapna GVT, Acton TB, Rost B and Montelione GT, Solution NMR structure of CC0527 from Caulobacter crescentus, Northeast Structural Genomics Consortium, 2007. [Google Scholar]
- 43.Aramini JM, Lee D, Ciccosanti C, Hamilton K, Nair R, Rost B, Acton TB, Xiao R, Swapna GVT, Everett JK and Montelione GT, Solution NMR structure of the CARDB domain of PF1109 from Pyrococcus furiosus, Northeast Structural Genomics Consortium, 2009. [Google Scholar]
- 44.McKnight CJ, Matsudaira PT and Kim PS, NMR structure of the 35-residue villin headpiece subdomain, Nat. Struct. Biol, 1997, 4, 180–184. [DOI] [PubMed] [Google Scholar]
- 45.Graf J, Nguyen PH, Stock G and Schwalbe H, Structure and dynamics of the homologous series of alanine peptides: A joint molecular dynamics/NMR study, J. Am. Chem. Soc, 2007, 129, 1179–1189. [DOI] [PubMed] [Google Scholar]
- 46.Sgourakis NG, Yan YL, McCallum SA, Wang CY and Garcia AE, The Alzheimer’s peptides A beta 40 and 42 adopt distinct conformations in water: a combined MD/NMR study, J. Mol. Biol, 2007, 368, 1448–1457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Iesmantavicius V, Jensen MR, Ozenne V, Blackledge M, Poulsen FM and Kjaergaard M, Modulation of the Intrinsic Helix Propensity of an Intrinsically Disordered Protein Reveals Long-Range Helix-Helix Interactions, J. Am. Chem. Soc, 2013, 135, 10155–10163. [DOI] [PubMed] [Google Scholar]
- 48.Zhang O and Forman-Kay JD, Structural characterization of folded and unfolded states of an SH3 domain in equilibrium in aqueous buffer, Biochemistry, 1995, 34, 6784–6794. [DOI] [PubMed] [Google Scholar]
- 49.Hoffmann KQ, McGovern M, Chiu CC and de Pablo JJ, Secondary Structure of Rat and Human Amylin across Force Fields, PLoS One, 2015, 10, e0134091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Raj PA, Marcus E and Sukumaran DK, Structure of human salivary histatin 5 in aqueous and nonaqueous solutions, Biopolymers, 1998, 45, 51–67. [DOI] [PubMed] [Google Scholar]
- 51.Hou L, Shao H, Zhang Y, Li H, Menon NK, Neuhaus EB, Brewer JM, Byeon IJ, Ray DG and Vitek MP, Solution NMR studies of the A beta(1–40) and A beta(1–42) peptides establish that the Met35 oxidation state affects the mechanism of amyloid formation, J. Am. Chem. Soc, 2004, 126, 1992–2005. [DOI] [PubMed] [Google Scholar]
- 52.Walti MA, Orts J, Vogeli B, Campioni S and Riek R, Solution NMR studies of recombinant Abeta(1–42): from the presence of a micellar entity to residual beta-sheet structure in the soluble species, ChemBioChem, 2015, 16, 659–669. [DOI] [PubMed] [Google Scholar]
- 53.Roche J, Shen Y, Lee JH, Ying JF and Bax A, Monomeric A beta(1–40) and A beta(1–42) Peptides in Solution Adopt Very Similar Ramachandran Map Distributions That Closely Resemble Random Coil, Biochemistry, 2016, 55, 762–775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Robustelli P, Piana S and Shaw DE, Developing a molecular dynamics force field for both folded and disordered protein states, Proc. Natl. Acad. Sci. U. S. A, 2018, 115, E4758–E4766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Mao BC, Tejero R, Baker D and Montelione GT, Protein NMR Structures Refined with Rosetta Have Higher Accuracy Relative to Corresponding X-ray Crystal Structures, J. Am. Chem. Soc, 2014, 136, 1893–1906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Balasubramanian S, Nirmala R, Beveridge DL and Bolton PH, Comparison of the 13C relaxation times and proton scalar couplings of BPTI with values predicted by molecular dynamics, J. Magn. Reson., Ser. B, 1994, 104, 240–249. [DOI] [PubMed] [Google Scholar]
- 57.Vogeli B, Ying JF, Grishaev A and Bax A, Limits on variations in protein backbone dynamics from precise measurements of scalar couplings, J. Am. Chem. Soc, 2007, 129, 9377–9385. [DOI] [PubMed] [Google Scholar]
- 58.Yao LS, Grishaev A, Cornilescu G and Bax A, Site-Specific Backbone Amide N-15 Chemical Shift Anisotropy Tensors in a Small Protein from Liquid Crystal and Cross-Correlated Relaxation Measurements, J. Am. Chem. Soc, 2010, 132, 4295–4309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Buck M, Boyd J, Redfield C, MacKenzie DA, Jeenes DJ, Archer DB and Dobson CM, Structural Determinants of Protein Dynamics: Analysis of 15N NMR Relaxation Measurements for Main-Chain and Side-Chain Nuclei of Hen Egg White Lysozyme, Biochemistry, 1995, 34, 4041–4055. [DOI] [PubMed] [Google Scholar]
- 60.Kjaergaard M, Norholm AB, Hendus-Altenburger R, Pedersen SF, Poulsen FM and Kragelund BB, Temperature-dependent structural changes in intrinsically disordered proteins: formation of alpha-helices or loss of polyproline II?, Protein Sci, 2010, 19, 1555–1564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Choy WY, Mulder FAA, Crowhurst KA, Muhandiram DR, Millett IS, Doniach S, Forman-Kay JD and Kay LE, Distribution of molecular size within an unfolded state ensemble using small-angle X-ray scattering and pulse field gradient NMR techniques, J. Mol. Biol, 2002, 316, 101–112. [DOI] [PubMed] [Google Scholar]
- 62.Cragnell C, Durand D, Cabane B and Skepo M, Coarsegrained modeling of the intrinsically disordered protein Histatin 5 in solution: Monte Carlo simulations in combination with SAXS, Proteins: Struct., Funct., Bioinf, 2016, 84, 777–791. [DOI] [PubMed] [Google Scholar]
- 63.Granata D, Baftizadeh F, Habchi J, Galvagnion C, De Simone A, Camilloni C, Laio A and Vendruscolo M, The inverted free energy landscape of an intrinsically disordered peptide by simulations and experiments, Sci. Rep, 2015, 5, 15449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Camilloni C, De Simone A, Vranken WF and Vendruscolo M, Determination of Secondary Structure Populations in Disordered States of Proteins Using Nuclear Magnetic Resonance Chemical Shifts, Biochemistry, 2012, 51, 2224–2231. [DOI] [PubMed] [Google Scholar]
- 65.Bitan G, Kirkitadze MD, Lomakin A, Vollers SS, Benedek GB and Teplow DB, Amyloid beta-protein (A beta) assembly: A beta 40 and A beta 42 oligomerize through distinct pathways, Proc. Natl. Acad. Sci. U. S. A, 2003, 100, 330–335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Varadi M, Kosol S, Lebrun P, Valentini E, Blackledge M, Dunker AK, Felli IC, Forman-Kay JD, Kriwacki RW, Pierattelli R, Sussman J, Svergun DI, Uversky VN, Vendruscolo M, Wishart D, Wright PE and Tompa P, pE-DB: a database of structural ensembles of intrinsically disordered and of unfolded proteins, Nucleic Acids Res, 2014, 42, D326–D335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Honda S, Akiba T, Kato YS, Sawada Y, Sekijima M, Ishimura M, Ooishi A, Watanabe H, Odahara T and Harata K, Crystal Structure of a Ten-Amino Acid Protein, J. Am. Chem. Soc, 2008, 130, 15327–15331. [DOI] [PubMed] [Google Scholar]
- 68.Gallagher T, Alexander P, Bryan P and Gilliland GL, Two crystal structures of the B1 immunoglobulin-binding domain of streptococcal protein G and comparison with NMR, Biochemistry, 1994, 33, 4721–4729. [PubMed] [Google Scholar]
- 69.Shalongo W, Dugad L and Stellwagen E, Distribution of Helicity within the Model Peptide Acetyl(AAQAA)3amide, J. Am. Chem. Soc, 1994, 116, 8288–8293. [Google Scholar]
- 70.Kubelka J, Chiu TK, Davies DR, Eaton WA and Hofrichter J, Sub-microsecond protein folding, J. Mol. Biol, 2006, 359, 546–553. [DOI] [PubMed] [Google Scholar]
- 71.Munoz V, Thompson PA, Hofrichter J and Eaton WA, Folding dynamics and mechanism of β-hairpin formation, Nature, 1997, 390, 196–199. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


