Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Mar 17;14(4):4224–4234. doi: 10.1021/acsnano.9b09339

Direct vs Delayed Triplet Energy Transfer from Organic Semiconductors to Quantum Dots and Implications for Luminescent Harvesting of Triplet Excitons

Victor Gray †,‡, Jesse R Allardice †, Zhilong Zhang †, Simon Dowland †, James Xiao †, Anthony J Petty II §, John E Anthony §, Neil C Greenham †, Akshay Rao †,*
PMCID: PMC7199217  PMID: 32181633

Abstract

graphic file with name nn9b09339_0007.jpg

Hybrid inorganic–organic materials such as quantum dots (QDs) coupled with organic semiconductors have a wide range of optoelectronic applications, taking advantage of the respective materials’ strengths. A key area of investigation in such systems is the transfer of triplet exciton states to and from QDs, which has potential applications in the luminescent harvesting of triplet excitons generated by singlet fission, in photocatalysis and photochemical upconversion. While the transfer of energy from QDs to the triplet state of organic semiconductors has been intensely studied in recent years, the mechanism and materials parameters controlling the reverse process, triplet transfer to QDs, have not been well investigated. Here, through a combination of steady-state and time-resolved optical spectroscopy we study the mechanism and energetic dependence of triplet energy transfer from an organic ligand (TIPS-tetracene carboxylic acid) to PbS QDs. Over an energetic range spanning from exothermic (−0.3 eV) to endothermic (+0.1 eV) triplet energy transfer we find that the triplet energy transfer to the QD occurs through a single step process with a clear energy dependence that is consistent with an electron exchange mechanism as described by Marcus–Hush theory. In contrast, the reverse process, energy transfer from the QD to the triplet state of the ligand, does not show any energy dependence in the studied energy range; interestingly, a delayed formation of the triplet state occurs relative to the quantum dots’ decay. Based on the energetic dependence of triplet energy transfer we also suggest design criteria for future materials systems where triplet excitons from organic semiconductors are harvested via QDs, for instance in light emitting structures or the harvesting of triplet excitons generated via singlet fission.

Keywords: triplet energy transfer, singlet fission, quantum dots, photon multiplication, solar energy

Semiconductor quantum dots (QDs) are a class of materials with a wide range of possible applications. With their superb optical properties, QDs are particularly well suited as absorbing and emitting species in optoelectronic devices.1−8 Since the bright–dark state splitting in QDs is small, much smaller than kT at room temperature, efficient emission with no losses due to dark spin states is common.9,10 In contrast, spin-1 triplet states in organic semiconductors are spin forbidden to relax to the ground state by photon emission; i.e., they are dark states. However, it has been shown that it is possible to transfer such dark triplet excitons from organic semiconductors to QDs, where the excitation energy subsequently can be emitted as a photon,11−15 thus converting the dark states into bright states.

Following the first demonstrations that it was possible to transfer energy from the triplet state of an organic semiconductor to a QD,11,12 there has been a growing interest in such hybrid organic–inorganic systems and their potential applications in photocatalysis and photochemical upconversion.16−18 The key photophysical process in such systems, the transfer of energy from the QD to organic, has gained considerable attention.13,16−19 For example, the transfer from CdSe to anthracene ligands has been studied for photon upconversion applications using both steady-state and time-resolved approaches.16,17,20,21 It is generally accepted that the triplet energy transfer in these CdSe–anthracene materials occurs through a Dexter exchange mechanism.19,21,22 It would be expected that triplet transfer from other QDs, such as PbS and PbSe, would occur through a similar mechanism. In some instances there is evidence supporting a similar direct transfer mechanism in PbS–tetracene systems.23−25 Surprisingly, recent observations indicate that in other cases the triplet exciton transfer from PbS QDs to organic ligands occurs via an intermediate state.26,27 Luo et al. recently showed that triplet transfer from perovskite QDs to organic ligands can occur through a simultaneous or stepwise two electron process depending on the band alignment.28

In contrast, the transfer of triplet excitons to QDs has been much less studied following the initial demonstrations of these hybrid systems. The mechanism of triplet energy transfer from organics to PbS has not been elucidated, and the question still remains if it occurs via a direct exchange mechanism or via an intermediate state. Furthermore, in both cases (triplet transfer to and from QDs), thermodynamic considerations, with regards to the energetic driving force for triplet energy transfer, have only been reported in a few cases.13,25 Understanding the energetic requirements for exciton transfer is crucial for modeling device behavior, which in turn can directly aid in the design of future, more suitable materials. In the case of triplet transfer to QDs, this process could form the underlying working principal of LEDs based on triplet harvesting from organics and also a recently proposed device concept—the singlet fission photon multiplier (PM)—which this work will examine in some detail.

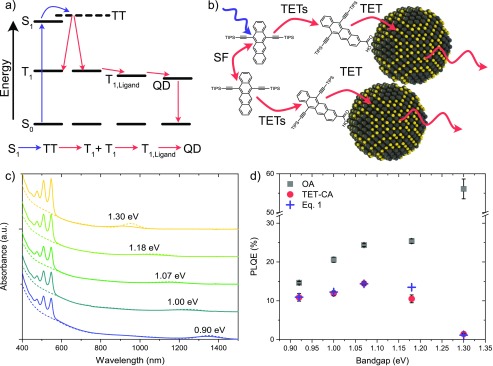
Singlet fission (SF) is a spin-allowed process in organic semiconductors forming two triplet excitons from an initial photoexcited singlet excited state (Figure 1a).29,30 As an exciton multiplication process, SF has been suggested as a possible way of overcoming thermalization losses in photovoltaic (PV) devices, increasing the theoretical maximum efficiency of a single-junction device from 33% to 44%.30−32 A few SF-based PV devices have been demonstrated;31,33−37 however, overall efficiencies are still low. Moreover, as suggested by Dexter 50 years ago,38 it would be a great gain if traditional Si-based PVs could be coupled with an SF material, and efforts toward this end are being made.39,40 A major difficulty is how to transfer the generated triplet excitons to the Si–PV efficiently as the diffusion length of triplets is limited, and the efficiency of Si–PV is sensitive to surface passivation.39,40 Emissive states, such as singlet spin-0 states, are easier to transfer long distances, either through FRET or photon emission with subsequent photon absorption in the acceptor. It has therefore been proposed that combining emissive QDs with an exciton multiplication material (such as an SF material) could constitute a photon multiplication (PM) material.14,15,30,32 The working principle of such a PM material is as follows (see Figure 1a,b): Absorption of a high-energy photon by the SF material generates two triplet excitons. These triplets are then transferred into emissive QDs, generating two excited QDs that efficiently emit two photons. The emitted photons are then absorbed in a conventional PV cell, such as Si. Examples of PM materials have been demonstrated in solution recently.14,15 Important in developing these materials further and of fundamental interest for many other optoelectronic materials is to gain a detailed understanding of the mechanism of triplet energy transfer from organic molecules to inorganic QDs.

Figure 1.

Figure 1

Open in a new tab

(a) Schematic energy diagram illustrating the singlet-fission process and photon multiplication pathway where a singlet excited state (S1) generates two triplet states (T1) via an intermediate TT state, followed by triplet energy transfer (TET) to a quantum dot (QD) via an intermediate ligand state. (b) Schematic illustration of the photon-multiplication process described in part a. (c) Absorption spectra of the series of PbS QDs studied herein, with excitonic band gaps ranging from 0.9 to 1.3 eV. Dotted lines are absorption from the as-synthesized OA-capped PbS QDs, and solid lines are the absorption after ligand exchange with TIPS-tetracene carboxylic acid, TET-CA. (d) Photoluminescence quantum efficiencies, PLQEs, at 658 nm excitation of the as-synthesized OA-capped QDs (gray squares), QDs with TET-CA ligand (red circles), and calculated quantum yields from eq 1 (blue crosses).

Here, we elucidate the mechanism and energy dependence of triplet exciton transfer to QDs from organic ligands. Our model system consists of 6,11-bis((triisopropylsilyl)ethynyltetracene-2-carboxylic acid (TET-CA) ligands attached to PbS QDs, as well as 5,12-bis((triisopropylsilyl)ethynyltetracene (TIPS-Tc) in concentrated solution as a singlet-fission material to generate free triplets. The triplet transfer is studied both indirectly through steady-state absolute photoluminescence efficiency (PLQE) measurements as well as directly through transient absorption spectroscopy. We vary the QD size and hence the exciton energy to achieve systems with different driving energies for triplet transfer to the QDs, ranging from exothermic (−0.3 eV) to endothermic (+0.1 eV). We find that triplet energy transfer to the QD occurs via a single step process, consistent with an electron exchange mechanism with a Marcus–Hush energy dependence, in line with previous indications in solution.25 An energy offset of about −0.1 eV between the QD and triplet mediator ligand is required for efficient net transfer. We can accurately model the PM behavior and use the developed model to propose future design criteria for efficient PM systems suitable for Si-PVs. We conclude that SF materials with higher triplet energies (1.4–1.5 eV) will be required for practical applications.

Results/Discussion

Ligand Exchange of PbS QDs

Oleic acid (OA)-capped PbS quantum dots with excitonic absorption peaks from 0.9 to 1.3 eV (Figure 1c) were synthesized according to previously reported methods.41 To achieve efficient triplet energy transfer to and from semiconductor quantum dots, a mediator ligand is often required.15−17 We therefore partly exchanged the native oleic acid ligands to TIPS-tetracene-carboxylic acid (TET-CA, Figure S1) as described previously15 (details of the ligand exchange can be found in the SI). The ligand coverage was within the range 1.6–1.9 TET-CA/nm2 for all sizes of QDs (as determined from UV/vis absorption, Supporting Information, Figure S2 and Table S1). The absolute photoluminescence quantum yield (PLQE) of the OA-capped dots increases from 10% to almost 60% when the band gap increases from 0.9 to 1.3 eV, shown in Figure 1d. The trend of increasing PLQE with band gap is well-known for QDs.42 After ligand exchange, the PLQE is quenched, and two distinct quenching behaviors are observed. For low-band-gap dots (0.9–1.1 eV), the PLQE quenching is about 25–40%. For band gaps above 1.1 eV, however, the quenching is even more severe, approaching 99% for 1.3 eV dots.

From ps and ns transient absorption measurements of the QDs capped with either OA or TET-CA (Figures S3 and S4), we conclude that the quenching mechanism is 2-fold; first the ligand exchange introduces some surface traps which are rapidly populated within hundreds of picoseconds after QD excitation. These traps can repopulate the QD excitonic state and only result in a net quenching of roughly 30%. Second, in the case when the QD band gap is close to or larger than the T1 energy of the TET-CA ligand (approximately 1.2 eV, see below), triplet energy transfer (TET) from the PbS QD to TET-CA is possible, resulting in more significant quenching. Based on the dual quenching mechanism, we can derive an expression for the QD PLQE, eq 1 (see the SI for the derivation):

graphic file with name nn9b09339_m001.jpg 1

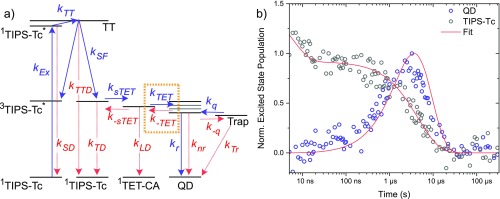
where kr and knr are the radiative and nonradiative decay constants of the QDs, respectively. kTET and k–TET are the rates of triplet energy transfer to and from the QD, respectively. Similarly, kq and k–q are the rates of quenching to the trap state and QD repopulation rate from the trap, respectively. kLD and kTr are the decay constants for the ligand triplet and QD trap state, respectively. The rate constants are also defined in the Jablonski diagram in Figure 4, which describes the studied PM system in whole. For the three low-energy QDs the triplet transfer rates (kTET and k–TET) can be neglected in the case where the QDs are directly excited, as the uphill transfer to the ligand is slow compared to the quenching. Therefore, the quenching of the ps TA dynamics seen in Figure S3a–c solely originates from trap quenching. From these decays we approximate the trap quenching rate to kq ≈ 1.0 × 1010 s–1. We find that k–q = 0.3 × 1010 s–1 and kTr = 1.0 × 105 s–1 reproduce the quenched PLQE values in Figure 1d for QDs with band gaps 0.9–1.07 eV. For the higher-energy QDs (band gaps 1.18–1.3 eV), there is the additional quenching via triplet energy transfer, and the quenching seen in the decays in Figure S3 cannot exclude contributions from TET. However, by assuming that the trap quenching is constant over the band gap range studied here and with triplet energy transfer rates (kTET and k–TET) determined from our ns TA measurements (see below), we can accurately reproduce the PLQEs of all the ligand-exchanged QDs (Figure 1d). The excellent agreement to the experimental PLQEs allows us for further modeling to assume that the trap quenching and repopulation dynamics do not change significantly with band gap, but only an additional quenching by triplet transfer to the ligand appears when it becomes energetically favorable.

Figure 4.

Figure 4

Open in a new tab

(a) Jablonski diagram illustrating the excited states involved in the photon multiplication (PM) process. Processes leading toward the desired quantum dot (QD) excited state are colored in blue; detrimental relaxation and quenching processes are shown as red dotted lines. Rate constants for a process are shown next to the corresponding arrow. The unknown rate constants kTET and k–TET determined from the fitting are highlighted in the orange dashed box. (b) Excited state population kinetics of TIPS-Tc triplets (black circles) and 0.9 eV quantum dots (QDs, blue circles) obtained by decomposing the QD and TIPS-Tc only spectra from the transient absorption maps in Figure 3. Red line shows the fitted population dynamics.

Singlet-Fission and Triplet Energy Transfer to PbS QDs in Solution

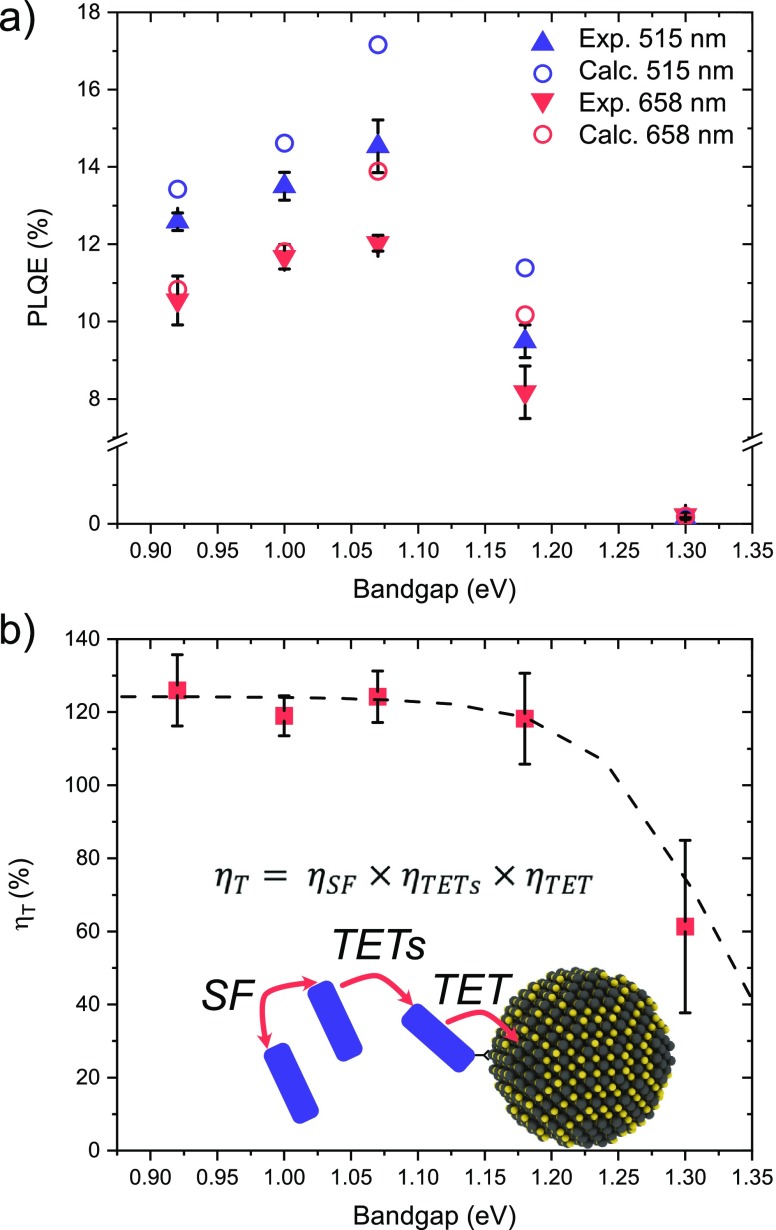
We choose TIPS-tetracene (TIPS-Tc, Figure S1) as the SF material as it is an extremely soluble tetracene derivative that is known to undergo SF in both concentrated solution and films.15,43,44 In solution, the free triplet yield has been reported to be 120–140%15,43 at concentrations of 200 mg/mL (0.34 M). Figure 2a displays the PLQE of the TET-CA covered dots in a 200 mg/mL TIPS-Tc solution, exciting either TIPS-Tc (515 nm) or the QDs (658 nm). For QDs with energies <1.25 eV there is an enhancement of the PLQE when the singlet-fission material TIPS-Tc is excited, suggesting exciton multiplication through SF followed by triplet energy transfer (TET) to the QDs. From the PLQE values in Figure 2a and taking into account the fractional absorption of the two components in the samples, we estimate the number of triplets transferred to a QD per photon absorbed (ηT) according to eq 2:12,15

graphic file with name nn9b09339_m002.jpg 2

where ΦPM is the measured PLQE when exciting the SF material TIPS-Tc, and ΦQD is the PLQE when exciting the QD directly. The total absorption at the excitation wavelength 515 nm (AbsTot515nm) is the sum of the absorption of the two components TIPS-Tc (AbsTIPS–Tc) and QD (AbsQD515nm) estimated from the concentrations and molar absorption coefficients. In Figure 2b it can be seen that the triplet transfer efficiency is 120 ± 5% for QDs with energies <1.25 eV. Our observations are in line with a triplet yield of 130 ± 10% in TIPS-Tc solutions followed by close to quantitative TET to the QDs, as we have recently reported.15

Figure 2.

Figure 2

Open in a new tab

(a) Measured and modeled photoluminescence quantum efficiencies (PLQEs) of PbS quantum dots (QDs) of various band gaps. Samples are 0.2 mM QDs with TET-CA ligands in 200 mg/mL TIPS-Tc solutions. Excitation with 515 nm mainly excites the singlet-fission material TIPS-Tc, and excitation at 658 nm directly excites the PbS QDs. (b) Triplet transfer efficiency (ηT) from TIPS-Tc to the QDs, determined from the PLQE enhancement following eq 2; dashed line is the theoretical triplet transfer efficiency obtained from the kinetic modeling described below. Inset shows the schematic energy transfer process and the equation highlights that the triplet transfer efficiency is a product of the singlet-fission (SF) yield, the efficiency of triplet transfer in solution (TETs), and the efficiency of triple transfer from the ligand to the QD (TET).

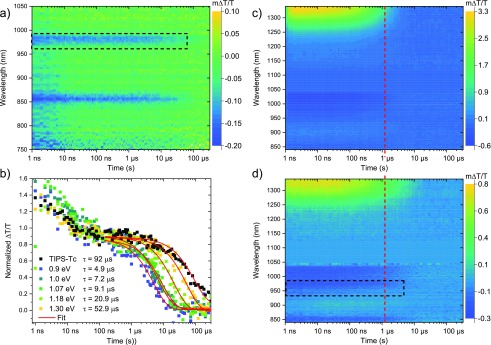
To further study the triplet energy transfer dynamics, we turn to ns-resolved transient absorption (TA) spectroscopy. Transient absorption spectra of TIPS-Tc solutions excited at 515 nm correspond well to previous reports, with the characteristic triplet absorption peaks at 860 and 970 nm (Figure 3a).15,43 Analyzing the kinetics of SF in our TIPS-Tc solutions, we conclude that the triplet decay occurs mainly though intrinsic first-order decay at fluences below 4 μJ/cm2, with a rate constant, kTc, of 1.1 × 104 s–1 (Figure S5). When TET-CA covered PbS QDs are added to the TIPS-Tc solution, a quenching of the triplet signal is observed, as shown Figure 3b. The TIPS-Tc is quenched by up to 95% by the 0.9 eV QD/TET-CA system, suggesting efficient TET from TIPS-Tc to the QDs and supporting the steady-state PLQE measurements. Another telling sign of TET to the QDs is the fact that the QD lifetimes are extended when TIPS-Tc is excited, compared to directly exciting the QDs at 658 nm (Figure 3c,d and Figure S6). The extended lifetime arises due to the delayed formation of QD excitons from TET.

Figure 3.

Figure 3

Open in a new tab

(a) Transient absorption (TA) map of a concentrated TIPS-Tc solution (200 mg/mL) excited at 515 nm (4 μJ/cm2) with clear triplet absorption features at 855 and 970 nm. (b) Triplet decay kinetics of the TIPS-Tc solutions in part a compared with TIPS-Tc solutions containing PbS quantum dots (2 mM) covered with TET-CA ligands. Legend shows fitted monoexponential lifetimes. (c) TA map of 0.9 eV QDs with TET-CA ligands in 200 mg/mL TIPS-Tc, excited directly at 650 nm, 3 μJ/cm2. (d) TA map of 0.9 eV QDs in part c but exciting TIPS-Tc at 515 nm (4 μJ/cm2). Dashed box highlights triplet signal at 970 nm. Red dashed line is a guide for the eye highlighting the extension in QD lifetime in part d due to triplet transfer from TIPS-Tc.

We decompose the QD features and the TIPS-Tc triplet features from the combined TA maps, as described in the SI. In this way the kinetics of the QD and TIPS-Tc triplet populations are obtained. To recover the QD population originating from TET from TIPS-Tc, the intrinsic QD kinetics, obtained by direct excitation at 658 nm, are subtracted from the decomposed QD kinetics at 515 nm excitation. Figure 4b and Figure S7 show these extracted kinetic traces where a delayed growth of the QD ground state bleach is clearly observed in the time scale of TET for QDs with exciton energies below 1.25 eV. For the 1.3 eV QD there is no QD ground state bleach in the time-resolution of our experiment. In fact, when the 1.3 eV QD is excited directly, there is a growth of the ligand triplet feature until 1 μs (Figure S8). For the 1.3 eV QD, there is no QD ground state bleach in the time-resolution of our experiment. In fact, when the 1.3 eV QD is excited directly, there is a growth of the ligand triplet feature until 1 μs (Figure S8). Considering that QD ground state bleach of the 1.3 eV QD/TET-CA recovers up to 95% in the first 2 ns, the delayed triplet formation could indicate a stepwise TET process or a competition of two separate processes: trap quenching and triplet transfer. In PbS–pentacene systems, reports suggest either a charge-separated or a localized surface state intermediate giving rise to a delayed triplet formation;26,27 however, a stepwise TET process has not been observed in previous PbS–tetraene systems in the literature.23−25 The reason for the delayed triplet formation is currently unknown. We did not observe any electroabsorption features, which have been associated with surface states, or signals associated with a charged intermediate in our TA data. Future studies with other techniques, such as electron spin resonance, may provide answers by examining the spin states involved in the process and identifying possible intermediates. Further, in the presence of TIPS-Tc, both the 1.3 and 1.18 eV QDs show evidence of triplet transfer from the QD, via the ligand, to TIPS-Tc (Figure S6). Since the 1.18 eV QD can both accept and donate triplets from/to the ligand, we conclude that the TET-CAT1 energy is close to resonant to the 1.18 eV QD. Thus, TET-CA has a slightly lower T1 energy than TIPS-Tc, by approximately 0.1 eV, allowing for an efficient energy cascade into lower-energy dots.

Even though the isoenergetic system of 1.18 eV QDs with TET-CA ligands has a high triplet transfer efficiency of 120% (Figure 2b), the absolute PLQE of the 1.18 eV QD/TET-CA system is lower than the lower-energy QDs. The possibility for exciton equilibration between QD and ligand states in the isoenergetic system would explain this lower PLQE. Thus, we can conclude that even though efficient triplet transfer can occur in the isoenergetic system, the QD/TET-CA exciton equilibrium leads to the need for an energy offset of 0.1 eV to achieve an overall efficient PM system. By modeling the triplet transfer dynamics in the PM systems we hope to gain a better understanding of the triplet transfer dependence on energetic driving force (ΔE) to aid future design of hybrid organic–inorganic optoelectronic materials.

Kinetic Model of PM and Fitting of Steady-State and Transient Data

We can now build a model describing the PM system. The Jablonski diagram in Figure 4 illustrates the states and processes involved, including possible quenching routes. In the following description, the rate constants of the described process are given in brackets. The first step that needs to happen is the absorption of a photon (kEx/s–1) by TIPS-Tc to form the first excited singlet state 1TIPS-Tc*. From here, singlet fission (kTT/s–1) forming a correlated triplet pair (TT) state, involving two TIPS-Tc molecules, competes with intrinsic radiative and nonradiative singlet decay (kSD/s–1). At high concentrations the formation of TT can be considered to be pseudo-first-order in [1TIPS-Tc*]. The TT state can dissociate (kSF/s–1) into two free triplets, 3TIPS-Tc*. However, the TT state can also decay through radiative and nonradiative pathways (kTTD/s–1). Triplet transfer from 3TIPS-Tc* to the ligand (ksTET/M–1 s–1) generates the triplet excited ligand 3TET-CA*. The triplet exciton can then either be transferred to the QD (kTET/s–1) or back to a TIPS-Tc molecule (k–sTET/M–1 s–1). Both 3TIPS-Tc* and 3TET-CA* can decay through intrinsic triplet decay channels, (kTD/s–1) and (kLD/s–1), respectively. As discussed above, there are a number of quenching pathways in the QD that compete with radiative emission (kr/s–1): back triplet transfer to the ligand (k–TET/s–1), quenching to a surface trap kq/s–1, and intrinsic nonradiative decay (knr/s–1).

Eight coupled differential rate equations govern the above-described system. The rate equations are defined in the SI as Equations S5–S13 together with a detailed description of the fitting analysis, and only a brief account of the modeling is given here in the main text. Using rate constants from Stern et al.,43 the kinetics of the 3TIPS-Tc* species, extracted from the TA measurement for a concentrated TIPS-Tc solution, can be accurately reproduced. The initial fast singlet-fission process will not be affected by the addition of QDs,15 and we therefore use the rate constants from Stern et al.43 for our modeling. However, we use a slightly larger kSF (factor of 1.3) to obtain a singlet-fission triplet yield of 130% which is in accordance with previous work.15,43 From the ps-TA measurements of the ligand-exchanged QDs we can also estimate rates for the trap quenching and repopulation rates. For our modeling we use an average rate of trap quenching kq of 1/100 ps–1 and a kq/k–q ratio of 1.7 to accurately reproduce the PLQE data in Figure 2 for all QD sizes. The remaining unknowns in our system are the triplet energy transfer rates: kTET, k–TET, ksTET, and k–sTET. To reduce the number of unknowns for the fitting, we set ksTET to a reasonable value for substituted acenes in toluene15,45 of 1 × 109 M–1 s–1. Using a detailed balance and microscopic reversibility of the rates, the reverse rate constant k–sTET is determined to be 1 × 107 M–1 s–1 based on the energetic offset of 0.1 eV between the ligand TET-CA and TIPS-Tc. To determine the triplet transfer rates kTET and k–TET, we solve Equations S5–S13 numerically and fit the results to the kinetic traces in Figure 4b and Figure S7; see the SI for details. The fit is also constrained by the added criterion that the steady-state PLQE values should be reproduced within 20% relative of the experimental values. Table 1 summarizes the obtained fitting parameters, and Figure 4b and Figure S7 show the resulting fits. Errors of the fitted parameters are estimated by varying the obtained rate constants 2 orders of magnitude while keeping other constants fixed and monitoring the goodness of the fit. The error is then taken as the values that maintain the goodness of fit within ±5% of the minimum while also maintaining the PLQE within 20% of the experimental value.

Table 1. Rate Constants Used for Fitting the Kinetic Model in Equations S5–S13; Rate Constants Are Defined in Figure 4.

  0.9 eV 1.0 eV 1.07 eV 1.18 eV 1.30 eV
kExa (s–1) 1.8 × 10–4 1.8 × 10–4 1.8 × 10–4 1.8 × 10–4 1.8 × 10–4
kEx-SSb (s–1) 0.031 0.032 0.034 0.035 0.037
kExQD-515nmc (s–1) 1.01 0.91 0.67 0.62 0.29
kExQD-658nmd (s–1) 20.2 20.2 20.2 20.2 20.2
kSDe (s–1) 6.8 × 107 6.8 × 107 6.8 × 107 6.8 × 107 6.8 × 107
kTTf (s–1) 5.6 × 109 5.6 × 109 5.6 × 109 5.6 × 109 5.6 × 109
kSFg (s–1) 1.11 × 108 1.11 × 108 1.11 × 108 1.11 × 108 1.11 × 108
kTTDe (s–1) 5.74 × 107 5.74 × 107 5.74 × 107 5.74 × 107 5.74 × 107
kTD (s–1) 1.1 × 104 1.1 × 104 1.1 × 104 1.1 × 104 1.1 × 104
ksTET (s–1 M–1) 1 × 109 1 × 109 1 × 109 1 × 109 1 × 109
k–sTET (s–1 M–1) 1 × 107 1 × 107 1 × 107 1 × 107 1 × 107
kLD (s–1) 3.45 × 104 3.45 × 104 3.45 × 104 3.45 × 104 3.45 × 104
kTETh (s–1) 2 × 108 9 × 107 5 × 107 1.5 × 106 0.7 × 106
k–TETh (s–1) 2 × 107 2 × 107 1 × 107 0.4 × 107 4 × 108
kQD = kr + knr (s–1) 1.0 × 106 0.50 × 106 0.50 × 106 0.50 × 106 0.42 × 106
kq (s–1) 1.0 × 1010 1.0 × 1010 1.0 × 1010 1.0 × 1010 1.0 × 1010
k–q (s–1) 0.3 × 1010 0.3 × 1010 0.3 × 1010 0.3 × 1010 0.3 × 1010
kTr (s–1) 1.0 × 105 1.0 × 105 1.0 × 105 1.0 × 105 1.0 × 105
Open in a new tab
a

Rate of excitation for the time-dependent solution, kEx, is used to calculate the initial concentration of TIPS-Tc singlets and then set to 0 for the numerical solution. Estimated from the experimental excitation density 4 μJ/cm2/pulse

b

Rate of excitation of TIPS-Tc only used for the steady-state solution for calculating PLQEs, estimated from 800 μW/cm2 excitation density.

c

The rate of direct excitation of the QD at 515 nm, considering the competitive absorption between TIPS-Tc and QD, estimated from 800 μW/cm2 excitation density, only used for the steady-state solution to calculate the PLQEs.

d

Excitation rate of QDs at 658 nm excitation used for the steady-state calculations, estimated from the experimental excitation density 8 mW/cm2.

e

Taken from Stern et al.39

f

Value interpolated from concentration dependent rates in Stern et al.6

g

Value from Stern et al.39 multiplied by 1.3, in line with a 130% SF yield.

h

Free parameters used in the fitting.

The rate of triplet transfer from the QD to ligand did not show any clear trend with energetic driving force; k–TET was consistently around 107 s–1 except for the highest-energy QD (1.30 eV) which was an order of magnitude faster (Table 1 and Figure S9). The lack of a clear trend could indicate that the triplet energy transfer from the QD to ligand does not proceed directly but is rather mediated by an intermediate, rate-determining step as observed for pentacene ligands.26,27 However, an indirect mechanism was not suggested by Kroupa et al. in the PbS-TET-CA system they studied.25 However, we note that their ps-TA data indicate a quick ground state recovery of the QDs and a slower triplet feature growth, as also observed by us (Figures S4e and S8).

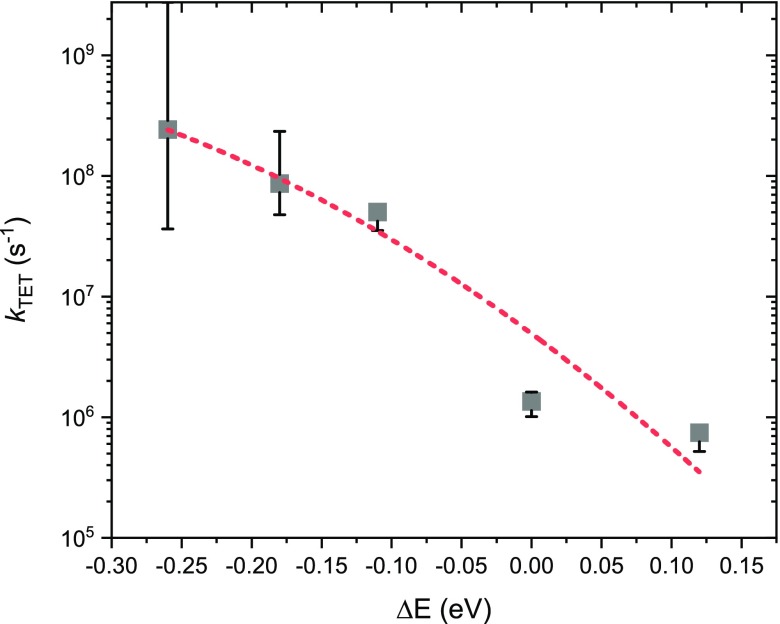
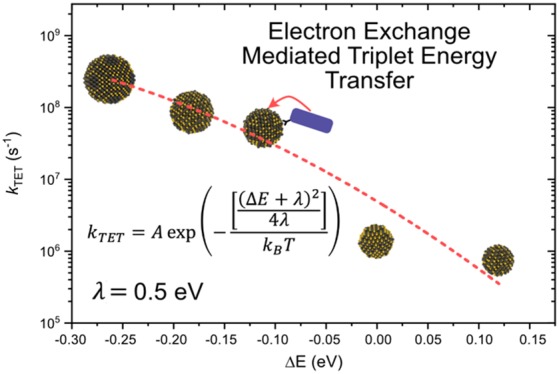
Interestingly, the reverse process, namely, triplet transfer from the ligand to QD, does not seem to be mediated by an intermediate rate-determining step. Instead, kTET shows a typical Marcus–Hush-like behavior with energetic driving force, as expected for an electron exchange mechanism.46−49 Such energy dependence is in contradiction to the initial report of resonant energy transfer to PbSe from a pentacene film.11 However, our findings are in line with the previous reports for CdSe QDs with pyrene ligands.13 The small band gap of pentacene, the relative band alignment with PbSe, and the bilayer structure could allow for competing electron transfer processes possibly interfering with the TET process, explaining the difference in energy dependence. Figure 5 shows the extracted kTET values plotted as a function of energetic offset (ΔE) between the TET-CA ligand T1 energy (taken to be 1.18 eV) and the QD exciton peak. The relatively slow rates for TET indicate that the coupling between the ligand and QD is weak, suggesting that Marcus–Hush theory is a reasonable description of the energetic dependence for TET.50 The error in kTET increases for the more exothermic systems; we suspect the reason is that the triplet transfer to the dot is no longer the rate-limiting step and becomes difficult to estimate solely from kinetic modeling. The dashed line in Figure 5 is a fit to eq 3 according to Marcus–Hush theory for electron and energy transfer:46−49,51,52

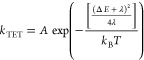graphic file with name nn9b09339_m003.jpg 3

Figure 5.

Figure 5

Open in a new tab

Obtained rate constants kTET from the fitting to transient absorption and photoluminescence measurements, plotted as a function of energetic offset (ΔE) between ligand TET-CA and QD band gap. Dashed red line is a fit to Marcus–Hush theory for electron transfer reactions (eq 3).

Here, A is a pre-exponential factor related to the probability of transfer which can be expressed in terms of the coupling (|V|2) between the initial and final state as 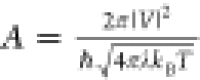Inline graphic. λ is the reorganization energy, kB the Boltzmann constant, and T the temperature. The fit to eq 3 returns a reorganization energy λ of 0.53 eV and a pre-exponential factor of 1 × 109 s–1,similar to values reported for TET in semiconducting polymers.53,54 By obtaining A and λ from our fit, we can predict kTET for any energy offset. We can then use our model to predict the PM behavior of other singlet-fission–ligand combinations in the search for better materials.

Designing PM Materials

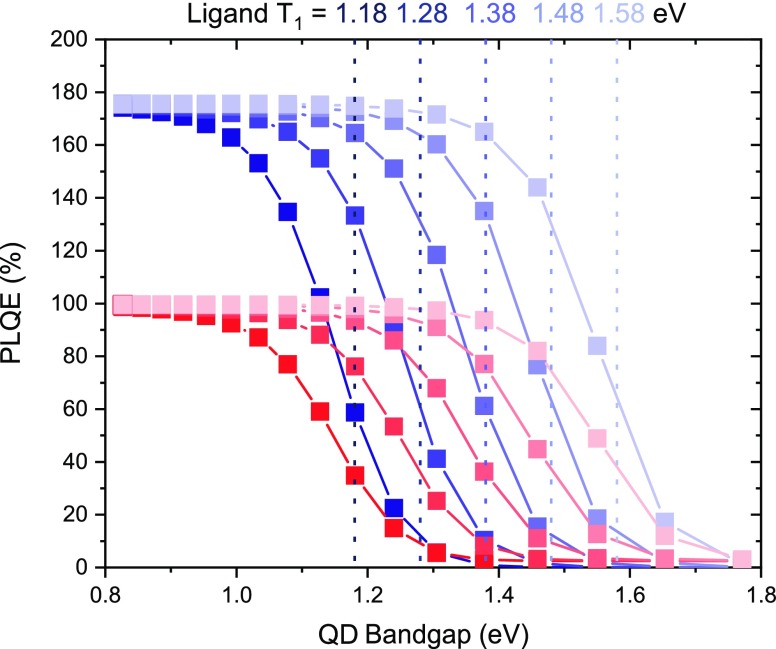
The most useful PM material combination would couple to existing Si-PVs. Therefore, an ideal PM material must emit photons above the band gap of silicon and ideally with photon energies around 1.2 eV.30,32 In Figure 6, we use our model to predict the PM behavior for QD–ligand systems with different ligand triplet energies. All the rate constants described above are kept constant, and only kTET is varied as a function of QD–ligand energy offset according to eq 3. To predict the behavior of an optimized system, the intrinsic QD PLQEs is assumed to be 100%, regardless of the band gap. The effect of surface trapping is also neglected, by setting kq to zero. The only quenching of QD PLQE is therefore due to triplet energy transfer to the ligand. k–TET, the rate of triplet transfer to the ligand, is kept at 2.0 × 107 s–1, similar to the determined k–TET values. Further, the singlet-fission material is modeled to generate triplets with 185% efficiency, which is reasonable for an efficient singlet-fission material.55−57 To achieve a singlet-fission yield of 185%, the rate of SF, kSF, is increased to 8.6 × 108 s–1. The bimolecular rate constants ksTET and k–sTET are kept constant throughout the series. Therefore, the effect on PM behavior solely originates from the effect of ligand–QD interactions.

Figure 6.

Figure 6

Open in a new tab

Modeling of an optimized photon multiplication (PM) material based on an absorbing singlet-fission material with 185% triplet yield. Triplet transfer to a PbS quantum dot is governed solely by the ligand triplet energy relative to the QD band gap. The energy difference between ligand and singlet-fission material is 0.1 eV as in the case for TIPS-Tc and TET-CA. Red squares correspond to direct excitation of the quantum dot, and the blue squares are the PM photoluminescence quantum efficiency when exciting the singlet-fission material.

Figure 6 shows the predicted PLQEs for systems with ligand T1 energies ranging from 1.18 to 1.58 eV, for direct QD excitation (red) and SF excitation (blue). From the data in Figure 6 we can conclude that, to achieve a PM above 150% for a 1.2 eV PbS QD, a ligand T1 energy of above 1.3 eV is necessary. Assuming that the SF material also needs another 0.1 eV to efficiently funnel triplets to the ligand, we propose that future SF materials with T1 energies of 1.4–1.5 eV will be required.

Conclusions

Here, we have answered a number of fundamental questions related to the triplet energy transfer from organic molecules to QDs. We have studied the energetic dependence of triplet energy transfer to PbS quantum dots. A photon multiplication scheme is used to estimate the efficiency of triplet transfer from steady-state PLQE measurements. Combined with the kinetic insight gained from ns-transient absorption measurements, we are able to extract the rate constants, kTET, of triplet energy transfer from a surface-bound TET-CA ligand to the PbS QD core. kTET is found to follow an electron exchange mechanism, as described by Marcus–Hush theory, addressing the issue of how the triplet transfer is mediated. Interestingly, the triplet energy transfer in the reverse direction, from QD to ligand, occurs at a slower time scale than the QD ground state bleach recovery possibly indicating a stepwise process.26,27 We are also able to accurately model a singlet-fission-based photon multiplication process and conclude that an energetic driving force of 0.1 eV is necessary for efficient net transfer to the QD. Furthermore, we highlight the need for singlet-fission materials with triplet energies around 1.4–1.5 eV to achieve a photon-multiplication material matched to Si-PVs. Overall, we report a detailed thermodynamic and mechanistic study of the triplet energy transfer to PbS QDs, with implications for the future design of QD optoelectronic devices and photon multiplication devices.

Methods and Experimental Section

Chemicals

5,12-Bis((triisopropylsilyl)ethynyltetracene (TIPS-Tc; Figure S1, left) was purchased from Ark Pharm. 6,11-Bis((triisopropylsilyl)ethynyl)tetracene-2-carboxylic acid (TET-CA; Figure S1, right) was synthesized as described previously.25 All other material was bought from Sigma-Aldrich and used as received.

Quantum Dot Synthesis and Ligand Exchange

Synthesis of PbS QDs was carried out following the procedure by Hines and Scholes with modifications.41,58 In summary, PbO (0.45 g), oleic acid (1.6–14 g, depending on the targeted band gap), and 1-octadecene (10 g) were degassed in a three necked flask at 110 °C for 2 h. The temperature was then reduced to 95 °C. Under nitrogen, a solution of bis(trimethylsilyl)sulfide (210 μL) in 1-octadecene (5 mL) was rapidly injected into the lead precursor solution. After cooling naturally to room temperature the PbS QDs were washed 4 times by precipitation/redispersion with acetone and hexane. The purified QDs were stored in a nitrogen-filled glovebox at high concentration (>40 mg/mL/>100 μM) until use.

Ligand exchange was carried out under nitrogen. QDs in toluene were diluted to 42 μM in a toluene/THF mixture of 4:1. The ligand in 100 mg/mL THF solutions was added to the QD solution, keeping a ligand to QD mass ratio of 1:2 for all sizes of QDs. Ligand coverage and size distribution are summarized in the Supporting Information, Table S1.

Optical Spectroscopy

Steady-State Absorption

A Shimadzu UV3600Plus spectrometer was used to measure the absorbance spectra of the solutions. The high concentration of the PM solutions required samples to be measured in rectangular capillary tubes with a 200 μm path length.

PLQE

The integrating sphere and PLQE measurement procedure has been described previously.15,59 An integrating sphere with a Spectralon-coated interior (Newport 819C-SL-5.3) was used for the absolute measurement. 515 and 658 nm laser diodes (Thorlabs) with a beam diameter at the sample of 3 mm were used as the excitation source. Light from the sphere was coupled into an Andor Kymera 328i spectrograph equipped with an InGaAs detector (Andor, iDus InGaAs 490). A NIST certified calibration lamp from Newport, 200 W quartz tungsten halogen lamp driven by an OPS-Q250 power supply, was used to generate a photons/count calibration file. The calibration file was generated by producing an irised beam of light from the calibration source into the integrating sphere; the spectral response was recorded with and without a series of long pass filters in order to resolve the longer wavelength response absent of the second harmonics from the shorter wavelengths. These were then also corrected for by measuring the transmission spectra of the filters. The calibration file was generated by comparing this data set to the calibrated spectrum of the lamp. To validate the calibration, a Rhodamine 6G sample in ethanol was measured in the sphere with 520 nm excitation. Three spectra were taken, with laser excitation on and off the sample and a blank sample. Each recorded spectra were multiplied with the generated correction curve to obtain the corrected spectra. From the corrected spectra, the PLQE was calculated to 92–95%, in good agreement with the literature.60

ps-Transient Absorption

The short-time (fs–ns) transient absorption setup has been described previously.15 In summary, a light conversion PHAROS laser system with 400 μJ per pulse at 1030 nm with a repetition rate of 38 kHz was used. The output is divided; one part is focused onto a 4 mm YAG substrate to produce the continuum probe beam from 520 to 950 nm. The second part of the PHAROS output is led into a narrow band optical parametric oscillator system (ORPHEUS-LYRA, light conversion) outputting the pump beam. The probe pulse is delayed up to 2 ns with a mechanical delay-stage (Newport). A mechanical chopper (Thorlabs) is used to create an on–off pump–probe pulse series. The pump size on the sample is approximately 0.065 mm2 and the probe about 0.015 mm2. A silicon line scan camera (JAI SW-2000M-CL-80) fitted onto a visible spectrograph (Andor Solis, Shamrock) is used to record the transmitted probe light.

ns-Transient Absorption

The long-time ns-transient absorption setup has also been described previously.15 In short, the pump–probe setup consists of a probe from a LEUKOS Disco 1 UV super continuum laser (STM-1-UV, 1 kHz) and a pump generated in a TOPAS optical amplifier, pumped with the output from a Spectra-Physics Solstice Ace Ti:sapphire amplifier (1 kHz). The probe beam is split into a reference and probe, and both are focused onto the sample. A pair of line image sensors (Hamamatsu, G11608) mounted on a spectrograph (Andor Solis, Shamrock SR303i) are used to detect the signal, using a custom built board from Stresing Entwickslungsburo to read out the signal.

Acknowledgments

We thank the Winton Programme for the Physics of Sustainability and the Engineering and Physical Sciences Research Council for funding. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement 758826). V.G. acknowledges funding from the Swedish research council, Vetenskapsrådet 2018-00238. J.R.A. acknowledges Cambridge Commonwealth European and International Trust for financial support. Z.Z. acknowledges funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie Actions grant (842271—TRITON project). J.X. acknowledges EPSRC Cambridge NanoDTC, EP/L015978/1 for financial support. J.E.A. and A.P. acknowledge the U.S. National Science Foundation (DMREF-1627428) for support of organic semiconductor synthesis.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.9b09339.

  • Additional details and data for the calculation of QD ligand coverage and size distribution. Additional data from the transient absorption measurements and details on data analysis and kinetic modeling (PDF)

  • Data underlying the figures and conclusions in this article is available at the University of Cambridge data repository at https://doi.org/10.17863/CAM50420.

The authors declare no competing financial interest.

Supplementary Material

nn9b09339_si_001.pdf (1.2MB, pdf)

References

  1. Kamat P. V. Quantum Dot Solar Cells. Semiconductor Nanocrystals as Light Harvesters. J. Phys. Chem. C 2008, 112, 18737–18753. 10.1021/jp806791s. [DOI] [Google Scholar]
  2. Kamat P. V. Quantum Dot Solar Cells. The Next Big Thing in Photovoltaics. J. Phys. Chem. Lett. 2013, 4, 908–918. 10.1021/jz400052e. [DOI] [PubMed] [Google Scholar]
  3. Dai X.; Zhang Z.; Jin Y.; Niu Y.; Cao H.; Liang X.; Chen L.; Wang J.; Peng X. Solution-Processed, High-Performance Light-Emitting Diodes Based on Quantum Dots. Nature 2014, 515, 96–99. 10.1038/nature13829. [DOI] [PubMed] [Google Scholar]
  4. Sargent E. H. Colloidal Quantum Dot Solar Cells. Nat. Photonics 2012, 6, 133–135. 10.1038/nphoton.2012.33. [DOI] [Google Scholar]
  5. Zhang Z.; Yang J.; Wen X.; Yuan L.; Shrestha S.; Stride J. A.; Conibeer G. J.; Patterson R. J.; Huang S. Effect of Halide Treatments on PbSe Quantum Dot Thin Films: Stability, Hot Carrier Lifetime, and Application to Photovoltaics. J. Phys. Chem. C 2015, 119, 24149–24155. 10.1021/acs.jpcc.5b08021. [DOI] [Google Scholar]
  6. Zhang Z.; Chen Z.; Zhang J.; Chen W.; Yang J.; Wen X.; Wang B.; Kobamoto N.; Yuan L.; Stride J. A.; Conibeer G. J.; Patterson R. J.; Huang S. Significant Improvement in the Performance of PbSe Quantum Dot Solar Cell by Introducing a CsPbBr3 Perovskite Colloidal Nanocrystal Back Layer. Adv. Energy Mater. 2017, 7, 1601773. 10.1002/aenm.201601773. [DOI] [Google Scholar]
  7. Zhang Z.; Chen Z.; Yuan L.; Chen W.; Yang J.; Wang B.; Wen X.; Zhang J.; Hu L.; Stride J. A.; Conibeer G. J.; Patterson R. J.; Huang S. A New Passivation Route Leading to Over 8% Efficient PbSe Quantum-Dot Solar Cells via Direct Ion Exchange with Perovskite Nanocrystals. Adv. Mater. 2017, 29, 1703214. 10.1002/adma.201703214. [DOI] [PubMed] [Google Scholar]
  8. Pan Z.; Rao H.; Mora-Seró I.; Bisquert J.; Zhong X. Quantum Dot-Sensitized Solar Cells. Chem. Soc. Rev. 2018, 47, 7659–7702. 10.1039/C8CS00431E. [DOI] [PubMed] [Google Scholar]
  9. Efros A. L.; Rosen M.; Kuno M.; Nirmal M.; Norris D.; Bawendi M. Band-Edge Exciton in Quantum Dots of Semiconductors with a Degenerate Valence Band: Dark and Bright Exciton States. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 4843–4856. 10.1103/PhysRevB.54.4843. [DOI] [PubMed] [Google Scholar]
  10. Scholes G. D.; Kim J.; Wong C. Y.; Huxter V. M.; Nair P. S.; Fritz K. P.; Kumar S. Nanocrystal Shape and the Mechanisme of Exciton Spin Relaxation. Nano Lett. 2006, 6, 1765–1771. 10.1021/nl061414e. [DOI] [PubMed] [Google Scholar]
  11. Tabachnyk M.; Ehrler B.; Gélinas S.; Böhm M. L.; Walker B. J.; Musselman K. P.; Greenham N. C.; Friend R. H.; Rao A. Resonant Energy Transfer of Triplet Excitons from Pentacene to PbSe Nanocrystals. Nat. Mater. 2014, 13, 1033–1038. 10.1038/nmat4093. [DOI] [PubMed] [Google Scholar]
  12. Thompson N. J.; Wilson M. W. B.; Congreve D. N.; Brown P. R.; Scherer J. M.; Bischof T. S.; Wu M.; Geva N.; Welborn M.; Voorhis T. V.; Bulović V.; Bawendi M. G.; Baldo M. A. Energy Harvesting of Non-Emissive Triplet Excitons in Tetracene by Emissive PbS Nanocrystals. Nat. Mater. 2014, 13, 1039–1043. 10.1038/nmat4097. [DOI] [PubMed] [Google Scholar]
  13. Mongin C.; Moroz P.; Zamkov M.; Castellano F. N. Thermally Activated Delayed Photoluminescence from Pyrenyl-Functionalized CdSe Quantum Dots. Nat. Chem. 2018, 10, 225–230. 10.1038/nchem.2906. [DOI] [PubMed] [Google Scholar]
  14. Davis N. J. L. K.; Allardice J. R.; Xiao J.; Petty A. J.; Greenham N. C.; Anthony J. E.; Rao A. Singlet Fission and Triplet Transfer to PbS Quantum Dots in TIPS-Tetracene Carboxylic Acid Ligands. J. Phys. Chem. Lett. 2018, 9, 1454–1460. 10.1021/acs.jpclett.8b00099. [DOI] [PubMed] [Google Scholar]
  15. Allardice J. R.; Thampi A.; Dowland S.; Xiao J.; Gray V.; Zhang Z.; Budden P.; Petty A. J.; Davis N. J. L. K.; Greenham N. C.; Anthony J. E.; Rao A. Engineering Molecular Ligand Shells on Quantum Dots for Quantitative Harvesting of Triplet Excitons Generated by Singlet Fission. J. Am. Chem. Soc. 2019, 141, 12907–12915. 10.1021/jacs.9b06584. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Mongin C.; Garakyaraghi S.; Razgoniaeva N.; Zamkov M.; Castellano F. N. Direct Observation of Triplet Energy Transfer from Semiconductor Nanocrystals. Science 2016, 351, 369–372. 10.1126/science.aad6378. [DOI] [PubMed] [Google Scholar]
  17. Huang Z.; Li X.; Mahboub M.; Hanson K. M.; Nichols V. M.; Le H.; Tang M. L.; Bardeen C. J. Hybrid Molecule-Nanocrystal Photon Upconversion across the Visible and Near-Infrared. Nano Lett. 2015, 15, 5552–5557. 10.1021/acs.nanolett.5b02130. [DOI] [PubMed] [Google Scholar]
  18. Jiang Y.; Wang C.; Rogers C. R.; Kodaimati M. S.; Weiss E. A. Regio- and Diastereoselective Intermolecular [2 + 2] Cycloadditions Photocatalysed by Quantum Dots. Nat. Chem. 2019, 11, 1034–1040. 10.1038/s41557-019-0344-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Huang Z.; Tang M. L. Designing Transmitter Ligands That Mediate Energy Transfer between Semiconductor Nanocrystals and Molecules. J. Am. Chem. Soc. 2017, 139, 9412–9418. 10.1021/jacs.6b08783. [DOI] [PubMed] [Google Scholar]
  20. Piland G. B.; Huang Z.; Lee Tang M.; Bardeen C. J. Dynamics of Energy Transfer from CdSe Nanocrystals to Triplet States of Anthracene Ligand Molecules. J. Phys. Chem. C 2016, 120, 5883–5889. 10.1021/acs.jpcc.5b12021. [DOI] [Google Scholar]
  21. Li X.; Huang Z.; Zavala R.; Tang M. L. Distance-Dependent Triplet Energy Transfer between CdSe Nanocrystals and Surface Bound Anthracene. J. Phys. Chem. Lett. 2016, 7, 1955–1959. 10.1021/acs.jpclett.6b00761. [DOI] [PubMed] [Google Scholar]
  22. Wang Y. A.; Li J. J.; Chen H.; Peng X. Stabilization of Inorganic Nanocrystals by Organic Dendrons. J. Am. Chem. Soc. 2002, 124, 2293–2298. 10.1021/ja016711u. [DOI] [PubMed] [Google Scholar]
  23. Mahboub M.; Huang Z.; Tang M. L. Efficient Infrared-to-Visible Upconversion with Subsolar Irradiance. Nano Lett. 2016, 16, 7169–7175. 10.1021/acs.nanolett.6b03503. [DOI] [PubMed] [Google Scholar]
  24. Huang Z.; Xu Z.; Mahboub M.; Li X.; Taylor J. W.; Harman W. H.; Lian T.; Tang M. L. PbS/CdS Core–Shell Quantum Dots Suppress Charge Transfer and Enhance Triplet Transfer. Angew. Chem., Int. Ed. 2017, 56, 16583–16587. 10.1002/anie.201710224. [DOI] [PubMed] [Google Scholar]
  25. Kroupa D. M.; Arias D. H.; Blackburn J. L.; Carroll G. M.; Granger D. B.; Anthony J. E.; Beard M. C.; Johnson J. C. Control of Energy Flow Dynamics between Tetracene Ligands and PbS Quantum Dots by Size Tuning and Ligand Coverage. Nano Lett. 2018, 18, 865–873. 10.1021/acs.nanolett.7b04144. [DOI] [PubMed] [Google Scholar]
  26. Garakyaraghi S.; Mongin C.; Granger D. B.; Anthony J. E.; Castellano F. N. Delayed Molecular Triplet Generation from Energized Lead Sulfide Quantum Dots. J. Phys. Chem. Lett. 2017, 8, 1458–1463. 10.1021/acs.jpclett.7b00546. [DOI] [PubMed] [Google Scholar]
  27. Bender J. A.; Raulerson E. K.; Li X.; Goldzak T.; Xia P.; Van Voorhis T.; Tang M. L.; Roberts S. T. Surface States Mediate Triplet Energy Transfer in Nanocrystal-Acene Composite Systems. J. Am. Chem. Soc. 2018, 140, 7543–7553. 10.1021/jacs.8b01966. [DOI] [PubMed] [Google Scholar]
  28. Luo X.; Han Y.; Chen Z.; Li Y.; Liang G.; Liu X.; Ding T.; Nie C.; Wang M.; Castellano F. N.; Wu K. Mechanisms of Triplet Energy Transfer across the Inorganic Nanocrystal/Organic Molecule Interface. Nat. Commun. 2020, 11, 28. 10.1038/s41467-019-13951-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Smith M. B.; Michl J. Singlet Fission. Chem. Rev. 2010, 110, 6891–6936. 10.1021/cr1002613. [DOI] [PubMed] [Google Scholar]
  30. Rao A.; Friend R. H. Harnessing Singlet Exciton Fission to Break the Shockley-Queisser Limit. Nat. Rev. Mater. 2017, 2, 17063. 10.1038/natrevmats.2017.63. [DOI] [Google Scholar]
  31. Lee J.; Jadhav P.; Reusswig P. D.; Yost S. R.; Thompson N. J.; Congreve D. N.; Hontz E.; Van Voorhis T.; Baldo M. A. Singlet Exciton Fission Photovoltaics. Acc. Chem. Res. 2013, 46, 1300–1311. 10.1021/ar300288e. [DOI] [PubMed] [Google Scholar]
  32. Futscher M. H.; Rao A.; Ehrler B. The Potential of Singlet Fission Photon Multipliers as an Alternative to Silicon-Based Tandem Solar Cells. ACS Energy Lett. 2018, 3, 2587–2592. 10.1021/acsenergylett.8b01322. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Ehrler B.; Musselman K. P.; Böhm M. L.; Friend R. H.; Greenham N. C. Hybrid Pentacene/a-Silicon Solar Cells Utilizing Multiple Carrier Generation via Singlet Exciton Fission. Appl. Phys. Lett. 2012, 101, 2010–2013. 10.1063/1.4757612. [DOI] [Google Scholar]
  34. Ehrler B.; Wilson M. W. B.; Rao A.; Friend R. H.; Greenham N. C. Singlet Exciton Fission-Sensitized Infrared Quantum Dot Solar Cells. Nano Lett. 2012, 12, 1053–1057. 10.1021/nl204297u. [DOI] [PubMed] [Google Scholar]
  35. Reusswig P. D.; Congreve D. N.; Thompson N. J.; Baldo M. A. Enhanced External Quantum Efficiency in an Organic Photovoltaic Cell via Singlet Fission Exciton Sensitizer. Appl. Phys. Lett. 2012, 101, 113304. 10.1063/1.4752445. [DOI] [Google Scholar]
  36. Wu T. C.; Thompson N. J.; Congreve D. N.; Hontz E.; Yost S. R.; Van Voorhis T.; Baldo M. A. Singlet Fission Efficiency in Tetracene-Based Organic Solar Cells. Appl. Phys. Lett. 2014, 104, 193901. 10.1063/1.4876600. [DOI] [Google Scholar]
  37. Thompson N. J.; Hontz E.; Congreve D. N.; Bahlke M. E.; Reineke S.; Van Voorhis T.; Baldo M. A. Nanostructured Singlet Fission Photovoltaics Subject to Triplet-Charge Annihilation. Adv. Mater. 2014, 26, 1366–1371. 10.1002/adma.201304588. [DOI] [PubMed] [Google Scholar]
  38. Dexter D. L. Two Ideas on Energy Transfer Phenomena: Ion-Pair Effects Involving the OH Stretching Mode, and Sensitization of Photovoltaic Cells. J. Lumin. 1979, 18–19, 779–784. 10.1016/0022-2313(79)90235-7. [DOI] [Google Scholar]
  39. MacQueen R.; Liebhaber M.; Niederhausen J.; Mews M.; Gersmann C.; Jäckle S.; Jäger K.; Tayebjee M.; Jehangir Y.; Schmidt T. W.; Rech B.; Lips K. Crystalline Silicon Solar Cells with Tetracene Interlayers: The Path to Silicon-Singlet Fission Heterojunction Devices. Mater. Horiz. 2018, 5, 1065–1075. 10.1039/C8MH00853A. [DOI] [Google Scholar]
  40. Einzinger M.; Wu T.; Kompalla J. F.; Smith H. L.; Perkinson C. F.; Nienhaus L.; Wieghold S.; Congreve D. N.; Kahn A.; Bawendi M. G.; Baldo M. A. Sensitization of Silicon by Singlet Exciton Fission in Tetracene. Nature 2019, 571, 90–94. 10.1038/s41586-019-1339-4. [DOI] [PubMed] [Google Scholar]
  41. Hines M. A.; Scholes G. D. Colloidal PbS Nanocrystals with Size-Tunable Near-Infrared Emission: Observation of Post-Synthesis Self-Narrowing of the Particle Size Distribution. Adv. Mater. 2003, 15, 1844–1849. 10.1002/adma.200305395. [DOI] [Google Scholar]
  42. Semonin O. E.; Johnson J. C.; Luther J. M.; Midgett A. G.; Nozik A. J.; Beard M. C. Absolute Photoluminescence Quantum Yields of IR-26 Dye, PbS, and PbSe Quantum Dots. J. Phys. Chem. Lett. 2010, 1, 2445–2450. 10.1021/jz100830r. [DOI] [Google Scholar]
  43. Stern H. L.; Musser A. J.; Gelinas S.; Parkinson P.; Herz L. M.; Bruzek M. J.; Anthony J.; Friend R. H.; Walker B. J. Identification of a Triplet Pair Intermediate in Singlet Exciton Fission in Solution. Proc. Natl. Acad. Sci. U. S. A. 2015, 112, 7656–7661. 10.1073/pnas.1503471112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Stern H. L.; Cheminal A.; Yost S. R.; Broch K.; Bayliss S. L.; Chen K.; Tabachnyk M.; Thorley K.; Greenham N.; Hodgkiss J. M.; Anthony J.; Head-Gordon M.; Musser A. J.; Rao A.; Friend R. H. Vibronically Coherent Ultrafast Triplet-Pair Formation and Subsequent Thermally Activated Dissociation Control Efficient Endothermic Singlet Fission. Nat. Chem. 2017, 9, 1205–1212. 10.1038/nchem.2856. [DOI] [PubMed] [Google Scholar]
  45. Gray V.; Dreos A.; Erhart P.; Albinsson B.; Moth-Poulsen K.; Abrahamsson M. Loss Channels in Triplet–Triplet Annihilation Photon Upconversion: Importance of Annihilator Singlet and Triplet Surface Shapes. Phys. Chem. Chem. Phys. 2017, 19, 10931–10939. 10.1039/C7CP01368J. [DOI] [PubMed] [Google Scholar]
  46. Albinsson B.; Mårtensson J. Long-Range Electron and Excitation Energy Transfer in Donor-Bridge-Acceptor Systems. J. Photochem. Photobiol., C 2008, 9, 138–155. 10.1016/j.jphotochemrev.2008.01.002. [DOI] [PubMed] [Google Scholar]
  47. Subotnik J. E.; Vura-weis J.; Sodt A. J.; Ratner M. A. Predicting Accurate Electronic Excitation Transfer Rates via Marcus Theory with Boys or Edmiston-Ruedenberg Localized Diabatization. J. Phys. Chem. A 2010, 114, 8665–8675. 10.1021/jp101235a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Closs G. L.; Piotrowiak P.; MacInnis J. M.; Fleming G. R. Determination of Long Distance Intramolecular Triplet Energy Transfer Rates. A Quantitative Comparison with Electron Transfer. J. Am. Chem. Soc. 1988, 110, 2652–2653. 10.1021/ja00216a051. [DOI] [Google Scholar]
  49. Closs G. L.; Piotrowiak P.; Johnson M. D.; Miller J. R. A Connection between Intramolecular Long-Range Electron, Hole, and Triplet Energy Transfers. J. Am. Chem. Soc. 1989, 111, 3751–3753. 10.1021/ja00192a044. [DOI] [Google Scholar]
  50. Tisdale W. A.; Zhu X. Y. Artificial Atoms on Semiconductor Surfaces. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 965–970. 10.1073/pnas.1006665107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Marcus R. A. Chemical and Electrochemical Electron-Transfer Theory. Annu. Rev. Phys. Chem. 1964, 15, 155–196. 10.1146/annurev.pc.15.100164.001103. [DOI] [Google Scholar]
  52. Balzani V.; Bolletta F.; Scandola F. Vertical and Nonvertical” Energy Transfer Processes. A General Classical Treatment “. J. Am. Chem. Soc. 1980, 102, 2152–2163. 10.1021/ja00527a002. [DOI] [Google Scholar]
  53. Sudha Devi L.; Al-Suti M. K.; Dosche C.; Khan M. S.; Friend R. H.; Köhler A. Triplet Energy Transfer in Conjugated Polymers. I. Experimental Investigation of a Weakly Disordered Compound. Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 78, 045210. 10.1103/PhysRevB.78.045210. [DOI] [Google Scholar]
  54. Hoffmann S. T.; Scheler E.; Koenen J. M.; Forster M.; Scherf U.; Strohriegl P.; Bässler H.; Köhler A. Triplet Energy Transfer in Conjugated Polymers. III. An Experimental Assessment Regarding the Influence of Disorder on Polaronic Transport. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 81, 165208. 10.1103/PhysRevB.81.165208. [DOI] [Google Scholar]
  55. Johnson J. C.; Nozik A. J.; Michl J. High Triplet Yield from Singlet Fission in a Thin Film of 1,3-Diphenylisobenzofuran. J. Am. Chem. Soc. 2010, 132, 16302–16303. 10.1021/ja104123r. [DOI] [PubMed] [Google Scholar]
  56. Walker B. J.; Musser A. J.; Beljonne D.; Friend R. H. Singlet Exciton Fission in Solution. Nat. Chem. 2013, 5, 1019–1024. 10.1038/nchem.1801. [DOI] [PubMed] [Google Scholar]
  57. Sanders S. N.; Kumarasamy E.; Pun A. B.; Trinh M. T.; Choi B.; Xia J.; Taffet E. J.; Low J. Z.; Miller J. R.; Roy X.; Zhu X. Y.; Steigerwald M. L.; Sfeir M. Y.; Campos L. M. Quantitative Intramolecular Singlet Fission in Bipentacenes. J. Am. Chem. Soc. 2015, 137, 8965–8972. 10.1021/jacs.5b04986. [DOI] [PubMed] [Google Scholar]
  58. Zhang J.; Crisp R. W.; Gao J.; Kroupa D. M.; Beard M. C.; Luther J. M. Synthetic Conditions for High-Accuracy Size Control of PbS Quantum Dots. J. Phys. Chem. Lett. 2015, 6, 1830–1833. 10.1021/acs.jpclett.5b00689. [DOI] [PubMed] [Google Scholar]
  59. De Mello J. C.; Wittmann H. F.; Friend R. H. An Improved Experimental Determination of External Photoluminescence Quantum Efficiency. Adv. Mater. 1997, 9, 230–232. 10.1002/adma.19970090308. [DOI] [Google Scholar]
  60. Kubin R. F.; Fletcher A. N. Fluorescence Quantum Yields of Some Rhodamine Dyes. J. Lumin. 1982, 27, 455–462. 10.1016/0022-2313(82)90045-X. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn9b09339_si_001.pdf (1.2MB, pdf)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES