An Open Access Database for the Evaluation of Heart Sound Algorithms

Abstract

In the past few decades, analysis of heart sound signals (i.e., the phonocardiogram or PCG), especially for automated heart sound segmentation and classification, has been widely studied and has been reported to have the potential value to detect pathology accurately in clinical applications. However, comparative analyses of algorithms in the literature have been hindered by the lack of high-quality, rigorously validated, and standardized open databases of heart sound recordings. This paper describes a public heart sound database, assembled for an international competition, the PhysioNet/Computing in Cardiology (CinC) Challenge 2016. The archive comprises nine different heart sound databases sourced from multiple research groups around the world. It includes 2,435 heart sound recordings in total collected from 1,297 healthy subjects and patients with a variety of conditions, including heart valve disease and coronary artery disease. The recordings were collected from a variety of clinical or nonclinical (such as in-home visits) environments and equipment. The length of recording varied from several seconds to several minutes. This article reports detailed information about the subjects/patients including demographics (number, age, gender), recordings (number, location, state and time length), associated synchronously recorded signals, sampling frequency and sensor type used. We also provide a brief summary of the commonly used heart sound segmentation and classification methods, including open source code provided concurrently for the Challenge. A description of the PhysioNet/CinC Challenge 2016, including the main aims, the training and test sets, the hand corrected annotations for different heart sound states, the scoring mechanism, and associated open source code are provided. In addition, several potential benefits from the public heart sound database are discussed.

1. Introduction

Cardiovascular diseases (CVDs) continue to be the leading cause of morbidity and mortality worldwide. An estimated 17.5 million people died from CVDs in 2012, representing 31% of all global deaths (WHO, 2015). One of the first steps in evaluating the cardiovascular system in clinical practice is physical examination. Auscultation of the heart sounds is an essential part of the physical examination and may reveal many pathologic cardiac conditions such as arrhythmias, valve disease, heart failure, and more. Heart sounds provide important initial clues in disease evaluation, serve as a guide for further diagnostic examination, and thus play an important role in the early detection for CVDs.

During the cardiac cycle, the heart first experiences electrical activation, which then leads to mechanical activity in the form of atrial and ventricular contractions. This in turn forces blood between the chambers of the heart and around the body, as a result of the opening and closure of the heart valves. This mechanical activity, and the sudden start or stop of the flow of blood within the heart, gives rise to vibrations of the entire cardiac structure (Leatham, 1975). These vibrations are audible on the chest wall, and listening for specific heart sounds can give an indication of the health of the heart. An audio recording (or graphical) time series representation of the resultant sounds, transduced at the chest surface is known as a heart sound recording or phonocardiogram (PCG).

Four locations are most often used to listen to and transduce the heart sounds, which are named according to the positions in which the valves can be best heard (Springer, 2015):

• Aortic area - centred at the second right intercostal space.

• Pulmonic area - in the second intercostal space along the left sternal border.

• Tricuspid area - in the fourth intercostal space along the left sternal edge.

• Mitral area - at the cardiac apex, in the fifth intercostal space on the midclavicular line.

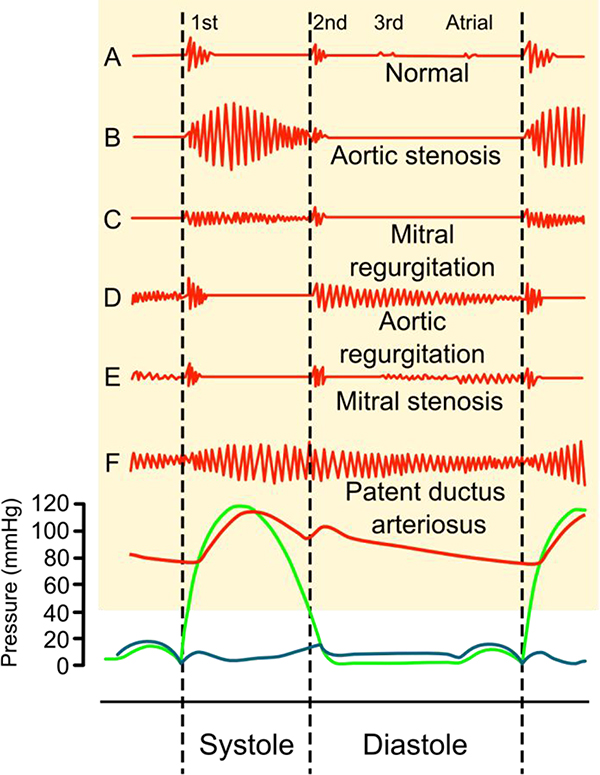
Fundamental heart sounds (FHSs) usually include the first (S1) and second (S2) heart sounds (Leatham, 1975). S1 occurs at the beginning of isovolumetric ventricular contraction, when already closed mitral and tricuspid valves suddenly reach their elastic limit due to the rapid increase in pressure within the ventricles. S2 occurs at the beginning of diastole with the closure of the aortic and pulmonic valves (See Figure 1.) While the FHSs are the most recognizable sounds of the heart cycle, the mechanical activity of the heart may also cause other audible sounds, such as the third heart sound (S3), the fourth heart sound (S4), systolic ejection click (EC), mid-systolic click (MC), the diastolic sound or opening snap (OS), as well as heart murmurs caused by turbulent, high-velocity flow of blood.

Figure 1.

Phonocardiograms (above) from normal and abnormal heart sounds with pressure diagrams (below). Red indicates aortic pressure, green ventricular pressure and blue atrial pressure. Reproduced under the CC BY-SA 3.0 license and adapted from (Madhero, 2010).

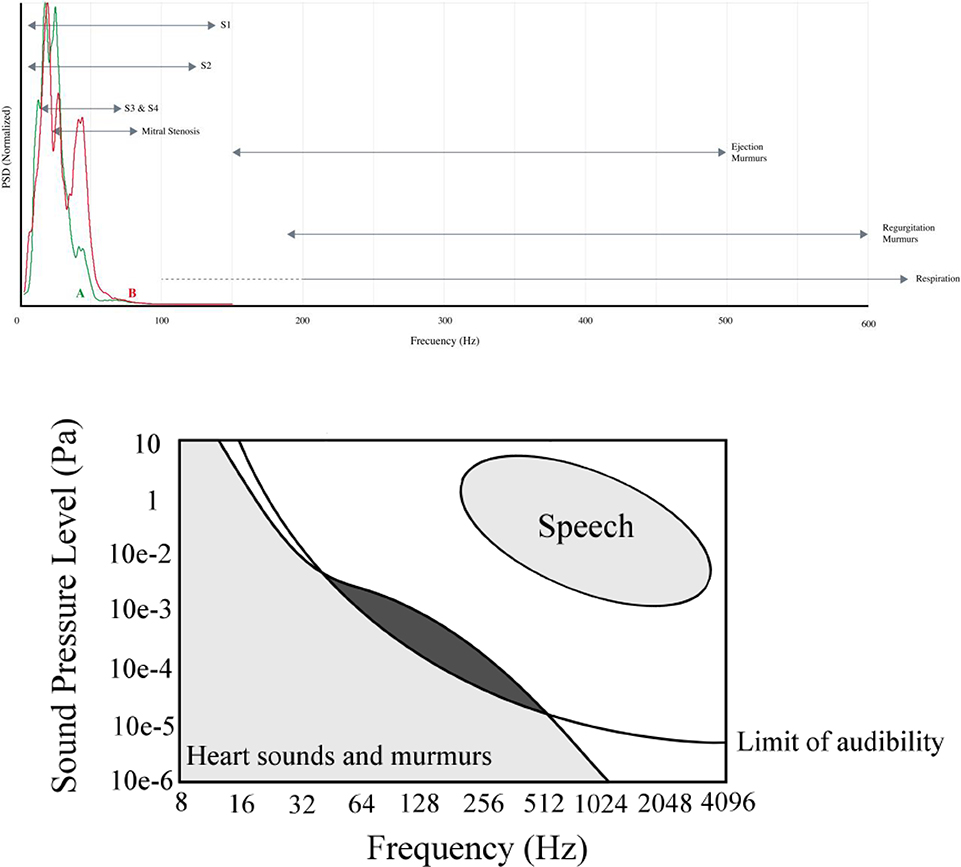
The spectral properties of heart sounds and PCG recording artifacts have been well described (Leatham, 1975). In particular, the first, second and third heart sounds overlap with each other and several conditions (see Figure 2). Similarly, murmurs and artifacts from respiration and other non-physiological events overlap significantly in the frequency domain. This makes the separation of heart sounds from each other, and from abnormal sounds or artifacts impossible in the frequency domain. The similarity of the noise to normal and abnormal heart sounds makes identification of the latter also extremely difficult in the time domain.

Figure 2.

General spectral regions for different heart sounds, and other physiological sounds during heart sound recordings. Adapted from (Springer, 2015; Leatham, 1975).

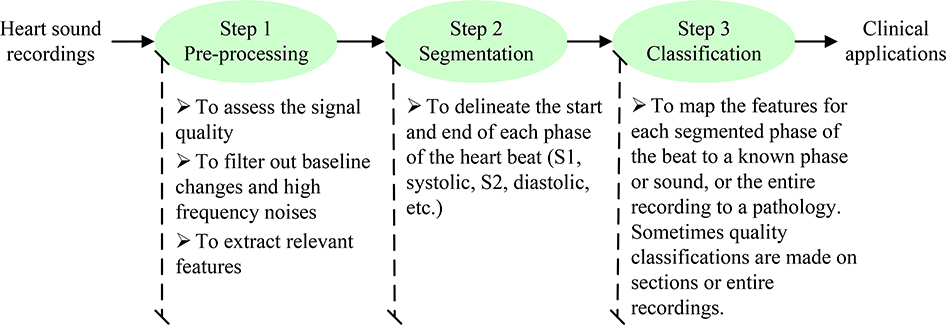
Automated analysis of the heart sound in clinical applications usually consists of three steps shown in Figure 3; pre-processing, segmentation and classification. Over the past few decades, methods for automated segmentation and classification of heart sounds have been widely studied. Many methods have demonstrated potential to accurately detect pathologies in clinical applications. Unfortunately, comparisons between techniques have been hindered by the lack of high-quality, rigorously validated, and standardized databases of heart sound signals obtained from a variety of healthy and pathological conditions. In many cases, both experimental and clinical data are collected at considerable expense, but only analyzed once by their collectors and then filed away indefinitely, because funding climates change, and collaborators move on. Moreover, the activation energy needed to document data for external use, store and share data in a semi-permanent manner is rarely available at the end of a research project.

Figure 3.

Typical three steps for automated analysis of heart sound in clinical applications.

The PhysioNet/Computing in Cardiology Challenge 2016 (PhysioNet/CinC Challenge 2016) attempts to address some of these issues by assembling the research community to contribute multiple promising databases. Prior to the PhysioNet/CinC Challenge 2016 there were only three public heart sound databases available: i) The Michigan Heart Sound and Murmur database (UMHS), ii) The PASCAL database (Bentley et al., 2011) and iii) The Cardiac Auscultation of Heart Murmurs database (eGeneralMedical). These three databases can be summarized as follows:

• The Michigan Heart Sound and Murmur database (MHSDB) was provided by the University of Michigan Health System. It includes only 23 heart sound recordings with a total of time length of 1496.8 s and is available from http://www.med.umich.edu/lrc/psb/heartsounds/index.htm

• The PASCAL database comprises 176 recordings for heart sound segmentation and 656 recordings for heart sound classification. Although the number of the recordings is relatively large, the recordings have the limited time length from 1 s to 30 s. They also have a limited frequency range below 195 Hz due to the applied low-pass filter, which removes many of the useful heart sound components for clinical diagnosis. It is available from http://www.peterjbentlev.com/heartchallenge

• The Cardiac Auscultation of Heart Murmurs database is provided by eGeneral Medical Inc., includes 64 recordings. It is not open and requires payment for access from: http://www.egeneralmedical.com/listohearmur.html

It is important to note that these three databases are limited by the recording number, length or signal frequency range. In addition, two of these databases are intended to teach medical students auscultation, and therefore comprise high-quality recordings of very pronounced murmurs, not often seen in real-world recordings. In the PhysioNet/CinC Challenge 2016, a large collection of heart sound recordings was obtained from different real-world clinical and nonclinical environments (such as in-home visits). The data include not only clean heart sounds but also very noisy recordings, providing authenticity to the challenge. The data were recorded from both normal subjects and pathological patients, and from both children and adults. Although a limited portion of the data has been held back for test purposes (Challenge scoring), much of the hidden test data will be released on PhysioNet after the conclusion of the Challenge and subsequent special issue in the Journal Physiological Measurement. The purpose of this paper is to provide a detailed description of the heart sound data that comprise the training and test sets for the PhysioNet/CinC Challenge 2016, and to help researchers improve their algorithms in the Official Phase of the Challenge.

2. Description of the assembled heart sound databases

Table 1 details the composition of the assembled heart sound database. There are a total of nine heart sound databases collected independently by seven different research teams from seven countries and three continents, over a period of more than a decade. As a result, the hardware, recording locations, data quality and patient types differ substantially, and the methods for identifying gold standard diagnoses also vary. A description of each composite database is now given. The acoustic data were saved in either the text format or the .wav format.

Table 1.

Detailed profiles for the assembled heart sound databases for the 2016 PhysioNet/CinC Challenge.

Database	Subject type	Subject number	Age	Gender (F/M)	Recording position	Recording state	Recording number	Recording length (s)	Simultaneous signal	Sample rate	Sensor	Sensor frequency bandwidth
MITHSDB	Normal	38	unknown	unknown	Nine different recording positions	Recorded in-home visits or in hospital, uncontrolled recording environment	117	33±5	One PCG One ECG	44,100 Hz	Welch Allyn Meditron electronic stethoscope	20 Hz – 20 kHz
	MVP	37					134
	Benign	34					118
	AD	5					17
	MPC	7					23
AADHSDB	Normal	121	unknown	58/93	Tricuspid area	Rest	544	8	One PCG	4,000 Hz	3M Littmann E4000	20 Hz – 1,000 Hz
	CAD	30					151
AUTHHSDB	Normal	11	29±8	5/6	Apex	Rest	11	47±25	Two PCGs	4,000 Hz	Welch Allyn Meditron electronic stethoscope	unknown
	MR	17	75±7	12/5	Auscultation		17	60±30
	AS	17	76±10	11/6	positions		17	43±21
TUTHSDB	Normal	28	unknown	unknown	Four typical auscultation positions	Rest	174	15	One PCG	4,000 Hz	unknown	unknown
	Pathologic	16
UHAHSDB	Normal: NHC	19	18–40	unknown	unknown	Rest	19	14±5	One PCG	8,000 Hz	Prototype (Infral Corporation)	unknown
	Normal: MARS500	6	unknown	unknown			20	10±3
	Pathologic	30	44–90	10/20			40	16±9
DLUTHSDB	Normal	174	25±3	2/172	Multi-position at chest	Rest or after exercise	338	209±78	PCG, PPG, RESP	ECG, 800 Hz and – 22,050 Hz	MLT201 or piezoelectric sensor	unknown
	CAD	335	60±12	227/108	Mitral	Rest	335	17±12	One PCG	8,000 Hz	3M Littmann	1–1,000 Hz
SUAHSDB	Normal	79	56±16	69/43	Apex	Rest	81	33±5	One PCG	8,000 Hz	JABES electronic stethoscope	20–1000 Hz
	Pathologic	33					33
SSHHSDB	Normal	12	unknown	unknown	2th intercostal	Rest	12	36±12	One PCG	8,000 Hz	unknown	unknown
	Pathological	23					23
SUFHSDB	Fetal	116	--	--	Maternal abdomen	Rest	119	90	One PCG	8,000 Hz, 44,100	JABES electronic stethoscope	20–1000 Hz
	Maternal	109	29±6	109/0	unknown	Rest	92	90	One PCG
										Hz
Total	--	1,297	--	--	--	--	2,435	--	--	--	--	--

Note: MIT: Massachusetts Institute of Technology, AAD: Aalborg University, AUTH: Aristotle University of Thessaloniki, TUT: K.N. Toosi University of Technology, UHA: University of Haute Alsace, DLUT: Dalian University of Technology, SU: Shiraz University, SSH: Skejby Sygehus Hospital, MVP: mitral valve prolapse, Benign: innocent or benign murmurs, AD: aortic disease, MPC: miscellaneous pathological conditions, CAD: coronary artery disease, MR: mitral regurgitation, AS: aortic stenosis, PCG: phonocardiogram, ECG: electrocardiogram, PPG: photoplethysmogram, RESP: respiratory.

2.1. MIT heart sounds database

The Massachusetts Institute of Technology heart sounds database (hereafter referred to as MITHSDB) was contributed by Prof John Guttag, Dr Zeeshan Syed and colleagues. An extensive description of the data can be found in Syed et al. (Syed, 2003; Syed et al., 2007). Heart sounds were recorded simultaneously with an electrocardiogram (ECG) using a Welch Allyn Meditron electronic stethoscope (Skaneateles Falls, New York, USA), with a frequency response of 20 Hz to 20 kHz. Both PCG and ECG signals were sampled at 44,100 Hz with 16-bit quantization. A total of 409 PCG recordings were made at nine different recording positions and orientations from 121 subjects. Each subject contributed several recordings. The subjects were divided into 5 groups: 1) normal control group: 117 recordings from 38 subjects, 2) murmurs relating to mitral valve prolapse (MVP): 134 recordings from 37 patients, 3) innocent or benign murmurs group (Benign): 118 recordings from 34 patients, 4) aortic disease (AD): 17 recordings from 5 patients, and 5) other miscellaneous pathological conditions (MPC): 23 recordings from 7 patients. The diagnosis for each patient was verified through echocardiographic examination at the Massachusetts General Hospital, Boston, MA, USA. These recordings were either performed during in-home visits or in the hospital, and were performed in an uncontrolled environment, resulting in many of the recordings being corrupted by various sources of noise, such as talking, dogs barking and children playing. Other noise sources included stethoscope motion, breathing and intestinal sounds. The recording length varied from 9 s to 37 s, with mean and standard deviation (SD) of 33±5 s. For the purposes of the competition, the ECGs were extracted and stored in a WFDB-compliant format.

2.2. AAD heart sounds database

The Aalborg University heart sounds database (AADHSDB) was contributed by Dr. Samuel E. Schmidt and colleagues (Schmidt et al., 2010a; Schmidt et al., 2015; Schmidt et al., 2010b). Heart sound recordings were made from the 4th intercostal space at the left sternal border on the chest of subjects using a Littmann E4000 electronic stethoscope (3M, Maplewood, Minnesota). The frequency response of the stethoscope was 20 to 1,000 Hz. The sample rate was 4,000 Hz with 16-bit quantization. A total of 151 subjects were recorded from patients were referred for coronary angiography at the Cardiology Department at Aalborg Hospital, Denmark. The aim of the study was diagnosis of CAD from heart sound, however in the current database normal and abnormal are defined base on if the patient has a heart valve defect either identified in the patient record or identified by a clear systolic or diastolic murmur. A total of 30 subjects had heart valve defect and where defined as abnormal. Patients were asked to breathe normally during the heart sound acquisition and between one and six PCG recordings were collected from each subject, resulting in a total of 695 recordings. Most of the recordings have a fixed time length of 8 s while a few recordings have a time length less than 8 s.

2.3. AUTHheart sounds database

The Aristotle University of Thessaloniki heart sounds database (AUTHHSDB) was contributed by Dr. Chrysa D. Papadaniil and colleagues (Papadaniil and Hadjileontiadis, 2014). Heart sounds were recorded in the first Cardiac Clinic of Papanikolaou General Hospital in Thessaloniki, Greece, using AUDIOSCOPE, a custom-made electronic stethoscope that records signals amplified and unfiltered. The sample rate was 4,000 Hz with 16-bit quantization. Forty-five subjects were enrolled within an age range of 18–95 years; in particular, 11 normal subjects, 17 patients with aortic stenosis (AS) and 17 patients with mitral regurgitation (MR). The diagnosis and the severity of the heart valve diseases were determined by the doctors, based on the echocardiogram of the patient. The recordings were recorded from the auscultation position of the chest where the murmur is best heard for each valve dysfunction, while the normal heart sounds were recorded from the apex. Each subject gave one PCG recording (total 45 recordings) and the recordings had varied time length from 10 s to 122 s (mean±SD: 50±26 s).

2.4. TUT heart sounds database

The K. N. Toosi University of Technology heart sounds database (TUTHSDB) was contributed by Dr. Hosein Naseri (Naseri and Homaeinezhad, 2013; Naseri et al., 2013). It includes a total of 28 healthy volunteers and 16 patients with different types of valve diseases. The actual diagnoses were determined by echocardiography prior to recording of PCG signals. PCG signals were recorded by using an electronic stethoscope (3M Littmanns 3200) at four different locations (not simultaneously): pulmonic, aortic, tricuspid and apex at a sampling rate of 4,000 Hz with 16-bit amplitude resolution for exactly 15 s each. Two subjects only had 3 PCG recordings, resulting in a total of 174 PCG recordings.

2.5. UHA heart sounds database

The University of Haute Alsace heart sounds database (UHAHSDB) was contributed by Dr. Ali Moukadema (Moukadem et al., 2013; Moukadem et al., 2011). Heart sound signals were recorded using prototype stethoscopes produced by Infral Corporation (Strasbourg, France). The sample rate was 8,000 Hz with 16-bit quantization. The dataset contains total 79 PCG recordings, including 39 normal sounds and 40 pathological cardiac sounds. The normal sound recordings were separated into two sub-files: ‘NHC’ (19 recordings) and ‘MARS500’ (20 recordings). ‘NHC’ recordings were collected from 19 normal subjects, aged from 18 to 40 years. The recording length varied from 7 s to 29 s (mean±SD: 14±5 s). ‘MARS500’ recordings were collected from 6 volunteers (astronauts), dedicating to the Cardio-Psy experience as a part of the MARS500 project (IBMP-Russia) promoted by European Spatial Agency. The recording length varied from 7 s to 17 s (mean±SD: 10±3 s). The pathologic recordings were from 30 patients (10 female and 20 male), who were recruited during hospitalization in the Hospital of Strasbourg. They were aged from 44 to 90 years. Ten of them were recorded twice generally before and after valvular surgery. The diagnoses of the pathologic patients were made by an experienced cardiologist using additional information from the ECG and echocardiography-Doppler. Among 30 patients, 9 patients had prosthetic valves with 1 bioprosthesis, 4 patients had double prostheses (in aortic and mitral positions), and the other patients presented rhythm disturbances (ventricular extra systoles, AV block and tachyarrhythmia) in the context of ischemic cardiomyopathy. The recordings varied in length from 6 s to 49 s (mean±SD: 16±9 s).

2.6. DLUTheart sounds database

The Dalian University of Technology heart sounds database (DLUTHSDB) was contributed by Dr. Hong Tang (Li et al., 2011; Tang et al., 2010a; Tang et al., 2010b; Tang et al., 2012). Subjects included 174 healthy volunteers (2 female and 172 male, aged from 4 to 35 years, mean±SD: 25±3 years) and 335 CAD patients (227 female and 108 male, aged from 10 to 88 years, mean±SD: 60±12 years). Heart sounds from the CAD patients were recorded in the Second Hospital of Dalian Medical University using an electronic stethoscope (3M Littmann). CAD patients were confirmed based on the cardiologist’s diagnosis. Only PCG signals were available and all of them were collected from the mitral position at the chest. Data were saved in the .wav format using a sampling rate of 8,000 Hz with 16-bit quantization. Each patient provided one PCG recording and there were a total of 335 recordings. The recording length varied from about 3 s to 98 s (mean±SD: 17±12 s). Heart sound signals from the healthy volunteers were recorded using a microphone sensor (MLT201, ADinstrument, Australia) or a piezoelectric sensor (Xinhangxingye Technology Co. Lt., China) at the Biomedical Engineering Lab in DLUT, China. Each subject contributed one or several recordings and a total of 338 recordings were collected. Recordings included either a single channel (PCG) or several channels (PCG combined with ECG, photoplethysmogram or respiratory signals). ECG signals were the standard lead-II ECG. Photoplethysmogram signals were recorded from the carotid artery or finger. Respiratory signals were collected using a MLT1132 belt transducer (ADinstrument, Australia) to record chest movement. The recording lengths varied from about 27.5 s to 312.5 s (mean±SD: 209±78 s). Various sampling rates were used (800 Hz, 1,000 Hz, 2,000 Hz, 3,000Hz, 4,000 Hz, 8,000 Hz or 22,050 Hz) depending on different research aims. All 338 recordings could be separated into two sub-types: recordings during rest (218 recordings) where the subjects were in peaceful calm states, and recordings during non-resting states (120 recordings). Non-resting recordings were collected immediately after step climbing (116 recordings), during cycles of breath holding (3 recordings), and after the bike cycling (1 recording).

2.7. SUA heart sounds database

The Shiraz University adult heart sounds database (SUAHSDB) was contributed by Dr. Reza Sameni and colleagues (Samieinasab and Sameni, 2015). This database was constructed using recordings made from 79 healthy subjects and 33 patients (total 69 female and 43 male, aged from 16 to 88 years, mean±SD: 56±16 years). The JABES digital electronic stethoscope (GS Technology Co. Ltd., South Korea) was used, placed on the chest, commonly above the apex region of the heart. The Audacity cross-platform audio software was used for recording and editing the signals on a PC. The subjects were asked to relax and breathe normally during the recording session. The database consists of 114 recordings (each subject/patient had one heart sound signal but one healthy subject had three), resulting in 81 normal recordings and 33 pathological recordings. The recording length varied from approximately 30 s to 60 s (mean±SD: 33±5 s). The sampling rate was 8,000 Hz with 16-bit quantization except for three recordings at 44,100 Hz and one at 384,000 Hz. The data were recorded in wideband mode of the digital stethoscope, with a frequency response of 20 Hz to 1 kHz.

2.8. SUF heart sounds database

The Shiraz University fetal heart sounds database (SUFHSDB) was also contributed by Dr. Reza Sameni and colleagues (Samieinasab and Sameni, 2015). This database was constructed using recordings made from 109 pregnant women (mothers aged from 16 to 47 years, mean±SD: 29±6 years with BMI from 19.5 to 38.9, mean±SD: 29.2±4.0). The JABES digital electronic stethoscope (GS Technology Co. Ltd., South Korea) was used, and placed on the lower maternal abdomen as described in (Samieinasab and Sameni, 2015). In the case of twins (seven cases) the data were collected twice according to the locations advised by the expert gynecologist. The Audacity cross-platform audio software was used for recording and editing the signals on a PC. In total, 99 subjects had one signal recorded, three subjects had two and seven cases of twins were recorded individually, resulting in 119 total recordings. The average duration of each record was about 90 seconds. The sampling rate was generally 8,000 Hz with 16-bit quantization and a few recordings were sampled at 44,100 Hz. The data were recorded in wideband mode of the digital stethoscope, with a frequency response of 20 Hz to 1 kHz. In most cases (91 subjects), the heart sounds of the mothers were also recorded before each fetal PCG recording session. As a result, a total number of 92 maternal heart sounds data (90 subjects had one heart sound signal but one had two signals recorded) are also available in the dataset.

2.9. SSH heart sounds database

The Skejby Sygehus Hospital heart sounds database (SSHHSDB) was assembled from patients referred to Skejby Sygehus Hospital, Denmark. It comprises 35 recordings from 12 normal subjects and 23 pathological patients with heart valve defect. All recordings are obtained from the 2nd intercostal room just right to sternum. The recording length varied from approximately 15 s to 69 s (mean±SD: 36±12 s) and the sampling rate was 8,000 Hz.

3. Brief review on heart sound segmentation methods

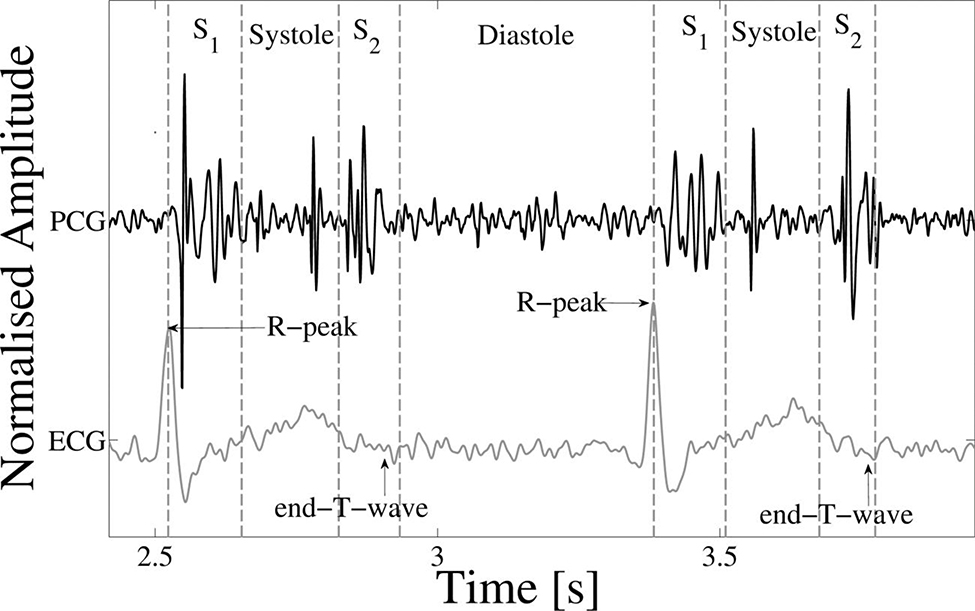
The segmentation of the FHSs is a first step in the automatic analysis of heart sounds. The accurate localization of the FHSs is a prerequisite for the identification of the systolic or diastolic regions, allowing the subsequent classification of pathological situations in these regions (Liang et al., 1997b; Springer, 2015; Springer et al., 2014). S1 is initiated by the closure of the atrioventricular valves at the beginning of the systole and occurs immediately after the R-peak (ventricular depolarization) of the ECG. S2 is initiated by the closure of the semilunar valves at the beginning of the diastole and occurs at approximately at the end-T-wave of the ECG (the end of ventricular depolarization). The time order of these features in ECG and PCG is shown in Figure 4 (Springer, 2015). In clinical practice, the criteria adopted by the cardiologist to annote the beginning and the ending of each sound was to define: the Mitral closure initiating S1 with high frequency vibration, the aortic closure generating the high frequencies beginning S2 and the end of S1 and S2 are annotated by the end of the high amplitude vibrations (Moukadem et al., 2013).

Figure 4.

Example of an ECG-labelled PCG, with the ECG, PCG and four states of the heart cycle (S1, systole, S2 and diastole) shown. The R-peak and end-T-wave are labelled as references for defining the approximate positions of S1 and S2 respectively. Mid-systolic clicks, typical of mitral valve prolapse, can be seen. Adapted from (Springer, 2015).

Many methods of heart sound segmentation have been studied over the past few decades. The typical methods can be classified into four types: the first type is envelope-based method, i.e., using a variety of techniques to construct the envelopes of heart sound and thus to perform the heart sound segmentation; the second one is feature-based method, i.e., by calculating the features of heart sounds to segment the signal; the third one is the machine learning method and the last one, also as the state-of-the-art method, is hidden Markov model (HMM) method. We will give a brief summary for the aforementioned four types of heart sound segmentation methods. The size of the database of subjects and recordings used in each study, as well as the numerical results, will be also presented (see Table 2).

Table 2.

Summary of the major heart sound segmentation works. Se: sensitivity, P+: positive predictivity and Acc: accuracy.

Author	Subject type	Subject number	Recording number	Recording length	Cycle number	Sample rate (Hz)	Segmentation results
							Se (%)	P+ (%)	Acc (%)
Envelope-based method
(Liang et al., 1997a)	Normal and pathological children	--	37	Each 7–12 s	515	11,025	--	--	93
(Liang et al., 1997b)	Normal and pathological children	--	77	Each 6–13 s	1,165	11,025	--	--	93
(Moukadem et al., 2013)	Normal	--	80	Each 6–12 s	--	8,000	96	95	--
	Pathological						97	95	--
(Sun et al., 2014)	Normal	45	--	Total 600 s	--	44,100	--	--	96.69
	Pathological	76		Total 7,730 s
	MHSDB	--	23	Total 1,497 s
(Choi and Jiang, 2008)	Normal	--	--	--	500	--	--	--	100
	Pathological						--	--	88.2
(Yan et al., 2010)	Normal and pathological	--	9	Each < 5 s	--	--	--	--	99.0
(Ari et al., 2008)	Normal and pathological	71	71	--	357	Varied	--	--	97.47
Feature-based method
(Naseri and Homaeinezhad, 2013)	Pathological	--	--	Total 42 min	--	4,000	99.00	98.60	--
(Kumar et al., 2006)	Pathological	55	55	Each < 120 s	7,530	44,100	97.95	98.20	--
(Varghees and Ramachandran, 2014)	Normal and pathological	--	64	Each < 10 s	701	Varied	99.43	93.56	--
(Pedrosa et al., 2014)	Pathological adults and PASCAL database	72	72	Each 60 s	--	--	89.2	98.6	--
(Vepa et al., 2008)	Normal and pathological	--	--	--	166	--	--	--	84.0
(Papadaniil and Hadjileontiadis, 2014)	Normal and pathological	43	43	--	2,602	44,100	--	--	83.05
(Gharehbaghi et al., 2011)	Normal and pathological children	120	120	Each 10 s	1,976	44,100	--	--	S1: 97 S2: 94
Machine learning method
(Oskiper and Watrous, 2002)	Normal	30	--	Each 20 s	--	--	--	--	S1 96.2
(Sepehri et al., 2010)	Normal and pathological children	60	120	Total 1,200 s	--	--	--	--	93.6
(Chen et al., 2009)	Normal	--	27	Each 30 s	997	--	92.1	88.4	--
(Gupta et al., 2007)	Normal and pathological	--	41	--	340	8,000	--	--	90.29
(Tang et al., 2012)	Normal	3	3	--	565	2,000	--	--	S1 94.9 S2 95.9
	Pathological	23	23
(Rajan et al., 2006)	Normal and pathological	42	42	Each 13 s	--	--	--	--	90.5
Hidden Markov Model (HMM) methods
(Gamero and Watrous, 2003)	Normal	80	80	Each 20 s	--	11,000	95	97	--
(Ricke et al., 2005)	--	9	9	--	--	997	--	--	98
(Gill et al., 2005)	Normal	17	44	Each 30–60 s	--	4,000	S1:98.6 S2:98.3	S1:96.9 S2:96.5	--
(Sedighian et al., 2014)	PASCAL database	--	84	Total 416 s	S1: 639 S2: 626	4,000	--	--	S1: 92.4 S2: 93.5
(Castro et al., 2013)	PASCAL database	--	84	Total 416 s	S1: 639 S2: 630	4,000	--	--	S1: 90.9 S2: 933
(Schmidt et al., 2010a)	Normal and pathological	--	113	Each 8 s	--	4,000	98.8	98.6	--
(Springer et al., 2015)	Normal and pathological	112	--	Total 10,172 s	S1: 12,181 S2: 11,627	Varied	--	--	F1 score 95.63

3.1. Envelope-based methods

Shannon energy envelope is the most used envelope for PCG envelope extraction. Liang et al proposed a normalized average Shannon energy envelope (Liang et al., 1997a), which emphasized the medium-intensity sounds while attenuating the low-intensity components. The performance of this method was evaluated using 515 PCG cycles from 37 recordings acquired from children with murmurs and achieved 93% accuracy for PCG segmentation. Another study from Liang et al employed wavelet decomposition before estimation of the Shannon envelope and segmented heart sound into four parts: S1, systole, S2 and diastole (Liang et al., 1997b). This method was evaluated using 1,165 cardiac cycles and got an improved accuracy from 84% to 93% on a noisy 77 recordings including both normal and abnormal heart sounds. Moukadem et al proposed a method to calculate the Shannon energy envelope of the local spectrum calculated by the S-transform for each sample of heart sound signal. This method was evaluated on 40 normal and 40 pathological heart sound recordings. The sensitivity and positive predictivity were both higher than 95% for normal and pathological heart sound segmentation (Moukadem et al., 2013).

Envelope extraction based on Hilbert transform can be divided into two aspects: 1) the envelope is the decimated signal of the real part of a complex analytic signal, and 2) the instantaneous frequency is the derivative of the imaginary part of complex analytic signal. Sun et al proposed an automatic segmentation method based on Hilbert transform (Sun et al., 2014). This method considered the characteristics of envelopes near the peaks of S1, the peaks of S2, the transmission points T12 from S1 to S2, and the transmission points T21 from S2 to S1. It was validated using 7,730 s of heart sounds from pathological patients, 600 s from normal subjects, and 1496.8 s from Michigan MHSDB database. For the sounds where S1 cannot be separated from S2, an average accuracy of 96.69% was achieved. For the sounds where S1 can be separated from S2, an average accuracy of 97.37% was achieved.

Jiang and Choi proposed an envelope extraction method named cardiac sound characteristic waveform (CSCW) (Jiang and Choi, 2006). However, they only reported the example figures without reporting any quantitative results. In their following study, they compared this CSCW method with other two popular envelope-based methods: Shannon energy and Hilbert transform envelopes, and found the CSCW method to be superior to both of these, concluding that their method led to more accurate segmentation results: 100% and 88.2% on normal and pathological patients respectively, as compared to 78.2% and 89.4% for the Shannon energy envelope and 51.4% and 47.3% for the Hilbert transform envelope (Choi and Jiang, 2008). However, these results were only evaluated on 500 selected cardiac cycles without a split between their training and test sets. Yan et al also used a similar characteristic moment waveform envelope method for segmenting heart sound (Yan et al., 2010). This method was only evaluated on a small dataset of 9 recordings and reported an accuracy of 99.0%, again without a train-test split.

A simple squared-energy envelope was proposed by Ari et al (Ari et al., 2008). It is primarily based on the use of frequency content present in the signal, calculation of energy in time windows and timing relations of signal components. It was shown to have a better performance than Shannon energy envelope when employing a threshold-based detection method. Testing on a total of 357 cycles from 71 recordings showed the segmentation accuracy is 97.47% (without a train-test split).

3.2. Feature-based methods

Naseri and Homaeinezhad used frequency- and amplitude-based features, and then employed a synthetic decision making algorithm for heart sound segmentation (Naseri and Homaeinezhad, 2013). The proposed method was applied to 52 PCG signals gathered from patients with different valve diseases and achieved an average sensitivity of 99.00% and positive predictivity of 98.60%. Kumar et al proposed a detection method based on a high frequency feature, which is extracted from the heart sound using the fast wavelet decomposition (Kumar et al., 2006). This feature is physiologically motivated by the accentuated pressure differences found across heart valves, both in native and prosthetic valves. The method was validated on patients with mechanical and bioprosthetic heart valve implants in different locations, as well as with patients with native valves, and achieved an averaged sensitivity of 97.95% and positive predictivity of 98.20%.

Varghees and Ramachandran used an instantaneous phase feature from the analytical signal after calculating the Shannon entropy (Varghees and Ramachandran, 2014). This method is a quite straightforward approach that does not use any search-back steps. It was tested using both clean and noisy PCG signals with both normal and pathological heart sounds (701 cycles), and achieved an average sensitivity of 99.43% and positive predictivity of 93.56% without a train-test split. Pedrosa et al used periodic component features from the analysis signal of the autocorrelation function to segment heart sound signal (Pedrosa et al., 2014). Their method was tested on 72 recordings and had sensitivity and positive predictivity of 89.2% and 98.6% respectively.

Unlike using the absolute amplitude or frequency characteristics of heart sounds, Nigam and Priemer used complexity-based features by utilizing the underlying complexity of the dynamical heart sound for PCG segmentation and this method showed good performance on the synthetic data (Nigam and Priemer, 2005). However, this study did not provide any quantitative results for evaluation. Vepa et al also used complexity-based features for heart sound segmentation, which combined energy-based and simplicity-based features computed from multi-level wavelet decomposition coefficients (Vepa et al., 2008). The method was evaluated on only 166 cycles and achieved an accuracy of 84.0%.

Papadaniil and Hadjileontiadis employed kurtosis-based features alongside ensemble empirical mode decomposition to select non-Gaussian intrinsic mode functions (IMFs), and then detected the start and end positions of heart sounds within the selected IMFs (Papadaniil and Hadjileontiadis, 2014). The method was tested on 11 normal subjects and 32 pathological patients, and achieved an accuracy of 83.05%. In addition, an ECG-referred pediatric heart sound segmentation method was proposed in (Gharehbaghi et al., 2011). This algorithm was applied on 120 recordings of normal and pathological children, totally containing 1,976 cardiac cycles, and achieved accuracy of 97% for S1 and 94% for S2.

3.3. Machine learning methods

Neural network technology is widely used as a typical machine learning method for heart sound segmentation. Oskiper and Watrous proposed a time-delay neural network method for detecting the S1 sound (Oskiper and Watrous, 2002). The method consists of a single hidden layer network, with time-delay links connecting the hidden units to the time-frequency energy coefficients of Morlet wavelet decomposition. The results tested on 30 healthy subjects (without a train-test split) showed an accuracy of 96.2%. Sepehri et al used a multi-layer perceptron neural network classifier for heart sound segmentation, which paid special attention to the physiological effects of respiration on pediatric heart sounds (Sepehri et al., 2010). A total of 823 cycles from 40 recordings of normal children and 80 recordings of children with congenital heart diseases were tested and an accuracy of 93.6% was achieved when splitting the recordings equally between training and test datasets.

K-means clustering is another widely used method. Chen et al used a K-means clustering and a threshold method to identify the heart sounds, achieving 92.1% sensitivity and 88.4% positive predictivity tested on 27 recordings from healthy subjects (Chen et al., 2009). Gupta et al also used K-means clustering combined with homomorphic filtering for segmenting heart sounds into single cardiac cycle (S1-systole-S2-diastole) (Gupta et al., 2007). This method was tested on 340 cycles and achieved an accuracy of 90.29%. Tang et al employed dynamic clustering for segmenting heart sounds (Tang et al., 2012). In this method, the heart sound signal was first separated into cardiac cycles based on the instantaneous cycle frequency and then was decomposed into time-frequency atoms, and finally the atoms of heart sounds were clustered in time-frequency plane allowing the classification of S1 and S2. The results tested on 25 subjects showed an accuracy of 94.9% for S1 and 95.9% for S2.

Rajan et al developed an unsupervised segmentation method by first using Morlet wavelet decomposition to obtain a time-scale representation of the heart sounds and then using an energy profile of the time-scale representation and a singular value decomposition technique to identify heart sound segments (Rajan et al., 2006). This method was tested on a dataset of 42 adult patients and achieved an accuracy of 90.5%.

3.4. Hidden Markov Model (HMM) methods

Gamero and Watrous proposed an HMM-based methodology, which employed a probabilistic finite state-machine to model systolic and diastolic interval duration (Gamero and Watrous, 2003). The detection of S1 and S2 was performed using a network of two HMM with grammar constraints to parse the sequence of systolic and diastolic intervals. Results were evaluated on 80 subjects and a sensitivity of 95% and a positive predictivity of 97% were achieved (without a train-test split). Ricke et al also used an HMM method for segmenting heart sounds into four components (S1-systole-S2-diastole), and achieved an accuracy of 98% when using eight-fold cross-validation (Ricke et al., 2005). However, this study was only performed on a relative small subject size of 9.

Gill et al were the first researchers to incorporate timing durations within the HMM method for heart sound segmentation (Gill et al., 2005). In their method, homomorphic filtering was first performed and then sequences of features were extracted to be used as observations within the HMM. Evaluation on 44 PCG recordings taken from 17 subjects showed that for S1 detection, sensitivity and positive predictivity were 98.6% and 96.9% respectively, and for S2 detection, they were 98.3% and 96.5% respectively. Sedighian et al (Sedighian et al., 2014) also used homomorphic filtering and an HMM method on the PASCAL database (Bentley et al., 2011) and obtained an average accuracy of 92.4% for S1 segmentation and 93.5% for S2 segmentation. By comparison, Costra et al (Castro et al., 2013) used the wavelet analysis on the same database and achieved an average accuracy of 90.9% for S1 segmentation and 93.3% for S2 segmentation.

Schmidt et al were the first researchers to explicitly model the expected duration of heart sounds within the HMM using a hidden semi-Markov model (HSMM) (Schmidt et al., 2010a). They first hand-labelled the positions of the S1 and S2 sounds in 113 recordings, and then used the average duration of these sounds and autocorrelation analysis of systolic and diastolic durations to derive Gaussian distributions for the expected duration of each of the four states, i.e., S1, systole, S2 and diastole. The employed features were the homomorphic envelope and three frequency band features (25–50, 50–100 and 100–150 Hz). These features, along with the hand-labelled positions of the states, were used to derive Gaussian distribution-based emission probabilities for the HMM. The duration distributions were then incorporated into the forward and backward paths of the Viterbi algorithm. The results on the separate test set were 98.8% sensitivity and 98.6% positive predictivity.

Based on Schmidt et al’s work (Schmidt et al., 2010a), Springer et al used the HSMM method and extended it with the use of logistic regression for emission probability estimation, to address the problem of accurate segmentation of noisy, real-world heart sound recordings (Springer et al., 2015). Meanwhile, a modified Viterbi algorithm for decoding the most-likely sequence of states was also implemented. This method is regarded as the state-of-the-art method in heart sound segmentation studies. It was evaluated on a large dataset of 10,172 s of heart sounds recorded from 112 patients and achieved an average F1 score of 95.63% on a separate test dataset, significantly improving upon the highest score of 86.28% achieved by the other reported methods in the literature when evaluated on the same test data.

4. Brief review on heart sound classification methods

The automated classification of pathology in heart sounds has been described in the literature for over 50 years, but accurate diagnosis remains a significant challenge. Gerbarg et al (Gerbarg et al., 1963) were the first to publish on the automatic classification of pathology in heart sounds, (specifically to aid the identification of children with rheumatic heart disease) and used a threshold-based method. The typical methods for heart sound classification can be grouped into four categories: 1) artificial neural network-based classification; 2) support vector machine-based classification; 3) hidden Markov model-based classification and 4) clustering-based classification. The current prominent works in this field are summarized in Table 3. The important notes about the evaluation of the method, such as whether the data was split into training and test sets, are also reported. For relative brevity, only the notable studies with sizeable datasets are summarized in detail below.

Table 3.

Summary of the previous heart sound classification works. Se: sensitivity, Sp: specificity and Acc: accuracy.

Author	Database	Recording length	Classification method	Features	Se (%)	Sp (%)	Acc (%)	Notes on database
(Akay et al., 1994)	42 normal and 72 CAD patients	Each 10 cycles	ANN	Wavelet	85	89	86	30 training, 82 test
(Liang and Hartimo, 1998)	40 normal and 45 pathological children	Each 7–12 s	ANN	Wavelet	80	90	85	65 training, 20 test
(Uguz, 2012a)	40 normal, 40 pulmonary and 40 mitral stenosis	--	ANN	Wavelet	100	95.24	98.33	50–50 train-test split
(Bhatikar et al., 2005)	88 innocent murmurs and 153 pathological murmurs	Each 10–15 s	ANN	Frequency	83	90	--	188 training, 53 test
(Sepehri et al., 2008)	36 normal and 54 pathological	Each 10 s	ANN	Frequency	95	93.33	--	40 training, 50 test
(Ahlstrom et al., 2006)	7 normal, 23 aortic stenosis and 6 mitral regurgitation	Each 12 cycles	ANN	Complexity	--	--	86	Cross-validation
(De Vos and Blanckenberg, 2007)	113 normal and 50 pathological	Each 6 cycles	ANN	Time-frequency	90	96.5	--	Cross-validation
(Uguz, 2012b)	40 normal, 40 pulmonary and 40 mitral stenosis	--	ANN	Time-frequency	90.48	97.44	95	50–50 train-test split
(Ari et al., 2010)	64 patients (normal and pathological)	Each 8 cycles	SVM	Wavelet	--	--	86.72	50–50 train-test split
(Zheng et al., 2015)	40 normal and 67 pathological	--	SVM	Wavelet	93.48	98.55	97.17	Cross-validation
(Patidar et al., 2015)	Total 4,628 heart cycles, 626 normal and 4,002 pathological	--	SVM	Wavelet	98.8	99.3	98.9	80% training, 20% test
(Maglogiannis et al., 2009)	38 normal and 160 heart valve disease patients	--	SVM	Frequency	87.5	94.74	91.43	Cross-validation
(Gharehbaghi et al., 2015)	30 normal, 26 innocent and 30 aortic stenosis	Each 10 s	SVM	Frequency	86.4	89.3	--	50–50 train-test split
(Wang et al., 2007)	20 normal and 21 murmurs patients	--	HMM	Signal amplitude, STFT and MFCC	≥95.2	≥95.3	--	No separate training and test
(Chauhan et al., 2008)	20 normal and 21 murmurs patients	--	HMM	Signal amplitude, STFT and MFCC	--	--	99.21	No separate training and test
(Saracoglu, 2012)	40 normal, 40 pulmonary and 40 mitral stenosis		HMM	DFT and PCA	95	98.8	97.5	50–50 train-test split
(Bentley et al., 1998)	Unspecified size: native and prosthetic heart valves patients	--	kNN	Wavelet	--	--	100 for native and 87 for prosthetic	Cross-validation
(Quiceno-Manrique et al., 2010)	16 normal and 6 pathological	--	kNN	Time-frequency	--	--	98	Cross-validation
(Avendano-Valencia et al., 2010)	26 normal and 19 pathological	--	kNN	Time-frequency	99.56	98.45	99.0	Cross-validation

4.1. Artificial neural network-based classification

The artificial neural network (ANN) is the most widely used machine learning-based approach for heart sound classification. Unless auto-associative in nature, ANN classifiers require discriminative signal features as inputs. (Relatively little work has been performed on optimizing network architectures in this context.) Typical signal features include: wavelet features, time, frequency and complexity-based features and time-frequency features.

Wavelet-based features are most widely employed in ANN approaches to classification of heart sounds. Akay et al combined wavelet features with an ANN for the automatic detection of CAD patients (Akay et al., 1994). They computed four features (mean, variance, skewness and kurtosis) of the extracted coefficients of wavelet transform from the diastolic period of heart cycles. These features, alongside physical characteristics (sex, age, weight, blood pressure), were fed into a fuzzy neural network, and a sensitivity of 85% and a specificity of 89% on a separate test set of 82 recordings were reported. (Liang and Hartimo, 1998) employed wavelet packed decomposition with the aim of differentiating between pathological and innocent murmurs in children when using ANN classification. Eight nodes of the wavelet packet tree were selected automatically using on an information-based cost function. The cost function values then served as the feature vector. With a 65/20 patient train/test split they achieved 80% sensitivity and 90% specificity on the test data. (Uguz, 2012a). employed an ANN with the features from a discrete wavelet transform and a fuzzy logic approach to perform three-class classification: normal, pulmonary stenosis, and mitral stenosis. With a 50/50 train/test split of a dataset of 120 subjects, they reported 100% sensitivity, 95.24% specificity, and 98.33% average accuracy for the three-classes.

(Bhatikar et al., 2005) used the fast Fourier transform (FFT) to extract the energy spectrum features in frequency domain, and then used these as inputs to an ANN. Using a separate test set of 53 patients they reported 83% sensitivity and 90% specificity when differentiating between innocent and pathological murmurs. (Sepehri et al., 2008) identified the five frequency bands that led to the greatest difference in spectral energy between normal and pathological recordings and used the spectral energy in these bands as the input features for the ANN. Reported results on 50 test records were 95% sensitivity and 93.33% specificity for a binary classification. (Ahlstrom et al., 2006) assessed a range of non-linear complexity-based features that had not previously been used for murmur classification. They included up to 207 features and finally selected 14 features to present to an ANN. They reported 86% classification accuracy for a three-class problem: normal, aortic stenosis and mitral regurgitation.

(De Vos and Blanckenberg, 2007) used time-frequency features and extracted the energy in 12 frequency bins at 10 equally-spaced time intervals over each heart cycle to presents to an ANN. They reported a sensitivity and specificity of 90% and 96.5% respectively on 163 test patients (aged between 2 months and 16 years). (Uguz, 2012b) also used time-frequency as an input to an ANN. A total of 120 heart sound recordings, split 50/50 into train/test, and reported 90.48% sensitivity, 97.44% specificity and 95% accuracy for a three-class classification problem (normal, pulmonary and mitral stenosis heart valve diseases).

4.2. Support vector machine-based classification

A number of researchers have applied a support vector machine (SVM) approach to the heart sound classification in recent years. Since SVMs are another form of supervised machine learning, the features chosen are rather similar to those based on ANN approaches.

Wavelet-based features are therefore widely employed in SVM-based methods. (Ari et al., 2010) used a least square SVM (LSSVM) method for classification of normal and abnormal heart sounds based on the wavelet features. The performance of the proposed method was evaluated on 64 recordings comprising of normal and pathological cases. The LSSVM was trained and tested on a 50/50 split (32 patients in each set) and the authors reported an 86.72% accuracy on their test dataset. (Zheng et al., 2015) decomposed heart sounds using wavelet packets and then extracted the energy fraction and sample entropy as features for the SVM input. Tested on 40 normal and 67 pathological patients, they reported a 97.17% accuracy, 93.48% sensitivity and 98.55% specificity. (Patidar et al., 2015) investigated the use of the tunable-Q wavelet transform as an input to LSSVM with varying kernel functions. Testing on a dataset of 4,628 cycles from 163 heart sound recordings (and an unknown number of patients) they reported a 98.8% sensitivity and 99.3% specificity, but without stratifying patients (having mutually exclusive patients in testing and training sets), and therefore over-fitting to their data.

(Maglogiannis et al., 2009) used Shannon energy and frequency features from four frequency bands (50–250, 100–300, 150–350, 200–400 Hz) to develop an automated diagnosis system for the identification of heart valve diseases based on an SVM classifier. Testing on 38 normal and 160 heart valve disease patients they reported an 87.5% sensitivity, 94.74% specificity and 91.43% accuracy. (Gharehbaghi et al., 2015) used frequency band power over varying length frames during systole as input features and used a growing-time SVM (GTSVM) to classify pathological and innocent murmurs. When using a 50/50 train/test split (from a total of 30 patients with aortic stenosis, 26 with innocent murmurs and 30 normals), they reported 86.4% sensitivity and 89.3% specificity.

4.3. Hidden Markov model-based classification

HMM methods are not only widely employed for heart sound segmentation, but are also used for pathology classification of heart sounds. In the case of classifying pathology, the posterior probability of the heart sound signal or the extracted features given a trained HMM can be used to differentiate between healthy and pathological recordings.

(Wang et al., 2007) used a combination of HMM and mel-frequency cepstral coefficients (MFCCs) to classify heart sound signals. The feature extraction was performed using three methods: time-domain feature, short-time Fourier transforms (STFT) and MFCCs. Testing on 20 normal and 21 abnormal patients with murmurs they reported a sensitivity of 95.2% and a specificity of 95.3%. In a subsequent study, they also used MFCCs to extract representative features and developed a HMM-based method for heart sound classification (Chauhan et al., 2008). The method was applied to 1,381 cycles of real and simulated, normal and abnormal heart sounds and they reported an accuracy of 99.21%. However, both studies failed to make use of a separate test set when evaluating their classification methods and the methods are likely to be highly over-trained. (Saracoglu, 2012) applied a HMM in an unconventional manner, by fitting an HMM to the frequency spectrum extracted from entire heart cycles. The exact classification procedure of using the HMMs is unclear, but it is thought that they trained four HMMs, and then evaluated the posterior probability of the features given each model to classify the recordings. They optimized the HMM parameters and PCA-based feature selection on a training set and reported 95% sensitivity, 98.8% specificity and 97.5% accuracy on a test dataset of 60 recordings.

In summary, although HMM-based approaches are regarded as the state-of-the-art heart sound segmentation method, their potential to classify heart sounds has not yet been adequately demonstrated.

4.4. Clustering-based classification

A number of researchers have made use of the unsupervised k-nearest neighbours (kNN) algorithm to classify pathology in heart sounds. (Bentley et al., 1998) showed that discrete wavelet transform features outperformed morphological features (time and frequency features from S1 and S2) when performing heart sound classification using such a method. They used a binary kNN classifier and reported 100% and 87% accuracy when detecting pathology in patients with heart valve disease and prosthetic heart valves respectively on an unspecified sized database. (Quiceno-Manrique et al., 2010) used a simple kNN classifier with features from various time-frequency representations on a subset of 16 normal and 6 pathological patients. They reported 98% accuracy for discriminating between normal and pathologic beats. However, the kNN classifier parameters were optimized on the test set, indicating a likelihood of over-training. (Avendano-Valencia et al., 2010).also employed time-frequency features and kNN approach for classifying normal and murmur patients. In order to extract the most relevant time-frequency features, two specific approaches for dimensionality reduction were presented in their method: feature extraction by linear decomposition, and tiling partition of the time-frequency plane. The experiments were carried out using 26 normal and 19 pathological recordings and they reported an average accuracy of 99.0% when using 11-fold cross-validation with grid-based dimensionality reduction.

5. Description of the 2016 PhysioNet/CinC Challenge

5.1. Main aim

The 2016 PhysioNet/CinC Challenge aims to encourage the development of algorithms to classify heart sound recordings collected from a variety of clinical or nonclinical environments (such as in-home visits). The practical aim is to identify, from a single short recording (10–60s) from a single precordial location, whether the subject of the recording should be referred on for an expert diagnosis.

As pointed out in the above reviews, a number of studies have investigated the performances of different methods for heart sound segmentation and classification. However, many of these investigations are flawed because: 1) the studies were marred by poor methodology, often without the use of a separate test set or by allowing data from the same patient to appear in both the training and test sets, almost certainly resulting in over-fitting of the model and inflated statistics; 2) the studies did not clearly describe the database used (type of patient, size, etc.) and did not report the method/location for heart sound recording; 3) the studies tended to use hand-picked clean data in their database, used manual labels, and excluded noisy data, which leads to an algorithm that is of little use in the real world; 4) failure to use enough or a variety of heart sound recordings; and 5) failure to post the data (and any code to process the data) publicly so others may compare their results directly. The latter issue is often due to lack of time and resources, and therefore this challenge is an attempt to address both this and the aforementioned issues.

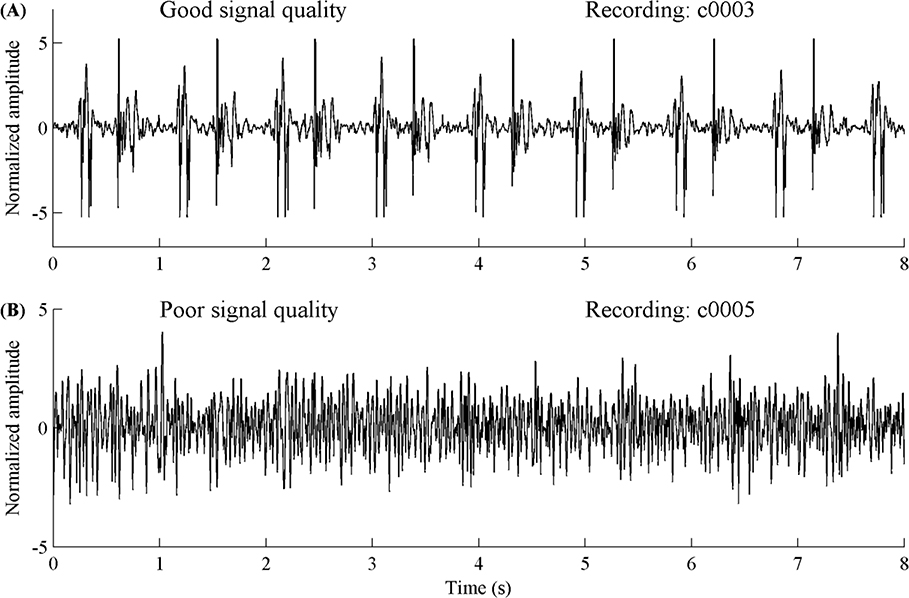
In this Challenge, we focused only on the accurate classification of normal and abnormal heart sound recordings, particularly in the context of real world (extremely noisy) recordings with low signal quality. By providing the largest public collection of heart sound recordings from a variety of clinical and nonclinical environments, the Challenge permits the challengers to develop accurate and robust algorithms. In addition, due to the uncontrolled environment of the recordings, many recordings provided in this Challenge are corrupted by various noise sources, such as speech, stethoscope motion, breathing and intestinal activity. Some recordings were difficult or even impossible to classify as normal or abnormal. Figure 5 shows an example of a section of a heart sound recording with good (upper plot) and poor (lower plot) signal quality respectively. Therefore the challengers were given the choice to classify some recordings as ‘unsure’ and the Challenge penalizes this in a different manner (see section 5.3: Scoring Mechanism). Classifications for the heart sound recordings were therefore three-level: normal (do not refer), abnormal (refer for further diagnostics) and unsure (too noisy to make a decision; retake the recording). In this way, any algorithm developed could be employed in an expert-free environment and used as decision support.

Figure 5.

Example of a heart sound recording segment with good signal quality (A) and poor signal quality (B).

5.2. Challenge data

Heart sound recordings (nine independent databases) sourced from seven contributing research groups described in section 2 (with the exception of the SUFHSDB since it was from fetal and maternal heart sounds), were divided into training and test sets. The Challenge training set consists of six databases (with file names prefixed alphabetically, a through f, training sets a through e were provided before the official phase and training set f was added after the beginning of the official phase) containing a total of 3,240 heart sound recordings from 764 subjects/patients, lasting from 5 s to just over 120 s. The Challenge test set also consists of six databases (b through e, plus g and i) containing a total of 1,353 heart sound recordings from 308 subjects/patients, lasting from 6 s to 104 s. The total number of recordings created for the Challenge was 4,593 and is different from the reported number of 2,435 in Table 1. This is because the 338 recordings from normal subjects in the DLUTHSDB are usually longer than 100 s and each recording was segmented into several relatively short recordings. All recordings were resampled to 2,000 Hz using an anti-alias filter and provided as .wav format. Each recording contains only one PCG lead, except for training set a, which also contains a simultaneously recorded ECG.

In each of the databases, each recording begins with the same letter followed by a sequential, but random number. Files from the same patient are unlikely to be numerically adjacent. The training and test sets have each been divided so that they are two sets of mutually exclusive populations (i.e., no recordings from the same subject/patient were in both training and test sets). Moreover, there are four collected databases that have been placed exclusively in either the training or test sets (to ensure there are ‘novel’ recording types and to reduce over-fitting on the recording methods). Databases a and f are exclusively in the training set and g and i are exclusively in the test set. The test set is unavailable to the public and will remain private for the purpose of scoring. (In the future, as more data are added, we may release all the data to the public.) Participants may note the existence of a validation dataset in the data folder. This data is a copy of 300 recordings from the training set, and is used to validate uploaded entries before their evaluation on the test set.

In both training and test sets, heart sound recordings were divided into two types: normal and abnormal recordings. The normal recordings were from healthy subjects and the abnormal ones were from patients with a confirmed cardiac diagnosis. The patients were noted to suffer from a variety of illnesses (which is not provided here on a case-by-case basis but is detailed in an online appendix to this article), but typically they are heart valve defects and CAD patients. Heart valve defects include mitral valve prolapse, mitral regurgitation, aortic regurgitation, aortic stenosis and valvular surgery. All the recordings from the patients were generally labeled as abnormal. We do not provide more specific classification for these abnormal recordings. Please note that both training and test sets are unbalanced, i.e., the number of normal recordings does not equal that of abnormal ones. Challengers will have to consider this when they train and test their algorithms.

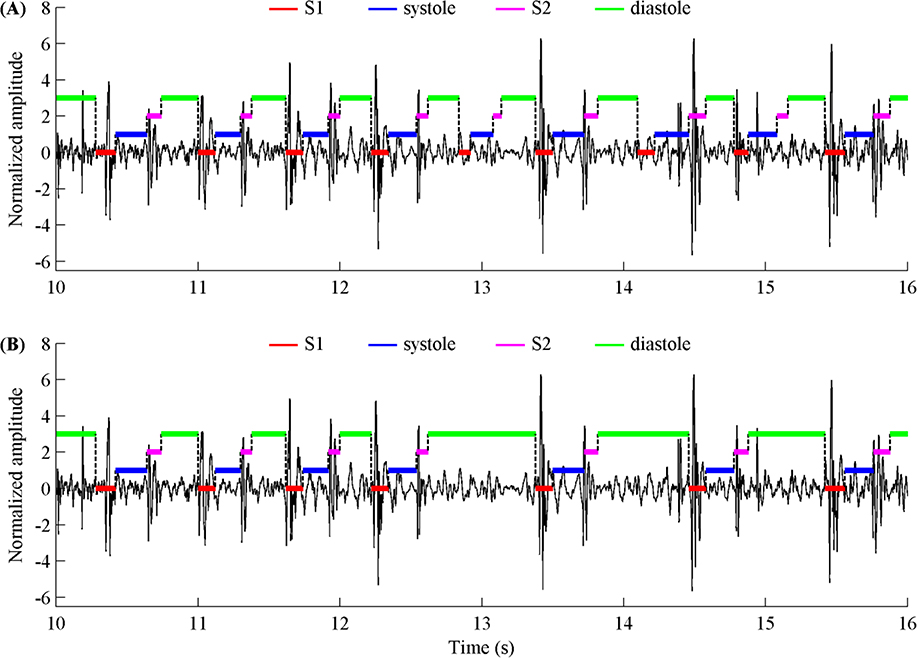
In addition, to facilitate the challengers in training their algorithms to identify low signal quality recordings, we provided the labels for ‘unsure’ recordings with poor signal quality in all training data. We also provided reference annotations for the four heart sound states (S1, systole, S2 and diastole) for each beat for all recordings that were not belong to ‘unsure’ type. The reference annotations were obtained by using Springer’s segmentation algorithm (Springer et al., 2015) and subsequently manually reviewing and correcting each beat labels, resulting in a total of 84,467 beats in training set and 32,575 beats in test set after hand correction. Figure 6 illustrates an example where the automatic segmentation algorithm outputs the wrong annotation and the corresponding correct annotation from hand-correction. Table 4 summarizes the number of patients and recordings, the recording percentages and time lengths, the percentages of hand corrected recordings and heart beats, as well as the corresponding number of hand corrected recordings/beats for each database, for both training and test sets. As shown in Table 4, 22.8% of the recordings in the training set and 20.2% of the recordings in the test set required hand correction, with corresponding percentages of hand corrected heart beats at 13.8% and 14.3% respectively.

Figure 6.

(A) An example of the state labels of a heart sound segment with automatically generated annotations (using Springer’s segmentation algorithm) and (B) the same data and annotations after hand-correction.

Table 4.

Summary of the training and test sets used in 2016 PhysioNet/CinC Challenge.

Proportion of recordings (%)								Recording length (s)			Hand corrected recordings (%)	Hand corrected beats (%)	# beats (after hand corrected)
Challenge set	Sub-set	Data source	# patients	# recordings	Abnormal	Normal	Unsure	Min	Median	Max			Min	Median	Max	Total
Training	training-a	MITHSDB	121	409	67.5	28.4	4.2	9.3	35.6	36.5	28.9	11.6	12	37	78	14,559
	training-b	AADHSDB	106	490	14.9	60.2	24.9	5.3	8	8	32.9	25.9	4	9	15	3,353
	training-c	AUTHHSDB	31	31	64.5	22.6	12.9	9.6	44.4	122.0	67.7	31.5	15	67	143	1,808
	training-d	UHAHSDB	38	55	47.3	47.3	5.5	6.6	12.3	48.5	56.4	19.5	6	14	72	853
	training-e	DLUTHSDB	356	2,141	6.8	83.2	9.9	8.1	21.1	101.7	17.1	12.7	4	27	174	59,635
	training-f	SUAHSDB	112	114	27.2	68.4	4.4	29.4	31.7	59.6	35.1	16.9	7	39	75	4,259
Total/Average			764	3,240	17.7	71.1	11.2	5.3	20.8	122.0	22.8	13.8	4	26	174	84,467
Test	test-b	AADHSDB	45	205	15.6	48.8	35.6	6.3	8	8	35.6	33.7	6	9	16	1,269
	test-c	AUTHHSDB	14	14	64.3	28.6	7.1	19.3	54.4	86.9	42.9	20.9	32	57	107	988
	test-d	UHAHSDB	17	24	45.8	45.8	8.3	6.1	11.4	17.1	37.5	19.7	7	11	24	260
	test-e	DLUTHSDB	153	901	6.5	84.7	8.8	8.1	21.8	103.6	13.2	10.4	3	28	169	26,724
	test-g	TUTHSDB	44	174	12.1	54.6	33.3	15	15	15	33.3	31.2	9	18	29	2,048
	test-i	SSHHSDB	35	35	60	34.3	5.7	15.0	31.7	68.8	22.9	26.4	18	36	59	1,286
Total/Average			308	1,353	11.3	72.8	15.9	6.1	17.7	103.6	20.2	14.3	3	24	169	32,575

5.3. Scoring mechanism

The overall score is computed based on the number of recordings classified as normal, abnormal or unsure, in each of the two reference categories. These numbers are denoted by Aa, Aq, An, Na, Nq, Nn, as shown in Table 5.

Table 5:

Rules for determining the classification result of current recording from Challenger’s algorithm.

		Challenger report result
		Abnormal	Unsure	Normal
Reference label	Abnormal	Aa	Aq	An
	Normal	Na	Nq	Nn

The modified sensitivity (Se) and specificity (Sp) are defined as:

$$Se=\frac{Aa+w\times Aq}{Aa+Aq+An}$$ (1)

$$Sp=\frac{Nn+w\times Nq}{Nn+Nq+Na}$$ (2)

where w is a weight (<1.0) for penalizing incorrect labels of ‘unsure’ less than incorrect classifications of abnormal or normal heart sounds. In this way, we encourage the algorithms to refuse to make a judgment call, and request a re-recording (when possible), rather than blindly guessing with low quality recordings. The weight, w, was arbitrarily set to be 0.5 initially. The overall Challenge ‘Score’ is then the average of the Se and Sp values: (Se+Sp)/2.

6. A simple benchmark classifier for the 2016 PhysioNet/CinC Challenge

As a basic starting point for the Challenge we provided a benchmark classifier that relied on relatively obvious parameters extracted from the heart sound segmentation code. Here we briefly describe the approach for training and testing the code on the Challenge training data only.

6.1. Selected balanced database from training set

Since both training and test sets are unbalanced, first, a balanced heart sound database from training set was selected. (Otherwise, without prior probabilities on the illness, a prevalence bias would be created.) Table 6 summarizes the numbers of the raw heart sound recordings in training set, and the numbers of the selected recordings for each training database.

Table 6.

Numbers of raw and selected recordings for each database in the training set.

Database name	# Raw recordings			# Recordings after balanced
	Abnormal	Normal	Total	Abnormal	Normal	Total
training-a	292	117	409	117	117	234
training-b	104	386	490	104	104	208
training-c	24	7	31	7	7	14
training-d	28	27	55	27	27	54
training-e	183	1,958	2,141	183	183	366
training-f	34	80	114	34	34	68
Total	665	2,575	3,240	472	472	944

6.2. Definition for features

Springer’s segmentation code (Springer et al., 2015) was used to segment each selected heart sound recording to generate the time durations for the four states: S1, systole, S2 and diastole. Twenty features were extracted from the position information of the four states as follows:

1. m_RR: mean value of RR intervals

2. sd_RR: standard deviation (SD) of RR intervals

3. m_IntS1: mean value of S1 intervals

4. sd_IntS1: SD of S1 intervals

5. m_IntS2: mean value of S2 intervals

6. sd_IntS2: SD of S2 intervals

7. m_IntSys: mean of systolic intervals

8. sd_IntSys: SD of systolic intervals

9. m_IntDia: mean of diastolic intervals

10. sd_IntDia: SD of diastolic intervals

11. m_Ratio_SysRR: mean of the ratio of systolic interval to RR of each heart beat

12. sd_Ratio_SysRR: SD of the ratio of systolic interval to RR of each heart beat

13. m_Ratio_DiaRR: mean of ratio of diastolic interval to RR of each heart beat

14. sd_Ratio_DiaRR: SD of ratio of diastolic interval to RR of each heart beat

15. m_Ratio_SysDia: mean of the ratio of systolic to diastolic interval of each heart beat

16. sd_Ratio_SysDia: SD of the ratio of systolic to diastolic interval of each heart beat

17. m_Amp_SysS1: mean of the ratio of the mean absolute amplitude during systole to that during the S1 period in each heart beat

18. sd_Amp_SysS1: SD of the ratio of the mean absolute amplitude during systole to that during the S1 period in each heart beat

19. m_Amp_DiaS2: mean of the ratio of the mean absolute amplitude during diastole to that during the S2 period in each heart beat

20. sd_Amp_DiaS2: SD of the ratio of the mean absolute amplitude during diastole to that during the S2 period in each heart beat

6.3. Logistic regression for feature selection

Logistic regression (LR) allows the identification of the impact of multiple independent variables in predicting the membership of one of the multiple dependent categories. Binary logistic regression (BLR) is an extension of linear regression, to address the fact that the latter struggles with dichotomous problems. This difficulty is overcome by applying a mathematical transformation of the output of the classifier, transforming it into a bounded value between 0 and 1 more appropriate for binary predictions.

In the current study, the output variable Y is a positive (1, abnormal) or negative (−1, normal) classification for heart sound recording,[duumy_incomplete para]

All 20 features were tested and a forward likelihood ratio selection was used, in order of likelihood. If the statistical difference between the accuracy of the model before and after adding of a feature, the feature was included in the updated model. The forward selection is terminated if the newly added feature did not significantly improve the normal/abnormal classification results. In this way, correlated predictors are unlikely to be included in the model, but it does not guarantee an optimal combination of features. Moreover, we note that the features we have chosen are by no means likely to include the most useful features.

6.4. Feature results comparison between the selected balanced data from training set

Table 7 shows the average values of all 20 features for normal and abnormal heart sound recordings on the selected balanced data from training set. A group t test (for features with normal distribution) or non-parametric test (for features without normal distribution) demonstrates that 16 features had significant differences between the two groups whereas 4 features did not have.

Table 7.

Statistical results for comparison between normal and abnormal heart sound recordings on all selected balanced data from training set.

Feature	Abnormal	Normal	P-value
m_RR (ms)	919 ± 279	876 ± 232	<0.05
sd_RR (ms)	54 ± 40	44 ± 30	<0.01
m_IntS1 (ms)	131 ± 9	130 ± 8	<0.01
sd_IntS1 (ms)	18 ± 6	15 ± 5	<0.01
m_IntS2 (ms)	105 ± 10	106 ± 10	0.6
sd_IntS2 (ms)	16 ± 6	13 ± 5	<0.01
m_IntSys (ms)	213 ± 112	199 ± 82	<0.05
sd_IntSys (ms)	20 ± 9	15 ± 7	<0.01
m_IntDia (ms)	470 ± 216	442 ± 176	<0.05
sd_IntDia (ms)	39 ± 29	33 ± 22	<0.01
m_Ratio_SysRR (%)	23 ± 3	23 ± 3	0.9
sd_Ratio_SysRR (%)	4.0 ± 1.7	3.5 ± 1.6	<0.01
m_Ratio_DiaRR (%)	44 ± 5	44 ± 5	0.3
sd_Ratio_DiaRR (%)	6.4 ± 2.9	5.7 ± 2.6	<0.01
m_Ratio_SysDia (%)	55 ± 12	54 ± 12	0.2
sd_Ratio_SysDia (%)	15 ± 6	13 ± 6	<0.01
m_Amp_SysS1 (%)	48 ± 22	44 ± 22	<0.01
sd_Amp_SysS1 (%)	29 ± 16	24 ± 19	<0.01
m_Amp_DiaS2 (%)	64± 24	60 ± 27	<0.01
sd_Amp_DiaS2 (%)	37 ± 23	33 ± 19	<0.01

6.5. Classification results using Logistic Regression

Equation (3) shows the derived BLR prediction formula with the corresponding regression coefficients for normal/abnormal heart sound recordings classification on all selected balanced data from training set. Seven features were identified as the predictable features, including: sd_RR, sd_IntS1, m_IntS2, sd_IntS2, sd_IntSys, m_IntDia and sd_Ratio_SysDia.

$$\begin{gathered} z=w^{T}X=0.062-0.013\times \text{sd\_RR}+0.067\times \text{sd\_IntS}1-0.032\times \text{m\_IntS}2 \\ +0.041\times \text{sd\_IntS}2+0.058\times \text{sd\_IntSys} \\ +0.002\times \text{m\_IntDia}+0.035\times \text{sd\_Ratio\_SysDia} \end{gathered}$$ (3)

Table 8 provides the results of Aa, An, Na and Nn numbers and the three evaluation metrics (Se, Sp and Score) defined in section 5.3. Using equation (3), the normal/abnormal classification results were 0.62 for Se, 0.70 for Sp and a Challenge Score of 0.66 on the training data.

Table 8.

BLR results (equation (3)) of the Aa, An, Na and Nn numbers and the three indices (Se, Sp and Score) for all selected balanced training database: 472 abnormal and 472 normal recordings.

Aa	An	Na	Nn	Se	Sp	Score
293	179	141	331	0.62	0.70	0.66

We also use both a K=10-fold cross validation, stratifying by patient, and a leave-one-out (database) cross validation, stratifying by database to test the performances of BLR model on all selected balanced training data. This is important to note, since including patients in the training data and reporting on test data that includes the same data will give a falsely inflated accuracy. Similarly, using a leave-one-out approach to each database, provides a deeper understanding of which databases can result in heavy biases, and may help provide an more accurate estimate of the out of sample accuracy of the algorithm. Tables 9 and 10 show the corresponding results from 10-fold cross validation and leave-one-out cross validation. Note that the results are subject to statistical variation because of the subsampling. We also note that the average running time on the training set used 5.26% of quota and 5.22% of quota on the hidden test set using Matlab 2016a. We note that this classification algorithm is not intended to provide a sensible way to classify the recordings, but rather to illustrate how a simple algorithm can achieve basic results, but that the results will also vary highly based on which databases are used to train and test the classifiers. We also note that improving the segmentation algorithm may be key to improving the results of any given classifier. Finally, we note that our classifier did not attempt to label any recordings as unknown or unreadable. Any useful algorithm must endeavor to do so, since the intention is for this algorithm to be used at the source of recording, where a re-recording can be triggered in the event that an automated algorithm is likely to fail. Differentiating abnormality from noise is often a difficult but critical issue in biomedical signal analysis, as we have noted in previous competitions (Clifford and Moody, 2012).

Table 9.

K=10-fold cross validation results for all selected balanced training database: 472 abnormal and 472 normal recordings.

Fold iterate	K-fold (10-fold) cross validation on the selected balanced training set
	Aa	An	Na	Nn	Se	Sp	Score
1	30	17	13	34	0.64	0.72	0.68
2	25	22	18	29	0.53	0.62	0.57
3	30	17	16	32	0.64	0.67	0.65
4	31	17	14	33	0.65	0.70	0.67
5	31	16	11	36	0.66	0.77	0.71
6	30	17	16	31	0.64	0.66	0.65
7	21	26	18	29	0.45	0.62	0.53
8	29	18	16	31	0.62	0.66	0.64
9	30	18	10	38	0.63	0.79	0.71
10	30	17	14	33	0.64	0.70	0.67
Mean	29	19	15	33	0.61	0.69	0.65
SD	3	3	3	3	0.07	0.06	0.06

Note: SD, standard deviation.

Table 10.

Balanced leave-one-out cross validation results for all training databases: 472 abnormal and 472 normal recordings.

Excluded database	Leave-one-out cross validation on the balanced training set
	Aa	An	Na	Nn	Se	Sp	Score
training-a	28	89	23	94	0.24	0.80	0.52
training-b	84	20	91	13	0.81	0.13	0.47
training-c	6	1	1	6	0.86	0.86	0.86
training-d	4	23	5	22	0.15	0.81	0.48
training-e	134	49	69	114	0.73	0.62	0.68
training-f	33	1	30	4	0.97	0.12	0.54
Mean	--	--	--	--	0.63	0.56	0.59
SD	--	--	--	--	0.34	0.34	0.15

Note: SD, standard deviation.

7. Potential benefits from the public heart sound data

The public release of the heart sound database has many potential benefits to a wide range of users. First, those who lack access to well-characterized real clinical signals may benefit from access to these data for developing prototype algorithms. The availability of these data can encourage researchers from a variety of backgrounds to develop innovative methods to tackle problems in heart sound signal processing that they might not otherwise have attempted.

An additional benefit is that the data can be re-evaluated with new advances in machine learning and signal processing as they become available. The public data are also essential resources for developers and evaluators who need to test their algorithms with realistic data and to perform these tests repeatedly and reproducibly on a public platform.

In addition, these databases have value in medical and biomedical engineering education by providing well-documented heart sound recordings from both healthy subjects and patients with a variety of clinically significant diseases. By making well-characterized clinical data available to educational institutions, these databases will make it possible to answer numerous physiological or pathological questions without the need to develop a new set of reference data.

The availability of open source state of the art signal processing algorithms for heart sound segmentation provided for the competition, and the subsequent open source classification algorithms provided by competitors is likely to provide an impulse into the field and raise the benchmark for FDA approval and diagnostic performance of industrial systems (Goldberger et al., 2000). We hope that this new heart sound database will help realize these benefits and their often-unanticipated rewards to those with an interest in heart sound signal processing.