Autocorrelation Structure in the Macaque Dorsolateral, But not Orbital or Polar, Prefrontal Cortex Predicts Response-Coding Strength in a Visually Cued Strategy Task

Abstract

In previous work, we studied the activity of neurons in the dorsolateral (PFdl), orbital (PFo), and polar (PFp) prefrontal cortex while monkeys performed a strategy task with 2 spatial goals. A cue instructed 1 of 2 strategies in each trial: stay with the previous goal or shift to the alternative goal. Each trial started with a fixation period, followed by a cue. Subsequently, a delay period was followed by a “go” signal that instructed the monkeys to choose one goal. After each choice, feedback was provided. In this study, we focused on the temporal receptive fields of the neurons, as measured by the decay in autocorrelation (time constant) during the fixation period, and examined the relationship with response and strategy coding. The temporal receptive field in PFdl correlated with the response-related but not with the strategy-related modulation in the delay and the feedback periods: neurons with longer time constants in PFdl tended to show stronger and more prolonged response coding. No such correlation was found in PFp or PFo. These findings demonstrate that the temporal specialization of neurons for temporally extended computations is predictive of response coding, and neurons in PFdl, but not PFp or PFo, develop such predictive properties.

Introduction

Neurons in various cortical areas differ with regard to their task-related firing activities and the temporal stability of their firing rates (Ogawa and Komatsu 2010; Murray et al. 2014). Such temporal stability can be defined as the ability of a neuron to sustain its firing rate over time. It can be quantified as the decay constant of the spike-count autocorrelation and can be considered the neuronal temporal receptive field of integration. For example, Ogawa and Komatsu (2010) reported higher temporal stability in the baseline activity of neurons in the frontal eye field (FEF) than in the visual area 4 (V4), consistent with the finding that neurons in the FEF (Bruce and Goldberg 1985; Chafee and Goldman-Rakic 2000) but not V4 (Bisley et al. 2004) sustain their activity in the absence of visual stimulation. Similarly, Murray et al. (2014) compared a wide range of cortical areas and showed that the prefrontal cortex (PF) has the longest timescale, followed by the posterior parietal cortex and somatosensory cortex. Based on these data, it has been proposed that the temporal receptive field can be regarded as an organizing principle of the primate cortex (Chen et al. 2015), analogous to the spatial receptive field in the visual cortical hierarchy (Lennie 1998).

Heterogeneity in baseline firing rate stabilities has been observed across areas and within the same cortical area for various functional classes of neurons. Specifically, Nishida et al. (2014) reported that the temporal stability of the baseline activity of neurons in the lateral intraparietal area (LIP) correlates with their persistent firing activity during a delay period. Thus, temporal stability appears to reflect the function of cortical neurons, that is, neurons with fast but reliable computations can capture fast changing stimuli, whereas those that experience slow integration and maintenance of information must rely on long timescales.

Consistent with this model, Cavanagh et al. (2016) reported that the temporal receptive field of neurons in the orbital PF (PFo) is related to the coding strength of the choice value. Notably, they did not observe such a relationship in the dorsolateral PF (PFdl), notwithstanding its importance in the generation and maintenance of selective activity (Badre and D’Esposito 2009), for working memory of various domains (Funahashi et al. 1989; Brody et al. 2003; Genovesio et al. 2009, 2011; Merchant et al. 2011; Eiselt and Nieder 2016) and for decision-making processes (Kim and Shadlen 1999; Seo et al. 2007). Thus, the persistent activity in PFdl, which is associated with the reverberation of activity that is mediated by NMDA receptors (Wang 2001; Wang et al. 2013), does not appear to rely on the intrinsic ability of the neurons to sustain activity. One alternative interpretation is that the functional neuronal temporal specialization that is determined by the intrinsic properties of self-sustained activity is not needed for all computations in the PF—only for specific functions in each area, such as working memory and response-related processes in PFdl and value computations in PFo. To test this hypothesis, we analyzed data that were recorded in a visually cued strategy task from the polar PF (PFp), PFdl, and PFo (Tsujimoto et al. 2010, 2011a,b, 2012). We have reported that response-related spatial signals appear after presentation of the cue in PFdl, whereas they emerge only after the response in PFo and PFp (Tsujimoto et al. 2010, 2012). In this study, we tested whether long intrinsic timescales are associated with stronger and more prolonged coding in the 3 areas of the PF.

Materials and Methods

Subjects

Two male rhesus monkeys (Macaca mulatta), 10–11 kg in weight, were operantly conditioned to perform a visually cued strategy task before the beginning of the recordings. During the task, each monkey sat in a primate chair, with its head stabilized and oriented toward a video monitor 32 cm away. An infrared oculometer (Arrington Research, Inc., Scottsdale, AZ) recorded their eye positions. All procedures conformed to the Guide for the Care and Use of Laboratory Animals and were approved by the National Institute of Mental Health Animal Care and Use Committee.

Behavioral Task

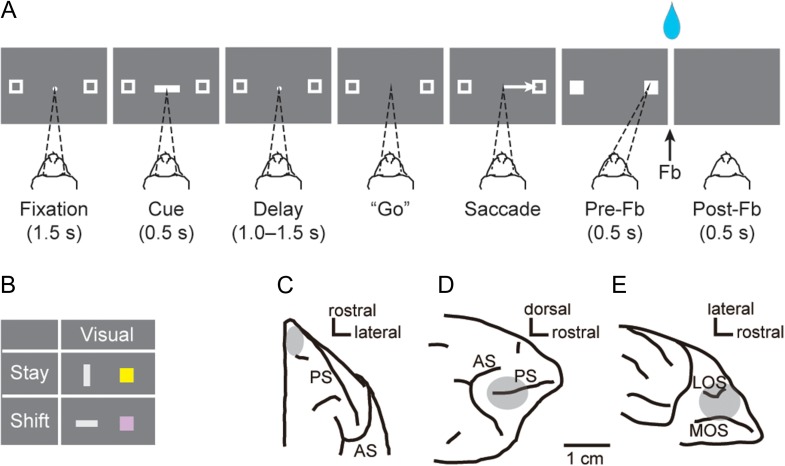
Figure 1A shows a schematic of the visually cued strategy task (Tsujimoto et al. 2010, 2011a, 2012). In each trial, the monkey had to choose 1 of 2 targets by making a saccade toward it, according to a shift or stay strategy cue (Fig. 1B). Each trial began with the appearance of a fixation point (a 0.6° filled white circle) located at the center of the video screen, with 2 peripheral targets (2.0° unfilled white squares) placed 11.6° to the left and right of the fixation point. After the monkeys attained and maintained fixation on the central spot for 1.5 s, a cue period of 0.5 s followed. During the cue period, a visual cue appeared at the fixation point. In each trial, 1 cue was selected pseudorandomly from a set of 4: a vertical (light gray) or horizontal rectangle with the same dimensions (1.0° × 4.9°) and brightness or a yellow or purple square with the same size (2.0° × 2.0°) (Fig. 1B). The vertical rectangle and the yellow square instructed a “stay” strategy. The “stay” strategy required the monkeys to make a saccade to the same target that was chosen in the previous trial. Conversely, the horizontal rectangle and the purple square required a “shift” strategy, wherein the monkeys had to make a saccade toward the target that was not selected in the previous trial. The number of alternative visual cues and responses (left or right) were approximately equal in each experimental session. An intertrial interval of 1 s separated the end of one trial from the beginning of the next one.

Figure 1.

Behavioral task, cues, and recording sites. (A) Sequence of task events for the visually cued strategy task, temporally ordered from left to right. Each dark gray rectangle represents the video screen as viewed by the monkey. Dashed lines indicate the target of the monkey’s gaze. (B) Strategy cues presented to the monkey. Each colored shape instructed the strategy to be applied. (C–E) Recording zones for PFp (C), PFdl (D), and PFo (E). Fb, feedback; LOS, lateral orbital sulcus; MOS, medial orbital sulcus; PS, principal sulcus; AS, arcuate sulcus.

The monkeys were required to fixate on the central point during the fixation period and the cue period (0.5 s) as well as during a subsequent delay of 1.0, 1.25, or 1.5 s, pseudorandomly selected. The fixation window was a ±3° square area that was centered on the fixation point. Both monkeys maintained fixation more accurately than required and rarely made a saccade within the fixation window (Tsujimoto et al. 2009). Fixation breaks during the cue or delay periods led to abortion of the trial. During the delay period that followed the cue, the fixation spot and the 2 peripheral targets were kept on the screen. The disappearance of the fixation spot constituted a “go” signal that instructed the monkeys to make a saccadic eye movement toward 1 of the 2 targets. When the monkeys fixated on one of the targets (±3.75°), both squares were filled in and became solid white. Entry of gaze into the response window was labeled “target acquisition.” The monkeys had to fixate on the target for 0.5 s (prefeedback period). Fixation breaks during the prefeedback period led to abortion of the trial. After the prefeedback period, feedback was provided as a reward (a 0.2-ml drop of fluid) in the case of correct responses or as red squares over both targets for incorrect responses. In the case of an error, the same cue was presented again in a “correction trial.” Correction trials were presented until the monkey responded correctly. Usually, the monkeys did not require more than one correction trial after making an error (Tsujimoto et al. 2009).

Data Collection

Once the monkeys completed the training phase, we implanted a recording chamber (10.65-mm inner diameter) over the exposed dura mater of PFp in the right hemisphere; the activity was recorded from this chamber. The detailed procedures for PFp, including the chamber design, and the surgical and recording techniques have been previously described (Mitz et al. 2009). Once data collection from PFp was completed, we implanted another chamber (18-mm inner diameter) over a more caudal part of the frontal lobe in the same hemisphere. The position and angle of this chamber were adjusted, based on magnetic resonance images, allowing us to access PFdl and PFo simultaneously through the same chamber (Tsujimoto et al. 2009). Up to 16 platinum–iridium electrodes (0.5–1.5 MΩ at 1 KHz; Thomas Recording, Giessen, Germany) recorded the single-cell activity simultaneously. The electrodes were inserted individually using a multielectrode drive (Thomas Recording), enabling independent control of each electrode.

In typical recording sessions for the caudal chamber, approximately half of the electrodes were introduced into PFo, whereas the others were maintained more superficially in PFdl. A multichannel acquisition processor (Plexon, Dallas, TX) was used to record the signals from each electrode. We used a cluster cutting technique (Off Line Sorter, Plexon) to isolate single-cell potentials online and sort them offline. Spike sorting was performed based on several criteria, such as principal component analysis (PCA), minimum interspike intervals, and close visual inspection of the entire waveform for each cell.

Histology

The recording sites were reconstructed by histological analysis, complemented by structural MRI. After the data collection was completed, electrolytic lesions (20 μA for 20 s, anodal current) were placed in selected locations at 2 depths per penetration in the caudal chamber. After 10 days, the monkey was deeply anesthetized and then perfused through the heart with 10% (v/v) formol saline. Immediately before and during the perfusion, we inserted a pin through the center of the rostral and caudal chambers. The penetration sites and tracks were reconstructed in Nissl-strained sections, referenced to the recovered electrolytic lesions and the marking pins that were inserted at the time of the perfusion. By cytoarchitectonic analysis, we verified that the recording sites in PFo originated from granular areas. The locations of recording sites have been illustrated elsewhere (Fig. 1C–E) (Tsujimoto et al. 2010, 2011a).

Data Analysis

We analyzed the activity of neurons in PFdl, PFo, and PFp (Tsujimoto et al. 2012; Tsujimoto and Genovesio 2017). Correction and error trials were discarded from all analyses. The task periods in the analyses were defined according to the task events: the fixation period (0.0–1.0 s after fixation onset), cue period (0.0–0.5 s after cue onset), early–delay period (0.0–0.5 s after cue offset), late–delay period (0.5–1.0 s after cue offset), and feedback period. The feedback period was considered the interval from 0.3 s before feedback onset to 0.2 s afterward (Tsujimoto et al. 2012). Only neurons that satisfied the following requirements were analyzed (Ogawa and Komatsu 2010; Murray et al. 2014):

$$\begin{array}{c}\mathrm{1}\mathrm{.}\text{at least 20 completed trials};\hfill \\ \mathrm{2}\mathrm{.}\text{at least 1 Hz of mean activity during the fixation period};\hfill \\ \mathrm{3}\mathrm{.}\text{each 50-ms time bin during fixation with nonzero mean activity}\mathrm{.}\hfill \end{array}$$ (1)

The analyses were performed using MatLab (The MathWorks, Inc., Natick, MA, USA).

Autocorrelation Structure During Fixation Period

To assess the spike-count autocorrelation, we subdivided the fixation period of each trial into time bins of 50 ms. The results were similar if we applied a change of ±20% on the 50-ms bin length. For each neuron, the spike-count autocorrelation across trials between time bins i and j (i, j integer numbers), separated by a time lag that was equal to |i − j| × Δ (Δ = 50 ms), was calculated using Pearson’s correlation coefficient, ρ (Murray et al. 2014):

$$\rho =\frac{Cov(N\left(i\right),N(j))}{\sqrt{Var(N\left(i\right))\times Var(N(j))}}=\frac{\langle \left({\rm N}\left(i\right)-\overline{{\rm N}}\left(i\right)\right)(N\left(j\right)-\overline{{\rm N}}(j))\rangle }{\sqrt{Var(N\left(i\right))\times Var(N(j))}},$$ (2)

where, N(i) and N(j) are the spike-counts in the i and j time bins, respectively, and $\overline{N}\left(i\right)$ and $\overline{N}\left(j\right)$ are the mean spike-counts across trials for the same time bins. The covariance (Cov) and variance (Var) were computed across trials for the i and j bins. The coefficient ρ was calculated using all pair-combinations of bins at various time lags. To study the autocorrelation structure at the population level for each brain area, the coefficient ρ was averaged across neurons for each time lag. The autocorrelation decay, as a function of time lag, was fitted to the population of neurons within each area using an exponential function (Murray et al. 2014), defined as follows:

$$\rho \left(k\mathrm{\Delta }\right)=A[\exp \left(-\frac{k\mathrm{\Delta }}{\tau }\right)+B],$$ (3)

where, kΔ refers to the time lag between i and j bins (k = |i − j|, k = 1, 2 … 19), ρ is the Pearson’s correlation coefficient at time lag $k\mathrm{\Delta }$, A is the amplitude, τ is the intrinsic timescale (decay constant), and B is the offset value that reflects the contribution of long timescales (much longer than our 1-s time window) (Murray et al. 2014). The same fit procedure was applied to single-neuron autocorrelation decay to assign the intrinsic timescales τ that were obtained from Equation (3) to each cell. This single-neuron analysis reduced further the population of neurons because neurons that did not satisfy the criteria listed in (1) and the following restrictions in their autocorrelation structure were excluded from further analyses:

$$\begin{array}{c}\mathrm{1}\mathrm{.}\mathrm{\text{decline in auto correlation within 150}}–\text{250 ms}\hfill \\ \text{of time lag after fixation onset};\hfill \\ \mathrm{2}\mathrm{.}\text{intrinsic timescale}(\mathrm{\tau })\text{larger than 0}\mathrm{ms}\mathrm{.}\hfill \end{array}$$ (4)

The first requirement followed some considerations on the autocorrelation structure of the neurons as a function of the time lag. Indeed, we observed that neurons showed a maximum value of their autocorrelation values in the range between 50 and 150 ms time lag after fixation onset. To accommodate this feature, the fitting procedure started at that time lag within the first 150 ms time lags (i.e., 50, 100, or 150 ms) after which the autocorrelation value decreased. Once the maximum value has been reached, in order to ensure that the exponential fitting curve from Equation 3 described as best as possible the descent ramp of the autocorrelation structure, we required no further increasing in the autocorrelation values at least between 150 and 250 ms time lags. This ensured that the exponential fitting curve was applied to decreasing values of the autocorrelation—at least in the first time lags just after the autocorrelation maximum-value—and leading then to a better estimation of the decay constant.

Concerning the second requirement, a negative or 0 ms value for τ is meaningless. Moreover, after visual inspection, neurons that were poorly fit by the exponential function were discarded (Cavanagh et al. 2016). More precisely, by visual inspection, we removed a neuron from further analyses if at least one of the 4 following dynamics was observed: (1) the autocorrelation values showed an oscillatory behavior as time lags increased; (2) the autocorrelation values did not decay as time lags increased; (3) the autocorrelation values were more linearly decreasing rather than exponentially; and (4) more than 40% of autocorrelation values (∼8/19 autocorrelation values) had the fitting curve outside their error bars. The last requirement implied at least 11/19 autocorrelation values for which the fitting curve was within the error bars. This was done to have a trade-off between the willingness to keep the highest number of neurons and in parallel to guarantee a good fit result for each of them. After applying this requirement, we found that our working point was at 80% of the efficiency (i.e., the number of accepted neurons out of the number of total neurons).

Correlation Analysis Between Strength of Neuronal Selectivity and Intrinsic Timescale

Neuronal selectivity indicates the ability of a neuron to encode a signal. In particular, the difference in spike activity between a preferred and anti-preferred condition can be used as a measure of neuronal selectivity (Tsujimoto et al. 2012). Preferred and anti-preferred conditions indicate the condition for which a neuron shows the highest and the lowest activity, respectively.

To quantify the strength of the selectivity for the spatial response (right or left) and strategy (stay or shift), we performed a receiver operating characteristic (ROC) analysis, which quantifies how strongly a neuron encodes a variable (Dayan and Abbott 2005). The ROC values were defined as the area under the ROC curve. The ROC values range from 0 to 1, where 0 and 1 indicate the maximum selectivity for the opposing preferences. The normalized values of ROC were computed with respect to the preferred condition—that is, highest activity—and range from 0.5 (no selectivity) to 1 (maximum selectivity).

We performed ROC analysis for a 0.5 s fixed time window using the task periods in which the ROC value of the population exceeded chance values for strategy or response, as reported by Tsujimoto et al. (2012) (see Results). That is, in PFdl, we considered the cue, early–delay, late–delay, and feedback periods for the response signal, and the cue and the early–delay periods for the strategy signal; in PFo, we considered the feedback period for the response signal and the cue, early–delay, late–delay, and feedback periods for the strategy signal; and in PFp we considered only the feedback period for the response signal. It is worth to note that the feedback period was a perifeedback period defined across the feedback event including both a prefeedback and a postfeedback periods. In both periods, the response signal is not a predictive signal because the response has already been made, but only in the postfeedback the monkeys were informed on the behavioral outcome.

For each neuron, we computed the normalized ROC values in the task periods of interest and the intrinsic timescales during fixation. To determine whether the intrinsic timescales during fixation and the ROC values correlated, we computed the Pearson’s correlation coefficient between the 2 variables in each brain area. Next, we compared the Pearson’s correlation coefficient previously calculated against those obtained from 1000 iterations of the permutations test. For each permutation test, all the correlation coefficients were recalculated by keeping the intrinsic timescale for each neuron as in the original analysis but randomizing the ROC values. We fixed a significance cutoff at the 95th percentile of the correlation coefficients from the permutation analysis.

Time Course and Temporal Maintenance of the Population Activity

To visually illustrate the temporal stability of the neurons within trials, we sorted the neurons according to increasing timescales and, using a median split, classified them into 2 groups: long and short timescale populations, defined as neurons with a timescale above and below the median value, respectively (Cavanagh et al. 2016).

To provide an intuitive and graphical explanation of the meaning of the autocorrelation for the long and short timescale populations, within each population, we divided the trials into high and low activity groups according to the magnitude of the neuron spike count calculated in an arbitrary 100-ms interval during the fixation period. For each trial, we divided the 1.5 s period after fixation onset into 50-ms successive bins and we computed the spike count in each time bin. We then averaged spike counts among trials within an activity group and then among neurons within long and short timescale populations. To assess whether the long timescale population exhibited a more sustained neuronal activity than the short population, we computed the difference between the mean spike counts of high and low activity group in each 50-ms time bin, for each timescale population. We identified a descent ramp, defined as the difference in mean activity after the arbitrary 100-ms interval from fixation onset. We performed a fit, for each timescale population, on the descent ramp using an exponential function to estimate the decay constant of the difference between the high and low activity groups approaching zero:

$$y=\alpha \times [\exp (-t/\beta )+\gamma ],$$

where, y is the dependent variable, that is, the mean activity difference between high and low activity groups, t is the time, β is the decay constant, γ is an offset that reflects the contribution to the mean activity difference at times much longer than the observation time window and α is an overall multiplication factor.

To examine the time course of neuronal selectivity, we calculated the normalized ROC values for the long and short timescale populations using a sliding window of 200 ms, increasing in steps of 20 ms with 2 alignments: cue onset and feedback onset (Tsujimoto et al. 2012). Subsequently, the normalized ROC values were averaged across neurons in each timescale population. In addition, to determine whether the population selectivity was sustained over time, we performed a cross-temporal analysis between the non-normalized ROC values in each timescale population (Cavanagh et al. 2016). These ROC values were computed in a fixed time bin Δ of 50 ms for each neuron. We defined a matrix of non-normalized ROC values in which each row was a neuron and each column was the time bin Δ where the ROC values were computed. The correlation between 2 population vectors of non-normalized ROC values at 2 time bins, separated by |k| × Δ (k integer number), was computed using Pearson’s correlation coefficient. The correlation analysis was applied to all pair-combinations of time bins. Moreover, to investigate a possible difference between the 2 timescale populations, we compared the correlation coefficients in each pixel of the 2 populations using a Fisher’s r-to-z transformation.

Results

Figure 1A illustrates the visually cued strategy task that has been described in our previous work (Tsujimoto et al. 2010, 2011a, 2012) and in more details in Materials and Methods. Briefly, in this task, each trial started with a fixation period in which the monkeys were required to maintain fixation on a central spot. Subsequently, a visual cue was presented (Fig. 1B) instructing the monkeys either to “stay” with the goal chosen on the previous trial or to “shift” to a different goal. After the cue period and a following delay period, the monkeys made a saccade to a left or right goal and had to maintain fixation of the chosen goal until feedback was provided.

The behavioral results have been described previously in detail (Tsujimoto et al. 2009, 2012). Briefly, both monkeys performed the task with an average performance greater than 90% of correct responses. Both monkeys maintained stable and accurate fixation throughout both the fixation and cue periods, within ±1° on more than 90% of the trials.

The database for this study consisted of 1494 neurons (871 and 623 from Monkey 1 and Monkey 2, respectively) that were recorded during the visually cued strategy task—566 cells were located in PFp, 551 resided in PFdl, and 377 were in PFo.

The Decay Time Constant in PFp, PFdl, and PFo

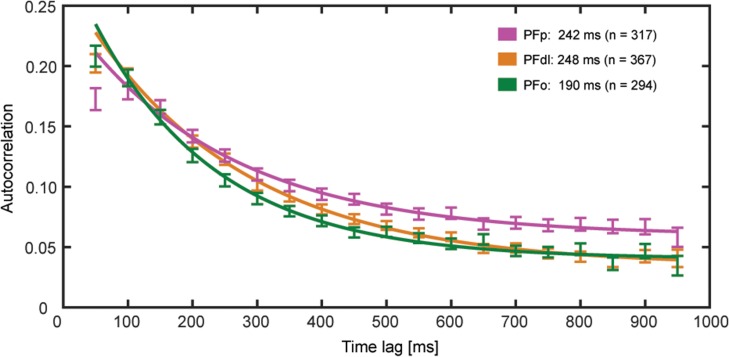
To determine temporal hierarchical ordering of the 3 areas, we assessed the intrinsic temporal properties of their neuronal populations by estimating the decay time constant (intrinsic timescale, τ) of the autocorrelation structure in the fixation period. Only neurons with 20 or more completed trials, at least 1 Hz of mean activity during the fixation period, and nonzero mean activity in each 50-ms time bin during fixation were analyzed (see Materials and Methods). In particular, 317/566 neurons in PFp, 367/551 in PFdl, and 294/377 in PFo survived the previous requirements. Figure 2 shows the autocorrelation values (averaged across neurons and times) during the fixation period at various time lags for PFp, PFdl, and PFo. We fitted the autocorrelation with an exponential function, which allowed us to have an estimate of the decay time constant (τ) for each brain area (see Materials and Methods). Notably, PFo (τ = 190 [167, 213] ms) had a shorter τ within 95% confidence level (C.L.) than PFp (τ = 242 [212, 272] ms), and PFdl (τ = 248 [230, 265] ms).

Figure 2.

Spike count autocorrelation decay computed using 50-ms time bins in a 1-s time window of the fixation period (mean ± standard error of the mean [SEM]). The solid lines are the exponential fits. The autocorrelation value of PFp for the shortest time lag of 50 ms shows refractory adaptation and it has been excluded from the fit procedure. The intrinsic timescale obtained from the exponential fit is shown for each brain area.

To exclude the possibility that our results depended on the coding of previous signals during the fixation period, we repeated the analysis, considering only the neurons that were not significantly modulated (one-way ANOVA) by the previous response in this period (the number of eliminated neurons were: 22/317 in PFp, 39/367 in PFdl, and 22/294 in PFo). We applied the exponential fit to the reduced neuronal sample and obtained consistent results within 95% C.L. (τ = 252 [220, 280] ms for PFp, τ = 250 [232, 267] ms for PFdl, τ = 197 [170, 225] ms for PFo).

To examine the relationship between the intrinsic timescale and the strength of neuronal selectivity for individual neurons, we calculated the intrinsic timescale for each neuron during the fixation period and its ROC value for the periods in which the ROC value of the population of each area for response and strategy was significantly above chance levels (Tsujimoto et al. 2012). To assess the intrinsic timescale for each neuron, we discarded most of the neurons by requiring a decline in the autocorrelation within 150–250 ms of time lag after fixation onset and an intrinsic timescale larger than zero (see Materials and Methods). In particular, 115/317 neurons of PFp, 149/367 of PFdl, and 138/294 of PFo survived the previous requirements. Afterwards, we further selected the remaining neurons by visual inspection (see Materials and Methods), ending up with 58 neurons in PFp, 84 in PFdl, and 76 in PFo.

Supplementary Figure S1 shows the scatter plot of the mean firing rate computed during fixation for each neuron within each brain area against the R² value obtained from the fit of the autocorrelation values. We plotted both the neurons included and those excluded by visual inspection (see Materials and Methods) from the 3 brain areas. The mean value of R² was 0.5 ± 0.3 (mean ± standard deviation [SD]) for the discarded neurons and 0.8 ± 0.1 (mean ± SD) for the included neurons. These results show that the selection by visual inspection tended to include neurons with higher R² but with some exceptions. Supplementary Figure S2 shows some examples of these exceptions. In particular it shows examples of neurons that were included albeit their relatively low R² values and others that were excluded with a relatively high R².

Relationship With Rate-Coding Strength

To assess the strength of neuronal selectivity, we computed the normalized ROC values for the response signal in the feedback period for the 3 areas and in the cue, early–delay and late–delay periods only for PFdl. For the strategy signal, the normalized ROC values were calculated in the late–delay and feedback periods for PFo and in the cue and early–delay periods for PFdl and PFo, whereas no strategy signal was found in PFp in any task period (Tsujimoto et al. 2012). The intrinsic timescales during fixation correlated significantly (P < 0.05) with the normalized ROC values for the response in PFdl during the late delay (Pearson’s correlation, r = 0.25, P < 0.05, Supplementary Fig. S3C) and feedback (Pearson’s correlation, r = 0.25, P < 0.05, Supplementary Fig. S3D) periods. In contrast, we did not observe any significant correlation in PFp and PFo in the feedback period (Supplementary Fig. S3G,H), although both areas showed significant response selectivity in this period (Tsujimoto et al. 2012). For the strategy signal, no significant correlation was observed between the timescales and ROC values in any PF area (Supplementary Fig. S3E,F,I–L). Table 1 shows the results of this correlation analysis. Thus, PFdl was the only area of the PF with a significant correlation (P < 0.05) between the intrinsic timescales of the individual neurons during fixation and their response selectivity in subsequent task periods. We confirmed a significant correlation for PFdl using the Spearman rank correlation in the late delay (Spearman’s correlation, r_s = 0.35, P = 0.001, n = 84), and feedback (Spearman’s correlation, r_s = 0. 37, P = 7 × 10^–4, n = 84) periods. We further confirmed the significance of the Pearson’s correlation obtained for PFdl in the late–delay and feedback period by implementing a permutation test (see Materials and Methods).

Table 1.

Results of the correlation analysis for each PF area between the intrinsic timescales in the fixation period and the ROC values in subsequent periods of the task. The ROC value was computed in each PF area only for the task periods in which that area encoded the spatial response or the strategy (or both) signal (Tsujimoto et al. 2012). The number of neurons analyzed was 58 for PFp, 84 for PFdl, and 76 for PFo. The correlation coefficient (Pearson’s coefficient, r) and the corresponding P-value (P) are shown. Only PFdl shows a significant correlation (P < 0.05) for the response signal during the late–delay and feedback periods

	PFdl						PFp	PFo
Signal selectivity	Response (right–left)				Strategy (stay–shift)		Response (right–left)	Response (right–left)	Strategy (stay–shift)
Task period	Cue	Early–delay	Late–delay	Feedback	Cue	Early–delay	Feedback	Feedback	Cue	Early–delay	Late–delay	Feedback
Pearson’s coeff., r	0.06	0.08	0.25	0.25	−0.21	−0.09	−0.04	0.02	−0.07	−0.005	0.16	−0.05
P-value	0.57	0.45	0.02	0.02	0.06	0.44	0.79	0.84	0.54	0.96	0.17	0.67

Afterwards, we compared the correlation coefficients shown in Table 1 for the response coding during the feedback period between the 3 areas. We applied the Fisher’s r-to-z transformation, computing the correspondent z value for the r Pearson’s coefficient and after comparing the obtained z values. No significant difference emerged from the comparison between PFdl and PFo (z = 1.46, P = 0.14, Fisher’s transformation), PFp and PFo (z = 0.31, P = 0.76, Fisher’s transformation), PFdl and PFp (z = 1.69, P = 0.09, Fisher’s transformation), albeit we observed a significant linear relation in PFdl but not in PFp and PFo.

We investigated whether there was a relationship between firing rates and estimated intrinsic timescales. We computed the mean firing rate in the 1-s fixation period that is the baseline period in which the intrinsic timescale was calculated. We calculated the correlation between intrinsic timescales and mean firing rates for the 218 neurons recorded from the 3 brain areas with a meaningful intrinsic timescale (58 neurons in PFp, 84 in PFdl, and 76 in PFo). No significant correlation emerged (r = 0.09, P = 0.17, n = 218, Pearson’s correlation). Similarly, looking at each area independently we did not observe a significant correlation between intrinsic timescales and mean firing rates in PFp (r = 0.06, P = 0.64, n = 58, Pearson’s correlation) and in PFo (r = −0.19, P = 0.09, n = 76, Pearson’s correlation). A significant correlation emerged only in PFdl (r = 0.24, P = 0.03, n = 84, Pearson’s correlation) and we will later examine the relationship between intrinsic timescale and response coding after matching the firing rates.

Implication for Neural Function in PFdl

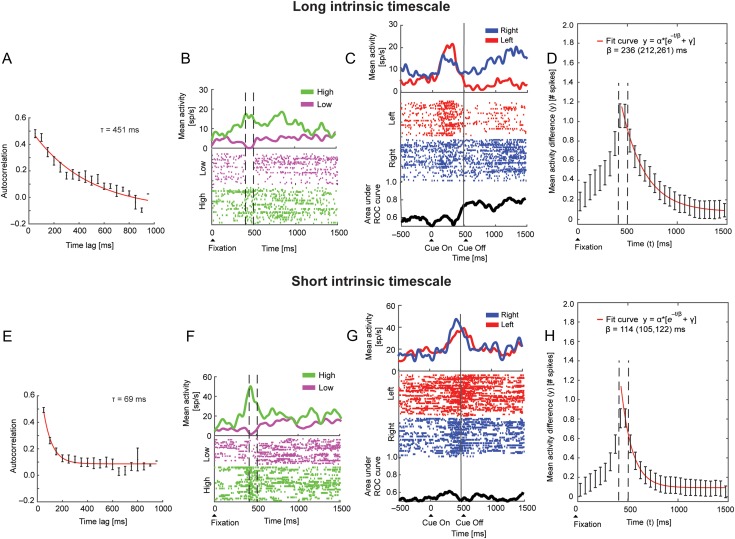
To understand the neural implications of the individual intrinsic timescales, we divided the neurons into 2 groups based on the magnitude of their intrinsic timescale (see Materials and Methods). Figure 3A–C, E–G shows 2 PFdl neurons with long and short intrinsic timescales, respectively. Figure 3A,E shows the decay of the autocorrelation (mean ± SEM) in the fixation period, defined as the decay constant τ. To illustrate what the long and short intrinsic timescales represent, we subdivided the trials of each of the 2 neurons into 2 groups according to the magnitude of their spike count, computed in an arbitrary 100-ms interval from 400 to 500 ms after fixation onset (see Materials and Methods) (Ogawa and Komatsu 2010; Nishida et al. 2014). We determined the mean spike count for each neuron within this interval and used this value as a threshold to separate the trials into low or high firing rate categories. In other words, trials with a spike count that was lower or higher than the mean spike count in that interval were classified as low or high trials activity, respectively. We expected that for a neuron with a long intrinsic timescale, the difference in the defined 100-ms interval would persist beyond that time period more than for a neuron with a short intrinsic timescale, which should exhibit a sudden decline in the activity difference after the interval. Indeed, the neuron with long τ (Fig. 3B) exhibited a difference between high and low activity trials that extended beyond the 100-ms interval that was used to split the trials, whereas the neuron with short τ (Fig. 3F) did not show a persistent difference in activity beyond this interval. Moreover, the neuron with a long intrinsic timescale encoded the correct response during the early–delay and late–delay periods (Fig. 3C). Conversely, the example neuron with the short intrinsic timescale was not response-selective in the delay periods (Fig. 3G). We extended to all neurons of PFdl the same analysis shown for the example neurons of Figure 3B, F. We computed the difference between the mean spike counts of the low and high activity groups in each 50-ms time bin, for each timescale population (see Materials and Methods). We observed, as expected, the highest difference between low and high activity in the 100-ms time bin used to classify the trials. Figure 3D,H shows the time course of the difference between high and low activity groups for the long and short timescale populations, respectively—the error on the difference between high and low activity was obtained by the error propagation of the difference. From the exponential fitting procedures, we obtained the following decay constants with the 95% C.L. for the short and long timescale populations (see Materials and Methods):

• β_shortTimescale = 114 (105, 122) ms;

• β_longTimescale = 236 (212, 261) ms.

Figure 3.

Example of 2 neurons with long and short intrinsic timescales and population analysis. (A–D) Example neuron with long intrinsic timescale encoding the response in the delay period and long intrinsic timescale population analysis. (A) Autocorrelation decay in the fixation period. The red line is the exponential fit with timescale τ = 451 ms. (B) Example of high activity maintenance during the fixation period by dividing high and low trials activity. Trials were subdivided in 2 groups according to the spike count computed in the 100-ms interval from 400 to 500 ms after fixation onset, as indicated by vertical dashed lines. The difference in activity was maintained for nearly the entire fixation period—not merely in the 100-ms interval. Raster plot for low (purple) and high (green) activity trials aligned to fixation onset. Each dot indicates when a spike occurred. Spike density averages are shown on top of the raster. (C) Raster plot for right (blue) and left trials (red) aligned to cue onset. Spike density averages are shown on top of the raster. The ROC values for the response are shown at the bottom. (D) Difference between high and low activity groups for the population of long timescales neurons. Dashed lines indicate the 100-ms interval from 400 to 500 ms after fixation onset. The decay constant (β) from the exponential fit is reported with the 95% C.L. (E–H) Example neuron with short intrinsic timescale and no response-related activity in the delay period and population analysis. (E) Same analysis as in A. The red line is the exponential fit with timescale τ = 69 ms. (F) Example of low activity maintenance during the fixation period. The low and high activity trials were defined as in B. The difference in activity between the 2 groups of trials did not extend beyond the period after the 100-ms interval. (G) Same analysis as in C. (H) Same analysis as in D for the population of short timescales neurons.

These β parameters represent the time period after which the initial difference between high and low activity is reduced by a factor 1/e (e ~ 2.72, Euler’s constant).

These results indicate that for neurons with long intrinsic timescale the activity was more sustained in time since, as time increased, the difference between high and low activity trials decreased slower over time (236 ms) than that for neurons with short intrinsic timescale (114 ms).

We also repeated the analysis dividing trials according to the spike count computed in the 100-ms time bin from 300 to 400 ms and in the 200-ms time bin from 300 to 500 ms after fixation onset. The results were essentially the same when we shifted or enlarged the time bin. It proved that the length and the time from fixation of the selected time bin were not critical and did not change our main findings.

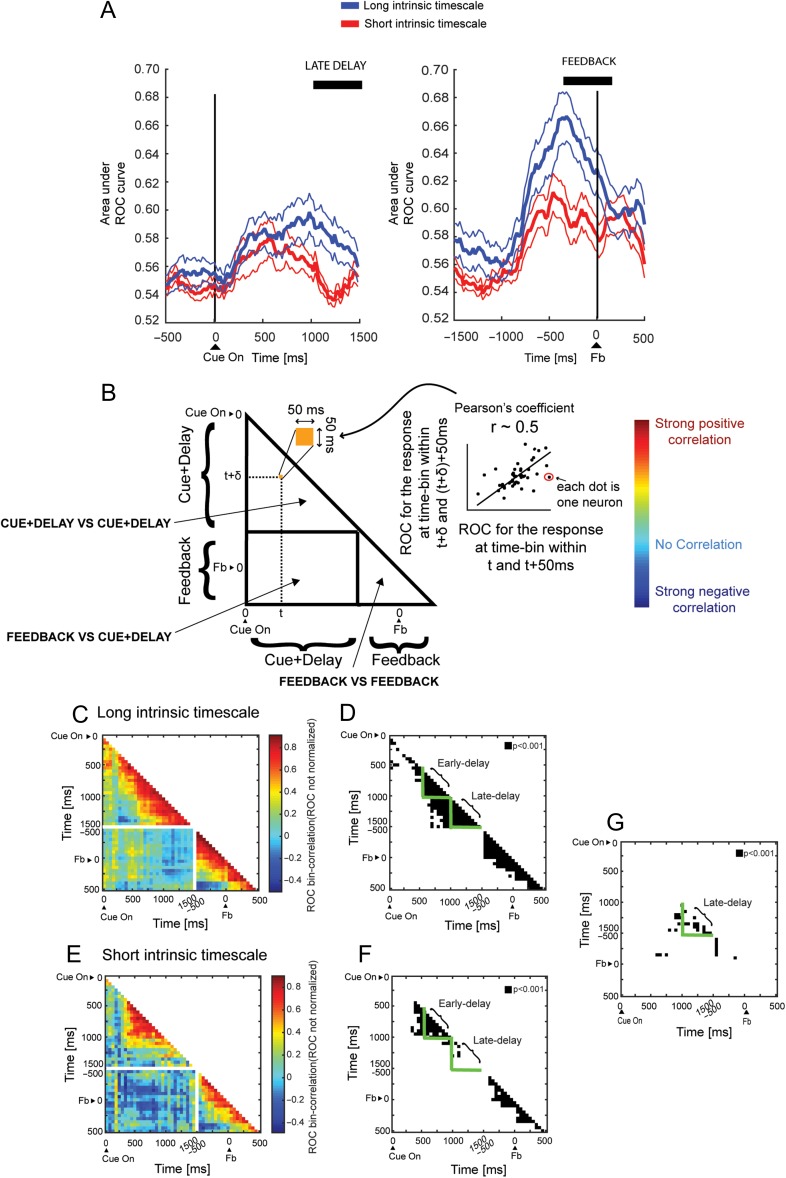
Next, we compared the temporal dynamics of the ROC values of the 2 populations with long and short intrinsic timescales in PFdl (see Materials and Methods). The population intrinsic timescales calculated for these groups of neurons were 130 and 362 ms, respectively in the short and long timescales populations. We expected based on the correlation results that the latter would show stronger neuronal response selectivity than the former population. Figure 4A shows the time course of the response selectivity during the delay (left) and feedback periods (right). The population with long intrinsic timescales (blue line, mean ± SEM) encoded the response more strongly in the late–delay (Kruskal–Wallis test, P = 0.004) and feedback (Kruskal–Wallis test, P = 0.005) periods than its counterpart (red line, mean ± SEM). Filtering out the 8/84 neurons that were selective for the previous trial response from the analysis (one-way ANOVA) did not affect the difference in response coding, which remained significant in the late–delay (Kruskal–Wallis test, P = 0.02) and feedback (Kruskal–Wallis test, P = 0.003) periods.

Figure 4.

Intrinsic timescale during fixation predicts neuronal response selectivity in PFdl. (A) Time course of the ROC for the spatial response aligned on the cue (left) and feedback (right) onsets. The population of neurons with long intrinsic timescale (blue line, mean ± SEM) has higher ROC values for the response than those with short intrinsic timescale (red line, mean ± SEM). The black lines indicate a significant difference in the late–delay and feedback periods (Kruskal–Wallis, P < 0.05). (B) Schematic of cross-temporal correlation between ROC values. Each pixel in the triangle is the correlation coefficient between the ROC values computed for 2 time bins for the neuronal population. Sustained population response coding is reflected by high positive correlation, a transient population response is indicated by low correlation, and an inversion of population coding is manifested by negative correlation. (C) Cross-correlation between non-normalized ROC values at time t and t + Δ for PFdl neurons with long intrinsic timescale. Each pixel represents the correlation coefficient between two 50-ms time bins. The population code for the response was maintained for nearly the entire delay but was more transient in the feedback period. (D) Significant P values of each pixel for Pearson’s correlation coefficient in C (black pixel, P < 0.001).The green triangles identify the early–delay and late–delay periods. (E) Cross-correlation between non-normalized ROC values at time t and t + Δ for PFdl neurons with short intrinsic timescale. The population code for the response is inconsistent through the late–delay period. The correlations lose significance in the late–delay period. (F) Significant P-values of each pixel for Pearson’s correlation coefficient in E (black pixel, P < 0.001). The green triangles identify the early–delay and late–delay periods. (G) Comparison between the correlation coefficients at each corresponding pixel (50 ms pixel length) of the short and long timescale populations of Fig 4C,E using Fisher's r-to-z transformation. All pixels with correlation coefficients significantly different between the 2 populations (P < 0.001) are highlighted in black. It is evident that a significant difference emerged in the late–delay period (green triangle), in which the response coding of the neurons with long intrinsic timescale was consistent and sustained to a greater extent than in neurons with short intrinsic timescales.

To check if an average difference in baseline firing rates between the short and long intrinsic timescale neurons could explain differences in response coding, we computed the mean firing rate during 1-s of fixation for the long and short intrinsic timescales neurons. We observed a mean firing rate of 12 ± 1 sp/s (mean ± SEM) for the long intrinsic timescale neurons and of 8 ± 1 sp/s (mean ± SEM) for the short intrinsic timescale neurons. To investigate whether some neurons with higher activity in the population of neurons with long intrinsic timescale could be responsible for the difference observed in response coding, we removed from this population the neurons with the highest firing rate during fixation, in order to match the mean firing rate of the short timescale population. To achieve such a match, we ranked the neurons by firing rate and we removed a number of neurons (10) from this long timescale population, to reach a mean firing rate equal to 8.1 ± 0.7 sp/s comparable to the average firing rate of the short timescale population. We repeated the analysis with this long timescale population subsample, and the result shown in Figure 4A was confirmed. Indeed, as previously observed, the population with long intrinsic timescales encoded the response more strongly in the late–delay (Kruskal–Wallis test, P = 0.02) and feedback (Kruskal–Wallis test, P = 0.005) periods than the population with short intrinsic timescale.

To determine how long the response signal was maintained over time, we performed a cross-temporal pattern analysis between the non-normalized ROC values that were computed in a fixed time window Δ of 50 ms for the long and short intrinsic timescale populations in PFdl (Cavanagh et al. 2016) (see Materials and Methods). High correlation between time t and t + Δ indicates that ROC values were consistent across these 2-time points. A schematic of the ROC correlation is shown in Figure 4B. Each pixel in the triangle is the correlation coefficient between the ROC values that were computed for 2 time bins for each neuron. Figure 4C,E shows the correlation coefficients for various time lags for the long and short timescale populations, respectively. For the long timescale population (Fig. 4C,D), we observed population response coding that was significantly sustained in both the early–delay and late–delay periods in all bins (Pearson’s correlation, P < 0.001; Fig. 4D, green triangles). In contrast, in the short timescale population (Fig. 4E,F), the correlation was significantly sustained in almost all bins in the early–delay (Pearson’s correlation, P < 0.001) but only in few bins in the late–delay period (Fig. 4F, green triangles). These results show that response coding in neurons with long intrinsic timescale was stronger and more consistent and sustained than in neurons with short intrinsic timescales. To compare the temporal maintenance of the population response of the 2 timescale populations, we compared the correlation coefficients in each pixel of the 2 populations using Fisher’s r-to-z transformation (Fig. 4G). We found that a significant difference emerged in many pixels in the late–delay period, in which indeed the response coding for neurons with long intrinsic timescale was more consistent and sustained than in neurons with short intrinsic timescales.

Notably, in the long and short timescale populations, there was no significant correlation between response selectivity in the delay and feedback periods, indicating that the population coding in various periods of the task represents distinct processes (white rectangle in Fig. 4C, E). To check whether there was an actual absence of correlation between these 2 task periods, we correlated the normalized ROC values computed in the 500-ms late–delay with those obtained in the 500-ms feedback period. No correlation was observed neither in the short timescale (r = 0.11, P = 0.47, n = 42, Pearson’s correlation) nor in the long timescale (r = 0.12, P = 0.44, n = 42, Pearson’s correlation) populations.

Discussion

We have examined the relationship between the intrinsic timescales, defined as the decay in the autocorrelation function in the initial fixation period of a visually cued strategy task, and the response and strategy coding in 3 prefrontal areas in which they have been previously described (Tsujimoto et al. 2012). We found that the individual intrinsic timescales predicted the response-coding strength of neurons in PFdl during the delay and feedback periods but not in PFo and PFp. Neurons from PFdl with longer intrinsic timescales tended to develop stronger and more prolonged response coding in the late–delay period and a more robust response coding in the feedback period than those with shorter timescales. However, we did not find a significant correlation between population response coding, measured as ROC values, between the delay and feedback periods, indicating that the working memory and monitoring processes are separate in PFdl (white rectangle in Fig. 4C, E) and that the second is not merely the continuation of the first.

Persistent Delay-Period Activity and Intrinsic Time Constant in the PF

Persistent activity in PF has been associated to features of its microcircuits. The persistent activity of neurons with spatial tuning can be affected by a recurrent neural microcircuit of pyramidal interconnected neurons within layer III and refined by lateral inhibition that is mediated by GABAergic interneurons (Goldman-Rakic 1995; Wang 2001). More recently, it has been shown that persistent activity is mediated specifically by the NR2B NMDA receptors in layer III and not by AMPA receptors (Wang et al. 2013), as predicted by computational models on the basis of the slower kinetics of NR2B, which favors persistent firing (Wang 2001).

Our study identified a relationship between the intrinsic timescales of neurons and their ability to support cognitive functions. The relationship between the intrinsic timescales of the neurons and the strength of their response coding in PFdl is not surprising, considering that PFdl neurons mediate a variety of high-level cognitive functions that require integration of past and future events (Fuster et al. 2000; Fuster 2001). PFdl is involved in sustaining activity, even in the absence of sensory stimuli; maintaining spatial information in working memory in trained (Funahashi et al. 1989; Constantinidis et al. 2001) and untrained monkeys (Meyer et al. 2007); directing spatial attention (Lebedev et al. 2004; Gregoriou et al. 2014); and maintaining the goal information of self (Genovesio et al. 2005, 2008, 2012, 2014a; Genovesio and Tsujimoto 2014) and others in time (Falcone et al. 2016). Although persistent activity is also seen in the parietal and temporal cortex, parietal (Constantinidis and Steinmetz 1996) and inferior temporal (IT) (Miller et al. 1993) neurons represent only the most recent stimulus, whereas persistent-coding in PF neurons can resist the influence of distracting stimuli (di Pellegrino and Wise 1993; Miller et al. 1996; Qi et al. 2010).

Further, PFdl neurons maintain information across trials with and without working memory demands (Genovesio et al. 2006, 2014b; Histed et al. 2009; Curtis and Lee 2010; Genovesio and Ferraina 2014; Marcos et al. 2016), and working memory deficits can depend on the ability to select between currently and previously relevant locations rather than forgetting (Tsujimoto and Postle 2012). Outcome information, even when it is not directly related to task performance, can persist from one trial to the next until new events occur, such as the presentation of a new stimulus or mere decay as a function of time (Marcos et al. 2016). We have found that under a free-choice condition using a strategy paradigm, the prestimulus activity before the potential targets are known can bias future choices (Marcos and Genovesio 2016), suggesting that persistent activity in PFdl can also affect future decisions, likely due to its significant temporal stability. However, that study did not examine the relationship between the neuronal timescales and the response coding. In the current study, we provide evidence that intrinsic neural properties can support at least the maintenance of response-related information in working memory and its monitoring after response execution in PFdl. This result suggests that the persistent activity that supports a memory signal relies on neurons with a higher degree of stable activity. Nevertheless, the maintenance of the response signal cannot rely entirely on the intrinsic neural stability but should depend also on computations at the network level as indicated by a duration of the persistence of the response coding longer than what is expected just by the intrinsic timescales.

We also examined the relationship between the intrinsic timescales and the strategy coding. We did not find any significant effect in any area of the PF but, interestingly, we observed a close to significant negative correlation in PFdl between the intrinsic timescales and the strategy coding in the cue period. Possibly, this negative result is due to the brief temporal window in which the strategy was coded in PFdl and PFo, in contrast to the more prolonged delay in response coding in PFdl. The small and nonsignificant negative correlation observed in PFdl can be only suggestive of the possibility that neurons with short timescales might play a role in coding signals that do not require to be maintained in time. Future experiments should examine whether neurons can flexibly become temporally specialized and recruited, based on their intrinsic timescale, when the time window of a computation is varied.

Comparison Across PFp, PFdl, and PFo

In contrast to PFdl, we did not observe a significant correlation in the feedback period for PFp and PFo, although both areas showed comparable response-coding during feedback (Tsujimoto et al. 2012). PFp and PFo lacked persistent delay-period activity for spatial responses, as reported by Tsujimoto et al. (2012) and Padoa-Schioppa and Assad (2006) for PFo. Thus, in these 2 areas, the response was represented in a narrower time window during the feedback period, obviating the need for temporally specialized neurons with large temporal receptive fields.

Our findings in PFdl and PFo for response coding appear to contrast with those from Cavanagh et al. (2016), which showed that the intrinsic timescale was predictive of the reward value coding strength and its persistence in PFo but not in PFdl. They suggested that a mechanism of credit assignment is represented by the ability to maintain the chosen value activity until the outcome is known. Notably PFo was the only area in their study with a significant difference in reward value coding between neurons with long and short timescales, although its timescale was comparable to PFdl’s timescale. Their findings indicate that neurons from an area with a high intrinsic timescale, such as PFdl, are unable to maintain value information, although persistent activity in PFdl is important to perform cognitive processes and integrative functions. The contrasting results between the study of Cavanagh et al. (2016) and ours suggest that between various areas of the PF, neurons with higher temporal receptive fields perform different computations. Thus, the intrinsic timescale is not simply organized in a hierarchical manner, as suggested by Murray et al. (2014), in the anterior cingulate cortex, LIP, and PFdl. Each area must function over a broad range of timescales so that, for instance, Yaron et al. (2012) described slow processes in sensory areas, such as the auditory cortex. Our study also extended the examination of the intrinsic timescale to PFp, wherein the time constant of PFp was comparable with that of PFdl and higher than that of PFo.

Further studies should determine whether temporal specialization that is similar to that in PFdl could emerge in PFo in tasks that require rapid learning or during the initial self-initiated exploration of novel alternatives (Boschin et al. 2015). The functional specialization of neurons in our study extends the list of types of functional specialization that have been identified, based on cortical layer and cell type (Hussar and Pasternak 2009, 2012; Opris et al. 2011; Pinto and Dan 2015), to intrinsic timescales. In conclusion, our findings provide evidence of a link between the higher timescales of PFdl—but not PFo and PFp—neurons and their greater response coding, in contrast to the more extensive involvement of neurons with longer time constants in PFo but not in PFdl in value coding (Cavanagh et al. 2016).

Authors’ Contributions

S.T. conceived and designed the experiments. S.T. and A.G. performed the experiments. V.F., S.T., A.G., and E.M. analyzed the data and wrote the article.

Funding

Division of Intramural Research of the National Institute of Mental Health (Z01MH-01092) and in part by Grants-in-Aid from JSPS (15K12049 and 26282218) and ImPACT Program of Council for Science, Technology and Innovation (Cabinet Office, Government of Japan).