Feedback control of calcium driven alternans in cardiac myocytes

Abstract

Cardiac alternans is a beat-to-beat alternation of the action potential duration (APD), which has been implicated as a possible cause of ventricular fibrillation. Previous studies have shown that alternans can originate via a period doubling bifurcation caused by the nonlinear dependence of the APD on the previous diastolic interval. In this case, it has been demonstrated that alternans can be eliminated by applying feedback control on the pacing cycle length. However, studies have shown that alternans can also originate due to unstable calcium (Ca) cycling in cardiac myocytes. In this study, we explore the effectiveness of APD feedback control to suppress alternans when the underlying instability is due to unstable Ca cycling. In particular, we explore the role of the bi-directional coupling between Ca and voltage and determine the effectiveness of feedback control under a wide range of conditions. We also analyze the applicability of feedback control on a coupled two cell system and show that APD control induces spatially out-of-phase alternans. We analyze the onset and the necessary conditions for the emergence of these out-of-phase patterns and assess the effectiveness of feedback control to suppress Ca driven alternans in a multi-cellular system.

Cardiac alternans is a heart rhythm disorder where the electrical response of the heart alternates from beat to beat. Detection of alternans is believed to underlie a wide range of cardiac arrythmias, and treatment strategies have been proposed which seek to eliminate alternans. One approach to eliminate alternans is to apply feedback control where the pacing rate is perturbed at each beat in order to eliminate the alternating response. However, alternans can occur due to a variety of subcellular mechanisms, and it is unclear if feedback control will be effective. In this study, we explore the effectiveness of feedback control when the underlying instability for cardiac alternans is due to calcium cycling. This work will guide experimentalists on how to design feedback control strategies that can be applied to cardiac cells under a wide range of physiological conditions.

INTRODUCTION

It is well known that when a cardiac cell is rapidly paced it undergoes a period doubling bifurcation to alternans where the action potential duration (APD) alternates in a long-short-long pattern.^1–3 This phenomenon has traditionally been explained by the restitution relation $A_{n+1}=f(D_n)$, where $A_{n+1}$ is the APD at beat $n+1$ and $D_n$ is the diastolic interval (DI) at beat n. Given this approximate nonlinear mapping, it is then straightforward to show that when the slope of the restitution curve is larger than one, a period doubling bifurcation to alternans will occur. While this theory has been shown to apply in some cell types, it is now established that there are alternative mechanisms for alternans. In particular, it is well known that APD alternans can also occur due to unstable Ca cycling.⁴ In this case, alternans originates from intracellular Ca cycling where Ca is released periodically from the sarcoplasmic reticulum (SR) and then pumped back into the SR during the relaxation phase. However, Ca cycling is bi-directionally coupled to membrane currents mainly via the L-type Ca current (LCC) which inactivates in a Ca dependent manner, and the sodium–calcium exchanger (NCX) which supplies an inward current that increases in magnitude with the Ca released in the cell. Thus, when the action potential (AP) is unclamped, it is difficult to determine the underlying mechanism that drives the instability of alternans. Numerous studies have explored the dynamics of voltage and Ca alternans and found that the source of the instability depends on cell type and physiological conditions.^5–7 However, it is generally difficult to pinpoint which mechanism drives alternans since Ca and voltage are bi-directionally coupled.

The detection of alternans in heart patients reveals an underlying nonlinear instability that may be fundamental to the induction of cardiac arrhythmias.⁸ As a result, several groups have applied real time control in order to suppress alternans.^9–12 In these studies, the APD is measured on alternate beats and the cell is paced at beat n with a cycle length $(T_n)$ given by

$$\begin{array}{c}{T}_n=T+g(A_n-A_{n-1}),\end{array}$$ (1)

where T is the basic cycle length and g is the gain of the feedback. This control scheme can be applied to the standard restitution based map to show that the amplitude of alternans can be eliminated for a sufficiently large gain parameter g. Several experimental studies have shown that this approach is effective in suppressing alternans under a range of experimental conditions.^10,11,13 Also, recent theoretical studies have explored the effectiveness of feedback control when the restitution relation gives an incomplete description of the beat-to-beat dynamics, i.e., in the presence of memory effects.^14,15 However, it is unclear whether this control scheme is effective when applied to a cardiac cell where the underlying instability is driven specifically by unstable Ca cycling.

In an elegant experimental study, Gaeta et al.⁵ demonstrated that applying feedback control to a cardiac cell can induce spatially discordant alternans of subcellular Ca. They found that when the feedback gain g exceeded a critical threshold, then APD alternans was controlled, while the Ca release within two halves of the cell alternated out of phase. Later, Gaeta et al.¹⁶ argued that this out-of-phase pattern occurred because feedback control modified the bi-directional coupling between Ca and voltage. This result was based on previous work showing that if the bi-directional coupling been Ca and voltage is negative, where a large (small) Ca transient shortened (prolonged) the APD, then a Turing-like pattern forming instability can drive Ca alternans out of phase.^17,18 Thus, they argued that feedback control applied to a cell with positive coupling, where a large (small) Ca transient corresponds to a long (short) APD, induced negative coupling, and thus unmasked the pattern forming instability. However, this study did not analyze the system stability, and, therefore, it is still not understood how much gain g is necessary to induce the spatially out-of-phase patterns observed.

In this study, we develop a general theory of feedback control applied to a physiologically motivated nonlinear map describing both Ca and voltage dynamics. In this approach, we account for nonlinear instabilities that can originate due to APD restitution, Ca cycling, or a combination of both. More importantly, we analyze the critical role of the bidirectional coupling between Ca and voltage that is mediated by Ca sensitive membrane currents that dictate the APD. We analyze the full parameter space of the system and provide quantitative criteria for the effectiveness of feedback control in the case where Ca cycling is the primary driver for alternans. We also analyze a system of coupled cells in order to quantify a criterion for the formation of spatially out-of-phase alternans of Ca when feedback control is applied.

A NONLINEAR MAP MODEL FOR VOLTAGE AND Ca DYNAMICS

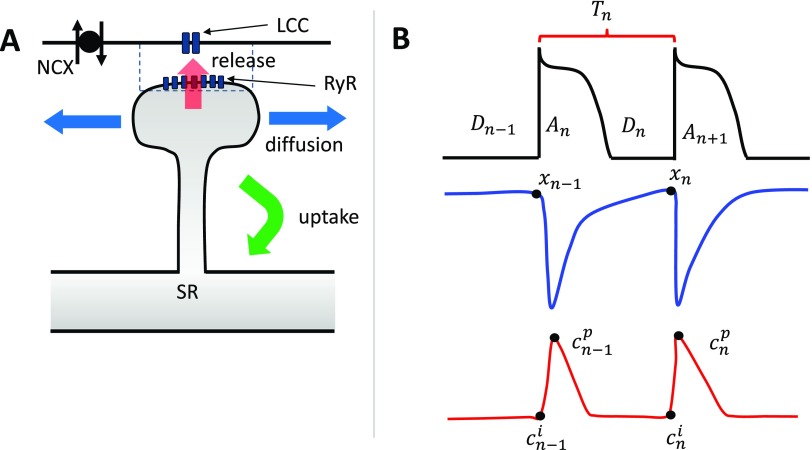
The basic architecture of local Ca signaling is illustrated in Fig. 1(a). Here, Ca is released from the sarcoplasmic reticulum (SR) at a dyadic junction (dashed rectangle), where LCC channels are in close proximity to a ryanodine receptor (RyR) cluster. Ca released from the junction then diffuses into the cytosol and is then pumped back into the SR.¹⁹ In this study, we follow Romero et al.²⁰ and assume that the cell is spatially uniform and develop a beat-to-beat map of the key variables describing voltage and Ca. The key variables describing Ca cycling and voltage are shown in Fig. 1(b), where the cell is paced at a cycle length $T_n$ at beat n. To account for Ca cycling, we keep track of the SR load at the beginning of beat n, which is denoted as $x_{n-1}$. We also keep track of the Ca concentration outside the SR, denoted as $c_{n-1}^i$, before Ca is released following the AP upstroke. Once Ca is released into the cytosol, the Ca concentration rises and peaks at $c_{n-1}^p$, which is referred to as the peak of the Ca transient. Now, during the AP, LCCs open in the cell and deliver Ca in the thousands of dyadic junctions in the cell. The amount of Ca release by sparks depends on the total LCC current, denoted as $I_{Ca}$, which itself is sensitive to the diastolic interval on the previous beat $D_{n-1}$. To capture these functional relationships, we say that at beat n, the total amount of Ca released into the cell is

$$\begin{array}{c}{R}_n=rP(x_{n-1},D_{n-1})x_{n-1},\end{array}$$ (2)

where r is a proportionality constant, and where $P(x,D)$ gives the SR load and DI dependence of the total number of Ca sparks recruited at that beat. Here, we have included a factor $x_{n-1}$ since the local spark amplitude itself should increase in proportion to the SR load. To develop the beat-to-beat map, we first note that Ca release from the SR occurs much faster $(\sim 10\text{ms})$ than the typical pacing cycle length $(\sim 500\text{ms})$. Thus, the peak of the Ca transient at beat n is determined by the amount of Ca released so that $c_{n-1}^p=c_{n-1}^i+R_n$. Now, once Ca is released in the cell, it has to be pumped back into the SR via the sarcoplasmic reticulum Ca-ATPase (SERCA) pump.¹⁹ The amount of Ca pumped by SERCA in one beat is roughly proportional to the cytosolic Ca which can be parameterized by the peak of the Ca transient on that beat $(c_{n-1}^p)$. Also, the amount of Ca pumped is roughly proportional to the amount of time before the next Ca release event. Thus, the total uptake at beat n can be modeled as

$$\begin{array}{c}{U}_n=a{T}_n{c}_{n-1}^p,\end{array}$$ (3)

where a is a constant and $T_n$ is the pacing period. Here, we note that since the amount of Ca pumped back into the SR cannot exceed the amount in the cytosol, then we require that $a{T}_n<1$. Also, for simplicity we will assume conservation of total Ca so that $x_{n-1}+c_{n-1}^i=1$. Therefore, we can write

$$\begin{array}{c}{U}_n=a{T}_n(1-x_{n-1}+R_n),\end{array}$$ (4)

and the beat-to-beat evolution of the SR load is given by

$$\begin{array}{c}{x}_n=x_{n-1}-R_n+U_n.\end{array}$$ (5)

FIG. 1.

(a) Illustration of the basic architecture of Ca signaling in cardiac myocytes. Here, LCC open and inject Ca into the vicinity of an RyR cluster that induces Ca release from the SR. The Ca released into the cell then diffuses and gets pumped back into the SR via uptake pumps. The sodium–Ca exchanger (NCX) regulates the local Ca concentration and couples Ca release to the membrane voltage. (b) Illustration of the beat-to-beat map describing voltage and Ca in a cardiac myocyte. The key variables are the APD $(A_n)$, the diastolic interval $D_n$, the pacing period $T_n$, the SR load $x_n$, the diastolic Ca concentration $c_{n-1}^i$, and the peak of the Ca transient $c_{n-1}^p$.

To couple Ca and voltage, we use the fact that the APD is dependent on the Ca sensitive membrane currents $I_{Ca}$, and the sodium–calcium exchanger current, denoted as $I_{NCX}$. On the one hand, $I_{Ca}$ decreases as more Ca is released into the cell because LCCs inactivate in a Ca dependent manner so that the APD will tend to shorten as Ca release is increased. Also, inward $I_{NCX}$ increases with Ca release so that more Ca release prolongs the APD.¹⁹ Which effect dominates is determined by the cell type and physiological conditions so that the effect of Ca on APD will be taken to be a variable. To model this effect, we use

$$\begin{array}{c}{A}_n=F(D_{n-1})+\gamma R_n,\end{array}$$ (6)

where $\gamma$ is a parameter that determines the sign of the coupling between Ca and voltage. Thus, if the effect of $I_{NCX}$ dominates over $I_{\text{Ca}},$ then the system is said to be in the positive coupling regime and $\gamma >0$. Likewise, if Ca induced inactivation of $I_{Ca}$ is the dominant feedback mechanism, then the coupling is designated as negative coupling, and $\gamma <0$. Here, the function $F(D)$ represents the standard restitution approximation which describes how the APD depends on the previous DI.

NONLINEAR DYNAMICS OF THE TWO VARIABLE MAP

Stability analysis

To analyze the nonlinear dynamics of the two variable map, we compute the stability of the periodic fixed point where

$$\begin{array}{c}\left(\begin{array}{c}\delta x_{n+1}\\ \delta A_{n+1}\end{array}\right)=\left(\begin{array}{cc}{J}_{cc}& J_{cv}\\ J_{vc}& J_{vv}\end{array}\right)\left(\begin{array}{c}\delta x_n\\ \delta A_n\end{array}\right)\end{array}$$ (7)

and where the Jacobian matrix elements are given by

$$\begin{array}{c}{J}_{cc}=\beta (1-R_x),\end{array}$$ (8)

$$\begin{array}{c}{J}_{cv}=\beta R_D,\end{array}$$ (9)

$$\begin{array}{c}{J}_{vv}=-(F_D+\gamma R_D),\end{array}$$ (10)

$$\begin{array}{c}{J}_{vc}=\gamma R_x,\end{array}$$ (11)

where $\beta =1-aT$. Here, we denote $F_D=\mathrm{\partial }F/\mathrm{\partial }D$, $R_D=\mathrm{\partial }R/\mathrm{\partial }D$, $R_x=\mathrm{\partial }R/\mathrm{\partial }x$, and where the partial derivatives are evaluated at the periodic fixed point. The alternans’ instability is determined by the most negative eigenvalue given by

$$\begin{array}{c}\lambda =\frac{J_{cc}+J_{vv}-\sqrt{A}}{2},\end{array}$$ (12)

where $A={(J_{cc}-J_{vv})}^2+4J_{cv}{J}_{vc}$, and where the instability to alternans occurs when $\lambda <-1$. The matrix elements of the Jacobian determine how the physiological properties of the voltage and Ca dynamics effect the instability to alternans. In particular, $J_{cc}$ represents the instability of the Ca cycling system which drives the alternans’ instability when the release vs SR load slope $R_x$ is large. Here, we note that when the Ca cycling system is unstable to alternans, then $R_x\gg 1$, and we have $J_{cc}<0$. On the other hand, the term $J_{vv}$ determines the voltage instability which is driven mainly by a steep restitution slope $F_D>0$, so that $J_{vv}<0$. The coupling between voltage on Ca is dictated by the cross term $J_{cv}=\beta R_D$. Here, we will fix $J_{cv}>0$ since it is known from cell electrophysiology that Ca release increases monotonically with DI, so that $R_D>0$ and $\beta >0$ since $a{T}_n<1$. Likewise, the coupling between Ca on voltage is governed by the matrix element $J_{vc}=\gamma R_x$. In this case, since Ca release is known to be a monotonically increasing function of the SR load, then $R_x>0$, so that the sign of $J_{vc}$ is dictated by $\gamma$. As shown previously,²¹ this two variable map can be classified into three main regimes. These are (i) the Ca driven regime, where $J_{cc}\ll J_{vv}$, i.e., $J_{cc}$ is more negative than $J_{vv}$, (ii) the voltage driven regime, where $J_{vv}\ll J_{cc}$, and (iii) the quasi-periodic regime, where $A<0$ so that the leading eigenvalue is complex. Quasiperiodicity has been observed experimentally,²² but it is rare given the more stringent requirement imposed. In this study, we will focus on the case where Ca cycling is the dominant instability so that $J_{cc}\ll J_{vv}$. In this case, it is useful to consider the limit where the bi-directional coupling is weak compared to the Ca cycling instability $(|J_{cv}{J}_{vc}|\ll J_{cc}^2)$, and the most negative eigenvalue can be well approximated as

$$\begin{array}{c}\lambda \approx J_{cc}-\frac{J_{cv}{J}_{vc}}{|J_{cc}|}.\end{array}$$ (13)

This expression demonstrates how the Ca cycling instability is perturbed by the bi-directional coupling terms $J_{cv}$ and $J_{vc}$ in the limit of weak coupling. Here, we note that since cell electrophysiology requires that $J_{cv}>0$, then the perturbation to the instability threshold is determined by the sign of $J_{vc}=\gamma R_x$.

STABILITY ANALYSIS OF FEEDBACK CONTROL

To apply feedback control, we apply Eq. (1) so that the DI can be written as

$$\begin{array}{c}{D}_{n-1}=T+(g-1)A_{n-1}-g{A}_{n-2}.\end{array}$$ (14)

To simplify further the beat-to-beat mapping, we introduce an auxiliary variable $u_{n-1}=A_{n-2}$, so that our two variable map with feedback control is governed by a three variable mapping. To the first order in g, the Jacobian reads

$$\begin{array}{c}\hat{J}=\left(\begin{array}{ccc}{J}_{cc}+g{a}_{cc}& J_{cv}+g{a}_{cv}& g{a}_{cu}\\ J_{vc}& J_{vv}+g{a}_{vv}& -g{a}_{vv}\\ 0& 1& 0\end{array}\right),\end{array}$$ (15)

where

$$\begin{array}{c}{a}_{cc}=\gamma h{R}_x,\end{array}$$ (16)

$$\begin{array}{c}{a}_{cv}=-\beta R_D-hs-h,\end{array}$$ (17)

$$\begin{array}{c}{a}_{vv}=s,\end{array}$$ (18)

$$\begin{array}{c}{a}_{cu}=\beta R_D,\end{array}$$ (19)

and where $s=F_D+\gamma R_D$, $h=a{c}^{\ast }$, and $c^{\ast }=1-x^{\ast }+R(D^{\ast },x^{\ast })$. Here, $x^{\ast }$ and $D^{\ast }$ denote the SR load and DI at the fixed point, respectively, and where $c^{\ast }$ is the peak of the Ca transient.

To determine the effect of feedback control on the stability of the leading eigenvalue, we will apply perturbation theory to the characteristic polynomial of the Jacobian. We find that to the first order in g the most negative eigenvalue can be expanded in the form

$$\begin{array}{c}\lambda (g)=\lambda +\mathrm{\Gamma }g+\cdots +O(g^2),\end{array}$$ (20)

where $\lambda$ is the eigenvalue in the absence of control, given by Eq. (12), and where

$$\begin{array}{c}\mathrm{\Gamma }=\frac{(b_2{\lambda }^2+b_1\lambda +b_0)}{-\lambda \sqrt{A}},\end{array}$$ (21)

with

$$\begin{array}{c}{b}_2=a_{cc}+a_{vv},\end{array}$$ (22)

$$\begin{array}{c}{b}_1=a_{cv}{J}_{vc}-a_{cc}{J}_{vv}+J_{vv}{J}_{cc}+J_{vv},\end{array}$$ (23)

$$\begin{array}{c}{b}_0=J_{cv}{J}_{vc}-J_{vv}{J}_{cc}.\end{array}$$ (24)

Thus, for small gain g, the effect of control on the coupled system is dictated by the magnitude and sign of the coefficient $\mathrm{\Gamma }$.

Physiological interpretation

In order to understand the effect of feedback control on the system dynamics, it is necessary to interpret the terms that contribute to the quantity $\mathrm{\Gamma }$. First, we note that feedback control is applied when the system is unstable and $|\lambda |>1$ so that the leading order term in the numerator of Eq. (21) is determined by the coefficient

$$\begin{array}{c}{b}_2=\gamma R_D+\gamma h{R}_x+F_D.\end{array}$$ (25)

To interpret the physiological origin of each term, we note that feedback control modifies the cycle length $T_n$ from beat to beat. This perturbation of cycle length can affect the Ca cycling system in two distinct ways. First, changes in $T_n$ have a direct effect on the Ca release on the next beat since release depends on DI via the term $R_n(x_n,D_n)$. This effect modifies the system instability via the term $\gamma R_D$. A second independent mechanism is that $T_n$ determines how long SERCA can pump Ca back into the SR, and, therefore, perturbs the SR load at the next beat. This effect is captured by the term $\gamma h{R}_x$. Finally, feedback control also perturbs the voltage dynamics which is driven by the restitution slope $F_D$. Thus, these three effects contribute to the term $b_2$ and determine whether or not APD feedback control can suppress or enhance Ca alternans. Here, we should point out that numerically the terms $b_1$ and $b_0$ can, under specific conditions, dominate the expression for $\mathrm{\Gamma }$. In this case, the effectiveness of feedback control does not have a direct physiological interpretation and it will be advantageous to simply evaluate $\mathrm{\Gamma }$ numerically.

To simplify further, we will first consider the Ca dominated regime where $J_{cc}\ll J_{vv}$ and where the voltage instability is small $|J_{vv}|\ll 1$. In this regime, we will assume a relatively flat restitution so that $F_D\ll 1$, so that the effectiveness of control is dictated by the leading terms in Eq. (25) so that $\mathrm{\Gamma }\propto \gamma$. Thus, for positive coupling $(\gamma >0)$, feedback control with $g>0$ will stabilize the leading eigenvector and suppress alternans with an effect proportional to $\gamma$. However, for negative coupling $(\gamma <0)$, control with $g>0$ is destabilizing and will promote a faster alternans’ growth rate. In this regime, it is necessary to apply a feedback gain, where $g<0$. Finally, we also mention that in the case when Ca cycling is stable, the dynamical instability is driven by the restitution slope $\mathrm{\Gamma }\propto F_D$ so that control is stabilizing for $g>0$ independently of the coupling between Ca and voltage.

APPLICATION OF FEEDBACK CONTROL TO AN EXPLICIT MAPPING MODEL

To analyze the effect of control on the Ca and voltage dynamics, we will analyze an explicit 2D nonlinear map given by Eqs. (5) and (6). Following our previous study, we will use explicit functions that mimic known physiological dependencies.²⁰ In particular, we will take the probability of release to be a product

$$\begin{array}{c}P(D_{n-1},x_{n-1})=P_{\text{Ca}}(D_{n-1})\cdot P_{sr}(x_{n-1}).\end{array}$$ (26)

To model the voltage dependence of release, we follow the approach of Qu et al.²³ and use a simple functional form

$$\begin{array}{c}{P}_{\text{Ca}}(D)=\frac{1}{1+e^{-(D-\tilde{D})/{\tau }_{\text{Ca}}}},\end{array}$$ (27)

where ${\tau }_{\text{Ca}}$ is the time scale of recovery of the LCC channel, and $\tilde{D}$ determines the onset at which a steep diastolic dependence is engaged. In this study, we will use this parameter to control the steepness of the DI dependence in order to probe the map dynamics for a range of system parameters. To model the SR load dependence, we rely on previous experimental data showing that the amount of Ca released in the cell increases substantially at high SR loads.^24–26 To model this nonlinear dependence, we use a functional form

$$\begin{array}{c}{P}_{sr}(x)=\frac{1}{1+{\left(\frac{x^{\ast }}{x}\right)}^{\nu }}\end{array}$$ (28)

where the Hill coefficients $\nu$ and $x^{\ast }$ determine the steepness and onset, respectively, of the SR load dependence. Finally, to model APD restitution, we will use the functional form

$$\begin{array}{c}F(D)=A_o\left(\frac{1}{1+e^{-(D-D^{\ast })/{\tau }_{APD}}}\right),\end{array}$$ (29)

which models the shape of the restitution curve typically measured in cardiac cells.²⁷ Here, ${\tau }_{APD}$ sets the timescale of recovery of the APD and $D^{\ast }$ determines the DI when the APD falls to half of its maximum value $A_0$.

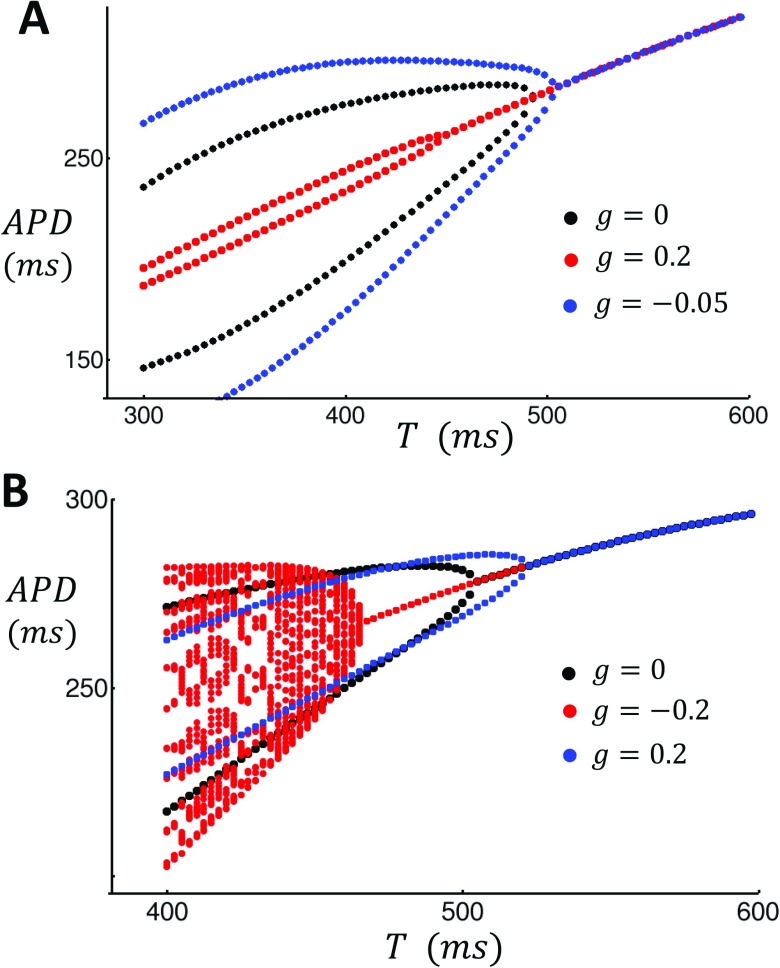
In this study, we will develop two nonlinear map models that exhibit positive and negative coupling, respectively. The model parameters used are given in Table I. As a starting point, we will first consider a nonlinear map model with positive Ca on voltage coupling $(\gamma >0)$. In Fig. 2(a), we plot the steady state APD as a function of the pacing period T for the case of no control (black), control with $g=0.2$ (red), and control with $g=-0.05$ (blue). In these simulations, we observe that turning on control decreases the amplitude of steady state APD alternans and also shifts the onset of alternans $T_c$ to shorter cycle lengths. Also, as expected, we find that turning on control with $g<0$ enhances APD alternans, as it destabilizes the system. In Fig. 2(b), we analyze the response of the negative coupling model. In this case, we find that when $g=0.2$ (blue), the onset for alternans occurs at a longer cycle length $T_c$. Thus, the application of control in this case destabilizes the system. However, when $g=-0.2$, the presence of feedback control stabilizes the system. In this case, we find that the system is unstable to a quasi-periodic solution that emerges at a lower cycle length than the alternans’ instability for the case $g=0$. This result is consistent with our perturbation analysis showing that for $\gamma <0$ control is stabilizing only for the negative g. Thus, our explicit map model confirms our finding that the effectiveness of feedback control is dependent on the sign of the bi-directional coupling between Ca and voltage. To demonstrate this effect over a wider range of parameters, in Fig. 3(a), we plot the steady state amplitude of alternans $\mathrm{\Delta }A=|A_{n+1}-A_n|$ as a function of the gain parameter g for the last 10 beats after iterating the map for 1000 iterations at $T=400\text{ms}$. Indeed, we find that the dependence of $\mathrm{\Delta }A$ on the gain parameter g is crucially dependent on the sign of the bidirectional coupling. For $\gamma >0$, we see that control is effective only for $g>0$ (black line). On the other hand, for $\gamma <0$, control is effective for $g<0$ and is largely ineffective for $g>0$. In Fig. 3(b), we plot the period of alternans’ onset $T_c$ as a function of the gain parameter g. Consistent with our analysis, we find that increasing g decreases $T_c$ in the case, where $\gamma >0$. Thus, control shifts the onset of alternans to faster rates and, therefore, makes the cell more stable. On the other hand, for $\gamma <0$, the onset of alternans decreases with decreasing g. Thus, the system is more stable with decreasing g.

TABLE I.

Ca and voltage map model parameters.

Parameter	Description	Value
$x^{\ast }$	Threshold SR concentration	0.75
$\nu$	Hill coefficient for SR load dependence	35
$r$	Release coefficient	0.7
$a$	Uptake strength	${10}^{-3}(\text{m}{\text{s}}^{-1})$
$\tilde{D}$	LCC restitution parameter	100 ms
${\tau }_{Ca}$	LCC channel recovery time	350 ms
${\tau }_{APD}$	Restitution decay time	100 ms
$A_o$	Restitution parameter	350 ms
$D^{\ast }$	Restitution parameter	50 ms
$\gamma$ (positive)	Ca on V coupling parameter	70 ms
$\gamma$ (negative)	Ca on V coupling parameter	−90 ms

FIG. 2.

Feedback control applied to a nonlinear map model of voltage and Ca. (a) Positive coupling. Nonlinear map is iterated 1000 times for different pacing periods T and the last 10 APDs are plotted. (b) Same as in (a) but using the negative coupling model. The strength of the feedback gain applied is shown in the inset.

FIG. 3.

(a) Steady state alternans amplitude $\mathrm{\Delta }A$, plotted as a function of the gain g, when the cell is paced at $T=400\text{ms}$ for 1000 beats. (b) Alternans’ onset $T_c$ plotted as a function of the gain g. The black (Red) line corresponds to the positive (negative) coupling models.

APPLICATION OF FEEDBACK CONTROL TO A PHYSIOLOGICALLY BASED AP MODEL

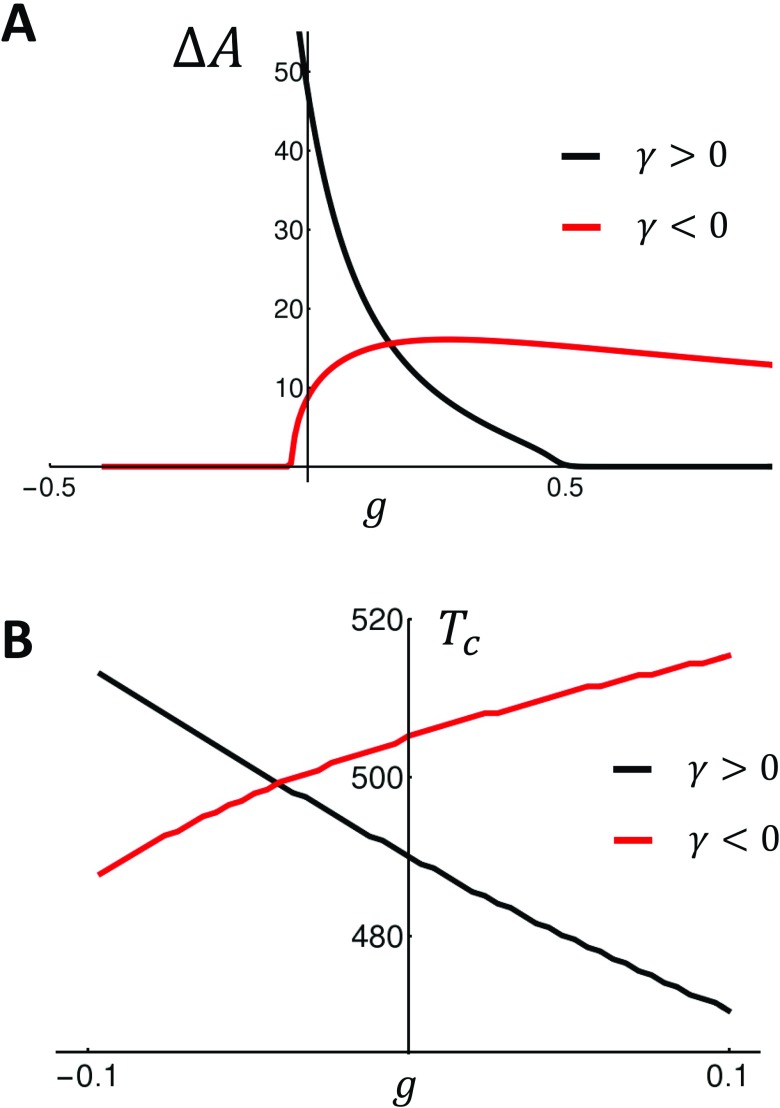
In order to test the qualitative predictions of our nonlinear map analysis, we have also applied feedback control to a physiologically detailed ionic model. The model that we implement is the Mahajan ionic model²⁷ which is based on experimentally measured ion currents from the rabbit myocyte. An important feature of this model is that, at rapid pacing rates, it exhibits APD alternans that are driven by an instability of Ca cycling. By construction, this instability is due to a steep dependence between Ca release on SR Ca load, which is engaged at rapid pacing rates when Ca accumulates in the cell. Thus, this model naturally corresponds to the Ca driven scenario analyzed above in our nonlinear map approach. To analyze the coupling between Ca release and APD in the Mahajan model, we first note that for positive coupling the APD alternates in-phase with the alternation of the peak Ca transient. Indeed, when the Mahajan model exhibits alternans, a long-short-long-short sequence of APD corresponds to a large-small-large-small sequence of Ca transients. Thus, consistent with experimental measurements, the Mahajan model exhibits positive Ca on voltage coupling. Now, to explore the scenario of negative coupling, it is necessary to adjust the Mahajan model so that a long-short-long-short sequence of APD corresponds to a small-large-small-large Ca transient. To accomplish this, it is necessary to enhance the contribution of $I_{\text{Ca}}$ to the APD and reduce the effect of $I_{NCX}$, which promotes positive coupling. Thus, we have reduced the conductance of $I_{NCX}$ by a factor of 0.4. Also, we have enhanced the effect of Ca induced inactivation, which promotes negative coupling, by shifting the threshold for Ca induced inactivation from $3\mu \text{M}$ to $10\mu \text{M}$ and increasing the Hill coefficient from 3 to 4. After these changes are implemented in the ionic model, we find that during alternans the Ca transient and the APD are out of phase during steady state pacing. This confirms that these parameter changes lead to negative coupling of the cell model.

To compare to our nonlinear map model, we will first consider the response of the original Mahajan model to APD feedback control. In Fig. 4(a), we plot the steady state $\mathrm{\Delta }A$ for the last 10 beats after pacing for 400 beats at $T=200\text{ms}$ (black circles). Indeed, by construction at $g=0$, the Mahajan model exhibits Ca driven APD alternans. Alternans’ amplitude is then suppressed as control is turned on for $g>0$ and is enhanced for $g<0$. Now, when the parameters of the Mahajan model are modified so that the model exhibits negative coupling, we find that the system response to control is altered. In Fig. 4(a) (red circles), we find that APD alternans is indeed suppressed for $g<0$. This result is similar to the mapping model prediction [Fig. 3(a)]. However, we find that the onset of control where $\mathrm{\Delta }A=0$ occurs more abruptly in the ionic model. To further analyze the effect of feedback control, we have also computed the onset of alternans $T_c$ as a function of the gain parameter g. In Fig. 4(b), we plot $T_c$ vs g for the Mahajan model (black squares) and the modified model that exhibits negative coupling (red squares). Indeed, consistent with our analysis, we find that increasing the gain stabilizes the Mahajan model, i.e., decreases the onset of alternans $T_c$. On the other hand, when the system exhibits negative coupling, increasing the gain destabilizes the model. Thus, the ionic model response to control is qualitatively similar to our mapping analysis which identified the sign of Ca on voltage coupling as the key variable that dictates the effectiveness of feedback control.

FIG. 4.

Feedback control applied to a physiologically based ionic model. (a) Steady state amplitude of APD alternans $\mathrm{\Delta }A$ vs the feedback gain g. In this simulation, the cell is paced for 100 beats at 200 ms and $\mathrm{\Delta }A$ is computed using the last two beats. (b) The onset of alternans $T_c$ as a function of the feedback control g.

TWO ELECTRICALLY COUPLED CELLS

In this section, we will explore the response of two electrically coupled cells to APD feedback control. Our two cell system is illustrated in Fig. 5(a) where the Ca dynamics within each cell is described by the SR load $x_n$ and $y_n$, respectively. The two cells are electrically coupled so that both share the same APD denoted as $A_n$. Also, we will assume that there is no diffusion of Ca between cells since it is known that the flow of Ca from cell to cell is negligible on the timescale of one beat.²⁸ The mapping model for the two cell system is given by

$$\begin{array}{c}{x}_n=x_{n-1}-R_n(D_{n-1},x_{n-1})+U_n(D_{n-1},x_{n-1}),\end{array}$$ (30)

$$\begin{array}{c}{y}_n=y_{n-1}-R_n(D_{n-1},y_{n-1})+U_n(D_{n-1},y_{n-1}),\end{array}$$ (31)

and where the voltage of both cells evolves from beat to beat according to

$$\begin{array}{c}{A}_n=F(D_{n-1})+\left(\frac{\gamma }{2}\right)[R(D_{n-1},x_{n-1})+R(D_{n-1},y_{n-1})].\end{array}$$ (32)

FIG. 5.

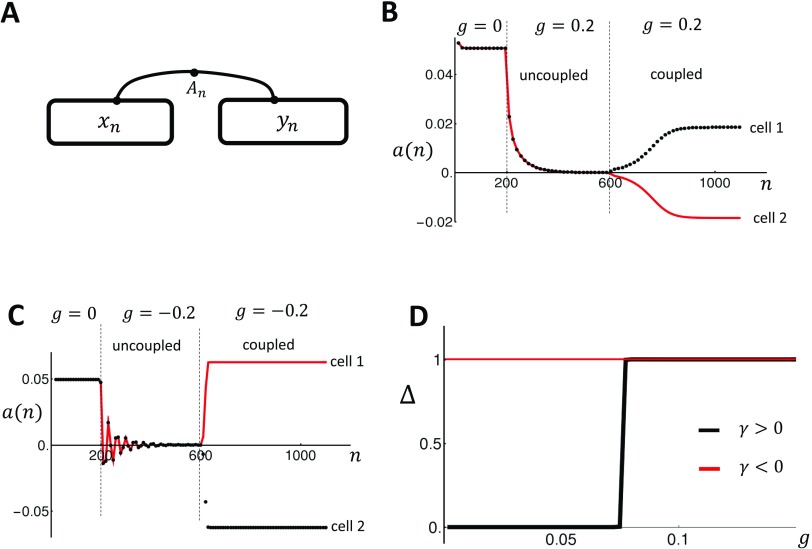
(a) Illustration of two electrically coupled cells. The variables $x_n$ and $y_n$ describe the beat-to-beat dynamics of Ca within each cell, and $A_n$ denotes the APD driving both cells. (b) Beat-to-beat evolution of the alternans’ amplitude $a(n)$ for the two coupled cells in the case of positive coupling. The two cells are initially uncoupled and paced in the absence of control for 200 beats. Control is then turned on with gain $g=0.2$, after which the cells are stabilized after pacing for 400 beats. At the 600th beat, the two cells are connected and pacing is continued. (c) Same as (b) in the case of negative coupling. (d) Plot of the steady state cell-to-cell difference $\mathrm{\Delta }=|x(n)-y(n)|$ as a function of the gain g. Here, we have normalized $\mathrm{\Delta }$ so that the steady state value is $\mathrm{\Delta }=1$. The two cell system is paced at $T=470\text{ms}$.

Here, we have assumed that APD prolongation is proportional to the average Ca release at both cells. After implementing feedback control, we find that to first order in g the Jacobian of the map has the form

$$\begin{array}{c}{J}_2=\left(\begin{array}{cc}\begin{array}{cc}{J}_{cc}+g{a}_{cc}/2& g{a}_{cc}/2\\ g{a}_{cc}/2& J_{cc}+g{a}_{cc}/2\end{array}& \begin{array}{cc}{J}_{cv}+g{a}_{cv}& g{a}_{cu}\\ J_{cv}+g{a}_{cv}& g{a}_{cu}\end{array}\\ \begin{array}{cc}{J}_{vc}/2& J_{vc}/2\\ 0& 0\end{array}& \begin{array}{cc}{J}_{vv}+g{a}_{vv}& -g{a}_{vv}\\ 1& 0\end{array}\end{array}\right).\end{array}$$ (33)

An analysis of the characteristic equation reveals that $J_2$ shares 3 eigenvalues with the single cell Jacobian J given in Eq. (15). These eigenvalues correspond to spatially homogeneous eigenvector solutions to the characteristic equation, while the fourth unique eigenvalue is given by $J_{cc}$ with the corresponding eigenvector

$$\begin{array}{c}\overrightarrow{v}=\left(\begin{array}{c}\begin{array}{c}1\\ -1\end{array}\\ \begin{array}{c}0\\ 0\end{array}\end{array}\right),\end{array}$$ (34)

which represents the mode where Ca cycling in both cells are out of phase, and where $|A_{n+1}-A_n|=0$. Thus, APD control has no effect on this mode and the stability is determined only by the Ca cycling instability $J_{cc}$. Therefore, the two cell system can transition to alternans via a spatially homogeneous mode when $\lambda (g)<J_{cc}$, or alternatively, to a spatially out-of-phase mode when $J_{cc}<\lambda (g)$. To linear order in g, this condition is $J_{cc}<\lambda +\mathrm{\Gamma }g$, which, in the limit where $J_{cc}\ll J_{vv}$, yields the criterion $g>g_c$, where

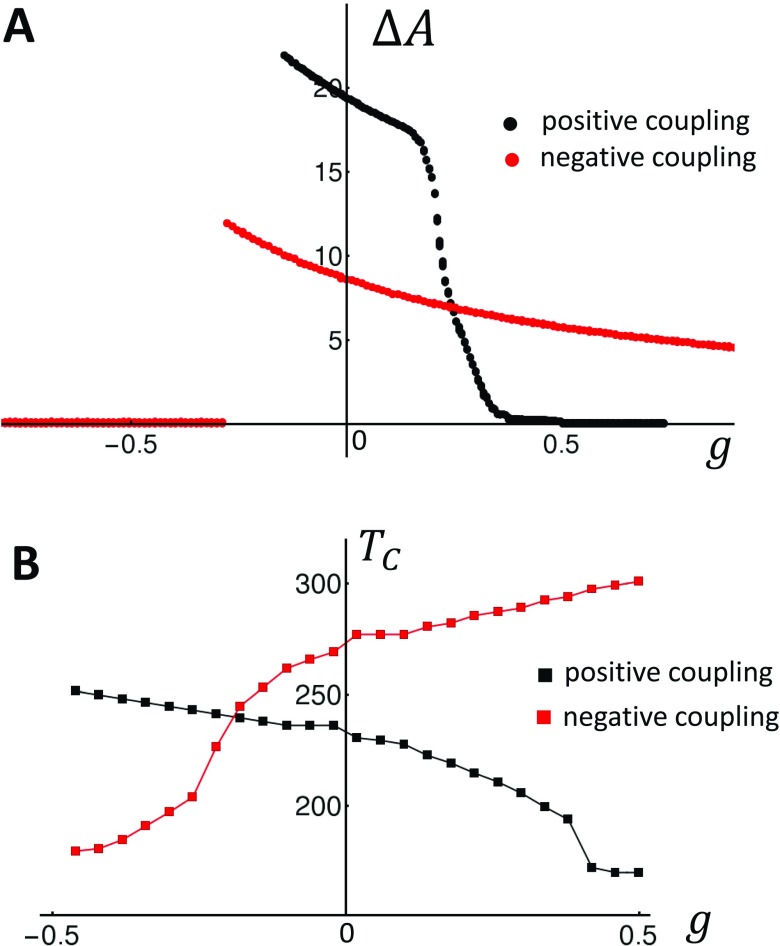
$$\begin{array}{c}{g}_c\approx \frac{1}{\mathrm{\Gamma }}\frac{J_{cv}{J}_{vc}}{|J_{cc}|}\end{array}.$$ (35)

Therefore, the nonlinear map predicts that for positive coupling $J_{cv}{J}_{vc}>0$, spatially out-of-phase alternans in Ca will form for a feedback gain $g>g_c$. However, for negative coupling $J_{cv}{J}_{vc}<0$, spatially discordant alternans form providing $g\ge 0$. This result is consistent with the original study of Shiferaw and Karma,¹⁷ who showed that subcellular Ca becomes spatially out of phase under periodic pacing $(g=0)$ providing the Ca on voltage coupling is negative. Also, Eq. (35) confirms the experimental findings of Gaeta et al.^5,16 who showed that the application of feedback control on myocytes that exhibited positive coupling induced spatially out-of-phase alternans for a gain that exceeded a critical value. In this study, we provide, for the first time, an analytic expression for this critical gain and its dependence on system parameters.

In order to test our prediction for the dynamics of the two cell system, we have applied APD control to our coupled nonlinear map system. To test the prediction of the stability analysis, it is necessary to study the beat-to-beat dynamics near the periodic fixed point. Thus, our procedure is to first apply feedback control to stabilize two uncoupled cells. Once this is achieved, we then electrically couple the cells and then determine the subsequent time evolution of the coupled 2 cell system. In order to keep track of the alternans phase, we measure the beat-to-beat amplitude of alternans given by

$$\begin{array}{c}a(n)={(-1)}^n(x(n)-x(n-1)).\end{array}$$ (36)

This measure ensures that if the two cells are out of phase, then the corresponding alternans amplitude $a(n)$ will have an opposite sign. To proceed, our protocol is to first pace two independent cells to alternans for 200 beats. Once alternans are fully developed, we apply control for 400 beats until alternans is stabilized, after which the two cells are electrically coupled and the system is paced for an additional 600 beats. Also, since both cells are identical, it is necessary to add a small perturbation to the SR load to assess whether the spatially out-of-phase mode will grow or not. Thus, on the 600th beat, we set $x_n\to x_n+\delta$ and $y_n\to y_n-\delta$, where $\delta ={10}^{-3}$. This protocol is applied in Fig. 5(b), where we pace the positive coupling model from Fig. 2(a) at $T=470\text{ms}$. After 200 beats, we apply control with $g=0.2$ so that both cells are stabilized. At beat $n=600$, both cells are connected electrically and we observe that the alternans amplitude of both cells begins to grow to an out-of-phase steady state. Thus, electrical coupling amplifies the small SR load difference and drives the coupled cells so that they alternate out of phase. In Fig. 5(c), we repeat the same simulation for the negative coupling case shown in Fig. 2(b). Here, we apply control with $g=-0.2$ to stabilize the two independent cells after which they are connected. As in the positive coupling case, once the cells are connected, the two cells evolve to an out-of-phase steady state pattern. In order to assess how the steady state depends on the gain parameter g, we have repeated the simulation shown in Figs. 5(b) and 5(c) for a range of gain g. In these simulations, we vary the gain g after electrical coupling at beat $n=600$. To measure the relative phase, we compute the difference in SR load of the two cells at steady state $\mathrm{\Delta }=|x(n)-y(n)|$, so that $\mathrm{\Delta }=0$ if the coupled cells are synchronized and $\mathrm{\Delta }>0$ if they are out of phase. In Fig. 5(d), we plot $\mathrm{\Delta }$ vs g for the positive (black line) and negative (red line) coupling cases. Indeed, we find that for $\gamma >0$, there is a critical $g_c$ after which both cells are out of phase. On the other hand, for $\gamma <0$, the cells are out of phase for any gain $g\ge 0$. This result confirms Eq. (35) which shows that the onset for spatially out-of-phase alternans is proportional to the sign of the bi-directional coupling.

THE MULTICELLULAR SYSTEM

The generalization of our two cell analysis to the case of many cells is straightforward. In the case with N electrically coupled cells, the Jacobian has the dimension $N+2$ and has the form

$$\begin{array}{c}{J}_n=\left(\begin{array}{ccccc}{J}_{cc}+\frac{g{a}_{cc}}{N}& \frac{g{a}_{cc}}{N}& \cdots & J_{cv}+g{a}_{cv}& g{a}_{cu}\\ \frac{g{a}_{cc}}{N}& J_{cc}+\frac{g{a}_{cc}}{N}& \cdots & J_{cv}+g{a}_{cv}& g{a}_{cu}\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ \frac{J_{vc}}{N}& \frac{J_{vc}}{N}& \cdots & J_{vv}+g{a}_{vv}& -g{a}_{vv}\\ 0& 0& \cdots & 1& 0\end{array}\right)\end{array}.$$ (37)

To determine the eigenvectors of this matrix, we first note that the spatially homogeneous mode, where the eigenvector $\overrightarrow{v}$ has equal components, will have the same eigenvalues as the single cell Jacobian J. Thus, for the spatially homogeneous solution, the dominant eigenvalue is simply the single cell eigenvalue $\lambda (g)$ given in Eq. (12). To search for non-homogeneous solutions, we look for solutions $\overrightarrow{v}$, where $v_i=0$ for $i\ge N+1$. Then, we have

$$\begin{array}{c}{J}_n\overrightarrow{v}=\left(\begin{array}{c}{J}_{cc}{v}_1+\frac{g}{N}\sum _{i=1}^N{v}_i\\ J_{cc}{v}_2+\frac{g}{N}\sum _{i=1}^N{v}_i\\ ⋮\\ 0\\ 0\end{array}\right),\end{array}$$ (38)

so that if ${\sum }_i{v}_i=0$, then $\overrightarrow{v}$ is an eigenvector of $J_n$ with eigenvalue $\lambda =J_{cc}$. Thus, all solutions of this form satisfy the eigenvalue equation and have a growth rate that depends only on the Ca cycling instability. Thus, these solutions will grow faster than the spatially homogeneous state providing $J_{cc}<\lambda (g)$. Therefore, in a multicellular system, the conditions for spatially out-of-phase patterns to form is identical to the two cell case and is given by $g\ge g_c$. However, in the multicellular system, there is a multitude of solutions which satisfy the condition ${\sum }_{i=1,N}{v}_i=0$. Thus, the spatial solution that is observed at steady state will be determined by the initial conditions.

DISCUSSION

In this study, we have analyzed the effectiveness of APD feedback control applied to cardiac cells where the period doubling instability is driven primarily by Ca cycling. Our main finding is that the essential variable that determines control is the sign of the coupling between Ca and voltage. Effectively, if a large (small) Ca transient induces a long (short) APD, then the system exhibits positive coupling, and control with the positive gain g is effective in suppressing alternans. On the other hand, if a large (small) Ca transient induces a short (long) APD, then the cell is said to exhibit negative coupling, and it is necessary to apply control with $g<0$. In this case, the application of feedback control with $g>0$ is destabilizing and will enhance rather than suppress APD alternans. These findings are confirmed using a physiologically based nonlinear map that describes voltage and Ca, along with a detailed ionic model. Consistent with our simplified nonlinear map model, we find that it is the bi-directional coupling between Ca and voltage that dictates the effectiveness of feedback control in this system.

In the second part of this study, we explored the effectiveness of APD control to suppress alternans in an electrically coupled two cell system. In this case, we find that the application of control can induce spatially out-of-phase alternans where one cell alternates with a large-small-large-small Ca transient and the coupled cell alternates with a small-large-small-large sequence. When this occurs, we find that APD alternans amplitude is zero and that the stability of the out-of-phase mode is dictated only by the instability of the Ca cycling system $(J_{cc})$. Our analysis shows that there is the critical $g_c$ after which the spatially out-of-phase mode is unstable, and, therefore, dictates the steady state dynamics of the two cell system. Furthermore, we find that $g_c\propto \gamma$ so that for $\gamma <0$, spatially out-of-phase alternans emerge in the case, where $g\ge 0$. This result is consistent with the work of Shiferaw and Karma¹⁷ who demonstrated a pattern forming instability of subcellular Ca in cardiac myocytes exhibiting negative coupling $(J_{cv}{J}_{vc}<0)$. However, in that study, the cell was divided further into sarcomeres, where each sarcomere was treated as an independent unit and Ca was allowed to diffuse across sarcomeres. In that case, spatially out-of-phase subcellular alternans were found to develop in the cell from the spatially homogeneous solution in the presence of a small noise amplitude. Here, we note that when Ca is allowed to diffuse between sarcomeres, the spatially out-of-phase regions will be joined by a smooth interface where the amplitude of alternans crosses a zero point referred to as a node. Here, we point out that while the underlying dynamics will drive two sarcomeres out of phase, Ca diffusion will also tend to synchronize their dynamics. Thus, in the presence of Ca diffusion, we expect that the growth of the spatially out-of-phase mode decreases with an increasing number of nodes. This result is consistent with the results of Shiferaw and Karma, who showed that the growth rate of a pattern with wave number $q>0$ has the form $\mathrm{\Omega }(q\text{)}=\delta -D_{Ca}{q}^2$, where $D_{Ca}$ is the diffusion coefficient of the subcellular Ca. From this perspective, the condition for a pattern forming instability is that $\delta >0$, along with the condition that $\delta >\mathrm{\Omega }(0),$ which is the requirement that the spatially out-of-phase state is more unstable than the spatially homogeneous mode. Consequently, it is straightforward to show that this condition is equivalent to the condition $J_{cv}{J}_{vc}\le 0$, and $J_{cc}<-1$, i.e., the case of negative coupling and unstable Ca cycling.

In the case of positive coupling with $\gamma >0$, there is a critical $g_c>0$ after which the spatially out-of-phase mode is unstable and dominates the steady state behavior. This critical threshold corresponds to the necessary gain such that the spatially out-of-phase solutions grow at a faster rate than the homogeneous solution. This condition is given by $J_{cc}<\lambda (g)$, which occurs as the gain is increased above $g_c$. This result is consistent with the experimental work of Gaeta et al.⁵ who showed that spatially discordant alternans of Ca emerge in cardiac myocytes when control is applied to a Guinea pig ventricular myocyte. They found that at a critical gain, subcellular Ca in two or three regions of the cell exhibited out-of-phase alternans. This finding is consistent with our analysis showing that there is a critical gain after which spatially out-of-phase alternans develop from the spatially homogeneous periodic solution.

DATA AVAILABILITY

The data that support the findings of this study are available within the article.