Leveraging multi-shell diffusion for studies of brain development in youth and young adulthood

Highlights

• •Multi-shell imaging sequences may improve sensitivity to developmental effects.
• •Models that leverage multi-shell information are often less sensitive to the confounding effects of motion.
• •Multi-shell sequences and models that leverage this data may be of particular utility for studying the developing brain.

Abstract

Diffusion weighted imaging (DWI) has advanced our understanding of brain microstructure evolution over development. Recently, the use of multi-shell diffusion imaging sequences has coincided with advances in modeling the diffusion signal, such as Neurite Orientation Dispersion and Density Imaging (NODDI) and Laplacian-regularized Mean Apparent Propagator MRI (MAPL). However, the relative utility of recently-developed diffusion models for understanding brain maturation remains sparsely investigated. Additionally, despite evidence that motion artifact is a major confound for studies of development, the vulnerability of metrics derived from contemporary models to in-scanner motion has not been described. Accordingly, in a sample of 120 youth and young adults (ages 12–30) we evaluated metrics derived from diffusion tensor imaging (DTI), NODDI, and MAPL for associations with age and in-scanner head motion at multiple scales. Specifically, we examined mean white matter values, white matter tracts, white matter voxels, and connections in structural brain networks. Our results revealed that multi-shell diffusion imaging data can be leveraged to robustly characterize neurodevelopment, and demonstrate stronger age effects than equivalent single-shell data. Additionally, MAPL-derived metrics were less sensitive to the confounding effects of head motion. Our findings suggest that multi-shell imaging data and contemporary modeling techniques confer important advantages for studies of neurodevelopment.

1. Introduction

Diffusion-weighted imaging (DWI) has informed our understanding of both local tissue (Basser and Pierpaoli, 1996; Koh and Padhani, 2006; Svolos et al., 2014) and distributed network properties of the brain in vivo (Sporns et al., 2005; Gollo et al., 2018). DWI has proven to be particularly useful for studying neurodevelopment, and has provided critical evidence of the protracted maturation of white matter from infancy into adulthood (Lebel et al., 2008; Schmithorst and Yuan, 2010; Asato et al., 2010; Larsen et al., 2018; Jalbrzikowski et al., 2017). Recent studies have leveraged tools from network neuroscience and established that structural networks reconfigure in development to promote efficient communication (Hagmann et al., 2010; Fan et al., 2011; Grayson et al., 2014; Baum et al., 2017; Uddin et al., 2011; Baker et al., 2015; Bassett et al., 2018; Huang et al., 2015).

Most DWI studies have used single b-value diffusion acquisitions (“single shell”) and applied a diffusion tensor imaging (DTI) model to characterize observed diffusion patterns as indices of neuronal microstructure (Lebel and Deoni, 2018; Lebel et al., 2017). While valuable, these studies may have been limited by certain characteristics of the diffusion tensor model and single-shell imaging sequences. In practice, metrics derived from the diffusion tensor model underestimate diffusion restriction in voxels within crossing fibers (Jeurissen et al., 2013; Jones and Cercignani, 2010; Volz et al., 2018; De Santis et al., 2014) and are systematically impacted by in-scanner motion, which is often prominent in children (Yendiki et al., 2014; Ling et al., 2012; Baum et al., 2018; Roalf et al., 2016). More recently, a new generation of models have been developed to leverage multiple b-values (“multi-shell”). Although it is unknown if these new models ameliorate the potential impact of motion or other artifacts, they do offer promising advances in characterizing white matter. When systematically varied over a DWI acquisition, the differential tissue responses elicited by different b-values can be used to model more detailed features of the cellular environment (Stanisz et al., 1997; Clark et al., 2002; Assaf and Basser, 2005). These models can be broadly separated into “tissue” and “signal” models (Alexander et al., 2017; Ferizi et al., 2017): tissue models attempt to classify signal attributable to different components of biological tissues, while signal models model the diffusion process directly and do not attempt to delineate tissue composition.

Although several tissue models were foundational for tissue modeling of diffusion images (Assaf and Basser, 2005; Alexander et al., 2010), Neurite Orientation Dispersion and Density Imaging has become the most widely used (NODDI; Zhang et al., 2012). NODDI provides estimates of the directional distribution of neurites (axons and dendrites) as well as compartmental volume fractions. Volume fractions convey the proportion of volume posited to be intracellular, extracellular and isotropic in each voxel based on the estimated contributions of these compartments to the diffusion signal. In contrast to DTI metrics, NODDI estimates separate parameters for the directional spread of water diffusion and the degree of microstructural restriction of water diffusion. This distinction allows more specific tissue properties to be discerned, like fiber direction coherence and intracellular volume fraction. As such, NODDI provides an advance in disambiguating properties of putative cellular microstructure over DTI (Chang et al., 2015; Eaton-Rosen et al., 2015; Mah et al., 2017; Zhang et al., 2012; Kodiweera et al., 2016; Timmers et al., 2016). These differences may have particular importance for developmental studies as recent work suggests that NODDI may be more sensitive to brain development than DTI (Chang et al., 2015; Genc et al., 2017; Nazeri et al., 2015; Mah et al., 2017; Ota et al., 2017). However, it remains unclear as to how useful NODDI-based measures are for studies of brain networks, or how they are impacted by in-scanner motion.

In contrast to tissue-based models like NODDI, “signal” based methods remain agnostic to tissue composition when characterizing the intra-voxel diffusion process. Two recently-introduced techniques which model the intra-voxel diffusion process are Mean Apparent Propagator MRI (MAP-MRI; Özarslan et al., 2013) and Laplacian-regularized MAP-MRI (MAPL; Fick et al., 2016a). Laplacian regularization makes MAPL more resilient to noisy data, which is a particularly important issue in studies of brain development. Notably, signal-based models estimate water molecule displacement patterns without a priori assumptions about the underlying tissue environment (Özarslan et al., 2013; Karmacharya et al., 2018). In contrast to the accumulating number of studies using NODDI to investigate brain development, MAPL has not previously been used in studies of brain maturation. Furthermore, like NODDI, it remains unknown how in-scanner motion may impact MAPL-based measures.

Here, we sought to describe the relationships between three diffusion models, brain development, and in-scanner motion. We evaluated how diffusion metrics from DTI, NODDI, and MAPL are associated with both age and in-scanner motion in a sample of 120 youth and young adults who completed multi-shell diffusion imaging. Importantly, we included DTI metrics derived from solely the b = 800 shell (to more closely match a traditional DTI scan), as well as the full multi-shell scheme. Statistical associations were examined across multiple scales of analysis, including global white matter values, tract values, edges in structural brain networks, and individual voxels. As described below, we present new evidence that multi-shell diffusion data can be leveraged to provide important advantages for studies of the developing brain.

2. Methods

2.1. Participant characteristics

After quality assurance (section 2.3), we studied 120 participants between the ages of 12 and 30 years old (M = 21.27, SD = 3.36, 68 females). Potential participants were excluded due to metallic implants, claustrophobia, pregnancy, acute intoxication, as well as significant medical and/or developmental conditions that could impact brain function. Parental consent and assent was obtained for minors participating in the study (n = 21; 18 after quality assurance). All protocols were approved by the University of Pennsylvania’s Institutional Review Board.

2.2. Image acquisition

All participants were imaged on a 3-Tesla Siemens MAGNETOM Prisma with a T1-weighted structural and diffusion-weighted scan. Our structural scan was a 3 min 28 s MPRAGE sequence with 0.9 × 0.9 × 1.0 mm³ resolution (TR =1810 ms, TE =3.45 ms, inversion time =1100 ms, flip angle = 9 degrees, acceleration factor = 2). Our DWI sequence was a single-shot, multiband, multi-shell acquisition protocol (TR =3027 ms, TE =82.80 ms, flip angle = 78 degrees, voxel size = 1.5 mm³ isotropic, FOV = 210 mm, acquisition time =6 min 12 s, multi-band GRAPPA acceleration factor = 4, phase-encoding direction = anterior to posterior) with 3 diffusion-weighted shells at b = 300 s/mm² (15 volumes), b = 800 s/mm² (30 volumes), and b = 2000s/mm² (64 volumes). The sequence included 9 b = 0 s/mm² scans interspersed throughout. We also acquired a b = 0 s/mm² reference scan with the opposite phase-encoding direction (posterior to anterior) to correct for phase-encoding direction-induced distortions.

2.3. Pre-processing and quality assurance

Distortions induced by phase encoding were corrected using topup from the FMRIB Software Library (FSL; Jenkinson et al., 2012). Eddy-current distortions and in-scanner movement were corrected using eddy from FSL version 5.0.11 with both single slice and multiband outlier replacement (Jenkinson et al., 2012; Andersson et al., 2016, 2017); this processing step also rotated the initial b-vectors from our sequence to align with estimated subject head motions. Motion-, distortion-, and eddy-corrected images served as the common input to all diffusion modeling methods.

Following prior work, we quantified in-scanner motion using the root mean squared displacement over the course of the scan (mean relative RMS; Baum et al., 2018; Roalf et al., 2016). To ensure robustness of our findings across different measurements of diffusion image quality, we also quantified and assessed temporal signal-to-noise ratio (tSNR). Mean relative RMS displacement was calculated between the interspersed b = 0 images, while tSNR was calculated from exclusively the b = 800 shell as in prior work (Roalf et al., 2016). Both metrics were calculated with publicly available tools (https://www.med.upenn.edu/cmroi/qascripts.html). Subsequently, three participants were removed for high in-scanner motion (mean relative RMS ≥ 2.95 SD above the mean) and one participant was removed for low signal-to-noise ratio (tSNR = 3.47 SD below the mean). Manual inspection of all T1 images led to one additional participant being removed for poor T1 image quality.

2.4. Overview of diffusion metrics

We evaluated 14 diffusion metrics from three DWI modeling techniques. From DTI, we calculated fractional anisotropy (FA), mean diffusivity (MD), axial diffusivity (AD), and radial diffusivity (RD; Basser et al., 1994). In accordance with previous applications of DTI to multi-shell data, we fit the DTI model using only the shell where gaussian diffusion patterns were expected (b = 800; Jones and Basser, 2004). We also fit a DTI model to the entire multi-shell dataset using an iteratively reweighted linear least squares estimator tensor fit (Veerart et al., 2013), yielding a multi-shell version of each of the same 4 diffusion metrics. From NODDI, we calculated orientation dispersion indices (ODI), the intracellular volume fraction (ICVF), and the isotropic volume fraction (ISOVF; Zhang et al., 2012). From MAPL, we evaluated the return-to-origin (RTOP), return-to-axis (RTAP), and return-to-plane (RTPP) probabilities (Özarslan et al., 2013; Fick et al., 2016a).

2.4.1. DTI metrics

DTI assesses the directionality and magnitude of water diffusion by assuming a Gaussian diffusion process in each voxel. DTI utilizes a 6 degrees of freedom symmetric tensor model that is fit to the observed signal. Subsequently, the primary direction of diffusion in a voxel is calculated by finding the largest eigenvalue of the tensor. After tensors are fit to a voxel, FA, MD, AD, and RD can be calculated from the corresponding eigenvalues. While MD is the averaged sum of these eigenvalues (representing the average magnitude of water diffusion), AD is derived from only the largest eigenvalue (representing the primary direction of diffusion). RD is the average of the remaining two eigenvalues, both representing eigenvectors orthogonal to the primary one. Finally, FA evaluates the magnitude of the eigenvalue associated with the primary direction of diffusion relative to the remaining eigenvalues. Thus, FA represents the fraction of anisotropy in a voxel aligned with a primary direction of diffusion. As diffusion shows increasing directional preference, FA increases (Soares et al., 2013; Basser et al., 1994).

All DTI metrics were calculated in MRtrix3 using an iteratively reweighted linear tensor fitting procedure (Tournier et al., 2012; Veerart et al., 2013). As mentioned, we included FA, MD, AD, and RD derived from a DTI fit to all of the shells, as well as the same DTI metrics derived from the b = 800 shell only. This processing choice was made to account for the possibility that the utility of including more diffusion directions was outweighed by the non-Gaussian contribution of high b-value acquisitions.

2.4.2. NODDI metrics

NODDI estimates the directional distribution of neurites (axons and dendrites) in a voxel, and then matches diffusion patterns to that distribution. Like DTI, this model is informed by restriction of diffusion unaligned with neuronal fibers, and unhindered diffusion along their prominent axes. Unlike DTI, the introduction of a 3D neurite distribution allows for modeling diffusion restriction in fiber populations with dispersed orientations.

NODDI attempts to parse the diffusion signal into discrete contributions of cellular compartments. The total signal is set to equal the sum of the contributions from each compartment, such that $A=(1-V_{iso})(V_{ic}{A}_{ic}+(1-V_{ic})A_{ec})+V_{iso}{A}_{iso}$, where A is the full diffusion signal, $A_{ic}$, $A_{ec}$, and $A_{iso}$ are the signal attributable to the intracellular, extracellular, and isotropic compartments, and $V_{iso}$, $V_{ic}$, and $V_{ec}$ represent the fraction of tissue volume attributable to the corresponding compartments. In order to assign diffusion signal to one of these compartments, the method assumes neurites can be modeled as zero-radius cylinders, or sticks. NODDI then fits an estimated distribution of these sticks to a spherical distribution, which captures the estimated spread of neurite orientations. ODI measures this spread, which ranges from 0 (non-dispersed) to 1 (highly dispersed). A_ic is calculated with respect to this posited orientation dispersion in any given voxel. Intracellular signal is estimated by comparing the spherical distribution of neurite orientations with the distribution of unimpeded diffusion, yielding $V_{ic}$, or the ICVF metric. Isotropic diffusion signal is attributed to a cerebrospinal fluid compartment, which yields the ISOVF metric (Zhang et al., 2012). Recent advances have markedly accelerated fitting the NODDI model; here we calculated NODDI using AMICO, which has been shown to accelerate fitting the NODDI model by several orders of magnitude without substantially impacting accuracy (Daducci et al., 2015).

2.4.3. MAPL metrics

Unlike tissue-based models such as NODDI, signal-based techniques seek to model the diffusion process directly and do not assume the separability of specific tissue compartments. In contrast to DTI, MAPL is not limited to representing diffusion as ellipsoids, and can therefore in theory capture arbitrary fiber configurations. MAP-MRI characterizes observed DWI signal as a linear combination of angular and radial basis functions. Once fit to the DWI signal, analytic transforms can be directly applied to estimate both the 3D diffusion propagator and the angular diffusion orientation distribution function (Özarslan et al., 2013; Walter, 1977). Building on MAP-MRI, Fick et al. (2016a) recently introduced Laplacian-regularized MAP-MRI (MAPL). MAPL imposes additional smoothness on MAP-MRI’s coefficient estimation using the norm of the Laplacian of the reconstructed signal. This approach effectively penalizes model fits with physiologically improbable high local variances, which are more likely to be artifactual than reflective of signals of interest (Descoteaux et al., 2007). The authors also demonstrated that this method reduces error over MAP-MRI in voxels with crossing fibers (Fick et al., 2016a).

MAP-MRI and MAPL allow for quantification of the likelihood that diffusing molecules undergo zero net displacement in one, two, or three dimensions. More specifically, RTOP estimates the probability of water molecules undergoing no net displacement in any direction. RTAP estimates the probability that molecules undergo no net displacement from their primary axis of diffusion; this axis typically represents the average neuronal tract direction within any given voxel (Assaf and Ofer, 2008; Basser et al., 2000). Finally, RTPP estimates the probability that molecules are not displaced from their original plane perpendicular to the primary direction of diffusion, but is not sensitive towards movement of molecules within that plane (Özarslan et al., 2013). It is important to note that these values reflect probabilities but are not scaled to reflect formal probabilities in the range of 0–1 (Fick et al., 2016a). We fit the MAPL model with a radial order of 8, without anisotropic scaling, using generalized cross-validation for determining optimal regularization weighting. We conducted model fitting and generated RTOP, RTAP, and RTPP with dipy, an open-source diffusion imaging toolbox in Python (Fick et al., 2016a; Garyfallidis et al., 2014).

2.5. Structural image processing

T1 images were processed using the ANTs Cortical Thickness Pipeline (Tustison et al., 2014). Images were bias field corrected using N4ITK (Tustison et al., 2010), and brains were extracted from T1 images using study-specific tissue priors (Avants, Tustison, Wu, et al., 2011). We utilized a custom young-adult template constructed via the buildtemplateparallel procedure in ANTs (Avants et al., 2011a, 2011b). A custom template was used due to evidence demonstrating the utility of custom templates in reducing registration biases (Tustison et al., 2014). The T1 to template affine and diffeomorphic transformations were calculated with the top-performing symmetric diffeomorphic normalization (SyN) tool in ANTs (Klein et al., 2009). The transforms between T1 and the initial b = 0 DWI images were calculated using boundary-based registration with 6 degrees of freedom (Greve and Fischl, 2009). All transforms were concatenated so that only one interpolation was performed.

2.6. Network construction

Accumulating evidence suggests that structural brain networks undergo substantial maturation during youth (Hagmann et al., 2010; Fan et al., 2011; Grayson et al., 2014; Baum et al., 2017; Uddin et al., 2011; Baker et al., 2015). Accordingly, in addition to analysis of summary measures and scalar maps, we evaluated each measure in the context of structural networks. Networks were constructed using the Schaefer 200 cortical parcellation (Schaefer et al., 2014). The parcellation was warped to the custom template, and then projected back to each subject’s T1 and native diffusion space using the inverse of each transform. Whole-brain connectomes were constructed by representing each of the 200 regions as a network node, while deterministic tractography was used to create network edges. Tractography was conducted in Camino (Cook et al., 2006) using the Euler tracking algorithm in native diffusion space (Basser et al., 2000). The intersections between gray and 1mm-dilated white matter were used as both seed regions and termination points for tractography. We used voxels defined as CSF by the segmented T1 image as termination boundaries for streamlines. Voxels defined as white matter by the segmented T1 image were used as an inclusion mask for streamlines, ensuring that streamlines had to pass through white matter. Additionally, we imposed a curvature restriction on all streamlines. Fibers determined to curve more than 60 degrees over a 5 mm interval were discarded in order to mitigate the impact of noise on tractography (Bastiani et al., 2012). Lastly, the mean value of each diffusion metric was calculated along each edge in this network; these values were used as edge weights between nodes connected via tractography. As higher values of ODI and ISOVF both indicate reduced anisotropic diffusivity, ODI and ISOVF values were transformed as 1 – ODI and 1 – ISOVF for weighted structural networks. Similarly, as higher MD and RD also indicate reduced anisotropy, their inverse values (1/RD and 1/MD) were utilized for weighting structural networks.

2.7. Statistical analyses

In order to determine how the spatial distribution of the different diffusion metrics covary, we first evaluated their spatial covariance within subjects across white matter. Specifically, within subjects, we calculated the Spearman’s ρ between each diffusion metric across all white matter voxels. To do so, we masked native-space diffusion images, vectorized diffusion metric values across voxels, and correlated the 14 vectors for each participant. Metric by metric correlations were averaged across all participants.

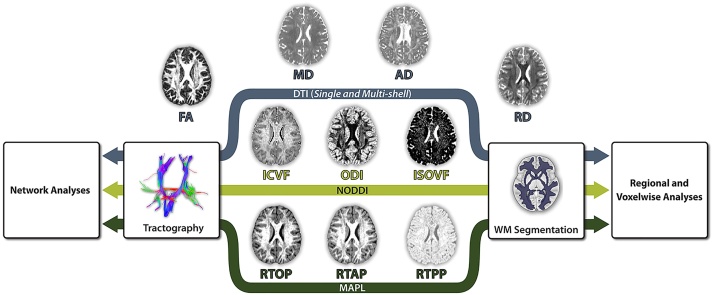
Next, we sought to evaluate the sensitivity of each diffusion metric for investigating neurodevelopment across four levels of features (see schematic in Fig. 1). First, we evaluated age associations with mean diffusion metric values within a global white matter mask. Second, we analyzed regional effects using a common white matter atlas (Mori et al., 2008). Third, we conducted mass-univariate voxelwise analyses within white matter. Finally, we evaluated associations between age and edges within tractography-based structural networks.

Fig. 1.

Analytic workflow. The DTI, NODDI, and MAPL models were fit to the same motion-, distortion-, and eddy-current corrected images, with the exception of the single-shell DTI fit, which only utilized the corrected b = 800 data. The resulting scalar maps were evaluated for associations with both age and data quality at multiple levels of analysis, including mean white matter values, mean values within tracts, white matter voxels, and network edges reconstructed by deterministic tractography that were weighted by each metric.

For all analyses, age effects were estimated with penalized splines and generalized additive models (GAMs; Wood, 2001, 2004) in R (Version 3.5.1) using the mgcv package (R Core Team, 2013; Wood, 2011). To avoid over-fitting, nonlinearity was penalized using restricted maximum likelihood (REML). Sex and in-scanner motion were included as linear covariates. For voxel and edge-level analyses, statistical significance maps were thresholded at p < 0.001 (uncorrected). In order to identify periods of significant neurodevelopment, we quantified the slope of the spline fit for age in each GAM from its derivative. We operationalized the window of significant age-related change as the period at which the 95 % confidence interval of the spline’s estimated slope did not include 0. These calculations were conducted with the gratia package in R (Simpson, 2018).

Additionally, to compare the strength of the age effects across metrics, we calculated an estimate of effect size. As conventional effect size estimates are not available for smoothed terms in GAMs, we calculated effect sizes with polynomial models. We calculated the difference in variance explained (change in R²) between a model that included motion and sex terms only and a model that also included polynomial age terms (linear, quadratic and cubic). As such, the reduced models took the form of y = β_{Head Motion}+ β_Sex. The full polynomial models were: y = β_{Head Motion} + β_Sex + β_Age + β_Age² + β_Age3. In both models, y was the diffusion metric of interest. We calculated the change in R² (ΔR²) between the full and reduced model to provide an estimate of the combined effect size of both linear and non-linear age terms; this was applied to all diffusion metrics evaluated.

In order to estimate the vulnerability of each metric to in-scanner motion, we calculated the correlation of each diffusion metric with our measurement of head motion. In order to remove age and sex effects from all head motion correlations, we first regressed out the effects of age and sex as estimated from GAMs to obtain model residuals. These residuals were then correlated with head motion. We used this correlation coefficient to quantify the relationships between each diffusion metric and head motion while controlling for common sources of variance.

2.8. Code availability

All analysis code is available at: https://github.com/PennBBL/multishell_diffusion.

3. Results

3.1. Measures of diffusion show differential patterns of covariance

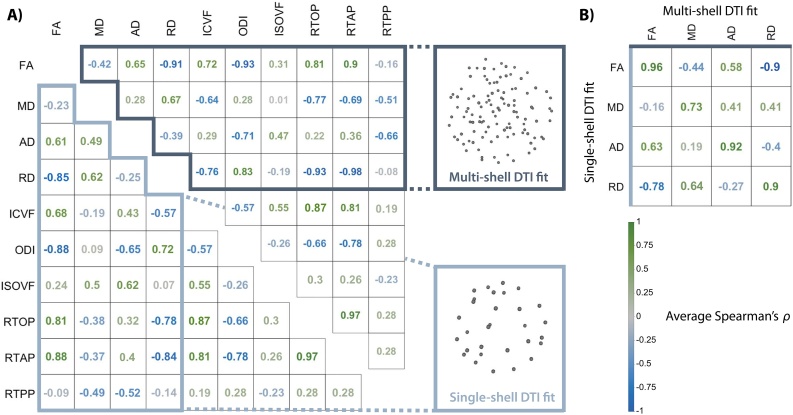
As an initial step, we investigated the relationships between all diffusion metrics of interest with Spearman’s correlations within white matter, and averaged these correlations across participants. This included correlations obtained when using a multi-shell DTI fit (Fig. 2A, top triangle), and single-shell DTI fits (Fig. 2A, bottom triangle). As expected, metrics of diffusion restriction were highly correlated with each other (i.e., FA, ICVF, and RTOP), and negatively correlated with metrics of diffusion dispersion (i.e., MD, ODI). In contrast, measures like RTPP demonstrated less systemic covariation with other metrics. Multi- and single-shell DTI metrics were generally quite similar (Fig. 2B), with MD being the least similar across shell schemes (r = 0.73). Next, we sought to understand the differential utility of these measures of diffusion for studies of brain development.

Fig. 2.

Measures of diffusion are differentially related. A. Average Spearman’s correlations between diffusion metrics in white matter. The top triangle depicts correlations derived from multi-shell DTI fitting, and the bottom triangle reflects correlations derived from single-shell fits. In the corresponding sampling schemes, the distance of each dot from the center of the sphere represents the b-value of a single volume, and the angle represents its b-vector. B. Average correlations between single and multi-shell DTI metrics. FA = fractional anisotropy, MD = mean diffusivity, AD = axial diffusivity, RD = radial diffusivity, ICVF = intracellular volume fraction, ODI = orientation dispersion index, ISOVF = isotropic volume fraction, RTOP = return-to-origin probability, RTAP = return-to-axis probability, RTPP = return-to-plane probability.

3.2. Associations with age vary by diffusion measure

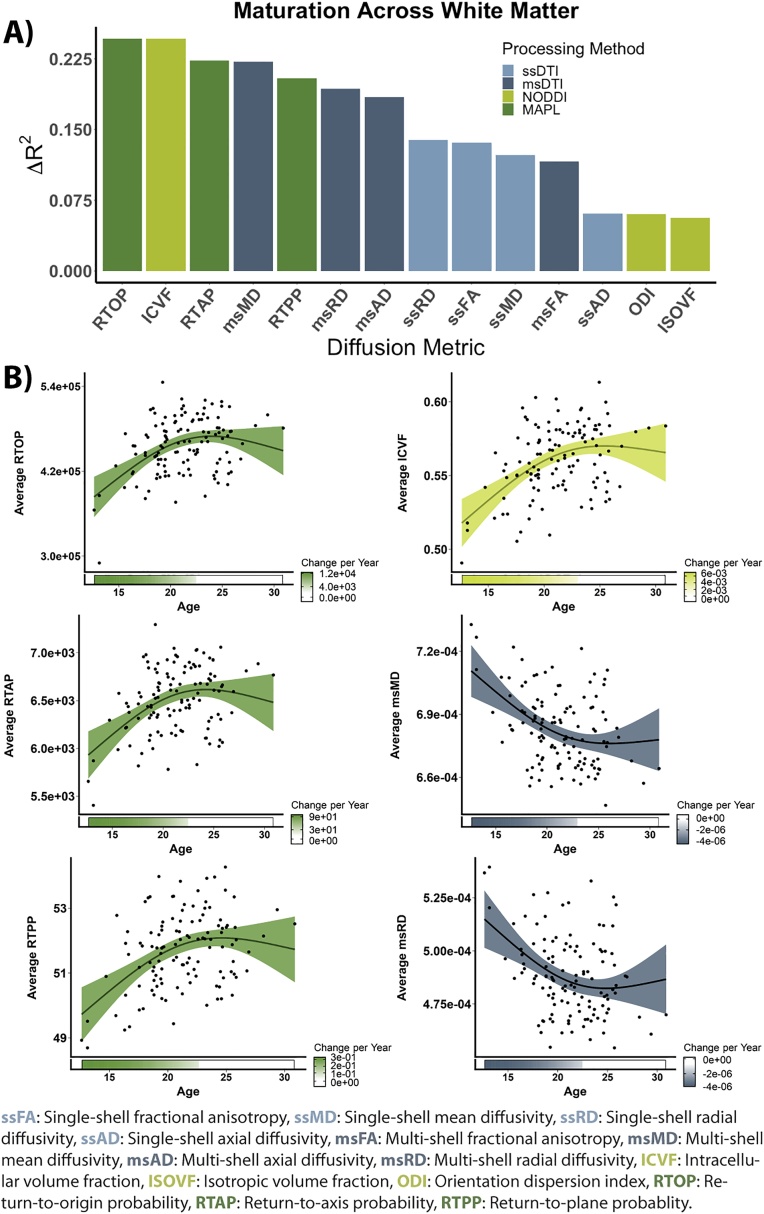
We evaluated the association of each diffusion metric with age at multiple scales. Specifically, we examined mean white matter values, mean values within white matter tracts, and high-resolution voxelwise mass-univariate analyses. While mean white matter values were significantly associated with age across all 14 diffusion metrics, metrics that incorporated data from multiple shells tended to yield the largest age effect sizes (Fig. 3A, Table 1, Fig. S1). When we examined the fitted age trajectories, as expected, we observed that associations with age were strongest at the younger end of the age range sampled and diminished during the transition to adulthood (Fig. 3B). For most diffusion metrics, the slopes of the age effects were no longer significant by the early 20’s. ODI, ISOVF, and ssAD were notable exceptions in that their respective values significantly increased across the entire age range of our sample (Table 1, Fig. S2).

Fig. 3.

Diffusion models leveraging multi-shell data show variable associations with age in white matter. A. Change in R² after the addition of linear, quadratic, and cubic age terms for each diffusion metric. Models included head motion and sex as linear covariates. B. Relationships between mean white matter values and age, after controlling for sex and data quality. GAMs were leveraged to more precisely estimate linear and non-linear effects as one spline. The derivative of these splines, representing the estimated rate of change, are depicted below the x-axis. Shaded area indicates where the confidence interval of the slope does not include 0.

Table 1.

Statistical relationships between mean white matter values and age for each metric. The second and third columns contains the F-statistic and p-value derived from the penalized spline for age in each GAM. The fourth column contains change in R² between polynomial models only accounting for sex and head motion effects and those that include age terms as well. The last column represents the age range at which the 95 % confidence interval for the estimated age effect does not include 0 in each GAM.

Metric	FAge	pAge	ΔR2	Age Spline Slope CI ≠ 0
msFA	4.24	0.034	0.116	12.7−21.3
msMD	14.04	1.20 × 10−5	0.222	12.7−22.9
msAD	14.37	2.07 × 10−5	0.184	12.7−23.8
msRD	10.33	2.16 × 10−4	0.193	12.7−22.4
ssFA	4.91	0.018	0.136	12.7−21.4
ssMD	6.12	0.001	0.123	12.7−22.2
ssAD	6.57	0.012	0.061	NA
ssRD	5.83	0.010	0.139	12.7−21.9
ICVF	18.23	3.41 × 10−7	0.246	12.7−23.0
ODI	5.66	0.019	0.060	NA
ISOVF	5.55	0.020	0.057	NA
RTOP	15.20	2.77 × 10−6	0.247	12.7−22.4
RTAP	13.17	1.64 × 10−5	0.223	12.7−22.4
RTPP	13.87	1.01 × 10−5	0.204	12.7−22.6

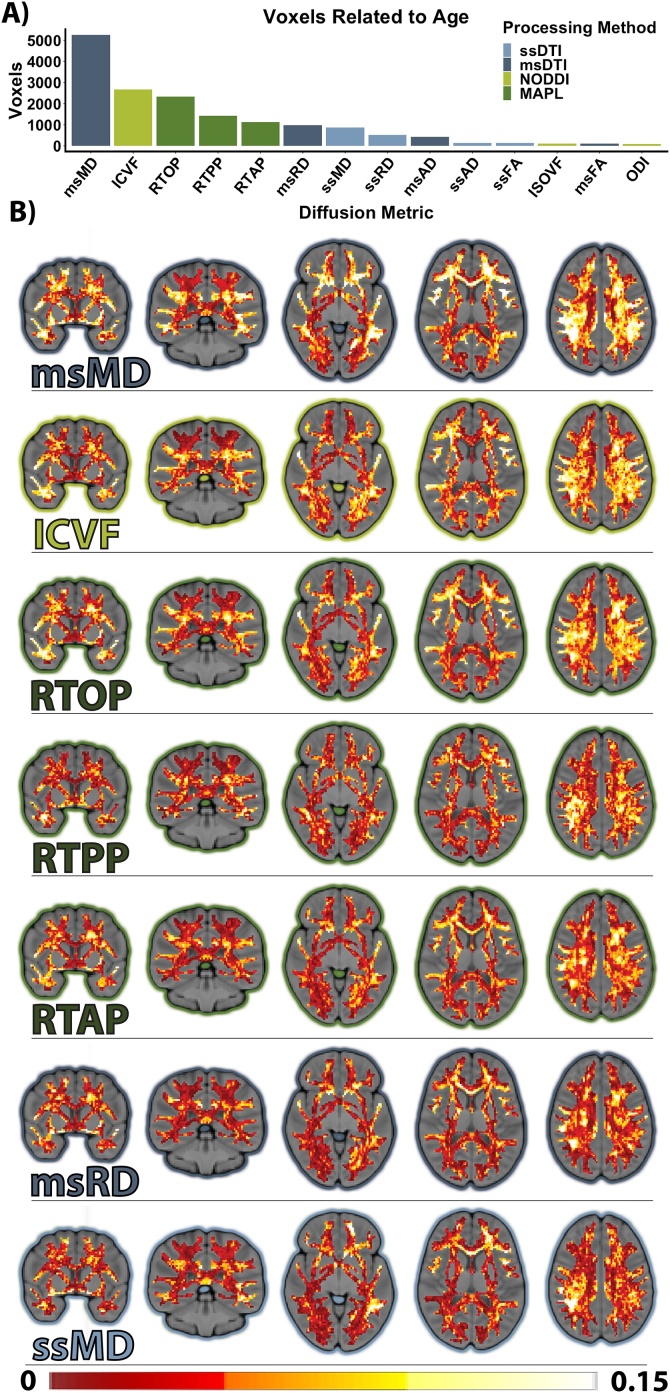
Tractwise analyses revealed a similar pattern of effects to whole brain analyses, further suggesting enhanced developmental sensitivity of multi-shell derived metrics (Table S1). Voxelwise analyses within white matter yielded more heterogenous results. While some metrics demonstrated only sparse associations with age, RTOP, ICVF, and MD derived from all of the shells displayed widespread effects encompassing thousands of voxels (Fig. 4).

Fig. 4.

Regional patterns of neurodevelopment are differentially associated with diffusion metrics. A. Number of voxels related to age (threshold of p < 0.001, uncorrected). B. The 7 diffusion metrics yielding the most voxels associated with age. Voxel color depicts age effect sizes (ΔR²) at each voxel. Note that the color bar only extends to 0.15 for equitable contrast across metrics, but many voxels demonstrated higher changes in R² (msMD_max = 0.44, ICVF_max = 0.30, RTOP_max = 0.59).

3.3. Estimates of network development vary according to diffusion metric

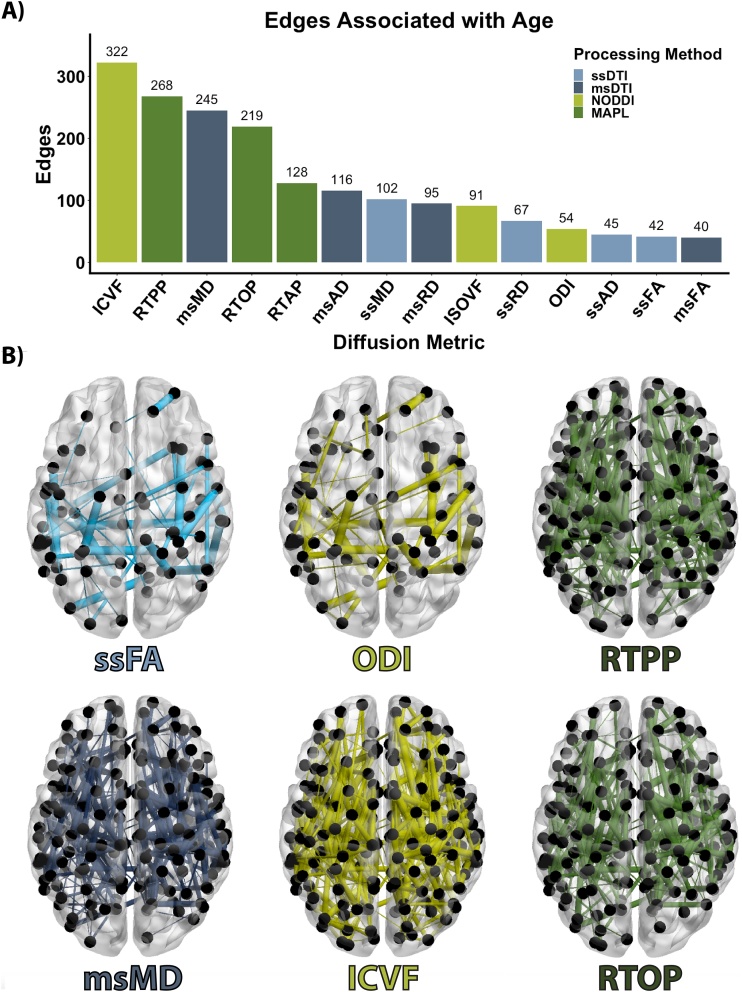
Given that tools from network science are increasingly used to study the developing brain, we next evaluated associations with age within networks where edges were weighted by diffusion metrics. These analyses yielded similar results to the voxelwise analyses described above, with network edges weighted by ICVF, RTPP, msMD, and RTOP displaying the most associations with age (Fig. 5).

Fig. 5.

Scalar-weighted structural networks show differential associations with age. A. Number of edges that displayed significant associations with age while controlling for sex and head motion. B. Associations between age and selected structural networks; thickness of edges is scaled to their transformed p-values, with lower p-values depicted by thicker edges.

3.4. Diffusion measures are differentially impacted by data quality

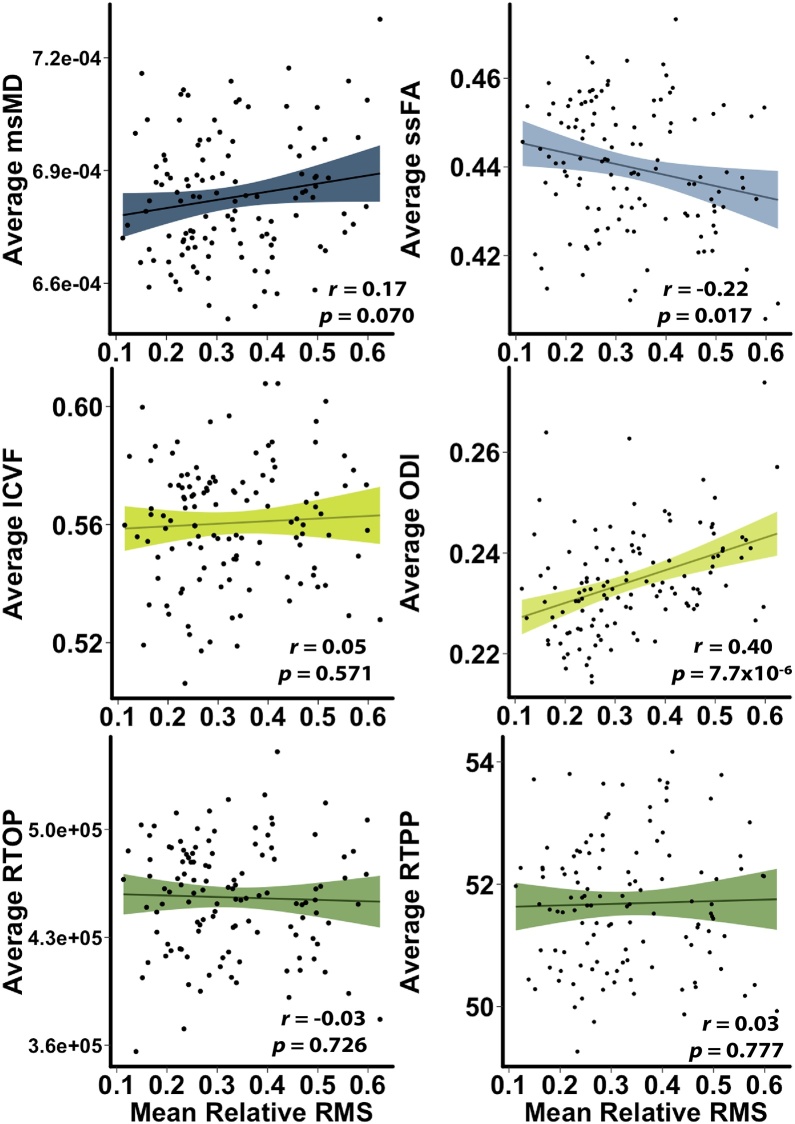
As a final step, we sought to characterize the impact of motion on all diffusion metrics. Evaluation of mean white matter values revealed that several diffusion measures were related to head motion after controlling for age and sex, including FA, RD, ssMD, ODI, and ISOVF (Table 2, Fig. 6). We observed similar patterns at the voxel level, with MAPL metrics and AD being least impacted by motion. Analyses of networks weighted by each of these values revealed relatively similar associations with head motion across metrics, except for ISOVF, which had 118 edges significantly associated with head motion.

Table 2.

Head motion and diffusion metric relations. All correlations were obtained after controlling for age and sex effects, and were derived from mean white matter values. Motion-metric relations were evaluated for statistical significance at the p < 0.001 level across all voxels and edges.

Metric	Global White Matter rrelRMS	Global White Matter prelRMS	# Voxels Related to motion (p<0.001)	# Edges Related to motion (p<0.001)
msFA	−0.30	7.8 × 10−4	143	48
msMD	0.17	0.070	116	52
msAD	−0.07	0.452	57	49
msRD	0.26	4.9 × 10−3	220	51
ssFA	−0.22	0.017	113	45
ssMD	0.23	0.013	278	54
ssAD	0.11	0.219	102	53
ssRD	0.25	0.006	210	49
ICVF	0.05	0.571	138	48
ODI	0.40	7.7 × 10−6	162	59
ISOVF	0.39	1.33 × 10−5	480	118
RTOP	−0.03	0.726	54	42
RTAP	−0.15	0.114	114	44
RTPP	0.03	0.767	71	50

Fig. 6.

Mean measures of diffusion are differentially impacted by in-scanner motion. Selected measures displayed; see Table 2 for full results. All analyses control for age and sex.

4. Discussion

Our findings suggest that diffusion models leveraging multi-shell data have important advantages for studying the developing brain. These advantages include increased sensitivity to developmental effects and reduced impact of in-scanner motion. Benefits of multi-shell data were present at multiple scales, including mean white matter values, white matter tracts, voxelwise analyses, and network edges. The context, implications, and limitations of these results are discussed below.

4.1. Metrics derived from multi-shell data demonstrate superior sensitivity to brain development

In our dataset, diffusion models that leveraged the full multi-shell acquisition had strong associations with age. For some metrics, stronger age associations were present despite relatively high correlations with equivalent single-shell metrics (Fig. 2B). This discrepancy implies that the unique diffusion patterns captured by multi-shell measures may drive associations with age. Specifically, the “slow” diffusion elicited by higher b-values (Stanisz et al., 1997) may change more with age than water diffusion patterns observed at b-values typically used in single-shell sequences. Indeed, additional recent evidence also suggests that high b-value diffusion images may be more sensitive to age effects in many white matter tracts (Genc et al., 2020). Some metrics, like RTPP, were robustly related to age but not highly correlated with other metrics. Because RTPP may capture specific white matter properties, it could be particularly useful as a complementary measure in studies using multiple diffusion metrics to characterize microstructure (Chamberland et al., 2019).

The similar neurodevelopmental patterns observed across the majority of diffusion metrics implicate a common pattern of microstructural changes that plateau in the early 20’s. Prior work has strongly suggested continued myelination throughout adolescence and into adulthood (Lebel et al., 2008; Asato et al., 2010), and persistent myelination may, at least in part, explain developmental effects observed here. However, other important neurobiological factors can affect diffusion properties independent of myelination. Among other factors, increased axonal packing may also contribute to restricted diffusion over neurodevelopment (Neil et al., 2002; Beaulieu, 2002).

In contrast to NODDI, MAPL, and DTI metrics derived from all shells, single-shell DTI metrics tended to demonstrate fewer age associations across all analyses. Although these metrics were calculated from less diffusion directions than their multi-shell counterparts, DTI-based neurodevelopmental inquiries have effectively characterized microstructure with far fewer sampling directions (Lebel et al., 2008). It is important to consider that the diffusion tensor model does not explicitly account for the non-gaussianity of water diffusion that is common at higher b-values. While our estimates of single-shell DTI, NODDI, and MAPL values aligned with previous literature (Lebel et al., 2008; Zhang et al., 2012; Fick et al., 2016a), the combination of high b-value data and the DTI model likely produced the relatively low values of multi-shell DTI metrics. Despite limitations of using the DTI model with multi-shell data, most DTI-derived metrics fit using all shells demonstrated substantial associations with age, particularly MD. This indicates that complete fulfillment of the assumptions of gaussian diffusion underlying the diffusion tensor model may not be necessary for probing broad, albeit potentially non-specific, developmental effects.

These results move beyond previous findings in several respects. To our knowledge, this is the first study to demonstrate that MAPL-derived metrics are highly sensitive to brain development in youth. RTOP, RTAP, and RTPP likely reflect multifaceted aspects of water diffusion becoming more restricted as the brain develops. Age-related changes in RTOP likely reflect aggregate water restriction from developmental factors like myelination and axonal packing (Aung et al., 2013; Beaulieu, 2002; Feldman et al., 2010; Neil et al., 2002), as RTOP is equally sensitive to water movement in all directions in all voxels. However, the neurodevelopmental effects that RTAP and RTPP track may reflect more specific fiber geometry in addition to generalized diffusion restriction. RTAP tracks water displacement from the principal axis of diffusion in a voxel. In white matter voxels with unidirectional fiber populations, RTAP is thought to correspond to cross-sectional area of cylindrically-shaped cellular compartments. Conversely, RTPP tracks water displacement from the plane that is perpendicular to that principal axis of diffusion and may correspond to the length of cellular compartments along that axis (Özarslan et al., 2013). However, like DTI (Volz et al., 2018; Jeurissen et al., 2013; Wheeler-Kingshott and Cercignani, 2009) and NODDI (Farooq et al., 2016), the neurobiological interpretation of MAPL metrics changes in voxels with crossing fibers. Efforts to explicitly model crossing fibers will undoubtedly play a role in disambiguating the relationship between diffusion metrics and fiber properties (Volz et al., 2018; Farooq et al., 2016; Raffelt et al., 2015).

Second, our results demonstrate that multi-shell measures of structural brain network connectivity, such as ICVF and RTPP, are more strongly associated with age than traditional FA-weighted networks. This result builds upon prior studies, which have shown that ICVF derived from NODDI is more strongly associated with age than traditional measures such as FA (Chang et al., 2015; Genc et al., 2017; Ota et al., 2017), and that weighting streamlines with DTI and NODDI metrics may offer complementary information (Deligianni et al., 2016). As previous developmental studies have indicated, these advantages may be driven by greater biological specificity from multi-shell models (Chang et al., 2015; Eaton-Rosen et al., 2015; Mah et al., 2017; Timmers et al., 2016). Overall, the age associations we have presented across analyses emphasize the utility of multi-shell data for studying brain development. These advantages of multi-shell data likely stem from the ability to successfully capture differential tissue responses across b-values and the evolution of complex white matter architecture during development (Jeurissen et al., 2013; Volz et al., 2018).

4.2. MAPL metrics are less impacted by head motion than NODDI and DTI

As children are more likely to move during scanning than adults, motion artifact remains a major concern for studies of brain development (Theys et al., 2014; Satterthwaite et al., 2012; Satterthwaite et al., 2013; Fair et al., 2012). For diffusion imaging and other sequences, the primary determinant of scan quality for diffusion imaging is in-scanner head motion (Yendiki et al., 2014; Ling et al., 2012). Importantly, higher in-scanner motion was associated with reduced mean white matter FA, and increased MD, RD, ODI, and ISOVF while accounting for age. This finding aligns with prior reports of in-scanner motion systematically impacting DTI metrics (Yendiki et al., 2014; Ling et al., 2012; Roalf et al., 2016; Baum et al., 2018).

However, to our knowledge there has been no prior work documenting the impact of in-scanner head motion on ODI and ISOVF, or any measure derived from MAPL. ODI and ISOVF were both significantly positively correlated with in-scanner head motion. Investigators should consider and account for this confound when utilizing the NODDI model. Notably, measures derived from MAPL were minimally impacted by motion. This may be due to the Laplacian signal regularization in MAPL, which was designed to mitigate the impact of noise in DWI acquisitions. Especially when considered alongside the robust associations between MAPL-derived measures and age, noise-resistance may strengthen the rationale for using MAPL in studies of brain development.

4.3. Limitations and future directions

Several limitations should be noted. First, our results were only derived from one study. Replication of these results using multiple datasets, scanners, and acquisition schemes would strengthen evidence for the relative advantages of multi-shell models. Specifically, MAPL has typically been fit on data with b-value shells higher than 2000, raising the possibility that it may perform better in acquisitions with b = 3000 shells (including those used for the HCP and ABCD efforts) (Özarslan et al., 2013; Fick et al., 2016a; Casey et al., 2018). A second limitation of our study is the lack of cellular specificity, which is a limitation of all non-invasive imaging techniques. However, several ex vivo studies of NODDI have suggested a degree of histological correspondence (Schiling et al., 2018; Sato et al., 2017; Grussu et al., 2017). Notably, although MAPL is also sensitive to cellular-level properties, it does not use an explicit model of tissue compartments like NODDI. However, preliminary animal work has tied MAPL diffusion metrics to neurodegenerative tissue abnormalities (Fick et al., 2016b). Third, we used deterministic DTI-based tractography to define streamlines, which results in a sparse structural network biased towards major white matter tracts. While these network analyses demonstrated enhanced associations with several diffusion metrics, networks constructed using multi-fiber tractography techniques might provide additional advantages (Maier-Hein et al., 2017; Reddy and Rathi, 2016; Farooq et al., 2016; Christiaens et al., 2015; Bonilha et al., 2015). Finally, our study mainly included young adults and older adolescents. Studies of younger children would provide complementary data, as prior literature in younger ages has demonstrated dramatic changes in FA during childhood and early adolescence (Lebel et al., 2008; Simmonds et al., 2014). Consequently, we anticipate that inclusion of younger participants could yield stronger FA-measured effects than those observed in our sample. Despite the relatively older age range of our sample, our results demonstrate that diffusion metrics incorporating tissue responses across multiple b-values are sensitive to protracted neurodevelopmental processes that single-shelled metrics may not be able to discern.

4.4. Conclusion

In summary, we provide novel evidence that diffusion metrics are differentially associated with age and motion in youth. Measures that are more tightly linked to brain maturation and less related to data quality are likely to be particularly useful for developmental studies or clinical samples. Through free open-access software, these advanced diffusion methods are relatively easy for investigators to implement (Alimi et al., 2018; Daducci et al., 2015; Fick et al., 2018; Garyfallidis et al., 2014). In the context of these results, we anticipate that multi-shell diffusion models will be increasingly adopted by the developmental and clinical neuroscience community.

Appendix A. Supplementary data

The following are Supplementary data to this article: