Abstract
Interrelationships between retained energy (RE) and retained protein (RP) that are essential in determining the efficiency of use of feeds and the assessment of energy and protein requirements of growing cattle were analyzed. Two concerns were identified. The first concern was the conundrum of a satisfactory correlation between observed and predicted RE (r = 0.93) or between observed and predicted RP when using predicted RE to estimate RP (r = 0.939), but a much lower correlation between observed and predicted RP when using observed RE to estimate RP (r = 0.679). The higher correlation when using predicted vs. observed RE is a concern because it indicates an interdependency between predicted RP and predicted RE that is needed to predict RP with a higher precision. These internal offsetting errors create an apparent overall adequacy of nutrition modeling that is elusive, thus potentially destabilizing the predictability of nutrition models when submodels are changed independently. In part, the unsatisfactory prediction of RP from observed RE might be related to the fact that body fat has a caloric value that is 1.65 times greater than body protein and the body deposition of fat increases exponentially as an animal matures, whereas body deposition of protein tends to plateau. Thus, body fat is more influential than body protein in determining RE, and inaccuracies in measuring body protein will be reflected in the RP comparison but suppressed in the RE calculation. The second concern is related to the disconnection when predicting partial efficiency of use of metabolizable energy for growth (kG) using the proportion of RE deposited as protein—carcass approach—vs. using the concentration of metabolizable energy of the diet—diet approach. The culprit of this disconnection might be related to how energy losses that are associated with supporting energy-expending processes (HiEv) are allocated between these approaches. When computing kG, the diet approach likely assigns the HiEv to the RE pool, whereas the carcass approach ignores the HiEV, assigning it to the overall heat production that is used to support the tissue metabolism. Opportunities exist for improving the California Net Energy System regarding the relationships of RE and RP in computing the requirements for energy and protein by growing cattle, but procedural changes might be needed such as increased accuracy in the determination of body composition and better partitioning of energy.
Keywords: bioenergetics, body composition, calorimetry, growth and development, modeling and simulation, ruminants
INTRODUCTION
The determination of the amounts of retained fat (RF) and retained protein (RP) is the objective of the California Net Energy System (CNES) comparative slaughter technique, and their accurate measurement is the most critical step in calculating the retained energy (RE) by growing cattle consuming known amounts of feeds (Lofgreen, 1965). The RE and RP are essential variables in determining the efficiency of use of feeds and the requirements of energy and protein for maintenance and growth of growing animals (Meyer and Garrett, 1960; Lofgreen and Garrett, 1968). As with any scientific method, standard and reliable methods for measuring body fat and protein are needed to ensure the accurate calculation of RE.
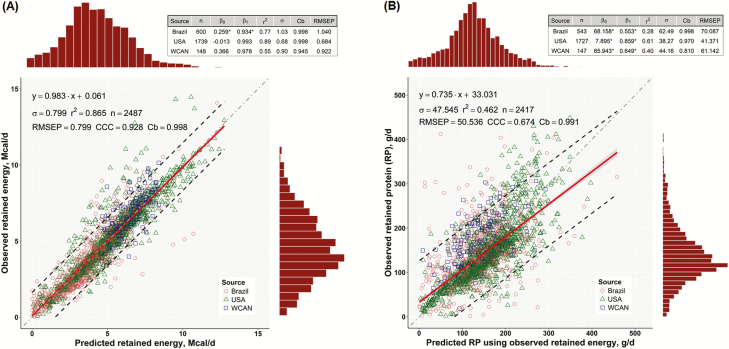
In recent years, two major concerns have been raised regarding the use of RE and RP in computing energy and protein requirements of growing cattle. The first concern was recently described in the publication of the Nutrient Requirements of Beef Cattle by the National Academies of Sciences, Engineering, and Medicine (NASEM, 2016, Ch. 12), which reported a less-than-expected correlation between observed and predicted RP (r = 0.86), but a satisfactory correlation between observed and predicted RE (r = 0.975) when evaluating seven independent studies. The NASEM’s (2016) evaluation, however, used means of animal groups rather than individual values. When the values of individual animals were investigated, the correlation between observed and predicted RE (Figure 1A) decreased slightly from 0.975 to 0.93. In contrast, the correlation between observed and predicted RP was much lower when using observed RE to predict RP (r = 0.679; Figure 1B) than when using predicted RE to predict RP (r = 0.939). These disturbing findings were initially reported by Tedeschi and Fox,(2018) and discussed in a subsequent review of advances in estimating protein and energy requirement of ruminants (Tedeschi et al., 2017). These authors also highlighted additional areas of research that need clarifications. The greater correlation between observed and predicted RP when using predicted RE (r = 0.939) to predict RP vs. using observed RE (r = 0.679) is, by itself, a concern because it indicates a clear interdependency between predicted RP and predicted RE that is needed to predict RP with a higher precision. These internal offsetting errors result in an apparent overall adequacy of the CNES to predict net energy (NE) and net protein (NP) requirements, thereby potentially destabilizing the predictability of nutrition models when submodels are changed independently (Tedeschi et al., 2017). The second concern was previously raised by Tedeschi (2001) and recently discussed by Tedeschi et al. (2002), Williams and Jenkins (2003b), and Tedeschi et al. (2004). These authors independently indicated that the partial efficiency of use of metabolizable energy (ME) for growth (kG) could be estimated based on the proportion of RE deposited as protein (REP) rather than using the concentration of ME of the diet as proposed by Garrett (1980) and adopted by the NRC (1984) and its subsequent revisions. However, intrinsic differences exist between these options in computing kG. The objective of this paper is to provide discussion points and opportunities for improving the CNES regarding the relationships of RE and RP in computing the requirements for energy and protein by growing cattle.
Figure 1.
(A) Relationship between observed and predicted RE (Mcal/d) and (B) relationship between observed and predicted RP (g/d) using observed RE (Mcal/d) for the Brazilian (circles), USA (triangles), and western Canadian (squares) datasets. The solid red lines represent the linear regression of observed on predicted values, the shaded areas represent the 95% confidence interval, and the dashed lines define the 95% prediction interval of all data points. The top- and right-side histograms represent the distribution of the predicted and observed values, respectively. The dashed gray lines represent the y = x, unity line. The adequacy statistics shown at the top grid were computed with the Model Evaluation System [http://www.nutritionmodels.com/mes.html; (Tedeschi, 2006)]. Panels were reproduced from Tedeschi and Fox (2018) with permission.
UNDERSTANDING THE RELATIONSHIP BETWEEN RETAINED ENERGY, BODY FAT, AND BODY PROTEIN
The prediction of RE requires accurate assessment of body composition, more specifically fat and protein, so the amount of RF and RP can be estimated. Besides having a different heat of combustion (i.e., gross energy), however, the relationship between body fat and protein is not linear; it changes as the animal matures. One way to assess body fat and protein is to relate them to body weight (BW). Simpfendorfer (1974) developed empirical regressions to determine chemical body compositions (e.g., fat, protein, ash, and water) at different empty BW (EBW) of 101 British beef steers from five studies, varying from birth to maturity. The author reported that within cattle of similar mature size, 95.6% to 98.9% of the variation in chemical composition was associated with the variation of EBW. More recently, Tedeschi and Fox (2018) updated Simpfendorfer’s original database by including two additional studies (Simpfendorfer, 1974; Tedeschi et al., 2002) and developed Equations 1 and 2 for predictive purposes of empty body fat (EBF) and empty body protein (EBP) contents from EBW, respectively. The revised dataset contains an unbalanced number of steers, heifers, and bulls of Angus, Hereford, Holstein, Nellore, and Shorthorns purebreds, and Angus x Jersey or Hereford x Shorthorn crossbreds. In this database, there were no major differences in body composition among Bos taurus, Holsteins, and Nellore breeds (Tedeschi and Fox, 2018),
| (1) |
| (2) |
where EBF is empty body fat, kg; EBP is empty body protein, kg; EBW is empty body weight, kg; and SE is standard error, kg.
Equations 1 and 2 are not based on longitudinal data in which data are obtained on the same individual multiple times over a period of interest. Rather, these equations are from cross-sectional data in which the points reflect the body composition (e.g., fat and protein) of different animals at different stages of growth, and one point does not have a relationship with another point. Therefore, temporal changes in body composition (and subsequently RE) may not be predicted correctly. But, it can be used to illustrate the aforementioned concept. Eventually, the inclusion of degree of maturity (or equivalent BW) would likely increase the goodness of fit of Equations 1 and 2, but for predictive purposes, it would add another hurdle in predicting body composition because the degree of maturity is not surely known a priori, and it would cause a cyclic dilemma because predicted EBF would depend on maturity degree and vice versa.
Developing a Synthetic Database for Empty Body Fat and Protein Contents
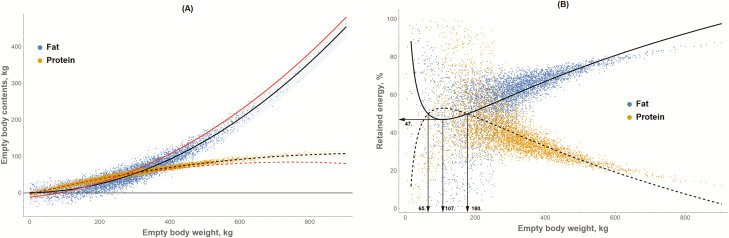
The relationship between RE and RP vs. EBW was evaluated using Monte Carlo simulations (Tedeschi and Fox, 2018) to reconstruct the EBF, EBP, and EBW databases. In a Monte Carlo simulation, the probability density functions of key inputs are used to draw samples to build the desired distributions (McKay et al., 1979; Law, 2007). For EBF and EBP, normal distributions assuming means zero and SE of 13.652 and 3.509 kg, respectively, were used to randomly draw 5,000 points to obtain the uncontrolled, random residue associated with Equations 1 and 2. For EBW, a logistic distribution assuming a mean of 279 kg and a scale parameter of 75.7 kg was used to randomly draw 5,000 points, but negative values were later removed. The Monte Carlo analyses were conducted with Mathematica 11.2 (Wolfram Research Inc., Champaign, IL). The logistic distribution parameters for the EBW were obtained by fitting the original EBW values to different distributions using the @Risk for Excel 7.5 (Palisade Corp., Ithaca, NY). Then, EBF and EBP were estimated for each EBW, using Equations 1 and 2, respectively, and the uncontrolled, random residues obtained with the normal distributions were added to the EBF and EBP estimates. Figure 2A shows the relationship between EBF and EBP vs. EBW of the synthetic database (n = 4,898). For comparative purposes, Figure 2A also depicts the polynomial regressions derived by Owens et al. (1995) from the average means of 12 studies to predict EBF and EBP. For the most part, the Owens et al. (1995) regressions overlap the confidence interval of Equations 1 and 2.
Figure 2.
(A) Predicted empty body fat (blue) and empty body protein (orange) vs. empty body weight (EBW). The solid and dashed black lines represent the polynomial equations 1 and 2, respectively; and the solid and dashed red lines represent the polynomial regressions derived by Owens et al. (1995) to predict fat and protein, respectively. The shaded areas represent the 95% confidence interval. (B) depicts the percentage of energy retained as fat (blue points and solid black line) or protein (orange points and dashed black line) vs. EBW.
Computing Retained Energy and Retained Protein
The body RE was computed assuming the heat of combustion of fat is 9.367 Mcal/kg and protein is 5.686 Mcal/kg (Garrett et al., 1959), yielding Equation 3, which can be used to estimate body RE. Different caloric values for fat and protein have been reported (Tedeschi and Fox, 2018, p. 379), ranging from 9.368 to 9.499 and 5.447 to 5.7 Mcal/kg, respectively. Although this difference might not drastically alter the prediction of RE, it is important to determine the caloric value of the fat and protein and use similar values across studies,
| (3) |
Equation 3 might not be suitable to predict RE for empty weight gain (EWG) because it does not take into account the greater energy density of faster rates of EWG at the same BW. Owens et al. (1995) indicated that the rate of fat accretion increased at different levels of intensity as the rate of EWG increased up to 1.9 kg EBW/d, after which it tended to decrease (Owens et al., 1995).
Figure 2B shows the percentage of RE as fat and as protein across EBW, assuming Equations 1 and 2 and the caloric values of fat (9.367 Mcal/kg) and protein (5.686 Mcal/kg). Equations 4 and 5 have the predicted RF and RP as a percentage of RE, respectively; they were derived based on average values shown in Figure 2B. There is a considerable variation in RF and RP (% of RE) for animals that have an EBW of less than about 250 kg, but there is a clear linear tendency of increasing RF (% of RE) and decreasing RP (% of RP) as EBW exceeds the 250-kg threshold. Many factors can affect the large variation observed in the synthetic database. Different breeds and mature weight influence the rate of deposition of fat and protein. Bailey and Mears (1990) reported that large mature-size calves tend to gain more and deposit less fat than cattle of small mature size at the same BW. Energy level and composition of the diet (Greenwood and Cafe, 2007) and milk intake (Robelin and Chilliard, 1989) also influence the lean-to-fat ratio during the postnatal phase of young calves,
| (4) |
| (5) |
where EBW is the empty body weight, kg; LN is the natural log; RF is the retained fat, % of RE; and RP is the retained protein, % of RE.
Despite the large variation, the patterns of RE and RP (% of RE) pre-250 kg EBW (Figure 2B) suggest that preweaned calves tend to mobilize adipose tissue (i.e., fat) and gain muscle (i.e., protein) until about 113 kg EBW, after which they start depositing more fat than protein. This suggests that, on average, for a short period (from approximately 72 to 180 kg EBW), the energy cost of depositing muscle (i.e., protein) is greater than depositing adipose tissue (i.e., fat). In agreement with this finding, Bonnet et al. (2010) indicated that although fat and protein accretions are concomitant during the postnatal growth of calves, protein accretion has preference over fat accretion during early growth but is reversed later. In part, the loss of adipose tissue could be a result of the oxidation of fat from the brown adipose tissue in support of nonshivering thermogenesis (Carstens, 1994), but this fat depot represents about 2% of BW (Alexander et al., 1975). Additionally, animals that undergo feed restrictions also deposit more protein than fat during the compensation period (Fox et al., 1972; Ryan, 1990), but they usually achieve the same body composition at a later stage of growth if adequate nutrition is provided during the compensatory growth. Based on these facts, the pattern of fat and protein deposition (% of RE) shown in Figure 2B seems to be reasonable.
Assuming that the pattern in Figure 2B represents the changes in body RE from RF and RP, as the animal grows, fat deposition will account for the majority of RE (up to 80%) closer to maturity (approximate EBW > 600 kg). This suggests that prediction of fat composition based on RE should have a greater correlation with the amount of fat being retained. Therefore, without accounting for the impact of the rate of gain on body composition as discussed above, accuracy in predicting RE will increase as the accuracy in measuring RF increases and for animals that are heavier than 180 kg EBW. Because the majority of data points are above this threshold, one would expect a greater precision and accuracy in predicting RE (Figure 1A) rather than predicting RP (Figure 1B). The precision in predicting RP shown in Figure 1B is lower than the precision previously reported by Tylutki et al. (1994) and the National Research Council (NRC, 1996, 2000) of 91% with an underprediction of 2% (i.e., mean bias).
THE RETAINED PROTEIN PREDICTION THAT YIELDS DISPARATE OUTCOMES
Perhaps the major discrepancy in the relationships among RE, RF, and RP for growing cattle is the prediction of RP. The NRC (1996, 2000) and the NASEM (2016) compute the requirement of NP for growth (i.e., RP, g/d) from RE and shrunk weight gain (SWG), as shown in the following equation:
| (6) |
where RE is the retained energy, Mcal/d; RP is the retained protein, g/d; and SWG is the shrunk weight gain, kg/d. The RE/SWG is also known as the concentration of retained energy (REc, Mcal/kg).
As reported by Garrett (1987) and derived by Tedeschi and Fox (2018, pp. 378–379), the proportion of protein in the gain (PIG) can be theoretically established. Assuming that the daily RE (Equation 7) is a function of PIG and fat in the gain (FIG), and their caloric values are constant at 5.686 and 9.367 Mcal/kg, respectively, and that fat-free matter deposition contains water, protein, and ash with only protein deposition contributing energy, PIG can be computed from FIG and protein in the fat-free matter (Equation 8), yielding Equations 9 and 10,
| (7) |
| (8) |
| (9) |
| (10) |
where EWG is the empty weight gain, kg/d; FFMP is the fat-free matter protein, g/g; FIG is the proportion of fat in the gain; PIG is the proportion of protein in the gain; RE is the retained energy, Mcal/d; and REc is the concentration of retained energy in the EWG, Mcal/kg.
Therefore, assuming that fat-free matter of empty body is constant and approximately 73% water, 22% protein, and 5% ash (Reid et al., 1955; Garrett and Hinman, 1969), RP can be theoretically derived from PIG (Equation 9), as shown in Equation 11. Assuming that EWG is 95.6% of SWG, Equation 11 collapses to Equation 12. Similarly, RF can be theoretically derived from FIG (Equation 10), as shown in Equations 13 and 14,
| (11) |
| (12) |
| (13) |
| (14) |
where EWG is the empty weight gain, kg/d; RE is the retained energy, Mcal/d; RF is the retained fat, g/d; RP is the retained protein, g/d; and SWG is the shrunk weight gain, kg/d. The RE/SWG is also known as the concentration of retained energy (REc, Mcal/kg).
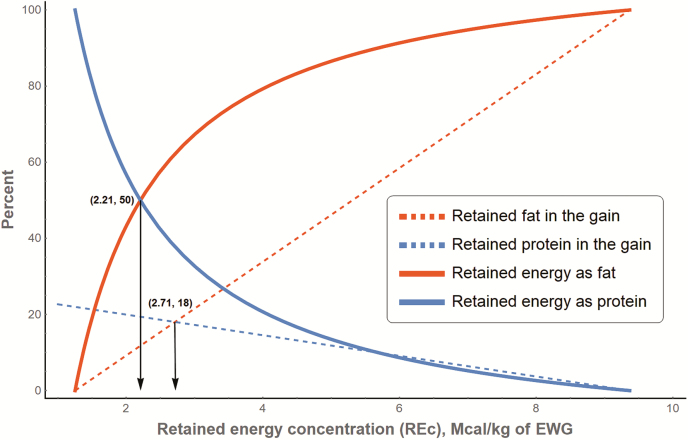
Figure 3 depicts the RF and RP in the gain (dashed lines; i.e., Equations 11 and 14 divided by EWG), and the percentage of RF or RP in the gain as RE (solid lines). When the RE concentration (REc, RE/SWG, Mcal/kg) is about 2.71 Mcal/kg EWG, both fat and protein are deposited at the same proportion (i.e., 18%) that means 18% of the EWG is fat and 18% is protein. Nonetheless, because fat has 1.65 times more energy than protein (9.367 vs. 5.686 Mcal/kg), at 2.71 Mcal/kg EWG, 62% of the RE is used for fat deposition, and the remaining (38%) is protein. When REc is 2.21 Mcal/kg EWG, 50% of the RE is used for fat, and the other 50% is used for protein.
Figure 3.
Partitioning of retained energy (REc, Mcal/kg) into retained fat and retained protein in the gain. Adapted from Tedeschi and Fox (2018) with permission.
Failures in data collection and analysis at the experimental level might partially explain the inadequacy in predicting RP and RF (Tedeschi et al., 2017). Most of the experiments used in the evaluation of RE (Figure 1A) and RP (Figure 1B) used the comparative slaughter technique in which the amounts of RE (Mcal) and RP (kilograms) are determined by difference (final minus initial amounts over a feeding period of at least 30 d), assuming a predetermined initial body composition of the animals slaughtered at the end of the feeding period, and RE and RP are computed by difference. The initial body composition of the animals relies on the body composition of the baseline (i.e., reference group), which is selected to be representative of all animals in the study and is slaughtered at the beginning of the feeding period. The initial composition of the remaining animals is then predicted using either the average of the body composition of the baseline or regressions that relate the body component of interest and EBW or shrunk body weight (SBW) obtained with the baseline animals (Tedeschi et al., 2002). Most experiments have around 5 to 10 animals in the baseline, which may not adequately represent the actual body composition of the remaining animals. Figure 2A clearly shows the variation associated with EBF and EBP around 200 kg, which is a good approximation of the initial BW of animals in many comparative slaughter trials. Scanning technologies such as the computerized tomography (Font-i-Furnols et al., 2014) and dual-energy X-ray absorptiometry (Ribeiro et al., 2011) have been used to estimate body composition of rib sections, but might also be used in determining the composition of live animals in the near future (Scholz et al., 2015).
Another factor affecting the predictability of RE and RP is variability in EWG throughout the feeding period. Animals could have a variable EWG throughout the feeding period because of either receiving different diets or other exogenous factors that affect animal performance, including variable feed intake and environment. Thus, the predicted RF and RP for the whole period do not match the sum of the RF and RP for each period. In part, this difference stems from the nonlinearity associated with the equations used to predict growth requirements (NASEM, 2016). A Monte Carlo simulation (n = 10,000) was used to test this hypothesis and assess the size of the discrepancy in predicting RF and RP either using the EWG and different days on feed (DOF) of four feeding periods or the average EWG and the sum of DOF for the whole period. The initial SBW, EWG, and DOF were assumed to follow normal distributions with means and standard deviations of 200 and 20 kg, 1.5 and 0.1 kg/d, and 50 and 10 d (for each feeding period), respectively. The difference (Δ) was computed as the sum of RF and RP accumulated over the four feeding periods minus the RF and RP predicted for the whole feeding period. The ΔRF was mostly negative (−0.823 ± 0.26 kg) indicating that predicted RF for the whole feeding period was greater than the sum of RF across the four feeding periods. In contrast, the ΔRP was mostly positive (0.181 ± 0.058 kg), but the ΔRE was negative (−6.68 ± 2.14 Mcal). These findings support the idea that dynamic growth models might likely be more sensitive to variation in body composition, possibly yielding improved predictions of feed intake, than steady-state growth models. When expressed on a daily and average EBW basis, the ΔRF was −0.00405 ± 0.00102 kg/d and −0.268 ± 0.0805% EBW, the ΔRF was 0.000892 ± 0.000223 kg/d and 0.059 ± 0.0177% EBW, and the ΔRE was −0.0329 ± 0.00824 Mcal/d and −0.0218 ± 0.00653 Mcal/kg EBW, respectively. Although these values might not improve the predictability of RE (Figure 1A) and RP (Figure 1B), they are a source of variation when using long feeding periods to compute RF and RP because body deposition is not linearly correlated with EWG, as shown in Figure 3.
DETERMINING THE PARTIAL EFFICIENCY OF USE OF METABOLIZABLE ENERGY FOR GROWTH
If the amounts of fat and protein deposited per unit of gain and their efficiencies of deposition are known, a generalized efficiency of energy deposition can be computed. For quite some time, it has been known that the utilization of ME in nonruminants depends on the composition of the gain (Thorbek, 1977; Roberts and Young, 1988). Since the 1970s, the fractionation of RE into RF and RP has been proposed to improve the assessment of the maintenance requirements (Van Es, 1980) because variations in maintenance requirement have been associated with levels of protein accretion (Geay and Robelin, 1979). The variability associated with the efficiency of deposition of fat and protein (Reid et al., 1980; Rompala et al., 1987) was small, likely as a result of the high collinearity among RF, RP, and RE (Roux et al., 1982). Average efficiency values of 75% and 20% have been proposed for fat and protein, respectively (Geay et al., 1980).
The amount of ME needed for growth can, therefore, be computed by assuming the amounts of RE deposited as fat and protein, divided by their efficiencies of deposition, as shown in Equation 15. Assuming that REP represents the proportion of energy that was retained as protein (Equation 16), the amount of RE as fat can be computed as shown in Equation 17, and the partial efficiency of ME used for growth (i.e., kG) can be computed as shown in Equation 18 when replacing kFat by 0.75 and kProt by 0.20 (Tedeschi and Fox, 2018),
| (15) |
| (16) |
| (17) |
| (18) |
where kFat is the net efficiency of deposition of fat, Mcal/Mcal; kG is the partial efficiency of use of ME for growth, Mcal/Mcal; kProt is the net efficiency of deposition of protein, Mcal/Mcal; ME is the metabolizable energy, Mcal/d; RE is the retained energy, Mcal/d; REFat is RE as fat, Mcal/d; REP is the proportion of RE deposited as protein, kg/kg; and REProt is RE as protein, Mcal/d.
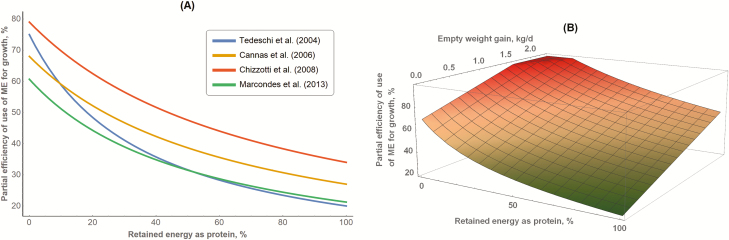
The efficiency of protein deposition from dietary sources (i.e., kProt) varies greatly, however, depending on the physiological stage, feeding level, feed quality, and amino acid profile (Commonwealth Scientific and Industrial Research Organization, 1990, 2007). Unlike protein, the efficiency of fat deposition from dietary sources (i.e., kFat) is believed to have a lower variability and a greater value (97% to 98.9%) than protein, based on biochemical pathway calculations (Armstrong, 1969; Baldwin, 1995, p. 4; Wu, 2017, p. 465), but it varies depending on the substrate it is synthesized from. Therefore, the 20% and 75% efficiencies of deposition of protein and fat, respectively, do not represent all types of feeds. In fact, empirical determination of these efficiencies has led to different values, and the calculation of kG using Equation 18 resulted in different patterns (Figure 4A). Besides the difference between kFat and kProt, the ratio of kFat to kProt (Equation 18) varies as follows: 3.75 (Tedeschi et al., 2004), 2.52 (Cannas et al., 2006; Tedeschi et al., 2010), 2.32 (Chizzotti et al., 2008), and 2.85 (Marcondes et al., 2013). Although the empirically derived values are closer among themselves and lesser (2.32 to 2.85) than the 3.75 kFat-to-kProt ratio, they are relatively greater than previously reported values of 1.856 for growing bulls (Schiemann et al., 1976), likely because the efficiency of protein is being overpredicted (i.e., not accounting for protein turnover inefficiencies).
Figure 4.
The relationship between the predicted efficiency of use of metabolizable energy (ME) for growth (kG) and RE as a protein. (A) Comparison of different studies: the ratio of kFat to kProt (equation 18) was 3.75 (Tedeschi et al., 2004), 2.52 (Cannas et al., 2006; Tedeschi et al., 2010), 2.32 (Chizzotti et al., 2008), and 2.85 (Marcondes et al., 2013). (B) Assuming variable kFat to kProt as a function of EWG based on equations 21 and 22, and assuming a maximum kG of 98%. (A) was adapted from Tedeschi and Fox (2018) with permission.
For growing pigs, Koong (1980) estimated the maximum deposition of fat and the partial efficiencies of depositing fat and protein by solving two nonlinear equations (one for fat gain and another for protein gain) simultaneously and assuming a Michaelis–Menten relationship between fat or protein gains and ME intake. The author also assumed that the partial efficiencies of fat and protein deposition (i.e., kFat and kProt, respectively) were linearly correlated with BW. Equations 19 and 20 indicate that although kFat may increase with BW, kProt likely decreases. This result indicated that kFat and kProt might not be constant throughout the growing and finishing phases; they depend on BW. Furthermore, the proportion of ME used for fat deposition followed a goal-seeking pattern with MEI, reaching a plateau around 84.6%, corroborating with the trend observed in Figure 2B,
| (19) |
| (20) |
Recently, the work of Marcondes et al. (2013) provided additional insights about the variability of kFat and kProt in which they are not constant; they rather vary (linearly) with EWG (Equations 21 and 22, respectively). Based on these Equations, when EWG is zero, the efficiencies become 0.691 and 0.198, respectively, with a ratio of 3.49, closer to the values of 3.75 adopted by Tedeschi et al. (2004). The range of EWG was −0.164 to 2.3 kg/d (Marcondes et al., 2013), but extrapolations of Equations 21 and 22 will yield unrealistic efficiency values. Figure 4B depicts the impact of variables kFat and kProt predicted with Equations 21 and 22, respectively, and RE as protein on the calculation of kG, assuming a maximum kFat of 98%. For the same RE as protein, animals with greater EWG had greater kG, suggesting that regardless the RE as protein, animals can achieve the same kG with different EWG because the efficiency of deposition of fat and protein increases as EWG increases,
| (21) |
| (22) |
Equation 18 assumes that kG can be predicted based on the composition of the gain—carcass approach—whereas Garrett (1980) developed empirical equations to compute NE available for growth (NEg, Mcal/kg) from ME (Mcal/kg), thus leading to the calculation of kG when NEg was divided by dietary ME—dietary approach. The dietary approach assumes that diet ME is the major component in dictating the partial efficiency of use of ME for growth (i.e., kG) regardless of the composition of the gain, or that the composition of the gain is largely dictated by the dietary ME.
As discussed by Tedeschi and Fox (2018, p. 382), additional inconsistencies exist between these approaches in computing kG. The inconsistency of interest here is the possible incorrect allocation of additional energy necessary to support growth that is not part of the RE (i.e., it neither belongs to the RE component nor it is used with the same efficiency). Animals at higher planes of nutrition (and greater rate of gain) have greater maintenance requirement than animals fed at maintenance level (Ferrell et al., 1986; Milligan and Summers, 1986), suggesting the existence of an additional energy expenditure to support growth that does not directly contribute to RE. Williams and Jenkins (2003a) divided the heat increment associated with production (HiEg) into two parts, as follows: 1) energy costs that are directly involved in the synthesis of RE (HiEr) and 2) energy costs that are associated with supporting energy-expending processes that are not directly part of the pathways from precursors absorbed to products synthesized, meaning they are associated with maintenance to support growth (HiEv). As shown by Tedeschi and Fox (2018, p. 376), the CNES assigns both HiEr and HiEv into RE because it computes RE by the difference (Equation 23). In contrast, Equations 15 to 18 correctly assign only the HiEr into RE because it computes RE from the efficiency of tissue deposition and so does not include the HE used to support the tissue metabolism (i.e., HiEv). That is why Equations 15 to 18 overpredicted the kG measured by Marcondes et al. (2013). Their kG values were estimated using the NE system with the approach derived by Lofgreen and Garrett (1968). Consequently, if computing a fixed ME required for maintenance with the NE system, the kG as predicted by Equations 15 to 18 cannot be used because they will not account for HiEv, likely resulting in an underfeeding situation. Furthermore, as expected, HiEv increases with the rate of gain, so the greater the gain, the greater the underprediction of energy requirement. Equation 24 shows the correct calculation for RE given the calculations of kG when using Equations 15 to 18,
| (23) |
| (24) |
where HiEv is the energy necessary to support the growth of the animal that is associated with maintenance, Mcal/d; kG is the partial efficiency of use of ME for growth, Mcal/Mcal; MEI is the metabolizable energy (ME) intake, Mcal/d; MEmr is the ME required for maintenance, Mcal/d; and RE is the retained energy, Mcal/d.
Williams and Jenkins (2003c) provided a way to account for the HiEv component as shown in Equation 24. Through a series of mathematical manipulations, Williams and Jenkins (2003a, 2003c) obtained Equation 25 to predict RE and Equation 26 to predict an adjustment factor that is a function of the ratio of HiEv to ME required for maintenance. Williams and Jenkins (2003a) listed different fixed values of C for different breeds. In their derivation; however, HiEv is a function of BW. A cautionary note for the C adjustment factor (Equation 26) is that the NE required for maintenance (NEmr, Mcal/d) is also adjusted for different breeds (NASEM, 2016), so simultaneously adjusting NEmr and kG might not be appropriate. One might suspect that the composition of the gain would affect the heat production of support metabolism (i.e., HiEv). Thus, an adjustment for degree of maturity rather than breeds might be warranted in future derivations,
| (25) |
| (26) |
In conclusion, two main concerns that plague the CNES were discussed. The first concern was related to the unsatisfactory correlation between observed and predicted RP when using observed RE to predict RP (r = 0.679). It highlighted some inconsistencies in the CNES that may not be easily isolated because of internal offsetting errors that create apparent overall adequacy of nutrition modeling that could potentially destabilize their predictability when submodels are changed independently. The second concern might be more critical as it exposed the disconnection when kG using the proportion of RE deposited as protein—carcass approach—vs. using the concentration of dietary ME—diet approach. This discrepancy essentially illustrated the situation in which the sum of the parts does not add up to the whole, and when the sum of the parts is initiated from different ends (from diet-based vs. carcass-based energetics), the whole differs. It was discussed that this disconnection might be related to how energy losses that are associated with supporting energy-expending processes (i.e., HiEv) are allocated between these approaches. When computing kG, the diet approach likely assigns the HiEv to the RE pool, whereas the carcass approach ignores the HiEV, assigning it to the overall heat production that is used to support the tissue metabolism. The diet approach, however, seems relatively easier to calculate than the carcass approach in practice, although advancements in scanning technologies might facilitate the assessment of body composition. On the other hand, the diet approach requires knowledge of dietary ME that is often calculated from predicted total digestible nutrients of the diet, and in many instances, this prediction raises concerns about its appropriateness in predicting kG. Opportunities exist for improving the CNES regarding the relationships of RE and RP in computing the requirements for energy and protein by growing cattle, but procedural changes might be needed, such as increased accuracy in the determination of body composition and better partitioning of energy. Further modifications in the conceptual partitioning of energy might be needed to eliminate offsetting errors in the CNES calculations, and complete and robust sets of comparative slaughter data will be necessary to evaluate the challenger–defender approach.
LITERATURE CITED
- Alexander G., Bennett J W, and Gemmell R. T.. 1975. Brown adipose tissue in the new-born calf (Bos taurus). J. Physiol. 244:223–234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armstrong D G. 1969. Cell bioenergetics and energy metabolism. In Lenkeit W., Breirem K. and Crasemann E, editors, in Handbuch der Tierernährung. Hamburg, Germany:Paul Parey; p. 385–414. [Google Scholar]
- Bailey C B, and Mears G. J.. 1990. Birth weight in calves and its relation to growth rates from birth to weaning and weaning to slaughter. Can. J. Anim. Sci. 70:167–173. doi: 10.4141/cjas90-019 [DOI] [Google Scholar]
- Baldwin R L. 1995. Modeling ruminant digestion and metabolism. New York, NY:Chapman & Hall. [DOI] [PubMed] [Google Scholar]
- Bonnet M., Cassar-Malek I, Chilliard Y, and Picard B.. 2010. Ontogenesis of muscle and adipose tissues and their interactions in ruminants and other species. Animal. 4:1093–1109. doi: 10.1017/S1751731110000601 [DOI] [PubMed] [Google Scholar]
- Cannas A, Tedeschi L. O., and Fox D. G.. 2006. Small ruminant nutrition system: A computer model to develop feeding programs for sheep and goats.Proceedings of the Joint Annual Meeting of American Society of Animal Science and American Dairy Science AssociationJ. Anim. Sci. Vol. 84, Suppl. 1/J. Dairy Sci. Vol. 89, Suppl. 1, 84Minneapolis, MN: Federation of Animal Science Societies; p. 376—[accessed May 21, 2016]. http://www.jtmtg.org/JAM/2006/abstracts/toc.htm. [Google Scholar]
- Carstens G E. 1994. Cold thermoregulation in the newborn calf. Vet. Clin. North Am. Food Anim. Pract. 10:69–106. doi: 10.1016/S0749-0720(15)30590-9 [DOI] [PubMed] [Google Scholar]
- Chizzotti M. L., Tedeschi L O, and Valadares Filho S. C.. 2008. A meta-analysis of energy and protein requirements for maintenance and growth of Nellore cattle. J. Anim. Sci. 86:1588–1597. doi: 10.2527/jas.2007-0309 [DOI] [PubMed] [Google Scholar]
- Commonwealth Scientific and Industrial Research Organization 1990. Feeding standards for Australian livestock ruminants. Melbourne, Australia:Commonwealth Scientific and Industrial Research Organization. [Google Scholar]
- Commonwealth Scientific and Industrial Research Organization 2007. Nutrient requirements of domesticated ruminants. Collingwood, VIC:Commonwealth Scientific and Industrial Research Organization. [Google Scholar]
- Ferrell C. L., Koong L J, and Nienaber J. A.. 1986. Effect of previous nutrition on body composition and maintenance energy costs of growing lambs. Br. J. Nutr. 56:595–605. doi: 10.1079/BJN19860140 [DOI] [PubMed] [Google Scholar]
- Font-i-Furnols M, Brun A., Marti S., Realini C. E., Pérez-Juan M., Gonzalez J. S., and Devant M.. 2014. Composition and intramuscular fat estimation of Holstein bull and steer rib sections by using one or more computed tomography cross-sectional images. Livest. Sci. 170:210–218. doi: 10.1016/j.livsci.2014.10.009 [DOI] [Google Scholar]
- Fox D G, Johnson R. R., Preston R. L., Dockerty T. R., and Klosterman E. W.. 1972. Protein and energy utilization during compensatory growth in beef cattle. J. Anim. Sci. 34:310–318. doi: 10.2527/jas1972.342310x [DOI] [Google Scholar]
- Garrett W N. 1980. Energy utilization by growing cattle as determined in 72 comparative slaughter experiments. In: Mount L E, editor. Proceedings of the 8th Symposium on Energy Metabolism of Farm Animals, No. 26 Cambridge, UK:Butterworths & Co; p. 3–7. [Google Scholar]
- Garrett W N. 1987. Relationship between energy metabolism and the amounts of protein and fat deposited in growing cattle. In: Moe P. W., Tyrrell H. F. and Reynolds P J, editors. Proceedings of the 10th Symposium on Energy Metabolism of Farm Animals, 32 Airlie, Virginia:Rowman & Littlefield; p. 98–101. [Google Scholar]
- Garrett R P, and Hinman H.. 1969. Re-evaluation of the relationship between carcass density and body composition of beef steers. J. Anim. Sci. 28:1–5. doi: 10.2527/jas1969.2811 [DOI] [Google Scholar]
- Garrett W N, Meyer J. H., and Lofgreen G. P.. 1959. The comparative energy requirements of sheep and cattle for maintenance and gain. J. Anim. Sci. 18:528–547. doi: 10.2527/jas1959.182528x [DOI] [Google Scholar]
- Geay Y, and Robelin J.. 1979. Variation of meat production capacity in cattle due to genotype and level of feeding: genotype-nutrition interaction. Livest. Prod. Sci. 6:263–276. doi: 10.1016/0301-6226(79)90044-7 [DOI] [Google Scholar]
- Geay Y, Robelin J., and Vermorel M.. 1980. Influence of the metabolizable energy content on the diet on energy utilization for growth in bulls and heifers. In: Mount L E, editor. Proceedings of the 8th Symposium on Energy Metabolism of Farm Animals, 26 Cambridge, UK:Butterworths & Co; p. 9–12. [Google Scholar]
- Greenwood P. L., and Cafe L. M.. 2007. Prenatal and pre-weaning growth and nutrition of cattle: long-term consequences for beef production. Animal. 1:1283–1296. doi: 10.1017/S175173110700050X [DOI] [PubMed] [Google Scholar]
- Koong L J. 1980. Effects of body weight on partitioning of available energy to fat and lean gains and on partial efficiencies. In: Mount L E, editor. Proceedings of the 8th Symposium on Energy Metabolism of Farm Animals, 26 Cambridge, UK:Butterworths & Co; p. 231–234. [Google Scholar]
- Law A M. 2007. Simulation modeling and analysis. (4th ed.). McGraw-Hill, Boston:Industrial Engineering and Management Science. [Google Scholar]
- Lofgreen G P. 1965. A comparative slaughter technique for determining net energy values with beef cattle. In: Blaxter K L, editor. Proceedings of the 3rd Symposium of Energy Metabolism Troon, Scotland:Academic Press; p. 309–317. [Google Scholar]
- Lofgreen G P, and Garrett W. N.. 1968. A system for expressing net energy requirements and feed values for growing and finishing beef cattle. J. Anim. Sci. 27:793–806. doi: 10.2527/jas1968.273793x [DOI] [Google Scholar]
- Marcondes M. I., Tedeschi L O, Valadares Filho S C, and Gionbelli M. P.. 2013. Predicting efficiency of use of metabolizable energy to net energy for gain and maintenance of Nellore cattle. J. Anim. Sci. 91:4887–4898. doi: 10.2527/jas.2011-4051 [DOI] [PubMed] [Google Scholar]
- McKay M D, Beckman R. J., and Conover W. J.. 1979. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics. 21:239–245. doi: 10.1080/00401706.2000.10485979 [DOI] [Google Scholar]
- Meyer J H, and Garrett W. N.. 1960. Efficiency of feed utilization. J. Anim. Sci. 26:638–646. doi: 10.2527/1990.6851201x [DOI] [Google Scholar]
- Milligan L. P., and Summers M.. 1986. The biological basis of maintenance and its relevance to assessing responses to nutrients. Proc. Nutr. Soc. 45:185–193. doi:10.1079/PNS19860053 [DOI] [PubMed] [Google Scholar]
- National Academies of Sciences, Engineering, and Medicine 2016. Nutrient requirements of beef cattle. (8th ed.). Nutrient requirements of domestic animals. Washington, DC:National Academy Press. [Google Scholar]
- National Research Council 1984. Nutrient requirements of beef cattle. (6th ed.). Nutrient requirements of domestic animals. Washington, DC:National Academy Press. [Google Scholar]
- National Research Council 1996. Nutrient requirements of beef cattle. (7th ed.). Nutrient requirements of domestic animals. Washington, DC:National Academy Press. [Google Scholar]
- National Research Council 2000. Nutrient requirements of beef cattle. (updated 7th ed). Nutrient requirements of domestic animals. Washington, DC:National Academy Press. [Google Scholar]
- Owens F. N., Gill D R, Secrist D S, and Coleman S. W.. 1995. Review of some aspects of growth and development of feedlot cattle. J. Anim. Sci. 73:3152–3172. doi: 10.2527/1995.73103152x [DOI] [PubMed] [Google Scholar]
- Reid J T, Wellington G. H., and Dunn H. O.. 1955. Some relationships among the major chemical components of the bovine body and their application to nutritional investigations. J. Dairy Sci. 38:1344–1359. doi: 10.3168/jds.S0022-0302(55)95117-1 [DOI] [Google Scholar]
- Reid J T, White O. D., Anrique R. G., and Fortin A.. 1980. Nutritional energetics of livestock: some present boundaries of knowledge and future research needs. J. Anim. Sci. 51:1393–1415. doi: 10.2527/jas1981.5161393x [DOI] [Google Scholar]
- Ribeiro F R B, Tedeschi L. O., Rhoades R. D., Smith S. B., Martin S. E., and Crouse S. F.. 2011. Evaluating the application of dual X-ray energy absorptiometry to assess dissectible and chemical fat and muscle from the 9th-to-11th rib section of beef cattle. Prof. Anim. Scient. 27:472–476. doi: 10.15232/S1080-7446(15)30521-0 [DOI] [Google Scholar]
- Robelin J., and Chilliard Y.. 1989. Short-term and long-term effects of early nutritional deprivation on adipose tissue growth and metabolism in calves. J. Dairy Sci. 72:505–513. doi: 10.3168/jds.S0022-0302(89)79133-5 [DOI] [PubMed] [Google Scholar]
- Roberts S. B., and Young V. R.. 1988. Energy costs of fat and protein deposition in the human infant. Am. J. Clin. Nutr. 48:951–955. doi: 10.1093/ajcn/48.4.951 [DOI] [PubMed] [Google Scholar]
- Rompala R E, Jones S. D. M., Buchaman-Smith J. G., and Bayley H. S.. 1987. Utilization of dietary energy for protein and lipid deposition in late maturing cattle. In: Moe P. W., Tyrrell H. F. and Reynolds P J, editors. Proceedings of the 10th Symposium on Energy Metabolism of Farm Animals, 32. Virginia: Rowman & Littlefield; p. 94–97. [Google Scholar]
- Roux C Z, Hofmeyer H. S., and Jordaan E.. 1982. The problem of multicollinearity in the estimation of partial efficiencies of protein and fat by regression methods. In: Ekern A. and Sundstøl F, editors. Proceedings of the 9th Symposium on Energy Metabolism of Farm Animals, 29 Lillehammer, Norway:EAAP; p. 138–140. [Google Scholar]
- Ryan W J. 1990. Compensatory growth in cattle and sheep. Nutr. Abstr. Rev. (Series B). 60:653–664. [Google Scholar]
- Schiemann R, Jentsch W., Wittenburg H., and Hoffmann L.. 1976. Die Verwertung der Futterenergie durch wachsende Bullen. Archiv für Tierernaehrung. 26:491–517. doi: 10.1080/17450397609426720 [DOI] [Google Scholar]
- Scholz A. M., Bünger L, Kongsro J, Baulain U, and Mitchell A. D.. 2015. Non-invasive methods for the determination of body and carcass composition in livestock: dual-energy X-ray absorptiometry, computed tomography, magnetic resonance imaging and ultrasound: invited review. Animal. 9:1250–1264. doi: 10.1017/S1751731115000336 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simpfendorfer S. 1974. Relationship of body type, size, sex, and energy intake to the body composition of cattle [dissertation]. Ithaca, NY:Cornell University. [Google Scholar]
- Tedeschi L O. 2001. Development and evaluation of models for the Cornell net carbohydrate and protein system: 1. feed libraries, 2. ruminal nitrogen and branched-chain volatile fatty acid deficiencies, 3. diet optimization, 4. energy requirement for maintenance and growth [dissertation]. Ithaca, NY:Cornell University. [Google Scholar]
- Tedeschi L O. 2006. Assessment of the adequacy of mathematical models. Agric. Syst. 89:225–247. doi: 10.1016/j.agsy.2005.11.004 [DOI] [Google Scholar]
- Tedeschi L. O., Boin C, Fox D G, Leme P R, Alleoni G F, and Lanna D. P.. 2002. Energy requirement for maintenance and growth of Nellore bulls and steers fed high-forage diets. J. Anim. Sci. 80:1671–1682. doi:10.2527/2002.8061671x [DOI] [PubMed] [Google Scholar]
- Tedeschi L O, Cannas A., and Fox D. G.. 2010. A nutrition mathematical model to account for dietary supply and requirements of energy and nutrients for domesticated small ruminants: the development and evaluation of the Small Ruminant Nutrition System. Small Ruminant Res. 89:174–184. doi: 10.1016/j.smallrumres.2009.12.041 [DOI] [Google Scholar]
- Tedeschi L O, and Fox D. G.. 2018. The ruminant nutrition system: an applied model for predicting nutrient requirements and feed utilization in ruminants. (2nd ed.). Acton, MA:XanEdu. [Google Scholar]
- Tedeschi L O, Fox D. G., and Guiroy P. J.. 2004. A decision support system to improve individual cattle management. 1. A mechanistic, dynamic model for animal growth. Agric. Syst. 79:171–204. doi: 10.1016/S0308-521X(03)00070-2 [DOI] [Google Scholar]
- Tedeschi L O, Galyean M. L., and Hales K. E.. 2017. Recent advances in estimating protein and energy requirements of ruminants. Anim. Prod. Sci. 57:2237–2249. doi: 10.1071/AN17341 [DOI] [Google Scholar]
- Thorbek G. 1977. The energetics of protein deposition during growth. Nutr. Metab. 21:105–118. doi: 10.1159/000175757 [DOI] [PubMed] [Google Scholar]
- Tylutki T. P., Fox D G, and Anrique R. G.. 1994. Predicting net energy and protein requirements for growth of implanted and nonimplanted heifers and steers and nonimplanted bulls varying in body size. J. Anim. Sci. 72:1806–1813. doi: 10.2527/1994.7271806x [DOI] [PubMed] [Google Scholar]
- Van Es A J H. 1980. Net requirements for maintenance as dependent on weight, feeding level, sex and genotype, estimated from balance trials. Ann. Zootech. 29:73–84. doi: 10.1051/animres:19800504 [Google Scholar]
- Williams C. B., and Jenkins T. G.. 2003a. A dynamic model of metabolizable energy utilization in growing and mature cattle. I. Metabolizable energy utilization for maintenance and support metabolism. J. Anim. Sci. 81:1371–1381. doi: 10.2527/2003.8161371x [DOI] [PubMed] [Google Scholar]
- Williams C. B., and Jenkins T. G.. 2003b. A dynamic model of metabolizable energy utilization in growing and mature cattle. II. Metabolizable energy utilization for gain. J. Anim. Sci. 81:1382–1389. doi: 10.2527/2003.8161382x [DOI] [PubMed] [Google Scholar]
- Williams C. B., and Jenkins T. G.. 2003c. A dynamic model of metabolizable energy utilization in growing and mature cattle. III. Model evaluation. J. Anim. Sci. 81:1390–1398. doi: 10.2527/2003.8161390x [DOI] [PubMed] [Google Scholar]
- Wu G. 2017. Principles of animal nutrition. Milton, UK:Chapman and Hall/CRC. [Google Scholar]