How did Lofgreen and Garrett do the math?

Abstract

Lofgreen and Garrett introduced a new system for predicting growing and finishing beef cattle energy requirements and feed values using net energy concepts. Based on data from comparative slaughter experiments they mathematically derived the California Net Energy System. Scaling values to body weight to the ¾ power, they summarized metabolizable energy intake (ME), energy retained (energy balance [EB]), and heat production (HP) data. They regressed the logarithm of HP on ME and extended the line to zero intake, and estimated fasting HP at 0.077 Mcal/kg^0.75, similar to previous estimates. They found no significant difference in fasting HP between steers and heifers. Above maintenance, however, a logarithmic fit of EB on ME does not allow for increased EB once ME is greater than 340 kcal/kg^0.75, or about three times maintenance intake. So based on their previous work, they used a linear fit so that partial efficiency of gain above maintenance was constant for a given feed. They show that with increasing roughage level efficiency of gain (slope) decreases, consistent with increasing efficiency of gain and maintenance with greater metabolizable energy of the feed. Making the system useful required that gain in body weight be related to EB. They settled on a parabolic equation, with significant differences between steers and heifers. Lofgreen and Garrett also used data from a number of experiments to relate ME and EB to estimate the ME required for maintenance (ME = HP) and then related the amount of feed that provided that amount of ME to the metabolizable energy content of the feed (MEc), resulting in a logarithmic equation. Then they related that amount of feed to the net energy for gain calculated as the slope of the EB line when regressed against feed intake. Combining the two equations, they estimate the net energy for maintenance and gain per unit feed (Mcal/kg dry matter) as a function of MEc: 0.4258 × 1.663^MEc and 2.544–5.670 × 0.6012^MEc, respectively. Finally, they show how to calculate net energy for maintenance and gain from experiments where two levels of a ration are fed and EB measured, where one level is fed and a metabolism trial is conducted, or when just a metabolism trial is conducted—but results are not consistent between designs.

INTRODUCTION

Lofgreen and Garrett (1968) introduced a new system for predicting growing and finishing beef cattle energy requirements and feed values using net energy concepts. They were not the first to use net energy concepts (Armsby and Fries, 1915), but they were the first to put into practice what Kleiber (1961) showed—that the partial efficiency of energy used for maintenance was greater than that used for gain. Lofgreen et al. (1963) and Garrett et al. (1964) further showed that the partial efficiency above maintenance energy intake was constant for a given feed. Also, as Kleiber (1961) suggested, since fasting heat production (HP) is relatively constant, the partial efficiency for maintenance is also constant for a feed. Based on these concepts, Lofgreen and Garrett (1968) analyzed data from comparative slaughter experiments to mathematically derive the California Net Energy System.

MATHEMATICAL DERIVATION OF THE CALIFORNIA NET ENERGY SYSTEM

Maintenance and Fasting HP

Table 1 of Lofgreen and Garrett (1968) summarized the mean energy values of groups of either six or eight animals. Both steers and heifers were fed rations of 2%, 20%, 25%, 40%, and 100% roughage, at intakes of about maintenance (“low” in Table 1), 1.5 times maintenance, and ad libitum (although the steers fed 20% and 40% roughage only received the low and ad libitum levels). Values were scaled to metabolic body weight (BW^0.75), and metabolizable energy intake (ME), energy retained (EB), and HP were calculated (HP = ME − EB). To get an estimate of fasting HP, HP was regressed on ME (Figure 1), using both HP and log₁₀(HP). Since the fit of the data was similar (R² = 0.93), Lofgreen and Garrett (1968) chose the logarithmic line because if extended to zero intake, fasting HP was 77 kcal/kg^0.75, which is much closer to the original Kleiber (1947) 70 kcal/kg^0.75 than the linear HP intercept of 39 kcal/kg^0.75. Also, the points at which EB = 0, energy equilibrium or maintenance intake (ME = HP) were 121 and 116 kcal/kg^0.75 for the logarithmic and linear HP fits, respectively. These result in an efficiency of feed metabolizable energy for maintenance (k_m, fasting HP per ME at maintenance) of 0.64 and 0.34 for the logarithmic and linear fits, respectively. Therefore, and consistent with indirect calorimeter measurements made later (Moe et al., 1972), the logarithmic fits were used for fasting HP. Also, the data in table 2 of Lofgreen and Garrett (1968) result in no significant difference in fasting HP between steers (81.5 kcal/kg^0.75) and heifers (82.8 kcal/kg^0.75) using the logarithmic fit of HP.

Table 1.

Estimation of net energy of maintenance (NEm) and gain (NEg) in the ration dry matter for the 20% roughage fed steers in table 1 of Lofgreen and Garrett (1968) for different EB or metabolism (determine metabolizable energy of the feed MEc) experiments

	Measure EB a 1 level
	Measure EB at 2 levels	Determine MEc	Determine MEc
NEm, Mcal/kg	1.66	1.71	1.65
NEg, Mcal/kg	0.90	1.02	1.08

Figure 1.

Heat production per BW^0.75 (HP) of beef cattle for table 1 of Lofgreen and Garrett (1968), with best linear fit of HP (dashed line) and log₁₀ of HP (solid line) on ME per BW^0.75. Data points are means of six or eight animals.

Energy Retained and Efficiency of Gain

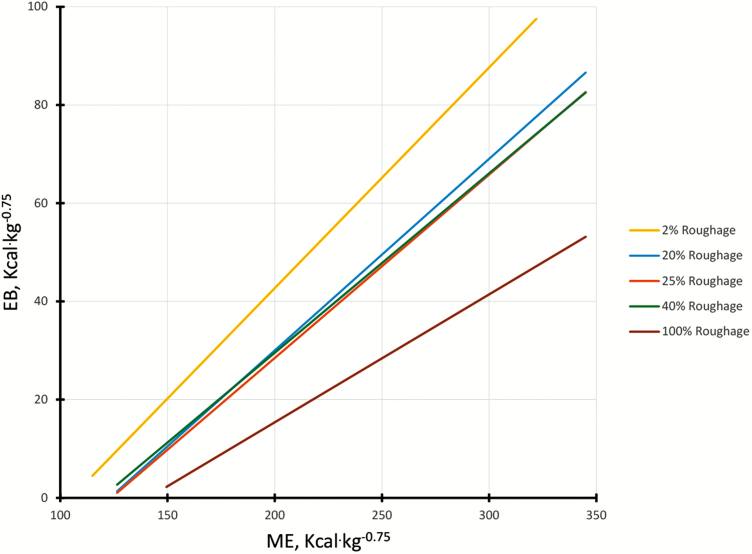
Table 1 of Lofgreen and Garrett showed the EB (Figure 2). However, unlike the case for fasting HP, the logarithmic fit does not allow for increased EB once ME is greater than 340 kcal/kg^0.75, or about three times maintenance intake. Clearly this would not work, consistent with results from their previous research (Lofgreen et al., 1963; Garrett et al., 1964) showing that partial efficiency of gain above maintenance was constant for a given feed. Therefore, a linear fit of HP above maintenance ME was used. Further demonstrating this (Figure 3), the fits for each of the different rations in table 1 of Lofgreen and Garrett (1968) show that with increasing roughage level efficiency of gain (slope) decreases. The efficiency (Figure 4) of gain (k_g) calculated for these data were 0.26, 0.37, 0.37, 0.39, and 0.45 for roughage levels of 100%, 40%, 25%, 20%, and 2%, respectively. Corresponding maintenance ME were 144, 116, 125, 126, and 109 kcal/kg^0.75; and k_m (fasting HP per maintenance ME) were 0.56, 0.59, 0.64, 0.62, and 0.66, respectively. These are consistent with increasing efficiency of gain and maintenance with greater metabolizable energy of the feed.

Figure 2.

Energy retained per BW^0.75 (EB) of beef cattle for table 1 of Lofgreen and Garrett (1968), using the best linear fit of HP (dashed line) and log₁₀ of HP (solid line) on ME per BW^0.75. Data points are means of six or eight animals.

Figure 3.

Energy retained per BW^0.75 (EB) of beef cattle for table 1 of Lofgreen and Garrett (1968), using the best linear fit of EB for each roughage level on ME per BW^0.75.

Figure 4.

Efficiency of ME use for maintenance energy use (k_m) and energy for gain (k_g) of beef cattle in table 1 of Lofgreen and Garrett (1968), using the best logarithmic fit of HP for maintenance (dotted line) and the best linear fit of HP for gain (dashed line).

Energy in Empty Body Weight Gain

To make the system useful, gain in body weight must be related to EB. Lofgreen and Garrett (1968) tested power and parabolic equations, comparing the parabolic both with and without an intercept (Figure 5). They found significant differences between steers and heifers, and that the parabolic equation had better fit. They chose the parabolic equation that passed through the origin (no intercept term); however, this forces empty body weight gain to equal zero when EB is zero (maintenance). These relationships can be compared with equations used in the current beef cattle feeding standards, also shown on Figure 5, which are quite similar for implanted British breed steers. The power function (EB = 56.8 × empty body weight gain^1.02) did not fit the data as well as the other equations. It should be noted that later models allow for gain of empty body protein and loss of fat at maintenance, consistent with observation (Oltjen and Sainz, 2001).

Figure 5.

Effect of rate of empty body weight gain on retained energy (EB) for steers (Lofgreen and Garrett, 1968) with fits of second-order polynomials, a power function, and the relationship in the current beef feeding standards (NASEM, 2016).

Relationship of Net Energy and Metabolizable Energy in Feed

Lofgreen and Garrett (1968) used the relationship of ME and EB to estimate the ME required for maintenance (ME = HP) and then related the amount of feed that provided that amount of ME to the metabolizable energy content of the feed (MEc) in their Figure 5, resulting in a logarithmic equation shown on that figure. Then they related that amount of feed to the net energy for gain calculated as the slope of the EB line when regressed against feed intake. Combining the two equations, one may calculate the net energy for gain and maintenance per unit feed (NEg and NEm, respectively) as a function of MEc:

$$\text{NEm},\text{Mcal}/\text{kg}=0.\text{4258}\times \text{1}.{\text{663}}^{\text{MEc}}$$

$$\text{NEg},\text{Mcal}/\text{kg}=\text{2}.\text{544}-\text{5}.\text{67}0\times 0.\text{6}0{\text{12}}^{\text{MEc}}$$

These can be compared with the equations later developed by Garrett (1980 e symp) and currently used (NASEM, 2016):

$$\text{NEm},\text{ Mcal}/\text{kg }=\text{ 1}.\text{37}\times \text{MEc}-0.\text{138}\times {\text{MEc}}^{\text{2}}+0.0\text{1}0\text{5}\times {\text{MEc}}^{\text{3}}-\text{1}.\text{12}$$

$$\text{NEg},\text{ Mcal}/\text{kg }=\text{ 1}.\text{42}\times \text{MEc}-0.\text{174}\times {\text{MEc}}^{\text{2}}+0.0\text{122}\times {\text{MEc}}^{\text{3}}-\text{1}.\text{65}$$

The newer equations suggest that the original Lofgreen and Garrett (1968) relationships slightly underestimated the feed net energy (Figure 6).

Figure 6.

Net energy for maintenance (NEm) and gain (NEg) as a function of ME of the ration (MEc) for Lofgreen and Garrett (1968) and NASEM (2016).

CALCULATION OF NET ENERGY FROM EXPERIMENTS

Lofgreen and Garrett (1968) show how to calculate net energy for maintenance and gain with an experiment measuring at least two levels of dry matter intake (DMI) and energy balance (EB) above maintenance (Figure 7). The slope of the regression line through the two experimental points is NEg, and the DM intake at zero EB is subtracted is that required for maintenance. NEm is fasting HP divided by the DMI for maintenance. Calculation of net energy for maintenance and gain with an experiment measuring only one level of DMI and EB above maintenance and another experiment measuring the metabolizable energy of the feed is shown in Figure 8. A line through the measured experimental point and fasting HP is used to calculate where ME intake is equal to HP. Dry matter intake at maintenance is thus HP divided by the MEc of the feed, so NEm is fasting HP divided by maintenance DMI. NEg is the EB divided by the DMI for gain, which is total DMI minus that for maintenance. If one only conducts a metabolism trial, then the equations relating MEc to NEm and NEg are used. Results of these three methods for the 20% roughage level in table 1 of Lofgreen and Garrett (1968) are shown in Table 1. Results do vary by up to 10%.

Figure 7.

Calculation of net energy for maintenance (NEm) and gain (NEg) with an experiment measuring at least two levels of daily DMI and daily EB above maintenance. The slope of the regression line through the two experimental points is NEg, and the DM intake at zero EB is subtracted is that required for maintenance. NEm is fasting HP (0.077 BW^0.75, BW is body weight) divided by this DMI for maintenance. Coefficients are from Table 1, 20% roughage (Lofgreen and Garrett, 1968).

Figure 8.

Calculation of net energy for maintenance (NEm) and gain (NEg) with an experiment measuring one level of daily DMI and daily EB above maintenance and another experiment measuring the ME of the feed (MEc). A line through the measured experimental point and fasting HP is used to calculate where ME intake is equal to HP. DMI at maintenance is thus HP divided by the MEc of the feed, so NEm is fasting HP divided by maintenance DMI. NEg is the EB divided by the DMI for gain, which is total DMI minus that for maintenance. Coefficients are from Table 1, ad libitum 20% roughage (Lofgreen and Garrett, 1968), data are scaled to body weight (BW).

SUMMARY

Lofgreen and Garrett (1968) proposed a system based on measurement of EB over a feeding period of the same feed fed at different levels. Net energy required for maintenance was estimated by regressing HP on ME of a number of previous studies, and extrapolating to zero intake. Then net energy for gain of the feed under study is the slope of the regression line of EB on feed intake, and the net energy for maintenance of the feed is the net energy for maintenance divided by the feed required for zero EB, calculated by solving the EB regression equation for zero EB. So it is a simple system, requiring at minimum only two feeding levels, with measurements of retained energy at the beginning and end of the trial, and feed intake. Studies relating energy in gain are used to develop relationships between net energy and metabolizable energy of rations and body weight gain. Different types of experiments can be used to estimate net energy using assumptions in the system related to fasting HP, but results can vary, setting the stage for subsequent research and adaptation of the net energy system for the past half century.