Opportunities to improve the accuracy of the United States Department of Agriculture beef yield grade equation through precision agriculture

Abstract

The U.S. Department of Agriculture (USDA) yield grade (YG) equation is used to predict the retail yield of beef carcasses, which facilitates a more accurate payment for cattle when they are sold on a grid pricing system that considers carcass composition instead of body weight alone. The current USDA YG equation was developed over 50 yr ago. Arguably, the population of cattle used to develop the YG equation is different than the current diverse U.S. beef cattle supply today. The objectives of this manuscript are to promote the adoption and use of precision agriculture technologies (i.e., camera grading and electronic animal identification) throughout the U.S. beef supply chain as a means to enhance the ability of the USDA YG equation to more accurately predict the retail yield across the population of cattle that contributes to the current U.S. beef supply. Camera grading has improved the accuracy of determining beef carcass retail yield; however, the use of electronic animal identification would allow for additional information to be passed back and forth between the packer, cattle feeder, and producer. Information, such as sex, genetics, medical treatment history, diets consumed, and growth promotant administration, as well as other information could be used to create additional variables for a new augmented USDA YG equation. Herein, fabrication yields demonstrated a 5.6 USDA YG and 12.8% boneless closely trimmed retail cut difference between actual cutout measurements and calculated values from the USDA YG equation for Jersey-influenced cattle. Evidence of such disparities between calculated and actual values warrants a reevaluation of the USDA YG system and consideration for implementing advancements in precision agriculture to improve the prediction of beef carcass retail yield to more accurately account for the large amount of variation in beef carcass retail yield from the cattle in the United States.

INTRODUCTION

In the United States, beef carcasses can be assigned a quality grade (QG) indicative of eating satisfaction and a yield grade (YG) indicative of the amount of saleable retail product retrieved by fabrication of the carcass (USDA, 2016). Carcass value is largely determined by hot carcass weight (HCW), but it can also be influenced by premiums and discounts received based on the predicted meat quality and retail yield. The beef grading systems used in the United States allows packers to more accurately pay cattle producers and feeders based on the estimated value of their cattle. Premiums and discounts assigned to the price of beef act as the signals sent from both customers purchasing beef and packers processing the cattle back to beef producers to indicate the demand for cattle that produce carcasses and resulting beef products that meet the supply chain’s specifications and desired expectations.

Research conducted by Murphey et al. (1960) was used to develop the current USDA YG equation to predict the percent boneless closely trimmed retail cuts (BCTRC) produced. Predictor variables used to estimate percent BCTRC retrieved from the beef carcass include HCW, back fat thickness (BFT), kidney, pelvic, and heart fat percentage (KPH), and longissimus muscle area (LMA). With the current USDA YG equation (percent BCTRC = −2.3 × YG + 56.9), a change of one YG represents a 2.3% change in the percentage of BCTRC retrieved from the carcass. Yield grades are awarded on a 1–5 scale, where a YG 1 carcass would be expected to produce greater than 52.3% BCTRC, while a YG 5 carcass would be expected to produce less than 45.4% BCTRC from the beef carcass (USDA, 2016).

The current USDA YG equation has been used in the beef industry for over 50 yr, with a “one size fits all” approach. However, the cattle population that currently contributes to the U.S. beef supply is quite diverse and is comprised of a variety of purebred and crossbred cattle. Different cattle breeds or cattle types were designed for different purposes or combination of purposes, such as beef production, draft, dairy production, and environmental tolerance, among others. As a result, cattle in the United States can have extremely different growth curves that represent differences in birth weight, rate of growth, and mature body weight (Owens et al., 1995). Even at the same stage of physiological maturity, cattle in the United States can vary widely in carcass composition, mostly due to differences in the location of carcass fat deposition (i.e., subcutaneous, intermuscular, and kidney fat). However, cattle with varying phenotypes and genotypes (i.e., beef type vs. dairy type) can also produce carcasses with vastly different muscle:bone ratios, which can contribute to differences in carcass composition.

In the last two decades, advances in technology have been used to augment the application of USDA YG to beef carcasses with the use of camera grading systems in packing plants. The use of camera grading systems has improved the accuracy and repeatability of determining beef carcass USDA YG by reducing some of the human bias or human error in the USDA YG prediction (Hueth et al., 2007). In addition, other technological advances, such as the adoption and use of electronic animal identification, allows for individual animal information to be passed back and forth through the supply chain between the packer and feedlot or producer. Information, such as sex, genetics, medical treatment history, diets consumed, growth promotant administration (i.e., exogenous hormone implants and β-agonists), and carcass YG and QG, as well as other information, would all travel with the animal and resulting carcass as it progresses through the beef supply chain. This information could be incorporated into additional variables in an augmented YG equation for improved accuracy in predicting beef carcass retail yield.

The goal of this technical note is to discuss the opportunities of adopting precision agriculture technologies to improve upon the accuracy and efficacy of the USDA YG equation and grading system. As an example of this opportunity, a recent study conducted by Jaborek et al. (2019a, 2019b) will be used to demonstrate the inability of the USDA YG equation to predict beef carcass yield with the use of Jersey-influenced cattle.

MATERIALS AND METHODS

Animal procedures and husbandry practices were approved by the Institutional Animal Care and Use Committee (protocol number 2015A00000093) of The Ohio State University and followed the guidelines recommended in the Guide for the Care and Use of Agricultural Animals in Agricultural Research and Teaching (FASS, 2010).

Details regarding the animals used in this technical note have been reported previously by Jaborek et al. (2019a, 2019b). Briefly, purebred Jersey steers and crossbred Jersey steers and heifers were raised over the course of 2 yr at the Ohio Agricultural Research and Development Center feedlot (Wooster, OH) where animals consumed similar feedlot diets. Cattle were not administered exogenous growth promotants (i.e., hormonal implants or β-adrenergic agonists) and were raised to obtain premium USDA QG to meet the requirements of a niche market that demands high-quality, naturally raised beef. Cattle (n = 91) were harvested and fabricated at The Ohio State University meat laboratory (Columbus, OH). Retail cuts were weighed to determine the retail yield of each carcass. Actual kidney fat percentage was used to determine beef carcass YG, instead of estimated kidney, pelvic, and heart fat. The current equations used to calculate the percent BCTRC (Murphey et al., 1960) and USDA YG (USDA, 2016) are shown in Table 1.

Table 1.

Comparison between current USDA regression equations for boneless closely trimmed retail cuts and YG and new regression equations for Jersey-influenced cattle

	USDA	Jersey		95% CI
Parameter	Estimate	Estimate	SE	Lower	Upper	CCC
%BCTRC						0.0108
Intercept	51.34	34.68	2.734	29.231	40.121
HCW	−0.0210	−0.0119	0.007	−0.026	0.002
BFT	−2.28	−1.01	0.427	−1.858	−0.158
LMA	0.115	0.081	0.024	0.033	0.129
KPH	0.462	−0.192	0.141	−0.472	0.088
YG						0.0108
Intercept	2.50	9.66	1.188	7.296	12.029
HCW	0.0084	0.0052	0.003	−0.001	0.011
BFT	0.99	0.44	0.186	0.069	0.808
LMA	0.050	−0.035	0.010	−0.056	−0.014
KPH	0.200	0.083	0.061	−0.038	0.205

Statistical analysis was performed using PROC REG and PROC IML in SAS (SAS Inst. Inc., Cary, NC). Missing kidney fat measurements from nine cattle prevented their use for the analysis of YG but not BCTRC. The statistical model used in PROC REG was: Y_ijkl = μ + HCW_i + BFT_j + LMA_k + KPH_l + e_ijkl, where HCW_i = hot carcass weight, BFT_j = backfat thickness, LMA_k = longissimus muscle area, KPH_l = percent kidney, pelvic, and heart fat as continuous variables, and e_ijkl = random error. The calculated USDA data had minimal SE because they predicted values from using the current USDA YG equation. The estimate statement and 95% CIs and concordance correlation coefficient (CCC) were used to determine differences between the calculated USDA and actual Jersey data. The use of the backward selection procedure in PROC REG selected only predictor variables with significant contributions (P ≤ 0.05) for the reduced equations, while the full models included all four predictor variables (HCW, BFT, LMA, and KPH). All significant differences were established at P ≤ 0.05.

RESULTS AND DISCUSSION

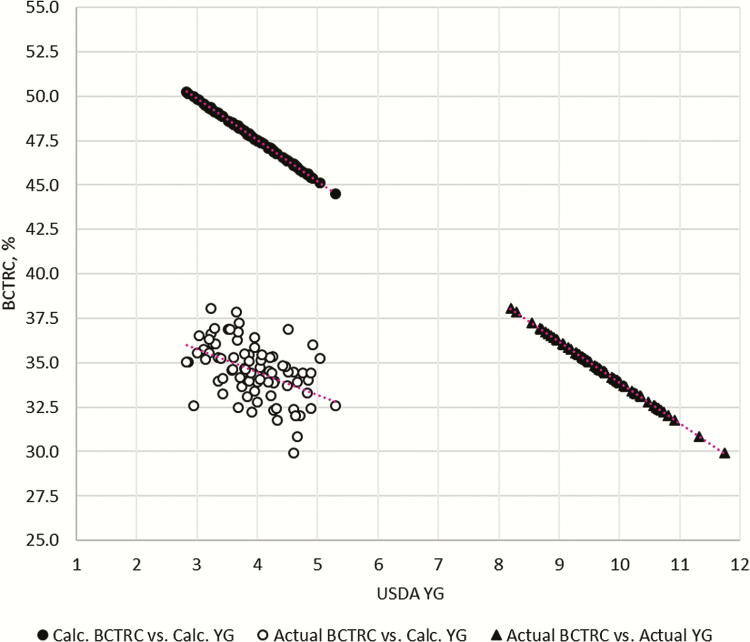
The USDA YG and BCTRC equations were created to gain a rapid prediction for the cutability of beef carcasses and, therefore, more accurately price beef carcasses. The YG of beef carcasses can be calculated from the USDA YG equation shown in Table 1. Likewise, the percent BCTRC can also be calculated with the USDA percent BCTRC equation (Murphey et al., 1960) shown in Table 1. When the USDA YG and USDA percent BCTRC equations are used to predict the retail yield of the Jersey-influenced cattle used in the present study, the data points in the upper left corner of Fig. 1 are created (calculated percent BCTRC vs. calculated YG; black circles). The relationship of the calculated USDA YG and calculated USDA percent BCTRC place the data points on the line where percent BCTRC = −2.3(YG) + 56.9, representing a 2.3% change in BCTRC or retail yield for a difference of 1 in YG score.

Figure 1.

Three relationships between percent BCTRC and USDA YG of purebred and crossbred Jersey cattle. The relationship between the calculated percent BCTRC and calculated USDA YG (black circles) is plotted in the upper left corner and follows the relationship Y = −2.3x + 56.9. The relationship between the actual percent BCTRC and calculated USDA YG (white circles) is plotted in the bottom left corner and follows the relationship Y = −1.29x + 39.6 (R2 = 0.22). The relationship between the actual percent BCTRC and actual USDA YG (black triangles) is plotted in the bottom right corner and follows the relationship Y = −2.3x + 56.9.

The USDA YG and BCTRC equations predict or calculate the Jersey-influenced cattle used in the present study to receive a USDA YG ranging from 2.8 to 5.3 ($\overline{x}$= 4.0) and produce carcasses ranging from 44.5% to 50.3% BCTRC ($\overline{x}$= 47.6%). However, after fabricating these beef carcasses into BCTRC as mentioned by Jaborek et al. (2019a, 2019b), the actual percentage of BCTRC was much lower than the calculated percentage of BCTRC determined by the USDA equation as shown in the lower-left corner of Fig. 1 created (actual BCTRC vs. calculated YG; white circles). The USDA percent BCTRC equation overestimated (P ≤ 0.01) the actual percent BCTRC by 12.8%. The actual percentage of BCTRC of Jersey-influenced cattle in the present study ranged from 29.9% to 41.7% BCTRC ($\overline{x}$ = 34.8%). Aware that the percent BCTRC was overestimated by the USDA percent BCTRC equation, we expected that the USDA YG equation would overestimate the retail yield of the Jersey beef carcasses. In order to determine the actual YG of the Jersey-influenced cattle used in the present study, the regression equation between the USDA YG and USDA percent BCTRC needed to be rearranged [YG = (percent BCTRC − 56.9)/−2.3]. Data points in the bottom right corner of Fig. 1 were created when the actual percentage of BCTRC was used to determine the actual YG of the Jersey-influenced cattle used in the present study. As a result, the actual USDA YG for the Jersey-influenced cattle ranged from 6.6 to 11.7 ($\overline{x}$= 9.6), with all cattle receiving a YG outside the USDA’s 1–5 scale for YG. The difference (P ≤ 0.01) between the calculated USDA YG and actual YG was 5.6 USDA YG, which was a 140% increase in USDA YG. Concordance correlation coefficient analysis (0.01 for YG and BCTRC) demonstrates the inability of the USDA YG and BCTRC equations to predict or calculate the actual YG and BCTRC of the Jersey-influenced cattle used in the present study.

Linear regression equations were developed to demonstrate the relationships between the calculated USDA data and the actual Jersey data for percent BCTRC and YG (Table 2). A perfect fit between the calculated USDA data and the actual Jersey data would produce an equation with a slope equal to 1 and a y-intercept equal to 0. However, for percent BCTRC and YG, the y-intercepts (P ≤ 0.16 and 0.01) and slopes (P ≤ 0.01 and 0.01) differed from 1 and 0, respectively. The adjusted R² values (Adj. R² = 0.21) indicate that these linear regression equations are not closely related to each other.

Table 2.

Linear regression equation for the prediction of percent boneless closely trimmed retail cuts and YG of Jersey-influenced cattle from the USDA percent boneless closely trimmed retail cuts and YG

Parameter	Estimate	SE	P value	Adj. R2	RMSEa
Jersey %BCTRC
Intercept (β 0)	8.153	5.612	0.1502	0.21	1.411
USDA %BCTRC (β1)	0.554	0.118	0.0003
Jersey YG
Intercept (β 0)	7.509	0.473	<0.0001	0.21	0.613
USDA YG (β1)	0.560	0.119	0.0004

^aRoot mean square error.

Multiple linear regressions for Jersey YG (Adj. R² = 0.02) and percent BCTRC (Adj. R² = 0.03) equations were created with the same predictor variables (HCW, BFT, KPH, and LMA) as the current USDA YG and percent BCTRC equations (Table 1). There were significant differences between the intercept (P ≤ 0.01), BFT (P ≤ 0.01), and a tendency for the LMA (P = 0.06) parameter estimates between the USDA and Jersey percent BCTRC and YG equations. Reduced Jersey models for YG (Adj. R² = 0.06) and percent BCTRC (Adj. R² = 0.18) were created (Table 3) when percent KPH (P = 0.18) and HCW (P = 0.09) were dropped from the full Jersey YG and percent BCTRC models. Based on the adjusted R² values from these multiple linear regression equations, the use of HCW, BFT, KPH, and LMA in the full Jersey model, or only BFT and LMA in the reduced Jersey model, either equation does not accurately predict the BCTRC and YG of Jersey-influenced cattle in the present study. Similarly, Crouse et al. (1975) reported that HCW was not a great predictor of carcass cutability. Crouse et al. (1975) reported that HCW was a better predictor within breed groups than for the entire population containing multiple cattle breeds. Results presented by Crouse et al. (1975) also demonstrated that HCW was a better predictor variable for British and Continental cattle breeds compared with Jersey-influenced cattle. Interestingly, KPH was the first variable removed from the full models (Table 1) in the present study, even though Murphey et al. (1960) and Crouse et al. (1975) reported that KPH was a significant contributor to predicting the percent BCTRC of beef carcasses. The lack of fit from the models shown in Tables 1 and 3 demonstrate the inability of the USDA YG equation to accurately predict beef carcass cutability with only HCW, BFT, KPH, and LMA as the predictor variables in the equation. Additional variables or coefficients are needed to improve the accuracy of the USDA YG equation’s ability to predict percent BCTRC of the cattle contributing to the U.S. beef supply.

Table 3.

Reduced equations of new boneless closely trimmed retail cut and YG regressions for Jersey-influenced cattle

Parameter	Estimate	SE	P value
Jersey %BCTRC
Intercept	29.679	1.458	<0.0001
HCW	—	—	0.0888
BFT	−0.983	0.419	0.0216
LMA	0.080	0.020	0.0002
KPH	---	—	0.1768
Jersey YG
Intercept	11.835	0.634	<0.0001
HCW	—	—	0.0888
BFT	0.428	0.182	0.0215
LMA	−0.349	0.009	0.0002
KPH	—	—	0.1765

As previously mentioned, the USDA YG equation was developed over 50 yr ago to fit the cattle in the U.S. beef industry at that time. However, the same USDA YG equation is being erroneously used 50 yr later with a “one size fits all” approach. Over the past 50 yr, the beef industry has evolved, and changes in genetics and the use of growth-promoting and carcass-enhancing technologies have contributed to the variation of beef carcass retail yield. Though a byproduct of the dairy industry, a greater number of purebred dairy steers and dairy crossbred cattle are being raised for beef production. According to the 2016 National Beef Quality Audit (Boykin et al., 2017), 16.3% of the fed cattle harvested were dairy-type compared with 8.3% from the National Beef Quality Audit in 2005 (Garcia et al., 2008). The present manuscript has demonstrated the inability of the USDA YG equation to accurately predict the retail yield of the Jersey-influenced cattle (purebred Jersey steers, Angus sired, SimAngus sired, and Red Wagyu sired steers and heifers) used in the present study. Koch and Dikeman (1977) reported implanted Jersey-influenced (Jersey × Hereford and Jersey × Angus) steers to have a total lean yield (retail yield + lean trim), fat trim yield, and bone yield of 64.2% to 67.3%, 20.0% to 24.3%, and 11.4% to 12.7%, respectively, for three different harvest groups. In comparison, Jersey-influenced cattle from the present study produced a total lean yield, fat trim yield, and bone yield of 55.3%, 24.1%, and 20.0%, respectively. The percentages of total lean yield (e.g., muscle) and bone yield are noticeably different between the carcasses of the Jersey-influenced cattle in the present study and of the Jersey-influenced cattle in the Koch and Dikeman (1977) study. A lesser muscle to bone ratio for cattle used in the present study may be due to the genetic selection of Jersey cattle for dairy type and milk production traits compared with carcass retail value over the past 40 yr. Likewise, Lawrence et al. (2010) reported that the USDA YG equation was not able to accurately predict the retail yield of implanted calf-fed Holstein steers (Adj. R² = 0.01). The Holstein steer carcasses produced a total lean yield, fat trim yield, and bone yield of 68.2%, 10.5%, and 21.2%, respectively (Lawrence et al., 2010). Lawrence et al. (2010) believe a predictor of bone quantity is needed in the USDA YG equation to improve the prediction of calf-fed Holstein carcass retail yield. In addition to dairy-type beef carcasses, Lawrence et al. (2010) reported that the ability of USDA YG equation to predict the beef retail yield of the control beef-type steers used in their study was poor (Adj. R² = 0.38). Growth promoting technologies (i.e., implants and β-adrenergic agonists) are commonly used to promote efficient body weight gains and increase muscle mass of feedlot cattle. While exogenous hormone implants were approved for use before the USDA YG equation was developed, β-adrenergic agonists have only been approved for use in the last 20 yr. In comparison to carcasses from nonimplanted steers, Foutz et al. (1997) reported a greater percentage of boneless chuck and striploin from carcasses of implanted steers. Some of the additional weight in the chuck of implanted steers may have been due to a greater splenius muscle weight as steers administered a trenbolone acetate implant had a greater splenius to chuck ratio (Foutz et al., 1997). When comparing β-agonist supplemented and nonsupplemented steer carcasses, Hilton et al. (2010) reported that the majority of the subprimal cuts in the round and loin primals, plus the brisket and ribeye roll, contributed a greater percentage of weight in the carcasses from steers supplemented with the β-agonist (Zilmax). Therefore, the use of growth-promoting technologies, such as implants and β- agonists, can alter the distribution of muscle weight within the carcass of cattle. The use of ribeye area alone in the USDA YG equation is unable to account for alterations in the distribution of muscle weight in the carcass. This claim is further supported by Lawrence et al. (2010) who reported a greater total lean yield from carcasses of steers (beef-type and Holstein steers) supplemented with Zilmax compared to carcasses from nonsupplemented steers when compared at a similar calculated USDA YG.

As reported by Jaborek et al. (2019a, 2019b), carcass fat deposition can vary by breed, with Jersey cattle having a greater percentage of kidney fat and a lesser BFT compared with Angus cattle, for example. The USDA YG equation considers subcutaneous and kidney fat measurements for the prediction of YG. However, the estimation of KPH fat percentage introduces subjectivity and error into the estimation of carcass retail yield. In the studies conducted by Jaborek et al. (2019a, 2019b), KPH percentage was estimated and kidney fat was objectively weighed to control for human error. An experienced carcass grader estimated a mean KPH fat percentage of 2.24% (SD = 0.469) for the Jersey-influenced cattle used in the present study. However, the actual kidney fat weight contributed 6.84% (SD = 1.351) of the carcass weight for the Jersey-influenced cattle used in the present study. The objective kidney fat measurement was three times greater and resulted in nearly an entire (0.9) YG score difference when compared with the subjective KPH percentage measurement. Farrow et al. (2009) reported that an actual measure of KPH increased the ability to predict beef carcass retail yield (Adj. R² = 0.63) compared with using an estimated KPH value or when excluding KPH as a predictor variable in the YG equation (Adj. R² = 0.57). Therefore, if KPH percentage is to be used as a predictor variable in the USDA YG equation, it should be as the actual kidney fat percentage to improve the accuracy of the prediction and eliminate human error.

In the packing plant, USDA graders are under immense pressure to assign USDA grades in the limited amount of time allowed as beef carcasses travel down the line. Adopting the use of precision agriculture technologies, such as camera grading, can augment the application of predicting the USDA YG (Hueth et al., 2007) and QG (Jang et al., 2017) of beef carcasses by eliminating grader bias. Cannell et al. (1999, 2002) reported that camera grading accounted for similar amounts of variation in predicting beef carcass retail yield as an expert offline grader, which increased the amount of variation accounted for by 17% to 25% compared with online graders. Additionally, the use of camera grading in the packing plant can be used for the development of a new and improved USDA YG equation. McEvers et al. (2012) used camera grading technology to develop new predictor variables at the 12th/13th rib separation to improve the accuracy of predicting beef carcass retail yield. Newly developed equations by McEvers et al. (2012) were able to account for significantly more variation in predicting beef carcass retail yield compared with the current USDA YG equation (Adj. R² = 0.62 vs. 0.39, respectively). McEvers et al. (2012) were also able to incorporate a coefficient for Zilmax treatment in their study to enhance the accuracy of the YG equation. The additional use of another precision agricultural technology in the beef industry, electronic animal identification, could allow for the sharing of information between the producer, cattle feeder, and packer. Similar to accounting for β-agonist supplementation in the YG equation model of McEvers et al. (2012), additional variables such as sex, genetics, medical treatment history, diets consumed, growth promotant administration (i.e., exogenous hormone implants and β-agonists), and carcass YG and QG, as well as other information, would all travel with the animal and resulting carcass as it progresses through the beef supply chain. Not only would this enhance the efficacy of the USDA YG in predicting retail yield and the true value of beef carcasses but also provide more accurate information for the supply chain and stimulate additional opportunities for production-level management practices and technology transfer to enhance production efficiencies and sustainability.

In conclusion, we have reported and referenced additional supporting data to present the lack of accuracy the current USDA YG equation provides in predicting beef carcass retail yield for cattle that represent a growing portion of the current U.S. beef supply. We also propose that the beef industry capitalizes on the opportunity to effectively incorporate precision agriculture into the USDA beef grading system to enhance its accuracy, which will help build confidence and drive adoption of precision agriculture technologies within the beef supply chain.

Conflict of interest statement. The authors do not perceive any conflict of interest.