Abstract
The concept of critical concentration (CC) is central to understanding the behavior of microtubules (MTs) and other cytoskeletal polymers. Traditionally, these polymers are understood to have one CC, measured in multiple ways and assumed to be the subunit concentration necessary for polymer assembly. However, this framework does not incorporate dynamic instability (DI), and there is work indicating that MTs have two CCs. We use our previously established simulations to confirm that MTs have (at least) two experimentally relevant CCs and to clarify the behavior of individuals and populations relative to the CCs. At free subunit concentrations above the lower CC (CCElongation), growth phases of individual filaments can occur transiently; above the higher CC (CCNetAssembly), the population’s polymer mass will increase persistently. Our results demonstrate that most experimental CC measurements correspond to CCNetAssembly, meaning that “typical” DI occurs below the concentration traditionally considered necessary for polymer assembly. We report that [free tubulin] at steady state does not equal CCNetAssembly, but instead approaches CCNetAssembly asymptotically as [total tubulin] increases, and depends on the number of stable MT nucleation sites. We show that the degree of separation between CCElongation and CCNetAssembly depends on the rate of nucleotide hydrolysis. This clarified framework helps explain and unify many experimental observations.
INTRODUCTION
The concept of critical concentration (CC) is fundamental to experimental studies of biological polymers, including microtubules (MTs) and actin, because CC is commonly understood to be the amount of subunit needed to obtain polymer. CC is used to characterize different polymers and to interpret the effects of polymer assembly regulators. In the standard framework for predicting the behavior of biological polymers, there is one CC, at which polymer assembly commences (e.g., Mirigian et al., 2013; Alberts et al., 2015). However, as indicated by other work (Hill and Chen, 1984; Walker et al., 1988), this framework fails to account for the dynamic instability (DI) displayed by MTs and other dynamically unstable polymers (e.g., PhuZ, ParM; Mitchison and Kirschner, 1984a; Garner et al., 2004; Erb et al., 2014). One purpose of the work presented here is to examine the many experimental and theoretical definitions of CC in order to show how the definitions relate to each other. Another purpose is to clarify how the behaviors of individual dynamically unstable filaments and those of their populations relate to each other and to experimental measurements of CC. To address these problems, we simulated systems of dynamic MTs with one of the two ends of each MT fixed at a stable seed (also called a nucleation site or template), similar to MTs growing from centrosomes. We performed analyses that are directly comparable to those used in experiments. A significant advantage of computational modeling for this work is that it allows simultaneous examination of the behaviors of individual subunits, individual MTs, and the population’s bulk polymer mass.
Traditional understanding of critical concentration based on equilibrium polymers
Traditionally, “the critical concentration” is understood to be the concentration of subunits needed for polymer assembly to occur (CCPolAssem). Specifically, the textbook understanding is that polymers will grow at concentrations above CCPolAssem, and will not grow below it. CCPolAssem can be measured by determining Q1 in a competing system (Figure 1, A and D). Equivalently, the CC has been defined as the concentration of free subunits left in solution once polymer assembly has reached a steady-state level in such a competing system (CCSubSoln, measured by Q2 in Figure 1, A and D). This set of ideas is based on early empirical observations with actin (Oosawa et al., 1959). These observations were initially given a theoretical framework by Oosawa and colleagues, who explained the behavior of actin by developing a theory for the equilibrium assembly behavior of helical polymers (Oosawa and Kasai, 1962; Oosawa, 1970). This equilibrium theory was extended to tubulin by Johnson and Borisy (1975).
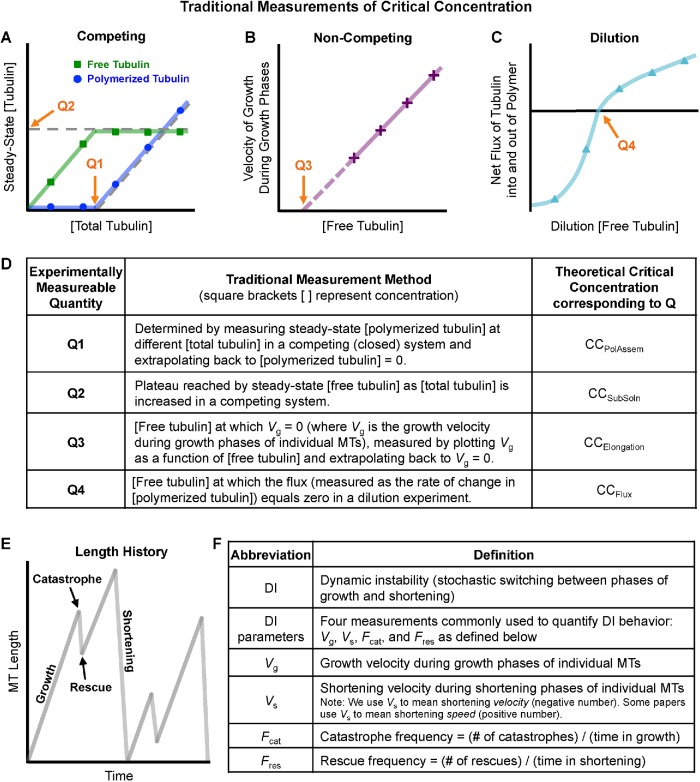
FIGURE 1:
Classical understanding of MT polymer assembly behavior. See Table 1 for additional description of the CC measurements depicted here. [Free tubulin] is the concentration of tubulin dimers in solution, [polymerized tubulin] is the concentration of tubulin dimers in polymerized form, and [total tubulin] = [free tubulin] + [polymerized tubulin]. (A) In a competing (closed) system, [total tubulin] is held constant over time and MTs compete for tubulin. As typically presented in textbooks, the CC can be measured in a competing system by observing either the concentration of total tubulin at which MT polymer appears (Q1) or the concentration of free tubulin left in solution once the amount of polymer has reached steady state (Q2). (B) In a noncompeting (open) system, [free tubulin] is held constant over time. In such a system, CC is considered to be the minimum concentration of tubulin necessary for MT polymers to grow, which is estimated by measuring the growth rate of individual filaments (Vg) and extrapolating back to Vg = 0 (Q3). (C) In dilution experiments, MTs are grown under competing conditions until the system reaches polymer-mass steady state and then diluted into various [free tubulin]. The initial rate of change in [polymerized tubulin] is measured. Here, CC is the concentration of dilution [free tubulin] at which the rate of change in [polymerized tubulin] is zero (i.e., the dilution [free tubulin] at which the net flux of tubulin into and out of MT polymer is zero) (Q4). (D) Summary table of the definitions of the experimentally measurable quantities Q1–Q4 depicted in panels A–C. (E) Individual MTs exhibit a behavior called dynamic instability (DI), in which the individuals undergo phases of growth and shortening separated by approximately random transitions termed catastrophe and rescue. (F) Table of definitions of DI parameters (four measurements commonly used to quantify DI behavior).
The idea that polymer assembly commences at the CC is now used routinely to design and interpret experiments involving cytoskeletal polymers (e.g., Amayed et al., 2002; Buey et al., 2005; Wieczorek et al., 2015; Concha-Marambio et al., 2017; Díaz-Celis et al., 2017; Schummel et al., 2017), and it is a standard topic in cell biology textbooks (e.g., Alberts et al., 2015; Lodish et al., 2016). Over time, a set of experimental measurements and definitions of CC have emerged (Table 1 and Figure 1), all of which would be equivalent for an equilibrium polymer, that is, a polymer that reaches maximum assembly at thermodynamic equilibrium. In other words, for an equilibrium polymer, there is one CC that can be measured in multiple ways.
TABLE 1:
Traditional critical concentration definitions used in the literature.
| Classical CC definition | Abbreviation | Experimental measurement of CC as applied to MT systems |
|---|---|---|
| Minimal concentration of total subunits (e.g., tubulin dimers) necessary for polymer assembly ( Oosawa, 1970; Johnson and Borisy, 1975) | CCPolAssem | CCPolAssem is determined by measuring steady-state [polymerized tubulin] at different [total tubulin] in a competing system and extrapolating back to [polymerized tubulin] = 0. See Q1 in Figure 1A (also Figures 3, A and B, and 4). |
| Concentration of free subunits left in solution once equilibrium or steady-state assembly has been achieved ( Oosawa, 1970; Johnson and Borisy, 1975)a | CCSubSoln | CCSubSoln is determined by measuring [free tubulin] left in solution at steady state for different [total tubulin] in a competing system and determining the position of the plateau reached by [free tubulin]. See Q2 in Figure 1A (also Figures 3, A and B, and 4). |
| Dissociation equilibrium constant for the binding of subunit to polymer, i.e., CC = KD = koff/kon ( Oosawa and Asakura, 1975)b | CCKD | CCKD can be determined by separate experimental measurement of kon and koff for addition/loss of tubulin subunits to/from MT polymer, respectively, and then calculating the ratio koff/kon. |
| Concentration of free subunit at which the rate of association equals the rate of dissociation during the elongation phase (called Sce in Walker et al., 1988; similar to c1 in Hill and Chen, 1984)c | CCElongation | CCElongation is determined by measuring the growth rate during the growth state (Vg) at various values of [free tubulin] and extrapolating back to the [free tubulin] at which Vg = 0. See Q3 in Figure 1B (also Figure 7, A and B). |
| Concentration of free subunit at which the fluxes of subunits into and out of polymer are balanced, that is, where the net flux is zero (called c0 in Hill and Chen, 1984) | CCFlux | CCFlux is determined by growing MTs to steady state at very high [total tubulin], then rapidly diluting to a new [free tubulin] and measuring the initial rate of change in [polymerized tubulin] (i.e., measuring [polymerized tubulin] flux). CCFlux is the value of [free tubulin] where [polymerized tubulin] flux = 0. See Q4 in Figure 1C (also Figure 6). |
| Concentration of free subunit at which polymers transition from “bounded growth” to “unbounded growth” (called ccr in Dogterom and Leibler, 1993) | CCUnbounded | CCUnbounded is the [free tubulin] at which the rate of change in average MT length transitions from equaling zero to being positive (Q5 in Figure 5). CCUnbounded can be identified by measuring DI parameters from MT length histories (Figure 1, E and F) across a range of different [free tubulin] and determining the [free tubulin] at which VgFres = |Vs|Fcat. |
These definitions of CC are interchangeable for equilibrium polymers, but have not all been compared in a single analysis for DI polymers. For each CC definition, we have assigned a specific abbreviation and provided an example of an early publication where that definition was used. The terms CCPolAssem, CCSubSoln, etc., refer to theoretical values (concepts), and Q1, Q2, etc., refer to experimentally measurable quantities (i.e., values obtained through experimental approaches as indicated in the figures). All definitions except CCKD can be applied to both equilibrium and steady-state polymers (CCKD assumes that the system is at equilibrium and therefore can be applied to only equilibrium polymers). The traditional framework outlined here will be revised in Results, where we will show that these definitions are not all equivalent for DI polymers (see Tables 3 and 4 for a summary).
aAssuming that assembly starts from a state with no polymer, maximal polymer assembly will occur at equilibrium for equilibrium polymers, and at polymer-mass steady state for steady-state polymers. Steady-state polymers will be (mostly) disassembled at thermodynamic equilibrium because the nucleotides in the system will be (effectively) entirely hydrolyzed.
bThe idea that CC = KD for simple equilibrium polymers is derived as follows. The net rate of polymer length change at a single filament tip = rate of addition – rate of loss. The rate of addition is assumed to be kon[free subunit], and the rate of loss is assumed to be koff. Therefore, the rate at which new subunits add to a population of n polymers is n × kon[free subunit], and the rate at which subunits detach from a population of n polymers is n × koff. At equilibrium, rate of polymerization = rate of depolymerization, so n × kon[free subunit] = n × koff . Therefore, at equilibrium, [free subunit] = koff/kon = KD = CCKD.
cCCElongation has been interpreted as the minimal concentration of free subunit needed to elongate from a growing polymer. The derivation of CCElongation is similar to that for CCKD, but considers the behavior of a single filament, not a population, and can apply to steady-state polymers because it does not require equilibrium. For polymers displaying DI, measurements of CCElongation are performed during the growth state of DI. The derivation of CCElongation assumes that Vg is a linear function of [free subunit], i.e.,  , where
, where  and
and  are observed rate constants during growth. Thus, the [free subunit] at which Vg = 0 is
are observed rate constants during growth. Thus, the [free subunit] at which Vg = 0 is 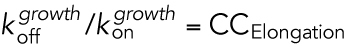 .
.
Nucleotide hydrolysis allows microtubules to exhibit dynamic instability
MTs (composed of subunits called tubulin dimers) are steady-state polymers, not equilibrium polymers, because they require a constant input of energy in the form of GTP (guanosine triphosphate) nucleotides to maintain a (highly) polymerized state. MTs exhibit a behavior known as DI, in which they stochastically switch between phases of growth and shortening via transitions known as catastrophe and rescue (Figure 1E) (Mitchison and Kirschner, 1984a; Walker et al., 1988). The DI behavior of MTs is driven by GTP hydrolysis (conversion of GTP–tubulin to GDP–tubulin): tubulin subunits containing GTP assemble into MTs, while tubulin subunits containing GDP do not (this occurs because the kon and koff values for GTP–tubulin differ from those for GDP–tubulin). In contrast, tubulin subunits containing non- or slowly hydrolyzable GTP analogues (e.g., GMPCPP) assemble into stable MTs that do not display DI (Hyman et al., 1992). Though some details about the mechanism of DI remain unclear, the consensus explanation for DI behavior is that growing MTs have a cap of GTP–tubulin subunits (the “GTP cap”) that stabilizes the underlying GDP–tubulin lattice. The MTs switch to rapid disassembly (i.e., undergo catastrophe) when they lose their stabilizing caps, exposing the unstable GDP–tubulin lattice below. When MTs regain their caps, they undergo rescue (transition from shortening to growth) (reviewed in Goodson and Jonasson, 2018). In contrast to equilibrium polymers, where individual filaments behave similarly to their populations, individual MTs and their populations can behave differently; for example, individual MTs can have shortening phases even when the overall polymer mass of the population is increasing.
Problems with applying equilibrium polymer theory to dynamically unstable polymers
On the surface, it may seem reasonable to apply the traditional CC framework as outlined above (see also Table 1) to understanding DI polymers such as MTs, because this framework is founded on theory (albeit equilibrium polymer theory) and appears to be consistent with many experimental results (Howard, 2001). However, further consideration reveals problems with this approach.
For a theoretical equilibrium polymer, the CC has been defined as koff/kon = KD (CCKD, Table 1), where kon and koff are the rate constants for attachment/detachment of a subunit to/from a filament tip and KD is the equilibrium dissociation constant for addition of subunits to polymer (e.g., Oosawa and Asakura, 1975; Howard, 2001; see also Pollard, 2010, for general information about KD for bimolecular reactions). Thus, polymer will undergo net assembly when [free subunit] is greater than CCKD, because the rate of attachment (kon × [free subunit]) will be greater than the rate of detachment (koff). Though this is frequently stated in textbooks, it is well recognized that the idea that “the CC” is the KD is a serious oversimplification when applied to MTs, or to steady-state polymers more generally (Alberts et al., 2015). More specifically, experimentally observed CCs for systems of dynamic MTs (however measured) cannot be equated to simple koff/kon = KD values because the GTP and GDP forms of tubulin have significantly different values of koff/kon. For example, the CC for GMPCPP (GTP-like) tubulin has been reported to be less than 1 µM (Hyman et al., 1992), while that for GDP–tubulin is very high, perhaps immeasurably so (Howard, 2001).
Exactly how the measured CC value(s) for a system of dynamic MTs relate to the KD values for GTP– and GDP–tubulin has not been established. However, intuition suggests that any CCs must lie between the respective KD values for GTP– and GDP–tubulin (Howard, 2001). Consistent with this idea, experimentally reported values for mammalian brain tubulin CC typically lie between ∼1 and ∼20 µM (e.g., Verdier-Pinard et al., 2000; Bonfils et al., 2007; Mirigian et al., 2013; Wieczorek et al., 2015).
Note that although the idea that CC = KD cannot apply in a simple way to a system of dynamic MTs, it can apply to tubulin polymers in the absence of hydrolysis, where assembly is an equilibrium phenomenon. Examples include systems containing only GDP–tubulin (when polymerized with certain drugs) or tubulin bound to non-/slowly hydrolyzable GTP analogues (e.g., GTP-γS, GMPCPP) (Hyman et al., 1992; Díaz et al., 1993; Buey et al., 2005). However, even for an equilibrium polymer, the KD might not equate to a simple koff/kon value (e.g., if the off rate is concentration-dependent [ Gardner et al., 2011]).
A related problem with applying equilibrium polymer theory to DI polymers is that it leaves open questions regarding how DI and energy utilization fit into the traditional CC framework. For example, how does the DI behavior of an individual filament in Figure 1, B and E, relate to the population-level behavior in Figure 1, A and C? Is there one experimentally relevant CC (as assumed from equilibrium polymer theory) or more than one? More broadly, why do some steady-state polymers (e.g., MTs) display DI, while others (e.g., actin) do not?
Previous efforts to clarify critical concentration as it applies to steady-state polymers
As one might imagine, some of these questions have been studied previously. However, ambiguity in understanding CC(s) of steady-state polymers still exists, in part because these earlier studies did not clearly relate their results to the classical definitions of CC, and few compared results between competing and noncompeting systems (Tables 1 and 2). A brief summary of some key previous efforts on CC for MTs is as follows (note that these focused on noncompeting systems):
In the 1980s, Hill and colleagues investigated some of the questions outlined above and worked to develop a theory of steady-state polymer assembly. Their conclusions included the idea that growth of MTs is governed by two distinct critical concentrations: a lower CC, which is the [free subunit] where “the mean subunit flux per polymer” during “phase 1″ (the growth phase) equals zero, and an upper CC, which is the [free subunit] where “the mean net subunit flux per polymer” is zero (similar to Figure 1C; e.g., Hill and Chen, 1984, elaborated on in Hill, 1987). However, the published work did not clarify for readers the biological significance of these two CCs nor how they relate to the behaviors of individual filaments and their populations.
Later in the 1980s, Walker et al. used video microscopy to analyze in detail the behavior of individual MTs undergoing DI. They demonstrated that MTs observed in vitro have a “critical concentration for elongation” (CCElongation), which they described as the [free subunit] at which the rate of tubulin association (
 [free tubulin]) is equal to the rate of dissociation (
[free tubulin]) is equal to the rate of dissociation ( ) during the elongation phase (Walker et al., 1988; Figure 1B; Table 1 and its footnotes). Consequently, at tubulin concentrations below CCElongation, there is no elongation. Later in this same paper, the authors discussed the existence of a higher CC above which a population of polymers will undergo “net assembly” (we refer to this as CCNetAssembly). Thus, the analysis in this article clearly indicates that MTs have two CCs. However, this conclusion is not stated explicitly, and the article does not address the question of how either of the two Walker et al. CCs relates to the two CCs predicted by Hill.
) during the elongation phase (Walker et al., 1988; Figure 1B; Table 1 and its footnotes). Consequently, at tubulin concentrations below CCElongation, there is no elongation. Later in this same paper, the authors discussed the existence of a higher CC above which a population of polymers will undergo “net assembly” (we refer to this as CCNetAssembly). Thus, the analysis in this article clearly indicates that MTs have two CCs. However, this conclusion is not stated explicitly, and the article does not address the question of how either of the two Walker et al. CCs relates to the two CCs predicted by Hill.In the 1990s, Dogterom et al. and Fygenson et al. used a combination of modeling (Dogterom and Leibler, 1993) and experiments (Fygenson et al., 1994) to show that there is a “critical value of monomer density, c = ccr,” above which MT growth is “unbounded” (i.e., the average length increases indefinitely and does not level off with time; Dogterom and Leibler, 1993; Dogterom et al., 1995; Fygenson et al., 1994). Hereafter, we refer to this ccr as CCUnbounded. Dogterom et al. also provided equations (similar to those proposed initially by Hill and Chen, 1984, and Walker et al., 1988) that can be used to relate CCUnbounded, which is a population-level characteristic, to the DI parameters (Figure 1, E and F), which describe individual-level behavior. One of the many significant outcomes of these papers was that they encouraged readers to think about how small changes to DI parameters (e.g., as caused by regulatory changes to MT binding proteins) could change the behavior of a system of MTs, especially in a cellular context. However, the implications of these articles for understanding CCs more broadly remained poorly appreciated because they did not explicitly relate CCUnbounded to the more classical CC definitions and measurements in Table 1 or to those discussed by Hill and Chen (1984) and Walker et al. (1988).
TABLE 2:
Types of experiments/simulations.
| Type of experiment/simulation | Description |
|---|---|
| Competing | Closed system where [total tubulin] is held constant for the duration of the experiment and MTs compete for tubulin (e.g., in a test tube) |
| Noncompeting | Open system where [free tubulin] is held constant for the duration of the experiment (e.g., in a flow cell) |
| Dilution | System where MTs are grown to polymer-mass steady state under competing conditions at very high [total tubulin] and then moved into noncompeting conditions at various values of [free tubulin] |
Thus, although DI has been studied for more than 30 years, confusion remains about how the traditionally equivalent definitions of CC and the interpretation of CC measurements should be adjusted to account for DI. Remarkably, the literature as yet still lacks a clear discussion of how the CCElongation and CCUnbounded mentioned above relate to each other, to the CCs predicted by Hill, or to the classical experimental measurements of CC depicted in Figure 1A. To address this problem, we will investigate the following questions:
How many distinct CCs are produced by the different experimentally measurable quantities (Q values, Figure 1 and Table 1), which measurements yield which CC, and what is the practical significance of each?
How do these values relate to behaviors at the scales of subunits, individual MTs (e.g., Figure 1, B and E), and the bulk polymer mass of populations of MTs (e.g., Figure 1, A and C)?
How does the separation between distinct CCs relate to DI, and can the separation help to explain differences between steady-state polymers that display DI (e.g., tubulin) and those that do not (e.g., actin)?
Undoubtedly, many researchers have an intuitive understanding of the answers to at least some of these questions. However, the observation that even recent literature contains many references to “the” CC for MT assembly (e.g., Alfaro-Aco and Petry, 2015; Wieczorek et al., 2015; Hussmann et al., 2016; Schummel et al., 2017) indicates that this problem deserves attention.
Biological implications of critical concentrations and practical significance for experimental design and interpretation
While these issues are interesting from a basic science perspective, they also have significant practical relevance: proper design and interpretation of experiments that involve perturbing MT dynamics (e.g., characterization of MT-directed drugs or proteins) require an unambiguous understanding of CCs and how they are measured (e.g., Verdier-Pinard et al., 2000; Bonfils et al., 2007; Hussmann et al., 2016; Cytoskeleton Inc., n.d.).
For example, measuring the values of the CCs provides a way to characterize tubulin from different cell types and effects of polymer-binding proteins. The measured CCs serve as reference points separating concentration ranges where a system’s qualitative behaviors differ, analogous to a KM for an enzyme–substrate system or a KD for a binding reaction. Correspondingly, the relationship between the subunit concentration set by an experimenter or a cell and the CCs affects various properties of the resulting polymer population, such as the total amount of polymer present, the length distribution of filaments in the population, and the DI behavior of the filaments.
Examples of practical implications include the following: 1) Measuring the effect of a polymer-binding protein on the CCs can be used not only to characterize the protein, but also to provide an intuitive understanding of its effects on polymer assembly over a range of subunit concentrations. 2) As we will return to in the Discussion, CCs are of value for understanding how MT behaviors studied in vitro pertain to in vivo behaviors, and relatedly, for understanding how cells can manipulate CCs for regulatory purposes. 3) Clarifying which CC is obtained from which measurement is necessary for correct interpretation of experiments (e.g., as our results below show, measurements commonly expected to yield the minimum subunit concentration needed for polymer assembly actually yield CCNetAssembly). 4) Finally, we propose that the separation between different CCs can be used to understand behavioral differences between MTs and actin.
Additionally, even if measuring CCs is not the goal of an experiment, understanding the CCs is still relevant to experimental design and interpretation, because the relationship between the starting subunit concentration and the CCs affects the resulting polymer behavior and amount of polymer. For example, if the subunit concentration in an experiment is close to a CC, then a small variation in experimental conditions could lead to a drastic change in polymer mass and behavior. More specifically, if the control conditions and test conditions in an experiment with a MT binding protein have slightly different [free tubulin], with one just below CCNetAssembly and the other just above, then the predictable dramatic difference in results could be incorrectly attributed to the MT binding protein. Indeed, we suggest that incomplete understanding of CCs and their impact on designing and interpreting experiments is one reason for variability in the reported effects of MT binding proteins.
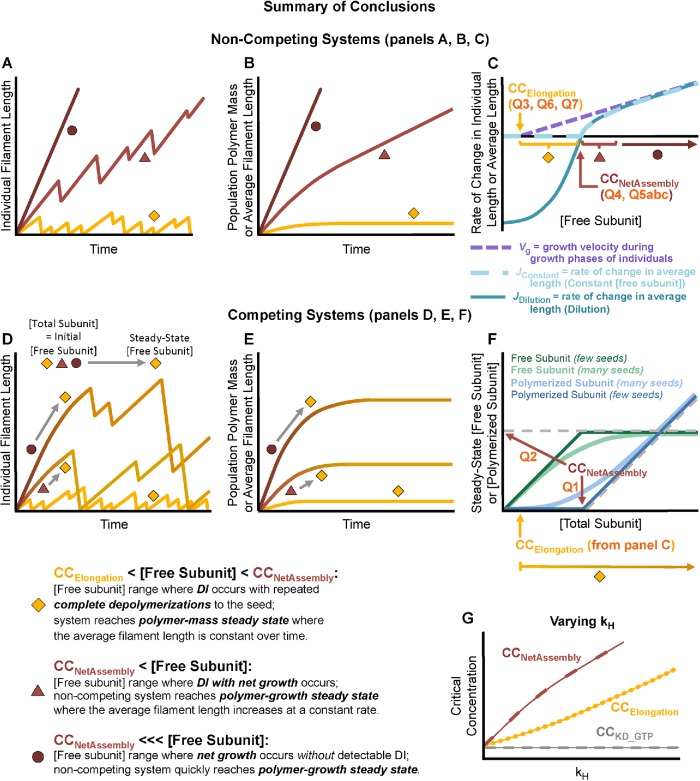
Summary of conclusions
Using systems of simulated MTs, we show that classical interpretations of experiments such as those in Figure 1 can be misleading in terms of understanding the behavior of individual MTs. In particular, we use the simulations to illustrate the fact that dynamically unstable polymers such as MTs do have (at least) two major experimentally distinguishable CCs, as originally proposed by Hill and colleagues (summarized in Hill, 1987). We clarify how the CCs relate to behaviors of individual MTs and populations of MTs. At [free tubulin] above the lower CC, growth phases of individual filaments can occur transiently, though experimentally observable growth phases may not occur until well above this CC. At [free tubulin] above the higher CC, the polymer mass of a large population will increase steadily; individual filaments in the population potentially still exhibit DI, but with net growth over sufficient time. We show that the lower CC corresponds to CCElongation (Table 1) as measured by Walker et al. (1988), which can be described as the free tubulin concentration above which individual MTs can elongate during the growth phase. This CC can be measured by experimental quantity Q3 in Figure 1B. The higher CC corresponds to CCUnbounded (Table 1) as identified by Dogterom et al., that is, the concentration of free tubulin above which “unbounded growth” occurs (Dogterom and Leibler, 1993; Dogterom et al., 1995; Fygenson et al., 1994). This upper CC can be measured by Q1, Q2, and Q4 in Figure 1, A and C. To clearly distinguish these two CCs and avoid confusing either with a situation where a physical boundary is involved, we suggest calling them CCElongation and CCNetAssembly, based on the terminology in Walker et al. (1988).
We show that most experiments intended to measure “the CC” actually measure CCNetAssembly (i.e., the higher CC). This conclusion means that “typical” MT DI (where MTs grow and depolymerize back to the seed) is limited to concentrations below what has traditionally been considered “the” CC needed for polymer assembly (i.e., Q1, Q2 in Figure 1A; Table 1). Related to the discussion above, this provides one example of why clarifying which CC is obtained from which measurement is relevant to experimental biology: if one thinks that an experiment is measuring the minimum concentration needed for polymer assembly, but it is actually measuring the CC for net assembly, then the biological implications of the experiment could be seriously misinterpreted.
Furthermore, we show that in competing systems (i.e., closed systems where MTs compete for a limited total number of tubulin subunits), the concentration of free tubulin at steady state ([free tubulin]SteadyState) does not equal CCNetAssembly, as would be expected from traditional interpretations of classic CC experiments (Figure 1A). Instead, [free tubulin]SteadyState asymptotically approaches CCNetAssembly as [total tubulin] increases.
In addition to the experimentally accessible CCElongation and CCNetAssembly, there are two more CCs (perhaps not experimentally accessible) that correspond to the KD for the GTP and GDP forms of tubulin subunits. We suggest calling these CCKD_GTP and CCKD_GDP, respectively. For an equilibrium polymer system (e.g., one composed of only the GTP form), CCElongation and CCNetAssembly would be equal to each other and to the relevant CCKD. In addition, we demonstrate that the degree of separation between CCElongation and CCNetAssembly depends on the GTP hydrolysis rate constant (kH). We also show that CCElongation can differ from CCKD_GTP, contrary to previous assumptions that growing MTs always have GTP–tubulin at their tips (topmost subunits; e.g., Bowne-Anderson et al., 2015).
Finally, we demonstrate that DI itself, in combination with detection limitations, can produce results (e.g., lack of detectable growth phases at concentrations near CCElongation, and sigmoidal seed occupancy plots) previously interpreted as evidence that growth from stable seeds requires a nucleation step.
This article focuses on systems composed of a predefined number of MTs with one end free and the other end anchored at a stable nucleation site, such as would exist for MTs growing from centrosomes. In other cases, MTs can have two free ends (plus and minus). For each of CCElongation and CCNetAssembly, the numerical value at the plus end could differ from the value at the minus end (Walker et al., 1988). While our studies focus on MTs, we suggest that these CC definitions and interpretations can apply to steady-state polymers more generally, but are especially significant for those that exhibit DI.
RESULTS
Computational models: simplified model and detailed model
To investigate and clarify the concept of CC as it applies to dynamically unstable polymers, we used computational modeling. Computational models are ideal for addressing this type of problem because the biochemistry of the reactions can be explicitly controlled, and in silico experiments can be performed quickly and easily. Furthermore, it is possible to follow the behavior of the system at all relevant scales simultaneously: addition/loss of individual subunits to/from the free end of each filament, DI of individual filaments, and any changes in polymer mass of the population of filaments. In comparison, it is challenging to address these questions using physical systems because experiments have thus far been limited technically to measurements of one (or at most two) of these scales at a time.
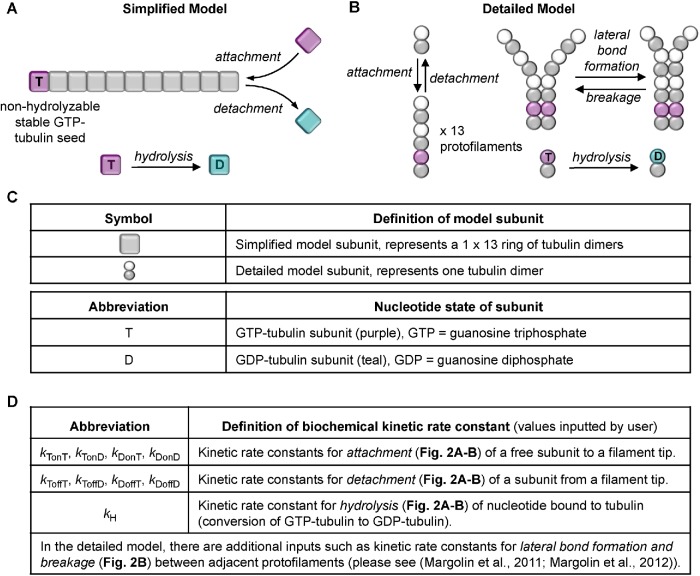
In this work, we used both a “simplified” model of MT dynamics, in which MTs are modeled as simple linear polymers (Gregoretti et al., 2006), and a “detailed” model, where MTs are composed of 13 protofilaments (PFs), with lateral and longitudinal bonds between subunits (tubulin dimers) modeled explicitly (Margolin et al., 2011, 2012) (Figure 2). The simulations were designed to be intuitively understandable to researchers familiar with biochemical aspects of cytoskeletal polymers. Consequently, the rules governing the simulations correspond directly to biochemical reaction kinetics. Key elements of these models are described in Box 1.
FIGURE 2:
Processes that occur in the computational models. (A) In the simplified model, MTs are approximated as simple linear filaments that can undergo three processes: subunit addition, loss, and hydrolysis. Addition and loss can occur only at the tip. Hydrolysis can occur anywhere in the filament where there is a GTP subunit. (B) In the detailed model, there are 13 protofilaments, each of which undergoes the same processes as in the simplified model but also undergoes lateral bonding and breaking between adjacent protofilaments. (C) Information about the subunits in the models. In both models, the kinetic rate constants (panel D) controlling these processes are input by the user, and the MTs grow off of a user-defined constant number of stable MT seeds (composed of nonhydrolyzable GTP–tubulin). The standard DI parameters (Vg,Vs, Fcat, Fres; see Figure 1, E and F) are emergent properties of the input rate constants, [free tubulin], and other aspects of the environment, such as the number of stable seeds. For more information about the models and their parameter sets, see Box 1, Materials and Methods, Gregoretti et al. (2006), and Margolin et al. (2011, 2012).
We utilized both the simplified and detailed computational models because each has particular strengths for addressing problems related to MT dynamics. The simplified model has fewer kinetic parameters, all of which are directly comparable to parameters in typical analytical models (i.e., mathematical equations), and it is similar to single-protofilament models that have been used by other authors (e.g., Padinhateeri et al., 2012; Li and Kolomeisky, 2014; Aparna et al., 2017). Thus, the simplified model is useful for testing analytical model predictions relating biochemical properties to individual filament level and bulk population level behaviors. In contrast, the increased resolution of the detailed model is important for testing the generality and relevance of conclusions derived from the simplified model.
In addition, the input kinetic rate constants in the two models were tuned to produce dynamic instability behavior that is quantitatively different between the two models (measured DI parameter values are in the Supplemental Excel file). It follows that the specific numerical values for CCs extracted from these two models will be different. However, as demonstrated by the results that follow, the behavioral changes that occur at each CC are qualitatively similar in the two models. Thus, these two models enable us to determine which conclusions are general and to avoid making conclusions that are specific to particular parameter sets or polymer types.
Box 1: Key elements of the two computational models (simplified and detailed) used in this study.
The behaviors of the evolving systems of dynamic MTs in the simulations can be followed at the scales of subunits, individual filaments, or populations of filaments. For both models, the simulations spontaneously undergo the full range of DI behaviors (including rescue), and they can simulate systems of dynamic MTs for hours of simulated time (Gregoretti et al., 2006; Margolin et al., 2012).
Subunit addition/loss and GTP hydrolysis (both models) and lateral bond formation/breaking (detailed model only) are modeled as stochastic events that occur according to kinetic rate equations based on the biochemistry of these processes (Figure 2). In the detailed model, longitudinal bonds form first (i.e., subunits attach to a PF), and lateral bonds between a pair of subunits in two neighboring PFs can form only if the pair of subunits immediately below is already laterally bonded. Similarly, lateral bonds between PFs can break only at the interface between bonded and unbonded regions. In other words, lateral bonds between PFs zip open or closed, enabling dynamic cracks to exist between PFs at the MT tip, as was recently observed experimentally (McIntosh et al., 2018). For more information about the effect of the lateral bonds in the simulations, see Margolin et al., 2011, 2012, and Li et al., 2014.
The user-defined (adjustable) parameters correspond to the following: the biochemistry of the proteins being studied (i.e., kinetic rate constants for the reactions listed above) and attributes of the environment that would be set by either the experimenter or the cell (e.g., the concentration of tubulin in the system, whether the system is competing (closed) or noncompeting (open), the number of stable seeds, and the system volume).
Because MTs in cells and in many in vitro experiments grow from stable seeds (nucleation sites such as centrosomes, axonemes, or GMPCPP seeds), our simulations assume that one end of each MT is fixed (as would be the case for growth from centrosomes) and that all addition and loss occur at the free end. In our simulations, the seeds are composed of nonhydrolyzable GTP–tubulin. Except where otherwise noted, the number of stable seeds was set to 100 in the simplified model and 40 in the detailed model.
As in physical experiments, emergent properties of the simulated systems include the DI parameters (Vg, Vs, Fcat, Fres; see Figure 1, E and F) and the concentrations of free and polymerized tubulin at steady state. In particular, transitions between growth and shortening (catastrophe and rescue) are spontaneous processes that occur when the stabilizing GTP cap happens to be lost or regained as a result of the biochemical reactions described.
The kinetic rate constants used as input parameters for the detailed model were previously tuned to approximate the DI parameters of mammalian brain MTs in vitro (Margolin et al., 2012). The simplified model parameters used here are modified from those of Gregoretti et al. (2006) and were chosen for use here because they produce DI behavior that is quantitatively different from that of the detailed model.
These attributes make these simulations ideal for studying the relationships between the concentration of tubulin, the behaviors of individual MTs, and the behaviors of populations of dynamic MTs. See Materials and Methods, Gregoretti et al. (2006), and Margolin et al. (2012) for additional details including input parameters.
Approach to understanding the relationship between microtubule behaviors and critical concentrations
The term “critical concentration” can have a specific thermodynamic meaning as the solute concentration at which a phase change occurs. Here we use the term operationally, as the concentration at which a behavioral change occurs. To clarify the concept of CC as it applies to MTs, we examined which of the commonly used CC definitions (outlined in Table 1) are meaningful in studying MTs, and for the set that are meaningful, which are equivalent. We determined how the various CC definitions in Table 1 relate to each other and to DI.
To perform this work, we used the simulations to examine simultaneously the behaviors of individual MTs and populations of MTs. More specifically, we ran sets of simulations for both the simplified and detailed models at various tubulin concentrations in both competing systems (closed systems with constant [total tubulin], as might happen in a test tube) and noncompeting systems (open systems with constant [free tubulin], similar to what might happen in a microscope flow cell). This approach mimics various experiments (Table 2) that are classically used to measure MT CC (Table 1). We then assessed and compared the behaviors of the individual MTs (e.g., DI parameters), population-level properties (e.g., [free tubulin] at steady state), and CCs as determined by the traditional definitions (Table 1).
For the work presented here, it is important to recognize that the relevant observations are the behaviors of the systems at different scales and the concurrence (or disagreement) between the values of CC that result from various definitions or measurement approaches; the specific numerical CC values observed are simply outcomes of the particular input kinetic rate constants used and so are not by themselves significant. This situation is analogous to physical MTs, where DI parameters and CC values depend on the protein sequences, temperatures, and buffer conditions used (e.g., Williams et al., 1985; Gildersleeve et al., 1992; Fygenson et al., 1994; Hussmann et al., 2016; Schummel et al., 2017).
We use the terms Q1, Q2, etc., to refer to specific experimentally measurable quantities (i.e., values obtained through experimental approaches, as indicated in the figures), and the terms CCKD, CCPolAssem, CCSubSoln, etc., to refer to theoretical values (concepts) that may or may not correspond to particular experimentally measurable quantities and may or may not be equivalent. Table 1 summarizes traditional CC definitions and measurements used in the literature. Tables 3 and 4 summarize our clarifications of CC definitions and additional Q value measurements based on the results that will be presented in this work.
TABLE 3:
Revised understanding of critical concentration for dynamically unstable polymers.
| Critical concentration | Representative figures | Critical concentration description | Equivalent to (see Table 1)a | Measured by (see Table 4) |
|---|---|---|---|---|
| CCNetAssembly | 1, A and C, 3–6 | CC above which the polymer mass of a population will increase persistently, and individual filaments will undergo net growth over time | CCSubSoln,b CCFlux,c CCUnbounded |
Q1, Q2, Q4, Q5 |
| CCElongation | 1B, 7, 8 | CC above which individual filaments can exhibit the transient growth phases of DI | CCElongation | Q3, Q6, Q7 |
| CCKD_GTP | 9 | Equilibrium dissociation constant for binding of a free GTP subunit to a GTP subunit at a polymer tip | Any of the Q values above, under conditions where GTP is not hydrolyzed | |
| CCKD_GDP | Equilibrium dissociation constant for binding of a free GDP subunit to a GDP subunit at a polymer tip | GDP–tubulin alone does not form MTs, so CCKD_GDP is not straightforwardly measured |
For steady-state polymers (including DI polymers), CCKD_GTP ≤ CCElongation ≤ CCNetAssembly ≤ CCKD_GDP, but for equilibrium polymers, CCKD = CCElongation = CCNetAssembly.
aCCPolAssem is not listed here because there is no threshold concentration at which polymers abruptly appear. Instead, the measurement classically expected to yield CCPolAssem (see Q1 in Table 4) actually yields CCNetAssembly.
bCCSubSoln is classically defined as the value of [free tubulin]SteadyState in a competing system whenever [total tubulin] is above “CCPolAssem” (Table 1; Figure 1A). However, CCSubSoln is more accurately defined as the asymptote approached by [free tubulin]SteadyState as [total tubulin] is increased (Q2 in Figures 3, A and B, and 4).
It should be stressed that CCFlux is the [free tubulin] at which the population-level fluxes of tubulin into and out of polymer are balanced, while individual MTs may grow and shorten when [free tubulin] = CCFlux.
TABLE 4:
Summary of experimentally measurable quantities (Q values) used to estimate CCs.
| Q value | Representative figures | Description of experimentally measurable quantity | CC estimated by Q |
|---|---|---|---|
| Q1 | 1A, 3, A and B, 4 | Q1 is the x-intercept of the line (with slope = 1) approached by steady-state [polymerized tubulin] as [total tubulin] is increased in a competing system. | CCNetAssembly |
| Q2 | 1A, 3, A and B, 4 | Q2 is the horizontal asymptote approached by [free tubulin]SteadyState as [total tubulin] is increased in a competing system. | CCNetAssembly ( = CCSubSoln) |
| Q3 | 1B, 7, A and B | Q3 is the [free tubulin] at which Vg = 0. Q3 is estimated by plotting Vg as a function of [free tubulin], fitting a regression line to the approximately linear part of the Vg data, and extrapolating back to the [free tubulin] at which Vg = 0. | CCElongation |
| Q4 | 1C, 6 | Q4 is the [free tubulin] at which J, the rate of change in [polymerized tubulin], equals zero in a dilution experiment (J < 0 when dilution [free tubulin] < Q4; J > 0 when dilution [free tubulin] > Q4).a Q4 is determined by growing MTs to polymer-mass steady state at high [total tubulin], then rapidly diluting to a new [free tubulin] and measuring the rate of change in [polymerized tubulin] after a short delay.b | CCNetAssembly ( = CCFlux) |
| Q5 (a, b, and c) |
5, C–F | Q5 is the [free tubulin] above which the rate of change in average MT length is positive in an experiment where [free tubulin] is held constant and the population has reached polymer-mass or polymer-growth steady state (J = 0 when [free tubulin] < Q5; J > 0 when [free tubulin] > Q5).c Q5 can also be described as the concentration above which the population drift coefficient is positive. We use the name Q5a, Q5b, or Q5c depending on how J is measured. | CCNetAssembly ( = CCUnbounded) |
| Q5a | 5, C–F, 6, C and D | Q5a is Q5 with J calculated from the net rate of change in a population’s average MT length between two time points; that is, J = (average length at time B – average length at time A)/(time B – time A), called JNet in Mauro et al. (2019). | |
| Q5b | 5, C and D | Q5b is Q5 with J calculated from measured DI parameters using the JDI_piecewise equation ( Eq. 1b). Q5b is the [free tubulin] at which VgFres = |Vs|Fcat. | |
| Q5c | 5, E and F | Q5c is Q5 with J calculated by summing displacements measured over short time steps (see the Supplemental Methods subsection on measuring drift coefficient, called JTimeStep in Mauro et al., 2019). | |
| Q6 | 7, C and D | Q6 is measured in the same way as Q3, but using growth phases from a dilution experiment after the system has been diluted into constant [free tubulin] conditions (instead of [free tubulin] being constant for the entire experiment, as with Q3). | CCElongation |
| Q7 | 8, C and D | Q7 is the x-intercept of the line approached by J as [free tubulin] is increased (note that J approaches the line when [free tubulin] >> CCNetAssembly). | CCElongation |
See Table 3 for descriptions of the CCs.
aJ can be defined in terms of polymer mass or average MT length (Supplemental Table S1; see also Section 1.3.2 of Mauro et al., 2019): J = rate of change in [polymerized tubulin] = flux of tubulin into and out of polymer (e.g., in µM/s) or J = rate of change in average MT length = drift coefficient (e.g., in µm/s).
bThe delay allows the GTP cap size to adjust in response to the new [free tubulin] after the dilution.
cThe closer [free tubulin] is to CCNetAssembly, the longer it will take for the system to reach steady state. If J is measured before polymer-mass steady state has been reached for [free tubulin] < CCNetAssembly, then J will appear to be positive for [free tubulin] near but below CCNetAssembly; this would make it difficult to identity the precise value of Q5. The transition from J = 0 to J > 0 at Q5 will be sharper the longer the system is allowed to run (see also Mauro et al., 2019).
The results of our in silico experiments are presented in the following order:
We first present experiments with the computational simulations under competing conditions to assess the classical CC measurements.
Next, we present experiments with the simulations under noncompeting conditions to assess DI behavior relative to the CCs and to compare the results with those of the competing experiments.
Once we have established which CC is provided by each measurement and the behavioral significance of the CCs, we then present simulations in which we alter kH to investigate the relationship between kH, the CCs, and DI behavior.
At the end, we examine how our improved understanding of the relationship between CCs and DI can help explain experimental observations that growth of MTs from stable seeds appears to require a nucleation step.
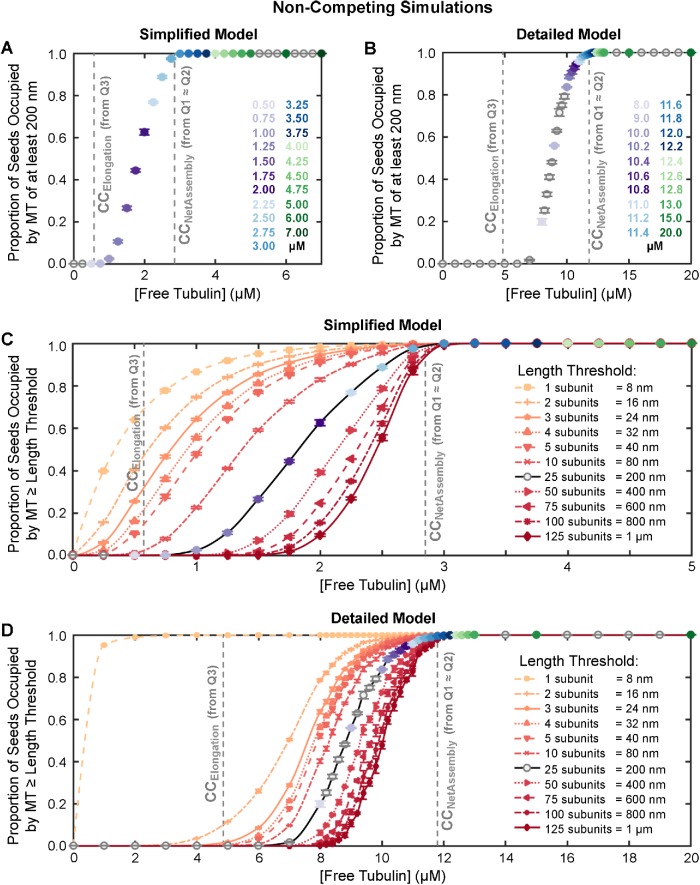
Dynamically unstable polymers grow at concentrations below standard experimental quantities commonly thought to measure the critical concentration for polymer assembly
A typical way to measure “the CC” for MT assembly is to determine the [total tubulin] at which polymer assembles in a competing (closed) experiment such as that portrayed in Figure 1A, where Q1 measures what is traditionally considered to be the CC for polymer assembly (CCPolAssem; e.g., Mirigian et al., 2013). An alternative approach treated as equivalent is to measure the concentration of free tubulin left in solution once steady-state polymer assembly has occurred (Figure 1A, Q2), traditionally considered to yield CCSubSoln (Mirigian et al., 2013). In other words, the expectation is that Q1 ≈ Q2, and that these experimentally obtained quantities provide equivalent ways to measure the CC for polymer assembly, where CCPolAssem = CCSubSoln (Table 1).
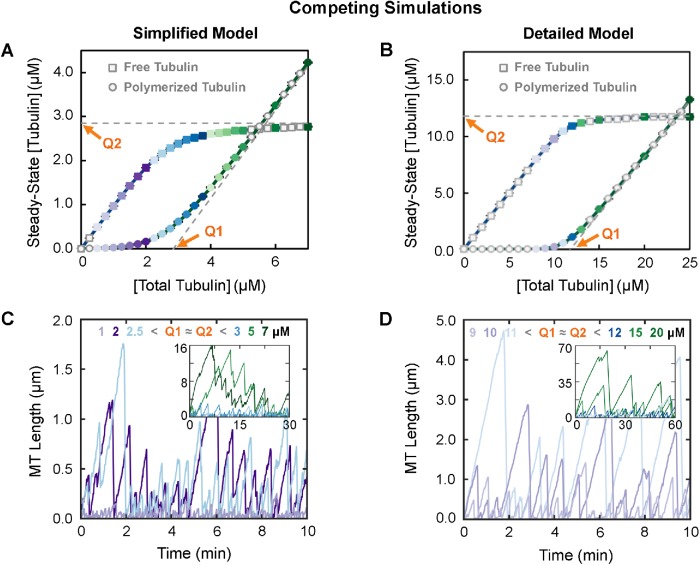
We tested these predictions by performing simulations of competing systems where individual MTs growing from stable seeds compete for a limited pool of tubulin (i.e., [total tubulin] is constant). This situation is analogous to a test-tube experiment in which MTs grow from preformed MT seeds, and both [polymerized tubulin] and [free tubulin] are measured after the system has reached polymer-mass steady state (Supplemental Figure S1, A–D). 1 Initial inspection of Figure 3, A and B shows that the [polymerized tubulin] and [free tubulin] curves are roughly similar to the expectations from the common understanding depicted in Figure 1A, and Q1 ≈ Q2 (Figure 3, A and B).
FIGURE 3:
Behavior of MTs (populations and individuals) under conditions of constant total tubulin. Left panels: simplified model; right panels: detailed model. Colors of data points reflect the concentrations of total tubulin. (A, B) Classical CC measurements (compare with Figure 1A). Systems of competing MTs at total tubulin concentrations as indicated on the horizontal axes were each allowed to reach polymer-mass steady state (shown in Supplemental Figure S1, A–D). Then the steady-state concentrations of free (squares) and polymerized (circles) tubulin were plotted as functions of [total tubulin]. (C,D) Representative length history plots for individual MTs from the simulation runs used in panels A and B. The value of [total tubulin] for each length history is indicated in the color keys at the top of panels C and D. Interpretation: Classically, Q1 estimates CCPolAssem, and Q2 estimates CCSubSoln. However, as can be seen in panels C and D, MTs grow in both models at [total tubulin] below Q1 ≈ Q2 (∼2.85 µM in the simplified model and ∼11.8 µM in the detailed model). Consistent with this observation, the main text provides justification for the idea that CC as estimated by Q1 ≈ Q2 instead measures CCNetAssembly, the CC for persistent growth of a population’s polymer mass and net growth of individual MTs over time. Note that the difference in the values of Q1 ≈ Q2 between the two models is expected from the fact that the input kinetic parameters for the models were chosen to produce quantitatively different DI measurements in order to provide a test of the generality of conclusions about qualitative behaviors; the results show that the behaviors are indeed qualitatively similar between the two models. For additional data related to the competing simulations (e.g., plots of [free tubulin] and [polymerized tubulin] as functions of time), see Supplemental Figure S1. Methods: Data points in panels A and B represent the mean ± one SD of the values obtained in three independent runs of the simulations. The values from each of three runs are averages over 15–30 min for the simplified model (panel 3A) and over 30–60 min for the detailed model (panel 3B). These time periods were chosen so that [free tubulin] and [polymerized tubulin] had reached their steady-state values (Supplemental Figure S1, A–D).
However, closer examination of these data shows a key difference from the common understanding (Figure 1A): there is no sharp transition at either Q1 or Q2 (Figure 3, A and B). Significantly, small but nonzero amounts of polymer exist at [total tubulin] below reasonable estimates for Q1 (Figure 3, A and B; Supplemental Figure S1, E and F). In addition, the steady-state concentration of free tubulin ([free tubulin]SteadyState) is not constant with respect to [total tubulin] for [total tubulin] > Q1. Instead, [free tubulin]SteadyState approaches an asymptote represented by Q2 (Figure 3, A and B). Nonetheless, Q1 is still approximately equal to Q2. 2 Consistent with these observations, examination of individual MTs in these simulations shows MTs growing and exhibiting DI at [total tubulin] below Q1 ≈ Q2 (Figure 3, C and D; compare with Figure 3, A and B).
These data (Figure 3) suggest that one of the most commonly accepted predictions of traditional CC understanding is invalid when applied to systems of dynamic MTs: instead of both Q1 and Q2 providing an experimental measure of the minimum concentration of tubulin needed for polymer assembly (CCPolAssem), neither does, since MTs exhibiting DI appear at concentrations below Q1 ≈ Q2. Correspondingly, the results in Figure 3, A and B, indicate that the CC called CCSubSoln would be more accurately defined as the asymptote approached by the [free tubulin]SteadyState as [total tubulin] increases, not the value of [free tubulin]SteadyState itself (Figure 1A).
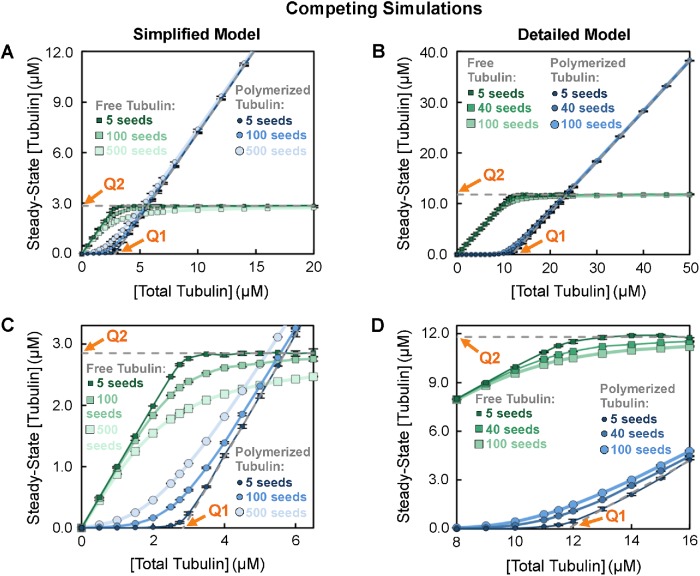
The number of stable MT seeds impacts the sharpness of the transition at Q1 and Q2.
Why is the transition at Q1 and Q2 in Figure 3, A and B, more gradual than the theoretical transition as depicted in Figure 1A? Previous results of our simplified model (Gregoretti et al., 2006) and other models (e.g., Vorobjev and Maly, 2008; Mourão et al., 2011) indicate that [free tubulin]SteadyState depends on the number of stable MT seeds. Therefore, we investigated how changing the number of stable MT seeds affects the shape of the curves in classical CC plots. Examination of the results (Figure 4, A and B; zoom-ins in Figure 4, C and D) shows that changing the number of MT seeds does change the sharpness of the transitions at Q1 and Q2. More specifically, when the number of MT seeds is small, a relatively sharp transition is seen at both Q1 and Q2 in graphs of steady-state [free tubulin] and [polymerized tubulin]; little if any bulk polymer is observed at [total tubulin] below Q1 (Figure 4, fewer seeds, darkest curves, similar to Figure 1A). In contrast, when the number of MT seeds is large, measurable amounts of polymer appear at concentrations well below Q1, and consequently [free tubulin]SteadyState approaches the Q2 asymptote more gradually (Figure 4, more seeds, lightest curves). Moreover, the data for various numbers of seeds all approach the same asymptotes (gray dashed lines, Figure 4). These observations indicate that the number of MT seeds does not impact the value of Q1 ≈ Q2, but does affect how sharply steady-state [free tubulin] approaches the Q2 asymptote.
FIGURE 4:
Impact of changing the number of MT seeds in competing systems. Steady-state concentrations of free (squares) and polymerized (circles) tubulin in competing systems as in Figure 3, A and B. (A, C) Simplified model with MTs growing from 5, 100, or 500 stable MT seeds (data for 100 seeds replotted from Figure 3A). (B, D) Detailed model with MTs growing from 5, 40, or 100 stable MT seeds (data for 40 seeds replotted from Figure 3B). Panels C and D show zoom-ins on the data plotted in panels A and B, respectively. The darker curves with smaller symbols correspond to fewer seeds and the lighter curves with larger symbols correspond to more seeds. Interpretation: These data show that changing the number of stable MT seeds alters the approach to the asymptotes determining Q1 and Q2 (dashed gray lines replotted here from Figure 3, A and B), but does not change the value of Q1 ≈ Q2. Methods: Data points represent the mean ± one SD of the values obtained in three independent runs of the simulations. Similar to Figure 3, [free tubulin] and [polymerized tubulin] from each run were averaged over a period of time after polymer-mass steady state was reached. The time to reach this steady state depends on the number of stable MT seeds (see Supplemental Figure S2). For the simplified model, the averages of [free tubulin] and [polymerized tubulin] were taken from 120 to 150 min for five MT seeds and from 15 to 30 min for 100 and 500 MT seeds. For the detailed model, the averages were taken from 100 to 150 min for five MT seeds and from 30 to 60 min for 40 and 100 MT seeds. We were able to use a larger number of seeds in the simplified model than in the detailed model because it is more computationally efficient.
The observations thus far raise a question: because CCSubSoln is not the minimum tubulin concentration needed for polymer assembly (CCPolAssem), what is the significance of Q1 ≈ Q2 ≈ CCSubSoln for MT behavior?
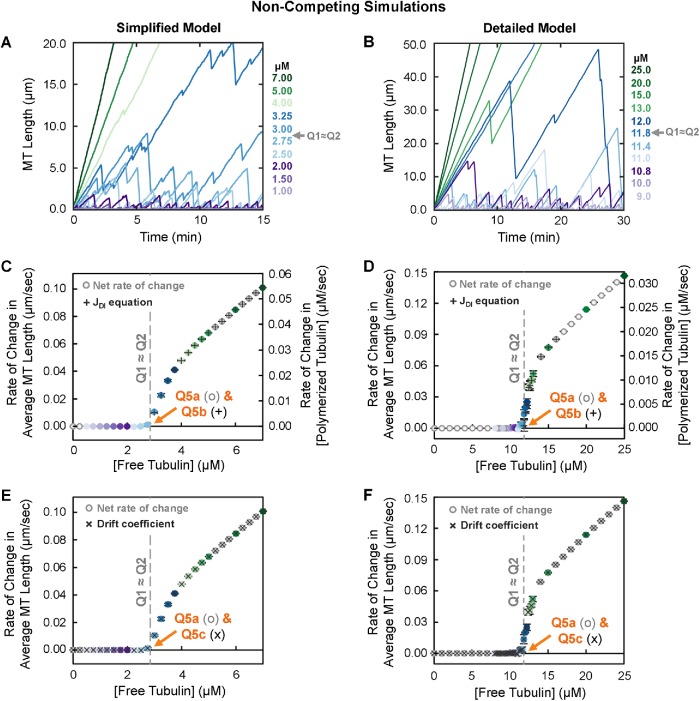
A critical concentration for net growth of individual microtubules and persistent growth of a population’s polymer mass (CC NetAssembly)
To investigate the significance of Q2 (i.e., the asymptote approached by [free tubulin]SteadyState as [total tubulin] is increased; Figures 3, A and B, and 4), we examined the dependence of MT behavior on the concentration of free tubulin in noncompeting simulations. For these studies, we fixed [free tubulin] at various values instead of allowing polymer growth to deplete the free tubulin over time. This set of conditions is analogous to a laboratory experiment involving MTs polymerizing from stable seeds in a constantly replenishing pool of free tubulin at a known concentration, such as might exist in a flow cell.
As described above, Q1 and Q2 from competing systems do not yield the CC for polymer assembly (CCPolAssem) as expected from traditional understanding. Instead, comparison with the noncompeting simulations (Figure 5) shows that Q1 and Q2 correspond to a different CC, which can be described as the [free tubulin] above which individual MTs will exhibit net growth over long periods of time (Figure 5, A and B). Equivalently, this CC can be described as the [free tubulin] above which the polymer mass of a large population of MTs will grow persistently (Figure 5, C and D); we use this terminology based on the experimentally observed “persistent growth” in Komarova et al. (2002).
FIGURE 5:
Behavior of MTs (individuals and populations) under conditions of constant free tubulin. Left panels: simplified model; right panels: detailed model. Colors of data points reflect the concentrations of free tubulin. (A, B) Representative length history plots for one individual MT at each indicated constant free tubulin concentration. (C, D) Steady-state net rate of change (o symbols) in average MT length (left axes) or in concentration of polymerized tubulin (right axes) for the free tubulin concentrations shown. Q5a indicates the concentration at which this rate becomes positive. This panel also shows the theoretical rate of change in average MT length (+ symbols) as calculated from the extracted DI measurements (Supplemental Excel file) using the equation JDI = (Vg Fres – |Vs|Fcat)/(Fcat + Fres) in the [free tubulin] range where JDI > 0 (Eq. 1 in the “unbounded growth” regime) (Hill and Chen, 1984; Walker et al., 1988; Verde et al., 1992; Dogterom and Leibler, 1993). Q5b is the concentration at which JDI becomes positive. (E, F) Drift coefficient (Komarova et al., 2002) of MT populations as a function of [free tubulin] (x symbols). Q5c is the concentration above which drift is positive. For ease of comparison, the rate of change in average MT length (o symbols) from panels C and D is replotted in panels E and F, respectively. For additional data related to these simulations, see Supplemental Figure S3. Interpretation: The results show that Q5a ≈ Q5b ≈ Q5c, hereafter referred to as Q5. At concentrations below Q5, populations of MTs reach a polymer-mass steady state where the average MT length is constant over time (the rate of change in average MT length or polymer mass is approximately zero; panels C and D), and the system of MTs exhibits zero drift (panels E and F). At free tubulin concentrations above Q5, populations of MTs reach a polymer-growth steady state where the average MT length and polymer mass increase over time at constant average rates that depend on [free tubulin] (panels C and D), and the system of MTs exhibits positive drift (panels E and F). Plots of average MT length vs. time are shown in Supplemental Figure S3, A and B. Note that the concentration range below Q5 corresponds to the “bounded” regime as discussed by Dogterom et al., while that above Q5 corresponds to the “unbounded” regime (Dogterom and Leibler, 1993). The overall conclusions of the data in this figure are that 1) MTs exhibit net growth (as averaged over time or over individuals in a population) at [free tubulin] above the value Q5 (Q5a ≈ Q5b ≈ Q5c) and 2) Q5 is similar to the value Q1 ≈ Q2 (gray dashed line) as determined in Figure 3, A and B. Thus, Q1, Q2, and Q5 all provide measurements of the same CC, defined as CCNetAssembly in the main text. Methods: All population data points (panels C–F) represent the mean ± one SD of the values obtained in three independent runs of the simulations. In panels C and D, the net rate of change was calculated from 15 to 30 min. In panels E and F, the drift coefficient was calculated using a method based on Komarova et al. (2002) (Supplemental Methods). See also Supplemental Table S1B for a summary of the measurement methods used in panels C–F.
As discussed more below, this CC is the same as that previously identified by Dogterom et al. as the CC at which the transition from “bounded growth” to “unbounded growth” occurs (Dogterom and Leibler, 1993; Dogterom et al., 1995; Fygenson et al., 1994), by Walker et al. as the CC for “net assembly” (Walker et al., 1988), and by Hill and Chen (1984) as the CC where net subunit flux equals zero. Note that a “bounded” system refers to one that has a constant steady-state polymer mass or average MT length; “unbounded” refers to a system where the polymer mass or average MT length exhibits net growth over time (Dogterom and Leibler, 1993; Dogterom et al., 1995). This situation should not be confused with one in which the system of MTs experiences a physical boundary (e.g., MTs in cells). To avoid implying that a physical boundary is involved, we suggest using Walker’s terminology: CC for net assembly, which we abbreviate CCNetAssembly.
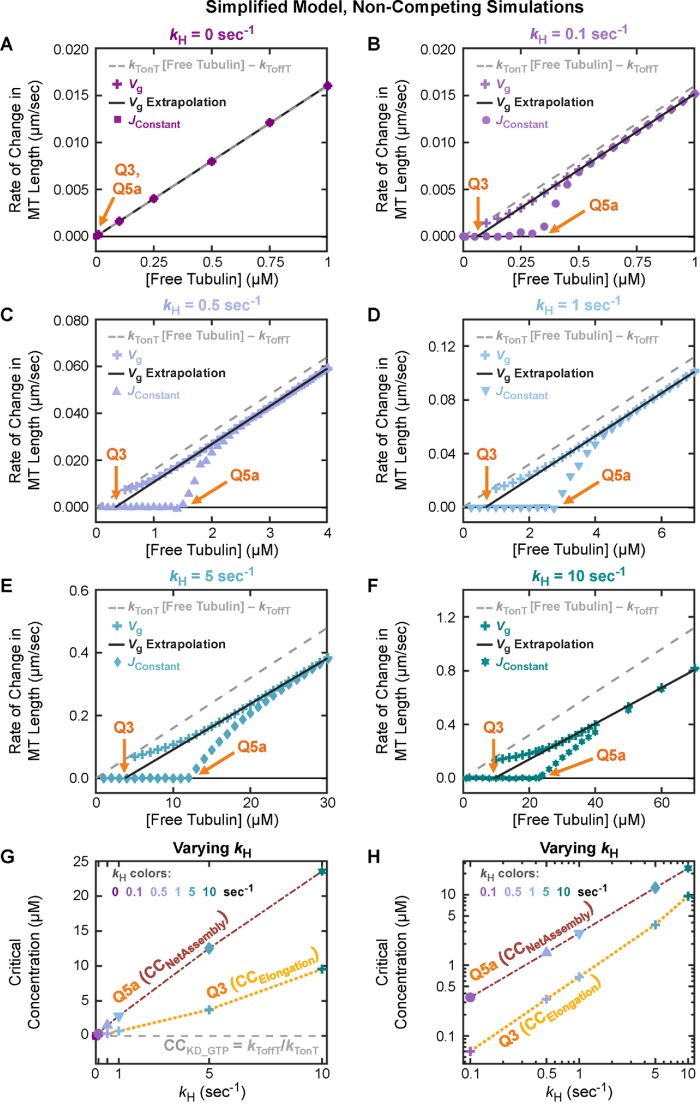
CCNetAssembly can be measured by Q5a, the [free tubulin] at which the steady-state net rate of change in average MT length (Figure 5, C and D, left axes) or in polymer mass (Figure 5, C and D, right axes) transitions from zero to positive. Additional approaches to measuring CCNetAssembly are discussed later.
The rate of change in [polymerized tubulin] is also described as the flux of tubulin into and out of polymer, typically abbreviated as J. We will use the abbreviation JConstant for J as measured in constant [free tubulin] experiments, to distinguish it from J as obtained from other experiments discussed below and summarized in Supplemental Table S1. Using this terminology, Q5a is the [free tubulin] at which JConstant transitions from equaling zero to being positive. Note that when the number of individual MTs is constant, the rate of change in the population’s [polymerized tubulin] (Figure 5, C and D, right axes) is equivalent to the rate of change in average MT length (Figure 5, C and D, left axes) after converting units and dividing by the number of individual MTs (see also Mauro et al., 2019).
How microtubule behaviors relate to CC NetAssembly.
Examination of Figure 5 shows that MT polymerization behavior under noncompeting conditions (i.e., where [free tubulin] is constant) can be divided into two regimes:
Polymer-mass steady state: At concentrations of free tubulin below CCNetAssembly (measured by Q5a), both average MT length and [polymerized tubulin] within a population reach steady-state values that increase with [free tubulin] but are constant with time (JConstant = 0, Figure 5, C and D; Supplemental Figure S3, A and B). Individual MTs in these systems exhibit what might be called “typical” DI: they undergo periods of growth and shortening, but they eventually and repeatedly depolymerize back to the stable MT seed (Figure 5, A and B).
Polymer-growth steady state: At CCNetAssembly, the populations of dynamic MTs undergo a major change in behavior: they begin to persistently grow in polymer mass. More specifically, when [free tubulin] is above label Q5a in Figure 5, C and D, there is no polymer-mass steady state where [polymerized tubulin] is constant over time (Supplemental Figure S3, A and B). Instead, the system of MTs arrives at a different type of steady state where [polymerized tubulin] increases at a constant rate (JConstant > 0; Figure 5, C and D; Supplemental Figure S3, A and B). Individual MTs within these populations still exhibit DI (except perhaps at very high [free tubulin]), but they exhibit net assembly (Walker et al., 1988) if their behavior is assessed over sufficient time (Figure 5, A and B). This type of behavior is also described as unbounded growth by Dogterom and Leibler (1993).
Significantly, for both models, Q5a (Figure 5, C and D) lies at approximately the value of Q1 ≈ Q2 (Figure 3, A and B). This observation indicates that [free tubulin]SteadyState in competing systems asymptotically approaches the same [free tubulin] at which MTs begin to exhibit net growth (i.e., unbounded growth) in noncompeting systems. In other words, these data show that CCSubSoln ≈ CCNetAssembly. This conclusion means that classical methods for measuring “the CC for polymer assembly” do not yield the CC at which individual DI polymers appear, but instead yield the CC above which the polymer mass of a population increases persistently and individual filaments exhibit net growth over sufficient time.
Other experimental methods for measuring CC NetAssembly.
As noted above, Dogterom and colleagues previously predicted the existence of a CCUnbounded, the [free tubulin] at which MTs will transition from exhibiting “bounded growth” to exhibiting “unbounded growth” (Dogterom and Leibler, 1993; Dogterom et al., 1995). These growth regimes are characterized by the average MT length reaching a steady-state value (bounded) or increasing indefinitely (unbounded). The predicted existence of a CCUnbounded was experimentally verified by Fygenson et al. (1994).
An equation for the rate of change in average MT length as a function of the DI parameters had been presented previously (Hill and Chen, 1984; Walker et al., 1988):
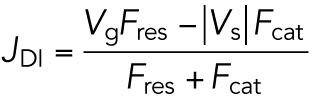 |
1a |
Dogterom and colleagues (Verde et al., 1992; Dogterom and Leibler, 1993) then applied this equation to characterize bounded and unbounded growth in constant [free tubulin] systems:
 |
1b |
Dogterom et al. identified CCUnbounded as the [free tubulin] at which Vg Fres = |Vs|Fcat (indicated by the label Q5b in Figure 5, C and D). Significantly, CCUnbounded as predicted by Q5b from this equation evaluated with our DI parameter measurements matches Q5a (compare + symbols to o symbols in Figure 5, C and D; DI measurements in the Supplemental Excel file). Hence, CCNetAssembly corresponds to CCUnbounded, and polymer-mass steady state and polymer-growth steady state correspond to “bounded growth” and “unbounded growth,” respectively.
Determination of Q5b may not be an experimentally practical way to identify CCNetAssembly, because measuring DI parameters across a range of concentrations requires extended (e.g., >tens of minutes) analysis of many individual MTs, which is laborious and time-consuming. An alternative approach to measuring CCNetAssembly that may be more tractable experimentally is to use video microscopy to simultaneously analyze the behavior of many individual MTs within a population according to the drift paradigm of Borisy and colleagues (Vorobjev et al., 1997, 1999; Komarova et al., 2002). The drift coefficient is the mean rate of change in the position of the MT ends (for plus or minus ends separately), also described as the mean velocity of displacement of the MT ends. In cases where one end is fixed, as in our simulations, the drift coefficient is equivalent to the rate of change in average MT length. For a mathematical explanation of how MT behavior can be approximated by a drift-diffusion process, see Maly, 2002; Vorobjev and Maly, 2008; and Mirny and Needleman, 2010.
Here we used a method based on Komarova et al. (2002), which calculates the drift coefficient from the displacements of MT ends over small time steps, for example, between consecutive frames of a movie (see the Supplemental Methods for additional information). As shown in Figure 5, E and F (x symbols), and Supplemental Figure S3, G and H (all symbols), Q5c is the [free tubulin] below which a population of MTs at steady state exhibits zero drift and above which the population exhibits positive drift. Furthermore, zero drift corresponds to the state where the average length of MTs in the population is constant with time, and positive drift corresponds to the average MT length increasing persistently. As one might intuitively predict, Q5a ≈ Q5b ≈ Q5c (Figure 5, C–F).
The evident similarity between the different measurements in Figure 5, C–F, suggests that the JDI equation using DI parameters (Eq. 1; + symbols in Figure 5, C and D) (Hill and Chen, 1984; Walker et al., 1988; Verde et al., 1992; Dogterom and Leibler, 1993) and the drift equation using short-term displacements (Eq. S1 in the Supplemental Methods; x symbols in Figure 5, E and F) (Komarova et al., 2002) are simply two different representations of the same relationship. Indeed, both yield the rate of change in average MT length as functions of experimentally observed growth and depolymerization behaviors, which we examined in more detail in Mauro et al. (2019).
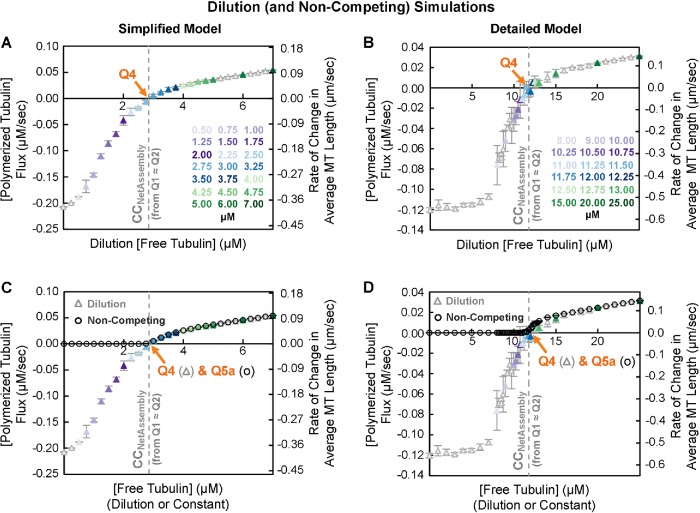
Measuring CC NetAssembly using population dilution experiments.
Next we tested whether CCNetAssembly is the same as the CC obtained from the population dilution experiments in early studies of steady-state polymers (e.g., Carlier et al., 1984a, b; see Q4 in Table 1 and Figure 1C). These experiments measure the rate of change in [polymerized tubulin]. As noted above, this rate of change is also described the flux (J) of tubulin into or out of polymer. We refer to this flux measured in dilution experiments as JDilution to distinguish it from JConstant discussed above, which is determined from constant [free tubulin] experiments. The measurement of JDilution is performed after a population of MTs at steady state is diluted into a large pool of free tubulin at a new concentration. The measured data from the dilution experiments are then used to produce J(c) plots, where JDilution is plotted as a function of subunit concentration “c” (Figure 6, A and B). In these plots, “the CC” is identified as the dilution [free tubulin] at which JDilution = 0 (i.e., where the plotted curve crosses the horizontal axis, Q4). At this concentration, individual MTs undergo periods of growth and shortening, but the population-level fluxes into and out of polymer are balanced (i.e., net growth is zero). We refer to the CC measured via J(c) plots as CCFlux (Table 1). CCFlux corresponds to one of the CCs that was identified by Hill and colleagues, variously named co in Hill and Chen (1984) and Chen and Hill (1985b) and aα in Hill (1987).
FIGURE 6:
Flux of tubulin subunits into and out of MT polymer as a function of dilution [free tubulin] (i.e., a J(c) plot as in Carlier et al., 1984a, b and Figure 1C). Left panels: simplified model; right panels: detailed model. (A, B) In the dilution simulations, competing systems of MTs at high [total tubulin] were allowed to polymerize until they reached polymer-mass steady state. The MTs were then transferred into (“diluted into”) the free tubulin concentrations shown on the horizontal axes. After a brief delay, the initial flux (rate of change in [polymerized tubulin] (left axes) or in average MT length (right axes)) was measured. (C, D) Data replotted to show that the J(c) curves from the dilution simulations (i.e., JDilution) in panels A and B (triangle symbols) and the net rate of change in average MT length from the constant [free tubulin] simulations (i.e., JConstant) in Figure 5, C and D (circle symbols), overlay each other for [free tubulin] above CCNetAssembly. Interpretation: These data show that CC as determined by Q4 from J(c) plots is approximately the same value as Q1 ≈ Q2 (gray dashed line), and thus Q4 also provides a measurement of CCNetAssembly. Methods: Competing systems of MTs at 22 µM total tubulin were allowed to reach polymer-mass steady state. Then, at minute 10 of the simulation in the simplified model and at minute 20 of the simulation in the detailed model, the MTs were transferred into the free tubulin concentrations shown on the horizontal axes. After a 5-s delay, the flux was measured over a 10-s period (see Supplemental Figure S4 for plots of [free tubulin] and [polymerized tubulin] as functions of time). Note that the delay after dilution was necessary in the original experiments because of instrument dead time, but it is important for obtaining accurate J(c) measurements because it allows the GTP cap size to respond to the new [free tubulin] (Duellberg et al., 2016; Bowne-Anderson et al., 2013; Mauro et al., 2019). For accurate measurements of J at low values of dilution [free tubulin], the predilution MTs should be sufficiently long so that none completely depolymerize during the 15-s period after dilution (Mauro et al., 2019). Data points for different concentrations of dilution [free tubulin] (see color key) represent the mean ± one SD of the values obtained in three independent runs of the simulations.
Significantly, the value of CCFlux as measured by Q4 in the dilution simulations corresponds to CCNetAssembly (gray dashed line, Figure 6, A and B) as measured by Q1 ≈ Q2 in the competing simulations (Figure 3, A and B) and by Q5abc in the noncompeting simulations (Figure 5, C–F). Note also that for (dilution) [free tubulin] above CCNetAssembly, JDilution is superimposable with JConstant (Figure 6, C and D). This observation might seem surprising, given the differences in the experimental approaches; however, it makes sense, because in each case the measurement is performed during a time period when [free tubulin] is constant and the rate of change, J, has reached its steady-state value for each [free tubulin] (Supplemental Figures S3, A and B, and S4, C–F). In contrast, JDilution and JConstant differ from each other below CCNetAssembly. This difference occurs because MTs in dilution experiments are sufficiently long so that they rarely depolymerize back to the MT seed during the measurement period, whereas MTs in constant [free tubulin] below CCNetAssembly repeatedly depolymerize to the seed. See Mauro et al. (2019) for a discussion of how the shape of the J(c) curve relates to individual growth and shortening behaviors (e.g., Vg, Vs, fractions of MTs that are growing or shortening).
Thus, all of the experimental approaches for measuring CC discussed thus far yield the CC for persistent growth of a population’s polymer mass and net growth of individual MTs over time (CCNetAssembly ≈ Q1 ≈ Q2 ≈ Q4 ≈ Q5abc). This conclusion leaves us with an unresolved question: What is the significance of the remaining common experimental CC measurement, Q3, which is obtained from experiments measuring growth velocity during growth phases for individual MTs as a function of [free tubulin] (see Figure 1B and Table 1)?
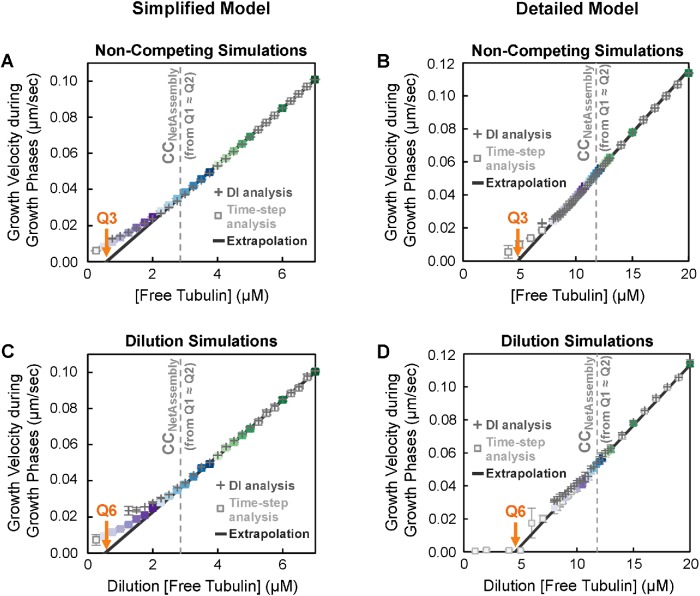
A critical concentration for transient elongation phases (growth phases) of individual filaments (CC Elongation)
Q3 (Figure 1B) has previously been used as a measure of the “critical concentration for elongation” (CCElongation; Walker et al., 1988). According to standard models, CCElongation is the free subunit concentration where the rate of subunit addition to an individual filament in the growth phase exactly matches the rate of subunit loss from that individual filament, meaning that individual filaments would be expected to grow at subunit concentrations above Q3 ≈ CCElongation (see Table 1 and its footnotes).
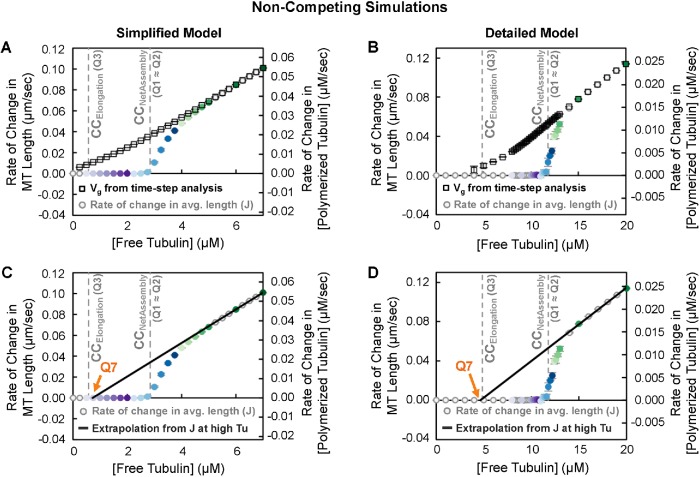
To determine the value of Q3 in our simulations, we used the standard approach for MTs as outlined in Table 1 (experiments in Walker et al., 1988; see also the theory in Hill and Chen, 1984; Hill, 1987). We plotted the growth velocity (Vg) of individual filaments observed during the growth phase of DI as a function of [free tubulin] and extrapolated a linear fit back to the [free tubulin] at which Vg is zero. 3 In addition to performing these measurements on the constant [free tubulin] simulations (Q3, Figure 7, A and B), we also used the growth phases that occurred in the dilution experiments to obtain a measurement of CCElongation (Q6 in Figure 7, C and D). Comparing these measurements of CCElongation in Figure 7, A–D, with the data in Figures 3 – 6 shows that in both models CCElongation (as determined by Q3 ≈ Q6) is well below CCNetAssembly as measured by any of the other approaches (Q1 ≈ Q2 ≈ Q4 ≈ Q5abc).
FIGURE 7:
Growth velocity of individual MTs during the growth state as a function of [free tubulin]. Left panels: simplified model; right panels: detailed model. Colors of data points reflect the concentrations of free tubulin. (A–D) Growth velocity (Vg) measured using growth phases from either the constant [free tubulin] simulations of Figure 5 (panels 7A and 7B) or the dilution simulations of Figure 6, A and B (panels 7C and 7D). Each of panels A–D shows Vg as measured by a standard DI-based analysis method (+ symbols) and a time-step method (square symbols) inspired by Komarova et al. (2002). Regression lines (solid black) were fitted to the linear range of these data and extrapolated back to Vg = 0 to obtain Q3 for the constant [free tubulin] simulations (panels A and B) and Q6 for the dilution simulations (panels C and D). Interpretation: These data show that the CC as measured by Q3 is approximately equal to that measured by Q6 and is different from CCNetAssembly (gray dashed line) as measured by Q1 ≈ Q2 (≈ Q4 ≈ Q5) from Figures 3– 6. The text provides justification for the idea that Q3 and Q6 estimate CCElongation, the CC above which individual filaments can exhibit the transient growth phases of DI. Methods: In panels A and B (constant [free tubulin]), the Vg measurements were taken during the time period from minute 15 to minute 30 of the simulations (chosen so that the system has reached either polymer-mass or polymer-growth steady state). In panels C and D (dilution simulations), the Vg data were acquired from 5 to 15 s after the dilution, that is, the J(c) measurement period described in Figure 6. For the DI-based analyses (panels A–D, + symbols), we used a custom MATLAB program to identify and quantify growth phases by finding peaks in the length history data. The time-step method (panels A–D, square symbols) divides each length history into 2-s intervals and identifies intervals during which there is a positive change in the MT length. See the Supplemental Methods for more information about both methods. Regression lines were fitted to the time-step measurements of Vg for [free tubulin] in ranges where the Vg data are approximately linear as a function of [free tubulin]: from 3 to 7 µM for the simplified model (panels A and C) and from 7 to 15 µM for the detailed model (panels B and D). All data points represent the mean ± one SD of the values obtained in three independent runs of the simulations. Data points are shown only at concentrations where at least one detected growth segment occurred in each of the three replicates.
This observation demonstrates that Q3 ≈ Q6 provides information about MT behavior not provided by the other measurements. Specifically, because Q3 and Q6 are determined from measurements of the growth velocity of individual MTs during the growth phase of DI, Q3 and Q6 provide estimates of the [free tubulin] above which individual filaments can grow transiently (i.e., can extend during the transient growth phases of DI). Whether growth phases will occur also depends on other factors, including the rescue frequency and the frequency of initiating growth from seeds. Additionally, whether growth phases that occur are observed depends on length detection thresholds (further discussed below).
Comparison of V g and J illustrates the relationship between CC Elongation, CC NetAssembly, and dynamic instability.
To relate the observations thus far, note that Vg and CCElongation come from measurements on individual MTs during only the growth state of DI, whereas J and CCNetAssembly are based on population-level measurements that encompass both growth and shortening phases. At any concentration at which both growth and shortening phases occur, Vg and J will necessarily differ (Figure 8, A and B, shows Vg and J replotted on the same axes). Hence, the difference between Vg and J, and correspondingly the difference between CCElongation and CCNetAssembly, are observable features of polymers that display DI (see also Mauro et al., 2019).
FIGURE 8:
Comparison of Vg and J (panels A and B) and an alternative method for measuring CCElongation (panels C and D). Left panels: simplified model; right panels: detailed model. In all panels, the gray dashed lines represent CCElongation as measured by Q3 (Figure 7, A and B) and CCNetAssembly as measured by Q1 ≈ Q2 (Figure 3, A and B). (A, B) Overlay of Vg measured from the time-step analysis of growing individual MTs (square symbols; replotted from Figure 7, A and B) and JConstant measured from the net rate of change in average MT length of the MT population (circle symbols; replotted from Figure 5, C and D), both from the constant [free tubulin] simulations. Interpretation of panels A, B: These data show that at high [free tubulin], JConstant approaches the Vg of individual MTs. These two data sets converge because at sufficiently high [free tubulin] individual MTs are growing (nearly) all the time, as seen in the length histories (Figure 5, A and B). Thus, CCElongation, which was obtained from Vg in Figure 7, should also be obtainable by extrapolating from the JConstant data at sufficiently high [free tubulin]. (C,D) Extrapolation to obtain Q7 from JConstant. Interpretation of panels C, D: In each of the models, the value of Q7 is approximately equal to Q3 ≈ Q6 (Figure 7). Thus, Q7 provides another way of estimating CCElongation. Methods: Regression lines were fitted to JConstant for [free tubulin] in ranges where the JConstant data are approximately linear as a function of [free tubulin]: from 6 to 7 µM for the simplified model (panel C) and from 14 to 20 µM for the detailed model (panel D). Q7 is the x-intercept of the regression line. Note that the [free tubulin] ranges used for determination of Q7 are higher than those used for Q3 and Q6 because the Q7 extrapolation requires conditions where (almost) all MTs in the population are growing (few if any depolymerization phases).
As discussed earlier (Figure 5), at [free tubulin] above CCNetAssembly, individual MTs experience net growth over sufficient time. Note that there is a range of [free tubulin] that is above CCNetAssembly but below the point where Vg and J become indistinguishable (Figure 8, A and B). This is the [free tubulin] range where net growth with appreciable DI occurs; in other words, the shortening phases that occur in this range are sufficient to create a noticeable separation between Vg and J. If shortening were not occurring above CCNetAssembly, then Vg and J would be equal for all values of [free tubulin] above CCNetAssembly.
Farther above CCNetAssembly, Vg and J converge on each other at very high [free tubulin] (Figure 8, A and B). This convergence occurs when [free tubulin] is sufficiently high so that catastrophe is rare and almost all MTs are growing (see the Supplemental Excel file for measured values of Fcat, time in growth, and time in shortening). Thus, in this range, measurements of individuals and populations give approximately the same results, leading to additional conclusions with practical significance for measuring the CCs. Specifically, linear extrapolation from JConstant at high [free tubulin] to obtain Q7 as shown in Figure 8, C and D, yields approximately the same value for CCElongation as Q3 ≈ Q6. Additionally, because JConstant and JDilution match each other at high [free tubulin] (Figure 6, C and D), the Q7 extrapolation can also be performed on the JDilution data to approximate CCElongation. Thus, both constant [free tubulin] experiments and dilution experiments can be used to obtain not only CCNetAssembly (via Q4 ≈ Q5abc) but also CCElongation (via Q3 ≈ Q6 ≈ Q7).
CC Elongation is not CC PolAssem.
The information above leads to the conclusion that CCElongation represents a lower limit for individual MTs to exhibit the transient growth phases of DI. One might be tempted to use this idea to predict that CCElongation is the concentration of free tubulin at which polymer appears (i.e., that CCElongation = CCPolAssem). However, this prediction fails. Contrary to traditional expectations, there is no total or free tubulin concentration at which polymer assembly commences abruptly. Instead, the amount of polymer initially increases in a slow and nonlinear way with respect to [free tubulin], increasing more rapidly only as [free tubulin] approaches CCNetAssembly (Supplemental Figure S3, A–F). The same conclusion is reached whether polymer mass (Supplemental Figure S3, A and B), average MT length (Supplemental Figure S3, A–F), or maximal MT length (Supplemental Figure S3, C–F) is examined.
Additionally, the appearance of detectable polymer mass in a population will depend not only on whether individual MTs are exhibiting growth phases, but also on the number of individual MTs in the population. The results in Figure 4 demonstrate that the number of MT seeds strongly affects the [total tubulin] at which a population’s [polymerized tubulin] first becomes noticeably nonzero. If there are few seeds for individual MTs to grow from, the appearance of noticeable [polymerized tubulin] does not occur until [total tubulin] is near or at CCNetAssembly. As the number of seeds is increased, [polymerized tubulin] becomes detectable at lower values of [total tubulin] (Figure 4; compare progression from darker to lighter curves).
These observations indicate that MTs (and DI polymers more broadly) do not have a CC for polymer appearance (CCPolAssem) as traditionally understood. CCElongation is the tubulin concentration above which DI growth phases can occur, but significant amounts of polymer generally do not accumulate in experiments with bulk polymer until [free tubulin] nears or exceeds CCNetAssembly (Figure 3; Supplemental Figures S1–S3).
These behaviors might seem counterintuitive, but can be explained by the following reasoning. First, when [free tubulin] is just above CCElongation, the growth velocity during the growth phase is low (Vg = 0 at Q3) and the frequency of catastrophe (Fcat) is high (measured DI parameter values in the Supplemental Excel file). Then, under these conditions, individual MTs will be both short (Figure 5, A and B; Supplemental Figure S3, A–F) and short-lived (Figure 5, A and B), and thus difficult to detect. As [free tubulin] rises, MTs will experience growth phases that last longer (because Fcat drops) and also have higher growth velocity (Figure 7). The combined impact of these two effects creates a nonlinear relationship between [free tubulin] and [polymerized tubulin] or equivalently the average MT length observed at steady state; it similarly creates a nonlinear relationship between [free tubulin] and maximal MT length as observed within a period of time (Supplemental Figure S3, C–F).
Measurement of CC Elongation by Q3, Q6, or Q7 is approximate.
CCElongation and CCNetAssembly are intrinsic properties of a system (i.e., a particular protein sequence in a particular buffer or cell type), whereas the experimental measurements (Q values) are subject to measurement error and are therefore approximate. The measurements of CCElongation by Q3, Q6, or Q7 can be particularly sensitive to measurement error and noise because they are based on extrapolations.
More specifically, because Q3 and Q6 are determined by extrapolations from regression lines fitted to plots of Vg versus [free tubulin], small changes in the Vg data (e.g., from noise) can be amplified in extrapolating to the Vg = 0 intercept. Additionally, in the simulation results, nonlinearities are observed in the Vg versus [free tubulin] plots in both models. In the presence of noise and/or nonlinearities, the values of Q3 and Q6 will depend on the [free tubulin] range where the regression lines are fitted to the Vg plots.
The deviations from linearity in the simulation plots are explained in part by measurement bias: at the lowest [free tubulin], there are few growing MTs, all of which are short (Figure 5, A and B; Supplemental Figure S3, C–F). The measured Vg data are biased toward the MTs that happened to grow fast enough and long enough to be detected. In particular, at low concentrations, there are very few detected growth phases, and the time in detected growth phases is a small fraction of the total time (see the DI measurements in the Supplemental Excel files). These observations indicate that the lowest concentrations should not be used in the linear extrapolation to identify Q3 or Q6. To our knowledge, such deviations from linearity at low concentrations have not been detected experimentally. However, the simulations generate considerably more data and at smaller length thresholds than is possible with typical experiments. Because measurement bias could also be a problem in physical systems, we speculate that similar effects may eventually be seen experimentally.
Given the nonlinearities and the measurement bias described above, one might be concerned that detection thresholds would affect the measured value of CCElongation. We therefore compared two different analysis methods for determining Vg (Figure 7). Specifically, for the DI analysis method (Figure 7, + symbols), we set a threshold of 25 subunits (200 nm) of length change to detect growth or shortening phases (we set this threshold to be comparable to typical length detection limits in light microscopy experiments). In contrast, for the time-step method (Figure 7, square symbols), we did not impose a threshold on the length change during each time step (see the Supplemental Methods). The Vg results from the two methods agree well with each other in the [free tubulin] range used to determine CCElongation (i.e., the range where Vg is approximately linear). Thus, in implementing Vg analysis to estimate CCElongation, the regression lines should be fitted to the linear region to avoid the effect of detection thresholds. If the regression lines are not fitted in the tubulin range where Vg is linear, then Q3 and Q6 will be less accurate approximations of CCElongation.
Depending on the specific system, Q7 may be a less accurate approximation than Q3 or Q6. Q7 is obtained from JConstant at free tubulin concentrations that are sufficiently high so that (almost) all MTs are growing (i.e., where Vg and JConstant overlap, Figure 8). Because the Q7 extrapolation is performed from higher concentrations than the Q3 or Q6 extrapolations, measurement error or noise in the data can be further amplified. Moreover, Vg and JConstant may not overlap until tubulin concentrations are so high that experimental measurements may no longer be feasible (e.g., because of problems such as free nucleation).
Both in the detailed model and in physical MTs, an additional factor can cause Vg to have nonlinearities as a function of [free tubulin] and therefore likely interferes with the accuracy of identifying CCElongation via Q3, Q6, or Q7. Previous work has provided experimental and theoretical evidence that the GTP–tubulin detachment rate depends on the tubulin concentration (Gardner et al., 2011), which is contrary to the assumptions classically used to determine CCElongation and would contribute to nonlinearity of Vg versus [free tubulin]. This observation has been explained by the occurrence of concentration-dependent changes in the MT tip structure (Coombes et al., 2013).
If one wished to estimate CCElongation from a competing system at steady state, Vg would need to be plotted as a function of the emergent [free tubulin]SteadyState. However, measuring Vg and the emergent [free tubulin]SteadyState in the same experiment might be impractical. Additionally, [free tubulin]SteadyState in a competing system is below CCNetAssembly, so this approach might not provide data over a range of [free tubulin] sufficient for the extrapolation to determine CCElongation. In other words, depending on the specific system, most or all of the [free tubulin] range where the measured Vg is linear might be above CCNetAssembly, and would therefore not be accessible in a steady-state competing system.
In summary, both detection issues and actual structural features can potentially make observed Vg measurements nonlinear with respect to [free tubulin]. As a result, the value obtained for CCElongation from Q3 ≈ Q6 ≈ Q7 may depend on what [free tubulin] range is used for the linear fit. These observations mean that these values (Q3, Q6, Q7) provide at best approximate measurements of CCElongation.
Effect of the hydrolysis rate constant ( k H) on CC Elongation and CC NetAssembly
The results above show that CCElongation is obtained from measurements of individual MTs that are in the growth phase, while CCNetAssembly is obtained from measurements performed on populations (or on individual MTs over sufficient time) that include both growth and shortening phases (see also Hill, 1987; Walker et al., 1988). Thus, the coexistence of growth and shortening phases (i.e., DI itself) occurs in conjunction with the separation between CCElongation and CCNetAssembly. DI in turn depends on nucleotide hydrolysis, since GTP–tubulin is prone to polymerization and GDP–tubulin is prone to depolymerization. Therefore, to develop an improved understanding of the separation between CCElongation and CCNetAssembly in DI polymers, we next examined the effect of the hydrolysis rate constant kH on CCElongation and CCNetAssembly. To allow a straightforward comparison between the observed behaviors and the input kinetic parameters, we utilized the simplified model.
More specifically, we ran simulations in the simplified model across a range of kH values, while holding the other biochemical kinetic parameters constant, under both constant [free tubulin] (Figure 9; Supplemental Figures S5 and S6) and competing (Supplemental Figure S7) conditions. From these data, we determined CCElongation as measured by Q3 (Figure 9; Supplemental Figure S5A), and CCNetAssembly as measured by Q5a (Figure 9; Supplemental Figure S5B) and also by Q1 ≈ Q2 (Supplemental Figure S7). As an additional test of the effect of varying kH, we also performed competing and noncompeting simulations in a parameter set with a higher value of CCKD_GTP (Supplemental Figure S8).
FIGURE 9:
Effect of varying the rate constant for nucleotide hydrolysis (kH) in the simplified model. Noncompeting simulations of the simplified model were performed for various values of kH (all other input kinetic rate constants are the same as in the other figures). Each of panels A–F corresponds to a different value of kH, ranging from 0 to 10 s-1, as indicated in the panel titles. (A–F) The growth velocity during growth phases (Vg; + symbols; color-coded by kH value) and the rate of change in average MT length (JConstant; color and symbol vary by kH value) as functions of [free tubulin]. We also plot the theoretical equation for Vg, which assumes that growing ends have only GTP–tubulin at the tips (gray dashed line). Note that the scales of the axes vary among panels A–F; for data replotted at the same scale, see Supplemental Figure S5. (G, H) CCElongation and CCNetAssembly as functions of kH, with CCElongation and CCNetAssembly measured respectively by Q3 and Q5a from panels A–F. The axes have linear scales in panel G and log scales in panel H. The vertical separation between CCElongation and CCNetAssembly at each kH in the log–log plot (panel H) represents their ratio CCNetAssembly/CCElongation. Interpretation: When kH is zero (panel G; see also panel A), CCElongation and CCNetAssembly are equal to each other and to CCKD_GTP. As kH increases (panels G and H; see also panels B–F), the values of CCElongation and CCNetAssembly increase; they also diverge from each other and from CCKD_GTP. Thus, the separations between CCKD_GTP, CCElongation, and CCNetAssembly depend on kH. To see how DI behavior relates to the CCs, see Supplemental Figure S6 for representative length-history plots of individual MTs at each kH value presented here. At any given [free tubulin], as kH increases, Vg and J each decrease relative to the rate for an equilibrium polymer with only GTP–tubulin (kTonT [free tubulin] – kToffT). Vg and J also diverge from each other. As discussed above, Vg and J differ from each other in the [free tubulin] range where DI occurs. Methods: The simulations were performed using the simplified model with 50 stable MT seeds. Vg was measured using the DI analysis method (Supplemental Methods). The steady-state JConstant was measured from the net change method (Supplemental Table S1B; see also Q5a, Table 4). All measurements were taken from 40 to 60 min. Vg data points are plotted only at concentrations where detected growth phases constituted at least 2% of the total time analyzed (20 min × 50 MTs = 1000 min analyzed). Regression lines (black solid line) were fitted to the Vg data points in the [free tubulin] range above CCNetAssembly and then extrapolated back to Vg = 0.
When the hydrolysis rate constant kH equals zero, only GTP–tubulin subunits are present. As would be expected, the behavior is that of an equilibrium polymer: no DI occurs (see length histories in Supplemental Figure S6A), and all observed CC values correspond to the KD for GTP–tubulin as defined by the input rate constants. In other words, when kH is zero, CCElongation = CCNetAssembly = CCKD_GTP = kToffT/kTonT (Figure 9A). When kH is greater than zero in these simulations, both GTP– and GDP–tubulin subunits contribute to polymer dynamics, concurrent with the appearance of DI (Supplemental Figure S6, B–F). As kH increases, CCElongation (Q3) and CCNetAssembly (Q5a) both increase and diverge from each other (Figure 9; Supplemental Figures S5 and S8), and DI occurs over a wider range of [free tubulin] (Supplemental Figure S6). In all cases, the value of CCNetAssembly as measured by Q1 and Q2 is similar to the value as measured by Q5a (Figure 9; Supplemental Figures S5, S7, and S8).
CC Elongation can differ from CC KD_GTP.
In addition to showing that nucleotide hydrolysis drives CCElongation (Q3) and CCNetAssembly (Q5a) apart, the results in Figure 9 also show that hydrolysis drives both away from CCKD_GTP (x-intercept of gray dashed line in Figure 9, A–F; gray dashed line in Figure 9G). In particular, while the relationship CCKD_GTP = kToffT/kTonT is independent of kH, we observe that CCElongation changes with kH. This could be viewed as surprising because one might expect CCElongation to equal CCKD_GTP even in the presence of DI. The reasoning behind this expectation is as follows.
First, the rate of growth of an individual MT in the growth state has been assumed to change linearly with [free tubulin] according to the following relationship (Walker et al., 1988): 4
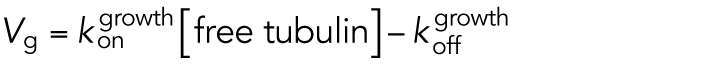 |
2 |
where  and
and  (called
(called  and
and 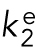 in Walker et al., 1988) are effective (observed) rate constants for loss and addition of GTP–tubulin subunits on a growing tip. By “effective” we mean that they are emergent quantities extracted from the Vg data, as opposed to directly measured kinetic rate constants. More specifically, the values of
in Walker et al., 1988) are effective (observed) rate constants for loss and addition of GTP–tubulin subunits on a growing tip. By “effective” we mean that they are emergent quantities extracted from the Vg data, as opposed to directly measured kinetic rate constants. More specifically, the values of  and
and  are measured from the slope and the y-intercept, respectively, of a regression line fitted to Vg data, given Eq. 2. Because CCElongation is measured as the value of [free tubulin] at which Vg is zero, setting Eq. 2 equal to zero and solving for [free tubulin] leads to the conclusion that CCElongation =
are measured from the slope and the y-intercept, respectively, of a regression line fitted to Vg data, given Eq. 2. Because CCElongation is measured as the value of [free tubulin] at which Vg is zero, setting Eq. 2 equal to zero and solving for [free tubulin] leads to the conclusion that CCElongation = 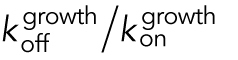 . This ratio
. This ratio 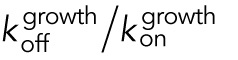 is measured as the x-intercept of the regression line (Eq. 2; Walker et al., 1988).
is measured as the x-intercept of the regression line (Eq. 2; Walker et al., 1988).
Second, it is commonly assumed that rapidly growing tips have only GTP-subunits at the end (e.g., Howard, 2001; Bowne-Anderson et al., 2015). Under this assumption, and also assuming that all unpolymerized tubulin is bound to GTP, Eq. 2 becomes
 |
3 |
which leads to the prediction that CCElongation = kToffT/kTonT = CCKD_GTP.
Instead, the results (Figure 9, A–F; Supplemental Figures S5A and S8) show that Eq. 3 fits the data well only when kH is close to zero. As kH increases, the Vg regression line and CCElongation diverge from the values that would be predicted from Eq. 3. More specifically, when kH is greater than zero, the effective  and
and  (slope and intercept of Vg in Eq. 2) in the simulations diverge from kTonT and kToffT; in this case, Vg does not satisfy Eq. 3, and CCElongation diverges from CCKD_GTP. In considering these observations, recall that the kinetic rate constants (e.g., kTonT, kH) in our simulations are input by the user. In contrast, the values of Vg and CCElongation are emergent properties of the system. Taken together, the results indicate that GDP subunits can influence behavior during growth phases.
(slope and intercept of Vg in Eq. 2) in the simulations diverge from kTonT and kToffT; in this case, Vg does not satisfy Eq. 3, and CCElongation diverges from CCKD_GTP. In considering these observations, recall that the kinetic rate constants (e.g., kTonT, kH) in our simulations are input by the user. In contrast, the values of Vg and CCElongation are emergent properties of the system. Taken together, the results indicate that GDP subunits can influence behavior during growth phases.
Possible mechanisms for exposure of GDP–tubulin at growing microtubule tips.
There are strong reasons to expect that GDP subunits will influence growth phase behavior in physical MTs. The idea that growing MT tips could have GDP–tubulin subunits might seem surprising, but GDP–tubulin subunits could become exposed on the surface of a growing tip either by detachment of a surface GTP subunit from a GDP subunit below it or by direct hydrolysis. The first mechanism conflicts with earlier ideas that GTP subunits rarely detach, but is consistent with recent experimental data indicating rapid exchange (attachment and detachment) of GTP subunits on MT tips (Gardner et al., 2011; Coombes et al., 2013; see also Margolin et al., 2012).
The idea that GDP–tubulin cannot be exposed at MT tips during growth phases may be a remnant of vectorial hydrolysis models, 5 where GDP–tubulin would become exposed only when the GTP cap is entirely lost (at least for single-protofilament models). However, various authors have shown that vectorial hydrolysis is neither sufficient (Flyvbjerg et al., 1994, 1996; Padinhateeri et al., 2012) nor necessary (Margolin et al., 2012; Padinhateeri et al., 2012) to explain MT DI behavior.
Additionally, Hill and colleagues examined both vectorial and random hydrolysis models. In the vectorial hydrolysis model, the growth velocity satisfied an equation equivalent to Eq. 2, which assumes only GTP tips during growth (Hill, 1987). In their random hydrolysis model, the observed (emergent) slope and intercept of Vg did not equal the input rate constants for addition and loss of GTP subunits, as explicitly pointed out in (Hill and Chen, 1984; Hill, 1987). This conclusion from Hill’s random hydrolysis model is consistent with the results of our model, which also has random hydrolysis.
The conclusion that CCElongation ≠ CCKD also helps explain the observation from earlier in the paper that there is no concentration at which polymer assembly abruptly commences (i.e., there is no CCPolAssem). Instead, the amount of polymer increases slowly with increasing [free tubulin] (Supplemental Figure S3, A–F). More specifically, although the MTs typically reach experimentally detectable lengths (e.g., >200 nm, depending on the method used) at some concentration above CCElongation (Supplemental Figure S3, A–F), polymerization of a few subunits can occur even below CCElongation (Supplemental Figure S3, E and F; square symbols in Figure 7). When [free tubulin] is above CCKD_GTP, attachment to a GTP subunit will be more favorable than detachment; thus, small flickers of growth can occur. In contrast, CCElongation is the [free tubulin] above which a MT may exhibit the extended growth phases of DI. The dependence of CCElongation on kH indicates that attachment must in some sense outweigh both detachment and hydrolysis of GTP subunits in order for extended growth phases to occur.
Dynamic instability can produce relationships previously interpreted as evidence of a nucleation process for growth from stable seeds
Previously, two experimental observations have been interpreted as evidence that growth of MTs from stable templates (e.g., centrosomes, axonemes, GMPCPP seeds) involves a nucleation process (e.g., conformational maturation or sheet closure; Wieczorek et al., 2015; Roostalu and Surrey, 2017). First, MTs are generally not observed growing at [free tubulin] near CCElongation. Second, when the fraction of seeds occupied is plotted as a function of [free tubulin], the shape of the resulting curve is sigmoidal, suggesting a cooperative process and/or a thermodynamic barrier. In this section, we show that these two nucleation-associated behaviors are observed in our simulations, which is notable because neither model incorporates an explicit nucleation step (our seeds are composed of nonhydrolyzable GTP–tubulin, so the rates of attachment to and detachment from the seed are the same as those for a GTP–tubulin tip). We show that both experimentally observed relationships can result from DI in combination with length detection thresholds. The behavior of DI polymers relative to CCElongation and CCNetAssembly, as described above (e.g., Figure 5, A and B; Supplemental Figure S3, A–F), can therefore be helpful in understanding these relationships.
Failure to detect MT growth events in experiments at [free tubulin] near CC Elongation can result from physical detection limitations coupled with DI.
As described above, when [free tubulin] is near CCElongation, Vg is small and Fcat is high, meaning that MTs are short (Supplemental Figure S3, A–F) and short-lived (Figure 5, A and B); the average MT length remains small until [free tubulin] is closer to CCNetAssembly (Supplemental Figure S3, A–F). This behavior, coupled with length detection thresholds (such as would be imposed by physical experiments), could make it difficult to detect MTs at [free tubulin] near CCElongation. To test this hypothesis, we used the simulations (which output the MT length without any detection threshold) to examine the effect of imposing length detection thresholds similar to those in physical experiments.
Indeed, when we imposed a 200-nm detection threshold (comparable to light microscopy) on the length change needed for a growth phase to be recognized (Figure 7, + symbols), we saw that MT growth that was detected in the absence of this threshold (Figure 7, square symbols) was no longer detected. These results indicate that failure to observe MTs growing from stable seeds at [free tubulin] near CCElongation can result from using experimental methods that have length detection limitations, providing evidence that such behavior can result from processes other than nucleation.
A sigmoidal P occ curve is predictable from detection thresholds and microtubule population length distributions resulting from dynamic instability.
Pocc is the proportion of stable MT templates/seeds that are occupied by a (detectable) MT (Figure 10, A and B). Previous experimental work has shown that Pocc has a sigmoidal shape when plotted as a function of [free tubulin] (e.g., Mitchison and Kirschner, 1984b; Walker et al., 1988; Wieczorek et al., 2015). This shape has been interpreted as evidence that starting a new MT from a seed is harder than extending an existing MT and thus that growth from seeds involves a nucleation process (e.g., Wieczorek et al., 2015; compare Figure 11, A and B). However, the Vg analysis described above led us to hypothesize that this sigmoidal Pocc shape can also result from the combination of length detection thresholds and DI.
FIGURE 10:
Relationship between Pocc (proportion of stable MT seeds that are occupied) and [free tubulin]. Simplified model in panels A, C; detailed model in panels B, D. The raw data analyzed in this figure are from the same noncompeting (constant [free tubulin]) simulations used in Figures 5, 6, C and D, 7, A and B, and 8. In all panels, the gray dashed lines represent CCElongation (Q3 from Figure 7, A and B) and CCNetAssembly (Q1, Q2 from Figure 3, A and B). (A, B) Proportion of stable seeds bearing “experimentally detectable” MTs (Pocc) as a function of [free tubulin]. Here detectable MTs are those with length ≥25 subunits = 200 nm (chosen because the Abbe diffraction limit for 540-nm (green) light in a 1.4 NA objective is ∼200 nm). (C, D) Pocc with detection thresholds varied from 1 subunit (8 nm) to 125 subunits (1000 nm). The data with the 25-subunit threshold are replotted from panels A and B. Interpretation: The data in panels A and B show that with a detection threshold similar to that in typical fluorescence microscopy experiments, little polymer is observed growing off of the GTP–tubulin seeds in either model until [free tubulin] is well above CCElongation. More specifically, with this 200-nm threshold, Pocc does not reach 0.5 until [free tubulin] is more than halfway from CCElongation to CCNetAssembly. Note that the lowest value of [free tubulin] at which 100% of the seeds have a detectable MT corresponds to ∼CCNetAssembly (see also Fygenson et al., 1994; Dogterom et al., 1995). The data in panels C and D show that short MTs (with lengths below the 200-nm detection threshold from panels A and B) are present at free tubulin concentrations near CCElongation (see also maximum MT length data in Supplemental Figure S3, C–F). Additionally, we note that the Pocc curve of the detailed model is steeper than that of the simplified model when the same threshold is compared. We suggest that this results from the more cooperative nature of growth in the detailed (13-protofilament) model, which is an outcome of interactions between protofilaments. Methods: All data points represent the mean ± one SD of the Pocc values obtained in three independent runs of the simulations. The values from each run are averages from 25 to 30 min, chosen so that Pocc has reached its steady-state value. MT length is measured as the number of subunit lengths above the seed. Note that in the detailed model, the MT length is the average of the 13 protofilament lengths and can therefore have noninteger values; see Supplemental Figure S9 for fractional thresholds below 2 subunits, which fill in the large gap between the thresholds of 1 and 2 subunits.
FIGURE 11:
Hypothetical Pocc vs. [free tubulin] curves, where Pocc is the proportion of seeds that are occupied by MTs. It might have been expected that GTP-like seeds should start growing once [free tubulin] is above CCElongation, and that Pocc would therefore increase abruptly from 0 to 1 for [free tubulin] at or just above CCElongation, similarly to the step function in panel A. In contrast, sigmoidal Pocc curves, similar to panel B, have been observed experimentally (Mitchison and Kirschner, 1984b; Walker et al., 1988; Dogterom et al., 1995; Wieczorek et al., 2015). Obtaining a sigmoidal shape (B) instead of a step function (A) has been interpreted as evidence of a nucleation process that makes growth of MTs from stable seeds more difficult than extension from a growing end (e.g., Wieczorek et al., 2015). However, as discussed in the text, this sigmoidal shape can be a consequence of DI in combination with experimental length-detection limitations, and therefore is not necessarily evidence of a nucleation process. Note that a nucleation process that makes growth from seeds more difficult would lead to a Pocc curve that increases more rapidly from 0 to 1 and does so at [free tubulin] near CCNetAssembly, similarly to the step function in panel C. This behavior can be explained in the following way. When [free tubulin] is below CCNetAssembly, MTs will repeatedly depolymerize back to the seed. When nucleation from seeds is difficult, it will take longer for a new growth phase to initiate after each complete depolymerization; seeds will therefore remain unoccupied for longer times and the proportion of seeds in the population that are occupied at any particular time be will smaller. Thus, as the difficulty of nucleation increases, the shape of the Pocc curve would change from a sigmoid (as in panel B) to a step function at CCNetAssembly (as in panel C).
To test this hypothesis, we examined Pocc as a function of [free tubulin] with varying detection thresholds (Figure 10, C and D; Supplemental Figure S9). The results show that at each [free tubulin] (below CCNetAssembly), as the detection threshold is increased, the detected Pocc decreases (i.e., fewer MTs are longer than the threshold), resulting in a sigmoidal shape emerging. The steepness of the sigmoid increases as the length detection threshold is increased. These observations indicate that the sigmoidal shape can result simply from imposing a length detection threshold on a system (such as dynamic MTs) where some of the filaments are shorter than the detection threshold. In the presence of DI with complete depolymerizations back to the seeds (as occurs below CCNetAssembly), MTs will necessarily be below any nonzero detection threshold for at least some amount of time (see also Fygenson et al., 1994). Indeed, Hill previously presented a formula for Pocc as a function of the DI parameters and length detection thresholds (Hill, 1984).
The P occ curve reaches 1 at [free tubulin] near CC NetAssembly.
The results in Figure 10 and Supplemental Figure S9 provide another observation relevant to understanding CCs: in both models, Pocc approaches 1 as [free tubulin] approaches CCNetAssembly (except possibly at very small thresholds, where Pocc nears 1 at lower [free tubulin]). This result is predictable, with or without a nucleation process, because only at [free tubulin] above CCNetAssembly (where the population undergoes net growth) would all active seeds be occupied by MTs longer than an arbitrarily chosen length threshold. This full occupancy would occur if sufficient time were allowed, because at [free tubulin] above CCNetAssembly, all MTs will eventually become long enough to escape depolymerizing back to the seed. Thus, the idea that Pocc = 1 at [free tubulin] above CCNetAssembly after sufficient time may provide a practical way to identify CCNetAssembly experimentally (see also Chen and Hill, 1985a; Fygenson et al., 1994; Dogterom et al., 1995).
Taking all this information together, we propose that a combination of DI itself and the existence of detection thresholds contributes to phenomena (failure to observe growing MTs at [free tubulin] near CCElongation, Figure 7; and sigmoidal Pocc plots, Figure 10, Supplemental Figure S9) that have previously been interpreted as evidence that growth of MTs from stable seeds involves a nucleation process (e.g., Wieczorek et al., 2015). In fact, any process that makes growth from a seed more difficult than extension of a growing tip (e.g., a nucleation process such as sheet closure) would make the Pocc curve more steplike, not less so (Figure 11: compare panels B and C). While we cannot exclude the existence of nucleation processes such as conformational maturation or sheet closure in physical MTs, our work suggests that neither sigmoidal Pocc curves nor absence of detectable MTs on seeds at [free tubulin] near CCElongation is sufficient evidence to conclude that growth from templates (e.g., centrosomes, stable seeds) involves a physical nucleation process.
DISCUSSION
The behavior of microtubules is governed by two major critical concentrations
Using dynamic MTs in our computational simulations, we examined the relationships between subunit concentration and polymer assembly behaviors for DI polymers. Our results show that there is no CCPolAssem as traditionally defined, meaning that there is no concentration where MTs abruptly come into existence. Instead, there are at least two major CCs. There is a lower CC (CCElongation), above which individual filaments can grow transiently, and an upper CC (CCNetAssembly), above which the polymer mass of a population of filaments will increase persistently (Figure 12, A–C). For [free tubulin] above CCNetAssembly, individual MTs may still undergo DI (Figure 12A, length history with triangle symbol), but will exhibit net growth over time (Figure 12A, triangle and circle symbols). What might be considered “typical” or “bounded” DI (where individual MTs repeatedly depolymerize back to the seeds) occurs at [free tubulin] between CCElongation and CCNetAssembly (Figure 12, A and D, diamond symbols).
FIGURE 12:
Schematic summary of the relationships between DI behavior and CCs for DI polymers. First row: noncompeting systems ([free subunit] is held constant over time). Second row: competing systems ([total subunit] is held constant over time). Symbol key at bottom left. CCs and Q values are summarized in Tables 3 and 4. (A, D) Length histories of individual filaments in systems with three different values of [free subunit] (panel A) or [total subunit] (panel D). (B, E) The polymer mass or average filament length of populations containing the individuals in panels A or D as indicated by the corresponding symbols (similar to Supplemental Figures S3, A and B, and S1, C and D, respectively). (C) Rate of polymerization/depolymerization vs. [free subunit] for individual filaments during growth phases (Vg) and populations of filaments (JConstant, JDilution). More specifically, the panel shows 1) the growth velocity of individual filaments during the growth phase (Vg, purple dashed line; similar to Figure 7); 2) the net rate of change in average filament length of a population of filaments as assessed from experiments with [free subunit] held constant for the entire time of the experiment (JConstant, light turquoise dashed curve; similar to Figure 5, C–F); and 3) the net rate of change in average filament length of a population of filaments as assessed from dilution experiments (JDilution, dark turquoise solid curve; similar to Figure 6). Notice that JConstant and JDilution are superimposed for any [free subunit] > CCNetAssembly, and that these two curves approach Vg for [free subunit] >>> CCNetAssembly. (F) Emergent [free subunit] (green) or [polymerized subunit] (blue) as functions of input [total subunit] for competing systems at polymer-mass steady state (similar to Figures 3, A and B, and 4). (G) Effect of changing kH, the rate constant for nucleotide hydrolysis (similar to Figure 9G). Interpretations:
Behavior of individual filaments for [free subunit] below and above CCNetAssembly: In both competing and noncompeting systems, when [free subunit] is between CCElongation and CCNetAssembly, individual filaments display steady-state DI in which they eventually and repeatedly depolymerize back to the seed (panels A and D, diamond symbols). When [free subunit] is above CCNetAssembly, individual filaments display net growth over time, while still undergoing DI (panel A, triangle symbol) except perhaps at very high concentrations (panel A, circle symbol).
•Behavior of individual filaments in competing systems over time: If initial [free subunit] > CCNetAssembly in a competing system, then individual filaments initially experience net growth (panel D, triangle and circle symbols). Because [total subunit] is constant in competing systems, [free subunit] decreases as subunits polymerize. Net growth of individual filaments continues until [free subunit] drops below CCNetAssembly.
•Polymer-mass and polymer-growth steady states: Given sufficient time, competing systems reach polymer-mass steady state, where the average filament length (panel E), the population’s [polymerized subunit] (panels E and F), and [free subunit] (panel F) have finite steady-state values governed by the input [total subunit]. In noncompeting systems, polymer-mass steady state is reached only if [free subunit] is below CCNetAssembly (panel B, diamond symbol). In contrast, noncompeting systems with [free subunit] above CCNetAssembly reach polymer-growth steady state (panel B, triangle and circle symbols), where the average filament length increases at a constant rate J (panel C).
•Effect of number of stable MT seeds in competing systems: [Free subunit]SteadyState in competing systems does not equal CCNetAssembly but approaches CCNetAssembly as [total subunit] is increased, and the sharpness of the approach depends on the number of seeds (panel F; compare light and dark curves). In particular, for many seeds, [free subunit]SteadyState is noticeably below CCNetAssembly even at very high [total subunit].
•Varying kH: When kH = 0 (equilibrium polymer), there is one CC: CCKD_GTP = CCElongation = CCNetAssembly. When kH > 0 (steady-state polymer), CCElongation and CCNetAssembly are distinct from each other and from CCKD_GTP. At sufficiently low kH, CCElongation and CCNetAssembly would be experimentally indistinguishable. As kH increases, CCElongation and CCNetAssembly both increase, but CCKD_GTP does not change with kH. The [free subunit] range where DI with complete depolymerizations occurs, that is, the range between CCNetAssembly and CCElongation (bracket with diamond symbol in panel C), increases with kH.
CCElongation is estimated by Q3, Q6, and Q7, and CCNetAssembly is estimated by Q1, Q2, Q4, and Q5abc (Figure 12, C and F; Tables 3 and 4). Classical CC measurements (Q1 and Q2 in Figure 1A) do not yield the traditionally expected CCPolAssem, but instead yield CCNetAssembly (Q1 and Q2 in Figure 12F). Importantly, [free tubulin]SteadyState in a competing system does not equal CCNetAssembly, but approaches CCNetAssembly asymptotically as [total tubulin] increases and depends on the number of stable seeds (Figure 12F; compare dark and light green lines).
Bulk polymer experiments can create the illusion that CC NetAssembly corresponds to CC PolAssem.
The conclusion that MTs grow transiently at [free tubulin] between CCElongation and CCNetAssembly might appear to conflict with experimental observations reporting that bulk polymer is detectable only above Q1 (Figure 1A; see, e.g., Johnson and Borisy, 1975; Mirigian et al., 2013). As discussed, Q1 provides a measure of CCNetAssembly, but is traditionally expected to provide the CC for polymer assembly, CCPolAssem. This apparent conflict can be resolved by recognizing that the fraction of total subunits converted to polymer will be small until the total tubulin concentration nears CCNetAssembly and will depend on the number of individual MTs in the population. In particular, for [total tubulin] < CCNetAssembly, [free tubulin] will be approximately equal to [total tubulin], and [polymerized tubulin] will be low (Figure 12F, dark lines), unless there are many stable seeds (Figure 12F, light curves). In contrast, for [total tubulin] > CCNetAssembly, all free tubulin in excess of CCNetAssembly will be converted from free to polymerized form if sufficient time is allowed (Supplemental Figure S1, A–D). 6 This conversion will happen because the average MT filament will experience net growth until [free tubulin] falls below CCNetAssembly (Figure 12D; compare early in time to later in time). The outcome of these relationships is that in bulk polymer experiments with few individual MTs, little if any MT polymer mass will be detected 7 until the total tubulin concentration is above CCNetAssembly (Figure 12F, dark blue line), even though dynamic individual MT filaments can exist transiently at tubulin concentrations below CCNetAssembly (Figure 3, C and D). Thus, the experimental quantities Q1 and Q2 may look like the traditionally expected minimum concentration for polymer assembly (CCPolAssem), but they actually represent the CC for persistent growth of a population’s polymer mass and net growth of individual MTs over time (CCNetAssembly).
P occ plots can create the illusion that there is a [free tubulin] at which microtubule assembly commences abruptly, i.e., that CC PolAssem exists.
Pocc plots with length detection thresholds (such as thresholds intrinsic to microscope-based experiments) (Figure 10, A and B) may have led to the conclusion that there is a CCPolAssem at which Pocc first becomes positive. However, at low [free tubulin], MTs are short and short-lived as a result of low Vg and high Fcat, as described above, and therefore can be undetectable by standard microscopy. By varying the length detection threshold imposed on simulation data (Figure 10, C and D), it can be seen that the [free tubulin] at which Pocc first becomes positive depends on the threshold. These results, together with the polymer mass, average length, and maximal length data (Supplemental Figures S1, C–F, and S3, A–F), indicate that there is no concentration at which assembly of DI polymers commences abruptly.
Two additional critical concentrations help define polymer behaviors.
In addition to the major CCs (CCElongation and CCNetAssembly), there are at least two additional CCs that impact MT assembly. The first of these is CCKD_GTP = kToffT/kTonT, which corresponds to the KD for binding of a free GTP–tubulin subunit to a GTP–tubulin at a MT tip. The second additional CC is the KD for binding of a free GDP–tubulin subunit to a GDP–tubulin at a MT tip, CCKD_GDP = kDoffD/kDonD. Because CCKD_GTP and CCKD_GDP provide biochemical limits on the behavior of GTP–tubulin and GDP–tubulin, any CCs must lie between these two nucleotide-specific CCs (CCKD_GTP ≤ CCElongation ≤ CCNetAssembly ≤ CCKD_GDP). CCKD_GTP is the [free tubulin] above which GTP–tubulin polymers will grow in the absence of hydrolysis and provides the lower limit for short-term assembly of polymers in the presence of hydrolysis. As the hydrolysis rate constant increases, CCElongation (the [free tubulin] above which the growth phases of DI can occur) can diverge from CCKD_GTP (Figure 12G; compare yellow CCElongation line to gray CCKD_GTP line). Unlike CCKD_GTP, CCKD_GDP is not straightforwardly measurable for MTs, because GDP–tubulin subunits alone do not polymerize into MTs (Howard, 2001), but could be relevant to other steady-state polymers (e.g., actin).
Separation between the critical concentrations is created by GTP hydrolysis.
By running simulations in the simplified model at different kH values, we show that increasing kH causes CCElongation and CCNetAssembly to diverge from each other and from CCKD_GTP (Figure 9; Supplemental Figures S5 and S8). We expect that the magnitude of the separation between the various CCs will depend not on the value of kH per se, nor on any individual rate constants, but rather on the relationships between the various rate constants. This is a topic of ongoing investigation. We speculate that the separation between the CCs has significance for understanding the difference between actin and tubulin, as discussed more below.
Relationship to previous work
As discussed above, the idea that MTs and other steady-state (energy-using) polymers have two major CCs was first investigated in depth by Hill and colleagues, who studied the behavior of these systems using a combination of theory, computational simulations, and experiments (Carlier et al., 1984a; Hill and Chen, 1984; Hill, 1987). Their c1 corresponds to our CCElongation; their c0 corresponds to our CCNetAssembly (Hill and Chen, 1984; note that these CCs were given other variable names elsewhere in Hill’s works). Moreover, Hill and Chen concluded that “rather long” MTs grow at concentrations “well below” what they referred to as the “real” CC (corresponding to our Q4 in Figure 1C), in contrast to equilibrium polymers, where the average length is very small until [free subunit] is “extremely close” to the CC (Hill and Chen, 1984). However, the significance of this work for MT DI behavior was not fully incorporated into the CC literature, perhaps because it was not clear how Hill’s two CCs related to classical CC measurements (e.g., Q1 and Q2 in Figure 1A).
Walker et al.’s (1988) seminal article on DI parameters included measurements of two different CCs, which they termed the CC for elongation (CCElongation in our notation) and the CC for net assembly (CCNetAssembly in our notation). They calculated their value of the CC for net assembly from their measured DI parameters using a version of the JDI equation (see equation on p. 1445 of Walker et al., 1988). However, perhaps because the article focused on CCElongation and did not directly relate either of these CCs to those predicted by Hill and colleagues, the idea that MTs have two CCs still did not become widely acknowledged. Soon thereafter, the articles of Dogterom et al. and Fygenson et al. were important in showing clearly and intuitively how the behavior of MTs changes at the CC for unbounded growth (equivalent to CCNetAssembly), which they described using the JDI equation shown in Eq. 1 (Dogterom and Leibler, 1993; Dogterom et al., 1995; Fygenson et al., 1994). However, these authors did not relate their CC for unbounded growth to the CCs discussed by Hill or Walker et al. or to more classical CCs (Table 1; Figure 1).
Some of the continued confusion about CC may have resulted from the fact that published experimental work typically involved either competing conditions or noncompeting conditions but not both. More specifically, classical experiments for determining “the critical concentration” (e.g., Figure 1A) involved competing conditions, but much of the previous work described above was performed under conditions of constant [free tubulin] (e.g., Figure 1, B and C). Walker et al. (1988) did note in their Discussion section that the concentration of free tubulin at steady state in their competing system was below their calculated CC for net assembly, contrary to the expectation that [free tubulin]SteadyState would equal the CC for net assembly. They attributed this difference to “uncertainties inherent in [their] assumptions and measurements” (Walker et al., 1988). Instead, as shown above, the observation that [free tubulin]SteadyState approaches CCNetAssembly without actually reaching it is a predictable aspect of DI. More specifically, [free tubulin]SteadyState will be measurably below CCNetAssembly if [total tubulin] is not high enough relative to the value of CCNetAssembly and/or if the number of stable seeds is large (Figures 3, A and B, and 4).
More recently, Mourão et al. (2011) focused on systems of MTs growing under competing conditions. Using stochastic simulations and mathematical analysis to study MT growth from stable seeds, they examined a quantity that they called “a baseline steady state free subunit concentration (MDSS),” which is conceptually similar to our CCSubSoln (measured by Q2). They concluded that [free tubulin]SteadyState is not equal to MDSS but below it; our results are consistent with this conclusion. In particular, they demonstrated how the separation between [free tubulin]SteadyState and MDSS depends on various factors including the number of stable MT seeds. The dependence of MT behavior on subunit concentration was not their primary focus, so they did not explicitly show that [free tubulin]SteadyState asymptotically approaches MDSS = CCNetAssembly as [total tubulin] increases (Figures 3, A and B, and 4); however, they did perform simulations at three different values of [total tubulin], and their results are consistent with our conclusions. Additionally, the criterion that they used to determine the value of MDSS is that MDSS is the free tubulin concentration at which Vg/|Vs| = Fcat/Fres. We note that this equation is algebraically equivalent to |Vs|Fcat = Vg Fres, which was the criterion given by Dogterom and Leibler (1993) for identifying the CC for unbounded growth (equivalent to our CCNetAssembly).
Thus, there has been a need for a unified understanding of how CCs relate to each other and to MT behaviors at different scales. Our work fills this gap by clearly showing how the behaviors of individual MTs and populations of MTs relate to each other, to [free subunit] and [total subunit], and to a range of different experimental measurements in both competing and noncompeting systems (conclusions summarized in Figure 12 and Tables 3 and 4). Taken together, our simulations and analyses should provide a more solid foundation for understanding the behavior of MTs and other DI polymers under varied concentrations and experimental conditions.
Implications for systems with free nucleation
As discussed above, all of our studies in this article are performed with a defined number of stable MT seeds and one free end. For systems with two free ends (plus and minus), each end would have its own values of CCElongation and CCNetAssembly, and behaviors of the individual ends would depend on the system’s [free tubulin] relative to the CCs. Additional behaviors such as filament treadmilling could arise.
In systems with free nucleation and disappearance of MTs, the number of MTs in a population can change over time. If the number of MTs is increasing with time, then the population’s polymer mass could increase while the average filament length stays the same or even decreases; this could occur, for example, with constant [free tubulin] below CCNetAssembly and a high rate of free nucleation, as could occur if there is autocatalytic nucleation (Ishihara et al., 2016).
In a competing system with free nucleation at steady state, the sharpness of the transition at Q1 and Q2 would likely depend on the difficulty of nucleation; difficult nucleation would lead to a sharp transition, whereas the transition would become more gradual with an increasing rate of nucleation (Johnson and Borisy, 1975). For biologically relevant free nucleation rates, the transition would likely be sharp, and one might mistakenly conclude that CCNetAssembly corresponds to a hypothetical CC for nucleation. This is because only when [free tubulin] > CCNetAssembly would newly nucleated MTs be likely to persist.
Studies of systems with two free ends and free nucleation are a topic for future work.
Concurrence between different approaches for measuring microtubule behavior has practical significance
As shown in Figure 5, C–F, there is concurrence between three seemingly disparate ways of analyzing MT behavior by measurements of J (flux of subunits into and out of polymer): 1) the net rate of change in [polymerized tubulin] (Figure 5, C–F, o symbols), which is a bulk property obtained by assessing the change in mass of the population of polymers between two points in time; 2) the JDI equation (Figure 5, C and D, + symbols), which uses DI parameters extracted from individual filament length history plots obtained over tens of minutes; 3) the drift coefficient (Figure 5, E and F, x symbols; Supplemental Figure S3, G and H, all symbols) as measured by observing individual MTs in a population of MTs for short periods of time (e.g., 2-s time steps across as little as 1 min). These approaches differ in attributes including physical scale, temporal scale, and experimental design. While the similarity of the data produced by these different approaches may initially be surprising, it can be shown that the equations underlying these measurements are algebraically equivalent if certain assumptions are met (Mauro et al., 2019). The agreement between the results of these measurements indicates that the experimentally more tractable time-step approach (Komarova et al., 2002) can be used to measure CCNetAssembly and should be used more frequently to quantitatively assess MT assembly behavior in the future (see Mauro et al., 2019, for additional considerations relevant to implementing this approach).
Biological significance of having two major critical concentrations
The understanding of critical concentration as presented above should help resolve apparently contradictory results in the MT literature. In particular, our results indicate that reported measurements of “the” CC for MT polymerization vary at least in part because some experiments measure CCElongation (e.g., Walker et al., 1988; Wieczorek et al., 2015), while others measure CCNetAssembly (e.g., Carlier et al., 1984a; Dogterom et al., 1995; Mirigian et al., 2013). This clarification should help in design and interpretation of experiments involving CC, especially those investigating the effects of MT-binding proteins (e.g., Amayed et al., 2002; Wieczorek et al., 2015; Hussmann et al., 2016), osmolytes (e.g, Schummel et al., 2017), or drugs (e.g., Buey et al., 2005; Verma et al., 2016).
Furthermore, it is important to emphasize that CCElongation and CCNetAssembly are fundamental attributes of a specific type of tubulin in a particular environment, similarly to the way a KD characterizes a protein–protein interaction or a KM characterizes an enzyme–substrate reaction. Thus, we suggest using CCElongation (e.g., as measured by Q3) and CCNetAssembly (especially as measured by Q5c from the time-step drift coefficient approach) in addition to using DI parameters as a way to characterize tubulin (or other proteins that form polymers) and the activities of proteins that alter polymer assembly (see also the discussion in Komarova et al., 2002).
CCs can also be helpful in connecting the behavior of MTs between in vitro and in vivo studies, including studies of how cells can exploit CCs for regulatory purposes. For example, MTs in many interphase cell types grow persistently (perhaps with catastrophe and rescue, but with net positive drift) until they reach the cell edge, where they undergo repeated cycles of catastrophe and rescue with rare complete depolymerizations (Komarova et al., 2002). We showed previously that this persistent growth is a predictable outcome of having enough tubulin in a confined space: if sufficient tubulin is present, the MTs grow long enough to contact the cell boundary, which causes catastrophe; this drives the [free tubulin] above its natural steady-state value, which reduces catastrophe, enhances rescue, and induces the persistent growth behavior (Gregoretti et al., 2006). In light of the current results, we can now phrase this previous work more succinctly: persistent growth of MTs in interphase cells occurs when catastrophes induced by the cell boundary drive [free tubulin] above CCNetAssembly. In contrast, at mitosis, when the MTs are more numerous and thus shorter, [free tubulin] remains below CCNetAssembly. Furthermore, a cell can potentially regulate the transition from interphase to mitosis through MT binding proteins that alter the value of CCNetAssembly and/or the degree of nucleation. See also Verde et al., 1992; Dogterom and Leibler, 1993; Dogterom et al., 1995; Gregoretti et al., 2006; Vorobjev and Maly, 2008; and Mourão et al., 2011, for relevant data and discussions.
Relevance to other steady-state polymers
Though our studies presented here were formulated specifically for MTs, we suggest that they can be applied to any nucleated steady-state polymers that display DI, and perhaps to steady-state polymers more broadly. In particular, we propose that the key characteristic that distinguishes dynamically unstable steady-state polymers (e.g., mammalian MTs) from other steady-state polymers (e.g., mammalian actin) is as follows: for DI polymers, CCElongation and CCNetAssembly are separable values driven apart by hydrolysis, but for other polymers, they are either identical (as is true for equilibrium polymers) or so close as to be nearly superimposed (e.g., mammalian actin). Whether or not DI is physiologically relevant for a given polymer type in a specific cellular environment will depend on how the values of CCElongation and CCNetAssembly relate to the cellular subunit concentration.
MATERIALS AND METHODS
Simulations
Simplified model ( Figure 2A )
The simplified model of stochastic MT dynamics was described previously (Gregoretti et al., 2006), but the implementation used here was updated significantly. First, the code was rewritten in Java so that it could be implemented more easily on personal computers. Second, the time between events is now sampled using an exact version of the Gillespie algorithm (Gillespie, 1976), instead of an approximate version with a fixed time step. This change improves the accuracy with which the simulation carries out the underlying biochemical model with user-input rate constants. Third, the simulation was adjusted so that each simulated subunit now corresponds to an 8-nm MT ring (1 × 13 dimers) instead of a 20-nm MT brick (2.5 × 10 dimers) as in Gregoretti et al. (2006). Also, the simulations in Gregoretti et al. (2006) had a cell edge, which limited the MT lengths; the simulations presented here have no physical constraints on the MT lengths. The change in subunit size and the lack of a physical boundary in the present simulation mean that the numerical values of the DI parameters and Q measurements (Figures 3 – 8, left panels) are not directly comparable between this implementation and our earlier publication (Gregoretti et al., 2006). However, the general behavior of the simulation is the same. The input parameters used here are as follows:
kTonT 2.0 /µM s kinetic rate constant for addition of GTP–tubulin onto GTP MT end
kTonD 0.1 /µM s kinetic rate constant for addition of GTP–tubulin onto GDP MT end
kToffT, kToffD 0.0 /s kinetic rate constant for loss of GTP–tubulin from GTP or GDP MT end
kDoffT, kDoffD 48 /s kinetic rate constant for loss of GDP–tubulin from GTP or GDP MT end
kH 1 /s kinetic rate constant for nucleotide hydrolysis (GTP–tubulin → GDP–tubulin)
Vol 500 fL volume of simulation
Unless otherwise indicated, each of the simplified model simulations was run with MTs growing from 100 stable seeds composed of nonhydrolyzable GTP–tubulin.
Detailed model ( Figure 2B )
The detailed model of stochastic MT dynamics was first developed in Margolin et al. (2011, 2012) and later utilized in Gupta et al., 2013; Li et al., 2014; Duan et al., 2017, and Mauro et al., 2019. The core simulation is the same as in these prior publications, but this version has minor modifications including the addition of a dilution function to enable production of J(c) plots such as those in Figure 6. Please refer to Margolin et al. (2012) for detailed information on the model, its parameter set C, and how its behavior compares with that of in vitro DI. Briefly, parameter set C (used here) was tuned in Margolin et al. (2012) to approximate Walker’s DI parameters for in vitro dynamics of mammalian brain MTs at [free tubulin] = 10 µM (Walker et al., 1988). Unless otherwise indicated, each of the detailed model simulations was run with MTs growing from 40 stable seeds composed of nonhydrolyzable GTP–tubulin in a volume of 500 fl.
For both models, the Supplemental Excel file provides the numerical values of the DI parameters, the numbers of growth and shortening phases, total times in growth and shortening, and total length changes during growth and shortening, as measured by our automated DI analysis tool (described in the Supplemental Methods). The values of the DI parameters for the detailed model are similar to those that we published previously for this model (Margolin et al., 2012; Duan et al., 2017).
Analysis
CCNetAssembly is estimated by determining Q1, Q2, Q4, or Q5abc (Figures 3 – 6). CCElongation is estimated (perhaps poorly) by determining Q3, Q6, or Q7 (Figures 7 and 8). See Table 4 for information on how to perform each of the Q measurements. The figure legends provide details about applying the measurements to the simulation data, including information about the time periods during which measurements were performed. The time periods were chosen to ensure that the variable being measured (e.g., rate of change in average length) has reached its steady-state value. For most of the measurements, this occurs when the simulated system has reached either polymer-mass steady state (noncompeting systems with [free tubulin] < CCNetAssembly, Supplemental Figure S3, A and B; competing systems, Supplemental Figure S1, A–D) or polymer-growth steady state (noncompeting systems with [free tubulin] > CCNetAssembly, Supplemental Figure S3, A and B). In the Supplemental Methods, we describe the time-step analysis method (based on Komarova et al., 2002) used to measure drift and Vg, as well as our DI analysis method, used to measure Vg, Vs, Fcat, and Fres.
Code availability
The simulation codes (written in Java) and analysis codes (written in MATLAB) are available upon request.
Supplementary Material
Acknowledgments
This work was supported by National Science Foundation Grants MCB-1244593 to H.V.G. and M.A., MCB-1817966 to H.V.G., and MCB-1817632 to E.M.J. Portions of the work were also supported by funding from the University of Massachusetts Amherst (A.J.M.) and by a fellowship from the Dolores Zohrab Liebmann Fund (S.M.M.). We thank the members of the Chicago Cytoskeleton community and the Goodson laboratory for their insightful discussions.
Abbreviations used:
- CC
critical concentration
- DI
dynamic instability
- GDP
guanosine disphosphate
- GTP
guanosine triphosphate
- J
flux
- MT
microtubule
- PF
protofilament
- SD
standard deviation.
This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E19-02-0101) on October 2, 2019.
Polymer-mass steady state describes a situation where the polymer mass has reached a plateau and no longer changes with time (other than small fluctuations around the steady-state value; Supplemental Figure S1, A–D). Systems of dynamic MTs can also have other steady states (e.g., polymer-length steady state; see also Mourão et al., 2011).
Because the transitions are not sharp, it can be difficult to determine the exact values of Q1 and Q2. Depending on how the measurements are performed, the values of Q1 and Q2 might appear different from each other. However, Q1 = Q2 does hold if the measurements are performed as follows: Q2 is the value of the horizontal asymptote that [free tubulin]SteadyState approaches as [total tubulin] increases; Q1 is the [polymerized tubulin] = 0 intercept of the line with slope 1 that [polymerized tubulin] approaches as [total tubulin] increases (Figure 3, A and B). Note that Q1 would be exactly equal to Q2 in a system with no measurement error, no noise, and no nonfunctional tubulin, but for a physical experiment these factors can interfere with the measurements.
This Vg versus [free tubulin] relationship is expected to be linear on the basis of the assumption that growth occurs according to the equation Vg = kTonT [free tubulin] – kToffT, where the first term corresponds to the rate at which GTP–tubulin attaches to a GTP tip, and the second term corresponds to the rate at which GTP–tubulin detaches from a GTP tip (Bowne-Anderson et al., 2015). We return to this relationship later in the main text.
The symbol ≈ may be more appropriate than = because this equation assumes 1) that Vg increases linearly with [free tubulin] and 2) that the detachment rate is independent of [free tubulin]. Our Vg results presented above indicate that assumption 1) may be inaccurate. See Gardner et al. (2011) for evidence against assumption 2).
In vectorial hydrolysis models, hydrolysis occurs only at the interface between the GDP–tubulin lattice and the GTP–tubulin cap (e.g., Carlier et al., 1987; Hill, 1987). In contrast, in random hydrolysis models, any internal GTP subunit can hydrolyze (terminal GTP subunits may also hydrolyze, depending on the model).
More precisely, as indicated by the earlier discussion of Figure 3, A and B, all subunits in excess of [free tubulin]SteadyState will be converted to polymer; [free tubulin] SteadyState is necessarily below but perhaps close to CCNetAssembly.
The amount of polymer present depends on the kinetic rate constants of the particular system and the number of stable seeds (Figure 4). The amount of polymer detected depends on the amount of polymer actually present and on what the experimental setup can detect.
REFERENCES
- Alberts B, Johnson A, Lewis J, Morgan D, Raff M, Roberts K, Walter P. (2015). Molecular Biology of the Cell, 6th ed, New York: Garland Science. [Google Scholar]
- Alfaro-Aco R, Petry S. (2015). Building the microtubule cytoskeleton piece by piece. J Biol Chem , 17154–17162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amayed P, Pantaloni D, Carlier MF. (2002). The effect of stathmin phosphorylation on microtubule assembly depends on tubulin critical concentration. J Biol Chem , 22718–22724. [DOI] [PubMed] [Google Scholar]
- Aparna JS, Padinhateeri R, Das D. (2017). Signatures of a macroscopic switching transition for a dynamic microtubule. Sci Rep , 45747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonfils C, Bec N, Lacroix B, Harricane MC, Larroque C. (2007). Kinetic analysis of tubulin assembly in the presence of the microtubule-associated protein TOGp. J Biol Chem , 5570–5581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowne-Anderson H, Hibbel A, Howard J. (2015). Regulation of microtubule growth and catastrophe: unifying theory and experiment. Trends Cell Biol , 769–779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowne-Anderson H, Zanic M, Kauer M, Howard J. (2013). Microtubule dynamic instability: a new model with coupled GTP hydrolysis and multistep catastrophe. Bioessays , 452–461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buey RM, Barasoain I, Jackson E, Meyer A, Giannakakou P, Paterson I, Mooberry S, Andreu JM, Díaz JF. (2005). Microtubule interactions with chemically diverse stabilizing agents: thermodynamics of binding to the paclitaxel site predicts cytotoxicity. Chem Biol , 1269–1279. [DOI] [PubMed] [Google Scholar]
- Carlier MF, Didry D, Pantaloni D. (1987). Microtubule elongation and guanosine 5’-triphosphate hydrolysis. Role of guanine nucleotides in microtubule dynamics. Biochemistry , 4428–4437. [DOI] [PubMed] [Google Scholar]
- Carlier MF, Hill TL, Chen Y. (1984a). Interference of GTP hydrolysis in the mechanism of microtubule assembly: an experimental study. Proc Natl Acad Sci USA , 771–775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlier MF, Pantaloni D, Korn ED. (1984b). Evidence for an ATP cap at the ends of actin filaments and its regulation of the F-actin steady state. J Biol Chem , 9983–9986. [PubMed] [Google Scholar]
- Chen Y, Hill TL. (1985a). Theoretical treatment of microtubules disappearing in solution. Proc Natl Acad Sci USA , 4127–4131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen YD, Hill TL. (1985b). Monte Carlo study of the GTP cap in a five-start helix model of a microtubule. Proc Natl Acad Sci USA , 1131–1135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Concha-Marambio L, Maldonado P, Lagos R, Monasterio O, Montecinos-Franjola F. (2017). Thermal adaptation of mesophilic and thermophilic FtsZ assembly by modulation of the critical concentration. PLoS One , e0185707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coombes CE, Yamamoto A, Kenzie MR, Odde DJ, Gardner MK. (2013). Evolving tip structures can explain age-dependent microtubule catastrophe. Curr Biol , 1342–1348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cytoskeleton, Inc. (n.d). Tubulin and microtubule based assays, compound screening, drug screening, pre-clinical drug screen for tubulin inhibitors and microtubule inhibitors. www.cytoskeleton.com/custom-services3-compound-screening-tubulin-microtubules.
- Díaz JF, Menéndez M, Andreu JM. (1993). Thermodynamics of ligand-induced assembly of tubulin. Biochemistry , 10067–10077. [DOI] [PubMed] [Google Scholar]
- Díaz-Celis C, Risca VI, Hurtado F, Polka JK, Hansen SD, Maturana D, Lagos R, Mullins RD, Monasterio O. (2017). Bacterial tubulins A and B exhibit polarized growth, mixed-polarity bundling, and destabilization by GTP hydrolysis. J Bacteriol , e00211–217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dogterom M, Leibler S. (1993). Physical aspects of the growth and regulation of microtubule structures. Phys Rev Lett , 1347–1350. [DOI] [PubMed] [Google Scholar]
- Dogterom M, Maggs AC, Leibler S. (1995). Diffusion and formation of microtubule asters: physical processes versus biochemical regulation. Proc Natl Acad Sci USA , 6683–6688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duan AR, Jonasson EM, Alberico EO, Li C, Scripture JP, Miller RA, Alber MS, Goodson HV. (2017). Interactions between tau and different conformations of tubulin: implications for tau function and mechanism. J Mol Biol , 1424–1438. [DOI] [PubMed] [Google Scholar]
- Duellberg C, Cade NI, Holmes D, Surrey T. (2016). The size of the EB cap determines instantaneous microtubule stability. Elife , e13470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erb ML, Kraemer JA, Coker JK, Chaikeeratisak V, Nonejuie P, Agard DA, Pogliano J. (2014). A bacteriophage tubulin harnesses dynamic instability to center DNA in infected cells. Elife , e03197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flyvbjerg H, Holy TE, Leibler S. (1994). Stochastic dynamics of microtubules: a model for caps and catastrophes. Phys Rev Lett , 2372–2375. [DOI] [PubMed] [Google Scholar]
- Flyvbjerg H, Holy TE, Leibler S. (1996). Microtubule dynamics: caps, catastrophes, and coupled hydrolysis. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics , 5538–5560. [DOI] [PubMed] [Google Scholar]
- Fygenson DK, Braun E, Libchaber A. (1994). Phase diagram of microtubules. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics , 1579–1588. [DOI] [PubMed] [Google Scholar]
- Gardner MK, Charlebois BD, Jánosi IM, Howard J, Hunt AJ, Odde DJ. (2011). Rapid microtubule self-assembly kinetics. Cell , 582–592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garner EC, Campbell CS, Mullins RD. (2004). Dynamic instability in a DNA-segregating prokaryotic actin homolog. Science , 1021–1025. [DOI] [PubMed] [Google Scholar]
- Gildersleeve RF, Cross AR, Cullen KE, Fagen AP, Williams RC. (1992). Microtubules grow and shorten at intrinsically variable rates. J Biol Chem , 7995–8006. [PubMed] [Google Scholar]
- Gillespie DT. (1976). A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J Comp Phys , 403–434. [Google Scholar]
- Goodson HV, Jonasson EM. (2018). Microtubules and microtubule-associated proteins. Cold Spring Harb Perspect Biol , a022608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gregoretti IV, Margolin G, Alber MS, Goodson HV. (2006). Insights into cytoskeletal behavior from computational modeling of dynamic microtubules in a cell-like environment. J Cell Sci , 4781–4788. [DOI] [PubMed] [Google Scholar]
- Gupta KK, Li C, Duan A, Alberico EO, Kim OV, Alber MS, Goodson HV. (2013). Mechanism for the catastrophe-promoting activity of the microtubule destabilizer Op18/stathmin. Proc Natl Acad Sci USA , 20449–20454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill TL. (1984). Introductory analysis of the GTP-cap phase-change kinetics at the end of a microtubule. Proc Natl Acad Sci USA , 6728–6732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill TL. (1987). Linear Aggregation Theory in Cell Biology, New York: Springer-Verlag. [Google Scholar]
- Hill TL, Chen Y. (1984). Phase changes at the end of a microtubule with a GTP cap. Proc Natl Acad Sci USA , 5772–5776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howard J. (2001). Mechanics of Motor Proteins and the Cytoskeleton, Sunderland, MA: Sinauer Associates. [Google Scholar]
- Hussmann F, Drummond DR, Peet DR, Martin DS, Cross RA. (2016). Alp7/TACC-Alp14/TOG generates long-lived, fast-growing MTs by an unconventional mechanism. Sci Rep , 20653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyman AA, Salser S, Drechsel DN, Unwin N, Mitchison TJ. (1992). Role of GTP hydrolysis in microtubule dynamics: information from a slowly hydrolyzable analogue, GMPCPP. Mol Biol Cell , 1155–1167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishihara K, Korolev KS, Mitchison TJ. (2016). Physical basis of large microtubule aster growth. Elife , e19145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson KA, Borisy GG. (1975). The equilibrium assembly of microtubules in vitro. Soc Gen Physiol Ser , 119–141. [PubMed] [Google Scholar]
- Komarova YA, Vorobjev IA, Borisy GG. (2002). Life cycle of MTs: persistent growth in the cell interior, asymmetric transition frequencies and effects of the cell boundary. J Cell Sci , 3527–3539. [DOI] [PubMed] [Google Scholar]
- Li C, Li J, Goodson HV, Alber MS. (2014). Microtubule dynamic instability: the role of cracks between protofilaments. Soft Matter , 2069–2080. [DOI] [PubMed] [Google Scholar]
- Li X, Kolomeisky AB. (2014). Theoretical analysis of microtubule dynamics at all times. J Phys Chem B , 13777–13784. [DOI] [PubMed] [Google Scholar]
- Lodish H, Berk A, Kaiser CA, Krieger M. (2016). Molecular Cell Biology, New York: W. H. Freeman. [Google Scholar]
- Maly IV. (2002). Diffusion approximation of the stochastic process of microtubule assembly. Bull Math Biol , 213–238. [DOI] [PubMed] [Google Scholar]
- Margolin G, Goodson HV, Alber MS. (2011). Mean-field study of the role of lateral cracks in microtubule dynamics. Phys Rev E Stat Nonlin Soft Matter Phys , 041905. [DOI] [PubMed] [Google Scholar]
- Margolin G, Gregoretti IV, Cickovski TM, Li C, Shi W, Alber MS, Goodson HV. (2012). The mechanisms of microtubule catastrophe and rescue: implications from analysis of a dimer-scale computational model. Mol Biol Cell , 642–656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mauro AJ, Jonasson EM, Goodson HV. (2019). Relationship between dynamic instability of individual microtubules and flux of subunits into and out of polymer. Cytoskeleton , 495–516. [DOI] [PubMed] [Google Scholar]
- McIntosh JR, O’Toole E, Morgan G, Austin J, Ulyanov E, Ataullakhanov F, and Gudimchuk N. (2018). Microtubules grow by the addition of bent guanosine triphosphate tubulin to the tips of curved protofilaments. J Cell Biol , 2691–2708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mirigian M, Mukherjee K, Bane SL, Sackett DL. (2013). Measurement of in vitro microtubule polymerization by turbidity and fluorescence. Methods Cell Biol , 215–229. [DOI] [PubMed] [Google Scholar]
- Mirny LA, Needleman DJ. (2010). Quantitative characterization of filament dynamics by single-molecule lifetime measurements. Methods Cell Biol , 583–600. [DOI] [PubMed] [Google Scholar]
- Mitchison T, Kirschner M. (1984a). Dynamic instability of microtubule growth. Nature , 237–242. [DOI] [PubMed] [Google Scholar]
- Mitchison T, Kirschner M. (1984b). Microtubule assembly nucleated by isolated centrosomes. Nature , 232–237. [DOI] [PubMed] [Google Scholar]
- Mourão M, Schnell S, Shaw SL. (2011). Macroscopic simulations of microtubule dynamics predict two steady-state processes governing array morphology. Comput Biol Chem , 269–281. [DOI] [PubMed] [Google Scholar]
- Oosawa F. (1970). Size distribution of protein polymers. J Theor Biol , 69–86. [DOI] [PubMed] [Google Scholar]
- Oosawa F, Asakura S. (1975). Thermodynamics of the Polymerization of Proteins, New York: Academic Press. [Google Scholar]
- Oosawa F, Asakura S, Hotta K, Imai N, Ooi T. (1959). G-F transformation of actin as a fibrous condensation. Jf Polym Sci Part A: Polym Chem , 323–336. [Google Scholar]
- Oosawa F, Kasai M. (1962). A theory of linear and helical aggregations of macromolecules. J Mol Biol , 10–21. [DOI] [PubMed] [Google Scholar]
- Padinhateeri R, Kolomeisky AB, Lacoste D. (2012). Random hydrolysis controls the dynamic instability of microtubules. Biophys J , 1274–1283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollard TD. (2010). A guide to simple and informative binding assays. Mol Biol Cell , 4061–4067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roostalu J, Surrey T. (2017). Microtubule nucleation: beyond the template. Nat Rev Mol Cell Biol , 702–710. [DOI] [PubMed] [Google Scholar]
- Schummel PH, Gao M, Winter R. (2017). Modulation of the polymerization kinetics of α/β-tubulin by osmolytes and macromolecular crowding. Chemphyschem , 189–197. [DOI] [PubMed] [Google Scholar]
- Verde F, Dogterom M, Stelzer E, Karsenti E, Leibler S. (1992). Control of microtubule dynamics and length by cyclin A- and cyclin B-dependent kinases in Xenopus egg extracts. J Cell Biol , 1097–1108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verdier-Pinard P, Wang Z, Mohanakrishnan AK, Cushman M, Hamel E. (2000). A steroid derivative with paclitaxel-like effects on tubulin polymerization. Mol Pharmacol , 568–575. [DOI] [PubMed] [Google Scholar]
- Verma S, Kumar N, Verma V. (2016). Role of paclitaxel on critical nucleation concentration of tubulin and its effects thereof. Biochem Biophys Res Commun , 1350–1354. [DOI] [PubMed] [Google Scholar]
- Vorobjev IA, Maly IV. (2008). Microtubule length and dynamics: boundary effect and properties of extended radial array. Cell Tissue Biol , 272–281. [PubMed] [Google Scholar]
- Vorobjev IA, Rodionov VI, Maly IV, Borisy GG. (1999). Contribution of plus and minus end pathways to microtubule turnover. J Cell Sci , 2277–2289. [DOI] [PubMed] [Google Scholar]
- Vorobjev IA, Svitkina TM, Borisy GG. (1997). Cytoplasmic assembly of microtubules in cultured cells. J Cell Sci , 2635–2645. [DOI] [PubMed] [Google Scholar]
- Walker RA, O’Brien ET, Pryer NK, Soboeiro MF, Voter WA, Erickson HP, Salmon ED. (1988). Dynamic instability of individual microtubules analyzed by video light microscopy: rate constants and transition frequencies. J Cell Biol , 1437–1448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wieczorek M, Bechstedt S, Chaaban S, Brouhard GJ. (2015). Microtubule-associated proteins control the kinetics of microtubule nucleation. Nat Cell Biol , 907–916. [DOI] [PubMed] [Google Scholar]
- Williams RC, Correia JJ, DeVries AL. (1985). Formation of microtubules at low temperature by tubulin from antarctic fish. Biochemistry , 2790–2798. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.