Image-derived models of cell organization changes during differentiation and drug treatments

Abstract

PC12 cells are a popular model system to study changes driving and accompanying neuronal differentiation. While attention has been paid to changes in transcriptional regulation and protein signaling, much less is known about the changes in organization that accompany PC12 differentiation. Fluorescence microscopy can provide extensive information about these changes, although it is difficult to continuously observe changes over many days of differentiation. We describe a generative model of differentiation-associated changes in cell and nuclear shape and their relationship to mitochondrial distribution constructed from images of different cells at discrete time points. We show that the model accurately represents complex cell and nuclear shapes and learn a regression model that relates cell and nuclear shape to mitochondrial distribution; the predictive accuracy of the model increases during differentiation. Most importantly, we propose a method, based on cell matching and interpolation, to produce realistic simulations of the dynamics of cell differentiation from only static images. We also found that the distribution of cell shapes is hollow: most shapes are very different from the average shape. Finally, we show how the method can be used to model nuclear shape changes of human-induced pluripotent stem cells resulting from drug treatments.

INTRODUCTION

Cellular differentiation is a highly complex process that is incompletely understood. While fluorescence microscopy provides a widely used tool for investigating the organization of cell components, given the number and complexity of the resulting images it is clear that there exists a need for automated methods for their analysis (Eliceiri et al., 2012). Tools are needed not just for describing these images, but also for creating models of cell organization that incorporate information from many cells (Murphy, 2016).

Owing to the intimate relationship between neuron morphology and function, particular attention has been paid to how to model and represent cell shapes. Tools have been described for tracking neurites (Meijering, 2010) and modeling neuronal structure (Ascoli et al., 2001; Vallotton et al., 2007; Koene et al., 2009) using segmented electron or fluorescence microscope images. While some methods are primarily concerned with representing neuron shape via summary statistics such as shape and skeleton features (Vallotton et al., 2007), the software L-NEURON and ARBORVITAE (Ascoli et al., 2001) use distributions over semiparametric tree representations to construct generative models of neuron morphology capable of synthesizing cell shapes. The NETMORPH software (Koene et al., 2009) likewise uses a generative modeling framework, but is additionally capable of constructing large networks of interconnected cells. Modeling of the dynamics of cell shape and organization during processes such as differentiation has received less attention. The tree-based procedures above do not fully address cell shape because they do not consider neurite or cell body thickness. While they could be interpreted as growth models, they are based on investigator interpretation and conceptualization of neuronal shapes rather than being learned directly from images. Obtaining continuous time series images of a differentiation process to learn from is difficult due to the compounded effects of both phototoxicity and photobleaching and the difficulty of tracking individual cells from sparse time points in long time series. The ability to infer models of heterogeneous differentiation dynamics from collections of static images would address these issues.

Mitochondria have been shown to have a role in cell differentiation fate (Mandal et al., 2011), but their spatial distributions are difficult to represent due to the fact that they form complex dynamic networks. Furthermore, there has been little work on describing the relationship between cell morphology and mitochondrial distribution.

Of the many model systems for cell differentiation, rat pheochromocytoma cell line PC12 is particularly useful for studying neuronal differentiation and survival (Greene and Tischler, 1976; Burstein et al., 1982; Cowley et al., 1994). After stimulation with nerve growth factor (NGF), PC12 cells differentiate into sympathetic neuron-like cells, a process which is morphologically marked by neurite outgrowth over a time course of up to 6 d (Levi-Montalcini, 1987; Chao, 1992; Fiore et al., 2009; Weber et al., 2013). To address the goal of building continuous models of cell shape and mitochondrial distribution during differentiation, we collected images of PC12 cells at various times after treatment with NGF. From these we constructed a joint cell and nuclear shape model based on spherical harmonic descriptors (Ruan and Murphy, 2019) and a probabilistic model of mitochondrial localization (Peng and Murphy, 2011) and combined them into a generative model of shape and mitochondrial distribution over all time points. We then developed a novel approach for combining these models to predict likely sequences of changes that single cells undergo through the differentiation process despite the fact that movies of single cells were not available. Moreover, to see how we can generate representative trajectories from unobserved cells, we explored the structure of the shape space, and found the shape space is hollow. Some arbitrary points may be not good for realistic shape evolution.

As a further illustration of the potential of the inference method, we applied it to study changes in nuclear shape after drug treatment of human induced pluripotent stem cells (hiPSC; Takahashi et al., 2007). HiPSCs are very important for the study of cell development, aging, and disease treatment (Yamanaka, 2012). As mentioned before, cell and nuclear shapes are both great indicators and contributors to cellular functions. Using a public data set created by the Allen Institute for Cell Science, we applied the shape modeling method to build a shape space of three-dimensional (3D) nuclear shapes for hiPSCs after treatment with and without five drugs. From the model, we are able to characterize nuclear shape changes associated with the drugs.

RESULTS

Cell-component representation

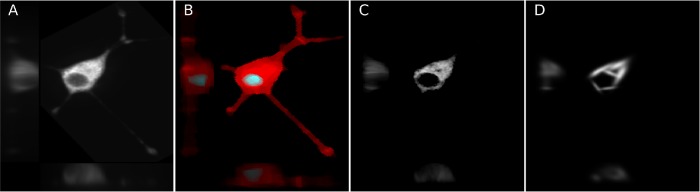
As described in Materials and Methods, we collected 3D images of mitochondrial staining of PC12 cells at various times after treatment with NGF. This was done in two large experiments: one consisting of images taken every 12 h up to 48 h, and one of images taken every 24 h up to 96 h; the experimental setup is illustrated in Supplemental Figure S1. We decomposed the image of each cell into three components: a cell shape, a nuclear shape, and a mitochondrial spatial distribution. The cell shape and nuclear shapes were inferred from autofluorescence in the mitochondrial staining image. Figure 1 shows this procedure on a typical cell image.

FIGURE 1:

Cell shape and mitochondria localization modeling procedure. Images were segmented into cell and nuclear shapes and these were aligned using the SPHARM-RPDM method. An aligned original image (A) and the segmented cell (red) and nuclear (gray) shapes (B) are shown; these were used to create a shape-space model. The individual mitochondrial objects from the original image were found using a Gaussian mixture model (C); their positions were modeled as a probability density function (D).

Models of cell and nuclear shape

3D cell and nuclear shapes were first converted into spherical harmonic descriptors using Robust SPHARM-PDM (SPHARM-RPDM; Ruan and Murphy, 2019) as described in Materials and Methods. Spherical harmonic descriptors are vectors of coefficients resulting from a spherical harmonic transform (similar to a Fourier transform), giving a representation with an orthogonal basis. We aligned all shapes to the same orientation and also normalized cell size, so that only variation in shape is contained in the shape descriptors. Out of 997 cells in the original data set, eight cells that were not well represented by the descriptors were removed from the analysis. Dimension reduction was done on the descriptors using principal components analysis (PCA) to generate a specified number of latent features. We found that models constructed with 300 dimensions were able to capture the cell shapes of individual cells with high accuracy, as shown in Supplemental Table S1. Some examples of reconstructed shapes from the models with the corresponding original shapes are shown in Supplemental Figure S2. The models were constructed with two different methods of shape alignment, using the first-order ellipse as done previously (Ruan and Murphy, 2019) or using the major axis (see Materials and Methods). The reconstruction errors were similar, but because they were slightly better for the major axis alignment approach, all subsequent analyses were done using that method.

To provide a loose illustration of the major trends in shape as a function of differentiation, low-dimensional shape spaces constructed from the latent features are shown in Figure 2 and Supplemental Figure S3 with or without the scale factors that were removed during the initial normalization. Cells from different time points overlap in shape fairly extensively, but there is a trend toward an increase in size and in the first shape component (PC1, which corresponds approximately to elongation); this is consistent with previous observations that PC12 cells start from a roughly spherical morphology and gradually flatten and spread out with more and longer neurites after NGF treatment. It is important to note that these two-dimensional representations do not allow full visualization of the cell and nuclear shape variation. The first principal component captures 33.6% of that variation and the second captures 7.9%, leaving 58.5% unvisualized in these two-dimensional maps. However, all operations using the models described below were done in the high-dimensional shape space.

FIGURE 2:

Shape space for the joint model of cell and nuclear shapes constructed from all cells for all the time points in the two experiments. Here the cell size and first principal component of shape are shown. Panel A shows the space with images projected in the xy-plane in the corresponding locations. Panel B shows a scatter plot with points for each cell shape; the line links the centroids of adjacent time points to indicate the trend as differentiation proceeds. In both panels, blue indicates untreated cells and warmer colors indicate later time points. To expand visualization of the lower left corner, scale is plotted as 1.4 * log(1.2 + x), where x is the normalized scale obtained by subtracting the mean scale and dividing by the maximum absolute value.

Relationship between mitochondrial localization and cell and nuclear shape

For each cell in the collection, the distribution of mitochondrial localization was described as the probability of a mitochondrial object occurring at a position inside of the cell according to a standardized coordinate system relative to the cell and nuclear membranes. We used the CellOrganizer implementation of the previously described method (Peng and Murphy, 2011) in which each object is represented by its relative distance from the nucleus and the azimuth and angle from the major axis and the positions of all objects are fitted using a logistic model (see Materials and Methods). The mitochondrial distribution for each cell is thus represented by the six parameters of the model. Given these parameters, we asked how the relationship between the mitochondrial location pattern and the cell shape changes as a function of differentiation.

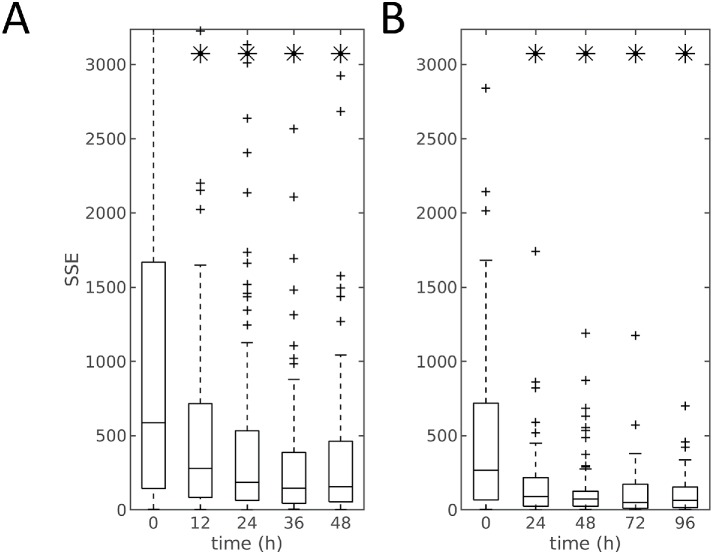
To evaluate this relationship, we used regularized multiresponse regression to predict the mitochondria localization model given the cell and nuclear shapes, as described in Materials and Methods. In the regression model, we use the shape descriptors (after removing cell scale) for cell and nuclear shapes as the independent variable vector X and used the six mitochondrial parameters as the dependent variable vector Y. A regularized linear model was learned to infer the relationship between X and Y, as shown in Eq. 5. We used nested leave-one-out cross-validation to first determine the optimal regularization parameters λ₁, λ₂, and λ₃ and then the model parameters 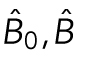. The parameters of the held-out cell were predicted, and the error between the predicted and measured mitochondrial parameters was recorded (this error serves as an inverse measure of the extent to which cell shape and mitochondrial localization pattern are related). Boxplots illustrating the distribution of errors at each time point and experiment with or without scale factor are shown in Supplemental Figure S4 and Figure 3. There is a distinct trend toward a decrease in the error of predicting the mitochondrial localization pattern as a function of time after treatment. We compared the errors between treated time points with the initial time point without treatment (0 h) via the t test and corrected for multiple tests using Bonferroni-Holm correction (Holm, 1979). An asterisk indicates a significant difference in the ability to predict the mitochondrial location pattern from the cell and nuclear shape between this time point and 0 h. As can be seen in Figure 3 for predictions with only shape models, the prediction errors decreased significantly over time, compared with those in the initial untreated condition. Also, the decrease is most dramatic in the beginning (12 h for the 48-h experiment and 24 h for the 96-h experiment). We repeated this analysis using the shape descriptors including scale (cell size) and observed that the patterns of prediction errors were similar, as shown in Supplemental Figure S4. The similarity between results for models with or without scale suggests shape variation rather than cell size is the dominant contributor to the prediction of mitochondrial pattern.

FIGURE 3:

Prediction error of mitochondrial localization parameters as a function of time for the model between shapes (without size) and mitochondria patterns. Panels A and B show the results for the 48- and 96-h dosing experiments, respectively. At each time point (x-axis) the central box mark indicates population median, and the lower and upper bounds of the box indicate 25th and 75th percentiles. Whisker bounds cover ∼95% of the data, with outliers shown in small crosses. An asterisk indicates that the error for that time point is statistically different from the error at the 0 h time point.

One potential explanation for the decrease of the prediction errors across time could be that the variation in the mitochondrial distribution from cell to cell decreases with treatment time (and thus predicting a close mitochondrial distribution is made easier). To test this, we determined whether the errors for a mitochondrial distribution predicted from a cell’s shape-space position were significantly smaller than those resulting from random choice of a cell from all cells in a given experiment. The models were all significant at α < 0.05 after Bonferroni-Holm correction as shown in Supplemental Table S2. These results indicate that a significant relationship exists between mitochondrial localization and cell shape and that the relationship becomes stronger as a function of time.

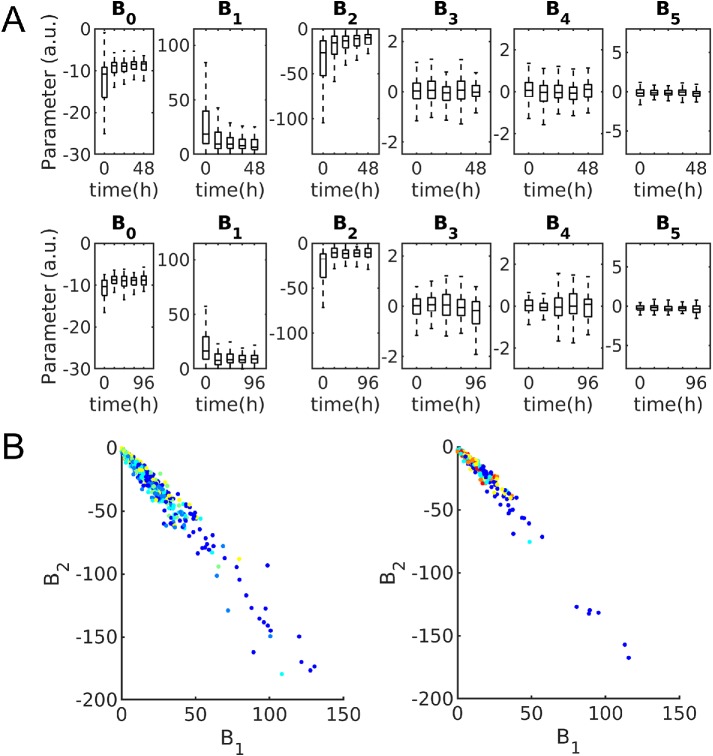
Figure 4 shows the distributions of the parameters of the mitochondria model for each time point for the 48- and 96-h experiments. B₁ and B₂ (parameters weighting the distance from the nucleus) show a strong relationship to time after treatment; they also show a high degree of correlation (Figure 4B), becoming more constrained as a function of time after treatment. To illustrate variation in mitochondrial patterns across time, Supplemental Figure S5 shows example cell shapes, segmented mitochondria patterns, and modeled and predicted spatial probability density models, for average cell shapes every 24 h for the 96-h data set.

FIGURE 4:

Mitochondria distribution parameters. (A) Boxplots showing distribution of parameters for 48-h (top) and 96-h (bottom) experiments. Box centers indicate population median with bounds indicating 25th and 75th percentiles, respectively. Whiskers indicate 99% coverage of data. (B) Mitochondria distribution parameters corresponding most with time plotted against each other and colored by time for 48-h (left) and 96-h (right) experiments. Blue indicates untreated cells and warmer colors indicate later time points at either 12- or 24-h intervals.

Modeling kinetics of differentiating cells

We next sought to construct a model of shape dynamics, such that we could generate movies of synthetic shapes for cells as they differentiate. Because we do not have images of the same cell at different time points, we cannot directly learn a dynamic model using the approach we have previously described (Johnson et al., 2015). We therefore propose an alternative model for learning shape dynamics. The basic idea is to assume that the populations of cells at each time point are large enough that we can consider that for each cell in our collection for a given time point there is a cell in the collection for the next time point that is reasonably similar to what the first cell would have looked like at the later time. We find the matches between cells at adjacent time points that give the lowest total difference in shape between them (by weighted maximum bipartite matching, as described in Materials and Methods). This gives us a “trajectory” in time and in shape space for each cell at the 0 h time point (without NGF treatment). Using shape evolution synthesis (Ruan and Murphy, 2019) we can construct intermediate shapes within each trajectory by interpolating along a linear path in the shape space between each pair of shapes in adjacent time points. Because cell size varies during differentiation, we use a shape space constructed from shape descriptors that include size for the cell matching and shape evolution processes.

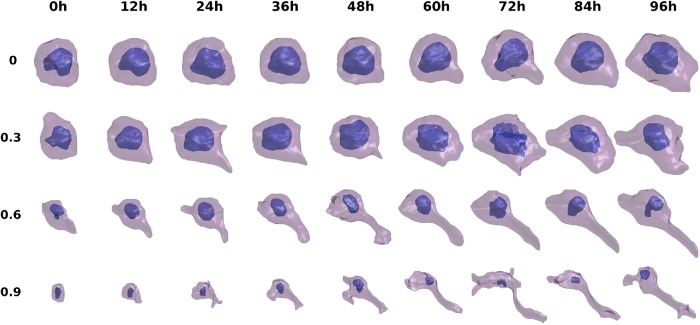
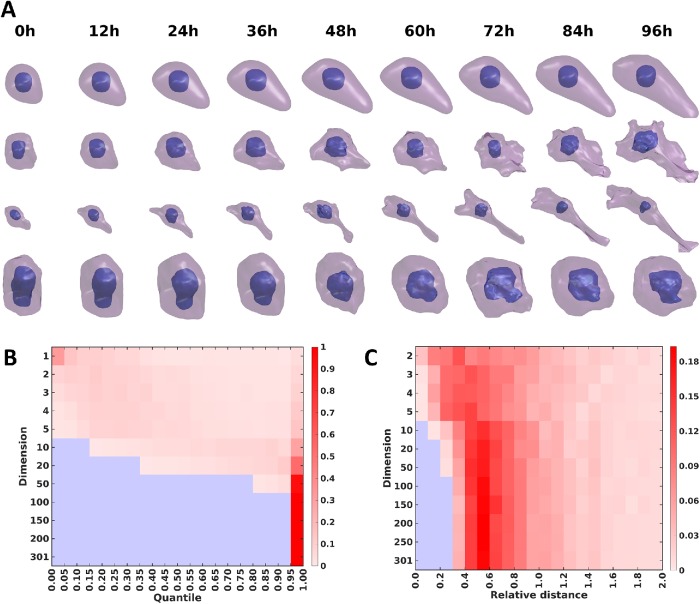
Examples of the resulting shape differentiation trajectories are shown in Supplemental Figure S6 and Figure 5 for the 48- and 96-h experiments, respectively, with finer and smoother synthesis of the trajectories from Figure 5 shown in Supplemental Videos S1–S4. In both figures, each row shows the evolution of cell and nuclear shape for a given cell from 0 h to 48/96 h. The four cells are chosen based on quantiles of total distances between the matched cells of adjacent time points across all time points. From the figures, we can see that the shape evolution method appears reasonable in terms of the reconstructions of cell shapes for either observed or unobserved cells (interpolated time points), and captures the expected trend from round cells to complicated shapes with long neurites (for most trajectories). Also, the total distances in the shape space for the trajectories reflect the overall shape variation across time; for example, the final shapes generally become more and more complicated as the quantile increases. Moreover, the sensitivity to NGF treatment is clearly heterogeneous among PC12 cells, as some of the matched cells do not appear to differentiate after treatment (the presence of these cells in the late time points of course also indicates this). In Supplemental Figures S7 and S8, the expected directions for the transitions of cell shapes for different size time steps are shown. The figures confirm the last observation, as different positions in the shape space are predicted to move toward quite heterogeneous directions at the next time point (especially during the early stages). This finding of heterogeneity agrees with previous experimental studies (Burstein et al., 1982; Clementi et al., 1993). Overall, we conclude that the method can generate very realistic intermediate cell shapes and synthetic trajectories, even though no prior knowledge or constraint on allowable shape changes was provided.

FIGURE 5:

Illustration of synthetic cell and nuclear shape differentiation for 12-h time steps interpolated between the time points of the 96-h experiment. Four trajectories chosen based on the quantiles of total distances between matched cell pairs in the trajectory are shown.

Video S1.

Download video file ^{(487.6KB, mov)}

Synthesized PC12 cell differentiation in response to treatment of NGF for the first cell in Figure 5. Cell shapes were inferred at 2.4h time steps aiming to illustrating smoother and more realistic transitions.

Video S2.

Download video file ^{(662.9KB, mov)}

Synthesized PC12 cell differentiation in response to treatment of NGF for the second cell in Figure 5. Cell shapes were inferred at 2.4h time steps aiming to illustrating smoother and more realistic transitions.

Video S3.

Download video file ^{(567.4KB, mov)}

Synthesized PC12 cell differentiation in response to treatment of NGF for the third cell in Figure 5. Cell shapes were inferred at 2.4h time steps aiming to illustrating smoother and more realistic transitions.

Video S4.

Download video file ^{(730.6KB, mov)}

Synthesized PC12 cell differentiation in response to treatment of NGF for the fourth cell in Figure 5. Cell shapes were inferred at 2.4h time steps aiming to illustrating smoother and more realistic transitions.

Generative model of the relationship between cell shape and mitochondrial location pattern

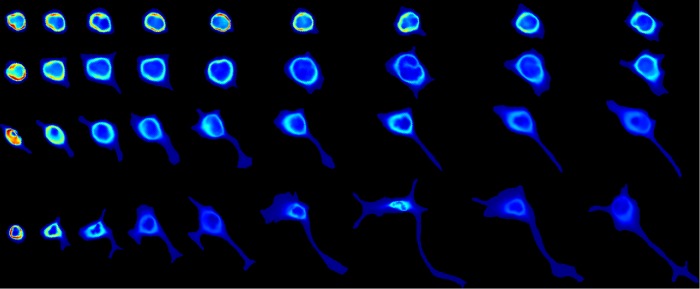
In addition to simulating dynamics for cell shape, we can also model the dynamics of changes in mitochondrial distribution. Using the regression model between cell/nuclear shapes and mitochondrial patterns, we inferred parameters of the mitochondria model for each of the interpolated cell and nuclear shapes along our estimated cell trajectories. This allows a probability density distribution for mitochondria to be synthesized using the inferred parameters and the volume images of cell and nuclear shape (using the image synthesis function in CellOrganizer). Figure 6 shows the mitochondrial probability densities for the same four cells as in Figure 5. The complete sets of frames of mitochondrial patterns for these four cells are shown in Supplemental Videos S5–S8.

FIGURE 6:

Illustration of mitochondria localization patterns during differentiation for 12-h time steps in the 96-h experiment. Each row shows 2D mean value projections of the 3D mitochondrial probability density maps in a trajectory. The trajectories are the same as shown in Figure 5. Each column represents a time point from 0 to 96 h with time step of 12 h from left to right. The maps are shown with a hot-cold color map (blue indicates low probability of observing a mitochondrion at that location).

Video S5.

Download video file ^{(775.8KB, mov)}

Synthesized probability density maps for mitochondria during PC12 cell differentiation in response to treatment of NGF for the first cell in Figure 6. Cell shapes were inferred in 2.4h time steps to provide smoother transitions. The density is shown with a hotcold color map similar to Figure 6.

Video S6.

Download video file ^{(951.6KB, mov)}

Synthesized probability density maps for mitochondria during PC12 cell differentiation in response to treatment of NGF for the second cell in Figure 6. Cell shapes were inferred in 2.4h time steps to provide smoother transitions. The density is shown with a hotcold color map similar to Figure 6.

Video S7.

Download video file ^{(649.4KB, mov)}

Synthesized probability density maps for mitochondria patterns during PC12 cell differentiation in response to treatment of NGF for the third cell in Figure 6. Cell shapes were inferred in 2.4h time steps to provide smoother transitions. The density is shown with a hot-cold color map similar to Figure 6.

Video S8.

Download video file ^{(825.4KB, mov)}

Synthesized probability density maps for mitochondria patterns during PC12 cell differentiation in response to treatment of NGF for the fourth cell in Figure 6. Cell shapes were inferred in 2.4h time steps to provide smoother transitions. The density is shown with a hot-cold color map similar to Figure 6.

Allowable shapes and evolution trajectories

In the preceding two sections, we used nearby pairs of existing observations to evolve shapes along the pseudotrajectories by interpolation, and showed that the synthetic shapes appeared realistic. An important question is whether shapes and trajectories derived from arbitrary points in the shape space are also realistic. To address this question, we first explored the path between the centroids in the shape space for each time point. The idea is to determine whether this “average” path is representative of the overall differentiation process. We generated a shape trajectory connecting the centroids for the 48- and 96-h experiments as shown in the top rows of Supplemental Figure S9 and Figure 7A, respectively. As can be seen, in both cases, the shapes in the centroid path are very smooth, and they are not similar to any of the cells observed in the experiments. Because centroids are calculated using all cells for a given time point, only the consistent components of the shape are retained and shape variation is inappropriately averaged out. As another approach to generating a realistic, purely synthetic trajectory, we considered interpolating a trajectory between two trajectories. To do this, we first chose the two trajectories that were the farthest apart while still being within the 95th percentile of distances from the centroid. As expected, interpolation between these trajectories gave very elongated shapes unlike any observed in the experiments (second rows, Supplemental Figure S9 and Figure 7A). We then reasoned that interpolation between two close trajectories would be more realistic. For each of the farthest apart trajectories, we chose the trajectory closest to it. Interpolation of a trajectory between these close pairs that are from very different regions of the shape space (third and fourth rows, Supplemental Figure S9 and Figure 7A) gave very different results but ones that were both clearly realistic. We conclude that only interpolations between nearby examples of real trajectories yield reasonable results.

FIGURE 7:

Creation of synthetic shape trajectories by various approaches from models of the 96-h experiment. (A) The top row shows a shape trajectory formed by creating shapes corresponding to the centroid shape coordinates in each original time point as well as shapes corresponding to points interpolated between them. The second row shows the trajectory formed by creating shapes corresponding to the mean of the shape coordinates for the pair of trajectories that have the 95% farthest distance between them (trajectories a and b). The third row shows the trajectory formed by the mean of a and the trajectory closest to a. The fourth row shows the trajectory formed by the mean of b and the trajectory closest to b. (B) The heatmap shows the number of points in each quantile of a Gaussian distribution within the shape space of a given number of specific dimensions. The colors indicate increasing number of points from blue (zero) to dark red. (C) The heatmap shows histograms of the number of points at a given distance from the fitted surface of a hyperellipsoid for shape spaces of different numbers of dimensions. The colors indicate increasing number of points from blue (zero) to dark red.

The result that shapes from some “interior” portions of the shape space (and hence some shape trajectories) are not realistic suggests that actual cell shapes may form a “hollow” distribution in shape space. That is, rather than forming clusters with high densities in the middle, actual shapes may be thought of as existing on or near the surface of something like a hyperellipsoid or hypertuboid in shape space (and shape trajectories as being paths along that surface). To explore this, we performed a simple test (related to the quantile–quantile test) to determine the Gaussianity of the shape distributions for shape spaces of various number of dimensions: we fitted the data with a Gaussian distribution and made a histogram of the distance from the centroid with bins at 0.05 intervals in Gaussian probability. If the distribution is close to a Gaussian distribution, the number of points in the bins should be similar. As shown in Figure 7B, as the dimension of the shape space increases, the distribution becomes farther and farther from a Gaussian distribution. Above 50 dimensions, almost all points are in the last bin. This is consistent with the “hollowness” hypothesis. To test whether the shape distribution is approximately hyperellipsoidal, we performed a similar analysis using a fit to a hyperellipsoidal distribution followed by measuring the signed distance from the estimated hyperellipsoidal surface. As the dimension of the shape space increases, the shapes increasingly move farther from the centroid and become closer to the estimated surface (Figure 7C).

Diverse drug effects on nuclear shapes

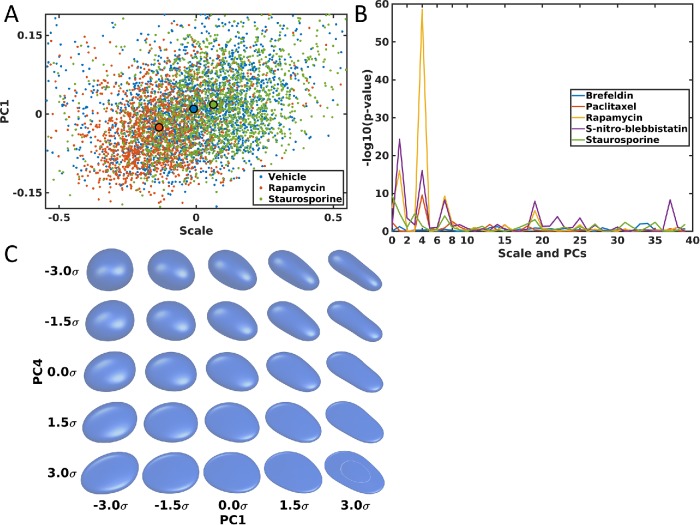
As an illustration of another application of the shape model approach, we constructed models of changes in nuclear shape resulting from drug treatment. For this, we used a public data set of images of hiPSCs with and without treatment with various drugs. The detailed description of the generation of these images is provided on the data set website (see Materials and Methods). A shape space for cells treated with vehicle only, with rapamycin, or with staurosporine is shown in Figure 8A, with the shape space for all five drugs and vehicle shown in Supplemental Figure S10. As shown in the figures, major shape variation after drug treatment for all five drugs is captured. Among the five drugs, rapamycin and staurosporine have the most significant effects on the nuclear shape and occur in opposite directions: rapamycin treatment significantly reduces nuclear size while staurosporine increases it. The effect of rapamycin is consistent with previous findings that rapamycin is an mTOR inhibitor and can reduce cell size (Fingar et al., 2002), and nuclear size is considered to be highly correlated with cell size (Huber and Gerace, 2007; Edens et al., 2013). However, to our knowledge, there is no strong previous evidence on how staurosporine relates to nuclear size.

FIGURE 8:

Shape space and shape variances comparison of nuclear shapes for hiPSCs. (A) Nuclear shape spaces for vehicle (blue), rapamycin (red), and staurosporine (green). A large dot with a black boundary shows the centroid of shape distributions for each group. (B) p values of t tests between a drug and its vehicle for size (shown on the left) and the first 39 PCs (separately). (C) Shape variance visualization for PC1 and PC4 in the shape space. The variations in PC1 and PC4 are shown along the x-axix and y-axis, with different standard deviations (SDs) as indicated. The center shows the mean shape.

To determine the statistical significance of any shape changes caused by the different drugs, we compared means and standard deviations for size and the first five PCs, along with the difference of distribution for these six components using Hotelling’s T-squared test (a multivariate version of the t test), followed by Bonferroni-Holm correction, as listed in Supplemental Table S3. Surprisingly, with the exception of brefeldin, all drugs show very significant changes over their vehicle controls. Paclitaxel and (S)-nitro-blebbistatin (SNB) do not change nuclear size very much but significantly change nuclear shape.

To see which shape components are strongly affected by the drug treatment, we compared size and the first 39 shape PCs between a drug and its vehicle, because the first 39 PCs represent ∼95% of overall shape variance. The p values for the comparison are shown in Figure 8B. Size, PC1, PC4, PC7, and PC19 show very significant changes, especially PC1 and PC4. To see what shape aspects these two PCs reflect, we visualized shapes at different numbers of standard deviations across these components. As shown in Figure 8C, PC1 is associated with the roundness of the nuclear shape (with some subtle remaining rotation), while PC4 seems to be associated with thickness. Supplemental Figure S11 shows similar results for PC7 and PC19, but their effects on shape are not obvious. From the figure, PC7 might associate with sharpness along the z-axis (from flat to sharp). The overall conclusions are that nuclear shapes under rapamycin or SNB treatment are generally rounder than those in normal condition, and are thicker under treatment with paclitaxel, rapamycin, or SNB.

DISCUSSION

One of the objectives of systems biology is to understand the relationships between cell components such that cell fate and the organization of unobserved components may be predicted. An additional objective is that these models not rely on human interpretation, such as hypothesized mechanisms for biochemical processes, but rather be learned directly from experimental measurements.

With these considerations in mind, we developed a tool to model the relationship between cell morphology and organelle organization and demonstrated that this relationship varies during differentiation of PC12 cells. We found that there is a decrease in variation of mitochondrial localization with respect to time after differentiation.

Given population snapshots, we constructed a model to describe shape evolution in response to NGF treatment; the model is capable of producing movies by statistically sampling differentiating cell shapes. Here we make very simple assumptions for shape dynamics in terms of both cell/nuclear shapes and mitochondria localization by interpolating across linear paths in the shape space for the cell and nuclear shape models and then estimating parameters for the localization model from those shapes. The synthetic movies appear reasonable in terms of shape dynamics even without using any prior knowledge of how PC12 cells actually differentiate. Of course the model of mitochondrial localization is quite simplistic, only considering the spatial probability distribution, rather than trying to predict individual mitochondrial shapes, sizes, and intensities. Thus, one potential future direction is to apply other generative methods for organelle or protein dynamics, for example, the 3D equivalent to optimal transport models (Kolouri et al., 2015).

An important finding was that, at least for the PC12 images, shape models that were sufficiently detailed to capture most variation yielded shape spaces that are effectively hollow, with most cell shapes and trajectories away from the mean shape coordinates. This has important consequences both for synthesis of shapes (allowing synthesis only between similar measured shapes) and for comparison of image sets.

The method we have described is capable of constructing models in a range of time-varying cell-component localization applications, including but not limited to changes associated with division and cell migration. Recent findings have shown that population heterogeneity is inherent in the PC12 signaling networks (Ryu et al., 2015). The relationship between proliferation and differentiation is sharply defined by mutually exclusive pAKT and pERK concentrations (Chen et al., 2012). This suggests an influence of stochastic effects on the cell fate decision, and that on the single-cell level cells are either proliferating or differentiating. As a consequence, homogeneity of the population can be reduced by optimal growth conditions, but never completely abrogated (Mouri and Sako, 2013; Chung et al., 2014).

Moreover, the method can allow us to model nuclear shape changes of hiPSCs after drug treatment. The most significant shape variances after treatment are the nuclear size and roundness. These findings are consistent with previous findings.

The image-derived modeling technique described here is able to model single-cell decisions and is therefore a small step in the development of tools to automatically learn relationships among cell populations and between cell shapes and their components, as well as provide compact representations of these relationships.

MATERIALS AND METHODS

Cell culture and experimental conditions

PC12 cells (between 6 and 10 passages) were obtained from the American Type Culture Collection (UK) and were cultured in RPMi medium containing 10% horse serum (HS), 5% fetal calf serum, 1% l-glutamine, and penicillin/streptomycin at 37°C in 5% CO₂. Cells were plated on collagen-coated 35-mm glass-bottom ibiTreat dishes and were allowed to adhere for 24 h. Two types of experiments were performed. Cells were either treated with 50 ng/ml rat NGF (Promega, Madison, WI) at 0, 12, 24, 36, and 48 h before imaging at the same time, or were treated at the same time and imaged at 24-h increments up to 96 h after treatment. Before imaging (1 h), cells were stained at 37°C with a 0.5 μM solution of mito red (Sigma-Aldrich, Munich, Germany) for 5 min, rinsed with phosphate-buffered saline, and placed in 1 ml of growth media without phenol red.

Microscopy

Cells were imaged on an Axio Observer.Z1 (Carl Zeiss Microscopy, Jena, Germany) microscope equipped with a spinning disk (CSU-22; Yokogawa, Japan) with an EX-Plan-Neofluar 40×/1.30 oil objective. The sample voxel size was 0.161 μm × 0.161 μm × 0.340 μm and 59 slices were taken with a 150-ms exposure time at 12-bit pixel depth. Imaged cells were manually selected to not be in contact with other cells. Due to the sensitivity of cells to phototoxicity, approximately 10 fields were imaged per plate. Between 172 and 98 cells were imaged at each time point for the 48-h experiment and between 46 and 89 cells per time point in the 96-h experiment.

Cell shape segmentation

To find the outline of each cell, each slice of an image was convolved with a 2D Hessian filter with a 3-pixel SD and eigen-edges were extracted (Ronneberger et al., 2008). Dilation and erosion operations were performed on each slice with a disk structuring element of 14 and 24 pixels, respectively. The final shape was regularized by convolving with a Gaussian with a SD of 7 pixels and retaining all pixels with a value greater than 0.5. The result was a “shell” of the cell shape, and thus a fill operation was performed on each region (cell) in the image.

Nuclear shape segmentation

Given a masked cell shape, the intensity image was thresholded via Ridler–Calvard thresholding (Ridler and Calvard, 1978). The nucleus was defined as the volume not containing a signal within the convex hull of each cell. Because this may result in multiple objects, a distance transform was performed, segmented with an active contour, and the largest object returned as the final nuclear shape. An example of this pipeline is shown in Supplemental Figure S12.

Cell and nuclear shape model with spherical harmonic framework

Shape alignment and modeling.

Joint models for cell and nuclear shapes were constructed using the spherical harmonic framework as described (Ruan and Murphy, 2019). To make different shapes comparable, this framework aligns shapes using the first-order ellipse before creating the model. As an alternative we also did alignment using the major axis, as illustrated in Supplemental Figure S13. The surface points were projected to the xy-plane, and PCA was used to find the major axis. The cell shape was then rotated around the z-axis to align it to this axis (Supplemental Figure S13A). After that, if the skewness along the x-axis was negative, the shape was flipped in the xy-plane. The cell shape was mapped to a unit sphere as described previously (Ruan and Murphy, 2019). This assigns each point on the surface of the shape to a point on a unit sphere, referred to as a parameterization of the shape. This parameterization needs further alignment so that the final descriptors of different cells are comparable, and further alignments were done on the parameterization vectors. The basic idea is to find some landmarks from the parameterization in specific directions and then rotate the parameterization using the landmarks. The first step is to pick a pair of vertices whose direction is closest to the x-axis to define the oriented poles in the spherical parameterization. To do this, vertices in the object were first paired with each other such that the projection to the unit sphere of one point is closest to the antipodal point of the other point (i.e., the two points are [approximately] diametrically opposite to each other after mapping). The 1% of pairs whose vector directions have the smallest angles to the xy-plane (those that are approximately in the xy-plane) were chosen, and the subset of those chosen for which the direction vectors were within 0.01% of the x-axis. The pair in this subset with the largest distance between them was chosen as the south and north poles for the parameterization. The second step is to find landmarks in the equator (analogous to points with 0° and 180° longitudes). The pairs of points whose direction vectors had inclinations (polar angles) closest to zero were chosen, and finally the pair with the minimum differences in the z coordinate selected. Given the poles and equator landmarks, a rotation matrix was defined as the rotation from the projected coordinate of the equator landmark with the larger y coordinate to the coordinate of (0, 1, 0) (see Supplemental Figure S13, B and C). After rotation, the spherical parameterization is flipped along the x-axis if the point in the object space with coordinate (1, 0, 0) in the parameter space has a smaller z coordinate than that of the centroid of all surface points.

The final parameterizations were converted to spherical harmonic descriptors, and shape spaces of various dimensions were created from various numbers of principal components of the descriptors. To analyze the distributions in the shape space, fits to Gaussian or hyperellipsoidal distributions were done for each number of dimensions. Hyperellipsoidal fits were done using various methods from the HYPERELLIPSOIDFIT package (www.mathworks.com/matlabcentral/fileexchange/59186-hyperellipsoidfit), namely, the sum of discriminants method (SOD), ellipsoid-specific method (HES), quadratic constraint-based methods (BOOK and TAUB), fixed constant term method (FC), or fixed sum of squares method (2-NORM). Fits for these methods were calculated with the regularization parameter set to log values from 2 to −2 in increments of 0.1 and the combination of method and regularization parameter that gave the lowest residual error was chosen.

Shape reconstruction.

Shape reconstruction from a SPHARM-RPDM model was done as described previously (Ruan and Murphy, 2019). The accuracy of shape reconstruction was measured using the Hausdorff distance, which is defined as

1

where X and Y are two sets of points and d (x, y) is a metric of distance between two points (Euclidean distance in our case). The 3D volume images of shapes were converted to surface meshes, and vertices in the meshes for the original and reconstructed surfaces were used to calculate the Hausdorff distance. Hausdorff distances are measured in voxels, and therefore cannot be readily compared between shapes of difference sizes. An additional error metric, peak signal-to-noise ratios (PSNR) between the original and reconstructed shape, was therefore also included to provide a scale-free estimate of the reconstruction quality. PSNR is calculated based on the Hausdorff distance with the following form:

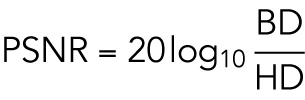2

where BD is the diagonal of the minimum bounding box of the cell and HD is the Hausdorff distance. For the joint model, the joint reconstruction error was defined as the average of those for the two components (cell and nuclear shapes).

Mitochondrial localization model

Mitochondrial localization models were learned as described previously (Peng and Murphy, 2011). Briefly, the mitochondrial image after masking to the cell boundary was preprocessed by removing intensity below the Ridler–Calvard threshold. A spherical Gaussian mixture model was fitted using seeds at each intensity local maxima after convolving the image with a Gaussian filter of one voxel SD. The position of each voxel in the cell was parameterized according to its ratio of distance to the nuclear surface over the nuclear distance plus the distance to the cell surface, s, and the inclination and azimuth angles, θ and φ, respectively, from the nuclear center. A logistic function was fitted to the probability that each pixel contains an object centroid,

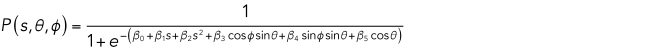3

The spatial probability distribution for each cell was parameterized by the six-element vector β.

Regression model between shape and mitochondrial distribution

We used a multiresponse regression to model and predict the mitochondrial localization model given the cell and nuclear shapes:

4

where 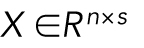is a matrix of joint shape-space positions of dimension s, with each row corresponding to a cell and nuclear shape, and each column a dimension of the shape space (in this case 300 dimensions without scale, and 301 dimensions including scale factors as an additional feature). 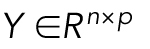is a matrix of mitochondrial localization models, with each row being a model corresponding to the cell at the same row in X. 1_n×1 is the n-dimensional column vector with all elements as 1. B₀ and B are model parameters, where is the parameter for the intercept and 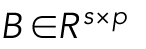is the regression matrix describing the relationship between the shape space and mitochondria localization models. W ∈ R^n×p is a matrix of random noise following multivariate Gaussian distribution with zero mean (the residual variation in the localization parameters not explained by model parameters). Here we combined elastic net regression (Zou and Hastie, 2005) with a group-penalized estimator (Simon et al., 2013a) of model parameters defined as

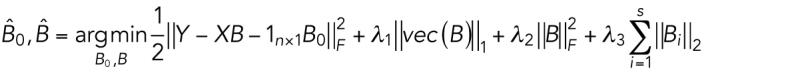5

where 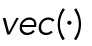is the operator of reshaping a matrix into a column vector, 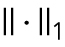represents the l₁ norm of a vector, 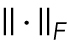stands for the Frobenius norm of a matrix, and 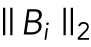indicates the l₂ norm of the ith row of B. The regularization parameters λ₁, λ₂, and λ₃ function as penalization terms on B to control the structure of B, as well as to avoid overfitting of the model. These regularization parameters were chosen by sweeping over combined sets of possible candidate values, and selecting the set that results in the lowest mean-squared prediction error of Y via 10-fold cross-validation. In the cross-validation, we allowed λ₂ and/or λ₃ to be zero, which means that the model may degenerate into lasso regression (Tibshirani, 1996; if both λ₂ and λ₃ are zeros), elastic net regression (Zou and Hastie, 2005; if λ₃ is zero), or sparse group lasso regression (Simon et al., 2013b; if λ₂ is zero). The reason for the possibility of degeneration in the model is to allow more flexible control of the model in response to different situations in the data sets. We implemented the regression model with the alternating direction method of multipliers framework (Boyd et al., 2011).

Modeling kinetics of differentiating cells

Given cell populations at sequential time points, we sought to find plausible and most similar cell shapes at the subsequent time point; such a shape pair can be treated as a “trace” in time series models. This essentially becomes a matching problem, where we want to find a matching of each cell in one time point to one cell in the next time point that minimizes the total shape-space distance between pairs of matched cell shapes. More formally, given the shape-space positions of equal numbers of cells at subsequent time points, 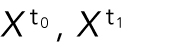, we can construct a matrix of cell shape distances between cells at subsequent time points,

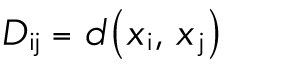6

where 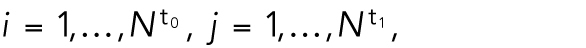and 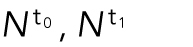are the number of cells for t₀ and t₁, respectively. We want to minimize the function

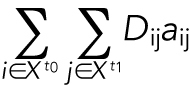7

where a_ij is binary matrix of assignments taking a value of 1 if there is an assignment and 0 otherwise, subject to the constraints 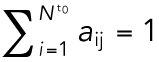and 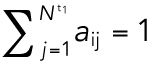(Christofides, 1975). This problem was solved through the Hungarian algorithm (Kuhn, 1955).

Modeling drug-induced nuclear shape changes

Image source.

The images are obtained from the drug perturba­tion pilot study at Allen Institute of Cell Science (www.allencell.org/drug-perturbation-pilot.html). The detailed experimental setup and image acquisition procedure are described on the website. Briefly, green fluorescent protein–tagged hiPSCs were treated with different drugs, followed by 3D high-resolution imaging. Five drugs were used: brefeldin A, paclitaxel (Taxol), rapamycin, SNB, and staurosporine. After drug treatment, 3D z-stack images were acquired with high magnification (120×). For the nuclear channel, images were 624 × 924 × 65 pixels and each pixel represented 0.108 μm × 0.108 μm × 0.29 μm.

Nuclear segmentation

A seeded watershed method (Meyer, 1994) was used for segmentation, in which a 2D projected image was segmented and the segmented objects were used as seeds for the 3D seeded watershed algorithm. There are two basic steps: the projected 2D image segmentation and 3D image segmentation. The detailed procedure is as follows:

1. Projected 2D image segmentation.

First, because some images have very low SNRs, which makes the segmentation difficult, we skip images with low contrast with a contrast threshold (the root mean square contrast 15 in the implementation) for the mean of the top three contrasts across all slices. Then, we project the nuclear image to the xy-plane by averaging the 15 slices centered by the slice with the highest contrast. Second, we first smooth the projected image with a Gaussian filter, and binarized the image with 0.9 folds of Otsu’s threshold, followed by hole filling and image smoothing. Third, if an object is considered as multiple cells touching together based on some criteria such as area, length of major axis, eccentricity, and so on, we split the object into multiple regions using a bottleneck detection method. In the method, we extract the skeleton and find paths for each pair of endpoints in the skeleton. For each path, we calculate the minimum distance from each pixel in the path to the two sides of the object boundary. A bottleneck is considered if there is a local minimum distance, where we can find two points that form the local minimum in each side of the boundary as bottleneck points. We do this for all paths. After that, we split the object into two parts by cutting the line across a pair of bottleneck points, if both parts have a reasonable size (>500 pixels). We repeat the cutting process for all pairs of bottleneck points. Fourth, we refine the segmentation of the projected image with the seeded watershed algorithm followed by local segmentation with Otsu’s method. We first use the results from the third step as seeds for the watershed algorithm to define regions. For each region, we use Otsu’s algorithm to get a local threshold for the object in order to better match the local background to obtain a more accurate nuclear shape. The region is binarized with 0.9 folds of Otsu’s threshold, followed by hole filling and image smoothing. Also, we split touching objects using the method as described in the third step.

1. 3D nuclear shape segmentation.

After obtaining 2D nuclear shapes in the projected image, we create a mask with the same size as the original 3D nuclear image and then place the segmented objects as the central slice in the mask as well as setting the boundary as an object (so that we can remove cells touching the boundary in the segmentation). Then, we smooth the nuclear image with a 3D Gaussian filter and apply the watershed algorithm using the mask as the seeds. For each region obtained from the watershed algorithm, we apply Otsu’s method to obtain a specific threshold for each region and binarize the region with a threshold of 0.95 folds of Otsu’s threshold. Then, we fill holes and smooth the nuclear shape with image close and open filters. Finally, bad segmentations are moved with criteria such as the area of the projected object in the xy-plane, the volume, the number of z-stacks, area touching the boundary, length of principal axis, solidity, surface area, length of equivalent diameter, and so on.

Nuclear shape modeling

We build a nuclear shape-space model using the SPHARM-RPDM model in the same way as described above, except that the model was only for nuclear shape.

Availability

The CellOrganizer software used here for modeling these relationships is available at http://cellorganizer.org. The source code for performing all analyses in this article, as well as analysis results, is available at http://murphylab.cbd.cmu.edu/software. The original PC12 images are available from the Dryad Digital Repository at https://doi.org/10.5061/dryad.hc8037v.

Abbreviations used:

HD

Hausdorff distance

hiPSC

human induced pluripotent stem cells

NGF

nerve growth factor

PCA

principal components analysis

SNB

(S)-nitro-blebbistatin

SNR

signal-to-noise ratio

SPHARM-RPDM

spherical harmonic robust Point Distribution Model.