Abstract
How do early embryos allocate the resources stored in the sperm and egg? Recently, we established isothermal calorimetry to measure heat dissipation by living zebrafish embryos and to estimate the energetics of specific developmental events. During the reductive cleavage divisions, the rate of heat dissipation increases from ∼60 nJ · s−1 at the two-cell stage to ∼90 nJ · s−1 at the 1024-cell stage. Here we ask which cellular process(es) drive this increasing energetic cost. We present evidence that the cost is due to the increase in the total surface area of all the cells of the embryo. First, embryo volume stays constant during the cleavage stage, indicating that the increase is not due to growth. Second, the heat increase is blocked by nocodazole, which inhibits DNA replication, mitosis, and cell division; this suggests some aspect of cell proliferation contributes to these costs. Third, the heat increases in proportion to the total cell surface area rather than total cell number. Fourth, the heat increase falls within the range of the estimated costs of maintaining and assembling plasma membranes and associated proteins. Thus, the increase in total plasma membrane associated with cell proliferation is likely to contribute appreciably to the total energy budget of the embryo.
INTRODUCTION
During early embryogenesis in oviparous animals, there is often a stage during which the cells divide without a change in the total volume of the zygote (Kimmel et al., 1995; Tadros and Lipshitz, 2009). During this so-called reductive cleavage stage, components provided by the mother and stored in the oocyte, for example, in the yolk, are used to build the early embryo. Because there is no growth, the cleavage stage provides an opportunity to study the energetic costs associated with cellular processes such as proliferation (e.g., DNA replication and cell division) and development (e.g., the specification of cell identity and fate). The reason why the absence of volume growth is important is that the metabolic cost of growth, mainly due to protein synthesis, is much larger than the basal metabolic costs without growth: for example, if a cell were to double its volume in 15 min, the cell cycle time during the cleavage stage in zebrafish, the energetic costs associated with growth (Eq. 1b in Lynch and Marinov, 2017) would be some 1000 times larger than the maintenance costs (using the initial heat dissipation rate equivalent to 25 μM ATP/s from Rodenfels et al., 2019). Thus, the cleavage stage offers a window for making sensitive measurements of the energetics of cellular processes independent of growth.
Metabolism during embryogenesis has been assayed in frogs (Nagano and Ode, 2014), fish (Rodenfels et al., 2019) and flies (Song et al., 2019) using isothermal calorimetry (ITC) to measure heat dissipation, which is equal to the net enthalpic change associated with all of the biochemical reactions taking place in the embryo (Rodenfels et al., 2019). The measurements show that embryogenesis is exothermic, meaning that the medium surrounding the embryos heats up. In the zebrafish Danio rerio, the cleavage stage lasts for 10 divisions producing 1024 cells, referred to as the 1K stage. We recently showed that, during this stage, the heat dissipation oscillates with an amplitude of ∼2% of the total heat dissipation (Rodenfels et al., 2019). The oscillations have a period equal to the cell cycle time and are unchanged when DNA replication and cell division are blocked. The heat oscillations likely arise from heat dissipated by the biochemical reactions associated with the cell cycle oscillator, which coordinates events taking place during the cell division cycles. Thus, noninvasive ITC measurements during the cleavage stage are a sensitive probe of cellular energetics during development.
During the cleavage stage in zebrafish, and concurrent with the oscillations, there is an overall increase in heat dissipation from ∼60 nJ · s−1 at the two-cell stage to ∼90 nJ · s−1 at the 1K stage (Rodenfels et al., 2019). We call this the “increasing trend.” In this work, we use a combination of pharmacological and computational approaches to identify cellular events that may account for the increasing trend.
RESULTS and discussion
Temperature dependence of the increasing trend
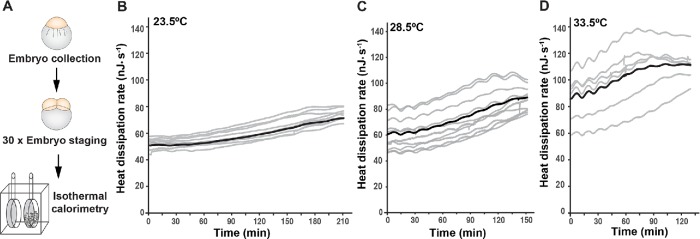
To confirm that the increasing trend is present under different experimental conditions, we measured heat dissipation during embryogenesis in zebrafish at three different temperatures. Thirty embryos from one mother were manually synchronized to begin the second cleavage (defined as time zero) within 3 min of each other and placed in an isothermal calorimeter (Figure 1A). At 23.5°C, the dissipation rate increased from 51 ± 8 nJ · s−1 per embryo (mean ± SD, n = 9 experiments, each using 30 embryos) to 69 ± 10 nJ · s−1 after 210 min, when the 10th cleavage was complete (Figure 1B). At 28.5°C, the heat dissipation rate increased from 60 ± 13 nJ · s−1 (n = 10 experiments) to 88 ± 10 nJ · s−1 after 150 min, when the 10th cleavage was complete (Figure 1C). At 33.5°C, the dissipation rate increased from 82 ± 18 nJ · s−1 (n = 6 experiments) to 119 ± 22 nJ · s−1 after 130 min (Figure 1D). Thus, the relative amplitude of the increasing trend is roughly independent of temperature (35% at 23.5°C, 47% at 28.5°C, and 45% at 33.5°C), even though the initial dissipation rate and the cell cycle period increased 1.6-fold over the 10°C temperature range.
FIGURE 1:
Heat dissipation in the early zebrafish embryo. (A) Schematic of an ITC experiment. Thirty embryos from a single pair of parents were collected and staged at the two-cell stage. Following staging, the embryonic heat dissipation rate during development was measured using ITC. (B) The time course of heat dissipation for nine experiments at 23.5°C (gray lines) together with the mean (black line). Time zero corresponds to the beginning of cleavage at the two-cell stage. Positive heat dissipation corresponds to heat transfer from the embryo to the surroundings. (C) The time course of heat dissipation for nine experiments at 28.5°C (gray lines) together with the mean (black line). (D) The time course of heat dissipation for six experiments at 33.5°C (gray lines) together with the mean (black line).
The increasing trend is blocked by nocodazole
We then asked whether the increasing trend depends on cell division. To test this possibility, we treated two-cell embryos with 10 μM of the microtubule poison nocodazole, which blocks DNA replication, mitosis, and cell division (Ikegami et al., 1997; Rodenfels et al., 2019). Nocodazole arrests development: the number of nuclei and cells remain at two throughout the first 135 min of development (Rodenfels et al., 2019). After addition of 10 μM nocodazole, the early embryos continued to dissipate heat at the initial rate, and the oscillation remained. The increasing trend, however, was greatly attenuated (Figure 2). The relative increase in heat dissipation dropped from 47 ± 15% in untreated cells (mean ± SD, n = 10) and 40 ± 23% in dimethyl sulfoxide (DMSO)-treated cells (n = 6) to 13.5 ± 1.5% in nocodazole-treated cells (n = 6). Thus, blocking cell proliferation also blocks the increasing trend.
FIGURE 2:
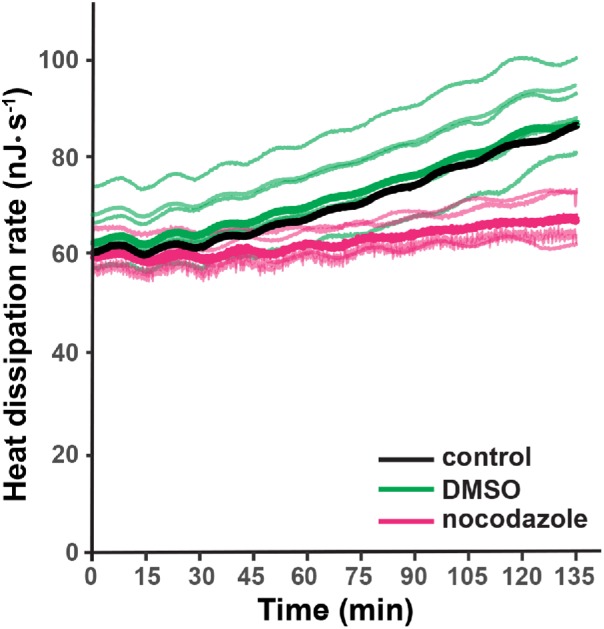
Nocodazole inhibits the increase in heat dissipation rate. Heat dissipation rates in which 10 μM nocodazole was added at the two-cell stage. The thin magenta lines show individual traces (n = 6), and the thick magenta line is the mean. The thin green lines are control traces in which the same DMSO-containing buffer but without nocodazole was added (n = 6), and the thick green line is the mean. The thick black line shows the mean trace from Figure 1B.
The increasing trend grows more slowly than the number of cells
The results of nocodazole treatment suggest that the increasing trend is related to the number of cells, N. Therefore, we considered a model in which the total heat dissipation, 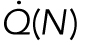 , has a term proportional to the number of cells:
, has a term proportional to the number of cells: 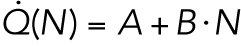 . Here A and B are constants, with A assumed to be proportional to the (constant) total cell volume. Because the number of cells doubles during every cell cycle and the cell cycle has a nearly constant period (T ≈ 17 min),
. Here A and B are constants, with A assumed to be proportional to the (constant) total cell volume. Because the number of cells doubles during every cell cycle and the cell cycle has a nearly constant period (T ≈ 17 min), 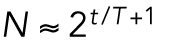 . At the start of the experiment, t = 0 and N = 2. Thus,
. At the start of the experiment, t = 0 and N = 2. Thus,
| 1 |
To test whether Eq. 1 is a good empirical description of the heat curves, we first fit the exponential equation
| 2 |
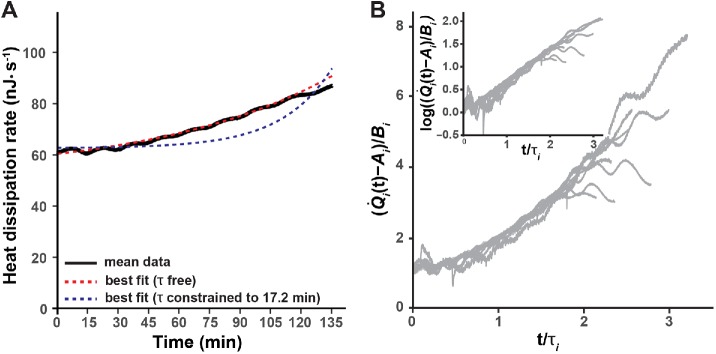
to the heat curves measured in each experiment. τ is a free parameter corresponding to the heat-doubling time (not necessarily equal to the cell doubling time T). A and B are free parameters. Comparison of the average fitted curve (using the average parameters from the individual fits) to the experimental traces at 28.5°C shows that Eq. 2 provides a good fit to the averaged data (Figure 3A). To determine how good the fit was for the individual experiments, we rescaled the data from the 10 traces (Qi(t), i = 1,…,10) by subtracting Ai, dividing by Bi, and plotting against time divided by τi (Figure 3B). The rescaled curves showed a “data collapse” (Bhattacharjee and Seno, 2001), indicating that the model in Eq. 2 provides a good fit to the individual traces. Next, we plotted the rescaled data on a semi–log plot to better visualize the form of the increasing trend (Figure 3B, inset). The curves were approximately linear, indicating that the individual traces are roughly exponential, though some traces stopped increasing during the last two cell divisions. Thus, Eq. 2 is a good empirical description of the increasing trend during the cleavage stage.
FIGURE 3:
The heat dissipation doubles approximately three times more slowly than the number of cells. (A) Least-squares fit of the heat dissipation curves to an exponential plus a constant, (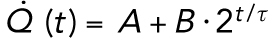 ). A, B, and τ are free parameters. The fits were done on the individual experimental curves (gray lines in Figure 1) and averaged (the red dotted line). The mean of the experimental heat dissipation curves is shown in black. The blue dotted curve is the least-squares fit with τ constrained to be equal to the average cell cycle time of 17.2 min with A and B free parameters. (B) The heat dissipation trajectories from 10 individual experiments (Qi (t), i = 1, …, 10) were rescaled by subtracting Ai and dividing by Bi plotted against time divided by τi. The superimposed curves illustrate the exponential rise, which is also apparent in the linear increase on a log-linear scale (inset).
). A, B, and τ are free parameters. The fits were done on the individual experimental curves (gray lines in Figure 1) and averaged (the red dotted line). The mean of the experimental heat dissipation curves is shown in black. The blue dotted curve is the least-squares fit with τ constrained to be equal to the average cell cycle time of 17.2 min with A and B free parameters. (B) The heat dissipation trajectories from 10 individual experiments (Qi (t), i = 1, …, 10) were rescaled by subtracting Ai and dividing by Bi plotted against time divided by τi. The superimposed curves illustrate the exponential rise, which is also apparent in the linear increase on a log-linear scale (inset).
The mean and SDs of A, B, and τ from the individual fits are compiled in Table 1 together with the mean and SD of the cell cycle period T. It is clear that, at 28.5°C, the doubling time of the increasing trend, τ = 60 ± 10 min (mean ± SD, n = 10), is three to four times longer than the average period of the cell cycle (T = 17.2 ± 0.8 min). In other words, the heat dissipation increased considerably more slowly than expected if the heat dissipation had a component proportional to the number of cells. This result is confirmed by the poor fit of the blue curve in Figure 3A to the data; this curve is the fit with τ constrained to the cell division time of 17.2 min. We therefore conclude that the data are not consistent with the increasing trend doubling every cell cycle.
TABLE 1:
Mean and SD of the model parameters.
| Mean ± SD | |||
|---|---|---|---|
| Parameter | 28.5°C | 23.5°C | 33.5°C |
| Volume term, A | 52 ± 12 nJ ⋅ s−1 | 47 ± 1.8 nJ ⋅ s−1 | 88.4 ± 22.4 nJ ⋅ s−1 |
| Area term, B | 8.2 ± 3.2 nJ ⋅ s−1 | 5.12 ± 2.9 nJ ⋅ s−1 | 4.22 ± 0.9 nJ ⋅ s−1 |
| Heat doubling time, τ | 60.4 ± 10.4 min | 74.3 ± 14.9 min | 68 min |
| Cell doubling time, T | 17.2 ± 0.8 min | 23.4 ± 1.4 min | 14.2 ± 0.8 min |
The increasing trend was also well fit by Eq. 2 at lower temperatures (Table 1 and Supplemental Figure 1A). At 23.5°C, the doubling time of the increasing trend, τ = 74 ± 15 min, was about three times longer than the average period of the cleavage divisions, T = 23 ± 2 min (Table 1). At 33.5°C, the doubling time of the increasing trend, τ = 68 min, was about five times longer than the average period of the cleavage divisions, T = 14.2 ± 0.8 min (Table 1), though the curves at 33.5°C were more variable from experiment to experiment: some curves showed decreasing heat dissipation at the end of cleavage stage (Figure 1D), raising the possibility that the health of the embryos may be compromised at high temperatures. Thus, at all temperatures, the increasing trend was much slower than expected if it were to scale with cell number.
The surface-area model
What process accounts for the increasing trend? One possibility is that the slower doubling time is due to the heat dissipation rate being proportional to the total cell surface area, which increases at a slower rate than the number of cells. To explore this possibility, we considered a simple model for the total surface area of the cells in the embryos. The model, schematically depicted in Figure 4, assumes that 1) the cells are the same size and are spherical; 2) the total volume of all cells is constant throughout cleavage stage (the initial volume is 60⋅106 μm3); and 3) the cell doubling time is constant throughout the cleavage stage. The parameters of the model are defined in Table 2.
FIGURE 4:
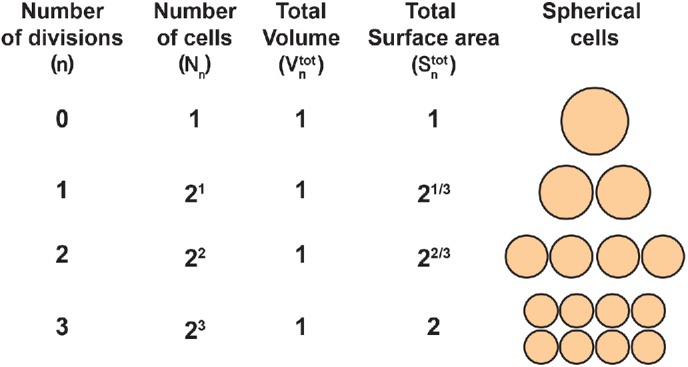
Surface-area model assuming spherical cells with constant total volume. As the number of divisions (n) increases, the number of cells (Nn), depicted as spheres on the right, increases exponentially. The total embryonic volume (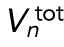 ) remains constant throughout cleavage stage, and the total surface area (
) remains constant throughout cleavage stage, and the total surface area (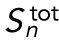 ) increases exponentially but three time slower than the number of cells. The model parameters and their initial values are defined in Table 2.
) increases exponentially but three time slower than the number of cells. The model parameters and their initial values are defined in Table 2.
TABLE 2:
Surface model parameters.
| Parameter | Meaning | Value |
|---|---|---|
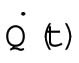 |
Heat dissipation rate | 60–85 nJ ⋅s−1 |
| t | Time from the beginning of cell 2 cleavage | 0–150 min |
| n = t/T + 1 | Number of divisions, T is the division period | 1–10 |
| Nn = 2n | Number of cells | 2–1024 |
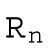 |
Cell radius after the nth division | R0 = 243 μm |
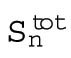 |
Total surface area after the nth division |
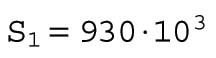 μm2 μm2
|
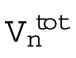 |
Total volume after the after the nth division |
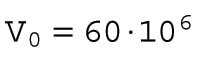 μm3 μm3
|
Summary of model parameters and their estimated range of values (for 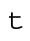 ,
, 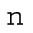 , and
, and 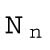 ) or their values at the initial state (for the rest of the parameters).
) or their values at the initial state (for the rest of the parameters).
When the number of divisions is n = 0, the number of cells is N0 =1, and the embryonic volume and surface area at the zeroth division and the one-cell stage are
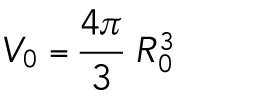 |
3 |
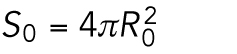 |
4 |
After n divisions, there are Nn = 2n cells, and each cell has a volume 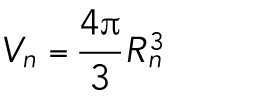 , with Rn the radius of a cell after n rounds of division. The total volume of all cells is then
, with Rn the radius of a cell after n rounds of division. The total volume of all cells is then
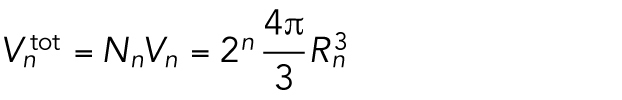 |
5 |
Because the total volume is constant throughout the developmental process, Vn = V0, the cell radius decreases with n divisions as
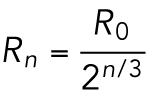 |
6 |
The cell radius halves every three divisions. The surface area of each cell decreases as 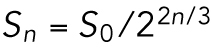 . It then follows that the total surface area,
. It then follows that the total surface area,  , increases as
, increases as
| 7 |
In other words, we have calculated that the total surface area of all the cells in the embryo is predicted to double after every third division. To write the area as a function of time, rather than the number of cell divisions, we proceed as in Eq. 1 and take n = t/T + 1, where T is the doubling time. Thus, in continuous time,
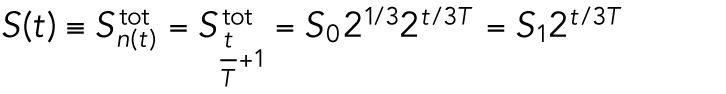 |
8 |
where S1 = 930 ⋅ 103 μm2 is the area at the two-cell stage, and we have defined S(t) as the continuous time total surface area. Note that
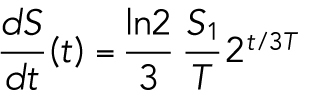 |
9 |
which shows that the change in total surface area dS/dt is also proportional to 2t/3T. Thus, the doubling time of the surface area and its change are the same.
This simple model shows that the total cell surface area, as well as the change in total cell surface area, doubles three times more slowly than the number of cells. Thus, our measured data showing that the embryonic heat dissipation doubles three times slower than the number of cells agree with the predictions of the cell surface model (Table 1).
There are number of caveats to the model assumptions. First, the cells are not spherical. At the two-cell stage, the two cells appear hemispherical and are open at their bases. Therefore, we may be overestimating the initial surface area at the two-cell stage. Second, cellularization is not complete until the 64-cell stage (Kane and Kimmel, 1993; Karlstrom and Kane, 1996), after which the constant volume assumption is well accepted. Before the 64-cell stage, we may be underestimating the cytoplasmic volume contributing to the embryo’s energetics. Third, the cell cycle time is not constant but slows down by ∼30% over the last three cell divisions. This will dilate the time axis toward the end of the cleavage stage (see the Supplemental Material and Supplemental Figure 2). Despite these caveats, we believe that our surface-area model captures at least qualitatively the changes in surface area that take place during the cleavage stage.
Estimated metabolic costs
To test the plausibility of the cell surface model, we asked whether the measured energetic costs are within the range of literature values. To make this comparison, we model the heat dissipation rate as
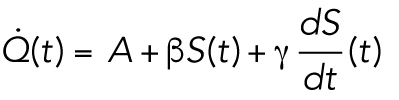 |
10 |
A is a constant that depends on the cell volume (nJ ⋅ s −1), β is the heat dissipation incurred in maintaining membrane per unit time (nJ ⋅ s −1 ⋅ μm−2), and γ is the heat dissipation incurred in building new membrane (nJ ⋅ μm−2). By comparing Eq. 10 to Eqs. 2 and 9, we can identify τ ≈ 3T, and
| 11 |
where S1 is the total surface area (μm2) at the two-cell stage (assuming spherical cells). We now estimate A and B.
The parameter A corresponds to the energetic cost of maintaining the fixed volume of cytoplasm in the early embryo and is measured to be 52 nJ ⋅ s−1 at 28.5°C and 47 nJ ⋅ s−1 at 23.5°C (Table 1). These values are similar to the basal maintenance cost estimated for prokaryotes and unicellular eukaryotes to equal 77 nJ ⋅ s−1 at 28.5°C and 60 nJ ⋅ s−1 at 23.5°C (correcting for volume [ Lynch and Marinov, 2015] and temperature using a Q10 of 1.65 for fish [ Makarieva et al., 2008]). These values are also within the range of 43 to 96 nJ ⋅ s−1 for the basal metabolic rates of the small fish Esomus danricus and Oryzias latipes at 25°C (Makarieva et al., 2008). Thus, the initial rate of heat dissipation, which is mainly determined by the parameter A in our model, is well accounted for by the typical energetic demands of cells.
The parameter B, with contributions from β and γ, corresponds to the energetic costs of maintaining and building plasma membrane. The maintenance costs (β) include the work done by ion pumps to maintain the membrane potential against leakage through ion channels and transporters, work done by flippases and floppases to maintain the asymmetry of the two leaflets of the bilayer, and work done by fission and fusion machinery such as the GTPase dynamin and the ATPase NSF associated with vesicular endocytosis and exocytosis. To estimate the total maintenance cost, we assume a total membrane protein density of 40 ×103 μm−2 (Quinn et al., 1984; Itzhak et al., 2016) and that 3% of plasma membrane proteins are ATPases with activities ranging from 10 to 100 s−1 (BionumbersID 104181; Milo et al., 2010). Membrane protein turnover is another maintenance cost, which we estimate assuming an average protein half-life of 42 h (Peshkin et al., 2015), protein degradation by lysosomes, and resynthesis by the ribosome. Assuming that the enthalpic change associated with ATP hydrolysis is 40 kJ ⋅ mol−1, the energy cost of maintaining the plasma membrane ATPase activity βATPase ranges from 0.8 to 8 fJ ⋅ s−1 μm−2, and the cost of plasma membrane protein turnover is much smaller, βturnover = 0.02 fJ ⋅ s−1 μm−2 (Table 3).
TABLE 3:
Estimated energetic parameters at 28.5°C.
| Parameter | Estimates | Values from fits | |
|---|---|---|---|
| Volume term, A | 80 nJ ⋅ s−1 | 52 ± 12 nJ ⋅ s−1 | |
Area term, 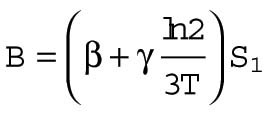 (i.e., area contribution at the two-cell stage) (i.e., area contribution at the two-cell stage) |
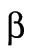 (maintenance) fJ⋅s−1⋅μm−2 (maintenance) fJ⋅s−1⋅μm−2
|
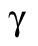 (building) (building) 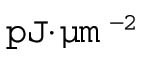
|
|
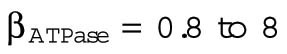 |
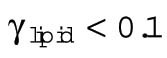 |
||
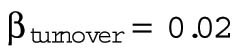 |
 |
||
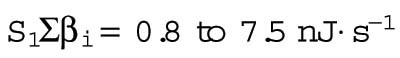 |
 |
||
| Total | 0.8 to 8.4 nJ⋅s−1 | 8.2 ± 3.2 nJ⋅s−1 | |
See text for calculations. Note that B has contributions from maintenance (β) and building (γ). The maintenance term can be decomposed into ATPase activity (βATPase) and protein turnover (βturnover), so that β = βATPase + βturnover. The building term can be decomposed into building of lipids ( ) and proteins
) and proteins ), so that
), so that 
 .
.
The building costs of new plasma membrane lipids (γ) may be close to zero if all the lipid and protein components are preassembled in the ER (or other stores) and all that is required is the cost of fusion with the plasma membrane. Indeed, the one-cell embryo has high levels of maternally loaded phospholipids, cholesterol, and cholesteryl-esters; de novo synthesis of membrane lipids is therefore probably absent during cleavage stage development in zebrafish (Fraher et al., 2016). Even if new phospholipids need to be assembled from diacyl chains derived from triglycerides in lipoprotein-like yolk granules (i.e., no synthesis of fatty acids) and pre-existing head groups, the cost will be quite modest. The removal of one fatty acid and the addition of the head group is estimated to utilize 2 CTPs (Lynch and Marinov, 2017), corresponding to 2 ATP-equivalents per lipid. The number of phospholipids and cholesterol molecules is calculated from the lipid area (0.65 nm2), assuming that 70% of the membrane is occupied by 60% phospholipid and 40% cholesterol. This results in a lipid production cost of 0.12 pJ ⋅ μm−2 (γlipid, Table 3). If proteins need to be assembled from existing amino acids, the production cost of membrane proteins will be around 4 pJ ⋅ μm−2, assuming a density of 40 × 103 μm−2, an average size of 400 amino acids, and 4 ATPs per amino acid (Lynch and Marinov, 2015) (γProtein, Table 3).
These calculations show that the maintenance costs are equal to or larger than the building costs (using Eq. 11 to convert γ into a cost per unit time; Table 2, bottom line). These costs are estimated to be 10% or more of the cost measured from fitting the heat-dissipation measurements to the surface-area model (B = 8.2 nJ ⋅ s−1 at the two-cell stage, Table 3). Therefore, the idea that the increasing trend is due to the cost of new plasma membrane is plausible. Another way of looking at the increasing trend, is to note that, over nine cell divisions, the surface area increases roughly eightfold (= 29/3) and the membrane-associated costs increase from about 8 nJ ⋅ s−1 to 60 nJ ⋅ s−1. If we are correctly attributing the increasing trend to membrane metabolic costs, then these costs will correspond to roughly 50% of total heat dissipation at the 1K stage. Such a contribution from the plasma membrane is not unreasonable, because just the sodium-potassium ATPases are thought to contribute up to 50% of the total metabolic output of a cell (Whittam and Willis, 1963; Swaminathan et al., 1989; Milo et al., 2010). Thus, it appears reasonable that the membrane has significant metabolic cost during early development.
In this work, we have investigated the overall energetics of cell proliferation during early development when there is no overall growth of the embryo. Our experimental measurements in the early zebrafish embryo show that the rate of heat dissipation increases from an initial value of ∼60 nJ · s−1 at the two-cell stage to ∼90 nJ · s−1 (at 28.5°C) at completion of the 10th division. A similar increase is observed during the cleavage stage of Xenopus laevis (Nagano and Ode, 2014). This suggests a conserved energetic cost of proliferation in early embryos, leading us to consider several hypotheses for the source of this cost. Because the volume of the embryo is constant, we ruled out growth. Instead, experimental and computational approaches were used to evaluate the potential contributions of DNA replication, mitosis, the production of new plasma membranes, or any other process. On the basis of our findings, we argue that the energetic cost is likely due to the increase in the total surface area of all of the cells of the embryo and the maintenance costs associated with the plasma membrane. We discuss the key experiments driving our conclusions here.
Two findings implicate cell proliferation in the increasing trend. First, the heat increase is greatly reduced by nocodazole, which blocks proliferation. This drug inhibits microtubule polymerization and thus prevents mitosis, cell division, and DNA replication but does not kill the embryo. A caveat of the nocodazole treatment is that we cannot exclude the possibility that nocodazole has indirect effects on another cytoplasmic process(es) besides DNA replication, mitosis, and cell division. In agreement with our interpretation, however, speeding up proliferation by changing the cell cycle frequency with higher temperature speeds up the increasing trend. This correlation, together with the nocodazole result, indicates that the increasing trend is closely associated with cell proliferation.
Though the increasing trend is associated with cell proliferation, the increase is slower than expected if it were proportional to the number of cells and nuclei. The heat increases exponentially (with an added constant) with a doubling time that is three times longer than the doubling time of the cells. The slow doubling time is inconsistent with increased cost due to increasing DNA, chromatin, nuclear volume, and nuclear area (Gerhart, 1980; Keller et al., 2008). Instead, a doubling time three times longer than the cell doubling time is expected if the heat increase scales with total cell surface area, which increases more slowly than the number of cells.
Estimates of the energetic costs associated with plasma membrane are consistent with changing cellular surface area driving the increasing trend. Based on literature values of energy dissipation by plasma membrane ATPases and the assembly costs of lipids and membrane proteins (from premade lipid and amino acid components), the maintenance and addition of plasma membrane surface area may account for 10% or more of our measured energetic increase. If either the membrane ATPase activity is higher and/or some de novo synthesis is required for phospholipids, cholesterol, and proteins, then up to 100% of the measured increase might be accounted for. It is therefore reasonable to propose that the costs of maintaining and/or assembling plasma membranes and associated proteins accounts for a significant proportion of the heat increase. A potential caveat is that we assume no increase in embryo volume, yet small volumetric increases that contribute to the increasing trend cannot be ruled out. This issue notwithstanding, we expect our findings to be generalizable to other species and proliferative processes because of the basic requirement for plasma membranes. Future experimental work is needed to dissect the costs of de novo biosynthesis of precursors and the assembly and maintenance of plasma membranes.
MATERIALS AND METHODS
Zebrafish husbandry and staging
Adult zebrafish were maintained and bred under standard conditions. Wild-type (AB) embryos were left to develop in E3 medium (5 mM NaCl, 0.17 mM KCl, 0.33 mM CaCl2, 0.33 mM MgSO4) to the desired stage. The temperature was 28.5°C unless otherwise indicated. Pairs of fish were paired for a maximum of 10 min, after which eggs were collected and allowed to develop for 30 min at 28.5°C. Staging was done based on morphology. Thirty embryos were selected such that their first cleavage furrows initiated within 3 min of each other. In this way, the population of embryos was synchronized at the two-cell stage.
ITC
Calorimetry experiments were carried out using a Malvern MicroCal VP-ITC (Malvern Instruments, Worcestershire, UK). The temperature in the instrument was set to desired temperatures of 22.5°C, 28.5°C, and 33.5 °C. The reference power (μcal s−1) was set to 11.5, the initial injection delay after calibration was set at 240 s, the feedback mode/gain was set to high, and the ITC equilibration options were set to “fast equilibration & auto.” The injection syringe parameters were set as follows: injection volume, 2 μl; duration, 2 s; spacing, 14,400 s (240 min); number of injections, 3. The ITC experiments were performed without the injection syringe and stirring, and the ITC chambers were covered with a plastic lid. The sample cell was filled with either 1.57 ml of E3 medium or E3 medium with the desired concentration of chemical inhibitors. The reference cell was filled with water.
Data analysis and curve fitting
Data analysis was performed in R (v. 3.5.3) using RStudio (v. 1.2.1335) with the additional libraries ggplot2, tidyr, stats, and dplyr. Each experiment, corresponding to a biological replicate, is an ITC measurement of a group of 30 staged zebrafish embryos; n represents the number of experiments. Statistical parameters including the exact value of n are reported in the text or figure/table legends Curve fitting was performed by nonlinear least-squares fits of Eq. 2 to single heat-dissipation trajectories (groups of 30 embryos) using the nls() function in R.
Supplementary Material
Acknowledgments
The analysis of these data was initiated in the 2019 Physical Biology of the Cell course at the Marine Biological Laboratory in Woods Hole, MA. We acknowledge the support and feedback from the course directors and participants. This work was supported by funding from EMBO Long-Term Fellowship ALTF 754–2015 (to J.R.), the Eric and Wendy Schmidt Membership in Biology at the Institute for Advanced Study (to P.S.), National Institutes of Health (NIH) R21 HD094013 (to K.M.N.), and NIH R01 GM110386 (to J.H.). Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the NIH.
Abbreviations used:
- DMSO
dimethyl sulfoxide
- ITC
isothermal calorimetry.
Footnotes
This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E19-09-0529) on February 12, 2020.
REFERENCES
- Bhattacharjee SM, Seno F. (2001). A measure of data collapse for scaling. J Phys A Math Gen , 6375. [Google Scholar]
- Fraher D, Sanigorski A, Mellett NA, Meikle PJ, Sinclair AJ, Gibert Y. (2016). Zebrafish embryonic lipidomic analysis reveals that the yolk cell is metabolically active in processing lipid. Cell Rep , 1317–1329. [DOI] [PubMed] [Google Scholar]
- Gerhart J. (1980). Mechanisms regulating pattern formation in the amphibian egg and early embryo. In: Biological Regulation and Development, vol. 2, ed. Goldberger RE, New York: Plenum. [Google Scholar]
- Ikegami R, Hunter P, Yager ID. (1997). Activation of the metaphase checkpoint and an apoptosis programme in the early zebrafish embryo, by treatment with the spindle-destabilising agent nocodazole. Zygote , 329–350. [DOI] [PubMed] [Google Scholar]
- Itzhak DN, Tyanova S, Cox J, Borner GHH. (2016). Global, quantitative and dynamic mapping of protein subcellular localization. eLife , e16950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kane DA, Kimmel CB. (1993). The zebrafish midblastula transition. Development , 447–456. [DOI] [PubMed] [Google Scholar]
- Karlstrom RO, Kane DA. (1996). A flipbook of zebrafish embryogenesis. Development , 461. [DOI] [PubMed] [Google Scholar]
- Keller PJ, Schmidt AD, Wittbrodt J, Steltzer EHK. (2008). Reconstruction of zebrafish early embryonic development by scanned light sheet microscopy. Science , 1065–1069. [DOI] [PubMed] [Google Scholar]
- Kimmel CB, Bollard WW, Kimmel SR, Ullmann B, Schilling TF. (1995). Stages of embryonic development of the zebrafish. Dev Dyn , 253–310. [DOI] [PubMed] [Google Scholar]
- Lynch M, Marinov GK. (2015). The bioenergetic costs of a gene. Proc Natl Acad Sci USA , 15690–15695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M, Marinov GK. (2017). Membranes, energetics, and evolution across the prokaryotic-eukaryotic divide. eLife , e20437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makarieva AM, Gorshkov VG, Li B-L, Chown SL, Reich PB, Gavrilov VM. (2008). Mean mass-specific metabolic rates are strikingly similar across life’s major domains: evidence for life’s metabolic optimum. Proc Natl Acad Sci USA , 16994–16999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milo R, Jorgensen P, Moran U, Weber G, Springer M. (2010). BioNumbers—the database of key numbers in molecular and cell biology. Nucleic Acids Res (Database issue), D750–D753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagano Y, Ode KL. (2014). Temperature-independent energy expenditure in early development of the African clawed frog Xenopus laevis. Phys Biol , 046008–046013. [DOI] [PubMed] [Google Scholar]
- Peshkin L, Wühr M, Pearl E, Haas W, Freeman RM, Gerhart JC, Klein AM, Horb M, Gyge SP, Kirschner MW. (2015). On the relationship of protein and mRNA dynamics in vertebrate embryonic development. Dev Cell , 383–394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quinn P, Griffiths G, Warren G. (1984). Density of newly synthesized plasma membrane proteins in intracellular membranes II. Biochemical studies. J Cell Biol , 2142–2147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodenfels J, Neugebauer KM, Howard J. (2019). Heat oscillations driven by the embryonic cell cycle reveal the energetic costs of signaling. Dev Cell , 646–658.e6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song Y, Park JO, Tanner L, Nagano Y, Rabinowitz JD, Shvartsman SY. (2019). Energy budget of Drosophila embryogenesis. Curr Biol , R566–R567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swaminathan R, Chan ELP, Sin LY, King NGS, Fun NGS, Chan AYS. (1989). The effect of ouabain on metabolic rate in guinea-pigs: estimation of energy cost of sodium pump activity. Br J Nutr, , 467–473. [DOI] [PubMed] [Google Scholar]
- Tadros W, Lipshitz HD. (2009). The maternal-to-zygotic transition: a play in two acts. Development , 3033–3042. [DOI] [PubMed] [Google Scholar]
- Whittam R, Willis JS. (1963). Ion movements and oxygen consumption in kidney cortex slices. J Physiol , 158–177. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.