How to Benchmark RNA Secondary Structure Prediction Accuracy

Abstract

RNA secondary structure prediction is widely used. As new methods are developed, these are often benchmarked for accuracy against existing methods. This review discusses good practices for performing these benchmarks, including the choice of benchmarking structures, metrics to quantify accuracy, the importance of allowing flexibility for pairs in the accepted structure, and the importance of statistical testing for significance.

1. Introduction

RNA sequences serve a variety of roles in Biology. It was appreciated early that RNA has core roles in the expression of proteins as outlined in the Central Dogma of Molecular Biology [1]. These roles include coding of genetic information, as served by messenger RNA, and noncoding roles, served by ribosomal RNA and transfer RNA. Since the discovery of these roles, we came to appreciate that RNA sequences serve a variety of non-coding roles [2], including catalysis [3], site-recognition [4, 5], and gene expression regulation [6–8].

RNA structure is hierarchical, from primary, to secondary, to tertiary, and to quaternary structure [9]. The primary structure is the covalent structure, i.e. the sequence of nucleotides. The secondary structure is the set of canonical base pairs, including A-U, G-C, and G-U pairs. These base pairs are organized in A-form helices, which flank nucleotides that are said to be in loops. The tertiary structure is the three-dimensional positions of the atoms in space, which demonstrate the additional intramolecular contacts beyond canonical base pairing. These contacts include non-canonical base pairs, stacks, and base-backbone interactions. The quaternary structure is the interactions with other RNA, macromolecules, or small molecules.

The secondary structure of RNA provides important information about the function of a sequence. It can characterize a family of RNA sequences that are homologous [10, 11]. It also provides a framework for understanding the mechanism by which an RNA sequence functions. Additionally, the secondary structure is informative for designing constructs for tertiary structure determination by NMR, x-ray crystallography, or cryogenic electron microscopy.

RNA secondary structure prediction is widely used. It is popular to predict secondary structure using a dynamic programming algorithm to find the lowest free energy structure, where nearest neighbor parameters are used to estimate folding stability [12–15]. Dynamic programming algorithms have also been developed to characterize the thermodynamic ensemble of structures, including estimating the probability of base pairs and sampling structures from the ensemble [16]. Alternative structure scoring methods have been developed using parameters learned from the database of RNA sequences with known structures [17–19]. It has been demonstrated that the thermodynamic methods and the scoring schemes are rooted in the same principles [17, 20].

The accuracy of RNA secondary structure prediction is improved by the use of additional information to inform the modeling. Structure probing data can guide structure prediction [21, 22]. Multiple homologous sequences can be used to predict a conserved structure [15, 23, 24]. It has also been shown that these two sources of information can be synergistic [25, 26]. In particular, developing improved methods for secondary structure prediction that use additional information is a field of active research.

The definition of secondary structure has also been broadened to include “extended” secondary structures. The extended secondary structure includes both canonical and non-canonical base pairs. Although non-canonical pairs are traditionally considered tertiary structure, recent advances have made it possible to predict non-canonical base pairs. First, a clear nomenclature was developed by Leontis and Westhof to describe these pairs [27, 28]. Next, software tools were developed to automate the identification of non-canonical pairs from atomic coordinates of structures [29, 30]. Finally, scoring functions and algorithms were developed to predict extended secondary structures from sequence [31–34].

This review discusses methods and good practices for benchmarking the accuracy of RNA secondary structure prediction. As new RNA secondary structure prediction methods are developed, they are typically benchmarked against existing methods by predicting structures for a set of sequences with accepted structures and then comparing the predictions to the accepted structures. This can highlight the strengths and weaknesses of the new method, informing potential users and providing direction for additional method development.

2. Choosing structures for benchmarks.

An informative benchmark requires a variety of high-quality structures. To have a sufficient number of tests, the structures are generally drawn from a set of structures determined by comparative sequence analysis, which infers a conserved structure using a large set of homologs [35, 36]. RNA sequences drift across evolution, but the secondary structure is more highly conserved because structure dictates function. This results in the phenomenon of compensating base pair changes, by which a base pair is conserved by two changes in sequence, such as an A-U base pair observed in one species that is replaced by a G-C pair observed in the sequence homolog in the second species. Although some differences can be observed between comparative analysis structure predictions and subsequently solved crystal structures, the accuracy of comparative analysis can be quite excellent. For example, over 97% of base pairs modeled for rRNA structures were observed in subsequent crystal structures [37].

For our benchmarks, we use structures from RNA families that were determined by comparative analysis where the structures have been carefully studied by specific investigators and refined over time using a wide phylogeny of sequences. We currently use secondary structures from the 5S ribosomal RNA (rRNA), group I intron, group II intron, large subunit rRNA, RNase P RNA, signal recognition particle RNA (SRP RNA), small subunit rRNA, tRNA, tmRNA, and telomerase RNA families. We largely stayed away from using structures drawn from the Rfam database [11]. The Rfam database is an excellent resource, but the secondary structure models were deposited by the community and therefore the structures vary in quality as compared to structures that were refined as the specific focus of an investigator or group. A recent study [38], for example, noted that the Rfam-curated 5S rRNA structure contains errors as compared to the consensus structure from the 5S database [39].

In our benchmark dataset, the 5S rRNA structures are drawn from the 5S rRNA database maintained by Maciej Szymanski at Adam Mickiewicz University [39]. Group I introns, small subunit rRNA, and large subunit rRNA structures are studied by Robin Gutell and his lab. They are available from the Comparative RNA Web Site from the University of Texas at Austin [40]. The group II introns were studied and assembled by Francois Michel and published in a review [41]. RNase P RNA are studied by James Brown and his lab. They provide structures at the RNase P Database from North Carolina State University [42]. The SRP RNA and tmRNA structures were assembled and maintained by Christian Zwieb [43]. The databases are provided by a consortium of investigators and hosted at the Center for noncoding RNA in Technology and Health (RTH) at the University of Copenhagen (https://rth.dk/resources/rnp/SRPDB/SRPDB.html; https://rth.dk/resources/rnp/tmRDB/). The tRNA database was assembled by Mathias Sprinzl and coworkers, and is now hosted at the University of Leipzig as a collaboration between the Universities at Leipzig, Marburg, and Strasbourg [44]. The telomerase RNA structures were assembled and studied by Julian Chen and his group at Arizona State University. They provide a database of structures that are available as images [45], but we found it convenient to retrieve machine-readable files with the same information from the Rfam database [11]. The collection of benchmarking structures we collected, called archive II, is available for download from our lab website at https://rna.urmc.rochester.edu/publications.html [46].

Benchmarks can also use secondary structures derived from solved tertiary structures. When testing the accuracy of prediction for extended secondary structures that include non-canonical base pairs, the use of these data is important because comparative analysis generally does not identify non-canonical base pairs. The RNA Strand database (http://www.rnasoft.ca/strand/) provides a combination of secondary structures determined by comparative sequence analysis and secondary structures extracted from tertiary structures [47]. The CompaRNA online benchmark uses the RNA Strand database and an additional database of structures that were extracted from tertiary structures. The tertiary structures for both these databases were derived from the protein databank [48] and the secondary structures determined using the RNAView program [29], which identifies base pairs from 3D coordinates.

3. Characterizing Accuracy.

Benchmarks of secondary structure prediction focus on the accuracy of predicted base pairs as compared to a known structure. This is a binary classification, in that a pair is either predicted or not and a pair is known to occur or not. It is therefore helpful to clarify the successes and failures of the prediction using a confusion matrix (Fig. 1). Pairs that are predicted and are also in the accepted structure are termed true positives. However, pairs that are predicted that are not in the accepted structure are termed false positives. Likewise, a pair in the accepted structure that is not predicted is a false negative, and a pair that is neither predicted nor in the accepted structure is a true negative.

Figure 1.

The confusion matrix for binary classification. Base pairs that are in the accepted structure and are predicted are true positives. Base pairs that are not in the accepted structure and also not in the prediction are true negatives. Base pairs that are in the accepted structure, but not predicted, are false negatives. Base pairs that are not in the accepted structure, but are predicted, are false positives. The true positives and true negatives are therefore correct predictions (labeled in green). The false negatives and false positives are incorrect predictions (labeled in red).

It is clear that a prediction that contains only true positives and true negatives is a perfect prediction. To quantify the accuracy, we use terms from epidemiology. The sensitivity, also known as recall, is the fraction of pairs in the accepted structure that are predicted:

$$\mathit{\text{sensitivity}}=\frac{\mathit{\text{true positives}}}{\mathit{\text{true positives}}+\mathit{\text{false negatives}}}$$ (eq. 1)

The positive predictive value (PPV), also known as precision, is the fraction of predicted pairs that are in the accepted the structure:

$$PPV=\frac{\mathit{\text{true positives}}}{\mathit{\text{true positives}}+\mathit{\text{false positives}}}$$ (eq. 2)

The sensitivity is therefore reduced from 1 (100%) when pairs in the known structure are missed by the prediction (false negatives) and the PPV is reduced from 1 (100%) when there are incorrectly predicted pairs (false positives). Both are needed to fully characterize the successes and failures of structure prediction. To summarize the sensitivity and PPV, the F₁ score, the harmonic mean of sensitivity and PPV, can be calculated:

$$F_1=\frac{2\times \mathit{\text{sensitivity}}\times PPV}{\mathit{\text{sensitivity}}+PPV}=\frac{2\times \mathit{\text{true positives}}}{2\times \mathit{\text{true positives}}+\mathit{\text{false positives}}+\mathit{\text{false negatives}}}$$ (eq. 3)

The harmonic mean has the property of being conservative (i.e. pessimistic about the accuracy) as compared to the arithmetic mean. This is because, if either sensitivity or PPV is substantially lower than the other, the harmonic mean tends towards the lower value. Alternatively, the geometric mean can also be used to summarize the overall prediction quality, and geometric mean is also conservative as compared to the arithmetic mean.

Another metric from epidemiology is specificity, but that is uninformative for RNA secondary structure prediction. Specificity is the fraction of pairs not in the accepted structure that are also not predicted:

$$\mathit{\text{specificity}}=\frac{\mathit{\text{true negatives}}}{\mathit{\text{true negatives}}+\mathit{\text{false positives}}}$$ (eq. 4)

The number of true negatives, however, is quite large compared to the false positives because the number of possible pairs for a sequence tends to increase with the square of the length, but the number of predicted pairs can only increase linearly with length (a nucleotide can be in only one pair in a valid structure). Therefore, especially for long sequences, specificity will be close to 1.

The PPV for free energy minimization has been observed to be lower on average than sensitivity [18, 49, 50]. This is in part because accepted structures can be missing pairs that are experimentally known to occur. A good example of this is the fact that the Sprinzl database of tRNA structures does not annotate base pairs in the variable loop region of leucine, serine, and tyrosine tRNAs, for which some sequences have fifth arms in their cloverleaf structures [51]. A correct prediction of one of these pairs would lower the PPV. The other reason for lower PPV, and the larger contributor, is that free energy minimization tends to overestimate the number of canonical base pairs because the canonical pairs lower the folding free energy change [52].

When reporting a mean sensitivity, PPV, and F₁ score, we prefer to report the mean taken across the families, where each family contributes equally to the mean. This is important because the total number of base pairs and sequences in each family varies. The mean across families is an estimate of the accuracy that would be observed for a new RNA family on which the benchmarked program might be used.

The small and large subunit rRNA families contain sequences that are longer than the other families. RNA secondary structure prediction is a harder problem for longer sequences because the number of possible structures increases exponentially with sequence length [53]. Historically, when benchmarking single sequence secondary structure prediction accuracy, we divided these long families into folding domains based on the known structure to provide average structure prediction accuracy for sequences shorter than 800 nucleotides [54–57]. We also provided the accuracy for the full-length sequences, but did not include that accuracy in the mean across families. It is important that a benchmark clearly report details, such as this, so that users are well informed about the accuracy they might have on their sequences.

4. Accounting for Conformational Dynamics.

RNA structures are intrinsically dynamic, and this is important for function [58–61]. The dynamics are most pronounced for non-canonical pairs, i.e. the loop regions of secondary structures [62, 63]. Secondary structure, however, is also dynamic. For example, it is well-established using NMR that terminal base pairs in nucleic acid helices are subject to opening, called fraying [64–67].

When assessing base pair prediction accuracy, it is important to account for conformational dynamics. We do this by considering a predicted pair to be consistent with a known pair even if it is displaced by up to one nucleotide on one side [54]. In other words, for base pair (i)-(j) in the accepted structure between nucleotides i and j, the following predicted base pairs would also be considered correct: (i+1)-(j), (i−1)-(j), (i)-(j+1), and (i)-(j−1).

There is considerable evidence supporting that base pairs sample multiple structures. First, measurements of folding free energy change at 37 °C for single-nucleotide bulges adjacent to one or more paired nucleotides of the same identity are consistent with the bulge migrating across multiple positions [55, 68]. The stability of these loops is similar to other single-nucleotide bulges when an entropic stability bonus is applied that reflects the multiple states available at equilibrium (Fig. 2).

Figure 2.

The comparison of folding free energy for two duplexes with a single U bulge. The top duplex has a single state. The second duplex has two states because the bulged U can migrate between two positions. The bulged U is assumed to not interrupt the helix, and therefore the two states in the second duplex have identical base pair stacks. In free energy, the entropic bonus for populating multiple states is [55, 69]:

$$\Delta {\text{G}}^{\circ }{}_{\text{bonus}}=-\text{RT ln}\left(\text{number of states}\right).$$

For the lower duplex, the number of states populated by the bulge is 2, and the bonus is estimated as:

$$\Delta {\text{G}}^{\circ }{}_{\text{bonus}}=-\left(1.9859{\text{ cal K}}^{-1}{\text{ mol}}^{-1}\right)\left(310.15\text{ K}\right)\text{ ln}\left(2\right)=-0.43\text{ kcal}/\text{mol},$$

which is consistent with the observed difference of stability of −0.84 ± 0.64 kcal/mol [68, 97]. The average stability of all measured single nucleotide bulges in one state is 3.7 ± 0.2 kcal/mol at 37 °C [68, 98–103]. The average stability of all measured single nucleotide bulges in two states, excluding C bulges that are known to have additional stability [55], is 2.0 ± 0.1 kcal/mol. Although this neglects sequence-specific affects, the average additional stability for a single nucleotide bulge that populates two states is therefore −1.7 ± 0.2 kcal/mol.

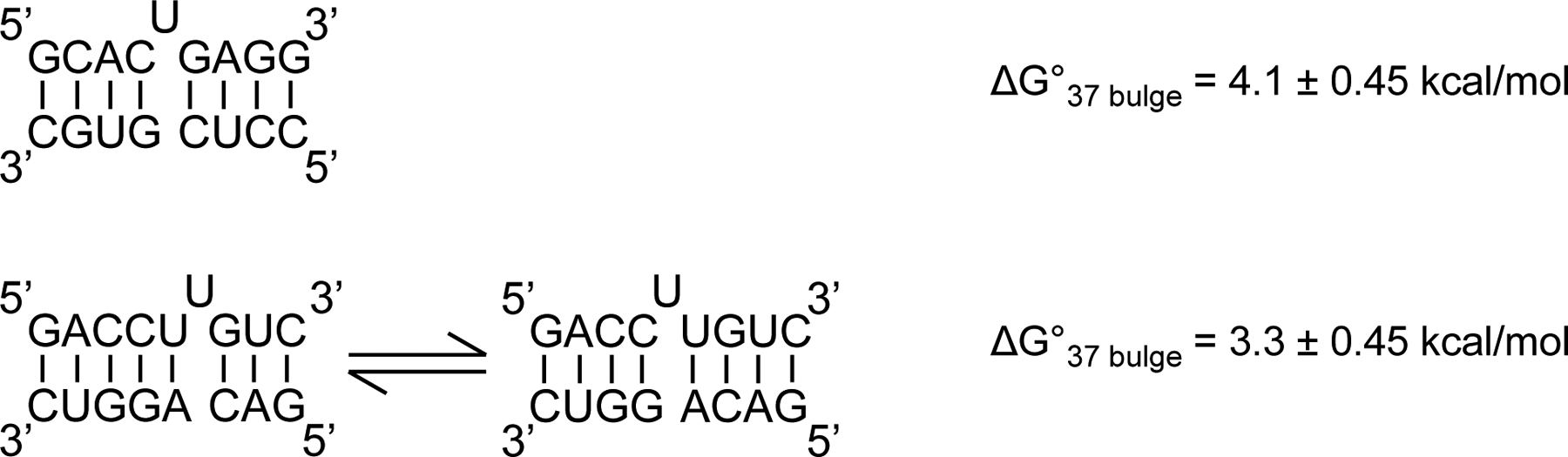
Fluctuating pairs are also observed by NMR. Woodson & Crothers observed that the bulged C nucleotide in the DNA helix 5’GATGGGCAG3’−5’CTGccccATC3’) fluctuated across the four possible positions on the NMR timescale [69]. Dethoff et al. observed a minor conformation for the HIV-1 RNA stem-loop 1 that exchanges with the major conformation on the NMR timescale. The major and minor conformations differ by two canonical base pairs (Fig. 3), and the minor conformation is approximately 1/10 as populated as the major conformation.

Figure 3.

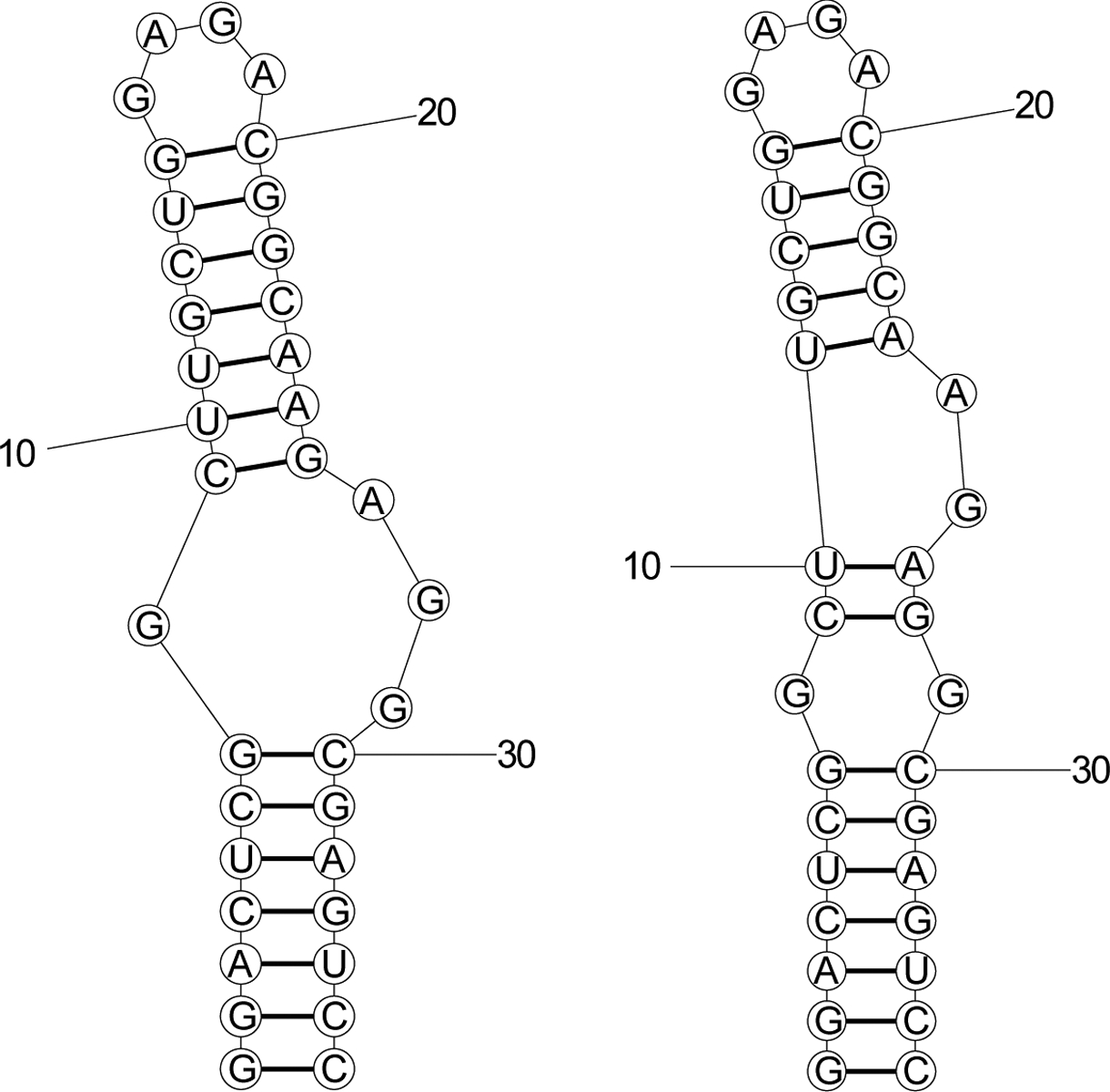
The two NMR-observed conformations for the HIV-1 stem-loop 1 [104]. The left is the major conformation and the right is the minor conformation. Interestingly, RNAstructure predicts the left structure as the lowest free energy structure and the right structure as the maximum expected accuracy (MEA) structure [56, 78, 105]. In this case, the fluctuating pairs are displaced by two nucleotides on one side (i.e. pairs from nucleotides 9 and 10 to nucleotides 25 and 26 switch to pairs to nucleotides 27 and 28).

Given that base pairs can fluctuate, a secondary structure model from either structure prediction or comparative sequence analysis should be considered as a representation of these alternative states, not as a rigid structure. Likewise, crystal structures can also be considered as one model of possible multiple states. Careful analyses of ribosome crystal structures reveal the flexibility (especially in non-canonical base pairs) across the conformational states that occur as part of ribosome function [70–74].

The Gutell lab provides high quality models of rRNA secondary structures [40] based on the comparison of over 7,000 small subunit and 1,000 large subunit rRNA sequences [37]. When the T. thermophilus small subunit [75] and H. marismortui large subunit [76] ribosome crystal structures became available, Gutell et al. analyzed and reported discrepancies between their secondary structure models and the crystal structures [37]. As expected, their models were excellent, and, as noted above, the models had 97% PPV against the crystal structures. Interestingly, using the information they provided, there are two cases in the 16S rRNA and three cases in the 23S rRNA where one side of a canonical base pair was displaced by one nucleotide in the comparative analysis model as compared to the crystal structure. The number of these types of discrepancies increases to 19 when non-canonical base pairs are also considered. These discrepancies between the models and the crystal structures are likely inconsequential because they might simply reflect situations where a structure is flexible as noted above. The prevalence of these discrepancies for high quality comparative analysis models also supports our choice to allow the one-nucleotide displacement when we score predicted structures against comparative models.

When we calculated the accuracy both allowing displacement and also requiring an exact match, we find the two scores generally differ by approximately 2%. For example, in a recent benchmark we reported sensitivity and PPV for Dynalign II, an algorithm that predicts the lowest free energy structure conserved for two sequences, and Fold, an algorithm that predicts the lowest free energy structure using a single sequence [77]. For 5S rRNA, the sensitivity was 91.8% and 73.1% for Dynalign II and Fold, respectively, when allowing the single-nucleotide displacement. The sensitivity was 90.6% and 70.9% for Dynalign II and Fold, respectively, when an exact match was required. PPV was also similar with the two scoring methods for 5S rRNA. It was 83.3% and 63.5% with single-nucleotide displacement allowed and 79.7% and 61.4% for exact match for Dynalign II and Fold, respectively.

5. The scorer program in RNAstructure.

The program scorer is available as a component of the RNAstructure package to compare a predicted secondary structure against an established structure [78]. It takes a connection table (ct) file of the predicted structure, which can contain multiple predicted structures, and a ct file of the known structure. It reports the sensitivity and PPV, along with the number of true positives, the number of predicted pairs, and the number of pairs in the known structure. By default, scorer allows pairs to be displaced by one nucleotide position on either the 5’ or the 3’ side of the pair. For comparison, this behavior can be changed to require exact match between predicted and accepted pairs.

A helpful adjunct to scorer is CircleCompare, which produces a postscript illustration of the predicted pairs and the accepted pairs (Fig. 4). The illustration shows the sequence in a circle and pairs as chords of the circle. The color of pairs provides information about whether pairs are predicted and/or in the accepted structure. Green pairs are those that are predicted and in the accepted structure. Black pairs are present in the accepted structure and not in the predicted structure. Red pairs are those in the predicted structure and not in the accepted structure. CircleCompare also reports the sensitivity and PPV for the prediction.

Figure 4.

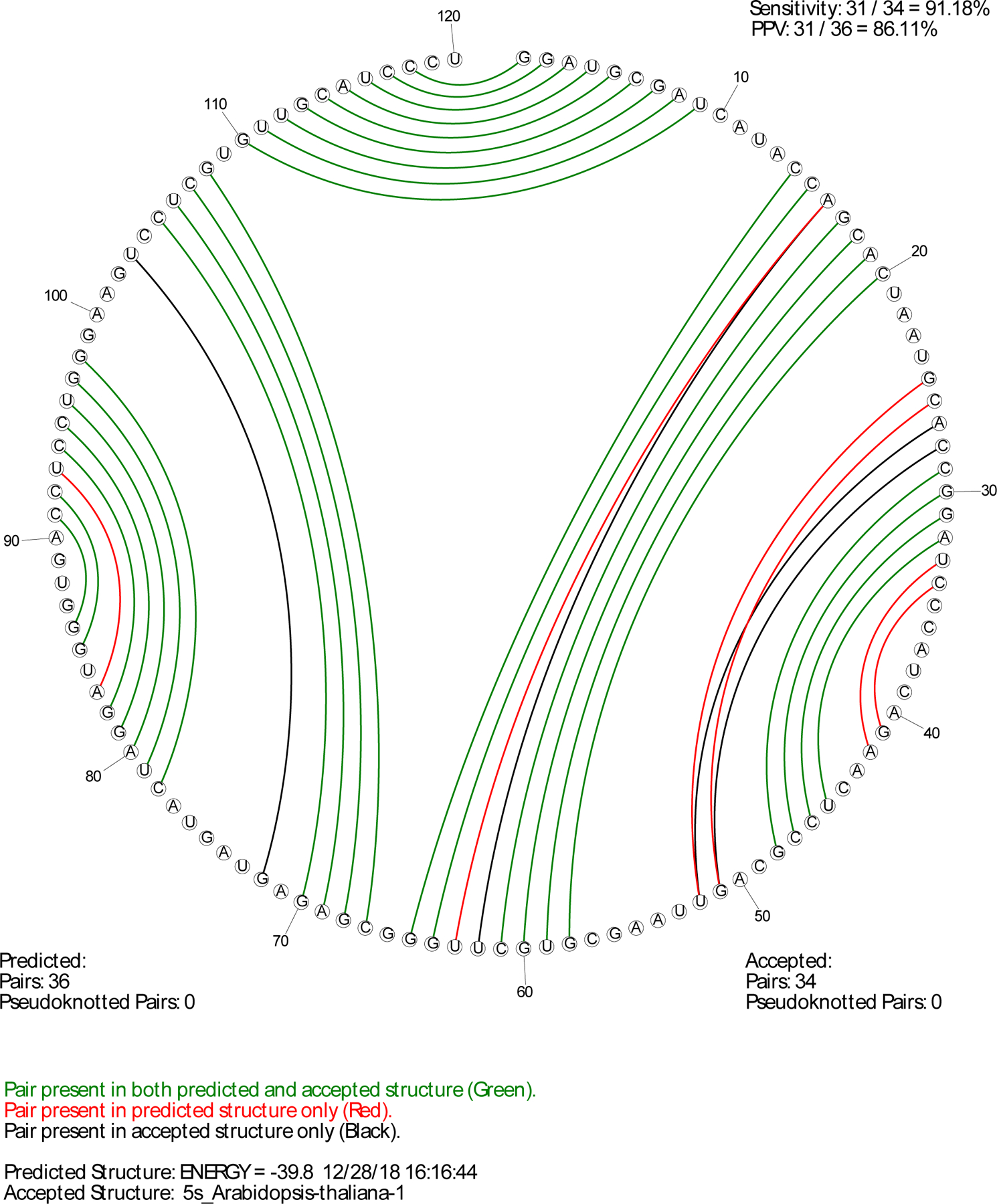
Example output for CircleCompare. Here, the predicted lowest free energy structure [78] for the Arabidopsis thaliana 5S rRNA is compared against the accepted structure [39]. The sensitivity of the prediction is 91% and the PPV is 86%. A key in the lower left explains the color code for the pairs.

6. Statistical testing.

In addition to comparing mean performance in benchmarks, it is also essential to determine whether differences in performance are statistically significant. For example, we reported a small improvement in PPV when using maximum expected accuracy (MEA) structure prediction to assemble structures with pairs of high equilibrium pairing probability as compared to free energy minimization [56]. This followed previous work that developed MEA using parameters learned from known structures [18, 79]. This small improvement was found subsequently to not be statistically significant on the RNA Strand dataset using a bootstrap to assess significance [80]. Therefore, although MEA provides an ability to tune predictions to higher sensitivity or higher PPV (at the cost of the other) and MEA provides helpful alternative hypotheses for the predicted structure, it is not reliably more accurate than free energy minimization.

For statistical testing, we use paired t-tests, which assess whether the mean difference in performance (either sensitivity or PPV) of two methods is significantly different than zero [81]. It uses the natural pairing of predictions made with two methods on the same sequence to compare the differences in performance. We also discussed ways to add structures to a benchmark set to test for significance if an initial set of structures does not have enough power to establish that a difference in performance is significant [81].

A second assessment for an improvement in one prediction method over another is whether the improvement is substantial. Generally, we believe that any statistically significant improvement is substantial because secondary structure prediction is well used. Additionally, it can be helpful to assess whether an improvement is substantial by assessing the improvement on individual calculations rather than just the mean improvement. For example, we examined the accuracy performance for each sequence individually in a benchmark testing whether TurboFold [82], which predicts conserved structures using a set of homologous sequences, is improved with the addition of SHAPE mapping data, which reveals nucleotides that are unpaired [25]. We plotted the F₁ score of structure prediction including SHAPE mapping data [83] as a function of F₁ score without using SHAPE. For some families, such as tRNA [44] and group I introns [40], we observed that the structure prediction improvement was greatest for sequences that were poorly predicted without the benefit of SHAPE data. For these families, a modest improvement in mean performance was really a large improvement for sequences that needed improvement. Additionally, even for families where the improvement was modest, such as 5S rRNA [40], the accuracy of a vast majority of calculations were improved by adding SHAPE. Therefore, for these families, we could demonstrate modest improvements across the sequences, without observing a loss of accuracy for individual calculations.

7. Pseudoknots.

We consider base pairs in pseudoknots to be part of secondary structure [84]. These base pairs span from one loop segment to another loop segment. Formally, a pseudoknot occurs if there are two base pairs (i)-(j) and (i’)-(j’) with i < i’ < j < j’. This distinction is important because many of the standard dynamic programming algorithms are not capable of predicting pseudoknotted base pairs; they can predict (i)-(j) or (i’)-(j’), but not both pairs in the same structure.

In our benchmarks, we keep pseudoknotted pairs present in the predicted structure. Therefore, methods that predict secondary structure without including pseudoknotted pairs are not capable of achieving 100% sensitivity.

When benchmarking methods that predict pseudoknots, it is also important to verify that pseudoknotted pairs are being predicted and to report the sensitivity and PPV of pseudoknotted base pairs. In our benchmark of programs that predict pseudoknotted secondary structures using a single input sequence, we found that the PPV of pseudoknotted base pair prediction was less than 30% and the sensitivity was 3% for the programs with highest PPV and highest sensitivity, respectively [57]. A good mean performance across all base pairs disguised the fact that the accuracy pseudoknot prediction using a single sequence is quite poor. In a follow-up benchmark of methods that predict pseudoknotted secondary structures using multiple homologous sequences, the PPV of the best method was 30%, but the sensitivity was still 5% [85]. Although the accuracy is greatly improved with the help of multiple homologs, there is still a large need to improve the prediction of pseudoknots.

8. The importance of separate training and testing sets.

A number of secondary structure prediction methods were explicitly trained using known RNA secondary structures. The database of secondary structures can be used to train parameters that are free energy nearest neighbor parameters [19, 50] or are similar to free energy nearest neighbor parameters [18, 31, 86]. Alternatively, parameters can be estimated for probabilistic models, such as stochastic context-free grammars [17, 79, 87, 88]. These training methods have been discussed in detail [20]. Also, methods can have adjustable parameters that were optimized to sets of structures, such as the sequence alignment components of Dynalign [77, 89], Foldalign [90], locARNA [91], and TurboFold [82], which are programs that predict a conserved structure and sequence alignment for two or more homologous sequences.

To prevent the training from inflating the apparent accuracy, the test set of structures must be independent of the training structures. This extends to RNA families because the structures within families are similar [17, 56]. Therefore, the testing dataset should use different RNA families from any training dataset that was used.

9. The focus on base pairs and prospectus.

Since 1999, our benchmarks focused on the accuracy of predicting base pairs because it is clear and simple to convey [54]. At that time, at least two previous papers had started to focus on the accuracy of individual base pairs because they reported methods to identify the base pairs more likely to be correctly predicted using folding free energy change or base pair probabilities [92, 93]. Prior to this, benchmarks had focused on helices as the basic unit, but this required interpretation of what constitutes a helix [94, 95].

Going forward, one approach to expanding benchmarks might be approaches that focus more on the topology of the overall fold than on individual pairs. Abstract shapes, for example, provide a means for abstracting structure to the helix or to the branch level [96]. Benchmarks could be developed to use the branching representation to characterize topology.

10. Conclusions.

Benchmarks are commonly performed when new secondary structure prediction methods are developed. Here, good practices are outlined for performing and reporting these benchmarks. It is important to use a variety of high-quality secondary structures, it is important to test for statistical significance, and it is important to use separate testing structure datasets from training datasets.

• Benchmarks of RNA secondary structure prediction should use a large set of well determined structures.

• Benchmarks must include a test of statistical significance.

• Benchmarks should consider a base pair correctly predicted even if it is displaced by up to one nucleotide on either the 5’ or 3’ side as compared to the accepted structure.

• Benchmarks should use entirely different RNA families than those used for training the methods being benchmarked.