SUMMARY AND CONCLUSIONS
1. We studied the contribution of the individual semicircular canals to the generation of horizontal and torsional eye movements in cynomolgus monkeys. Eye movements were elicited by sinusoidal rotation about a vertical (gravitational) axis at 0.2 Hz with the animals tilted in various attitudes of static forward or backward pitch. The gains of the horizontal and torsional components of the vestibuloocular reflex (VOR) were measured for each tilt position. The gains as a function of tilt position were fit with sinusoidal functions, and spatial gains and phases were determined. After control responses were recorded, the semicircular canals were plugged, animals were allowed to adapt, and the test procedure was repeated. Animals were prepared with only the anterior and posterior canals intact [vertical canal (VC) animals], with only the lateral canals intact [lateral canal (LC) animal], and with only one anterior and the contralateral posterior canals intact [right anterior and left posterior canal (RALP) animals; left anterior and right posterior canal (LARP) animals].
2. In normal animals, the gain of the horizontal (yaw axis) velocity of the compensatory eye movements decreased as they were pitched forward or backward, and a torsional velocity appeared, reversing phase at the peak of the horizontal gain. After the anterior and posterior canals were plugged (LC animal), the horizontal component was reduced when the animal was tilted backward; the gain was zero with about −60° of backward tilt. The spatial phase of the torsional component had the same characteristics. This is consistent with the fact that both responses were produced by the lateral canals, which from our results are tilted between 28 and 39° above the horizontal stereotaxic plane.
3. After both lateral canals were plugged (VC animals), horizontal velocity was reduced in the upright position but increased as the animals were pitched backward relative to the axis of rotation. Torsional velocities, which were zero in the upright position in the normal animal, were now 180° out of phase with the horizontal velocity. The peak values of the horizontal and torsional components were significantly shifted from the normal data and were closely aligned with each other, reaching peak values at approximately −56° pitched back (−53° horizontal, −58° torsional). The same was true for the LARP and RALP animals; the peak values were at −59° pitched back (−55° horizontal, −62° torsional). Likewise, in the LC animal the peak yaw and roll gains occurred at about the same angle of forward tilt, 35° (30° horizontal, 39° torsional). Thus, in each case, the canal plugging had transformed the VOR from a compensatory to a direction-fixed response with regard to the head. Therefore there was no adaptation of the response planes of the individual canals after plugging.
4. The data were compared with eye velocity predictions of a model based on the geometric organization of the canals and their relation to a head coordinate frame. The model used the normal to the canal planes to form a nonorthogonal coordinate basis for representing eye velocity. An analysis of variance was used to define the goodness of fit of model predictions to the data. Model predictions and experimental data agreed closely for both normal animals and for the animals with canal lesions. Moreover, if horizontal and roll components from the LC and VC animals were combined, the summation overlay the response of the normal monkeys and the predictions of the model. In addition, a combination of the RALP and LARP animals predicted the response of the lateral-canal-plugged (VC) animals.
5. When operated animals were tested in light, the gains, peak values, and spatial phases of horizontal and roll eye velocity returned to the preoperative values, regardless of the type of surgery performed. This indicates that vision compensated for the lack of spatial adaptation of the response planes after plugging. It converted a noncompensatory, direction-fixed response with regard to the head to an appropriate compensatory response.
6. These results indicate that both the vertical and lateral canals contribute a horizontal and torsional component to the VOR in the monkey according to the vector projection of head velocity onto the normals of the individual canals. The individual components can be predicted according to the position of the canals in the head with regard to the plane of rotation. The nonorthogonality of the canal planes must be considered when predicting canal activation of eye movements in response to rotation around any axis.
INTRODUCTION
The lateral and vertical semicircular canals activate the angular vestibuloocular reflex (VOR) to generate compensatory eye movement during angular head movement. A great deal is known about how the canals respond to rotation (see Wilson and Melvill Jones 1979 for review), but how complementary canal pairs contribute to horizontal, vertical, and roll components of compensatory eye velocity has not been adequately evaluated.
One approach to this problem is to study the VOR before and after canal plugging (Baker and Peterson 1991; Baker et al. 1982, 1986; Böhmer et al. 1985; Minor and Goldberg 1990). This operation, devised by Ewald (1892), was modified by Money and Scott (1962). If the bony and membranous canals are interrupted by grinding across them with a fine diamond burr, a strong bony plug is left on recovery that blocks the flow of endolymph when the head is turned. Canal plugging eliminates the response to angular accelerations along specific canal axes (Baker et al. 1982; Böhmer et al. 1985; Cohen et al. 1983; Correia and Money 1970; Igarashi et al. 1987; Paige 1983; Raphan et al. 1983) while maintaining a relatively normal spontaneous discharge in the afferents of the plugged canals (Barmack and Pettorossi 1988; Goldberg and Fernandez 1975; Paige 1983).
An analytic study of squirrel monkeys with caloric and rotational stimulation has led to the conclusion that the lateral canals are essentially responsible for producing the horizontal VOR (Minor and Goldberg 1990). This conclusion arose from examining the spatial phase of the maximum horizontal VOR gain as a function of pitch angle. The maximum compensatory eye velocity occurred when the head was pitched forward ~15°. It was argued that because the peak gains occurred close to the angle at which the semicircular canals were pitched back relative to the stereotaxic frame, the lateral canals must be producing the horizontal VOR. By studying lateral and medial rectus activation during sinusoidal rotation in decerebrate cats, the conclusion was reached that there is little vertical canal input to horizontal rectus muscles and little horizontal canal input to vertical rectus and oblique muscles (Baker and Peterson 1991; also Baker et al. 1988).
The question of whether a horizontal component of eye movement is induced by the vertical canals has been addressed in several studies (Baker et al. 1982; Böhmer et al. 1985; Cohen et al. 1988). After the lateral canals were plugged, a prominent horizontal component emerged when animals were statically pitched backward and sinusoidally rotated about a vertical axis (Baker et al. 1982; Böhmer et al. 1985; Cohen et al. 1988). It was postulated that the vertical canals produce this horizontal component as a result of normal or increased coupling following inactivation of the lateral canals (Baker et al. 1982; Böhmer et al. 1985). The precise relationship between the canals and the eye velocities that they produce, however, has not been defined. Moreover, because the semicircular canals are nonorthogonal (Blanks et al. 1975, 1985; Reisine et al. 1988), we felt it worthwhile to assess the contribution of the vertical canals to the horizontal component of the VOR and the corresponding lateral canal contribution to the roll component of the VOR using a nonorthogonal model.
From the geometric relationship of the vertical canals to the head coordinate frame, it has been suggested that the canals make a contribution to the horizontal VOR according to the projection of their activation into the horizontal plane (Robinson 1982). In support of this, activity of type I anterior and posterior canal neurons in the vestibular nuclei is related to the component of angular acceleration that excites that canal, expressed as a vector normal to the canal plane. These vertical-canal-related neurons have significant activity when animals are rotated around a yaw axis (Duensing and Schaefer 1958; Reisine and Raphan 1992; Shimazu and Precht 1965). Because only horizontal eye velocity is generated during yaw rotation, it is likely that the vertical canals make a substantial contribution to the yaw VOR in the normal animal. The substrate for this probably includes projections of vertical-canal-related neurons to the abducens nucleus (McCrea et al. 1987).
In this study we determine the contribution of individual semicircular canals to the generation of compensatory horizontal and torsional eye velocity and compare experimental results with predictions of the contributions of the individual canals based on a geometric model. The aim was to explore whether removing input from individual canals would affect the plane of response from the remaining canals. The hypothesis was that the horizontal and torsional components of eye velocity will be a sum of the response of the individual canals, and that when individual canals are removed the resultant eye movements will be predicted by summing the components produced by the remaining canals.
METHODS
Experiments were performed on eight cynomolgus monkeys that had one or more semicircular canal pairs plugged. The experiments conformed to the Principles of Laboratory Animal Care (National Institutes of Health Publication 85–23, Revised 1985) and were approved by the Institutional Animal Care and Use Committee.
Surgical procedures
Under anesthesia (ketamine induction, halothane-NO2 gas anesthesia) using sterile surgical conditions, head bolts were implanted on the skull in dental acrylic cement in the stereotaxic vertical plane. The bolts provided painless fixation of the head in stereotaxic coordinates during testing. With the animals upright, the normal to the horizontal stereotaxic plane or the yaw axis was along the spatial vertical. During the same surgery, two three-turn coils were implanted on one eye. One 14-mm coil was placed symmetrically around the iris in the frontal plane with its normal aligned with the optic axis (Judge et al. 1980; Robinson 1963). This coil was used to measure horizontal and vertical eye position. An 11- to 12-mm coil, threaded under the superior rectus muscle, was implanted on top of the same eye (Cohen et al. 1992; Dai et al. 1994). The top coil, which was used to measure roll eye position, was approximately orthogonal to the frontal coil. The animals were allowed to recover and then received baseline testing. About 1 mo later, the monkeys were anesthetized and the middle ear was approached posteriorly. The canals were identified under an operating microscope. Plugging was accomplished by grinding across each canal with a diamond burr until the membranous canal was interrupted. The region of the canal was packed with bone and covered with a small piece of muscle. Animals received steroids for 3 days, antibiotics for 5 days, and analgesics for 2 days to reduce swelling, infection, and pain, respectively. Animals were allowed to recover for 1 mo after plugging before testing began, and testing continued at monthly intervals until the results stabilized. After this, animals were tested up to 18 mo after surgery. The last two tests were used for the data analysis. During the recovery period, the animals moved freely in their cages. By the time of testing, postural control was good, and the uncoordinated head movements in the plane of the plugged canals observed in the first weeks after surgery had largely disappeared. Thus the results that will be reported were from animals that had recovered from the effects of operation.
Canal plugging was verified by the lack of response to sinusoidal rotation at 0.2 Hz and 60°/s in a plane perpendicular to the average plane of the remaining canals. This midband frequency was high enough to activate the direct vestibular pathway but not velocity storage. At the end of testing, the three animals reported in Figs. 7 and 8 (LC M9008, VC M9003, LARP M9006) were perfused through the heart with saline and a paraformaldehyde-Formalin solution. The temporal bones were removed, decalcified, embedded in celloidin, and processed for anatomic study. It was verified that the appropriate canals had been plugged, that their ampullae and nerves were intact, and that the other canals were patent.
FIG. 7.

Comparison of data from a VC animal (monkey M9354; A and B) with summed left anterior and right posterior canals left intact (LARP) and RALP data (M9355 + M9356, C and D; M9223 + M9306, E and F). The spatial phases were similar in all 3 cases, but the gains were slightly higher in the summed data from the LARP and RALP animals (C–F). Also see Fig. 5, C and D, for comparison. Dotted phase error markers are not shown in E because the phase error, determined from the critical value of the E statistic, was 0°. Therefore the curve for the yaw axis component could not be shifted and still significantly fit the data.
FIG. 8.
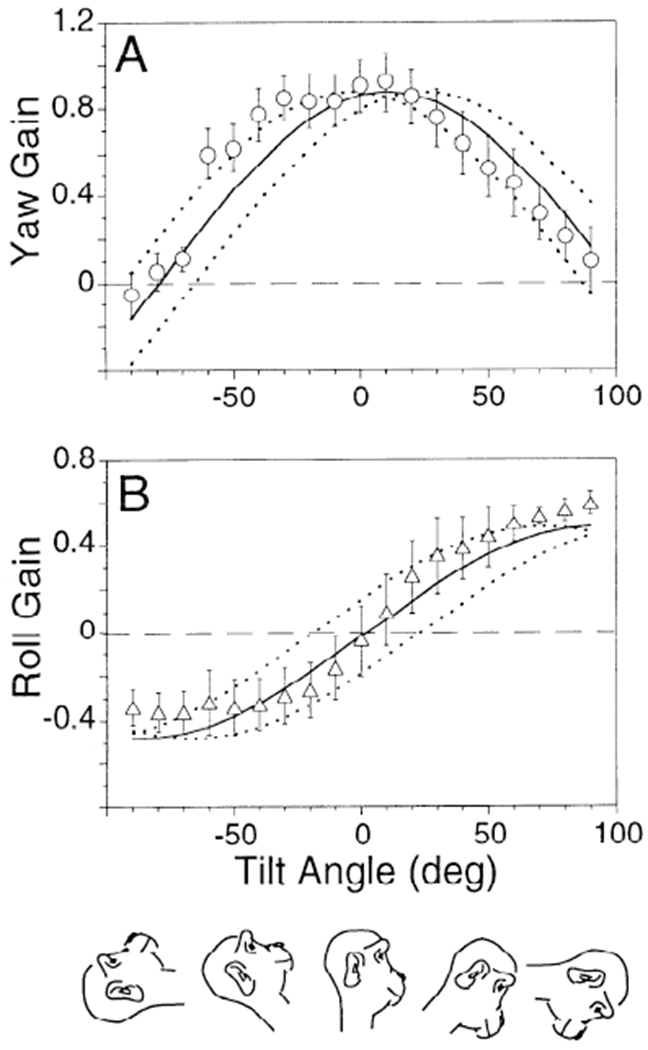
Yaw (A) and roll (B) vestibuloocular reflex (VOR) gains of 6 canal-plugged animals as a function of head tilt when tested in light (open symbols ° 1 SD). Also shown is the best fit curve for the 8 normal monkeys tested in darkness (solid line) and the phase error for the normal data (dotted lines) from Fig. 6, A and B. The data from the canal-plugged monkeys recorded in light lay in or close to the mean and phase error of the data from the normal monkeys recorded in darkness.
Techniques for measuring eye position and eye velocity
During testing, the monkey’s head was fixed to a 13-cm plastic frame that held two sets of field coils that generated orthogonal oscillating magnetic fields at the same frequency (24.7 kHz). The axes of the field coils were along the interaural and dorsoventral axes of the head, establishing a head-fixed reference frame for measuring the orientation of the frontal and top search coils. The head frame axes for the field coils were the X and Z directions, respectively.
It should be noted that the coordinate frame utilized in this study was different from that used by Böhmer et al. (1985)), Minor and Goldberg (1990)), and Baker and Peterson (1991). They pitched the head at various angles relative to the horizontal stereotaxic plane to bring the lateral canals to the spatial horizontal.
The eye with the search coils was centered in the magnetic fields, and its orientation relative to the head was determined from the orientation of the search coils. If the two search coils were not orthogonal, a portion of the horizontal voltage was fed back and subtracted from the roll voltage. As a result, there was no cross talk in the roll recording when the upright animal was rotated around a spatial vertical axis. This method electronically orthogonalized the eye axes so that the effective normal to the top coil was aligned with axis from the bottom to the top pole of the eye. Studies on monkeys have shown that there is a small nonorthogonal relationship between the maximum direction for roll and yaw (Crawford and Vilis 1991), but the angles are well within the error bounds of the data reported in this study. Therefore orthogonalization was warranted.
Calibration procedures
To calibrate eye movements, the animals were rotated in light at 30°/s about the pitch, roll, and yaw axes. It was assumed that horizontal and vertical gains were close to unity in this condition (Crawford and Vilis 1991; Dai et al. 1991; Raphan et al. 1979; Robinson 1963). Roll gains were assumed to be 0.6 when rotation was around a nasooccipital axis aligned with the spatial vertical (Crawford and Vilis 1991; Henn et al. 1992). This agrees with roll gains determined for monkeys using other techniques (Dai et al. 1994; Yue et al. 1994). (See APPENDIX for calibration and computation of eye velocity in head coordinates, and Figs. 1 and 11 for a comparison of these velocities with eye velocity derived from differentiation of coil voltages.) Calibrations that were determined before surgery for each animal were used after canal plugging. Calibrated eye velocities obtained during sinusoidal rotation in light after plugging matched the preoperative values. Eye velocities to the left, down, and counterclockwise (from the animal’s point of view) are represented by downward deflections in the velocity traces in the figures.
FIG. 1.
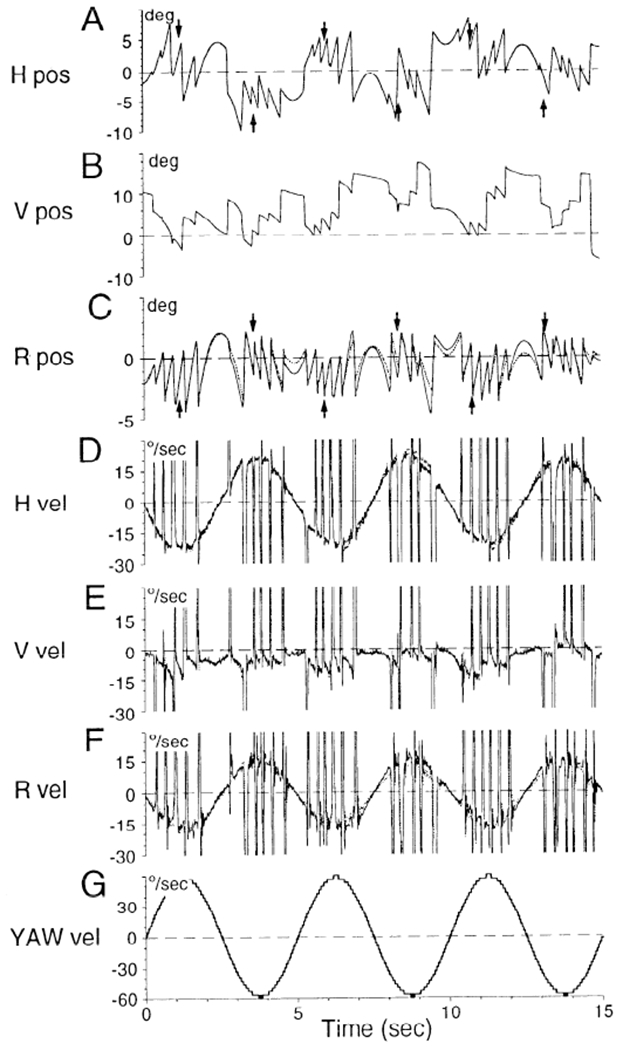
Comparison of coil voltages (A–C, solid lines) and derivatives of coil voltages (D–F, solid lines) with Euler angle derivations of eye position (A–C, dotted lines) and eye velocity (D–F, dotted lines) in head coordinates. See APPENDIX for derivation of Euler angle representations. G: stimulus velocity. Dashed horizontal lines in A–C: reference position of the eye. Dashed horizontal lines in D–G: 0 velocity. Arrows in A and C are the points at which gain measurements were taken. Solid and dotted lines were indistinguishable in A, B, D, and E. There were small differences between them in torsional position (C) and velocity (F), but these were minimal at the points were measurements were taken. Ordinates in A–C: deviation (°) around the reference position. Ordinates in D–G: eye velocity (°/s).
FIG. 11.
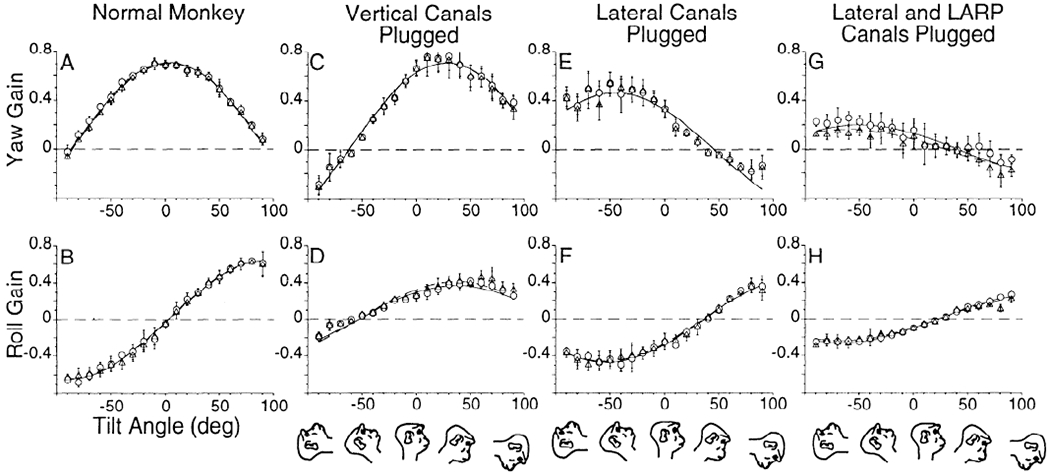
Comparison of spatial gains derived from measurements of derivatives of coil voltages (◯) with derived Euler angle velocities (Δ). The scheme of representation is identical to that in Fig. 10. Solid lines: best fitting curves for the derivatives of the coil voltages. Dashed lines: best fitting curves for the Euler angle velocities. The curves overlap, and small differences between them were not significant (P = 0.05).
To determine eye velocity in a head frame coordinate system, eye orientation was determined relative to a reference position. This position was obtained from the average voltage of each coil during 10 cycles of sinusoidal rotation about a vertical axis at 0.20 Hz in darkness (60°/s peak velocity). We then determined the slope of the voltage change for a slow phase during step rotation at 30°/s in light about the yaw axis where the other two voltages were close to the reference value. The same was done for pitch and roll during rotation about the pitch and roll axes of the head, respectively. The average absolute value of the slope corresponded to an eye velocity of 30°/s for yaw and pitch and 18°/s for roll (roll gain 0.6). The voltages were normalized to values between −1 and 1.
Data collection
During testing, animals sat in a primate chair in a four-axis vestibular stimulator surrounded by an optokinetic drum. Each axis went through the center of rotation of the head. The stimulator and drum have been described in detail in previous publications (Dai et al. 1991; Raphan et al. 1981; Reisine and Raphan 1992). The animals were pitched about their interaural axes to a given angle and then rotated about an axis that was spatially vertical. This stimulus induced yaw eye movements when the animals were upright and both yaw and roll eye movements when the animals were pitched. This paradigm was similar to that utilized in previous studies of horizontal eye movements induced after semicircular canal plugging (Baker and Peterson 1991; Baker et al. 1982, 1986; Böhmer et al. 1985; Minor and Goldberg 1990). Unless otherwise specified (as in Fig. 8), all testing was done in darkness.
Eye position voltages and voltages related to the velocity or position of the axes of rotation were recorded with amplifiers with a bandpass of DC to 40 Hz. An MS DOS-based PC/AT computer, running programs written in DAOS (Data Acquisition and Operating System, Mycon Technology, Australia), was used to control the vestibular stimulator, collect the data, and analyze the results. Voltages were digitized at 600 Hz per channel with 12-bit resolution and stored on optical disk. Eye position voltages were smoothed by sequentially averaging four sampling intervals. The smoothed waveform was digitally differentiated by finding the slope of the least-squares linear fit to 11 data points. This corresponded to a filter that had a 3-dB cutoff above 40 Hz, the cutoff frequency of the filters used for data acquisition. Saccades were then removed from the record using a maximum likelihood detection criterion (Singh et al. 1981).
Small angle approximation used for measurement of eye velocity
Coil voltages are close approximations of eye position for small angular deviations, usually taken as 15° from some reference position (Ferman et al. 1987a,b; Paige and Tomko 1991). This is dictated by the fact that the cosine of 15° is ~1 and the sine is approximately linear over ±15°. In this study, eye position shifts were <15° from the reference position on average. In addition, because eye velocity is taken as an average measurement over 10 cycles in our plots, variations due to deviations beyond this limit are necessarily small. In four monkeys (M9223, M9354, M9355, and M9356), we computed the Euler angles from the coil voltages, used the Euler angles to compute eye velocity in head coordinates, and compared the velocities with the derivatives of the coil voltages (see appendix). Figure 1 shows sample presurgery data from monkey M9223 tilted 50° forward where the gain of each component was close to maximum and the eyes were maximally deviated vertically (Fig. 4). Coil voltages in Fig. 1 are shown by solid lines and the values of the Euler angle by dotted lines. The two horizontal representations of eye position (Fig. 1A) and eye velocity (Fig. 1D) were indistinguishable. The same was true for vertical position and velocity (Fig. 1, B and E). There were small differences between the voltage and Euler angle representations of torsion (Fig. 1C) at times when there were large horizontal and vertical deviations. The roll velocities, however, were indistinguishable at the peaks where the measurements for roll velocity were taken (Fig. 1, A and C, arrows).
FIG. 4.
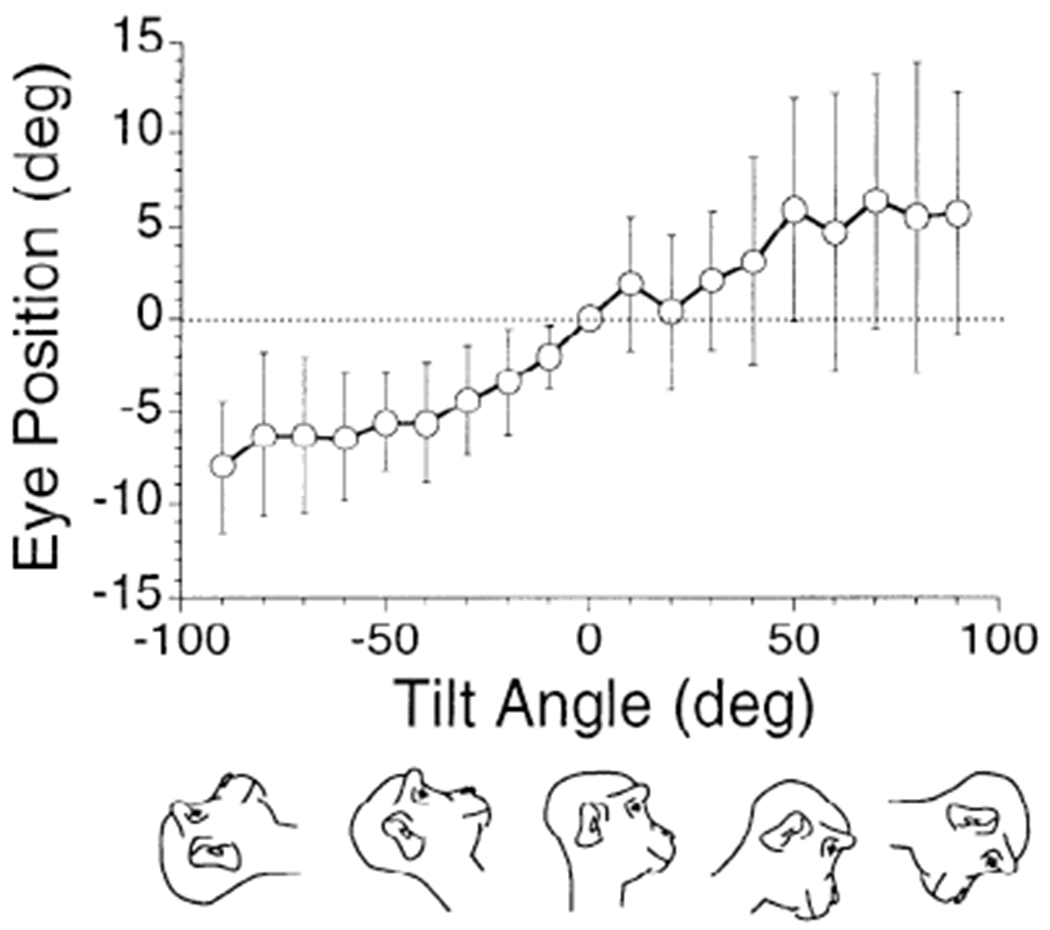
Average vertical eye position at different pitch angles for 8 normal animals. Eye position was calculated from 10 cycles of rotation in darkness at 0.20 Hz. Abscissa: pitch angles in forward (positive values) and backward (negative values) directions. It was assumed that the average vertical eye position was 0 when the animal was upright. Vertical bars in this and subsequent graphs: ±1 SD.
The conclusion is that because the computed eye velocity represents changes in eye orientation that remain within 15° of the reference position, eye velocity in head coordinates was not significantly different from the derivatives of the coil voltages. Thus we used the coil voltage derivatives to represent eye velocity in head coordinates in this study. A similar approximation was used by Paige and Tomko (1991).
Data analysis
Animals were sinusoidally rotated about a vertical axis at a frequency of 0.20 Hz with a peak velocity of ±60°/s. They were tested upright (0°) and statically tilted forward (nose down, +) or backward (nose up, −) in 10° increments up to 90°. Ten cycles were collected in each position. The tests were repeated three to seven times for each animal on different days before and after canal plugging. The gains (peak eye velocity/peak stimulus velocity) of the horizontal, vertical, and torsional VOR components were calculated for each cycle. The mean gains and standard deviations were obtained for 10 cycles of data. The temporal phase of the responses was determined by fitting the average of 10 cycles of eye velocity with a single sinusoid, the dominant harmonic, and computing the phase relative to the stimulus velocity. This procedure was done for tilt angles ranging over ±90°. Mean gain curves as a function of tilt angle were fitted with a sinusoid. The peak value of this function was the spatial gain. The tilt angle at which the peak value occurred defined the spatial phase relative to the upright (0°). The primary interest of this study were the spatial gains and phases, which are shown in Figs. 5–8 and 11 and in Table 1.
FIG. 5.

Gain curves of yaw (A, C, and E) and roll (B, D, and F) eye velocity over tilt angles of −90 to +90° in 10° intervals. Yaw and roll gains after plugging the vertical canals [animal with only the lateral canals left intact (LC animal); A and B, monkey M9003], lateral canals [animal with only the anterior and posterior canals left intact (VC animal); C and D, monkey M9008], and lateral, left anterior, and right posterior canals (RALP animal; E and F, monkey M9006). Diagrams at top: plugging. Ac, anterior canal; Lc, lateral canal; Pc, posterior canal. Drawings at bottom: head position at these pitch angles. Each symbol represents the mean of gain values obtained at that tilt angle. Vertical bars: ±1 SD. In this and subsequent graphs, the 2 dotted lines show the region over which the approximation curve can be shifted and still significantly fit the data. Arrows: tilt position with maximal gain response.
TABLE 1.
Maximal yaw and roll spatial gains and angles of tilt at which peak gains occurred
| Intact Canals | Yaw |
Roll |
Monkey | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Before |
After |
Before |
After |
||||||
| Gain | Phase | Gain | Phase | Gain | Phase | Gain | Phase | ||
| A. Experimental data | |||||||||
| Lateral canals (LC animal) | 0.88 | −1 | 0.71 | 30 | 0.53 | −88 | 0.37 | 39 | 9008 |
| Vertical canals (VC animal) | 0.83 | 10 | 0.46 | −46 | 0.53 | 78 | 0.47 | −52 | 9003 |
| 0.94 | 14 | 0.40 | −59 | 0.42 | −81 | 0.39 | −64 | 9354 | |
| LARP canals (LARP animal) | 0.71 | 3 | 0.20 | −55 | 0.64 | −87 | 0.26 | −67 | 9006 |
| 0.94 | 9 | 0.23 | −57 | 0.56 | −88 | 0.23 | −66 | 9306 | |
| 0.89 | 17 | 0.28 | −60 | 0.58 | 85 | 0.32 | −64 | 9356 | |
| RALP canals (RALP animal) | 0.81 | 19 | 0.36 | −44 | 0.48 | −86 | 0.29 | −52 | 9223 |
| 0.97 | 16 | 0.29 | −58 | 0.41 | 89 | 0.31 | −62 | 9355 | |
| B. Model prediction | |||||||||
| Lateral canals (LC animal) | 0.87 | 0 | 0.68 | 30 | 0.52 | 90, −90 | 0.34 | 30 | |
| Vertical canals (VC animal) | 0.87 | 0 | 0.44 | −50 | 0.52 | 90, −90 | 0.46 | −50 | |
| LARP/RALP canals (LARP/RALP animal) | 0.87 | 0 | 0.22 | −50 | 0.52 | 90, −90 | 0.23 | −50 | |
A: maximal yaw and roll spatial gains and angles of tilt (spatial phase) at which the peak gains occurred in the 8 animals before and after surgery. Testing was done in darkness. B: same values as in A derived from predictions based on the geometric model of the canals and their projections to the oculomotor system. Using only the gains and phases of the normal monkeys, the model predicted the results after canal plugging. LC, lateral canals intact; VC, vertical canals intact; LARP, left anterior and right posterior canals intact; RALP, right anterior and left posterior canals intact.
CONVENTIONS FOR DATA REPRESENTATION.
The coordinate frame for the semicircular canals, described by the normals to the canal planes, is approximately an orthogonal frame, rotated 45° and tilted up relative to the pitch, roll, and yaw axes of the head (Blanks et al. 1975, 1985; Reisine et al. 1988). The pitch axis is interaural, the roll axis is nasooccipital, and the yaw axis lies in the sagittal and coronal planes perpendicular to the pitch and roll axes. Because the horizontal stereotaxic plane is perpendicular to the coronal frame, we define horizontal eye movements as movements that are confined to the horizontal stereotaxic plane. They are about the yaw axis and have no roll or vertical components. The conventions for describing eye velocity in the head followed a right-hand rule. The positive direction for the stimulus is along the spatial vertical (Fig. 2, A and E), and peak positive values occur during rotations to the left (Fig. 2, B and F). Horizontal or yaw eye velocity, which is also positive for rotations to the left, has a vector pointing out the top of the head (Fig. 2, A and E, Z-axis). The positive direction for roll or torsion is along the nasooccipital axis, toward the back of the head (Fig. 2, A and E, Y-axis). This represents a counterclockwise rotation from the animal’s perspective. The positive direction for the vertical or pitch component is out of the left ear (not shown).
FIG. 2.
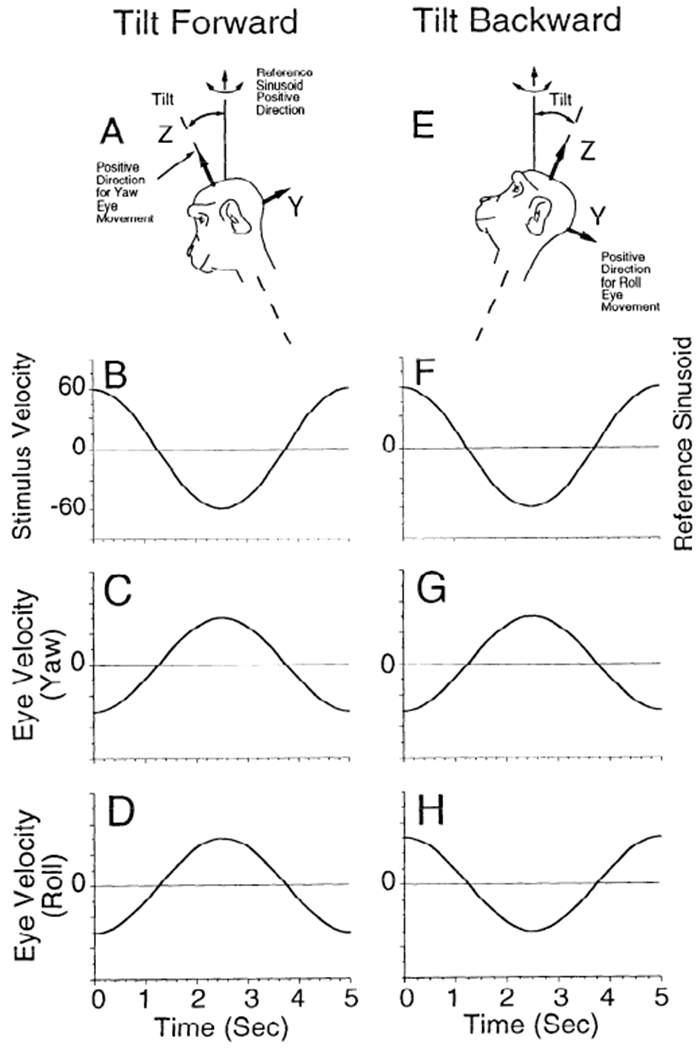
Conventions for describing eye velocity in the head. A and E: positive directions associated with the vector components of head and eye movements referenced to a head-based coordinate frame. A positive value along the reference directions corresponds to a rotation according to a right-hand rule. Thus a positive value for Z corresponds to a leftward movement, and a positive value for Y corresponds to a counterclockwise rotation from the animal’s viewpoint. The reference sinusoid for computing gains was along the spatial vertical (B and F). For the tilted forward condition, the components of head velocity along the yaw (Z) and roll (Y) axes are positive, and the corresponding compensatory eye velocity components are 180° out of phase (C and D). This has been taken as a positive gain. G and H: with the head tilted backward, the component of head velocity along the yaw axis is positive and the component along the roll axis is negative. This corresponds to a yaw eye velocity that is 180° out of phase (G) with the reference and a roll eye velocity that is in phase with the reference sinusoid (H). The gain of the yaw component was therefore taken as positive, whereas the gain of the roll component was taken as negative.
When the animal is tilted forward (Fig. 2A), the reference sinusoid (Fig. 2B) has peak velocity to the left at zero phase along the spatial vertical at the frequency of rotation (0.20 Hz). The horizontal (Fig. 2C, Yaw) and torsional (Fig. 2D, Roll) components are 180° out of phase, having peak velocity to the right when the stimulus has its peak velocity to the left. When the animal is tilted backward (Fig. 2E), the reference sinusoid (Fig. 2F) is the same as in Fig. 2B. The horizontal component has the same phase relationship to the stimulus sinusoid (compare Fig. 2, C and G), but the torsional component oscillates in phase with the stimulus (Fig. 2H).
In each case all components of eye velocity are either in phase or 180° out of phase with the reference sinusoid as a sinusoidal function of time. The phase difference between the stimulus sinusoid and the eye velocity sinusoid is the temporal phase. For forward tilts, when the horizontal and roll components of eye velocity are out of phase with the reference sinusoid (Fig. 2, C and D), the gain will be considered as positive. With the animal tilted back, when the zero phase of the torsional component is in phase with the reference sinusoid (Fig. 2, F and H), the gain will be considered negative. The positive and negative gains are represented on the ordinates of graphs displaying the average gains of horizontal and torsional (roll) eye velocity as functions of tilt with regard to gravity (Figs. 5–8 and 11). The abscissa shows the direction of tilt (0°, upright; +, forward; −, backward). In the equations, bold characters represent vectors.
STATISTICAL ANALYSIS OF DATA.
An analysis of variance (ANOVA) was used to evaluate how closely the sinusoids describing gain as a function of tilt angle fit the data (Keppel 199 1). The null hypothesis was that for each tilt angle the mean gain of the data was equal to the value obtained from the optimal fit to the data over all angles of tilt. The function used to fit the data was a cosine function, A * cos (x + B), where x is the tilt angle, A is the spatial gain, and B is the spatial phase. We tested this hypothesis by examining the ratio of the variance of the data relative to the mean and the variance relative to the fitted value. Because each measurement of gain at each tilt angle was done independently, the ratio follows an F distribution (Keppel 1991) and is called an F statistic.
In this model-based study, the F statistic is a ratio of the mean square error of the model prediction and the data around the mean (F = MSerr model/MSerr data). The F statistic is not affected by variance of data around the mean, it simply measures the goodness of fit of the model to the data. Because the mean value is the best predictor for the data, the F statistic will be close to 1 only when the model prediction overlaps the mean value of the data. As long as the data follow the sinusoidal fit, an increase in variance will not cause an increase in the F value or an increase in the phase error term. When the data deviate from the sinusoidal fit, however, the F statistic will increase. If the F statistic was less than the critical value (95% confidence level), we assumed that there was no significant difference between the data and the model prediction.
Because the variances of each distributions were derived from the same data set using the hypothesis that it could be fit by a cosine function, the F statistic had 1 degree of freedom (df = 2–1) and is given by F(1,N) (where N is the number of data points minus 1). If this value was larger than the critical value at the 95% confidence level, then the null hypothesis was rejected, and the data were not considered to be well fit (Fcr, Table A-1 of Keppel 1991).
The maximum deviation of the spatial phase from the optimal fit that maintained the F statistic within critical limits (P < 0.05) was calculated. To do this, the best fit curve was shifted in both directions in increments of 1° on the abscissa until a critical value was obtained for the F statistic. This was called the phase error. The criterion for assessing model fits was that the phase predicted by the model should fall within the range of the phase error. The gains of the model were chosen on the basis of average gains of the normal monkeys. They could be adjusted to fit the data for individual spatial gain curves.
Data from pairs of monkeys with different canal lesions were summated to compare with data from normal monkeys or with data from monkeys with the same lesions. To create the summated response, 10 individual gain measurements that were taken from each pair of monkeys in each tilt position were sequentially summated to get 10 gain values (Keppel 1991). These gain values were used to construct a best fit curve. This curve was then compared with preoperative data from other monkeys using the F statistic described above. The vertical bars in all of the graphs represent ±1 SD.
RESULTS
Figure 3 shows the eye velocities produced before (A) and after surgery (B and C) when an animal with only the right anterior and left posterior canals left intact (RALP animal) (monkey M9223) was statically tilted back and rotated sinusoidally about a spatial vertical axis in darkness (A and B) or in light (C). Preoperatively, the horizontal component was largest when the animal was upright and gradually decreased as it was tilted backward (Fig. 3A). Complementing this, the torsional component (roll) was close to zero when the animal was upright and increased as a function of tilt angle. This occurred for both forward and backward tilts, but in reverse phase.
FIG. 3.

Horizontal , vertical , and roll eye velocity of an animal with only the right anterior and left posterior canals left intact (RALP animal) (monkey M9223) during sinusoidal rotation about a spatial vertical axis (Turntable). Represented are responses upright (left) and during backward tilts along the pitch axis at angles of −30, −60, and −90°. Drawings at bottom: attitude of tilt and the axes of rotation are shown by the position of the monkey’s head. Vertical line below the monkey: axis of gravity that was coincident with the axis of rotation. Three conditions are represented: preoperative in darkness (A), postoperative in darkness (B), and postoperative in light (C). Before operation (A) and in light after operation (C), there was a decrease in the peak horizontal component and an increase in the peak roll component with increases in tilt angle along the pitch axis. B: when the animal was rotated in darkness after operation, horizontal and roll eye velocity increased with tilt backward for −30 and −60°. There was a vertical component during the rotation at all angles that was also predicted by the model (see text). The calibrations for eye velocity and turntable velocity, which are the same for each component and for each panel, are shown in A, right.
Vertical velocities were small or absent in the normal monkeys during the sinusoidal rotation. Therefore we concentrated on horizontal and torsional velocities in this study. [There were vertical components in the animals with only the left anterior and right posterior canals left intact (LARP animals) and RALP animals after surgery when they were tested in darkness (Fig. 3B). These will be considered below.] There was, on average, a shift in vertical eye position as a function of tilt (Fig. 4). When the animals were tilted forward the eyes moved up, and when the animals were tilted back the eyes moved down. Consistent with Haslwanter et al. (1992)) the curves tended to saturate at ≈6° shift at about ±50° of tilt. Variance was large, however, and the difference between the upright and tilted positions was significant only for backward tilts (P < 0.05).
To determine the contribution of individual canals to the total response, we first considered the gain and phase of the responses produced by the lateral canals after the vertical canals were plugged. Then the response due to the vertical canals was examined by plugging the lateral canals. From this we determined how they combined. We then compared the summed response with the normal response. These determinations were performed in animals in which the canal plugging was both physiologically and anatomically verified (LARP M9006; LC M9008; VC M9003).
The mean value for the temporal phase between stimulus velocity and horizontal and torsional eye velocity for normal animals was −5 ± 2° (mean ± SD) and −7 ± 2°, respectively, over all tilt angles. After vertical canal plugging [only the lateral canals intact (LC animal)], the temporal phases were 0 and 3° for horizontal and roll eye velocity, respectively. After lateral canal plugging [only the vertical canals intact (VC animal)], the phases were 6° for horizontal and 2° for torsional eye velocity. Differences in phase angles were similarly small for the LARP and RALP animals (8 ± 3° horizontal, 5 ± 4° torsion). Therefore the differences in phase angles before and after plugging were not significant, and the peak gain values would not be significantly affected by correcting for temporal phases.
Contribution of the lateral canals (LC animals)
When the anterior and posterior canals are plugged (LC animals), all compensatory eye movements due to the angular VOR originate in the lateral canals. As a result, the horizontal and roll velocities produced by the lateral canals should be in phase at each tilt angle and direction-fixed with regard to the head. Gains were plotted as a function of tilt angle to determine spatial phases (Fig. 5, A and B). The standard deviations of the gains were small. Data were approximated with cosine curves (monkey M9008, Table 1), and these curves were used to measure the gain and phase of the response. The maximum gain of the horizontal component was 0.71 after plugging, and it occurred at 30° pitch forward (Fig. 5A, arrow; ±9° phase error; Table 1). Similarly, the peak gain of the roll component due to lateral canal activation was 0.37, and it occurred at 39° pitch forward (Fig. 5 B, arrow; ±11° phase error; Table 1). Considering the variation, there was no significant difference between these sinusoidal data fits. Therefore both sets of data could be approximated with a single curve that could have phase shifts between 28 and 39° (P = 0.05). This is consistent with the postulate that only the horizontal canals were active in this animal.
Contributions of the anterior and posterior canals (VC animals)
With the lateral canals plugged, only the vertical canals can generate the angular VOR. Because the vertical canals are tilted back relative to the stereotaxic coordinate frame (Blanks et al. 1975, 1985; Reisine et al. 1988), they should produce both horizontal and roll components during sinusoidal rotation in the upright condition. As with the lateral canal animal, the horizontal and roll velocities should be in phase and direction-fixed with regard to the head, and their gains should also reflect the projection of the vertical canals into head coordinates.
The peak gain of the horizontal velocity was 0.46 after lateral canal plugging in monkey M9003 (Fig. 5C, up arrow). This was achieved for −46° tilt back (phase error ±7°; Table 1). The peak gain of the roll component was 0.47 at −52° tilt back (Fig. 5D, down arrow; phase error ±7°; Table 1). Discounting the phase difference of 180° and phase error of ±7°, the difference between the horizontal and torsional curves was not significant for fits with phases between −45 and −53°. Differences between the horizontal and torsional phases in a second VC animal (monkey M9354) were similar (Fig. 7, A and B; Table 1).
These findings confirm findings of Baker et al. (1982) and Böhmer et al. (1985) that a horizontal component of eye velocity is produced by the vertical canals after lateral canal plugging. They demonstrate, moreover, that the lateral and vertical canals each contribute both horizontal and roll components to the VOR, and that if the 180° phase difference between the horizontal and roll components is discounted, their spatial gain characteristics are not significantly different.
RALP and LARP animals
The characteristics of the compensatory eye movements in the RALP and LARP animals were similar to those of the VC animals, but the gain was lower (Fig. 5, E and F; Table 1). The average peak horizontal gains for the LARP and RALP monkeys were 0.27 ± 0.05, occurring at −55 ± 6° tilt backward (Table 1) with a null point at 35 ± 6° tilt forward. The peak roll gains were 0.28 ± 0.03 at −62 ± 5° tilt backward with a null point at 28 ± 5 tilt forward. Thus the gain of both components of the VOR in the LARP and RALP animals was about half as large as in the VC animals, indicating that each pair of vertical canals contributes approximately equally to the gain of the horizontal and roll VOR. As before, if the 180° phase difference between horizontal and roll was discounted, the spatial gain curves of the horizontal and roll components were not significantly different.
Comparison of normal responses with summed responses from canal-plugged animals
The VOR can be spatially adapted by interacting vestibular and optokinetic inputs (Schultheis and Robinson 1981). This has been termed “cross-axis adaptation” (Baker et al. 1986, 1987). It is possible that the responses of the canals after plugging represented spatial adaptation of the VOR. If so, there should be a significant difference between the responses of the intact animal and a sum of the responses from animals with their lateral and vertical canals plugged. If not, the responses from an LC animal should add to the responses from a VC animal to reproduce the normal response. This would demonstrate that the spatial gain is determined solely according to the vector projection of head velocity onto the normals of the individual canals.
The averaged gains of the horizontal and torsional components for the eight normal monkeys are shown in Fig. 6, A and B. In the upright position, the peak gain of the horizontal component of the VOR was 0.87 ± 0.08, occurring at 11° tilt forward (Fig. 6A, ↑; phase error ±14°). The peak torsional gain was 0.52 ± 0.07. The zero crossing occurred at 0° tilt (Fig. 6B, ↓; phase error ±21°).
FIG. 6.
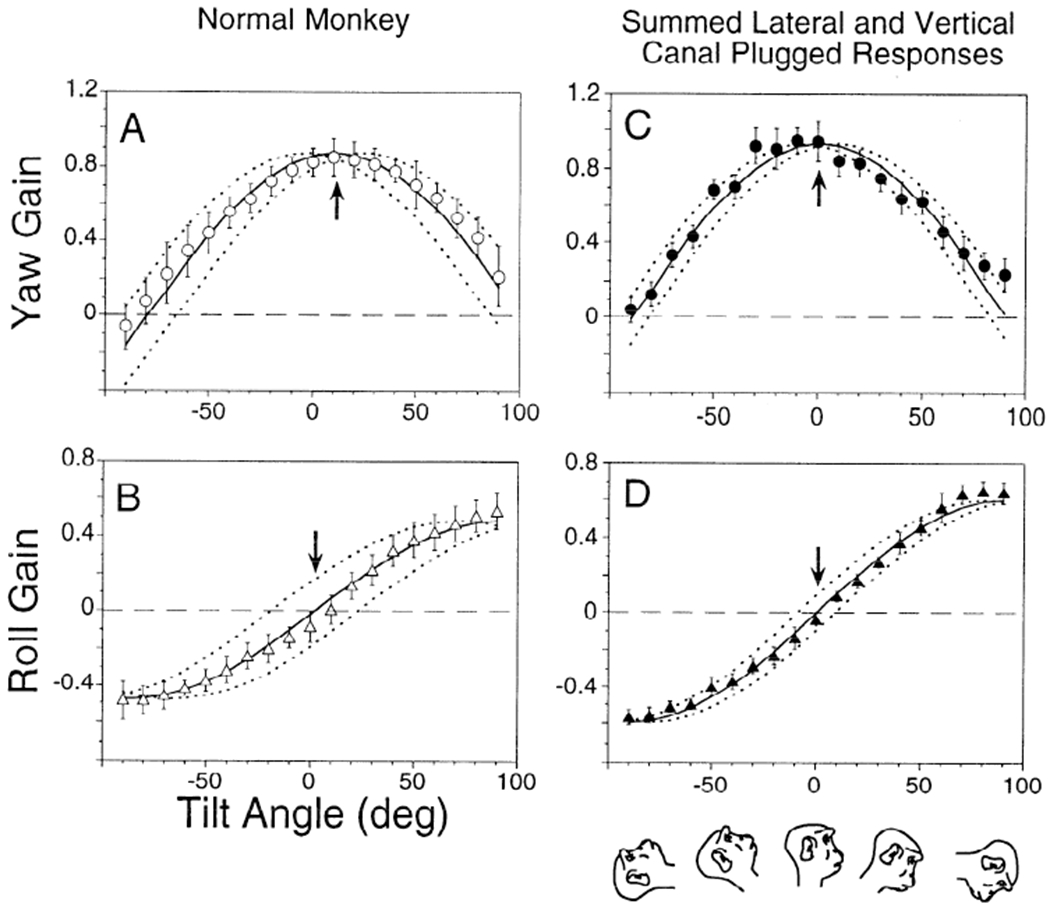
Averaged gains of the yaw (A) and roll (B) components from 8 normal monkeys and corresponding yaw (C) and roll (D) gains summated from 2 canal-plugged monkeys. One had its lateral canals plugged (VC animal, M9008), another had anterior and posterior canal plugging (LC animal, M9003). Solid lines: best sinusoidal fit to the horizontal and torsional gains. Dotted lines: range over which the fit for horizontal and roll gains could be phase shifted and still significantly fit the data (P = 0.05). The range of fits for both normal and summated responses overlap, and they are not significantly different.
Data from LC and VC animals were summated to form the curves shown in Fig. 6, C and D. The spatial phasor representing the gain and angle of the average vertical-canal-plugged animals (0.71 at 30°; Table 1, monkey M9008) was added to that from the average horizontal-canal-plugged condition (0.46 at −46°, Table 1). The summed gain was 0.93 at 1° tilt forward (phase error ±8°). The summed spatial roll gain was 0.60 with a zero crossing at −1° tilt backward (phase error ±9°). Differences between the curves from the normal and summed canal-plugged animal data were not significant (P > 0.05). Thus the average summated gains and phases of both horizontal and roll components of the canal-plugged animals matched the corresponding gains and phases of the normal monkeys.
Data from two RALP and two LARP animals were also summated (Fig. 7, C and D and E and F) and compared with the those from the VC animals (Figs. 6, C and D, and 7, A and B). The postulate was that the addition of responses from RALP and LARP animals, which have no lateral canals and only one vertical canal pair, should reconstitute the responses of the VC animals.
The summated horizontal gains for the two pairs of monkeys (M9355 + M9356; M9223 + M9306) had a maximum at 0.57 for −59° tilt backward (±9° phase error) and 0.60 at −49° (0° phase error). The summated torsional gains were 0.63 at −63° (±7° phase error) and 0.51 at −58° (±11° phase error). The gains were slightly higher than the gains in the two VC animals but the phases were comparable. From this we conclude that, disregarding small changes in gain, the normal or plugged-canal responses can be approximated by summating the response from animals with different canal lesions. This indicates that although there was some increase in temporal gain after surgery in the LARP and RALP animals, there was little or no change in the spatial gain and phase after the lesions despite the long periods of recovery after surgery.
Rotation in light after plugging
The previous data show that when animals were rotated in darkness after canal plugging, the roll and horizontal movements were approximately in spatial phase so that there were significant roll eye movements associated with horizontal eye movements (Fig. 5). This was different from the normal animals, where the roll and horizontal eye movements were 90° out of phase (Fig. 6, A and B). Therefore the horizontal and roll components of the VOR recorded in darkness after surgery were anticompensatory in that they would not have improved stabilization of gaze on the surround during head movement.
We determined whether vision would alter the spatial relationship between horizontal and roll components to improve retinal stability during rotation. In six animals with various canal pluggings available for testing in this paradigm (Fig. 8), vision caused the spatial phases to return to those recorded in the normal animals in darkness (Fig. 8, A and B: horizontal, spatial phase ±14°; roll, spatial phase ±21°). The peak spatial gain for canal-plugged animals in light at 10° forward was 0.93 for horizontal and 0.60 for roll at +90° tilt forward (Fig. 8).1 This can be compared with gains and phases of 0.87 at 11° and 0.48 at ±90°, respectively, for the normal animals. This demonstrates that the visual system can compensate for lesions of the peripheral vestibular system. It also indicates that the horizontal and torsional components of the VOR had not been cross-adapted in any of the canal-plugged animals when tested in darkness, although the ocular compensatory movements were correctly phased in light in all of them.
Modeling the canal contributions to the VOR
The data were compared with a model that projects the head velocity into a coordinate frame defined by the normals to the average canal planes and projects the eye velocity command into the head coordinate frame to drive the oculomotor system. This is similar to the approach first used by Robinson (1982) except that that model was based on specific measurements of canal planes relative to the head described by Curthoys et al. (1977) and a muscle transformation. From these two matrices, Robinson derived a brain stem matrix to give an overall VOR gain of −1.0.
In the model presented in this study, the components of eye velocity along the canal axes were derived assuming general angular relationships between the lateral canals θ1 and vertical canals θv relative to the head yaw axis (Fig. 9). Only the angle between the anterior and posterior canals was assumed fixed at 90° and rotated 45° (ψv = 45°). These more general equations relating average canal plane axes in terms of θ1 and θv are explicit in the transformation equations to allow greater flexibility in fitting data to specific animals. Furthermore, because we were interested in the relationship between head velocity and eye velocity, but not the eye muscle or brain stem matrix, we also collapsed the muscle and brain stem matrices into gain parameters.
FIG. 9.
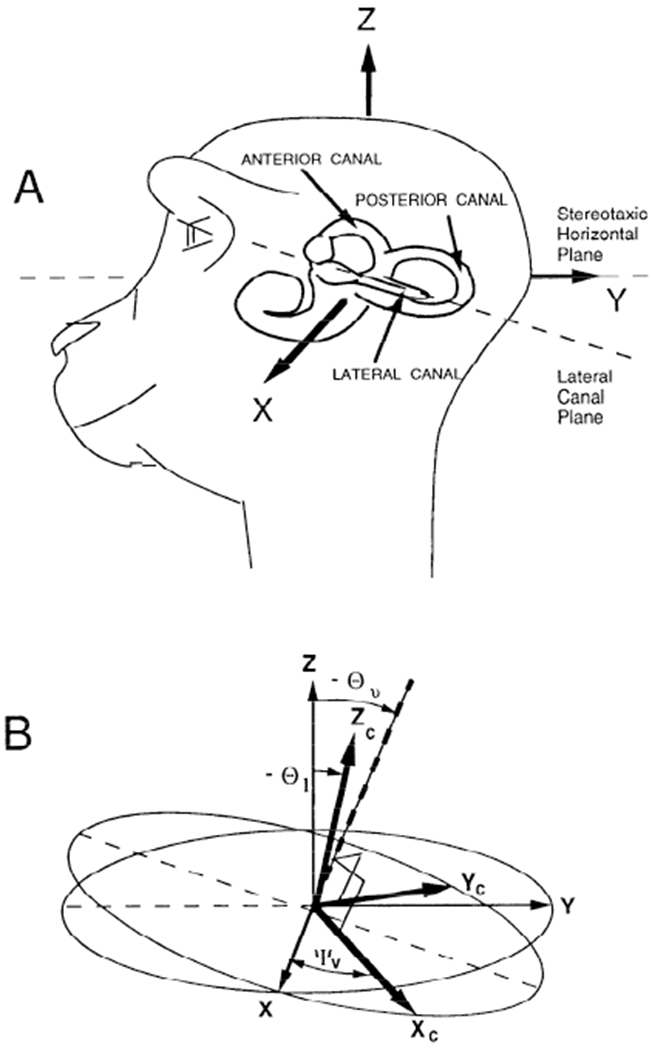
A: position of the left labyrinth of a monkey relative to its head. The coordinate frame of the head has been taken as the stereotaxic frame. It is the coordinate frame in which pitch (vertical), roll (torsion), and yaw (horizontal) eye movements are measured. X: pitch axis. Y: roll axis. Z: yaw axis. B: representation of the relative orientation of the coordinate axes of the stereotaxic frame (X, Y, Z) and the coordinate axes determined by the normals to the semicircular canal planes. The positive direction of these normals is determined by using a right-hand rule for the rotation direction that excites an individual canal. Xc: positive direction for the anterior canal. Yc: positive direction for the posterior canal. Zc: positive direction for the lateral canal. Θ1 is the angle between the stereotaxic vertical axis (Z) and the average direction of the lateral canal axis (Zc). Θυ is the angle between Z and the normal to the plane determined by Xc and Yc. The Xc and Yc axes are orthogonal to each other and rotated relative to the head frame about an axis normal their plane (dashed axis) by an angle ψv. The difference between Θυ and Θ1, represents the nonorthogonality of the canal system coordinate frame.
The coordinate system of the semicircular canals, defined by the normals to their planes, is not coincident with the stereotaxic coordinate frame of the head (Blanks et al. 1975, 1985; Reisine et al. 1988) (Fig. 9, A and B). The normal to the lateral canal (Zc) is tilted back relative to the head yaw axis (Z) by an angle θ1. The normals to the anterior and posterior canal planes (Xc and Yc, Fig. 11B) are tilted back relative to the yaw axis of the head (Z) by an angle θv, which is greater than θ1. These normals are also rotated by an angle ψ about a virtual axis (Fig. 9B, dashed line) that is normal to the plane determined by Xc and Yc. Thus the vertical canals are assumed to be perpendicular to each other. Together, the lateral and vertical canals form a nonorthogonal coordinate frame for encoding the head velocity vector (Blanks et al. 1975, 1985; Ezure and Graf 1984a,b; Reisine et al. 1988; Simpson and Graf 1981).
A head velocity vector ωh relative to the head coordinate frame can be mapped onto the canal frame by taking each of the components of ωh (ωhpit, ωhroll, ωhyaw) and projecting them onto the normals of the canals according to the rotation of the canal plane within the head frame (see appendix for derivation of the relationship between coordinate frames due to a rotation). The component ωhpit has no projection along the normal to the lateral canal and will have a projected value of zero. The relationships between the velocity components along the anterior, posterior, and lateral canal normals can then be given in terms of the pitch, yaw, and roll head velocities as follows:
| (1) |
| (2) |
| (3) |
where (ωhpit, ωhroll, and ωhyaw are the pitch, roll, and yaw components of head velocity in head coordinates and ωant, ωpost, and ωlat are the head velocity components in canal coordinates. The canal activations are mapped back to the stereotaxic head frame by projecting their activations to each of the head coordinate basis vectors. They are given by the following equations
| (4) |
| (5) |
| (6) |
where ωepit, ωeroll, and ωeyaw are the pitch, roll, and yaw components of eye velocity in head coordinates.
A similar procedure was followed to obtain eye velocity in head coordinates by projecting each canal component to the eye velocity component. The orientation of a canal relative to a head coordinate axis multiplied by a gain (g) is the percentage of that canal activation along that coordinate axis of the head. The sum of the projections multiplied by its associated gain from all canals determines the gain of each component of eye velocity. It has been assumed that the complementary canals on both sides act in a push-pull combination, that they are coplanar, and that they contribute equally to the compensatory eye velocity vector (Cohen et al. 1964).
The spatial properties of the eye velocity characteristics were simulated with this model using θ1 = −30° and θv = −40°. The parameters g00 and g01 were chosen as 0.83, corresponding to the gain of the anterior and posterior contribution to the vertical VOR. Each lateral canal and a fortiori the average plane of the lateral canals on both sides are close to 90° with respect to the midsagittal plane in the monkey (Blanks et al. 1985). Therefore they do not significantly contribute to generating a vertical velocity (Suzuki et al. 1964), and g02, which represents the gain of the lateral canal contribution to the vertical VOR, was set to zero. Because g10, g11, and g12 represent the anterior, posterior, and lateral canal gain contributions to roll, they were chosen as 0.52, corresponding to the gain of the torsional VOR recorded in darkness. The gain parameters g20, g21, and g22 represent the anterior, posterior, and lateral canal gain contributions to the horizontal VOR. They were chosen as 0.87, corresponding to the yaw axis gain in our data.
For animals with normal labyrinths, the model predicted that the VOR gain of yaw and roll would vary sinusoidally as a function of tilt angle (Fig. 10, A and B), although the yaw and roll components were shifted 90° relative to each other. The peak of the yaw gain occurred at 0° and corresponded to the zero crossing of the roll gain. The normal monkeys had peak yaw and roll gains at 11 ± 14° and 90 ± 21°, respectively. The differences between the model predictions and the data were not significant. Thus, despite the fact that the canals are nonorthogonal and are tipped up reflex still has a neak at 0°. This corresponds to our data, which peaked on average at 11° tilt forward.
FIG. 10.

Model simulations of yaw and roll VOR gains as a function of tilt for a normal monkey (A and B) and for monkeys with plugged bilateral anterior and posterior canals (LC animals; C and D), bilateral lateral canals (VC animals; E and F), bilateral lateral, left anterior, and right posterior canals (RALP animals; G and H). For purposes of simulation, Θ1 = 30°, Θυ = 40°, and ψv = 45°. The simulations agree with the data of Figs. 5–7.
When the vertical canals were plugged, leaving the lateral canals intact (LC animal; Fig. 10, C and D), the model predicted a peak gain of 0.68 and 0.34 for yaw and roll, respectively, occurring for both at 30° tilt forward (Table 1). Corresponding gains in the LC animal (monkey M9008) were 0.71 (yaw) and 0.37 (roll), occurring at 30 and 39°, respectively (Table 1). When the lateral canals were plugged, leaving the vertical canals intact (VC animal; Fig. 10, E and F), the model predicted 0.44 and 0.46 peak yaw and roll gains, respectively, occurring at −50° tilt back (Table 1). Corresponding average gains for the two VC animals were 0.43 for both yaw and roll. The average phases were −53° for yaw and −58° for roll (monkeys M9003 and M9354, Table 1). After the lateral, left anterior, and right posterior canals were plugged (RALP animal; Fig. 10, G and H), the model predicted a reduction in the gain of both components to 0.22 and 0.23 for yaw and roll, respectively. The peak gains for both occurred at −50° tilt backward. The average peak yaw and roll gains for the five LARP and RALP animals were 0.27 and 0.28, occurring at −55 and −62°.
Thus, even though the model was based on average rather than specific normal responses, it was capable of approximately predicting both the normal and the plugged-canal animal data with a single set of parameters. Although the model predicted that the phases would occur at the same angle, there were small discrepancies in the LC, LARP, and RALP animals. These were not significant, however. The model also predicted the appearance of a vertical component with the same spatial phase as the horizontal component in the LARP and RALP animals at −50° tilt back. This vertical component was also present in the experimental data (, Fig. 3B).
DISCUSSION
The experiments support the idea that when the head is rotated, there is a geometric projection of the head velocity vector onto the planes of the semicircular canals to drive eye velocity. They show that each semicircular canal contributes horizontal and torsional components of eye velocity to the compensatory VOR independently according to its geometric orientation within the head in the normal or canal-plugged animal. It was possible to predict the data from the model for the normal and plugged animals using a nonorthogonal coordinate frame and a single set of parameters from the normal animals. Had there been significant spatial gain or phase adaptation after plugging, the spatial phases of the summated curves would be different from the model predictions. Therefore we conclude that there was no spatial adaptation after canal plugging, and that the geometric association between the canals and the oculomotor system, represented by the gain parameters of the model, was not altered by plugging. Regardless of variation from any source, the average phase error for the 95% confidence level in the 32 data sets from the eight animals was ±8°. The ANOVA indicated that on average, the model fits to the data were within this resolution.
Although the yaw and roll eye velocity components were spatially out of phase by ≈90° in the normal animals, they were in phase or 180° out of phase when the VOR was produced by one or more single canal pairs. As a result, the eyes had a torsional component associated with rotation about a yaw axis in darkness after lateral or vertical canal plugging (Figs. 5 and 7) where there was none in the normal animal (Fig. 6, A and B) or during rotation in light (Fig. 8). This inappropriate roll component must have caused visual-vestibular conflict when the animals moved their heads in light after plugging. That the animals did not adaptively suppress the roll component during yaw axis rotation in darkness was surprising considering the remarkable plasticity of the vestibular system, as well as the ability of the brain to alter spatial responses during visual-vestibular conflict stimulation (Baker et al. 1986, 1987; Schultheis and Robinson 1981).
The fact that both the horizontal and torsional gains were phase shifted in the same way when the vertical canals were plugged and only the lateral canals were intact demonstrates that a torsional component is produced by the lateral canals in the normal animal. When the normal animal is upright and rotated, the torsional component generated by the lateral canals superposes with that from the vertical canals to produce a zero torsional response. Similarly, there is a superposition of the yaw component of eye velocity produced by the lateral and vertical canals to generate a maximum response at zero spatial phase or close to the upright position.
Peak horizontal gains for the normal animal, calculated by Böhmer et al. (1985), occurred at 15° tilt forward. This value is close to the angle at which peak horizontal gains occurred in our normal animals (11°, range −1–19°, Table 1). It is different from the mean lateral canal orientation in our animals, however, which was predicted to be ~30°. The latter is close to predictions from the physiological data of Miles and Braitman (1980). Data in both Böhmer et al. (1985) and this study are consistent with the interpretation that the peak horizontal VOR response is dependent on activation of both the lateral and vertical canals. This would explain why the null point for the horizontal gain curve crossed zero away from the 15° tilt position after lateral canal plugging.
After surgery, the animals initially had postural instability as well as head titubation in the planes of the plugged canals. After recovery, their behavior was close to that of normal animals, with the exception of slight instability of the head during movement in the plugged-canal planes. There were small differences between the normal gains and those obtained from a summation of the responses after canal plugging. These differences were also present in a comparison of model predictions and observed post-canal-plugging responses. These small gain increases could not have been responsible for the behavioral adaptation that was present in each of the animals. Rather, recovery was likely to be due to the dependence on visual-oculomotor reflexes (Fig. 8), on enhanced cervicoocular reflexes (Böhmer et al. 1985; Dichgans et al. 1973), and on adaptation of posture (for review see Curthoys and Halmagyi 1995). This may have clinical significance in that recovery after labyrinthine lesions in humans may mask the effects of the lesion, and deficits may be expressed during appropriate stimulation.
There is evidence that the axis of eye velocity is not aligned with the axis of rotation when the eye looks up or down during rotation of the head about a yaw axis (Henn et al. 1992; Misslisch et al. 1994). However, the axis shift is variable, and for small vertical shifts of the eyes (<7–8°), the axis shift will be <3° in both monkeys and humans (Crawford and Vilis 1991; Misslisch et al. 1994). Thus our method of orthogonalization of the coils would not significantly impact our analysis or the conclusions drawn from it, particularly because the analysis is focused on the relative changes in horizontal and torsional changes in eye velocity before and after lesions. Computation of spatial gains using eye velocity in head coordinates (APPENDIX) would also not alter our results or conclusions. Data plotted for yaw and roll eye velocities as a function of tilt angle in the normal animal (Fig. 11, A and B), and after canal plugging (Fig. 11, C–H), confirmed that there was no significant difference between the results derived from a differentiation of coil voltages and from computation of eye velocity in head coordinates for any of the canal-plugged conditions (ANOVA, P > 0.05).
The zero crossings of the model predictions for the normal responses occurred at ±90° for yaw (Fig. 10A). These were close to the experimental data. Variation increased for yaw at ±90° (Fig. 6A). A likely explanation for the increase in variance is the change in vertical eye position when the animals were tilted forward or back, due to compensatory static otolith-ocular reflexes (Fig. 4). The horizontal component of eye velocity induced by rotation around a spatial vertical varied as the cosine of the angle between the axis of eye rotation and the yaw axis. The nature of the cosine function is such that the amplitude of the horizontal component is largest with the animal upright, but the sensitivity of change in the horizontal component is largest with the animal supine or prone and smallest with the animal upright. Thus small upward or downward movement of the eyes could easily increase the horizontal component of the VOR when the animals were in forward or backward pitch, although the same vertical deviations would have little effect when the animals were upright.
The peak yaw gain after vertical canal plugging occurred at ~30° (Fig. 5A). The maximum yaw gain after lateral canal plugging occurred at approximately −50° (Table 1). From these values we estimated that the average vertical canal planes were tilted ~30° back relative to the stereotaxic horizontal plane, whereas the vertical canals were tipped back ≈40°, the values used in simulating the data. There were variations among the monkeys that could easily be simulated by changing these angles in the model. In some instances there were phase shifts between the yaw and roll peaks for the plugged animals that cannot be encompassed by this model. These phase shifts were not significant from a statistical point of view, and at present we have ignored them. The angles of the lateral and vertical canal planes are ~10° more in our data than in the study of Reisine et al. (1988). They are in general agreement with calculations of others, however (Blanks et al. 1975, 1985). Differences between the various studies may be due to individual variation based on species or differences between animals or to differences in the placement of the head in the stereotaxic frames (Curthoys et al. 1977).
A critical factor in predicting the results was incorporating a nonorthogonal coordinate frame in the model. This was necessary to explain the finding that the maximal horizontal and roll components occurred at ≈30° tilt forward when the lateral canals were intact as compared with the maximal components at −50° tilt back when only the vertical canals were intact. The difference between the two is not 90°. As a result, it is not possible to activate the lateral canals maximally with rotation without activating the vertical canals. Conversely, it is not possible to activate the vertical canals maximally with rotation without activating the lateral canals. Despite the fact that there is a nonorthogonal frame, the normal animal would have a peak in the upright at 0° because of the contributions of all of the canals.
The nonorthgonality found in this behavioral study is supported by both anatomic and physiological data. In the rhesus monkey, the nonorthogonality of the relationship between the lateral and the vertical canals was on the order of 10° (Blanks et al. 1985; Reisine et al. 1988), as in this study. The nonorthogonality is greater in the guinea pig and in humans (Blanks et al. 1975). Minor and Goldberg (1990) tested the horizontal contribution to the VOR when the lateral canals were presumed vertical. They concluded that “signals from the horizontal, but not the vertical canals contribute to the HVOR,” whereas we have inferred an important vertical canal contribution. Differences between the studies are that Minor and Goldberg assumed orthogonality of the vertical and lateral canals, whereas we found that a nonorthogonal canal coordinate frame was better able to approximate the data in our animals.
Baker and Peterson (1991) assumed from the data of Curthoys et al. (1977) that the amount of nonorthogonality between the vertical and lateral canals in the cat was 6°. By tipping animals forward by 28°, they further assumed that the vertical canals were vertical. A larger angle of tilt of the vertical canals with regard to the lateral canals in individual cats could cause a greater contribution of the individual canals in the activation of individual muscles, perhaps accounting for differences between the study of Baker and Peterson and those utilizing mechanical or electrical stimulation of the canals (Cohen et al. 1964; Suzuki et al. 1964; Szentágothai 1950; Tokumasu et al. 1965).
There were differences in the gain values between the data from the normal animals and the summed LC and VC animals, as well as between the VC animals and the summed LARP and RALP animals (Figs. 5 and 7). The spatial gains were slightly greater for the operated animals, but the differences were not significant. This can be explained by an adaptive increase in the gains of the horizontal and torsional components. Such adaptation, however, would have to occur concurrently in the horizontal and torsional components; otherwise it would cause a change in the spatial phases of the response, which did not occur.
The conclusion about the spatial invariance of canal-induced components of the VOR with regard to the head is limited to the direct vestibular pathway, which is predominantly active during frequencies of sinusoidal rotation between 0.1 and 8 Hz, the range of normal head movements. Below this frequency, cross coupling of velocity storage would have converted the head-fixed, directional responses after canal plugging into responses that were oriented around gravity (Dai et al. 1991; Raphan and Sturm 1991; Raphan et al. 1992).
The model also predicted that a vertical component would appear in the RALP and LARP animals. This was observed, as is shown in Fig. 3B . The reason for this vertical component is that the activated canal pair in the RALP and LARP animals is shifted ≈45° from the midline, causing a vector projection onto the X-axis.
In summary, the data support the hypothesis that the individual canal pairs contribute eye velocity components according to the vector projection onto the individual canals. The gains and the spatial phases of the horizontal component were the same after lateral canal plugging as in previous studies (Baker et al. 1982; Böhmer et al. 1985; Cohen et al. 1988). The finding that the data from separate animals with different combinations of lesions could be combined to predict the response of the normal and the canal-plugged monkeys was internally consistent. These data suggest that despite considerable plasticity in the VOR, the canal coordinate system is hard-wired, and that the innate coordinate frame with regard to the head is not altered in adult animals by lesions of the individual canals.
Acknowledgments
We thank Dr. Yasuko Arai of Tokyo Women’s Medical College for aid in analyzing the anatomy and V. Rodriguez for technical assistance.
This work was supported by National Institutes of Health Grants NS-00294, EY-04148, and EY-01867.
APPENDIX
Computation of eye velocity in head coordinates and comparison with derivatives of coil voltages
The voltages, Vfx and Vfz, derived from the frontal coil are proportional to the inner products of the normal to the frontal coil, , with unit vectors, ex and ez, along the X- and Z-axes, respectively. The voltage Vtx is proportional to the inner product of the normal to the top coil, , with the unit vector along the X-axis, ex. These voltages can be related to the rotation matrix that describes the orientation of the eye with respect to the head using various parameterization techniques, including quaternions (Crawford and Vilis 1991; Tweed and Vilis 1987; Tweed et al. 1990; Westheimer 1957), rotation vectors (Haslwanter et al. 1992; Haustein 1989), Euler angles (Collewijn et al. 1988), and axis angle (Schnabolk and Raphan 1994). These different representations are not different coordinate frames but relate the eye coordinate frame to the head frame. These different parameterizations can in turn be related to each other. Because the computation of eye velocity is uniquely determined as a vector in head coordinates, it is independent of the formalism for describing eye orientation, which is not a vector. That is, any representation of eye position would lead to the same eye velocity that is the primary interest of this paper.
A simple parameterization of the rotation matrix is through Euler angles (Euler 1775). These can be chosen in a variety of ways, one of which corresponds to Fick angles (1854). This describes the rotation about a fixed point as a sequence of rotations given by three matrices
| (A1) |
| (A2) |
| (A3) |
where ϕ, θ, and ψ are the Euler angles representing rotations about the head yaw axis, a line of nodes axis (rotated pitch axis) of the eye, and the optic axis (doubly rotated axis). The positive directions for the head-based axes are shown in Figs. 2 and 9 and the rotations are in accordance with the right-hand rule. A vector in eye-based coordinates can be expressed in the head coordinate frame by the following transformation (Goldstein 1980)
| (A4) |
Because the coil moves with the eye, the normal to the frontal coil can be expressed as (0, −1, 0) in eye coordinates, independent of eye orientation. This vector can be obtained in head coordinates by multiplying it by the rotation matrix given in Eq. A4. Therefore, in head coordinates, the vector is given by . The top coil normal is given by (0, 0, 1) in eye coordinates. This vector can similarly be transformed by Eq. 4 to head coordinates to a vector, . The voltage output for the coil system, scaled to values between {−1, 1}, can be represented as inner products of the coil vectors, and with unit vectors along the field coil axes. Because in this study the horizontal, vertical, and roll voltages were recorded as positive for movements to the right, upward, and clockwise from the animal’s point of view, the negative of the voltages Vfx, Vfz, and Vtx are the inner products of with ex, with ez, and with ex, respectively. In terms of Euler angles, this can be expressed as follows
| (A5) |
The derivatives of these voltages can be expressed in terms of the Euler angles and their derivatives as follows
| (A6) |
A simple algorithm can be derived to compute the components of eye velocity in head coordinates, ω, from the coil voltages at each instance of time as follows.
From Eq. A5, the Euler angles representing eye orientation can be obtained sequentially from the coil voltages as follows
| (A7) |
Using the Euler angles computed in Eq. A7, the derivatives of the Euler angles can be obtained sequentially from Eq. A6 as follows
| (A8) |
The components of the angular velocity vector along the pitch (X), roll (Y), and yaw (Z) axes of the head are given in terms of the Euler angles and their derivatives by Goldstein (1980)
| (A9) |
where ωx, ωy, and ωz are the components of angular velocity of the eyes in head coordinates, and ϕ, , and are the derivatives of the Euler angles. Substituting the values obtained in Eqs. A7 and A8 into Eq. A9 generates the components of the angular velocity, ωx, ωy, and ωz, in head coordinates at each instant in time. It should be noted that for small angles (<15°) the angular velocity in head coordinates is approximately equal to the derivatives of the Euler angles, which are in turn approximately equal to the derivatives of the coil voltages.
Footnotes
Data in Fig. 8, derived from rotation of the canal-plugged monkeys in light, were not fitted. When the animals were tilted more than −60° back, they faced a frame on the ceiling of the drum that attached the primate chair to the primate axis. This provided a stationary field that covered the optokinetic stimulus and caused suppression of the VOR. It accounts for the sharp drop in the gain of the horizontal VOR for tilts between −70 and −90°. Therefore the data could not be approximated with a single best fit line, and only the mean values at the other tilt angles are shown (open symbols ± 1 SD). The solid and dotted lines in this figure show the fitted cosine curve and the phase error calculations for the eight normal monkeys for comparison.
REFERENCES
- Baker J, Wickland C, Goldberg J, and Peterson B Motor output to lateral rectus in cats during the vestibulo-ocular reflex in three-dimensional space. Neuroscience 25: 1–12, 1988. [DOI] [PubMed] [Google Scholar]
- Baker JF, Goldberg J, Peterson BW, and Schor R Oculomotor reflexes after semicircular canal plugging in cats. Brain Res. 252: 151–155, 1982. [DOI] [PubMed] [Google Scholar]
- Baker JF, Isu N, Wickland CR, and Peterson BW Dynamics of adaptive change in vestibulo-ocular reflex directions. II. Sagittal plane rotation. Brain Res. 371: 166–170, 1986. [DOI] [PubMed] [Google Scholar]
- Baker JF and Peterson BW Excitation of the extraocular muscles in decerebrate cats during the vestibulo-ocular reflex in three-dimensional space. Exp. Brain Res 84: 266–278, 1991. [DOI] [PubMed] [Google Scholar]
- Baker JF, Wickland C, and Peterson BW Dependence of cat vestibulo-ocular reflex direction adaptation on animal orientation during adaptation and rotation in darkness. Brain Res. 408: 339–343, 1987. [DOI] [PubMed] [Google Scholar]
- Barmack NH and Pettorossi VE The induction and compensation of asymmetric eye movements following unilateral blockage of horizontal semicircular canal in the rabbit. J. Neurosci 8: 2836–2843, 1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berthoz A, Melvill Jones G, and Begue AE Differential visual adaptation of vertical canal-dependent vestibulo-ocular reflexes. Exp. Brain Res 44: 19–26, 1981. [DOI] [PubMed] [Google Scholar]
- Blanks RHI, Curthoys IS, Bennett M, and Markham CH Planar relationships of the semicircular canals in rhesus and squirrel monkeys. Brain Res. 340: 315–324, 1985. [DOI] [PubMed] [Google Scholar]
- Blanks RHI, Curthoys IS, and Markham CH Planar relationships of the semicircular canals in man. Acta Otolaryngol. 80: 185–196, 1975. [DOI] [PubMed] [Google Scholar]
- Böhmer A, Henn V, and Suzuki JI Vestibuloocular reflex after selective plugging of the semicircular canals in the monkey—response plane determinations. Brain Res. 326: 291–298, 1985. [DOI] [PubMed] [Google Scholar]
- Camis M The Physiology of the Vestibular Apparatus. Oxford, UK: Clarendon, 1930. [Google Scholar]
- Cohen B, Helwig D, Raphan T, Suzuki JI, Kaga K, and Eden A Changes in visual and vestibular function after canal plugging in the monkey. Soc. Neurosci. Abstr 14: 173, 1988. [Google Scholar]
- Cohen B, Kozlovskaya I, Raphan T, Solomon D, Helwig D, Cohen N, Sirota M, and Yakushin S Vestibular reflex of rhesus monkeys after spaceflight. J. Appl. Physiol 73, Suppl. : 121–131, 1992. [DOI] [PubMed] [Google Scholar]
- Cohen B, Suzuki JI, and Bender MB Eye movements from semicircular canal nerve stimulation in the cat. Ann. Otorhinolaryngol. 73: 153–169, 1964. [DOI] [PubMed] [Google Scholar]
- Cohen B, Suzuki JI, and Raphan T Role of the otolith organs in generation of horizontal nystagmus: effects of selective labyrinthine lesions. Brain Res. 276: 159–164, 1983. [DOI] [PubMed] [Google Scholar]
- Collewijn H, Ferman L, and Van den Berg AV The behavior of human gaze in three dimensions In: Representation of Three-Dimensional Space in the Vestibular, Oculomotor, and Visual Systems, edited by Cohen B and Henn V. New York: NY: Acad. Sci., 1988, vol. 545, p. 105–127. [DOI] [PubMed] [Google Scholar]
- Correia MJ and Money KE The effect of all six semicircular canal ducts on nystagmus produced by linear acceleration in the cat. Acta Otolaryngol. 69: 7–16, 1970. [DOI] [PubMed] [Google Scholar]
- Crawford JD and Vilis T Axes of eye rotation and Listing’s law during rotations of the head. J. Neurophysiol 65: 407–423, 1991. [DOI] [PubMed] [Google Scholar]
- Curthoys IS, Blanks RHI, and Markham CH Semicircular canal functional anatomy in cat, guinea pig and man. Acta Otolaryngol. 83: 258–265, 1977. [DOI] [PubMed] [Google Scholar]
- Curthoys IS and Halmagyi GM Vestibular compensation: a review of the oculomotor, neural, and clinical consequences of unilateral vestibular loss. J. Vestib. Res 5: 67–107, 1995. [PubMed] [Google Scholar]
- Dai M, McGarvie L, Kozlovskaya I, Raphan T, and Cohen B Effects of spaceflight on ocular counterrolling and spatial orientation of the vestibular system. Exp. Brain Res 102: 45–56, 1994. [DOI] [PubMed] [Google Scholar]
- Dai MJ, Raphan T, and Cohen B Spatial orientation of the vestibular system: dependence of optokinetic afternystagmus on gravity. J. Neurophysiol 66: 1422–1438, 1991. [DOI] [PubMed] [Google Scholar]
- Dichgans J, Bizzi E, Morasso P, and Tagliasco V Mechanisms underlying recovery of eye-head coordination following bilateral labyrinthectomy in monkey. Exp. Brain Res 18: 548–562, 1973. [DOI] [PubMed] [Google Scholar]
- Duensing F and Schaefer KP Die Aktivität einzelner Neurone im Bereich der Vestibulariskerne bei Horizontal-beschleunigungen unter besonderer Berücksichtigung des vestibulären Nystagmus. Arch. Psychiatr. Nervenkr 198: 225–252, 1958. [DOI] [PubMed] [Google Scholar]
- Euler L Formulae generales pro translatione quacunque corporum rigidorum. Novi Comm. Acad. Sci. Imp. Petrop 20: 189–207, 1775. [Google Scholar]
- Ewald JR Physiologische Untersuchungen über das Endorgan des Nervus Octavus. Wiesbaden, Germany: Bergmann, 1892. [Google Scholar]
- Ezure K and Graf W A quantitative analysis of the spatial organization of the vestibulo-ocular reflexes in lateral- and frontal-eyed animals. I. Orientation of semicircular canals and extraocular muscles. Neuroscience 12: 85–93, 1984a. [DOI] [PubMed] [Google Scholar]
- Ezure K and Graf W A quantitative analysis of the spatial organization of the vestibulo-ocular reflexes in lateral- and frontal-eyed animals. II. Neuronal networks underlying vestibulo-oculomotor coordination. Neuroscience 12: 95–109, 1984b. [DOI] [PubMed] [Google Scholar]
- Ferman L, Collewijn H, Jansen TC, and Van den Berg AV Human gaze stability in the horizontal, vertical and torsional direction during voluntary head movement, evaluated with a three-dimensional scleral induction coil technique. Vision Res. 5: 811–828, 1987a. [DOI] [PubMed] [Google Scholar]
- Ferman L, Collewijn H, and Van den Berg AV A direct test of Listing’s law. II. Human ocular torsion measured under dynamic conditions. Vision Res. 27: 939–951, 1987b. [DOI] [PubMed] [Google Scholar]
- Fetter M, Hain TC, and Zee DS Influence of eye and head position on the vestibulo-ocular reflex. Exp. Brain Res 64: 208–216, 1986. [DOI] [PubMed] [Google Scholar]
- Fick A Die Bewegungen des menschlischen Augapfel. Z. Rationelle Med 4: 101–128, 1854. [Google Scholar]
- Goldberg JM and Fernandez C Responses of peripheral vestibular neurons to angular and linear accelerations in the squirrel monkey. Acta Otolaryngol. 80: 101–110, 1975. [DOI] [PubMed] [Google Scholar]
- Goldstein H Classical Mechanics. Reading, MA: Addison-Wesley, 1980. [Google Scholar]
- Haslwanter T, Straumann D, Hess BJM, and Henn V Static roll and pitch in the monkey: shift and rotation in Listing’s plane. Vision Res. 32: 1341–1348, 1992. [DOI] [PubMed] [Google Scholar]
- Haustein W Consideration on Listing’s law and the primary position by means of a matrix description of eye position control. Biol. Cybern 60: 411–420, 1989. [DOI] [PubMed] [Google Scholar]
- Henn V, Straumann D, Hess BJM, Haslwanter T, and Kawachi N Three-dimensional transformations from vestibular and visual input to oculomotor output. Ann. NY Acad. Sci 656: 166–180, 1992. [DOI] [PubMed] [Google Scholar]
- Igarashi M, Himi T, Kulecz WB, and Patel S The role of saccular afferents in vertical optokinetic nystagmus in primates. A study in relation to optokinetic nystagmus in microgravity. Arch. Otorhinolaryngol 244: 143–146, 1987. [DOI] [PubMed] [Google Scholar]
- Judge SJ, Richmond BJ, and Chu FC Implantation of magnetic search coils for measurement of eye position: an improved method. Vision Res. 20: 535–538, 1980. [DOI] [PubMed] [Google Scholar]
- Keppel G Design and Analysis: A Researcher’s Handbook (3rd ed.). Englewood Cliffs, NJ: Prentice-Hall, 1991. [Google Scholar]
- McCrea RA, Strassman A, and Highstein SM Anatomical and physiological characteristics of vestibular neurons mediating the vertical vestibulo-ocular reflexes of the squirrel monkey. J. Comp. Neurol 264: 571–594, 1987. [DOI] [PubMed] [Google Scholar]
- Miles FA and Braitman DJ Long-term adaptive changes in primate vestibulo-ocular reflex. II. Electrophysiological observations on semicircular canal primary afferents. J. Neurophysiol 43: 1426–1436, 1980. [DOI] [PubMed] [Google Scholar]
- Minor LB and Goldberg JM Influence of static head position on the horizontal nystagmus evoked by caloric, rotational and optokinetic stimulation in the squirrel monkey. Exp. Brain Res 82: 1–13, 1990. [DOI] [PubMed] [Google Scholar]
- Misslisch H, Tweed D, Fetter M, and Vilis T The influence of gravity on Donders’ Law for head movement. Vision Res. 34: 3017–3025, 1994. [DOI] [PubMed] [Google Scholar]
- Money KE and Scott JW Functions of separate sensory receptors of non-auditory labyrinth of the cat. Am. J. Physiol 202: 1211–1220, 1962. [DOI] [PubMed] [Google Scholar]
- Paige GD Vestibuloocular reflex and its interactions with visual following mechanisms in the squirrel monkey. II. Response characteristics and plasticity following unilateral inactivation of horizontal canal. J. Neurophysiol 49: 152–168, 1983. [DOI] [PubMed] [Google Scholar]
- Paige GD and Tomko DL Eye movement responses to linear head motion in the squirrel monkey. I. Basic characteristics. J. Neurophysiol 65: 1170–1182, 1991. [DOI] [PubMed] [Google Scholar]
- Raphan T, Cohen B, and Henn V Effects of gravity on rotatory nystagmus in monkeys In: Vestibular and Oculomotor Physiology: International Meeting of the Barany Society, edited by Cohen B. New York: NY: Acad. Sci., 1981, vol. 374, p. 44–55. [DOI] [PubMed] [Google Scholar]
- Raphan T, Cohen B, and Henn V Nystagmus generated by sinusoidal pitch while rotating. Brain Res. 276: 165–172, 1983. [DOI] [PubMed] [Google Scholar]
- Raphan T, Dai M, and Cohen B Spatial orientation of the vestibular system In: Sensing and Controlling Motion: Vestibular and Sensorimotor Function, edited by Cohen B, Tomko D, and Guedry F. New York: NY: Acad. Sci., 1992, vol. 656, p. 140–157. [DOI] [PubMed] [Google Scholar]
- Raphan T, Matsuo V, and Cohen B Velocity storage in the vestibuloocular reflex (VOR). Exp. Brain Res 35: 229–248, 1979. [DOI] [PubMed] [Google Scholar]
- Raphan T and Sturm D Modelling spatiotemporal organization of velocity storage in the vestibuloocular reflex by optokinetic studies. J. Neurophysiol 66: 1410–1421, 1991. [DOI] [PubMed] [Google Scholar]
- Reisine H and Raphan T Neural basis for eye velocity generation in the vestibular nuclei during off-vertical axis rotation (OVAR). Exp. Brain Res 92: 209–226, 1992. [DOI] [PubMed] [Google Scholar]
- Reisine H, Simpson JI, and Henn V A geometric analysis of semicircular canals and induced activity in their peripheral afferents in the rhesus monkey. Ann. NY Acad. Sci 545: 10–20, 1988. [DOI] [PubMed] [Google Scholar]
- Robinson DA A method of measuring eye movements using a scleral search coil in a magnetic field. IEEE Trans. Biomed. Eng 10: 137–145, 1963. [DOI] [PubMed] [Google Scholar]
- Robinson DA The use of matrices in analyzing the three-dimensional behavior of the vestibuloocular reflex. Biol. Cybern 46: 53–66, 1982. [DOI] [PubMed] [Google Scholar]
- Schnabolk C and Raphan T Modeling three dimensional velocity-to-position transformation in oculomotor control. J. Neurophysiol 71: 623–638, 1994. [DOI] [PubMed] [Google Scholar]
- Schultheis LW and Robinson DA Directional plasticity of the vestibulo-ocular reflex in the cat. In: Vestibular and Oculomotor Physiology: International Meeting of the Barany Society, edited by Cohen B. New York: NY Acad. Sci., 1981, vol. 374, p. 504–512. [Google Scholar]
- Shimazu H and Precht W Tonic and kinetic responses of cat’s vestibular neurons to horizontal angular acceleration. J. Neurophysiol 28: 991–1013, 1965. [DOI] [PubMed] [Google Scholar]
- Simpson J and Graf W Eye-Muscle Geometry and Compensatory Eye Movements in Lateral-Eyed and Frontal-Eyed Animals. In: Vestibular and Oculomotor Physiology: International Meeting of the Barany Society New York: NY Acad. Sci., 1981, vol. 374, p. 20–30. [DOI] [PubMed] [Google Scholar]
- Singh A, Thau FE, Raphan T, and Cohen B Detection of saccades by a maximum likelihood ratio criterion. In: Proc. 34th Annu. Conf. Eng. Biol. Houston, TX, 1981. [Google Scholar]
- Straumann D, Haslwanter T, Hepp-Reymond M-C, and Hepp K Listing’s law for eye, head and arm movements and their synergistic control. Exp. Brain Res 86: 209–215, 1991. [DOI] [PubMed] [Google Scholar]
- Suzuki J, Cohen B, and Bender MB Compensatory eye movements induced by vertical semicircular canal stimulation. Exp. Neurol 9: 137–160, 1964. [DOI] [PubMed] [Google Scholar]
- SzenthÁgothai J The elementary vestibuloocular reflex arc. J. Neurophysiol 13: 395–407, 1950. [DOI] [PubMed] [Google Scholar]
- Tokumasu K, Goto K, and Cohen B Eye movements produced by the superior oblique muscle. Arch. Ophthalmol 73: 851–862, 1965. [DOI] [PubMed] [Google Scholar]
- Tweed D, Cadera W, and Vilis T. Computing three-dimensional eye position quaternions and eye velocity for search coil signals. Vision Res. 30: 97–110, 1990. [DOI] [PubMed] [Google Scholar]
- Tweed D and Vilis T Implications of rotational kinematics for the oculomotor system in three dimensions. J. Neurophysiol 58: 832–849, 1987. [DOI] [PubMed] [Google Scholar]
- Westheimer G Kinematics of the eye. J. Opt. Soc. Am 47: 967–974, 1957. [DOI] [PubMed] [Google Scholar]
- Wilson VJ and Melvill Jones G Mammalian Vestibular Physiology. New York: Plenum, 1979. [Google Scholar]
- Yue Q, Straumann D, and Henn V Three-dimensional characteristics of rhesus monkey vestibular nystagmus after velocity steps. J. Vestib. Res 4: 313–323, 1994. [PubMed] [Google Scholar]


