A Nonlinear Support Vector Machine-Based Feature Selection Approach for Fault Detection and Diagnosis: Application to the Tennessee Eastman Process

Abstract

In this article, we present (1) a feature selection algorithm based on nonlinear support vector machine (SVM) for fault detection and diagnosis in continuous processes and (2) results for the Tennessee Eastman benchmark process. The presented feature selection algorithm is derived from the sensitivity analysis of the dual C-SVM objective function. This enables simultaneous modeling and feature selection paving the way for simultaneous fault detection and diagnosis, where feature ranking guides fault diagnosis. We train fault-specific two-class SVM models to detect faulty operations, while using the feature selection algorithm to improve the accuracy and perform the fault diagnosis. Our results show that the developed SVM models outperform the available ones in the literature both in terms of detection accuracy and latency. Moreover, it is shown that the loss of information is minimized with the use of feature selection techniques compared to feature extraction techniques such as principal component analysis (PCA). This further facilitates a more accurate interpretation of the results.

Introduction

The emergence of the fourth industrial revolution, Industry 4.0,^1,2 along with the recent Big Data initiatives has enabled a research breakthrough in the field of data-driven (or statistical) process monitoring. The main goal is to ensure Smart Manufacturing, a concept envisioned by numerous agencies including the US Department of Energy (DoE) and the National Institute of Standards and Technology (NIST), which describes the motivation to design intelligent factories that can rapidly adapt to changes/disturbances by sharing and analyzing process data during manufacturing operation. Thus, integration of the advancements in information technology (i.e., enhanced networking, cloud services, and data analytics) with operations technology (i.e., adaptive automation, sensor, and software technology) is of utmost importance to produce a network communication between process instruments known as industrial Internet of Things.³ As the industry is moving toward such automated and integrated process architecture, the analysis of process data produced in large amount in real time is becoming more practical in various engineering applications to understand underlying trends and subsequently improve decision-making for operation. Data-driven process monitoring, specifically fault detection and diagnosis, is one of these major fields where industrial process data play a significant role in accurate and timely decision-making to maintain a safe and profitable operation.

Data-driven process monitoring exploits multivariate statistics and data mining methods to determine whether a fault has occurred or not during industrial process operations. Here, fault is defined as abnormal process behavior that may have caused by equipment failure, equipment wear, or extreme process disturbances.⁴ When compared to traditional first-principle-based process monitoring methods, data-driven methods are advantageous in capturing intrinsic complexity of the industrial processes by benefiting of the abundance in process data. Thus, data-driven methodologies have sparked significant interest within the last two decades and their applications have become prevalent in wide range of industries including the chemical, energy, medical, photovoltaic, semiconductor manufacturing, and steel industries.^5–12 The widely accepted, the so-called traditional, technique for fault detection is anomaly/outlier, out-of-control situation, identification via the Hotelling’s T² and Q-statistics.^13,14 These multivariate statistical methods have found place in many applications. Yet, with the recent advancements in computational power along with the increased complexity in plant-wide process control structure, the focus has recently been shifted more toward the use of more advanced data mining algorithms with dimensionality reduction techniques. Prominent methods include latent variable-based models being principal component analysis (PCA), and partial least squares (PLSs) that aim to project the original data into a lower-dimensional space where accurate and simplified characterization can guide process monitoring.¹⁵ Nonlinear and dynamic extensions of these techniques (i.e., Kernel PCA/PLS,^16,17 dynamic PCA/PLS^18,19) have also been introduced to handle nonlinearity and serial (temporal) correlations of process data, respectively. However, the assumption of Gaussian distributed process data poses limitation in producing accurate fault detection and diagnosis with these techniques.²⁰ Other data-based methods centering around classification/regression-based analysis have been proposed that employ artificial neural network (ANN)²¹ and more recently deep learning algorithms,²² classification and regression decision trees (CART)^23,24 as well as different support vector machines (SVMs) formulations being support vector classification (SVC),^25–27 support vector regression (SVR),²⁸ and support vector data description (SVDD).²⁹ In particular, a major advantage of SVMs is their ability to provide nonlinear and robust models for non-Gaussian distributed process data, and due to their succinct representation as convex nonlinear optimization problem to obtain global parameters for models.

As the number of monitored process variables is increasing, the number of features that needs to be considered in the model development raises, which renders the dimensionality reduction as an essential component of data-driven process monitoring techniques. This further raises the need for development of novel data-driven fault detection and diagnosis techniques that employs powerful dimensionality reduction methodologies. Dimensionality reduction can be achieved via either by (1) feature extraction or by (2) feature selection. Here, features represent process variables used in model development. Feature extraction entails projection of the features of original space into a new, lower dimensional space, where the extracted features become linear combinations of the original ones. Latent variable models such as PCA and PLS inherently perform dimensionality reduction by performing feature extraction. However, a major disadvantage of these methods is the possibility of loss in information during the transformation of the original features into a lower dimensional space, which may impair fault diagnosis due to loss in physical interpretation. On the other hand, feature selection, which is the method of selecting optimal subset of original features, can reveal optimal set of original features that yield highest model accuracy without impairing fault diagnosis.

In our recent work, we have combined feature selection with nonlinear SVM classification algorithm by exploiting their optimization problem formulation and produced accurate fault detection and diagnosis models for batch process monitoring.³⁰ Here, we are presenting application of our framework in continuous processes. The rest of the article is organized as follows: section “SVM Classification: Key Concepts and Application in Continuous Process Monitoring” provides brief overview of SVMs and their application in continuous process monitoring. Section “Feature Selection Algorithm Based on Nonlinear SVMs: Motivation and Theoretical Background” introduces the modified SVM formulation to perform simultaneous modeling and dimensionality reduction, which enables simultaneous fault detection and diagnosis. Section “Tennessee Eastman Process: Model and Dataset” introduces Tennessee Eastman process.³¹ The implementation of the proposed data-driven algorithm for fault detection and diagnosis is given in the “Proposed Framework for Fault Detection and Diagnosis in Continuous Processes” section. Finally, we provide the results and comparison in “Results” section and conclude within “Conclusion” section.

SVM Classification: Key Concepts and Application in Continuous Process Monitoring

SVMs are popular machine learning algorithms that are introduced by Cortes and Vapnik.³² Given a set of training data with known labels, categorical (for classification) or continuous (for regression), SVMs analyze the patterns to derive supervised learning models. These models are built based on the structural risk minimization (SRM) principle,³³ where the selection of the simplest model, in terms of complexity (i.e., order) and empirical error on the trained data, is induced.³⁴ SVM formulations have been continuously improved to tackle wide range of engineering problems involving classification,^35–37 regression,^38,39 outlier detection^40,41 as well as clustering⁴² analysis. They have drawn significant interest for fault detection due to their high generalization and effective nonlinear data handling ability.^26,27,30 The main idea behind SVM classification is the following. By mapping the original data into a higher (possibly infinite) dimensional space (feature space), an optimal linear hyperplane in the mapped space that can maximally separate data points belonging to different classes can be determined. In the case of nonlinear SVMs, the optimal linear hyperplane of the mapped space (also known as feature space) corresponds to a nonlinear separating function in the original (input) space. The mappings are achieved via Kernel methods which rely on the similarity among data samples.

In this work, we train two-class C-parameterized SVM (C-SVM) classification models that can predict whether the operation performs under faulty (positive classification where y_i = + 1) or nominal condition (negative classification where y_i = − 1) given a continuous operation process variables. We have l training instances (i.e., input data samples), corresponding to l different continuous operations, where $x_i\in {ℝ}^n$. Indices i, j = 1, 2, …, l represent different continuous operations, whereas indices k, k′ = 1, 2, …, n belong to input features (i.e., process variable measurements). The primary C-SVM classification problem is formulated as a convex optimization with hinge loss, ℓ₂-norm penalty, and linear Kernel as shown as follows^32,33:

$$\begin{gathered} \underset{w,b,\xi }{\text{min}}\frac{1}{2}\Vert w{\Vert }^2+C\sum _{i=1}^l{\xi }_i \\ \text{s}.\text{t}.y_i\left(w^T\cdot x_i+b\right)\ge 1-{\xi }_{i}i=1,\dots ,l \\ {\xi }_i\ge 0i=1,\dots ,l \end{gathered}$$ (1)

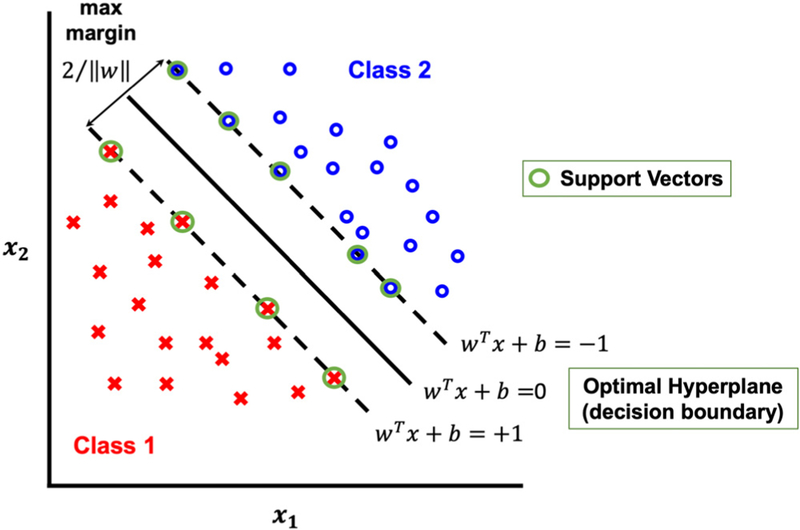
where w is the vector including weights of features, which is normal to the optimal separating hyperplane of the mapped space (Figure 1). The margin separating the instances of the two classes (where class labels are denoted via y_i) from each other is defined by $\frac{2}{\Vert w\Vert }$, where ∥w∥ is the magnitude of the vector w. The offset of the separating hyperplane from the origin is given by $\frac{b}{\Vert w\Vert }$. The optimal separating hyperplane is achieved by maximizing the margin between two classes. Maximization of the margin, $\frac{2}{\Vert w\Vert }$, is equivalent to the minimization of ∥w∥² as shown in Eq. 1. The problem formulation shown above and is referred as “soft margin” formulation, which allows for misclassification of the instances. This is important for the frequently encountered cases where training data cannot be separated without error. Hence, slack variable ξ is introduced to represent the extent of misclassification of vector x_i. C is the cost parameter penalizing the objective of Eq. 1 due to any misclassification. Use of such a soft margin formulation is common practice to minimize the training error during model development, thereby plays an essential role in increasing the generalization of the developed models. Note that Eq. 1 is a convex nonlinear problem (NLP) satisfying the first-order constraint qualification; therefore strong duality holds and the Lagrange dual problem can be written as follows:

$$\begin{gathered} \underset{\alpha }{\text{max}}\sum _{i=1}^l{\alpha }_i-\frac{1}{2}\sum _{i=1}^l\sum _{j=1}^l{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i,x_j\right) \\ \text{s}.\text{t}.\sum _{i=1}^l{\alpha }_i{y}_i=0 \\ {\alpha }_i\in [0,C]i=1,\dots ,l \end{gathered}$$ (2)

Figure 1.

Two-class classification via soft margin C-SVM formulation.

A nonlinear Kernel function, K(x_i, x_j), is introduced in the dual problem formulation to enable implicit mapping of the data points to a higher dimensional feature space for better separation as follows:

$$\begin{gathered} {\text{max}}_{\alpha }\sum _{i=1}^l{\alpha }_i-\frac{1}{2}\sum _{i=1}^l\sum _{j=1}^l{\alpha }_i{\alpha }_j{y}_i{y}_{j}K\left(x_i,x_j\right) \\ \text{s}.\text{t}.\sum _{i=1}^l{\alpha }_i{y}_i=0 \\ {\alpha }_i\in [0,C]i=1,\dots ,l \end{gathered}$$ (3)

Note that Eq. 3 generates a nonlinear decision function in the input (linear in the mapped) space shown as follows:

$$f(x)=w^{*}\cdot \varphi (x)+b^{*}=\sum _{i=1}^l{\alpha }_i^{*}{y}_{i}K\left(x_i,x\right)+b^{*}$$ (4)

where α_i are Lagrange multipliers, and ϕ(x) is the function providing Kernel-induced implicit mapping. With the implicit mapping enabled by the Kernel trick, w* can reach infinite dimension where instances of different classes are separated effectively. The linear decision function or optimal separating hyperplane (Eq. 4) is specified by a subset of training samples of which Lagrange multipliers are larger than zero. These training samples are referred as support vectors. As the name suggests, they are the ones nearby the optimal separating hyperplane (Figure 1). The Lagrange multipliers of other training samples are null, thus they do not have any effect on the f (x) value, where f(x) value determines the group membership of the new samples (i.e., operations). Specifically, the group membership of a new operation x is determined as positive (i.e., faulty, y_i = + 1) when f(x) > 0, or negative (i.e., normal or fault-free, y_i = − 1) when f(x) < 0.

Feature Selection Algorithm Based on Nonlinear SVMs: Motivation and Theoretical Background

With the advances in sensor technology, a large number of process measurements have become available to be used in data-driven process monitoring. Although the number of features to be considered during predictive model development has increased significantly, turning the data-driven process monitoring into a high-dimensional data analysis problem, not all of these process measurements (i.e., features) may be valuable in knowledge extraction. On the other hand, redundant features may lead to overfitting problem and deteriorate model performance significantly. Therefore, the use of effective dimensionality reduction techniques is essential to achieve high-performance models for accurate detection and isolation of the process faults during operation. There are two main categories to perform dimensionality reduction: (1) feature extraction and (2) feature elimination (i.e., feature selection) techniques. Feature extraction techniques transform the input space onto a lower space where the most relevant information is preserved, whereas feature elimination reduces the dimensionality of space without altering the original representation of features, by selecting the most informative feature subset. Major drawbacks of feature extraction include (1) the possible loss in information during the transformation to a lower feature space and (2) difficulty in interpretation due to having features as linear combination of transformed features. In our previous work, we have introduced a novel feature selection algorithm based on nonlinear SVM formulation utilized in bioinformatics⁴³ and process systems engineering applications (process monitoring^30,44) for accurate predictive model development. In this study, we incorporate previously introduced feature selection algorithm, which enables simultaneous modeling and dimensionality reduction via greedy (i.e., recursive) feature elimination, for continuous process monitoring. The use of our algorithm is highly valuable for rigorous fault detection and diagnosis, where the selected top descriptive features yield the major causes of the detected fault instantaneously. Simultaneous detection and diagnosis of process faults is crucial in order to take rapid actions to correct the detected fault.

To perform model-informed feature selection, we introduce binary variables z ∈ {0, 1}ⁿ in Model 3 for the selection of feature k to be involved in the optimal feature subset. z_k = 1 corresponds to the selection, whereas z_k = 0 corresponds to the elimination of feature k. The resulting model becomes a min–max problem as follows:

$$\begin{gathered} \underset{z}{\text{min}}\underset{\alpha }{\text{max}}\sum _{i=1}^l{\alpha }_i-\frac{1}{2}\sum _{i=1}^l\sum _{j=1}^l{\alpha }_i{\alpha }_j{y}_i{y}_{j}K\left(x_i\circ z,x_j\circ z\right) \\ \text{s}.\text{t}.\sum _{i=1}^l{\alpha }_i{y}_i=0 \\ {\alpha }_i\in [0,C]i=1,\dots ,l \\ \sum _k{z}_k=m \\ {z}_k\in \left\{0,1\right\}k=1,\dots ,n \end{gathered}$$ (5)

where m is the size of the optimally reduced feature subset, and operator ∘ is the Hadamard product operator⁴⁵ for component-wise multiplication. Model 5 can be used for dot-product Kernel functions that include linear, polynomial, and sigmoid Kernel functions, and isotropic stationary Kernel functions that involve Gaussian radial basis, exponential, circular, spherical, rational quadratic, Matérn, inverse multiquadric, log, power distance, wave, and triangular Kernel functions.^46–48 Model 5 is the formal representation of the feature selection problem via nonlinear SVMs, which is highly challenging and impractical to solve to global optimality in real-life applications. Therefore, instead of solving Model 5 to global optimality, we adopt heuristic algorithms to achieve high-quality feasible solutions. Specifically, we perform sensitivity analysis on the inner maximization problem of Model 5 with respect to z_k at (α*; z), where α* is the optimal solution of the inner maximization problem over α at some fixed z, and z_k is treated as a fixed parameter. Thus, to attain the first-order sensitivity of the objective function of the Model 5 at an optimal solution with respect to the parameter z_k, which is located in the objective function and constraints, we use the partial derivative of the Lagrange function of the Model 5 as shown as follows⁴⁹:

$$\frac{\partial \zeta }{\partial z_k}=\frac{\partial }{\partial z_k}\left[\sum _{i=1}^l{\alpha }_i^{*}-\frac{1}{2}\sum _{i=1}^l\sum _{j=1}^l{\alpha }_i^{*}{\alpha }_j^{*}{y}_i{y}_j{K}_z\left(x_i,x_j\right)+\lambda \left(\sum _{i=1}^l{\alpha }_i^{*}{y}_i\right)-\sum _{i=1}^l{\mu }_i^{\left(1\right)}{\alpha }_i^{*}+\sum _{i=1}^l{\mu }_i^{\left(2\right)}\left({\alpha }_i^{*}-C\right)\right]{|}_{z=z^{*}}=-\frac{1}{2}\sum _{i=1}^l\sum _{j=1}^l{\alpha }_i^{*}{\alpha }_j^{*}{y}_i{y}_j\frac{\partial K_z\left(x_i,x_j\right)}{\partial z_k}{|}_{z=z^{*}}$$

where $\lambda \in ℝ$, μ⁽¹⁾, μ⁽²⁾ ∈ [0, ∞)ⁿ are Lagrange multipliers. z does not appear in the constraints of Model 5. The final criterion contains only terms from the inner maximization objective function as shown as follows:

$${\text{crit}}_k=-\frac{1}{2}\sum _{i=1}^l\sum _{j=1}^l{\alpha }_i^{*}{\alpha }_j^{*}{y}_i{y}_j\frac{\partial K\left(x_i\circ z,x_j\circ z\right)}{\partial z_k}{|}_{z=z^{*}}$$ (6)

$$k_{\text{worst}}=\text{arg }\underset{\text{k}}{\text{max}}{\text{crit}}_{\text{k}}.$$ (7)

Equation 6 results from the Lagrangian sensitivity-based analysis and forms the perturbation criterion for greedy reductive feature elimination algorithm. Specifically, we follow an iterative procedure where we build nonlinear SVM models, rank features based on the derived criterion (Eq. 6), and finally eliminate one feature (feature k_worst) in each iteration. One can also eliminate features in blocks (i.e., as % of total features). The presented feature selection algorithm is equivalent to well-known recursive feature elimination (RFE)-SVM classification algorithm⁵⁰ when performing SVM classification with linear Kernels. The detailed derivation of the presented feature selection algorithm can be found elsewhere.⁵¹

Tennessee Eastman Process: Model and Dataset

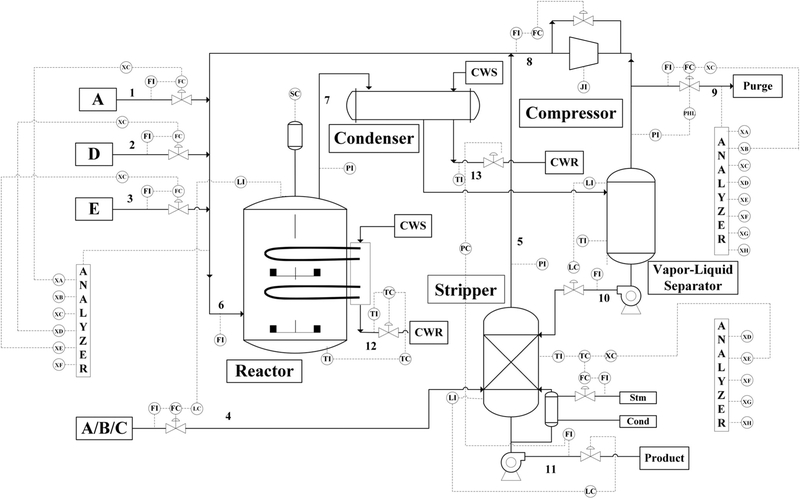
The Tennessee Eastman process (Figure 2), an extensively used benchmark case for comparative assessment of process monitoring algorithms, was designed by the Eastman Chemical Company.³¹ Numerous data-driven fault detection and diagnosis methodologies tested with the Tennessee Eastman process are available in the literature.^13,14,25,27 The process is based on a real industrial process, in which the components, kinetics, and operating conditions have been modified for proprietary reasons.¹³ There are five primary units in the process being: a reactor, condenser, compressor, separator, and a stripper, where chemicals G and H are produced from feedstocks A, C, D, and E with byproduct F and inert compound B. The process contains 11 manipulated and 41 measured variables. The detail for the process variables is provided in the Supporting Information.

Figure 2.

Tennessee Eastman process flowsheet with the second control structure in Lyman and Georgakis.⁵²

Among several simulation designs, we adopt the one whose plant-wide control structure is provided by Lyman and Georgakis.⁵² In this study, we use two sets of simulation dataset based on the Tennessee Eastman process with the second control structure in Lyman and Georgakis. The first simulation dataset is adopted from the study by Chiang et al.,¹³ which includes measurements from normal and 21 distinct faulty operations (Table 1). It includes single set of simulation for normal and 21 faulty operations separately (yielding 22 simulation datasets). The latter is taken from the study by Rieth et al.⁵³ having measurements from normal and first 20 faults provided in Table 1. It involves 500 set of simulations for normal and 20 faulty operations separately (yielding 10,500 simulation datasets). In this work, we have randomly selected 2 out of 500 sets of simulations from the study by Rieth et al. dataset, which lead us to employ a twice size of Chiang et al. data for model building. The aim in using two different simulation datasets with different size is to test the importance of data size involved in model development for fault detection and diagnosis. Training and test sets have been collected by running 25 and 48 h of simulations, respectively, where faults have been introduced 1 and 8 h into the simulation and each variable is sampled every 3 min. Thus, training sets consists of 500 samples, whereas test sets contain 960 samples per set of simulation. Further information on the process and simulation can be found in other references 13,31,53.

Table 1.

Overview of Faults and Corresponding Fault Types in the Tennessee Eastman Process Dataset

Fault no	Fault	Fault type
1	A/C feed ratio	Step
2	B composition	Step
3	D feed temperature	Step
4	Reactor cooling water inlet temperature	Step
5	Condenser cooling water inlet temperature	Step
6	A feed loss	Step
7	C header pressure loss	Step
8	A,B,C feed composition	Random variation
9	D feed temperature	Random variation
10	C feed temperature	Random variation
11	Reactor cooling water inlet temperature	Random variation
12	Condenser cooling water inlet temperature	Random variation
13	Reaction kinetics	Slow drift
14	Reactor cooling water valve	Sticking
15	Condenser cooling water valve	Sticking
16	Unknown	N/A
17	Unknown	N/A
18	Unknown	N/A
19	Unknown	N/A
20	Unknown	N/A
21	The valve for Stream 4	Constant position

Proposed Framework for Fault Detection and Diagnosis in Continuous Processes

In this study, we are building SVM binary classifiers for 21 (20 for Rieth et al.) different faults (fault-specific classifier) introduced in the process data. Thus, for each of the model building phase, we combine data from normal and relevant faulty operation. The proposed framework consists of two phases: (1) Offline phase includes the formulation of the fault-specific models for fault detection and diagnosis via signal process data where the optimization-backed feature selection algorithm is used; (2) Online phase monitors ongoing process in real time by employing the fault-specific models, raises alarm when faults occur and reports diagnosis of the detected fault simultaneously. Common to both phases, data need to be re-organized and/or processed a priori.

Data preprocessing

The common first step in data-driven modeling is the assessment of data quality. This is achieved via several different data preprocessing techniques such as (1) data cleaning that involves identification and removing outliers, smoothening the noisy data, and imputation of any missing values and (2) data transformation that includes scaling and normalization of the data to give all features equal weight, thus avoid bias during model development. In this study, we are using simulation-based dataset, which is free of outliers or missing values and solely involves Gaussian white noise.¹³ Therefore, only normalization is performed on process data by calculating their corresponding z-scores, by subtracting the mean of relevant measurements and then dividing into the standard deviation of them, prior to the offline phase. In the online phase, where actual process data are monitored in real time, both data cleaning and transformation steps are performed prior to the use of the developed models.

Offline phase: Model building

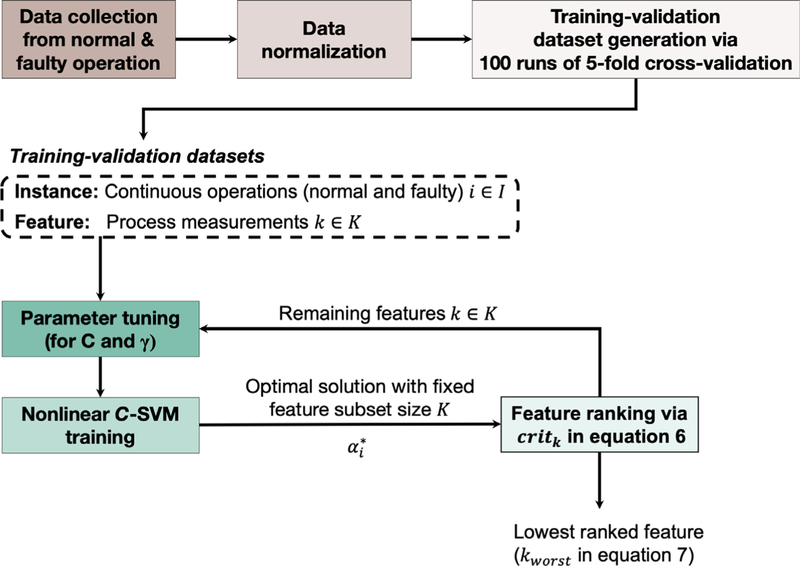
In this phase, we build fault-specific two-class C-SVM models using simulation-based process signal data. Here, the initial step is to collect relevant faulty operation process data and process data under normal operation. Next, we normalize the process data as described in the “Step 1: Tuning C-SVM Hyperparameters with the Active Set of Features” section and construct balanced training and validation sets to be used in model building. Use of imbalanced datasets may cause insufficient learning of one class than the other, thus may lead to inaccurate models. Therefore, we initially create balanced training and validation sets via 100 runs of fivefold cross validation where each fold includes 480 (960) normal and 480 (960) faulty samples for Chiang et al. dataset (Rieth et al.). Next, we build binary fault-specific C-SVM classifier models for each of the 21 (20) faults separately. Specifically, as we have 52 process variables in Tennessee Eastman process, we build 52 C-SVM classifiers for each 21 (20) faults (one per each feature subset). Finally, we select the end-model for each fault (fault-specific end-model), which has the optimal feature subset yielding best model performance, for online implementation. The performance metrics utilized throughout model building phase are provided in the Supporting Information. The iterative model building procedure, which consists of three main steps, is described below and illustrated in Figure 3.

Figure 3. Schematic representation of the offline phase–model building section.

Gaussian Radial Basis kernel is used for nonlinear C-SVM training. Iterative procedure is performed for each fault separately.

Step 1: Tuning C-SVM Hyperparameters with the Active Set of Features.

Parameter tuning is essential and required for developing generalizable models that will be implemented as a decision tool in online phase. In this work, we build C-SVM classification models by adopting one of the widely used nonlinear Kernel function, Gaussian radial basis function (RBF) (Eq. 8).

$$K\left(x_i,x_j\right)=\text{exp}\left(-\gamma \Vert x_i-x_j{\Vert }^2\right),$$ (8)

Hence, we have hyperparameters C and γ that are tuned using training and validation datasets with the active set of features (whole feature set in the first iteration). During the selection of hyperparameter γ, data density plays a critical role to prevent overfitting in the obtained decision function. Thus, we tune parameter $\widehat{\gamma }$ where

$$\gamma =\frac{2^{\widehat{\gamma }}}{n}.$$ (9)

In each iteration of model building, where features are eliminated in a greedy reductive manner (Section “Step 2: Training Fault-Specific C-SVM Classifiers for each Feature Subset”), $\widehat{\gamma }$ is updated with the available set of features as follows:

$$\gamma =\frac{2^{\widehat{\gamma }}}{z^{\text{T}}1}$$ (10)

In addition, we tune parameter Ĉ where C = 2^ĉ. We perform a grid search to tune parameters Ĉ, and $\widehat{\gamma }$ for all value combinations between −10 and 10. In each iteration, we train and validate two-class C-SVM models using 500 training-validation dataset pairs that include the corresponding active set of features. Then, the hyperparameter combination yielding the highest average testing AUC, accuracy, recall along with minimum false alarm rate across the 500 dataset pairs for each feature subset are chosen for further modeling steps.

Step 2: Training Fault-Specific C-SVM Classifiers for each Feature Subset.

We adopt the selected hyperparameters from the previous step and build C-SVM classifiers with Gaussian RBF, where the class probabilities are smoothened using median of probabilities with a window size of 3.

Step 3: Feature Rank Criteria Calculation and Elimination of the Least Informative Feature.

We obtain feature ranks using Eq. 6. Then, according to the criteria formulated as in Eq. 7, we eliminate the “worst,” which is most redundant or least informative, feature from the dataset.

This iterative framework involving greedy reductive feature elimination leads us to have fault-specific C-SVM models for each feature subset. Thus, we attain one C-SVM model per feature subset per fault. This leads to 52 model generation for each fault classification, which renders 1092 (1040 for Rieth et al. dataset) fault-specific classifiers. The final step of the offline phase is the selection of the fault-specific end-models. These are the fault-specific models that yield highest model performance with the optimal feature subset. Specifically, these models produce highest AUC along with minimum number of features, false alarm rate, false negative rate, and latency (fault detection time). In this work, we have picked 21 (20 for Rieth et al. dataset) fault-specific end-models among 1092 (1040) developed models.

Online phase: Fault Detection and Diagnosis in real time

In this phase, 21 fault-specific end models, which are chosen at the end of the offline phase, are implemented to monitor the online process data. Here, we are using the test datasets obtained from the simulation of Tennessee Eastman process, which includes 160 normal and 800 faulty samples, to assess the performance of the selected models. The test datasets are normalized with the mean and standard deviation obtained from the training sets (to attain z-scores) before being sent into the end-models. In an industrial setting, the real-time process data need to be preprocessed with cleaning and transformation (i.e., normalization) steps as described in the “Data Preprocessing” section before use of the implemented C-SVM models for fault detection and diagnosis. Fault-specific end-models generate binary answer for detection of each fault independently. Here, we adopt an alarm policy to identify the fault occurrence. In compliance with the studies of Mahadevan and Shah²⁵ and Russell et al.,¹⁸ fault occurrence is reported after we observe six consecutive positive alarms within the system. Once a fault is detected from any of the end-models, the developed framework simultaneously produces the root-cause analysis by solely checking the corresponding optimal set of features (process variables).

Results

Fault-specific C-SVM binary classifier models have been built using the training datasets created from the two different simulation datasets of different size. The adopted simulation datasets, namely Chiang et al. and Rieth et al. datasets, include all of the 52 process variables but differ in terms of the number of simulated continuous operations where the latter is the twice size of the former one. The evaluation of the proposed framework for continuous processes is examined via fault detection performance in the “Fault detection” section, where increasing number of instances have been observed to increase the model accuracy for the detection of distinct faults. The “Fault detection” section compares the fault-detection latency of the reported end-models with the ones in the literature. Finally, diagnosis of the successfully detected faults is provided according to the most accurate C-SVM model in the “Fault detection” section.

Fault detection

In this section, we evaluate the performance of the chosen fault-specific end-models for fault detection. The 21 (20 for Rieth et al. dataset) end-models yield highest AUC along with minimum number of features, false alarm rate, false negative rate, and latency (fault detection time). The results are tabulated in Tables 2 and 4, respectively, for Chiang et al. and Rieth et al. datasets. As mentioned earlier, in compliance with the studies of Mahadevan and Shah,²⁵ and Russell et al.,¹⁸ we report fault occurrence at the end of six consecutive positive alarms within the system. This policy is widely adopted in industry to minimize the number of false alarm rates, thus disruption of the operator. Furthermore, in accordance with the same studies, the fault-detection latency is reported as the first time when the initial alarm is raised.

Table 2.

Performance Results of the Selected Models Developed with Chiang et al. Dataset

Fault	Optimal feature subset size	AUC	Accuracy	Detection rate	False negative rate	False alarm rate	Latency (min)
1*	2	100.0	99.9	99.9	0.1	0.0	6
2*	5	99.5	98.1	97.8	2.3	0.0	57
3	13	62.0	67.8	72.1	27.9	53.8	3
4	1	100.0	100.0	100.0	0.0	0.0	3
5	4	100.0	99.9	99.9	0.1	0.0	6
6	2	100.0	100.0	100.0	0.0	0.0	3
7*	3	100.0	100.0	100.0	0.0	0.0	3
8	7	99.4	96.5	95.8	4.3	0.0	60
9	17	66.3	65.2	69.0	31.0	53.8	3
10*	14	90.2	83.3	85.8	14.3	28.8	12
11	29	84.9	86.8	96.6	3.4	62.5	3
12	9	99.9	95.7	100.0	0.0	25.6	3
13*	7	98.2	93.2	91.9	8.1	0.0	153
14	3	100.0	100.0	100.0	0.0	0.0	3
15	27	75.6	67.2	65.5	34.5	24.4	3
16	5	86.9	87.7	96.9	3.1	58.1	3
17	32	99.5	94.1	92.9	7.1	0.0	72
18	34	94.4	91.7	90.0	10.0	0.0	231
19	2	29.8	75.4	88.5	11.5	90.0	3
20	14	94.5	86.8	85.0	15.0	4.4	45
21*	1	99.7	100.0	100.0	0.0	0.6	3

^*Imply that the end-model is selected for online implementation.

Table 4.

Performance Results of the Selected Models Developed with Rieth et al. Dataset

Fault	Optimal feature subset size	AUC	Accuracy	Detection rate	False negative rate	False alarm rate	Latency (min)
1	18	100.0	99.8	99.8	0.3	0.0	15
2	10	99.7	99.2	99.1	0.9	0.0	24
3	10	50.2	17.0	0.4	99.6	0.0	2442
4*	1	100.0	100.0	100.0	0.0	0.0	3
5	14	100.0	100.0	100.0	0.0	0.0	3
6*	2	100.0	100.0	100.0	0.0	0.0	3
7	4	100.0	100.0	100.0	0.0	0.0	3
8	12	99.0	94.5	93.4	6.6	0.0	54
9	2	54.3	55.1	55.9	44.1	49.4	15
10	15	87.9	80.1	77.6	22.4	7.5	72
11*	2	99.8	95.9	95.1	4.9	0.0	18
12*	5	99.9	99.4	99.3	0.7	0.0	15
13	8	95.5	87.3	84.8	15.2	0.0	90
14*	2	100.0	100.0	100.0	0.0	0.0	3
15	16	56.0	17.6	1.1	98.9	0.0	1635
16*	2	96.7	88.3	87.4	12.6	7.2	9
17	28	96.9	92.9	91.5	8.5	0.0	210
18	5	98.6	96.1	95.3	4.7	0.0	75
19	10	100.0	99.6	99.6	0.4	0.0	18
20	14	97.1	92.7	91.2	8.8	0.0	99

^*Imply that the end-model is selected for online implementation.

The end-models reported in Table 2 are obtained with the Chiang et al. dataset, which is smaller compared to Rieth et al. data. In particular, fault-specific models are trained with 480 normal and 480 faulty samples and tested on 48 h simulation data where each fault is introduced at the end of eighth hour, which corresponds to having 160 normal and 800 faulty samples sequentially.

An ideal model would give 100% AUC, accuracy, detection rate along with 0% false alarm and negative rates. Among the introduced performance metrics (Supporting Information), accuracy and fault detection rate (recall) are the two common ones used for model performance evaluation in the literature.^25,26 Yet, evaluation based on only these two metrics would be insufficient for a thorough analysis. In this study, we inspect the model performance via collective evaluation of AUC, fault-detection rate, accuracy as well as false alarm rate and false negative rate. We believe collective judgment of AUC, fault-detection rate, accuracy along with false alarm rate and false negative rate is essential and required because a model may simultaneously yield high accuracy, and fault detection rate, but also high false alarm rates which would lead to misleading conclusions. Such models would be very sensitive and frequently raise fault alarm, consequently making them unreliable.

As shown in Table 2, fault-specific models perform well excluding Faults 3, 9, 11, 15, 16, and 19. Specifically, Faults 3, 9, and 15 are the ones that could not be detected with the available algorithms in the literature. This is due to the absence of observable change in the process variable behavior (mean and standard deviation) between their corresponding faulty and normal operation.¹⁸ In other words, these faults could not be detected with the set of provided process variables; however models can always be improved by considering additional process variable information. For instance, for Fault 15, which is sticking condenser cooling water valve, additional process variables such as position of the valve and/or condenser pressure would have been extremely helpful for the detection. Then, using the presented simultaneous modeling and feature selection algorithm (“Feature Selection Algorithm based on Nonlinear Support Vector Machines: Motivation and Theoretical Background” section), we can obtain the optimal feature subset that would produce the most accurate model to detect these faults. Particularly for Faults 3, 9, and 15, although high fault detection rate and accuracy have been obtained in particular models built for the detection, high false alarm rates have also been recorded, whereas corresponding AUC metric has fluctuated around 42.8%–64.51%, 42.51%–66.29%, and 42.08%–75.71%, respectively. Of note, 50% of AUC indicates random assignment of the class label. Specifically, highest AUC received for Fault 3, 64.51%, is recorded for the fault-specific model developed with 35 optimal features yielding 82.19% accuracy, 98.62% fault detection rate but with 100% false alarm rate. This means that the model is very sensitive and raises alarm for fault detection frequently regardless of the operation characteristics, which turns the model into an inaccurate tool. Similarly, for Fault 9, highest AUC yielding model is obtained with 17 features which produce 65.21% accuracy, 69.00% fault detection rate together with 53.75% false alarm rate; whereas for Fault 15, highest AUC. This shows that AUC metric becomes significantly informative in data-driven model selection, especially when the testing dataset is unbalanced with the number of samples from two different classes. Moreover, as unbalanced dataset would be very common in continuous operation online data, we offer use of AUC metric in the future fault detection studies, where problem is formulated as classification problem, to attain a more complete picture of the results.

Moreover, Table 2 reveals that our proposed data-driven algorithm has achieved to detect Fault 21, regarding a fixed Stream 4 valve at the steady-state position, successfully with an AUC of 99.7%, accuracy and detection rate of 100% with 0% false negative rate and 0.6% false alarm rate. Here, we would like to highlight that this is one of the most challenging faults of the Tenneessee Eastman process simulation, where, to the best of our knowledge, highest fault detection rate recorded in the literature is 59.4% along with 26.1% false alarm rate via one-class SVM algorithm.²⁷ Again, to have a detailed analysis of this model, we strongly suggest to evaluate AUC and false negative rate metrics as well. Here, we show that with the advances in C-SVM formulation for feature selection, we achieve to detect Fault 21 with high AUC, accuracy, detection rate and minimum false negative and alarm rates by considering solely one feature, which is a manipulated process variable—total feed-flow rate of Stream 4. This also demonstrates the requirement for feature elimination during model development. Consideration of any further process variable in addition to 45th process variable has deteriorated the model performance significantly. In other words, other process variables become redundant to detect this fault.

The selection of end-models is a multi-objective task. The fault-specific end-models are the ones producing the highest AUC with minimum number of features, false alarm and negative rates, and latency (Tables 2 and 4). Here, we also report alternative models demonstrating similar performance to end-models but with lower number of features (process variables) (Tables 3 and 5).

Table 3.

Performance Results of the Selected Alternative Models Developed with Chiang et al. Dataset

Fault	Optimal feature subset size	AUC	Accuracy	Detection rate	False negative rate	False alarm rate	Latency (min)
8*	4	99.2	95.9	95.8	4.2	3.1	63
17*	27	99.1	93.4	92.1	7.9	0.0	75

^*Imply that the end-model is selected for online implementation.

Table 5.

Performance Results of the Selected Alternative Models Developed with Rieth et al. Dataset

Fault	Optimal feature subset size	AUC	Accuracy	Detection rate	False negative rate	False alarm rate	Latency (min)
5*	3	100.0	99.9	99.9	0.1	0.0	6
18*	2	98.2	95.3	94.3	5.7	0.0	105
19*	3	99.7	99.2	99.0	1.0	0.0	9
20*	13	97.2	92.1	90.5	9.5	0.0	102

^*Imply that the end-model is selected for online implementation.

On the other hand, the end-models trained via Rieth et al. dataset perform well for all faults excluding only Faults 3, 9, and 15. This shows that models can be improved with the addition of more simulation data. As the Big Data era has started playing significant role in industrial decision making, today large amount of process data collection has been extremely facilitated. Therefore, accessibility to further process data is assumed not to be an issue. As for the opposite scenario, where historical process data are not available or not adequate, one can simulate more process data with the dynamic model of a process to improve model performance with the proposed framework. Here, we see that using larger data has improved fault detection model performances for Faults 11, 16, 19, and 20. This is the result of the fact that the models have learned much better by being trained with increased number of scenarios (i.e., simulations) for both normal and faulty operation. Furthermore, we would like to highlight that the addition of new and more training data (scenarios) also affects the learning pattern of the models and due to the nonlinear dynamics of the process, this may lead to the selection of different feature sets with two different datasets used in this study. Yet the key goal in data-driven modeling is to obtain generalizable models and, in this study, we ensure this using 100 runs of fivefold cross validation technique during model development.

Next, we compare the obtained end-models with Chiang et al. and Rieth et al. datasets provided in Tables 2 and 4 as well as the alternative models given in Tables 3 and 5. We select the most simple end-models for the online decision-making. According to the scientific interpretation of the Occam’s razor philosophy, if one has two competing theories that would yield the same predictions, the simpler one is the better.⁵⁴ By following this principle, we select the fault-specific end-models (for Faults 1–20) with lower number of features if they demonstrate similar performance between the two datasets. The selected “simple” end-models are marked with asterisks. This also facilitates relevant sample data collection and analysis due to decreased number of sample collection and analysis.

Finally, we pick our fault-specific models yielding highest fault detection rate among the developed 1092 and 1040 fault-specific models from two simulation datasets and compare our results with the available data-driven methods performed on the Tennessee Eastman process data.^14,25,27 These methodologies are based on well-known and widely used algorithms, where in some of them only normal operating data is used^25,27 and in the others normal and faulty operation data is utilized simultaneously.¹⁴ Table 6 shows that our proposed framework produces better results than the other methods; however, we need to highlight that the models producing highest detection rate do not necessarily produce the most reliable models for all faults. As mentioned earlier, a model can produce not only high fault detection rate but also high false alarm rate. In fact, this is the case for Faults 8, 10, 11, 13, 16, 17, 19, and 20 reported in Table 6. For these faults, although we achieve high fault detection rates as reported in Table 6, we observe false alarm rate of 68.1%, 91.2%, 100.0%, 83.8%, 81.9%, 100.0%, and 97.5%, respectively. Therefore, we strongly suggest to evaluate all metrics described in the Supporting Information in order to make a fair comparison between models. Specifically, the end-models reported in this study are selected based on AUC, which considers fault detection rate and false alarm rate, false negative rate, and latency (fault detection time).

Table 6.

Comparison of Fault Detection Rate between the Fault-Specific Models Producing Highest Fault Detection Rate of this Study and the Models Reported in the Literature.^14,25,52 Best results of Xiao et al. are adopted. (Highest fault detection rates are bolded.)

Ref.	Mahadevan and Shah25					Xiao et al.52	Yin et al.26	This study
Faults	PCA-T2	PCA-Q	DPCA-T2	DPCA-Q	One-class SVM	Two-class SVM	Two-class SVM	Two-class SVM
1	99.2	99.8	99.4	99.5	99.8	99.5	99.5	99.9
2	98.0	98.6	98.1	98.5	98.6	98.3	98.1	99.1
4	4.4	96.2	6.1	100.0	99.6	47.4	99.9	100.0
5	22.5	25.4	24.2	25.2	100.0	45.2	90.8	100.0
6	98.9	100.0	98.7	100.0	100.0	99.2	60.1	100.0
7	91.5	100.0	84.1	100.0	100.0	70.1	98.9	100.0
8	96.6	97.6	97.2	97.5	97.9	97.4	96.0	100.0
10	33.4	34.1	42.0	33.5	87.6	68.0	81.0	99.4
11	20.6	64.4	19.9	80.7	69.8	65.8	80.2	100.0
12	97.1	97.5	99.0	97.6	99.9	98.8	97.8	100.0
13	94.0	95.5	95.1	95.1	95.5	95.0	92.5	100.0
14	84.2	100.0	93.9	100.0	100.0	93.9	91.0	100.0
16	16.6	24.5	21.7	29.2	89.8	73.1	89.4	100.0
17	74.1	89.2	76.0	94.7	95.3	75.2	81.6	98.2
18	88.7	89.9	88.9	90.0	90.0	89.3	89.5	95.3
19	0.4	12.7	0.7	24.7	83.9	43.6	85.9	100.0
20	29.9	45.0	35.6	51.0	90.0	69.0	80.5	100.0
21	26.4	43.0	35.6	44.2	52.8	59.4	-	100.0

Fault-detection latency

The average latency among the reported faults, all faults excluding Faults 3, 9, and 15, has been stated as 306.19, 145.58, 263.12, 151.00, and 98.50 min for PCA-T², PCA-Q, DPCA-T², DPCA-Q, and 1-class SVM,²⁵ respectively, whereas the latency information is not provided by Yin et al.²⁶ In this work, we report significantly lower fault detection latency along with higher detection accuracy as reported in Tables 2 and 4. When we exclude Faults 3, 9, and 15, faults that cannot be detectable from the available process variable data accurately, the average fault detection latency among the remaining 18 (17) faults of Chiang et al. (Rieth et al.) dataset is 37.50 (42.00) min. Moreover, the average fault detection latency for the selected “simple” end-models for online implementation, which are marked with asterisks, is 35.83 min. This reveals the power of the proposed framework for rapid and precise fault detection and diagnosis.

Fault diagnosis

Here, we present the root cause diagnosis of the detected faults using the chosen end-models for online implementation (the models with asterisks). Below, we discuss the obtained diagnosis results for the selected faults (Table 7). The diagnosis with the end-models reported in Tables 2 and 4 is provided in the Supporting Information. Of note, we may observe distinct feature sets for different types of faults but related with the same unit in the process (e.g., Faults 5 and 12 in Supporting Information, Table S7). This is mainly because of the fact that varying fault types realize themselves in distinct ways due to the nonlinear dynamics of the process, which leads to the selection of different process variables as key ones for fault diagnosis.

Table 7.

Diagnosis from the Selected End-Models (Marked with Asterisks in Tables 2–5) via Occam’s Razor Principle. Faults 3, 9, and 15 are excluded

Faults	Optimal feature subset size	Selected process variables
1	2	16, 44
2	5	7, 16, 10, 47, 13
4	1	51
5	3	52, 11, 17
6	2	44, 1
7	3	45, 7, 13
8	4	39, 44, 16, 20
10	14	41, 39, 38, 37, 40, 50, 19, 18, 20, 7, 13, 16, 31, 29
11	2	9, 51
12	5	16, 38, 35, 25, 11
13	7	39, 40, 18, 7, 38, 23, 3
14	2	51, 9
16	2	19, 50
17	27	38, 39, 40, 41, 21, 37, 19, 20, 33, 27, 34, 30, 1, 11, 25, 28, 24, 23, 35, 36, 26, 10, 3, 2, 22, 14, 48
18	2	22, 8
19	3	13, 16, 46
20	13	38, 39, 41, 16, 52, 17, 18, 30, 35, 29, 40, 13, 7
21	1	45

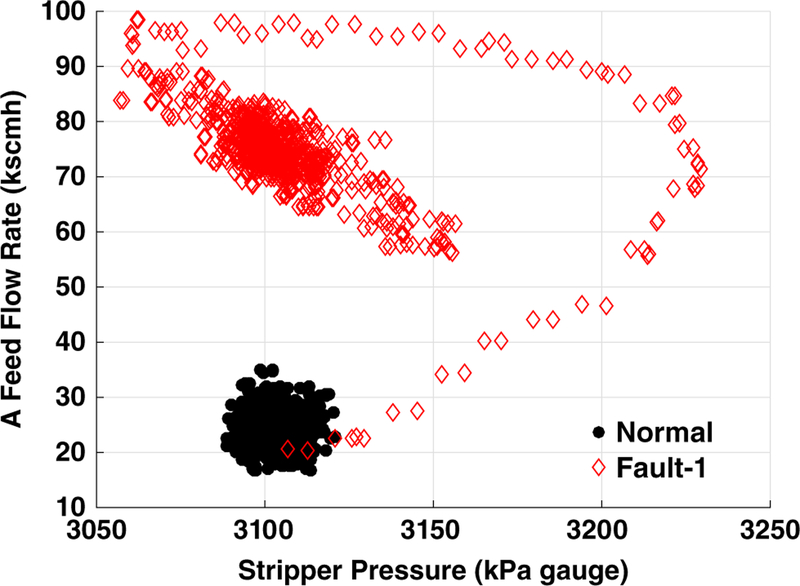
Fault 1: Sudden Decrease in A/C Feed Ratio (Stream 4).

Fault 1 occurs due to a step change in the A/C feed ratio which also changes B composition constant at Stream 4. The chosen end-model (Table 2) is able to detect this fault by monitoring process variables 16, and 44, that are stripper pressure on Stream 5 and A feed flow rate, respectively. Here, sudden increase in C flow rate causes an increase in the stripper pressure, which is a measured process variable. To compensate this sudden effect and maintain the B composition constant on Stream 4, the flow controller increases the feed-flow rate of A. This, in turn, reverses the stripper pressure to the original operating range, however, the raise in the A feed-flow rate carries the operation to a new steady state which can be clearly observed in Figure 4.

Figure 4.

Fault 1 diagnosis–plot of the root cause variables.

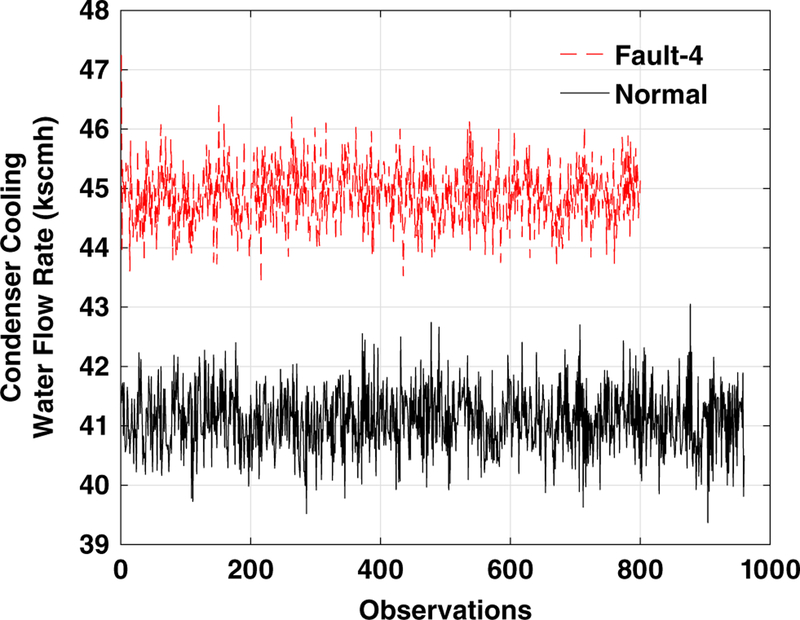
Fault 4: Step Change in Reactor Cooling Water Inlet Temperature.

The end-model selected for detection of this fault is given in Table 4. By monitoring the manipulated process variable 51, we are able to detect this fault with 100.0% accuracy along with 0% false negative and alarm rates in 3 min. To decrease the elevated reactor cooling water inlet temperature, the controller increases the condenser cooling water flow rate (Figure 5). Therefore, monitoring of this process variable provides valuable insights for the identification of this fault.

Figure 5.

Fault 4 diagnosis–plot of the root cause variables.

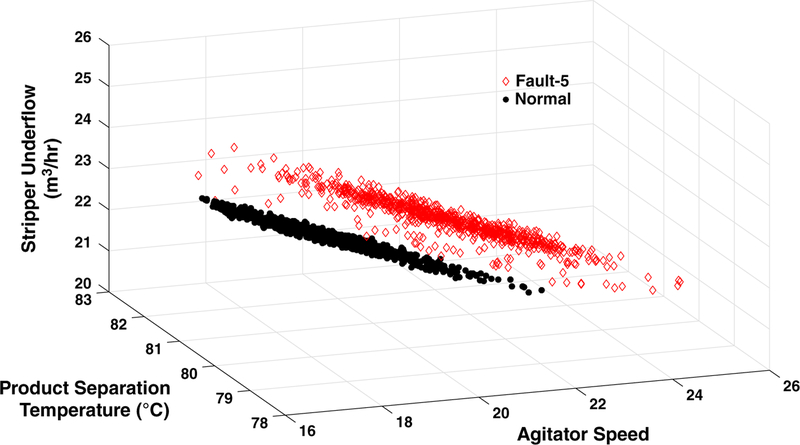
Fault 5: Step Change in Condenser Cooling Water Inlet Temperature.

Fault 5 is generated with a step change in the condenser cooling water inlet temperature in the simulations. We are able diagnose this fault by monitoring process variables 52, 11, and 17, which are agitator speed (manipulated variable), product separation temperature (measured variable), and stripper underflow (measured variable), respectively. Because of the temperature increase in the cooling water, the cooling performance of the condenser decreases. To compensate this adverse effect, the flow controller increases the flow rate of the condenser cooling water by increasing the agitator speed (process variable 52). The step change in cooling water temperature also affects the product separation temperature and accordingly stripper flow rate. We have plotted the selected process variables, which provide the most informative set of samples to detect this fault, and clearly seen the distinction between normal and faulty operation (Figure 6). By monitoring these three process variables, the fault-specific model reported for Fault 5 in Table 5 is able to detect the fault with 99.9% accuracy with 0.0% false alarm rate and 0.1% false negative rate in 6 min.

Figure 6.

Fault 5 diagnosis–plot of the root cause variables.

Fault 7: C Header Pressure Loss.

The selected end-model, given in Table 2, detects this fault with 100.0% accuracy with 0% false alarm and false negative rates in 3 min. The diagnosis of this fault is obtained from process variables 45, 7, and 13, which are manipulated process variable—total feed-flow rate on Stream 4, measured process variables reactor pressure and product separation pressure, respectively. Here, to compensate the decreased C header pressure, total feed-flow rate is increased via the adjustment of the flow valve on Stream 4, which in turn affects the reactor pressure and product separation pressure within the process. Therefore, monitoring these three key process variables has enabled accurate detection of the Fault 7.

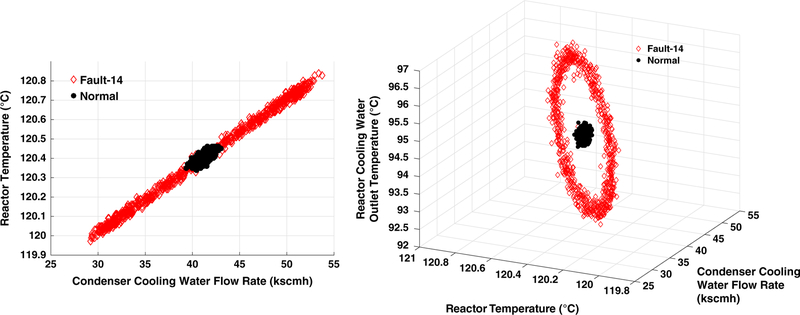
Fault 14: Sticking Reactor Cooling Water Valve.

We detect this fault using the end-model provided in Table 4, where we achieve 100.0% accuracy with 0% false alarm and false negative rates in 3 min. The analysis reveals that process variables 51 (manipulated) and 9 (measured) are the two key process variables to identify this fault. Here, if the reactor cooling water temperature is elevated, thus there occurs a lost cooling effect on the reactor, we observe a direct temperature increase in the reactor (measured process variable 9). The controller then tries to decrease the elevated reactor temperature by increasing the condenser cooling water flow rate (manipulated process variable 51). On the other hand, if the reactor cooling water temperature decreases due to the sticking valve, creating increased cooling effect on the reactor, we notice a decline in the reactor temperature, where the controller would decrease the condenser cooling water flow rate for balance (Figure 7—left plot). Moreover, we are able to achieve same model performance by observing an additional process variables along with process variables 51 and 9, whereas the model with less number of process variables was favored due to the simplicity. The third ranked key process variable is the measured process variable 21, reactor cooling water outlet temperature, which is directly affected with the sticking reactor cooling water valve. When we consider this third ranked key process variable and visualize the sampling data, the distinction between normal and faulty operation becomes more evident (Figure 7—right plot).

Figure 7.

Fault 14 diagnosis–plot of the root cause variables. Left: With top two key process variables. Right: With top three key process variables.

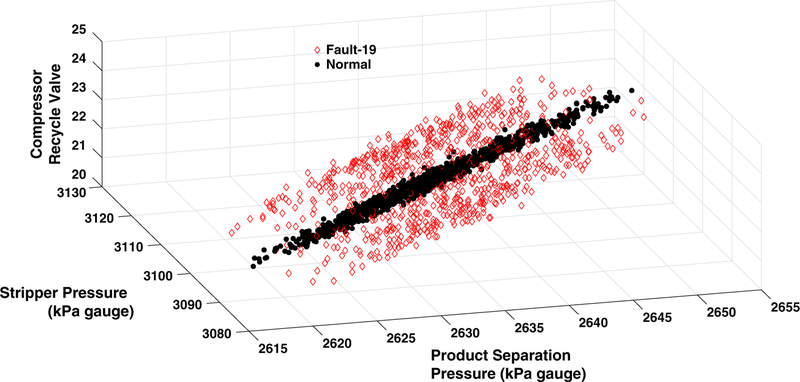
Fault 19—Unknown.

The cause of this fault is not provided in Downs and Vogel³¹ However, we observe the clear distinction between normal and faulty operation with the optimal set of diagnosed process variables (Figure 8). These are measured process variables 13, and 16, as well as a manipulated process variable 46, which are product separation pressure, stripper pressure, and compressor recycle valve, respectively.

Figure 8.

Fault 19 diagnosis–plot of the root cause variables.

Conclusions

Dimensionality reduction is a key task in most data-driven applications, in areas such as multiscale systems engineering, where vast amounts of data must be reduced to an essential subset that is used to provide actionable insights. Process monitoring, specifically fault detection and diagnosis, is one of the major fields in process systems engineering that benefits the advances in data-driven modeling and dimensionality reduction techniques with the increased availability of process data. In this article, we present theoretical advances in the feature selection algorithm based on nonlinear SVMs, describe a data-driven framework for fault detection and diagnosis in continuous processes, and finally apply it to the Tennessee Eastman benchmark process. The presented feature selection algorithm is based on nonlinear Kernel-dependent SVM feature rank criteria, which is derived from the sensitivity analysis of the dual C-SVM objective function. This enables simultaneous modeling and feature elimination which paves the way for simultaneous fault detection and diagnosis, where feature ranking guides fault diagnosis. Thus, once the implemented fault detection models detect a fault within the process, they are able to instantly report the diagnosed process variables. Moreover, by adopting feature selection techniques which list the most informative features in the original space rather than feature extraction (i.e., PCA and PLS) where features become linear combination of the original features in a transformed space, loss of information is highly minimized and interpretation of the results become more convenient.

In this work, we have developed 1092 and 1040 fault-specific C-SVM binary classifier models for 52 feature subsets of the 21 and 20 faults simulated in Chiang et al. and Rieth et al. datasets, respectively. The fault-specific end models that yield highest Area Under the ROC Curve (AUC) along with minimum number of features, false alarm rate, false negative rate, and latency (fault-detection time) are selected for online implementation. For the cases where we have observed similar model performances for the detection of a fault, we have followed the Occam’s razor principle and selected the one that provides diagnosis with minimum process variables, for simplicity. The achieved results with the presented framework are highly promising. Specifically, excluding the Faults 3, 9, and 15, the models that we report in this study outperforms the available ones in the literature not only in terms of detection accuracy but also in terms of detection latency. The detection latency is attained as low as 35.83 min for the 18 faults (excluding Faults 3,9, and 15) analyzed with our framework. Of note, Faults 3, 9, and 15 are the ones that are not accurately detected neither in this work nor previous studies. This is due to the fact that available process variable set does not provide a distinct observable change between normal and corresponding faulty operation. However, we also note that consideration of further process variables for certain faults, specifically Faults 3, 9, and 15, can highly improve the model performances. Furthermore, for distinct set of faults (i.e., Faults 11, 16, 19, and 20), we have benefited from the larger simulation dataset (Rieth et al.) where added samples have contributed the learning of the developed models.

Finally, we highlight the importance of utilizing additional evaluation metrics (i.e., AUC, accuracy, false alarm rate, and false negative rate) for detailed model performance assessment. Commonly used metric in the previous studies is fault detection rate. However, one can end up with a model producing high fault detection rates along with high false alarm and false negative rates, meaning that the model would become very sensitive, thus unreliable. Therefore, collective interpretation of these metrics is critical to avoid such unstable models that would obfuscate the decision-making process.