Role of particle clusters on the rheology of magneto-polymer fluids and gels

Abstract

Even in the absence of cross-linking, at large enough concentration, long polymer strands have a strong influence on the rheology of aqueous systems. In this work, we show that solutions of medium molecular weight (120 000–190 000 g mol⁻¹) alginate polymer retained a liquid-like behaviour even for concentrations as large as 20% w/v. On the contrary, solutions of alginate polymer of larger (and also polydisperse) molecular weight (up to 600 000 g mol⁻¹) presented a gel-like behaviour already at concentrations of 7% w/v. We dispersed micrometre-sized iron particles at a concentration of 5% v/v in these solutions, which resulted in either stable magnetic fluids or gels, depending on the type of alginate polymer employed (medium or large molecular weight, respectively). These magneto-polymer composites presented a shear-thinning behaviour that allowed injection through a syringe and recovery of the original properties afterwards. More interestingly, application of a magnetic field resulted in the formation of particle clusters elongated along the field direction. The presence of these clusters intensely affected the rheology of the systems, allowing a reversible control of their stiffness. We finally developed theoretical modelling for the prediction of the magnetic-sensitive rheological properties of these magneto-polymer colloids.

This article is part of the theme issue ‘Patterns in soft and biological matters'.

1. Introduction

Systems composed of polymeric chains and magnetizable particles dispersed in a liquid medium are of a high technological interest as a consequence of their soft consistency and the possibility of controlling their physical properties at a distance through magnetic fields [1]. Broadly speaking, these ‘smart’ materials can be classified into magnetorheological fluids and magnetic gels. The former are basically suspensions of magnetizable particles in a liquid medium, in which polymers can be added to reach different aims, including improving the colloidal stability of the dispersed particles. From the rheological point of view, in the absence of a magnetic field, the magnetorheological fluids behave like viscoelastic liquids, achieving a reversible liquid–solid transition under the application of a magnetic field. On the other hand, magnetic gels are characterized by showing a viscoelastic solid behaviour even in the absence of an applied magnetic field. Typically, this behaviour has its origin in the formation of a cross-linked network of flexible polymer chains that retain (by absorption) a large amount of liquid. This is what is known as a polymeric gel and, by extension, a magneto-polymeric gel would be one that also contains dispersed magnetic particles.

The scientific field of magneto-polymeric gels experienced in its beginnings a development similar to that of magnetorheological fluids, finding for them applications mainly in the field of magnetorheological damping. However, in the last decade, the interest in magneto-polymeric gels has resurged with novel applications in the field of biomedicine, in parallel to the growing importance of hydrogels (i.e. gels in which water is the medium of dispersion). In biomedicine, hydrogels stand out from the rest of biomedical materials because of their mechanical and chemical versatility and biocompatibility [2]. Consequently, hydrogels have been employed in various biomedical applications, being in many cases already commercially available. The current applications range from tissue engineering, to prepare extracellular matrices for different artificial tissues, to their use as drug delivery and cell-encapsulation systems.

The dispersion of magnetic particles in polymeric hydrogels allows them to be endowed with very interesting properties from the point of view of biomedical applications. First, the presence of magnetic particles allows the visualization and monitoring of magnetic hydrogels by magnetic resonance for in vivo applications [3]. In addition, several studies indicate that, when used in tissue engineering, the magnetic material stimulates cell adhesion, proliferation and differentiation [4]. Finally, recent works of our research group show that artificial biological tissues based on magnetic hydrogels, with microstructural and mechanical properties modulated by external magnetic fields, can be prepared [5,6]. This is a unique advantage compared to other biomaterials because it is possible to generate smart materials suitable for mimicking native tissues and, therefore, with great potential in the field of tissue engineering.

Despite the advances achieved so far in the field of magneto-polymer hydrogels, there are several aspects that need improvement. For example, from the perspective of their applications in tissue engineering, an important advance would be that, in the absence of the applied magnetic field, hydrogels could be deformable enough to be injected through small cavities [7]. In this way, the hydrogels could be implanted by simple injection (without invasive surgery) and successively, in the post-injection stage, the gels could be activated by magnetic forces at a distance, until their mechanical properties are adapted to those of the native tissues that they need to mimic. In short, obtaining hydrogels with these new characteristics would be a step forward in the field of biomaterials.

With this objective (preparation of injectable hydrogels with mechanical properties controllable by magnetic fields) in mind, we aimed for the preparation of magneto-polymer composites that could present shear-thinning properties. The mechanism of the self-assembly process, due to weak physical associations, is specific to the shear-thinning system. Therefore, we tried to target the above-mentioned objective by preparing highly concentrated solutions of polymers that could demonstrate a defined gel-like character, as a consequence of the impediment of movement of the polymer chains due to their high concentration. Iron particles were subsequently dispersed in the carrier solutions in order to provide the hydrogels with responsiveness to applied magnetic fields. We explored systems consisting of alginate polymers of two different molecular weights: medium molecular weight (120 000–190 000 g mol⁻¹) alginate polymer, as well as larger (and also polydisperse) molecular weight (up to 600 000 g mol⁻¹) alginate polymer. As will be shown, a gel-like behaviour was observed only in the systems prepared with the highest molecular weight alginate. Nevertheless, both systems gave rise to stable suspensions of magnetic particles with a rich (magneto)rheological behaviour.

2. Materials and methods

(a). Materials

As polymer material, we used sodium alginate [empirical formula (C₆H₇NaO₆)_n], obtained from the extracellular matrix of brown macroalgae, and supplied by two different enterprises (Sigma-Aldrich, USA, and BioChemica, Germany). The fundamental difference between these two samples was related to their molecular weight. Sodium alginate with molecular weight 120 000–190 000 g mol⁻¹ was purchased from Sigma-Aldrich, while sodium alginate with molecular weight 10 000–600 000 g mol⁻¹ was purchased from BioChemica. The differences in molecular weight were reflected in the viscosity of the solutions, ranging from 15–25 mPa s for 1% Sigma-Aldrich sodium alginate solutions in water, to 350–550 mPa s for similar solutions of sodium alginate from BioChemica, according to the respective manufacturers. We will refer to these polymer materials as low-viscosity sodium alginate (LVSA) polymer and medium-viscosity sodium alginate (MVSA) polymer throughout this paper, respectively.

We used distilled water as a dispersion medium, and bare iron particles (Fe-HQ powder) supplied by BASF (Germany) as a magnetic phase. This powder consisted of spherical micrometre-sized particles of diameter 0.9 ± 0.3 µm, as obtained by electron microscopy images, and showed a volumetric mass density of 7.88 ± 0.16 g cm⁻³, as measured by a pycnometer. The powder presented a typical paramagnetic behaviour with saturation magnetization M_s = 1721 ± 2 kA m⁻¹, as measured by superconducting quantum interference device magnetometry.

(b). Preparation of solutions of alginate polymer

Both LVSA and MVSA polymers were dissolved separately in distilled water at concentrations ranging from 5 to 20% w/v. We used mechanical mixing at a speed of 3500 r.p.m. for 10 min to accelerate the dissolution and homogenize the resulting alginate solutions.

(c). Preparation of suspensions of magnetic particles in alginate polymer solutions

For the preparation of suspensions of magnetic particles, we took HQ iron particles and suspended them in the alginate solutions at a concentration of 5% v/v. The resulting mixtures were homogenized by mechanical mixing.

(d). Stability of the suspensions against particle settling

For the evaluation of the settling behaviour of the suspensions of iron particles in alginate solutions, we placed aliquots of the samples in test tubes and waited for the appearance of a sediment/supernatant interface, due to gravitational forces.

(e). Rheological characterization of the solutions and suspensions

First, we determined whether the alginate polymer solutions in water behaved as fluids or gels. For this aim, we considered a rheological point of view, from which gels are characterized by the values of the storage modulus (G′) larger than the values of the loss modulus (G′′) within the linear viscoelastic region (LVR). Otherwise, we will refer to the solutions as fluid-like samples. The precise experiments (amplitude sweeps) carried out for the determination of G′ and G′′ within the LVR are described below in detail.

We determined the rheological properties under shear of both polymer solutions and iron suspensions by using a rotational (magneto)rheometer (Physica MCR 300) with a plate–plate geometry of 20 mm diameter and at a constant temperature of 25 ± 0.1°C.

We subjected the samples to two different kinds of experiments. Steady-state measurements, where the samples were subjected to ramps of shear rate, $\dot{\gamma }$, of increasing value and the resulting shear stress, σ, and viscosity, η, were monitored. And oscillatory measurements, where the samples were subjected to oscillatory shear strains, monitoring the resulting oscillatory shear stress. From oscillatory measurements, we obtained the values of the storage (G′) and loss (G′′) moduli. We performed two different oscillatory tests. In the first one, we subjected the samples to oscillatory shear strains of constant frequency (1 Hz) and increasing amplitude—these tests are known as amplitude sweeps and allow the determination of the extension of the LVR. Secondly, we subjected the samples to oscillatory shear strains of constant amplitude (within the LVR) and increasing frequency from 1 to 100 Hz, in order to obtain the frequency response of the samples. For iron suspensions, all kinds of measurements were carried out in both the absence and presence of the applied magnetic field. For the application of the magnetic field of different strengths, we used the commercial magneto-cell provided with the Physica MCR 300 rheometer.

We also analysed the self-healing capacity of the samples, after subjecting them to a shear rate that breaks the internal structure. For this aim, we subjected the samples to an oscillatory shear strain of constant amplitude within the LVR and 1 Hz frequency, and monitored the resulting viscoelastic moduli as a function of time. At time t = 80 s, and for a total duration of 80 s, we stopped the oscillatory shear strain and subjected the samples to shear rates of large magnitude, in order to break the internal structure of the samples. Immediately afterwards (t = 160 s), the shear rate was stopped and the samples were subjected again to oscillatory shear strain of constant amplitude within the LVR and 1 Hz frequency, and the resulting viscoelastic moduli were monitored again as a function of time, to check if the rheological state previous to the large shearing was regained. For this self-healing analysis, we used a controlled-stress Haake Mars III rheometer, provided with a measuring system consisting of coaxial cylinders of 16 mm and 17 mm internal and external diameter, respectively, where the samples were previously placed and left at rest before the experiment.

For all kinds of rheological experiments, the results shown in this paper for each experimental condition represent the average of separate measurements; for at least three aliquots of each sample.

(f). Optical microscopy of the internal structure of suspensions

For the investigation of the microstructure of the suspensions of iron particles, we used optical microscopy connected to a charge-coupled device camera. We performed observations in both the absence and presence of the applied magnetic field.

3. Experimental results

(a). Stability of the suspensions against particle settling

The colloidal stability was studied by monitoring, through direct observation, the appearance and evolution of phase separation in suspensions contained in test tubes (figure 1).

Figure 1.

Images of suspensions of iron particles (5% v/v) in solutions of alginate polymer at different times after preparation as indicated (days: hours: minutes: seconds). In each image, from left to right samples corresponding to the following concentrations of alginate polymer are seen: 5% w/v of LVSA polymer; 10% of LVSA polymer; 15% of LVSA polymer; 20% of LVSA polymer; and 8% of MVSA polymer. (Online version in colour.)

As observed, particle settling with appreciable phase separation appeared in suspensions of iron particles in LVSA polymer for the concentration of polymer up to 15% w/v, while no signs of phase separation were observed, even after 16 days of rest, for an LVSA polymer concentration of 20% w/v. As expected, the smaller the concentration of LVSA polymer, the faster was the phase separation. For suspensions of iron particles in MVSA polymer, no phase separation was observed for the total duration of the observations, even for a polymer concentration as low as 8% w/v.

(b). Rheological characterization of the solutions and suspensions

(i). Analysis of fluid-like/gel-like behaviour of the solutions of alginate polymer

We checked if solutions of LVSA polymer and MVSA polymer presented a fluid-like or a gel-like behaviour. For this aim, we first subjected the samples to oscillatory strains of fixed frequency and increasing amplitude (amplitude sweeps), and from these curves (not shown here for brevity), we determined the extension of the LVR. Then, we took the average value of both G′ and G′′ corresponding to the LVR. The obtained results are plotted in figure 2 as a function of alginate concentration, for both LVSA and MVSA.

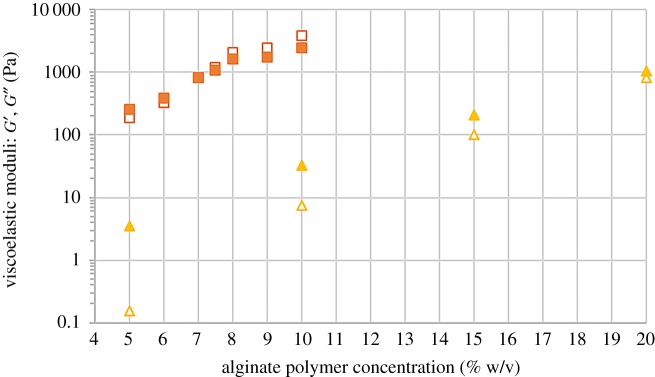
Figure 2.

Average value of the viscoelastic moduli of solutions of alginate polymer, within the LVR; standard deviations are about one order of magnitude smaller than the average values. Triangles and squares correspond, respectively, to solutions of LVSA polymer and MVSA polymer. Open symbols are for the storage modulus (G′) and full symbols are for the loss modulus (G′′). (Online version in colour.)

As observed, for both LVSA and MVSA polymer solutions, the loss modulus (G′′) and the storage modulus (G′) increased strongly with polymer concentration. For LVSA polymer, the loss modulus (G′′) was higher than the storage modulus (G′) for the whole range of concentrations under study (up to 20% w/v), and thus we can conclude that LVSA polymer solutions showed a fluid-like behaviour. Note, nevertheless, that the difference between G′′ and G′ diminished with polymer concentration, and at the highest LVSA polymer concentration (20% w/v) the value of G′ almost reached that of G′′. On the other hand, for MVSA polymer solutions, although the loss modulus was higher than the storage modulus at polymer concentration smaller than 7% w/v, a cross-over of these magnitudes took place for higher polymer concentration. Thus, we can conclude that, for concentrations higher than 7.5% w/v, the storage modulus dominated over the loss modulus and, consequently, the solutions presented a gel-like behaviour—note that the standard deviations are smaller than the differences between G′ and G′′ for this range of concentrations of MVSA polymer.

This gel-like behaviour was certainly responsible for the stability against particle settling observed in figure 1 for suspensions of iron particles in MVSA polymer solutions. In the case of LVSA polymer solutions, the increase in the loss (viscous) modulus with the concentration of polymer justifies the progressive diminution of settling inferred from observations in figure 1.

In what follows, and in view of the existence of two different behaviours for polymer solutions (fluid-like for LVSA polymer and low concentration of MVSA polymer, and gel-like for the medium to high concentration of MVSA polymer), we will restrict the samples studied in this work to those described in table 1.

Table 1.

Experimental systems for which the rheological properties were thoroughly investigated in the present work.

sample name	iron particle (HQ type) concentration	alginate polymer type/concentration	carrier liquid	rheological nature
0Fe-10LVSA	0% v/v	LVSA/10% w/v	water	fluid-like
0Fe-15LVSA	0% v/v	LVSA/15% w/v	water	fluid-like
0Fe-20LVSA	0% v/v	LVSA/20% w/v	water	fluid-like
0Fe-8MVSA	0% v/v	MVSA/8% w/v	water	gel-like
5Fe-10LVSA	5% v/v	LVSA/10% w/v	water	fluid-like
5Fe-15LVSA	5% v/v	LVSA/15% w/v	water	fluid-like
5Fe-20LVSA	5% v/v	LVSA/20% w/v	water	fluid-like
5Fe-8MVSA	5% v/v	MVSA/8% w/v	water	gel-like

(ii). Analysis of the steady-state rheology in the absence of an applied magnetic field

From steady-state measurements, we obtained the viscosity as a function of the shear rate (figure 3). As expected, the viscosity of the LVSA polymer solutions increased strongly with the concentration of alginate polymer. Also, for a given concentration of LVSA polymer, a shear-thinning phenomenon was observed, which was characterized by a decrease of the viscosity as the value of the shear rate increased. This shear-thinning phenomenon was found to be relatively stronger at higher concentrations of the polymer. With respect to the solution of MVSA polymer, it showed the largest values of viscosity at the low shear rate, despite its relatively low polymer concentration, with respect to solutions of LVSA polymer. In addition, this sample showed the strongest shear-thinning behaviour, as anticipated by its gel-like behaviour, demonstrated by data of figure 2.

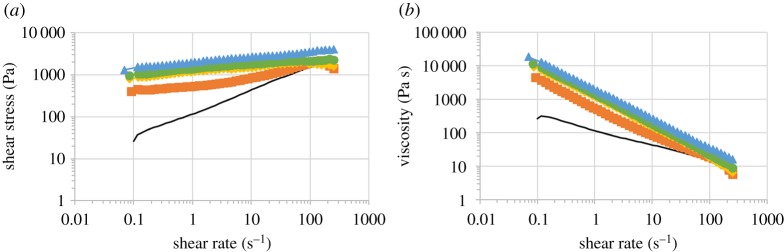
Figure 3.

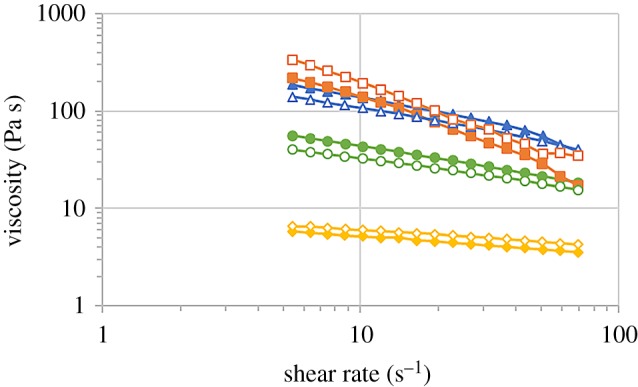
Viscosity as a function of shear rate for solutions of alginate polymer (open symbols) and suspensions of iron particles in alginate polymer solutions (full symbols): unfilled diamond/filled diamond, samples 0Fe-10LVSA/5Fe-10LVSA; unfilled circle/filled circle, samples 0Fe-15LVSA/5Fe-15LVSA; unfilled triangle/filled triangle, samples 0Fe-20LVSA/5Fe-20LVSA; unfilled square/filled square, samples 0Fe-8MVSA/5Fe-8MVSA. (Online version in colour.)

When magnetic particles were added to the solutions of sodium alginate, similar trends to those exhibited by the solutions of sodium alginate were obtained (figure 3). Furthermore, the values of the viscosity for each given value of the shear rate were not much affected by the introduction of the particles, with respect to those of solutions of sodium alginate. This result was expected since, in the absence of interaction between particles and polymers, the presence of 5% v/v of particles only induces a limited modification of the viscosity, according to Batchelor's formula [8]. Nevertheless, to investigate better the effect of iron particle concentration, we studied the viscosity of 10% alginate solutions for increasing concentrations of iron particles (up to 20% v/v of iron particles—results not shown here), and we observed an increase in viscosity with increasing concentration of iron particles. Note that the effect of particle concentration on the viscosity of fluids and gels has been extensively investigated from both experimental and theoretical points of view in previous works [8–11].

(iii). Analysis of the dynamic (oscillatory) state rheology in the absence of an applied magnetic field

We subjected the samples to oscillatory shear strains of constant frequency, f (1 Hz), and increasing amplitude, as well as to oscillatory shear strains of constant amplitude, γ, and increasing frequency (figures 4 and 5). For the samples based on LVSA polymer (both the solutions and the suspensions), the loss modulus (G′′) was higher than the storage modulus (G′), which is typical of a liquid-like system (table 2). Nevertheless, as the concentration of LVSA polymer within the solution increased, the values of G′ increased faster than those of G′′, and for the higher concentration under study (20%), both the storage and the loss moduli were within the same order of magnitude. On the other hand, for the samples based on MVSA polymer (both the solution and the suspension) G′ dominated over G′′ (table 2), i.e. a gel-like behaviour was obtained.

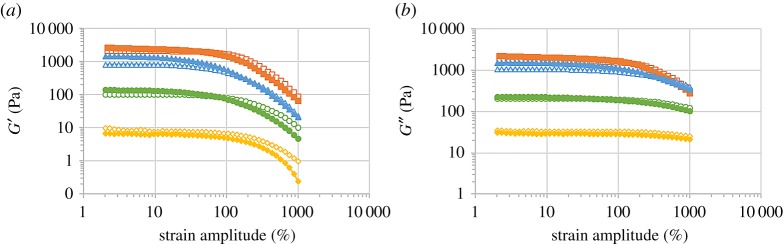
Figure 4.

Viscoelastic moduli as a function of shear strain amplitude for fixed frequency of 1 Hz, for solutions of alginate polymer (open symbols) and suspensions of iron particles in alginate polymer solutions (full symbols): unfilled diamond/filled diamond, samples 0Fe-10LVSA/5Fe-10LVSA; unfilled circle/filled circle, samples 0Fe-15LVSA/5Fe-15LVSA; unfilled triangle/filled triangle, samples 0Fe-20LVSA/5Fe-20LVSA; unfilled square/filled square, samples 0Fe-8MVSA/5Fe-8MVSA. (a) Storage modulus (G′) and (b) loss modulus (G′′). (Online version in colour.)

Figure 5.

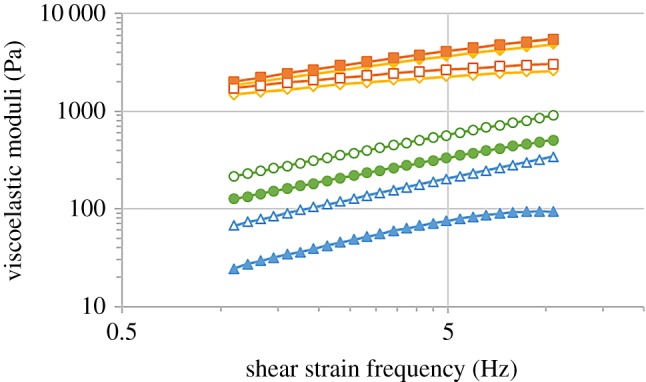
Viscoelastic moduli as a function of shear strain frequency for fixed shear strain amplitude within the LVR, for solutions of alginate polymer and suspensions of iron particles in alginate polymer solutions: unfilled triangle/filled triangle, sample 0Fe-15LVSA; unfilled circle/filled circle, sample 5Fe-15LVSA; unfilled diamond/filled diamond, sample 0Fe-8MVSA; unfilled square/filled square, sample 5Fe-8MVSA. Full symbols represent values of the storage modulus (G′) and open symbols represent values of the loss modulus (G′′). (Online version in colour.)

Table 2.

Values corresponding to the LVR, as obtained by oscillatory measurements of constant frequency and increasing shear strain amplitude.

sample name	storage modulus, G′ (Pa)	loss modulus, G′′ (Pa)	G′′/G′ ratio
0Fe-10LVSA	7.5 ± 0.8	33 ± 5	4.4 ± 1.1
0Fe-15LVSA	103 ± 12	210 ± 30	2.0 ± 0.5
0Fe-20LVSA	820 ± 90	1060 ± 120	1.3 ± 0.3
0Fe-8MVSA	2070 ± 240	1650 ± 170	0.80 ± 0.17
5Fe-10LVSA	6 ± 0.5	29 ± 3	4.8 ± 0.9
5Fe-15LVSA	132 ± 14	220 ± 30	1.7 ± 0.4
5Fe-20LVSA	1340 ± 140	1500 ± 180	1.1 ± 0.3
5Fe-8MVSA	2350 ± 180	2030 ± 150	0.86 ± 0.12

Another feature observed in figure 4 is the fact that both G′ and G′′ presented approximately constant values at low strain amplitude (something that defines the LVR), while showing decreasing trends at large amplitude (above 100% of strain amplitude), with the drop being more acute for G′ than for G′′. Concerning the dependence of these quantities with strain frequency within the LVR, as demonstrated by figure 5, in all cases both log G′ and log G′′ increased almost linearly with log f, a characteristic that is typical of solutions of polymers measured at low to medium frequency [12]. Note at this point that the linear trends in double logarithmic scale observed in figure 5 imply a power-law dependence of the viscoelastic moduli with frequency. We have calculated the exponent of this power-law dependence and we obtained values in the approximate range 0.6–0.7 (for both G′ and G′′) for the samples based on LVSA, and values of approximately 0.25 (for G′′) and 0.44 (for G′) for the samples based on MVSA. Note that typically G′ is constant at low frequency for highly cross-linked systems, such as rubber [12]. On the contrary, for concentrated polymer liquids, G′ scales with f² and G′′ with f in the limit of low frequency [12].

As for the comparison between results for solutions and suspensions, as observed (figures 4 and 5), the introduction of a content of 5% v/v of iron particles within the formulation provokes, in general, some enhancements of the values of G′ and G′′ (figure 3).

(iv). Analysis of the steady-state rheology of suspensions of iron particles in alginate solutions in the presence of an applied magnetic field

We analysed the steady-state behaviour under a magnetic field. As illustrated (figure 6) for the sample containing 5% v/v of iron particles in the solution of 15% w/v of LVSA polymer, there is a clear magnetorheological (MR) effect, characterized by an enhancement of both the shear stress and the viscosity for a given value of the shear rate, as the strength of the magnetic field increased. Similar curves were obtained for the other samples, not shown here for brevity.

Figure 6.

Shear stress (a) and viscosity (b) as a function of shear rate for sample 5Fe-15LVSA, under the application of magnetic fields of different strengths, H: solid line, H = 0 kA m⁻¹; filled square, H = 73.5 kA m⁻¹; filled diamond, H = 156 kA m⁻¹; filled circle, 229 kA m⁻¹; filled triangle, 282 kA m⁻¹. (Online version in colour.)

In order to better analyse the effect of the applied magnetic field on the characteristic rheological parameters of the samples, we obtained the dynamic yield stress, σ_y, of the samples from curves like those shown in figure 6a, by fitting them to the Bingham equation [13]:

$$\sigma ={\sigma }_{\mathrm{y}}+{\eta }_{\mathrm{p}}\dot{\gamma },$$ 3.1

with η_p being the plastic viscosity. As observed in figure 7, samples based on LVSA polymer did not show any yield stress in the absence of the applied magnetic field, which is consistent with their liquid-like behaviour. On the contrary, the sample based on MVSA polymer presented a non-negligible yield stress in the absence of the applied magnetic field, as expected for a gel-like material. Under an applied magnetic field, all samples presented a yield stress, which increased strongly with the intensity of the field. The stronger enhancement was obtained for sample 5Fe-8MVSA in spite of its gel-like behaviour in the absence of the applied field. For the samples based on LVSA polymer, the tunability of the rheological properties by magnetic field application was higher for the solution of 10% of alginate than for the formulation containing 20%, as a consequence of the stronger hindering of particle movement in the latter case due to the dense polymer chains at the microscopic level.

Figure 7.

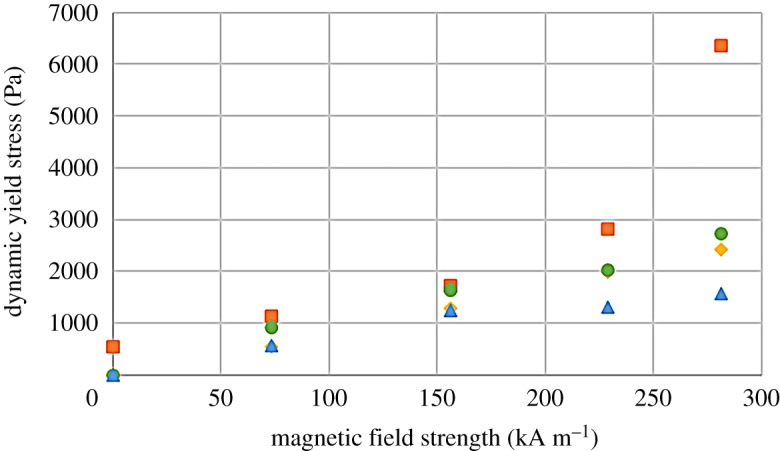
Dynamic yield stress as a function of the applied magnetic field strength, for suspensions of magnetic particles in solutions of alginate polymer: filled diamond, sample 5Fe-10LVSA; filled circle, sample 5Fe-15LVSA; filled triangle, sample 5Fe-20LVSA; filled square, sample 5Fe-8MVSA. (Online version in colour.)

(v). Analysis of the dynamic (oscillatory) state rheology of suspensions of iron particles in alginate solutions in the presence of an applied magnetic field

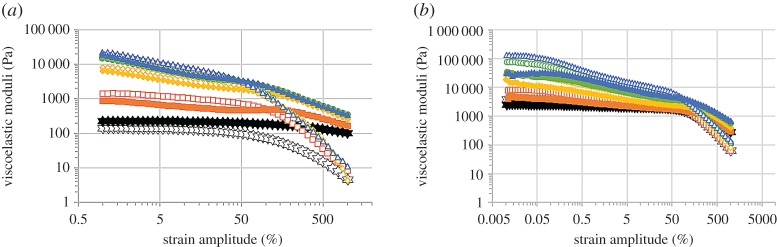
Finally, we analysed the effect of an applied magnetic field on the response of samples to oscillatory shear strains of fixed frequency (1 Hz) and stepwise increasing amplitude (figure 8). As observed, the application of a magnetic field had a strong impact on the response of the suspensions. First, under a magnetic field, at low shear strain amplitude, the storage modulus is higher than the loss modulus, which is characteristic of a viscoelastic solid. The reason is the aggregation of the particles into chain-like structures under the application of a magnetic field, which gives to the samples a gel-like microstructure. Note that, for samples based on LVSA polymer, in the absence of an applied magnetic field, a viscoelastic liquid behaviour (G′′ > G′) was obtained. Another remarkable feature of figure 8 is the fact that, as the magnetic field increases, the magnitudes of both G′ and G′′ increase, as a consequence of the MR effect. Finally, we observe the appearance of a maximum in G′′ under a field in the range 10–100% of strain. These maxima represent yielding points, for which the magnetic field-induced particle structures are broken by the applied shear.

Figure 8.

Viscoelastic moduli of suspensions of magnetic particles in solutions of alginate polymer, as a function of shear strain amplitude, for imposed oscillatory shear strain of fixed frequency (1 Hz), and under the application of magnetic fields of different strengths, H: unfilled star/filled star, H = 0 kA m⁻¹; unfilled square/filled square, H = 73.5 kA m⁻¹; unfilled diamond/filled diamond, H = 156 kA m⁻¹; unfilled circle/filled circle, 229 kA m⁻¹; unfilled triangle/filled triangle, 282 kA m⁻¹. (a) Sample 5Fe-15LVSA and (b) 5Fe-8MVSA. Open symbols represent values of the storage modulus (G′) and full symbols represent values of the loss modulus (G′′). (Online version in colour.)

We also analysed the behaviour of the samples under oscillatory shear strains of constant amplitude (within the LVR) and increasing frequency. Results are illustrated for sample 5Fe-8MVSA as an example in figure 9. As observed, for all the values of the applied magnetic field under study, both G′ and G′′ increased with frequency, which is typical of viscoelastic materials. It is also observed that both G′ and G′′ increased with the intensity of the applied magnetic field.

Figure 9.

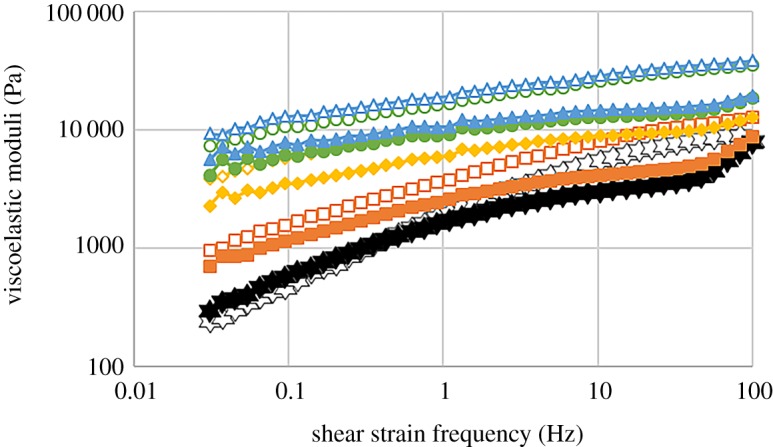
Viscoelastic moduli of sample 5Fe-8MVSA as a function of shear strain frequency, for imposed oscillatory shear strain of fixed amplitude within the LVR, and under the application of magnetic fields of different strengths, H: unfilled star/filled star, H = 0 kA m⁻¹; unfilled square/filled square, H = 73.5 kA m⁻¹; unfilled diamond/filled diamond, H = 156 kA m⁻¹; unfilled circle/filled circle, 229 kA m⁻¹; unfilled triangle/filled triangle, 282 kA m⁻¹. Open symbols represent values of the storage modulus (G′) and full symbols represent values of the loss modulus (G′′). (Online version in colour.)

Finally, and in order to better analyse the effect of the applied magnetic field, we obtained the values of the viscoelastic moduli corresponding to the LVR from curves like those shown in figure 8 (frequency 1 Hz), and plotted them as a function of the magnetic field strength (figure 10)—note that we took the viscoelastic moduli for shear strain amplitudes of 0.05 and 0.1, respectively, for MVSA and LVSA samples, as representative of the LVR. As observed, there is a strong enhancement of the viscoelastic moduli (both G′ and G′′) with the increase of the magnetic field strength. This enhancement was higher for sample 5Fe-8MVSA, in spite of its gel-like behaviour in the absence of an applied magnetic field. For the samples based on LVSA polymer, at the highest field, the stronger enhancement was obtained for the sample containing the intermediate content of alginate (15%). A larger amount of sodium alginate very likely hindered the magnetic field-induced particle chaining, thus preventing a strong MR effect. At the lowest value of the applied magnetic field (73.5 kA m⁻¹), no significant differences were obtained for the different samples based on LVSA polymer, very likely because the polymer prevented strong particle chaining.

Figure 10.

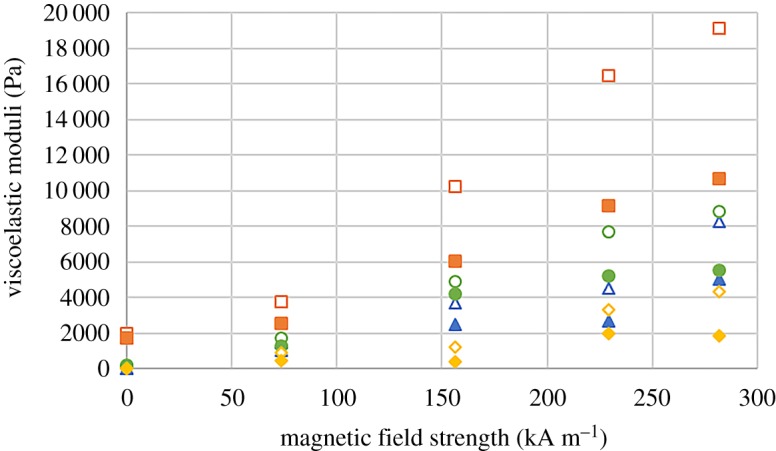
Values of the viscoelastic moduli corresponding to the LVR for a frequency of 1 Hz, as a function of the magnetic field strength for suspensions of magnetic particles in solutions of alginate polymer: unfilled diamond/filled diamond, sample 5Fe-10LVSA; unfilled circle/filled circle, sample 5Fe-15VSA; unfilled triangle/filled triangle, sample 5Fe-20LVSA; unfilled square/filled square, sample 5Fe-8MVSA. Open symbols represent values of the storage modulus (G′) and full symbols represent values of the loss modulus (G′′). (Online version in colour.)

(vi). Self-healing behaviour

The study of the self-healing behaviour makes sense for gel-like samples, for which a large shearing (such as the one used when injecting in biomedical applications) provokes a breakage of the internal network structure. Because of this, here we only present results for gel-like samples, i.e. samples based on MVSA polymer. As an example, figure 11 shows the results for sample 5Fe-8MVSA, when subjected to a shear rate of 1000 s⁻¹ (during the time interval 80–160 s). As observed, the sample demonstrated a gel-like behaviour (G′ > G′′) prior to the application of the large shear rate (t < 80 s). On the contrary, immediately after the application of the large shear rate (t approx. 160 s), the sample demonstrated a liquid-like behaviour (G′ < G′′), i.e. the internal structure (and thus the gel-like structure) was broken. Note also the large decrease of the values of the viscoelastic moduli after the large shearing. However, as the time advanced after the breakage, the gel-like behaviour was regained very quickly, accompanied by an enhancement of the values of both G′ and G′′, although the values of the viscoelastic moduli measured prior to the large shearing were not recuperated for the total duration of the experiment. Similar results were obtained for other values of the applied shear rate, as well as for the gel-like samples not containing magnetic particles (0Fe-8MVSA).

Figure 11.

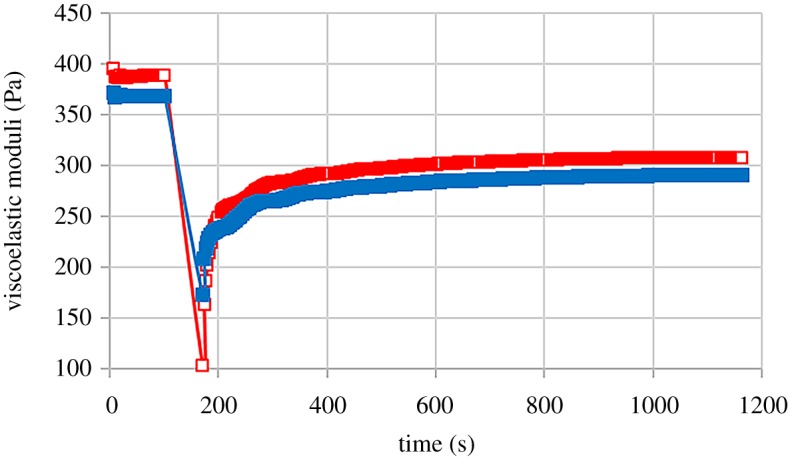
Self-healing study of sample 5Fe-8MVSA. The sample was subjected to a shear rate of 1000 s⁻¹ during the time interval 80–160 s. Before and after this time, the viscoelastic moduli resulting from an oscillatory shear strain of fixed amplitude within the LVR and 1 Hz frequency were monitored. Open squares (red) represent the storage modulus and full symbols (blue) represent the loss modulus. (Online version in colour.)

(c). Optical microscopy of the internal structure

Finally, we analysed the internal structure of the magnetic samples by means of optical microscopy (figure 12). As observed, some roughly spherical clusters were observed in all samples in the absence of a magnetic field (figure 12a,c,e,g,i). These clusters should consist of magnetic particles aggregated mainly by van der Waals attraction, as well as a consequence of the remnant magnetization. Under a magnetic field (figure 12b,d,f,h,j), these primary clusters should aggregate into secondary, elongated, chain-like clusters, as observed particularly in figure 12b and j. These chain-like clusters are less in number in those samples containing a larger amount of alginate polymer (compare figure 12f and h with b and j), as the polymer hindered the movement of the primary clusters in response to the applied magnetic field. These results are in agreement with the results of magnetorheological experiments, where we obtained a stronger enhancement of the rheological properties under a magnetic field for samples 5Fe-8MVSA and 5Fe-10LVSA than for those containing larger amounts of polymer.

Figure 12.

Images of optical microscopy of diluted suspensions of magnetic particles (about 0.2% v/v of particles) in solutions of alginate polymer. Images (a,c,e,g,i) were taken in the absence of the applied magnetic field; (b,d,f,h,j) were taken under the application of a magnetic field of 40 mT. Solutions of alginate polymer used as a dispersing medium were as follows: (a,b) 5LVSA; (c,d) 10LVSA; (e,f) 15LVSA; (g,h) 20LVSA and (i,j) 8MVSA.

4. Theory

In this part, we present a theoretical model of the observed magnetoviscous effects in the alginate suspensions, involved in the low-frequency motion, which can be considered as a quasi-stationary one. The model is based on observations of [10], which demonstrate that without an applied field the particles of the magnetic filler unify into dense aggregates (primary agglomerates—PAs), which, in the first approximation, can be considered as spherical clusters. Under the action of the applied magnetic field, these clusters magnetize and form linear chain-like aggregates. In the gelated polymer, the number of the PAs in the chain is determined by a competition between the force of magnetic attraction between the agglomerates, and the resistance to their displacement in the elastic host gel.

In motionless liquid suspensions of magnetizable non-Brownian particles (PAs), the number of particles (PAs) in the chain is, in principle, restricted only by the size of the sample. Theoretically, these chains can overlap the suspension, bridging the opposite walls of the container. If the suspension is involved in macroscopic deformation flow, the longest chains are destroyed by the viscous forces and the size of the chains is determined by the competition between the forces of magnetic interparticle (interagglomerate) attraction and the destroying hydrodynamic forces [14,15].

However, photos in figure 12 show that, because of the high viscosity of the carrier alginate solution, the clusters do not have time to form the long chains overlapping the measuring cell. It is natural to suppose that initially, right after the field switching on, the rate of chain formation is relatively high. Then, with depletion of the single PA concentration, the rate falls down to negligible values. Note that the similar time dependence of the rate of chain formation has been detected in computer simulations [16]. One can suppose also that the chains, which can appear for the duration of a real experiment, are significantly shorter than the maximal (stable) size of the chains, estimated in [14,15], corresponding to the given stationary shear rate of the suspension flow. That is why, in the flowing suspension, at least in the studied range of the macroscopic shear rate, these chains can be considered as undestroyed. When the shear rate exceeds some threshold value, the chains rupture. The analysis and comparison of the obtained theoretical results with the experimental ones, presented below, confirms the concept of the transition from regimes with undestroyed chains to ruptured chains.

Let us start with analysis of the suspension with undestroyed chains, corresponding to the relatively low shear rate of the suspension flow. For maximal simplification of analysis, we consider a system of identical chains, consisting of identical spherical primary agglomerates. Like in the experiments, an external magnetic field is applied in the direction of the suspension velocity gradient. We suppose that the number n of the PAs in the chain is given and does not depend on the shear rate.

We will use an approach based on the models [10,14,15] of magnetic suspensions with the chains. Like in these models, suppose that they magnetically interact in the dipole–dipole way and neglect their hydrodynamic interactions.

The magnetic moment of a PA in the chain can be presented as m = Mv, where M is the chain magnetization and v is the agglomerate volume. The magnetization can be estimated by using the well-known Fröhlich–Kennelly approximation [17]:

$$M=\frac{{\chi }_0{H}_{\mathrm{in}}{M}_{\mathrm{s}}}{{\chi }_0{H}_{\mathrm{in}}+M_{\mathrm{s}}},$$ 4.1

where χ₀ and M_s are the initial susceptibility and the saturated magnetization of the primary agglomerate, i.e. of the chain, and H_in is the mean magnetic field inside the chain. This field can be estimated as follows [18]:

$$H_{\mathrm{in}}=H-MN,$$ 4.2

where N is the demagnetizing factor of the chain, and H is the magnetic field in the suspension. Taking into account that the particles' volume concentration in our experiments is low, the field H is approximately equal to the external field with respect to the suspension.

We estimate parameter N by using the explicit relation (e.g. [18]) for the demagnetizing factor of an ellipsoid of revolution with aspect ratio equal to the number n of agglomerates in the chain:

$$N=\frac{1}{2{(n^2-1)}^{3/2}}\left[n\hspace{0.17em}\text{ln}\left(\frac{n+\sqrt{n^2-1}}{n-\sqrt{n^2-1}}\right)-2\sqrt{n^2-1}\right].$$ 4.3

The magnetic susceptibility and saturated magnetization of the agglomerates, which appear in the alginate suspension with an internal composition similar to that in the present experiments, have been estimated in [10] as χ₀ ≈ 6.4 and M_s ≈ 800 kA m⁻¹.

Combining equations (4.1) and (4.2), one gets

$$\begin{array}{rl}M& =\frac{b-\sqrt{b^2-4{\chi }_0^2{M}_{\mathrm{s}}HN}}{2N{\chi }_0}\\ \text{with}b& ={\chi }_{0}H+M_{\mathrm{s}}(1+{\chi }_{0}N).\end{array}\}$$ 4.4

The strong magnetoviscous effect, observed in the experiments presented in figures 6–10, can be obtained for long chains with n significantly greater than one. In this case, the demagnetizing factor N is much less than 1, and the relation (4.4) gives

$$M=\frac{{\chi }_{0}H{M}_{\mathrm{s}}}{{\chi }_{0}H+M_{\mathrm{s}}}.$$ 4.5

Under the action of the shear flow, the chain deviates from the applied field H. This leads to the appearance of a magnetic torque, which tends to return the chain to the field direction. The angle θ of the chain deviation from the field direction is determined by the balance of the hydrodynamic Γ^h and magnetic Γ^m torques, acting on the chains. These torques can be estimated as follows [14,15]:

$$\begin{array}{rl}{\mathrm{\Gamma }}_n^{\mathrm{h}}& =\frac{1}{12}\dot{\gamma }\beta d^2{\cos }^2\hspace{0.17em}\theta \hspace{0.17em}n(n^2-1)\\ \text{with}\beta & =3\pi {\eta }_{0}d\end{array}\}$$ 4.6

and

$${\mathrm{\Gamma }}_n^{\mathrm{m}}=-6(n-1)\frac{{\mu }_0}{4\pi }\frac{m^2}{d^3}\sin \hspace{0.17em}\theta \cos \hspace{0.17em}\theta ,$$ 4.7

where μ₀ is the vacuum magnetic permeability, d is the PA diameter and η₀ is the viscosity of the carrier liquid. In the case of the alginate suspension, η₀ is not equal to the viscosity of the pure alginate solution without the particles (figure 3) but, approximately, it can be estimated as the viscosity of the suspension without the field (since the concentration of the particles is small). Balancing the torques (4.6) and (4.7), we come to the relation for the deviation angle θ, shown in figure 13:

$$\text{tan}\hspace{0.17em}\theta =\frac{{\pi }^2}{6}\dot{\gamma }\frac{{\eta }_0{d}^6}{{\mu }_0{m}^2}n(n+1).$$ 4.8

Figure 13.

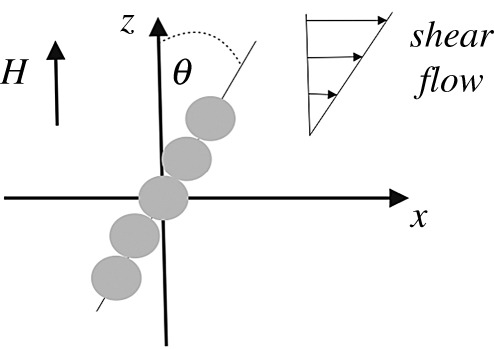
Illustration of the chains. The circles represent the clusters.

The stress produced by the chains can be estimated as follows [14,15]:

$${\sigma }_{\mathrm{ch}}\approx \frac{N_{\mathrm{ch}}}{V}|{\mathrm{\Gamma }}_n^{\mathrm{m}}|,$$ 4.9

where V is the total volume of the suspension, and N_ch is the total number of chains in this system.

Combining equations (4.7)–(4.9), after simple transformations, one gets

$$\begin{array}{rl}\sigma & \approx {\sigma }_{\mathrm{ch}}+{\eta }_0\dot{\gamma }\\ \text{with}{\sigma }_{\mathrm{ch}}& =\frac{3}{2}\mathrm{\Phi }(n^2-1)\frac{{\eta }_0\dot{\gamma }}{1+{(\text{tan}\hspace{0.17em}\theta )}^2},\end{array}\}$$ 4.10

where Φ is the volume concentration of the primary agglomerates and ${\eta }_0\dot{\gamma }$ is the stress in the host medium. The volume concentration Φ of the clusters cannot be calculated theoretically; the estimate Φ ≈ 0.25 was obtained in [10] by comparing the experimental and theoretical results. Note that the number n of agglomerates in the undestroyed chain is determined by the details of the kinetics of chain formation. Analysis of this kinetics requires a special investigation that is outside of the scope of the present paper. That is why we determine n as a fitting parameter from the condition of agreement between theory and experiment.

Let us consider the regime of the ruptured chains. The stress σ_ch now can be estimated by using the results of [14,15]. Assuming $n\gg 1$, we can present the results of [15] as follows:

$${\sigma }_{\mathrm{ch}}=\mathrm{\Phi }{\mu }_0\frac{M^2}{36\sqrt{2}}.$$ 4.11

For small values of the shear rate $\dot{\gamma }$, the stress σ_ch, determined by equation (4.10), is less than that given by equation (4.11). For large $\dot{\gamma }$, the opposite relation holds. Following the principle of a minimum of energy dissipation in a non-equilibrium system, it is natural to suppose that the transition from the state with undestroyed chains to the state with ruptured chains must take place when the values of stress σ_ch, estimated by equations (4.10) and (4.11), coincide. Thus, we can present the final form for the total stress as

$$\begin{array}{rl}\sigma & \approx {\sigma }_{\mathrm{ch}}+{\eta }_0\dot{\gamma }\\ \text{with}{\sigma }_{\mathrm{ch}}& =\text{min}\left(\frac{3}{2}\mathrm{\Phi }(n^2-1)\frac{{\eta }_0\dot{\gamma }}{1+{(\text{tan}\hspace{0.17em}\theta )}^2};\mathrm{\Phi }{\mu }_0\frac{M^2}{36\sqrt{2}}\right).\end{array}\}$$ 4.12

The fitted agglomerates' volume concentration Φ = 0.2 slightly differs from that Φ = 0.25 estimated in [10], because the conditions of the systems' synthesis are not identical.

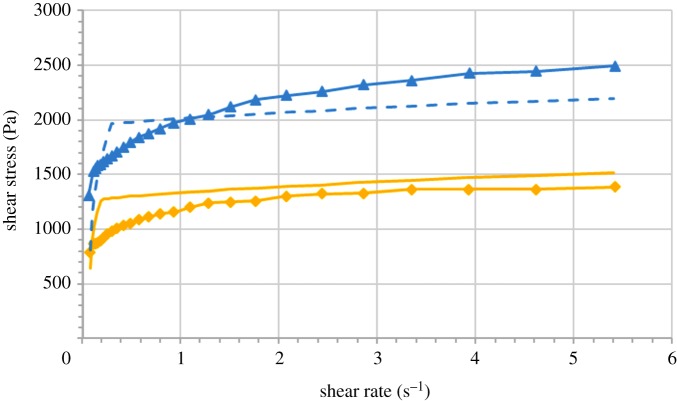
Results of calculations of equation (4.12) are shown in figure 14 for two values of the applied magnetic field. Experimental values are also included for comparison. As observed, the theoretical predictions reproduce the general tendency exhibited by the experimental values.

Figure 14.

Theory–experiment comparison for curves of shear stress versus shear rate, for sample 5Fe-15LVSA, under the application of magnetic fields of different strengths, H. Filled diamond, full curve, H = 156 kA m⁻¹; filled triangle, dashed curve, H = 282 kA m⁻¹. Filled diamond and filled triangle represent experimental data; full curve and dashed curve are predictions of the theoretical model (equation (4.12)). Parameters of the system for theoretical calculations: number of primary agglomerates in the undestroyed chains obtained by fitting are n = 8 and n = 9 for the magnetic fields of 156 kA m⁻¹ and 282 kA m⁻¹, respectively; volume concentration of clusters $\mathrm{\Phi }=0.25$ and viscosity ${\eta }_0=\sigma (H=0)/\dot{\gamma }$. (Online version in colour.)

The fitting numbers n = 8 and n = 9 of the agglomerates in the undestroyed chains look quite reasonable from the physical point of view. The agreement between theory and experiment indicates that the proposed model is adequate, at least, in its main physical points. The dynamic yield stress σ_y can also be estimated by extrapolation of the quasi-linear parts of the theoretical curves in a linear–linear scale, corresponding to large shear rates, to zero shear rate. The extrapolations gave the following theoretical values of the yield stress: σ_y ≈ 1200 Pa for H = 156 kA m⁻¹ and σ_y ≈ 1900 Pa for H = 282 kA m⁻¹. These results are not far from the experimental data: σ_y ≈ 1629 Pa for H = 156 kA m⁻¹ and σ_y ≈ 2731 Pa for H = 282 kA m⁻¹.

5. Conclusion

We report a straightforward strategy to develop and characterize novel ‘smart’ alginate-based fluids and gels, containing a dispersion of micrometre-sized Fe-HQ magnetic particles. Our study demonstrates the fabrication of magnetorheological polymer suspensions in a controlled manner and according to the physical needs in terms of colloidal stability, shear-thinning properties and viscoelastic moduli, through the modulation of the polymer concentration and molecular weight. In the presence of an applied magnetic field, we found a clear magnetorheological effect, as the viscoelastic moduli of all polymer formulations increased with increasing concentration of magnetic particles and strength of the magnetic field. Tuning the polymer concentration of the magnetorheological formulations permitted enhancement of their rheological properties, by controlling the movement and the structural distribution of the magnetic particle clusters within the polymeric matrix, as demonstrated through optical microscopy evaluation. In support of our hypothesis, here we presented a theoretical model able to properly reproduce the general trend exhibited by the experimental values in the stationary regime of the suspension flow. With further improvements, the capability to master the interaction between polymeric chains, magnetic particle clusters and its distribution within biocompatible matrices could allow the generation of novel magnetorheological fluids and gels with novel properties and with new potential applications in the field of biomedicine and tissue engineering.

Data accessibility

This article does not contain any additional data.

Authors' contributions

W.R.S.-F.: substantial contributions to acquisition of data; drafting the article; final approval of the version to be published. G.S.: substantial contributions to conception and design; revising the article critically for important intellectual content; final approval of the version to be published. J.D.G.D. and A.Y.Z.: substantial contributions to conception and design, and analysis and interpretation of data; revising the article critically for important intellectual content; final approval of the version to be published. M.T.L.-L.: substantial contributions to conception and design, analysis and interpretation of data; drafting the article; final approval of the version to be published.

Competing interests

We declare we have no competing interests.

Funding

W.R.S.-F. acknowledges financial support by the UTE University of Ecuador through paid licenses for trips and stays from Ecuador to Spain. J.D.G.D. received support from the Ministerio de Economía, Industria y Competitividad, MINECO, and Agencia Estatal de Investigación, AEI, Spain, cofounded by Fondo Europeo de Desarrollo Regional, FEDER, European Union, project FIS2017-85954-R. A.Y.Z. acknowledges the programme of the Ministry of Education and Science of the Russian Federation, project FEUZ-2020-0051, as well as the Russian Fund of Basic Researches, project 19-52-12028. M.T.L.-L. received support from the Ministerio de Economía, Industria y Competitividad, MINECO, and Agencia Estatal de Investigación, AEI, Spain, cofounded by Fondo Europeo de Desarrollo Regional, FEDER, European Union, project FIS2017-85954-R.