Dissolution of polydisperse ensembles of crystals in channels with a forced flow

Abstract

A non-stationary integro-differential model describing the dissolution of polydisperse ensembles of crystals in channels filled with flowing liquid is analysed. The particle-size distribution function, the particle flux through an arbitrary cross-section of the channel, the particle concentration profile, as well as the disappearance intensity of particles are found analytically. It is shown that a nonlinear behaviour of solutions is completely defined by the source term of particles introduced into the channel. In particular, the model approximately describes the processes of dissolution and transport of drug microcrystals to the target sites in a living organism, taking into account complex dissolution kinetics of drug particles.

This article is part of the theme issue ‘Patterns in soft and biological matters’.

1. Introduction

The processes of phase transformations from the metastable state of a system completely determine its physico-chemical properties, particle-size distribution and dynamics of growing structures. Here such applications as dissolution of dispersed solids, evapo- ration of polydispersed mists, combustion of liquid and solid dispersed fuels, as well as nucleation and crystallization of particulate assemblages in metastable media may be mentioned as examples having a great practical significance [1–13]. Mathematical models of such processes of phase transformations represent a system of integro-differential equations in partial derivatives, the general methods of solution of which do not exist. Therefore, the construction of a solution in each case requires the development of unique mathematical methods and techniques for finding solutions to a nonlinear model with moving boundaries of phase transformations of evolving particles in a polydisperse ensemble. Here such approaches as the saddle-point technique, the method of variable separation, the method of integral transforms, the small parameter expansion method, the perturbation technique or a combination of these approaches may be used as a powerful tool for constructing a solution to the concrete phase transformation model (see, among others, [14–23]).

The present study is concerned with a new analytical approach developed for a nonlinear dissolution problem of particulate assemblages in a channel in the presence of well-developed flow. Such dissolution processes play an important role in different areas of applied science ranging from metallurgy and chemical industry to production of food and delivery of drugs to the target sites [24–28]. For example, different drugs are used in the form of microcrystals compressed into tablets. When microcrystals of the drug enter the body fluid, they undergo dissolution and transfer to the sites of their destination [29]. As this takes place, some microcrystals dissolve earlier, not reaching the goal of their impact due to the presence of different barriers in the organism. At the same time, other microcrystals do not have time to dissolve and are carried away by the fluid flow from the target. This leads to insufficient drug concentrations at the sites of destination (e.g. a receptor in the brain). Therefore, the urgent task is to control the process of transfer and dissolution of microcrystals in a living organism, so that the maximum number of dissolved particles of the drug would be able to achieve the final target. Another important example is the transport mechanism of drugs from blood vessels to tumour tissue. To reach a solid tumour, drugs are first introduced into an intravenous infusion site and then they are transferred through a living organism (its system of veins, heart, lungs and arteries) to peripheral microvessels [30]. Then drugs penetrate through microvessel walls and extravascular tissues to cancer cells. Therefore, it is important to control the process of dissolution and transport of the drug microcrystals to obtain the maximum concentration of drugs at the point of their destination.

This article is organized as follows. Section 2 is devoted to the formulation of a mathematical model that describes the dissolution of particulate assemblages in a channel filled with fluid flow. Analytical solutions to this model are constructed in §3. Numerical examples showing behaviour of the analytical theory under consideration are given in §4. The concluding §5 summarizes the main outcomes following from the present analysis.

2. Governing equations

Let us now formulate the mathematical model describing the non-stationary dissolution process of a polydisperse assemblage of solid particles in a channel with a forced steady-state flow. We assume that the distances at which the flow parameters of the mixture change significantly are much larger than the sizes of the particles and the distances between them. We also assume that the solid particles are introduced into the channel cross-section l₀, and their spatio-temporal behaviour is described by means of the size distribution function f(r, l, t), where r is the particle radius, l is the channel axis and t is time (figure 1). Neglecting fluctuations in a particle dissolution rate, we have the following kinetic equation in the case of well-developed turbulent flow

$$\begin{array}{rl}\hspace{0.17em}& \frac{\mathrm{\partial }f}{\mathrm{\partial }t}+w\frac{\mathrm{\partial }f}{\mathrm{\partial }l}+\frac{\mathrm{\partial }}{\mathrm{\partial }r}(vf)-D\frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }{l}^2}=\frac{I_0}{L}\delta (l-l_0)w{f}_0(r,t),\\ \hspace{0.17em}& -\mathrm{\infty }<l<\mathrm{\infty },\hspace{0.17em}r>0,\hspace{0.17em}t>0,\end{array}$$ 2.1

where w is the mean solid phase flow velocity, v is the particle dissolution rate, D is the coefficient of longitudinal flow mixing, I₀ is the intensity of particle source, L is a length scale of channel, δ is the Dirac delta function and f₀(r, t) is the size distribution function corresponding to the particle source at the channel cross-section l₀. The right-hand side of equation (2.1) describes the solid phase input into a channel at l = l₀.

Figure 1.

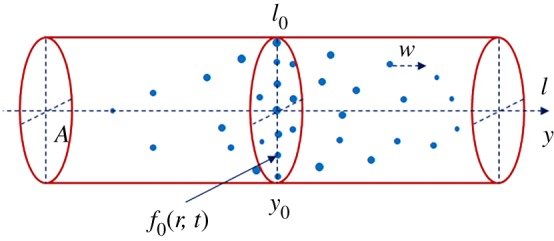
Schematic illustration of the dissolution of a polydisperse ensemble of particles introduced into the channel cross-section l₀ (A designates the channel cross-sectional area). (Online version in colour.)

The size distribution function f satisfies the following boundary and initial conditions at l → ±∞, r → ∞ and t = 0

$$f\to 0,\hspace{0.17em}l\to \pm \mathrm{\infty };\hspace{0.17em}f\to 0,\hspace{0.17em}r\to \mathrm{\infty };\hspace{0.17em}f=0,\hspace{0.17em}t=0.$$ 2.2

Note that the first boundary condition (2.2) shows that the solid particles completely dissolve far from the channel cross-section l₀.

For the sake of simplicity, we assume that the dissolution rate v is a linear function of supersaturation $\mathrm{\Delta }C=C_{\ast }-C$

$$v=-\chi \beta (r)\mathrm{\Delta }C,$$ 2.3

where C and $C_{\ast }$ are the solute concentrations in the flow and on the surface of a solid particle, β(r) is the mass transfer coefficient and χ is a constant coefficient (χ = k_w/(3ρk_v) [24], k_w and k_v represent the surface and volume form factors of particles, ρ is the solid phase density). Note that the driving force ΔC of the dissolution process generally varies along the channel, and the current concentration C is related to the mass of the soluble substance by the conservation equation. This makes the problem under consideration highly nonlinear. To simplify the model, we assume that dissolution occurs in a large volume and the driving force ΔC remains constant.

Let us now chose the length scale r_m of particles and a characteristic length scale L, which is the distance travelled by a particle having the size r_m at the beginning when moving along the channel axis with an average velocity w until its complete dissolution

$$L=\frac{w}{\chi \mathrm{\Delta }C}{\int }_0^{r_m}\frac{\text{d}r}{\beta (r)}=\frac{w{r}_m}{v_0}\text{and}{v}_0=\chi \mathrm{\Delta }C{r}_m{\left({\int }_0^{r_m}\frac{\text{d}r}{\beta (r)}\right)}^{-1}.$$ 2.4

Also, introducing the dimensionless variables and parameters

$$\begin{array}{rl}\hspace{0.17em}& x=\frac{r}{r_m},\hspace{0.17em}y=\frac{l}{L},\hspace{0.17em}{y}_0=\frac{l_0}{L},\hspace{0.17em}\tau =\frac{v_{0}t}{L},\hspace{0.17em}R=\frac{v_{0}L}{D},\hspace{0.17em}\kappa =\frac{L}{r_m},\hspace{0.17em}P=\frac{wL}{D},\hspace{0.17em}v=-v_0{\beta }_0(x)\\ \text{and}& {\beta }_0(x)=\frac{\beta (x{r}_m)}{r_m}{\int }_0^{r_m}\frac{\text{d}r}{\beta (r)},\hspace{0.17em}F(x,y,\tau )=r_{m}ALf(r,l,t),\hspace{0.17em}{F}_0(x,\tau )=r_{m}AL{f}_0(r,t),\end{array}\}$$ 2.5

we get from (2.1) to (2.4)

$$\begin{array}{rl}\hspace{0.17em}& R\frac{\mathrm{\partial }F}{\mathrm{\partial }\tau }+P\frac{\mathrm{\partial }F}{\mathrm{\partial }y}-\kappa R\frac{\mathrm{\partial }}{\mathrm{\partial }x}[{\beta }_0(x)F]-\frac{{\mathrm{\partial }}^{2}F}{\mathrm{\partial }{y}^2}=P{I}_0\delta (y-y_0)F_0(x,\tau ),\\ \hspace{0.17em}& -\mathrm{\infty }<y<\mathrm{\infty },\hspace{0.17em}x>0,\hspace{0.17em}\tau >0\end{array}$$ 2.6

and

$$F\to 0,\hspace{0.17em}y\to \pm \mathrm{\infty };\hspace{0.17em}F\to 0,\hspace{0.17em}x\to \mathrm{\infty };\hspace{0.17em}F=0,\hspace{0.17em}\tau =0.$$ 2.7

To simplify the problem (2.6), (2.7), we use the following substitutions:

$$G(x,y,\tau )={\beta }_0(x)F(x,y,\tau )\exp [-\alpha y-\gamma z(x)],\hspace{0.17em}\alpha =\frac{P}{2},\hspace{0.17em}z(x)={\int }_0^x\frac{\text{d}\xi }{{\beta }_0(\xi )},\hspace{0.17em}\gamma =\frac{P^2}{4\kappa R}.$$ 2.8

Now rewriting the model (2.6), (2.7) in terms of (2.8), we arrive at

$$\begin{array}{rl}\hspace{0.17em}& R\frac{\mathrm{\partial }G}{\mathrm{\partial }\tau }-\kappa R{\beta }_0(x)\frac{\mathrm{\partial }G}{\mathrm{\partial }x}-\frac{{\mathrm{\partial }}^{2}G}{\mathrm{\partial }{y}^2}=P{I}_0{\beta }_0(x)\delta (y-y_0)F_0(x,\tau )\exp [-\alpha y-\gamma z(x)],\\ \hspace{0.17em}& -\mathrm{\infty }<y<\mathrm{\infty },\hspace{0.17em}x>0,\hspace{0.17em}\tau >0\end{array}$$ 2.9

and

$$G\to 0,\hspace{0.17em}y\to \pm \mathrm{\infty };\hspace{0.17em}G\to 0,\hspace{0.17em}x\to \mathrm{\infty };\hspace{0.17em}G=0,\hspace{0.17em}\tau =0.$$ 2.10

3. Analytical solutions

Now applying the exponential Fourier transform with respect to variable y and the Laplace transform with respect to τ, we come to

$$\kappa R{\beta }_0(x)\frac{\text{d}{G}_{FL}}{\text{d}x}=(Rs+{\omega }^2)G_{FL}-{\phi }_L(x).$$ 3.1

Here, subscripts F and L denote the Fourier and Laplace transforms, ω and s represent the Fourier and Laplace variables, and

$$\phi (x,\tau )=\frac{P{I}_0}{\sqrt{2\pi }}{\beta }_0(x)F_0(x,\tau )\exp (-i\omega y_0-\alpha y_0-\gamma z(x)),$$

where i is the imaginary unit.

The solution of differential equation (3.1) satisfying the boundary condition G_FL → 0 at x → ∞ (z → ∞) takes the form

$$G_{FL}=\frac{1}{\kappa R}{\int }_x^{\mathrm{\infty }}\frac{{\phi }_L(x_1)}{{\beta }_0(x_1)}\exp [-\frac{Rs+{\omega }^2}{\kappa R}(z(x_1)-z(x))]\text{d}{x}_1.$$ 3.2

Applying the inverse Laplace and Fourier transforms to expression (3.2), we obtain

$$G(x,y,\tau )=\frac{P{I}_0\exp (-P{y}_0/2)}{2\sqrt{\pi \kappa R}}{\int }_x^{\mathrm{\infty }}\frac{\exp [-\frac{\kappa R{(y-y_0)}^2}{4(z(x_1)-z(x))}-\frac{P^{2}z(x_1)}{4\kappa R}]}{\sqrt{z(x_1)-z(x)}}{F}_0(x_1,\tau -\frac{z(x_1)-z(x)}{\kappa })\text{d}{x}_1.$$ 3.3

Combining now expressions (2.8) and (3.3), we find the dimensionless size distribution function as

$$\begin{array}{rl}F(x,y,\tau )& =\frac{P{I}_0\exp [P(y-y_0)/2]}{2{\beta }_0(x)\sqrt{\pi \kappa R}}{\int }_x^{\mathrm{\infty }}\frac{\exp [-\frac{\kappa R{(y-y_0)}^2}{4(z(x_1)-z(x))}-\frac{P^2(z(x_1)-z(x))}{4\kappa R}]}{\sqrt{z(x_1)-z(x)}}\\ \hspace{0.17em}& \times F_0(x_1,\tau -\frac{z(x_1)-z(x)}{\kappa })\text{d}{x}_1.\end{array}$$ 3.4

One of the important characteristics of the particle dissolution process in a channel with flow is the particle flux J through an arbitrary section of the channel, which is determined as

$$J(r,l,t)=f(r,l,t)-\frac{D}{w}\frac{\mathrm{\partial }f}{\mathrm{\partial }l}=\frac{1}{r_{m}AL}(F(x,y,\tau )-\frac{1}{P}\frac{\mathrm{\partial }F}{\mathrm{\partial }y}).$$ 3.5

Introducing the relative particle flux $J_r=4\sqrt{\pi \kappa R}{r}_{m}ALJ/I_0$ and substituting (3.4) into (3.5), we get

$$\begin{array}{rl}{J}_r(x,y,\tau )& =\frac{P\exp [P(y-y_0)/2]}{{\beta }_0(x)}{\int }_x^{\mathrm{\infty }}\frac{{\displaystyle \exp [-\frac{\kappa R{(y-y_0)}^2}{4(z(x_1)-z(x))}-\frac{P^2(z(x_1)-z(x))}{4\kappa R}]}}{\sqrt{z(x_1)-z(x)}}\\ \hspace{0.17em}& \times F_0(x_1,\tau -\frac{z(x_1)-z(x)}{\kappa })[1+\frac{\kappa R(y-y_0)}{P(z(x_1)-z(x))}]\text{d}{x}_1.\end{array}$$ 3.6

The initial moment μ₀(l, t) of the zero order of the particle-size distribution function describes the particle concentration profile along the channel length

$${\mu }_0(l,t)={\int }_0^{R_m}f(r,l,t)\hspace{0.17em}\text{d}r=\frac{1}{AL}{\int }_0^{R_m/r_m}F(x,y,\tau )\hspace{0.17em}\text{d}x,$$ 3.7

where R_m stands for the maximum particle size.

The particle disappearance intensity f|v| at r → 0 determines the dissolution rate of a polydisperse ensemble of crystals

$$f(r,l,t)|v|=\frac{v_0{\beta }_0(x)F(x,y,\tau )}{r_{m}AL},\hspace{0.17em}x\to 0.$$ 3.8

Expressions (3.4)–(3.8) represent exact analytical solutions of the problem under consideration. Below we analyse their behaviour when changing different variables and parameters.

4. Behaviour of solutions

Let us now analyse the main features of the analytical solution constructed in §3. For the sake of definiteness, we choose the size distribution function f₀ at the channel cross-section l₀ as

$$f_0(r,t)=\frac{F_0(x,\tau )}{r_{m}AL}=\frac{N_0\delta (r-r_m)\overline{F}(\tau )}{r_{m}AL},\hspace{0.17em}\overline{F}(\tau )=\tau \exp (-\tau ),$$ 4.1

where N₀ is the normalization factor, and function $\overline{F}(\tau )$ takes into account an increase in the influx of particles at short times and its weakening at long times (for example, short-term drug input). We also consider a simple case when β₀ (x) = 1. Keeping this in mind and substituting (4.1) into (3.4), we arrive at the following dimensionless distribution function:

$$\begin{array}{rl}\mathrm{\Phi }(x,y,\tau )& =\frac{2\sqrt{\pi \kappa R}F(x,y,\tau )}{I_0{N}_0}\\ \hspace{0.17em}& =\frac{P\exp [-\frac{\kappa R{(y-y_0)}^2}{4(1-x)}-\frac{P^2(1-x)}{4\kappa R}+\frac{P(y-y_0)}{2}]}{\sqrt{1-x}}\overline{F}(\tau -\frac{1-x}{\kappa }).\end{array}$$ 4.2

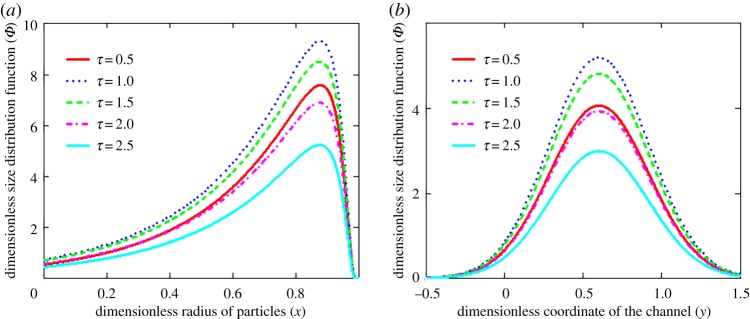
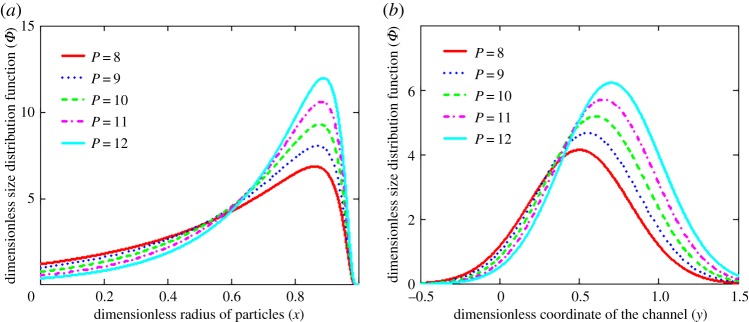
The evolutionary behaviour of this rescaled distribution function is shown in figure 2. It is seen that the distribution function first increases and then decreases with increasing time. Such a behaviour completely corresponds to the dynamics of particle influx at the channel cross-section y₀ (or l₀). In addition, the distribution function of fixed particle size at different channel cross-sections (figure 2b) represents a bell-shaped curve that is shifted to the right relative to the particle entry point y₀. This effect is caused by the presence of flow velocity directed to the right. The influence of Péclet number P = wL/D on the particle-size distribution function is illustrated in figure 3. As is easily seen, the number of smaller particles decreases and the number of larger particles increases with increasing Péclet number (figure 3a). This is due to the fact that larger particles are transported faster by the fluid flow, and smaller particles dissolve faster with increasing Péclet number. What is more, an increase in the Péclet number symmetrically shifts the distribution function to the right, towards larger values of the channel coordinate y (figure 3b).

Figure 2.

The dimensionless size distribution function Φ versus radius x of crystals (a, y = 0.3) and coordinate y of the channel (b, x = 0.5) at different times τ (y₀ = 0.1 and P = 10). (Online version in colour.)

Figure 3.

The dimensionless size distribution function Φ versus radius x of crystals (a, y = 0.3) and coordinate y of the channel (b, x = 0.5) at different Péclet numbers P (y₀ = 0.1 and τ = 1). (Online version in colour.)

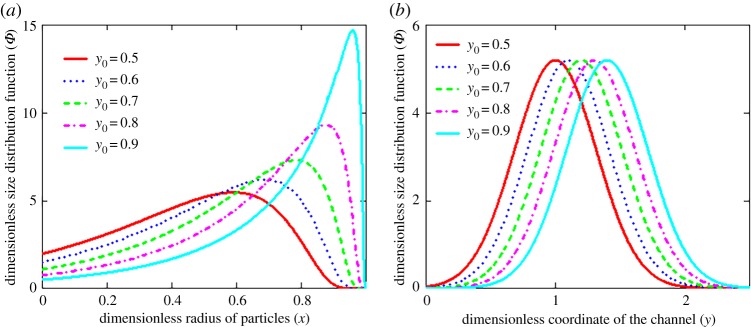
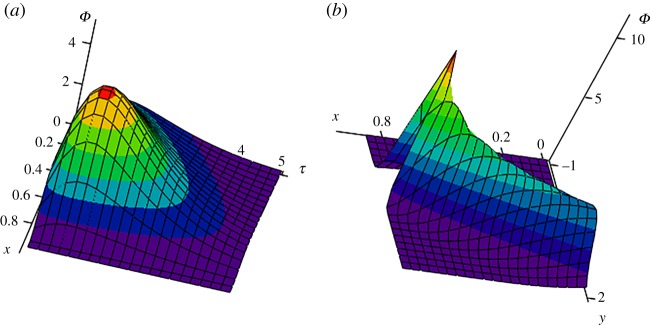
Figure 4 demonstrates the influence of various source cross-sections y₀ (where particles come into the channel) on the distribution function. First, the closer y₀ to y, the narrower and steeper the distribution function, and its maximum lies higher (figure 4a). Secondly, the distribution function of particles of a fixed size uniformly shifts toward larger values of the channel coordinate y with increasing y₀ (figure 4b). Note that the shift of a maximum point to the right for y₀ is explained by the presence of fluid flow in the same direction. Figure 5 illustrates the three-dimensional behaviour of the distribution function. This function moves along the time variable τ, changing its shape and amplitude (figure 5a). Strongly nonlinear behaviour of the distribution function in the plane of spatial variables x and y at a fixed point in time is shown in figure 5b.

Figure 4.

The dimensionless size distribution function Φ versus radius x of crystals (a, y = 1) and coordinate y of the channel (b, x = 0.5) at different cross-sections y₀, where particles are introduced into the channel (τ = 1 and P = 10). (Online version in colour.)

Figure 5.

The dimensionless size distribution function Φ versus x and τ (a, y = 0.5) and versus x and y (b, τ = 1), y₀ = 0.1 and P = 10. (Online version in colour.)

Now combining expressions (3.6) and (4.1), we simplify the dimensionless particle flux going through an arbitrary section of the channel as

$$\begin{array}{rl}I(x,y,\tau )& =\frac{J_r(x,y,\tau )}{N_0}=\frac{{\displaystyle P\exp [-\frac{\kappa R{(y-y_0)}^2}{4(1-x)}-\frac{P^2(1-x)}{4\kappa R}+\frac{P(y-y_0)}{2}]}}{\sqrt{1-x}}\\ \hspace{0.17em}& \times \overline{F}(\tau -\frac{1-x}{\kappa })[1+\frac{\kappa R(y-y_0)}{P(1-x)}].\end{array}$$ 4.3

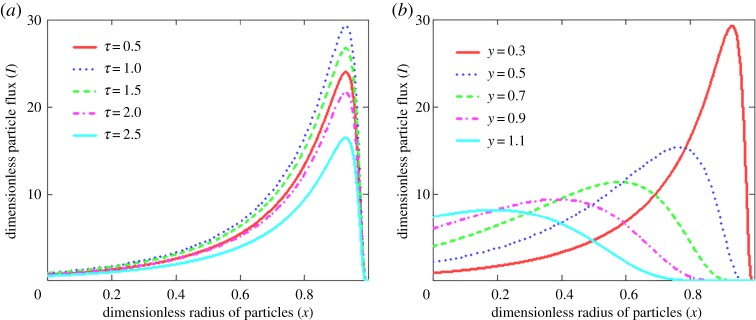
An important point is that the particle flux at a fixed channel cross-section y attains its maximum at a certain time due to an increase in the introduced particles at short times and a decrease in their number at long times in the source cross-section y₀ (figure 6a). Another important feature is that the particles are capable to dissolve with increasing y and their flux decreases (figure 6b).

Figure 6.

The dimensionless particle flux I versus radius x of crystals at different times (a, y = 0.3) and coordinates y of the channel (b, τ = 1), y₀ = 0.1 and P = 10.

Now rewriting expressions (3.7) and (3.8) in dimensionless form, choosing R_m = r_m, and taking into account (4.1), we have

$$\begin{array}{rl}\nu (y,\tau )& =\frac{2\sqrt{\pi \kappa R}AL{\mu }_0(l,t)}{I_0{N}_0}=P\exp \left[\frac{P(y-y_0)}{2}\right]\\ \hspace{0.17em}& \times {\int }_0^1\frac{{\displaystyle \exp [-\frac{\kappa R{(y-y_0)}^2}{4(1-x)}-\frac{P^2(1-x)}{4\kappa R}]}}{\sqrt{1-x}}\overline{F}(\tau -\frac{1-x}{\kappa })\text{d}x\end{array}$$ 4.4

and

$$\begin{array}{rl}\sigma (y,\tau )& =\frac{2\sqrt{\pi \kappa R}{r}_{m}ALf(0,l,t)|v|}{v_0{I}_0{N}_0}\\ \hspace{0.17em}& =P\exp [\frac{P(y-y_0)}{2}-\frac{\kappa R{(y-y_0)}^2}{4}-\frac{P^2}{4\kappa R}]\overline{F}(\tau -\frac{1}{\kappa }).\end{array}$$ 4.5

Here, ν(y, τ) and σ(y, τ) represent the dimensionless initial moment of the zero order and the particle disappearance intensity.

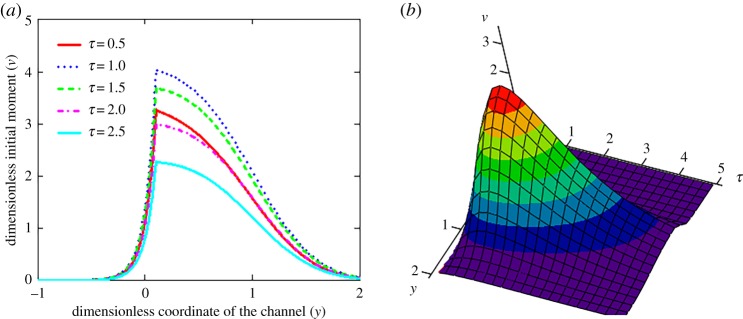
Figure 7 illustrates the particle concentration profile along the channel length at different times. It is easy to note that the profile of this function increases at short times, reaches a maximum and then decreases at long times. What is more, the fluid flow spreads this profile to the right in the direction of flow. Note that the particle source is located at y₀ = 0.1.

Figure 7.

The dimensionless initial moment ν of the zero order (particle concentration profile along the channel length) versus coordinate y of the channel (a) and versus y and τ (b), y₀ = 0.1 and P = 10. (Online version in colour.)

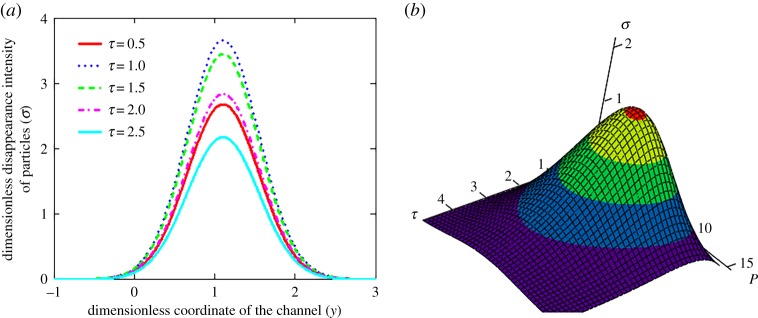
The particle disappearance intensity shown in figure 8 has a maximum point, which is dependent on time τ, Péclet number P and the channel cross-section y₀ where the particle source is located. In other words, these parameters determine the maximum point of dissolution of a particulate assemblage in a channel. So, for example, if we are dealing with the dissolution and transport processes of drugs in a living organism, we can find the target site where the soluble dose of the drug attains its maximum.

Figure 8.

The dimensionless disappearance intensity σ of particles versus coordinate y of the channel (a, P = 10) and versus τ and P (b, y = 0.5), y₀ = 0.1. (Online version in colour.)

5. Concluding remarks

In summary, a new theoretical description of the dissolution process of a polydisperse ensemble of particles in the presence of a forced flow is presented. The model is based on the kinetic equation for the particle-size distribution function and on the assumption that the phase transition occurs in a sufficiently large volume, where the driving force is constant. An exact analytical solution of the problem under consideration is constructed by means of the Laplace and Fourier integral transforms. It is demonstrated that a nonlinear behaviour of solutions is completely determined by the source term of particles introduced into the channel cross-section y₀ (or l₀). So, for example, the distribution function first increases and then decreases, inheriting the dynamic behaviour of the particle influx into the source cross-section y₀ of the channel. The intensity of fluid flow (Péclet number P) has a decisive role in the dissolution process. Namely, an increase in the Péclet number shifts the distribution function to the right in the direction of fluid flow. It is shown that the particle flux at an arbitrary channel cross-section, the particle concentration profile, as well as the disappearance intensity of particles, are substantially dependent on time, the channel coordinate, Péclet number, and the source cross-section.

The theory under consideration can be generalized to the more general case when the driving force ΔC is determined from the integral equation of mass balance. It can be done in the spirit of works [31–34], where some special approaches to the integro-differential model of nucleation and growth of particulate assemblages were detailed.

Data accessibility

This article has no additional data.

Authors' contributions

All authors contributed equally to the present research article.

Competing interests

The authors declare that they have no competing interests.

Funding

This work was supported by the Russian Science Foundation(grant no. 18-19-00008).