From nucleation and coarsening to coalescence in metastable liquids

Abstract

The transition of a metastable liquid (supersaturated solution or supercooled melt) occurring from the intermediate stage (where the crystals nucleate and grow) to the concluding stage (where the larger particles evolve at the expense of the dissolution of smaller particles) is theoretically described, with allowance for various mass transfer mechanisms (reaction on the interface surface, volume diffusion, grain-boundary diffusion, diffusion along the dislocations) arising at the stage of Ostwald ripening (coalescence). The initial distribution function (its ‘tail’) for the concluding stage (forming as a result of the evolution of a particulate assemblage during the intermediate stage) is taken into account to determine the particle-size distribution function at the stage of Ostwald ripening. This modified distribution function essentially differs from the universal Lifshitz–Slyozov (LS) solutions for several mass transfer mechanisms. Namely, its maximum lies below and is shifted to the left in comparison with the LS asymptotic distribution function. In addition, the right branch of the particle-size distribution lies above and is shifted to the right of the LS blocking point. It is shown that the initial ‘tail’ of the particle-size distribution function completely determines its behaviour at the concluding stage of Ostwald ripening. The present theory agrees well with experimental data.

This article is part of the theme issue ‘Patterns in soft and biological matters’.

1. Introduction

The processes of phase and structural transformations in metastable liquids completely determine the nonlinear dynamics of the system, the evolving patterns in it, the evolution of polydisperse particulate assemblages as well as the final state and microstructure of the material. Such processes take place in different areas of applied science ranging from condensed matter physics, materials science and geophysics to chemical industry, biophysics and life science [1–19].

Generally speaking, the phase transformation processes in metastable liquids occur in several stages, each of which is described by the corresponding mathematical model. So, for example, at the initial stage, the supercooling (supersaturation) of the liquid practically does not change, and the solid phase particles nucleate on small impurity inclusions. At the intermediate stage of the phase transformation, the nucleation of crystals of a new phase and their further growth occur. As this takes place, the growing particles release the latent heat of crystallization (in the case of crystallization processes in supercooled melts) or absorb impurities from solutions (in the case of crystallization process in supersaturated solutions). This process reduces the liquid metastability (its supercooling or supersaturation) and leads to the formation of a polydisperse ensemble of particles evolving in a metastable liquid. Note that at this stage, the particles grow almost without interacting with each other. When the supercooling (supersaturation) of the liquid becomes very small, and the number of crystals becomes sufficiently large, the process of phase transformation goes to the final stage. Here such transformations as Ostwald ripening, agglomeration and disintegration of particles are capable to occur. In the case of Ostwald ripening, smaller crystals dissolve and larger crystals continue to grow at the expense of this dissolution process.

The theory of evolution of particulate assemblages at the intermediate stage with allowance for the diffusion mechanism of the particle-size distribution function in the space of particle radii was recently developed in articles [20–22]. This theory enables us to find an unsteady-state behaviour of the distribution function as well as the liquid supercooling (supersaturation) as a function of time. In 1978, Slezov developed a theory of Ostwald ripening (coalescence) process [23] taking into account the initial particle-size distribution function that forms to the beginning of ripening stage. He showed that this initial distribution function depends on the power-law ‘tail’ that forms to the beginning of this phase transition stage. This power-law dependence can be found from the exact analytical solutions that describe the final states of the intermediate stage from the analytical solutions [20–22]. Thus, a transition between the intermediate and ripening stages becomes described analytically. The present article develops such a theory for several types of mass transfer mechanisms occurring at the stage of Ostwald ripening.

This article is organized as follows. Section 2 is devoted to the theory of the intermediate stage, where the model equations and their analytical solutions are written out. The ‘tail’ of the particle-size distribution function that forms to the concluding phase of the intermediate stage (or to the beginning of the Ostwald ripening stage) is analytically found in §3. Keeping in mind this power-law ‘tail’ of the distribution function, new analytical solutions for the Ostwald ripening stage are constructed in §4. Our concluding remarks are formulated in §5. Two appendices give more detailed information on the theory presented in §4.

2. Analytical solutions describing the intermediate stage of a phase transition process

Let us first formulate a mathematical model describing a phase transformation process in a metastable liquid that occurs at its intermediate stage. A metastable medium is supercooled (or supersaturated) to a great degree so that nucleation and growth of solid-phase crystals are capable to occur. Their evolution is described by an integro-differential model of kinetic and balance equations that govern the dynamics of the particle-radius distribution function f(r, t) and liquid supercooling (or supersaturation) Δ(τ) of the form [20–22]

$$\frac{\mathrm{\partial }f}{\mathrm{\partial }\tau }+\frac{\mathrm{\partial }}{\mathrm{\partial }r}(\frac{\text{d}r}{\text{d}\tau }f(r,\tau ))=\frac{\mathrm{\partial }}{\mathrm{\partial }r}\left(D\frac{\mathrm{\partial }f}{\mathrm{\partial }r}\right),\hspace{0.17em}r>r_{\ast },\hspace{0.17em}\tau >0$$ 2.1

and

$$\mathrm{\Delta }(\tau )={\mathrm{\Delta }}_0-b{\mathrm{\Delta }}_0{\int }_{r_{\ast }}^{\mathrm{\infty }}{r}^{3}f(r,\tau )\hspace{0.17em}\text{d}r,\hspace{0.17em}\tau >0,$$ 2.2

where r and τ are the spherical coordinate and time, dr/dτ is the particle growth rate, D is the coefficient of mutual Brownian diffusion of particles, $r_{\ast }$ is the radius of critical nuclei, Δ₀ is the initial supercooling (or supersaturation) and b = 4πL_V/(3ρ_mc_mΔ₀), if the phase transition occurs in a single-component supercooled melt (or b = 4πC_p/(3Δ₀) if the phase transition occurs in a supersaturated solution). Here, ρ_m and c_m represent the density and specific heat of a metastable mixuture, and L_V and C_p are the latent heat parameter and concentration at saturation. Note that the coefficient of mutual Brownian diffusion is defined by an ‘Einstein relation’ in the r space [24]. Generally speaking, its exact determination is a difficult task of statistical physics. Therefore, for the sake of simplicity, let us use the following simple approximation $D=d_{1}dr/d\tau =d_1{\beta }_{\ast }\mathrm{\Delta }(\tau )$, where ${\beta }_{\ast }$ and d₁ stand for the kinetic coefficient and a pertinent factor.

The boundary and initial conditions to the model equations (2.1) and (2.2) can be written out in the form [20–22]

$$\begin{array}{rl}\hspace{0.17em}& \frac{\text{d}r}{\text{d}\tau }\hspace{0.17em}f(r,\tau )-D\frac{\mathrm{\partial }f}{\mathrm{\partial }r}=I(\mathrm{\Delta }),\hspace{0.17em}r=r_{\ast },\\ \hspace{0.17em}& f(r,\tau )\to 0,\hspace{0.17em}r\to \mathrm{\infty }\\ \text{and}& f(r,\tau )=0,\hspace{0.17em}\mathrm{\Delta }(\tau )={\mathrm{\Delta }}_0,\hspace{0.17em}\tau =0.\end{array}\}$$ 2.3

Note that the first boundary condition (2.3) defines the flux of particles passing through a critical nucleation barrier. The nucleation rate I(Δ) should be calculated theoretically or determined from experimental data. Let us use here the frequently used expression known as the Meirs nucleation rate [25–32] $I(\mathrm{\Delta })=I_{\ast }{(\mathrm{\Delta })}^p$, where p and $I_{\ast }$ represent empirical parameters.

Let us now introduce the following dimensionless variables and parameters:

$$\begin{array}{rl}\hspace{0.17em}& F(s,t)=l_0^{4}f(r,\tau ),\hspace{0.17em}t=\frac{\tau }{{\tau }_0},\hspace{0.17em}s=\frac{r}{l_0},\hspace{0.17em}{u}_0=\frac{d_1}{l_0},\hspace{0.17em}w(t)=\frac{\mathrm{\Delta }(\tau )}{{\mathrm{\Delta }}_0}\\ \text{and}& l_0={\left(\frac{{\beta }_{\ast }{\mathrm{\Delta }}_0}{I_0}\right)}^{1/4},\hspace{0.17em}{\tau }_0=\frac{l_0}{{\beta }_{\ast }{\mathrm{\Delta }}_0},\hspace{0.17em}{I}_0=I({\mathrm{\Delta }}_0),\end{array}\}$$ 2.4

where F(s, t) and w(t) are the dimensionless particle-radius distribution function and metastability degree (supercooling or supersaturation), and s and t are the dimensionless spatial and time variables.

The model (2.1)–(2.3) was analytically solved in the case of Meirs and Weber–Volmer–Frenkel–Zeldovich nucleation kinetics in our previous papers [20–22]. Let us write down here a simplest analytical solution that describes the Meirs kinetics as [21]

$$\begin{array}{rl}F(s,x)& =\exp \left(\frac{s}{2u_0}\right){\int }_0^x\frac{w^{p-1}(x-y)}{\sqrt{u_0}}\exp (-\frac{y}{4u_0})[\frac{1}{\sqrt{\pi y}}\exp (-\frac{s^2}{4u_{0}y})\\ \hspace{0.17em}& -\frac{1}{2\sqrt{u_0}}\exp (\frac{s}{2u_0}+\frac{y}{4u_0})\text{erfc}(\frac{s}{2\sqrt{u_{0}y}}+\frac{\sqrt{y}}{2\sqrt{u_0}})]\text{d}y\end{array}$$ 2.5

and

$$w(x)=\{\begin{array}{l}{[(2-p)H(x)+1]}^{1/(2-p)},\hspace{0.17em}p\ne 2\\ \exp [H(x)],\hspace{0.17em}p=2\end{array},$$ 2.6

where

$$\begin{array}{rl}x(t)& ={\int }_0^{t}w(t_1)\hspace{0.17em}\text{d}{t}_1,\hspace{0.17em}H(x)=-b{\int }_0^{x}h(y)\hspace{0.17em}\text{d}y\\ \text{and}h(y)& =\frac{2}{\sqrt{\pi }}[\exp (-\frac{y}{4u_0})(\frac{1}{2}{u}_0^{1/2}{y}^{5/2}+\frac{7}{2}{u}_0^{3/2}{y}^{3/2}-3u_0^{5/2}{y}^{1/2})\\ \hspace{0.17em}& +\sqrt{\pi }(\frac{9}{2}{u}_0{y}^2+3u_0^3+\frac{y^3}{2})]-\text{erfc}\left(\frac{\sqrt{y}}{2\sqrt{u_0}}\right)[6u_0^3+\frac{9}{2}{u}_0{y}^2+\frac{y^3}{2}].\end{array}\}$$ 2.7

The analytical solutions (2.5)–(2.7) found in a parametric form (x is the parameter playing the role of modified time variable) describe the particle-radius distribution function F(s, x) and the metastability degree w(x) at the intermediate stage of a phase transformation process. To study a behaviour of the metastable system at its concluding (coalescence) stage, we should determine the ‘tail’ of the distribution function F(s, x) that forms at the end of intermediate stage or at the beginning of Ostwald ripening stage.

3. The ‘tail’ of the particle-size distribution function

In 1978, Slezov showed that the ‘tail’ of the particle-radius distribution function that is formed at the beginning of the Ostwald ripening stage completely characterizes the system states during the concluding (coalescence) stage of a phase transformation process [23]. To find this ‘tail’, let us use the analytical solutions (2.5)–(2.7) at the end of the intermediate stage.

First of all, we take into account that the complementary error function entering in the analytical solutions (2.5) and (2.7) has an asymptotic expansion at small values of the system parameter u₀ ≪ 1 [20–22], i.e.

$$\text{erfc}(\alpha )\approx \frac{\exp (-{\alpha }^2)}{\sqrt{\pi }\alpha },\hspace{0.17em}\alpha \gg 1.$$ 3.1

Now combining (2.5) and (3.1), we estimate the particle-size distribution function as

$$F(s,x)\approx {\int }_0^x\frac{w^{p-1}(x-y)}{\sqrt{\pi u_{0}y}}\frac{s}{s+y}\exp [-\frac{1}{4u_0}{(\frac{s}{\sqrt{y}}-\sqrt{y})}^2]\text{d}y.$$ 3.2

The integral contribution (3.2) can be estimated by means of the saddle-point method [33–36]. So, introducing

$$S(y)={(\frac{s}{\sqrt{y}}-\sqrt{y})}^2\text{and}\lambda =\frac{1}{4u_0}\gg 1,$$

we estimate the distribution function (3.2) as

$$F(s,x)\approx \frac{s{w}^{p-1}(x-y_o)}{\sqrt{\pi u_0{y}_o}(s+y_o)}\exp [-\frac{1}{4u_0}{(\frac{s}{\sqrt{y_o}}-\sqrt{y_o})}^2]\sqrt{\frac{2\pi }{\lambda S^{\mathrm{\prime }\mathrm{\prime }}(y_o)}},$$ 3.3

where y_o = s is the minimum point of S(y). Substitution of y_o and S^′′(y_o) = 2/s into formula (3.3) leads to

$$F(s,x)\approx w^{p-1}(x-s).$$ 3.4

Now estimating functions h(y) and H(x) from (2.7) at u₀ ≪ 1, we arrive at the following simple expressions

$$h(y)\approx y^3\text{and}H(x)\approx -\frac{b{x}^4}{4}.$$ 3.5

Substituting (3.5) into (2.6) and (3.4), we finally obtain the ‘tail’ of the distribution function, which reads as

$$F(s)\approx \frac{A}{s^n},\hspace{0.17em}A={\left[\frac{4}{b(p-2)}\right]}^{(p-1)/(p-2)},\hspace{0.17em}n=\frac{4(p-1)}{p-2}.$$ 3.6

If we put, for example, p = 3 (or p = 4), we get n = 8 (or n = 6). An important point is that the ‘tail’ (3.6) of the distribution function completely characterizes the relaxation process of the distribution function at the concluding stage of Ostwald ripening from its initial state described by the distribution (3.6) to the universal distribution function derived by Lifshitz and Slyozov (Slezov) for different mass transfer mechanisms [37–41]. Expression (3.6) shows that the ‘tail’ of the distribution function represents the power-dependent distribution predicted for the first time by Slezov [23]. Note that his approach was developed for unknown parameters A and n. The present theory taking into account the intermediate stage of a phase transformation phenomenon enables us to find these parameters and describe the concluding stage more precisely.

4. Analytical solutions describing the stage of Ostwald ripening

Let us now describe the particle-size distribution function at the stage of Ostwald ripening process where larger particles grow at the expense of dissolution of smaller particles. To define the initial distribution of particles at this stage, we use the analytical distribution (3.6), which determines the initial distribution function in dimensional form as $f(r,0)=l_0^{n-4}A{r}^{-n}$. This power-dependent function defines a transition zone in the vicinity of the Lifshitz–Slyozov (LS) blocking point u_0k = k/(k − 1) [23,39–43]. Note that the blocking point depends on the mass transfer mechanism so that u_0k = u₀₂ = 2, k = 2 (reaction on the interphase surface), u_0k = u₀₃ = 3/2, k = 3 (volume diffusion), u_0k = u₀₄ = 4/3, k = 4 (grain-boundary diffusion) and u_0k = u₀₅ = 5/4, k = 5 (diffusion along the dislocations). Following articles [42,43], we introduce the scaled variables and parameters, which read as

$$\begin{array}{rl}\hspace{0.17em}& {\phi }_k(u,{\tau }_k)=r_{\ast }f=A_k\exp (-\frac{3{\tau }_k}{k})P_k(u),\hspace{0.17em}{\tau }_k=k\ln \frac{r_{\ast }(\tau )}{r_{\ast }(0)}\\ \text{and}& u=\frac{r}{r_{\ast }(\tau )},\hspace{0.17em}{A}_k^{-1}=\kappa {\int }_0^{\mathrm{\infty }}{\tilde{u}}^3{P}_k(\tilde{u})\text{d}\tilde{u},\hspace{0.17em}\kappa =\frac{4\pi r_{\ast }^3(0){\omega }_p}{3Q\omega }.\end{array}\}$$ 4.1

Here, $r_{\ast }$ represents the critical radius of crystals, $r_{\ast }(0)$ is its value at the beginning of ripening stage, Q is the total initial quantity of the material (supersaturation), ω_p is the volume per atom of pure solvent, ω is the volume of a single atom in the precipitate, u and τ_k stand for the rescaled space and time variables and P_k(u) represents the rescaled distribution function. We use here the standard designations and scales in the theory of Ostwald ripening processes [24]. Namely, the time scale is measured in units of $r_{\ast }^3(0)/(D_d\sigma )$, where D_d stands for the diffusion coefficient of the dissolved component, and σ = 2βv^′ c_0∞/(k_BT) (β is the interface surface tension, v^′ is the volume per atom of the dissolved component, c_0∞ is the equilibrium concentration at the plane boundary, k_B is the Boltzmann constant and T is the absolute temperature).

In the case of different mass transfer mechanisms under consideration, the growth rates of particles take the form [42,43]

$$\begin{array}{rl}\hspace{0.17em}& v_{uk}=\frac{\text{d}u}{\text{d}{\tau }_k}=\frac{1}{k{u}^{k-1}}[U_k(u)+{\gamma }_{0k}(u-1)(1-\frac{{\lambda }_k}{{\tau }_k^2(u)})],\hspace{0.17em}{\gamma }_{0k}=\frac{k^k}{{(k-1)}^{k-1}}\\ \hspace{0.17em}& U_k(u)=u_{0k}^{k-1}[k(u_{0k}-u)-u_{0k}]-\frac{k(k-1)u_{0k}^{k-2}{(u-u_{0k})}^2}{2}[1+\frac{(k-2)(u-u_{0k})}{3u_{0k}}\\ \hspace{0.17em}& +\frac{(k-2)(k-3){(u-u_{0k})}^2}{12u_{0k}^2}+\frac{(k-2)(k-3)(k-4){(u-u_{0k})}^3}{60u_{0k}^3}],\end{array}\}$$ 4.2

where the coefficients λ_k (k = 2, 3, 4, 5) are determined in table 1.

Table 1.

Parameters entering in the growth rate of particles (4.2) for several mass transfer mechanisms [42,43].

mass transfer mechanism	k	δk	λk	u2k	u1k
reaction on the interphase surface	2	${\displaystyle \frac{\pi }{\ln \frac{n-1}{2}}}$	$1+4{\delta }_2^2$	1	3
volume diffusion	3	${\displaystyle \frac{\pi }{\ln \frac{n-1}{3}}}$	${\displaystyle \frac{3}{4}}(1+4{\delta }_3^2)$	1.182	1.786
grain-boundary diffusion	4	${\displaystyle \frac{\pi }{\ln \frac{n-1}{4}}}$	${\displaystyle \frac{2}{3}}(1+4{\delta }_4^2)$	1.183	1.467
diffusion along the dislocations	5	${\displaystyle \frac{\pi }{\ln \frac{n-1}{5}}}$	${\displaystyle \frac{5}{8}}(1+4{\delta }_5^2)$	1.153	1.336

Here, functions τ_k(u) are defined from the following Cauchy problem [42,43]:

$$\frac{\text{d}{\tau }_k}{\text{d}u}=\frac{k{u}^{k-1}{\tau }_k^2}{[{\gamma }_{0k}(u-1)+U_k(u)]{\tau }_k^2-{\gamma }_{0k}{\lambda }_k(u-1)},\hspace{0.17em}\tau ={\tau }_{0k}\hspace{0.17em}\text{at}\hspace{0.17em}u=0$$ 4.3

and

$${\tau }_{0k}=\frac{(n-1)\psi (u_{1k})}{n-k-1}-\frac{k\psi (u_{2k})}{n-k-1}+\frac{k}{n-k-1}\ln \left[\frac{{(r_{\ast }(0))}^{n-3}Q(n-1)}{A{l}_0^{n-4}}\right],$$ 4.4

where

$$\psi (u)=-\frac{{\nu }_k{u}_{0k}}{u-u_{0k}},$$

ν₂ = 2, ν₃ = 1, ν₄ = 2/3 and ν₅ = 1/2 [42,43]. Note that the explicit differential equations for the evaluation of functions τ_k(u) for several mass transfer mechanisms are presented in appendix A.

The rescaled distribution function P_k(u) entering in (4.1) is determined by means of the following law [42,43]:

$$P_k(u)=-\frac{3}{k{v}_{uk}(u)}\exp \left(\frac{3}{k}{\int }_0^u\frac{\text{d}\tilde{u}}{v_{uk}(\tilde{u})}\right),k=2,3,4,5,$$ 4.5

where v_uk is given by formulae (4.2).

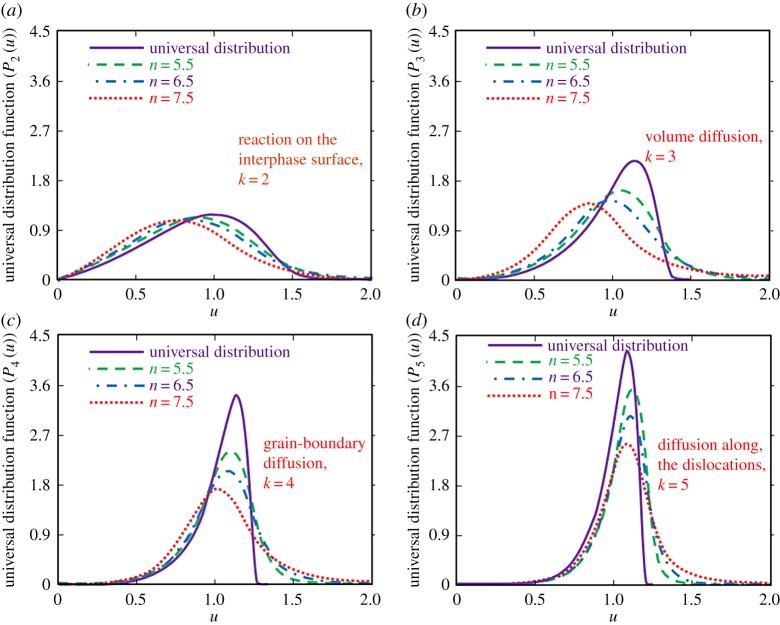
A limiting transition to the classical LS theory can be easily obtained from expressions (4.2) and (4.5) at large times τ_k → ∞. In this asymptotic case, one can obtain from solutions (4.2) and (4.5) the universal distribution functions P_k(u) given in table 2 for different mass transfer mechanisms k = 2, 3, 4, 5. These universal (limiting) distributions forming at large times are shown in figure 1. Note that each distribution function P_k(u) is defined to the left of its blocking point u_0k. As this universal state attains only in the asymptotic limit of large times, it is important to determine the distribution function at smaller times. In this more realistic case, the solution is represented by the analytical expressions (4.2) and (4.5).

Table 2.

Universal distribution functions for several mass transfer mechanisms (these functions follow from expressions (4.2) and (4.5) at large times τ_k → ∞ [42,43]). Expressions for C₄, C₅, j(u), s, ξ, θ, η, ζ and h are presented in appendix B.

k	Pk(u)
2	$P_2(u)=\{\begin{array}{ll}{\displaystyle \frac{24u\exp (3-{\displaystyle \frac{6}{2-u}})}{{(2-u)}^5}},& u\le u_{02}\\ 0,& u>u_{02}\end{array}$
3	$P_3(u)=\{\begin{array}{ll}{\displaystyle \frac{81u^2\exp (1-{\displaystyle \frac{1}{1-2u/3}})}{2^{5/3}{(u+3)}^{7/3}{(3/2-u)}^{11/3}}},& u\le u_{03}\\ 0,& u>u_{03}\end{array}$
4	$P_4(u)=\{\begin{array}{ll}{\displaystyle \frac{C_4{u}^3\exp ({\displaystyle \frac{2}{3u-4}}-{\displaystyle \frac{1}{6\sqrt{2}}}\text{arctan}{\displaystyle \frac{u+4/3}{4\sqrt{2}/3}})}{{(4/3-u)}^{19/6}{(u^2+8u/3+16/3)}^{23/12}}},& u\le u_{04}\\ 0,& u>u_{04}\end{array}$
5	$P_5(u)=\{\begin{array}{ll}{\displaystyle \frac{C_5{u}^4\exp [-{\displaystyle \frac{1}{2(1-4u/5)}}-\theta \hspace{0.17em}\text{arctan}({\displaystyle \frac{2u+(3+s)u_{05}}{2h}})]}{{(u_{05}-u)}^{2+\eta }j(u){[{(u+(3+s)u_{05}/2)}^2+h^2]}^{\xi }{[u-(1+s)u_{05}]}^{\zeta }}},& u\le u_{05}\\ 0,& u>u_{05}\end{array}$

Figure 1.

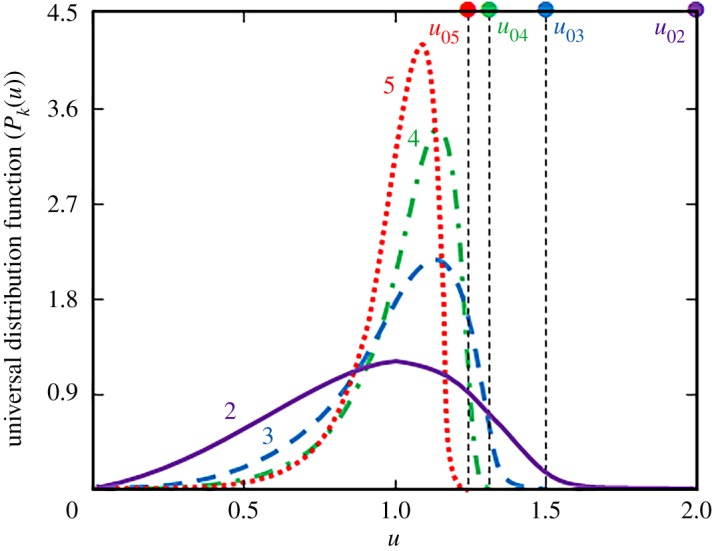
The universal distribution function (or the asymptotic state of a metastable system at the stage of Ostwald ripening) for several mass transfer mechanisms (numbers at the curves show different values of k). The mass transfer mechanisms are demonstrated by the solid (k = 2), dashed (k = 3), dash-dotted (k = 4) and dotted (k = 5) lines. The blocking points u_0k for several mass transfer mechanisms are u₀₂ = 2 (reaction on the interphase surface), u₀₃ = 3/2 (volume diffusion), u₀₄ = 4/3 (grain-boundary diffusion) and u₀₅ = 5/4 (diffusion along the dislocations). (Online version in colour.)

Figure 2 shows the distribution functions (4.5) plotted for several mass transfer mechanisms with allowance for the ‘tail’ (3.6) of the initial particle-size distribution at the stage of Ostwald ripening process (here we use three shapes of the ‘tail’ (3.6) with n = 5.5, n = 6.5 and n = 7.5). Now the blocking point does not determine the behaviour of curves. The distribution function lies to the right of the corresponding blocking point and its decreasing behaviour at large values of u is determined by the transition region u_2k < u < u_1k for a concrete mass transfer mechanism (see, for details, table 1 and [42,43]). An important point is that the maximum point of the distribution function P_k(u) decreases and shifts to the left with increasing the exponent n of the initial ‘tail’ (3.6). As a result, the real distribution functions during the Ostwald ripening process essentially differ from the universal asymptotic distributions shown in figure 2 by the solid lines.

Figure 2.

The particle-size distribution function P_k(u) shown accordingly to expressions (4.5) for different mass transfer mechanisms. The solid lines demonstrate universal (asymptotic) solutions presented in table 2 at large times τ_k → ∞. (Online version in colour.)

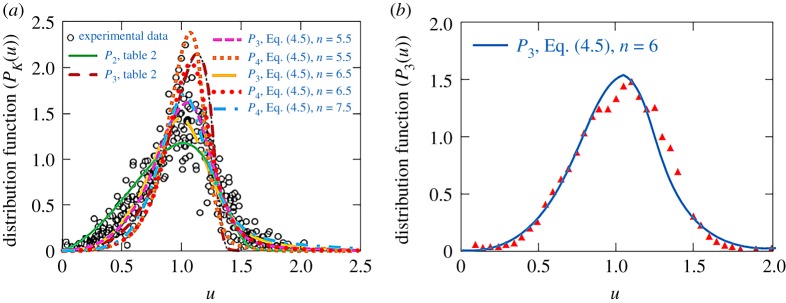
Figure 3 compares the theory under consideration with experimental data [44,45] for different mass transfer mechanisms and different shapes of the initial ‘tail’ of the particle-size distribution function. Twenty years of experiments [44] (figure 3a) confirm that the universal distribution functions P₂ (u) and P₃(u) given in table 2 cannot satisfactory describe experimental data: the corresponding distribution functions lie below or above of experimental points, and their behaviour is limited by the blocking points u_0k. Taking into account the initial ‘tail’ (3.6) of the distribution function at the stage of Ostwald ripening we can describe experimental data. As is easily seen from figure 3, the maximum point of P_k(u) shifts closer to experimental points, its left branch has the correct inflection whereas its right branch lies above the blocking point and tends to the region of larger values of u. An important point is that this behaviour highly depends on the exponent n of the initial ‘tail’ (3.6). In other words, this ‘tail’ completely determines the particle-size distribution function at the concluding stage of Ostwald ripening process as previously predicted by Slezov [23,39].

Figure 3.

The distribution function P_k(u) (table 2 and solution (4.5)) is compared with experimental data ([44] (a) and [45] (b) for several mass transfer mechanisms, $4\pi A{l}_0^{n-4}/(3Q{r}_{\ast }^{n-3}(0))={10}^{-10}$. (Online version in colour.)

5. Concluding remarks

In summary, a transition of the phase transformation process occurring in metastable liquids between the intermediate stage and the concluding stage of Ostwald ripening is theoretically described by sewing together two different analytical theories. First of all, from the analytical solutions describing the intermediate stage, we derived the initial ‘tail’ of the particle-size distribution function that forms at the beginning of the Ostwald ripening stage. Taking this ‘tail’ into account, we then found the distribution function that determines the state of a metastable system during the ripening stage when the smaller particles dissolve and the larger particles exist and evolve at the expense of this dissolution. Comparing our analytical theory with experimental data we conclude that the exponent n of the initial ‘tail’ (3.6) completely defines the behaviour of experimental data at the stage of Ostwald ripening. Namely, the shape of the distribution function changes drastically. Its maximum point becomes lower and shifts to the left side (to smaller values of u) with increasing n. As this takes place, the blocking point disappears, the right branch of the distribution function becomes higher and goes much to the right in comparison with the universal asymptotic (LS) distribution function. In addition, the left branch of the distribution function has a correct inflection that is confirmed by experimental points (if k = 2, 3, 4 this branch lies above the LS distribution curve).

Different mass transfer mechanisms at the stage of Ostwald ripening also have a decisive role in the particle-size distribution. As is easily seen from figures 1 to 3, the distribution function becomes broader and lower with decreasing the mass transfer constant k. Let us especially underline that several mass transfer mechanisms can occur simultaneously in real Ostwald ripening processes [46] (e.g. the mass transfer always happens along the grain boundaries and dislocation lines simultaneously with the volume diffusion [46]). Such a phase transformation theory represents an interesting and important task for future investigations that can be studied in the spirit of previous works [39,42,43,46]. Another important task is to combine the theories of directional and bulk crystallization (when dendritic growth, nucleation and particle growth occur simultaneously), the solution of which can be performed using the described approach and the theory of a two-phase (mushy) layer (see, among others, [47–52]).

Appendix A. Explicit differential equations for the functions τ_k(u)

$$\begin{array}{rl}\hspace{0.17em}& \frac{\text{d}{\tau }_2}{\text{d}u}=\frac{-2u{\tau }_2^2}{{(u-u_{02})}^2{\tau }_2^2+4(u-1)(1+4{\delta }_2^2)},\\ \hspace{0.17em}& \frac{\text{d}{\tau }_3}{\text{d}u}=\frac{-48u^2{\tau }_3^2}{16{(u-u_{03})}^2(u+3){\tau }_3^2+81(u-1)(1+4{\delta }_3^2)},\\ \hspace{0.17em}& \frac{\text{d}{\tau }_4}{\text{d}u}=\frac{-324u^3{\tau }_4^2}{81{(u-u_{04})}^2{p}_0(u){\tau }_4^2+512(u-1)(1+4{\delta }_4^2)},\hspace{0.17em}{p}_0(u)=u^2+2u_{04}u+3u_{04}^2\\ \text{and}& \frac{\text{d}{\tau }_5}{\text{d}u}=\frac{-10240u^4{\tau }_5^2}{2048{(u-u_{05})}^{2}j(u){\tau }_5^2+15625(u-1)(1+4{\delta }_5^2)}.\end{array}$$

The boundary-value problem for these differential equations is formulated by means of the initial condition (4.4) at u = 0 for a concrete mass transfer mechanism.

Appendix B. Coefficients used in the universal distribution functions (table 2)

$$\begin{array}{rl}\hspace{0.17em}& C_4^{-1}={\int }_0^{4/3}\hspace{0.17em}\frac{u^3\exp (\frac{2}{3u-4}-\frac{1}{6\sqrt{2}}\text{arctan}\frac{u+4/3}{4\sqrt{2}/3})}{{(4/3-u)}^{19/6}{(u^2+8u/3+16/3)}^{23/12}}\hspace{0.17em}\text{d}u,\\ \hspace{0.17em}& C_5^{-1}={\int }_0^{5/4}\hspace{0.17em}\frac{u^4\exp [-\frac{1}{2(1-4u/5)}-\theta \hspace{0.17em}\text{arctan}\left(\frac{2u+(3+s)u_{05}}{2h}\right)]}{{(u_{05}-u)}^{2+\eta }j(u){[{(u+(3+s)u_{05}/2)}^2+h^2]}^{\xi }{[u-(1+s)u_{05}]}^{\zeta }}\text{d}u,\\ \hspace{0.17em}& C_4\approx 34.51,\hspace{0.17em}{C}_5\approx 129.66,\hspace{0.17em}j(u)=u^3+2u_{05}{u}^2+3u_{05}^{2}u+4u_{05}^3,\\ \hspace{0.17em}& s={\left(\frac{5}{9}\right)}^{1/3}[{(\sqrt{6}-\frac{7}{3})}^{1/3}-{(\sqrt{6}+\frac{7}{3})}^{1/3}]-\frac{5}{3},\\ \hspace{0.17em}& \xi =5q_1,\hspace{0.17em}\theta =5q_2,\hspace{0.17em}\eta =5q_3,\hspace{0.17em}\zeta =\frac{5{(s+1)}^4}{s(2s^3+5s^2-10)},\\ \hspace{0.17em}& q_1=-\frac{2s^5+15s^4+5s^3+110s^2+600s+1000}{200(2s^3+5s^2-10)},\hspace{0.17em}{q}_3=\frac{s^3+5s^2+40s+10}{100s},\\ \hspace{0.17em}& q_2=-\sqrt{\frac{-s}{s^3+10s^2+25s+40}}\frac{2s^6+25s^5+280s^4+1375s^3+3450s^2+4800s+3000}{100(2s^3+5s^2-10)}\\ \text{and}& h=\frac{u_{05}}{2}\sqrt{-\frac{s^3+10s^2+25s+40}{s}}.\end{array}$$

Data accessibility

This article has no additional data.

Authors' contributions

All authors contributed equally to the present research article.

Competing interests

The authors declare that they have no competing interests.

Funding

This work was supported by the Russian Science Foundation(grant no. 18-19-00008).