Abstract
Sanitary Emergency Measures (SEM) were implemented in Mexico on March 30th, 2020 requiring the suspension of non-essential activities. This action followed a Healthy Distance Sanitary action on March 23rd, 2020. The aim of both measures was to reduce community transmission of COVID-19 in Mexico by lowering the effective contact rate. Using a modification of the Kermack–McKendrick SEIR model we explore the effect of behavioral changes required to lower community transmission by introducing a time-varying contact rate, and the consequences of disease spread in a population subject to suspension of non-essential activities. Our study shows that there exists a trade-off between the proportion of the population under SEM and the average time an individual is committed to all the behavioral changes needed to achieve an effective social distancing. This trade-off generates an optimum value for the proportion of the population under strict mitigation measures, significantly below 1 in some cases, that minimizes maximum COVID-19 incidence. We study the population-level impact of three key factors: the implementation of behavior change control measures, the time horizon necessary to reduce the effective contact rate and the proportion of people under SEM in combating COVID-19. Our model is fitted to the available data. The initial phase of the epidemic, from February 17th to March 23rd, 2020, is used to estimate the contact rates, infectious periods and mortality rate using both confirmed cases (by date of symptoms initiation), and daily mortality. Data on deaths after March 23rd, 2020 is used to estimate the mortality rate after the mitigation measures are implemented. Our simulations indicate that the most likely dates for maximum incidence are between late May and early June, 2020 under a scenario of high SEM compliance and low SEM abandonment rate.
Keywords: Behavioral change, Contact rate reduction, Isolation, Disease dispersal, COVID-19, Bayesian inference
Highlights
-
•
A CoVID-19 model is presented considering suspension of non-essential activities.
-
•
The model explores the effect of behavioral changes required to reduce transmission.
-
•
Key parameters of the model are estimated using Bayesian inference.
-
•
There is an optimum value of the lockdown proportion which minimizes incidence.
-
•
Our scenarios show that incidence peak date occurs later than government estimates.
1. Introduction
Mexico confirmed its first case of the novel coronavirus pandemic (COVID-19) on February 28th, 2020 [1]. On March 18th, 2020 the Mexican Health Secretariat reported that a total of 250,656 COVID-19 cases were expected in the country (this amounts to roughly a 0.19% of the total population of Mexico estimated around 130.8 million in 2018 [2]). If the pandemic is expected to last 90 days approximately (using the Wuhan case as an example), then a straightforward calculation shows that this number amounts to an average daily attack rate of 21.5 per million people. On March 19th, 2020 the Heath Secretariat informed [3] that 140,367 (56% of the expected cases) would be mild not requiring hospitalization, 24,564 (9.8%) will require hospitalization, but will not be critical, and 10,528 (4.2%) would be critical patients. Thus, the remaining 75,197 (30% of the expected cases) are asymptomatic carriers. This percentage agrees with the percentage reported by [4] which estimated the size of this population in 30.8%. On the same date, March 19th, it was informed [3] that the Mexican Health Federal Sector at that time had 4,291 intensive care unit (ICU) beds and 2,053 ventilators ready for the contingency. On March 23rd, 2020 schools were closed and on March 30th, 2020 the general suspension of non-essential activities was announced [1]. All the recommendations pertained to so-called non-pharmaceutical interventions such as washing hands, keeping cough/sneeze etiquette, avoiding handshakes, keeping distance from other people, working at home. These activities require changes in behavior and, therefore, have a learning curve. Importantly, they can be forgotten, relaxed or only partially implemented in any given population.
We take into account, together with the suspension of non-essential activities, a time-varying effective contact rate. We model the efficacy of the Sanitary Emergency Measures (SEM) using two parameters, namely, , the parameter representing the proportion of the population that strictly follows the required actions, and the parameter where represents the average time that an average resident of Mexico keeps his/her low-risk community contact behavior. With respect to the time-varying effective contact rate, we introduce three parameters: the proportion of contact rate reduction desired to achieve (), the expected time to achieve that reduction from its original value to the desired fraction (), and the time lapse between the identification of the first cases to the implementation of the anti-COVID-19 control and mitigation measures (). For the incubation period distribution we use the infection-to-onset time reported in [5], [6], [7] that postulate a Gamma distribution with mean 5.1 days, and coefficient of variation 0.86 (but also see [8], [9], [10], [11] for similar estimates).
The model is parametrized with the available information on confirmed cases and mortality. It allows the exploration of scenarios dictated by the adopted public health control and mitigation measures vis a vis the transmission dynamics of the COVID-19 pandemic in Mexico. We have used realistic parameter values and estimated contact rates and reproductive numbers using the publicly available incidence and mortality data for Mexico City [12].
In Section 2 we present a modification of the Kermack–McKendrick SEIR model used and describe the parameter estimation for Mexico City. In Section 3 we assess the population level impact of the implementation of containment measures for community contact rate reduction. Here we also analyze the effect of contact rate reduction in combination with suspension of non-essential activities, exemplifying our findings for the case of Mexico City. Finally, we present our discussion and conclusions in Section 4.
2. COVID-19 transmission dynamics under suspension of non-essential activities in Mexico
A flow diagram of the mathematical model considered in this study is depicted in Fig. 1. COVID-19 is transmitted by both symptomatic and asymptomatic individuals. Asymptomatic transmission exists, it is not negligible, but its true magnitude is not known. Symptomatic individuals are the ones that develop severe conditions and therefore, on average, are expected to have reduced mobility compared with asymptomatic cases. The consequence of this fact is that the contact rates of symptomatic and asymptomatic individuals are different [13]. Thus, in this model, we incorporate both symptomatic and asymptomatic carriers, each class with a different and variable contact rate. The population is considered constant for the duration of the current epidemic event (January–August) and therefore the mixing function is a max action law (equivalent to proportionate mixing in this case).
Fig. 1.
Flow diagram of the mathematical model. The state variables , , , , , represent the populations of susceptible, exposed, asymptomatically infected, symptomatically infected, recovered and dead individuals, respectively. Before time , the dynamics of the pandemic is represented in diagram (A). Once SEM are implemented at time , the population splits into two: one with a proportion that follows the mitigation actions (B), and the other, with proportion that does not (C). These two populations do not mix. We have variable effective contact rates for asymptomatically () and symptomatically () infected populations. The parameter is the proportion of asymptomatically infectious individuals, is the incubation period, and are the infectious periods. Finally, is the average time an individual strictly adheres to all the behavioral requirements of effective SEM or social distancing measures (e.g., not leaving home, washing hands, frequently cleaning common surfaces, using masks, etc.).
In Mexico, mitigation actions are not mandatory. They are recommendations for the general population and private sector. This implies that, once the sanitary actions are implemented at day , certain fraction of the population will adhere to those directives, while another proportion will not. Consequently, there are, after this date, two dynamics: one describing the fraction () of the population adhering to the sanitary actions, and the other describing the fraction () of the population not adhering to the directives. We also assume that the population following the mitigation indicatives, do so strictly in such a way that the two populations do not mix. We see the parameter as a measure of the efficacy of suspension, for instance if 90% of the population is following the sanitary actions.
In the first part of our model, we keep record of the number of people in each of the SEIR compartments up to day when the sanitary actions are implemented. The contact rates before are and for the symptomatically and asymptomatically infected populations, respectively. The equations for the first part (pre-dating the application of SEM ) of the model are given by the following deterministic system of non-linear differential equations:
| (1) |
where , , , , and represent respectively the number of susceptible, exposed, asymptomatically infected, symptomatically infected, recovered, and dead individuals. After the sanitary actions are implemented, the population is split into two as described above with a proportion , of individuals following the actions and, the remaining proportion not adhering to the sanitary actions. Thus, the dynamics of the population adhering to SEM is given by the following differential equations:
| (2) |
Similarly the dynamics of the non-adhering subpopulation is given by the following differential equations:
| (3) |
where , , , , and represent, respectively, the number of susceptible, exposed, asymptomatically infected, symptomatically infected, and recovered individuals. Deaths from both subpopulations are described by the following differential equation:
| (4) |
For this second instance of the model, we define two time dependent contact rates. The first for the population under SEM, given by:
| (5) |
and the second for the non-adhering subpopulation given by:
| (6) |
Here, or are used for asymptomatically and symptomatically infectious individuals, respectively. The form of these contact rates is shown in Fig. 2. The equations are the standard Kermack–McKendrick SEIR for a flu-like illness. The total population is assumed to be constant. There exists a continuum of disease free equilibria for the pre-SEM population and likewise, for the post-SEM populations of the form where , are the proportions of the population that are susceptible at the initial time in each case. The basic reproductive number of the pre-SEM epidemic was computed as the spectral radius of the next-generation operator [14] of the equation and it is given as:
It is clearly a weighted average determined by the proportion of asymptomatically infected individuals, . In summary, for the pandemic follows the standard SEIR Kermack–McKendrick formulation with two infectious compartments. Once is reached, the population is split into two.
Fig. 2.
Schematic diagram of the general effective contact rate function for the model in Fig. 1. Orange line represents the starting contact rate until sanitary actions are enforced at time . Blue line shows the time dependent contact rate , and is the target contact rate. is the time to achieve the desired reduction in contact rate. The parameter follows the same behavior.
In Mexico City, the COVID-19 outbreak started with imported cases. Mitigation measures announced on March 23rd and March 30th, 2020 attempted to reduce the effective contact rate. We consider February 17th, 2020 as the initial date of the pandemic introduction in Mexico since we are using confirmed cases by day of initiation of symptoms. The date of the initial control and mitigation measures is March 23rd, 2020. It was followed by a more strict suspension of non-essential activities on March 30th, 2020. In our model, after March 23rd, 2020 the original effective contact rate , where or corresponds to asymptomatically or symptomatically individuals, starts to decline towards a target contact rate . Here is the desired proportion of reduction after days. The parameter is the “learning” time, that is, the average time it takes the population to reach the desired target reduction in the effective contact rate. The index indicates the fraction of the population that is under SEM (), and the fraction that is not (). The suspension of non-essential activities of March 30th, 2020 is seen as a reinforcement of the already ongoing reduction in contact rate.
2.1. Parameter estimation
The initial phase of the pandemic in Mexico covers from February 17th, 2020 to March 22nd, 2020. SEM was implemented on March 23rd, 2020. We use the number of daily confirmed COVID-19 cases in Mexico City by date of symptoms onset, and the daily number of deaths [12]. The initial (pre-SEM) effective contact rates, , , the infectious periods, , , and mortality rate were estimated using a Bayesian inference approach. Technical details can be found in Appendix A. We also estimated the mortality rate after March 23rd, 2020 (post-SEM) denoted by . Table 1 shows the median values and 95% intervals for each parameter. Fig. 3 shows the trajectory of the epidemic and the observed data. Using the median values presented in Table 1 for the effective contact rates and infectious periods, our median basic reproduction number works out to be , with a credible interval of . This reproduction number is below the recently reported value for China given in [15].
Fig. 3.
Model fit and observed data. Daily confirmed COVID-19 cases in Mexico City from February 17th, 2020 to March 22nd, 2020 are represented by gray bars. The red line is the median estimate for the model and black lines are 95% point-wise probability intervals..
Table 1.
Parameter estimates. Data from February 17th, 2020 to March 22nd, 2020 was used to generate posterior median estimates and 95% credible intervals for parameters , , , and . Data up to April 25th, 2020 was used to estimate parameter .
| Lower bound | Median | Upper bound | |
|---|---|---|---|
| 5.03 | 5.97 | 11.58 | |
| 5.52 | 10.81 | 23.13 | |
| 0.39 | 0.50 | 0.70 | |
| 0.31 | 0.40 | 0.53 | |
| 2.95 | 3.87 | 5.89 | |
| 0.00 | 0.02 | 0.04 | |
| 0.10 | 0.11 | 0.12 |
3. Results
In this section we present the main results of our analysis.
3.1. Target proportion of individuals following the actions
At the time of writing, there were no estimates of the learning times for contact rate reduction. Therefore, we set days and days as the average learning times for the population fractions and , respectively. With these values, the contact rate reduction by April 30th, 2020, the announced initial date of lifting of SEM measures, are, respectively, 23% and 18% on average for both population fractions. On April 6th, 2020, this SEM end date was extended to May 30th, 2020, where our projected contact rate reductions are 41% and 32%, respectively. This assumption gives us a worst-case scenario where the behavioral changes required to lower the effective contact rate take a relatively long time to be adopted. The effective contact rate decreases linearly over time until the target reductions of and for the adherent and non-adherent sub-populations (reductions of 90% and 70%) were reached, respectively. Finally, we set days. The parameter represents the average time an individual is committed to all the behavioral requirements of effective social distancing (not leaving home, washing hands, frequently cleaning common surfaces, using masks, etc.). All these assumptions imply that the mitigation measures are always leaky, not every member of the community follows them but also that a substantial part of the population under SEM will keep a low-risk behavior even beyond the formal termination of SEM.
3.2. Date and size of maximum incidence and prevalence: a trade-off between lockdown and compliance
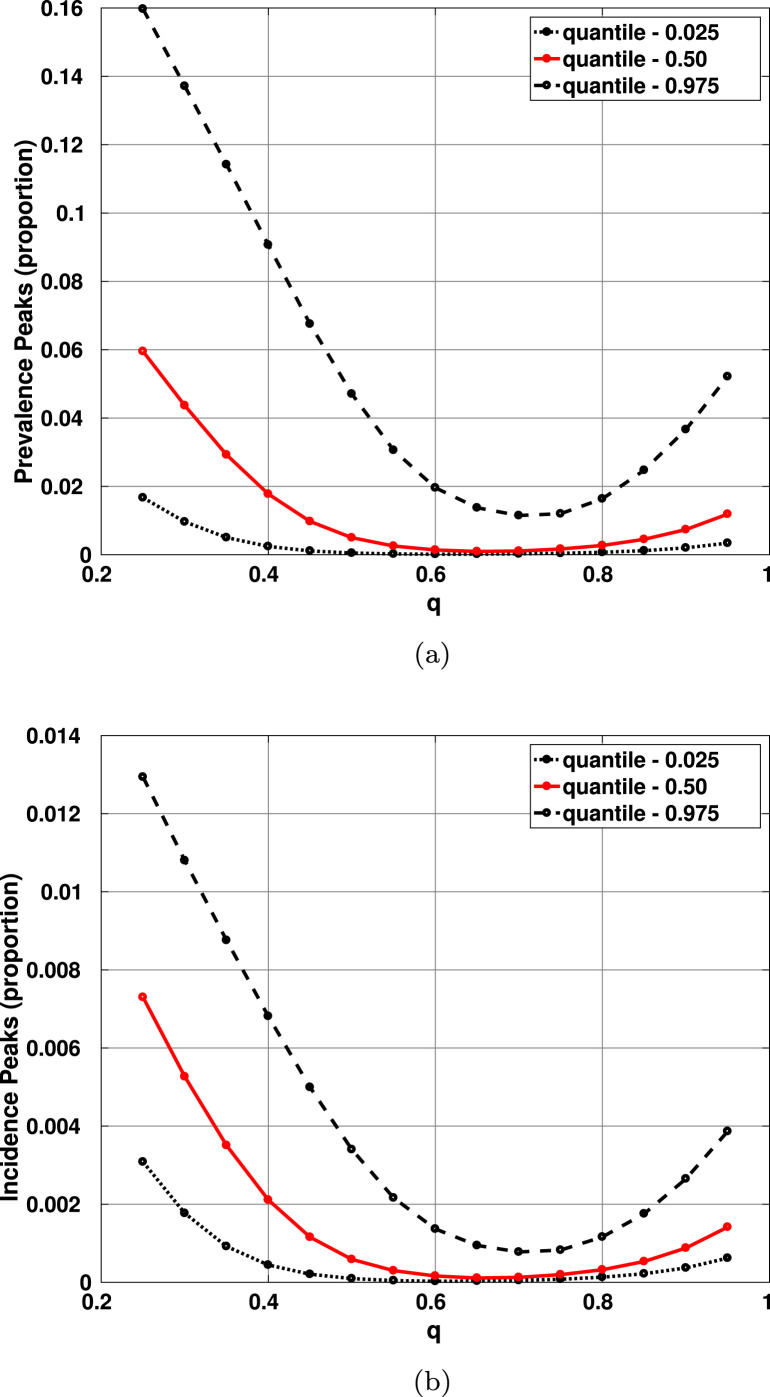
Letting the pandemic run its course, we measure the maximum prevalence and maximum incidence, as well as the dates when they occur. Fig. 4 shows the median and 95% credible interval for the dates where maximum prevalence and maximum incidence are projected to occur as a function of . On the other hand, Fig. 5 shows the same statistics for the values of the maximum prevalence and maximum incidence, as a function of . Observe that there is a value of that appears to be optimum (produces minimum prevalence and earlier peak date). We will come back to this issue later in Section 4.
Fig. 4.
95% credible intervals and median estimates for the dates when the peaks in prevalence and incidence are projected to occur. Notice that the earliest date occurs . (a) Date of maximum prevalence as a function of ; (b) date of maximum incidence as a function of . All other parameters are set at their baseline values. The upper black lines are broken because the simulations are stopped in middle August.
Fig. 5.
95% credible intervals and median estimates for the maximum prevalence and incidence as functions of . Notice that the smaller magnitudes occur for . (a) Maximum prevalence as a function of ; (b) maximum incidence as a function of . All other parameters are set at their baseline values. The upper black lines are broken because the simulations are stopped in middle August.
The existence of this optimum value of , for the maximum incidence, made us explore the behavior of the epidemic curve before and after the epidemic peak. We show in Fig. 6 how the total cumulative incidence for a given depends on the observation date. On April 30th, 2020, for both the best and the worst case scenarios, the minimum cumulative incidence is achieved for , while on August 31st, 2020, the minimum occurs for (for the best case) and (for the worst case). Symptomatically infected individuals are the most vulnerable sector of the population since these are the cases that can end up at the hospital or Emergency Units. Fig. 7 shows how the maximum incidence of symptomatic patients depends on , the proportion of the population under SEM, and , the average time an individual is committed to all the behavioral requirements of effective social distancing. Note that the surface shows a region for minima corresponding to values of and for all in the interval days (5 to 9 months approximately). This clearly suggest an interesting balance between the parameter and the “leak” rate .
Fig. 6.
95% credible intervals and median estimates for the cumulative incidence as a function of before and after the maximum peak. (a) Cumulative incidence for April 30th; (b) cumulative incidence for August 31st. All other parameters are set at their baseline values.
Fig. 7.
Symptomatic maximum incidence as a function of , the proportion of the population under SEM, and , the average time an individual is committed to all the behavioral requirements of effective social distancing. The trade-off between SEM and adequate behavioral traits associated with effective social distancing is apparent. All other parameters at their baseline values.
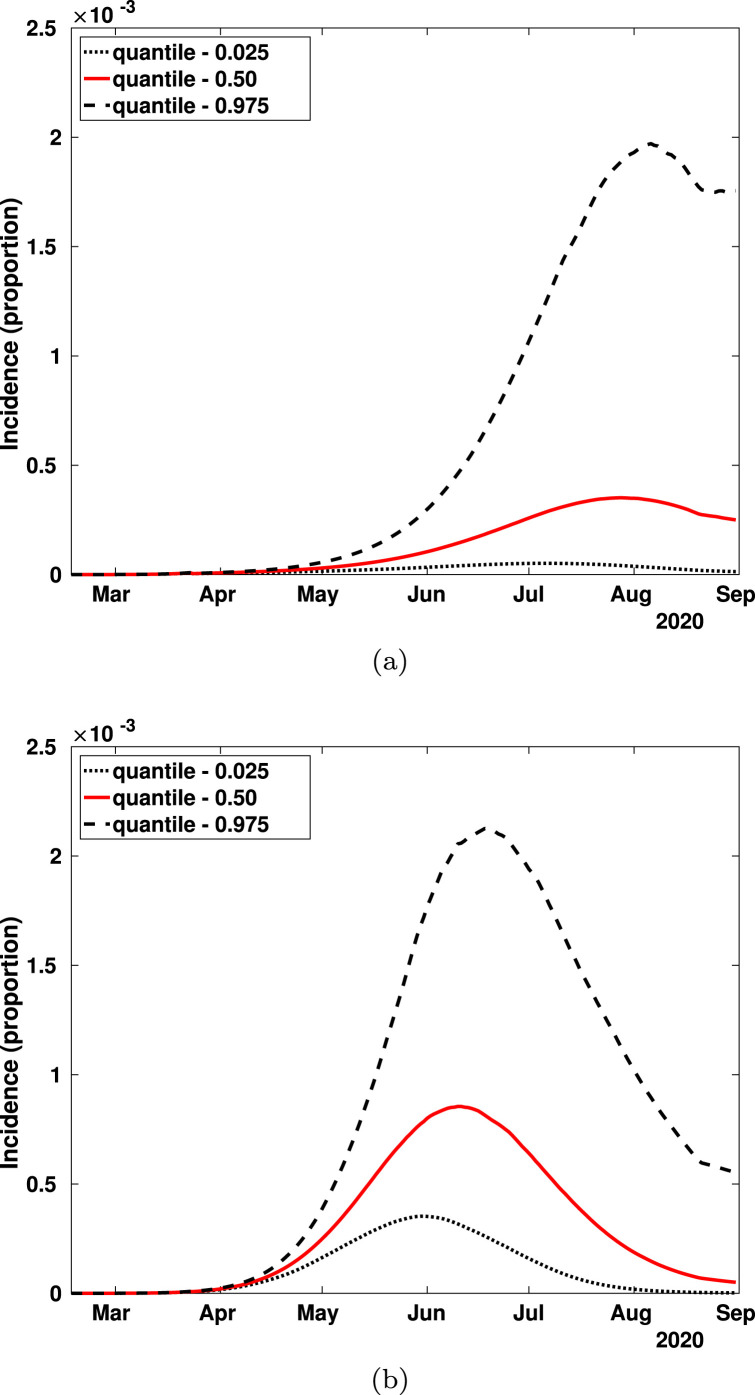
This trade-off between and is also reflected in the overall dynamics of the epidemic giving rise to an interesting and curious, perhaps important, theoretical result. Fig. 8(a)–(b) show 95% credible intervals and median estimates for the symptomatic incidence. Here 50% and 95% of the population follows the mitigation indicatives, respectively. Note that the symptomatic incidence level is higher when is greater (compliance of 95%) than when it is only of 50%.
Fig. 8.
95% credible intervals and median estimates for incidence as a function of . (a) 50% of individuals obey SEM ; (b) 95% of individuals obey SEM .
As we vary , the more likely dates for the incidence peaks also change. This is shown in Fig. 9. If SEM compliance is 50%, the peaks occur on early August, 2020 (median value of Fig. 9(a)) and, when compliance is 95%, they occur in early June, 2020 (median value of Fig. 9(b)).
Fig. 9.
Histogram for the maximum incidence dates. (a) 50% of individuals obey SEM ; (b) 95% of individuals SEM . We run the simulations for , and varying within their corresponding 95% credible intervals as reported in Table 1.
In Fig. 10, we present the scenario for , when maximum incidence is minimized. Under this scenario, our likely dates for maximum incidence coincide with the projection of middle to late May, 2020 suggested by the Mexican Secretariat of Health [16]. However, in this scenario, the interval of dates for the maximum incidence is wide (Fig. 10(a)). This effect is due to (i), the existence of different infectious periods for asymptomatically and symptomatically infectious individuals , and (ii) the size of the confidence interval of compared to that of (Table 1). When both infectious periods are the same, the empirical distribution of dates for the maximum incidence has less dispersion (Fig. 10(b)).
Fig. 10.
Histogram for the maximum incidence dates for . We run the simulations for , , and varying within their corresponding 95% credible intervals reported in Table 1. (a) Estimated infectious periods for asymptomatically () and symptomatically () infectious individuals. (b) Infectious periods for asymptomatically and symptomatically infected individuals are equal (). Note that the mode of the empirical distribution is located around the middle of May and that the distribution allows for later peak dates.
To end this section we show in Fig. 11 the trend of the instantaneous reproduction number [17]. Since there is no estimation of the serial interval for the pandemic in Mexico City or Mexico, we adopt the results in [18] where a Gamma distribution is used with median of 4.7 and standard deviation of 2.9 days. It can be appreciated that, at least in terms of the instantaneous reproduction number under the assumptions made on the serial interval descriptors, the SEM is at least maintaining the epidemic curve under control (low attack rate).
Fig. 11.
Instantaneous reproduction number for Mexico City using a median serial interval of 4.9 days [18]. The Figure shows the estimates from the start of the pandemic up to March 23rd, 2020 (start of SEM); from March 24th, 2020 to March, 30th, 2020 (suspension of non-essential activities) and from March 31st, to April 10th, 2020. SEM measures where implemented on March 23rd, and March 30th, 2020.
4. Conclusions
The control, containment, mitigation and possible elimination of the coronavirus pandemic requires rapid and consistent implementation of control and mitigation strategies as described in [6]. Mathematical models are central to this effort but certain issues have to be considered and measured for an increased efficacy in their application. Mexico has the lowest testing rate among the OCDE countries [19]. As this same study points out, a high testing rate is recommended to adequately plan the lifting of mitigation restrictions already in place in many countries, including Mexico. Testing is necessary to have a good estimate of the true size of the epidemic. In Mexico, several hundred Health Units constitute the country’s sentinel surveillance system. Here cases are detected and then a methodology is followed to identify contacts and other relevant information [20]. However, the identification of a suspected case detected by symptomatic surveillance has to be confirmed by testing. Limitations in testing correlate with a higher number of confirmed cases [21]. The positivity test rate in Mexico was around 20% on April [22], comparable to that of the US [21]. This high rate may mislead conclusions on the true growth rate of the epidemic and, in particular, on the date where the maximum incidence is expected.
The model presented in this work, using the official data on confirmed cases [12], is presented to evaluate the mitigation actions implemented by the Mexican Federal government based on information consistent in confirmed cases and mortality. The voluntary stay-at-home strategy in effect at the time of writing, requires a level of awareness and behavioral change that take time to become established in the population. Behavioral change is one of the main public health control mechanisms for reducing effective contact rates (in the form of so-called non-pharmaceutical interventions [6]). However, when dealing with behavioral issues, we enter into the psychological realm of individuals and groups of individuals. In our simulations we assume that education or awareness and rational decisions regarding the behavioral change associated with reducing effective contact rates is the same for asymptomatic and symptomatic individuals, although there is some evidence that this might not be the case as one can directly witness in the street of large metropolitan areas like Mexico City. We find that there exists a trade-off between the percentage of the population put into SEM () and the average time an individual is committed to all the behavioral requirements of effective social distancing (). This trade-off generates and optimum value of , not necessarily very high, that minimizes maximum incidence. Parameter can be thought of as a “leak rate”. The reason behind the existence of an optimal rate that minimizes the maximum COVID-19 incidence is as follows. When is small, there is a large quantity of individuals outside SEM. Therefore, the net flux of individuals leaking from the population complying with SEM, is relatively small and does not affect the positive effect of which is to reduce the effective contact rate and therefore the incidence. However, as more people adhere to SEM protocols, the net flux of leaked individuals becomes more important until we reach a point where the negative effect of abandoning safe social-distancing and behavioral practices counter-balances the beneficial effect of SEM. Recall that, in our model, the population outside SEM has a higher effective contact rate even though they also reduce it when the government indicative is announced. On the other hand we assume that before March 23rd, 2020, the epidemic follows the standard Kermack–McKendrick model and therefore both contact rates (for asymptomatically and symptomatically infected individuals) are constant. After March 23rd, 2020, social-distancing measures are implemented with the aim of reducing these two original contact rates. We model this by assuming that there is 1) a target effective contact rate reduction (modeled by the proportions for each subpopulation), and 2) a time during which awareness develops implying a gradual but decreasing contact rate over time. Since reducing the effective contact rate is a demand on a behavioral trait, we assume it is not automatic, that it takes time.
Our model does not account for the conditions and actions associated with lifting SEM. Therefore, in the model, the reduction when achieved, remains in place for a long period of time. Under this conditions, assuming that the educational/promotional efforts of the government to enforce the non-pharmaceutical interventions are effective for at least 6 months after the implementation of SEM ( days), we show that the scenario with the optimal , when maximum incidence is minimized (Fig. 10), coincides with the projection of having maximum incidence in middle to late May, 2020 made by the Secretary of Health [16]. However, our model shows that the incidence peak date is rather sensitive to changes in the values of and . In summary our model is looking only at the scenario where SEM is maintained. Our model exploration finishes in late August. It is expected that (a gradual) lifting of SEM restrictions will start on the first week of June. However, this fact may change in the following weeks since incidence and deaths are increasing quickly at present.
Mathematical models are important tools to assess and evaluate mitigation objectives as minimizing morbidity and mortality, diminishing an epidemic peak that otherwise could saturate health-care services, soften the impact on the economy, give time for vaccine development and manufacture of antiviral drug therapies [23]. A recent model by [24] has explored in great detail the impact of several non-pharmaceutical interventions that our work confirms. Adherence to strict social-distancing is reported there as of utmost importance to control and mitigate the pandemic. In [24] the very important role of face-masks in the containment and mitigation of COVID-19 is demonstrated. These authors find that the efficacious face-mask use (high compliance) can lead, in combination with other intervention strategies, to the eradication of COVID-19. This effect is confirmed in our model through the interplay of two parameters, , the fraction of the population that follows the protocols of the SEM implemented by the Mexican government, and the leak (or escape) rate of individuals from the adherence to SEM. We have found that there exist a balance between these two parameters to achieve a minimum (or optimal) incidence peak. In Mexico, the mitigation strategy is showing signs of reducing the effective contact rate, which is reflected in the average instantaneous reproduction number holding slightly above 1 since March 23rd, 2020 without significant increase (Fig. 11). Finally, we underline the need of timely interventions accompanied by an efficient public awareness campaign to reduce together with a well managed and controlled implantation of SEM protocols to maintain a high and a low target effective reproduction numbers, are all important factors for a successful control and mitigation of the epidemic curve. As our simulations indicate, assuming compliance with SEM with high and a low abandonment rate , the most likely dates for maximum incidence are late May and early June, 2020 (Fig. 4(b), Fig. 8(b)). According to our results, alternative scenarios for the maximum incidence being reached in early May, 2020 are improbable.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
JXVH acknowledges support from grant PAPIIT UNAM IN115720, Mexico and the Department of Mathematics of the University of Miami, USA , particularly Prof. Steve Cantrell and Prof. Chris Costner. We thank Dr. David Baca Carrasco, Nancy Gonzalez and Ruth Corona for their help during the preparation of this manuscript. Finally, we would like to thank Abba Gumel and Santiago Schnell for their helpful advise in the preparation of this manuscript.
Appendix A. Parameter estimation
We estimate key parameters of the model using publicly available data from the Mexican Secretariat of Health [12]. We use the reports on the daily confirmed COVID-19 cases and deaths in Mexico City from February 17th, 2020 to April 25th, 2020.
Case fatality rates are estimated as the ratio , where represents the cumulative number of confirmed COVID cases at time , is the number of deaths at time and is the average time from symptom onset to death. This formula is a correction of the naive estimator . We calculate two case fatality rates, before SEM (before March 23rd, 2020), and one after this date . Table 1 shows the 95% intervals for this parameters. It is important to point out that the pandemic in Mexico City before SEM implantation had 475 confirmed cases but only 2 deaths. This is the reason why is considerably smaller than .
Now, assume that the proportion of susceptible, exposed, asymptomatically and symptomatically infected, recovered and dead individuals in a closed population of size can be described by Eq. (1), where and are the infectious periods, and are the effective contact rates before the mitigation measures, respectively, with subscripts and denoting asymptomatically and symptomatically infected populations; denotes the incubation rate, is the proportion of exposed cases that become asymptomatic carriers and is the percentage of symptomatically infected that die. We set and . The parameters are estimated from data. Time is February 17th, 2020 the date of initiation of symptoms of the first confirmed COVID-19 case in Mexico City. The ODE system (1) is written in proportions for each state variable. In order to compare the solutions of the system with the data, these proportions were converted to number of cases by scaling them with the population size million. For the rest of this section, we will consider that the state variables are number of individuals in each compartment. The initial number of exposed, recovered and dead individuals are set to . The number of asymptomatic and symptomatic cases at time are set to . Then, .
To account for the variability in the data, we consider that the observed number of daily symptomatically infected cases at time , , , are random variables that follow a Poisson distribution with mean parameter given by the integral
| (7) |
expressing the incidence predicted by the model. The variables , come from Eq. (1). They depend on the vector of parameters fitted from the data, namely . The likelihood function of observing the data under both the Poisson model assumption and Eq. (1), is given by
| (8) |
We use a Bayesian inference approach were is treated as a random vector and inferences are drawn from its posterior distribution. To construct this function, we first assign prior probability distributions to each parameter in . We assume that infectious periods are between 5 and 25 days. Then, follows a uniform distribution in , and (conditionally on ) follows a uniform distribution in Likewise, the effective contact rate follows a uniform distribution in , and (conditionally on ) follows a uniform distribution in . Consequently, the joint density function of is
| (9) |
with the posterior distribution of the parameters of interest given as
This expression does not have an analytical form because the likelihood function depends on the solution of the ODE system. The posterior distribution is analyzed through simulation using an MCMC algorithm that does not require tuning called t-walk [25]. This algorithm generates samples from the posterior distribution that can be used to estimate marginal posterior densities, as well as the mean, variance and quantiles of the parameters. We run the t-walk for 500,000 iterations, discard the first 10,000 and use 5,000 samples to generate estimates of the parameters. Table 1 shows the median posterior estimates for each parameter and 95% probability intervals.
The samples generated above are also used to generate the credibility intervals shown in this work. To generate the histograms, for each sample of we calculate the solution of the differential equation given in (1). This results in a set of solutions that can be used to calculate the distribution of the maximum prevalence and incidence at each time, the distribution of the dates when these maxima occur, and any other statistic of interest. We refer the reader to [26] for more details on MCMC methods and to [27] for an introduction to Bayesian inference with differential equations.
Appendix B. Supplementary data
The code used in our simulations is available, as recommended in [28], at the link below
www.github.com/ProjectsEpi/SARS-CoV-2/tree/master/Behavioral_Change
References
- 1.de Epidemiologia D.G. March 2020. Comunicado tecnico 238449. [Online]. Available: https://www.gob.mx/salud/documentos/ [Google Scholar]
- 2.Review W.P. May 2020. Mexico Population 2020. [Online]. Available: https://worldpopulationreview.com/countries/mexico-population/ [Google Scholar]
- 3.Miranda P. March 2020. Sector salud con 4291 camas y 2053 ventiladores para combatir coronavirus. El Universal. [Online]. Available: www.eluniversal.com.mx/nacion/sector-salud-con-4291-camas-y-2053-ventiladores-para-combatir-coronavirus. [Google Scholar]
- 4.Nishiura P., Kobayashi, Yang, Hayashi, Miyama, Kinoshita, Linton, Jung, Yuan, Suzuki, Akhmetzhanov The rate of underascertainment of Novel Coronavirus (2019-nCoV) infection: Estimation using Japanese passengers data on evacuation flights. J. Clin. Med. 2020;9(2):419. doi: 10.3390/jcm9020419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Flaxman S., Mishra S., Gandy A., Unwin H.J.T., Coupland H., Mellan T.A., Berah T., Eaton J.W., Guzman P.N.P., Schmit N., Cilloni L., Ainslie K.E.C., Blake I., Boonyasiri A., Boyd O., Cattarino L., Ciavarella C., Cooper L., Cucunubá Z., Cuomo-dannenburg G., Dighe A., Djaafara B., Dorigatti I., Elsland S.V. Imperial College COVID-19 Response Team; March 2020. Estimating the Number of Infections and the Impact of Non- Pharmaceutical Interventions on COVID-19 in 11 European Countries: Tech. Rep. pp. 1–35. [Google Scholar]
- 6.Ferguson N.M., Laydon D., Nedjati-gilani G., Imai N., Ainslie K., Baguelin M., Bhatia S., Boonyasiri A., Cucunubá Z., Cuomo-dannenburg G., Dighe A., Fu H., Gaythorpe K., Green W., Hamlet A., Hinsley W., Okell L.C., Van S., Thompson H., Verity R., Volz E., Wang H., Wang Y., Walker P.G.T., Walters C., Winskill P., Whittaker C., Donnelly C.A., Riley S., Ghani A.C. Imperial College COVID-19 Response Team; March 2020. Impact of Non-Pharmaceutical Interventions (NPIs) to reduce COVID- 19 Mortality and Healthcare Demand: Tech. Rep. [Google Scholar]
- 7.Verity R., Okell L.C., Dorigatti I., Winskill P., Whittaker C., Imai N., Cuomo-dannenburg G., Thompson H., Walker P.G.T., Fu H., Dighe A., Griffin J.T., Baguelin M., Bhatia S., Boonyasiri A., Cori A., Cucunubá Z., Fitzjohn R., Gaythorpe K., Green W., Hamlet A., Hinsley W., Laydon D., Nedjati-gilani G., Riley S., Elsland S.V., Volz E., Wang H., Wang Y., Xi X., Donnelly C.A., Ghani A.C., Ferguson N.M. Estimates of the severity of coronavirus disease 2019 : a model-based analysis. Lancet Infect. Diseases. 2020;3099(20):1–9. doi: 10.1016/S1473-3099(20)30243-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Baud D., Qi X., Nielsen-saines K., Musso D., Pomar L.Ã., Favre G. Real estimates of mortality following COVID-19 infection. Lancet Infect. Diseases. 2020;3099(20):30195. doi: 10.1016/S1473-3099(20)30195-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Huang C., Wang Y., Li X., Ren L., Zhao J., Hu Y., Zhang L., Fan G., Xu J., Gu X., Cheng Z., Yu T., Xia J., Wei Y., Wu W., Xie X., Yin W., Li H., Liu M., Xiao Y., Gao H., Guo L., Xie J., Wang G., Jiang R., Gao Z., Jin Q., Wang J., Cao B. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet. 2020;395(10223):497–506. doi: 10.1016/S0140-6736(20)30183-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Backer J.A., Klinkenberg D., Wallinga J. Incubation period of 2019 novel coronavirus (2019-ncov) infections among travellers from wuhan, China, 20-28 January 2020. Euro Surv. : Bull. Eur. Mal. Transmiss. = Eur. Commun. Dis. Bull. 2020;25(5):1–6. doi: 10.2807/1560-7917.ES.2020.25.5.2000062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Read J.M., Bridgen J.R., Cummings D.A., Ho A., Jewell C.P. MedRxiv. 2020. Novel coronavirus 2019-nCoV: early estimation of epidemiological parameters and epidemic predictions. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.G. CONACyT, CentroGeo J.M. 2020. COVID-19 nacional. Gobierno de Mexico. [Online]. Available: https://datos.covid-19.conacyt.mx/fHDMap/#. [Google Scholar]
- 13.Park S.W., Cornforth D.M., Dushoff J., Weitz J.S. The time scale of asymptomatic transmission affects estimates of epidemic potential in the COVID-19 outbreak. medRxiv. 2020 doi: 10.1016/j.epidem.2020.100392. 2020.03.09.20033514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.van den Driessche P., Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002;180:29–48. doi: 10.1016/s0025-5564(02)00108-6. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/12387915. [DOI] [PubMed] [Google Scholar]
- 15.Early release - High contagiousness and rapid spread of severe acute respiratory syndrome Coronavirus 2. Emerg. Infect. Diseases. 2020;26(7) doi: 10.3201/eid2607.200282. E.R.H. Contagiousness and N..-J.E.I.D.j.C.h.-. Rapid Spread of Severe Acute Respiratory Syndrome Coronavirus 2 Volume 26. CDC https://wwwnc.cdc.gov/eid/article/26/7/20-0282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.2020 April [Online]. Available: https://www.conacyt.gob.mx/index.php/kit-informativo-coronavirus.
- 17.Thompson R.N., Stockwin J.E., van Gaalen R.D., Polonsky J.A., Kamvar Z.N., Demarsh P.A., Dahlqwist E., Li S., Miguel E., Jombart T., Lessler J., Cauchemez S., Cori A. Improved inference of time-varying reproduction numbers during infectious disease outbreaks. Epidemics. 2019;29(March) doi: 10.1016/j.epidem.2019.100356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Nishiura H., Linton N.M., Akhmetzhanov A.R. Serial interval of novel coronavirus (COVID-19) infections. Int. J. Inf. Dis. : IJID : Official publication of the International Society for Infectious Diseases. 2020 doi: 10.1016/j.ijid.2020.02.060. [Online]. Available: http://www.ncbi.nlm.nih.gov/pubmed/32145466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.OCDE H. 2020. Testing for COVID-19 : A Way to Lift Confinement Restrictions: Tech. Rep. pp. 1–21. [Online]. Available: http://www.oecd.org/coronavirus/en/ [Google Scholar]
- 20.Secretaria de Salud Gobierno de Mexico H. May 2020. Lineamiento estandarizado para la vigilancia epidemiologica y por laboratorio de COVID-19; pp. 1–27. [Google Scholar]
- 21.Meyer R., Madrigal A. A new statistic reveals why America’s COVID-19 numbers are flat. The Atlantic. April 2020 [Google Scholar]
- 22.Secretaria de Salud R. Secretaria de Salud; 2020. COVID-19 Comunicado Técnico Diario. 19 de abril. [Online]. Available: https://www.gob.mx/cms/uploads/attachment/file/547330/CP_Salud_CTD_coronavirus_COVID-19__19abr20.pdf. [Google Scholar]
- 23.Anderson R.M., Heesterbeek H., Klinkenberg D., Hollingsworth T.D. How will country-based mitigation measures influence the course of the COVID-19 epidemic ? Lancet. 2020;(20) doi: 10.1016/S0140-6736(20)30567-5. 30567–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ngonghala C.N., Iboi E., Eikenberry S., Scotch M., MacIntyre C.R., Bonds M.H., Gumel A.B. Mathematical assessment of the impact of non-pharmaceutical interventions on curtailing the 2019 novel Coronavirus. Math. Biosci. 2020:108364. doi: 10.1016/j.mbs.2020.108364. [Online]. Available: https://www.sciencedirect.com/science/article/pii/S0025556420300560?via%3Dihub. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Christen J.A., Fox C. A general purpose sampling algorithm for continuous distributions (the t -walk) Bayesian Anal. 2010;5(2):263–281. [Google Scholar]
- 26.Robert C.P., Casella G. second ed. Springer Verlag; 2004. Monte Carlo Statistical Methods. [Google Scholar]
- 27.Kaipio J., Somersalo E. Springer-Verlag New York; 2005. Statistical and Computational Inverse Problems. [Google Scholar]
- 28.Barton M., Alberti M., Ames D., Atkinson J.-A., Bales J., Burke E., Chen M., Diallo S.Y., Earn D.J., Fath B., Feng Z., Gibbons C., Heffernan J., Hammond R., Houser H., Hovmand P.S., Kopainsky B., Mabry P.L., Mair C., Meier P., Niles R., Nosek B., Nathaniel O., Suzanne P., Polhill G., Prosser L., Robinson E., Rosenzweig C., Sankaran S., Stange K., Tucker G. Call for transparency of COVID-19 models. Science. 2020;368(6490):1 May 2020. doi: 10.1126/science.abb8637. [DOI] [PubMed] [Google Scholar]