Ensembles of Breathing Nucleosomes: A Computational Study

Abstract

About three-fourths of the human DNA molecules are wrapped into nucleosomes, protein spools with DNA. Nucleosomes are highly dynamic, transiently exposing their DNA through spontaneous unspooling. Recent experiments allowed to observe the DNA of an ensemble of such breathing nucleosomes through x-ray diffraction with contrast matching between the solvent and the protein core. In this study, we calculate such an ensemble through a Monte Carlo simulation of a coarse-grained nucleosome model with sequence-dependent DNA mechanics. Our analysis gives detailed insights into the sequence dependence of nucleosome breathing observed in the experiment and allows us to determine the adsorption energy of the DNA bound to the protein core as a function of the ionic strength. Moreover, we predict the breathing behavior of other potentially interesting sequences and compare the findings to earlier related experiments.

Significance

Nucleosomes—protein spools with wrapped DNA—have rather distinct physical properties that reflect the mechanics of the involved DNA sequences. In this case study, we demonstrate this idea by focusing on the most-studied nucleosome positioning sequence, Widom 601, and two variants thereof. We ask to what extent the wrapped DNA in a 601 nucleosome is accessible through spontaneous DNA unspooling and how much this accessibility is affected by the basepair sequence itself. To answer this question, we perform Monte Carlo simulations of a coarse-grained nucleosome model and compare our predictions to recent small angle x-ray scattering experiments on solutions of 601 nucleosomes.

Introduction

About three-quarters of the human genome is sequestered by nucleosomes, protein spools wrapping DNA. In each nucleosome, 147 basepairs (bps) of DNA are wrapped along a superhelical wrapping path of one and three-fourths turns around a protein cylinder, composed of eight histone proteins (1). Nucleosomes dictate a wide range of biological processes such as gene regulation, recombination, replication, and chromosome condensation. They have been shown to be dynamical structures that temporarily expose portions of their wrapped DNA through spontaneous unspooling from either end through a process called site exposure or nucleosome breathing (2). Other dynamical modes, not considered in this study, include nucleosome sliding (3,4) (via single-bp twist defects (5, 6, 7, 8, 9, 10) and 10-bp bulges (7,8,10, 11, 12, 13)) and slow spontaneous gaping (2,14,15).

Nucleosome breathing had already been observed in 1995 by measuring the accessibility of restriction sites inside nucleosomal DNA to the corresponding enzymes (16) (see also (17, 18, 19, 20, 21, 22)) and later by performing Förster resonance energy transfer (FRET) experiments in which pairs of dyes were placed at strategic positions inside nucleosomes (23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49) (for a review, see (50)). Such experiments demonstrate that nucleosomes temporarily expose their DNA, including even the stretch at the middle of the wrapped portion. The probability for a nucleosomal DNA site to be accessible decays roughly exponentially toward the dyad (51). Importantly, such experiments revealed that nucleosomes can be very different from each other as a result of post-translational modifications (19,20,30,33,42,43,46) (see (52) for a review) and of the sequence-dependent mechanical properties of their wrapped DNA (18,21,26,29,30,39) (cf. (53) for a review), the latter being the subject of our study. Especially, different bp sequences inside a nucleosome can have very different accessibilities for proteins, and the accessibility of a given sequence can have a pronounced left-right asymmetry (see, e.g., (18)).

A disadvantage of the above-mentioned experiments with restriction enzymes or FRET is that a given measurement can only probe one DNA portion at a time (by having a restriction site at a particular position in the wrapped DNA or a pair of fluorescent dyes placed at appropriate locations). This makes an interpretation of the experiments challenging no matter whether it is based on restriction enzymes (54) or on FRET (55). Moreover, such measurements do not reveal the whole set of unwrapping states that a particular nucleosome visits or, equivalently, the set of states a population of identical nucleosomes occupies at a given moment in time.

A recently published experiment by the Pollack lab (56) (see also (57,58)) has overcome these limitations. It is based on small angle x-ray scattering (SAXS) on a solution of nucleosomes all containing the same bp sequence, either the Widom 601 positioning sequence (59) or the sea urchin 5S ribosomal DNA (rDNA) sequence. By matching the contrast between the solvent and the protein core, only the DNA remains visible. What is detected is the ensemble average stemming from all nucleosomes in their different unwrapping states, each state contributing with its own scattering profile. To determine those different unwrapping states, together with their probabilities, an ensemble of theoretical unwrapping states was created that leads to a similar average scattering profile. These model states even include the fluctuations of the partially unwrapped DNA, modeled by cgDNA (60), a sequence-dependent coarse-grained DNA model. Remarkably, with this level of detail, this ensemble optimization method allows the authors to even distinguish the two ends of their nucleosomes. This is possible because the left and right unwrapped DNA portions feature different bp sequences with different elastic properties and thus different conformational fluctuations.

The nucleosomes were studied in a wide range of NaCl concentrations, from 0.2 to 2.0 M, allowing the experimentalists to observe how the set of structures shifts with ionic strength from predominantly fully wrapped to unwrapped (56). However, for the 601 nucleosome, the transition from the closed to the open states is not a continuous one. Instead, at intermediate salt concentrations, a highly asymmetric partially unwrapped state emerges with ∼65 bps unwrapped. The authors argue that a “spring-loaded latch” mechanism is at play here: as the salt concentration crosses beyond a certain threshold, a stiffer stretch of DNA causes the wrapped nucleosome to jump discontinuously into this asymmetric state. The findings for the 5S rDNA nucleosome are less well defined: it is less stable, already partially unwrapped at a 0.2 M salt concentration, and jumps (without an intermediate unwrapping state) to a nearly fully unwrapped state.

We are interested in how DNA mechanics can influence the physical properties of nucleosomes. In a series of studies (54,61, 62, 63, 64), we have used a coarse-grained nucleosome model that accounts for the sequence-dependent DNA elasticity in various experimental situations. Our model, together with similar models from other groups (65, 66, 67, 68, 69), lies somewhere in between very coarse-grained representations of nucleosomes (spheres or cylinders wrapped by homogeneous polymers (70, 71, 72, 73, 74, 75, 76, 77, 78, 79)) and molecular dynamics (MD) simulations of nucleosomes (fully atomistic (80, 81, 82, 83) or at near-atomic level (7, 8, 9, 10,84,85)). Whereas the simpler models do not account for bp sequence effects, the higher-resolution models account for them but—because of computational costs—can only look at relatively short timescales and few sequences. Our model is complex enough to include sequence effects but, at the same time, simple enough to allow us to study large numbers of sequences and can even be used to perform genome-wide calculations (86).

In (54), we specifically used our nucleosome model to study nucleosome breathing for the 601 and 5S rDNA nucleosome. In that study, however, we focused entirely on experiments employing restriction enzymes and thus determined the equilibrium constant for site exposure. We revisit here nucleosome breathing with our model, inspired by the new SAXS experiments. The aim of this study is threefold: first, we would like to study the whole probability distribution of nucleosomes and how it shifts when lowering the adsorption energy. This allows us to check whether our model is capable of reproducing the spring-loaded latch mechanism of the 601 nucleosome. Secondly, we would like to investigate the dependence of salt concentration on the effective binding energy of our simple nucleosome model. Finally, we present some results for other potentially interesting DNA sequences that shed additional light on the role of DNA elasticity on nucleosome breathing and might be worthwhile to study experimentally.

Methods

To investigate the sequence-dependent unwrapping, we use a Markov chain Monte Carlo (MCMC) simulation of a model nucleosome (61); see Fig. 1. This model has been previously applied to predict rotational nucleosome positioning (61), translational positioning (86), spontaneous unwrapping (54), force-induced unwrapping (62,63), and sequence selection (64). The DNA molecule is modeled by the rigid bp model (87), with quadratic interactions between nearest neighbors using a parameter set P characterizing these interactions from both crystal structures (87) and all-atom MD simulations (88). In this hybrid parameterization (89), intrinsic deformations are derived from protein-DNA crystals and the stiffnesses from atomistic simulations. Our simulation makes extensive use of the Armadillo linear algebra library (90). The elastic energy of a DNA molecule with sequence S of length N is thus given by

$$E_{\text{DNA}}\left(w,S,P\right)=\frac{1}{2}\left(w-\hat{w}\left(S,P\right)\right)\cdot K\left(S,P\right)\cdot \left(w-\hat{w}\left(S,P\right)\right),$$ (1)

with w a 6(N − 1)-vector of all internal degrees of freedom between neighboring bps, ŵ(S, P) a 6(N − 1)-vector representing the equilibrium shape of the DNA molecule with sequence S, and K(S, P) a 6(N − 1) × 6(N − 1) block-diagonal stiffness matrix with a block size of 6 × 6 describing interaction strengths between bps. All sequences used in this study can be found in Fig. S1.

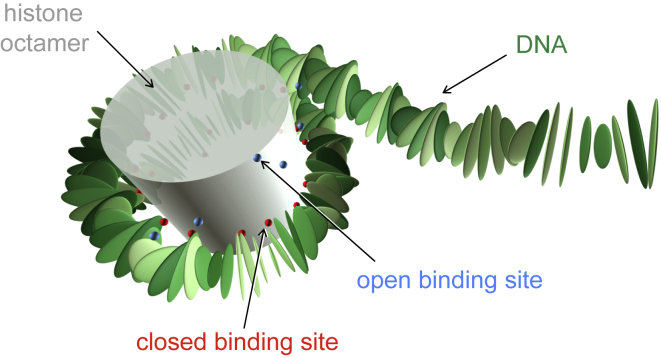
Figure 1.

Model nucleosome in a partially unwrapped configuration. To see this figure in color, go online.

Histone-DNA interactions mainly involve bonding between the negatively charged DNA phosphate groups and positively charged elements at the surface of the octamer, localized at 14 distinct binding sites where the minor groove of the DNA faces the octamer (1). In our model, the histone octamer is not modeled explicitly but is accounted for indirectly through the binding sites. Bound phosphates in real nucleosomes are represented in our model by a special treatment for the corresponding bp steps. This is necessary because the rigid bp model does not contain the phosphates explicitly. We have shown (61) that the location of a given phosphate can be predicted with high accuracy from the positions and orientations of the bps connected to it. Specifically, a given phosphate lies very close to the midplane of the corresponding bp step. We therefore model bound phosphates by imposing fixed midplanes for all the bp steps closest to such phosphates, 28 in total (two per binding site). We move the two bps around a bound phosphate not individually, but as a pair such that the rotation and translation of one bp determines that of the other, keeping the midframe fixed. Our choice of midframes thus does not allow for dynamic binding and unbinding. Therefore, all different unwrapping configurations are simulated independently from each other. We denote an unwrapping configuration by a pair of integers ($\ell$, r), which represent the number of binding sites released from the left, $\ell$, and from the right, r. We require $\ell$ + r ≤ 14.

We note that although an MCMC simulation samples the free energy of the rigid bp DNA, our histone core model does not contain binding entropy. Therefore, we choose to take out entropy completely and instead add a certain amount of binding energy E_ads to the total energy of the system for each binding site released. It is known from experiments that the binding energy of different binding sites is not constant (91). However, because there are no precise values available, we assume here for simplicity that all binding sites have the same strength. What we do account for is the fact that the binding strength depends on the salt concentration. We determine this salt-dependent binding strength through comparison with the SAXS experiment (56). For this purpose, we need to have our data points at the same bp spacing as the experimental data. The experimental data sample the unwrapping every 5 bps, whereas our simulation supplies us with unwrapping only at predetermined binding sites. We therefore linearly interpolate the simulation data to obtain values at the same bp spacing as the experiment and use these interpolated data to obtain a fit, using the LMFIT python library (92).

The total energy of our nucleosome model is the sum of the elastic energy of the DNA, Eq. 1, and that of the binding sites:

$$\begin{array}{c}{E}_{\text{total}}\left(\ell ,r\right)=E_{\text{DNA}}\left(\ell ,r\right)-E_{\text{binding sites}}\left(\ell ,r\right)\\ =\frac{1}{2}\left(w-\hat{w}\right)K\left(w-\hat{w}\right)-\left(14-\left(\ell +r\right)\right)E_{\text{ads}}\end{array},$$ (2)

which is a function of the unwrapping state ($\ell$, r). Increasing $\ell$ or r allows parts of the DNA to relax and thus lowers E_DNA, but at the same time, it comes at a price because binding sites have to open, i.e., E_{binding sites} increases. In the following, we report on the breathing behavior as predicted by our model for various sequences.

Results

The breathing behavior of the 601 nucleosome and of its variants

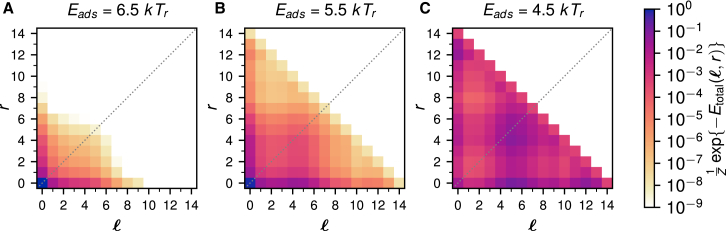
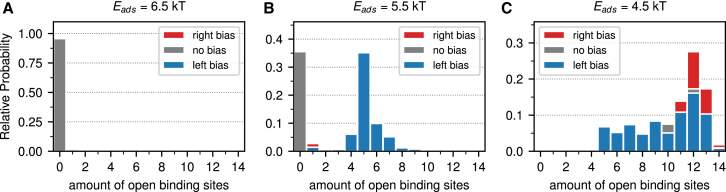
Because we perform independent simulations for each unwrapping state, we plot the relative occupancy $\left(1/Z\right)\exp \left\{-\beta E_{\text{total}}\left(\ell ,r\right)\right\}$ of each state ($\ell$, r) in a landscape with axes containing $\ell$ and r for different binding energies. Here, β is the reciprocal sampling temperature of the simulation, and Z is the partition function of the system to normalize the probabilities. The relative occupancies for a nucleosome with the 601 sequence are displayed in Fig. 2. Different plots show the occupancies for different values of the binding energy per binding site, ranging from E_ads = 6.5 kT_r (Fig. 2 A) to E_ads = 4.5 kT_r (Fig. 2 C) (see also Fig. S2 for more values of the adsorption energy). At higher binding energies, the 601 nucleosome occupies mostly the (0, 0) state, i.e., it is fully wrapped. As one lowers the binding energy, this remains the case up to about E_ads = 5.5 kT_r, at which point the system starts to prefer to be in state (5, 0). As the adsorption energy is reduced even further to 4.5 kT_r, the nucleosome is mostly found in the nearly fully unwrapped states (0, 12) and (12, 0).

Figure 2.

Relative occupancies of the unwrapping states of the 601 nucleosome for different binding energies per binding site, ranging from E_ads = 6.5 kT_r (A) to E_ads = 4.5 kT_r (C). $\ell$ denotes the number of binding sites released from the left and r from the right. To see this figure in color, go online.

Remarkably, for intermediate binding strengths, the 601 nucleosome skips over all states in between (0, 0) and (5, 0), jumping directly at about E_ads = 5.5 kT_r to the highly asymmetric state (5, 0). As mentioned in the introduction, the SAXS experiment led to the discovery of this effect, which was termed the spring-loaded latch mechanism by the authors (56). It was speculated that this effect is caused by a stiff stretch of DNA that unwraps all at once as soon as the salt concentration has been increased beyond a certain critical value, as opposed to a more gradual way of unpeeling each binding site separately. Before going into a more detailed investigation of this effect, let us first study a variant of the 601 sequence, called 601RTA, in which a supposedly stiff stretch inside the 601 sequence was softened by introducing three extra soft TA steps (93). In Fig. 3, we plot the relative occupancy landscapes of the 601RTA nucleosome for the same values of the binding energies as in Fig. 2 (see also Fig. S4 for more values of the adsorption energy). The addition of a mere three TA steps in the stiff part of the 601 sequence indeed has a dramatic effect on the occupancy plots. First of all, the asymmetry in the landscape is strongly reduced (cf. the plots for E_ads = 5.5 kT_r in Figs. 2 and 3). More importantly, the landscape does not show a strong preference for unwrapping state (5, 0) right away, but rather a smear across states (0, 0) to (5, 0), indicating that the 601RTA nucleosome unwraps in a smoother fashion than the 601 nucleosome.

Figure 3.

Relative occupancies of the unwrapping states of the 601RTA nucleosome, the 601 sequence with three added TA steps, for the same range of binding energies as in Fig. 2. To see this figure in color, go online.

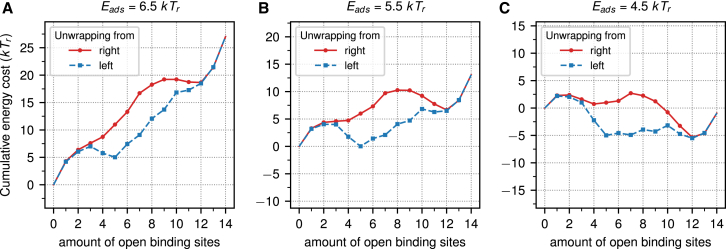
We now investigate in closer detail the spring-loaded latch mechanism. Specifically, we ask which part of the 601 DNA causes this behavior and why it is absent for the 601RTA nucleosome. Because we find in the occupancy plots that this behavior occurs along unwrapping states in which just one arm is unwrapped, we restrict our analysis to precisely those states. In Fig. 4, we plot the cumulative total energy of the 601 nucleosome as a function of the number of opened binding sites for three different adsorption energies, E_ads = 6.5 kT_r (Fig. 4 A) to E_ads = 4.5 kT_r (Fig. 4 C) (see also Fig. S3 for more values of the adsorption energy). All plots show two curves, one for unwrapping from the left and the other for unwrapping from the right. Both curves overlap for the fully wrapped nucleosome but start to strongly deviate from each other as the number of sites increases beyond three and finally come back together for the fully unwrapped state. Even for strong adsorption, E_ads = 6.5 kT_r, there is already a local minimum at (5, 0) with an energy that is about 5.0 kT_r higher than the ground state (0, 0). For E_ads = 5.5 kT_r, state (5, 0) has become the preferred configuration over the fully wrapped state, whereas the states between these two states constitute a 4-kT_r-high energy barrier. This very clearly shows that this region acts as a spring-loaded latch. In (56) the authors speculated, just by looking at the sequence, that there is a stiff region starting ∼30 bps from one end and that this region is ∼20 bps long. Inspecting Fig. 4, we come to a similar conclusion. The binding energy drops substantially as we open the fourth binding site which starts at bp 35 and finishes after the fifth binding site has opened, allowing the relaxation of the DNA up to bp 56.

Figure 4.

The cumulative energies for the unwrapping of the 601 sequence from the left (blue) and right (red) at adsorption energies of 6.5 kT_r (A) to 4.5 kT_r (C). To see this figure in color, go online.

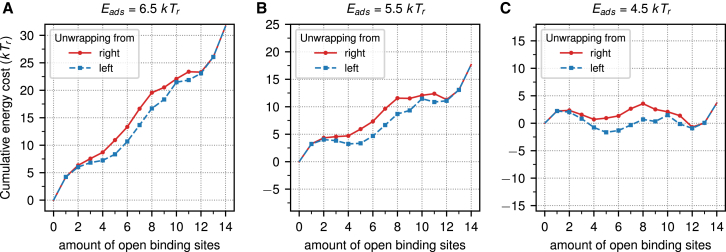
Fig. 5 shows the cumulative total energy for the 601RTA sequence for the same three values of the adsorption energy as in Fig. 4 (see also Fig. S5 for more values of the adsorption energy). As can be seen very clearly, the asymmetry of the 601 has almost disappeared. The local minimum at (5, 0) is not anymore present for E_ads = 6.5 kT_r (Fig. 5 A). Even though for E_ads = 5.5 kT_r, there is still a minimum for the (5, 0) state (Fig. 5 B), this minimum is only local. When looking at the differences between 601 and 601RTA, it turns out that just two of the three TA steps are inserted in the stiff region. These two steps at bp steps 38 and 48 from the end are sufficient to disrupt the spring-loaded latch.

Figure 5.

The cumulative energies for the unwrapping of the 601RTA sequence from the left (blue) and right (red) at adsorption energies of 6.5 kT_r (A) to 4.5 kT_r (C). To see this figure in color, go online.

We studied two other variants of the Widom 601 sequence, namely 601MF (93) and 601L (94). For sequence 601MF, the inner two quarters are flipped, whereas the outer 37 bps on each side stay unchanged. This means that after this operation, most of the stiff DNA stretch ends up on the other side. Interestingly, this is reflected in the occupancy plots, Fig. S6, and the cumulative total energy, Fig. S7, by a mirror reflection between the left and right side compared to the original 601 nucleosome, Figs. 2 and 4. This demonstrates that it is mostly the stiff DNA stretch that is responsible of the main features of the breathing 601 nucleosome, whereas the outer stretches are far less important. The other sequence, 601L, is a palindromic sequence built from the more strongly adsorbed half of the 601 sequence. As expected, the 601L landscape is symmetric, and the nucleosome is very stable, with the fully wrapped state being the most probable state even at E_ads = 4.5 kT_r; see Figs. S8 and S9. This sequence has also been used in a recent atomistic study of nucleosome breathing (83), in which it was observed that the 601L nucleosome is very stable at physiological ionic conditions and no breathing was observed. At higher ionic strength, the nucleosome featured breathing of the outer DNA regions, but the timescales were too short to observe more extensive unwrapping.

The other sequence that was studied in (56) is the 5S rDNA positioning sequence. The probability for the different unwrapping states is given in Fig. S10 and the cumulative total energy in Fig. S11. As one can see from Fig. S10, the occupancy landscape of the 5S nucleosome shifts gradually when lowering the adsorption energy. There is no spring-loaded latch that causes the system to jump into a partially unwrapped state, and there is no strong left-right asymmetry. The latter findings fit well with one of the SAXS experiments (56). However, it was found in the experiment that the 5S nucleosome opens rather abruptly from mostly wrapped states at low salt concentrations to mostly unwrapped states at high salt concentrations without substantial occupancy of intermediate states, unlike what we predict in Fig. S10. A possible explanation for this discrepancy might lie in the fact that the histone cores of 5S nucleosomes disrupt at substantially lower ionic strength than that of 601 nucleosomes, as has been demonstrated by FRET measurements (56). This could mean that intermediate states that would be energetically preferred on the basis of DNA elasticity do not survive in the experiment, and instead, the nucleosome is mostly seen in an open state with a disrupted histone core. We study this possibility further in the next section when we compare our model directly to experimental data.

Finally, it is also useful to look at the purely theoretical uniform sequence in which all bp step parameters are the corresponding average values from all 10 distinct bp steps. Even for this most simple case, it is not obvious how the system behaves. Because the positions of the binding sites in our model were extracted from the nucleosome crystal structure, their positions are not equally spaced. In addition, the DNA is forced into a superhelical configuration with nonuniform curvature. This is indeed reflected in the nonuniformity of both the occupancy landscape, Fig. S12, and the cumulative total energy for the unwrapping of the two DNA ends, Fig. S13. What is especially striking is that the system prefers for low adsorption energies, e.g., for E_ads = 4.0 kT_r, to be in the nearly fully unwrapped states (0, 12), (0, 13), (12, 0), and (13, 0). This simply reflects the fact that the outermost stretches of the wrapped DNA are nearly straight. A nearly fully unwrapped nucleosome therefore prefers to have one of these two stretches still wrapped. This explains also why the 601 nucleosome prefers the same set of states under such conditions; see Fig. 2. This also applies to the other sequences discussed here, 601RTA (Fig. 3), 601MF (Fig. S6), 601L (Fig. S8), and 5S (Fig. S10). Also, for larger adsorption energies, the landscapes of the uniform sequence in Fig. S12 show a preference for highly asymmetric unwrapping states in which one end is still wrapped, a feature that can also be seen for all the other sequences. The free-energy landscape calculated from a coarse-grained MD simulation of nucleosome breathing shows this preference as well (see Fig. 5 B in (85)).

Determining the binding site strength dependency on salt concentration

The SAXS experiments measured the degree of nucleosome breathing as a function of the salt concentration, namely NaCl concentrations in the range from 0.2 to 2.0 M. This opens the possibility to determine the binding strength per nucleosomal binding site through comparison to the predictions of our model. In particular, it is interesting to learn whether there is a simple linear or a rather complicated dependence.

We start by restructuring the information in the relative occupancy landscape of the 601 nucleosome in a way that is more closely related to the experiment. Instead of looking in the occupancy landscape at all unwrapping states individually (Fig. 2), we combine all states with the same number of unwrapped sites in a histogram (Fig. 6), which means to sum probabilities along diagonals in the occupancy plot. In addition, instead of plotting the number of opened binding sites, we plot the numbers of unwrapped bps that are simply related knowing the positions of the binding sites (see, e.g., Table 1 in (54) for the precise numbers). We continue to keep track of possible asymmetries by subdividing the bars by three colors: one for symmetric, one for dominantly unwrapped from the left, and one for dominantly unwrapped from the right. Fig. 6 shows these histograms for the 601 sequence and the asymmetric unwrapping preference for different adsorption energies ranging from E_ads = 6.5 kT_r (Fig. 6 A) to E_ads = 4.5 kT_r (Fig. 6 C). The plots clearly show the spring-loaded latch mechanism and the intermediate state with a very strong asymmetry. The same type of plot for the 601 nucleosome at 1.0 M NaCl is shown in the top of Fig. 3 in (56) and shows strong similarities with our plots. In fact, based on this comparison, we expect, for 1.0 M NaCl, the best agreement between the experimental and theoretical plots to be somewhere between E_ads = 5.5 kT_r and E_ads = 4.5 kT_r.

Figure 6.

Probabilities to find the 601 nucleosome in a state with a given number of open binding sites for adsorption energies of 6.5 kT_r (A) to 4.5 kT_r (C). Note that each vertical axis has a different range. To see this figure in color, go online.

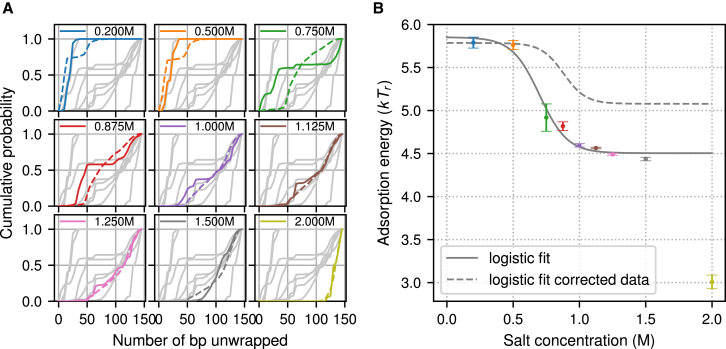
We simplify the analysis further by not keeping track of the symmetry of the unwrapping states, but only the total amount of unwrapping. We consider each bar in Fig. 6 as one set of states and create a cumulative distribution for each histogram. Our energies per unwrapping state, together with the adsorption energy, give a one-parameter family of curves of cumulative relative occupancies of states with the same number of released binding sites. For each salt concentration curve in the SAXS data, we fit our data and find the best fitting curve with a given adsorption energy. In Fig. 7, we plot both the SAXS data and our best fits (Fig. 7 A) and the adsorption energy as a function of the salt concentration (Fig. 7 B). We fit a logistic curve to the all points except the one for 2.0 M salt concentration and find

$$E_{\text{ads}}=\frac{1.29}{1+\exp \left(10.9\left(\left[{\text{Na}}^{+}\right]-0.67\right)\right)}+4.55,$$ (3)

where [Na⁺] is the concentration of counterions in molars. The error bars in Fig. 7 are the ones obtained by fitting.

Figure 7.

(A) The experimental cumulative probabilities (solid lines) for different salt concentrations and the best fitting probabilities from our model (dashed lines) for the 601 nucleosome. (B) The adsorption energy in our model from the fits in (A) as a function of the experimental salt concentrations (colored circles) and the best fitting logistic curve, given in Eq. 3 (gray solid curve), is shown. The error bars are the standard errors of the fitting on the left. The gray dashed curve shows the best fitting logistic curve to the SAXS data after removing the fraction of fully unwrapped structures (possibly free DNA); see Fig. S16. To see this figure in color, go online.

We note that the extended plateaus found in the experimental curves (for salt concentrations larger than 0.5 M) are not found in our fits to the data in Fig. 7 A. One explanation for this discrepancy could be our simplifying assumption of an equal binding strength for all binding sites. There might be another spring-loaded latch at work that could be caused by some strong sites beyond (0, 5). Once these sites are broken, the whole DNA would unravel from the histone core. However, there might be an entirely different explanation for the extended plateaus.

This can be best demonstrated by looking at the SAXS data of the 5S nucleosome. The experimental cumulative distributions, together with our fits, are provided in Fig. S14. As can be seen, our fits are unsatisfactory because they do not feature the extended plateaus observed for all salt concentrations. However, note that the 5S nucleosome is less stable than the 601 nucleosome (according to (95), the difference is ∼4–5 kT). In fact, the authors of the SAXS study (56) speculate as follows: “For this construct, a large population of fully unwrapped (120+ basepair) structures is present at all salt concentrations, which we attribute to free DNA in the sample.”

We therefore repeated the analysis of the 5S nucleosome with the population of free DNA removed. We achieved this by rescaling the experimental cumulative probabilities by moving the extended plateaus to the value of 1. The corresponding plots are given in Fig. S15. The fits in Fig. S15 A are now better, even though there are still some discrepancies. One could try to improve the fits by introducing extra fit parameters by, e.g., allowing different binding strengths for different binding sites. However, the small set of data and the problem with free DNA make such an approach questionable. Moreover, we would like to point out that the plot of the adsorption energy as a function of salt concentration does not change much despite the dramatic rescaling of the experimental curves; see Fig. S15 B.

We also redid the analysis for the 601 nucleosome, speculating that the population of fully unwrapped (120+ bps) structures also represents free DNA; see Fig. S16. The corresponding fits to the data improve substantially. As for the 5S case, the adsorption strength as a function of the salt concentration is not strongly affected by this modification; see Fig. 7 B.

Of interest is to check whether the binding strength for the two different sequences, 601 and 5S, is the same so that the affinity of a DNA stretch to be in a nucleosome just reflects the bending cost to wrap the corresponding DNA sequence. The curves are shown together in Fig. S16 B. Even though there are similarities in the overall dependence, the height of the two plateaus of the logistic curve are quite different. The 601 seems to be more strongly bound (about 0.5 kT for small and about 1 kT per binding site for large concentrations). However, it is hard to judge whether this is a real effect. On one hand, our mechanical DNA model underestimates the difference in binding energy between the two sequences (1 kT vs. 4–5 kT), which would partly have to be compensated for by an increase in binding strength. On the other hand, the histone octamer is partially disintegrated for larger unwrapping—especially for the 5S nucleosome—so that the estimates of the binding strengths for larger salt concentrations (at which the discrepancy between the curves is strongest) cannot be trusted.

Discussion

Relation to site exposure experiments

The SAXS experiments, analyzed here with our coarse-grained nucleosome model, are closely related to various other experiments. We discuss here and in the next subsection experiments we have studied previously using the same nucleosome model that shed some additional light on these findings. In this subsection, we discuss the relation to a series of experiments (16, 17, 18, 19, 20, 21, 22) measuring the accessibility of DNA target sites inside nucleosomes to DNA binding proteins. Specifically, in (18), the accessibility of restriction sites engineered into the 601 nucleosome to their corresponding enzymes was measured. This way, the equilibrium constant for site exposure as a function of the position inside the nucleosome was determined. This quantity is the probability that a given site is sufficiently unwrapped. Here, “sufficiently” means that enough room is available for a given restriction enzyme to access its site, which can be achieved by unwrapping some extra length beyond that site (51). This extra length is expected to depend on the size and shape of the enzyme, as well as its orientation on the DNA with respect to the nucleosome. The equilibrium constant for site exposure was found to decay, roughly exponentially, toward the center of the wrapped DNA portion. Interestingly, the accessibility measured for the 601 nucleosome was rather asymmetric, with one half substantially more accessible than the other. A similar experiment (16) performed earlier with the 5S rDNA nucleosome only looked at one half of the nucleosome. It is therefore not known whether the breathing profile of this nucleosome is more symmetric.

We have studied these experiments using precisely the same nucleosome model (54). The accessibility was determined by calculating the probabilities of all unwrapping states (as done in this study) and then by summing over the probabilities of all those states in which a given site is accessible. Also, in that computational study, the adsorption energy serves as a fit parameter and was found to be slightly above E_ads = 6.0 kT_r. Note that for each restriction site, the reaction was carried out in a different buffer with different ionic conditions, making a comparison to the SAXS experiment difficult. Regardless, the salt concentrations reported specifically in (16) were slightly lower throughout than in all SAXS measurements, so that the adsorption energy we found in (54) is compatible to what we would expect based on our study.

Relation to nucleosome pulling experiments

Over the last two decades, there has been a series of experiments in which DNA containing one or several nucleosomes was pulled on in micromanipulation setups (93,96, 97, 98, 99, 100). Nucleosomes turned out to be surprisingly stable against external forces, much more so than one would expect based on the effective adsorption energy of DNA on the histone octamer. This finding can be understood by the fact that a nucleosome needs to flip by 180° during unwrapping (78,79,101, 102, 103, 104). This flip is accompanied by a high energetic barrier caused by the strong deformation of two stretches of DNA. Specifically, the in- and outgoing DNA stretches need to make sharp 90° bends once the nucleosome has flipped halfway. As a result, there is a set of metastable states, namely states in which just one turn of DNA is wrapped and therefore the in- and outgoing DNA arms are essentially straight.

Sequence-dependent details of the unwrapping process only became available rather recently through combining a micromanipulation pulling experiment of the 601 nucleosome (and variants thereof) with FRET (93). It was found that the 601 nucleosome unwraps asymmetrically with one end unpeeled already at very small forces (between 0 and 5 pN) and the other side staying wrapped up to much higher forces (e.g., 15 pN). Based on our computational nucleosome model, this can be understood as follows (62): already, at rather small forces, the nucleosome unwraps to states in which just one DNA turn remains wrapped. In this state, the nucleosome is kinetically protected against further unwrapping even at much higher forces because this would cause a flipping and subsequent bending of the entering and exiting DNA. The 601 nucleosome could, in principle, visit all states that feature a single wrapped DNA turn because each such state features essentially straight DNA arms. However, because the 601 sequence is mechanically highly asymmetric, it very strongly prefers a highly asymmetric state in which one end is still fully wrapped, in agreement with the experimental observation (93). Remarkably, that preferred state is state (5, 0), the same state into which a freely breathing 601 nucleosome jumps as one lowers the binding energy (note that sequences in that study are flipped with respect to the sequences here and in (56)). In both situations, it is obvious that this state is energetically preferred because in this case, the stiffer stretch in the 601 sequence is released. However, the fact that a nucleosome under force and in its free state has a preference for precisely the same state is not trivial, but rather, a peculiarity of the 601 nucleosome. Based purely on geometry, one expects five unwrapped sites for a nucleosome under force because this allows essentially straight DNA arms along the force direction, whereas for a free nucleosome, the unwrapped DNA can always assume a straight configuration. In fact, all the other sequences we studied here did not show a particular preference for a state with five unwrapped sites.

The adsorption energy per binding site

We found that the adsorption energy per binding site displays roughly a sigmoidal shape (see Fig. 7 B). When fitting the data, we disregarded the data point at 2.0 M NaCl salt concentration because this might reflect disintegration of the 601 nucleosome at high ionic strength. We find that there is an intermediate range of salt concentrations in which the adsorption energy decays with increasing salt concentration. At large concentrations, it levels off to a value of about E_ads = 4.5 kT_r before the nucleosome disintegrates. At the other end, for small ionic strength, the adsorption energy seems to level off as well, namely slightly below E_ads = 6.0 kT_r.

This behavior might reflect several effects. One main mechanism that causes binding of the DNA molecule to the oppositely charged octamer is the release of counterions that were condensed on the (unbound) DNA molecule (105). Each counterion that is released gains entropy by being replaced by a fixed charged group on the histone octamer. The entropy gain is proportional to the logarithm of the ratio of the concentrations of the counterions in the condensed layer/their concentration in the bulk (76). This means that with increasing salt concentration, this entropy gain becomes smaller and smaller, whereas other effects such as, e.g., hydrogen bonds (106) gain in relative importance.

On the other hand, when going to small salt concentrations, the Debye screening length increases. Once that length is on the order of the spacing between the two turns of the wrapped DNA or even longer, e.g., of the size of the whole nucleosome, the concept of a linear adsorption energy density becomes questionable. Instead, the fact that the wrapped DNA overcharges the protein core becomes important and eventually leads to the unspooling of the DNA, as can be seen already in simple model systems (77). This might partially explain the leveling off of the adsorption energy that we find for small ionic strengths in Fig. 7 B. Fitting a “symmetric” sigmoid (logistic curve) function to the fitted data is therefore not physically motivated and might possibly not be the best choice, but given the limited agreement between the data and our model (see Fig. 7 A), it seems to be a reasonable approximation.

Finally, let us stress that we have assumed in our model that all binding sites have the same adsorption energy. In principle, one could make the model more general by allowing different binding strengths for different sites to, e.g., increase the agreement between the model and the experimental data in Fig. 7 A. However, the predictive power of such a model can only be assessed if there are more data available, especially for many different sequences. A starting point can be the study of the Wang group in which DNA was unzipped into a 601 nucleosome, which revealed the presence of the binding sites through pausing patterns in the unzipping process that occurred each time the zipping fork encountered a nucleosomal binding site (91). The pausing pattern did in fact suggest that there are weaker and stronger sites. In addition, a recent all-atom MD simulation (83) shows that the inner region of the nucleosomal DNA is more strongly bound than the outer ones. One could use such data to build a nucleosome model with different binding strengths for different binding sites, as we did in an earlier prototype of our nucleosome model (6) in which we studied nucleosome sliding via twist defects. There are, however, not enough data to assess whether this procedure improves the performance of our model. In addition, a change in salt concentration might affect different binding sites differently because they might, e.g., affect different numbers of counterions.

Another point of concern is the question whether we can assume that the binding strength of the different sites is independent of the bp sequence of the wrapped sequence. If this is the case, then the binding strength of sites that are symmetrically related are identical. However, it might be that if the local DNA shape, e.g., the minor groove width, is compatible with the geometry imposed by the interacting groups, one might have stronger binding. To some extent, our model takes this into account because each binding site involves two phosphates that sit across the minor groove. A DNA portion with a given sequence is thus forced in our model to deform its minor groove to fit into the structure (69). This, however, is the limiting case in which the DNA adjusts its shape to the one prescribed by an octamer that is assumed to be completely stiff. As discussed above, the quality of the SAXS data of the 5S nucleosome is not good enough, but having more SAXS data with different sequences available might allow us to answer these questions.

Biological relevance

Nucleosome breathing is a mechanism that gives regulatory proteins access to DNA target sites buried inside nucleosomes. One finding of our study suggests that this dynamical mode of the nucleosome is very sensitive to the involved DNA sequence such that small differences in sequence can have a strong impact (compare Figs. 2, 3, 4, and 5). This suggests that DNA sequence might play an important role not only in positioning some of the nucleosomes but also to equip them with special physical properties. This can have nontrivial consequences because it can affect the cooperativity between two DNA binding proteins, say proteins A and B: after A has bound at a more outward DNA site in the nucleosome, the target site for B further inside the wrapped portion becomes more easily accessible (107). This effect would be especially enhanced for a spring-loaded nucleosome like the 601 nucleosome: as A binds to the softer outer stretch, the stiffer inner stretch snaps open, and B can access its site at practically no cost.

A second finding of this study is that the effective adsorption energy per length seems not to change much as one moves toward physiological salt concentrations (cf. Fig. 7 B). This suggests that nucleosome breathing is rather insensitive to small changes around physiological ionic conditions, in contrast to the strong bp sequence dependence. As a result, this might give nucleosomes a sequence-dependent “individuality” that is not affected by the local electrostatic environment of, e.g., eu- and heterochromatic regions.

Finally, in a cell, nucleosomes are not isolated but connected via linker DNA. Attraction between nucleosomes might, e.g., cause them to stack, which requires the linker DNA to bend (108). The associated bending energies might be reduced by a partial unwrapping of the nucleosomal DNA. This can drive the breathing behavior of nucleosomes toward more open structures, something that has been deduced for dinucleosomes and 17-mers from the accessibility of restriction enzymes (109) and from FRET measurements on dinucleosomes (110). The increased unwrapping of nucleosomal DNA in multinucleosomal constructs might be key in understanding higher-order chromatin folding.

Conclusions

We have performed MCMC simulations on a coarse-grained nucleosome model to study nucleosome breathing at different binding strengths between DNA and the protein core. The DNA model accounts for the sequence-dependent elasticity, allowing us to learn how variations in stiffness in the wrapped DNA part affect the probability of different unwrapping states. For the most-studied nucleosome sequence, the Widom 601, we found a highly asymmetric breathing behavior and a spring-loaded latch effect that occurs when the binding strength is reduced below a certain threshold. These simulations reproduce observations in SAXS measurements of the 601 nucleosome for different ionic conditions well (56). This allowed us to couple our model’s adsorption energy to the experimental salt concentration. We found a sigmoid functional relationship between these two quantities. We also predicted the breathing behavior of nucleosomes containing three derivatives of the 601 sequence that have not been measured yet. We show how these sequences would allow to directly test in more detail how DNA mechanics affects nucleosome dynamics. In addition, given enough data from other sequences, it should be possible to make more detailed predictions on how much the adsorption energies of the binding sites are affected by the underlying sequence.

Author Contributions

H.S. and L.d.B. designed the study. L.d.B. contributed computational tools. K.v.D. performed the simulations. K.v.D. and L.d.B. performed the analyses. H.S. and L.d.B. contributed to the article.

Editor: Tamar Schlick.