Structural Studies of Overlapping Dinucleosomes in Solution

Abstract

An overlapping dinucleosome (OLDN) is a structure composed of one hexasome and one octasome and appears to be formed through nucleosome collision promoted by nucleosome remodeling factor(s). In this study, the solution structure of the OLDN was investigated through the integration of small-angle x-ray and neutron scattering (SAXS and SANS, respectively), computer modeling, and molecular dynamics simulations. Starting from the crystal structure, we generated a conformational ensemble based on normal mode analysis and searched for the conformations that reproduced the SAXS and SANS scattering curves well. We found that inclusion of histone tails, which are not observed in the crystal structure, greatly improved model quality. The obtained structural models suggest that OLDNs adopt a variety of conformations stabilized by histone tails situated at the interface between the hexasome and octasome, simultaneously binding to both the hexasomal and octasomal DNA. In addition, our models define a possible direction for the conformational changes or dynamics, which may provide important information that furthers our understanding of the role of chromatin dynamics in gene regulation.

Significance

Overlapping dinucleosomes (OLDNs) are intermediate structures formed through nucleosome collision promoted by nucleosome remodeling factor(s). To study the solution structure of OLDNs, a structural library containing a wide variety of conformations was prepared through simulations, and the structures that reproduced the small-angle x-ray and neutron scattering data well were selected from the library. Simultaneous evaluation of the conformational variation in the global OLDN structures and in the histone tails is difficult using conventional molecular dynamics simulations. We overcame this problem by combining multiple simulation techniques and showed the importance of the histone tails for stabilizing the structures of OLDNs in solution.

Introduction

Nucleosomes are fundamental structural units of chromatin that enable eukaryotic genomic DNA to be packaged into a nucleus. The canonical nucleosome consists of a histone octamer and ∼150 basepairs of DNA. The histone octamer is composed of two copies each of histones H2A, H2B, H3, and H4, and the DNA segment tightly wraps around its surface (1). For transcription, therefore, the DNA wrapped around the octamer must be unwrapped. This is accomplished by RNA polymerase II, which unwraps the nucleosomal DNA in stepwise fashion during the transcription elongation process (2,3).

Nucleosomes are dynamic entities that change their position along genomic DNA (e.g., Segal and Widom (4)). In particular, the rearrangement of nucleosome positioning around transcription initiation sites is thought to play a regulatory role in transcription initiation (5). This nucleosome remodeling process is likely mediated by nucleosome remodeling factors (6,7). It has been reported, for example, that if two nucleosomes are closely positioned, one of the nucleosomes will invade the DNA of its neighbor, probably through nucleosome remodeling, and adopt an unusual structure called an overlapping dinucleosome (OLDN) (8,9). We previously reconstituted an OLDN and determined its crystal structure (10). Within the OLDN structure, a histone hexasome lacking an H2A-H2B dimer associates with a canonical octasomal nucleosome, and a 250-basepair DNA segment wraps around the two histone subnucleosomal moieties. Sequence mapping using micrococcal-nuclease-digested HeLa cell chromatin showed that micrococcal-nuclease-protected, 250-basepair DNA segments accumulate in regions just downstream of transcription start sites (10), which suggests OLDNs are formed during the transcription initiation process.

The OLDN structure is asymmetric. To understand the structure and dynamics of OLDNs in solution, we measured its small-angle x-ray and neutron scattering (SAXS and SANS, respectively). The obtained scattering curves were in near agreement with one calculated from the crystal structure, indicating that the asymmetric structure is maintained in solution. However, the bump peak positions were shifted slightly to a lower Q, and the observed gyration radius was slightly enlarged. This may reflect structural fluctuation caused by adoption of several stable conformations and/or the lack of histone tails, which could not be observed in the crystal structure.

In our study, we used computer modeling and molecular dynamics (MD) simulations to model OLDN conformations, including the histone tails, and screened for structures that reproduced the experimental data well. To do this, we first generated a large number of conformations from the crystal structure by deforming the DNA along the lowest-frequency normal modes. We then looked for the conformations that reproduced the SAXS and SANS data well. Although, individually, the SAXS or SANS data were not sufficient to uniquely determine the solution conformations of OLDNs, integration of the SAXS and SANS data prevented the model structures from being overfitted to one data set or the other, which enabled us to successfully narrow the size of the conformational ensemble in solution. Finally, we conducted MD simulations by using each conformation of the ensemble as an initial structure to evaluate the structural stability of OLDNs and investigate their dynamic features in more detail. The results indicate that OLDNs adopt a wide variety of conformations in solution, each of which is stabilized by histone tails situated at the interface of the hexameric and octameric histones. Furthermore, analysis of the conformations can tell us the likely direction of the conformational changes. Such dynamics information may increase our understanding of the assembly and disassembly of OLDNs, which may provide the structural foundation for nucleosome rearrangement within chromatin.

Materials and Methods

Sample preparation

Recombinant human histone proteins (H2A, H2B, H3.1, and H4) were purified as described previously (11,12). Histone octamer was reconstituted and then purified using Superdex200 (GE Healthcare, Chicago, IL) gel filtration column chromatography (11). OLDNs were reconstituted with 250-bp DNA fragments and purified as described previously (10). For SAXS, purified samples were dialyzed against 20 mM Tris-HCl buffer (pH 7.5) containing 50 mM NaCl, 0.1 mM MgCl₂, and 1 mM dithiothreitol. For SANS, purified samples were dialyzed against 20 mM Tris-HCl (pH 7.5) buffer containing 50 mM NaCl, 0.2 mM MgCl₂, and 1 mM dithiothreitol with different amounts of D₂O (0, 40, 65, and 100%, respectively). The concentration of OLDNs was calculated from the absorbance by the DNA (260 nm) and determined as the DNA-histone 14-mer complex (1.00 mg/mL DNA corresponds to 2.26 mg/mL complex).

Solution scattering

SAXS and SANS were conducted to observe the structure of OLDNs in aqueous solution: SAXS was used to examine the overall shape of OLDNs, whereas SANS was employed to separately observe the structures of the elements comprising OLDNs, including the histone domains and the DNA.

SAXS experiments were performed with a SAXS camera installed at BL10C of the KEK Photon Factory (Ibaraki, Japan). Using a two-dimensional semiconductor detector (PILATUS3 2M; Dectris, Baden, Switzerland), SAXS intensity was measured for 300 s using a time slice of 15 s by checking the radiation damage on each sample: the SAXS data obtained in 0–150 s when the radiation damage was not observed were averaged and then used for this study. The covered Q-range was from 0.008 Å⁻¹ to 0.25 Å⁻¹: Q = (4π/λ)sin(θ/2), where λ and θ are the wavelength of the incident beam and the scattering angle, respectively. After checking the radiation damage, the SAXS pattern was converted to a one-dimensional scattering profile, after which standard corrections for the initial beam intensity, background scattering, and buffer scattering were applied. Finally, the obtained SAXS intensity of the sample was normalized to the absolute scale using a glassy carbon standard. The samples were solutions of the DNA-histone 14-mer complexes in buffer at a concentration of 0.5 or 3.0 mg/mL. No particle interference was observed with either solution.

SANS experiments were performed on D22 installed at the high-flux reactor of the Institut Laue-Langevin. To cover the Q-range from 0.008 to 0.25 Å⁻¹, the SANS intensity was measured at two sample-to-detector distances, 5.6 and 2.0 m, using a 6-Å neutron beam. The measured two-dimensional scattering pattern was converted to a one-dimensional scattering profile of solute by following the standard procedure: circular averaging, correction of transmission, and substations of buffer scattering and background. Thereafter, the SANS profiles with sample-to-detector distances of 5.6 and 2.0 m were merged into one profile using GRASP software (https://www.ill.eu/fr/users-en/scientific-groups/large-scale-structures/grasp/).

For small-angle scattering, scattering intensity I(Q) is described as follows:

$$I\left(Q\right)={\langle \left|\underset{V}{\int }\left(\rho \left(\mathit{r}\right)-{\rho }_s\right)exp\left(i\mathit{Q}·\mathit{r}\right)d\mathit{r}\right|\rangle }^2,$$ (1)

where V, ρ, and ρ_s are the volume of the solute and the scattering length densities of the solute and solvent, respectively, and the brackets indicate the spherical average. With neutron scattering, there is an isotope effect on scattering length, which is especially large between hydrogen (−3.74 fm) and deuterium (+6.67 fm). Reflecting this difference, ρ_s can be tuned by mixing H₂O and D₂O at a proper ratio. This is called the “contrast-variation technique.” As shown in Fig. S1, the scattering length densities of histone and DNA are matched to those of 40 and 65% D₂O, respectively. Following Eq. 1, this means that in 40% D₂O solution, a histone is invisible, and only the structures of the DNA in OLDNs can be observed; in the same manner, the structures of only histones in OLDNs can be observed in 65% D₂O solution. Using this approach, we measured the SANS profiles of OLDNs (3 mg/mL DNA-histone 14-mer complex) in solutions containing 0, 40, 65, and 100% D₂O.

DNA treated at basepair step level

One of the authors developed a method for studying the static and dynamic structures of double-stranded DNA using the basepair step parameters (tilt, roll, twist, shift, slide, rise) as internal coordinates (13, 14, 15). In our study, we used this method to model the missing basepairs of the DNA in the x-ray crystal structure and to deform the DNA.

With this method, basepaired residues in double-stranded DNA are treated as a rigid body, and the relative position and orientation of two adjacent rigid bodies (or basepairs) are described in terms of six basepair step parameters (tilt, roll, twist, shift, slide, rise). Deviation of the geometry from the equilibrium increases the conformational energy (dimer step energy) E_d described as

$$E_d=\sum _{ij}{f}_{ij}\left({\theta }_i-{\theta }_i^0\right)\left({\theta }_j-{\theta }_j^0\right)/2,$$ (2)

where θ_i and ${\theta }_i^0$ are the instantaneous and equilibrium values of the basepair step parameters and f_ij is the force constant. Olson et al. (16) derived these values (${\theta }_i^0$ and f_ij) in a sequence-dependent manner—i.e., different constants for different kinds of dimer steps—by analyzing a large number of crystal structures. In our study, we used those constants unless otherwise noted. The total conformational energy of the double-stranded DNA is described as the sum of E_d.

Deformation of OLDN by changing the DNA conformation

We deformed the crystal structure of OLDNs by changing the conformation of the DNA while the structures of the histone octamer and hexamer were fixed. Because the basepair step parameters were used as the internal coordinates, each conformation of the DNA was described by a 6 × (N − 1)-dimensional vector Θ, where N is the number of basepairs. The deformation of the DNA was performed by changing the basepair step parameters along the normal mode vectors as

$$\Theta ={\Theta }_0+\sum _k{\alpha }_k{\mathbf{u}}_k,$$ (3)

where Θ₀ describes the crystal structure, α_k is the magnitude of the deformation, and u_k is the k-th lowest-frequency normal mode vector. In our study, we used the five lowest-frequency modes (k = 1, 2, 3, 4, 5) in the summation. It should be noted that different conformations are obtained by giving different sets of numbers (α₁, α₂, α₃, α₄, α₅).

The normal mode vectors were obtained using a computational procedure that was nearly the same as that used for linear DNA (15). The differences were that in this computation, we assumed that the crystal structure was in the minimum energy conformation—i.e., the values of the basepair step parameters in the crystal structure were used as the equilibrium values ${\theta }_i^0$ in Eq. 2—and that we used very large force constants f_ij (100 times larger than those derived by Olson et al. (16)) for the DNA wrapped around the histone core proteins so that they would not change their conformations easily. We assigned normal force constants only to the basepair steps (chain I:129–152, chain J:99–122) in the linker DNA region, where the DNA did not wrap around the core proteins. To build the deformed atomic model of an OLDN, after deformation of the DNA, the histone octamer and hexamer were put into the same geometry as in the crystal structure with respect to the wrapping DNA.

Modeling OLDNs with histone tails

The crystal structure of the OLDN lacked the histone tails. However, to reproduce the experimental SAXS profile well, we found it necessary to include the histone tails in the models. We therefore modeled OLDNs with histone tails in the following way. We started from the structure with the minimum χ² for the SAXS profile, which was obtained by deforming the crystal structure without the histone tails. Based on this structure, the initial histone tail conformations were modeled using the program MODELER (17,18). We then performed 107 independent MD simulations using the simulated annealing method for OLDNs with the modeled histone tails to obtain distinct tail structures. The model was put in a box with dimension of 26.4 × 2.4 × 4.6 nm³, which was kept unchanged during the simulations (constant volume). The box was filled with TIP3P water containing Na⁺ and Cl⁻ ions to neutralize the system and maintain the salt concentration at 150 mM. The simulations started with a rapid increase of the temperature from 3 to 1500 K in 0.15 ns, followed by a gradual reduction of the temperature to 0 K in 1.5 ns. In all the simulations, only the modeled histone tails were allowed to move, whereas the DNA and histone core proteins were restrained. Different initial velocities to the atoms were assigned in different simulation runs to obtained different tail structures. The simulation was carried out using GROMACS (19, 20, 21, 22, 23, 24, 25) with the Amber 14sb+bsc1 force field (26). The temperature was controlled using the V-rescale method (27). The final conformation in each simulation run was collected. From the 107 collected models with different conformations of the histone tails, we selected 50 whose histone tails were bound to the nucleosomes and were not extended outward.

Ideally, the above computations should have been performed with all the different OLDN conformations built by deforming the crystal structure. That was not possible, however, because of the computational time and resources it would have required. Instead, we replaced the histone core proteins lacking histone tails with proteins with tails in the aforementioned 50 models. This enabled us to build 50 different conformations of OLDNs with histone tails from the model without them.

Selection scheme

To select appropriate atomic models that reproduce the experimental profiles well, we used the χ²-value defined as

$${\chi }^2=\frac{1}{N_p}\sum _{i=1}^{N_p}{\left(\frac{I_e\left(Q_i\right)-cI\left(Q_i\right)+a}{\sigma \left(Q_i\right)}\right)}^2,$$ (4)

where N_p is the number of experimental points Q_i; I_e(Q_i) and I(Q_i) are the experimental and computed profiles, respectively; σ(Q_i) is the experimental error; c is a scale factor given by

$$c=\sum _{i=1}^{N_p}\frac{I_e\left(Q_i\right)I\left(Q_i\right)}{\sigma {\left(Q_i\right)}^2}/\sum _{i=1}^{N_p}\frac{I{\left(Q_i\right)}^2}{\sigma {\left(Q_i\right)}^2};$$ (5)

and a is the offset that accounts for possible systematic errors due to mismatched buffers in the experimental data (28). The profiles were computed using crysol3 (29) for SAXS profiles and cryson (30) for SANS profiles. Smaller χ²-values indicated a better fit to the experimental profile.

Conformational analysis using six rigid-body parameters

To describe the global conformation of each OLDN model, six rigid-body parameters (dX, dY, dZ, dρ_X, dρ_Y, dρ_Z), which reflected the positions and orientations of the two nucleosomes relative to each other, were computed as follows. First, we defined the reference coordinate system on the x-ray crystal structure of a mononucleosome (Protein Data Bank, PDB: 3LZ0 (31)). The origin was set on the center of mass, and the xyz axes were defined by the principal axes of inertia (Fig. 1 a). Note that we included both the DNA and proteins in the calculation. The z axis appeared to coincide with the superhelical axis of the DNA, and the y axis appeared close to the dyad symmetry axis. Then, the histone core proteins of the mononucleosome were fitted to the corresponding proteins (RMS fitting) in the OLDN model. Through this fitting, the origin and xyz axes were defined locally in each nucleosome (Fig. 1 b). The xyz axes were described by a rotation matrix, R_i, and the origin was described by a vector, o_i. The subscript i was used to differentiate the two nucleosomes within an OLDN. We assigned R₁ and o₁ for the octasome and R₂ and o₂ for the hexasome. Finally, using the Cambridge University Engineering Department Helix computation Scheme (CEHS) (32,33), the six rigid-body parameters were computed. The angular parameters (dρ_X, dρ_Y, dρ_Z) were computed from the rotation matrices R₁ and R₂. The translational parameters (dX, dY, dZ) were computed as ${\mathbf{R}}_{mid}^{-1}$(o₂ − o₁), where R_mid described the “middle frame” between R₁ and R₂. The parameters dρ_X, dρ_Y, and dρ_Z, respectively, correspond to the basepair step parameters tilt, roll, and twist, whereas dX, dY, and dZ correspond to shift, slide, and rise.

Figure 1.

(a) The xyz coordinate system defined on the reference atomic model. The x (red arrow), y (green), and z axes (blue) were defined by the principal axes of inertia of the x-ray crystal structure of the mononucleosome (PDB: 3LZ0). The origin was set on the center of mass of the structure. (b) For both the octasome and hexasome, the xyz coordinate system was defined (x₁y₁z₁ and x₂y₂z₂, respectively) by fitting the x-ray crystal structure of the mononucleosome shown in (a). For easy understanding of the six rigid-body parameters, the octasome and hexasome are situated such that the z₁ and z₂ axes are parallel and the angle between the x₁ and x₂ axes is 45°, ignoring the connection between the two nucleosomes. Transparent red, octameric proteins; transparent blue, hexameric proteins. The middle frame (x_my_mz_m) is also shown. To see this figure in color, go online.

MD simulations for model verification

We performed MD simulations with the models that reproduced the experimental SAXS and SANS profiles well to see whether they were maintained stably in solution. As described above, the histone tails in these models were built for the specific structure with the smallest χ² for the SAXS profile. Here, we optimized the conformations of the histone tails for each model before each simulation run as follows. First, the histone tails were replaced with the extended tails modeled using the program MODELER. We then performed MD simulations using the simulated annealing technique to enhance the conformational changes in the histone tails while the rest of the structure remained fixed. The same procedure was applied when we added the histone tails to the model without tails. This time, we performed the simulation only once for each model. After remodeling the histone tails, we performed conventional MD simulations (NVT) at a temperature of 300 K with no restraint using GROMACS with the Amber 14sb+bsc1 force field. The temperature was controlled using the V-rescale method. The Na⁺ and Cl⁻ ions were added to neutralize the system and maintain the salt concentration at 50 mM. As Chen et al. (34) demonstrated, the NaCl concentration could play a crucial role on the conformation of nucleosomes. The salt concentration was set at the same value as the scattering experiment (see Sample Preparation).

Results and Discussion

Solution scattering

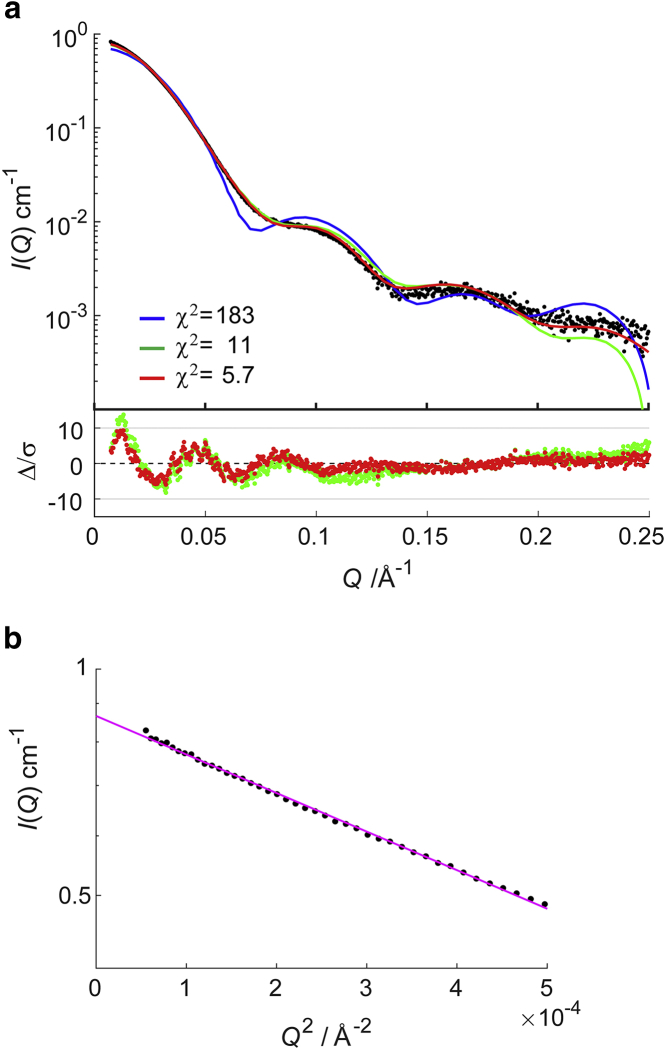
Fig. 2, a and b shows SAXS profiles in an aqueous solution and their Guinier plots (log I(Q) vs. Q²). Through least-square fitting at low Q with the Guinier formula (I(Q) = I₀exp(−$R_g^2{Q}^2$/3)), where R_g is the radius of gyration (Fig. 2 b), the radius of gyration was calculated to be 57.5 ± 0.3 Å. In Fig. 2 a, the SAXS profile calculated from the crystallographic data (PDB: 5GSE) is indicated by a blue line. Notably, the experimental and computational SAXS profiles have common points: both have peaks around 0.10 and 0.17 Å⁻¹, which correspond to the disk-like structures of hexasome and octasome domains (10,35). However, the peak positions in the experimental profile were shifted slightly to a lower Q and the gyration radius was larger. This indicates that the partial (domain) structures in aqueous solution was basically the same as in crystal, but there was a modulation in the whole structure. The radius of gyration of the crystal structure was calculated to be 46.3 Å (Table 1), which was smaller than that obtained from SAXS or SANS profiles. It should be noted that calculation of R_g for the crystal structure included no contribution from the missing histone tails, which were not observable.

Figure 2.

(a) The upper plot: SAXS profiles for OLDNs. Black dots show the experimental SAXS profile, and a blue line indicates the calculated profile based on the crystal structure (PDB: 5GSE). A green line is the calculated profile for the model with the smallest χ² for the SAXS profile in which histone tails were not considered, and a red line is the averaged profile for the model with the smallest χ² in which the multiple conformations of the histone tails were considered. Numerical values of χ² for the SAXS profile are also shown for the blue, green, and red lines. The lower plot shows the error-weighted residual difference plot for the computational models. The same color is used for the same model in the upper plot. (b) Guinier plots are shown. Solid circles are the experimental results, and the magenta line shows the result of the least-square fitting with the Guinier formula (see text). To see this figure in color, go online.

Table 1.

Radii of Gyration

	Solution D2O Concentration	Experiment	Crystal
SAXS	0%	57.5 ± 0.3 Å	46.3 Å
SANS	0%	55.3 ± 0.6 Å	46.4 Å
	40%	61.1 ± 1.6 Å	51.6 Å
	65%	50.1 ± 0.4 Å	39.3 Å
	100%	54.8 ± 0.4 Å	43.4 Å

To examine the structure of OLDNs in more detail, we conducted contrast-variation SANS (CV-SANS) measurements, which provide structural information about the histones and DNA within OLDNs separately (see Fig. S1). Fig. 3 shows the SANS profiles with their Guinier plots as insets for OLDNs in 0, 40, 65, and 100% D₂O. The radii of gyration are listed in Table 1. The SANS profiles in 40 and 65% D₂O, respectively, correspond to the profiles for the DNA and histones within OLDNs. As expected, therefore, the radius of gyration in 40% D₂O was the largest and that in 65% D₂O was the smallest, which indicates that the DNA was wrapping around histone cores. Interestingly, even though the radii of gyration were larger than those calculated from the crystal structure in all the contrast conditions, the SANS profiles were becoming more similar in the higher Q-region (roughly Q > 0.10 Å⁻¹). This suggests that the individual nucleosomes, hexasome and octasome, had basically the same structures in aqueous solution as those in crystal. However, all experimental CV-SANS profiles show larger R_g-values than those calculated with the crystal structure. Therefore, we assumed that the whole structure composed of the hexasome and octasome particles could dynamically fluctuate in solution. To elucidate these molecular structures at the atomic level, we constructed structural models by integrating the SAXS and CV-SANS experiments with the computational methods. In this modeling, the DNA and histone tails missing from the crystallographic data were explicitly considered.

Figure 3.

CV-SANS profiles, residual difference plots, and Guinier plots. (a) 0% D₂O (H₂O), (b) 40% D₂O, (c) 65% D₂O, and (d) 100% D₂O results are shown. Blue lines show the SANS profiles calculated based on the crystal structure (PDB: 5GSE). Green lines are the calculated profiles for the model with the smallest χ² for the SAXS profile in which histone tails were not considered, and red lines are the averaged profile for the model with the smallest χ² for the SAXS profile in which the multiple conformations of the histone tails were considered. Numerical values of χ² for each SANS profile are also shown for the blue, green, and red lines. The residual difference plots are shown only for the computational models. Insets are Guinier plots in which magenta lines show the results of the least-square fitting with the Guinier formula (see text). Error bars indicate experimental errors σ(Q_i). To see this figure in color, go online.

Overview of the construction of atomic models consistent with the scattering data

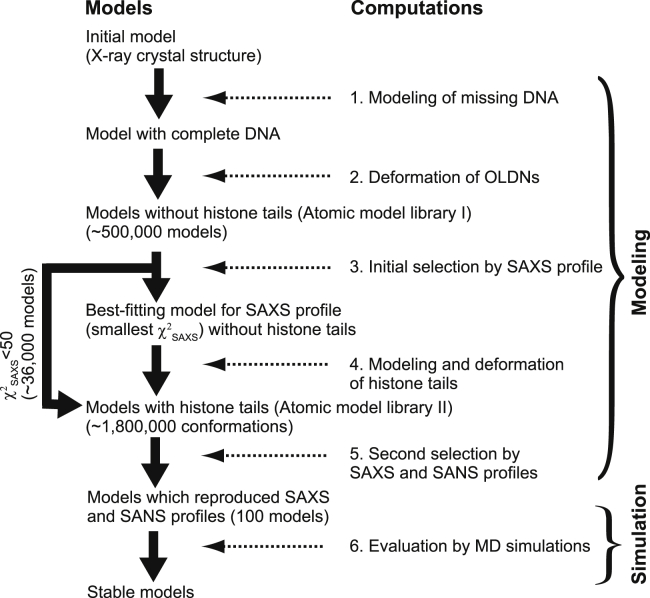
The computational procedure we used to obtain atomic models consistent with the scattering data and to investigate OLDN dynamics is outlined in Fig. 4. It consisted of six steps and started from the OLDN crystal structure (PDB: 5GSE (10)). Here, we provide an overview of each step. The steps are described in detail in the Supporting Materials and Methods and Figs. S2–S7 and in the Materials and Methods.

Figure 4.

Overview of the computations performed in this study.

Step 1: Modeling of the missing DNA

The x-ray crystal structure of an OLDN lacks five successive basepairs (chain I:131–135 and chain J:116–120). To model these basepairs (i.e., to fill the gap), we considered a DNA model with seven basepairs that had the same sequence as the missing basepairs plus two adjacent basepairs (chain I:130–136, chain J:115–121). We then minimized the total conformational energy of the DNA model, which included a penalty function to force the basepairs on both ends to have the same geometry as in the crystal structure. The resultant DNA model was inserted into the crystal structure by fitting the end basepairs to the corresponding ones in the crystal structure (RMS fitting). By the modeling of the missing DNA, there was a small improvement in the χ²-value for the SAXS profile (from 183 to 165). Hereafter, we will refer to this x-ray crystal structure with the DNA gap filled by the model as simply the crystal structure.

Step 2: Deformation of OLDNs

To construct the atomic model of OLDNs fitted to the SAXS and SANS data, we prepared a large number of different conformations. For this purpose, we first generated a wide variety of different DNA conformations by deforming the crystal structure using the five lowest-frequency normal modes (see Materials and Methods). Then, the histone octamer and hexamer, whose structures were fixed as the crystallographic structures, were put in the same geometry with respect to the wrapping DNA in the crystal structure. It should be noted that we assumed that the crystal structure was the minimum energy conformation and allowed only the linker DNA (chain I:129–152, chain J:99–122) to change its conformation. With this approach, we produced more than 500,000 atomic models of an OLDN (the atomic model library I), which differed from one another by at least 2 Å in root mean-square deviation (RMSD).

Step 3: Initial selection by SAXS profile

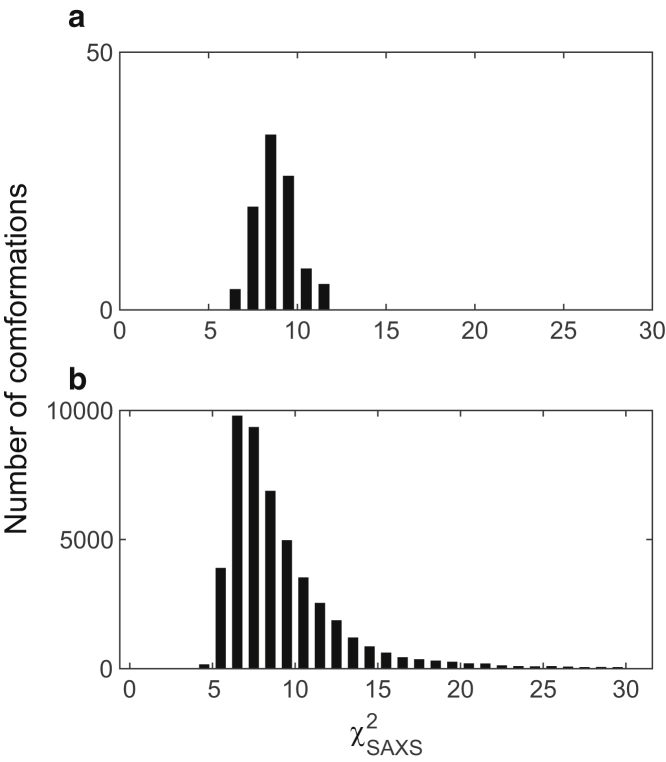
When we calculated χ² for each of the models in library I against the SAXS profile, the minimum χ² was 11, which suggested that the biggest decrease of the χ² (from 165 to 11) was brought by the configurational changes of the hexasome and octasome because we allowed only the linker DNA to change its conformations in step 2. This result supported our assumption made above in Solution Scattering. However, we considered the number (χ² = 11) too large for the model to reproduce the experimental profile well, and at the same time, we found that the models with the smallest χ² did not stay stably in water by the MD simulations (Fig. S8). This may have been due to the lack of the histone tails in the crystal structure. In fact, the tails occupy ∼20–25% of the total weight of the histones and so cannot be ignored in terms of scattering intensity (36). Therefore, for further analysis, we selected ∼36,000 OLDN models with a relatively small χ² (<50) in which the histone tails were to be modeled. Some models without tails that had higher χ² (>50) might drastically decrease χ² (e.g., <10) if the histone tails were modeled. It should be noted, however, that such a drastic decrease would not occur, as demonstrated in Fig. S7.

Step 4: Modeling and deformation of histone tails

The initial conformations of the histone tails were prepared using MODELER (17,18) based on the OLDN structure with the minimum χ² obtained at step 3. Because histone tails are highly flexible, using GROMACS (19, 20, 21, 22, 23, 24, 25) we repeated independent, simulated annealing MD simulations of this OLDN ∼100 times, starting from the same initial conformation. In the simulations, only the modeled histone tails were allowed to move; the DNA and histone core regions were restrained. From the ∼100 final models with different tail conformations, we selected 50 whose histone tails were bound and not extending outward (see Fig. S9). We then replaced the histone proteins without tails in the 36,000 models selected at step 3 with the proteins with tails in one of the 50 models through RMS fitting of the histone core atoms. As a result, we built a new structure library with 1.8 million (36,000 × 50) different conformations (atomic model library II).

Step 5: Second selection of structure with SAXS and SANS

Because the histone tails are very flexible, it is reasonable to consider their multiple conformations —i.e., we considered that in each OLDN model, the histone tails had 50 different conformations. To examine the reproducibility of the models against the experimental SAXS and SANS profiles, we used the mean value of χ² over the 50 conformations, which differed only in the histone tails. Hereafter, we will denote the mean value of χ² as <χ²>.

Selection using SAXS profiles

We calculated $<{\chi }_{\text{SAXS}}^2>$ (<χ²> for the SAXS profile) for all the models in the new library II, in which the models have tails. The minimum value of $<{\chi }_{\text{SAXS}}^2>$ was 5.7, showing that addition of the histone tails improved χ² (from 11 to 5.7). Indeed, $<{\chi }_{\text{SAXS}}^2>$ for most of the models was smaller after the histone tails were added (Fig. S7). In Fig. 2, two computed SAXS profiles were compared with the experimental profiles. The green line is the profile for the model with the smallest χ² when the histone tails were not considered, and the red line is for the model with the smallest $<{\chi }_{\text{SAXS}}^2>$. The latter was obtained by averaging 50 different profiles for the model in which multiple conformations of the histone tails were considered. In the lower region of q (<0.1 Å⁻¹), both profiles fit well to the experimental profile, indicating that the overall shape of OLDN is reproduced, even by the models without the histone tails. However, in the higher region of q, deviation of the former from the experimental profile was apparent, demonstrating that addition of the histone tails improved the reproduction of local OLDN structures.

Selection using SANS profiles

SANS profiles in 40 and 65% D₂O give information about the conformations of the DNA and proteins, respectively. We used these two different profiles as a kind of “low-pass filter” to exclude the models with $<{\chi }_{\text{SANS}40}^2>$ or $<{\chi }_{\text{SANS}65}^2>$ (<χ²> for the SANS profile in 40 and 65% D₂O) higher than given threshold values. By applying these filters to the models with small $<{\chi }_{\text{SAXS}}^2>$, we further limited them by excluding those that satisfied the SAXS profile, but not the SANS profiles, reflecting the conformations of the DNA or histones. The threshold values were set so that a quarter of the models with $<{\chi }_{\text{SAXS}}^2>$ < 10 were blocked by each filter (∼1.90 for both $<{\chi }_{\text{SANS}40}^2>$ and $<{\chi }_{\text{SANS}65}^2>$). Using these filters, 320 models were extracted from the 500 models with the smallest $<{\chi }_{\text{SAXS}}^2>$ (<∼7.5).

We analyzed the conformations of the models using the six rigid-body parameters, which described the positions and orientations of the two nucleosomes relative to each other within the OLDN (Fig. 1). Fig. 5 shows the distributions of the parameters for the 500 models (black open bar), as well as the 320 extracted models (green open bar) (left y axis). The most significant difference between the two distributions was observed in dX. The models with relatively large dX (>∼20 Å) were excluded by the SANS filters. It should be noted that application of the SANS profile filters in 0 and 100% D₂O did not noticeably change the distributions (data not shown). This is reasonable because these profiles included the scattering from both proteins and DNA as the SAXS profile, so they should be essentially the same as the SAXS profile.

Figure 5.

Distributions of the six rigid-body parameters for the atomic models of OLDNs in which multiple conformations of the histone tails are considered (left y axis). For the 500 models with the smallest $<{\chi }_{\text{SAXS}}^2>$, the distributions are denoted by open black bars. Among the 500 models, the 320 models in which both $<{\chi }_{\text{SANS}40}^2>$ and $<{\chi }_{\text{SANS}65}^2>$ are smaller than the threshold values are denoted by open green bars. Among the 320 models, the 100 atomic models with the smallest $<{\chi }_{\text{SAXS}}^2>$ were used as the initial conformations in MD simulations and are denoted by filled blue bars. The bin size was set to 5 (Å or degrees) in all the distributions. The smallest $<{\chi }_{\text{SAXS}}^2>$ of the models in each bin is also plotted (right y axis) as a black solid line for the models included in the open black bar and as the red dashed line for models included in the open green bar. To see this figure in color, go online.

The smallest $<{\chi }_{\text{SAXS}}^2>$ of the models included in each bin is also plotted in Fig. 5. The shape of the plot was similar to that of the distribution of models if inverted, and the conformation with the lowest $<{\chi }_{\text{SAXS}}^2>$ was nearly always located in the highest bin of the distribution. This suggests that a group of models with relatively small $<{\chi }_{\text{SAXS}}^2>$ were distributed around the conformation with the smallest $<{\chi }_{\text{SAXS}}^2>$ in the conformational space. Indeed, among the 100 final candidate models with the smallest$<{\chi }_{\text{SAXS}}^2>$ (< ∼6.75), most models (85 models) had RMSDs less than 6 Å, excluding the histone tail atoms, from the one with the smallest $<{\chi }_{\text{SAXS}}^2>$ (= 5.7), and the mean value was 4.3 Å.

Summary of the final candidate models

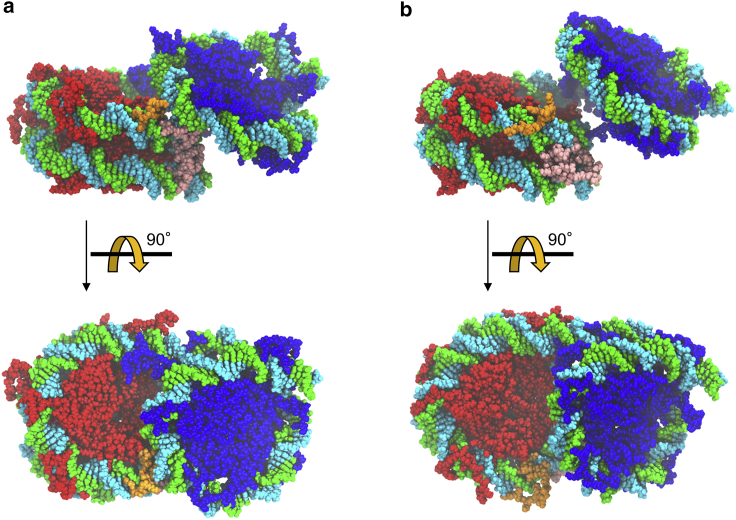
All of the distributions of the rigid-body parameters in Fig. 5 have a single peak, suggesting that we were able to successfully narrow down the candidate models to a group with similar conformations. When the histone tails were not included in the models (step 3), two peaks appeared in the distribution of dX (Fig. S4), which corresponded to two groups of models with significantly different conformations at the atomic level (Fig. S5). When the histone tails were included, one group of the models gave smaller $<{\chi }_{\text{SAXS}}^2>$-values and became more favorable, showing that inclusion of the histone tails contributed to the selection of the models. The model with the smallest $<{\chi }_{\text{SAXS}}^2>$ was included in this favorable group. The positions of the histone tails differed significantly between the two groups. As shown in Fig. 6 a, the histone tails in the models in the group with smaller $<{\chi }_{\text{SAXS}}^2>$ were observed more frequently at the interface between the two nucleosomes or, more specifically, in the region where sequentially distant DNA sites came into close proximity. This could be important for stabilizing the structure of OLDNs, as will be described later. On the other hand, tails in the other group were not observed in that region (Fig. 6 b). Note that the model with the smallest ${\chi }_{\text{SAXS}}^2$ obtained when not considering the tails belonged to the unfavorable group (Fig. 6 b).

Figure 6.

Atomic models of an OLDN. Octameric core proteins are shown in red and hexameric in blue. (a and b) Multiple conformations of histone tails are illustrated by averaging 50 images of the model with histone tails in different conformations viewed from the same angle. The histone tails of the octamer and hexamer are colored in yellow and orange, respectively. Thick orange and yellow indicate that the histone tails are observed frequently in the area. (a) The model with the smallest $<{\chi }_{\text{SAXS}}^2>$ is shown. (b) The model with the smallest ${\chi }_{\text{SAXS}}^2$ when the histone tails were not considered is shown. The dashed circles in yellow and red, respectively, indicate the positions of one of the H4 and H3 histone tails in the octamer. Note that these circles are closer to both the hexasomal and octasomal DNA in (a) than in (b). The H4 histone tail indicated by the yellow circle in (a) is mostly beneath the hexasomal DNA. (c) The crystal structure is compared with the model in (a). The octameric core proteins (red) are superimposed on each other. The computational model is represented with light colors. The RMSD between the two structures, excluding the histone tails atoms, was 19.6 Å. To see this figure in color, go online.

In Fig. 3, the computed SANS profiles are plotted for the model with the smallest $<{\chi }_{\text{SAXS}}^2>$ as well as for the one with the smallest ${\chi }_{\text{SAXS}}^2$, which had no tails. It is clearly shown that, compared to the latter model, the 65% D₂O profile (Fig. 3 c) was improved (smaller χ²), but the change of the 40% D₂O profile (Fig. 3 b) was small, indicating that only the conformations of the histone proteins were improved. In principle, it could be possible that the modeled histone tails compensated for erroneous DNA shapes of the model with high ${\chi }_{\text{SANS}40}^2$ and made $<{\chi }_{\text{SAXS}}^2>$ small. However, such compensation did not occur in the model with the smallest $<{\chi }_{\text{SAXS}}^2>$ in our modeling procedure.

Among the six rigid-body parameters, dX, dρ_X, and dρ_Y showed relatively wide distributions, suggesting that variations in these parameters had smaller effects on $<{\chi }_{\text{SAXS}}^2>$, which is also apparent from the less steep slopes of the plots of $<{\chi }_{\text{SAXS}}^2>$ in Fig. 5. This result can be interpreted in two ways. One is that the OLDN is fluctuating in these directions; another is that it is difficult to differentiate the models deformed in these directions through SAXS analysis. To determine which interpretation is more likely, we carried out MD simulations, the results of which support the first interpretation, as will be described in step 6. The distributions of dY, dZ, and dρ_Z in Fig. 5 were narrow, suggesting that the variations in these parameters have larger effects on $<{\chi }_{\text{SAXS}}^2>$.

Videos S1, S2, S3, S4, S5, and S6 show the conformational changes in an OLDN when one of the six rigid-body parameters in the model with the smallest $<{\chi }_{\text{SAXS}}^2>$ was forced to change while the other parameters were kept unchanged as much as possible (see Supporting Materials and Methods). When dY or dρ_Z was changed, however, other parameters also changed considerably (Fig. S10), which suggests these parameters are correlated with one another. This interpretation is described in detail in the Supporting Materials and Methods and Fig. S11.

Video S1. The Conformational Change of OLDN Increases dX

(Cyan and green) DNA chains, (red) the octamer proteins, (blue) the hexamer proteins.

Video S2. The Conformational Change of OLDN Increases dY

See legend of Video S1.

Video S3. The Conformational Change of OLDN Increases dZ

See legend of Video S1.

Video S4. The Conformational Change of OLDN Increases dρ_X

See legend of Video S1.

Video S5. The Conformational Change of OLDN Increases dρ_Y

See legend of Video S1.

Video S6. The Conformational Change of OLDN Increases dρ_X

See legend of Video S1.

Step 6: Model stability evaluated using MD simulations

To examine the stability of the models, we performed 10-ns-long all-atom MD simulations with an explicit solvent model. From the final candidate models, we selected the 100 OLDN models with the smallest $<{\chi }_{\text{SAXS}}^2>$ (<∼6.75) for the simulations. The distributions of the rigid-body parameters of these models are shown as blue bars in Fig. 5. Among the 100 simulations, three failed during the initial energy minimizations because of bad positioning of the atoms in the models. For each of the remaining 97 models, the trajectory was saved and analyzed every 20 ps. The χ²-values and the six rigid-body parameters were computed for these conformations, as were the means and the SDs of the values in each trajectory.

Fig. 7 shows the distributions of the ${\chi }_{\text{SAXS}}^2$-values for the initial conformations (or t = 0) (a) and for all ∼50,000 conformations (b) during the simulations. The distribution of the latter conformations became wider toward both sides. It is noteworthy that the peak shifted toward a smaller ${\chi }_{\text{SAXS}}^2$-value, indicating that conformations that better fit the SAXS profile were sampled during the simulations. The standard deviations (SDs) of ${\chi }_{\text{SAXS}}^2$ were generally small, and 33 of the 97 trajectories had SDs less than one (hereafter referred to as stable trajectories). One of the stable trajectories is shown in Videos S7, S8, and S9. Fig. S12 shows the distributions of the deviations in the six rigid-body parameters from the mean values in each trajectory. It is evident that dX and dρ_X had the largest variations among the translational (dX, dY, dZ) and rotational (dρ_X, dρ_Y, dρ_Z) parameters, respectively. On the other hand, the variations in dY and dρ_Z were the smallest. These results are consistent with the distribution widths in the final models shown in Fig. 5, which indicates that the distribution widths obtained from the final models reflect the rigidity or flexibility of OLDNs in those directions.

Figure 7.

Distribution of ${\chi }_{\text{SAXS}}^2$ for the initial conformations (a) and for all (∼50,000) conformations (b) during the 97 trajectories of the MD simulations. The bin size was set to 1 in both panels.

Video S7. The Conformations of OLDN in One of the Stable MD Trajectories

(Cyan and green) DNA chains, (red) the octamer proteins, (blue) the hexamer proteins, (orange) one of the H4 histone tails in the octamer proteins, (pink) one of the H3 histone tails in the octamer proteins.

Video S8. The Conformation in Video S7 Viewed from a Different Angle

See legend of Video S7.

Video S9. The Conformation in Video S8 Viewed from the Opposite Side

See legend of Video S7.

Some trajectories exhibited structural instability, which yielded conformations with large ${\chi }_{\text{SAXS}}^2$ and widened the ${\chi }_{\text{SAXS}}^2$ distribution (Fig. 7 b). In such unstable trajectories, the two nucleosomes were often widely separated (Fig. 8 b or Videos S10, S11, and S12). Fig. S13 shows the SD of ${\chi }_{\text{SAXS}}^2$ in each trajectory plotted against the mean value of the distance between the two nucleosomes, which was measured using the minimum interatomic distances between the hexasomal and octasomal DNA. The terminal 98 DNA basepairs wrapping the hexamer were regarded as the hexasomal DNA, whereas the other terminal 128 DNA basepairs were regarded as the octasomal DNA. Clearly, the deviation was large when the distance was more than 14 Å, and in all of the stable trajectories, the distances were less than 13 Å. We therefore concluded that the two nucleosomes comprising an OLDN were situated close to each other in the stable conformations, but the distance ranged from 2 to 13 Å.

Figure 8.

One of the conformations of OLDN in a stable trajectory for which the SD of ${\chi }_{\text{SAXS}}^2$ was less than 1 (a) and in an unstable trajectory for which the SD was large (b). Red, octameric proteins; blue, hexameric proteins; orange, one of the H4 histone tails in the octamer; pink. one of the H3 histone tails in the octamer. To see this figure in color, go online.

Video S10. The Conformation of OLDN in One of the Unstable MD Trajectories

See legend of Video S7.

Video S11. The Conformation in Video S10 Viewed from a Different Angle

See legend of Video S7.

Video S12. The Conformation in Video S11 Viewed from the Opposite Side

See legend of Video S7.

We found that the conformations of the histone tails in the trajectories with small ${\chi }_{\text{SAXS}}^2$ SDs clearly differed from those with larger SDs. In the small ${\chi }_{\text{SAXS}}^2$ conformations, at least one of the histone tails of the octamer always bound simultaneously to both the octasomal and hexasomal DNA, acting as a bridge or glue between two DNA sites on opposite sides of the linker DNA (Fig. 8 a or Videos S7, S8, and S9). By contrast, no such histone tails were observed in the trajectories with large SDs (Fig. 8 b or Videos S10, S11, and S12). Because DNA is negatively charged, two DNA sites are unable to closely approach one another without the positively charged histone tails. In most trajectories, one of the H4 histone tails (orange in Fig. 8 a) in the octamer served as this bridge. In some trajectories, one of the H3 histone tails (pink in Fig. 8 a) in the octamer also served as a bridge.

Conclusions

In this work, we constructed atomic models of OLDNs in solution. Starting from the crystal structure, we first produced a library of atomic models with different conformations by deforming the DNA chain while keeping the structures of the histone proteins fixed. However, these models did not reproduce the SAXS profiles well. We therefore added the histone tails, which were invisible in the crystal structure. We then conducted repeated annealing MD simulations to generate a large number of different conformations of the tails. The addition of the histone tails improved the χ²-values for the SAXS profiles and enabled us to reduce the number of candidate models. We then used the SANS profiles for further refinement and selection of conformational candidates. The stability of the modeled structures was finally evaluated using MD simulations with explicit solvent models. These MD simulations showed that in stable trajectories, the hexasomal and octasomal DNAs were close to one another and that one or more histone tails were simultaneously bound to both DNA segments, which enabled the negatively charged DNA chains from the octamer and hexamer to be in close proximity.

Author Contributions

A. Matsumoto, M.S., H. Kurumizaka, and H. Kono designed research. D.K. and A.O. prepared OLDN for SAXS and SANS. A. Matsumoto, M.S., Z.L., A. Martel, L.P., R.I., H. Kurumizaka, and H. Kono performed research. A. Matsumoto, M.S., Z.L., H. Kurumizaka, and H. Kono wrote the manuscript.

Editor: Tamar Schlick.