Summary
The human ability to imagine motor actions without executing them (i.e., motor imagery) is crucial to a number of cognitive functions, including motor planning and learning, and has been shown to improve response times and accuracy of subsequent motor actions [1, 2]. Although these behavioral findings suggest the possibility that imagined movements directly influence primary motor cortex (M1) how this might occur remains unknown [3]. Here, we use a non-BOLD method for collecting fMRI data, called vascular space occupancy (VASO) [4, 5], to measure neural activations across cortical laminae in M1 while participants either tapped their thumb and forefinger together or simply imagined doing so. We report that, while executed movements (i.e., finger tapping) evoked neural responses in both the superficial layers of M1 that receive cortical input and the deep layers of M1 that send output to the spinal cord to support movement, imagined movements evoked responses in superficial cortical layers only. Furthermore, we found that finger tapping preceded by both imagined and executed movements showed a reduced response in the superficial layers (repetition suppression) coupled with a heightened response in the deep layers (repetition enhancement). Taken together, our results provide evidence for a mechanism whereby imagined movements can directly affect motor performance and might explain how neural repetition effects lead to improvements in behavior (e.g., repetition priming).
Keywords: fMRI, motor Imagery, Primary Motor Cortex, cortical layers, repetition suppression, priming, VASO
eToc blurb
Persichetti et al. use a non-BOLD fMRI method called vascular space occupancy (VASO) to show that while actual hand movements evoke responses in superficial and deep layers of M1, imagined hand movements evoke responses in superficial layers only. Imagined movements also produce layer-specific repetition effects on subsequently executed movements.
Results & Discussion
A number of behavioral findings suggest the possibility that imagined movements directly influence primary motor cortex (M1), but how this might occur remains unknown [3]. Methodological limitations in neuroimaging are partially responsible for the ambiguity surrounding the role of M1 in motor imagery. Until now, the poor spatial specificity and vascular biases of conventional neuroimaging techniques that measure changes in blood oxygenation levels (i.e., BOLD signal) have made it difficult to detect functional changes across cortical layers [4, 5]. That said, a prior study found evidence for neural activity related to motor imagery in the superficial, but not deep, layers of M1 in the BOLD signal (Trampel et al., SFN 2011; OHBM 2012). However, the interpretation of their results is limited by the lack of spatial specificity of the BOLD signal across cortical layers, especially in deeper layers [e.g., 5, 6]. Therefore, we used a 7-Tesla MRI scanner and a cutting-edge method called vascular space occupancy (VASO) to simultaneously measure changes in cerebral blood volume (CBV) and the BOLD signal across cortical layers of the hand-selective region of M1. Using VASO to measure CBV, instead of using conventional fMRI methods that measure the BOLD signal only, we achieved sub-millimeter spatial specificity without the vasculature-bias of the BOLD signal [5, 6]. We also used an event-related design with counterbalanced stimulus presentations to measure both the neural response to the direct effect of each stimulus, as well as the carry-over effect of the prior stimulus (i.e., repetition effects) [7, 8]. Measuring repetition effects allowed us to further probe the laminar dynamics of M1 during motor tasks.
While little is known about the role of M1 in motor imagery, animal models of M1 have demonstrated that its laminar organization is such that cortico-cortical connections with M1 terminate predominately in superficial layers (II/III), while cortico-spinal output from M1 originates predominantly in the deep layers of cortex (Vb/VI) [9, 10]. Recently, a study using VASO found this same laminar circuitry in human motor cortex [6]. Given this laminar organization in M1, we predict that the superficial layers of M1 are involved in both motor imagery and execution, while deeper layers are involved in the execution of movements only.
Eleven healthy adult participants completed trials in which they either tapped their left thumb and index fingers together, imagined tapping their fingers together, or wiggled their left toes (Figure 1A) while we measured both VASO and BOLD responses in the contralateral hand-selective region of M1. In each participant, we functionally defined a hand-selective region of interest (ROI) in M1, by identifying the expected double-peak pattern of VASO responses to finger tapping across laminae in the anatomically-defined “hand knob” [11] (Figure 1B–F. See Methods for details). This double-peak pattern of responses in the VASO signal clearly functionally defines both the superficial and deep layers of M1 cortex (Figure 2A), while the pattern of BOLD responses does not (5) (Figure S1A). Therefore, we focused our analyses on the VASO signal.
Figure 1. Experimental design & ROI definition.
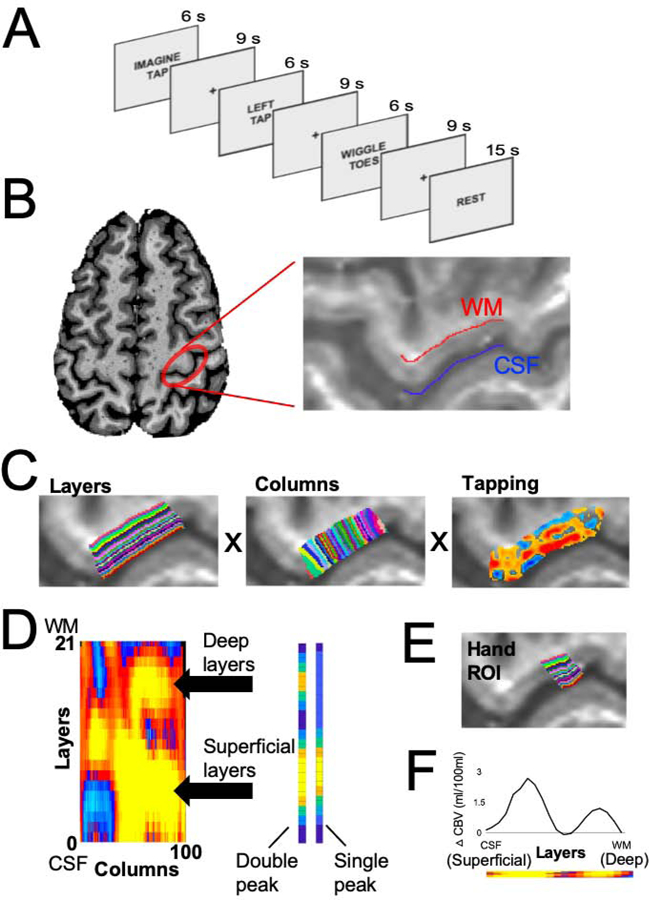
(A) In each trial, the participants either tapped their left thumb and forefinger together, imagined tapping their fingers together, or wiggled their left toes for 6s followed by 9s of rest. Several 15s rest trials were interspersed with the experimental conditions to be used as a baseline. (B) The hand ROI was defined in each participant by first locating the hand-selective area of M1 based on anatomical landmarks [10] and then further constrained by demarcating the cerebral spinal fluid (blue) and white matter (red) boundaries. (C) The anatomical hand ROI separated into 21 cortical layers (left) and 100 columns (middle). The VASO response to the tapping condition within the hand ROI (right). (D) A 21 layers X 100 columns matrix of activation shows the pattern of activation across the anatomical hand ROI. A multiple linear regression, in which an idealized double-peak response and a single-peak response was fit to each column of the matrix. (E) The columns of the matrix that were best fit by the double-peak response were used as a guide for functionally defining the hand ROI based on the response to finger tapping in each participant. Crucially, the direct response to finger tapping is not analyzed in further analyses, since doing so would be a non-independent analysis. (F) The VASO response profile to the tapping condition across the layers of the functionally defined hand ROI. Note that these data are non-independent, since the hand ROI was defined using the tapping data. It is displayed here simply to illustrate the efficacy of our ROI definition approach. Figures B-F are data from an example participant.
Figure 2. Responses to motor imagery in superficial, but not deep, layers of M1.
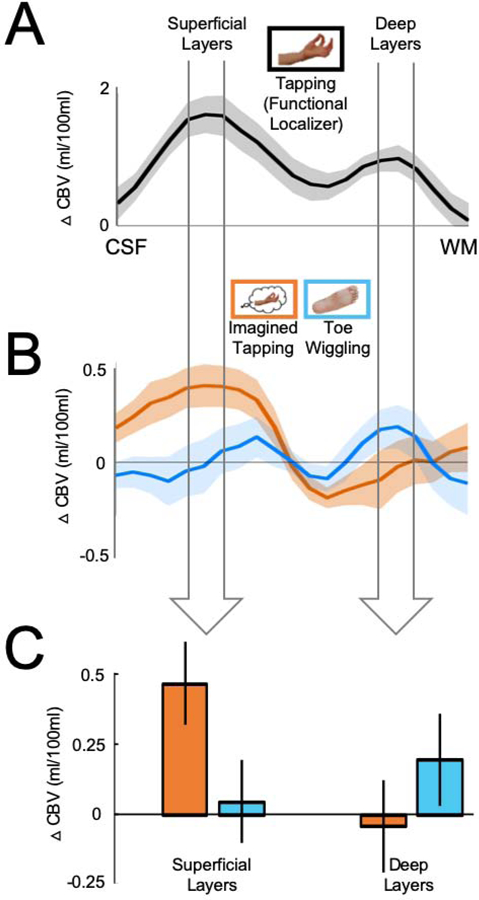
(A) The VASO response to the tapping condition was used to functionally localize the superficial and deep cortical layers based on the double-peak response profile. The widths of the arrows correspond to functional windows that comprise the peak and the data point on either side of it in the functionally defined superficial and deep layers, respectively. (B) The VASO responses to the Imagined tapping (orange) and toe wiggling (blue) conditions across the cortical layers. (C) The data in the bar graph are the same data shown in 2B, averaged across the functional window in the superficial and deep layers, respectively, in each participant. We found a significant interaction between responses in the superficial and deep cortical layers (F(1,10)=20.46, p<0.001), with a significantly greater response to Imagined tapping relative to the Toe wiggling condition in the superficial, but not deep cortical layers. Ten out of 11 participants showed a greater response to imagined finger tapping relative toe wiggling in the superficial layers of M1. Error bars on the line plots represent +/− 1 SEM. Error bars on the bar graph are 95% within-subject confidence intervals.
Responses to motor imagery in superficial, but not deep, layers of M1
First, we asked if imagined movements are represented in the hand-selective region of M1. As predicted, a 2 Layers (Superficial, Deep) x 2 Conditions (Imagined tapping, Toe wiggling) repeated-measures ANOVA revealed a significant interaction between responses in the superficial and deep cortical layers (F(1,10)=20.46, p<0.001, ηP2=0.67), with a significantly greater response in the superficial layers of the hand ROI when participants imagined tapping their thumb and index fingers together relative to wiggling their toes (t(10)=4.00, p=0.003, Cohen’s d=1.21), but not in the deep layers (t(10)=1.13, p=0.29, Cohen’s d=0.34) (Figure 2B–C). Importantly, a subset of six participants wore a motion detecting glove while in the scanner to ensure that the neural responses to imagined tapping were not due to inadvertent small finger movements during imagery trials (Figure S2). (Please note that if participants were in fact moving their fingers during imagining trials, this would be reflected in the deep cortical layers, and thus go against our hypothesis.) We then used independent data from a different subset of six participants who completed an additional functional run that included alternating 15 second blocks of the Finger tapping and Toe wiggling conditions to replicate the layer-specific responses to finger tapping in the hand ROI [12, 13] (see Methods and Figure S1B–C). These results demonstrate that the superficial cortical layers of a hand-selective region in M1 represent imagined movements, while the deep layers do not show a significant difference between the responses to Imagined tapping and Toe wiggling.
Layer-specific repetition suppression and enhancement effects in M1
Next, we asked how neural responses to executed hand movements (i.e., Tapping) were modulated by the preceding stimulus [14] within the superficial and deep layers of the functionally-defined hand ROI (Figure 3A–B). In the superficial layers, the response to repeated Tapping trials was significantly less than when Tapping was preceded by toe wiggling (t(10)=−3.66, p=0.004, Cohen’s d=1.10), thus displaying clear repetition suppression. We found a marginal repetition suppression effect when Tapping trials were preceded by Imagined tapping. Specifically, we found a marginal decrease in response to Tapping trials that were preceded by Imagined tapping compared to when Tapping trials were preceded by Toe wiggling (t(10)=−1.54, p=0.15, Cohen’s d=0.46), and no significant difference between Tapping trials preceded by Imagined tapping compared to when Tapping trials were repeated (t(10)=−1.20, p=0.26, Cohen’s d=0.36). By contrast, in the deep layers, we found an increased response to Tapping (i.e., repetition enhancement) both when Tapping trials were repeated (t(10)=2.62, p=0.03, Cohen’s d=0.79) and when Tapping was preceded by Imagined tapping (t(10)=3.09, p=0.01, Cohen’s d=0.93) compared to when Tapping trials were preceded by Toe wiggling (Figure 3C). A 2 Layer x 3 Condition repeated-measures ANOVA revealed a significant interaction (F(2,20)=6.53, p=0.007, ηP2=0.40), thus confirming the different patterns of responses between the superficial and deep layers. Finally, and most importantly, interaction contrasts revealed double dissociations between the repetition suppression effects in the superficial layers and the repetition enhancement effects in the deep layers: repeated Tapping trials compared to when Tapping trials were preceded by Toe wiggling (F(1,10)=12.08, p=0.006, ηP2=0.55) and Tapping trials preceded by Imagined tapping compared to when Tapping trials were preceded by Toe wiggling (F(1,10)=7.52, p=0.02, ηP2=0.43) (Figure 3C). Taken together, these data show that finger tapping preceded by both imagined and executed tapping showed a reduced response in the superficial layers (repetition suppression) coupled with a heightened response in the deep layers (repetition enhancement).
Figure 3. Layer-specific repetition suppression and enhancement effects in M1.
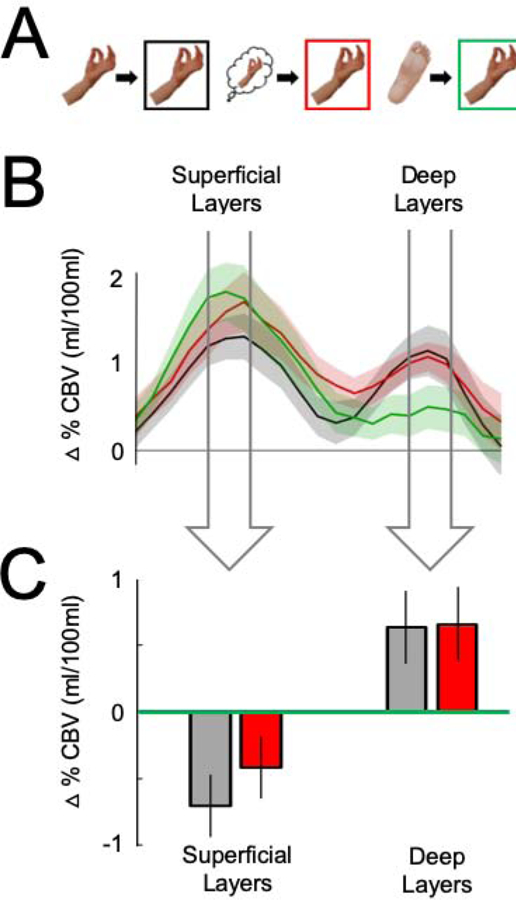
(A) In the graphs that follow, the responses to Tapping are separated by the type of trial that preceded it: Tapping preceded by Tapping is plotted in black, Tapping preceded by Imagined tapping in red, and Tapping preceded by Toe wiggling in green. (B) The VASO responses to Tapping across cortical layers, separated by which trial type preceded it. The widths of the arrows correspond to functional windows that comprise the peak and the data point on either side of it in the functionally defined superficial and deep layers, respectively. (C) The data in the bar graph are the same data shown in 3B, averaged across the functional window in the superficial and deep layers, respectively, in each participant. The data are plotted as difference scores – i.e. Tapping-preceded-by-toe-wiggling minus Tapping-preceded-by-tapping and Tapping-preceded-by-toe-wiggling minus Tapping-preceded-by-imagined tapping – in the superficial and deep layers. The responses to Tapping were attenuated both when it was preceded by Tapping and when it was preceded by Imagined tapping, relative to when Tapping was preceded by Toe wiggling (i.e., repetition suppression) in the superficial layers. By contrast, the responses to Tapping were enhanced both when it was preceded by Tapping and when it was preceded by Imagined tapping, relative to when Tapping was preceded by Toe wiggling (i.e., repetition enhancement) in the deep layers. Error bars on the line plots represent +/− 1 SEM. Error bars on the bar graphs are 95% within-subject confidence intervals.
Animal studies have established that the layers in a given patch of cortex are highly interconnected and the laminar circuitry is quite complex [10, 15]. Thus, it is reasonable to suspect that direct effects found exclusively in some layers (i.e., responses to Imagined tapping in the superficial layers only) will have a carry-over effect on the other layers. The pattern of repetition effects we found across laminae in the VASO signal may provide a clue to how neural signals propagate through the laminar circuitry of M1 in a manner that results in improved behavioral performance. Specifically, repetition suppression in the superficial layers might reflect improved coordination, or synchronization [16, 17], with other cortical areas involved in motor planning and learning of particular motor actions (e.g., premotor cortex and parietal regions), thus resulting in more efficient processing. This possibility is consistent with animal studies of the visual system that have reported increased neural synchrony in superficial relative to deeper layers of cortex in response to stimulus repetition [15, 18–20]. By contrast, repetition enhancement in the deep layers of M1 might reflect a boost in the gain of the signal, perhaps caused by increased attention to the motor action of finger tapping or by learned stimulus-response associations as a result of both the preceding imagined and actual tapping trials [14, 21]. This, in turn, could result in a more robust signal being sent out to the spinal cord, thus increasing the probability that it reaches the targeted spinal outputs with high precision.
In conclusion, our finding that the superficial layers of M1 represent imagined movements, while the deep layers do not, provides strong evidence that, while M1 is indeed involved in motor imagery, imagined and executed hand movements rely on different neural substrates within M1. Finally, the pattern of repetition effects we found across the cortical layers in M1 might explain how neural repetition effects lead to improvements in behavior (e.g., repetition priming), and thus reveal how using motor imagery to rehearse specific motor actions leads to improvements in motor execution during activities, such as athletic training and physical therapy [2].
STAR★Methods
Lead Contact and Materials Availability
Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Andrew Persichetti (persichettias@nih.gov). This study did not generate new unique reagents.
Experimental Model and Subject Details
Eleven healthy right-handed volunteers (age 22–50 years; 6 females) were recruited from the Washington D.C. metro area. We decided that the sample size of 11 participants would be adequate in our study based on the sample sizes used in prior comparable studies [6, 22, 23]. That said, it should be noted that the small sample size in our study could potentially result in low statistical power, and thus a reduced chance of detecting a true effect [24, 25]. All participants gave informed consent under an NIH Institutional Review Board-approved protocol (93-M-0170).
Method Details
Experimental Design
During experimental trials, participants were asked to either 1) tap their left thumb and forefinger together, 2) imagine tapping their left thumb and forefinger together without actually moving their fingers, or 3) wiggle the toes on their left foot. During each trial, participants saw instructions (“LEFT TAP”, “IMAGINE TAP”, “WIGGLE TOES”) displayed in black on the center of a neutral gray screen for 6 s followed by a black central fixation cross for 9 s (Figure 1A). Each participant completed 192 experimental trials (64 of each condition) intermixed with 64 trials in which the word “REST” was displayed for 15 s on the center of a blank neutral gray screen. During the rest trials, participants were asked to keep their hands and feet still. The rest trials were used as a baseline comparison for the conditions of interest.
The sequence of experimental trials was generated using four de Bruijn sequences (k=4, N=3) that were optimized to detect both the direct effect of the current trial and the carry-over effect of the preceding trial on the current trial (i.e., repetition effects) [7, 8]. Each sequence comprised 64 trials (43). Each sequence was split into two runs of 32 trials. To allow time for the hemodynamic response to build to a steady state, each run began with the first trial from the prior run (taken circularly, so that the last trial from the second run was prepended to the first run). An extra “rest” trial was added to the end of each run to ensure that the hemodynamic response to the last experimental trial of the run was resolved before ending data collection. The experiment was divided into eight runs, each with 34 trials, for a total of 510 s per run. In analysis, the data from the first trial of each run were discarded.
In addition to the experimental runs, six of the eleven participants also completed a “blocked” run at the end of the scan session to obtain a within-subject replication of the tapping result in the hand region of interest (Figure S1C–D). During the blocked run, participants alternated between tapping their left thumb and forefinger together and wiggling their left toes. Each block lasted 30 s (15 s of action followed by 15 s of rest) and participants completed eight blocks of each condition. The blocked run ended with an additional 15 s of fixation and lasted for a total of 495 s.
Before entering the scanner, each participant practiced each experimental condition for several minutes. In the scanner, six of the eleven participants wore a 5DT data glove ultra (Fifth Dimension Technologies), with a sampling rate of 60 Hz, on their left hand to detect motion during each trial. During the tapping condition, participants performed a ~3 Hz pinch-like tapping of thumb and forefinger (confirmed by data from the motion-detecting glove). During the imagined tapping condition, participants were asked to imagine tapping at approximately the same rate. During the toe wiggling condition, participants moved all of the toes on their left foot back and forth at roughly the same rate as the finger tapping condition (confirmed visually by the researcher during scanning).
fMRI Scanning
Slice-selective slab-inversion VASO [26, 27] was implemented on a MAGNETOM 7T scanner (Siemens Healthineers, Erlangen, Germany) using the vendor-provided IDEA environment (VB17A-UHF) and a 32-channel-receive head coil. A 3rd order B0-shimming was done with three iterations. The shim volume covered most of the right anterior part of the brain, extending down to the Circle of Willis to achieve optimal B0-homogeneity in the right motor cortex with residually homogeneous B0-field distribution for spin inversion. Imaging slice position and slice angle were adjusted individually for every participant to be perpendicular to the forefinger region of M1 (Figure S4). This was done at the beginning of the scan session based on short EPI test runs with 10 measurements (approx. 30 s per test scan) and their online depiction in the vendor-provided 3D-viewer. Eight slices (0.75x0.75x1.8mm) were acquired during each run with a repetition time of 3000 ms. The cortex in M1 is approximately 4mm thick [28]. In each participant, the hand knob in M1 spans roughly 5–6 voxels, each 0.75mm2, from CSF to WM. Therefore, across the participants in this study, the cortex in M1 is approximately 3.75–4.5mm thick.
VASO-specific scan parameters
The adiabatic VASO inversion pulse duration was 10 ms and the bandwidth was 6.3 kHz. The inversion-efficiency of the TR-FOCI pulse was adjusted by the implementation of a phase skip of 30° to minimize the risk of inflow of fresh non-inverted blood into the imaging region during the blood nulling time. One whole plane of k-space was acquired in every 3D-EPI shot [29]. The last excitation pulse of every readout was chosen to be nominally 90°. To keep a near-constant gray matter (GM) signal across k-space planes, the flip angles of the preceding planes were adjusted to be respectively smaller. The T1-relaxation between consecutive excitation pulses was estimated assuming a tissue T1-value of 1800 ms at 7 Tesla. The acquisition of the GRAPPA calibration data followed the FLASH approach to minimize segmentation artifacts and optimize conditioning of the subsequent GRAPPA reconstruction, resulting in increased tSNR. The GRAPPA reconstruction algorithms (Siemens software identifier: IcePAT WIP 571) were applied using a 3x2 (read direction 3 phase direction 2) kernel. Partial Fourier reconstruction was done with the projection-onto-convex-sets (POCS) algorithm [30] with 8 iterations. No Maxwell-correction was applied to minimize the number of data resampling steps.
The coil data were combined from the vendor provided image reconstruction pipeline with sum of squares. The coil-combined data consisted of interleaved BOLD and VASO contrasts (1500 ms BOLD, 1500 ms VASO contrast). The VASO contrast was corrected for BOLD contaminations by dynamic division [27].
Motion correction & anatomical alignment
Motion correction was performed using SPM12 [31], and was done separately for nulled and not-nulled time frames. Motion estimation was optimized on the motor cortex having the highest weights in the center of the FOV, decreasing toward the distortion-susceptible periphery of the FOV. A 4th order spline was used for motion estimation and resampling to minimize signal blurring. To ensure the most accurate definition of cortical depths, we used the functional data directly as an anatomical reference (5). Using functional data as an anatomical reference renders distortion corrections and spatial registration to other anatomical reference data unnecessary, thus avoiding registration errors and additional data resampling and hence, it helps to maintain the spatial specificity throughout the subsequent analyses [6, 32, 33].
Layering methods
Laminae were defined in reference to the borders between layer I and cerebral spinal fluid (CSF), and between layer VI and the white matter ribbon. First, to avoid singularities at the edges in angular voxel space, we upsampled the in-plane voxel dimensions by a factor of 4, so that we could define the cortical depths on a finer grid than the original EPI resolution (5). Next, we implemented an equidistant layering approach to estimate twenty-one cortical depths using the LN_GROW_LAYERS program in the LAYNII toolbox (https://github.com/layerfMRI/LAYNII). Based on known input-output characteristics of different cortical layers I-VI [6] and the position of the boundary between layer I and CSF, and the boundary between layer VI and the white matter ribbon, we were able to functionally localize the double-peak response to finger tapping in the VASO data approximately to layers II/III (“superficial layers”) and layer Vb (“deep layers”), respectively, based on the position of the boundary between layer I and CSF, and the boundary between layer VI and the white matter ribbon, and known input-output characteristics of different cortical layers I-VI [6].
Quantification and Statistical Analysis
Statistical analysis
Both the VASO and BOLD data were analyzed in AFNI [34] using a multiple linear regression model in each participant. The regression model contained a regressor for each condition of interest – i.e., tapping, imagined tapping, and toe wiggling – and another for the rest trials. These regressors were convolved with a gamma-variate hemodynamic response function with a peak amplitude of 1 and a peak at 4 seconds (as implemented in AFNI version 19.3.16). Beta weights associated with each covariate were extracted and each condition of interest was contrasted with the rest trials. Finally, the changes in cerebral blood volume associated with the VASO signal are reported as mL volume change per 100 mL of parenchyma volume (ml/100ml) [6, 35], while the BOLD data were converted to units of percent signal change by dividing each timepoint by the mean intensity across the time-course in each voxel and then multiplying by 100 for further analyses.
ROI definition
To functionally define the hand ROI in each participant, we first located the hand-selective area of M1 (i.e., the “hand knob”) based on anatomical landmarks in the contralateral (right) precentral gyrus [11] (Figure 1B). We then identified a single slice within the functional volume that exhibited a strong response to finger tapping in both the VASO and BOLD signals [6]. Next, we visually identified a region of the hand knob that showed a positive VASO response to finger tapping in the superficial layers and a separate positive response in the deep layers – i.e., a double-peak response profile across laminae (Figure 1C, right panel). Since we added the constraint that a particular pattern of response (i.e., the double-peak response profile) needed to be present in the functional ROI, we also used a more data-driven approach to confirm the location of the functional ROI. Specifically, we first created both a laminar mask and a columnar mask within the single slice of the hand knob (Figure 1C). To make the column mask, we manually delineated the CSF/Layer I and WM/Layer VI boundaries, and then drew boundaries at the medial and lateral ends of the hand knob in each participant. We then filled in that mask with 100 abutting columns that run orthogonal to the layers in the layer mask. We then created an orthogonal 2-dimensional coordinate space within the hand knob by combining the two masks. Next, we mapped the VASO response to the tapping condition onto this 2-dimensional coordinate space (the matrix in Figure 1D), and then ran a multiple linear regression that included an idealized double-peak response covariate and a single-peak response covariate to each column-wise vector of the matrix (Figure 1D). We then confirmed that the functionally defined tapping ROI approximately corresponded to the columns of the matrix in which the idealized double-peak response covariate explained more variance than the idealized single-peak covariate. Finally, we filled the tapping ROI in with twenty-one layers across the cortical depth to create a functionally defined hand ROI in each participant (Figure 1E). Crucially, we do not analyze the direct response to finger tapping in further analyses, since doing so would be a non-independent analysis.
We also defined a toe-selective ROI in primary motor cortex to serve as a control region of interest for the hand ROI and ensure that the toe wiggling condition was an appropriate control condition. Specifically, we functionally defined the toe-selective ROI as a region in the contralateral (right) paracentral lobule that responded more to toe wiggling than finger tapping during the experimental runs (Figure S3). We found a toe ROI in all eleven participants. Since, we were unable to measure layer-specific responses in the toe ROI due to its position relative to the angle of our field of view, we made an average hand ROI in each participant by averaging across the layers in the original hand ROI, so we could directly compare responses from the toe and hand ROIs. We then extracted both the BOLD and VASO responses to toe wiggling and finger tapping from the separate “blocked” run in six participants. We found a double dissociation between the ROIs in both the VASO and BOLD signals (Figure S3). Specifically, we found a significant interaction between the ROIs (VASO: F(1,5)=22.25, p=0.005, ηP2=0.82; BOLD: F(1,5)=12.27, p=0.02, ηP2=0.71), with a significantly greater response to the Tapping relative to Toe wiggling condition in the hand ROI (VASO: t(5)=3.71, p=0.01, Cohen’s d=1.51; BOLD: t(5)=3.29, p=0.02, Cohen’s d=1.34) and the opposite pattern of results in the toe ROI (VASO: t(5)=−3.47, p=0.02, Cohen’s d=1.41; BOLD: t(5)=−2.67, p=0.04, Cohen’s d=1.09). These independent data confirm that the hand ROI was indeed hand selective, and that the Toe wiggling condition was an appropriate motor control condition for our experiment (i.e., it evoked the expected response from a region of M1 that should be involved in toe movements).
Data and Code Availability
The data presented here are publicly available online at NIH Figshare 10.35092/yhjc.c.4808136. Processing and analysis code can be found at https://github.com/layerfMRI/LAYNII The authors are happy to share the 3D-VASO MR sequence upon request under the SIEMENS C2P agreement.
Supplementary Material
Key Resources Table
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Experimental Models: Organisms/Strains | ||
| healthy human volunteers | This manuscript | NIH Figshare identifier: 10.35092/yhjc.c.4808136 |
| Software and Algorithms | ||
| SIEMENS VB17A-UHF image reconstruction | SIEMENS Healthineers | IcePAT WIP 571 |
| Analysis of Functional NeuroImages (AFNI) v19.3.18 | NIMH | https://afni.nimh.nih.gov/ |
| Statistical Parametric Mapping (SPM) v12 | Wellcome Trust Centre for Neuroimaging, UCL | http://www.fil.ion.ucl.ac.uk/spm/ |
| Layer fMRI analysis software (LAYNII) | [6] |
https://github.com/layerfMRI/LAYNII And NIH Figshare identifier: 10.35092/yhjc.c.4808136 |
Highlights.
Finger tapping evokes responses in superficial and deep layers of M1
Imagined finger tapping evokes responses in superficial but not deep layers of M1
Imagined tapping suppresses response to finger tapping in superficial layers
Imagined tapping enhances response to finger tapping in deep layers
Acknowledgements
This work was supported by the NIMH Intramural Research Program (#ZIA-MH002588–29, clinical trials number NCT00001360). Laurentius Huber was also funded from the NWO VENI project 016.Veni.198.032. We thank B. Poser for the 3D-EPI readout that is used in the VASO sequence and Chung Kan for support operating the 7T scanner. We also thank Peter Bandettini for suggestions on experimental design.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declaration of interests
The authors declare no competing interests.
References
- 1.Guillot A, and Collet C (2008). Construction of the Motor Imagery Integrative Model in Sport: a review and theoretical investigation of motor imagery use. International Review of Sport and Exercise Psychology 1, 31–44. [Google Scholar]
- 2.Di Rienzo F, Debarnot U, Daligault S, Saruco E, Delpuech C, Doyon J, Collet C, and Guillot A (2016). Online and Offline Performance Gains Following Motor Imagery Practice: A Comprehensive Review of Behavioral and Neuroimaging Studies. Front Hum Neurosci 10, 315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hetu S, Gregoire M, Saimpont A, Coll MP, Eugene F, Michon PE, and Jackson PL (2013). The neural network of motor imagery: an ALE meta-analysis. Neurosci Biobehav Rev 37, 930–949. [DOI] [PubMed] [Google Scholar]
- 4.Turner R (2016). Uses, misuses, new uses and fundamental limitations of magnetic resonance imaging in cognitive science. Philos Trans R Soc Lond B Biol Sci 371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Huber L, Ivanov D, Handwerker DA, Marrett S, Guidi M, Uludag K, Bandettini PA, and Poser BA (2018). Techniques for blood volume fMRI with VASO: From low-resolution mapping towards sub-millimeter layer-dependent applications. Neuroimage 164, 131–143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Huber L, Handwerker DA, Jangraw DC, Chen G, Hall A, Stuber C, Gonzalez-Castillo J, Ivanov D, Marrett S, Guidi M, et al. (2017). High-Resolution CBV-fMRI Allows Mapping of Laminar Activity and Connectivity of Cortical Input and Output in Human M1. Neuron 96, 1253–1263 e1257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Aguirre GK (2007). Continuous carry-over designs for fMRI. Neuroimage 35, 1480–1494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Aguirre GK, Mattar MG, and Magis-Weinberg L (2011). de Bruijn cycles for neural decoding. Neuroimage 56, 1293–1300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mao T, Kusefoglu D, Hooks BM, Huber D, Petreanu L, and Svoboda K (2011). Long-range neuronal circuits underlying the interaction between sensory and motor cortex. Neuron 72, 111–123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Weiler N, Wood L, Yu J, Solla SA, and Shepherd GM (2008). Top-down laminar organization of the excitatory network in motor cortex. Nat Neurosci 11, 360–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yousry TA, Schmid UD, Alkadhi H, Schmidt D, Peraud A, Buettner A, and Winkler P (1997). Localization of the motor hand area to a knob on the precentral gyrus. A new landmark. Brain 120 (Pt 1), 141–157. [DOI] [PubMed] [Google Scholar]
- 12.Kriegeskorte N, Simmons WK, Bellgowan PS, and Baker CI (2009). Circular analysis in systems neuroscience: the dangers of double dipping. Nat Neurosci 12, 535–540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Vul E, Harris C, Winkielman P, and Pashler H (2009). Puzzlingly High Correlations in fMRI Studies of Emotion, Personality, and Social Cognition. Perspectives on Psychological Science 4, 274–290. [DOI] [PubMed] [Google Scholar]
- 14.Grill-Spector K, Henson R, and Martin A (2006). Repetition and the brain: neural models of stimulus-specific effects. Trends in Cognitive Sciences 10, 14–23. [DOI] [PubMed] [Google Scholar]
- 15.Westerberg JA, Cox MA, Dougherty K, and Maier A (2019). V1 microcircuit dynamics: altered signal propagation suggests intracortical origins for adaptation in response to visual repetition. J Neurophysiol 121, 1938–1952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gotts SJ, Chow CC, and Martin A (2012). Repetition Priming and Repetition Suppression: A Case for Enhanced Efficiency Through Neural Synchronization. Cogn Neurosci 3, 227–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gilbert JR, Gotts SJ, Carver FW, and Martin A (2010). Object repetition leads to local increases in the temporal coordination of neural responses. Front Hum Neurosci 4, 30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kaliukhovich DA, and Vogels R (2012). Stimulus repetition affects both strength and synchrony of macaque inferior temporal cortical activity. J Neurophysiol 107, 3509–3527. [DOI] [PubMed] [Google Scholar]
- 19.Hansen BJ, and Dragoi V (2011). Adaptation-induced synchronization in laminar cortical circuits. Proc Natl Acad Sci U S A 108, 10720–10725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Brunet NM, Bosman CA, Vinck M, Roberts M, Oostenveld R, Desimone R, De Weerd P, and Fries P (2014). Stimulus repetition modulates gamma-band synchronization in primate visual cortex. Proc Natl Acad Sci U S A 111, 3626–3631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Segaert K, Weber K, de Lange FP, Petersson KM, and Hagoort P (2013). The suppression of repetition enhancement: a review of fMRI studies. Neuropsychologia 51, 59–66. [DOI] [PubMed] [Google Scholar]
- 22.Finn ES, Huber L, Jangraw DC, Molfese PJ, and Bandettini PA (2019). Layer-dependent activity in human prefrontal cortex during working memory. Nat Neurosci 22, 1687–1695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Muckli L, De Martino F, Vizioli L, Petro LS, Smith FW, Ugurbil K, Goebel R, and Yacoub E (2015). Contextual Feedback to Superficial Layers of V1. Curr Biol 25, 2690–2695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Button KS, Ioannidis JP, Mokrysz C, Nosek BA, Flint J, Robinson ES, and Munafo MR (2013). Power failure: why small sample size undermines the reliability of neuroscience. Nat Rev Neurosci 14, 365–376. [DOI] [PubMed] [Google Scholar]
- 25.Turner DP, and Houle TT (2018). The Importance of Statistical Power Calculations. Headache 58, 1187–1191. [DOI] [PubMed] [Google Scholar]
- 26.Lu H, Golay X, Pekar JJ, and Van Zijl PC (2003). Functional magnetic resonance imaging based on changes in vascular space occupancy. Magn Reson Med 50, 263–274. [DOI] [PubMed] [Google Scholar]
- 27.Huber L, Ivanov D, Krieger SN, Streicher MN, Mildner T, Poser BA, Moller HE, and Turner R (2014). Slab-selective, BOLD-corrected VASO at 7 Tesla provides measures of cerebral blood volume reactivity with high signal-to-noise ratio. Magn Reson Med 72, 137–148. [DOI] [PubMed] [Google Scholar]
- 28.Fischl B, and Dale AM (2000). Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proc Natl Acad Sci U S A 97, 11050–11055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Poser BA, Koopmans PJ, Witzel T, Wald LL, and Barth M (2010). Three dimensional echo-planar imaging at 7 Tesla. Neuroimage 51, 261–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Haacke EM, Lindskogj ED, and Lin W (1991). A fast, iterative, partial-fourier technique capable of local phase recovery. Journal of Magnetic Resonance (1969) 92, 126–145. [Google Scholar]
- 31.Friston KJ, Holmes AP, Worsley KJ, Poline JP, Frith CD, and Frackowiak RSJ (1994). Statistical parametric maps in functional imaging: A general linear approach. Human Brain Mapping 2, 189–210. [Google Scholar]
- 32.Kashyap S, Ivanov D, Havlicek M, Poser BA, and Uludag K (2018). Impact of acquisition and analysis strategies on cortical depth-dependent fMRI. Neuroimage 168, 332–344. [DOI] [PubMed] [Google Scholar]
- 33.Renvall V, Witzel T, Wald LL, and Polimeni JR (2016). Automatic cortical surface reconstruction of high-resolution T1 echo planar imaging data. Neuroimage 134, 338–354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Cox RW (1996). AFNI: Software for Analysis and Visualization of Functional Magnetic Resonance Neuroimages. Computers and Biomedical Research 29, 162–173. [DOI] [PubMed] [Google Scholar]
- 35.Duvernoy HM, Delon S, and Vannson JL (1981). Cortical blood vessels of the human brain. Brain Research Bulletin 7, 519–579. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data presented here are publicly available online at NIH Figshare 10.35092/yhjc.c.4808136. Processing and analysis code can be found at https://github.com/layerfMRI/LAYNII The authors are happy to share the 3D-VASO MR sequence upon request under the SIEMENS C2P agreement.


