Abstract
Histone variants regulate replication, transcription, DNA damage repair, and chromosome segregation. Though widely accepted as a paradigm, it has not been rigorously demonstrated that histone variants encode unique mechanical properties. Here, we present a new theoretical approach called minimal cylinder analysis that uses strain fluctuations to determine the Young’s modulus of nucleosomes from all-atom molecular dynamics simulations. Recently, we validated this computational tool against in vitro single-molecule nanoindentation of histone variant nucleosomes. In this report, we further extend minimal cylinder analysis to study the biophysical properties of hybrid nucleosomes that are known to exist in human cancer cells and contain H3 histone variants CENP-A and H3.3. Here, we report that the heterotypic nucleosome has an intermediate elasticity (8.5 ± 0.5 MPa) compared to CENP-A (6.2 ± 0.4 MPa) and H3 (9.8 ± 0.7 MPa) and that the dynamics of both canonical and CENP-A nucleosomes are preserved and partitioned across the nucleosome pseudodyad. Furthermore, we investigate the mechanism by which the elasticity of these heterotypic nucleosomes augments cryptic binding surfaces. From these analyses, we predict that the heterotypic nucleosome is permissive to the binding of one copy of the kinetochore protein CENP-C while still retaining a closed DNA end configuration required for linker histone H1 to bind. We discuss that the ectopic deposition of CENP-A in cancer by H3.3 chaperones HIRA and DAXX may fortuitously result in hybrid nucleosome formation. Using these results, we propose biological outcomes that might arise when such heterotypic nucleosomes occupy large regions of the genome.
Significance
Nucleosomes are the base unit of eukaryotic genome organization. Histone variants create unique local chromatin structures that are thought to fine-tune transcription, replication, DNA damage repair, and faithful chromosome segregation. It is becoming evident that the mechanical response of chromatin, through material properties such as elasticity, regulates genetic function. We developed a theoretical method, validated by previous in vitro nanoindentation studies, called minimal cylinder analysis (MCA) to determine the Young’s modulus of nucleosomes from molecular dynamics simulations. Here, we apply MCA to oncogenic hybrid nucleosomes containing histone H3 variants from which we postulate biological predictions. MCA allows for inexpensive analysis of molecular dynamics simulations to discern how diverse, cylindrically shaped macromolecular systems respond to mechanical forces.
Introduction
The elastic properties of chromatin regulates genetic function in a manner distinct from classically understood properties such as key binding partners (1). Early evidence of the elastic behavior of chromatin comes from the classic micromanipulation experiments of grasshopper chromosomes (2). Several subsequent studies have shown that chromatin acts as an elastic medium and that its constituent linker DNA behaves as an entropically driven elastomer (3,4). Such studies on the physics of chromatin have led to new biological insight. For example, the pericentromere, a region flanking the site of microtubule attachment, can act as a mechanical spring, governing chromosome separation and spindle length during mitosis (5). Chromatin physics can help to address questions about chromatin ordering (6, 7, 8), how DNA is both stable and distortable (9,10), how glassy DNA dynamics give rise to cell-to-cell variability (11), and even how the mechanical microenvironment tunes genetic expression (12,13). Chromatin states are altered by posttranslational modifications (PTMs) (14) and by histone variant deposition at the macromolecular scale (9). Consequently, the additive effects of nanoscale modifications are an essential component of chromatin chemical signaling pathways and may alter chromatin’s mechanical behavior.
Previously, we carried out structural analysis of CENP-A dynamics in silico (15). In a subsequent recent study, we also investigated the material properties of CENP-A nucleosomes and binding partners, located primarily at centromeres, and H3 nucleosomes, found throughout the chromosome arms (16). More specifically, to gain new insights into the initial effects of kinetochore formation, we performed the first comprehensive in vitro nanoindentation study of nucleosomes, experimentally determining their Young’s moduli, and compared these measurements to our in silico predictions, carried out in parallel (16). This report presents our new algorithm, denoted minimal cylinder analysis (MCA), to perform elasticity measurements in silico and for the first time, outlines the theory and derivation for how to obtain Young’s modulus from stain fluctuations of nucleoprotein complexes.
Furthermore, in this work, we have applied MCA to investigate the material properties of hybrid nucleosomes simultaneously containing CENP-A and H3.3 histones. Such nucleosomes are found in human cancer cells and appear to be detrimental to chromosome integrity (17,18). In many aggressive forms of cancer, CENP-A, a centromeric histone H3 variant, is overexpressed (18, 19, 20). Studies have demonstrated that either in cancer cells derived from patient tumors or when artificially overexpressed, excess CENP-A is deposited outside the centromere and stably retained there in the form of unexpectedly stable (17) hybrid nucleosomes containing CENP-A and H3.3 (18,20,21). This complex has been technically challenging to study experimentally because of its low abundance in vivo, therefore motivating us to rely on MCA to explore the material properties and biological impacts of hybrid CENP-A:H3.3 nucleosomes in cancer cells.
Elasticity, as defined by Hooke’s law, is the ability of a material to return to its initial state after deformation by an applied force. The reversibility of this process implies that mechanical energy is stored as elastic strain energy during deformation and is conserved during recoil (22). Additionally, the proportion of stress/strain in the linear regime is described by Young’s modulus. Although Young’s modulus is a salient mechanical property of a material, it is applicable for small deformations and hence may not be sufficient to predict all biologically germane deformation processes. The function of elastic materials also depends on extensibility and the amount of work required to fracture the material, which is referred to as toughness (22). For example, exceptionally tough biological materials exist such as viscid spider silk, which is far more elastic (0.002 GPa) than Kevlar (130 GPa) and yet is remarkably tougher than Kevlar (150 vs. 50 MJ m−3, respectively (22)).
There exist several computational approaches to model the elastic properties of macromolecules. One such method is finite element analysis (FEA), in which a mesh network describes the structure, and energy is minimized in response to deformation (23,24). However, the accuracy of this method requires system-specific parameterization to account for atomic interactions such as Coulombic forces. FEA at the nanoscale has produced results consistent with molecular dynamics (MD) when informed by atomistic simulation (25), but FEA lacks the built-in portability and resolution of MD. To achieve all-atom resolution, force-probe MD simulations have been implemented (26,27). However, large systems such as macromolecular complexes are computationally costly, and unphysical force-loading rates are typically required because of the short simulation time. Lastly, coarse-grained MD force fields have also been developed that are, excitedly, able to study the nonelastic deformation and fracture of macromolecules to simulate nanoindentation (28). The longer timescales achieved by coarse-grained methods are promising, but they lack the resolution of all-atom models and may not resolve differences because of PTMs or variants. In the methodology we present here, we analyze all-atom resolution simulations of nucleosomes at extended timescales and then use surface fluctuations to derive the modulus of elasticity in the absence of applied forces. The strength of our methodology is that it does not require expensive computational resources beyond equilibrated simulations.
The elastic modulus is derived by connecting equilibrium strain fluctuations with stress response (29). We employ this logic to obtain the elasticity of nucleosomes without applying an external force. Furthermore, we have introduced a simple temporal hierarchy when implementing our algorithm: first, the equilibrium trajectory is averaged over short timescale windows, and the resulting structures snuggly fit into encompassing cylindrical bounding domains. Afterward, the sequence of fluctuating cylinders is analyzed using solid mechanics while also estimating the energy of the corresponding low-frequency vibrational mode from the equipartition theorem. Overall, our algorithm produces the absolute values of nucleosomes’ Young’s moduli without freely adjustable parameters that are tuned to fit any specific experiment.
Materials and Methods
The goal of our analysis method is to calculate the Young’s modulus of nucleosomes in the absence of applied forces. Essentially, this technique connects structural fluctuations observed in unbiased MD simulations, with the nucleosome’s mechanical response. To analyze all-atom simulation data in such a way, we first treat the nucleosomes as mechanically homogenous elastic cylinders vibrating in a thermal bath. Next, we calculate the dimensions and fluctuations of what we term “minimal” cylinders over the ensemble of each trajectory. We define the cylinder dimensions as the minimum volume that contains the rigid exterior surfaces of the nucleosome.
To develop a simplified model for elasticity calculations, we make assumptions based on the known physical properties of nucleosomes. First, we apply an averaging technique to the all-atom simulation data using continuum mechanics. Elastic continuum theory has been shown to predict material properties on the nanoscale when compared to experiments and analytical predictions (30,31). We further reduce degrees of freedom and variability by utilizing the pseudosymmetry and geometry of nucleosomes to treat them as homogenous circular cylinders. Next, we make simplifications on the mode of deformation studied. To compare to single-molecule nanoindentation, we assume that nucleosomes are compressed perpendicular to the axis of the cylinder. Therefore, we model nucleosome fluctuations as compression and expansion in the absence of shearing motions and attribute to this mode an equipartition of energy.
The workflow we used to determine the Young’s modulus of nucleosomes from atomistic trajectories is as follows:
-
1)
Define the all-atom nucleosome coordinate system.
-
2)
Probe for rigid external cylinder bases and lateral surfaces.
-
3)
Retrieve average cylinder dimensions and variances.
The output of these steps is then used to calculate the Young’s modulus. Next, we will describe in detail each of these steps.
Define the all-atom nucleosome coordinate system
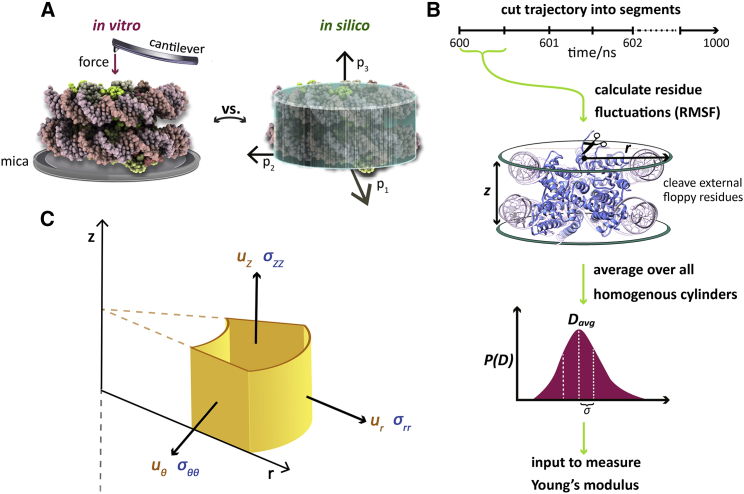
Analogous to the requirement of consistent orientation of nucleosomes in nanoindentation studies, we must first choose a standard nucleosome orientation. The question asked is this: if nucleosomes were to lie “flat” on a surface, what would this orientation be? The chosen alignment influences the cylinder dimensions that will be measured. Because we constrain our analysis to right circular cylinders, if the nucleosomes are tilted, the measured dimensions will be altered. Before analysis, we removed the nucleosome’s rotational and translational motions from our trajectories and moved the center of mass of residues analyzed in MCA to the origin. To define our coordinate system, we computed the principal axes of rotation and oriented the cylinder base to the plane of the first two principal axes (Fig. 1 A; Supporting Materials and Methods). The nucleosome core particles (NCPs), which we analyzed with MCA, were built as described in All-Atom Computational Modeling without flexible histone tails. After simulation, during MCA, we did not include in the data set the first and last 10 DNA basepairs from simulation so that the NCP fits more snugly into a cylinder. The coordinates of the protein C-α and nucleic phosphorus atoms were used to calculate the nucleosome dimensions, elaborated next.
Figure 1.
(A) Schematic that compares in vitro atomic force microscopy (AFM) single-molecule nanoindentation, left, to our in silico modeling and analysis, right. In AFM, the normal force from the cantilever to the mica surface is measured. For our computational analysis, nucleosomes were oriented by the principal axes of the moment of inertia and then modeled as homogenous elastic cylinders. (B) The workflow for calculating Young’s modulus in silico is shown. The protein C-α and nucleic phosphorus atom RMSFs are calculated for each segment of the simulation to obtain an ensemble of cylinders. The average dimensions, Davg, of the radius and height (r, z) and the standard deviation, σ, are then input to calculate Young’s modulus. (C) This is a diagram that shows the orientation of cylinders in relation to the variables introduced in Eqs. 2 and 4. Displacements (ur, uθ, uz) are shown in yellow. Stresses in the i-th direction from the forces applied in the j-th direction, σij, are shown in blue.
Probe for rigid external cylinder bases and lateral surfaces
Because we are measuring elasticity without an applied force, we consider the following thought experiment: if one were to hypothetically push down on the nucleosome surface, at what point would compression become more significantly hindered? Such determination would, in turn, suggest the coordinates of the rigid surface of the nucleosome. For example, an intrinsically disordered region or loop is configurationally highly distortable compared with regions comprised of α-helices of β-strands. The elastic moduli of the former structures, which are largely entropic in origin, are expected to be orders of magnitude smaller compared with the latter and hence are neglected in our subsequent analysis. Thus, we need a specific metric for local stiffness. The rigidity of residues can be quantified by the root mean-square fluctuations (RMSFs) of each residue throughout the simulation. High RMSF values correspond to increased fluctuation or decreased stiffness. Because RMSF is a time-averaged parameter, multiple time steps are required to calculate fluctuations of residues. Therefore, we divide the 1-μs simulation (from 0.6 to 1 μs) into a number of temporal segments and output each atom’s RMSF per segment.
There are two input parameters in MCA: the “averaging window length” (AWL), which defines the length of the temporal segments, and the “flexible exterior residue number” (FERN), which defines how many residues over an RMSF value; the “residue flexibility cutoffs” (RFCs) are excluded from the cylinder volume. We probed for how sensitive MCA is to AWL (Fig. S2 A) and FERN (Fig. S3, A and B) and explain our parameter choices to analyze NCPs (Supporting Material). MCA calculates the RFC value, which demarcates rigid and flexible residues and is dependent on AWL (Fig. S2 B). Additionally, we plot how the RFC value compares to the atom RMSFs (Fig. S2 C).
Retrieve average cylinder dimensions and variances
We first sort the C-α and phosphorus atoms by their z axis coordinates and select the z coordinate of the residue such that the number of residues specified by FERN are minimally excluded outside the cylinder bounds from the top and, subsequently, the bottom surface. For our analysis of NCPs, we rationally selected a FERN value of 10 residues (Fig. S3). Maximal separation among the remaining coordinates determines the cylinder height, z. We repeat this process for the radial coordinate to calculate the radius, r, of the cylinder per temporal segment. The collection of (r, z) tuples, which are treated as stochastic variables, are histogrammed as illustrated in Fig. 1 B for an example trajectory. From this stochastic realization for a given simulation, we compute the average of the distributions zavg and ravg and the standard deviations Δr and Δz. These data are then used in our derivation for the Young’s modulus as described below. We have made our MCA code for calculating the Young’s modulus available for academic use (32).
All-atom computational modeling
The software suite GROMACS version 5.0.4 (33) was used to perform all-atom MD simulations. The force fields used were amber99SB∗-ILDN (34,35) for proteins, amber99SB parmbsc0 (36) for DNA, ions08 (37) for ions, and the TIP3P water model. Two nucleosome systems were built for simulation and compared to our prior simulations of H3 as a control (15). First, the heterotypic CENP-A:H3.3 nucleosome was built from the crystallographic structure Protein Data Bank, PDB: 3WTP (17). Subsequently, the CENP-A nucleosome was built with PDB: 3AN2 (38). The unresolved residues CENP-A′ 79–83 from the crystal structure 3AN2 were inserted using MODELLER (39). Histone tails were not added to the experimentally solved structures. For energy minimization of the inserted residues, the N- and C-terminus were unconstrained. The 146-basepair α-satellite DNA PDB: 3WTP (17) was aligned to all systems as a control, using the combinatorial extension algorithm (40) of PyMOL (41).
We used Gromacs tool pdb2gmx to assign residue charges at a biological pH around 7 (42): a charge of +1 on Lys (side chain pKa = 10.67) and Arg (side chain pKa = 12.10), 0 for Gln, −1 for Asp (side chain pKa = 3.71) and Glu (side chain pKa = 4.15), and His with hydrogen on the ε nitrogen (side chain pKa 6.04) (43). The boundaries of the simulation were set to a cuboid box with a minimum distance of 1.5 nm from the nucleosome with periodic boundary conditions. Counterions of Na+ and Cl− were introduced to neutralize the system and to model an ionic physiological concentration of 150 mM NaCl. The particle mesh Ewald method was used for electrostatics with the Verlet cutoff scheme. Coulombic and van der Waals potentials were used for nonbonded interactions with a cutoff distance at 1.0 nm. The LINCS algorithm was used to constrain hydrogen bonds.
Energy minimization was performed using the steepest descent to a maximum energy of 100 kJ/mol. After this, equilibration of the structure was carried out. The systems were heated to 300 K for 2000 ps with a DNA position restraint of K = 1000 kJ mol−1 nm−2 in the canonical ensemble. Next, thermal equilibration was performed for both DNA and protein at 300 K for 2000 ps with weak position restraints defined as Khet = 2.1e−5 kJ mol−1 nm−2 assigned to the heterotypic nucleosome and Kcpa = 2.5e−5 kJ mol−1 nm−2 for the CENP-A nucleosome. These weak position constraints vary based on atom number in each simulation and restrain nucleosome rotations. Finally, the pressure was equilibrated for 1500 ps in the isothermal-isobaric ensemble at 300 K, 1.0 bar pressure, and weak position constraint (Fig. S1 A).
Each production simulation was run for 1 μs at 300 K. Simulation temperature was V-rescaled using the modified Berendsen thermostat (44) with time constant 1.0 ps. The Parrinello-Rahman barostat (45) was used for pressure regulation at 1.0 bar and a time constant of 2.0 ps. To investigate the possibility of barostat pressure regulation resonating with the thermal fluctuations of the nucleosomal dimensions, we calculated the natural frequency of our system (46,47), treating the nucleosome as a homogeneous elastic cylinder, and found two orders of magnitude difference between the faster barostat coordinate-rescaling frequency and the slower axisymmetric, acoustic deformation mode frequency considered in MCA.
A simulation time step of 2 fs was used, and coordinates, velocities, and energies were saved every 2 ps. The nonbonded neighbor lists were updated at intervals of 20 fs. To analyze equilibrated sections of the production runs, the first 600 ns were not included in the analysis. We checked for convergence of the production runs of the heterotypic nucleosome by tracking the change in root mean-square deviation from the initial production run configuration (Fig. S1 B). Published equilibrium analyses of trajectories CENP-A and CENP-A bound to CENP-C are available in Fig. S9 of (16). Equilibration analysis of the control system, H3, is available in Fig. S2 of (15). Detailed methods on all-atom structural analysis are provided in the Supporting Materials and Methods.
Results
Outline of the derivation of Young’s modulus from MCA
We will present here the main highlights from the derivation for Young’s modulus from MCA. For those interested, a full, extended derivation is also included (Supporting Materials and Methods). The work done in the deformation of an elastic material is stored in the form of strain energy, U. The strain energy density, u, the energy stored in small volume elements, can be useful to describe variable strains along a body that sum to the total strain energy:
| (1) |
Because the extent of cylinder fluctuations is relatively small, around the range of 0.5–1.5 percent of the average radial or lateral dimension, we rely on linear elasticity and the small-deformations’ theory. Under these conditions, the strain energy density in cylindrical coordinates can be calculated for low magnitude stresses from arbitrary directions (48) as
| (2) |
where σij is the stress in the i-th direction from the force applied in the j-th direction, and εij is the strain in the i-j plane (Fig. 1 C). Further explanation for the form of Eq. 2 in cylindrical coordinates is provided in Supporting Materials and Methods, Section S4, in which, briefly, we apply the cyclic property of trace on the second-order symmetric tensors, stress, and strain, to arrive at Eq. 2 (Supporting Materials and Methods). In the absence of shear stresses and using Hooke’s law, the strain energy density in Eq. 2 can also be written in the form
| (3) |
where μ is the shear modulus and is related to Young’s modulus E by μ = E/2 (1 + ν), and ν is the Poisson ratio (48). We used a value 0.4 used in prior nanoindentation simulations of macromolecules (49). For displacements (ur, uθ, uz) in cylindrical coordinates (r, θ, z) as shown in Fig. 1 C (50),
| (4) |
In the special case of a homogeneous axisymmetric cylinder where the center of mass is at the origin (Fig. 1 C), = 0, and at the walls of the cylinder, (6), which is from MCA. Therefore, in this specific case, εrr = εθθ in Eq. 4. More detail on how we arrive at these conclusions is provided (Supporting Materials and Methods).
To calculate the strain energy density in Eq. 3, we input the dependence of the shear modulus on E and relations found from Eq. 4 to obtain
| (5) |
Strain values in Eq. 5 are calculated from the measured quantities ravg, zavg, Δr, and Δz from MCA (Retrieve Average Cylinder Dimensions and Variances). We next focus on the acoustic cylindrical mode of motion that describes compression in the z axis along with radial extension (and vice versa). Because we are studying only small deformations or harmonic modes, we estimate the average potential energy from the equipartition theorem , where kb is the Boltzmann constant and T is the simulation temperature 300 K. We then integrate Eq. 5 over the body volume, Eq. 1, and with the abovementioned energy from the equipartition theorem, we solve for Young’s modulus:
| (6) |
This final form for the derivation of Young’s modulus, shown in Eq. 6, is one of the main findings of this work.
Experimental validation of MCA model
For our analyses from our previous work (16), we used the Hertz model with spherical indenter geometry for Young’s modulus measurements (51). The Hertz model assumes that the substrate is an isotropic, elastic solid and is valid for small indentations and low forces in the linear regime. To check for elastic dependence on the point probed, we experimentally measured the Young’s modulus across mononucleosomes and found that the effective elasticity is surprisingly homogenous across the surface (16). This finding is consistent with the model of MCA, which treats nucleosomes as homogenous elastic solids.
Experimental validation for in silico Young’s modulus calculations
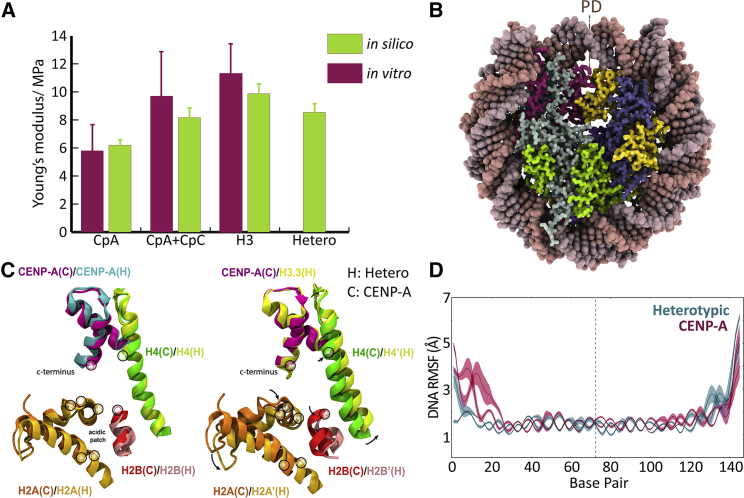
In our study of the mechanical properties of nucleosome variants on the chromatin fiber, we applied our in silico methodology to measure the Young’s modulus of nucleosomes (16). We measured the elasticity of three systems: 1) the canonical nucleosome, H3; 2) the centromeric variant of H3, CENP-A; and 3) CENP-A nucleosomes bound to CENP-C. We also measured the elasticity of these substrates in vitro using single-molecule nanoindentation force spectroscopy. Our in silico algorithm to determine Young’s modulus quantitatively agrees with in vitro nanoindentation measurements (Fig. 2 A). Thus, experimental nanoindentation studies provide a validation for our model and suggest that the various assumptions made in MCA are acceptable simplifications.
Figure 2.
(A) Young’s modulus of CENP-A nucleosomes, CpA; CENP-A bound to CENP-C, CpA + CpC; the canonical nucleosome, H3; and the CENP-A:H3.3-containing heterotypic nucleosome, hetero. AFM measurements in vitro are shown in magenta with Young’s moduli of CpA = 5.8 ± 3.0 MPa, CpA+CpC = 9.4 ± 5.8 MPa, and H3 = 11.3 ± 4.1 MPa. In silico measurements are shown in green with Young’s moduli of CpA = 6.2 ± 0.4 MPa, CpA+CpC = 8.2 ± 0.9 MPa, H3 = 9.8 ± 0.7 MPa, and Hetero = 8.5 ± 0.5 MPa. Experimental values are referenced from our companion work (16). (B) The structure of the heterotypic nucleosome is shown. Histones CENP-A are shown in magenta, H3.3 in yellow, H4 in dark slate blue, H2A in light gray, and H2B in green. (C) The overlay of the CENP-C binding sites by the minimum root mean-square deviation obtained from the representative structure of the first principal component (PC1) (Video S1) is shown. Histones labeled with a “C” are from the CENP-A nucleosome, and histones labeled with “H” are from the heterotypic nucleosome. Black circles indicate CENP-C-binding residues. (D) The RMSFs of DNA residues of the CENP-A nucleosome are in magenta, and the heterotypic nucleosome are in blue.
Young’s modulus of the hybrid CENP-A:H3.3 versus the CENP-A nucleosome
After validating MCA against in vitro single-molecule force studies previously (16), we applied this method to study the elastic properties of a heterotypic cancer-specific nucleosome. This unique variant nucleosome has one copy of CENP-A and one copy of H3.3 and is enriched at CENP-A ectopic sites in chromatin (20), some of which are well-documented fragile sites in the chromatin fiber (18). The heterotypic nucleosome was found to be surprisingly stable, regardless of the unique docking interface formed between two divergent H3 variants (17). What, then, causes the measured stability?
To explore this question, we computationally assessed the elastic properties of the heterotypic nucleosome. We discovered an intermediate Young’s modulus of hybrid CENP-A:H3.3 nucleosomes (8.5 ± 0.5 MPa) compared to CENP-A nucleosomes (6.2 ± 0.4 MPa) and canonical H3 nucleosomes (9.8 ± 0.7 MPa, Fig. 2 A). Values for nucleosome dimensions and standard deviations are provided for a trial from this data set (Table S1). This result contradicts the idea that unfavorable contacts may form between the CENP-A:H3.3 heterodimer and disrupt the stability of the hybrid nucleosome. Because our methodology uses an averaging technique over the structure of the nucleosome, we next asked how the dynamics of the heterotypic nucleosome gives rise to its intermediate elasticity. Two hypotheses were considered: first, the heterotypic nucleosome presents an averaged global shift in nucleosome dynamics; or secondly, there may be sequestered regions within the heterotypic nucleosome that display canonical or centromeric nucleosome dynamics.
The rigidified heterotypic nucleosome is permissive to CENP-C binding
The essential docking protein to initiate kinetochore formation is CENP-C, which binds to the surface of CENP-A (52). The structure of the CENP-C-binding domain on the surface of the CENP-A nucleosome can be found at Fig. S4 A. It is still unknown whether the heterotypic CENP-A:H3.3 nucleosome is implicated in the formation of neocentromeres. Consistent with reduced flexibility compared to CENP-A (Fig. 2 A), we found a more tightly bound four-helix bundle interface between H3.3 and CENP-A in the heterotypic nucleosome (Fig. S5 A). CENP-C docks by interaction with the C-terminal tail of CENP-A in this region and binds across the nucleosome surface with the basic residues of H2A (residues 60, 63, 89–91 in Drosophila melanogaster) and H2B (53).
Therefore, we analyzed the CENP-C-binding platform to see if the heterotypic nucleosome is permissive to CENP-C. To do so, we performed principal component analysis and animated the first major mode of motion, the first principal component (PC1). Visualization of PC1 revealed that the CENP-A-containing tetramer of the heterotypic nucleosome rocks apart less than the H3.3 tetramer and is more compact, similar to the CENP-A nucleosome (Video S1). Indeed, the heterotypic nucleosome contains asymmetric and partitioned dynamics in which features of CENP-A nucleosome behavior are maintained. In PC1, we see that the CENP-C-binding site from the CENP-A nucleosome is preserved in the heterotypic nucleosome (Fig. 2 C, left). The acidic patch and C-terminal CENP-A domain provide the scaffold for CENP-C binding (17). On the H3.3 face of the heterotypic nucleosome, the acidic patch, shown as H2A′(H) in light orange, is extended away from the C-terminus of H3.3 (Figs. 2 C and S5 B). This analysis shows that the correct coordination of binding residues for CENP-C is maintained in the CENP-A-facing side of the heterotypic nucleosome, making it permissive to the double-arginine anchor mechanism of both of the CENP-C central domains R522 and R525 (53), previously observed in vitro (17), and to the CENP-C motif R717, R719 (40), which we modeled in silico in our prior work (14). We further discuss the dynamics of the heterotypic nucleosome and the high exposure of the CENP-N-binding site, the CENP-A RG (Arg80/Gly81) loop (Supporting Materials and Methods).
DNA dynamics of histone variants is partitioned by the heterotypic nucleosome pseudodyad
Intriguingly, linker histones (LHs) are excluded from centromere-specific CENP-A nucleosomes, principally because of a clash with entry and exit dynamics of DNA (54,55). Thus, a fundamental question is whether CENP-A:H3.3 hybrid nucleosomes are able to bind LHs to form a chromatosome unit similar to the canonical nucleosome (56,57). The LH globular domain docks to the entry-exit sight of canonical nucleosomes (58), illustrated at Fig. S4 B. The LH disordered tails bind to linker DNA, holding DNA ends together (55). A distinctive difference between H3 nucleosomes and CENP-A nucleosomes is the markedly lower affinity of the latter for LHs (54).
It was experimentally demonstrated that the αN helix in canonical histones binds DNA and restricts DNA end motions, creating a more-closed DNA end configuration. In contrast, in CENP-A, the αN helix is shorter and experimentally resulted in more open DNA ends and a lack of H1 binding (54). Furthermore, experimentally, it was found that unstable entry and exit DNA strands inhibit LH binding (54). A picture of the solved chromatosome structure of the canonical nucleosome bound to the LH globular domain, with the αN helix indicated, is provided for structural reference (Fig. S4 B; (59)). We asked how the intermediate rigidity of the heterotypic nucleosome (Fig. 2 A) affects DNA dynamics.
First, we calculated the RMSF of DNA over three segments of our analyzed trajectories. We found that the presence of both CENP-A and H3.3 results in a symmetry breaking in DNA dynamics across the pseudodyad (Fig. 2 D). We observed increased DNA motion in the heterotypic nucleosome proximal to the CENP-A histone in contrast to the H3.3 histone. This region is of interest because the globular domain of H1 binds to the DNA minor groove on-dyad (60).
Furthermore, the asymmetry in DNA dynamics propagates to the DNA entry-exit ends. In the heterotypic nucleosome, we found increased DNA end fluctuations on the end proximal to CENP-A and decreased fluctuations proximal to H3.3 (Fig. 2 D). The disordered tails of H1 rely on the presence of DNA crossing at the entry and exit ends for nucleosome affinity and to compact the fiber (60,61). Therefore, we next measured the DNA end-to-end distance in comparison to CENP-A nucleosomes. We found that the DNA ends of the heterotypic are closer together, with a probability similar to that of canonical nucleosomes (Fig. S5 D). More open configurations were the least likely to occur by the heterotypic nucleosome Fig. S5 D). The increased likelihood of close DNA end configurations suggests that heterotypic nucleosomes may bind LHs.
The principal, and somewhat unexpected, finding from these simulation analyses is that neither the H3.3 or CENP-A histone dominates the hybrid particle’s properties. Indeed, the heterotypic nucleosome displays the dynamics of both canonical and centromeric nucleosomes, resulting in an overall intermediate elasticity. Our findings show that the presence of one H3.3 histone variant induces increased rigidity, whereas the CENP-A histone intrinsically induces a more elastic phenotype. These results provide further structural analysis for experimental findings that reported on the surprising thermal stability of the CENP-A:H3.3-containing nucleosome (17).
Discussion
When CENP-A is overexpressed in human cancer cells (18,62,63), CENP-A appears to take advantage of H3.3 chaperones such as HIRA and DAXX (19,20). The role of H3.3 chaperones in CENP-A deposition away from the centromere provides a logical pathway for the formation of hybrid CENP-A:H3.3 nucleosomes because dimer H3.3/H4 and CENP-A/H4 pairs may fortuitously coassemble into tetramers on the DNA at regions of high turnover (64, 65, 66). Indeed, H3.3 chaperones are implicated in the ectopic formation of heterotypic nucleosomes in cells with increased survivability in the presence of DNA damage (20) and with increased DNase I sensitivity (18,19).
The formation and retention of heterotypic nucleosomes on the chromatin fiber could be further augmented by our findings here that the CENP-A:H3.3 hybrid is more rigid (8.5 ± 0.5 MPa) than CENP-A alone (6.2 ± 0.4 MPa) (Fig. 2 A). It is important to note that elasticity in the linear regime cannot be extrapolated to either fracture or thermodynamic stability. However, it has been shown that CENP-A nucleosomes are less thermodynamically stable and disassemble more easily than H3 in vitro by NAP-1 or heparin destabilization (61) and by magnetic tweezers (67). Intriguingly, the cause for H3 stability was shown to be a more-closed DNA end configuration (61). We found that the heterotypic nucleosome had the highest likelihood of being in a closed DNA end configuration (Fig. S5 D). Indeed, the heterotypic nucleosome was measured to have higher thermal stability than CENP-A nucleosomes (17). The heterotypic nucleosome may then be a safe harbor for ectopically located CENP-A histones to be less easily evicted. In other words, the structural features of these hybrid particles might be part of the reason why they persist ectopically, whereas nonhybrid CENP-A nucleosomes may be more readily removed by transcription or remodeling, were they to stochastically accumulate ectopically in normal conditions (68).
Even more fascinating to consider is the dynamics of the heterotypic nucleosome, which is predicted to alter the accessibility of cryptic binding sites, resulting in downstream biological effects. For example, our findings suggest that heterotypic nucleosomes are competent to bind CENP-C, the structural scaffold for inner kinetochore assembly (69), while still retaining the ability to bind LH H1. The CENP-A:H3.3-containing nucleosome binds the CENP-C central region in vitro (17) and ectopic mislocalization of CENP-A results in neocentomeres (18,19,21,63,70). However, the biological impact of these phenomena depends on the subsequent recruitment of proteins for microtubule attachment and whether H1 could interfere with the binding affinities or steric space normally available to kinetochore proteins. At minimum, bound LHs or inner kinetochore proteins may further rigidify the heterotypic nucleosome and facilitate CENP-A retention ectopically.
Conclusions
The elasticity of nucleosomes has biological relevance because of the mechanical sensing of large macromolecules and histone variant-specific assemblies such as in the case of CENP-A, CENP-C, and the entire inner kinetochore complex. In the absence of irreversible distortions to the structure, in which binding partners or nanomachines exert forces in the elastic range, our newly developed method, MCA, can be applied to measure Young’s moduli of various nucleosome complexes that are of low abundance in cells of specific lineages.
Our quantitative elasticity measurements of nucleosomes are likely to also be tunable in varied contexts of biological systems. One process that could alter the elasticity of the nucleosome variants measured here is the presence of binding partners such as proteins, DNA, or RNA. The charge environment, considering the plethora of PTMs of nucleosomes (71), is also likely to affect the in vivo elasticity of nucleosomes and may differ noticeably from the Young’s moduli calculated here. Interestingly, nucleosomes are highly responsive to charge perturbations, and slight changes in the histone core charge from physiological values thermodynamically destabilize the nucleosome and can cause DNA unwrapping (72). In contrast to these thermodynamic studies, it is still unknown to what extent individual or combinations of site-specific charge modifications alter the elasticity of nucleosomes. Our specific quantitative elasticity measurements are, therefore, dependent on the environment and state of the nucleosome variant.
The specific structural features of nucleosomes or macromolecules are highly controlled in silico. When performing elastic studies in vitro, additional sources of potential error arise from structural inhomogeneity and orientation and must be rigorously controlled (16). To make testable predictions in vivo, it is then important to consider the specific state of the macromolecule of interest because of the increased complexity, inhomogeneity, and cell-cycle-dependent ensembles of structural states.
A significant benefit of MCA is that it can be applied to equilibrium trajectories, enabling a computationally efficient way to analyze new or existing time-continuous simulations. This has the advantage of providing a means to obtain elastic measurements without doing a series of stretching studies on large systems for which single all-atom trajectories are already costly. However, we would like to note that sufficiently long simulations, such as the microsecond simulations presented here, are required to produce a sufficient number of decorrelated segments needed to achieve convergence. In future research, MCA could be extended to different geometries and varied modes of deformation or augmented to calculate other mechanical properties.
Author Contributions
Conceptualization of MCA, M.P. and G.A.P.; conceptualization of the oncogenic project, Y.D. and G.A.P.; derivation, M.P.; methodology and code, M.P.; investigation, M.P.; writing, M.P., G.A.P., and Y.D.; funding acquisition, G.A.P. and Y.D.; visualization, M.P.; and supervision, G.A.P. and Y.D.
Acknowledgments
We thank our reviewers for their valuable contributions to improve our manuscript and method. We also thank Carlos S. Floyd for independent validation of the MCA code and Daniël P. Melters and Aravind Chandrasekaran for feedback. Furthermore, we thank David Winogradoff for simulation work of H3 nucleosomes.
This work was supported by the Intramural Research Program of the National Institutes of Health (to Y.D. and M.P.). G.A.P. is supported by the National Science Foundation grant CHE-1800418 and the Amazon Web Services Artificial Intelligence Award.
Editor: Tamar Schlick.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2020.01.042.
Contributor Information
Yamini Dalal, Email: dalaly@mail.nih.gov.
Garegin A. Papoian, Email: gpapoian@umd.edu.
Supporting Citations
References (73, 74, 75) appear in the Supporting Material.
Supporting Material
References
- 1.Marko J.F. Micromechanical studies of mitotic chromosomes. Chromosome Res. 2008;16:469–497. doi: 10.1007/s10577-008-1233-7. [DOI] [PubMed] [Google Scholar]
- 2.Nicklas R.B. A quantitative study of chromosomal elasticity and its influence on chromosome movement. Chromosoma. 1963;14:276–295. doi: 10.1007/BF00326816. [DOI] [PubMed] [Google Scholar]
- 3.de Vries A.H.B., Krenn B.E., Kanger J.S. Direct observation of nanomechanical properties of chromatin in living cells. Nano Lett. 2007;7:1424–1427. doi: 10.1021/nl070603+. [DOI] [PubMed] [Google Scholar]
- 4.Claudet C., Angelov D., Bednar J. Histone octamer instability under single molecule experiment conditions. J. Biol. Chem. 2005;280:19958–19965. doi: 10.1074/jbc.M500121200. [DOI] [PubMed] [Google Scholar]
- 5.Bouck D.C., Bloom K. Pericentric chromatin is an elastic component of the mitotic spindle. Curr. Biol. 2007;17:741–748. doi: 10.1016/j.cub.2007.03.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Di Pierro M., Cheng R.R., Onuchic J.N. De novo prediction of human chromosome structures: epigenetic marking patterns encode genome architecture. Proc. Natl. Acad. Sci. USA. 2017;114:12126–12131. doi: 10.1073/pnas.1714980114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Di Pierro M., Potoyan D.A., Onuchic J.N. Anomalous diffusion, spatial coherence, and viscoelasticity from the energy landscape of human chromosomes. Proc. Natl. Acad. Sci. USA. 2018;115:7753–7758. doi: 10.1073/pnas.1806297115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Collepardo-Guevara R., Schlick T. Insights into chromatin fibre structure by in vitro and in silico single-molecule stretching experiments. Biochem. Soc. Trans. 2013;41:494–500. doi: 10.1042/BST20120349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fenley A.T., Anandakrishnan R., Onufriev A.V. Modulation of nucleosomal DNA accessibility via charge-altering post-translational modifications in histone core. Epigenetics Chromatin. 2018;11:11. doi: 10.1186/s13072-018-0181-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Beard D.A., Schlick T. Computational modeling predicts the structure and dynamics of chromatin fiber. Structure. 2001;9:105–114. doi: 10.1016/s0969-2126(01)00572-x. [DOI] [PubMed] [Google Scholar]
- 11.Shi G., Liu L., Thirumalai D. Interphase human chromosome exhibits out of equilibrium glassy dynamics. Nat. Commun. 2018;9:3161. doi: 10.1038/s41467-018-05606-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Tajik A., Zhang Y., Wang N. Transcription upregulation via force-induced direct stretching of chromatin. Nat. Mater. 2016;15:1287–1296. doi: 10.1038/nmat4729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Levens D., Baranello L., Kouzine F. Controlling gene expression by DNA mechanics: emerging insights and challenges. Biophys. Rev. 2016;8(Suppl 1):23–32. doi: 10.1007/s12551-016-0243-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bui M., Pitman M., Dalal Y. Internal modifications in the CENP-A nucleosome modulate centromeric dynamics. Epigenetics Chromatin. 2017;10:17. doi: 10.1186/s13072-017-0124-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Winogradoff D., Zhao H., Papoian G.A. Shearing of the CENP-A dimerization interface mediates plasticity in the octameric centromeric nucleosome. Sci. Rep. 2015;5:17038. doi: 10.1038/srep17038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Melters D.P., Pitman M., Dalal Y. Intrinsic elasticity of nucleosomes is encoded by histone variants and calibrated by their binding partners. Proc. Natl. Acad. Sci. USA. 2019;116:24066–24074. doi: 10.1073/pnas.1911880116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Arimura Y., Shirayama K., Kurumizaka H. Crystal structure and stable property of the cancer-associated heterotypic nucleosome containing CENP-A and H3.3. Sci. Rep. 2014;4:7115. doi: 10.1038/srep07115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Athwal R.K., Walkiewicz M.P., Dalal Y. CENP-A nucleosomes localize to transcription factor hotspots and subtelomeric sites in human cancer cells. Epigenetics Chromatin. 2015;8:2. doi: 10.1186/1756-8935-8-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Nye J., Sturgill D., Dalal Y. HJURP antagonizes CENP-A mislocalization driven by the H3.3 chaperones HIRA and DAXX. PLoS One. 2018;13:e0205948. doi: 10.1371/journal.pone.0205948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lacoste N., Woolfe A., Almouzni G. Mislocalization of the centromeric histone variant CenH3/CENP-A in human cells depends on the chaperone DAXX. Mol. Cell. 2014;53:631–644. doi: 10.1016/j.molcel.2014.01.018. [DOI] [PubMed] [Google Scholar]
- 21.Heun P., Erhardt S., Karpen G.H. Mislocalization of the Drosophila centromere-specific histone CID promotes formation of functional ectopic kinetochores. Dev. Cell. 2006;10:303–315. doi: 10.1016/j.devcel.2006.01.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gosline J., Lillie M., Savage K. Elastic proteins: biological roles and mechanical properties. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2002;357:121–132. doi: 10.1098/rstb.2001.1022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Klug W.S., Roos W.H., Wuite G.J.L. Unlocking internal prestress from protein nanoshells. Phys. Rev. Lett. 2012;109:168104. doi: 10.1103/PhysRevLett.109.168104. [DOI] [PubMed] [Google Scholar]
- 24.Gibbons M.M., Klug W.S. Influence of nonuniform geometry on nanoindentation of viral capsids. Biophys. J. 2008;95:3640–3649. doi: 10.1529/biophysj.108.136176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lloyd J.T., Zimmerman J.A., McDowell D.L. Finite element analysis of an atomistically derived cohesive model for brittle fracture. Model. Simul. Mater. Sci. Eng. 2011;19:65007. [Google Scholar]
- 26.Zink M., Grubmüller H. Mechanical properties of the icosahedral shell of southern bean mosaic virus: a molecular dynamics study. Biophys. J. 2009;96:1350–1363. doi: 10.1016/j.bpj.2008.11.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zink M., Grubmüller H. Primary changes of the mechanical properties of Southern Bean Mosaic Virus upon calcium removal. Biophys. J. 2010;98:687–695. doi: 10.1016/j.bpj.2009.10.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kononova O., Marx K.A., Barsegov V. Nanoindentation in silico of biological particles. In: Tiwari A., Natarajan S., editors. Applied Nanoindentation in Advanced Materials. John Wiley & Sons; 2017. pp. 393–428. [Google Scholar]
- 29.Parrinello M., Rahman A. Strain fluctuations and elastic constants. J. Chem. Phys. 1982;76:2662–2666. [Google Scholar]
- 30.Montalenti F., Salvalaglio M., Schroeder T. Fully coherent growth of Ge on free-standing Si(001) nanomesas. Phys. Rev. B Condens. Matter Mater. Phys. 2014;89:014101. [Google Scholar]
- 31.Salvalaglio M., Voigt A., Elder K.R. Closing the gap between atomic-scale lattice deformations and continuum elasticity. npj Comput. Mater. 2019;5:48. [Google Scholar]
- 32.Pitman M. Minimal cylinder analysis. 2020 doi: 10.5281/zenodo.2641192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Abraham M., Van Der Spoel D., Lindahl E. GROMACS user manual version 5.0.4. 2014. www.Gromacs.org
- 34.Best R.B., Hummer G. Optimized molecular dynamics force fields applied to the helix-coil transition of polypeptides. J. Phys. Chem. B. 2009;113:9004–9015. doi: 10.1021/jp901540t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lindorff-Larsen K., Piana S., Shaw D.E. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins. 2010;78:1950–1958. doi: 10.1002/prot.22711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Pérez A., Marchán I., Orozco M. Refinement of the AMBER force field for nucleic acids: improving the description of α/γ conformers. Biophys. J. 2007;92:3817–3829. doi: 10.1529/biophysj.106.097782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Joung I.S., Cheatham T.E., III Determination of alkali and halide monovalent ion parameters for use in explicitly solvated biomolecular simulations. J. Phys. Chem. B. 2008;112:9020–9041. doi: 10.1021/jp8001614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tachiwana H., Kagawa W., Kurumizaka H. Crystal structure of the human centromeric nucleosome containing CENP-A. Nature. 2011;476:232–235. doi: 10.1038/nature10258. [DOI] [PubMed] [Google Scholar]
- 39.Šali A. Rockefeller University; 2013. MODELLER: a program for protein structure modeling release 9.12, r9480; pp. 779–815. [Google Scholar]
- 40.Shindyalov I.N., Bourne P.E. Protein structure alignment by incremental combinatorial extension (CE) of the optimal path. Protein Eng. 1998;11:739–747. doi: 10.1093/protein/11.9.739. [DOI] [PubMed] [Google Scholar]
- 41.Lee M.K., Lee K.H., Park C.Y. Impact of initial active engagement in self-monitoring with a telemonitoring device on glycemic control among patients with type 2 diabetes. Sci. Rep. 2017;7:3866. doi: 10.1038/s41598-017-03842-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Seksek O., Bolard J. Nuclear pH gradient in mammalian cells revealed by laser microspectrofluorimetry. J. Cell Sci. 1996;109:257–262. doi: 10.1242/jcs.109.1.257. [DOI] [PubMed] [Google Scholar]
- 43.Berg J.M., Tymoczko J.L., Stryer L. Seventh Edition. W.H. Freeman and Co.; New York: 2012. Biochemistry. [Google Scholar]
- 44.Lemak A.S., Balabaev N.K. On the berendsen thermostat. Mol. Simul. 1994;13:177–187. [Google Scholar]
- 45.Bussi G., Zykova-Timan T., Parrinello M. Isothermal-isobaric molecular dynamics using stochastic velocity rescaling. J. Chem. Phys. 2009;130:074101. doi: 10.1063/1.3073889. [DOI] [PubMed] [Google Scholar]
- 46.Chree C. Longitudinal vibrations in solid and hollow cylinders. Proc. Phys. Soc. Lond. 1897;16:304–322. [Google Scholar]
- 47.W L.R. The theory of sound. Nature. 1898;58:121–122. [Google Scholar]
- 48.Piaras K. 2015. Solid Mechanics Part 1: An Introduction to Solid Mechanics. Mechanics Lecture Notes; pp. 183–191. [Google Scholar]
- 49.Ahadi A., Johansson D., Evilevitch A. Modeling and simulation of the mechanical response from nanoindentation test of DNA-filled viral capsids. J. Biol. Phys. 2013;39:183–199. doi: 10.1007/s10867-013-9297-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Jaeger M.T. Basic relationships in elasticity theory. Available at. https://dspace.mit.edu/bitstream/handle/1721.1/39137/22–314JSpring2004/NR/rdonlyres/Nuclear-Engineering/22–314JSpring2004/ACF104D9–8C23–4EEB-B3CD-D350871D8EDE/0/elastic_theory.pdf
- 51.Hertz H. Ueber die Berührung fester elastischer Körper. J. Reine Angew. Math. 1882;1882:156–171. [Google Scholar]
- 52.Xiao H., Wang F., Wu C. Molecular basis of CENP-C association with the CENP-A nucleosome at yeast centromeres. Genes Dev. 2017;31:1958–1972. doi: 10.1101/gad.304782.117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Kato H., Jiang J., Bai Y. A conserved mechanism for centromeric nucleosome recognition by centromere protein CENP-C. Science. 2013;340:1110–1113. doi: 10.1126/science.1235532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Roulland Y., Ouararhni K., Dimitrov S. The flexible ends of CENP-A nucleosome are required for mitotic fidelity. Mol. Cell. 2016;63:674–685. doi: 10.1016/j.molcel.2016.06.023. [DOI] [PubMed] [Google Scholar]
- 55.Hamiche A., Schultz P., Prunell A. Linker histone-dependent DNA structure in linear mononucleosomes. J. Mol. Biol. 1996;257:30–42. doi: 10.1006/jmbi.1996.0144. [DOI] [PubMed] [Google Scholar]
- 56.Zlatanova J., Seebart C., Tomschik M. The linker-protein network: control of nucleosomal DNA accessibility. Trends Biochem. Sci. 2008;33:247–253. doi: 10.1016/j.tibs.2008.04.001. [DOI] [PubMed] [Google Scholar]
- 57.Simpson R.T. Structure of the chromatosome, a chromatin particle containing 160 base pairs of DNA and all the histones. Biochemistry. 1978;17:5524–5531. doi: 10.1021/bi00618a030. [DOI] [PubMed] [Google Scholar]
- 58.Cui F., Zhurkin V.B. Distinctive sequence patterns in metazoan and yeast nucleosomes: implications for linker histone binding to AT-rich and methylated DNA. Nucleic Acids Res. 2009;37:2818–2829. doi: 10.1093/nar/gkp113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Zhou B.R., Jiang J., Bai Y. Structural mechanisms of nucleosome recognition by linker histones. Mol. Cell. 2015;59:628–638. doi: 10.1016/j.molcel.2015.06.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Bednar J., Garcia-Saez I., Dimitrov S. Structure and dynamics of a 197 bp nucleosome in complex with linker histone H1. Mol. Cell. 2017;66:384–397.e8. doi: 10.1016/j.molcel.2017.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Conde e Silva N., Black B.E., Prunell A. CENP-A-containing nucleosomes: easier disassembly versus exclusive centromeric localization. J. Mol. Biol. 2007;370:555–573. doi: 10.1016/j.jmb.2007.04.064. [DOI] [PubMed] [Google Scholar]
- 62.McGovern S.L., Qi Y., Buchholz T.A. Centromere protein-A, an essential centromere protein, is a prognostic marker for relapse in estrogen receptor-positive breast cancer. Breast Cancer Res. 2012;14:R72. doi: 10.1186/bcr3181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Tomonaga T., Matsushita K., Nomura F. Overexpression and mistargeting of centromere protein-A in human primary colorectal cancer. Cancer Res. 2003;63:3511–3516. [PubMed] [Google Scholar]
- 64.Mito Y., Henikoff J.G., Henikoff S. Genome-scale profiling of histone H3.3 replacement patterns. Nat. Genet. 2005;37:1090–1097. doi: 10.1038/ng1637. [DOI] [PubMed] [Google Scholar]
- 65.Mattiroli F., Gu Y., Luger K. DNA-mediated association of two histone-bound complexes of yeast chromatin assembly factor-1 (CAF-1) drives tetrasome assembly in the wake of DNA replication. eLife. 2017;6:e22799. doi: 10.7554/eLife.22799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Liu W.H., Roemer S.C., Churchill M.E. The Cac1 subunit of histone chaperone CAF-1 organizes CAF-1-H3/H4 architecture and tetramerizes histones. eLife. 2016;5:e18023. doi: 10.7554/eLife.18023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Kim S.H., Vlijm R., Dekker C. CENP-A and H3 nucleosomes display a similar stability to force-mediated disassembly. PLoS One. 2016;11:e0165078. doi: 10.1371/journal.pone.0165078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Moreno-Moreno O., Torras-Llort M., Azorin F. The E3-ligases SCFPpa and APC/CCdh1 co-operate to regulate CENP-ACID expression across the cell cycle. Nucleic Acids Res. 2019;47:3395–3406. doi: 10.1093/nar/gkz060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Przewloka M.R., Venkei Z., Glover D.M. CENP-C is a structural platform for kinetochore assembly. Curr. Biol. 2011;21:399–405. doi: 10.1016/j.cub.2011.02.005. [DOI] [PubMed] [Google Scholar]
- 70.Amor D.J., Bentley K., Choo K.H.A. Human centromere repositioning “in progress”. Proc. Natl. Acad. Sci. USA. 2004;101:6542–6547. doi: 10.1073/pnas.0308637101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Tessarz P., Kouzarides T. Histone core modifications regulating nucleosome structure and dynamics. Nat. Rev. Mol. Cell Biol. 2014;15:703–708. doi: 10.1038/nrm3890. [DOI] [PubMed] [Google Scholar]
- 72.Fenley A.T., Adams D.A., Onufriev A.V. Charge state of the globular histone core controls stability of the nucleosome. Biophys. J. 2010;99:1577–1585. doi: 10.1016/j.bpj.2010.06.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Tian T., Li X., Zang J. Molecular basis for CENP-N recognition of CENP-A nucleosome on the human kinetochore. Cell Res. 2018;28:374–378. doi: 10.1038/cr.2018.13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Williams J.G., Gamonpilas C. Using the simple compression test to determine Young’s modulus, Poisson’s ratio and the Coulomb friction coefficient. Int. J. Solids Struct. 2008;45:4448–4459. [Google Scholar]
- 75.O’connor P.D.T. Advanced strength and applied elasticity, A.C. Ugural and S.K. Fenster, Second SI Edition, Elsevier Science Publishing Company Inc., 1987. Number of pages: 471. Price: $35.00 (hardback only) Qual. Reliab. Eng. Int. 1988;4:297–298. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.