Abstract
Design and optimization of the energy system with the efficient method is one the major problem in recent years. The combined emergy-exergy-economic-environmental analysis is one of new methods selected for the optimization of energy systems. At present paper, first, optimal design of thermodynamic, exergo economic and exergo environmental was developed; the geothermal power plant was used as a complement to concentrated solar power (CSP) and then combined emergy-exergy-economic-environmental analysis was conducted. A standalone geothermal cycle (first mode), as well as hybrid Geothermal-Solar cycle (second mode) were investigated to generate the heating/cooling power of the building. The close similarity of the results of the exergy and emerge-economic analysis was very interesting. For standalone geothermal cycle, both exergo and emerge-economic analysis implied that highest value (6.02E-04 $/s and 3.1915E+09 sej/s) was related to turbine due to the heat generated by the impact of the blade, and the lowest value was related to ORC condenser. The exergo and emergo-economic analysis for geothermal-solar hybrid cycle, due to the increase in refrigerant pressure drop inside the coil, the evaporator (4.50E-03 $/s and 4.4699E+09 sej/s) and turbine (2.40E-03 $/s and 2.1920E+09 sej/s) had the highest amount. Also for standalone cycle, exergo and emergo-environmental implied that ORC turbine had the highest value of 1.26E-06 pts/s and 9.7201E+09sej/s. For hybrid geothermal-solar cycle, the evaporator (3.77E-06 pts/s and 6.1814E+08sej/s) and turbine (3.27E-06 pts/s and 6.37E+08 sej/s) had the highest amount of exergo and emergo-environmental. Solar power plants have only an initial cost and because solar energy is freely available to the system, so its economical exergy degradation is very low and has the lowest environmental exergy degradation. According to the results of the exergo-economic analysis of the hybrid power plant, the highest investment cost is related to solar power plant. It also has the lowest cost of exergy degradation because the environmental impact of fuel flow of solar panel is zero. The highest emerge-environmental rate of 3.3250E+09 (sej/s) was belonged to the solar power plant, but its environmental destruction rate was minimal because it does not consume fuel.
Keywords: Energy, Mechanical engineering, Environmental analysis, Environmental economics, Hybrid solar – geothermal, Exergy analysis, Exergo-economic, Exergo-environmental, Emergy
Energy; Mechanical engineering; Environmental analysis; Environmental economics; Hybrid solar – geothermal; Exergy analysis; Exergo-economic; Exergo-environmental; Emergy
1. Introduction
Renewable energy is the endless source of energy without depleting earth's resources. The costs of renewable energy sources are high compared to fossil fuels such as coal, oil and gas. But in spite of many failures in the renewables sector and occasional acceptance, we will see it grow in the coming decades due to technological advances (Goodarzi, 2017; Sajid et al., 2016).
It is virtually impossible to adopt appropriate policies for the use of renewable energies, regardless of the obstacles to the development of these types of energy, because of the production of distributed renewable energy in areas away from the global power transmission grid (Beier et al., 2017; Ochoa et al., 2019). Another problem is the lack of continuous energy production within 24 h a day, which can be solved using several hybrid energy sources. For example, combining geothermal and solar energy takes advantage of both technologies. Because solar energy is inherently alternative, while geothermal energy can provide the base power. There are various methods for hybridizing solar and geothermal technologies, and the efficiency of some methods depends on factors such as location, relative quality of geothermal and solar resources. Most previous research has focused on retrofitting geothermal power plants. Typically decreasing the temperature, pressure, or mass velocity of the fluid stream over time is resulted in a decrease in geothermal power generation and equipment efficiency (McTigue et al., 2019).
Gonzalez et al. (2018) investigated theoretical advances to optimize the use of solar air conditioning by distributing vacuum tubes to several solar collectors in residential units. Javaherdeh et al. (2016) simulated the organic rankine cycle (ORC) in order to generate electricity and hot water with the simultaneous stimulation of geothermal and solar energy, and evaluated from an energy, exergy and exergo-economic standpoint. In this configuration, 90°C geothermal fluid was used for pre-heating and 150°C solar fluid was used for super heating the organic fluid. The heat exchanger in the condenser was also used to produce hot water. The simulation results showed that at the base state, the efficiency of energy and exergy were 0.566 and 0.156, respectively. Solar collectors, evaporators and organic cycle condensers have the highest initial cost and exergy destruction from an exergo-economic perspective. The results of parametric analysis indicated that evaporator temperature had a positive effect on cycle performance and increased electrical efficiency and reduced irreversibility. And increasing the pinch temperature has a negative effect on system performance. From an economic point of view, the increase in evaporator temperature and pinch temperature resulted in a lower overall cost rate. Also, the change in solar flux improved the performance of the system from exergo-economic point of view and resulted in increased energy and exergy efficiency. Yan and Xu (2018) reviewed the recent research on ground heat exchangers used in buildings. In order to better use of ground heat exchangers, several technologies are combined with it, including cooling towers and solar thermal collectors. Lee et al. (2017) investigated the hybrid ground source-photovoltaic heat pump (GSHP-PVT) and ground source heat pumps (GSHP) to be applied in fuzzy logic control strategy. For the GSHP, advanced fuzzy logic control was resulted in initial energy saving of approximately 9.5% during the heating period, of 18.3% in the cooling period, and of 12% within a year compared to the on-off control strategy. Zyvith et al. (2018) studied on multipurpose geothermal systems for large residential and commercial buildings. Their system consisted of five output products namely industry cooling, air heating for residential applications, hot water for drying household food, and electricity. Total energy and exergy efficiency were 69.6% and 42.8%, respectively. Other studies in the field of hybrid geothermal-solar can be found in (Heberle and Hofer, 2017; Islam and Dincer, 2017; Ramos et al., 2017; Cardemil et al., 2016; Khalid et al., 2017; Jeong et al., 2017; Carotenuto et al., 2017; and Bassetti et al., 2018; Lee et al., 2017; McTigue et al., 2018; Bicer and Dincer, 2017).
Even though the important studies developed in the analysis of ORC systems using the geothermal-solar hybrid resource as a thermal source, the identification of improvement opportunities have been evaluated independently, without integrating the exergy, economic, and environmental criteria. Therefore, no systemic approach involving exergy, economic and environmental criteria has been developed that seeks to optimize the operating and design parameters of each of the process subsystems. Thus, the main objective and scientific contribution of this study is to develop an exergy, economic and environmental evaluation through performance indicators of an ORC system that uses the solar resource integrated to the geothermal as a thermal source. A system with optimal design is proposed based on economic, environmental and thermodynamic criteria, then the standalone geothermal cycle (first mode) is studied, as well as a hybrid Geothermal-Solar cycle (second mode) to supply the thermal energy required both for heating and cooling a building, with the aim of obtaining a cleaner production of energy with lower environmental impacts.
The concept of emergy is an acceptable alternative for the word of conventional monetary index and the assessment of the environmental impact. In other word, the types of energy and resources needed can be considered as emergy or “energy memory” to create a specific product or service (Aghbashlo and Rosen, 2018; Zhang et al., 2018). The basic hypothesis of this concept is that life on Earth is created by sustainable solar energy. It is worth noting that any flow of energy, matter and even money can be expressed using the emergy concept, for example the solar equivalent joule (sej) of available energy. The monetary and environmental costs of a given energy flow can be combined using this concept (Chen et al., 2017; Wang et al., 2017). Emergy analysis is a widespread method for considering the energy efficiency and sustainability of complex systems using quantifying the direct and indirect contribution of nature to human-made systems (Gonzalez-Mejia and Ma, 2017; Zhao et al., 2019). Zhang and Ma (2020) evaluated the environmental sustainability of a new wastewater treatment plant in China based on emergy concept. The results illustrated that the emergy of the construction processes (approximately 92.6) was much more important than the emergy of the treatment process. Also, renewable energy sources are the main factor for the analysis of emergy, and revenue obtained (7%).
The researchers merged the concept of emergy with conventional economic and environmental ecosystem analysis and improved the results by converting the input values into the emergy unit. Aghbashlo and Rosen (2018) and Boyaghchi and Sabaghian (2016) studied on CHP system using emergy concept and compared the results with conventional exergo environmental and exergo economic analysis.
In this paper, to better understand energy conversion systems from a thermodynamic, economic and environmental point of view, economic and environmental exergy analysis was performed based on emergy concept. After presenting the theoretical concepts, the ORC Geothermal-Solar system is considered as an example. This example explains how emergy-exergy-economic-environmental analysis allows us to investigate energy conversion systems. It is anticipated that energy conversion systems will be better understood using developed methods based on environmental, economic and thermodynamic factors.
2. Material and methods
2.1. Thermodynamic modeling
The first step for thermodynamic analysis of the system is to calculate the unknown temperature, pressure, and enthalpy of each state of the system. Although this analysis can't define all aspects of the system, but it is a critical task since subsequent analysis is based on thermodynamic modeling. Therefore, in the first step, thermodynamic modeling was performed by thermo-flow software. Then, the first law of thermodynamics was analyzed using MATLAB software. The balance of mass (Eq. (1)) and energy (Eq.(2)) is one of the fundamental equations of the first law analysis.
| (1) |
| (2) |
2.2. Exergy analysis
To calculate the exergy rate of material flows, the specific exergy flow rate must be multiplied by their mass flow rate (Eq. (3)).
| (3) |
The calculation of fuel and flow of production for each component is one of the most important concepts of exergy analysis. In fact, for continuing the operation, each component needs a drive which is defined as the fuel flow of the equipment. After calculating the fuel, other outputs of exergy analysis namely exergy efficiency () and exergy destruction () of each component can be obtained through Eqs. (4) and (5).
| (4) |
| (5) |
where is exergy destruction of each component, and the and are the exergy rate of product and fuel of each component, respectively.
2.3. Exergo-economic analysis
Since economic issues are an integral component of engineering analysis, they are integrated into thermodynamic calculations which are called exergo-economic analysis (Ayub et al., 2015). The purchasing equipment cost (PEC) is calculated by equations given in Table 1
Table 1.
Purchase equipment cost of the equipment ($).
| Components | Equations |
|---|---|
| Heat exchanger (Khalid et al., 2017) | |
| Steam Turbine (Jiang et al., 2016) | |
| Condenser | |
| Pump | |
| Collector |
Table 2 gives the equations for the exergo-economic analysis.
Table 2.
Related equations for the exergo economic analysis.
| Description | Equation | Number of Eq. |
|---|---|---|
| The equipment cost rate (Dincer et al., 2017). | [6] | |
| The Capital Recovery Factor (Dincer et al., 2017). | [7] | |
| The cost rate of the streams (Bonyadi et al., 2018). | [8] | |
| The exergo-economic balance for each component (Bonyadi et al., 2018; Ochoa et al., 2020). | [9] | |
| The cost rate of exergy destruction of the equipment (Bonyadi et al., 2018). | [10] | |
| The exergo-economic factor (Bonyadi et al., 2018). | [11] | |
| The relative difference of equipment cost (Bonyadi et al., 2018). | [12] |
The equipment cost rate can be determined by Eq. (6). where is a coefficient of maintenance that determines how the maintenance costs will affect the overall cost of the equipment and can be considered 1.06. N is the life of power plant (in year) which is considered 25 years, and the Capital Recovery Factor (CRF) can be estimated by Eq. (7).
The economic exergy balance must be written for each component through Eqs. (8) and (9) to calculate the cost values for each exergy unit for all flows.where, is the equipment cost rate, is the cost rate of fuel flow and is the cost rate dependent on the capital cost rate and maintenance cost of each component.
2.4. Exergo-environmental analysis
Power production systems have significant impacts on the environment, so analyzing these systems to reduce losses in an environmentally friendly manner seems to be essential. See Table 3 for equations of the exergo-environmental analysis.
Table 3.
Related equations for the Exergo-environmental Analysis.
| Description | Equation | Number of Eq. |
|---|---|---|
| The relationship between environmental impact and exergy of each stream (Carotenuto et al., 2017). | (13) | |
| The exergo-environmental balances for the equipment (Carotenuto et al., 2017). | (14) | |
| The environmental impact of equipment (Carotenuto et al., 2017). | (15) | |
| The environmental impact of the fuel streams of equipment per exergy unit, pts/kJ (Cavalcanti, 2017). | (16) | |
| The environmental impact of the product streams of equipment per exergy unit,pts/kJ (Cavalcanti, 2017). | (17) | |
| The environmental impact rate of exergy destruction of equipment (Bassetti et al., 2018). | (18) | |
| The exergo-environmental factor (Bassetti et al., 2018). | (19) |
2.5. Emergy concept
For the proposed cycle analysis, all input variables must be converted to equivalent “solar emergy jules” (SEJs). These conversions can be done by multiplying the input variable by the corresponding unit energy value (UEV) or the conversion factor the emergy used to generate a given amount of energy, mass, etc (Rafat et al., 2019). Conversion coefficient values usually appear in the amount of energy-based emergy.
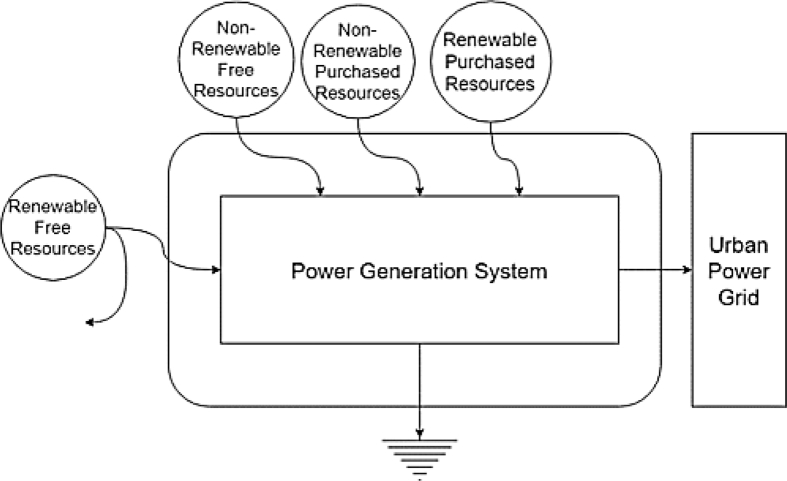
Figure 1 schematically represents the power generation cycles and system input/output flows of system. Inputs are divided into four categories: resources of renewable purchased (RP) and non-renewable purchased (NP), resources of free renewables (R1) and free non-renewable (NR). The sum of the input energies (Y) is called efficiency and can be calculated by Eq. (21):
| (21) |
Figure 1.
Boundary of the system.
EYR indicates the cycle's ability to exploit local resources. The more EYR means that more emergy will be returned to the system.
| (22) |
The ratio of environmental energy (ELR) is the ratio between non-renewable and renewable resources used in the system and can be calculated from the Eq. (23):
| (23) |
The energy sustainability index (ESI) is the ratio of energy efficiency and environmental loading. This parameter can measure environmental sustainability, local environmental impacts and social benefits (Pan et al., 2018). A system with an ESI greater than 5 is called a stable system, and if this index is lower than 1, it is not a stable system.
| (24) |
Finally, the conversion coefficient of the system is defined to determine the amount of emergy used to generate the required power (Rafat et al., 2019).
| (25) |
2.6. Emergo-economic analysis
The principles of emergo-economic analysis is similar to conventional exergo-economic analysis. The monetary values of emergy for all exergy flows are evaluated using specific exergy costing (SPECO) method. See Table 4 for the exergo-environmental analysis.
Table 4.
Related equations for the Exergo-environmental Analysis.
| Description | Equation | Number of Eq. |
|---|---|---|
| The monetary emergy rate for all exergy flows (Rafat et al., 2019). | (26) | |
| The monetary-based emergy rate of product (Aghbashlo and Rosen, 2018). | (27) | |
| The monetary emergy rate of component k (Aghbashlo and Rosen, 2018). | (28) | |
| The specific monetary value of the product of the equipment (Rafat et al., 2019). | (29) | |
| The specific monetary value of the fuel (Aghbashlo and Rosen, 2018). | (30) | |
| The destruction rate of monetary emergy (Rafat et al., 2019). | (31) | |
| Total rate of emergy of component (Aghbashlo and Rosen, 2018). | (32) | |
| The factor of emergo-economic of each component (Aghbashlo and Rosen, 2018). | (33) | |
| The monetary energy difference ratio of the equipment (Rafat et al., 2019). | (34) |
2.7. Emergo-environmental analysis
The EMergo-environmenal analysis is performed by applying the ecological emergy values to exergy flows. The equations for the emerge-environmental analysis are given in Table 5.
Table 5.
Related equations for the Emergo environmental Analysis.
| Description | Equation | Number of Eq. |
|---|---|---|
| The environmental emergy rate (Aghbashlo and Rosen, 2018). | (35) | |
| The environmental emergy balance of each component (Rafat et al., 2019). | (36) | |
| (37) | ||
| The specific emergy of product in the environmental analysis (Aghbashlo and Rosen, 2018). | (38) | |
| The specific emergy of fuel in the environmental analysis (Rafat et al., 2019). | (39) | |
| The destruction rate of environmental emergy (Aghbashlo and Rosen, 2018). | (40) | |
| Total emergy rate of a component in the environmental analysis (Rafat et al., 2019). | (41) | |
| The Emergo environmental factor for each component (Aghbashlo and Rosen, 2018). | (42) |
2.8. Project approach
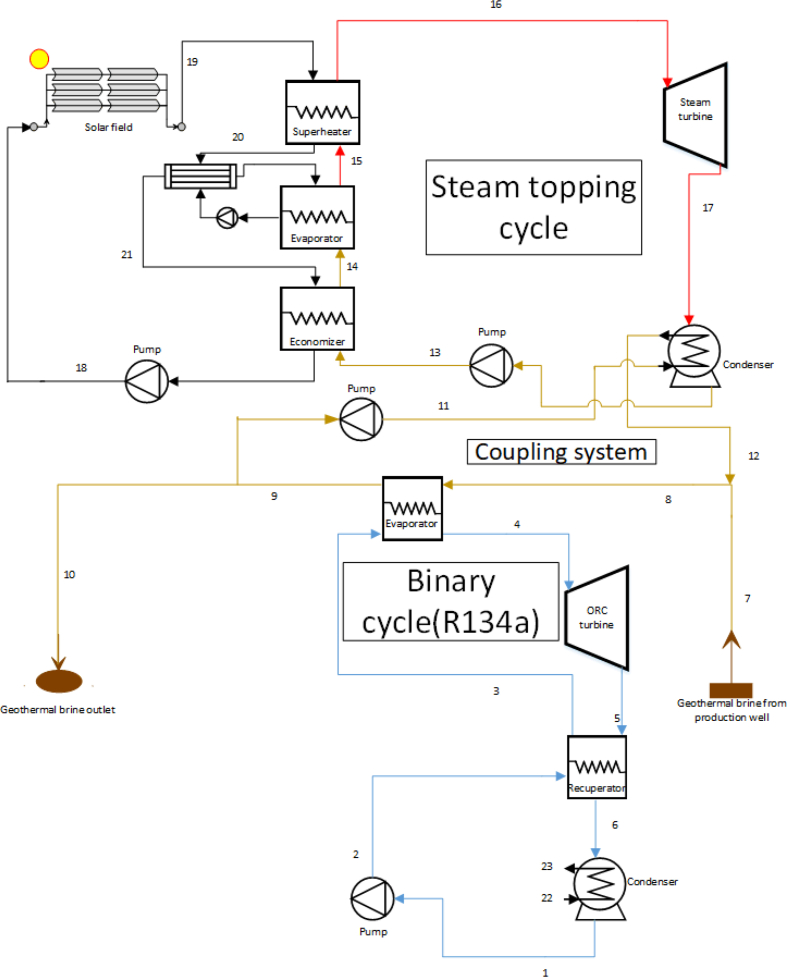
At present study, a new Geothermal-Solar hybrid power plant has been proposed to generate electrical power, in order to integrate the Solar-Steam Rankin cycle with the geothermal section and the organic Rankine cycle (Figure 2).
Figure 2.
Integration of Solar-Steam Rankin cycle with Geothermal and Organic Rankine Sections.
2.8.1. Geothermal source
The temperature and pressure of the boiler and the geothermal source is assumed to be 150 °C and 10 bar, respectively. This thermal source is coupled by a downstream heat exchanger. In order to minimize geothermal source cooling and reduce problems such as the formation of silica, it is assumed that the salt is released in minimum temperature of 70 °C. The flow rate is equal to the flow in the well and spring (Heberle and Hofer, 2017).
2.8.2. Downstream cycle
A review of the fluids normally used for this application has been carried out with priority given to the criteria mentioned above. Therefore, R134a has been selected as the Rankine's organic cycling fluid. This fluid receives the geothermal heat factor by a heat exchanger and reaches an approximate temperature of 150 °C. An improver is used at the turbine output to increase the efficiency of the downstream cycle (Bonyadi et al., 2018; Valencia Ochoa et al., 2020).
2.8.3. The solar section in upstream cycles
In the supposed hybrid power plant, the linear parabolic collectors with the lubricant oil (Therminol vp1) have been used as the heat transfer fluid interface. The solar part of the storage enclosure has no thermal energy and the exhaust temperature of the particle collectors used is 395 °C. In order to circulate the flow of fluid with controlled discharge, a pump is used to allow the fluid to reach the desired outlet temperature at the collector output. On the other hand, a series of heat exchangers have been used to transfer the direct heat of solar energy to the steam's Rankine cycle. In this study, solar power is considered to be 1.25, which means that the maximum output of the solar sector generates 25% more thermal energy than the required amount of cycle time required.
2.8.4. Rankine steam cycle in upstream cycles
As mentioned earlier, heat exchangers are used in three ways: economic optimizers, evaporators and superconductors to directly transfer solar heat to part of the Rankine cycle. The operating fluid (water) enters the turbine after heat absorption and eventually pumps after the heat transfer to the converter and the heat loss in the condenser. The equipment used in this cycle is high pressure equipment. The super heater steam enters the turbine at a constant temperature of 390°C and exits from turbine at 170°C (Bonyadi et al., 2018).
2.8.5. Thermal coupling for upstream and downstream cycles
In order to create heat and thermal coupling of the downstream and upstream cycles, the geothermal power plant is used as the heat transfer fluid interface. For reheating, the low-temperature rapid-flow fluid stream of the geothermal cycle is directed to the upstream condenser and, using a return cycle, the mixture is mixed with pure salt. This will only source the solar thermal cycle if the downstream cycle energy source is geothermal energy and the thermal energy delivered by the upstream cycle condenser is delivered. The pump and flow controller are used to adjust the water temperature of the solar cycle outlet from the condenser at a temperature of 150 °C (Bonyadi et al., 2018).
2.9. Modes of simulation
From a mass flow rate perspective of the geothermal, two mods are considered as below:
2.9.1. Standalone geothermal mode
In this case, the solar field is considered economical and only the downstream cycle is considered as the power generation sector. The boiler water is 100 kg/s, and the temperature and pressure of the source of the boiler are 150 °C and 10 bar (Heberle and Hofer, 2017).
2.9.2. Hybrid geothermal-solar mode
In this case, the geothermal sector is capable of producing a mass flow of 100 kg/s. This solar module is designed to provide a flow rate of 100 kg/s for 12 h a day. For a solar sector (during the day), the mass flow rate at node 8 is constant at 100 kg/s, but the heat source in the presence of solar sources is 0% sun and 100% geothermal at night.
2.9.3. Simulation by software
To simulate the cycles, Thermoflow software was used. The data required to simulate the organic part of the Rankine cycle has been considered in accordance with the referenced data. Given that the geothermal section has different divergences in all models and that the solar and steam sections are added to the organic Rankine cycle by the geothermal section, it was assumed that input data for the organic Rankin section is the same for all models. This data is summarized in Table 6.
Table 6.
Design parameters of simulation the case study.
| Design parameters | Value |
|---|---|
| The mass flow of geothermal fluid (kg/s) | 100 |
| The pressure of the geothermal fluid (bar) | 10 |
| The temperature of the geothermal fluid (°C) | 150 |
| A minimum temperature of the geothermal returned fluid (°C) | 70 |
| The inlet temperature of theturbine (°C) | 145 |
| Ambient temperature (°C) | 15 |
| Recuperator efficiency (%) | 95 |
| Isentropic efficiency of the turbine (%) | 85 |
| Condensing temperature (°C) | 27 |
3. Result and discussion
In order to evaluate more precisely, in both cases the proposed cycle, the design programming is performed in MATLAB software and its results are presented separately with the simulation results in Table 7. The results show that the main design parameters in both cases are very accurate and the calculation error for all of the first mode results parameters is below 5%. Also for validation, the results are compared with reference papers and are presented in Table 8. It should be noted that for accurate evaluation and optimization of the results, the performance of the condenser cooling fan is included in the coding to minimize the calculation error.
Table 7.
Validation of the first and second mode of simulation and Computer code results.
| Main parameters | first mode results |
second mode results |
||||
|---|---|---|---|---|---|---|
| Computer code | Simulation | Error (%) | Computer code | Simulation | Error (%) | |
| Flow rate of cooling water (kg/s) | 660.98 | 662 | 0.15 | 664.59 | 676.2 | 1.72 |
| Flow rate of organic Rankine cycle (kg/s) | 151.58 | 151.2 | 0.25 | 153.90 | 154.5 | 0.39 |
| Geothermal inlet heat (kW) | 32734 | 32730 | 0.01 | 33027 | 33600 | 1.71 |
| Net power output of organic Rankine cycle (kW) | 4728 | 4651 | 1.66 | |||
| Net power output of topping cycle (kW) | 1194.8 | 1155.2 | 3.43 | |||
| Net power output (kW) | 4592.2 | 4412 | 4.08 | 5922.7 | 5734.9 | 3.27 |
| Energy efficiency (%) | 14.03 | 13.48 | 4.08 | |||
| Energy efficiency of organic Rankine cycle (%) | 14.32 | 13.84 | 3.45 | |||
| Energy efficiency of topping cycle (%) | 15.53 | 15.01 | 3.46 | |||
| Steam cycle flowrate (kg/s) | 3.171 | 3.145 | 0.83 | |||
| Heat transfer fluid flowrate (kg/s) | 23.481 | 23.5 | 0.08 | |||
Table 8.
Validation of the first and second mode of simulation net output power.
| Main parameters of the first mode | Net output power in computer code results (kW) | Net output power in simulation results (kW) | Other references result (kW) |
|---|---|---|---|
| First mode | 4592.2 | 4412 | 4326.5 |
| Second mode | 5922.7 | 5734.9 | 5399.5 |
Depending on how the cycle operates, it can be mentioned that the plant consists of two sources of solar and geothermal energy. During the day both sources are involved in operating the plant simultaneously. During the night, both the solar and the Rankine cycle are eliminated and only the geothermal section is active.
The errors of the second mode results in Table 7 are below 4 % and represent that the simulation is acceptable. The power output validation is presented in Table 8.
Considering two cases and considering the results, the simulation results are consistent with the pure power output of the power plant for a specified discharge. Stream information of first and second mode including mass flow, temperature, pressure, enthalpy and exergy rate are given in Table 9. Flow data for a particular case of upstream and downstream couplings or the second mode (simulated to minimize the production of steam from the geothermal section) is shown in Table 9. In this case, the output flow from the upstream condenser can reach 100 kg per second.
Table 9.
Flow information of cycle simulations.
| State | First mode cycle simulation |
Second mode cycle simulation |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| T (°C) | P (bar) | h (kJ/kg) | (kw) | T (°C) | P (bar) | h (kJ/kg) | (kw) | |||
| 1 | 151.2 | 27.48 | 7.16 | -186.43 | 5344.7 | 154.5 | 27.48 | 7.16 | -186.43 | 5426.5 |
| 2 | 151.2 | 32.52 | 56.2 | -179.08 | 5967.4 | 154.5 | 32.52 | 56.20 | -179.08 | 6058.8 |
| 3 | 151.2 | 49.56 | 55.7 | -154.70 | 6256.2 | 154.5 | 52.43 | 55.70 | -150.4 | 6373.7 |
| 4 | 151.2 | 144.4 | 53.36 | 59.67 | 13709 | 154.5 | 147.6 | 53.36 | 64.93 | 13919 |
| 5 | 151.2 | 59.44 | 7.31 | 20.99 | 6958.7 | 154.5 | 63.754 | 7.31 | 25.28 | 6988.9 |
| 6 | 151.2 | 34.52 | 7.16 | -3.68 | 6524.1 | 154.5 | 34.525 | 7.16 | -3.68 | 6543.5 |
| 7 | 100 | 150 | 10 | -3.68 | 6524.1 | 8543.2 | ||||
| 8 | 100 | 150 | 10 | 632.4 | 10355 | 100 | 151.36 | 10 | 638.1 | 10355 |
| 9 | 100 | 72.7 | 10 | 305.10 | 2225.1 | 100 | 728 | 10 | 302.12 | 2176.4 |
| 10 | 82.50 | 72 | 10 | 302.20 | 1795.5 | |||||
| 11 | 17.5 | 72.01 | 10.2 | 302.12 | 381.2 | |||||
| 12 | 17.5 | 157.5 | 10 | 664.7 | 1812.2 | |||||
| 13 | 3.145 | 171.7 | 60.41 | 729.60 | 439.5 | |||||
| 14 | 3.145 | 270.8 | 60.21 | 1188.9 | 1051 | |||||
| 15 | 3.145 | 275.8 | 60.21 | 2784.6 | 3454 | |||||
| 16 | 3.145 | 390 | 60 | 3154 | 4058.3 | |||||
| 17 | 3.145 | 170 | 7.92 | 2756.4 | 2679.1 | |||||
| 18 | 23.5 | 258.1 | 1.54 | 894.8 | 5613.8 | |||||
| 19 | 23.5 | 395 | 1.4 | 1222.40 | 10653 | |||||
| 20 | 23.5 | 375.6 | 1.3 | 1172.5 | 9847.3 | |||||
| 21 | 23.5 | 285.8 | 1.2 | 1188.9 | 6511.1 | |||||
| 22 | 662 | 15 | 1.014 | 63.03 | 0 | 676.2 | 15 | 1.013 | 63.03 | 0 |
| 23 | 662 | 24.98 | 0.9936 | 104.80 | 467.6 | 676.2 | 24.98 | 0.9931 | 104.80 | 470.2 |
Exergy is an indicator for quantization of the stability of the process and involves quantitative and qualitative aspects of energy together.
Exergy illustrates the quality of the energy and matter flow that gives the useful part of energy. Energy conversion is always associated with the loss of energy quality.
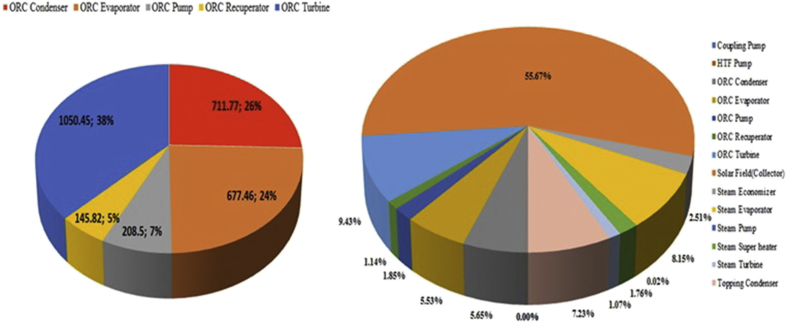
The exergy destruction results for the first and second mode of simulation have been given in the Figure 3. These results show that the ORC turbine with 1050 kW has the highest rate of the exergy destruction. This amount has a share of 38% of total exergy destruction. The ORC condenser has a share about 26% of the total exergy destruction.
Figure 3.
Exergy destruction of the first and second mode components.
In addition, Figure 3 illustrates the results of exergy destruction of each component in the Geothermal-Solar cycle. It has been indicated that the solar field has a share about 56% of the total exergy destruction of the cycle. The higher rate of exergy destruction can be observed in power plant implemented by solar. This is because of higher temperature difference between hot and cold streams (Mohammadi et al., 2018). Also, by reducing the inlet temperature of the hot fluid in shell and tube heat exchangers, the rate of exergy destruction can be decreased (Mehrpooya et al., 2018). The ORC turbine has a share about 9% of the total exergy destruction in this case.
Economic exergy, a common branch of chemical and mechanical engineering, implies a unique integrated analysis of exergy and cost. Moreover, economic exergy is a very powerful tool for understanding the relation between economics and thermodynamics. Table 10 gives the results of exergo-economic analysis of the geothermal cycle (the first mode).
Table 10.
Exergo economic analysis results of the geothermal cycle (first mode).
| Component | (kW) | (kW) | ($/s) | ($/kJ) | ($/kJ) | ($/s) | ($/s) | ($/s) | r | f (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| ORC Condenser | - | - | 8.06E-04 | - | - | - | - | - | - | - |
| ORC Evaporator | 8130.4 | 7452.9 | 3.11E-04 | 1.75E-06 | 1.95E-06 | 0.0142 | 0.0145 | 0.0012 | 0.1147 | 20.78 |
| ORC Pump | 831.2 | 622.7 | 0.0013 | 4.69E-06 | 8.28E-06 | 0.0039 | 0.0052 | 9.78E-04 | 0.7651 | 56.24 |
| ORC Recuperator | 434.6 | 288.8 | 2.76E-05 | 3.04E-06 | 4.67E-06 | 0.0013 | 0.0013 | 4.43E-04 | 0.5363 | 5.85 |
| ORC Turbine | 6750.5 | 5700 | 0.0062 | 3.04E-06 | 4.69E-06 | 0.0205 | 0.0267 | 0.0032 | 0.5420 | 66.00 |
The results of exergo economic analysis associated with the second mode of simulation determines that the maximum investment cost in the cycle is related to the ORC turbine. Also, the maximum cost of exergy destruction is associated with ORC turbine.
See Table 11 for additional information on the analysis of economic exergy, cost, and exergy and fuel and production costs. When the desired result is not achieved by conventional energy and exergy analysis, and economic analysis, this table provides useful information in designing and operating a cost-effective system. Defining the concepts of fuel and product is essential for economic exergy analysis.
Table 11.
Exergo economic results of each component in the Geothermal-Solar cycle (second mode of simulation).
| Component | (kW) | (kW) | ($/s) | ($/kJ) | ($/kJ) | ($/s) | ($/s) | ($/s) | r | f (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| Coupling Pump | 0.42 | 0.37 | 1.50E-06 | 2.43E-05 | 3.19E-05 | 1.03E-05 | 1.18E-05 | 1.28E-06 | 0.31 | 53.38 |
| HTF Pump | 2.3 | 1.9 | 3.56E-05 | 2.43E-05 | 4.88E-05 | 5.62E-05 | 9.18E-05 | 1.04E-05 | 1.00 | 77.38 |
| ORC Condenser | - | - | 8.19E-04 | - | - | - | - | - | ||
| ORC Evaporator | 8179.1 | 7545.4 | 5.14E-04 | 0.00E+00 | 6.81E-08 | 0.00E+00 | 5.14E-04 | 0.00E+00 | Inf | 100 |
| ORC Pump | 844 | 632.3 | 0.0013 | 1.80E-06 | 4.41E-06 | 0.0015 | 0.0028 | 3.80E-04 | 1.45 | 76.95 |
| ORC Recuperator | 445.4 | 314.9 | 3.02E-05 | 5.99E-07 | 9.43E-07 | 2.67E-04 | 2.97E-04 | 7.81E-05 | 0.57 | 27.85 |
| ORC Turbine | 6930.1 | 5850 | 0.0064 | 5.99E-07 | 1.80E-06 | 0.0041 | 0.0105 | 6.47E-04 | 2.00 | 90.77 |
| Solar Field (Collector) | 11415 | 5038.8 | 2.41E-02 | 0.00E+00 | 4.78E-06 | 0 | 0.0241 | 0.00E+00 | Inf | 100 |
| Steam Economizer | 899.2 | 611.5 | 3.09E-04 | 4.80E-06 | 7.56E-06 | 0.0043 | 0.0046 | 1.40E-03 | 0.57 | 18.32 |
| Steam Evaporator | 3336.2 | 2403.1 | 7.82E-04 | 4.80E-06 | 6.98E-06 | 0.016 | 0.0168 | 4.50E-03 | 0.45 | 14.88 |
| Steam Pump | 21.8 | 19.7 | 2.11E-05 | 2.43E-05 | 2.80E-05 | 5.30E-04 | 5.51E-04 | 5.16E-05 | 0.15 | 29.02 |
| Steam Super heater | 805.3 | 604.2 | 2.60E-04 | 4.80E-06 | 6.82E-06 | 0.0039 | 0.0041 | 9.64E-04 | 0.42 | 21.26 |
| Steam Turbine | 1379.1 | 1257 | 0.0032 | 1.99E-05 | 2.43E-05 | 0.0274 | 0.0306 | 2.40E-03 | 0.22 | 57.03 |
| Topping Condenser | - | - | 0.0013 | - | - | - | - | - | - | - |
The results of the exergo-economic analysis of the hybrid power plant showed that the solar power plant has the maximum investment cost. It also has the lowest cost of exergy destruction in the cycle. The maximum cost of exergy destruction is the evaporator. Exergo-economic results of each component in the Geothermal-Solar cycle (second mode) of simulation have been calculated as given in Table 11.
In this project, the environmental impacts of each flow are obtained in the first and second simulation modes using the Exergy method. The environmental results of first mode and second mode are presented in Tables 12 and 13, respectively.
Table 12.
Exergo-environmental calculations for standalone geothermal cycle.
| Component | (pts/s) | (pts/kJ) | (pts/kJ) | (pts/s) | (pts/s) | (pts/s) | (%) | |
|---|---|---|---|---|---|---|---|---|
| ORC Condenser | 6.25E-08 | - | - | - | - | - | - | - |
| ORC Evaporator | 4.77E-06 | 0 | 6.40E-10 | 0 | 4.77E-06 | 0 | Inf | 100 |
| ORC Pump | 2.61E-08 | 3.68E-09 | 4.96E-09 | 3.06E-06 | 3.09E-06 | 3.68E-07 | 0.3462 | 3.29 |
| ORC Recuperator | 1.75E-07 | 1.20E-09 | 2.41E-09 | 5.21E-07 | 6.96E-07 | 1.75E-07 | 1.0095 | 5.00E+01 |
| ORC Turbine | 1.29E-05 | 1.20E-09 | 3.68E-09 | 8.10E-06 | 2.10E-05 | 1.26E-06 | 2.0698 | 91.1 |
Table 13.
Exergo-environmental calculations for hybrid Geothermal-Solarcycle (second mode of simulation).
| Component | (pts/s) | (pts/kJ) | (pts/kJ) | (pts/s) | (pts/s) | (pts/s) | (%) | |
|---|---|---|---|---|---|---|---|---|
| Coupling Pump | 7.54E-10 | 3.57E-08 | 4.28E-08 | 1.50E-08 | 1.58E-08 | 1.88E-09 | 2.01E-01 | 2.86E+01 |
| HTF Pump | 3.79E-09 | 3.57E-08 | 4.58E-08 | 8.23E-08 | 8.61E-08 | 1.52E-08 | 2.84E-01 | 1.99E+01 |
| ORC Condenser | 6.28E-08 | - | - | - | - | - | - | - |
| ORC Evaporator | 4.80E-06 | 0 | 6.36E-10 | 0.00E+00 | 4.80E-06 | 0.00 | Inf | 1.00E+02 |
| ORC Pump | 2.64E-08 | 3.64E-09 | 4.90E-09 | 3.07E-06 | 3.10E-06 | 7.70E-07 | 3.46E-01 | 3.31 |
| ORC Recuperator | 1.83E-07 | 1.18E-09 | 2.24E-09 | 5.23E-07 | 7.07E-07 | 1.53E-07 | 9.10E-01 | 5.44E+01 |
| ORC Turbine | 1.31E-05 | 1.18E-09 | 3.64E-09 | 8.14E-06 | 2.13E-05 | 1.27E-06 | 2.10E+00 | 91.19 |
| Solar Field (Collector) | 2.03E-05 | 0 | 4.03E-09 | 0.00E+00 | 2.03E-05 | 0.00E+00 | Inf | 100 |
| Steam Economizer | 2.16E-07 | 4.04E-09 | 6.30E-09 | 3.64E-06 | 3.85E-06 | 1.16E-06 | 5.58E-01 | 15.63 |
| Steam Evaporator | 2.48E-06 | 4.04E-09 | 6.65E-09 | 1.35E-05 | 1.60E-05 | 3.77E-06 | 6.43E-01 | 39.65 |
| Steam Pump | 3.20E-08 | 3.57E-08 | 4.11E-08 | 7.77E-07 | 8.09E-07 | 7.57E-08 | 1.54E-01 | 2.97E+01 |
| Steam Super heater | 1.30E-05 | 4.04E-09 | 2.69E-08 | 3.26E-06 | 1.63E-05 | 8.13E-07 | 5.65E+00 | 94.11 |
| Steam Turbine | 7.91E-06 | 2.68E-08 | 3.57E-08 | 3.69E-05 | 4.48E-05 | 3.27E-06 | 3.32E-01 | 70.74 |
| Topping Condenser | 2.74E-08 | - | - | - | - | - | - | - |
According to the results presented in Table 12, the turbine was highest from the point of view of environmental impact on equipment and environmental impact of exergy destruction. After the turbine, the evaporator had the highest environmental impact but its exergy destruction was zero.
In hybrid cycle mode, the solar panel ranked the highest in terms of environmental impact of the equipment, but the environmental impact of its exergy degradation is zero because the environmental impacts of fuel flow of the solar panel is zero. The steam evaporator in the geothermal-solar cycle has the highest impact on environmental exergy degradation.
Results of Emergoeconomic analysis are summarized in Table 14. According to table, the ORC turbine has the highest total monetary emergy rate. This component has low monetary emergy, but the emergy destruction in this component is highest and thus the turbine has the highest total monetary emergy rate. Therefore, improving this component can improve the monetary performance of the cycle. The condenser was at second place in the total monetary emergy rate point of view.
Table 14.
Emergo economic analysis results of the standalone geothermal cycle (first mode).
| component | (sej/s) | (sej/kJ) | (sej/kJ) | (sej/s) | (sej/s) | (sej/s) | (%) | |
|---|---|---|---|---|---|---|---|---|
| ORC Condenser | 8.0563E+08 | - | - | - | - | - | - | - |
| ORC Evaporator | 3.1072E+08 | 1.7485E+06 | 1.9491E+06 | 1.4216E+10 | 1.4526E+10 | 1.1845E+08 | 0.1147 | 20.78 |
| ORC Pump | 1.2555E+09 | 4.6850E+06 | 8.2696E+06 | 3.8944E+09 | 5.1499E+10 | 9.7683E+08 | 0.7651 | 56.24 |
| ORC Recuperator | 2.7547E+07 | 3.0382E+06 | 4.6676E+06 | 1.3205E+09 | 1.3480E+09 | 4.4302E+08 | 0.5363 | 5.85 |
| ORC Turbine | 6.1952E+09 | 3.0382E+06 | 4.6850E+06 | 2.0509E+10 | 2.6705E+10 | 3.1915E+09 | 0.5420 | 66.00 |
Figure 4 illustrates the results of the exergo-economical and emergo-economic analysis of the equipment used in the standalone geothermal cycle (the first case) as well as the hybrid geothermal-solar cycle (the second state); each diagram showing the close similarity of the results. For example, in the standalone geothermal cycle, the ORC turbine had the highest value (6.02E-04 $/s and 3.1915E+09 sej/s) and the ORC condenser had the lowest value for both exergo and emergo-economic analysis. Exergy destruction in turbine was due to heat generated by fluid impact on turbine blade, fluid friction passing through surface of blade, head loss of nozzle and frictional resistance by air. Also in the hybrid geothermal-solar cycle, the evaporator (4.50E-03$/s and 4.4699E+09 sej/s) and turbine (2.40E-03 $/s and 2.1920E+09 sej/s) had the highest value of exergo and emergo economic. Solar power plant was ranked the lowest. Increased pressure drop of refrigerant flow inside coil or evaporator pipes is the main cause of its exergy destruction and can adversely affect system performance. Solar power plants have only an initial cost; and because solar energy is freely available to the system, so its exergy and emergy destruction is very low.
Figure 4.
Comparison between exergo and emergo economic analysis results (first and second mode).
Table 15 indicates that the solar power plant has the highest emergy destruction, whereas the coupling system (condenser, geothermal recuperator, and evaporator) has only a minor amount of exergy destruction. In the middle of the day, the monetary destruction of the coupling cycle is at its highest when the maximum monetary emergy occur in the upstream cycle condenser and the ORC cycle evaporator, respectively. At night, the destruction is only due to heat transfer in the binary cycle evaporator because the condenser does not work, and its destruction is minimal.
Table 15.
Emergo economic results of each component in the Geothermal-Solar cycle (second mode of simulation).
| Component | (sej/s) | (sej/kJ) | (sej/kJ) | (sej/s) | (sej/s) | (sej/s) | (%) | |
|---|---|---|---|---|---|---|---|---|
| Coupling Pump | 1.4997E+06 | 2.2250E+07 | 2.9502E+07 | 9.3771E+06 | 1.0877E+07 | 1.1743E+06 | 0.3260 | 56.08 |
| HTF Pump | 3.5546E+07 | 2.2250E+07 | 4.6195E+07 | 5.1367E+07 | 8.6913E+07 | 9.5054E+06 | 1.0762 | 78.90 |
| ORC Condenser | 8.1796E+08 | - | - | - | - | - | - | - |
| ORC Evaporator | 5.1369E+08 | 1.7485E+06 | 1.9634E+06 | 1.4301E+10 | 1.4814E+10 | 1.1080E+08 | 0.1229 | 31.68 |
| ORC Pump | 1.2691E + -09 | 4.6520E+06 | 8.2167E+06 | 3.9262E+09 | 5.1953E+09 | 9.8480E+08 | 0.7663 | 56.31 |
| ORC Recuperator | 3.0139E+07 | 3.0097E+06 | 4.3527E+06 | 1.3404E+09 | 1.3706E+09 | 3.9272E+08 | 0.4462 | 7.13 |
| ORC Turbine | 6.3565E+09 | 3.0097E+06 | 4.6520E+06 | 2.0858E+10 | 2.7214E+10 | 3.2509E+09 | 0.5457 | 66.16 |
| Solar Field (Collector) | 2.4059E+10 | 0.00E+00 | 4.7748E+06 | 0 | 2.4059E+10 | 0.00E+00 | Inf | 100 |
| Steam Economizer | 3.0915E+08 | 4.7903E+06 | 7.5493E+06 | 4.3072E+09 | 4.6164E+09 | 1.3780E+09 | 0.5760 | 18.32 |
| Steam Evaporator | 7.8142E+08 | 4.7903E+06 | 6.9755E+06 | 1.5981E+10 | 1.6763E+10 | 4.4699E+09 | 0.4562 | 14.88 |
| Steam Pump | 2.1089E+07 | 2.2250E+07 | 2.5722E+07 | 4.8482E+08 | 5.0590E+08 | 4.7202E+07 | 0.1561 | 30.88 |
| Steam Super heater | 2.6014E+08 | 4.7903E+06 | 6.8148E+06 | 3.8576E+09 | 4.1177E+09 | 9.6314E+08 | 0.4226 | 21.27 |
| Steam Turbine | 3.2151E+09 | 1.7948E+07 | 2.2250E+07 | 2.4753E+10 | 2.7968E+10 | 2.1920E+09 | 0.2397 | 59.46 |
| Topping Condenser | 1.2904E+09 | - | - | - | - | - | - | - |
Table 16 gives the results of the emerge-environmental analysis of standalone geothermal cycle. As can be seen, the turbine and ORC evaporator have the highest environmental destruction rate Therefore these components must be improved to increase the environmental performance of the cycle.
Table 16.
Emergo environmental calculations for standalone geothermal cycle (first mode).
| Component | (sej/s) | (sej/kJ) | (sej/kJ) | (sej/s) | (sej/s) | (sej/s) | (%) | |
|---|---|---|---|---|---|---|---|---|
| ORC Condenser | 8.4844E+06 | - | - | - | - | - | - | - |
| ORC Evaporator | 6.4780E+08 | 6.86E+09 | 7.5705E+06 | 5.5774E+10 | 5.6422E+10 | 4.6474E+08 | 0.1036 | 12.23 |
| ORC Pump | 5.7135E+05 | 1.1088E+07 | 1.4801E+07 | 9.2168E+09 | 9.2174E+09 | 2.3118E+09 | 0.3349 | 0.0247 |
| ORC Recuperator | 2.3728E+07 | 9.2533E+06 | 1.4007E+07 | 4.0217E+09 | 4.0454E+09 | 1.3493E+09 | 0.5138 | 1.73 |
| ORC Turbine | 7.3731E+08 | 9.2533E+06 | 1.1088E+07 | 6.2464E+10 | 6.3201E+10 | 9.7201E+09 | 0.1983 | 7.05 |
Table 17 represents the results of the Emergo-environmental analysis of the hybrid geothermal-solar system. The highest environmental emergy rate is belonged to solar power plant is, but its environmental destruction rate is minimal because it does not consume fuel.
Table 17.
Emergo environmental calculations for Geothermal-Solar cycle (second mode of simulation).
| Component | (sej/s) | (sej/kJ) | (sej/kJ) | (sej/s) | (sej/s) | (sej/s) | (%) | |
|---|---|---|---|---|---|---|---|---|
| Coupling Pump | 1.6503E+04 | 6.0885E+06 | 7.0048E+06 | 2.5660E+06 | 2.5825E+06 | 3.2133E+05 | 0.1505 | 4.88 |
| HTF Pump | 8.3033E+04 | 6.0885E+06 | 7.5151E+06 | 1.4056E+07 | 1.4139E+07 | 2.6011E+06 | 0.2343 | 3.09 |
| ORC Condenser | 8.5303E+06 | - | - | - | - | - | - | - |
| ORC Evaporator | 6.5174E+08 | 6.86E+06 | 7.5225E+06 | 5.6108E+10 | 5.6760E+10 | 4.3470E+09 | 0.0966 | 13.04 |
| ORC Pump | 5.7736E+05 | 1.0851E+07 | 1.4485E+07 | 9.1579E+09 | 9.1585E+09 | 2.2971E+09 | 0.3349 | 0.0251 |
| ORC Recuperator | 2.4876E+07 | 9.0513 + 06 | 1.2881E+07 | 4.0311E+09 | 4.0559E+09 | 1.1810E+09 | 0.4231 | 2.06 |
| ORC Turbine | 7.5142E+08 | 9.0513 + 06 | 1.0851E+07 | 6.2727E+10 | 6.3478E+10 | 9.7766E+09 | 0.1988 | 7.14 |
| Solar Field (Collector) | 3.3250E+09 | 1 | 6.5988E+05 | 1.1415E+04 | 3.3250E+09 | 6.3765E+03 | 6.5985E+05 | 100 |
| Steam Economizer | 2.9260E+07 | 6.6244E+05 | 1.0219E+06 | 5.9564E+08 | 6.2490E+08 | 1.9056E+08 | 0.5427 | 13.31 |
| Steam Evaporator | 3.3650E+08 | 6.6244E+05 | 1.0597E+06 | 2.2100E+09 | 2.5465E+09 | 6.1814E+08 | 0.5997 | 35.25 |
| Steam Pump | 7.0048E+05 | 6.0885E+06 | 6.7808E+06 | 1.3267E+08 | 1.3337E+08 | 1.2916E+07 | 0.1137 | 5.14 |
| Steam Super heater | 7.4364E+08 | 6.6244E+05 | 2.1136E+06 | 5.3346E+08 | 1.2771E+09 | 1.3319E+08 | 2.1906 | 84.81 |
| Steam Turbine | 4.5226E+08 | 5.2213E+06 | 6.0885E+06 | 7.2009E+09 | 7.6532E+09 | 6.3769E+08 | 0.1661 | 41.49 |
| Topping Condenser | 3.7184E+06 | - | - | - | - | - | - | - |
In Tables 12, 13, 16, and 17, the results of the exergo and emergy environmental analysis of the equipment used in the standalone geothermal cycle (the first mode) and the hybrid geothermal-solar cycle (the second mode) imply qualitative similarity in the cycles.
The quantitative dissimilarity in these cycles is due to the specific emergo-environmental coefficient. For example, in the standalone geothermal cycle, ORC turbine had the highest value of exergo and emergo environmental analysis (1.26E-06 pts/s and 9.7201E+09sej/s, respectively) and the ORC condenser ranked the lowest. Also in the hybrid geothermal-solar cycle, the evaporator (3.77E-06 pts/s and 6.1814E+08sej/s) and turbine (3.27E-06 pts/s and 6.3769E+08sej/s) had the highest amount of exergy degradation. Solar power plant was ranked lowest. Thus, using emergy concept with the advantage of the same global unit of sej/s, we obtain results that are qualitatively proportional to the exergo-environmental of the cycle.
4. Conclusion
In this research, simulation was performed by MATLAB software. The main design parameters are very accurate in both cases (standalone geothermal cycle and hybrid Geothermal-Solar cycle) and the calculated error for all parameters was below 5%. The simulation results are consistent with the net power of the plant for a given output.
Power generation systems have significant impacts on the environment, so analysis of these systems is environmentally necessary. The results of exergy degradation for the standalone geothermal cycle (first case) showed that the ORC turbine has the highest exergy degradation rate. Then the condenser and the evaporator had the highest environmental impact respectively (Bonyadi et al., 2018). In hybrid geothermal-solar cycle (second mode), the solar panel and turbine were ranked first and second with 56% and 9% of the total share of exergy cycle degradation, respectively. The results of economic exergy analysis also showed that solar power plant has the maximum cost of investment.
The results of the emerge-economic and emerge-environmental analysis of standalone geothermal cycle indicate that ORC turbines and evaporators need to be modified to improve cycle performance. Due to the heat generated by the impact of the fluid on the turbine blade, the friction of the fluid passing through the surface of the ORC turbine blade is highest.
Also, in the hybrid solar geothermal cycle, the monetary and environmental rate of emergy was the highest. During midday, monetary destruction of the coupling cycle energy is at its highest when the maximum monetary energy occurs in the upstream cycle condenser and the ORC cycle evaporator. Increasing pressure drop of refrigerant flow inside coil or evaporator tubes was the main cause of its economic exergy destruction.
At night, the destruction is only due to heat transfer in the binary cycle evaporator because the upstream cycle condenser does not work. Solar power plants have only an initial cost; on the other hand, solar energy is freely available, thus exergy destruction is very low.
The obtained results are similar to the results obtained by Rafat et al. (2019).
Declarations
Author contribution statement
Massomeh Alibaba: Performed the experiments.
Razieh Pourdarbani: Conceived and designed the experiments; Wrote the paper.
Mohammad Hasan Khoshgoftar Manesh: Analyzed and interpreted the data.
Guillermo Valencia Ochoa & Jorge Duarte Forero: Contributed reagents, materials, analysis tools or data.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Competing interest statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
References
- Aghbashlo M., Rosen M.A. Consolidating exergoeconomic and exergoenvironmental analyses using the emergy concept for better understanding energy conversion systems. J. Clean. Prod. 2018;172:696–708. [Google Scholar]
- Ayub M., Mitsos A., Ghasemi H. Thermo-economic analysis of a hybrid solar-binary geothermal power plant. Energy. 2015;87:326–335. [Google Scholar]
- Bassetti M., Consoli D., Manente G., Lazzaretto A. Design and off-design models of a hybrid geothermal-solar power plant enhanced by a thermal storage. Renew. Energy. 2018;128:460–472. [Google Scholar]
- Beier J., Thiede S., Herrmann C. Energy flexibility of manufacturing systems for variable renewable energy supply integration: real-time control method and simulation. J. Clean. Prod. 2017;141:648–661. [Google Scholar]
- Bicer Y., Dincer I. Development of a new solar and geothermal based combined system. Sol. Energy. 2017;127:269–284. [Google Scholar]
- Bonyadi N., Johnson E., Baker D. Technoeconomic and exergy analysis of a solar geothermal hybrid electric power plant using a novel combined cycle. Energy Convers. Manag. 2018;156:542–554. [Google Scholar]
- Boyaghchi F.A., Sabaghian M. Multi objective optimisation of a Kalina power cycle integrated with parabolic trough solar collectors based on exergy and exergoeconomic concept. Int. J. Energy Technol. Pol. 2016;12:154–180. [Google Scholar]
- Cardemil Jose Miguel, Cortes Felipe, Diaz Andres, Escobar Rodrigo. Thermodynamic evaluation of Geothermal-Solarhybrid power plants in northern Chile. Energy Convers. Manag. 2016;123:348–361. [Google Scholar]
- Carotenuto A., Figaj R., Vanoli L. A novel Geothermal-Solardistrict heating, cooling and domestic hot water system: dynamic simulation and energy-economic analysis. Energy. 2017;141:2652–2669. [Google Scholar]
- Cavalcanti E.J.C. Exergoeconomic and exergoenvironmental analyses of an integrated solar combined cycle system. Renew. Sustain. Energy Rev. 2017;67:507–519. [Google Scholar]
- Chen W., Liu W., Geng Y., Brown M.T., Gao C., Wu R. Recent progress on emergy research: a bibliometric analysis. Renew. Sustain. Energy Rev. 2017;73:1051–1060. [Google Scholar]
- Dincer I., Rosen M.A., Ahmadi P. Wile; 2017. Optimization of Energy Systems. [Google Scholar]
- Gonzalez G.I., Potes A.P., Junquera V.R., Lopez W.A., Pozo CA Del. Smart control system to optimize time of use in a solar-assisted air-conditioning by ejector for residential sector. Appl. Sci. 2018;8:350. [Google Scholar]
- Gonzalez-Mejia A.M., Ma X.C. The emergy perspective of sustainable trends in Puerto Rico from 1960 to 2013. Ecol. Econ. 2017;133:11–22. doi: 10.1016/j.ecolecon.2016.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodarzi A. Policy of the Islamic Republic of Iran in optimal utilization of renewable energy sources. J. Strat. Stud. Public Policy. 2017;7:23. [Google Scholar]
- Heberle F., Hofer M. Techno-economic analysis of a solar thermal retrofit for an air-cooled geothermal Organic Rankine Cycle power plant. Renew. Energy. 2017;113:494–502. [Google Scholar]
- Islam S., Dincer I. Development, analysis and performance assessment of a combined solar and geothermal energy-based integrated system for multigeneration. Sol. Energy. 2017;147:328–343. [Google Scholar]
- Javaherdeh Kourosh, Amin Fard Mehdi, Zoghi Mohammad. Thermo-economic analysis of organic Rankine cycle with cogeneration of heat and power operating with solar and geothermal energy in Ramsar. Modares Mech. Eng. 2016;16(13):56–63. [Google Scholar]
- Jeong Y.D., Yu M.G., Nam Y. Feasibility study of a heating, cooling and domestic hot water system combining a photovoltaic-thermal system and a ground source heat pump. Energies. 2017;10:1243. [Google Scholar]
- Jiang P., Zhanga F., Xu R. Thermodynamic analysis of a solar–enhanced geothermal hybrid power plant using CO2 as working fluid. Appl. Therm. Eng. 2016;116:463–472. [Google Scholar]
- Khalid F., Dincer I., Rosen M. Techno-economic assessment of a Geothermal-Solarmultigeneration system for buildings. Int. J. Hydrogen Energy. 2017;1(9):65–72. [Google Scholar]
- Lee K., Kangb E., Ghorabc M., Yangc L., Entchevc E., Lee E. Paper Presented at the 12th IEA Heat Pump Conference. 2017. Smart building heating, cooling and power generation with solar geothermal combined heat pump system. [Google Scholar]
- McTigue Joshua D., Castro Jose, Mungas Greg, Kramer Nick, King John, Turchi Craig, Zhu Guangdong. Hybridizing a geothermal power plant with concentrating solar power and thermal storage to increase power generation and dispatchability. Appl. Energy. 2018;228:1837–1852. [Google Scholar]
- McTigue Joshua, Castro Jose, Mungas Greg, King John, Kramer Nick, Wendt Daniel. Paper presented at the 44th Workshop on Geothermal Reservoir Engineering Stanford University, Stanford, California. 2019. Techno-economic assessment of geothermal power plants hybridized with solar heat and thermal storage. [Google Scholar]
- Mehrpooya M., Ghorbani R., Hosseini S.S. Thermodynamic and economic evaluation of a novel concentrated solar power system integrated with absorption refrigeration and desalination cycles. Energy Convers. Manag. 2018;175:337–356. [Google Scholar]
- Mohammadi A., Ahmadi M., Bidi M.H., Ghazvini M., Ming T. Exergy and economic analyses of replacing feedwater heaters in a Rankine cycle with parabolic trough collectors. Energy Rep. 2018;4:243–251. [Google Scholar]
- Ochoa G., Isaza-Roldan C., Duarte Forero J. A phenomenological base semi-physical thermodynamic model for the cylinder and exhaust manifold of a natural gas 2-megawatt four-stroke internal combustion engine. Heliyon. 2019;5(10):e02700. doi: 10.1016/j.heliyon.2019.e02700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ochoa G., Piero Rojas J., Duarte Forero J. Advance exergo-economic analysis of a waste heat recovery system using ORC for a bottoming natural gas engine. Energies. 2020;13(1):267. [Google Scholar]
- Pan H., Geng Y., Jiang P., Dong H., Sun L., Wu R. An emergy based sustainability evaluation on a combined landfill and LFG power generation system. Energy. 2018;143:310–322. [Google Scholar]
- Rafat E., Babaelahi M., Mofidipour E. Sustainability analysis of low temperature solar-driven kalina power plant using emergy concept. Int. J. Therm. (IJoT) 2019;22(3):118–126. [Google Scholar]
- Ramos A.L., Guarracino I.L., Mellor A.L., Alvarez D.I., Childs P.E., Daukes E.K., Markides C.H. Grantham Institute. Briefng paper; 2017. Solar-Thermal and Hybrid Photovoltaic-Thermal Systems for Renewable Heating; pp. 22–23. [Google Scholar]
- Sajid Z., Khan F., Zhang Y. Process simulation and life cycle analysis of biodiesel production. Renew. Energy. 2016;85:945–952. [Google Scholar]
- Valencia Ochoa G., Cárdenas Gutierrez J., Duarte Forero J. Exergy, economic, and life-cycle assessment of ORC system for waste heat recovery in a natural gas internal combustion engine. Resources. 2020;9(1):2. [Google Scholar]
- Wang X., Li Z., Long P., Yan L., Gao W., Chen Y., Sui P. Sustainability evaluation of recycling in agricultural systems by emergy accounting. Resour. Conserv. Recycl. 2017;117(B):114–124. [Google Scholar]
- Yan T., Xu X. Utilization of ground heat exchangers: a review. Curr. Sustain. Renew. Energy Rep. 2018;5:189–198. [Google Scholar]
- Zhang J., Ma L. Environmental sustainability assessment of a new sewage treatment plant in China based on infrastructure construction and operation phases emergy analysis. MDPI. Water. 2020;12:484. [Google Scholar]
- Zhang H., Guan X., Ding Y., Liu C. Emergy analysis of Organic Rankine Cycle (ORC) for waste heat power generation. J. Clean. Prod. 2018;183:1207–1215. [Google Scholar]
- Zhao H., Zhai X., Guo L., Liu K., Huang D., Yang Y., Li J., Xie S., Zhang C., Tang S., Wang K. Assessing the efficiency and sustainability of wheat production systems in different climate zones in China using emergy analysis. J. Clean. Prod. 2019 [Google Scholar]
- Zyvith Z.O., Trevena M.A., Lamantia R.Y., Sharp L.A., Yong A.N., Haghani S.A. Paper Presented at the 2018 ASEE Mid-Atlantic Section Spring Conference. American Society for Engineering Education; Washington, District of Columbia: 2018. Geothermal heating/Cooling in massachusetts general hospital. [Google Scholar]