Effects of network topologies on stochastic resonance in feedforward neural network

Abstract

The effects of network topologies on signal propagation are studied in noisy feedforward neural network in detail, where the network topologies are modulated by changing both the in-degree and out-degree distributions of FFNs as identical, uniform and exponential respectively. Stochastic resonance appeared in three FFNs when the same external stimuli and noise are applied to the three different network topologies. It is found that optimal noise intensity decreases with the increase of network’s layer index. Meanwhile, the Q index of FFN with identical distribution is higher than that of the other two FFNs, indicating that the synchronization between the neuronal firing activities and the external stimuli is more obvious in FFN with identical distribution. The optimal parameter regions for the time cycle of external stimuli and the noise intensity are found for three FFNs, in which the resonance is more easily induced when the parameters of stimuli are set in this region. Furthermore, the relationship between the in-degree, the average membrane potential and the resonance performance is studied at the neuronal level, where it is found that both the average membrane potentials and the Q indexes of neurons in FFN with identical degree distribution is more consistent with each other than that of the other two FFNs due to their network topologies. In summary, the simulations here indicate that the network topologies play essential roles in affecting the signal propagation of FFNs.

Introduction

Stimulus representation, interpretation, transformation and transmission are the four key functions during the neural encoding and decoding processes (Aertsen et al. 1996; Zhou and Yu 2018). There are amounts of studies trying to exploring the neural mechanism underlying the four processes and plenty of results have been found (Dai et al. 2015; Yuan et al. 2016; Zhao et al. 2016; Mizraji and Lin 2017; Kim and Lim 2018; Malagarriga et al. 2019). One of the most attracting phenomena in neural systems is stochastic resonance (SR), which is considered as a possible way participating in the propagation of neural information (Li et al. 2007; Guo 2011; Wang et al. 2012). It is found that the transmission of neural signal can not only be helped by noise with suitable intensity, but also be inhibited by noise at a certain intensity (e.g., the inverse stochastic resonance, ISR) (Yu et al. 2001; Uzuntarla et al. 2013; Qin et al. 2014; Uzuntarla et al. 2017a; Zhao et al. 2017; Yao and Ma 2018). Recently, a double ISR phenomenon induced by dynamic synaptic currents is observed in the Hodgkin-Huxley neuron model (Uzuntarla et al. 2017b). Due to the importance of ISR in signal propagation, a general theoretical framework that can be used to explain the ISR in natural systems is carried out, where it stated that the occurrence of ISR requires one metastable minimum with higher activity and the other global minimum with the lowest activity (Torres et al. 2020). As noise is inevitable in neural systems, different kinds of noises are used to represent the physiological disturbance in neural systems during the both the theoretical and experimental investigations. For example, by applying a time varying electric field and a Gaussian noise to a hippocampal slice from mammalian brain, Gluckman et al. (1996) found that resonance could be observed as a response of the neuronal network. Based on a scale-free network, Perc M. verified that the Gaussian noise can optimally assist the whole network to resonance with the network’s pacemaker (Perc 2008). Li et al. (2009) found that the Gaussian noise can enhance the propagation of weak signal in a self-organization network, and the evolved network can further increase the efficiency of signal propagation. Besides the effects of Gaussian white noise, the non-Gaussian noise is attracting attentions recently, which shows similar effects with that of Gaussian white noise on the detection or propagation process of weak signal (Guo 2011; Yao et al. 2017; Zhao et al. 2019). Therefore, these studies indicate that the effects of noise should be considered during the model simulation, which may make the results more abundant and meaningful.

Recently, the effects of network structure on signal propagation in neural networks become one of the most focused points due to its essential role in affecting the signal propagation in neural systems. Multilayer FFN, which contains multi-groups of neurons with convergent-divergent connections between adjacent groups, is usually used to study the propagation of neural signal (Guo and Li 2009; Kumar et al. 2010). FFN has reproduced many physiological phenomena due to its structure that neural information is propagated from one layer to the next layer. As the two main ways for the transmission of neural information in neural systems, both the rate coding and temporal coding are found in FFNs (Kumar et al. 2008). There are also studies about the optimal network parameters of FFNs for the transmission of neural signal, including the influence of neuronal heterogeneity and cell size, the effects of the linkage probability and synaptic strength between neurons (Reyes 2003; Masuda and Kori 2007; Ozer et al. 2010; Qin et al. 2018a). However, most of them are based on FFN with uniform linkage distribution between the adjacent layers. Little attention is paid on the effects of degree distribution on the transmission of neural signal, especially when the external stimuli are applied to the FFNs. Considering the real linkage between neurons, different neurons should have distinct numbers of presynaptic neurons and postsynaptic neurons, which are not identical for each neuron. In addition, there are many studies verified the distinct effects of network structures (e.g., the randomly connected network, scale-free network and the “rich-club”) on signal propagation (Deng et al. 2010; van den Heuvel and Sporns 2011; Mofakham et al. 2016; Kim and Lim 2019a). Therefore, it makes sense to study the effects of network topologies on signal propagation in FFNs by modulating both the in-degree distribution and out-degree distribution of neurons as identical, uniform and exponential distribution, which are similar with degree distribution of the randomly connected network, scale-free network and the recently “rich-hub” respectively.

In this study, we first established FFNs with three topologies, i.e., the in-degree and the out-degree of three FFNs are set differently as identical, uniform, and exponential respectively. Then the transmission of the same signal in three noisy FFNs is studied in detail. Finally, the discussion and conclusion are given.

Model and method

FFN model

As shown in Fig. 1, the multi-layer FFN is utilized to mimic the propagation of neural information between different neuron groups (Diesmann et al. 1999; Li and Greenside 2006). Here, each layer of the FFN contains 200 FHN neurons, and there are not recurrent or feedback couplings between neurons of different layers. Neurons in each layer only receive synaptic currents from its previous layer. The model of FFN is given in Eq. (1) as:

$$\begin{array}{cc}\hfill \epsilon \frac{d{x}_{i,j}}{\mathit{dt}}& =x_{i,j}-\frac{x_{i,j}^3}{3}-y_{i,j}+I_{i,j}^{\mathit{syn}}\left(t\right)\hfill \\ \hfill \frac{d{y}_{i,j}}{\mathit{dt}}& =x_{i,j}+a-b{y}_{i,j}+I_{\mathit{ext}}\left(t\right)+{\xi }_{i,j}\left(t\right)\hfill \\ \hfill I_{i,j}^{\mathit{syn}}\left(t\right)& =-\sum _{k=1}^{N_{i,j}^{\mathit{syn}}}{g}_{\mathit{syn}}\alpha \left(t-t_{i-1,k}\right)\left(x_{i,j}-V_{\mathit{syn}}\right)\hfill \\ \hfill \end{array}$$ 1

Here, the layer indices are $i=1,2,3\dots N_L$, and the neuron indices in each layer are $j=1,2,3\dots N$. $x_{i,j}$ and $y_{i,j}$ represent the membrane potential and recovery variable of neuron j in the layer i, and the total synaptic current of this neuron is $I_{i,j}^{\mathit{syn}}\left(t\right)$. $I_{\mathit{ext}}\left(t\right)$ stands for the external stimuli added to neurons, which has a form as $I_{\mathit{ext}}\left(t\right)=A·sin\left(2\pi /T_s·t\right)$. ${\xi }_{i,j}\left(t\right)$ represents the Gaussian white noise with zero mean and power D (i.e., $〈{\xi }_{i,j}\left(t\right){\xi }_{i,j}\left(t^{\prime }\right)=2D\delta \left(t-t^{\prime }\right)〉$), which is employed to simulate the physiological noise in neural systems. In Eq. (1), $\alpha \left(t\right)=\left(t/\tau \right)e^{-t/\tau }$, where $\tau$ represents the time constant of synapses. Moreover, $N_{i,j}^{\mathit{syn}}$ represents the number of synaptic couplings from (i −1)th layer to jth neuron in ith layer. $g_{\mathit{syn}}=0.04$ and $\tau =0.2$ are set for the connection strength $g_{\mathit{syn}}$ and time constant $\tau$, which are large enough to propagate signal through FFNs. $V_{\mathit{syn}}$ represents the synaptic reversal potential, which can control the kind of synapse. In this study, only excitatory synapses are used where the synaptic reversal potential is set as $V_{\mathit{syn}}=0$ (Qin et al. 2011). In addition, parameter $a$ is a critical parameter that could substantially influence the neuronal dynamics. When $a\approx 0.69$ ($\epsilon =0.08$ and $b=0.45$), the Andronov-Hopf bifurcation occurs in FHN neuron model. When $a>0.69$, the neuron can be excited with external stimuli or synaptic currents. When $a<0.69$, a stable periodic solution can be obtained from the neuron system. To make the neurons be excitable, the parameters for the neuronal model are set as $\epsilon =0.08$, $a=0.75$, and $b=0.45$ (Qin et al. 2014). The connection probability P between layers is set to 0.15, which means that there are 6000 synaptic connections between adjacent layers. In addition, the summation of $N_{i,j}^{\mathit{syn}}$ of the neurons in each layer is identical for all three FFNs.

Fig. 1.

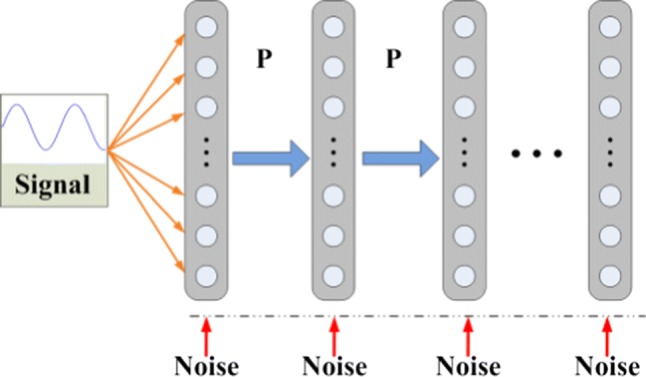
The network structure with linkage probability P between layers. There are no connections between neurons in the same layer

To study the effects of network topologies on signal propagation, FFNs with three degree distributions for neuron couplings are constructed by setting the connections between neurons. In detail, the total number of incoming connections for each layer in the three FFN topologies is set the same, but the in-degree and out-degree distributions of the neurons in each layer differ as identical, uniform or exponential distributions. The uniform distribution is defined with numbers drawn from the standard uniform distribution on the interval [0, 2 *P*N], where N is the number of neurons in one layer (here, $N=200$, $P=0.15$). Thus, the maximum in-degree of a neuron allowed in the uniform distribution is 60. The third in-degree distribution of neurons used here is drawn from the exponential distribution with a probability density function as $f\left(c\right)=\lambda e^{-\lambda c}$, and mean of $E\left(c\right)=1/\lambda$, where $\lambda$ is set as $1/\left(P\ast N\right)$.

Q Index

To evaluate the effects of topologies on SR in the FFNs, the Fourier coefficient Q is calculated as a function of the average membrane potential of neurons in one layer of the network. The Q index is frequently used to evaluate the transport of the information in the neural network, which is a compact tool with the form as follows (Gammaitoni et al. 1998; Deng et al. 2010)

$$\begin{array}{cc}\hfill Q_{sin}& =\frac{\omega }{2n\pi }{\int }_0^{2\pi n/\omega }2X\left(t\right)sin\left(\omega t\right)dt,\hfill \\ \hfill Q_{cos}& =\frac{\omega }{2n\pi }{\int }_0^{2\pi n/\omega }2X\left(t\right)cos\left(\omega t\right)dt,\hfill \\ \hfill Q& =\sqrt{Q_{sin}^2+Q_{cos}^2},\hfill \\ \hfill \end{array}$$ 2

Here, X(t) is the average membrane potential of neurons in one layer. n represents the number of periods, and $\omega =2\pi /T_s$, where T_s is the time cycle of the weak signal I_Ext(t). A big Q value indicates that there is a better phase synchronization between the average membrane potential and the input signal. Besides, the Q_j index is also calculated for each neuron in the network, which has the form as

$$\begin{array}{cc}\hfill Q_{j,sin}& =\frac{\omega }{2n\pi }{\int }_0^{2\pi n/\omega }2X_j\left(t\right)sin\left(\omega t\right)dt,\hfill \\ \hfill Q_{j,cos}& =\frac{\omega }{2n\pi }{\int }_0^{2\pi n/\omega }2X_j\left(t\right)cos\left(\omega t\right)dt,\hfill \\ \hfill Q_j& =\sqrt{Q_{j,sin}^2+Q_{j,cos}^2},\hfill \\ \hfill \end{array}$$ 3

In Eq. (3), X_j(t) represents the mean value of the membrane potential of neuron j in a certain layer, and Q_j is the Fourier coefficient of this neuron. Other parameters used in this paper are given in each case.

Results

Propagation of firing patterns in three FFNs

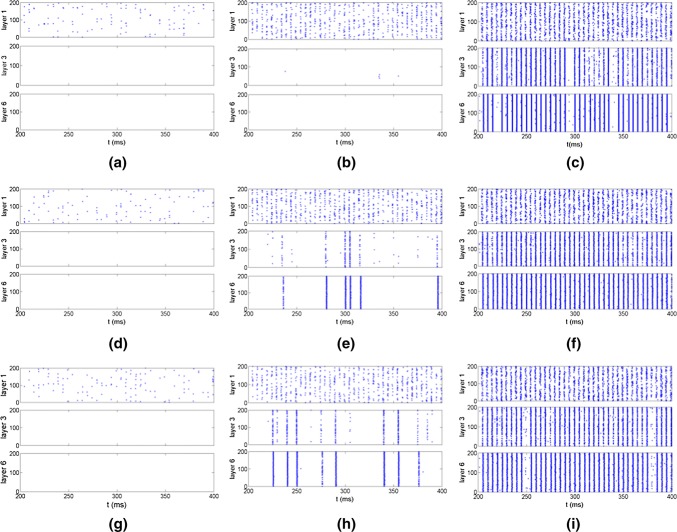
The effects of the network topologies and noise intensities on firing patterns of neurons are investigated based on three FFNs, i.e., the distributions of in-degree and out-degree of three FFNs are identical, uniform and exponential from up to bottom as shown in Fig. 2. When the noise intensity is lower, the firings of neurons in three FFNs are sparse and irregular (Fig. 2a d, g). With the increase of the noise intensity, the firing times of neurons are increased and become regular (Fig. 2b, e, h). Several firing trains are formed and transmitted successfully through layers in FFNs with uniform and exponential distributions, but there is not firing train in FFN with identical distribution. When the noise intensity is increased further, much more firing trains are formed and transmitted through layers, which indicates the important role of noise in the signal transmission (Fig. 2c, f, i). Meanwhile, it also displays the distinct effects of three topologies on the propagation of neural information in FFNs.

Fig. 2.

Raster plots of the spike trains for three representative layers in FFNs with three topologies as identical (a–c), uniform (d–f) and exponential (g–i) respectively. a Noise intensity D = 10⁻⁴; bD = 10^−3.7; cD = 10^−3.4; dD = 10⁻⁴; eD = 10^−3.7; fD = 10^−3.4; gD = 10⁻⁴; hD = 10^−3.7; iD = 10^−3.4. The connection probability between neurons is set as P = 0.2. The input signal here has the form as $I_{\mathit{ext}}\left(t\right)=Asin\left(2\pi /T_s·t\right)$, where A = 0.08 and T_s= 5 (Qin et al. 2014)

Effects of degree distribution on signal propagation in three FFNs

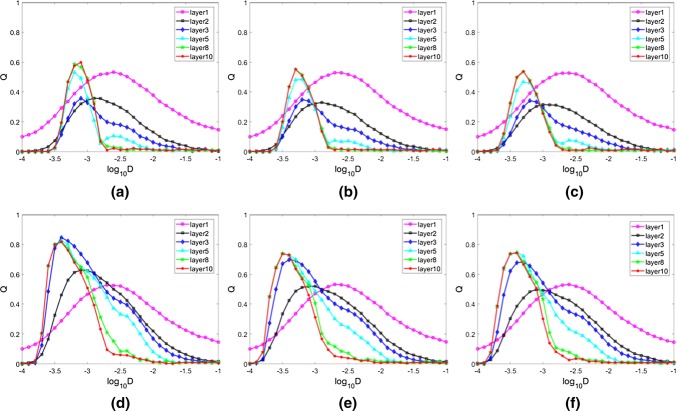
To study the effects of degree distribution on signal propagation through layers, Q index is calculated for each layer of three FFNs (Fig. 3). Bell-shaped curve is found for different layers of three FFNs, which indicate the appearance of SR. Meanwhile, it can be noticed that the optimal noise intensity for each layer is decreased with the increase of layer index, which means SR is more easily appeared at the latter layers. This should be related with the amplification effect of FFN, where the neuronal activities in the latter layers of the network become stronger and can easily be resonated with each other. It is also found that the changes and the distributions of Q indexes of different layers for three topologies are similar when the connection probability is set as P = 0.15 (Fig. 3a–c). When the connection probability between neurons is increased (Fig. 3d–f), the phase synchronization between the average membrane potential of the layers and the input signal is also enhanced for the latter layers. Meanwhile, the optimal noise intensities for different layers of three FFN topologies are decreased. This is reasonable that increased connectivity probability leads to the increase of firing activities of neurons, which further facilitates the resonance between neurons and the input signal. Moreover, it can be found that the maximal Q indexes in latter layers of FFN with identical topology are higher than the other FFN topologies. This should be related with the different topologies of three FFNs, where neurons in FFN with identical degree distribution are easier to be synchronization with each other than neurons in other two FFN topologies. It should be stated that the firing patterns of the FFNs are almost stable in the 10th layer, therefore we just calculate the Q index to this layer.

Fig. 3.

Linear response Q as a function of noise intensity for different layers of FFNs with identical distribution (a ,d), uniform distribution (b, e) and exponential distribution (c, f) respectively. aP = 0.15; bP = 0.15; cP = 0.15; dP = 0.3; eP = 0.3; fP = 0.3. The input signal is set the same as A = 0.08 and T_s= 5 for a–f

Effects of the noise intensity and stimuli frequency on signal propagation in three FFNs

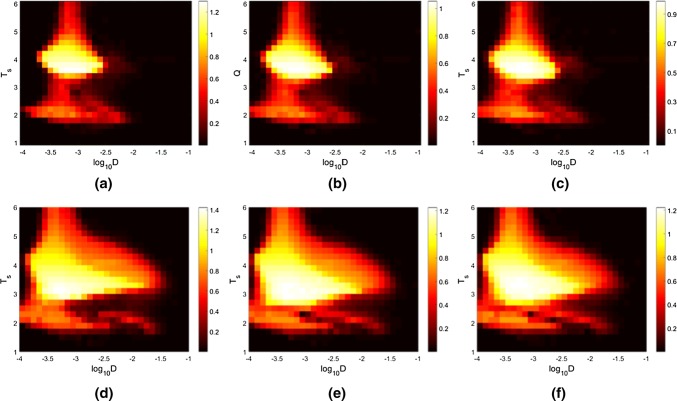
To be clearer with the effects of degree distribution on signal propagation in FFNs, Q is calculated as a function of both the noise intensity D and the time cycle T_s of input signal (Fig. 4), which can find the overall resonance performance corresponding to different parameters and the most optimal parameters for three FFNs. It is interesting that there appears an optimal region (the area with white and yellow color) where the phase synchronization between the activities of neuron and the input signal are strongest. Increasing the connection probability between neurons adds the number of synapses between layers of three FFNs, which further enhances the information propagation between layers and elevates the performance of SR (from Fig. 4a–c to d–f). In addition, it is found that the distributions of Q indexes for three FFNs are similar, but the maximal Q value for FFN with identical distribution is larger than that of FFNs with uniform and exponential distribution. This indicates the key effects of topologies on the propagation of input signal, where neurons in FFN with identical distribution are easier to be resonated with each other than the other two FFNs. The parameter distribution here also helps us to choose the suitable parameters for comparing the resonance performance between three FFNs.

Fig. 4.

Q as a function of noise intensity D and period T_s of input signal in FFNs with different connection probabilities. aP = 0.15, identical distribution; bP = 0.15, uniform distribution; cP = 0.15, exponential distribution; dP = 0.3, identical distribution; eP = 0.3, uniform distribution; fP = 0.3, exponential distribution. The input signal is set as A = 0.08

Relationship between the membrane potential and resonance performance for different neurons

To explore the corresponding relationship between the firing activity of each neuron and its in-degree, the average membrane potential and the Q index for each neuron are calculated for three FFNs, which can display the inner changes of the network at neuronal level. The parameters of neurons and the external input signal for three FFNs are set the same so that the network topology is the only one variation here. They are chosen from the bright region in Fig. 4 above, which are set as noise intensity D = 10⁻³, and input signal with A = 0.08 and time cycle T_s = 4. The results are shown in Figs. 5 and 6 below.

Fig. 5.

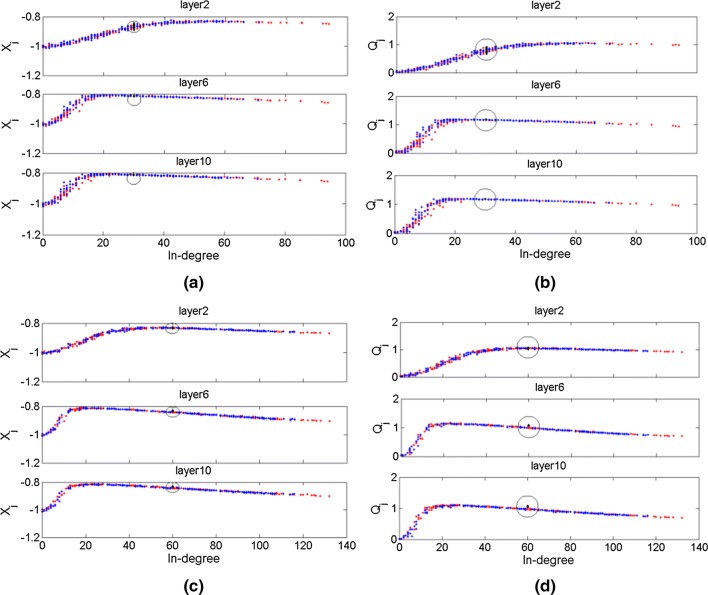
The average membrane potential of neurons in 10th layer (X_j) and response Q_j of each neuron versus the in-degree of neurons for three topologies. Points in three colors (Black, blue and red) indicate the three topologies (identical, uniform and exponent) respectively. aP = 0.15; bP = 0.15; cP = 0.3; dP = 0.3. The black cycle in figures are used to mark the location of average membrane potential and Q_j of neurons in FFN with identical distribution. The input signal is set as A = 0.08, T_s= 4, and the noise intensity is set as D = 10⁻³. (Color figure online)

Fig. 6.

Time series of membrane potential x_i,j of single neurons for different in-degree in three FFNs (identical, uniform and exponent) respectively. FFN with identical in-degree distribution: a–c the number of in-degree is the same as 30; FFN with identical in-degree distribution: d the number of in-degree is 10; e the number of in-degree is 20; f the number of in-degree is 60; g the number of in-degree is 10; h the number of in-degree is 20; i the number of in-degree is 60. P = 0.15. The input signal is set as A = 0.08, T_s= 4, and the noise intensity is set as D = 10⁻³. Here, the displayed amplitude of the input signal is enlarged 5 times to its real value

It can be found that the average membrane potential X_j of individual neurons in FFNs of uniform and exponent distribution is increasing with their in-degree obviously in layer 2 (Fig. 5a). For neurons in FFN with identical distribution, their average membrane potentials in layer 2 are distributed in a relatively smaller range (almost − 0.84 ~ − 0.90) than the average membrane potentials of neurons in other two FFNs. With the increase of the layer index (i.e., layers 6 and 10), the average membrane potentials of neurons in FFNs with uniform and exponential distributions are easier to attain the maximal value, then the average membrane potentials show a relatively decrease with the increase of in-degree. Meanwhile, the distribution range of average membrane potentials for neurons in high layers of FFN with identical distribution becomes smaller than that in layer 2. To be clear with the corresponding relationship between the resonance performance of neurons and their in-degree, Q_j of each neuron for three topologies are shown in Fig. 5b. It can be easily found that the variation trends of Q_j for neurons in three topologies are similar with that of their average membrane potentials, where the Q_j index in higher layers (i.e., layer 6 and 10) first increases with their in-degree and then decreases. The results here for three FFNs should be closely related with their topologies. When the in-degree distribution is identical for each neuron, the same number of synaptic connections makes the firing activities of different neurons become similar. For the firing activities of neurons in the other two FFNs, their in-degree distributions play main roles in the changes of firing activities and resonance performance in the initial layer (layer 2). Then, the amplification effects of FFNs take part in the propagation of weak signal in higher layers, which increases the number of neurons that have relatively high X_j. When the connection probability between neurons is increased, the average membrane potentials of neurons become quickly to be maximal and then Q_j decreases more obvious (comparing Fig. 5c, d with a, b). The increased connection probability leads to the increase of in-degree for most of neurons, thus increasing the amount of currents imposed on the postsynaptic neurons. But what leads to the decline for both the X_j and Q_j of neurons with large in-degree (> 20) is still unclear.

To be clear with this phenomenon, the firing waveforms of neurons with different in-degree in 10th layer are shown in Fig. 6. Neurons with three typical in-degree are selected to show the effects of in-degree of neuron on their firing waveforms. As the in-degree is the same for neurons in FFN of identical distribution, three neurons selected randomly in the 10th layer display similar waveforms with each other (Fig. 6a–c). Meanwhile, it can be easily found that the three neurons show good synchronization between their firing waveforms and the input signal. Neurons with different in-degree (10, 20 and 60) are selected from FFNs with uniform or exponential distribution respectively, which are distributed in the low, medium and high range of in-degree. For neurons with small in-degree (i.e., in-degree = 10), the phase synchronization between the firing of neuron and the input signal is worse than that of neurons in FFN with identical distribution. With the increase of in-degree, the phase synchronization between neurons and their firing waveforms become better. When the in-degree of neurons is further increased, the peak values of firing waveforms of neurons are decreased and the negative values in the trough of waveforms are not changed, which lead to the decrease of X_j and Q_j index. It can also be found that the changing trends of synchronization between the firing waveforms of neurons and the input signal in FFN of exponential distribution are similar with that in FFN of uniform distribution.

Therefore, it is clear in Fig. 5 that the neurons with suitable in-degree (i.e., about 20) can resonate well with the input signal as their Q_j indexes are large. When the in-degree of neurons is further increased, the redundant input currents reduces the X_j of these neurons, thus, the resonance between the average membrane potentials and the input signal is also decreased.

Discussion and conclusion

Throughout this study, it is verified that the network topology can influence the signal propagation in noisy FFNs. In each layer of FFNs, the Q index firstly increases with the increase of noise intensity, then it decreases when the noise intensity is increased further, indicating the appearance of SR. The amplification effects of FFN also plays an important role in affecting the signal propagation, where SR is much stronger in latter layers than in the previous layers as the maximal Q values are increased obviously (Fig. 3). Meanwhile, optimal parameter regions for the appearance of SR are found for three FFNs (Fig. 4). When the noise intensity and the signal frequency are set near this parameter region, SR can be easily induced. Increasing the connection probability between neurons also enhances the SR performance, which is similar with the previous studies (Qin et al. 2014; Zhao et al. 2017). In addition, it is found that the network topology can influence the firing waveforms of neurons, which further affect the SR performance (Fig. 5).

SR has been widely studied based on theoretical and experimental methods. By modeling three bidirectional coupled neurons, Li et al. (2007) found that the chemical synapses are more efficient than the electrical coupling (i.e., the linear coupling) for the transmission of signal that is applied on partial neurons. There are also investigations shown the enhancement effects of weak signal propagation by heterogeneous aperiodic high-frequency disturbances based on different network structures, which includes the regular network, the small-world network and the random network (Deng et al. 2010). In addition, SR induced by sine-wiener noise (SW-noise) is also studied systematically in different network structures (Yao et al. 2018; Yao and Ma 2018). However, the effects of network topologies on SR are still unexplored, which are the main point of this investigation. By studying the effects of degree distributions on signal propagation, it can help us understand the mechanisms of signal propagation through FFNs with different network topologies. The results here suggest that the resonance phenomenon between the FFN with identical degree distribution and the external stimuli is better than other two FFNs. This should be related with the network structure that each neuron has the same number of presynaptic neurons and can receive similar input currents, which makes the firing activities of neurons be easier to behave synchronously with each other (Qin et al. 2018a, b; Zhao et al. 2018).

The results here should also be related with the attracting neurological physiotherapy (e.g., the photic stimulation; the transcranial electric stimulation, TES; and the transcranial magnetic stimulation, TMS) in recent years. Hannah et al. found that light-emitting diode (LED) flicked at gamma frequency (40 Hz) could reduce the concentration of amyloid-β(Aβ) and Aβ isoforms in a mouse model of Alzheimer’s disease (AD) (Iaccarino et al. 2016). As the concentration of Aβ is strongly related with the severity level of AD, their results give a promising prospect for the potential use of the neurological physiotherapy. The TES and the TMS have also attracted many researchers’ attention in these years, which include curing psychiatric diseases (Fregni et al. 2007), elevating the cognitive function (Thomson et al. 2015) and so on. The effectiveness of the electrical stimuli on influencing the firing activities of neurons have been verified by Bikson et al. (2004) using a cluster of neurons. There are also several research groups studied the influence of electrical stimuli on neural activities with both the experimental and modeling methods (Deans et al. 2007; Reato et al. 2010; Qin et al. 2012; Kim and Lim 2017). Through this study, it should be noticed that the stimuli position must be considered in detail before its application. Neurons with big in-degree and out-degree will be active and act like a pacemaker of the network that always gives stimulus to its postsynaptic neurons, which may further influence the activities of the network. Meanwhile, neurons with smaller in-degree and out-degree often have little influence on the activities of the network as it is often inactive and can affect few neurons. For the brain regions of human, similar phenomenon is also appeared where different brain regions have different functions and linkages with other brain regions. Therefore, considering the important role of the independent brain functions and its linkages with other brain regions, it is essential to optimally select the stimuli position before the physical stimuli are applied. With an optimal stimuli position, its modulation effects should be more obvious.

In summary, the results here showed that the influence of network topologies on SR. It also shed light on the usage of the neurological physiotherapy, where the effects of applied stimuli on the transmission of neural information should be more effective when the stimuli are applied at the suitable brain region. As the neurological physiotherapy often needs multiple repetitive sessions to get an optimal treatment, it should be significant to investigate the mechanism of the neural plasticity (Li and Small 2010; Luz and Shamir 2016; Kim and Lim 2018; Kim and Lim 2019a, b) underlying the use of physiotherapy in the future.