A Bayesian approach to accurate and robust signature detection on LINCS L1000 data

Abstract

Motivation

LINCS L1000 dataset contains numerous cellular expression data induced by large sets of perturbagens. Although it provides invaluable resources for drug discovery as well as understanding of disease mechanisms, the existing peak deconvolution algorithms cannot recover the accurate expression level of genes in many cases, inducing severe noise in the dataset and limiting its applications in biomedical studies.

Results

Here, we present a novel Bayesian-based peak deconvolution algorithm that gives unbiased likelihood estimations for peak locations and characterize the peaks with probability based z-scores. Based on the above algorithm, we build a pipeline to process raw data from L1000 assay into signatures that represent the features of perturbagen. The performance of the proposed pipeline is evaluated using similarity between the signatures of bio-replicates and the drugs with shared targets, and the results show that signatures derived from our pipeline gives a substantially more reliable and informative representation for perturbagens than existing methods. Thus, the new pipeline may significantly boost the performance of L1000 data in the downstream applications such as drug repurposing, disease modeling and gene function prediction.

Availability and implementation

The code and the precomputed data for LINCS L1000 Phase II (GSE 70138) are available at https://github.com/njpipeorgan/L1000-bayesian.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

The library of integrated network-based cellular signatures (LINCS) created a resource of cellular state changes under treatment of perturbagens, including chemical compounds, RNAis and CRISPRs (Keenan et al., 2018). L1000 assay is used in LINCS as a low-cost, high-throughput gene expression profiling on cells treated by perturbagens (Subramanian et al., 2017). The application of L1000 assay allows the profiling on more than 1 million samples treated with more than 50 000 different perturbagens across 98 cell lines. These profiles are processed into molecular signatures to represent cellular effects of certain perturbagen treatment (Duan et al., 2014). This comprehensive profiling provided by L1000 is widely used in drug discovery and repurposing, greatly facilitating large-scale pharmacology analysis (Duan et al., 2016; Wang et al., 2016).

L1000 assay measures the expression of 978 landmark genes with The Luminex FlexMap 3D platform, which can identify 500 different bead colors as tags for different genes. To measure all landmark genes within one scan, L1000 separately coupled two different gene barcodes to aliquots of the same bead color and mixed them with a ratio of 2:1. In consequence, two peaks in the distribution of fluorescent intensity (FI) are expected, and a deconvolution step must be involved to access the expression level of a certain gene. LINCS adopted the k-means clustering algorithm to separate all reads of the same beads color into two distinct components, and the median FI values are assigned to each gene. Although the k-means clustering gives a good estimation on most of the data, cases with unexpected ratio between two peaks, classified into more than two categories, or large overlap between peaks cannot be well solved (Jin and Malthouse, 2015). This problem limits the quality of z-score profiles, and adds to the difficulty of utilizing the massive data provided by L1000 assay.

After L1000 data was released, efforts have been made to improve the peak deconvolution process. Liu et al. (2015) developed a method based on Gaussian mixture model (GMM) to improve the accuracy of peak deconvolution. They assume that each gene’s fluorescent intensities follow a Gaussian distribution and thus each sample with two genes will subject to a bimodal Gaussian distribution. GMM can avoid overclustering problem in k-means but raises a new problem that the z-scores are highly sensitive to frequent isolated reads and become unreliable. To solve this problem, Li et al. (2017) developed an aggregate Gaussian mixture model (AGMM) and associated software (l1kdeconv). They added an outlier identification step before deconvoluting peaks with GMM to make the algorithm more robust. However, there are still cases where the peaks cannot be well identified. Thus, it is necessary to develop a new algorithm that improves the data process of L1000 assay.

In this study, we describe a novel peak deconvolution algorithm based on Bayes’ theorem and a probability based z-score inference method. We model each measurement as a random sample from the population with two different components mixed by 2:1 ratio. The likelihoods for all different FI values are calculated by Bayes’ theorem. Then z-scores are inferred by the probabilities for the genes to have differential expression. The gene expression profiles deconvoluted by our Bayesian method achieve higher similarity between bio-replicates and drugs with shared targets than those generated from the existing methods. This suggests that the molecular signatures from our method are of better consistency and less noisy, which will be helpful for further pharmacology analysis.

We develop a pipeline to process raw data from L1000 assay into z-scores. The code and the precomputed data for LINCS L1000 Phase II (GSE 70138) are available at https://github.com/njpipeorgan/L1000-bayesian.

2 Materials and methods

2.1 Datasets

In this study, we use L1000 small molecule compound data from Broad Institute LINCS L1000 Phase II datasets (https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE70138), which are categorized into five levels as follows.

Level 1 data contain raw FI values and 3D color codes for each bead measured by the Luminex FlexMap 3D platform. An FI value is proportional to the transcript abundance of the gene associated with a type of beads. The types of the beads are inferred from their color codes and marked by numbers between 1 and 500 or marked by 0 meaning that they cannot be attributed to any one of the 500 types.

Level 2 data contain gene expression values for the 978 landmark genes, 976 of which are grouped into pairs and associated with 488 types of beads and the rest two of which are associated with two separate types of beads. A peak deconvolution process is employed to measure one or two expression values from the FI values for each type of beads in each well (Subramanian et al., 2017). A profile consisting 978 expression values is therefore obtained.

Level 3 data contain normalized gene expression values. The normalization process is divided into two parts: L1000 invariant set scaling (LISS) and quantile normalization. In LISS, all gene expression values in a well, i.e. a sample, are scaled to a set of predefined control genes. Then, the expression values are quantile normalized across all wells on each plate.

Level 4 data contain the z-scores for each gene with all expression values of that gene on a plate as the background. z-Scores indicate the levels at which genes are differentially expressed. They are then combined across biological replicates to obtain level 5 data.

2.2 Work flow

Based on a novel Bayesian analysis-based peak deconvolution and a new z-score inference method, we develop a pipeline to generate signature from raw data measured from L1000 assay. The pipeline takes raw FI data from LINCS L1000 datasets as input and gives a combined z-score profile for each experiment as its signature. As shown in Figure 1, our pipeline is composed of five steps as follows:

Fig. 1.

Illustration of pipeline for robust L1000 perturbagen signature detection

1. LISS and quality control. In this step, we perform a two-step linear scaling to calibrate the fluorescent intensities. Also, we identify the low-quality samples with goodness of fit ${\chi }^2>4.0$ or the slope a > 3.0.

2. Peak deconvolution. For beads coupled with two different transcript barcodes, a deconvolution step is involved to infer the peak position for each gene. Two probability distributions will be given to the transcripts as the estimations of their expression levels.

3. Quantile normalization. The shape of expression profile is standardized across all samples on the same plate so that different samples on the same plate are comparable to each other.

4. Probabilistic z-score inference. z-Scores are inferred by comparing the probability distribution for each gene with its background distribution. They represent relative gene expressions.

5. Combining replicates. z-Scores profiles from bio-replicates are combined into one signature by weighted average.

2.3 LISS and quality control

Since the amplification factor of each sample is different, L1000 added 80 control transcripts to each well, whose expression levels are empirically found to be invariant as calibration set. These genes are grouped into 10 levels with 8 each so that the median expression of each level should follow a similar increasing trend. The median expression levels in terms their fluorescent intensities are then compared with reference values and a relationship between them can be inferred by fitting various template functions on a logarithmic scale (Enache et al., 2018).

L1000 used a power law relation $y=a{x}^b+c$ in their pipeline, where x is the unscaled data and y the scaled data (Subramanian et al., 2017). In this study, we employ a two-step linear scaling as follows. First, we rescale the median expressions of 10 invariant sets by fitting them against the reference values linearly, and we obtain the averages and SDs of those scaled expressions within each perturbagen group, indicated by the first field of the distil_id of the sample. For example, the group of the sample with the distil_id (ID of an individual replicate profile) ‘LJP009_A549_24H_X1_DUO52HI53LO_A04’ is LJP009. The samples in the same perturbagen group are tested in the same batch. The resulting calibrated reference expressions shown in Figure 2a. Second, we fit the median expressions of the invariant sets against the calibrated expressions linearly and use this relation to rescale the expressions of the landmark genes.

Fig. 2.

(a) The calibrated reference expression values of the invariant set compared with the original ones. The error bars show the ranges corresponding to ±1 SD. The data points are horizontally offset for better visibility. (b) The distribution of the slope and ${\chi }^2$ of the fitted relationship between unscaled expression values and calibrated reference values

The two-step linear scaling have two advantages. First, since the median expressions of the invariant sets vary across plates (see Fig. 2a), calibrated reference expressions depending on the perturbagen groups are needed to capture this variability. Second, the linear scaling in the second step depends on only two fitted parameters, one less than the power law scaling.

We identify low-quality samples according to two parameters: the goodness of fit in terms of ${\chi }^2$ and the slope a of the relation, where an exceptionally large slope suggests a failed amplification. Figure 2b shows the distribution of these two parameters. L1000 level 1 data have 4.0% of the samples missing due to its quality control and we remove additional 3.0% of the samples with a > 3.0 or ${\chi }^2>4.0$ as our quality control.

2.4 Peak deconvolution

The Luminex FlexMap 3D platform can detect 500 different bead colors. To measure 978 transcripts in a sample within a single batch, almost all of them are grouped into pairs. For each pair, barcodes of two transcripts are coupled to beads with the same color and they are mixed in a ratio of 2:1. Therefore, the distributions of reads from these bead colors will form two peaks, whose expression levels should be measured by the peak deconvolution algorithm. In the design of L1000 system, the pairing of genes is optimized to minimize the confusion in peak deconvolution, but we note that it is inevitable that the peaks in some of the distributions are hard to be differentiated.

In this study, we develop a new peak deconvolution algorithm based on Bayesian probability model. L1000 samples typically have dozens of reads per bead color in each sample. In our model, each of these reads will either come from one of the genes that are coupled to that bead color or come from an arbitrary bead in the same sample due to color misidentification with a small rate ${\alpha }_{\mathrm{c}}\sim 1\%$. Suppose that N measurements are made for a specific color; we can derive the probability of the number of measurements that are associated with both genes $N_{\text{hi}},\hspace{0.17em}{N}_{\text{lo}}$ and the number of color misidentifications, or the background $N_{\text{bg}}$, where $N=N_{\text{hi}}+N_{\text{lo}}+N_{\text{bg}}$. Given that ${\alpha }_{\mathrm{c}}\ll 1$, we assume that $N_{\text{bg}}$ follows the Poisson distribution with $\lambda ={\alpha }_{\mathrm{c}}N$ and $N_{\text{hi}}$ follows the binomial distribution $B(N-N_{\text{bg}},2/3)$.

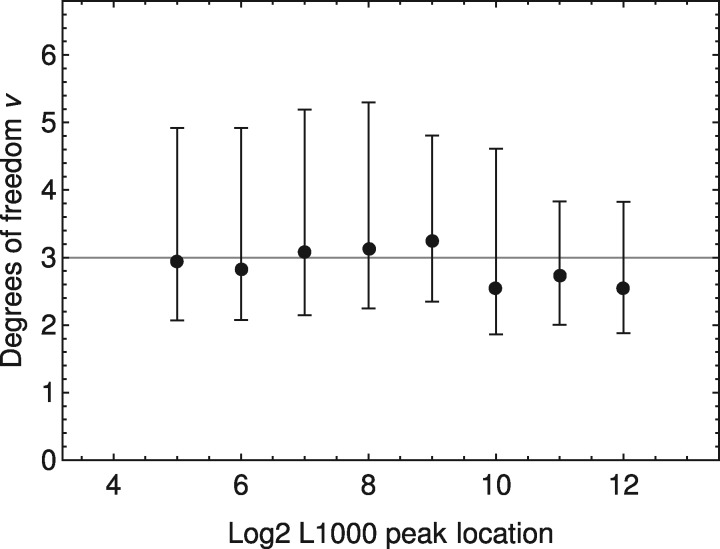
The shapes of the peaks reflect the spread of FI measurements, and they should depend on their expression levels only. We build the reference shapes of the peaks from L1000 level 2 data. First, we pick the profiles of reads that have well-separated peaks, i.e. the distance between the centers of two peaks is at least 3 in terms of log2 expression, so that individual peaks can be extracted with correct locations. Second, we fit the extracted peaks by Student’s t-distributions and check their best fitted degrees of freedom (DOF), shown in Figure 3. We find that a DOF of three is appropriate across all expression levels. Third, to measure the scale parameters of the distributions, we pick 11 discrete log2 expression levels between 4 and 12; for each expression level, we find all peaks with locations in its neighborhood (±0.01), gather all reads in the peaks into one profile, and measure its scale parameter and mean value by fitting a Student’s t-distribution with a fixed DOF of three. An empirical relation is measured between the scale parameter σ and the log2 expression value x, shown in Figure 4, which can be fitted by an analytical expression as

$${\sigma }_x=0.15+5.3{\mathrm{e}}^{-0.52x}$$ (1)

with a mean absolute error of 0.009. The shape of a single peak centered at log2 expression level x is therefore given by

$$f_x(u)=t(x,{\sigma }_x,\nu =3),$$ (2)

where u is the log2 FI. As for bead color misidentification, we assume that the distribution of these reads follows the distribution of all reads $f_{\text{bg}}(u)$ from the same well.

Fig. 3.

The median and 68% confidence interval of the best fit DOF of Student’s t-distribution. Each data point corresponds to the DOFs of all peaks within its neighborhood (±0.01 in terms of log2 peak location). Our choice of three DOF is shown by a gray line

Fig. 4.

The relationship between the scale parameter of the Student’s t-distribution and the log2 expression level, i.e. the center of an isolated peak

With the shape of peaks and background known, we can determine the probability of a read to be found with FI u_i described as a summation of probability for it to come from either of the two genes or background:

$$p(u_i|x_{\text{hi}},x_{\text{lo}})=\frac{N_{\text{hi}}}{N}{f}_{x_{\text{hi}}}(u_i)+\frac{N_{\text{lo}}}{N}{f}_{x_{\text{lo}}}(u_i)+\frac{N_{\text{bg}}}{N}{f}_{\text{bg}}(u_i),$$ (3)

where $x_{\text{hi}}$ and $x_{\text{lo}}$ are the center of the two peaks. The posterior distribution of $x_{\text{hi}}$ and $x_{\text{lo}}$ is given by

$$p(x_{\text{hi}},x_{\text{lo}}|\mathbf{u})=\frac{p(\mathbf{u}|x_{\text{hi}},x_{\text{lo}})p(x_{\text{hi}},x_{\text{lo}})}{p(\mathbf{u})},$$ (4)

where u denotes all of the measurements u_i ($i=1,2,\dots ,N$). We adopt a uniform prior on $x_{\text{hi}}$ and $x_{\text{lo}}$, and the posterior distribution becomes

$$\begin{array}{cc}p(x_{\text{hi}},x_{\text{lo}}|\mathbf{u})\hfill & =Ap(\mathbf{u}|x_{\text{hi}},x_{\text{lo}})\hfill \\ \hfill & =A\sum _{N_{\text{bg}},N_{\text{hi}}}\left(p(N_{\text{bg}},N_{\text{hi}})\prod _{i}p(u_i|x_{\text{hi}},x_{\text{lo}})\right),\hfill \end{array}$$ (5)

where A denotes a normalizing constant. We note that the calculation of the likelihood function is not trivial, and we show the simplifications of the function in Supplementary Materials.

To simplify further analysis, we marginalize $x_{\text{hi}}$ and $x_{\text{lo}}$ in all samples to get $p(x_g|\mathbf{u})$, or simply $p(x_g)$, where $g=1,2,\dots ,978$ are the indices of the genes. Compared to L1000 level 2 data, in which x_g have precise values, our algorithm of peak deconvolution gives two probability distributions, revealing the uncertainty of these estimations.

2.5 Quantile normalization

Quantile normalization standardize the shape of expression profile distributions among the wells on each plate. In L1000 level 3 data, quantile noramlization is done by first sorting the expression levels within samples, then setting the ith highest values in each sample by their median value.

In this study, we use a similar way to do quantile normalization. First, we add together all the marginal distributions of all genes in each sample to get the overall distribution of expression levels

$$p_{\text{total}}(x)=\frac{1}{978}\sum _{g=1}^{978}p(x_g).$$ (6)

Then, we define the relative FI r as

$$r(x)={\int }_{-\infty }^x{p}_{\text{total}}(x\prime )\mathrm{d}x\prime ,$$ (7)

which has a value in the interval of $[0,\hspace{0.17em}1]$. Finally, we standardize $p_{\text{total}}(x)$ as a uniform distribution U(0, 1) to get the quantile normalized distribution of individual expression levels as

$$p(r_g)=p(x_g){\left(\frac{\mathrm{d}{r}_g}{\mathrm{d}{x}_g}\right)}^{-1}.$$ (8)

2.6 z-Score inference

With quantile normalization done, the profiles of different samples are now comparable to each other. L1000 uses z-score to represent relative gene expression. In a normal distributed population, z-score is defined by $z_g=(x_g-{\mu }_g)/{\sigma }_g$, where μ_g denotes the average value of the population and σ_g the SD. Due to the fact that the distributions of gene expression typically have heavier tails, i.e. having more extreme values than the normal distribution, L1000 uses the median and median absolute difference (MAD) instead and defines the z-scores by

$$z_g=\sqrt{2}{\text{erf}}^{-1}\left(\frac{1}{2}\right)·\frac{x_g-\text{median}(X_g)}{\text{MAD}(X_g)},$$ (9)

which is equivalent to the original one in the case of normal distribution. A common choice of the population X_g is the expression levels x_g of all samples on a plate.

In our case, since we depict the expression level by a probability distribution instead of a single value, both definitions of the z-score cannot be used directly. However, we note that the z-score, assuming a normal distribution, is related to the quantile of the expression level in the population by

$$z_g=\sqrt{2}{\text{erf}}^{-1}(2q_g-1),$$ (10)

where the expected value of the quantile q_g is the probability that the expression level

$$q_g=P(r_g>R_g),$$ (11)

in which the probability distribution of R_g equals to the summation of those of all samples on a plate

$$p(R_g)=\frac{1}{N_{\text{sample}}}\sum _{s=1}^{N_{\text{sample}}}{p}^{(s)}(r_g).$$ (12)

2.7 Combining replicates

We follow the L1000 pipeline and use a weighted average in combining replicates based on the correlations among the bio-replicates. Denote the combined z-scores of all genes as ${\mathbf{z}}_{\mathrm{c}}$ and the z-scores of the ith bio-replicate as ${\mathbf{z}}^{(i)}$, we have

$${\mathbf{z}}_{\mathrm{c}}=\frac{{\sum }_{i=1}^{N_{\text{rep}}}{w}^{(i)}{\mathbf{z}}^{(i)}}{\sqrt{{\sum }_{i=1}^{N_{\text{rep}}}{(w^{(i)})}^2}},$$ (13)

where $N_{\text{rep}}$ is the number of replicates and the weights $w^{(i)}$ are defined as

$$w^{(i)}=\sum _{j\ne i}\text{Spearman}\hspace{0.17em}\text{Rho}\left({\mathbf{z}}^{(i)},{\mathbf{z}}^{(j)}\right).$$ (14)

3 Results

3.1 Peak deconvolution

3.1.1 Comparing Bayesian method with other methods on simulated data

We first construct a simulated dataset to test the performance of different peak deconvolution methods. We generate 10 000 samples with the characteristics of L1000 dataset as follows. For each simulated sample, reference peak positions are sampled from LINCS L1000 level 2 data. The probability distribution for each read in the sample is a mixture of two Student’s t-distributions centered on two peak positions with σ we fitted in Equation (1) and three DOF. Since the average number of reads in real data is around 50 and the ratio of noise reads is of order 1%, the number of reads we draw follows a Poisson distribution with mean of $49.5\hspace{0.17em}(50\times 99\%)$, then we add noise reads that are randomly picked from other samples, the number of which follows a Poisson distribution with mean of 0.5.

With this simulated dataset, we compare our Bayesian approach, k-means and AGMM for their performance in peak deconvolution. For our method, since the peak deconvolution process gives probability distributions instead of precise values for peak locations, we determine their locations by the maximum likelihood estimation (MLE) from marginal probability distributions, and the pipeline with this treatment is referred to as Bayesian MLE hereafter. Figure 5 shows the hexplot between the true and predicted peak positions from each method. We find that our Bayesian method shows a smaller mean squared error (MSE) and a higher correlation than two other methods.

Fig. 5.

Hexplots between the true peak and recovered peak positions from Bayesian MLE, k-means and AGMM. The darkness of the hexagon indicates the number of points in it. The Pearson correlation coefficient and MSE for each method are shown in each figure

We also tested on other simulated datasets with Gaussian distribution and other parameters if Student’s t-distribution, and the results are shown in Supplementary Figure S1. All results show that Bayesian method performs the best.

3.1.2 Comparing Bayesian method with other methods on real data

Unlike simulated data, we do not have true locations of the peaks for the real data. Hence, we test the performance of the three methods by comparing the peak locations they predicted with each other and find differences between them. We run three methods in a sample well REP.A028_MCF7_24H_X2_B25_D11, and the comparison between the methods are shown in Table 1.

Table 1.

The consistency in peak deconvolution between our Bayesian method, L1000 and AGMM

Case	Description	Number of genes
1	All are the same	773
2	All are different	22
3	Only L1000 is differenta	86
4	Only AGMM is differenta	79
5	Only Bayesian MLE is different a	18

^aThe last three cases show those where two of the methods give the same peak location while the third one gives a different locations.

When comparing the locations of a peak by two methods, we consider them to be different when the discrepancy in log2 expression value is larger than 0.2, which is based on the fact that the peaks have a typical scale parameter σ of $\gtrsim 0.2$. Also, all the methods are considered giving the same location for a peak when all three values are within ±0.2 range relative to the middle one.

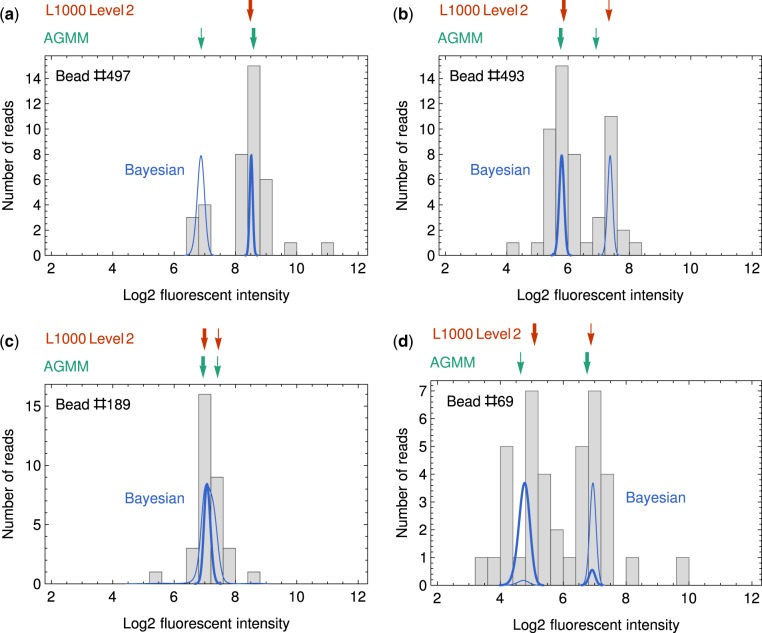
In most instances, all three methods agree with each other. It shows an overall consistency among all methods. Although all three methods may give a prediction that different from the other two, it happens less frequently to Bayesian MLE (18 verses 86 and 79 in Table 1). To further investigate the origin of those disagreements in Table 1, we show one typical example for each case in Figure 6. A full list of all peak locations by the three methods can be found in Supplementary Materials. Here, we give a brief analysis for each case:

Fig. 6.

Typical examples where discrepancies happens between Bayesian MLE, L1000 level 2 data and AGMM. For panel (a–d), the results from L1000 peak deconvolution and AGMM are shown in red and green arrows, where the thick and thin arrows indicate the peaks with high (2/3) and low (1/3) abundances, respectively. The results from our Bayesian method are shown as probability distributions in thick and thin blue curves, respectively. The peak locations used in Bayesian MLE are the fluorescent intensities where the probability distributions reach their maxima. The examples are from well REP.A028_MCF7_24H_X2_B25_D11

• Figure 6a is an example for Case 3 in Table 1. k-Means clustering sometimes fail to give two clusters of reads. In those scenarios, L1000 sets the expression level of both genes to be the median of all reads, which yields a different result from Bayesian MLE and AGMM.

• Figure 6b is an example for Case 4 in Table 1. AGMM sometimes fails to identify the peaks that are not well separated. In the case of Figure 6b, AGMM gives a scale parameter σ of 0.55, which overestimates the actual peak widths, and it makes AGMM to separate the peaks at a wrong location.

• Figure 6c is an example for Case 5 in Table 1. When the two peaks are mostly overlapped, Bayesian MLE tends to predict the peaks at roughly the same location, while both L1000 and AGMM tends to give two different peak locations. In this case, L1000 and AGMM agree with each other and Bayesian MLE gives a different result.

• Figure 6d is an example for Case 2 in Table 1. All three methods gives different predictions for the high abundance peak in this case. For L1000, reads with log2 FI smaller than 4 are discarded so the peak location is biased to have a higher expression. For AGMM, the separation of the two peaks is not correct, and the locations of the two peaks are flipped.

From these cases, we find that except when the information is not enough to decide the peak locations well, the Bayesian method always gives reasonable predictions but L1000 level 2 and AGMM sometimes make mistakes. It explains why the Bayesian MLE data have a lower chance of being different from two other methods simultaneously. We also find that the rate of disagreement between our method and L1000 is around 10%, which should be considered crucial. Given that the genes regulated under each treatment is very limited, the 10% noise signal will largely affect the quality of the dataset.

3.2 Similarity between replicates

After locating peaks from raw FI values, we quantile normalize the data and infer their z-scores. The z-scores can be interpreted as relative gene expression levels, where significantly up/downregulated genes will get a large positive/negative z-scores. The z-scores also serves as the final feature of expression for each sample.

L1000 dataset typically include three bio-replicates for each experiment. Since they are expected to be similar to each other in gene expression, a validation of this statistical property indicates good quality of the data and the processing pipeline. Here, we adopt gene set enrichment analysis (GSEA; Subramanian et al., 2005) to compare gene expression profiles, which is a non-parametric statistical method widely used in analyzing gene expression data. GSEA yields a score for the enrichment of a gene set (called a query hereafter) in an expression profile. Here, we directly take the z-scores as the expression profiles and build the queries by taking an equal number of genes that are most up/downregulated in terms of their z-scores. The higher enrichment score a query get, the more similar the query and expression profile are.

L1000 performs multiple experiments with each perturbagen on multiple cell lines with different doses. To maximize the difference between the perturbagens, we take experiments with the maximum dose in this performance test. We include three methods in the performance evaluation.

1. L1000 standard pipeline: We directly take z-scores from L1000 level 4 data.

2. Bayesian pipeline: We calculate the probabilistic distributions of the peak locations and employ specialized quantile normalizatoin and z-score inference as described in Sections 2.5 and 2.6.

3. Bayesian MLE pipeline: We obtain peak locations by the MLE from marginal probability distributions as in Section 3.1.1 and adopt L1000 quantile normalization and z-score inference methods.

We note that the most significant difference between Bayesian pipeline and Bayesian MLE pipeline is the modeling of peak locations. Because Bayesian MLE uses precise values to characterize peak locations like k-means and AGMM and performs the best in peak deconvolution tests (see Section 3.1), we use it as the control to study the impact of our probabilistic modeling together with specialized quantile normalization and z-score inference methods.

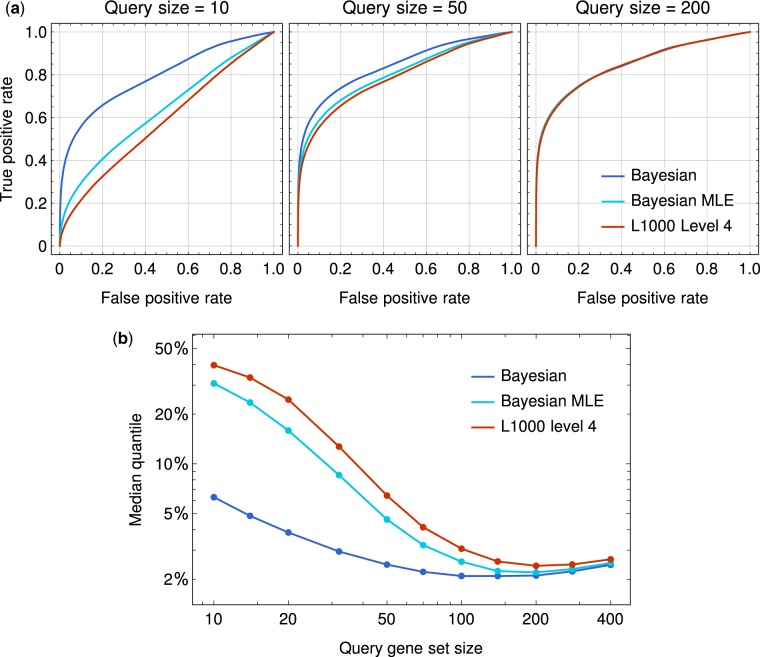
We test the performance of the three methods as follows. For each sample, we obtain its background distribution of GSEA scores by querying the sample against all other samples in the same cell line. Then we query the sample against one of its bio-replicates. For each false positive rate (FPR), i.e. a certain ratio of the highest background scores being picked, a true positive rate (TPR) can be calculated as the probability that its bio-replicate has a GSEA score higher than the threshold. Figure 7a shows the performance of all three methods with different query sizes. Among all query size we tested, our Bayesian method has higher TPR at the same FPR and the performance difference is the most significant when the query size is small.

Fig. 7.

(a) Receiver operating characteristic (ROC) curves for replicates identification. Expression profiles from our Bayesian pipeline, Bayesian MLE and L1000 standard pipeline are tested with GSEA under different query sizes. The three methods are labeled as Bayesian, Bayesian MLE and L1000 level 4 in the figure. (b) The comparison of the median quantile (FPR at $\text{TPR}=0.5$)

To better illustrate the performance of three methods under different query sizes, we follow Filzen et al. (2017) to show the median quantile of GSEA scores between bio-replicates, which is equivalent to the FPR at $\text{TPR}=0.5$. As shown in Figure 7b, the median quantile of bio-replicates by all methods become lower as the query size increases up to 200. We notice that the performance of Bayesian MLE is more similar to that of L1000 than the Bayesian method. As the only difference between Bayesian and Bayesian MLE is whether peak positions are determined for z-score calculation, we conclude that the probabilistic z-score inference have a great impact on the performance.

We find that the median quantile by our Bayesian method varies slowly with the query size, while L1000 method have a big improvement when the query size reaches above 50, after which its performance gets close to Bayesian. It indicates that the genes in the query set from our method is more informative when the query size is limited, and the most up/downregulated genes are more stable across bio-replicates by our method. Note that the robustness to small number of query genes is important in real applications. Novel discoveries in pharmacology often involve chemicals and/or cell lines that have not been tested in the L1000 assay, and in such cases, there is no guarantee that a large number of genes can be matched.

3.3 Similarity between perturbagens with shared targets

L1000 dataset is widely used in drug repurposing and discovery. Signatures in L1000 dataset are compared to each other or target gene sets to estimate the similarity between drugs. To demonstrate the performance in practical problems, we test if our method give similar z-score features for similar perturbagens.

Drug target information is obtained from ChEMBL23, and the drugs with the same target annotation are considered similar. In L1000 Phase II dataset, we find 77 groups of similar drugs with an average group size of 2.6 and take them as positive identifications. The list of these groups of similar drug can be found in Supplementary Table S1. We use a similar method in measuring the performance as Section 3.2 for the combined z-scores from our Bayesian pipeline, Bayesian MLE and L1000 level 5 data. But since the perturbagens are not the same for each cell line in the experiments, we use all the samples as the background instead of separating cell lines.

As shown in Figure 8a, the Bayesian method performs the best among three methods especially when the query size is small and in the high specificity (low FPR) region. At a query size of 100, TPR of our Bayesian method at $\text{FPR}=5\%$ is 16.9%, 41% higher than the TPR from L1000 level 5 data. When the query size is reduced to 10, the TPR of our Bayesian method is only reduced by 21%, while that of L1000 data is reduced by 63%. We also show the median quantile of similar drugs with different query sizes in Figure 8b. We find that the median quantile from our Bayesian method is lower than the other methods across all query sizes, and the best performance is about 34% when the query set contains about 100 genes.

Fig. 8.

(a) ROC curves for similar perturbagen recognition based on combined z-scores from Bayesian, Bayesian MLE and L1000 level 5 data. The area under the curve is also shown for each method. (b) The comparison of the median quantile (FPR at TPR = 0.5)

4 Discussion

The existence of outliers in FI values are considered a major problem that affects peak detection for the algorithms based on Gaussian models, such as GMM and AGMM. Instead of adding an empirical outlier removal step (Li et al., 2017), we address this problem by modeling outliers as bead color misidentification. The color of each bead is measured by the Luminex FlexMap 3D platform as three numbers, and there is a small chance that the error in measuring the numbers is large enough for the bead to be identified as a wrong color. We set the rate of misidentification ${\alpha }_{\mathrm{c}}$ to be 1% for our precomputed datasets. We notice that the z-scores are not sensitive to this rate, where changing ${\alpha }_{\mathrm{c}}$ to 3% or 0.3% will affect <1 z-score in each profile (∼1000 z-scores) on average. In addition, we model the shape of the peaks as Student’s t-distributions, which have a heavier tail than the Gaussian distribution, and the peak locations are less sensitive to outliers compared to Gaussian models.

Peak flip is another problem that is widely discussed (Li et al., 2017; Young et al., 2017). We address this problem by considering the number of reads in two peaks following a binomial distribution, which is built into our mathematical model. When the number of reads is very close for the two peaks, the likelihood function will show a similar probability for both ways of peak assignment, and the z-score from our pipeline is often close to zero which correctly describe the situation. We also note that peak flip is very rare in real data. For instance, a sample with 60 reads and a 2:1 mix ratio, the probability of peak flip is $\sim 0.5\%$.

As we find the performance of Bayesian MLE in Figures 7b and 8b is more similar to that of L1000 rather than Bayesian method, we speculate a possible explanation for this phenomenon as follows. Any deterministic method, regardless of its accuracy in modeling, picks a precise number for each peak according to some likelihood function. But in the real data, there are many cases where the peak positions are hard to decide. For example, the smaller peak contains too few reads thus hard to be distinguished from noise, or two peaks are not well separated and their locations have a large uncertainty. In those cases, a deterministic method has a small chance to give large z-scores to genes that are not regulated. Given that only a little fraction of the genes are actually regulated, the quality of highest and lowest z-scores are compromised.

In this paper, we used GSEA as a robust signature comparison method and top up/downregulated genes as the feature for a sample, which is a widely accepted non-parametric way to compare expression profiles. But with changes we made in the signature generation process, different comparison algorithm can be developed to better capture information in signatures.

5 Conclusion

We developed the Bayesian signature detection pipeline to generate robust z-score profiles from L1000 assay data. The new Bayesian approach has demonstrate high accuracy and robustness in signature detection, which will give better representation for perturbagens. Perturbagen signatures produced by this pipeline will largely facilitate in silico drug screening and repurposing, finding possible drug targets for different diseases and help understanding gene functions.

Funding

This work was supported by the National Library of Medicine (NLM) [R01LM011986]; the National Institute of General Medical Sciences (NIGMS) [R01GM122845]; National Institute on Aging of the National Institute of Health (NIH) [R01AD057555]; and CUNY High Performance Computing Center.

Conflict of Interest: none declared.