Abstract
Photoinduced intramolecular charge-transfer (ICT) molecules are important in various applications such as a probe for single-molecule spectroscopy, cell imaging, laser dyes, biomarkers, solar cells, in photosynthesis, etc. Here, we report a new set of substituted pyrene dye molecules, N,N-dimethylamino nitrilo pyrene and its higher analogues, containing pull–push donor (D)–chromophore (π)–acceptor (A) functional groups with enhanced photophysical characteristics like oscillator strength, light-harvesting, and ICT properties. The excited-state ICT process has been established by quantum chemical calculations using the density functional theory method in vacuo and in solvents of different polarity and hydrogen-bonding ability using linear-response (LR) and state-specific (SS) solvation approaches with gradually increasing the D–A distance. The studied molecules show solvent polarity-dependent larger Stokes’ shifts (3609–9016 cm–1, in acetonitrile), higher excited-state dipole moments (11.7–16.8 Debye, in acetonitrile), higher possibilities of highest occupied molecular orbital (HOMO)–lowest unoccupied molecular orbital (LUMO) electronic transitions, etc., which support the occurrence of the excited-state ICT process. Here, we demonstrate how to increase the efficiency of the ICT process and also tune the ICT fluorescence maximum. We find that with a variation of the D–A distance, studied molecules show a noticeable effect on the spectroscopic and molecular properties such as the position of absorption and fluorescence band maxima, Stokes’ shift, dipole moment, light-harvesting, and ICT properties. We also show that the SS solvation approach is more supportive than the LR method to the ICT process.
1. Introduction
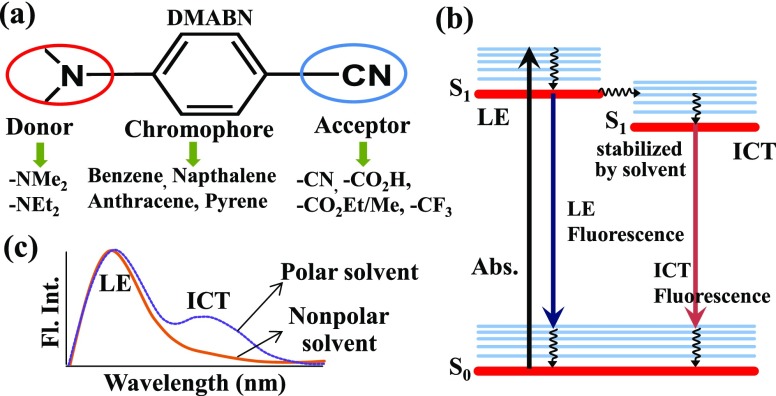
The photoinduced intramolecular charge-transfer (ICT) process has been found to produce polarity sensitive emission in a number of push–pull systems where donor and acceptor groups are connected to a central aromatic chromophore (Scheme 1a).1 A huge surge in the design and synthesis of such ICT compounds has been noted ever since the first observation of this behavior in the iconic molecule 4-(N,N-dimethylamino)benzonitrile (DMABN).2 Lippert et al. first observed a dual anomalous fluorescence in polar solvents for the DMABN molecule, where the higher-energy emission originates from the locally excited (LE) state and the lower-energy emission from the polar solvent-stabilized charge-transfer (CT) state (Scheme 1b,c).1,2 To date, varieties of ICT molecules have been studied due to their importance in various applications such as a probe for single-molecule spectroscopy, cell imaging, laser dyes, biomarkers, solar cells, etc.3−8 ICT molecules also have a crucial role in biological light-harvesting processes, e.g., photosynthesis.9,10 The ICT molecules containing a central benzene chromophore are mostly reported.1,11,12 In addition to that, ICT molecules having naphthalene13 and anthracene14 rings with extra flexibility between the donor and acceptor are also found.15−18 Recently, few reports containing a pyrene chromophore with more complicated molecular structures are also observed.19−21
Scheme 1. General Chemical Structure of ICT Molecules, Schematic of Electronic Transitions and Fluorescence Spectra.
(a) Chemical structure of ICT molecules, the DMABN, and others by mentioning the donor, chromophore, and acceptor groups. (b) The electronic energy-level diagram for the dual emission LE and ICT in a polar solvent. (c) Sketch of fluorescence spectra of an ICT molecule in polar and nonpolar solvents to show the dual emission.
Generally, the ICT molecules show low quantum yield and low-intensity fluorescence spectral properties due to n → π* type of forbidden electronic transition.22,23 For efficient applications of ICT molecules, it is recommended to have high quantum yield. At present, there are few commercial suppliers to provide the fluorescent ICT molecular probes with >60% quantum yield, which are also very expensive, thereby reducing their commercial viability.24,25 On the other hand, most of the fluorophore probe molecules are excited within the ultraviolet region.16,22,26 This is a limitation for the use of pyrene-based probe molecules in light microscopy and single-molecule spectroscopy for studying live cells and biomolecules like proteins, DNA, RNA, etc. For single-molecule spectroscopy, the photostable fluorescence molecular probe with very high quantum efficiency is recommended so that the photobleaching will be less by using very low energy excitation light.
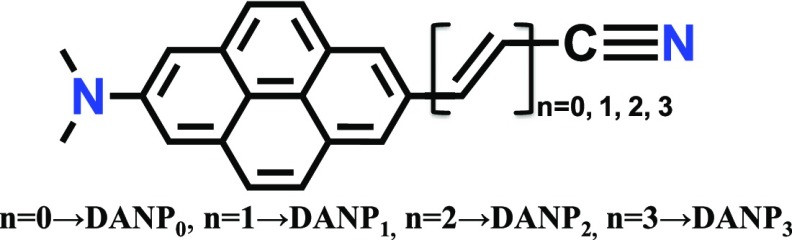
To resolve the above issues, we computationally designed a new class of ICT molecules containing donor (NMe2)–chromophore (pyrene)–acceptor (CN) groups with the variation of the D–A distance (Scheme 2). The pyrene chromophore will help to increase the quantum yield by π → π* type of allowed charge-transfer transition in addition to the weaker n → π* type.26−28 The gradual addition of π-conjugated alternate double and single bonds between the pyrene and nitrile groups will help to tune the absorption and fluorescence band maxima to the visible spectral range.22,29 Experimental data for analogous pyrene molecules also support our computational findings.21,26 The specific features of the pyrene charge-transfer molecules will attract attention due to a slower lifetime for real-time probe monitoring; the high quantum yield will help to use the probe even in a nanomolar concentration range to avoid excimer emission when measuring in a conventional fluorescence spectrometer.30 Pyrene is already used as a biomarker for labeling biomolecules due to its good fluorescence character.30−32 This probe also used in single-molecule spectroscopy and FRET study.33,34 On the other hand, the pyrene-containing donor (D)–chromophore (π)–acceptor (A) organic dye has shown much improved photovoltaic performance than others.28 As pyrene-chromophore-containing D−π–A groups can fulfill above criteria, therefore, development of a new class of pyrene ICT molecules and investigation of the D–A distance-dependent ICT phenomena are important and demanding.
Scheme 2. Schematic Diagram of the Studied Donor–Acceptor-Substituted Pyrene ICT Molecules.
The synthesis of 2,7-disubstituted D−π–A pyrene molecules is more expensive and complicated due to the availability of appropriate starting materials, catalysts and the presence of a multistep synthetic process, which results in a low yield.21,35 On the other hand, after the synthesis of the desired molecules, there remain some uncertainties as to whether these molecules will show the expected spectral properties. To avoid those uncertainties, we designed a series of donor–acceptor 2,7-disubstituted pyrene molecules and established the expected spectral properties using the computational methods and solvation techniques, which are more reliable to provide the results close to the experimental one.21,27 In recent times, the state-specific (SS) calculation using a solvation model is more powerful to provide the ICT results than the linear-response (LR) calculation27,36,37 using the Coulomb-attenuated B3LYP functional (CAM-B3LYP)21,30,38 and conductor-like polarizable continuum model (CPCM).21,30,39
Here, we quantum chemically examined the photophysical properties and established the ICT phenomenon of the designed D−π–A molecules (Scheme 2) by calculating the spectroscopic parameters in different solvents using quantum chemical methods. We investigated the nature of the charge-transfer character and how it depends on the D–A distance and also the effect of the π electron-rich bulky pyrene chromophore on the ICT phenomenon. We further optimized the molecules in the gas phase and within different solvents with increasing polarity as well as the hydrogen-bonding character by the SS and the LR approaches through nonequilibrium and equilibrium solvation processes. Calculated ground- and excited-state geometries, dipole moments, Stokes’ shifts, highest occupied molecular orbital (HOMO)–lowest unoccupied molecular orbital (LUMO) diagrams, etc. adequately support the charge-transfer nature and D–A distance-dependent charge-transfer property of the designed pyrene ICT molecules.
2. Computational Methods
2.1. Theoretical Background
The solute electron density of the ICT state differs significantly from that of the reference ground state and this electron density depends on the change of the dipole moment and stabilization of the state by surrounding solvent molecules. Therefore, the excited-state free energy critically depends on the solvent reorganization. During studying electronic processes like the formation and relaxation of excited states in solution, the solvent delay response has to be considered properly with respect to the ultrafast time scale of the excitation or emission processes. Therefore, consideration of the proper solvation model is important to get the accurate free energy of solvation. The approximated polarizable continuum model (CPCM)40 and the polarizable continuum model (PCM)41,42 are successful solvation methods among the others and their description are provided in the literature elaborately. Recently, the CPCM model has been widely used to get good results for long-range charge-transfer molecules.21,30,38 In the CPCM model, the solvation free energy (ΔGsol) expressed as follows by neglecting the other small-quantity terms.39
| 1 |
where ΔGel, ΔGcav, ΔGdis, and ΔGrep are the electrostatic component, cavitation, dispersion, and repulsion terms of ΔGsol. The electrostatic component can be calculated using the CPCM self-consistent reaction field (SCRF) method.39 The cavitation term is calculated by using Pierotti’s expression of the hard-sphere theory and applied for nonspherical cavities.39 Dispersion and repulsion terms are computed following Floris and Tomasi’s procedure, with the parameters proposed by Callet and Claverie.39
Depending upon the reorientation of the solvent dipoles around the solute molecule, the CPCM approach involves two solvation cases, i.e., the equilibrium and the nonequilibrium. In the equilibrium condition, all of the electronic and the nuclear solvent degrees of freedom are in equilibrium with the electron density of the solute. Therefore, the apparent surface charges are computed by employing the static dielectric constant. Whereas for the nonequilibrium condition, only the electronic polarization of the solvent molecule is in equilibrium with the excited-state electron density of the solute and the apparent surface charges are separated into two sets of charges, representing the electronic polarization (fast) and nuclear components (slow) whose values are computed by using the optical and static dielectric constants, respectively. In the case of the absorption process, the solvent molecules are in nonequilibrium with the excited-state electron density; therefore, the vertical excitation energy is computed in terms of free energy by the following equation27
| 2 |
where G represents the free energy. The superscript (1), (0) and subscript neq, eq denote the excited, ground states and nonequilibrium, equilibrium conditions, respectively.
As soon as the electronic excitation occurs, the solute molecule starts to relax toward the minimum of the excited-state potential energy surface. Simultaneously, the solvent molecules around the solute start to reorganize to reach the equilibrium with the excited-state electron density of the solute. As these two processes cannot be strictly decoupled, particularly when they exhibit similar time scales there is not a suitable single strategy to investigate all of the possible emission processes. To simplify this complex strategy, two limiting cases can be considered. Case 1: for the ultrafast excited-state decay, the equilibration of intramolecular degrees of freedom is faster than solvent equilibration and as a result, the emission occurs from the excited-state minimum. In that case, only the fast solvent degrees of freedom are in equilibrium with the excited-state density. Therefore, the ΔGem can be computed in the same way as ΔGabs in eq 2. Case 2: for molecules with very long excited-state lifetimes or strongly fluorescent compound, as in the case of donor–acceptor-substituted pyrene, it is possible to assume that all of the solvent degrees of freedom are in equilibrium with the excited-state density and the fluorescence can be computed by the following relation41
| 3 |
where the terms have usual significance as defined before. The expression for Geq and Gneq reported elsewhere in the literature.27,36,40,41
2.2. Geometry Optimization
The ground- and excited-state energy optimization of all of the molecules (Scheme 2) was carried out by density functional theory (DFT) and time-dependent density functional theory (TD-DFT) methods, respectively, using Coulomb-attenuated functional, CAM-B3LYP and 6-311++G(d,p) basis set. The CAM-B3LYP functional provides better Hartree–Fock (HF) exchange correlation, starting from 0.19 Hartree–Fock (HF) and 0.81 Becke exchange interaction at the short range to 0.65 HF and 0.35 Becke exchange interaction at the long range.43 Therefore, it is effective for both the pyrene and long-range charge-transfer systems, like our systems.21,30 We selected the above-mentioned calculation method, functional, and basis set to obtain reliable results in comparison to the experimental data of similar types of molecules and also to balance the effective computational cost.21,30,38 Even nowadays, quantum mechanical calculations of such types of molecules containing 47 atoms by using a 6-311++G(d,p) split valence basis set, which is equivalent to the triple-ζ basis set, containing diffusion function with polarization on hydrogen and heavy atoms are expensive mainly when the excited-state frequency calculations were performed using the solvent model. On the other hand, recent studies show that the CAM-B3LYP functional with the CPCM model provides better computational results when comparing with the experimental results for such types of D−π–A push–pull π-conjugated systems.21 Also, the additional functional B3LYP was used for comparison, considering the SS and LR solvation approaches, as we applied for the CAM-B3LYP functional. The computational calculations were performed in vacuo and in different solvents with the variation of polarity and hydrogen-bonding abilities. We used a wide range of solvents: n-hexane (n-hex), dioxan (DOX), chloroform (CHCl3), tetrahydrofuran (THF), acetonitrile (ACN), butanol (BuOH), ethanol (EtOH), methanol (MeOH), and water (H2O) with their specified dielectric constants, as mentioned in the Gaussian 09 package.44 All of the structures were optimized without freezing any parameters. To evaluate the solvent effect, the calculations were performed using the CPCM model without any constraints. The energy-optimized geometries were confirmed by frequency calculations without any imaginary frequencies. All of the computational works were carried out using Gaussian 09 suit program.44 To visualize the results, the Gauss view 5 software was used.
2.3. Absorption and Fluorescence Band Positions, Light-Harvesting Property, and Solvatochromism
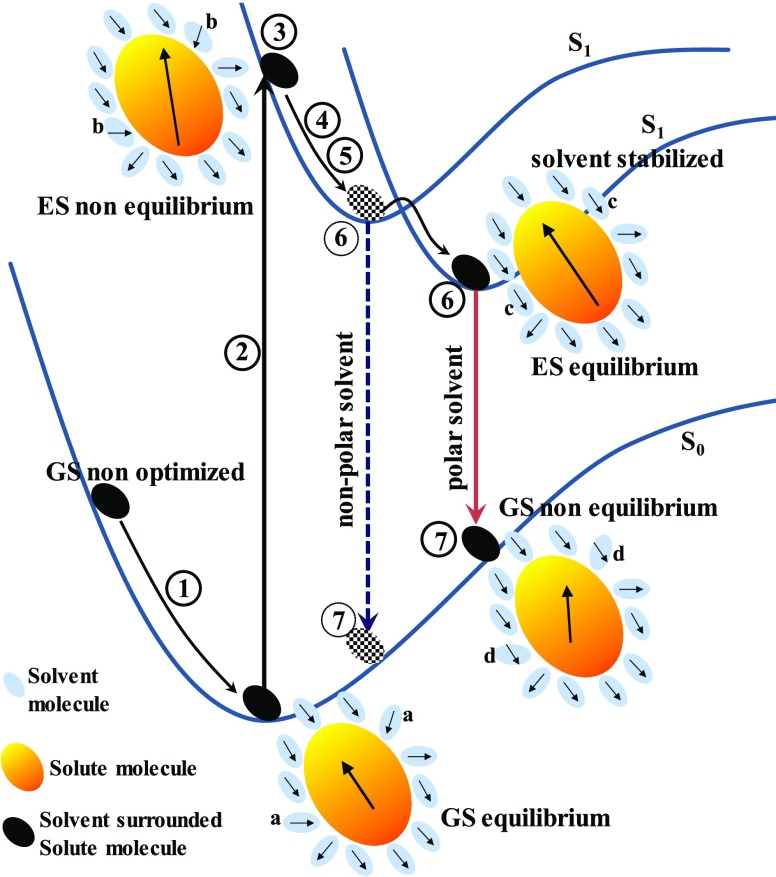
The absorption and fluorescence band positions were calculated in different solvents by seven consecutive stages, Scheme 3, and the data are presented considering state-specific and linear-response solvations. In the first stage, the ground-state geometry optimization was performed followed by frequency calculation. The second stage is the vertical excitation by a single-point TD-DFT calculation with linear-response solvation to know the excited state with a specific interest. The third is the state-specific solvation of the vertical excitation using TD-DFT calculation for the first excited state (S1) by reading previously calculated ground-state (S0) nonequilibrium solvation information. In the fourth stage, the excited-state geometry optimization was performed with the equilibrium condition and linear-response solvation. For this step, the parameters obtained from the checkpoint file of the second stage were used. The fifth stage is the most challenging and expensive step of excited-state frequency (S1) calculation to confirm the excited-state geometry optimization. Sixth and seventh stages are the emission state-specific solvation and emission to the final ground state, respectively. To get the absorption band position with state-specific solvation, the obtained energy in the third stage after PCM correction was subtracted from the transition energy obtained in the first stage. Similarly, the fluorescence band position considering state-specific solvation was extracted from the energy difference between the sixth and the seventh stages (Scheme 3).
Scheme 3. Schematic Diagram of Equilibrium, Nonequilibrium, State-Specific, Linear-Response Solvation, Excitation, and Fluorescence Processes.
The numbers within the circle represent different stages of the calculations. The dashed arrow, dotted circles, and dotted molecules indicate in nonpolar or less polar solvents. The arrow within the solute and the solvent molecules indicates the dipole moment. Solvent molecules, a, b, c, and d represent different equilibrium and nonequilibrium situations with respect to its previous state before the transition and the solute dipole after the transition.
The light-harvesting property of the investigated DANPn dye molecules has been studied by the calculation of the light-harvesting efficiency (LHE) using the following eq 4.28
| 4 |
where f is the calculated oscillator strength of DANPn molecules for the S0 → S1 electronic transition by the absorption of light.
For the solvatochromic study, the Lippert–Mataga relation has been used, as shown in eq 5.45 Stokes’ shift (Δν = νa – νf) was plotted against the solvent parameter Δf(εr,n) considering nonpolar n-hex to polar aprotic solvents with gradually increasing polarity. The nonpolar solvent n-hex was taken into account to show the inherent Stokes’ shift of the studied molecules.
| 5 |
Where
νa, νf, εr, and n are the absorption and the fluorescence band positions in cm–1, the dielectric constant, and the refractive index of the medium, respectively. The terms h, ε0, c, ρ, μg, and μe in the given equation are Planck’s constant, the permittivity of vacuum, the velocity of light, the Onsagar cavity radius, the ground- and excited-state dipole moments, respectively. The increasing solvatochromism of the investigated DANPn molecules has been explained from the positive slope and the linear nature of the fitted straight line of the above-mentioned plot.
2.4. Generation of HOMO and LUMO Diagrams
The HOMO – 1, HOMO, LUMO, and LUMO + 1 frontier orbital diagrams were generated from the optimized checkpoint files using the Gauss View 5 software in the ACN solvent for all types of substituted pyrene molecules. To generate the molecular orbital diagrams, a surface isovalue of ±0.02 [ea0–3]1/2, the default setting in Gauss View 5, was used for all of the DANPn molecules, pyrene, and other 2/7-substituted supporting pyrene molecules.19
3. Results and Discussion
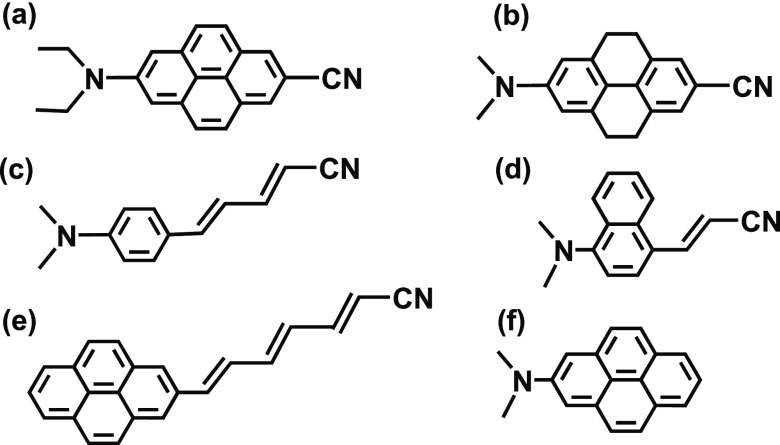
We compared the results obtained using CAM-B3LYP and B3LYP functionals considering both the SS and the LR solvation approaches with the experimental results of the analogous ICT molecules (Scheme 4a,b)21,26 and presented in Figure 1. After comparison of the results (discussed in details within each subsection), it is clear that the CAM-B3LYP functional with the SS solvation method well supports the ICT process than the LR solvation approach and even better than the B3LYP functional. Therefore, below we discuss the results of the CAM-B3LYP functional with the SS and the LR methods considering the CPCM solvation model in the main article and other results are presented in the Supporting Information.
Scheme 4. Chemical Structure of Supporting and Other Reported ICT Molecules.
(a) Molecule used in expt 1, (b) molecule used in expt 2, (c) DMAPPDN, (d) DMANAN, (e) NP3, and (f) DAP.
Figure 1.
Plot of spectroscopic parameters obtained using different calculation methods for the DANP0 molecule in n-hex, THF, and ACN solvents and experimentally reported results of two analogous ICT molecules. (a) Absorption, (b) fluorescence, and (c) Stokes’ shifts are plotted against different methods. Expt 1 and expt 2 are the experimental results taken from refs (21, 26), respectively. SS and LR represent state-specific and linear-response solvations, respectively, CB and B within the parenthesis indicate the results using CAM-B3LYP and B3LYP functionals, respectively. The data shown in the n-hex solvent for expt 2 are taken from the cyclohexane solvent. The dotted lines are presented to easily compare the closeness of expt 2 and the computational results.
3.1. Ground- and Excited-State Geometries
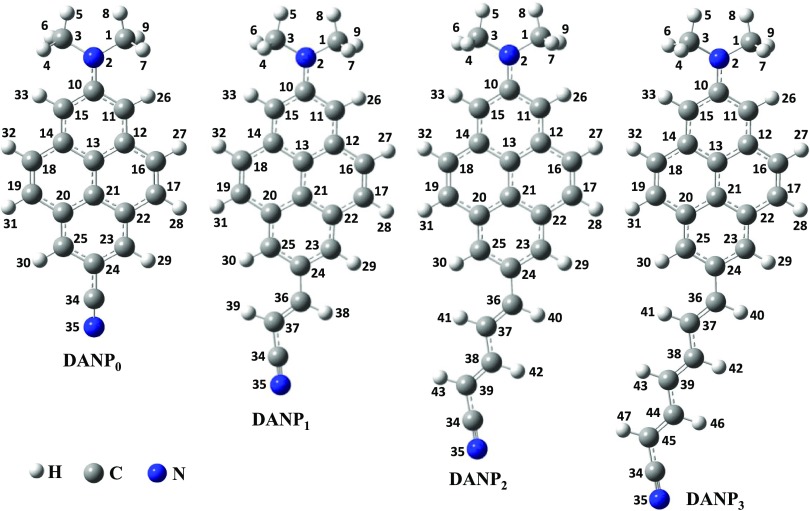
Since the ICT phenomenon and corresponding spectral properties are directly related to the ground- and excited-state structural changes of the molecules, we focused on the structural changes of the studied molecules. The important parameters, which are observed to change during the excitation from the ground (optimized structure from step 1) to the first excited state (optimized structure from step 4), are presented in Table 1. All-trans conformation of the acceptor side chain of DANPn (n = 0–3) molecules provides the lowest-energy structure, as also reported from the crystal structure for such types of acceptor groups in D−π–A charge-transfer molecules.15 We found that a number of parameters change significantly at the donor and acceptor sides, whereas no significant changes are observed within the pyrene ring. The data as shown in Table 1 show that the N2–C10 bond length (Scheme 5) is slightly shorter in the excited state by an amount of maximum 0.024 Å and this shortening increases with increasing solvent polarity (Table 1). The C1–N2–C3 bond angle shows a change in the studied DANPn molecules. For DANP0, this angle reduces by 0.3–2° with increasing solvent polarity, except in vacuum, where a small positive change is observed. For the other three DANPn=1–3 molecules, with increasing the additional C=C–C bond on the donor side, this angle increases (Table 1 and Scheme 5), but this is almost independent on the polarity of the solvents. The C1–N2–C3–C10 dihedral angle also significantly increases from ground-state to excited-state by 17.3 to 22.4° with increasing the value of n = 0–3. Another important dihedral angle C1–N2–C10–C11 is also found to decrease considerably by 8.9–11.8° to reach to the planer form except for the DANP0 molecule in THF and H2O solvents. Such types of dihedral angles between the donor and chromophore planes have already been observed for reported other planer ICT molecules.21,46,47 The planarization of the D−π–A molecule in the excited state supports the possibility of more electronic delocalization from the donor to the acceptor group. This results in a higher dipolar character of the excited state. As the delocalization increases with increasing the number of the C=C–C bond in DANPn molecules, the C–C single bonds become shorten and C=C double bonds become elongated within the side chain.
Table 1. Ground- and Excited-State-Optimized Parameters In Vacuo and Different Solventsa.
| molecules | parameters | Vacg | Vace | ΔVac | THFg | THFe | ΔTHF | ACNg | ACNe | ΔACN | H2Og | H2Oe | ΔH2O |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DANP0 | N2–C10 | 1.380 | 1.366 | –0.014 | 1.374 | 1.355 | –0.019 | 1.373 | 1.353 | –0.020 | 1.373 | 1.352 | –0.021 |
| C1–N2–C3 | 118.2 | 118.4 | 0.2 | 118.3 | 117.2 | –1.1 | 118.3 | 118.0 | –0.3 | 118.3 | 116.3 | –2.00 | |
| C1–N2–C3–C10 | 161.6 | 179.9 | 18.3 | 162.6 | 180.0 | 17.4 | 162.7 | 180.0 | 17.3 | 162.7 | 180.0 | 17.3 | |
| C1–N2–C10–C11 | 9.4 | 0.0 | –9.4 | 9.0 | 6.5 | –2.5 | 8.9 | 0.0 | –8.9 | 8.9 | 8.9 | 0.0 | |
| DANP1 | N2–C10 | 1.381 | 1.368 | –0.013 | 1.377 | 1.357 | –0.02 | 1.376 | 1.354 | –0.022 | 1.376 | 1.354 | –0.022 |
| C1–N2–C3 | 118.1 | 118.7 | 0.6 | 117.9 | 118.3 | 0.4 | 117.8 | 118.2 | 0.4 | 117.8 | 118.2 | 0.4 | |
| C1–N2–C3–C10 | 160.5 | 180.0 | 19.5 | 159.9 | 180.0 | 20.1 | 159.9 | 179.9 | 20.0 | 159.9 | 179.9 | 20.0 | |
| C1–N2–C10–C11 | 10.4 | 0.0 | –10.4 | 10.7 | 0.0 | –10.7 | 10.7 | 0.7 | –10.0 | 10.7 | 0.6 | –10.1 | |
| DANP2 | N2–C10 | 1.382 | 1.382 | 0 | 1.378 | 1.356 | –0.022 | 1.378 | 1.354 | –0.024 | 1.378 | 1.354 | –0.024 |
| C1–N2–C3 | 118.0 | 118.9 | 0.9 | 117.6 | 118.9 | 1.3 | 117.6 | 118.8 | 1.2 | 117.6 | 118.8 | 1.2 | |
| C1–N2–C3–C10 | 159.5 | 179.9 | 20.4 | 158.4 | 180.0 | 21.6 | 158.4 | 179.9 | 21.5 | 158.4 | 180.0 | 21.6 | |
| C1–N2–C10–C11 | 10.9 | 0.0 | –10.9 | 11.5 | 0.0 | –11.5 | 11.4 | 0.0 | –11.4 | 11.4 | 0.0 | –11.4 | |
| DANP3 | N2–C10 | 1.381 | 1.367 | –0.014 | 1.379 | 1.36 | –0.019 | 1.379 | 1.359 | –0.02 | 1.379 | 1.358 | –0.021 |
| C1–N2–C3 | 117.5 | 119.2 | 1.7 | 117.5 | 119.1 | 1.6 | 117.5 | 119.0 | 1.5 | 117.5 | 119.1 | 1.6 | |
| C1–N2–C3–C10 | 160.0 | 180.0 | 20.0 | 157.6 | 180.0 | 22.4 | 157.6 | 180.0 | 22.4 | 157.6 | 180.0 | 22.4 | |
| C1–N2–C10–C11 | 10.7 | 0.0 | –10.7 | 11.8 | 0.0 | –11.8 | 11.9 | 0.1 | –11.8 | 11.9 | 0.1 | –11.8 |
Where the subscript g and e denote the ground and excited states, respectively. Vac, THF, ACN, and H2O represent the vacuo, tetrahydrofuran, acetonitrile, and water solvents, respectively. Δ represents the difference from the excited to ground state.
Scheme 5. Atom Numbering of DANPn Molecules at the Ground-State Optimized Structures in the ACN Solvent.
3.2. Absorption Spectral Characteristic
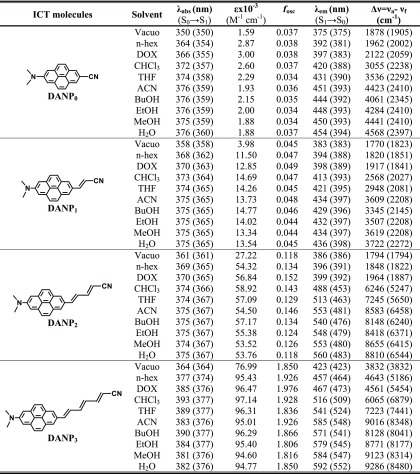
As shown in Figure 1a, the absorption band positions in different solvents obtained from the CAM-B3LYP/SS-CPCM results are well-matched with the reported literature, here we mentioned it as experiment 2 (expt 2)26 (Scheme 4b). We also compared the results with another literature, which reported an analogous ICT molecule in experiment 1 (expt 1).21 The molecule DANP0 shows the lowest-energy absorption band at 364 nm in n-hex (ca. expt 2 value 367 nm in cyclohexane); this band is originated from S0 → S1 electronic transition with ε = 2872 M–1 cm–1 (ca. experimental value 2800 M–1 cm–1 for the molecule in Scheme 4a)21,26 and oscillator strength f = 0.038 (Table 2). The lowest-energy absorption band is slightly red-shifted to 376 nm in ACN and H2O with f = 0.036 and 0.037, respectively. Such types of spectral shifts also reported in the literature for ICT molecules.15,16,22 The f value suggests that the transition is of π → π* nature. The results obtained using the B3LYP/SS-CPCM and LR-CPCM methods (Table S1) moderately correlate with expt 1 but fail to correlate with the results of absorption spectra from expt 2 (Figure 1a). Increasing the donor–acceptor distance of rest of the DANPn molecules (n = 1–3), the absorption band positions are gradually red-shifted from 368 to 377 nm in n-hex and 375 to 383 nm in ACN. The shift of the absorption maximum is reasonable as also observed in experimentally reported 2, 7-disubstituted pyrene molecules.19,21,28 A distinguishable shift of the absorption band position is observed between the DANP1 and DANP2 molecules (Table 2). When comparing the absorption maximum between n-hex and ACN solvents, a 12 nm difference is observed for DANP0, whereas this difference is almost constant to 6–7 nm for the rest of the DANPn=1–3 molecules. The oscillator strength value in polar protic and polar aprotic solvents is slightly less than that of the nonpolar solvent and the value gradually increases with increasing the value of n for DANPn molecules. A noticeable jump is observed for the DANP3 molecule, where the lowest-energy S0 → S1 electronic transition is more intense than the other higher-level transitions, unlike for the DANPn=0–2 molecules. The absorption band is independent of the hydrogen-bonding solvents for DANPn=0–2 molecules, whereas an 8 nm blue shift is observed for the DANP3 molecule (Table 2). Such type of blue-shifting of the absorption spectrum in hydrogen-bonding solvents is also reported for the D−π–A charge-transfer systems, like DMAPPDN22 and DMANAN13 (Scheme 4c,d). The light-harvesting property of the studied DANPn molecules gradually increases with increasing the value of n. DANP0–2 molecules show low LHE property, which is 8, 10, and 28%, respectively, in the ACN solvent, whereas for DANP3, it is 98%, which is relatively higher but comparable with other charge-transfer pyrene molecules.28
Table 2. Calculated Spectroscopic Parameters for Absorption and Fluorescence Processesa.
Where λabs and λem are the lowest-energy absorption and fluorescence wavelengths. ε, fosc, and Δν are the molar extinction coefficient, oscillator strength, and Stokes’ shift, respectively. The ε values are for the LR method and the values are calculated using default bandwidth of absorption spectra, as provided by Gauss View 5. The Stokes’ shifts are calculated for the ICT process. The values in parenthesis are calculated using CAM-B3LYP/LR-CPCM method.
3.3. Steady-State Emission
The CAM-B3LYP/SS-CPCM results for emission spectra and Stokes’ shift in n-hex, THF, and ACN solvents correlate well with expt 2 (Figure 1b,c), whereas the results obtained by B3LYP/SS-CPCM and LR-CPCM methods match less well. The fluorescence band positions for the S1 → S0 electronic transitions of the studied molecules in different polar aprotic and polar protic solvents with increasing polarity and hydrogen-bonding abilities are presented in Table 2. The DANP0 molecule shows the fluorescence band maximum at 392 and 451 nm in n-hex and ACN solvents, respectively (ca. 392 nm in cyclohexane and 442 nm in ACN from expt 2), with a positive emission solvatochromism, 59 nm (2447 cm–1), matched well with the experimentally reported values 50 and 46 nm for expt 2 and 1, respectively.21,26 For other intermediate polar aprotic DOX, CHCl3, and THF solvents, Stokes’ shift (Δν) gradually increases with increasing polarity of the solvents. 2447 cm–1 positive emission solvatochromism supports a weak charge transfer as reported for an analogous molecule.21 The spectral data obtained using the B3LYP/SS-CPCM and LR-CPCM methods correlate less with the experimental data in n-hex, THF, and ACN solvents, as presented in Table S1. The B3LYP functional overestimates the fluorescence band position for the DANP0 molecule. The fluorescence band is slightly red-shifted comparatively in more polar and hydrogen-bonding water solvents and appears at 454 nm when the CAM-B3LYP/SS-CPCM method is used. Overall, as increasing the solvent hydrogen-bonding character with the polarity, the fluorescence band is 10 nm red-shifted from BuOH to water (Table 2). Addition of an extra C=C–C moiety to the DANP0 molecule generates DANP1. The fluorescence band of DANP1 in n-hex and ACN solvents appears at 394 and 434 nm, respectively, with the 3609 cm–1 Stokes’ shift in the ACN solvent. Similarly, DANP2 and DANP3 show a more red-shifted fluorescence band in ACN at 553 (Δν = 8583 cm–1) and 585 nm (Δν = 9016 cm–1) in the n-hex solvent at 396 and 457 nm, respectively. The fluorescence band in water appears at 560 and 592 nm for DANP2 and DANP3 molecules, respectively (Table 2). Among all of the studied molecules, DANP3 shows the highest Stokes’ shift 9286 cm–1 in water. Such type of the huge Stokes’ shift is also experimentally reported for D−π–A pyrene and other charge-transfer systems (Scheme 4c,d).13,16,22 A maximum 21 nm red-shift is observed for the DANP3 molecule in hydrogen-bonding solvents. Overall, it is clear that the excited states of DANPn molecules are more polar in nature compared to the ground state. This polar character gradually increases and stabilizes by the more polar solvents with increasing the value of n in DANPn molecules. As a result, we see more red-shifted fluorescence with the larger Stokes’ shift (Table 2).
3.4. Excited-State Polarity and the Charge-Transfer Process
The change of the dipole moment of DANPn molecules due to electronic transition from the ground to the excited state and the stability of the polar excited state in different polar media through solvation are main evidence of the generation of the ICT state. Therefore, the dipole moments of the ground- and excited-state equilibrium geometries in vacuum, n-hex, ACN, and water solvents are estimated and summarized in Table 3. Dipole moments for other states in different solvents, as depicted in Scheme 3, are presented in Table S2. DANP0 shows the ground-state dipole moment 8.68 Debye in a vacuum and 11.07 Debye in the ACN solvent, which are also comparable to the D−π-–A types of ICT molecules containing −CN as an acceptor, −NMe2 as a donor, and different chromophores.13,14 The ground-state dipole moments are not much different as increasing the value of n for the DANPn molecules and the values are observed to change almost within 1 Debye. Whereas, the excited-state dipole moment in the more polar water solvent is observed to increase approximately 5 Debye. Also, the excited-state dipole moment of the DANP3 molecule in water and ACN solvents is almost 4.7 Debye larger than the ground-state geometry. The dipole moment differences of other nonequilibria states are ∼ 4 times more than the equilibria states (Table S2). The dipole moment difference between nonequilibrium and equilibrium states suggests the extent of stabilization of the ICT state through the solvation. Overall, the higher dipole moment of DANPn molecules in the excited state and the increasing dipole moment difference between ground and excited states with increasing the value of n as well as solvent polarity well supports the existence of the polar excited state. Such types of the dipole moment difference from the ground to the excited state are possible due to redistribution of the charge from the donor to the acceptor after electronic excitation. This clearly suggests the formation of the ICT state for DANPn molecules.
Table 3. Ground and Excited Equilibria State Dipole Moments of the ICT Molecules In Vacuo and Different Solventsa.
| ICT molecules | solvents | μg | μe | Δμ |
|---|---|---|---|---|
| DANP0 | vacuo | 8.68 | 9.05 | 0.37 |
| n-hex | 9.63 | 10.12 | 0.49 | |
| ACN | 11.07 | 11.75 | 0.68 | |
| H2O | 11.12 | 11.81 | 0.69 | |
| DANP1 | vacuo | 9.30 | 9.79 | 0.49 |
| n-hex | 10.16 | 10.80 | 0.64 | |
| ACN | 11.34 | 12.24 | 0.90 | |
| H2O | 11.38 | 12.29 | 0.91 | |
| DANP2 | vacuo | 9.77 | 10.38 | 0.61 |
| n-hex | 10.61 | 11.44 | 0.83 | |
| ACN | 11.73 | 15.53 | 3.80 | |
| H2O | 11.77 | 15.64 | 3.87 | |
| DANP3 | vacuo | 10.18 | 12.04 | 1.86 |
| n-hex | 11.05 | 13.75 | 2.70 | |
| ACN | 12.14 | 16.82 | 4.68 | |
| H2O | 12.18 | 16.96 | 4.78 |
where μg and μe are the ground- and excited-state dipole moments and Δμ is the dipole moment difference (μe – μg).
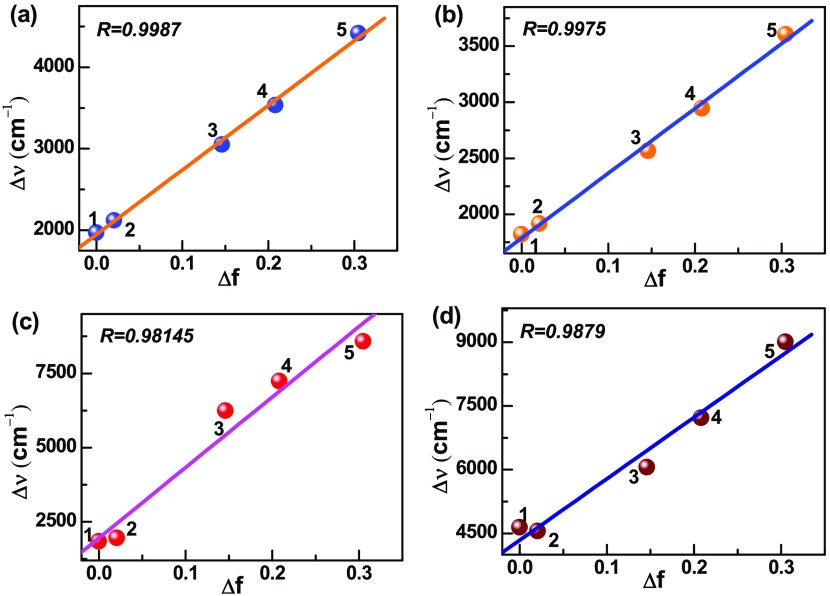
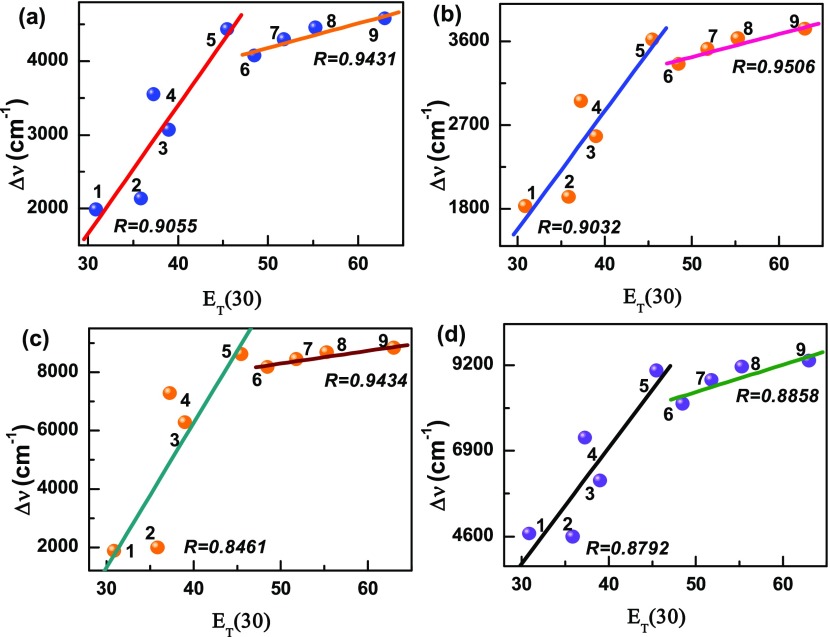
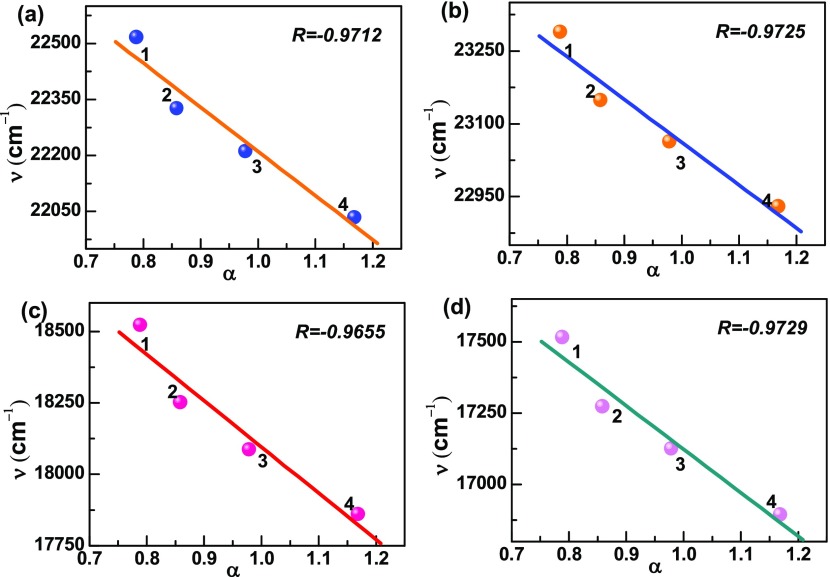
For confirming the evidence of the charge-transfer process, we calculated Stokes’ shift of DANPn molecules in nonpolar n-hex and different polar aprotic solvents with gradually increasing polarity and plotted the Lippart–Mataga relation (eq 5) of the solvent polarity parameter (Δf) against Stokes’ shift (Δν cm–1).45 As shown in Figure 2a, the plot shows linearity with the correlation coefficient, R = 0.9987. The rest of the DANPn=1–3 molecules also show clear linear relationship with R = 0.9975, 0.9814, 0.9879, respectively (Figure 2b–d). However, in the case of polar protic solvents like BuOH, EtOH, MeOH, and water, a deviation from linearity are observed in the Lippert–Mataga plot, which indicates that hydrogen-bonding solvents have different types of influence on the charge-transfer state of the studied molecules. To further examine the different effects of polar protic and aprotic solvents on the charge-transfer state, we used the Reichard ET(30) parameter and plotted against Stokes’ shift.48 The ET(30) plots in Figure 3a–d clearly show two different straight lines with different slopes for the DANPn molecules, one for the polar protic and another for the polar aprotic solvents. In polar aprotic solvents only dipolar interaction is present, whereas in polar protic solvents both the dipolar as well as the hydrogen-bonding interactions are present to stabilize the charge-transfer state. To get further evidence of the dependence of the charge-transfer emission on the hydrogen-bonding solvents, we plotted the emission band maximum (νf cm–1) against hydrogen-bonding strength (α) of different hydrogen-bonding solvents for the studied molecules.23,49 The results in Figure 4a–d show linear dependence with the satisfactory linear fitting of the data points. These plots indicate that hydrogen-bonding solvents stabilize the charge-transfer state through hydrogen-bonding interaction in a different fashion in addition to the dipolar interaction.22 Although, the effect of hydrogen-bonding solvents coincidentally matched with the experimental trend of other ICT molecules, these types of calculations did not consider explicit solvent model. To further check among the donor and acceptor which group is more important to the formation of the charge-transfer state, we carried out calculations in n-hex and ACN solvents for the NP3 molecule (DANP3 without the −NMe2 group) and 2-N,N-dimethylamino pyrene (DAP), the molecule without the acceptor (Scheme 4e,f). The results are presented in Table S3. Although the DAP molecule shows more solvent polarity-dependent Stokes’ shifted emission than NP3, both the molecules did not show any strong solvent polarity dependency as observed for the DANP3 molecule. Therefore, it is also clear that for the efficient charge-transfer process, the appropriate donor and acceptor groups have to be attached to the pyrene chromophore within the D−π–A system.
Figure 2.
Plot of Stokes’ shift (Δν) against the solvent polarity parameter (Δf), 1 → 5: n-hex, DOX, CHCl3, THF, and ACN solvents for (a) DANP0, (b) DANP1, (c) DANP2, and (d) DANP3 molecules.
Figure 3.
Plot of Stokes’ shift (Δν) against the Reichardt solvent polarity parameter, ET(30). 1 → 5 for nonpolar and polar aprotic solvents: n-hex, DOX, CHCl3, THF, and ACN; 6 → 9 for hydrogen-bonding solvents: BuOH, EtOH, MeOH, and H2O for (a) DANP0, (b) DANP1, (c) DANP2, and (d) DANP3 molecules.
Figure 4.
Plot of the fluorescence band maximum (ν) against the solvent hydrogen-bonding parameter (α), 1 → 4: BuOH, EtOH, MeOH, and H2O for (a) DANP0, (b) DANP1, (c) DANP2, and (d) DANP3 molecules.
3.5. Analysis of Molecular Orbital Diagrams
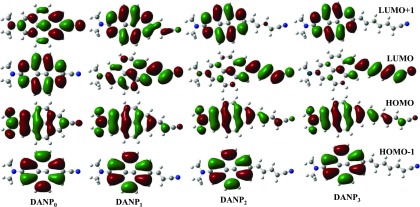
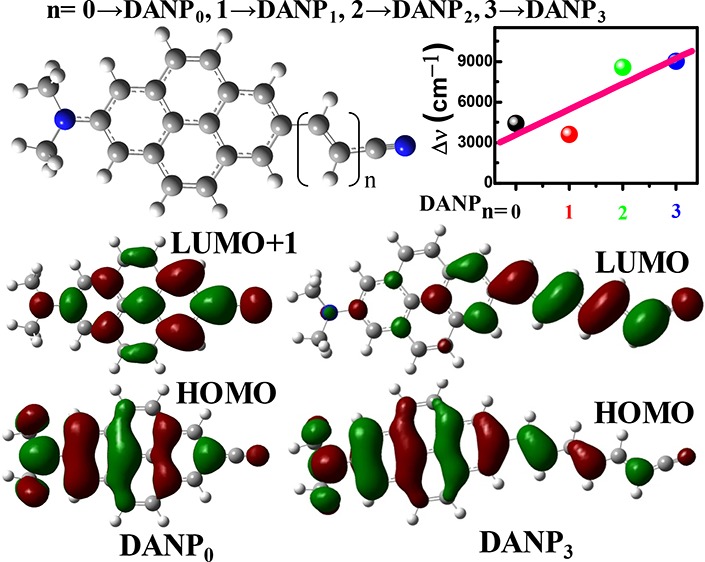
To further extract the evidence of the formation of the charge-transfer state and it’s dependence on the D–A distance, we generated the molecular orbital (MO) diagrams from the optimized structure of DANPn molecules in the ACN solvent (Figure 5). Comparing with the earlier reported molecular orbital diagrams of the parent unsubstituted pyrene molecule,19 we mainly focused on the HOMO – 1, HOMO, LUMO, and LUMO + 1 diagrams for the studied molecules. As shown in Figure 5, due to D–A 2,7-disubstitution to the parent pyrene molecule, the HOMO and HOMO – 1 orbitals shuffle their energy order with respect to unsubstituted pyrene (Figure S1).19,30 In addition to that, increasing the length of the acceptor chain, the LUMO and LUMO + 1 orbitals interchange their energy order from the DANP0 to DANP1 molecule and rest of the DANPn=2–3 molecules follow the MO energy order like DANP1. Such type of LUMO and LUMO + 1 energy order shuffling is also observed by Merz et al. for other D−π–A-substituted pyrene molecules.19,30 The orbital energy order shuffling reflects better optical and redox properties of these molecules as also reported for other substituted pyrene molecules.19 The HOMO of DANPn molecules is mainly localized on the −NMe2 group and pyrene ring, whereas a lesser extent on the acceptor side chain and this trend is gradually more prominent as increasing the value of n in DANPn molecules. Gradually increasing the length of the acceptor side chain, the LUMO (LUMO + 1 for DANP0) is gradually found to localize more on the acceptor side chain and to a lesser extent on the donor and chromophore groups. Therefore, the HOMO to LUMO electronic transition creates DANPn molecules of more dipolar nature. The less charge-transfer possibility of the DANP0 molecule also may be explained when comparing the LUMO + 1 of DANP0 with the LUMO of the rest of the molecules.14,28,30 The more electron density on the N atom of the −NMe2 group and pyrene ring remains for DANP0 (LUMO + 1), whereas it gradually decreases and shifts to the acceptor side chain through the pyrene moiety for DANPn=1–3 molecules (LUMO). To check the involvement of the donor and acceptor groups to the formation of the charge-transfer state, we also generated the MO diagrams of DAP and NP3 molecules (Figure S1). The HOMO and HOMO – 1 of DAP show the energy order shuffling in comparison to the MO of the unsubstituted pyrene. On the other hand, we see a similar situation between the LUMO and LUMO + 1 of NP3. When both the donor and acceptor groups are attached to the pyrene chromophore, i.e., DANP3 molecule, the nature of the HOMO–LUMO and the energy gap between them are observed to change, which may prompt the electronic transition and the formation of the ICT state.
Figure 5.
Molecular orbital diagrams of DANPn molecules in the ACN solvent.
3.6. Donor–Acceptor Distance-Dependent ICT Process
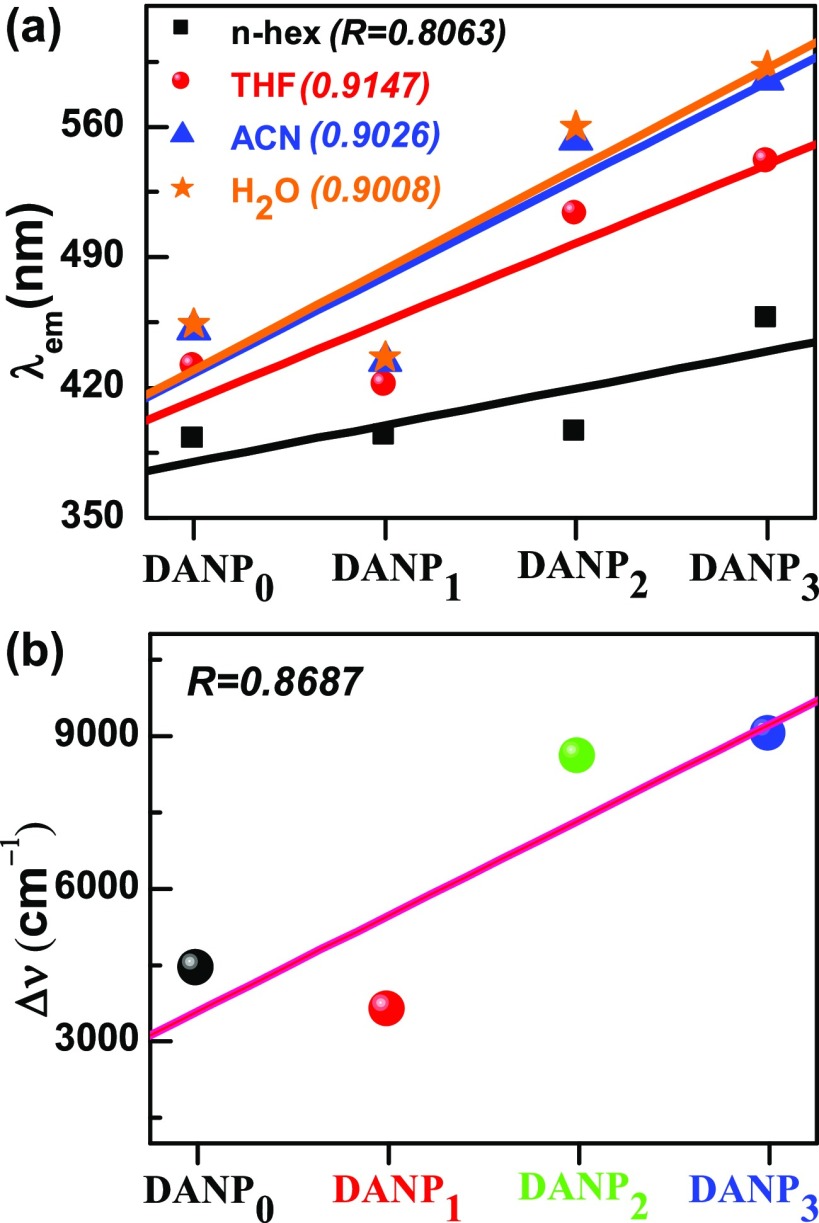
To investigate the D–A distance dependency on the ICT process, we compared the calculated dipole moment, fluorescence band position, Stokes’ shift, etc. as a function of the change of D–A distance, i.e., the number of C=C–C moieties, which is denoted by n for DANPn molecules. The presented data in Tables 2, 3 and S2, S3 clearly support that there are distinct changes in the above-mentioned parameters, which are responsible for the ICT phenomenon. Figure 6a shows the plot of the fluorescence band maxima against the change of D–A distance (n of DANPn molecules) in n-hex, THF, ACN, and H2O solvents. The data support a linear relationship between the fluorescence band maximum in different polar solvents and increased D–A distance. It is clear that with increasing the value of n, the emissive species is more stabilized in polar solvents, which is clear from the positive slope of the above plot in different solvents of increasing polarity. Figure 6b reveals that Stokes’ shift of the DANPn molecules in the ACN solvent increases linearly (R = 0.8687) as changing the D–A distance. The dipole moment difference between equilibrium ground and excited states in ACN solvent also increases from 0.68 to 4.68 Debye as increasing the value of n (Table 3). On the other hand, on increasing the D–A distance, the light-harvesting efficiency (LHE) in the ACN solvent increases from 8 to 98% for n = 0–3 of DANPn molecules. As a whole, the emission solvatochromism increases with increasing the donor–acceptor distance and we see the highest emission solvatochromism 9286 cm–1 for the DANP3 molecule in water. The MO energy order as well as MO distribution both change as the donor–acceptor distance increases, which also influences the ICT phenomenon.
Figure 6.
(a) Plot of the fluorescence band position in different solvents against ICT molecules of different donor–acceptor distances. (b) Stokes’ shift in the ACN solvent vs ICT molecules of different donor–acceptor distances. The donor–acceptor distance here is represented by the number of the C=C–C moiety within the chromophore and acceptor.
4. Conclusions
We have successfully designed and established the ICT phenomenon of a set of donor–acceptor-substituted pyrene dye molecules by quantum chemical calculations and reported the D–A distance-dependent ICT process. The computational results obtained from the CAM-B3LYP/SS-CPCM method better agree with the experimental results than other methods to support the ICT phenomenon. Solvatochromism, structural and dipolar changes between the ground and the excited states are well evidence for the ICT process, which passes through the planer ICT mechanism. Polar aprotic solvents have different influences on the stability of the ICT state than the polar aprotic solvents. The increase of the donor–acceptor distance maintains a linear trend with the properties of emission maxima, dipole moment difference between ground and excited states, Stokes’ shift, oscillator strength, and light-harvesting properties. Increasing the oscillator strength value as a function of the D–A distance well supports the enhanced optical properties and quantum yield. In the future, this work will help and motivate to further synthesize pyrene ICT molecules experimentally to use their physical and light-harvesting properties. Finally, it is evident that for the enhanced charge-transfer phenomenon and light-harvesting properties of pyrene dye molecules, D−π–A moieties are essential and require adequate distance between the donor and acceptor.
Acknowledgments
D.J. would like to acknowledge Bishnupada Sarkar College of Education. S.J. would like to acknowledge the University of St Andrews for the position and The Royal Society as Newton International Fellow (Grant No. NF170334).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c00265.
Calculated spectroscopic parameters for the DANP0 molecule in n-hex, THF, and ACN solvents using B3LYP functional and different methods (Table S1), dipole moments of different ground- and excited-state structures in different solvents (Table S2), calculated spectroscopic parameters for DAP and NP3 molecules in n-hex and ACN solvents (Table S3), MO diagrams of pyrene, DAP, and NP3 molecules in the ACN solvent (Figure S1) (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Grabowski Z. R.; Rotkiewicz K.; Rettig W. Structural Changes Accompanying Intramolecular Electron Transfer: Focus on Twisted Intramolecular Charge-Transfer States and Structures. Chem. Rev. 2003, 103, 3899–4032. 10.1021/cr940745l. [DOI] [PubMed] [Google Scholar]
- Lippert E.; Lüder W.; Moll F.; Nägele W.; Boos H.; Prigge H.; Seibold-Blankenstein I. Umwandlung von Elektronenanregungsenergie. Angew. Chem., Int. Ed. 1961, 73, 695–706. 10.1002/ange.19610732103. [DOI] [Google Scholar]
- Lai R. Y.; Fabrizio E. F.; Lu L.; Jenekhe S. A.; Bard A. J. Synthesis, Cyclic Voltammetric Studies, and Electrogenerated Chemiluminescence of a New Donor Acceptor Molecule: 3,7-[Bis[4-phenyl-2-quinolyl]]-10-methylphenothiazine. J. Am. Chem. Soc. 2001, 123, 9112–9118. 10.1021/ja0102235. [DOI] [PubMed] [Google Scholar]
- Yang Y.; Zou J.; Rong H.; Qian G. D.; Wang Z. Y.; Wang M. Q. Influence of various coumarin dyes on the laser performance of laser dyes co-doped into ORMOSILs. Appl. Phys. B 2007, 86, 309–313. 10.1007/s00340-006-2462-0. [DOI] [Google Scholar]
- Grimm J. B.; English B. P.; Chen J.; Slaughter J. P.; Zhang Z.; Revyakin A.; Patel R.; Macklin J. J.; Normanno D.; Singer R. H.; Lionnet T.; Lavis L. D. A general method to improve fluorophores for live-cell and single-molecule microscopy. Nat. Methods 2015, 12, 244–250. 10.1038/nmeth.3256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hara K.; Tachibana Y.; Ohga Y.; Shinpo A.; Suga S.; Sayama K.; Sugihara H.; Arakawa H. Dye-sensitized nanocrystalline TiO2 solar cells based on novel coumarin dyes. Sol. Energy Mater. Sol. Cells 2003, 77, 89–103. 10.1016/S0927-0248(02)00460-9. [DOI] [Google Scholar]
- Wang Z.-S.; Cui Y.; Hara K.; Dan-oh Y.; Kasada C.; Shinpo A. A High-Light-Harvesting-Efficiency Coumarin Dye for Stable Dye-Sensitized Solar Cells. Adv. Mater. 2007, 19, 1138–1141. 10.1002/adma.200601020. [DOI] [Google Scholar]
- Jana S.; Dalapati S.; Ghosh S.; Guchhait N. Potential charge transfer probe induced conformational changes of model plasma protein human serum albumin: Spectroscopic, molecular docking, and molecular dynamics simulation study. Biopolymers 2012, 97, 766–777. 10.1002/bip.22057. [DOI] [PubMed] [Google Scholar]
- Park S.; Steen C. J.; Lyska D.; Fischer A. L.; Endelman B.; Iwai M.; Niyogi K. K.; Fleming G. R. Chlorophyll–carotenoid excitation energy transfer and charge transfer in Nannochloropsis oceanica for the regulation of photosynthesis. Proc. Natl. Acad. Sci. U.S.A. 2019, 116, 3385–3390. 10.1073/pnas.1819011116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jana S.; Du T.; Nagao R.; Noguchi T.; Shibata Y. Redox-state dependent blinking of single photosystem I trimers at around liquid-nitrogen temperature. Biochim. Biophys. Acta, Bioenerg. 2018, 1860, 30–40. [DOI] [PubMed] [Google Scholar]
- Jana S.; Ghosh S.; Dalapati S.; Guchhait N. Exploring structural change of protein bovine serum albumin by external perturbation using extrinsic fluorescence probe: spectroscopic measurement, molecular docking and molecular dynamics simulation. Photochem. Photobiol. Sci. 2012, 11, 323–332. 10.1039/C1PP05180F. [DOI] [PubMed] [Google Scholar]
- Jana S.; Dalapati S.; Ghosh S.; Guchhait N. Study of microheterogeneous environment of protein Human Serum Albumin by an extrinsic fluorescent reporter: A spectroscopic study in combination with Molecular Docking and Molecular Dynamics Simulation. J. Photochem. Photobiol., B 2012, 112, 48–58. 10.1016/j.jphotobiol.2012.04.007. [DOI] [PubMed] [Google Scholar]
- Singh R. B.; Mahanta S.; Kar S.; Guchhait N. Spectroscopic and theoretical evidence for the photoinduced twisted intramolecular charge transfer state formation in N,N-dimethylaminonaphthyl-(acrylo)-nitrile. J. Lumin. 2008, 128, 1421–1430. 10.1016/j.jlumin.2008.01.015. [DOI] [Google Scholar]
- Muralidharan S.; Sinha H. K.; Yates K. Conformational effects on charge-transfer properties in selected 9,10-disubstituted anthracene derivatives: ground- and excited-state dipole moments. J. Phys. Chem. A 1991, 95, 8517–8520. 10.1021/j100175a020. [DOI] [Google Scholar]
- Jana S.; Dalapati S.; Ghosh S.; Guchhait N. Excited state intramolecular charge transfer process in 5-(4-dimethylamino-phenyl)-penta-2,4-dienoic acid ethyl ester and effect of acceptor functional groups. J. Photochem. Photobiol., A 2013, 261, 31–40. 10.1016/j.jphotochem.2013.04.005. [DOI] [Google Scholar]
- Jana S.; Ghosh S.; Dalapati S.; Kar S.; Guchhait N. Photoinduced intramolecular charge transfer phenomena in 5-(4-dimethylamino-phenyl)-penta-2,4-dienoic acid. Spectrochim. Acta, Part A 2011, 78, 463–468. 10.1016/j.saa.2010.11.010. [DOI] [PubMed] [Google Scholar]
- Ghosh S.; Jana S.; Nath D.; Guchhait N. Fluorescent Probing of Protein Bovine Serum Albumin Stability and Denaturation Using Polarity Sensitive Spectral Response of a Charge Transfer Probe. J. Fluoresc. 2011, 21, 365–374. 10.1007/s10895-010-0725-y. [DOI] [PubMed] [Google Scholar]
- Jana S.; Dalapati S.; Ghosh S.; Guchhait N. Binding interaction between plasma protein bovine serum albumin and flexible charge transfer fluorophore: A spectroscopic study in combination with molecular docking and molecular dynamics simulation. J. Photochem. Photobiol., A 2012, 231, 19–27. 10.1016/j.jphotochem.2011.12.002. [DOI] [Google Scholar]
- Merz J.; Fink J.; Friedrich A.; Krummenacher I.; Al Mamari H. H.; Lorenzen S.; Haehnel M.; Eichhorn A.; Moos M.; Holzapfel M.; Braunschweig H.; Lambert C.; Steffen A.; Ji L.; Marder T. B. Pyrene Molecular Orbital Shuffle—Controlling Excited State and Redox Properties by Changing the Nature of the Frontier Orbitals. Chem. Eur. J. 2017, 23, 13164–13180. 10.1002/chem.201702594. [DOI] [PubMed] [Google Scholar]
- Niko Y.; Sasaki S.; Narushima K.; Sharma D. K.; Vacha M.; Konishi G.-i. 1-, 3-, 6-, and 8-Tetrasubstituted Asymmetric Pyrene Derivatives with Electron Donors and Acceptors: High Photostability and Regioisomer-Specific Photophysical Properties. J. Org. Chem. 2015, 80, 10794–10805. 10.1021/acs.joc.5b01987. [DOI] [PubMed] [Google Scholar]
- Ji L.; Lorbach A.; Edkins R. M.; Marder T. B. Synthesis and Photophysics of a 2,7-Disubstituted Donor-Acceptor Pyrene Derivative: An Example of the Application of Sequential Ir-Catalyzed C–H Borylation and Substitution Chemistry. J. Org. Chem. 2015, 80, 5658–5665. 10.1021/acs.joc.5b00618. [DOI] [PubMed] [Google Scholar]
- Jana S.; Dalapati S.; Ghosh S.; Kar S.; Guchhait N. Excited State Charge Transfer reaction with dual emission from 5-(4-dimethylamino-phenyl)-penta-2,4-dienenitrile: Spectral measurement and theoretical density functional theory calculation. J. Mol. Struct. 2011, 998, 136–143. 10.1016/j.molstruc.2011.05.022. [DOI] [Google Scholar]
- Jana S.; Dalapati S.; Guchhait N. Excited State Intramolecular Charge Transfer Suppressed Proton Transfer Process in 4-(Diethylamino)-2-hydroxybenzaldehyde. J. Phys. Chem. A 2013, 117, 4367–4376. 10.1021/jp3120463. [DOI] [PubMed] [Google Scholar]
- Nandy R.; Sankararaman S. Donor-acceptor substituted phenylethynyltriphenylenes – excited state intramolecular charge transfer, solvatochromic absorption and fluorescence emission. Beilstein J. Org. Chem. 2010, 6, 992–1001. 10.3762/bjoc.6.112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferreira D. P.; Conceição D. S.; Prostota Y.; Santos P. F.; Ferreira L. F. V. Fluorescent “rhodamine-like” hemicyanines derived from the 6-(N,N-diethylamino)-1,2,3,4-tetrahydroxanthylium system. Dyes Pigm. 2015, 112, 73–80. 10.1016/j.dyepig.2014.06.021. [DOI] [Google Scholar]
- Sumalekshmy S.; Gopidas K. R. Photoinduced Intramolecular Charge Transfer in Donor–Acceptor Substituted Tetrahydropyrenes. J. Phys. Chem. B 2004, 108, 3705–3712. 10.1021/jp022549l. [DOI] [Google Scholar]
- Pedone A. Role of Solvent on Charge Transfer in 7-Aminocoumarin Dyes: New Hints from TD-CAM-B3LYP and State Specific PCM Calculations. J. Chem. Theory Comput. 2013, 9, 4087–4096. 10.1021/ct4004349. [DOI] [PubMed] [Google Scholar]
- Kathiravan A.; Panneerselvam M.; Sundaravel K.; Pavithra N.; Srinivasan V.; Anandan S.; Jaccob M. Unravelling the effect of anchoring groups on the ground and excited state properties of pyrene using computational and spectroscopic methods. Phys. Chem. Chem. Phys. 2016, 18, 13332–13345. 10.1039/C6CP00571C. [DOI] [PubMed] [Google Scholar]
- Sun F.; Jin R. DFT and TD-DFT study on the optical and electronic properties of derivatives of 1,4-bis(2-substituted-1,3,4-oxadiazole)benzene. Arabian J. Chem. 2017, 10, S2988–S2993. 10.1016/j.arabjc.2013.11.037. [DOI] [Google Scholar]
- Crawford A. G.; Dwyer A. D.; Liu Z.; Steffen A.; Beeby A.; Pålsson L.-O.; Tozer D. J.; Marder T. B. Experimental and Theoretical Studies of the Photophysical Properties of 2- and 2,7-Functionalized Pyrene Derivatives. J. Am. Chem. Soc. 2011, 133, 13349–13362. 10.1021/ja2006862. [DOI] [PubMed] [Google Scholar]
- Zhou Y.; Yang Q.; Cuan J.; Wang Y.; Gan N.; Cao Y.; Li T. A pyrene-involved luminescent MOF for monitoring 1-hydroxypyrene, a biomarker for human intoxication of PAH carcinogens. Analyst 2018, 143, 3628–3634. 10.1039/C8AN00909K. [DOI] [PubMed] [Google Scholar]
- Ifegwu C.; Osunjaye K.; Fashogbon F.; Oke K.; Adeniyi A.; Anyakora C. Urinary 1-Hydroxypyrene as a Biomarker to Carcinogenic Polycyclic Aromatic Hydrocarbon Exposure. Biomarkers Cancer 2012, 4, BIC.S10065 10.4137/BIC.S10065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masuko M.; Ohuchi S.; Sode K.; Ohtani H.; Shimadzu A. Fluorescence resonance energy transfer from pyrene to perylene labels for nucleic acid hybridization assays under homogeneous solution conditions. Nucleic Acids Res. 2000, 28, e34–00. 10.1093/nar/28.8.e34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conlon P.; Yang C. J.; Wu Y.; Chen Y.; Martinez K.; Kim Y.; Stevens N.; Marti A. A.; Jockusch S.; Turro N. J.; Tan W. Pyrene Excimer Signaling Molecular Beacons for Probing Nucleic Acids. J. Am. Chem. Soc. 2008, 130, 336–342. 10.1021/ja076411y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casas-Solvas J. M.; Howgego J. D.; Davis A. P. Synthesis of substituted pyrenes by indirect methods. Org. Biomol. Chem. 2014, 12, 212–232. 10.1039/C3OB41993B. [DOI] [PubMed] [Google Scholar]
- Improta R.; Barone V.; Scalmani G.; Frisch M. J. A state-specific polarizable continuum model time dependent density functional theory method for excited state calculations in solution. J. Chem. Phys. 2006, 125, 054103 10.1063/1.2222364. [DOI] [PubMed] [Google Scholar]
- Adamo C.; Jacquemin D. The calculations of excited-state properties with Time-Dependent Density Functional Theory. Chem. Soc. Rev. 2013, 42, 845–856. 10.1039/C2CS35394F. [DOI] [PubMed] [Google Scholar]
- Krawczyk P. Time-dependent density functional theory calculations of the solvatochromism of some azo sulfonamide fluorochromes. J. Mol. Model. 2015, 21, 118. 10.1007/s00894-015-2651-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takano Y.; Houk K. N. Benchmarking the Conductor-like Polarizable Continuum Model (CPCM) for Aqueous Solvation Free Energies of Neutral and Ionic Organic Molecules. J. Chem. Theory Comput. 2005, 1, 70–77. 10.1021/ct049977a. [DOI] [PubMed] [Google Scholar]
- Barone V.; Cossi M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. 10.1021/jp9716997. [DOI] [Google Scholar]
- Improta R.; Scalmani G.; Frisch M. J.; Barone V. Toward effective and reliable fluorescence energies in solution by a new state specific polarizable continuum model time dependent density functional theory approach. J. Chem. Phys. 2007, 127, 074504 10.1063/1.2757168. [DOI] [PubMed] [Google Scholar]
- Jana S.; Dalapati S.; Guchhait N. Functional group induced excited state intramolecular proton transfer process in 4-amino-2-methylsulfanyl-pyrimidine-5-carboxylic acid ethyl ester: a combined spectroscopic and density functional theory study. Photochem. Photobiol. Sci. 2013, 12, 1636–1648. 10.1039/c3pp50010a. [DOI] [PubMed] [Google Scholar]
- Yanai T.; Tew D. P.; Handy N. C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. 10.1016/j.cplett.2004.06.011. [DOI] [Google Scholar]
- Frisch M.; Trucks G.; Schlegel H.; Scuseria G.; Robb M.; Cheeseman J.; Scalmani G.; Barone V.; Mennucci B.; Petersson G.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H.; Izmaylov A.; Bloino J.; Zheng G.; Sonnenberg J.; Hada M.; Fox D.. Gaussian 09, revision D.01; Gaussian Inc.: Wallingford, CT, 2009.
- Mataga N.; Chosrowjan H.; Taniguchi S. Ultrafast charge transfer in excited electronic states and investigations into fundamental problems of exciplex chemistry: Our early studies and recent developments. J. Photochem. Photobiol., C 2005, 6, 37–79. 10.1016/j.jphotochemrev.2005.02.003. [DOI] [Google Scholar]
- Zachariasse K. A.; Grobys M.; von der Haar T.; Hebecker A.; Il’ichev Y. V.; Jiang Y. B.; Morawski O.; Kühnle W. Intramolecular charge transfer in the excited state. Kinetics and configurational changes. J. Photochem. Photobiol., A 1996, 102, 59–70. 10.1016/S1010-6030(96)04368-7. [DOI] [Google Scholar]
- Liu X.; Cole J. M.; Xu Z. Substantial Intramolecular Charge Transfer Induces Long Emission Wavelengths and Mega Stokes Shifts in 6-Aminocoumarins. J. Phys. Chem. C 2017, 121, 13274–13279. 10.1021/acs.jpcc.7b04176. [DOI] [Google Scholar]
- Reichardt C. Solvatochromic Dyes as Solvent Polarity Indicators. Chem. Rev. 1994, 94, 2319–2358. 10.1021/cr00032a005. [DOI] [Google Scholar]
- Jana S.; Dalapati S.; Guchhait N. Proton Transfer Assisted Charge Transfer Phenomena in Photochromic Schiff Bases and Effect of -NEt2 Groups to the Anil Schiff Bases. J. Phys. Chem. A 2012, 116, 10948–10958. 10.1021/jp3079698. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.