Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2020 Apr 21;5(17):9957–9968. doi: 10.1021/acsomega.0c00269

Experiment and Modeling of Permeability under Different Impact Loads in a Structural Anisotropic Coal Body

Minmin Li †, Weimin Liang †, Gaowei Yue †,*, Jiwei Yue ‡, Xinjun Zheng †
PMCID: PMC7203995  PMID: 32391483

Abstract

graphic file with name ao0c00269_0012.jpg

A mount of bedding and cleat in a coal body causes that the mechanical property and gas permeability are anisotropic in a coal seam, partly. To reveal the permeability change law of the impacted coal, a self-developed vertical split Hopkinson pressure bar (SHPB) device is used to carry out the dynamic impact mechanical property tests of coal samples in three different coring directions under five impact loads and then the permeability of the impacted coal samples is measured by a permeability measuring instrument under different gas pressures. Finally, a calculation model for the anisotropic coal permeability is established to analyze the permeability distribution law in any direction with different angles to the bedding plane. The results show that with an increase in impact height the dynamic peak stress of coal samples increases gradually, which shows a linear growth relationship. The permeability of the impacted coal samples is much larger than that of raw coal samples, and the bigger the impact load, the larger the permeability. Moreover, under the same impact load and gas pressure, the permeability is the largest in parallel to the bedding direction, followed by that in oblique 45° to the bedding direction, and the smallest in perpendicular to the bedding direction. The permeability calculated by the anisotropic model in oblique 45° to the bedding direction is in good agreement with the measured results, and the errors are no more than 10%, which will provide a theoretical basis for the permeability distribution law of the coal seam after deep-hole blasting.

1. Introduction

Gas drainage from a coal seam is one of the important measures to prevent coal and gas outburst in the process of coal mining.1−5 However, due to low permeability of the coal seam, gas drainage often fails to achieve the expected effect; therefore, some necessary measures have to be taken to destroy the coal body for improving permeability, and deep-hole blasting is one of the commonly used methods to increase the permeability of the coal seam.6,7 During the deep-hole blasting process in the coal seam, high-pressure gas impacts the coal body instantaneously, which makes the coal body to produce a fracture network and effectively increase the permeability of the coal seam.8−10 However, the blast wave decays very fast in the coal seam, which leads to the decrease of impact loads and a small damage degree at far positions. Therefore, the permeability at different distances from the blasting center is greatly different after blasting. According to the effect of blasting impact, the coal body is divided into three zones: crushing zone, cracking zone, and vibration zone. In the vibration zone, the coal body under the impact is in the elastic state and the structure of the coal body does not change after blasting. In the crushing zone, the coal body is completely destroyed. In the cracking zone, the structure of the coal body is damaged by blasting shock waves to form macroscopic or microscopic fissures, and in the far area of cracks, although blasting does not lead to visible cracks, it has a damaging effect on the coal body, which is equivalent to the impact of the low strain rate on the coal body. At the same time, after a long geological change, there are abundant bedding and cleat structures in the coal seam, which causes the permeability and mechanical properties of the coal body to show anisotropic characteristics, partly.11,12 During the deep-hole blasting process, the blast wave will cause different damage degrees of coal structure in different directions, which leads to a great difference in enhancing the permeability. Therefore, it has great engineering significance for the reasonable arrangement of blasting holes and extraction holes by developing the impact resistance and permeability change characteristics of structural anisotropic coal in different bedding directions under different impact loads.

It is very difficult to test different impact loads and permeabilities in a coal seam blasted in situ. Therefore, the impact and permeability tests have to be carried out in the laboratory using a split Hopkinson pressure bar (SHPB) device and a gas permeability instrument. The horizontal SHPB device is usually used to carry out the dynamic mechanical tests with strain rates ranging from 101 to 103 s–1, which is mostly concentrated in ranges of the medium strain rate (101–102 s–1) and high strain rate (102–104 s–1),13−15 and after impact, the coal samples are always broken and cannot be tested for permeability. Therefore, the self-developed vertical SHPB device was used to impact the coal samples with a low strain rate (<101 s–1), which can guarantee the integrity of coal samples for the next permeability test. Of course, the small impact loads represent the farther positions of deep-hole blasting in a coal seam.

Many scholars have done a lot of research on the anisotropic permeability of the coal seam and believed that the permeability of coal samples is the largest in parallel to the bedding direction.16−20 Yan et al.16 also pointed out that the permeability of coal samples in perpendicular to the bedding direction is the smallest and the permeability of coal samples in oblique to the bedding direction is between those of in parallel and perpendicular to the bedding direction. Yue et al.21 conducted underground in situ measurement of the borehole influence radius within 200 days and modeled the influence radius evolvement around borehole in an anisotropy coal seam. The underground in situ measurement revealed an anisotropy feature of the borehole influence radius associated with coal bedding and cleat structures. Ten permeability measurements of coal show that the permeability of coal in parallel to the bedding plane in the butt cleat direction is higher than that in perpendicular to the bedding plane. Chen et al.22,23 studied the influence of mechanical and permeability properties of coal samples with different intersection angles in parallel and perpendicular to the bedding direction on the process of full stress–strain. Wang et al.24 tested the permeability under the effective stress of 3.5–8.5 MPa, and the results show that the permeability of coal samples decreases exponentially with an increase in effective stress and the dimensionless permeability in parallel to the bedding direction is larger than that in perpendicular to the bedding direction. Yang et al.25 tested the anisotropic permeability of coal samples with different intersection angles (θ) in parallel to the bedding direction, and the results that the permeability decreases nonlinearly with an increase in intersection angles (θ) and the relationship between the permeability and θ can be quantified by the exponential model of the anisotropic parameter λ.

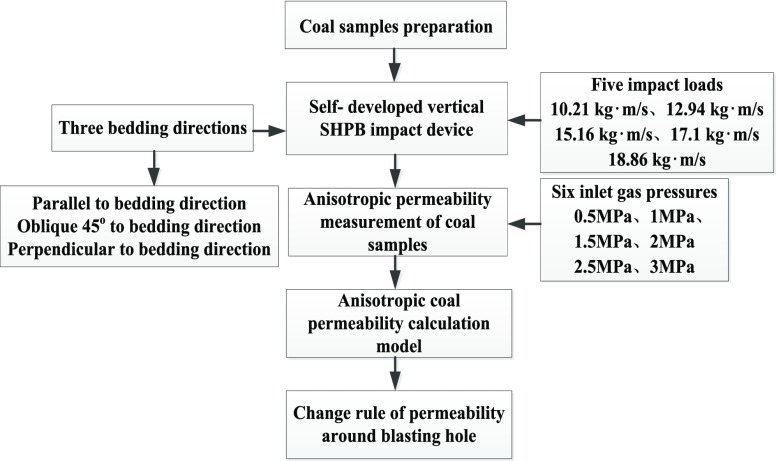
Although many useful achievements have been made in the research on anisotropic permeability of coal seams,26−28 the anisotropic permeability of coal samples under impact load is rarely reported. Therefore, to explore the permeability of the crack zone in a structural anisotropic coal seam after deep-hole blasting, different dynamic impact tests are carried out for coal samples with different coring directions by a self-developed vertical SHPB device and then the permeabilities of the above-impacted coal samples are measured. Finally, the calculation model is established to describe the permeability characteristics of coal seams in different directions. The test flow chart is shown in Figure 1.

Figure 1.

Figure 1

Open in a new tab

Test flow chart.

2. Methodology

2.1. Coal Sample Preparation

The samples used in this experiment are all primary structural coal, which were taken from 3# coal seam of Yangquan No. 2 coal mine, China, as shown in Figure 2. The metamorphic degree of coal is anthracite. The water content, ash content, and volatile matter of the coal sample are 1.27, 18.46, and 9.34%, respectively. The consistent coefficient of coal samples by the drop hammer method is 1.21. The bedding of the coal body is obvious, as shown in Figure 3a,b. The coal samples are prepared in three different directions (X, Y, and Z) from coal blocks, as shown in Figure 3c,d. Sample ①, the X direction is parallel to the bedding plane; sample ②, the Y direction is perpendicular to the bedding plane; and sample ③, the Z direction is oblique 45° to the bedding plane. The end face and circumference of coal samples shall be precisely processed and polished so that the unevenness and perpendicularity both of coal samples are less than 0.02 mm.

Figure 2.

Figure 2

Open in a new tab

Yangquan No. 2 coal mine: (a) Geographical coordinates of the mine and (b) coal-bearing stratigraphic column of the mine.

Figure 3.

Figure 3

Open in a new tab

Preparation of coal samples: (a) coal bedding structure, (b) enlarged drawing of the coal sample surface, (c) coal block after coring, (d) coring direction, and (e) part of coal samples.

The prepared coal samples are 50 mm in diameter and 50 mm in height, and a part of coal samples is shown in Figure 3e. There are 45 coal samples, which are divided into three groups, and in each direction, there are 15 coal samples for five different impact tests.

The quasi-static mechanical properties of the coal samples were measured by a SANS CMT5305 electronic universal testing machine. The uniaxial compression, point load splitting, and variable angle shear tests, the elastic modulus E, Poisson’s ratio μ, uniaxial compressive strength σc, uniaxial tensile strength σt, shear strength τf, and internal friction angle φ of the standard-sized coal samples are shown in Table 1.

Table 1. Mechanical Property Parameters of Coal Samples in Different Bedding Directions.

direction ρ (g/cm3) E (GPa) μ σc (MPa) σt (MPa) τf (MPa) φ (deg)
perpendicular to the bedding plane 1.417 3.772 0.295 25.37 1.273 7.41 20.35
oblique 45° to the bedding plane 1.415 3.812 0.327 13.13 1.096 7.216 18.79
parallel to the bedding plane 1.422 3.978 0.333 14.82 0.985 7.165 17.92
Open in a new tab

2.2. Dynamic Impact Test of Coal Samples

2.2.1. Experimental System and Device

The self-developed vertical SHPB device is used to determine the dynamic mechanical properties of coal samples. The principle of this device is similar to that of a horizontal SHPB device. The difference is that the driving device changes from the original pneumatic loading to the gravity impact loading. The main reason for not using the horizontal SHPB device is that when the loading speed is larger, the bullet exit speed of the SHPB device is very stable, but when the loading speed is smaller, the bullet exit speed is prone to deviation, and the air pressure of the bullet exit chamber has a minimum value. The vertical SHPB device occupies a small area and does not need high-pressure gas, which is superior to the traditional SHPB device in safety and economy.

The dynamic test device is shown in Figure 4, which is mainly composed of an impact bar (bullet) 4, an incident bar 5, a transmission bar 9, an absorbing bar 10, a damper 11, a jack 12, a clamp holder 6 (as shown in Figure 4d), a supporting device 7 (as shown in Figure 4c), and a strain gauge 13. During the test, the impact load can be adjusted by the height of the falling bullet. The diameter and length of the bullet are 50 and 30 mm, respectively. Both the incident bar and the transmission bar are equal-section steel bars with a diameter of 50 mm and a length of 1000 mm. The diameter and length of the absorbing bar are 50 and 700 mm, respectively.

Figure 4.

Figure 4

Open in a new tab

Self-developed vertical SHPB device: (a) schematic diagram, (b) impact test system, (c) partially enlarged drawing of the supporting device, (d) partially enlarged drawing of the clamp holder, and (e) Dh8302-1 dynamic tester.

The test operations and attention are shown as follows: (1) The generator 1 lifts the steel wire rope 3, and when the bullet reaches a certain height, it is released freely in the acceleration conduit 2 and impacts the incident bar after obtaining a certain speed. (2) At the moment of impact, the strain gauge 13 on the incident bar and the transmission bar immediately collects the pulse signal that is transmitted to the Dh8302-1 dynamic tester (as shown in Figure 4e). (3) After the clamper 6 is powered on, the confining pressure applied to the incident bar 5, the transmission bar 9, and the absorbing bar 10 can be adjusted until the confining pressure is increased to the maximum so that all of the bars are in a fixed state before and after the impact. (4) The function of the supporting device 7 is to adjust the perpendicularity of the bars so that the bar and the samples are on the same vertical line to ensure the accuracy of the test results.

2.2.2. Experimental Principle

The parameters of the steel bar used in the test are tested and calculated with relevant equipment. The density is 7850 kg/m3, the elastic modulus is 210 GPa, and the speed of wave propagation in the steel bar is 5.19 km/s.

The impact velocity (v) of the bullet is calculated according to eq 1

2.2.2. 1

where g is the acceleration of gravity, 9.8 m/s2, and H is the height of the free-falling bullet’s center of gravity.

In this paper, five free-falling heights (H) are 0.25, 0.40, 0.55, 0.70, and 0.85 m, and the impact velocities calculated by eq 1 are 2.21, 2.8, 3.28, 3.7, and 4.08 m/s.

The impulse of the bullet is calculated according to the momentum theorem of eq 2

2.2.2. 2

where F is the resultant force of all external forces including gravity, N; t is the impact time, s; m is the mass of the bullet, kg; and v and v0 are the end velocity and initial velocity of the object motion, m/s, respectively. According to the impact velocity obtained from eq 1, the different impulses under different H’s can be obtained, as listed in Table 2.

Table 2. Impact Test Parameters.
impact height (m) coal sample number impact velocity (m/s) impulse (kg·m/s)
0.25 X1-1, X1-2, X1-3 2.21 10.21
Y1-1, Y1-2, Y1-3
Z1-1, Z1-2, Z1-3
0.4 X2-1, X2-2, X2-3 2.8 12.94
Y2-1, Y2-2, Y2-3
Z2-1, Z2-2, Z2-3
0.55 X3-1, X3-2, X3-3 3.28 15.16
Y3-1, Y3-2, Y3-3
Z3-1, Z3-2, Z3-3
0.7 X4-1, X4-2, X4-3 3.7 17.1
Y4-1, Y4-2, Y4-3
Z4-1, Z4-2, Z4-3
0.85 X5-1, X5-2, X5-3 4.08 18.86
Y5-1, Y5-2, Y5-3
Z5-1, Z5-2, Z5-3
Open in a new tab

Based on the assumption of one-dimensional stress, the waveforms of the incident wave, reflected wave, and transmitted wave are obtained by a Dh8302-1 dynamic tester. The strain rate, strain, and stress in the coal samples are calculated according to the simplified “three-wave equation”, and the stress–strain curves of the coal samples under different strain rates are drawn to obtain the dynamic mechanical properties. The simplified equations are as follows

2.2.2. 3
2.2.2. 4
2.2.2. 5

where ε̇(t) is the loading strain rate of coal samples, s–1; ε(t) is the strain of coal samples, %; σ(t) is the loading stress of coal samples, MPa; εr(t) and εt(t) are the reflected wave strain and transmitted wave strain in the compression bar, respectively, %; E is the elastic modulus of the compression bar; C is the wave velocity of the compression bar, km/s; A is the cross-sectional area of the compression bar, m2; A0 is the cross-sectional area of the test sample, m2; and L0 is the length of the test sample, mm.

2.3. Anisotropic Permeability Test of Coal Samples

2.3.1. Test Device

The permeability test of coal samples was carried out by a TC-III multilayer superimposed gas reservoir joint development simulation device. The test system is mainly composed of a coal sample holder, a stress loading system, a vacuum degassing system, an inflation system, a temperature control system, and a data acquisition system. The test system is shown in Figure 5, and the main performance parameters are listed in Table 3.

Figure 5.

Figure 5

Open in a new tab

Schematic diagram of the permeability test system.

Table 3. Performance Parameters of the Test System.
parameter test range accuracy
temperature (°C) –20–100 ±0.01
axial compression (MPa) 0–50 ±0.25%
confining pressure (MPa) 0–50 ±0.25%
flowmeter range (mL/min) 0–500 ±0.01
displacement pressure (MPa) 0–15 ±0.1
Open in a new tab

2.3.2. Test Method

  • (1)

    Put the prepared coal sample into the coal sample holder for sealing treatment.

  • (2)

    Vacuum degas for more than 12 h to eliminate the error caused by gas impurity to the test.

  • (3)

    Adjust the constant-temperature device to carry out the test process in a constant-temperature environment of 28 °C.

  • (4)

    Use the manual high-pressure pump in the stress loading system to load the coal samples to the set confining pressure.

  • (5)

    When gas is introduced into the coal sample and the change in the adsorption pressure is less than 0.01 MPa within 2 h, the gas is considered to reach the adsorption equilibrium.

  • (6)

    Open the gas outlet end of the coal samples until the gas seepage reaches a stable state and measure the gas pressure and flow rate.

  • (7)

    Replace other coal samples, repeat the above steps, and complete all coal sample tests.

2.3.3. Test Principle for Permeability

In the experiment, the Darcy steady-flow method is used to measure the permeability of coal samples, and the gas flow rate in coal samples at a steady state is measured under different gas pressure conditions. The average permeability (K) of coal samples is calculated according to the gas flow rate and the pressure difference at both inlet and outlet ends of coal samples. The expression is

2.3.3. 6

where Q0 is the gas seepage flow under the standard condition, cm3/s; P0 is the standard atmospheric pressure, Pa; μ is the gas dynamic viscosity, Pa·s; L is the length of the coal samples, cm; P1 and P2 are the gas inlet and outlet pressures of the coal samples, respectively, Pa; and S is the cross-sectional area of the coal samples, cm2.

According to the buried depth of the coal samples (about 400 m) and the condition of the overlying strata, the test confining pressure is 8 MPa and the axial pressure is 3.5 MPa (the lateral pressure coefficient is 0.43).

3. Results and Discussion

3.1. Coal Impact Test Results and Analysis

According to eqs 3–5, the dynamic peak stress of coal samples was obtained in parallel to the bedding direction, perpendicular to the bedding direction, and oblique 45° to the bedding direction under different impact heights, which is presented in Table 4 and Figure 6. It can be seen from Table 4 that the strain rates of coal samples after the impact are concentrated in the range of low and medium strain rates. It can be seen from Figure 6 that the dynamic peak stress of coal samples is the largest in perpendicular to the bedding direction and the lowest in oblique 45° to the bedding direction under any impact loads. With an increase in impact height, the dynamic peak stress of coal samples increases gradually, which shows a linear growth relationship, and the fitting coefficient is above 0.98.

Table 4. Data Summary of Coal Samples in Different Directions under Different Impulses.

  X direction
 Y direction
 Z direction
impulse (kg·m/s) no. peak stress strain rate no. peak stress strain rate no. peak stress strain rate
10.21 X1-1 5.306 8.017 Y1-1 7.225 10.087 Z1-1 4.472 7.561
X1-2 5.701 8.454 Y1-2 6.909 9.534 Z1-2 4.638 8.044
X1-3 5.715 9.576 Y1-3 7.098 9.015 Z1-3 4.556 7.078
12.94 X2-1 7.540 15.112 Y2-1 9.774 16.213 Z2-1 6.758 14.339
X2-2 7.401 15.065 Y2-2 9.325 17.054 Z2-2 6.756 14.812
X2-3 7.626 15.948 Y2-3 8.496 16.156 Z2-3 6.732 14.556
15.16 X3-1 9.763 24.015 Y3-1 11.822 25.316 Z3-1 8.116 22.271
X3-2 9.837 23.238 Y3-2 11.184 24.323 Z3-2 7.936 22.047
X3-3 9.591 22.914 Y3-3 11.432 24.066 Z3-3 8.263 23.817
17.1 X4-1 12.115 34.021 Y4-1 14.006 34.043 Z4-1 10.573 31.815
X4-2 11.861 33.755 Y4-2 13.528 34.027 Z4-2 10.318 32.726
X4-3 12.148 33.366 Y4-3 13.213 35.583 Z4-3 9.832 33.542
18.86 X5-1 14.220 44.377 Y5-1 15.481 47.335 Z5-1 11.788 42.815
X5-2 13.952 45.231 Y5-2 15.356 46.512 Z5-2 12.213 43.942
X5-3 13.473 44.717 Y5-3 15.681 45.416 Z5-3 12.214 44.505
Open in a new tab

Figure 6.

Figure 6

Open in a new tab

Peak stress of coal samples in different directions under different impact loads.

3.2. Test Results and Analysis of the Anisotropic Coal Permeability

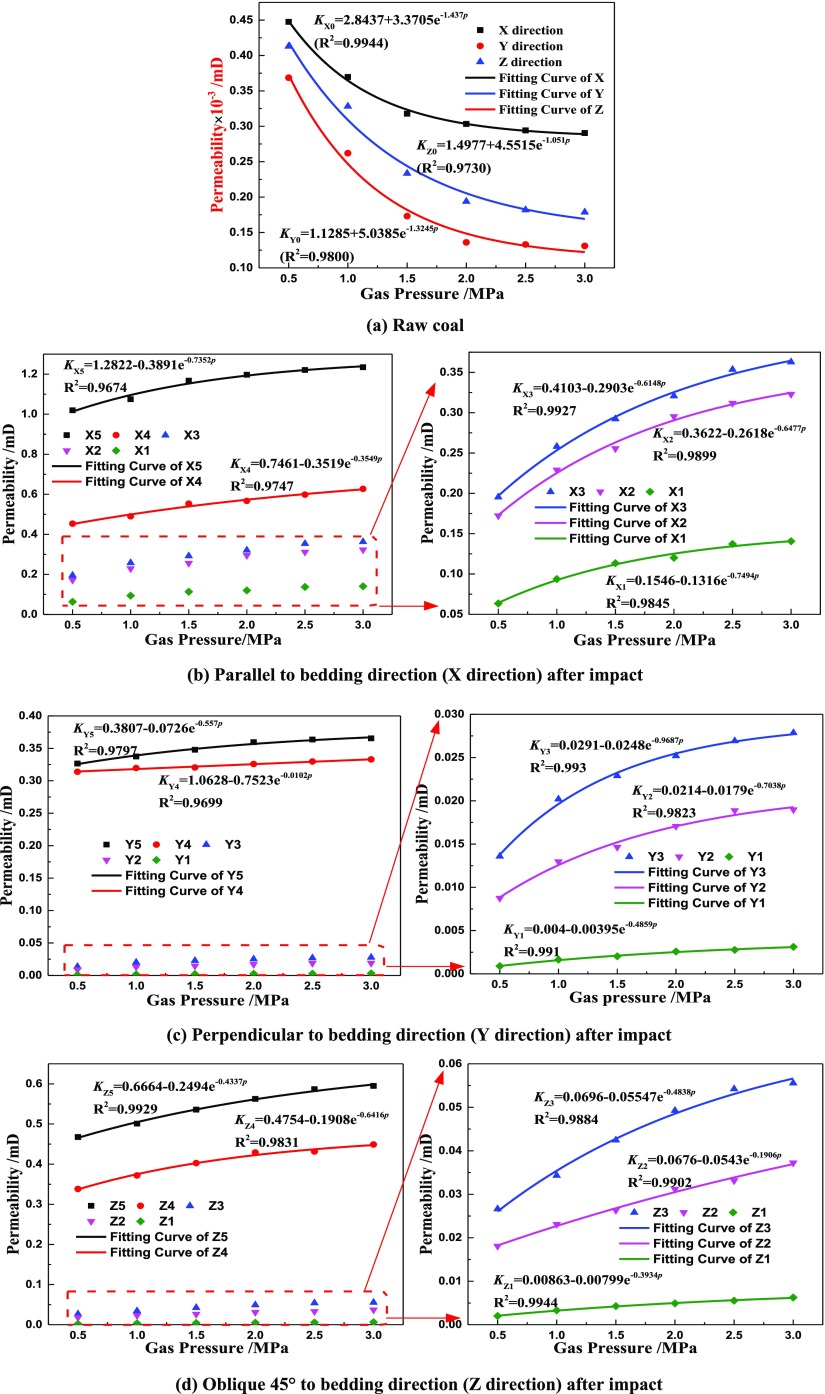
The test results of the permeability of impacted coal samples under different gas pressures are shown in Figure 7. KXi, KYi, and KZi are the permeabilities in parallel to the bedding direction (X direction), perpendicular to the bedding direction (Y direction), and oblique 45° to the bedding direction (Z direction), and the subscript i = 0, 1, 2, 3, 4, and 5, where “0” is the raw coal sample and “1–5” are impacted coal samples from a smaller impact load to a larger impact load.

Figure 7.

Figure 7

Open in a new tab

Permeability change laws in different directions before and after the impact.

In Figure 7a, the permeability of raw coal samples is very small and its magnitude is only several 10–4 mD. At the same time, the permeability shows its anisotropic characteristics in different directions. Coal samples in perpendicular to the bedding direction are more sensitive to gas pressure. The permeability in parallel to the bedding direction (X direction) is the largest, which is caused by the bedding plane in this direction, followed by that in oblique 45° to the bedding direction (Z direction), and the smallest in perpendicular to the bedding direction (Y direction). With an increase in gas inlet pressure, the permeability of coal samples decreases exponentially.

Obviously, the impact has a significant effect on the permeability of coal samples, as shown in Figure 7b–d. After the coal samples are impacted under five different impact loads (herein, it should be noted that the coal sample after the impact is not only not broken but also has no clearly visible cracks and transfixion cracks), the permeability increases in varying degrees in three different directions; however, with an increase in inlet gas pressure, the permeability change law of the impacted coal samples is different from that of raw coal samples, which increases exponentially, as shown in Figure 7b–d. The main reason is that in the low gas pressure stage the migration of gas molecules in coal pores will have the Klinkenberg slippage effect, which increases the flow momentum of gas and results in a rapid increase of permeability. When the pore pressure increases gradually, the Klinkenberg effect gradually weakens. At the same time, the effective stress on the coal body is gradually reduced.

It can be seen from Figure 7b–d that under the same impact load the permeability is the highest in the direction of parallel to the bedding plane, the second is in the direction of oblique 45° to the bedding plane, and the lowest is in the direction of perpendicular to the bedding plane. Moreover, for any direction, the larger the impact load, the more obvious the influence on coal permeability. This is because the impact causes the natural micropores and microfractures to expand to a certain extent, and even new microfractures will be generated and micropores become macropores, which will increase the gas flow. Therefore, under different impact loads, the permeability in each direction is far greater than that of raw coal samples.

To compare and analyze the influence of different impact loads on coal permeability, the permeability ratios of impacted coal samples and raw coal samples in each direction are shown in Figure 8. It can be seen from Figure 8 that with an increase in inlet gas pressure the ratio of permeability conforms to the exponential growth under the same impact load in different directions. Also, the ratios of permeability indicate that they are rather  surprising  results. The permeability of impacted coal samples is thousands of times than that of raw coal samples under larger impact loads and is hundreds of times than that of raw coal samples under smaller impact loads. For example, when the inlet gas pressure is 3.0 MPa and the impulse is the maximum (18.86 kg·m/s), the ratio of permeabilities KX5 and KX0 is up to more than 4000, in parallel to the bedding direction; the ratio of permeabilities KY5 and KY0 is up to more than 2500 in perpendicular to the bedding direction; and the ratio of permeabilities KZ5 and KZ0 is up to more than 3000 in oblique 45° to the bedding direction. Obviously, the impact load plays a positive role in coal gas permeability improvement.

Figure 8.

Figure 8

Open in a new tab

Ratios of permeabilities of impacted coal samples and raw coal samples under different impact loads in different directions.

3.3. Anisotropic Coal Permeability Calculation Model

3.3.1. Permeability Calculation Model

Coal is orthotropic; that is, the x-axis and y-axis in the rectangular coordinate system are consistent with the direction of maximum and minimum permeabilities. Here, the x-axis and y-axis refer to the directions of parallel and perpendicular to the bedding plane, respectively, as shown in Figure 9. In the model, the permeabilities of coal seam gas in the directions of parallel and perpendicular to the bedding plane are KX and KY, respectively. ∇pn is the gas driving pressure gradient in the n direction, and the displacement effect of ∇pn on coal seam gas can be equivalent to the component ∇pnx in the x direction and the component ∇pny in the y direction, which is called the equivalent displacement principle.29,30

Figure 9.

Figure 9

Open in a new tab

Anisotropic coal permeability calculation model.

In the process of anisotropic coal–rock permeability derivation, only considering the seepage velocity component parallel to the pressure gradient, and ignoring the seepage velocity component perpendicular to the pressure gradient, there will be great errors in the calculation results. Therefore, a numerical model is established that the seepage velocity is not parallel to the pressure gradient.31 According to Darcy’s law, the permeability can be expressed as eq 7 by seepage velocity, fluid viscosity, and the component of pressure gradient along the velocity direction at a certain position in the reservoir stratum.

3.3.1. 7

where v is the seepage velocity, μ is the fluid viscosity, θ is the included angle between the seepage velocity (v) and the pressure gradient (∇pn), α is the included angle between the seepage velocity (v) and the x-axis, and β is the included angle between the pressure gradient (∇pn) and the x-axis.

The cosine of the included angle (θ) between the seepage velocity (v) and the pressure gradient (∇pn) can be expressed as

3.3.1. 8

According to the equation of motion, the components of velocity vx and vy in x and y directions are as follows

3.3.1. 9

Combining eqs 7–9, the permeability (Kn) can be obtained

3.3.1. 10

Therefore, if the permeabilities in parallel and perpendicular to the bedding direction (i.e., KX and KY) are known, the permeability corresponding to any direction in the plane can be calculated by eq 10.

3.3.2. Calculation and Analysis of the Permeability in Anisotropic Coal Seam

To verify the reliability of the calculation model, the measured permeability in oblique 45° to the bedding direction is compared with the calculated values under different impact loads, as shown in Figure 10. It can be seen intuitively from Figure 10 that under the condition of a certain gas pressure the calculated permeability values are in good agreement with the measured values in the direction of oblique 45° to the bedding plane. Also, the relative errors of permeability between the calculated values and the measured values are no more than 10%. Most of the errors are less than 5%; only a few are more than 5%. Therefore, if the permeability of the coal seam in parallel and perpendicular to the bedding direction can be measured, the permeability of the coal seam in any direction of this plane can be obtained by the model. The method is simple and easy to operate, and the results are fast and accurate.

Figure 10.

Figure 10

Open in a new tab

Permeability comparison between calculated values and measured values in oblique 45° to the bedding direction under different impact loads.

Under the determined gas pressure of the coal seam, KX and KY can be obtained from Figure 7 and then the permeability (Kn) can be calculated via eq 10 with different α angles. Therefore, the permeability distribution laws in different bedding directions before and after the impact are shown in Figure 11. It can be seen from Figure 11 the permeability in the raw coal seam displays noncircular distribution under different gas pressures. The permeability in parallel to the bedding direction is the largest and then decreases to the minimum with an increase of α angle to 90°; that is, the permeability in perpendicular to the bedding direction is the smallest. In Figure 11a, the permeability in the original coal seam is very small and decreases with an increase in gas pressure. In Figure 11b–d, the permeability KX is much bigger than KY under the same impact load, which causes the closer the angle is to 90° (y direction), the faster the decrease in the permeability (Kn). At the same time, the larger the impact load, the bigger the permeability (Kn), which indicates that when deep-hole blasting is carried out in the coal seam, the closer the coal seam to the blasting center, the better the effect of coal cracking and the bigger the permeability. On the contrary, the farther away the coal seam from the blasting center, the worse the effect of coal cracking and the smaller the permeability. This fully reveals that the permeability of coal seam after deep-hole blasting is not only anisotropic but also decreases gradually from near to far until the original coal seam permeability. That is to say, the permeability changes gradually from the blasting center to the original coal seam, which will provide basic data for gas predrainage analysis after coal seam blasting.

Figure 11.

Figure 11

Open in a new tab

Permeability in different directions under different impact loads and gas pressures.

4. Conclusions

The dynamic impact mechanical properties of coal samples in different coring directions (parallel to the bedding direction, perpendicular to the bedding direction, and oblique 45° to the bedding direction) were tested by a self-developed vertical SHPB device under different impact loads. Then, the permeability of coal samples was measured under different inlet gas pressures. Finally, the calculation model of anisotropic coal permeability was established, and the permeability distribution law was calculated and analyzed. The main conclusions are as follows:

  • (1)

    The permeability of raw coal samples in three directions decreases exponentially with an increase in gas pressure. However, the permeability of impacted coal samples in three directions increases exponentially with an increase in gas pressure under the same impact load, and in each bedding direction, the permeability increases exponentially with an increase in impact load under the same gas pressure.

  • (2)

    Under the same bedding direction and gas pressure, the permeability of impacted coal samples is much larger than that of raw coal samples.

  • (3)

    The calculated permeability values in oblique 45° to the bedding direction are very consistent with the measured values, and the relative errors are no more than 10%.

  • (4)

    In anisotropic permeability of the coal seam, the permeability distribution laws are not noncircular, and the greater the impact load, the larger the permeability.

This study not only shows that the coal seam has anisotropic characteristics of the mechanical properties and gas permeability but also analyzes the distribution of permeability characteristics in each direction by measuring the permeability in perpendicular and parallel to the bedding direction, which will provide the basis for the layout of deep-hole blasting holes and the theoretical prediction of the gas predrainage effect.

Acknowledgments

This paper is supported by the National Natural Science Foundation of China (no. 41772163).

The authors declare no competing financial interest.

References

  1. Shen B. H.; Liu J. Z.; Zhang H. The technical measures of gas control in China coal mines. J. China Coal Soc. 2007, 32, 673–679. [Google Scholar]
  2. Yue G. W.; Liu H.; Yue J. W.; Li M. M.; Liang W. M. Influence radius of gas extraction borehole in an anisotropic coal seam: Underground in-situ measurement and modeling. Energy Sci. Eng. 2019, 7, 694–709. 10.1002/ese3.285. [DOI] [Google Scholar]
  3. Huang B.; Li X. H.; Fu C.; Wang Y.; Cheng H. R. The mechanism of drainage gas recovery and structure optimization of an internal vortex tool in a horizontal well. J. Nat. Gas Sci. Eng. 2019, 67, 233–241. 10.1016/j.jngse.2019.05.005. [DOI] [Google Scholar]
  4. Sun Z.; Li X. F.; Liu W. Y.; Zhang T.; He M. X.; Nasrabadi H. D. Molecular Dynamics of Methane Flow Behavior through Realistic Organic Nanopores under Geologic Shale Condition: Pore size and Kerogen Types. Chem. Eng. J. 2020, 124341 10.1016/j.cej.2020.124341. [DOI] [Google Scholar]
  5. Zou Q. L.; Liu H.; Zhang Y. J.; Li Q. M.; Fu J. W.; Hu Q. T. Rationality evaluation of production deployment of outburst-prone coal mines: A case study of nantong coal mine in Chongqing, China. Saf. Sci. 2020, 122, 104515 10.1016/j.ssci.2019.104515. [DOI] [Google Scholar]
  6. Chen X. Z.; Xue S.; Yuan L. Coal seam drainage enhancement using borehole pre-splitting basting technology-A case study in Huainan. Int. J. Min. Sci. Technol. 2017, 27, 771–775. 10.1016/j.ijmst.2017.07.015. [DOI] [Google Scholar]
  7. Roslin A.; Pokrajac D.; Zhou Y. F. Cleat structure analysis and permeability simulation of coal samples based on micro-computed tomography (micro-CT) and scan electron microscopy (SEM) technology. Fuel 2019, 254, 115579 10.1016/j.fuel.2019.05.162. [DOI] [Google Scholar]
  8. Ti Z. Y.; Zhang F.; Pan J.; Ma X. F.; Shang Z. Permeability enhancement of deep hole pre-splitting blasting in the low permeability coal seam of the Nanting coal mine. PLoS One 2018, 13, e0199835 10.1371/journal.pone.0199835. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Wang F. T.; Tu S. H.; Yuan Y.; Feng Y. F.; Chen F.; Tu H. S. Deep-hole pre-split blasting mechanism and its application for controlled roof caving in shallow depth seams. Int. J. Rock Mech. Min. Sci. 2013, 64, 112–121. 10.1016/j.ijrmms.2013.08.026. [DOI] [Google Scholar]
  10. Sun Z.; Shi J. T.; Wu K. L.; Liu W. Y.; Wang S. R.; Li X. F. A prediction model for desorption area propagation of coalbed methane wells with hydraulic fracturing. J. Pet. Sci. Eng.. 2019, 175, 286–293. 10.1016/j.petrol.2018.12.047. [DOI] [Google Scholar]
  11. Liu Y. B.; Yin G. Z.; Zhang D. M.; Li M. H.; Deng B. Z.; Liu C.; Zhao H. G.; Yin S. Y. Directional permeability evolution in intact and fractured coal subjected to true-triaxial stresses under dry and water-saturated conditions. Int. J. Rock Mech. Min. Sci. 2019, 119, 22–34. 10.1016/j.ijrmms.2019.04.007. [DOI] [Google Scholar]
  12. Li W.; Ren T. W.; Busch A.; Den Hartog S. A. M.; Cheng Y. P.; Qiao W.; Li B. Architecture, stress state and permeability of a fault zone in Jiulishan coal mine, China: Implication for coal and gas outbursts. Int. J. Coal Geol. 2018, 198, 1–13. 10.1016/j.coal.2018.09.002. [DOI] [Google Scholar]
  13. Xia K. W.; Wei Y. Dynamic rock tests using split Hopkinson(Kolsky) bar system-A review. J. Rock Mech. Geotech. Eng. 2015, 7, 27–59. 10.1016/j.jrmge.2014.07.008. [DOI] [Google Scholar]
  14. Cai M.; Kaiser P. K.; Suorineni F.; Su K. A study on the dynamic behavior of the Meuse/Haute-Marne argillite. Phys. Chem. Earth 2007, 32, 907–916. 10.1016/j.pce.2006.03.007. [DOI] [Google Scholar]
  15. Lu F. Y.; Chen R.; Lin Y. L.; Zhao P. Y.; Zhang D.. Hopkinson Rod Experimental Technology; Science Press: Beijing, 2013; pp 1–2. [Google Scholar]
  16. Yan Z. M.; Wang K.; Zang J.; Wang C.; Liu A. Anisotropic coal permeability and its stress sensitivity. Int. J. Min. Sci. Technol. 2019, 29, 507–511. 10.1016/j.ijmst.2018.10.005. [DOI] [Google Scholar]
  17. Li H.; Shimada S.; Zhang M. Anisotropy of gas permeability associated with cleat pattern in a coal seam of the Kushiro coalfield in Japan. Environ. Geol. 2004, 47, 45–50. 10.1007/s00254-004-1125-x. [DOI] [Google Scholar]
  18. Wang H.; Yue G. W.; Yue J. W.; Li M. M.; Zhen X. J. Permeability of coal associated with cleat and bedding structure: measurement and modeling. Energy Sources, Part A 2019, 32, 1 10.1080/15567036.2019.1675813. [DOI] [Google Scholar]
  19. Koenig P. A.; Stubbs P. B. In Interference Testing of a Coal-bed Methane Reservoir, SPE Unconventional Gas Technology Symposium, Louisville, Kentucky, 1986; pp 18–21.
  20. Liu S. Q.; Zhang S. J.; Chen F.; Wang C. H.; Liu M. Y. Variation of coal permeability under dehydrating and heating: A Case study of ulanqab lignite for underground coal gasification. Energy Fuels 2014, 28, 6869–6876. 10.1021/ef501696e. [DOI] [Google Scholar]
  21. Yue G. W.; Li M. M.; Wang L.; Liang W. M. Optimal layout of blasting holes in structural anisotropic coal seam. PLoS One 2019, 14, e0218105 10.1371/journal.pone.0218105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Chen Y. L.; Zhang Y. N.; Li X. L. Experimental study on influence of bedding angle on gas permeability in coal. J. Pet. Sci. Eng.. 2019, 179, 173–179. 10.1016/j.petrol.2019.04.010. [DOI] [Google Scholar]
  23. Chen Y. L.; Li X. L.; Li B. Coal anisotropic sorption and Permeability:An Experimental study. Processes 2018, 6, 104 10.3390/pr6080104. [DOI] [Google Scholar]
  24. Wang Z. Z.; Pan J. N.; Hou Q. L.; Niu Q. H.; Tian J. J.; Wang H. C.; Fu X. H. Changes in the anisotropic permeability of low-rank coal under varying effective stress in Fukang mining area, China. Fuel 2018, 234, 1481–1497. 10.1016/j.fuel.2018.08.013. [DOI] [Google Scholar]
  25. Yang D. S.; Qi X. Y.; Chen W. Z.; Wang S. G.; Yang J. P. Anisotropic Permeability of coal subjected to cyclic loading and unloading. Int. J. Geomech. 2018, 18, 04018093 10.1061/(ASCE)GM.1943-5622.0001229. [DOI] [Google Scholar]
  26. Raza S. S.; Ge L.; Rufford T. E.; Chen Z. W.; Rudolph V. Anisotropic coal permeability estimation by determining cleat compressibility using mercury intrusion porosimetry and stress-strain measurements. Int. J. Coal Geol. 2019, 205, 75–86. 10.1016/j.coal.2019.02.011. [DOI] [Google Scholar]
  27. Chen S.; Zhang L.; Zhang C.; Huang M. Q. Experimental study on the seepage characteristics of bituminous coal under the conditions of liquid nitrogen fracturing. Energy Sci. Eng. 2019, 7, 2138 10.1002/ese3.419. [DOI] [Google Scholar]
  28. Yan F. Z.; Xu J.; Lin B. Q.; Peng S. J.; Zou Q. L.; Zhang X. L. Changs in pore structure and permeability of anthracite coal before and after high-voltage electrical pulses treatment. Powder Technol. 2019, 343, 560–567. 10.1016/j.powtec.2018.11.083. [DOI] [Google Scholar]
  29. Wang D. P.; Zhou Y. Y.; Ma P. G.; Tian T. H. Vector properties and calculation model for directional rock permeability. Rock Soil Mech. 2005, 26, 1294–1297. [Google Scholar]
  30. Szabo Barna A. Permeability of orthotropic porous mediums. Water Resour. Res. 1968, 4, 801–808. 10.1029/WR004i004p00801. [DOI] [Google Scholar]
  31. Wang X. Directional permeability calculation model for anisotropic rock. Sci. Tech. Eng. 2013, 13, 5037–5039. [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES