Modulations of Insular Projections by Prior Belief Mediate the Precision of Prediction Error during Tactile Learning

Abstract

Awareness for surprising sensory events is shaped by prior belief inferred from past experience. Here, we combined hierarchical Bayesian modeling with fMRI on an associative learning task in 28 male human participants to characterize the effect of the prior belief of tactile events on connections mediating the outcome of perceptual decisions. Activity in anterior insular cortex (AIC), premotor cortex (PMd), and inferior parietal lobule (IPL) were modulated by prior belief on unexpected targets compared with expected targets. On expected targets, prior belief decreased the connection strength from AIC to IPL, whereas it increased the connection strength from AIC to PMd when targets were unexpected. Individual differences in the modulatory strength of prior belief on insular projections correlated with the precision that increases the influence of prediction errors on belief updating. These results suggest complementary effects of prior belief on insular-frontoparietal projections mediating the precision of prediction during probabilistic tactile learning.

SIGNIFICANCE STATEMENT In a probabilistic environment, the prior belief of sensory events can be inferred from past experiences. How this prior belief modulates effective brain connectivity for updating expectations for future decision-making remains unexplored. Combining hierarchical Bayesian modeling with fMRI, we show that during tactile associative learning, prior expectations modulate connections originating in the anterior insula cortex and targeting salience-related and attention-related frontoparietal areas (i.e., parietal and premotor cortex). These connections seem to be involved in updating evidence based on the precision of ascending inputs to guide future decision-making.

Introduction

The expectation for the occurrence of tactile events is modulated by prior experiences (Lovero et al., 2009; van Ede et al., 2010, 2014). In a probabilistic environment, prior belief about the causes of relevant stimuli, such as imminent tactile inputs, is continuously updated based on past experiences following the principle of predictive coding (Rao and Ballard, 1999) and free energy (Friston and Kiebel, 2009). In this framework, bottom-up sensations and top-down predictions are integrated by precision-dependent computational processes, where the precision or confidence increases the influence of ascending prediction error (PE) signals on perceptual inference via postsynaptic gain (i.e., cortical gain control or excitation–inhibition balance; Feldman and Friston, 2010).

Awareness of surprising or unexpected tactile sensations is thought to depend on interactions within a hierarchically organized somatosensory system. Somatosensory mismatch negativity, as a PE equivalent, elicited by an unexpected deviant has been shown to follow Bayesian rules (Ostwald et al., 2012; Allen et al., 2016; Fardo et al., 2017). These rules seem to be encoded by recurrent processing loops in a network encompassing primary/secondary somatosensory cortices (S1/S2), inferior frontal cortex, and anterior cingulate cortex (Ostwald et al., 2012). Unexpected tactile events particularly increase recurrent connectivity among S1/S2, inferior/middle frontal, and inferior parietal regions (Allen et al., 2016; Fardo et al., 2017), while the anterior insular cortex (AIC) seems crucial for the integration of afferent sensory inputs with top-down control arising in the frontal and cingulate cortex (Allen et al., 2016).

Behavioral performance and neural responses to expected and unexpected outcomes are modulated by prior beliefs about future states of the tactile environment. The degree of anticipation has been shown to improve the precision of tactile sensations (van Ede et al., 2014), whereas uncertainty (Rossi-Pool et al., 2016; Schröder et al., 2019) or the constitutive elements of perceptual inference (i.e., prediction error and precision weighting; Ostwald et al., 2012; Allen et al., 2016; Fardo et al., 2017) are well reflected by neural responses in the insular, cingulate, and premotor cortices. Despite all this evidence, how prior belief regulates effective connectivity in the somatosensory network for future decision-making remains unknown.

In an associative learning task, the association strength of the decision and the corresponding feedback is continuously updated on the basis of recent observations. Considerable evidence has shown that this inference can be conceptualized by hierarchical Bayesian modeling (Iglesias et al., 2013; Vossel et al., 2015; Kuhns et al., 2017; Weilnhammer et al., 2018). Here, we applied an adapted tactile associative learning task where participants had to learn the changing predictive strength of a sample stimulus in forecasting a subsequently presented target. Trialwise prior belief about the sample-target contingency were used as modulators of effective connectivity for expected and unexpected targets.

We hypothesized to identify a hierarchically organized somatosensory network, consisting of the insular cortex and frontoparietal regions, in which predicted outcomes (i.e., the awareness for expected and unexpected targets) are differentially modulated by prior belief. Since the insular cortex is considered as a core hub regulating the interaction of bodily, attentional, and anticipatory tactile signals (Sridharan et al., 2008; Lovero et al., 2009; Menon and Uddin, 2010; Allen et al., 2016), we further expected that efferent projections originating in the insula may change as a function of prior belief for expected and unexpected targets, which, in turn may signal the precision weighting for belief updating.

Materials and Methods

Participants

We recruited 33 healthy male participants (mean ± SD age, 25.1 ± 3.8 years). Only male participants were included to avoid the influences of hormonal fluctuations over the menstrual cycle on learning and associated blood oxygenation level-dependent (BOLD) signals (Dreher et al., 2007; Sacher et al., 2013; Wetherill et al., 2016). Five participants were excluded due to >20% invalid trials (i.e., missed or late response >1300 ms) or <60% correct responses. Consequently, 28 participants were included for further data analysis (mean ± SD age, 25.3 ± 3.9 years). All participants were right handed, as assessed by the Edinburgh Handedness Inventory (Oldfield, 1971), and had normal or corrected to normal vision, no history of psychiatric/neurologic disorders, or received regular medication. The study was approved by the ethics committee of the Ruhr-University Bochum.

Tactile stimuli

The tactile stimuli were generated and delivered using an MRI-compatible piezoelectric Braille stimulator (Metec). It consisted of eight plastic pins, aligned in two series of four (Fig. 1A; pin diameter, 1.2 mm; rounded top; interpin spacing, 2.45 mm). The Braille stimulator was controlled using Presentation software (version 20.1; Neurobehavioral Systems) through Metec Virtual Braille Device by TCP-IP (transmission control protocol/internet protocol) commands. The index fingertip of the right (dominant) hand was positioned over the Braille stimulator. We applied the following two alternative tactile stimulation patterns: either the upper four pins (distal) were raised or the lower four pins (proximal) were raised. To ensure that both tactile stimulation patterns (distal or proximal) were perceived correctly, participants performed an initial test before MRI scanning in which they had to distinguish both tactile stimulation patterns 100% correctly.

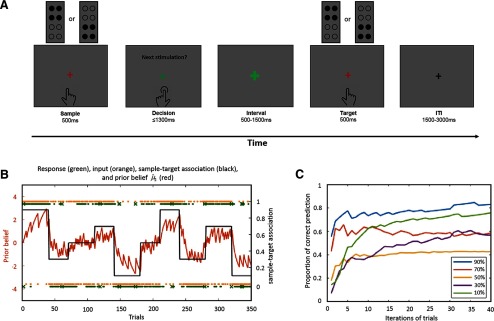
Figure 1.

Experimental design and participants' behavioral performance. A, Experimental design. Participants were instructed to predict the target stimulus as accurately as possible based on the predictability of the sample stimulus. Both sample and target stimuli were delivered to the dominant (right) hand. B, The sample-target association and a subject-specific example of prior belief (${\widehat{\mu }}_2$). Black line, Time-varying sample-target association strengths consisting of strongly predictive (90% and 10%), moderately predictive (70% and 30%), and nonpredictive (50%) blocks; red line, example of a subject-specific trajectory of prior beliefs about sample-target contingencies; orange dots, trial outcomes (or tactile inputs); green dots, participant's observed responses; green cross, participant's missing responses. C, The proportion of expected targets (Correct) over time for each of the five sample-target contingencies (i.e., 90%, 70%, 50%, 30%, and 10%). The colored lines show the difference in proportion of Correct trials between blocks with high predictability and low predictability indicating successful learning of sample-target contingencies.

Experimental design

We used a tactile associative learning task where participants were instructed to learn the predictability of a sample stimulus in forecasting the subsequently presented target stimulus (Fig. 1A). In each trial, participants first received the sample stimulus for 500 ms (distal or proximal). A red fixation cross was simultaneously presented on the screen together with the tactile stimulus via fMRI-compatible LCD goggles (VisuaStim Digital, Resonance Technology). Following the sample, the red fixation cross turned green and participants had to press one of two buttons (LumiTouch keypads, Photon Control) with the index or middle finger of the left hand to indicate which of the two target stimuli (distal or proximal) would follow. After the button press and a short interval of 500–1500 ms, the target stimulus (distal or proximal) was presented for 500 ms. Trials were presented with randomized intertrial intervals ranging between 1500 and 3000 ms, in 100 ms steps.

Throughout the experiment, participants were asked to maintain central fixation and to indicate their decision by pressing the button within 1300 ms. Moreover, they were instructed to learn the predictability of the sample stimulus (i.e., how much they believed that the target matches the sample). The predictability of the sample was manipulated by changing the strength of the sample-target contingency over time. The task consisted of strongly predictive (90% and 10%), moderately predictive (70% and 30%), and nonpredictive (50%) blocks (Fig. 1B). The whole experiment comprised 10 blocks, 2 blocks for each of the five sample-target contingencies. Each block based on one sample-target contingency and consisted of an equal number of the two tactile patterns, presented in random order as either sample or target stimulus. The sequence of blocks was pseudorandomized and fixed across participants to ensure intersubject comparability of the learning process (Iglesias et al., 2013; Vossel et al., 2014). Participants were informed that the sample-target contingency would change over time, but the exact probabilities (i.e., 90%/10%, 70%/30%, and 50%) were unknown to the participants. To avoid the prediction of a new block onset, the two blocks for each prediction strength were once presented with 30 trials, and the other time with 40 trials. The fMRI experiment consisted of 350 trials in total, which we split into three runs, each lasting ∼10 min. Overall, the fMRI session was 30 min long.

To motivate constantly high performance throughout the fMRI experiment, we offered a monetary reward of 1€ added to the general reimbursement (5€/run) for a 5% increase in correct predictions in each fMRI run. After each run, the participants were given a visual feedback (10 s) about the amount of correctly or incorrectly predicted trials, how many were missed, and how much money they made during the preceding run. After the reward feedback, the participants had a short rest of 60 s in which the word “pause” was shown on the display.

Modeling of behavioral data

The invalid trials with missed responses or excessively long reaction time (>1300 ms) were excluded from further analyses. The behavioral data were applied to a three-level hierarchical Gaussian filter (HGF), as implemented in the HGF version 5.2 toolbox (https://www.tnu.ethz.ch/de/software/tapas.html), to calculate the individual differences in trialwise prior belief about external states at different levels (Mathys et al., 2011; Iglesias et al., 2013; Vossel et al., 2014; Kuhns et al., 2017; Weilnhammer et al., 2018). The HGF consists of a perceptual and a response model, which describes a framework where an agent receives a sequence of inputs (stimuli) and generates behavioral responses based on perceptual inference. It describes how hidden states (χ^(t)) of the world generate sensory input (Mathys et al., 2011). The first level of the model represents tactile perception during each trial, χ₁^(t). In our study, it was represented by a binary input, with χ₁^(t) = 1 for when the target matched the sample and χ₁^(t) = 0 for when the target mismatched the sample. The second level, χ₂^(t), represents the sample-target contingency (i.e., the estimation of the predictive strength of the sample stimulus with respect to the target on a trial-by-trial basis). The probability distribution of χ₁^(t) = 1 was a Bernoulli distribution, determined by higher-level χ₂^(t) through sigmoid transformation. The value of χ₂^(t) was based on the previous trial (t − 1) and changed from trial to trial as a Gaussian random walk. The changing rate of χ₂^(t) was determined by both the third level, χ₃^(t), and a subject-specific parameter, ω₂. χ₃^(t) represented the volatility of tactile observation (i.e., how fast the predictive strength of the sample stimulus changed over time). The step size of Gaussian random walk on χ₃^(t) was determined by a second subject-specific parameter, ω₃. So, the variance of these environmental hidden states depended on the state at the next higher level, changing as a Gaussian random walk (Mathys et al., 2011).

To infer the subject-specific probabilistic representations from environmental states, the perceptual model needed to be inverted, which yields the posterior densities over the three hidden states χ^(t). The posterior belief is denoted by ${\mu }^{\left(t\right)}$ on a given trial t. The hat symbol (^) was used to denote predictions before the observation of three hidden states χ^(t) on a given trial t (i.e., prior belief). In the present study, we focused on trialwise ${\widehat{\mu }}_2^{\left(t\right)}$ at the second level; that is, the prior belief about the sample-target contingency. Prior belief ${\widehat{\mu }}_2^{\left(t\right)}$ evolves from the posterior belief of the previous trial (t − 1), as follows:

Posterior belief (${\mu }_2^{\left(t\right)}$) in this model is updated after each trial based on the weighted prediction error. These update equations provide Bayes-optimal rules for updating belief trial by trial. The update equation of belief is as follows:

where precision-weighted prediction error (${\mathrm{\epsilon }}_2$) is the outcome prediction error (${\delta }_1$) weighted by the precision of predictions (${\psi }_2$). At the second level of the HGF, the precision weight (${\psi }_2$) is updated with every trial, so that it also can be considered as the equivalence of a dynamic learning rate in reward-learning models (Preuschoff and Bossaerts, 2007; Mathys et al., 2011). The outcome PE ${\delta }_1$ is the difference between the actual and the predicted outcome on trial t, as follows:

We used the absolute value of prior belief about sample-target contingency ($\left|{\mu }_2^{\left(t\right)}\right|$) to create regressors that entered the general linear model (GLM), which we estimated for each participant. In addition, we also added prior belief about the volatility (${\widehat{\mu }}_3^{\left(t\right)}$) at the third level as another regressor to investigate the potential effect of prior belief about the volatility. For the derivation of mathematical details about prior belief at the third level, please see the study by Mathys et al. (2011).

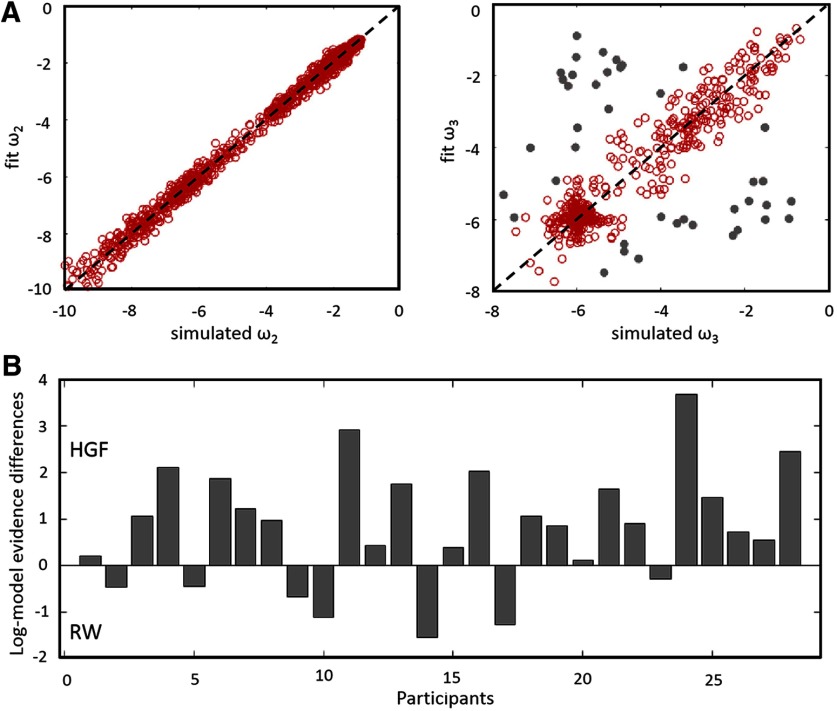
To check whether the model-fitting procedure derives meaningful parameter values when fitting simulated response data where the “true” parameter values are known, we performed a parameter recovery analysis using the HGF model. First, we simulated fake data with known parameter values (ω2 and ω3 were chosen as variable parameters). Next, we fitted the model to fake data to “recover” parameters. Finally, we compared recovered parameters to the true values used to simulate fake data. If there is only a weak correlation between the simulated and recovered parameters and/or a significant bias, the model might be problematic or the experimental design is underpowered to assess the model (Wilson and Collins, 2019). A range of ω₂ and ω₃ from 0 to −10 was chosen based on the range of estimates observed in the analysis of experimental data. We then repeated these steps 1000 times using new values for ω₂ and ω₃ each time.

To test whether a simpler reinforcement learning model better fits participants' performance, we compared the hierarchical Bayesian model with a standard Rescorla–Wagner (RW) learning model with a fixed learning rate (Rescorla and Wagner, 1972). The central idea behind the RW learning model is that it quantifies the evaluation of a choice option updated by the difference between the actual outcome and the expected outcome, as follows:

where α is the learning rate, which takes a value between 0 and 1, and captures the extent to which the prediction error, the difference between the actual outcome (r_t−1) and the expected outcome (V_t−1), updates the value of an option V_t.

For each model estimation, we calculated the log-model evidence as a measure of model goodness, which can also be used for model comparison. The log-evidence of a model is calculated as the negative variational free energy under the Laplace assumption. It represents a generic trade-off between the accuracy and complexity of a model that can be derived from first principles of probability theory (Penny et al., 2004; Stephan et al., 2009). To assess the relative plausibility of our models at the group level, we used random-effects Bayesian model selection (BMS), which evaluates the relative plausibility of competing models in terms of their log-evidence (Stephan et al., 2009), to identify the model with the higher likelihood.

fMRI data acquisition and preprocessing

fMRI data were collected on a Philips Achieva 3.0 T X-series scanner using a 32-channel head coil. For functional imaging, we used a T2*-weighted echoplanar imaging (EPI) sequence (voxel size, 2 × 2 × 3 mm³; field of view, 224 × 224 mm²; interslice gap, 0.6 mm; TR = 2800 ms; TE = 36 ms) to acquire 36 transaxial slices parallel to the anterior commissure-posterior commissure covering the whole brain. As anatomic reference, high-resolution T1-weighted structural images were acquired using an isotropic T1 turbo field echo sequence (voxel size, 1 × 1 × 1 mm³; field of view, 240 × 224 mm²) with 220 transversally oriented slices covering the whole brain.

Across the three fMRI runs, we acquired a total of 644 EPI volumes. To allow for T1 equilibration, five dummy scans preceded data acquisition in each run. These scans were removed before further processing. Each participant's EPI volumes were preprocessed and analyzed with the Statistical Parametric Mapping software SPM12 (Wellcome Department of Imaging Neuroscience, University College London, London, UK; http://www.fil.ion.ucl.ac.uk/spm) implemented in MATLAB R2017b (MathWorks). For preprocessing, images were first applied to slice time correction using sinc interpolation to the middle slice. Then, the T1-weighted image was normalized to the Montreal Neurologic Institute (MNI) reference space using the unified segmentation approach (Ashburner and Friston, 2005). Subsequently, the resulting transformation was applied to the individual EPI volumes to transform the images into standard MNI space and resample into 2 × 2 × 2 mm³ voxels. Finally, normalized images were spatially smoothed using a Gaussian filter with a full-width at half-maximum kernel of 8 mm. Data were high-pass filtered at 1/128 Hz to remove low-frequency signal drifts.

General linear modeling of fMRI data

The GLM in SPM 12 was used to analyze fMRI data. For each participant, we conducted a first-level GLM. Events were time locked to the onset of the target stimulus. Two regressors of interest were defined at the single-subject level, one for Correct (expected targets) and the other one for Wrong trials (unexpected targets). For each of these two regressors, two parametric modulators of prior belief were defined. The first parametric modulator was prior belief about the sample-target contingency (${\widehat{\mu }}_2^{\left(t\right)}$). The second modulator was prior belief about the volatility (${\widehat{\mu }}_3^{\left(t\right)}$), orthogonalized with respect to ${\widehat{\mu }}_2^{\left(t\right)}$. Onsets were convolved with the canonical hemodynamic responses function in an event-related fashion. Invalid trials (i.e., missing or late responses) were modeled separately. Functional data from the three runs were concatenated using the spm_fmri_concatenate.m function in SPM12. Using this function, the high-pass filtering and temporal nonsphericity calculations were corrected to account for the original session length (Berron et al., 2018; Ross et al., 2018). Furthermore, six head motion parameters, as estimated during the realignment procedure, were added as regressors of no interest to minimize false-positive activations due to task-correlated motion.

With the GLM, we aimed to identify brain areas in which BOLD responses were differentially modulated by prior belief for expected and unexpected targets. To this end, the comparison of the two main regressors (contrast Wrong > Correct for the main HRF regressor) were first analyzed to identify significant neural activity related to unexpected targets. Then, in the analyses of prior belief-related neural activity, we assessed the positive or negative effects with the contrasts [1, −1] and [−1, 1] applied to the two regressors representing the parametric modulation by prior belief ${\widehat{\mu }}_2^{\left(t\right)}$ or ${\widehat{\mu }}_3^{\left(t\right)}$. The respective t-contrast single-subject images were applied to the group-level one-sample t test. All analyses were thresholded at p < 0.05 familywise error (FWE) corrected for the whole brain.

Dynamic causal model

To investigate effective connectivity and compare different network models, we performed the bilinear deterministic dynamic causal model (DCM; Friston et al., 2003) using SPM12. DCM serves to compare different hypotheses about the mechanisms (in terms of neuronal coupling) that underlie regional neural responses detected in conventional analyses (Stephan et al., 2010).

Time series extraction

Following our GLM results and a priori hypotheses, we selected those brain regions as network nodes in which neural responses were modulated by prior belief [i.e., AIC, inferior parietal lobule (IPL), and dorsal premotor cortex (PMd) in the right hemisphere]. Subject-specific time series were extracted from the nearest local maximum within a sphere with a radius of 12 mm centered on the group maxima. The first Eigenvariate was then extracted across all voxels surviving p = 0.05 uncorrected within a 6 mm sphere centered on the individual peak voxel. The resulting BOLD time series were adjusted for effects of no interest (e.g., invalid trials and movement parameters). Following these procedures, time series for all three areas could be extracted in 26 of the 28 participants. Right AIC (rAIC) time series in one participant and right IPL (rIPL) time series in another participant could not be obtained because of a failure to meet the above criteria in the target regions. These two participants were excluded from DCM analyses.

Specification of DCMs and model space

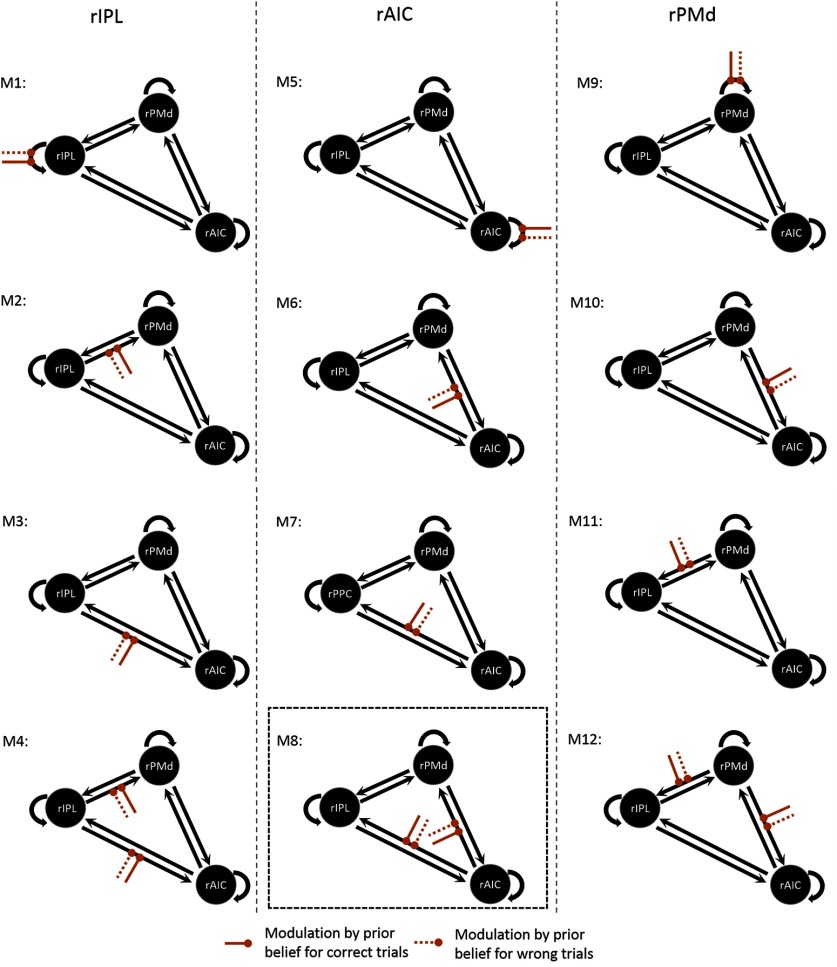
DCMs are specified in terms of fixed (endogenous) connections between brain areas and condition-specific changes in the strength of these connections (i.e., modulatory or bilinear effects). Since our DCM model considered the contrast of the main regressors (Wrong > Correct) as the input and prior belief-related brain activity as the modulatory factor, we only included the three regions that significantly overlapped at p = 0.05 (FWE corrected) in both contrasts (main regressor: Wrong vs Correct and parametric regressor: Wrong vs Correct by prior belief). All three regions (i.e., IPL, AIC, and PMd) were found in the right hemisphere. This finding is supported by empirical evidence suggesting that body-related awareness and attentional reorientation are mainly localized in right-lateralized brain networks (Craig, 2005; Vossel et al., 2015; Allen et al., 2016). Given that every brain region is connected reciprocally (Friston, 2011), we assumed reciprocal endogenous connectivity among the three regions; that is, all forward connections were accompanied by respective backward connections. Driving input was assumed to enter the terminals of the dorsal (rIPL) or ventral somatosensory pathway (rAIC). We specified three model families to determine the following tactile input drives: (1) rIPL; (2) rAIC; or (3) rIPL and rAIC. For each of these three families, we specified models with different modulatory (bilinear) effects. Specifically, we tested whether the source of prior belief-related neural activity was represented by the rIPL, rAIC, or right PMd (rPMd), and how self-connections or efferent connections between those regions changed as a function of prior belief for unexpected (Wrong) and expected (Correct) targets. This resulted in 12 models for each driving input family (see Fig. 4). Finally, 36 models were evaluated.

Figure 4.

Illustration of the model space for Bayesian model selection. First, we specified three model families to determine whether the tactile input drives rIPL, rAIC, or both regions (families not shown in the figure). For each of these three families, we then specified models based on whether prior belief modulates self-connections or efferent connections of the rIPL (M1–M4), rAIC (M5–M8), or rPMd (M9–M12). Bayesian model selection revealed that among the models with the tactile input directed to both rAIC and rIPL, model 8 (surrounded by the box) was superior to the other 11 models.

Model selection and parameter inference

We used a two-step fixed-effects Bayesian model comparison to infer the best fitting model for our observed responses in rIPL, rAIC, and rPMd. The fixed-effect analysis was applied as we assumed that all participants were best described by the same brain network, but with different connection strengths. To this end, we selected the model with the best balance between accuracy and complexity. First, we used family-level inference (Penny et al., 2010) to determine whether models with tactile input to rIPL, rAIC, or both regions best explained the observed data. Second, the models of the winning family were compared to identify the most plausible model explaining prior belief-related effects. The parameters of the winning model were summarized by Bayesian parameter averaging, which computes a joint posterior density for the entire group by combining the individual posterior densities (Neumann and Lohmann, 2003; Garrido et al., 2007). A posterior probability criterion of 90% was considered to reflect significant effective connectivity.

Correlate the modulation strength with updating parameters

To investigate whether the modulatory influences on the connections by prior belief could serve the updating process based on a precision-weighting mechanism, we tested the relationship between individual differences in the change ratio of the modulated connection strengths and the two crucial updating parameters (precision ${\psi }_2$ and prediction error ${\delta }_1$). For each participant, we averaged the two trialwise updating parameters of Wrong and Correct trials separately. The connections that were differently modulated by prior belief, namely, rAIC → rPMd and rAIC → rIPL (see Results), were separately correlated with the two averaged updating parameters across participants. For the connection rAIC → rPMd, the change ratio of modulation strength was defined by (Wrong-Correct)/Wrong. For the rAIC → rIPL connection, the change ratio of modulation strength was defined as (Correct-Wrong)/Correct. The change ratio of the two averaged parameters guiding the update process (precision ${\psi }_2$ and prediction error ${\delta }_1$) for Wrong and Correct trials was defined in the same way as for the connection strengths. Finally, data were applied to Pearson correlation analyses together with a Bonferroni-corrected threshold at p = 0.025 (i.e., corrected for the two parameters ${\psi }_2$ and ${\delta }_1$).

Results

Behavioral results

Before data analyses, each participant's behavioral data were examined for invalid trials (i.e., missed or late responses >1300 ms). Participants with >20% invalid trials or <60% correct responses were excluded from further analyses. These criteria led to the exclusion of five participants. The remaining 28 participants were included for further data analysis. The trials with missing or late responses (2.19 ± 0.53%, mean ± SEM) were excluded from the analysis of behavioral data and were modeled separately as a regressor of no interest in the analysis of the fMRI data. The proportion of expected targets (Correct) was analyzed across the five different sample-target contingencies (90%, 70%, 50%, 30%, and 10%; Fig. 1B) to assess whether probabilistic learning was successful. Figure 1C shows increases in expected targets over time and a significantly higher proportion of expected targets in blocks with high predictability (i.e., 90%/10%) than in blocks with low predictability (i.e., 70%/30%; t_(1,27) = 20.75, p < 0.001, Bonferroni corrected) or unpredictable blocks (i.e., 50%; t_(1,27) = 24.70, p < 0.001, Bonferroni corrected).

The parameter recovery analysis revealed that the parameter values (i.e., subject-specific parameters ω₂ and ω₃) can be recovered with good precision using the HGF model (Fig. 2A). Comparing relative log-model evidence between the HGF and RW model showed that HGF was superior in 21 of 28 participants (Fig. 2B). BMS revealed posterior model probabilities of 90% for the winning HGF (posterior probabilities, 0.90; exceedance probability, 1.00). This result provides evidence that our participants did learn the task-relevant conditional probabilities of sample stimuli and updated their learning rate dynamically.

Figure 2.

Parameter recovery for the HGF model and differences in log-model evidence for the HGF model as compared to the RW model. A, Parameter recovery for the HGF model. Grey dots correspond to points where parameter recovery for ω3 is bad (i.e., when |ωsim − ωfit |>1). As shown in the figure, there is fairly good correlation between the simulated and fitting parameter values, which indicates that the parameter values can be recovered with good precision using the HGF model. B, Individual difference of log-model evidence between the HGF model and the RW model. Positive values index participants who presented higher model evidence for the HGF model.

FMRI results

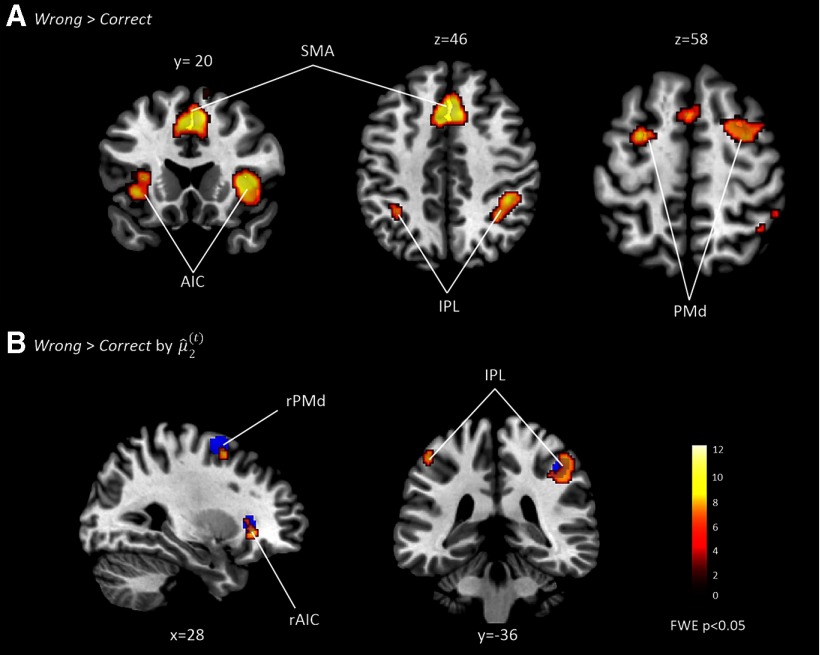
First, we investigated the neural substrates of unexpected targets (Wrong > Correct contrast). In line with our a priori hypotheses, the fMRI GLM analysis revealed bilateral activations in AIC, supplementary motor area (SMA), IPL, and PMd (p < 0.05, FWE whole-brain corrected; Fig. 3A, Table 1).

Figure 3.

Results of the GLM analysis. A, Bilateral brain regions that were activated by Wrong > Correct. B, Regions related to prior belief for unexpected trials as revealed by a t-contrast Wrong > Correct by the modulatory parameters (${\widehat{\mu }}_2^{\left(t\right)}$). The blue pattern represents activations revealed by comparing Wrong > Correct, as shown in A. Note that only regions in the right hemisphere significantly overlapped in both contrasts, as follows: Wrong > Correct by the modulatory parameters (${\widehat{\mu }}_2^{\left(t\right)}$) and Wrong > Correct. Since our DCM models were based on both contrasts, we only considered the three regions in the right hemisphere for DCM, but not left IPL. Significant activations (p < 0.05, FWE corrected) were superimposed on sagittal, coronal, and axial slices of a standard T1-weighted image, as implemented in SPM. Coordinates next to each slice index their location in MNI space. Red-yellow coding indexes the t scores of activation intensities.

Table 1.

Results of fMRI analysis for Wrong versus Correct trials

Regions	Hemisphere	Peak coordinates			Cluster size (voxels)	t score
		x	y	z
Main regressor: Wrong > Correct
Insula	R	34	22	4	455	10.92
Insula	L	−32	26	−2	258	9.40
Premotor cortex	R	46	30	34	118	7.59
Premotor cortex	L	−32	54	20	48	7.12
Supplementary motor cortex	L and R	2	22	44	820	10.73
Inferior parietal lobule	R	40	−40	46	313	8.20
Inferior parietal lobule	L	−34	−48	46	36	6.96
Parametric regressor ${\widehat{\mathit{\mu }}}_2^{\left(\mathit{t}\right)}$: Wrong > Correct
Insula	R	30	28	−4	64	7.62
Premotor cortex	R	28	6	54	30	7.52
Inferior parietal lobule	R	46	−38	40	188	7.25
Inferior parietal lobule	L	−48	−38	56	42	7.94
Parametric regressor ${\widehat{\mu }}_3^{\left(t\right)}$:
n.s.

n.s., Not significant; L, left; R, right.

Next, we tested how prior belief modulated neural activation related to unexpected targets (Wrong > Correct by prior belief). The interaction between Wrong > Correct and prior belief about the sample-target contingency ${\widehat{\mu }}_2^{\left(t\right)}$ revealed a significant effect in right AIC, right PMd, and bilateral IPL (Fig. 3B, Table 1; “parametric regressors” for MNI coordinates, cluster sizes, and t scores). The analysis of parametric effects related to prior belief about trail-specific volatility (${\widehat{\mu }}_3^{\left(t\right)}$) did not reveal any significant effects (p < 0.05, FWE whole-brain corrected). The comparison of expected and unexpected trials (Correct > Wrong) did not reveal any significant differences for both ${\widehat{\mu }}_2^{\left(t\right)}$ and ${\widehat{\mu }}_3^{\left(t\right)}$.

DCM results

DCM was used to unveil context-sensitive interactions between those regions in which the response was modulated by prior belief. First, family-level BMS was used to reveal the most likely region that receives the driving sensory inputs. Results revealed that models with the tactile input directed to both rAIC and rIPL were superior (posterior probability, 0.88) to models with the input directed to only one of the two regions. Among the 12 models in which the tactile input was directed to rAIC and rIPL (Fig. 4), model 8 was superior to the other 11 models (posterior probability, 1.00). This model consisted of efferent connections originating in rAIC and targeting rIPL and rPMd. These efferent connections were significantly modulated by prior belief when targets were unexpected (Wrong > Correct).

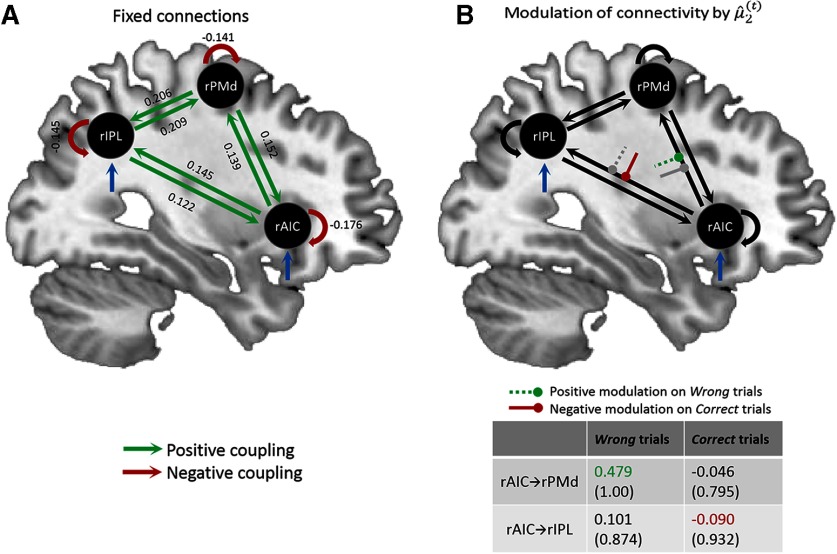
Bayesian parameter averaging of the winning model across all participants revealed significant endogenous (fixed) connections among all three regions and their self-connections (all connections: posterior probability, 1.00; Fig. 5A). Analysis of the modulatory influence of prior belief ${\widehat{\mu }}_2^{\left(t\right)}$ on Wrong and Correct trials showed complementary effects of prior belief (negative modulation for Correct trials, positive modulation for Wrong trials). Prior belief on expected targets (Correct) had a specific inhibitory influence on the connectivity from rAIC to rIPL (posterior probability, 0.932; Fig. 5B), whereas prior belief on unexpected targets (Wrong) strengthened the connectivity from rAIC to rPMd (posterior probability, 1.00; Fig. 5B).

Figure 5.

Bayesian parameter averaging across participants for the winning DCM model 8 (Fig. 4). A, Endogenous (fixed) connections. Green connections = significant positive coupling rates, red connections = significant negative coupling rates. The numbers alongside the connections indicate coupling parameters representing the strength of effective connectivity in Hz. All fixed connections were significant (posterior probability = 1.00). Blue arrows represent the driving inputs. B, Modulation of connectivity by prior belief. Bayesian parameter averaging revealed that prior belief positively modulated the connection rAIC → rPMd for unexpected targets (green dashed line). For expected targets, prior belief negatively modulated the connection rAIC → rIPL (red solid line). The corresponding gray lines represent the nonsignificant modulation effects. The table depicts the Bayesian parameter averages with posterior probabilities in brackets for the modulation of connections by prior belief the modulation of connections by prior belief.

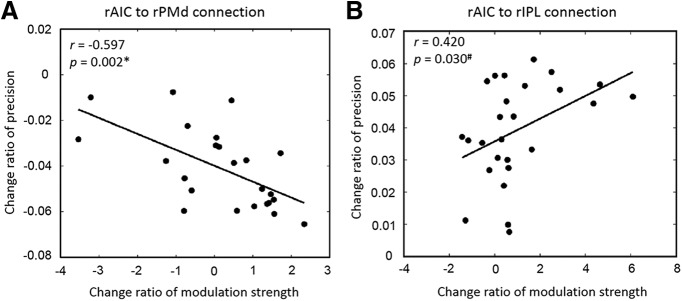
Pearson correlation analyses were applied to explore the relationship between individual differences in the change ratio of the modulatory influence of prior belief on rAIC projections [i.e., (Wrong-Correct)/Wrong for rAIC → rPMd connection; (Correct-Wrong)/Correct for rAIC → rIPL connection] and the change ratio of the two key parameters underpinning the belief updating process (precision ${\psi }_2$ and prediction error ${\delta }_1$), analyzed in the same way (i.e., Wrong-Correct)/Wrong; (Correct-Wrong)/Correct). The results revealed a significant negativecorrelation between prior belief-related changes in rAIC → rPMd connectivity and the precision of prediction error (r = −0.597, p = 0.002; Fig. 6). These findings suggest that the stronger the prior belief-related connection strength of rAIC → rPMd, the lower the precision of prediction error for unexpected targets. For expected targets, we only found a trend for a positive correlation, which failed to surpass the Bonferroni-corrected threshold (p = 0.025). This clear trend (r = 0.420, p = 0.030) nevertheless suggests that the stronger the prior belief-related connection strength of rAIC → rIPL, the higher also the precision of prediction error (Fig. 6). For the prediction error ${\delta }_1,$we revealed no significant relationship, not even at trend level.

Figure 6.

Correlation between change ratio of prior belief-related effective connections and the precision of prediction error. A, rAIC to rPMd connection. The change ratio is defined by (Wrong-Correct)/Wrong. The stronger the prior belief-related connection strength of rAIC → rPMd was, the lower was the precision of prediction error for unexpected targets. B, rAIC to rIPL connection. The change ratio is defined by (Correct-Wrong)/Correct. A clear trend for a positive correlation (r = 0.420, p = 0.030) was found for expected targets, suggesting that the stronger prior belief related connection strength of rAIC → rIPL was, the higher also the precision of prediction error was. The r and p values are based on a linear (Pearson) correlation analysis.*Significant correlation; ^#trend level correlation (Bonferroni-corrected (p < 0.025).

Discussion

In the present study, we demonstrate that neural responses to unexpected versus expected tactile targets are modulated by probabilistic inference through changes in effective connectivity. Unexpected compared with expected targets provoked bilateral activity in regions involved in attentional allocation (i.e., AIC and IPL) as well as areas involved in coordinating attention and cognitive control (i.e., SMA and PMd). Among these regions, the activity in right AIC, IPL, and PMd correlated with prior belief from trial to trial. DCM revealed that prior belief specifically modulated the effective connectivity either from AIC to PMd or from AIC to IPL, depending on whether the target was unexpected or expected. The connection strength from AIC to IPL decreased with prior belief on expected targets, whereas the connection strength from AIC to PMd increased with prior belief on unexpected targets. These context-sensitive changes in effective connectivity seem to signal the decision outcome depending on whether the concurrently presented tactile target was expected or not.

Unexpected compared with expected outcomes provoked activity in a hierarchically organized network assumed to serve the interactions of ascending body-related sensations and top-down prediction signals (Downar et al., 2000, 2002). Our observed activation pattern markedly overlapped in the AIC, IPL, SMA, and PMd with previously reported effects related to the encoding of deviant stimuli in the oddball task (Huang et al., 2005; Allen et al., 2016; Fardo et al., 2017). While processing surprising or unexpected tactile sensations, AIC and IPL were assumed to be specifically involved in guiding the orientation of attention to salient sensory events (Allen et al., 2016; Fardo et al., 2017), whereas SMA and PMd were, rather, expected to coordinate attention and cognitive control (Downar et al., 2000; Rossi-Pool et al., 2016). These functional implementations appear at the crossroad between processes that support awareness for the physical properties of a tactile input and their further cognitive implementation.

Analogous to the visual or auditory domain, Dijkerman and de Haan (2007) formulated a somatosensory model of perception and action, in which a perception/recognition-related ventral pathway terminates in the insular cortex after passing S1 and S2. A motor output-related dorsal pathway terminates in the posterior parietal cortex to relay event-related information to the corresponding motor output region. In our study, Bayesian comparison of different model families revealed that tactile inputs evoked by the target stimulus were primarily conveyed to terminal nodes of both somatosensory pathways, the dorsal one (represented by the IPL) and the ventral one (represented by the AIC), instead of a sole propagation of inputs from the ventral to the dorsal pathway, or vice versa. This suggests that both dorsal and ventral somatosensory pathways were required for the propagation of perceptual representations to higher attentional and cognitive implementation of tactile information.

Our findings also identified the AIC as the source region of prior belief-dependent effects projecting to IPL and PMd. In a probabilistic environment, activity in S1 and S2 mainly represents the transformation from physical to perceptual representations, whereas activity in the insular cortex is assumed to reflect the degree of perceptual uncertainty (Schröder et al., 2019). Empirical findings demonstrated that AIC, together with IPL and middle frontal gyrus, were involved in stimulus-driven, bottom-up control of attention, likely reflecting perceptual inference (Uddin, 2015; Fardo et al., 2017). These findings agree well with studies showing that the insular cortex acts as a core hub regulating the interaction of bodily, attentional, and anticipatory tactile signals (Sridharan et al., 2008; Craig, 2009; Lovero et al., 2009; Menon and Uddin, 2010; Allen et al., 2016). In line with these previous studies, our results suggest that the AIC also relays crucial decision outcome-related information to frontoparietal regions involved in attentional reorienting and perceptual inference (i.e., IPL and PMd).

In association with unexpected compared with expected outcomes, we found activity in the IPL. On expected outcomes, the IPL was furthermore the target of inhibitory prior belief-related AIC projections. These findings agree with several human studies, emphasizing that the IPL supports modality-independent attentional allocation to surprising (i.e., odd) sensory events (Kiehl and Liddle, 2001; Ardekani et al., 2002; Huang et al., 2005; Fardo et al., 2017). Violation of expectations was shown to strengthen recurrent connections from S1/S2 to the IPL, which supports the assumption that the IPL serves the reorientation of spatial attention (Limanowski and Blankenburg, 2015; Fardo et al., 2017).

The PMd, as the target of AIC projections on unexpected outcomes, was shown to maintain information necessary to evaluate the consequence of decision-making in the monkey brain (Rossi-Pool et al., 2016). This information serves future decision-making with respect to the behavioral context and environmental demands (i.e., whether the active evaluation is required or not). Electrophysiological studies in humans support these findings, showing that the comparison and updating of working memory contents, as required for perceptual decision-making, are well reflected by beta-band oscillations in the PMd (Spitzer and Blankenburg, 2011; Herding et al., 2016). According to the present findings, the PMd seems to specifically represent the comparison of predicted outcomes with a stronger sensitivity and update function when the concurrently presented tactile target is unexpected as when it is expected.

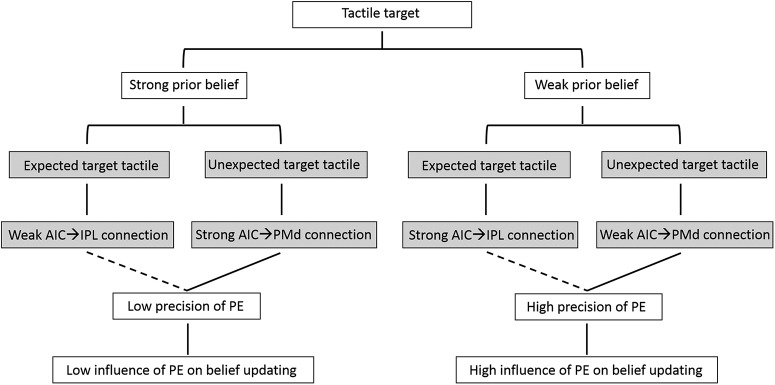
Prior belief seems to modulate insular projections to IPL and PMd with respect to the concurrently presented target. Recent theoretical accounts of predictive coding agree well with our findings, together assuming a central role for the AIC in integrating prior belief according to changes in tactile perception (Allen et al., 2016). In this context, the AIC has also been shown to host processes that contribute to the encoding of precision-weighted prediction errors or volatility based on Bayesian inference (Iglesias et al., 2013). During predictive coding, precision (i.e., certainty) of prediction errors has been shown to enhance the influence of ascending prediction errors on perceptual inference via the neuromodulatory regulation of postsynaptic cortical gain (Moran et al., 2013). Within this framework, sensory inputs and prior belief are jointly integrated and act via precision-weighting mechanisms to produce context-sensitive responses for perceptual inference (Friston, 2009). In our study, we found that strong prior belief increased the strength of connectivity from the AIC to the PMd on unexpected targets, whereas it decreased the connectivity from AIC to IPL when targets were expected. Individual differences in prior belief-related effective connectivity were correlated with the precision of the prediction error. Strong prior belief was finally associated with a low influence of the prediction error on belief updating, especially when the target was unexpected (Fig. 7). This increased the probability that the participant used the same decision strategy on the next trial. Low prior belief, in turn, was associated with a strong influence of the prediction error on belief updating (Fig. 7) and an increased probability for changing the decision strategy on the next trial. Our results emphasize that these processes are mediated by connections originating in the AIC and targeting salience and attention-related frontoparietal areas. These connections seem to be involved in updating evidence arising from expected and unexpected tactile targets to guide future decision-making (Vossel et al., 2015; Allen et al., 2016). These results are consistent with the concept of predictive coding, suggesting that bottom-up prediction errors and top-down expectations are integrated based on precision-dependent computational processes.

Figure 7.

The schematic summarizes the processing of expected and unexpected targets under different levels of environmental uncertainty (i.e., prior belief). The dashed lines indicate trend level correlation between the connection strength and the precision of PE. Strong prior belief was associated with a low influence of the prediction error on belief updating, especially when the target was unexpected. It also increased the strength of connectivity from the AIC to the PMd on unexpected targets, whereas it decreased the connectivity from AIC to IPL when targets were expected. Tactile targets in combination with weak prior belief were associated with a strong influence of the prediction error on belief updating, again especially for unexpected targets. Weak prior belief also decreased the strength of connectivity from the AIC to the PMd on unexpected targets, whereas it increased the connectivity from AIC to IPL when targets were expected.

Together, our study demonstrates that unexpected tactile outcomes evoke activity in a hierarchic ensemble of somatosensory-, salience-, and attention-related cortical regions. In a right-lateralized network consisting of insula, parietal, and premotor cortex, the probabilistic inference differentially modulated effective connectivity from the insula to the parietal cortex, as well as from the insula to the premotor cortex depending on whether the prediction was confirmed or violated. Our findings suggest that the insular cortex acts as a gate to control the awareness for prediction outcomes mediated by Bayesian inference.