Streaming of Repeated Noise in Primary and Secondary Fields of Auditory Cortex

Abstract

Statistical regularities in natural sounds facilitate the perceptual segregation of auditory sources, or streams. Repetition is one cue that drives stream segregation in humans, but the neural basis of this perceptual phenomenon remains unknown. We demonstrated a similar perceptual ability in animals by training ferrets of both sexes to detect a stream of repeating noise samples (foreground) embedded in a stream of random samples (background). During passive listening, we recorded neural activity in primary auditory cortex (A1) and secondary auditory cortex (posterior ectosylvian gyrus, PEG). We used two context-dependent encoding models to test for evidence of streaming of the repeating stimulus. The first was based on average evoked activity per noise sample and the second on the spectro-temporal receptive field. Both approaches tested whether differences in neural responses to repeating versus random stimuli were better modeled by scaling the response to both streams equally (global gain) or by separately scaling the response to the foreground versus background stream (stream-specific gain). Consistent with previous observations of adaptation, we found an overall reduction in global gain when the stimulus began to repeat. However, when we measured stream-specific changes in gain, responses to the foreground were enhanced relative to the background. This enhancement was stronger in PEG than A1. In A1, enhancement was strongest in units with low sparseness (i.e., broad sensory tuning) and with tuning selective for the repeated sample. Enhancement of responses to the foreground relative to the background provides evidence for stream segregation that emerges in A1 and is refined in PEG.

SIGNIFICANCE STATEMENT To interact with the world successfully, the brain must parse behaviorally important information from a complex sensory environment. Complex mixtures of sounds often arrive at the ears simultaneously or in close succession, yet they are effortlessly segregated into distinct perceptual sources. This process breaks down in hearing-impaired individuals and speech recognition devices. By identifying the underlying neural mechanisms that facilitate perceptual segregation, we can develop strategies for ameliorating hearing loss and improving speech recognition technology in the presence of background noise. Here, we present evidence to support a hierarchical process, present in primary auditory cortex and refined in secondary auditory cortex, in which sound repetition facilitates segregation.

Introduction

Sounds generated by different sources impinge on the ear as a complex mixture, with acoustic energy generated by each source overlapping in both time and frequency. The auditory system groups these dynamic spectro-temporal sound features into percepts of distinct sources, in a process known as auditory streaming (Bregman, 1990; Griffiths and Warren, 2004). Streaming requires statistical analysis of sound sources: streams that come from the same sound source share statistical regularities, and the brain uses these properties as cues for stream integration or segregation (Bregman, 1990; Darwin, 1997; Carlyon, 2004; McDermott, 2009; Winkler et al., 2009).

Basic acoustic features, such as separation in frequency and time, are key perceptual cues for segregating simple, alternating sequences of pure tones (van Noorden, 1975; Bregman, 1978; Bregman et al., 2000; Oberfeld, 2014). However, more complex natural sounds often overlap in frequency and time. Segregating spectrally overlapping sounds requires the use of perceptual cues such as pitch (Akeroyd et al., 2005; Mesgarani and Chang, 2012), timbre (Singh and Bregman, 1997; Cusack and Roberts, 2000; Roberts et al., 2002), spatial location (Singh and Bregman, 1997; Cusack and Roberts, 2000; Roberts et al., 2002; Carlyon, 2004; Micheyl et al., 2007; Mesgarani and Chang, 2012), common onset (Elhilali et al., 2009; Shamma et al., 2011), and temporal regularity (Agus et al., 2010; Bendixen et al., 2010; Andreou et al., 2011; Szalárdy et al., 2014). McDermott et al. (2011) specifically tested for the benefit of temporal regularity with a set of naturalistic noise samples that lacked other cues for streaming. Nonrepeating samples could not be distinguished from background noise, but humans could identify these samples when they were repeated. The neural basis of this perceptual pop-out remains unknown.

In contrast to the robust perceptual enhancement reported for a repeating foreground stream, studies of neurophysiological activity in auditory cortex demonstrate a suppressive effect of repetition (Pérez-González and Malmierca, 2014). Single neurons undergo stimulus-specific adaptation (SSA), where responses to repeated tones adapt, but responses to an oddball stimulus, such as a tone at a different frequency, are less adapted or even facilitated, reflecting perceptual pop-out of the oddball sound (Ulanovsky et al., 2003; Nelken, 2014). In human electroencephalography, a possibly related phenomenon is observed in a late event-related component, called the mismatch negativity (MMN). Although the dynamics are slower than SSA, MMN is also elicited by rare deviant sounds randomly interspersed among frequent standard sounds (Näätänen, 2001). There is no evidence that links SSA or MMN with repetition-based grouping, but it is possible that these processes share some of the same neural circuits. How the brain might use adaptation to a repeating sound to enhance its perception is not known.

In this study, we investigated neural correlates of streaming induced by the repetition of complex sounds in primary auditory cortex (A1) and secondary auditory cortex [posterior ectosylvian gyrus (PEG)]. We first established the ferret as an animal model for the streaming of repeating noise sounds by designing a behavioral paradigm that assessed the ability of animals to detect repetitions embedded in mixtures. We then recorded neural activity in A1 and PEG of passive, unanesthetized ferrets. We tested the prediction that auditory cortical neurons facilitate stream segregation by selectively enhancing their response to the repeating (i.e., foreground) stream. We used context-dependent sound-encoding models to quantify the relative contribution of the two overlapping streams to the evoked neural response (David, 2018). We found that neural responses to the repeated stimuli were reduced overall in both areas, relative to the nonrepeating stimuli, consistent with previous studies that reported adaptation for a single repeating stream (Ulanovsky et al., 2003). However, in addition, neurons in both cortical fields displayed foreground-specific responses that were enhanced relative to responses to the background stream. These results provide evidence for a mechanism of streaming cued by repetition that is present in primary and is refined in secondary fields of the auditory cortex.

Materials and Methods

All procedures were approved by the Oregon Health and Science University Institutional Animal Care and Use Committee and conform to the United States Department of Agriculture standards.

Surgical procedure

Animal care and procedures were similar to those described previously for neurophysiological recordings from awake ferrets (Slee and David, 2015). Five spayed, descented young adult ferrets (two females, three males) were obtained from an animal supplier (Marshall Farms). Normal auditory thresholds were confirmed by measuring auditory brainstem responses to clicks. A sterile surgery was then performed under isoflurane anesthesia to mount a custom stainless steel head-post for subsequent head fixation and expose a 10 mm² portion of the skull over the auditory cortex where the craniotomy would be subsequently opened. A light-cured composite (Charisma, Heraeus Kulzer) anchored the post on the midline in the posterior region of the skull. The stability of the implant was also supported by 8–10 stainless self-tapping set screws mounted in the skull (Synthes). The whole implant was then built up to its final shape with layers of Charisma and acrylic pink cement (AM Systems).

During the first week postsurgery, the animal was treated prophylactically with broad-spectrum antibiotics (10 mg/kg; Baytril). For the first 2 weeks, the wound was cleaned with antiseptics (Betadine and chlorhexidine) and bandaged daily. After the wound margin was healed, cleaning and bandaging occurred every 2–3 d through the life of the animal to minimize infection of the wound margin.

Experimental design

Stimuli and acoustics

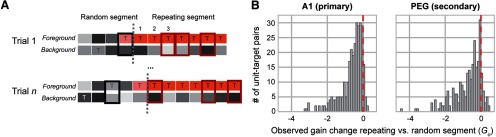
Repeated embedded noise stimuli used in the present study were generated using the algorithm from McDermott et al. (2011). Brief, 250 or 300 ms duration samples of broadband Gaussian noise were filtered to have spectro-temporal correlations matched to a large library of natural sound textures and vocalizations but without common grouping cues, such as harmonic regularities and common onsets. The spectral range of the noise (125–16,000 or 250–20,000 Hz) was chosen to span the tuning of the current recording site. Thus, the duration and spectral range of the stimuli differed from previous work in humans, but other statistical properties were identical (McDermott et al., 2011). An experimental trial consisted of continuous sequences of 10–12 noise samples (0 ms intersample interval) drawn randomly from a pool of 20 distinct samples (Figs. 1B, 2A). The order of samples varied between trials. Either one stream of samples was presented (single stream trial) or two streams were overlaid and presented simultaneously (dual-stream trial). At a random time (after 3–11 samples; median, 6 samples), the sample in one stream (target sample) began to repeat. In dual-stream trials, this repetition occurred only in one of the two streams, while samples in the other stream continued to be drawn randomly. In human studies, the repeating sample has been shown to pop out perceptually as a salient stream (McDermott et al., 2011). Thus, the stream containing the repeated sample is referred to here as the foreground, and the nonrepeating stream as the background (Fig. 1B). The period of the trial containing only random samples is referred to as the random segment, and the segment starting with the first repetition of the target sample is referred to as the repeating segment (Figs. 1B, 2A). With the exception of the spectro-temporal receptive field analysis, the first sample of the random segment was excluded from all analyses to minimize the effect of onset-related adaptation, which was consistently complete by 250 ms following trial onset.

Figure 1.

Ferrets are sensitive to repetitions embedded in mixtures. A, Ferrets were trained to respond to sound repetition by licking a waterspout. B, Schematic of the go/no-go task and spectrograms of repetition embedded noise stimuli from an example behavioral trial. Animals were exposed to the combination (bottom spectrogram) of the following two overlapping streams: a foreground stream containing a target sample (top); and a background stream, a nonrepeating sequence of noise samples (middle). In this example, the target sample (orange boxes, bottom) starts repeating after three random noise samples (gray boxes). The gray dashed line marks the first occurrence of the target sample (pale orange box), which is included in the random segment for analysis. The transition between random and repeating segment is marked by the orange dashed line and occurs when the target sample is first repeated. Animals were trained to withhold licking during the random segment (4–6 s). To receive a water reward, they had to lick the waterspout following repetition onset. C, Distribution of DI across behavior sessions for ferret O (n = 636; mean, 0.60; gray arrow) and ferret H (n = 504; mean, 0.64; black arrow) after training was completed. For both animals, average performance was significantly better than average performance computed after shuffling response times across trials (mean shuffled DI = 0.53 for both animals; dashed line, p < 0.0001). D, Mean reaction time relative to the onset of each noise sample slot in the random segment. Reaction times for target samples appearing in the random phase were identical to nontarget samples appearing at the same time relative to the onset of repetition, indicating that animals did not preferentially respond to the identity of the target sample. Shading indicates SEM. Only data from 250 ms noise samples are shown.

Figure 2.

Activity in both A1 and PEG was suppressed during the repeating segment. A, Schematic of two trials during electrophysiological recordings. The background stream consisted entirely of randomly chosen noise samples (gray). The foreground stream contained randomly chosen samples during the random segment, which sometimes included the target sample (T). The final pair of noise samples in the random segment included the target (light orange) as it had not yet begun to repeat. Average PSTH responses to each pair of samples that contained the target (thick rectangles) were computed separately for the random segment (black) and repeating segment (dark red). Target samples were subsampled from the repeating segment to match counts between random and repeating segments (see Materials and Methods). To minimize effects of stimulus onset adaptation, the very first pair of samples at the beginning of the trial was always excluded from the analysis, even if the pair included the target sample. B, Distribution of observed gain change ($G_o$) between random and repeating segments in A1 and PEG. The majority of target responses were suppressed ($G_o$< 0) during the repeating segment. Red dashed line indicates 0 (i.e., no difference between segments). Since results may depend on how well the unit responded to the target, all analyses of neural responses were performed separately for each unique unit–target pair (A1: mean ± SEM $G_o$ = −0.634 ± 0.038; n = 300; one-sample t test, null hypothesis population mean = 0, t statistic = −16.72; p < 0.0001; PEG: mean ± SEM $G_o$ −0.698 ± 0.049; n = 259; one-sample t test, null hypothesis population mean = 0, t statistic = −14.11; p < 0.0001).

All behavioral and physiological experiments were conducted inside a custom double-walled sound-isolating chamber with inside dimensions of 8 × 8 × 6 feet (length × weight × height). A custom second wall was added to a single-walled factory chamber (Professional Model, Gretch-Ken) with a wooden frame and an inner wall composed of three-quarter inch medium-density fiberboard board. The air gap between the outer and inner walls was 1.5 inches. The inside wall was lined with 3 inch sound-absorbing foam (Pinta Acoustics). The chamber attenuated sounds >2 kHz by >60 dB. Sounds from 0.2 to 2 kHz were attenuated 30–60 dB, falling off approximately linearly with log-frequency.

Stimulus presentation and behavioral control were provided by custom MATLAB software (MathWorks). Digitally generated sounds were digital-to-analog converted (100 kHz; PCI-6229, National Instruments) and presented through a sound transducer (W05, MANGER) driven with a power amplifier (D-75A, Crown). The speaker was placed 1 m from the head of the animal, 30° contralateral to the cortical hemisphere under study. Sound level was calibrated using a one-half inch microphone (4191, Brüel & Kjær). Stimuli were presented with 10 ms cos² onset and offset ramps.

Behavior

Two ferrets (one female, ferret O; one male, ferret H) were trained to report the occurrence of repeated target noise samples in the repeated embedded noise stimuli using a go/no-go paradigm (David et al., 2012). Starting 2 weeks after the implant surgery, each ferret was gradually habituated to head fixation by a custom stereotaxic apparatus in a Plexiglas tube. Habituation sessions initially lasted for 5 min and increased by increments of 5–10 min until the ferret lay comfortably for at least 1 h. At this time, the ferret was placed on a restricted water schedule and began behavioral training. During training and physiological recording sessions that involved behavior, the ferret was kept in water restriction for 5 d/week, and almost all the daily water intake (40–80 ml) was delivered through behavior. Their diet was supplemented with 20 ml/d high-protein Ensure (Abbott). Water restriction was to be discontinued if weight dropped to <20% of the initial weight, but this did not happen with either ferret. Water rewards were delivered through a spout positioned close to the nose of the ferret. Delivery was controlled electronically with a solenoid valve. Each time the ferret licked the waterspout, it caused a beam formed by an infrared LED and a photograph-diode placed across the spout to be discontinued (Fig. 1A). This system allowed us to precisely record the timing of each lick relative to stimulus presentation.

After trial onset, animals were required to refrain from licking until the onset of the repeating segment (i.e., after the occurrence of a repeated sample). Licks during the random segment were recorded as false alarms and punished with a 4–6 s time-out. Licks that occurred in the repeating segment were recorded as hits and always rewarded with one to two drops of water (Fig. 1B). Each behavioral block was defined as a continuous presentation of trials. For behavioral sessions, more than one block was acquired on a single day if the animal was performing well. For passive sessions (i.e., physiology), one block was typically acquired per recording site, but multiple recording sites may have been acquired on any given day. Each block contained two target samples presented randomly across trials. Target identity varied from block to block to prevent ferrets from learning to detect specific spectro-temporal features of the target. False alarm trials in which licks occurred before the target were repeated to prevent animals from simply responding with a short latency on every trial. The repeated trials were excluded from behavioral analysis (see below) to prevent artifactual increase in performance from a strategy in which response time was gradually increased following each false alarm (David et al., 2012).

To shape the behavior of the animal, training started with a high signal-to-noise ratio (SNR) between random and repeating segments. SNR was then gradually decreased over subsequent training sessions to 0 dB (i.e., random and repeating segments were presented at the same intensity). Parameters such as spectral modulation depth of the two streams and length of the random segment/false alarm window were also adjusted over the training period.

Electrophysiology

Single-unit and multiunit neural recordings were performed in one trained animal (ferret O) and four task-naive animals. A small (∼1- to 2-mm-diameter) craniotomy was opened over the right auditory cortex, in a location chosen based on stereotaxic coordinates and superficial landmarks on the skull marked during surgery. Initial recordings targeted the ferret A1, and recording location was confirmed by characteristic short-latency responses to tone stimuli and by tonotopic organization of frequency selectivity (Bizley et al., 2005). Recordings in secondary auditory cortex (PEG) were then performed in the field ventrolateral to A1. The border between A1 and PEG was identified functionally by a reversal in the tonotopic gradient.

Neurophysiological data were collected from animals in a passive state (i.e., while animals were head fixed and unanesthetized but not performing any explicit behavior). Recording sessions typically lasted 2–4 h. On each recording day, one to four high-impedance tungsten microelectrodes (impedance, 1–5 MΩ; FHC or A-M Systems) were slowly advanced into cortex with independent motorized microdrives (Alpha-Omega). The electrodes were positioned (Kopf Instruments) such that the angle was approximately perpendicular to the surface of the brain. Stimulus presentation and electrode advancement were controlled from outside the sound booth, and animals were monitored through a video camera. Neural signals were recorded using open-source data acquisition software (MANTA; Englitz et al., 2013). Raw traces were amplified (10,000x; 1800 or 3600 AC amplifier, A-M Systems), bandpass filtered (0.3-10kHz), digitized (20 kHz; National Instruments, PCI-6052E), and stored for subsequent offline analysis. Putative spikes were extracted from the continuous signal by collecting all events ≥4 SDs from zero. Different spike waves were separated from each other and from noise using principal component analysis and k-means clustering (David et al., 2009). Both single units (>95% isolation) and stable multiunits (>70% isolation) were included in this study, resulting in a total of 149 A1 and 136 PEG units.

Between recording sessions, the exposed recording chamber surrounding the craniotomy was covered with polysiloxane impression material (GC America). After several electrophysiological penetrations (usually ∼5–10), the craniotomy was expanded or a new craniotomy was opened to expose new regions of the auditory cortex. When possible, old craniotomies were covered with a layer of bone wax and allowed to heal.

Analysis

Behavior

Performance was assessed by a discrimination index (DI) computed from the area under the receiver operating characteristic (ROC) curve for detection of the target in the repeating segment (Yin et al., 2010; David et al., 2012). DI combines information about hit rate, false alarm rate, and reaction time. Higher values indicate better performance on the task. Repeated trials following a false alarm were excluded from DI measurements to prevent artifactual inflation of DI estimates if animals used the strategy of gradually increasing their response time following each false alarm. Criterion was reached as the ferret performed at DI >0.5, with 0 SNR and 0 modulation depth difference for 4 consecutive days. To determine the statistical significance of the performance of each animal, we compared the actual DI to the DI computed after shuffling response times across trials. We tested for a difference in mean actual and shuffled DI across behavioral blocks by a pairwise t test.

Although the identity of the target samples varied from day to day, the ferrets could have developed a strategy in which, during the first few trials of a session, they learn to detect the spectro-temporal features associated with the target. Since some trials contained the target samples during the random segment, we predicted that ferrets using a spectro-temporal feature detection strategy would have a faster reaction time when the target was present during the random segment, whereas ferrets using a repetition detection strategy would have similar reaction times for both target and nontarget samples. To test for this, we computed a reaction time for every noise sample in each trial. Reaction time was defined as the time from the onset of the noise sample to the first lick. We then aligned each trial relative to repetition onset, split the data by target versus nontarget, and computed the mean reaction time across trials (Fig. 1D). Reaction time was fit using a linear mixed model based on sample identity, time until repetition, and the interaction between them.

The majority of the experiments included only dual-stream trials, but a subset contained interleaved dual-stream and single-stream trials (ferret O, 224 of 635; ferret H, 85 of 495). We found a small but significant difference in performance favoring dual-stream trials in both animals (mean DI difference, 0.038; p < 0.001, pairwise t test). Only the dual-stream data were included in the behavior data reported in the Results.

Stream-dependent changes in sound-evoked activity

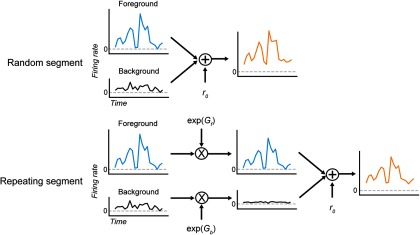
To assess the effect of repetition on overall responsiveness, we first measured changes in the response to the target sample between random and repeating trial segments. We computed the peristimulus time histogram (PSTH) response to each occurrence of a target sample in the stimulus separately for the random segment and repeating segment, using data from dual-stream trials only. The spontaneous rate was subtracted from the PSTH to ensure that the fraction term reflected changes in the evoked response. We then computed the observed gain change ($G_o$) that minimized the least-squares difference between evoked responses in the two segments. Log of the measured gain is reported to allow for direct comparison with the results of subsequent modeling analysis (see below).

PSTH-based models

Auditory cortical neurons could support the segregation of both streams either by changing the overall gain of their response to the repeating stream (stream independent) or by differentially enhancing responses to one or the other stream (stream dependent). To test these alternative predictions, we fit the data using stream-independent and stream-dependent models. In both models, responses were predicted using a weighted sum of time-varying responses to each noise sample. During the random segment, the time-varying response was the linear sum of a response to the foreground stream, response to the background stream, and spontaneous spike rate, as follows:

Here, $S_f$ and $S_b$ are the identity of samples in the foreground and background streams, respectively, and $r_0$ is the spontaneous rate. $\overline{r}\left(S,i\right)$ is the contribution of sample S to the evoked spike count in the ith time bin following sample onset.

For the stream-independent model, responses during the repeated segment, r_rep;ind, were computed as follows:

where a global gain term ($G_g$) scales responses to both streams. Forthe stream-dependent model, responses during the repeated segment,r_rep;dep, were computed, as follows:

where the gains for the foreground ($G_f$) and background ($G_b$) modulate the respective stream responses separately before they are summed. The use of an exponent simplifies the interpretation of gain changes such that values of $G\hspace{0.17em}>\hspace{0.17em}0$ indicate enhancement and values of $G\hspace{0.17em}<\hspace{0.17em}0$ indicate suppression. $\overline{r}\left(S,i\right)$ can be negative, which allows for suppressed responses relative to the spontaneous rate. In this case, if a unit has both enhanced and suppressed responses, $G$ will scale both responses equally (e.g., if $G$ > 0, there will be a decrease in spike rate during negative responses and an increase in spike rate during enhanced responses). The difference $G_f-G_b$ is the relative enhancement between streams, here referred to as foreground enhancement. If $G_f$ > $G_b$, then the neural response to the foreground stream is enhanced relative to the background stream.

The repeating segment had many more presentations of the target sample than the random segment. To minimize potential bias when fitting the data, we randomly discarded target samples from the repeating segment such that the number of target samples in the repeating segment matched the number of target samples in the random segment. As mentioned earlier, the first sample of the random segment (i.e., the very first sample in the trial) was excluded from analysis to minimize the effect of onset adaptation in our analysis.

In this model, $r\left(s,i\right)$ can contain negative values because it was added to the spontaneous rate, $r_0$ (Fig. 3). These negative values indicate that there was suppression of the spontaneous rate. The mechanisms producing this suppression are not specified (e.g., inhibition, adaptation), but similar suppression is captured by negative coefficients in a spectro-temporal receptive field (STRF).

Figure 3.

Schematic representation of the stream-dependent PSTH-based encoding model. During the random segment of each trial, the time-varying response of a neuron was modeled as the sum average responses to the two samples composing the stimulus at each point in time. During the repeating segment, responses to the foreground (repeating) and background samples were scaled by gain terms, G_f and G_b, respectively, before summing. Thus, the time course of the response to each sample was the same, but the relative magnitude of the foreground response versus background response varied between the random and repeating segments.

Models were fit to maximize Poisson likelihood of free parameters using Bayesian regression. A normal prior with a mean of 0 and an SD of 10 was set on both $r_0$ and $\overline{r}$. A normal prior with a mean of 0 and an SD of 1 was set on all $G$parameters. The model was fit three times using a different set of random starting values for each coefficient. Two thousand samples for each fit were acquired with a no-u-turn sampler, an extension to Hamiltonian Monte Carlo that eliminates the need to set a number of steps (Hoffman and Gelman, 2014). Gelman–Rubin statistics were computed for each fit to ensure that all the fits converged to the same final estimate ($\overline{r}$ < 1.1).

The posteriors for $G_g$, $G_f$, and $G_b$ were extracted from the model, and the posterior for enhancement, $E$, was computed by subtracting the posterior of $G_b$ from $G_f$. Units for which the 95% confidence interval (CI) for $E$ (as derived from the posterior) was <0 were considered to have significant suppression, and those with a 95% CI >0 were considered to have significant enhancement. For data shown in the Results, the mean of the relevant posterior is plotted.

To validate the stream-dependent model as a means of measuring stream-specific gain, we simulated the activity of 100 neurons with stream-dependent gain. For each neuron, we simulated the responses to 20 noise samples by generating a simulated PSTH for each sample from the sum of one to nine Gaussians (each amplitude, mean, and SD randomized). Eighty trials for each neuron were simulated by assembling two sequences of noise samples, one for the foreground stream and one for the background stream, as in the repeated embedded noise task. The sequences were then scaled by randomly chosen $G_f$ (uniform distribution, −0.5 to 1) and $G_b$ (uniform distribution, −1 to 1). The resulting PSTH for the trial provided a time-varying mean to a Poisson spike generator to produce simulated single-trial spiking responses. The regression model accurately recovered the responses to the individual samples (r = 0.87, p < 0.0001) and the baseline rate of each unit (r = 1.00, p < 0.0001). Predicted values for $G_f$, $G_b$, and $E$ were significantly correlated with the simulated values (r = 0.65, 0.92, and 0.82, respectively; p < 0.0001 for all). The model tended to underestimate foreground enhancement, suggesting that the results presented in this manuscript are a conservative estimate of foreground enhancement.

To validate results of the stream-dependent PSTH model applied to the data, measurements of prediction accuracy were obtained by 10-fold cross-validation, in which a separate Bayesian model was fit to 90% of the data then used to predict the remaining 10%. This procedure was repeated 10 times with nonoverlapping test sets, so that the final result was a prediction of the entire time-varying response. Prediction accuracy was then measured as the correlation coefficient (Pearson's r) between the predicted response and the actual response. Mean ± SEM correlation coefficients for A1 were 0.165 ± 0.01 for the stream-dependent model and 0.161 ± 0.01 for the stream-independent model. Mean correlation coefficients for PEG were 0.125 ± 0.01 for the stream-dependent model and 0.119 ± 0.010 for the stream-independent model. For both A1 and PEG, the stream-dependent model had significantly higher correlation coefficients than the stream-independent model (paired-sample t test; A1: t statistic, 3.27; p = 0.0014; PEG: t statistic, 4.88; p < 0.0001).

Lifetime sparseness and target preference

We quantified sparseness (S), a measure of unit selectivity for a given sample relative to the others in the collection (Vinje and Gallant, 2000), as follows:

where $r_i$ is the SD of the PSTH (computed using the average of the response to the noise sample in the random segment of single-stream trials) for the ith sample, and n is the total number of noise samples. We also quantified target preference (TP), a measure of how well the target sample modulates the unit's response, as follows:

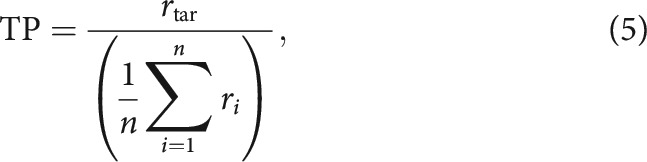where $r_{\mathrm{t}\mathrm{a}\mathrm{r}}$ is the SD of the target PSTH, and the other terms are defined as for sparseness. The use of SD to measure response magnitude means that strong suppression or enhancement yields similar response strength.

To assess whether there was a significant effect of sparseness, target preference, and/or area on foreground enhancement, E, we used the following general linear mixed model:

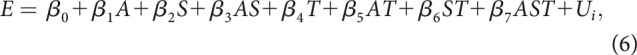where sparseness (S), target preference (T), and area (A) are fixed effects. Since each unit was tested with two target samples and, therefore, provided two measures of foreground enhancement, unit (U_i) was included as a random effect for the ith unit.

Data from the trained animal represented 40% of all units in A1 and 46% in PEG. To test for potential effects of training on neural coding, we included training status (i.e., trained vs naive), along with all possible one-, two-, and three-way interactions to the general linear mixed model. Results suggested that the effects were weaker in the trained subset (i.e., there was no significant effect of foreground enhancement in A1). However, since all the “trained” data were from one animal and the statistical power was weaker overall, we felt there were insufficient data to draw conclusions about differences between units from naive versus trained animals. Thus, we combined the data from naive and trained animals for the results reported in this article.

Spectro-temporal receptive field models

In addition to the PSTH-based models, which fit responses to individual noise samples, we confirmed that the same streaming effects were captured by a context-dependent STRF model (David, 2018). The classic linear-nonlinear (LN) STRF models neural activity as the linear weighted sum of the preceding stimulus spectrogram, the output of which passes through a static nonlinearity to predict the time-varying spike rate response (Aertsen and Johannesma, 1981; deCharms et al., 1998). The STRF, $h\left(x,u\right)$, is defined as a linear weight matrix that is convolved with the logarithm of the stimulus spectrogram, $s\left(x,t\right)$, to produce a linear model prediction, r_LIN

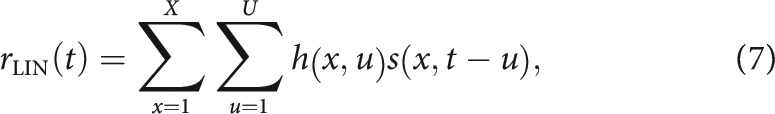where x = 1…X are the frequency channels, t = 1…T is time, and $u$ is the time lag of the convolution kernel. Taking the log of the stimulus spectrogram accounts for nonlinear gain in the cochlea. Free parameters in the weight matrix, $h$, indicate the gain applied to frequency channel x at time lag u to produce the predicted response. Positive values indicate components of the stimulus correlated with increased firing, and negative values indicate components correlated with decreased firing.

The output of the linear STRF is passed through a static nonlinear sigmoid function to account for spike threshold and saturation (Thorson et al., 2015), as follows:

where

Free parameters of the static nonlinearity are $x_0$, the inflection point of the sigmoid; $r_0$, the spontaneous spike rate; A, the maximum spike rate; and κ, the slope of the sigmoid.

We developed a modified LN STRF to account for stream-dependent changes in gain. The input spectrogram for each stream was scaled by a gain term that depended on stream identity (foreground or background) and trial segment (random or repeating). We refer to this model as the stream-dependent STRF model. The stimulus was modeled as the sum of two log spectrograms, computed separately for the foreground and background streams, s₁ and s₂, respectively. In the random segment, the total stimulus, $s\left(x,t\right)$, was modeled as the linear sum of these two stimuli, as follows:

In the repeating segment, each stimulus was scaled by the gain, $G$, for the respective stream, as follows:

All model parameters were estimated by gradient descent (Byrd et al., 1995; Thorson et al., 2015; David, 2018). STRF parameters were initialized to have flat tuning (i.e., uniform initial values of h) and were iteratively updated using small steps in the direction that optimally reduced the mean squared error between the time-varying spike rate of the unit and the model prediction. To maximize statistical power with the available data, the STRF was fit using both single-stream and dual-stream data. For single-stream trials, the second stimulus spectrogram was fixed at zero, $s_2\left(x,t\right)=0$, and a separate gain term was fit for those trials to prevent bias in estimates of $G_f$ and $G_b$. Gain parameters and STRF parameters were fit simultaneously (David, 2018). Measurements of prediction accuracy were obtained by 20-fold cross-validation, in which a separate model was fit to 95% of the data and then used to predict the remaining 5%. Fit and test data were taken from interleaved trials. This procedure was repeated 20 times with nonoverlapping test sets, so that the final result was a prediction of the entire time-varying response. Prediction accuracy was then measured as the correlation coefficient (Pearson's r) between the predicted response and the actual response. The SE on prediction correlation was measured by jackknifing (Efron and Tibshirani, 1986), and only units with prediction error significantly greater than zero were included in model comparisons (p < 0.05, jackknife t test).

To quantify the effects of segment-dependent and stream-dependent gain, we also fit models using the same data and fitting procedure, but where stream identity (stream-independent STRF model) or both segment and stream (baseline STRF model) were shuffled in time. An improvement in prediction accuracy for a model with a nonshuffled over shuffled variable indicated a beneficial effect of the corresponding gain parameter on model performance, and thus of a stream-dependent change in sound encoding. Significant differences in model performance were assessed by a Wilcoxon rank sum test between prediction correlations for the set of units fit with each model.

Statistical analysis

As described above, the effect of repetition on neural responses to the simultaneous streams was quantified using a Bayesian regression model. Unlike conventional (i.e., frequentist) approaches, Bayesian analysis does not generate standard p values. Instead, Bayesian analysis quantifies the probability that the true value for a parameter falls between two points. These distributions can be used to calculate the probability that there is a true difference between groups, which is typically the information that is intended to be reflected in p values (Nuzzo, 2014). In our analyses, we report the mean and 95% CI for all the gain terms. The CI should be interpreted as the interval in which we are 95% certain the true value is contained. Therefore, if the 95% CI does not include the reference value (e.g., $E=$ 0, which indicates no significant change in response from the random segment), we treat it as significant. Where possible, we have translated these determinations into more standardp value.

To quantify the relationship between neural tuning and the effects of repetition on stream segregation, we used a linear mixed-effects model fit with the Python statsmodels toolbox (Seabold and Perktold, 2010), using algorithms as described by Lindstrom and Bates (1988). Area (A1 vs PEG), target preference and sparseness were treated as fixed effects. All two-way and three-way interactions between the effects were included. Random intercepts for each unit were incorporated into the model. The effect size, z-score, p value, and 95% confidence interval are reported for all fixed effects and their interactions in Table 1.

Table 1.

Regression analysis of auditory tuning effects on foreground enhancement

Area	Effect	Coef.	Coef.	SE	z	p > z	CI lower	CI upper
A1	Intercept	${\beta }_0$	0.15	0.04	3.57	0.0004	0.07	0.23
	S	${\beta }_2$	−0.42	0.32	−1.33	0.1835	−1.04	0.20
	TP	${\beta }_4$	0.46	0.11	4.38	0.0000	0.26	0.67
	TP * S	${\beta }_0$	−1.04	0.27	−3.92	0.0001	−1.57	−0.52
PEG	Intercept	${\beta }_0+{\beta }_1$	0.42	0.04	9.42	0.0000	0.33	0.50
	S	${\beta }_2+{\beta }_3$	−0.32	0.32	−0.98	0.3293	−0.95	0.32
	TP	${\beta }_4+{\beta }_5$	0.05	0.10	0.50	0.6167	−0.14	0.24
	TP * S	${\beta }_6+{\beta }_7$	−0.11	0.35	−0.30	0.7644	−0.80	0.59
PEG-A1	Intercept	${\beta }_1$	0.27	0.06	4.40	0.0000	0.15	0.39
	S	${\beta }_3$	0.10	0.45	0.23	0.8210	−0.79	0.99
	TP	${\beta }_5$	−0.42	0.15	−2.86	0.0042	−0.70	−0.13
	TP * S	${\beta }_7$	0.94	0.44	2.12	0.0342	0.07	1.80

Results of the linear mixed model for foreground enhancement, with target preference, sparseness, and area as fixed effects. See text in Results and Materials and Methods for details of the model fit. Results presented are a post hoc test of contrasts. The effect and coefficient (Coef.) columns indicate the predictor/coefficients that were set to 1 for the post hoc test of contrasts. Since each unit contributes two measures of foreground enhancement (one for each target), the unit was included as a random effect in the model.

In the STRF model analysis, to assess statistical significance of the prediction correlation and thereby determine which units to include in the model comparisons, we used the jackknife t test (Efron and Tibshirani, 1986). The SE was computed by jackknife resampling of the predicted and actual responses. Significant units had a prediction correlation at least 2 SEs greater than zero (i.e., p < 0.05). Significant differences in performance by two models on a single neuron were also determined by a jackknife t test. In this case, the prediction correlation for the two models had to be separated by at least 2 SEs.

To test for differences between two neural populations (e.g., $G$ in A1 vs PEG), we used a Wilcoxon rank sum test, Student's t test, or independent two-sample t test. The specific test used, along with the test statistic, df, and p value are reported alongside the relevant result.

Results

Ferrets perceive repeated patterns embedded in noise

To investigate the physiological underpinnings of repetition-based streaming in an animal model, we first developed a behavioral paradigm to assess the ability of ferrets to detect repetitions embedded in noise. Repeated embedded noise stimuli were composed of two overlapping continuous streams of brief (250 or 300 ms) broadband noise samples. The noise samples had second-order statistics (i.e., spectral and temporal envelope correlations) matched to natural sounds (McDermott et al., 2011). Consistent with the goal of this study, the only streaming cue was repetition. These stimuli lacked other conventional streaming cues such as harmonicity and common onset time.

During the initial part of the stimulus, referred to as the random segment, samples for both streams were drawn randomly from a pool of 20 distinct noise samples (1–2.5 s duration; Fig. 1B). When all the samples are drawn randomly, they are perceived by human listeners as a single stream. The random segment was followed immediately by the repeating segment, in which a target noise sample started to repeat in one sequence but not in the other. In humans, this repetition leads to perceptual separation of the two sequences into discrete streams (McDermott et al., 2011). We refer to the sequence that contains the repeating target sample as the foreground stream, and the concurrent sequence with no repetition as the background stream (Fig. 1B).

Two ferrets (O and H) were trained to detect the repetition of the target using a go/no-go detection paradigm. Head-fixed animals were required to withhold from licking a waterspout during the random segment and to lick after the onset of the repeating segment (Fig. 1A,B). In each behavioral block (∼50–100 trials presented continuously), two noise samples were chosen as targets, each with a 50% chance of occurring in a trial. Changing the identity of the targets between blocks avoided overtraining on a specific target. To measure behavioral performance in a task with continuous distractors and variable target times, we used a DI. This metric uses hit rate (ferret O: mean ± SEM = 0.875 ± 0.007, n = 636; ferret H: mean ± SEM = 0.869 ± 0.007, n = 504), false alarm rate (ferret O: mean ± SEM = 0.522 ± 0.007; ferret H: mean ± SEM = 0.516 ± 0.010), and reaction time (250 ms noise samples: ferret O: mean ± SEM = 0.649 ± 0.017 s; ferret H: mean ± SEM = 0.826 ± 0.020 s; 300 ms noise samples: ferret O: mean ± SEM = 0.715 ± 0.014 s; ferret H: mean ± SEM = 1.006 ± 0.042) to compute the area under the ROC curve for target detection (Yin et al., 2010; David et al., 2012). Both ferrets were able to learn the task and perform significantly better than chance computed by shuffling reaction times across trials before computing the DI (ferret O: mean ± SEM = 0.603 ± 0.005, n = 636; ferret H: mean ± SEM = 0.634 ± 0.007, n = 504; ferret O: mean shuffled DI = 0.541 ± 0.004; ferret H: mean shuffled DI = 0.528 ± 0.005, p < 0.0001, pairwise t test; Fig. 1C). On average, ferrets responded after 2.9 target presentations (ferret O: mean ± SEM = 2.490 ± 0.041; ferret H: mean ± SEM = 3.315 ± 0.071). Thus, the animals were able to detect the repeating stream, and they responded after the target began repeating.

Because two unique targets were used throughout each experimental block, we considered the possibility that animals learned the identity of the target samples during the first few trials and then responded to unique spectro-temporal features of the target samples rather than the repetition. If this were the case, then we predicted that animals would be more likely to respond (i.e., false alarm) to a target sample in the random segment relative to a nontarget sample. Since the average reaction time was 2.9 samples and response rates increased over time within a trial, we could not attribute a response (i.e., lick) to a particular sample in the random segment. However, if animals did respond to the target sample, average reaction time measured from the onset of noise samples in the random phase would be expected to be shorter for target samples than for nontarget samples. We compared responses following target and nontarget samples and found no apparent difference in mean reaction time between them (Fig. 1D). To verify this similarity, we fit the reaction time data with a linear mixed model using sample duration, sample identity (i.e., target vs nontarget), time until repetition onset, and all two-way and three-way interactions as predictors. A post hoc test of contrasts demonstrated no significant effect of sample identity (p = 0.567), interaction between sample identity and time until repetition (p = 0.998), or interaction among sample identity, sample duration, and time until repetition (p = 0.823). The similar false alarm behavior for target and nontarget samples indicates that animals were not relying on spectro-temporal features of the target to perform the task.

In humans, repetition-based streaming was found to be a preattentive phenomenon (Masutomi et al., 2015). All electrophysiological data that follow were recorded while animals (trained and task naive) were passively listening to the stimuli.

Neuronal responses are suppressed during the repeating segment

We recorded multiunit and single-unit neural activity in primary (A1, n = 149) and secondary (PEG, n = 136) regions of the right auditory cortex of five ferrets of both sexes passively listening to the task stimuli. One animal was trained on the repetition-embedded noise task (ferret O), and four animals were naive to the task. Although all physiological data presented here were recorded in nonbehaving ferrets, we refer to the same trial structure terminology as in the previous section for consistency. During electrophysiological recordings, one of the target samples was chosen to match the tuning of each unit (eliciting a relatively strong response) while the other was chosen at random. The two targets had an equal probability of occurring as the repeating sample on any given trial.

To investigate the neurophysiological underpinnings of streaming due to repetition, we first looked at the raw firing rates of the recorded units in response to the repeated noise samples. Given the enhanced perception of repeating stimuli observed in behavioral experiments (Agus et al., 2010; McDermott et al., 2011; Masutomi et al., 2015), we reasoned that evidence for the selective enhancement of foreground representation should be observed at the level of the auditory cortex. If this were true, we would expect the neural response to a target sample to change between random and repeating segments.

To test this prediction, we computed the average PSTH response across all occurrences of the target noise samples in the random segment (excluding any occurrences during the first 250 ms of the trial), and compared it to the average PSTH response to a balanced number of targets in the repeating segment (Fig. 2A). Since the background sample was randomly selected for each presentation of the target, responses to the background sample were averaged out, and the PSTH primarily reflected responses to the target. To quantify changes in the response, we computed the observed gain ($G_o$) term that scaled the PSTH for the random segment to best match the PSTH for the repeating segment. To allow for a direct comparison between gains generated by encoding models (see below), the gain was log transformed. Thus, negative values indicate suppressed responses during repetition and positive values indicate enhanced responses. For most units in A1 and PEG, log gains were less than zero (Fig. 2B), indicating that the average target response in the repeating segment was suppressed with respect to the random segment (A1: mean ± SEM $G_o$ = −0.634 ± 0.038; n = 300; one-sample t test, null hypothesis population mean = 0; t statistic = −16.72; p < 0.0001; PEG: mean ± SEM $G_o$ −0.698 ± 0.049; n = 259; one-sample t test, null hypothesis population mean = 0; t statistic = −14.11; p < 0.0001). Considering previous observations of neural adaptation to repeated stimuli in auditory cortex (Ulanovsky et al., 2003; Pérez-González and Malmierca, 2014), a decreased response to the target in the repeating segment is not unexpected.

Relative enhancement of responses to the repeating foreground stream

Simply comparing the average neural response to the target in the repeating segment to the random segment does not provide insight into any stream-specific effect that might emerge as a consequence of the repetition. To test for evidence of streaming in the neural response, we needed to independently assess the responses to the two streams. Even if the total response was suppressed, activity in the foreground stream in response to the repetition could be enhanced or suppressed relative to the background stream.

To test this prediction, we developed an encoding model in which the neural response was computed as the sum of responses to samples in each stream (stream-dependent model; Fig. 3). Using regression analysis, the relative contribution of each noise sample to the PSTH response was computed from the response to the noise samples. In the random segment, the response was modeled as the sum of responses to each of the two concurrent samples and a baseline firing rate (Eq. 1). In the repeating segment, the response to each sample was scaled according to whether it occurred in the foreground or background stream before summing (respectively, gain terms $G_f$ and $G_b$; Eq. 3). We compared this model to a stream-independent model, in which responses to samples in both streams were scaled equally by a single gain term in the repeating segment ($G_g$, Eq. 2). The gain terms were exponentiated before scaling the response. Thus, positive gain indicates stronger modulation of the response of the unit (i.e., greater excitation and/or inhibition relative to the spontaneous firing rate), and negative gain indicates weaker modulation.

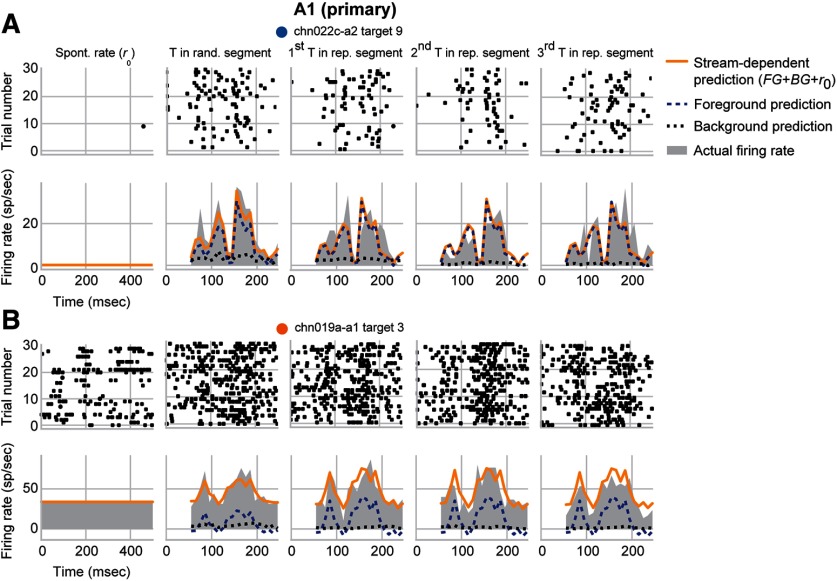
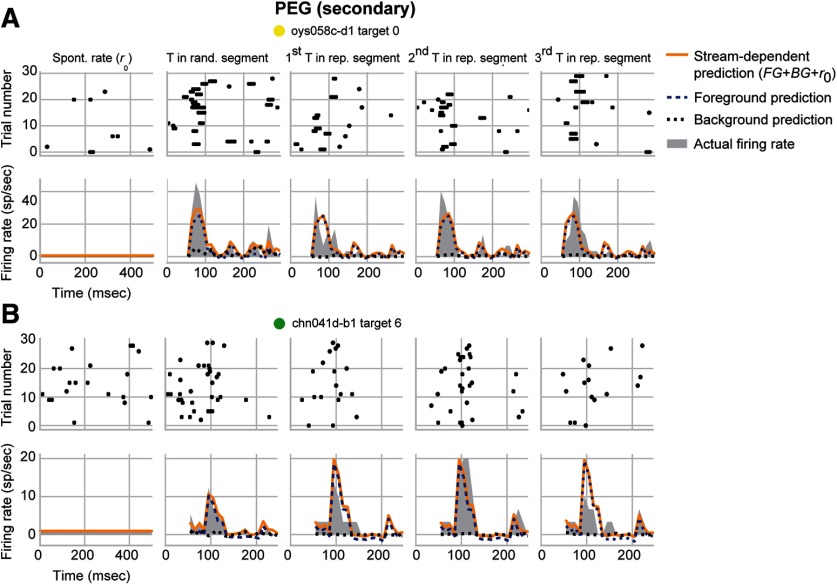
Figures 4 and 5 show the average response to the target samples and predictions by the stream-dependent model for example units in A1 and PEG, respectively. For some units in both areas, the gain during the repeating segment was unchanged for the foreground but negative for the background stream (Fig. 4A, $G_f$ = −0.014, $G_b$ = −1.332; Fig. 5A, $G_f$ = −0.009, $G_b$ = −1.316). In others, the change was negative for the background stream but positive for the foreground stream (Fig. 4B, $G_f$ = 0.552, $G_b$ = −1.014; Fig. 5B, $G_f$ = 0.612, $G_b$ = −1.551). In all of these cases, however, foreground gain was greater than background gain during the repeating segment. Thus, even if the overall gain was negative, there could be a relative enhancement of response to the foreground stream over the response to the background.

Figure 4.

Example A1 units showing foreground enhancement of responses to repeating noise. A, Raster plots (top) and PSTH responses (gray shading, bottom) of an A1 unit to the target sample (T) in the random segment and during the first three repetitions in the repeating segment. Each trace is a response to the target sample and a simultaneous random background sample. Spontaneous rate ($\mathrm{S}\mathrm{R}$) is shown (first column) for reference. Predictions from the stream-dependent model (orange) broken down into the constituent responses to foreground (blue, dashed) and background (black, dotted) streams. This unit had a smaller overall response to the repeating segment compared with the random segment ($G_o$ = −0.330; $G_g$ = −0.244), indicating some neural adaptation. Despite this adaptation, this unit had significant foreground enhancement (E = 1.318) resulting from the suppression of background ($G_b$= −1.332) but no change for foreground ($G_f$= −0.014). B, Same as in A for a second unit in A1. This unit showed some small facilitation of the overall response ($G_o$ = −0.080; $G_g$ = 0.147). When broken down by stream, there was significant foreground enhancement (E = 1.566) due to the suppression of background ($G_b$= −1.014) and the enhancement of foreground ($G_f$= 0.552). Colored dots near each unit name identify their points in Figure 6.

Figure 5.

Example PEG units showing foreground enhancement of responses to repeating noise. A, Raster and PSTH data for a unit from PEG, plotted as in Figure 4. This unit had a smaller overall response to the repeating segment compared with the random segment ($G_o$ = −0.493; $G_g$= −0.250), indicating some neural adaptation. Despite this adaptation, this unit had a significant foreground enhancement (E = 1.308) due to the suppression of background ($G_b$= −1.316) but no change of foreground ($G_f$ = −0.009). B, Same as in A for a second unit in PEG. This unit showed facilitation of the overall response ($G_o$ = 0.425; $G_g$ = 0.104). When broken down by stream, a second PEG unit underwent foreground enhancement (E = 2.163) due to the suppression of background ($G_b$ = −1.551) and the enhancement of foreground ($G_f$= 0.612). Colored dots near each unit name identify their points in Figure 6.

Across the population, gain was negative for both foreground and background streams in the majority of unit–target pairs (Fig. 6A; A1: mean ± SEM $G_b$ = −0.609 ± 0.041, mean ± SEM $G_f$ = −0.485 ± 0.035, n = 304 unit–target pairs; PEG: mean ± SEM $G_b$ = −0.935 ± 0.038, mean ± SEM $G_f$= −0.518 ± 0.040; n = 276 unit–target pairs). Consistent with this result, the stream-independent model also showed a decrease in gain during the repeating segment (A1: mean ± SEM $G_g$ = −0.498 ± 0.038, n = 304 unit–target pairs; PEG: mean ± SEM $G_g$ = −0.740 ± 0.042, n = 276 unit–target pairs). This overall suppression was also consistent with the decrease measured directly from the average target response (Fig. 2B; r = 0.626 between $G_g$ and $G_o$; p < 0.0001).

Figure 6.

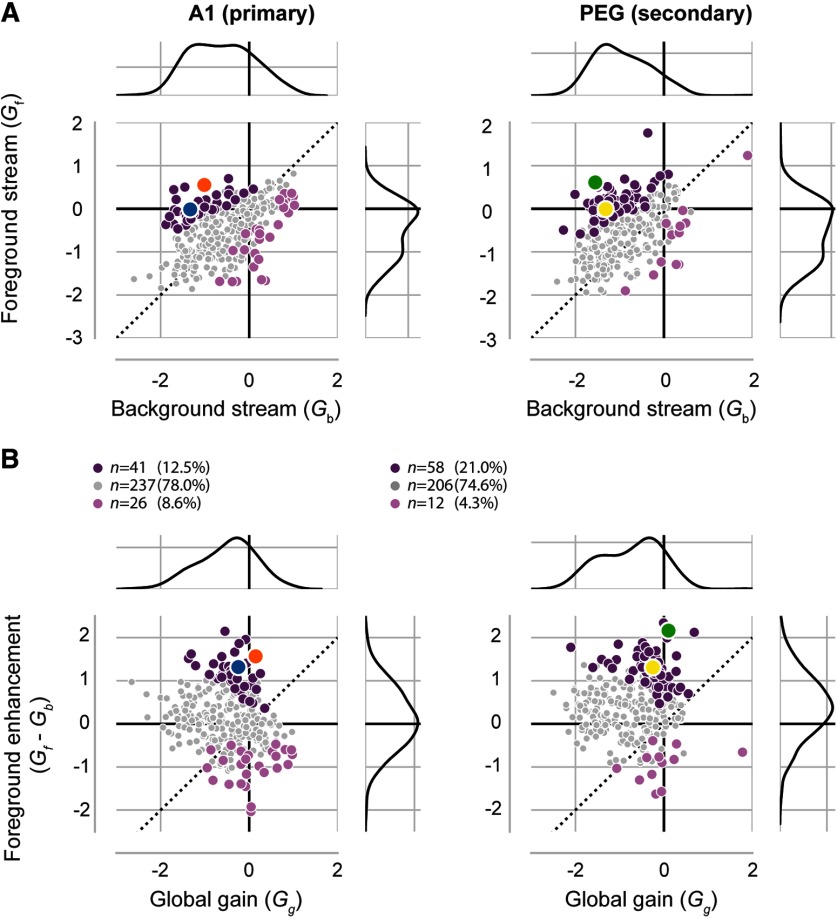
Selective foreground enhancement in A1 and PEG. A, Scatter plots of $G_f$ versus $G_b$ gain during the repeating segment of each trial. Gain parameters are plotted for the stream-dependent model fit to each unit–target pair in A1 (left) and PEG (right). Distributions for $G_f$ and $G_b$ are shown in the margins of each plot. Colored circles indicate significant foreground enhancement (dark purple) or suppression (light purple) as assessed by the 95% confidence interval not overlapping with 0. Gray indicates no significant difference. Orange and blue circles refer to A1 example units (Fig. 4), and green and yellow to PEG example units (Fig. 5). B, Foreground enhancement (E = $G_f-G_b$, stream-dependent model) plotted against global gain change ($G_g$, stream-independent model) in A1 (left) and PEG (right). Colors are as in A. Legend shows n. Mean foreground enhancement was significantly greater than zero in both areas (A1: mean ± SEM 0.124 ± 0.040; n = 304 unit–target pairs; p = 0.004, Wilcoxon signed-rank; sum of ranks = 18,778; PEG: mean ± SEM 0.416 ± 0.042; n = 276 unit–target pairs; p < 0.0001, Wilcoxon signed-rank; sum of ranks = 7610).

To test for the relative enhancement of responses to the repeated foreground, we measured foreground enhancement, the difference between $G_f$ and $G_b$, for each unit–target pair (Fig. 6B). Foreground enhancement was considered significant if the 95% CI for the fitted parameter did not bracket 0 (see Materials and Methods). A subset of unit–target pairs displayed significant foreground enhancement (41 of 304 in A1; 58 of 276 in PEG), meaning that, during the repeating segment, responses to the foreground stream were less suppressed than responses to the background stream. This could be due to a large suppression of responses to the background stream with no change in responses to the foreground stream (Figs. 4A, 5A) or to the enhancement of responses to the foreground stream combined with a moderate suppression of responses to the background stream (Figs. 4B, 5B). In contrast, fewer units showed foreground suppression in either area (26 of 304 in A1; 12 of 276 in PEG). Across the set of unit–target pairs, mean foreground enhancement was significantly greater than zero in A1 (mean ± SEM, 0.124 ± 0.040; n = 304 unit–target pairs; p = 0.004, Wilcoxon signed-rank test; sum of ranks = 18,778; Fig. 6A) and PEG (mean ± SEM, 0.416 ± 0.042; n = 276 unit–target pairs; p < 0.0001, Wilcoxon signed-rank test; sum of ranks = 7610; Fig. 6B). Mean foreground enhancement was greater in PEG than in A1 (p < 0.0001, independent two-sample t test; t statistic = −5.025).

Despite the overall suppression of activity during the repeating segment, these results support a model of selective enhancement of responses to the repeated foreground stream, consistent with the enhanced perception of the repeated stream relative to the random background (McDermott et al., 2011).

Auditory tuning properties predict the degree of foreground enhancement

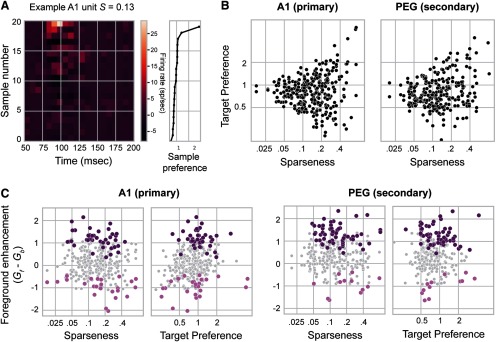
Next, we wondered whether the units showing significant foreground enhancement had distinct sensory-encoding properties. For each unit, we quantified lifetime sparseness, a measure of selectivity for any one sample relative to the others (see Materials and Methods; Eq. 4; Vinje and Gallant, 2000). This metric is bounded between 0 and 1, where 0 indicates low sparseness (unit responds equally to all stimuli) and 1 indicates high sparseness (unit responds well to only one stimulus). Many units were sparse, responding strongly to only a few noise samples (Fig. 7A, example). For each unit–target pair, we also computed target preference, the ratio of evoked response to the target versus the average response to all samples (see Materials and Methods;Eq. 5). A target preference of 1 indicates that the modulation of the unit firing rate by the target (increased or decreased spike rate) is equivalent to the average modulation across all samples for all samples.

Figure 7.

Relationship between target preference and sparseness in A1 and PEG units. A, Illustration of responses to individual noise samples for a unit with moderate sparseness (S = 0.13) that responded strongly to only a few samples. Each row of the heatmap represents the PSTH response of the unit to one of the noise samples. Rows are ordered according to the sample preference, as shown in the right panel (Eq. 5). B, Scatter plot of target versus lifetime sparseness for each unit recorded from A1 and PEG. Target preference quantifies the response of a given unit to a target sample compared with all 20 noise samples. Lifetime sparseness measures selectivity for the noise samples. Values of sparseness near 0 indicate units that responded similarly to all noise samples, and values near 1 indicate units that responded preferentially to a small number of samples. Units with high sparseness had a greater variability in target preference. C, Scatter plots of foreground enhancement as a function of target preference and sparseness in A1 (left) and PEG (right). Because sparseness and target preference are correlated, possible relationships with foreground enhancement were tested using a regression model, which is detailed in Table 1. Briefly, the regression identifies no significant relationship between sparseness and foreground enhancement in either area (p > 0.05). However, units in A1 with strong target preference tended to show stronger foreground enhancement (A1, p < 0.0001).

The relationship among the sparseness, target preference, and auditory area (A1 or PEG) of each unit and the foreground enhancement of the unit was quantified by a general linear mixed model with area, target preference, and sparseness as fixed effects and unit as a random effect (Eq. 6, Fig. 7B,C). All two-way and three-way interactions among the fixed parameters were included, and results, including significance tests, are shown in Table 1. This model identified a significant relationship between target preference and foreground enhancement in A1 (e.g., for every increase in target preference of 1.0, foreground enhancement increased by 0.46). The effect of target preference was significantly modulated by sparseness. That is, foreground enhancement was stronger in units with high target preference, but this effect decreased with increasing sparseness (e.g., for a unit with a sparseness of 0.05, the effect of target preference on foreground enhancement would be 0.41, whereas for a unit with a sparseness of 0.4, the effect of target preference on foreground enhancement would be 0.04). In contrast, in PEG there was no significant relationship between oreground enhancement and sparseness, target preference, or the interaction of target preference and sparseness (Table 1).

Thus, in A1, units that responded to many stimuli (low sparseness) but had a relatively strong response to a target (high target preference) tended to show the most foreground enhancement. In PEG, enhancement was stronger overall and affected responses more uniformly, regardless of auditory selectivity. These differences between PEG and A1 suggest a gradual emergence of repetition-related streaming along the cortical auditory pathway.

Foreground enhancement increases accuracy ofspectro-temporal receptive field models

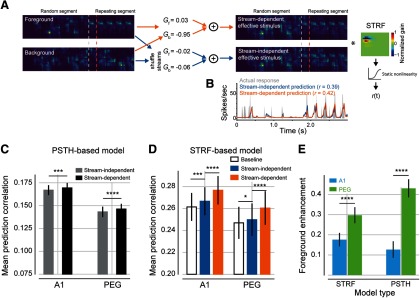
To validate the gain changes observed in the PSTH-based model and to quantify their effect on sound-evoked activity, we modeled the same data with an STRF. In the classic LN STRF (see Materials and Methods; Eqs. 7–9), the time-varying neural response is modeled as a linear weighted sum of the stimulus spectrogram, followed by a static nonlinearity to account for spike threshold (Depireux et al., 2001; Thorson et al., 2015). We developed a context-dependent model, in which spectrograms for each stream were scaled separately by a gain term before providing input to a traditional LN STRF (Fig. 8A,B, orange arrows; Eqs. 10, 11). This scaling followed the same logic as the stream-dependent PSTH-based model described above. That is, a separate spectrogram for each stream was scaled by free parameters that depended on segment (random or repeating) and, during the repeating segment, stream identity (foreground or background). If neural responses were enhanced selectively for one stream, then the gain applied to that spectrogram was greater than the gain for the other spectrogram. We refer to this model as the stream-dependent STRF.

Figure 8.

STRF-based model corroborates PSTH-based model findings of stream-specific gain changes in A1 and PEG. A, Schematic of the STRF-based encoding models. Left to right, Spectrograms of the foreground and background streams are scaled by context-dependent gain. Separate gain terms are applied to the $G_f$and $G_b$ streams during the repeating segment. The sum of the scaled spectrograms then provides input to a traditional linear–nonlinear STRF, which in turn predicts the time-varying response. For the stream-independent model (bottom right), stream identity was shuffled, leading to similar gain for both streams. For the stream-dependent model, gains could differ. In this example, the higher gain for the foreground emphasizes the repeating noise sample (top right). B, Time-varying response for example unit in A for the actual unit response (gray), stream-independent model prediction (blue), and stream-dependent model prediction (orange). Prediction correlation (Pearson's r) between predicted and actual time-varying neural responses is reported for the two models. C, Mean prediction correlation coefficient (Pearson's r) between the predicted and actual time-varying neural responses for A1 and PEG units, plotted for the stream-independent (gray) and stream-dependent (black) PSTH-based models (Fig. 6, scatter plots). D, Mean prediction correlation (Pearson's r) between the predicted and actual time-varying neural responses for STRF-based models across A1 and PEG units. Asterisks indicate significant differences for p values associated with Wilcoxon signed-rank test within-area model comparisons [baseline vs stream-independent for A1 (n = 141, p < 0.0001) and for PEG (n = 106, p < 0.0001); stream-dependent vs stream-independent for A1 (p = 0.0007) and PEG (p = 0.0139, Wilcoxon signed-rank test)]. E, Mean foreground enhancement for STRF-based models (A1, 0.180 ± 0.024; PEG, 0.298 ± 0.024) and PSTH-based models (A1, 0.124 ± 0.040; PEG, 0.416 ± 0.042). Asterisks indicate p values associated with an independent two-sample t test between values of foreground enhancement in A1 and PEG.

We compared prediction accuracy of the stream-dependent STRF to two control models: a stream-independent STRF, in which stream identity was shuffled in time before fitting (Fig. 8A,B, blue path), and a baseline STRF, in which both segment and stream identity were shuffled. By separately shuffling state variables related to repetition and stream identity, we controlled for the influence of each variable on response gain while keeping the number of free parameters in each model constant. We used a cross-validation procedure to prevent the possibility of overfitting to the model estimation data, testing the models on a common dataset that was not used for fitting.

The stream-dependent STRF predicted time-varying responses more accurately than the stream-independent STRF in both A1 (mean prediction correlation ± SEM, 0.277 ± 0.013 and 0.267 ± 0.013, respectively; p < 0.0001, Wilcoxon signed-rank test; Fig. 8D) and PEG (mean prediction correlation ± SEM, 0.260 ± 0.015 and 0.250 ± 0.015, respectively; p < 0.0001). Thus, the STRF-based models confirm a significant influence of stream identity on relative gain.

While incorporating stream-dependent gain improved prediction accuracy in both areas, predictions were generally more accurate in A1 than in PEG for both models. This difference is likely due to a greater prevalence of nonlinear encoding properties and nonauditory activity in PEG, compared with A1 (Atiani et al., 2014). The same pattern of enhanced prediction accuracy was observed for stream-dependent PSTH-based models, when compared with fits with stream identity shuffled (Fig. 8C).

The comparison of stream-independent and baseline STRFs measured the effect of repetition alone on evoked activity (independent of stream identity). On average, the stream-independent STRF had greater prediction accuracy than the baseline STRF in both areas (baseline STRF mean ± SEM prediction correlation: A1: 0.261 ± 0.013, p = 0.0007; PEG: 0.247 ± 0.015, p = 0.014, Wilcoxon signed-rank test; Fig. 8D). Moreover, overall gain was suppressed during the repeating segment (mean ± SEM: A1, −0.098 ± 0.009; PEG: −0.047 ± 0.010), as observed in the PSTH-based models above (Fig. 6). Thus, the STRF-based models provide additional evidence for a streaming mechanism in which repetition leads to overall suppression of the neural responses, but with less prominent suppression of the foreground stream relative to the background.

To measure the relative enhancement between the two streams, we compared the stream-specific gain terms from the model fits, equivalent to $G_f$ and $G_b$ in the stream-dependent PSTH model. We observed a significant foreground enhancement in both A1 (mean ± SEM, 0.180 ± 0.024; p < 0.0001) and PEG (mean 0.298 ± 0.024; p < 0.0001, Wilcoxon signed-rank test; Fig. 8E). These changes in gain followed the same pattern as in the PSTH-based model above (correlation between foreground enhancement for PSTH-based and STRF-based models, as follows: A1, r = 0.39, p < 0.0001; PEG, r = 0.22, p = 0.0005).

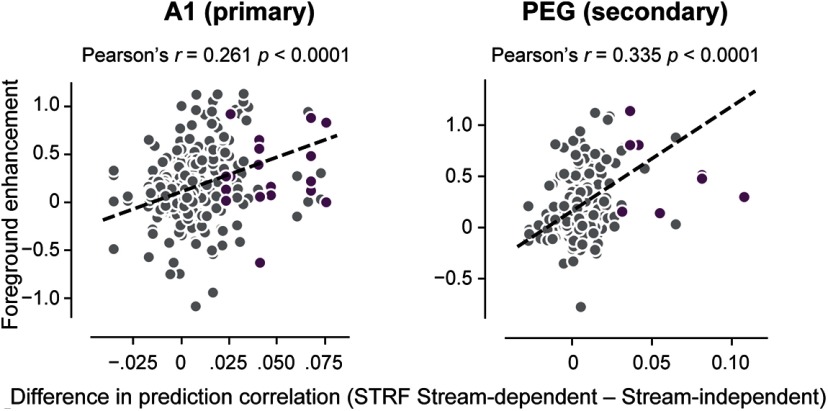
Since only some units in A1 or PEG showed foreground enhancement, we also expected that the performance of the stream-dependent STRF should vary and that the benefit of a stream-dependent model should be greatest for units showing the strongest foreground enhancement. We compared the difference in prediction accuracy between stream-dependent and stream-independent STRFs with foreground enhancement measured in the stream-dependent STRF (Fig. 9). In both A1 and PEG, these values were positively correlated (A1: r = 0.261, p < 0.0001; PEG: r = 0.335, p < 0.0001). Thus, in units showing enhanced gain for the repeating stream, models incorporating stream-dependent gain show the greatest improvement in prediction accuracy.

Figure 9.

Improved performance by the stream-dependent model predicts foreground enhancement. Scatter plot compares foreground enhancement against the difference in prediction correlation coefficient between stream-dependent and segment-only models in A1 (left) and PEG (right). Each circle represents a unit–target pair. Dashed line indicates a linear fit to the data. Units showing significant enhancement for the stream-dependent model are indicated in purple. Headings indicate the mean prediction correlation (Pearson's r) and corresponding p value.

Discussion

Temporally covarying sound features tend to be perceptually grouped into a single object (Bizley and Cohen, 2013). Consistent with this observation, subjects are able to identify novel noise samples when they are repeated simultaneously in a mixture with nonrepeating samples (McDermott et al., 2011). The goal of this study was to investigate the neural underpinnings of auditory streaming cued by repetition. We developed an animal model for repetition detection and found evidence for enhanced representation of a repeating foreground stream in single-unit activity in auditory cortex. This representation emerges hierarchically, as streaming effects are stronger in PEG than in A1 auditory cortical fields.

Mechanisms of repetition-induced stream segregation

Studies of streaming at the single-unit level have primarily used alternating sequences of pure tones (Fishman et al., 2001; Micheyl et al., 2005). Relevant to the current study, Micheyl et al. (2005) presented sequences of “ABA_” tone triplets to awake macaques and examined the activity evoked in A1. Tone A was chosen to be on the best frequency of the recorded unit, while tone B differed by 1–9 semitones from tone A. The authors found that, even if responses to both tones decreased relative to their presentation in isolation, responses to the nonpreferred B tones decreased more. We observed a similar effect, that relative enhancement of the foreground stream was more pronounced in units well tuned to the repeated noise sample. Thus, this study provides evidence that the same principles generalize to the streaming of simultaneous, naturalistic sounds.

Sound features that belong to the same source tend to occur at the same time. This phenomenon has been formalized in the temporal coherence model (Elhilali et al., 2009; Shamma et al., 2011). Teki et al. (2016) demonstrated that human listeners are sensitive to the repetition of sounds presented in the context of a random mixture of chords. Similar to our findings, the authors observed that repeating sounds tend to fuse together into a foreground that emerges from a randomly changing background (Teki et al., 2011, 2013). Here, we propose that the enhancement of neural responses to the foreground contributes to the streaming of repeating sounds. Streaming effects were heterogeneous across neurons, with the substantial variability in foreground enhancement explained by neural tuning (i.e., sparsity and target preference). This observation emphasizes that, for complex naturalistic stimuli, only a subset of neurons will show streaming effects, which may differ from when stimuli are optimized for each neuron studied.

It is important to note that an expectation of enhanced responses to “foreground” stimuli may reflect a biased expectation. There is no requirement for sounds that perceptually pop out to evoke enhanced neural responses. For example, Bar-Yosef et al. (2002) and Bar-Yosef and Nelken (2007) investigated cat A1 activity during the presentation of bird chirps in background noise, simulating a natural auditory scene. To their surprise, neural responses were dominated by the background noise. The authors interpreted this finding in an evolutionary context, in which it is advantageous for prey to detect subtle changes in the background, thereby preventing predators from masking their approach behind foreground sounds. Thus, it may be important to consider the behavioral context of the animal model. More experiments testing streaming in natural conditions will elucidate how behavioral relevance influences the streaming of repeated sound features.

Streaming analysis

Since the neural response measured in this study is the sum of responses to two simultaneous stimuli, the component responses cannot be separated in the raw neural firing rate. Therefore, we constructed encoding models to computationally tease apart stream-dependent activity. We found that, although most neural responses were suppressed by repetition (likely due to adaptation; Ulanovsky et al., 2004; Grill-Spector et al., 2006; Pérez-González and Malmierca, 2014), responses to the foreground stream were less suppressed than the background stream, or even were enhanced. The same methodology could be applied to other datasets where there is a need to separate neural responses to simultaneous inputs.

The challenge of separating responses to simultaneous sounds has been addressed in some human studies using a similar approach (Ding and Simon, 2012). Ding and Simon (2012) recorded human brain activity via magnetoencephalography (MEG) while subjects attended to one of two simultaneous speech samples. They fit a separate STRF [or more precisely a “TRF” (temporal receptive field) since MEG did not resolve spectral tuning] for each speech stream. Neural activity preferentially synchronized to the speech envelope of the attended speaker. Furthermore, the source location of the attended versus nonattended signals suggested a hierarchy of auditory processing in which representation of the attended object emerges in posterior auditory cortex (Ding and Simon, 2012). These results are consistent with the foreground enhancement observed in the current study, suggesting that top-down attention and bottom-up pop-out effects could be mediated by common mechanisms.

A related approach used to investigate the neural signature of streaming is stimulus decoding (Mesgarani et al., 2009; Ding and Simon, 2012; Mesgarani and Chang, 2012). A decoding model is effectively an inverse of the STRF, using neural population activity to reconstruct the sound stimulus. Using human MEG and electrocorticography recordings, attended stimuli can be reconstructed more accurately than simultaneous nonattended stimuli, indicating enhanced coding of the attended stream (Ding and Simon, 2012; Mesgarani and Chang, 2012). In the current study, stimuli were not fixed across experiments. Thus, the data do not support straightforward population decoding. However, with appropriate changes to experimental design, we predict that reconstruction should be more accurate for the foreground stream than the background stream.

Relation of repetition enhancement to stimulus-specific adaptation

The ability of the brain to detect regularities is not only crucial for identifying an auditory object embedded in a noisy scene, but also for making predictions about the environment, thereby making the system sensitive to deviance (Winkler et al., 2009; Bendixen et al., 2010). Substantial effort has been devoted to understanding the mechanisms of deviance detection, with a focus on the MMN in humans (Näätänen, 2001) and on SSA in animals (Ulanovsky et al., 2003; May and Tiitinen, 2010; Pérez-González and Malmierca, 2014). Evidence for SSA has been found in the nonlemniscal inferior colliculus and thalamus (Anderson et al., 2009; Malmierca et al., 2009; Antunes et al., 2010), but the first primary region in which SSA has been shown to be prominent is A1 (Nelken and Ulanovsky, 2007; Malmierca et al., 2015).

Selective enhancement of the neural response to a repeating sound might seem like an intuitive prediction, based on behavioral studies (Agus et al., 2010; McDermott et al., 2011). However, it may be surprising when viewed in the context of SSA (Ulanovsky et al., 2003; Taaseh et al., 2011). If SSA affects responses to simultaneous stimuli the same way as responses to sequential stimuli, one would expect a relative suppression of responses to the foreground stream. However, our results show the opposite effect (i.e., relative suppression of the simultaneous background). We propose that while SSA can account for the overall decreased response to both streams (Grill-Spector et al., 2006; Pérez-González and Malmierca, 2014), a separate mechanism must further suppress responses to sounds that occur simultaneously in the background. Furthermore, the fact that foreground enhancement is more prominent in PEG than in A1, suggests a hierarchical process by which the enhancement emerges.

Feedback from local inhibitory networks and short-term synaptic plasticity are both believed to play a role in contextual modulation of sensory coding. Inhibitory interneurons contribute to SSA (Natan et al., 2015), contrast gain control (Isaacson and Scanziani, 2011), and top-down effects of behavior (Kvitsiani et al., 2013). Short-term plasticity may play a role in robust encoding of noisy natural sounds (Mesgarani et al., 2014) and temporal integration of sound information (David and Shamma, 2013). The most prominent effect of repetition in the current study may be broad inhibition of neural responses to both streams. However, disinhibition or adaptation of inhibitory feedback along specific pathways could mediate the relative enhancement of the foreground stream.

Animal models for streaming

Most behavioral studies of auditory streaming have been performed in humans (Bregman, 1990; Darwin and Carlyon, 1995; Darwin, 1997; Carlyon, 2004; Yost et al., 2007). This is not surprising, as perceptual measurement of streaming in nonhuman species is challenging (Bee and Micheyl, 2008; Fay, 2008). Within a small number of animal studies, however, the ferret has been identified as a model for streaming of alternating tone sequences and tone clouds (Micheyl et al., 2007; Ma et al., 2010) and has been used to study its neurophysiological basis (Elhilali et al., 2009).

Here, we developed the ferret as a model for streaming complex, repeating sounds. Ferrets were able to report the occurrence of a repetition amid random overlapping noise samples. Since the identity of the repeated sample was changed across behavioral blocks, we excluded the possibility that they used specific spectro-temporal features of the target sample to perform the task. While the ability to report the occurrence of repetitions in one stream is not direct proof that ferrets perceived two separate streams in the same way as humans, it confirms that they did detect the repetitions.