Implementation of Clinical Diagnostic Criteria and Universal Symptom Survey Contributed to Lower Magnitude and Faster Resolution of the COVID-19 Epidemic in Wuhan

Abstract

The majority of cases infected with the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) in China centered in the city of Wuhan. Despite a rapid increase in the number of cases and deaths due to the coronavirus disease 2019 (COVID-19), the epidemic was stemmed via a combination of epidemic mitigation and control measures. This study evaluates how the implementation of clinical diagnostics and universal symptom surveys contributed to epidemic control in Wuhan. We extended the susceptibles-exposed-infectious-removed (SEIR) transmission dynamics model by considering three quarantined compartments (SEIR^+Q). The SEIR^+Q dynamics model was fitted using the daily reported number of confirmed infections and unconfirmed cases by clinical diagnostic criteria up to February 14, 2020, in Wuhan. Applying the model to carry forward the pre-February 14 trend in Wuhan, the number of daily new diagnosed cases would be expected to drop below 100 by March 25, below 10 by April 29, and reach 0 by May 31, 2020. The observed case counts after February 14 demonstrated that the daily new cases fell below 100 by March 6, below 10 by March 11, and reached 0 by March 18, respectively, 19, 49, and 74 d earlier than model predictions. By March 30, the observed number of cumulative confirmed cases was 50 006, which was 19 951 cases fewer than the predicted count. Effective reproductive number R(t) analysis using observed frequencies showed a remarkable decline after the implementation of clinical diagnostic criteria and universal symptom surveys, which was significantly below the R(t) curve estimated by the model assuming that the pre-February 14 trend was carried forward. In conclusion, the proposed SEIR^+Q dynamics model was a good fit for the epidemic data in Wuhan and explained the large increase in the number of infections during February 12–14, 2020. The implementation of clinical diagnostic criteria and universal symptom surveys contributed to a contraction in both the magnitude and the duration of the epidemic in Wuhan.

1. Introduction

In December 2019, a cluster of pneumonia cases with unclear pathogenesis was reported. On January 9, 2020, a novel coronavirus was identified as the cause of this condition. This virus was named by World Health Organization (WHO) as the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) and the disease it caused was named as coronavirus disease 2019 (COVID-19) [1]. The disease rapidly became an epidemic across China over January. Consequently, COVID-19 was urgently classified as a Class B communicable disease and was managed as a Class A communicable disease in accordance with the Law of the People’s Republic of China on the Prevention and Treatment of Infectious Disease [2]. Various mitigation measures led to effective containment of the virus in early February, significant declines in infection in late February, and nationwide control by mid-March.

At the same time, the COVID-19 epidemic continued to spread around the globe, with rapid increases in case numbers in European and American countries [3]. The WHO officially declared a global pandemic on March 11, 2020. As of March 31, the pandemic had spread to 178 countries on six continents, with a total of 788 522 diagnosed cases [4].

Wuhan placed high priority on constraining the COVID-19 epidemic. Both the state and the local government undertook a series of active prevention and control intervention measures in Wuhan. On January 23, Wuhan implemented traffic restrictions; immediately after, a first-level response to a major public health emergency was launched, which is the highest level of emergency response to a public health crisis in China, according to the scope and degree of its impact. Urban bus, subway, ferry, and long-distance passenger transportation in Wuhan were all suspended, and departure channels in airport and railway stations were also temporarily closed down. Consequently, during January 23–31, population outflow from Wuhan declined to 6% of that in the same period in 2019, and travel intensity within Wuhan declined to 23% of that in the same period in 2019 according to the Baidu Map's Migration Big Data Platform†. In addition, Wuhan initiated a universal symptom survey during February 6–10, followed by a second round during February 17–19, 2020.

On February 12, clinical diagnostic criteria—in addition to the diagnosis by positive laboratory nucleic acid test results of SARS-CoV-2—were implemented in Hubei Province. This criteria resulted in a sharp increment of cases in subsequent days, likely reflecting the number of cumulative unconfirmed cases identified during the initial universal symptom survey. The Diagnosis and treatment protocol for novel coronavirus pneumonia (trial version 5), released on February 5 by the National Health Commission of the People’s Republic of China, indicated that patients with clinical and radiological characteristics typical of COVID-19 could be diagnosed as positive, even in the absence of a positive nucleic acid test [5]. Diagnosed individuals were then isolated to prevent further transmission.

These various measures slowed down the growth of the epidemic in Wuhan. Effects of the travel ban in Wuhan on the spread of COVID-19 have been studied [6], [7]. However, the contribution of implementing universal symptom surveys and clinical diagnostic criteria to epidemic control in Wuhan has not yet been delineated. Here, we extend a transmission dynamics model to fit the epidemic trend in Wuhan and evaluate the effects attributable to these major interventions (i.e., universal symptom surveys and clinical diagnostic criteria). Our results may provide critical insight for the international community for current and future epidemic response.

2. Methods

2.1. Source of data

Data were collected from the official websites of the Wuhan Municipal Health Commission and the National Health Commission of the People’s Republic of China, as detailed in Table 1 . Numbers of daily new and cumulative confirmed cases were collected from January 15 to March 30, 2020. All confirmed cases had positive laboratory nucleic acid test results, confirming infection with SARS-CoV-2. In addition, we extracted the frequencies of cases reported during February 12–14 using clinical diagnostic criteria in the absence of positive nucleic acid testing, according to the Diagnosis and treatment protocol for novel coronavirus pneumonia (trial version 5) [5].

Table 1.

Number of officially reported cases of COVID-19 in Wuhan, 2020.

Date	Number of daily new cases	Number of cumulative cases	Date	Number of daily new cases	Number of cumulative cases
Jan 15	0	41	Feb 22	541	46 201
Jan 16	4	45	Feb 23	406a	46 607
Jan 17	17	62	Feb 24	464	47 071
Jan 18	59	121	Feb 25	370	47 441
Jan 19	77	198	Feb 26	383	47 824
Jan 20	60	258	Feb 27	313	48 137
Jan 21	105	363	Feb 28	420	48 557
Jan 22	62	425	Feb 29	565	49 122
Jan 23	70	495	Mar 1	193	49 315
Jan 24	77	572	Mar 2	111	49 426
Jan 25	46	618	Mar 3	114	49 540
Jan 26	80	698	Mar 4	131	49 671
Jan 27	892	1 590	Mar 5	126	49 797
Jan 28	315	1 905	Mar 6	74	49 871
Jan 29	356	2 261	Mar 7	41	49 912
Jan 30	378	2 639	Mar 8	36	49 948
Jan 31	576	3 215	Mar 9	17	49 965
Feb 1	894	4 109	Mar 10	13	49 978
Feb 2	1 033	5 142	Mar 11	8	49 986
Feb 3	1 242	6 384	Mar 12	5	49 991
Feb 4	1 967	8 351	Mar 13	4	49 995
Feb 5	1 766	10 117	Mar 14	4	49 999
Feb 6	1 501	11 618	Mar 15	4	50 003
Feb 7	1 985	13 603	Mar 16	1	50 004
Feb 8	1 379	14 982	Mar 17	1	50 005
Feb 9	1 920a	16 902	Mar 18	0	50 005
Feb 10	1 552	18 454	Mar 19	0	50 005
Feb 11	1 104	19 558	Mar 20	0	50 005
Feb 12	13 436	32 994 (12 364b)	Mar 21	0	50 005
Feb 13	2 997a	35 991 (14 031b)	Mar 22	0	50 005
Feb 14	1 923	37 914 (14 953b)	Mar 23	1	50 006
Feb 15	1 548	39 462	Mar 24	0	50 006
Feb 16	1 690	41 152	Mar 25	0	50 006
Feb 17	1 600	42 752	Mar 26	0	50 006
Feb 18	1 660	44 412	Mar 27	0	50 006
Feb 19	615	45 027	Mar 28	0	50 006
Feb 20	319	45 346	Mar 29	0	50 006
Feb 21	314	45 660	Mar 30	0	50 006

^aNumber of daily new cases was calibrated by the number of cumulative cases on the current day aside from that of the previous day.

^bNumber of cumulative cases by clinical diagnostic criteria.

2.2. Dynamics model definition and fitting

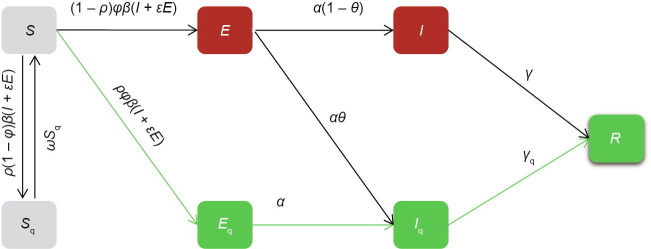
We extended the traditional susceptible-exposed-infectious-removed (SEIR) transmission dynamics model to account for unconfirmed infections and quarantine (the SEIR^+Q dynamics model). The population was divided into four traditional SEIR compartments—susceptibles (S), latent cases (exposed, E), unconfirmed cases (not quarantined, I), and removed individuals (R)—and three additional quarantined compartments—quarantined susceptibles (S _q), quarantined latent cases (E _q), and quarantined infections with laboratory-confirmed results (I _q) (Fig. 1 ). Ordinary differential equations and parameters are shown in Eq. (1) and Table 2 [5], [8], respectively.

$$\begin{array}{c}\frac{\text{d}S}{\text{d}t}=(\rho -1)\beta \mathit{\phi }(\epsilon E+I)S-\rho \beta (1-\mathit{\phi })(\epsilon E+I)S-\rho \beta \mathit{\phi }(\epsilon E+I)S+\omega S_{\text{q}}\hfill \\ \frac{\text{d}{S}_{\text{q}}}{\text{d}t}=\rho \beta \mathit{\phi }(\epsilon E+I)S-\omega S_{\text{q}}\hfill \\ \frac{\text{d}E}{\text{d}t}=(1-\rho )\beta \mathit{\phi }(\epsilon E+I)S-\alpha E\hfill \\ \frac{\text{d}{E}_{\text{q}}}{\text{d}t}=\rho \beta (1-\mathit{\phi })(\epsilon E+I)S-\alpha E_{\text{q}}\hfill \\ \frac{\text{d}I}{\text{d}t}=\alpha E(1-\theta )-\gamma I\hfill \\ \frac{\text{d}{I}_{\text{q}}}{\text{d}t}=\alpha E_{\text{q}}+\alpha E\theta -{\gamma }_{\text{q}}{I}_{\text{q}}\hfill \\ \frac{\text{d}R}{\text{d}t}=\gamma I+{\gamma }_{\text{q}}{I}_{\text{q}}\hfill \end{array}$$ (1)

where β is the contact rate of susceptible persons with incubation period or infected persons; ρ is the probability of susceptible population being tracked; φ is the probability of infection among population with close contacts; ε is the coefficient of transmission compared with infected persons; ω is the release rate of quarantined susceptible population; α is the rate of an incubator progressing to an infected person, the reciprocal of the incubation period; γ is the removal rate of undiagnosed (not quarantined) infected persons; γ _q is the removal rate of confirmed infected persons; θ is the proportion of confirmed isolates among infected persons.

Fig. 1.

Illustration of the extended SEIR^+Q dynamics model. β: contact rate of susceptible persons with incubation period or infected persons; ρ: probability of susceptible population being tracked; φ: probability of infection among population with close contacts; ε: coefficient of transmission compared with infected persons; ω: the release rate of quarantined susceptible population; α: the rate of an incubator progressing to an infected person, the reciprocal of the incubation period; γ: removal rate of undiagnosed (not quarantined) infected persons; γ_q: removal rate of confirmed infected persons; θ: proportion of confirmed isolates among infected persons.

Table 2.

Parameters in the SEIR^+Q dynamics model.

Parameter	Initial value	Range	Reference
S	8 × 104	5 × 104–1.5 × 105	RK4 and MCMC
Sq	0	Fixed	—
E	361	Fixed	Iq (0) × Incubation period
Eq	0	Fixed	—
I	26	Fixed	—
Iq	41	Fixed	Table 1
R	14	Fixed	Official website
β	1.45 × 10−4	1 × 10−5–1 × 10−3	RK4 and MCMC
ρ	0.05	0–0.10	RK4 and MCMC
φ	0.13	0.01–0.50	RK4 and MCMC
ε	0.07	0.10–0.90	RK4 and MCMC
ω	0.07	Fixed	—
α	0.19	Fixed	Ref. [5]
γ	0.1	Fixed	Ref. [8]
γq	0.1	Fixed	Ref. [8]
θ	0.6	0.2–0.8	RK4 and MCMC

RK4: fourth-order Runge‒Kutta method; MCMC: Markov chain Monte Carlo.

Directly fitting the reported number of cumulative confirmed cases was impractical due to a sharp increase in cases when the clinical diagnostic criteria were implemented during February 12–14. Instead, the 14 953 clinically diagnosed cases resultant in that short period were regarded as cumulative cases that were unconfirmed due to missing or negative nucleic acid testing results; these cases correspond to compartment I in the proposed SEIR^+Q dynamics model.

Daily frequencies of laboratory-confirmed cases from January 15 to February 14 (31 d) and unconfirmed cases from February 12 to 14 (3 d) were used simultaneously to fit the dynamics model (Model I). The fourth-order Runge‒Kutta method (RK4) was used to solve the differential equations; estimates from RK4 were used as initial settings for a Markov chain Monte Carlo (MCMC) to estimate the parameters. Implementation of universal symptom surveys (February 6–10 and 17–19) and clinical diagnostic criteria (February 12–14) was accompanied by the isolation of cases, and would therefore be expected to alter transmission. Thus, the contact rate β after February 14 was re-estimated by partitioned fitting using MCMC with initial values from the outputs at February 14 of Model I (Model II). In addition, smoothed sequential effective reproductive numbers R(t) [9] were estimated based on the outputs of the dynamics model.

2.3. Evaluation for intervention effect

2.3.1. Clinical diagnostic criteria

The Diagnosis and treatment protocol for novel coronavirus pneumonia (trial version 5) suggested implementing clinical diagnostic criteria only for Hubei Province [5]. Individuals could be classified as suspected infections if they had clinical manifestations of “fever and/or respiratory symptoms” and “normal or decreased white blood cell counts in the early stage of disease, or decreased lymphocyte count.” Suspected infections could be diagnosed as COVID-19 cases if typical viral pneumonia characteristics were demonstrated via computed tomography (CT) imaging of the lungs, without confirmatory results by nucleic acid testing.

2.3.2. Universal symptom survey

All communities were closed and all residents remained at home during the universal symptom survey period during February 6–10 (first round) and February 17–19 (second round). Thousands of community workers and volunteers screened all residents using grid searching of all communities in order to trace four categories of population: infected patients; suspected patients; fever patients with a body temperature ≥ 37.3 °C, who could not be ruled out of possible infection; and persons who had had close contact with the infections. The body temperature of the residents was collected through spontaneous reporting by recommended mobile applications or phone calling, or through door-to-door and individual-to-individual visiting by community workers and volunteers. The four categories of the population were centrally quarantined and given appropriate treatment if necessary.

2.3.3. Effect quantification

The effect of the implementation of a universal symptom survey and clinical diagnostic criteria was evaluated by comparing observed epidemic data from Wuhan with the trend predicted by the dynamics model fitted for data before February 14 (Model I). The effect of the interventions was quantified as days in advance for achieving daily emerging cases fewer than 100 or 10, days in advance for achieving the first day of zero increment, and the decrease in the number of cumulative confirmed cases as of March 30. In addition, sequential R(t) curves based on Model II were generated to show the impact of the mitigation strategies on the COVID-19 epidemic trajectory versus those based on Model I.

2.4. Statistical analysis

Berkeley Madonna Version 9.1.19 (Berkeley Madonna Inc., USA) was used to fit and explore the appropriate range of parameters. R version 3.6.3 (R Foundation for Statistical Computing, Austria) and the deBInfer version 0.4.2 package were used to perform MCMC for 200 000 simulations followed by 100 000 burn-ins.†

3. Results

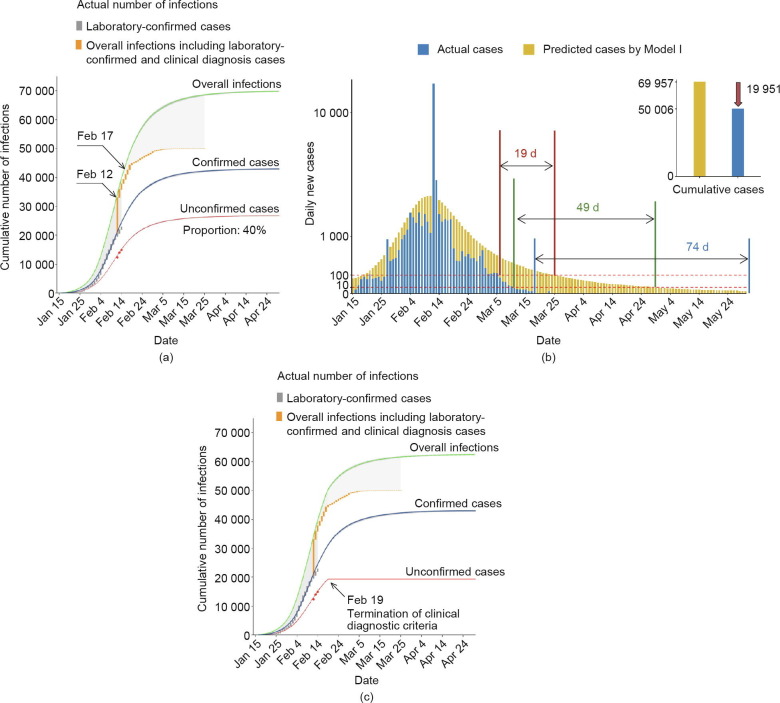
Clinically diagnosed cases reported during February 12–14 were considered to be unconfirmed infections, and the dynamics model for the epidemic trend in Wuhan through February 14 was fitted (Model I). Cumulative frequencies for unconfirmed cases identified by clinical diagnosis and laboratory-confirmed infections diagnosed by positive nucleic acid test results were fitted, respectively (Fig. 2 (a)). The number of overall infections, including both confirmed and unconfirmed cases, was summarized (Fig. 2(a)). The median proportion of unconfirmed cases was estimated as 40% of the total infections; the unconfirmed proportion was relatively high during the early phase of the epidemic in January (median, 55%; range, 42%–71%). When the trend of the epidemic in Wuhan up to February 14 was carried forward, the model predicted that the daily number of newly diagnosed cases would drop below 100 by March 25, and below 10 by April 29. In addition, the model predicted that the first day with 0 new cases would be expected by May 31, and that the number of overall infections (including laboratory-confirmed and unconfirmed cases) would eventually accumulate to 69 957 (Fig. 2(a)).

Fig. 2.

Wuhan COVID-19 epidemic trend fitted by the SEIR^+Q dynamics model. (a) The actual unconfirmed cases diagnosed by clinical symptoms (red dots) and laboratory-confirmed infections (gray stairs) before February 14, 2020 were used to fit the dynamics model. Orange stairs represent the actual overall infections including laboratory-confirmed and clinical diagnosis cases after February 12, 2020. The numbers of cumulative unconfirmed cases (red curve), confirmed infections (blue curve), and overall infections including confirmed and unconfirmed cases (green curve) were predicted by the SEIR^+Q dynamics model. Black arrows denote implementation of clinical diagnostic criteria from February 12 to 14 and universal symptom survey from February 17 to 19. The gray shadow before February 12 indicates the proportion of unreported unconfirmed cases. The gray shadow after February 14 indicates the effect of the interventions. (b) Summary of the effects of epidemic prevention and control interventions in Wuhan. (c) Considering that the Diagnosis and treatment protocol for novel coronavirus pneumonia (trial version 6)[10] released by February 19 no longer supported clinical diagnostic criteria for COVID-19, the predicted number of unconfirmed cases after February 19 was subtracted from the overall infections for sensitivity analysis.

Based on observed data, the number of daily emerging cases gradually dropped after February 14. Furthermore, a remarkable decline in daily new cases was observed beginning February 19, which aligned with the average expected incubation period of 5–7 d after the implementation of clinical diagnostic criteria. The dates on which daily new case counts fell below 100, fell below 10, and reached 0 in Wuhan were March 6, March 11, and March 18, respectively. These dates were 19, 49, and 74 d earlier than those predicted by Model I (Fig. 2(b)). By March 30, the number of cumulative observed infections was 50 006, which was 19 951 cases fewer than the number of cumulative infections predicted by Model I if the trend before February 14 were to be carried forward (Fig. 2(b)). Notably, the Diagnosis and treatment protocol for novel coronavirus pneumonia (trial version 6) [10] released on February 19 no longer supported clinical diagnostic criteria for COVID-19. For a conservative estimation, the predicted number of unconfirmed cases after February 19 was subtracted from the overall number of infections; nonetheless, the actual situation in Wuhan remained optimistic compared with the predicted trend (Fig. 2(c)).

Transmission parameters after February 14 would be expected to differ, due to the implementation of clinical diagnostic criteria and universal symptom surveys in Wuhan, both of which were paired with the isolation of identified cases in order to control transmission sources and cut off transmission routes. Thus, the contact rate (β) after February 14 was re-estimated by partitioned fitting using MCMC (Model II). Sequential effective reproductive numbers R(t) were estimated by the outputs of Model I and Model II, and by actual frequencies with calibration for the frequencies before February 12 (Fig. 3 ). R(t) demonstrated a steady downward trend since the first round of universal symptom survey during February 6–10, showed a remarkable decline after the implementation of the clinical diagnostic criteria during February 12–14, and closely approached 0 (< 0.1) after March 5. This curve aligned with the actual epidemic data for Wuhan.

Fig. 3.

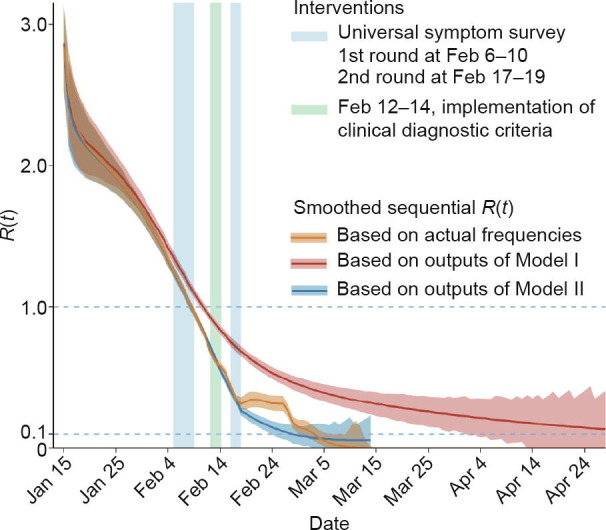
Sequential effective reproductive numbers (R(t)) for Wuhan’s epidemic trend estimated based on dynamics models. R(t) curves were estimated based on Model I using actual data from before February 14 (red curve), Model II by refitting the trend after February 14 (blue curve), and calibrated actual frequencies (orange curve). Three vertical bars denote the three key intervention periods: first-round universal symptom survey, clinical diagnostic criteria, and second-round universal symptom survey.

4. Discussion

Over the course of the COVID-19 epidemic in China, improved clinical understanding of the virus and disease enabled multiple refinements of diagnosis and treatment guidelines. By the time of this publication, seven versions of the Diagnosis and treatment protocol for novel coronavirus pneumonia had been released by the National Health Commission of the People’s Republic of China. In early February, a large number of suspected cases emerged in Wuhan, which was beyond the capacity for nucleic acid testing. Before the implementation of clinical diagnostic criteria, individuals with typical COVID-19 clinical symptoms but without the nucleic acid test, or with negative nucleic acid test results, were unable to be diagnosed and isolated in time to prevent potential transmission. Most suspected cases could be infectious, which increased the pressure on prevention and control efforts.

Implementation of the clinical diagnostic criteria produced a sharp increase in the number of COVID-19 cases reported over February 12–14, which led to a failure of almost all previous dynamic models. At the same time, the hospitalization and isolation of these cumulative suspected cases over a brief period was equivalent to cutting off transmission routes, significantly curbing viral spread in Wuhan. Indeed, 5–7 d later, by February 19, the number of daily new cases and effective reproduction decreased dramatically. A second round of universal symptom survey over February 17–19 further consolidated the effects of the mitigation efforts. Collectively, the implementation of clinical diagnosis and universal symptom surveys in Wuhan in early-to-mid-February reduced the number of infections by nearly 20 000 and advanced over two months of critical time points. It is notable that the actual data after February 19 deviated slightly from the epidemic pattern of infectious diseases as fitted by Model II, suggesting that some unconfirmed cases may exist.

A variety of traditional and extended dynamics models have been proposed using publicly accessible data on COVID-19 to predict outbreak trends [8], [11], [12], [13], [14]. A dynamics model applies theoretical assumptions and fits existing data to earlier epidemic patterns in order to predict the epidemic trend by carrying earlier patterns forward. However, in practice, dynamic introductions of multiple and varying interventions and criteria challenge the validity of dynamic models. These real-world changes affect the assumptions of such models and decrease their accuracy.

An analysis of the epidemic pattern in Wuhan requires consideration of the sharp jump in case counts over February 12–14. Previous reports either fitted the data before the implementation of clinical diagnostic criteria [14], or fitted the data without clinically diagnosed cases [7]. Notably, Song et al. [15] assumed the number of clinically diagnosed cases following exponential distribution and calibrated the frequencies before February 12 for future modeling. In contrast, our method considered clinically diagnosed infections as a compartment in the dynamics model. The curves for confirmed and unconfirmed infections were simultaneously fitted in order to obtain the trend for overall infections. As a result, the sharp increase in cases in Wuhan was well explained by the proposed model. In addition, our model estimated an average proportion of 40% unconfirmed cases, which was lower than the 59% unascertained infections estimated by Pan et al. [7].

We acknowledge some limitations in this study. First, unconfirmed infections as identified by clinical diagnosis were considered infectious in the SEIR^+Q dynamics model. However, some of these cases, due to the existence of clinical symptoms, were probably hospitalized and isolated prior to diagnosis and thus had limited infectious ability. Second, asymptomatic infections and clinical classifications of the infections were not considered in this study. Third, a better estimation for the COVID-19 epidemic trend should rely on the data of the onset information of the infections, which was not publicly accessible. Fourth, potential confounders, such as further improvement of the reporting system and nucleic acid testing facility and capacity, were non-negligible during the causal inference based on observational data. In general, a set of measures, such as improvements of the reporting system and nucleic acid testing facility and capacity, aimed to increase the efficiency and sensitivity of identifying cases; these measures, if further improved after February 14, should have contributed to an increase in the number of daily new cases after February 14, which was not in line with the facts. On the other hand, such confounding effects may have resulted in an underestimate of the effect. In addition, the effect of the interventions was the product of mitigation strategies, and is thus difficult to decompose precisely.

5. Conclusion

The proposed SEIR^+Q dynamics model fitted the Wuhan epidemic data well under a situation with an observed large short-term increase in the number of detected infections. Differences between the modeled outcomes and the actual data underscore that the implementation of clinical diagnostic criteria and universal symptom surveys contributed to a lower-than-anticipated magnitude and duration of the epidemic in Wuhan. With the continued rapid spread of SARS-CoV-2 globally, and for potential future infectious disease modeling, the reported findings may inform the international community on infectious disease prevention and control.