Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2021 May 5.
Published in final edited form as: Structure. 2020 Mar 31;28(5):548–554.e3. doi: 10.1016/j.str.2020.03.002

Markov State Model of Lassa Virus Nucleoprotein Reveals Large Structural Changes During the Trimer to Monomer Transition

Jason G Pattis 1,†, Eric R May 1,2,*
PMCID: PMC7205590  NIHMSID: NIHMS1576785  PMID: 32234493

Summary

Lassa virus contains a nucleoprotein (NP) that encapsulates the viral genomic RNA forming the ribonucleoprotein (RNP). The NP forms trimers which do not bind RNA, but a structure of only the NP N-terminal domain was co-crystalized with RNA bound. These structures suggested a model in which the NP forms a trimer to keep the RNA gate closed, but then is triggered to undergo a change to a form competent for RNA binding. Here we investigate the scenario in which the trimer is disrupted to observe if monomeric NP undergoes significant conformational changes. From multi-microsecond molecular dynamics simulations and an adaptive sampling scheme to sample the conformational space, a Markov State Model (MSM) is constructed. The MSM reveals an energetically favorable conformational change, with the most significant changes occurring at the domain interface. These results support a model in which significant structural reorganization of the NP is required for RNP formation.

eTOC Blurb

The Lassa virus nucleoprotein binds viral RNA, however experimental studies have not resolved this structure due to the nucleoprotein propensity to form trimers, which prevent RNA binding. Pattis and May have used advanced molecular simulation techniques to reveal large conformational changes in the nucleoprotein which may allow for RNA binding.

graphic file with name nihms-1576785-f0009.jpg

Introduction

Lassa virus is the causative agent of Lassa fever, a sever hemorrhagic fever which is estimated to infect between 100,000 and 300,000 people per year, primarily in western Africa, and leads to 5000 deaths per year(Falzarano and Feldmann, 2013; Haas et al., 2003). Transmission of Lassa virus to humans occurs through contact with Lassa infected rodent’s urine and feces. Both the NIH and the WHO have classified Lassa as a category A priority pathogen due to its high risk to public health. Lassa is also a threat to other parts of the world as it is the most frequent hemorrhagic fever to spread to Europe and the United States(Haas et al., 2003; Holmes et al., 1990; Macher and Wolfe, 2006).There have been an increasing number of large outbreaks in the last few years(Dan-Nwafor et al., 2019; Ilori et al., 2019).

Lassa currently has only one vaccine that recently entered stage I clinical trials but no vaccines that have progressed further than stage I(Purushotham et al., 2019). The other treatment options are limited to only preventative care, with Ribavirin being helpful if administered early after infection(Purushotham et al., 2019). There is a significant need for increased understanding of the Lassa protein structures and interactions to aid in the development of new therapeutics.

Lassa is an enveloped virus that has two strands of single stranded RNA. It has four genes and uses an ambisense coding strategy where the polymerase and nucleoprotein (NP) are transcribed first, then the Z protein and glycoprotein precursor protein are transcribed later in the life cycle after RNA replication(Yun and Walker, 2012). The single stranded RNA genome is encapsulated by the NP, forming the ribonucleoprotein (RNP) to protect the RNA from detection by the immune system. The RNP also acts as a scaffold for the polymerase. The RNA genome segments have reverse complementary tails, which stick together and form the promoter for the polymerase and cause the RNA to make a hairpin(Kranzusch et al., 2010). While the 3D structure of the Lassa RNP is not known, cryo-EM structures of similar negative strand RNA viruses show the RNP as a twisted helical structure(Moeller et al., 2012; Wang et al., 2012).

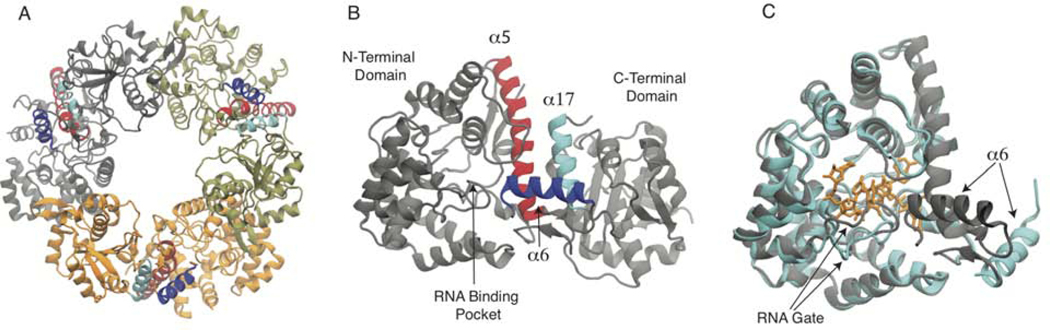
The NP contains 569 residues comprising two domains which are connected by an unstructured linker segment. The N-terminal domain is involved in RNA binding(Hastie et al., 2011a) while the C-terminal domain contains an exonuclease to digest double stranded RNA(Hastie et al., 2011b). The first crystal structure of Lassa NP was solved with three subunits in the asymmetric unit, which each form symmetric trimers through the crystallographic symmetric (P3). The NP trimer does not have an exposed RNA binding site, Figure 1A–B(Qi et al., 2010). A subsequent study was able to co-crystalize the N-terminal domain with a short strand of RNA bound to the NP, Figure 1C(Hastie et al., 2011a). In the RNA-bound structure some large conformational differences from the apo trimer structure were observed, mainly the shifting out of helix 6, the loss of helicity of helix 5 and the shifting down of a loop to the left of helix 6. Hydrogen deuterium exchange was also performed on the full length NP as well as a double mutant near the NP-NP interface, far from the RNA binding site, which elutes as a dimer. This double mutant showed much higher solvent exposure of helix 5, 6, and the RNA gate suggesting that disruption of the trimer may allow easier opening of the RNA binding pocket. Expression and purification of wild-type Lassa NP from several different cell lines, consistently shows the NP forms trimers, which are not associated with RNA.(Brunotte et al., 2011; Hastie et al., 2011a; Lennartz et al., 2013; Qi et al., 2010)

Figure 1. Lassa NP structure.

Figure 1.

Open in a new tab

A) Trimer structure from PBDID: 3MWP, each subunit is colored differently. B) Monomer structure, also from PDBID: 3MWP. In both A-B panels helices 5, 6, and 17 are colored red, blue and cyan, respectively. C) Comparison between the N-terminal domain of a monomer from the trimer/apo structure (grey), with an RNA bound conformation (cyan, RNA is orange) from PDBID: 3T5Q chain k.

The model put forward by Hastie and coworkers(Hastie et al., 2011a) was that NP trimerizes during viral transcription to prevent off-target RNA binding and to build up a large store of NP. Then during RNA-replication some signal will break up the NP trimer, causing the C-terminal domain to shift away from the N-terminal domain and expose the RNA binding pocket. It was proposed that in the shifted conformation the NP can bind RNA allowing for organization of NPs onto the newly formed viral genomic RNA and formation of the RNP. There is still much unknown about the molecular mechanisms of Lassa infection and more work is needed to understand them. Furthermore, these protein conformational changes may expose novel targets for drug discovery which block the proteins function.

The dynamics of the N-terminal domain have been studied previously(Pattis and May, 2016). It was found that the slow global motions primarily involve helix 6 motions. Apo NP was found to have a large barrier for helix 6 opening whereas RNA bound NP was found to have a fairly small barrier for opening. This along with correlated motions in intermediate states suggested a mechanism where the RNA binding pocket starts to open allowing RNA to form some contacts with the NP, which stimulate further conformational changes in NP to facilitate RNA becoming fully bound. It was also found that helix 6’s position in the open state is influenced by crystal contacts and when NP is free in solution the helix 6 position may be closer to the RNA binding pocket. This observation was also noted in another simulation study of Lassa NP(Omotuyi et al., 2019).

In the current work we extend the study on the dynamics of Lassa NP from just the N-terminal domain to the full-length NP. The Hastie model and the hydrogen deuterium exchange suggest that that disruption of the trimer would allow shifting away of the C-terminal domain and easier opening of the RNA binding pocket. In the present study, one monomer from the trimeric APO crystal structure is solvated and simulated on the multi-microsecond timescale. A large conformational change is witnessed which is resampled using a two stage adaptive sampling scheme allowing the construction of a Markov state model (MSM) describing this transition. The results we find are that NP undergoes an energetically favorable transition which involves reorganization of the domain interface, as well as displacement of helix 10. The significance of the helix 10 displacement is that it may allow for increased access to the RNA binding groove, while the domain level reorganization is supportive of the Hastie model. Further valuable insights from this study include the identification of metastable intermediates along the transition pathway, which could be targeted by small molecules to interrupt the viral life cycle.

Results and Discussion

Long timescale equilibrium simulations reveal domain level reorganization

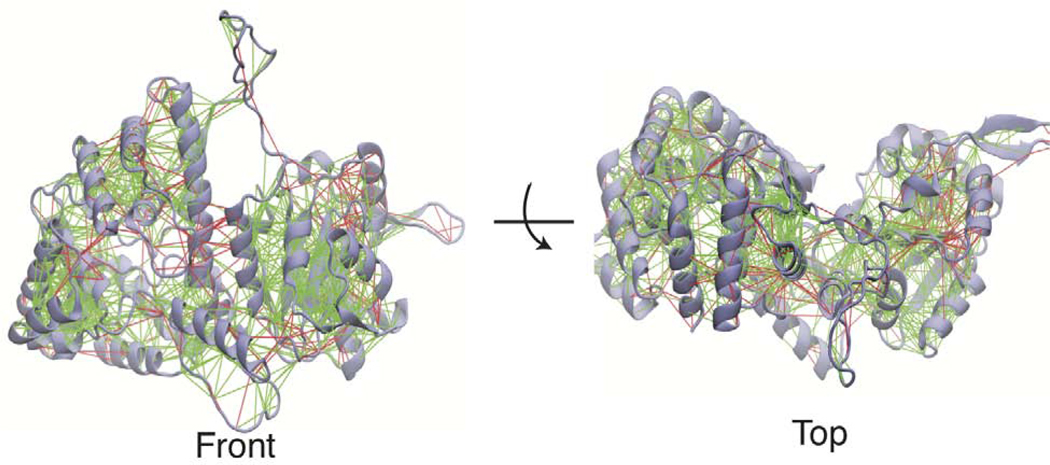
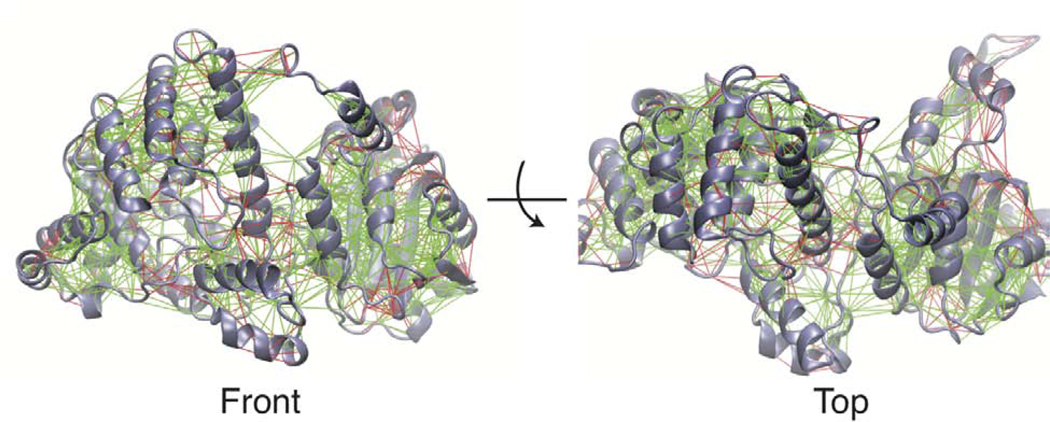
The Lassa NP is presumed to go through a large conformational change to switch from a trimeric structure where NP is being stored to the RNP structure, where the NP encapsulates the single stranded genomic RNA(Hastie et al., 2011a). Understanding this transition is important to gain insights into how the molecular machinery in Lassa virus acts to carry out its function and regulate its lifecycle. This large conformational change may also reveal pockets that can be targeted in drug discovery to identify novel inhibitors. The Hastie model of RNP formation suggests that disruption of the trimer would allow the C-terminal domain to swing away from the N-terminal domain and increase opening of helix 6 and helix 5. This is supported by hydrogen/deuterium exchange data, which indicated increased solvent exposure in helix 5, 6, and 17 (see Figure 1) in a double mutant which disrupts trimer contacts. Based upon structural analysis we have identified high energy (frustrated) interactions across the interface of the N and C-terminal domains. This analysis is performed on a monomer from the trimer crystal structure with the missing loops modeled in and the structure is run through the Frustratometer2 web server(Parra et al., 2016). This serve calculates the mutational frustration by comparing the energy of a native residue pair interaction with the average of many different mutations of that pair. Figure 2 shows that there are many highly frustrated residue pairs between helix 5 and helix 17. There are also highly frustrated residues between helix 6 and its surrounding loops and the C-terminal domain. This may suggest that the formation of the trimer is placing pressure on the domain interface and that without the trimer contacts these domains may reorganize to reduce frustration and adopt a more favorable configuration.

Figure 2. Frustration of Lassa NP in the trimeric state.

Figure 2.

Open in a new tab

Mutational frustration of Lassa NP monomer in the trimeric state (PDBID 3MWP.B), shown from front and top views. Green lines represent residue pairs which are minimally frustrated and red lines represent highly frustrated residue pairs.

Previous simulations have shown that in an isolated N-terminal domain there is a large energy barrier for helix 6 to open(Pattis and May, 2016). Another possibility is that the C-terminal domain shifting away could be coupled with a conformational change in helix 6 and the RNA binding pocket. To investigate this further one monomer from the trimeric structure was isolated, solvated and run on specialized hardware to generate long-time scale (multi-microsecond) simulations to observe if trimer disruption leads to structural relaxation to an alternate NP conformation.

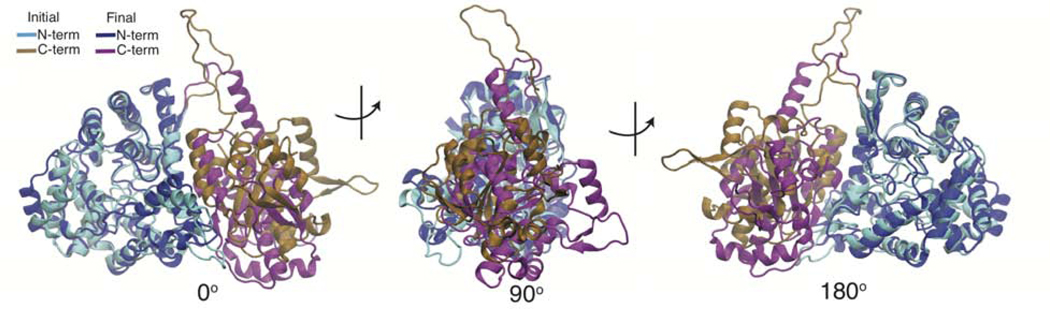
A 4 μs and an 825 ns simulation were run on the Anton supercomputer. In the 4 μ s simulation a large conformational change was observed (Figure 3). Here the C-terminal domain shifted to the back of the N-terminal domain, helix 6 shifted in, and helix 9 and 10 shifted out. Because this large conformational change only occurred once in the 4 μ s trajectory more sampling was needed to provide statistical significance of the thermodynamics and the kinetics of this transition. We used the tools of adaptive sampling and Markov State Modeling to improve the sampling of this transition and for analysis. Additional trajectories were spawned from the beginning, end, and a few midpoints from each of the Anton trajectories. Next a counts based adaptive sampling protocol was run for 12 rounds. Here new simulations are spawned from areas with poor sampling. This has been shown to be an efficient method to discover new states(Weber and Pande, 2011). Next population uncertainty adaptive sampling was performed. Here the uncertainty is calculated using a Bayesian MSM then new simulations are spawned from clusters that have a high standard deviation of possible stationary distributions. This second phase of adaptive sampling was run for 16 rounds, followed by construction of our final MSM. The enhancement in sampling is demonstrated by comparing the transitions counts matrix prior (Anton only) and after adaptive sampling in Figure S1.

Figure 3. Conformational Change of Lassa NP during 4 μs simulation.

Figure 3.

Open in a new tab

Overlay of initial and final structures of the 4 μs Anton simulation. The initial structure is consistent with the trimeric crystal structure (PDBID 3MWP.B) and is colored in cyan (N-term) and brown (C-term). The final structure is colored in blue (N-term) and purple (C-term). Structures are shown from front (0°), side (90°) and back (180°) views. Structures were aligned along the α5 helix.

Model Selection and Validation

An initial guess of parameters suggested an MSM lag time of 3.84 ns would generate a Markovian kinetic model. We next used the generalized matrix Rayleigh quotient (GMRQ) score to select the number of clusters, TICA lag time, and number of TICA components. K-means clustering was used for all models and commute map was used for TICA. The highest validation GMRQ score was from a TICA lag time of 18 ns, 3 TICA components, and 75 clusters (Figure S2). These parameters were used for the final model which we analyze and present here. The implied timescales of the MSM processes are related to the transition probability matrix eigenvalues by eq. 1

ti=−τlnλi (1)

where, τ is the MSM lag time, λi are the eigenvalues and ti are the implied timescales. An implied timescales test was run (Figure 4) by scanning lag time values. We identified the implied timescales were relatively insensitive to the lag time chosen (beyond ~ 2 ns), which indicated the model is Markovian. We selected a lag time of 3.84 ns, which was in the range of lag times where the implied timescales were not rapidly changing and produced the largest timescale for the slowest process. A Chapman–Kolmogorov test was run with a Bayesian MSM with 1000 transition matrices to construct a 95% confidence interval. Five macrostates were determined, and this number of macrostates was chosen due to the presence of four slow timescale processes. The Chapman–Kolmogorov test shows excellent agreement between the estimated and the predicted transition probabilities (Figure S3).

Figure 4. MSM Validation.

Figure 4.

Open in a new tab

Implied timescale plot of top 7 processes. Final MSM lag time is shown in red.

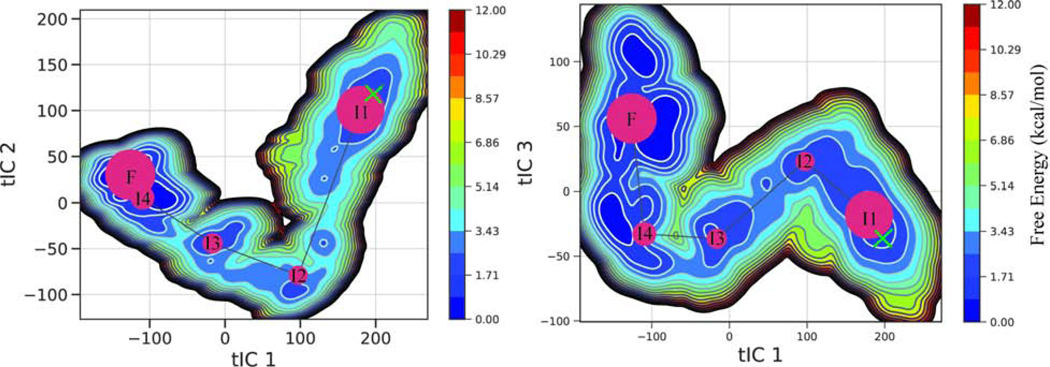
MSM Reveals Multiple Intermediate States

The model has five kinetic macro states which are shown on top of the free energy surface (Figure 5). The starting structure is shown with a green x. NP moves from its starting structure linearly through the different locally stable intermediates finally reaching the most favorable state(F). Representative structures are shown in (Figure 6). The mean first passage time from the starting state to the most favorable state was 20.47 μs, whereas the mean first passage time from the most favorable state back to the starting structure was 279.94 μs.

Figure 5. Free Energy Surface from MSM.

Figure 5.

Open in a new tab

Free energy surface of the final MSM. Kinetic macrostates (red circles) shown on top with the size proportional to their population. A green × marks the starting structure.

Figure 6. Stable and Metastable Conformational along NP Transition Pathway.

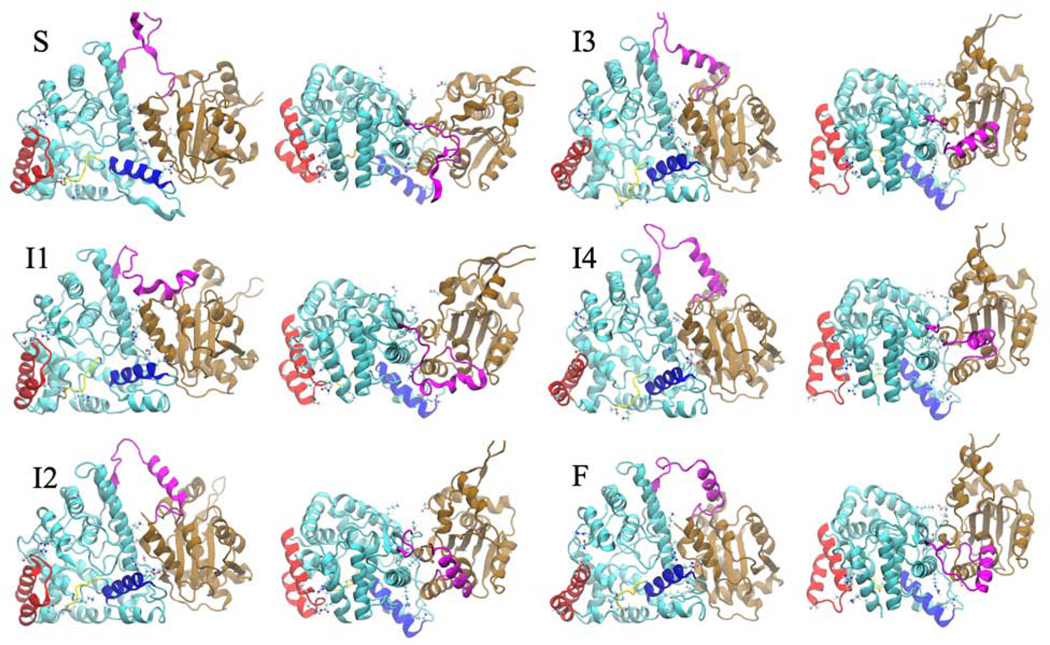
Figure 6.

Open in a new tab

Starting structure (S) and structures from the five macrostates (I1-I4 and F) l from the front view (left) and from top view (right). Structures progress in order from negative IC 1 to positive IC 1. The N-terminal domain is shown in cyan, the linker region in magenta, and the C-terminal domain in brown. Helix 6 is shown in blue, helix 9 and 10 are shown in red, and the gating loop is shown in yellow.

The transition from the starting state to the first intermediate (I1) involves separation being created between contacts in the N-terminal and C-terminal domain primarily between helix 5 and helix 17. A salt bridge between ARG115 and ASP375 is broken, as well as contacts between ASP557 with LYS110 and TRP331 during this stage of the transition. The gating loop shifts up and the loop between helix 6 and helix 7 shifts away from the C-terminal domain. Contact is also broken between THR34 and THR216 connecting the RNA gating loop (yellow) and helix 9 (red) (Figure 6). Transition between intermediate state 1 and intermediate state 2 involves the bottom of the C-terminal domain moving away from the bottom of the N-terminal domain while the top of the C-terminal domain maintains contact with the N-terminal domain

From intermediate state 2 to intermediate state 3 helix 10 (red) shifts out, the left side of the RNA gating loop moves down while the right side moves up. In addition, helix 6 moves in closer to the RNA binding groove. Also, the C-terminal domain shift back and a salt bridge is formed between ASP504 and LYS65 and contacts between ASN 168 and LEU 505 are formed which connects the bottom of the C-terminal domain to the back of the N-terminal domain. From intermediate state 3 to intermediate state 4 separation is created between THR210 of helix 10 and GLN14, while the domains start to compact together more. From intermediate state 4 to the most favorable state (F) the domains compact even more. This structure is very stable according to the MSM and also has much fewer frustrated contacts according to the Frustratometer (Figure 7).

Figure 7. Frustration of Lassa NP in the Relaxed Monomeric State.

Figure 7.

Open in a new tab

Mutational frustration of the most favorable microstate (F), shown from front and top views. Green lines represent residue pairs which are minimally frustrated and red lines represent highly frustrated residue pairs.

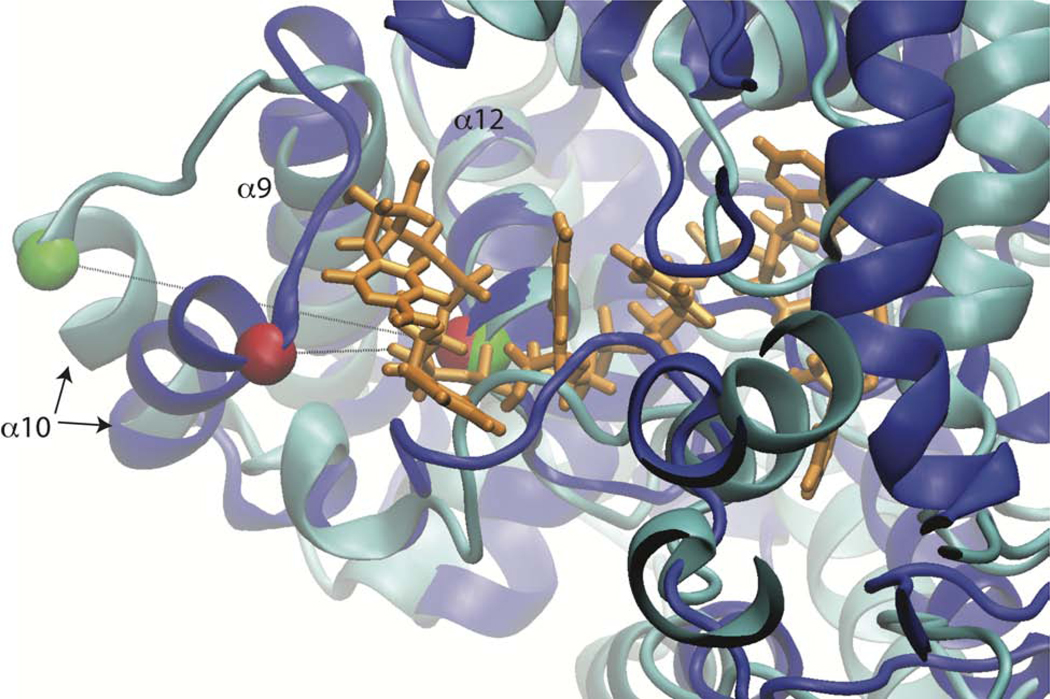
Several of the residues we have identified as having shifting contacts during the transition have been implicated to be functionally important for transcription. This was measured through a mini-genome assay, and mutations to ARG115, LYS110 and TRP331 all had significant effects on the transcriptional activity compared to wild-type(Hastie et al., 2011a). In addition, the structural transition we observe has some consistency with hydrogen-deuterium exchange mass spectrometry data. In a structure where the trimer has been disrupted through protein-protein interface mutations, increased exchange (compared to wt trimer) was observed in helices 5, 10 and 17, which are regions where we also observe structural changes(Hastie et al., 2011a). Lastly, we want to emphasize that the structural reorganization of helix 10 on the left side of the NP may facilitate RNA binding (Fig 5, red motif). Helix 10 can be considered a cap on the left side of the RNA binding groove and in our most favorable state helix 10 is swung away from the binding channel provide a potential access point for RNA to enter. The orientation of helix 10 in the most favorable and initial structure are compared with the RNA inserted from the N-terminal RNA bound structure (PDB ID:3T5Q), in Figure 8. The distance between the top of helix 10 (THR216) and the start of helix 12 (Leu 248) is changed by almost 10 Å, from 9.6 Å in the starting state (Figure 8 blue) to 19.2 Å the most favorable state (Figure 8 cyan).

Figure 8. Helix 10 Reorientation Allows Greater Accessibility to RNA Binding Groove.

Figure 8.

Open in a new tab

The position of helix 10 is compared in the initial (blue) and most favorable (cyan) conformations. RNA (orange) is copied in from PDB ID: 3T5Q.k. Structures are aligned on helix 12 in back of binding groove (residues 245–259). Ca of residues 216 and 248 are shown as green and red vdW spheres for the most favorable and initial conformations, respectively.

Conclusions

Our simulation study supports a model in which, when the Lassa NP trimeric structure is disrupted, the C-terminal domain moves away from the N-terminal domain, swings back, then compresses in making new contacts in the back of the N-terminal domain. This observation is consistent with the qualitive model put forth from Hastie et al, when they determined the RNA bound conformation of the Lassa NP N-terminal domain. The domain scale movements we observe are coupled with shifting in of helix 6, movement of the RNA gating loop, and shifting out of helix 9 and 10. This shows that loss of trimer contacts can cause global conformational changes in the RNA binding pocket. The shifting out of helix 9 and 10 exposes some of the RNA binding pocket. This may provide a surface or a gateway for RNA to make initial contact. Our observations and conclusions we have drawn are made under the assumption that the NP trimer becomes disrupted, we do not make any claims about how this disruption occurs. It would be ideal to understand how trimer disruption occurs and how disruption couples to the NP conformational change. However, undertaking simulations of the full trimer is computationally challenging and reaching the timescales we have achieved for the monomer would take an exorbitant time to complete. We do believe the conformational change we have observed would require trimer disruption as our most favorable conformation (F) would sterically clash with neighboring subunits in the trimer, as shown in Figure S4.

The model we observe has consistency with experimental data in that increased hydrogen exchange observed in helix 10 and helix 17 could be accounted for by the structural changes we observe. There are other experimental observations including the opening of helix 6 and the loss of helicity of helix 5 that are observed in the RNA bound structure that was not observed in our MSM. However, there are variety of factors which could explain these differences including i) the double mutant NP in which the trimer is disrupted was still oligomeric (dimers and tetramers) ii) the presence of RNA could induce those changes, where RNA was not present in these simulations. Indeed the double mutant NP had more RNA as measured by spectrophotometrically (A260/A280 ratio of 1.3 in double mutant vs. 0.95 for the wildtype)(Hastie et al., 2011a), iii) or, despite our extensive sampling (> 25 μs), we were unable to exhaustively explore all relevant conformations of Lassa NP. The H/D exchange experiments were quenched at 10 s and 1000 s,(Hastie et al., 2011a) and these timescales are not accessible with current computational resources.

The meta-stable and stable conformations we observe may be helpful in structural studies on determination of the Lassa RNP and also provide potential drug targets for anti-viral therapies. An approach could target trapping one of the intermediates with a small molecule which may cause non-native oligomers to form that would be detrimental to the virus. Other negative strand viruses have shown that conformational changes in mobile elements such as flexible helices or loops can play a role controlling the oligomeric states(Ruigrok et al., 2011), and we observe helix 6 may play this role for Lassa as new contacts within the C-terminal domain or a shift in position may allow contact with a neighboring NP and facilitate formation of the RNP.

STAR Methods

Lead Contact and Materials Availability

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Eric May (eric.may@uconn.edu). This study did not generate new unique reagents.

Methods Details

Simulation details

Anton simulations were prepared starting from chain B of the full length trimeric nucleoprotein (PDB ID: 3MWP)(Qi et al., 2010) which included one zinc atom. Missing loops were modeled in using MODELLER(Fiser et al., 2000; Sali and Blundell, 1993). The protein was solvated in a rectangular box with a 10 Å buffer on all sides and NaCl was added to a concentration of 150 mM. This system totaled approximately 137,000 atoms. Energy minimization and equilibration were run using NAMD v2.9(Phillips et al., 2005). 5000 steps of energy minimization were run followed by 5 ns of NPT equilibration with 1 kcal/mol restraints on all protein backbone atoms. This was followed by 5 ns of equilibration with 0.25 kcal/mol restraints on backbone atoms, and then 10 ns of unrestrained MD. The CHARMM27(Foloppe and MacKerell Jr, 2000; MacKerell Jr et al., 2004) force field including CMAP corrections and CHARMM TIP3P water model were used. 12 Å cutoffs were used with a switching function on van der Waals interactions starting 8 Å. Full electrostatic interactions were computed using the PME method.

Anton simulations were run in the NPT (isothermal, isobaric) ensemble, a Nose-Hoover thermostat at 300 K, and a Martyna-Tobias-Klein (MTK) barostat with isotropic scaling at 1 atmosphere. The simulations used the CHARMM27 force field with CMAP correction and the CHARMM TIP3P water. Frames were saved every 240 ps. The multigrator(Lippert et al., 2013) was used for the integrator, which calculated bonded and near non-bonded forces every 2 fs and far non-bonded forces, which are the long-range electrostatics in the Ewald decomposition, every 6 fs. Gaussian Split Ewald(Shan et al., 2005) was used for the far non-bonded term.

GROMACS simulations were run starting from the NAMD equilibrated starting structure or from solvated frames pulled out of the Anton simulation. They were run using GROMACS 5.0.1 with the CHARMM27 force field(Bjelkmar et al., 2010; Foloppe and MacKerell Jr, 2000; MacKerell Jr et al., 2004) with CMAP corrections and the CHARMM TIP3P water. These simulations were run using a leap-frog stochastic dynamics integrator using a timestep of 2 fs. Frames were saved every 240 ps. Short ranged non-bonded interactions were calculated with a cutoff of 12 Å and where smoothly shifted to zero at the cutoff. For the Lennard-Jones potential the shifting began at 10 Å, and the Coulomb potential was shifted over the whole range (starting from 0 Å). PME was used for long-range electrostatics. The temperature was maintained at 300 K using the v-rescale algorithm(Bussi et al., 2007) and pressure was maintained at 1 Atm using the Parrinello-Rahman isotropic pressure coupling.

Adaptive Sampling and Markov State Model Construction

MSMBuilder 2.8(Beauchamp et al., 2011) was used for all steps in constructing the Markov state model (MSM) except for the Bayesian MSM and the Chapman-Kolmogorov test, which were done in pyEmma 2.4(Scherer et al., 2015). A flow chart of the steps used for adaptive sampling and Markov State Model Construction is shown in Figure S5. To describe the conformational space the raw Cartesian coordinates were transformed into internal coordinates (featurized). We sought to identify pairwise residue contacts which changed during the Anton simulation. The specific set of coordinates we choose were the pairwise alpha carbon distances that were less that 13 Å apart for at least 2 % of the simulation and had a standard deviation of at least 1.5 Å during the 4 μs Anton simulation. The linker loop between domains was excluded from consideration in identifying the feature set. Our criteria led to 3290 pairwise distances. A visualization of these distances can be seen in Figure S6.

Time-lagged Independent component analysis (TICA) was used to transform the data into kinetic coordinates(Pérez-Hernández and Noé, 2016; Schwantes and Pande, 2013). In TICA a covariance matrix and a time-lagged covariance matrix of features (filtered C alpha distances) are put through a generalized eigenvalue problem. A set of linear combinations of input features (TICA components) and corresponding eigenvalues are returned.

In an MSM the number of transitions between discrete states are counted in some time interval (lagtime) τ from all trajectories to form a count matrix. From this a transition matrix is constructed which describes the conditional probability of transitioning from state i to state j at lagtime τ. MSMs were estimated using a maximum likelihood approach and a sliding window(Prinz et al., 2011). All MSMs are reversible and obey detailed balance(Prinz et al., 2011).

In order to improve sampling in undersampled regions of the NP transition phase space a counts-based adaptive sampling protocol was performed. In this approach, the data is featurized and TICA is performed with a lag time of 7.2 ns being fit to the Anton trajectory and using the kinetic map algorithm(Noé and Clementi, 2015) to scale the eigenvectors. K-centers clustering(Gonzalez, 1985) is performed on the top 5 independent components, which capture approximately 40% of the total kinetic variance. An MSM is then generated with a lag time of 3.84 ns. The sum of each row of the count matrix is used to see how well each state is sampled. The ten states with the lowest counts are then subjected to two independent 30 ns simulations with different starting velocities. The initial structure for these simulations is determined by identifying the frame with the smallest nearest neighbor distance in 5 dimensional TICA space to the average TICA values for that cluster. This protocol was repeated for 12 rounds, generating 7.2 μs of additional simulation data. An example visualization of the states selected for countsbased adaptive sampling can be seen in Figure S7.

In order to reduce the uncertainty in the MSM a second stage of adaptive sampling was performed. In this stage the data is featurized and TICA is performed with a lag time of 3.42 ns using the commute map algorithm(Noé et al., 2016). Again K-centers clustering is performed on the top 5 independent components to separate the space into 100 evenly spaced clusters. Next a Bayesian MSM using a sparse prior(Trendelkamp-Schroer et al., 2015) is constructed with 100,000 possible transition matrices that could have created the raw data. The standard deviation in the population is calculated for each state. The top five max flux pathways from the starting state to the highest population cluster are calculated from the net flux matrix(Metzner et al., 2009). The ten states that are part of one of the top five maximum flux pathways and have the highest standard deviation in their population are subjected to two independent 30 ns simulations with different starting velocities. This stage of adaptive sampling was repeated for 16 rounds, generating 9.6 μs of additional simulation data. A sample visualization of the states selected for uncertainty-based adaptive sampling can be seen in Figure S8.

The TICA lag time, number of TICA components, and number of clusters were chosen based on the generalized matrix Rayleigh quotient (GMRQ)(McGibbon and Pande, 2015). It was found that the variational theorem(Noé and Nüske, 2013; Nüske et al., 2014) bounds the GMRQ from above as the sum of the first m eigenvalues. when avoiding over fitting through cross-validation. This allows the GMRQ to be used as a score of how different parameter choices affect how well the MSM captures the slow subspace of the system’s propagator. Here trajectories over 80 ns were split into 40 ns chunks giving 860 trajectories. To avoid overfitting, cross-validation is performed by training a model on a portion of the data (“test set”) and evaluating the GRMQ score on the remaining data (“validation set”). To do this 30 iterations of shuffle split was performed where 50% of trajectories were placed in the training set and 50% of trajectories were placed in the validation set using Scikit-learn version 0.18.2. The ergodic cutoff was turned off and a prior count of 0.00000001 was placed in each cluster to ensure the calculation was done on the entire state space. The top three dynamical eigenvalues were examined making the max possible GMRQ score 4, since each eigenvalue has a maximum value of 1.

The model was validated using the implied timescale test and the Chapman Kolmogorov test. The implied timescales of a model are ti = − τ/ln|λi| where λi is the i-th eigenvalue of the MSM. In the implied timescale test the top 7 implied timescales are plotted for MSMs of increasing lagtimes (Figure 4). At a Markovian (memory-less) lag time, increasing the lag time should give the same implied timescales because the models are capturing the same processes. The Chapman Kolmogorov test compares the transition probabilities between the left and right side of equation (2).

P(kτ)=Pk(τ) eq. (2)

Here the right side of the equation is the original transition matrix at lag time τ propagated to the k-th power (prediction) and left side is a new transition matrix made at lag time kτ (estimation). For a full discussion see Prinz et. al.(Prinz et al., 2011). This test is performed using PCCA+(Deuflhard and Weber, 2005; Kube and Weber, 2007) to lump the 75 state MSM into 5 macrostates due to the MSM having 4 slow timescale processes ( > 200 ns) and a large gap in eigenvalues between the 4th and 5th slowest timescale process.

The free energy surface was constructed using the plot_free_energy tool from MSMExplorer version 1.2.0dev0(Hernández et al., 2017). The free energy surface is constructed by subsampling 1,500,000 frames, where microstates are selected with a probability proportional to the state population and a random frame is chosen from the selected state. The density of frames is calculated by a bivariate kernel density estimate (KDE) using Scott’s rule for bandwidth selection. KDE is a probability density estimation method which results in data smoothing and has been shown to provide better estimates of free energy surfaces than histogram-based methods when sampling is limited(Lee et al., 2013). This probability is converted to a free energy using F = -kBT* ln(P).The mean first passage time was calculated using transition path theory(Metzner et al., 2009). Clusters were lumped into macrostates using PCCA+(Deuflhard and Weber, 2005; Kube and Weber, 2007).

QUANTIFICATION AND STATISTICAL ANALYSIS

Uncertainty in the stationary population of microstates in the MSM was used as metric to adaptively sample and reduce uncertainty in the final MSM. The PyEMMA software was used to construct a Bayesian MSM based upon 100,000 transition matrices (n=100,000). The uncertainty in the microstates was based upon the standard deviations in the stationary populations. States which have the highest uncertainty and also are along the top 5 maximum flux pathways to the most populated state are selected for additional simulations in each adaptive sampling round.

DATA AND CODE AVAILABILTY

The datasets supporting the current study have not been deposited in a public repository because of the large size of the datasets and lack of standardized repository for hosting these datasets, but are available from the corresponding author on request.

Supplementary Material

1
2

Highlights.

  • Energetically favorable conformational change of Lassa NP is observed in simulations

  • New conformation has greater accessibility to RNA binding groove

  • Findings support model that requires domain level reorganization for RNP formation

  • Anton2 simulations and adaptive sampling procedure are combined to build MSM

Acknowledgments

The authors would like to thank Michael D. Ward for helpful advice and discussions. The authors would also like to thank Maxwell I. Zimmerman for the suggestion of adaptive sampling only along the maximum flux pathway. Funding for this project has been provided by the NIH to E.R.M. (R35-GM119762). Anton computer time was provided by the Pittsburgh Supercomputing Center (PSC) through Grant R01GM116961 from the National Institutes of Health. The Anton machine at PSC was generously made available by D.E. Shaw Research. Additional computational resources have been provided through the University of Connecticut Storrs HPC center.

Footnotes

Declaration of Interests

The authors declare no competing interests.

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Beauchamp KA, Bowman GR, Lane TJ, Maibaum L, Haque IS, and Pande VS (2011). MSMBuilder2: Modeling Conformational Dynamics on the Picosecond to Millisecond Scale. J. Chem. Theory Comput 7, 3412–3419. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bjelkmar P, Larsson P, Cuendet MA, Hess B, and Lindahl E. (2010). Implementation of the CHARMM Force Field in GROMACS: Analysis of Protein Stability Effects from Correction Maps, Virtual Interaction Sites, and Water Models. J. Chem. Theory Comput 6, 459–466. [DOI] [PubMed] [Google Scholar]
  3. Brunotte L, Kerber R, Shang W, Hauer F, Hass M, Gabriel M, Lelke M, Busch C, Stark H, Svergun DI, et al. (2011). Structure of the Lassa Virus Nucleoprotein Revealed by X-ray Crystallography, Small-angle X-ray Scattering, and Electron Microscopy. Journal of Biological Chemistry 286, 38748–38756. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bussi G, Donadio D, and Parrinello M. (2007). Canonical sampling through velocity rescaling. J. Chem. Phys 126, 014101. [DOI] [PubMed] [Google Scholar]
  5. Dan-Nwafor CC, Furuse Y, Ilori EA, Ipadeola O, Akabike KO, Ahumibe A, Ukponu W, Bakare L, Okwor TJ, Joseph G, et al. (2019). Measures to control protracted large Lassa fever outbreak in Nigeria, 1 January to 28 April 2019. Eurosurveillance 24, 1–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Deuflhard P, and Weber M. (2005). Robust Perron cluster analysis in conformation dynamics. Linear Algebra and Its Applications 398, 161–184. [Google Scholar]
  7. Falzarano D, and Feldmann H. (2013). Vaccines for viral hemorrhagic fevers — progress and shortcomings. Current Opinion in Virology 3, 343–351. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Fiser A, Do RKG, and Šali A. (2000). Modeling of loops in protein structures. Protein Science 9, 1753–1773. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Foloppe N, and MacKerell AD Jr (2000). All-atom empirical force field for nucleic acids: I. Parameter optimization based on small molecule and condensed phase macromolecular target data. J Comput Chem 21, 86–104. [Google Scholar]
  10. Gonzalez TF (1985). Clustering to minimize the maximum intercluster distance. Theoretical Computer Science 38, 293–306. [Google Scholar]
  11. Haas WH, Breuer T, Pfaff G, Schmitz H, Kohler P, Asper M, Emmerich P, Drosten C, Golnitz U, Fleischer K, et al. (2003). Imported Lassa fever in Germany: surveillance and management of contact persons. Clin. Infect. Dis 36, 1254–1258. [DOI] [PubMed] [Google Scholar]
  12. Hastie KM, Liu T, Li S, King LB, Ngo N, Zandonatti MA, Woods VL, de la Torre JC, and Saphire EO (2011a). Crystal structure of the Lassa virus nucleoprotein-RNA complex reveals a gating mechanism for RNA binding. P Natl Acad Sci Usa 108, 19365–19370. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Hastie KM, Kimberlin CR, Zandonatti MA, MacRae IJ, and Saphire EO (2011b). Structure of the Lassa virus nucleoprotein reveals a dsRNA-specific 3’ to 5’ exonuclease activity essential for immune suppression. P Natl Acad Sci Usa 108, 2396–2401. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Hernández CX, Harrigan MP, Sultan MM, and Pande VS (2017). MSMExplorer: Data Visualizations for Biomolecular Dynamics. JOSS 2, 188–3. [Google Scholar]
  15. Holmes GP, McCormick JB, Trock SC, Chase RA, Lewis SM, Mason CA, Hall PA, Brammer LS, Perez-Oronoz GI, McDonnell MK, et al. (1990). Lassa fever in the United States. Investigation of a case and new guidelines for management. N Engl J Med 323, 1120–1123. [DOI] [PubMed] [Google Scholar]
  16. Ilori EA, Furuse Y, Ipadeola OB, Dan-Nwafor CC, Abubakar A, Womi-Eteng OE, Ogbaini-Emovon E, Okogbenin S, Unigwe U, Ogah E, et al. (2019). Epidemiologic and Clinical Features of Lassa Fever Outbreak in Nigeria, January 1–May 6, 2018. Emerging Infect. Dis 25, 1066–1074. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Kranzusch PJ, Kranzusch PJ, Schenk AD, Schenk AD, Rahmeh AA, Rahmeh AA, Radoshitzky SR, Radoshitzky SR, Bavari S, Bavari S, et al. (2010). Assembly of a functional Machupo virus polymerase complex. Proc. Natl. Acad. Sci. U.S.A 107, 20069–20074. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Kube S, and Weber M. (2007). A coarse graining method for the identification of transition rates between molecular conformations. J. Chem. Phys 126, 024103–11. [DOI] [PubMed] [Google Scholar]
  19. Lee T-S, Radak BK, Huang M, Wong K-Y, and York DM (2013). Roadmaps through Free Energy Landscapes Calculated Using the Multidimensional vFEP Approach. J. Chem. Theory Comput 10, 24–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Lennartz F, Hoenen T, Lehmann M, Groseth A, and Garten W. (2013). The role of oligomerization for the biological functions of the arenavirus nucleoprotein. Arch. Virol 158, 1895–1905. [DOI] [PubMed] [Google Scholar]
  21. Lippert RA, Predescu C, Ierardi DJ, Mackenzie KM, Eastwood MP, Dror RO, and Shaw DE (2013). Accurate and efficient integration for molecular dynamics simulations at constant temperature and pressure. J. Chem. Phys 139, 164106. [DOI] [PubMed] [Google Scholar]
  22. Macher AM, and Wolfe MS (2006). Historical Lassa fever reports and 30-year clinical update. Emerging Infect. Dis 12, 835–837. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. MacKerell AD Jr, Feig M, and Brooks CL III (2004). Extending the treatment of backbone energetics in protein force fields: Limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J Comput Chem 25, 1400–1415. [DOI] [PubMed] [Google Scholar]
  24. McGibbon RT, and Pande VS (2015). Variational cross-validation of slow dynamical modes in molecular kinetics. J. Chem. Phys 142, 124105–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Metzner P, Schütte C, and Vanden-Eijnden E. (2009). Transition Path Theory for Markov Jump Processes. Multiscale Model. Simul 7, 1192–1219. [Google Scholar]
  26. Moeller A, Kirchdoerfer RN, Potter CS, Carragher B, and Wilson IA (2012). Organization of the Influenza Virus Replication Machinery. Science 338, 1631–1634. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Noé F, and Clementi C. (2015). Kinetic Distance and Kinetic Maps from Molecular Dynamics Simulation. J. Chem. Theory Comput 11, 5002–5011. [DOI] [PubMed] [Google Scholar]
  28. Noé F, and Nüske F. (2013). A Variational Approach to Modeling Slow Processes in Stochastic Dynamical Systems. Multiscale Model. Simul 11, 635–655. [Google Scholar]
  29. Noé F, Banisch R, and Clementi C. (2016). Commute Maps: Separating Slowly Mixing Molecular Configurations for Kinetic Modeling. J. Chem. Theory Comput 12, 5620–5630. [DOI] [PubMed] [Google Scholar]
  30. Nüske F, Keller BG, Pérez-Hernández G, Mey ASJS, and Noé F. (2014). Variational Approach to Molecular Kinetics. J. Chem. Theory Comput 10, 1739–1752. [DOI] [PubMed] [Google Scholar]
  31. Omotuyi OI, Nash O, Safronetz D, Ojo AA, Ogunwa TH, and Adelakun NS (2019). T-705-modified ssRNA in complex with Lassa virus nucleoprotein exhibits nucleotide splaying and increased water influx into the RNA-binding pocket. Chem Biol Drug Des 93, 544–555. [DOI] [PubMed] [Google Scholar]
  32. Parra RG, Schafer NP, Radusky LG, Tsai M-Y, Guzovsky AB, Wolynes PG, and Ferreiro DU (2016). Protein Frustratometer 2: a tool to localize energetic frustration in protein molecules, now with electrostatics. Nucleic Acids Research 44, W356–W360. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Pattis JG, and May ER (2016). Influence of RNA Binding on the Structure and Dynamics of the Lassa Virus Nucleoprotein. Biophysj 110, 1246–1254. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Pérez-Hernández G, and Noé F. (2016). Hierarchical Time-Lagged Independent Component Analysis: Computing Slow Modes and Reaction Coordinates for Large Molecular Systems. J. Chem. Theory Comput 12, 6118–6129. [DOI] [PubMed] [Google Scholar]
  35. Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kalé L, and Schulten K. (2005). Scalable molecular dynamics with NAMD. J Comput Chem 26, 1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Prinz J-H, Wu H, Sarich M, Keller B, Senne M, Held M, Chodera JD, Schütte C, and Noé F. (2011). Markov models of molecular kinetics: Generation and validation. J. Chem. Phys 134, 174105–23. [DOI] [PubMed] [Google Scholar]
  37. Purushotham J, Lambe T, and Gilbert SC (2019). Vaccine platforms for the prevention of Lassa fever. Immunology Letters 1–0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Qi X, Lan S, Wang W, Schelde LM, Dong H, Wallat GD, Ly H, Liang Y, and Dong C. (2010). Cap binding and immune evasion revealed by Lassa nucleoprotein structure. Nature 468, 779–783. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Ruigrok RW, Crépin T, and Kolakofsky D. (2011). Nucleoproteins and nucleocapsids of negative-strand RNA viruses. Current Opinion in Microbiology 14, 504–510. [DOI] [PubMed] [Google Scholar]
  40. Sali A, and Blundell TL (1993). Comparative protein modelling by satisfaction of spatial restraints. Journal of Molecular Biology 234, 779–815. [DOI] [PubMed] [Google Scholar]
  41. Scherer MK, Trendelkamp-Schroer B, Paul F, Pérez-Hernández G, Hoffmann M, Plattner N, Wehmeyer C, Prinz J-H, and Noé F. (2015). PyEMMA 2: A Software Package for Estimation, Validation, and Analysis of Markov Models. J. Chem. Theory Comput 11, 5525–5542. [DOI] [PubMed] [Google Scholar]
  42. Schwantes CR, and Pande VS (2013). Improvements in Markov State Model Construction Reveal Many Non-Native Interactions in the Folding of NTL9. 9, 2000–2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Shan Y, Klepeis JL, Eastwood MP, Dror RO, and Shaw DE (2005). Gaussian split Ewald: A fast Ewald mesh method for molecular simulation. J. Chem. Phys 122, 054101. [DOI] [PubMed] [Google Scholar]
  44. Trendelkamp-Schroer B, Wu H, Paul F, and Noé F. (2015). Estimation and uncertainty of reversible Markov models. J. Chem. Phys 143, 174101–21. [DOI] [PubMed] [Google Scholar]
  45. Wang Y, Dutta S, Karlberg H, Devignot S, Weber F, Hao Q, Tan YJ, Mirazimi A, and Kotaka M. (2012). Structure of Crimean-Congo Hemorrhagic Fever Virus Nucleoprotein: Superhelical Homo-Oligomers and the Role of Caspase-3 Cleavage. Journal of Virology 86, 12294–12303. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Weber JK, and Pande VS (2011). Characterization and Rapid Sampling of Protein Folding Markov State Model Topologies. J. Chem. Theory Comput 7, 3405–3411. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Yun NE, and Walker DH (2012). Pathogenesis of Lassa fever. Viruses 4, 2031–2048. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1
NIHMS1576785-supplement-1.pdf (3.3MB, pdf)
2
NIHMS1576785-supplement-2.docx (33.6KB, docx)

RESOURCES