Skip to main content
PMC home page
Elsevier - PMC COVID-19 Collection logoLink to Elsevier - PMC COVID-19 Collection
. 2020 May 8;135:109864. doi: 10.1016/j.chaos.2020.109864

Time series forecasting of COVID-19 transmission in Canada using LSTM networks☆

Vinay Kumar Reddy Chimmula 1,⁎, Lei Zhang 1
PMCID: PMC7205623  PMID: 32390691

Highlights

  • •

    A fully automated, real-time forecasting model for COVID-19 transmission to help frontline health workers and government policy makers.

  • •

    Use of Artificial intelligence (AI) and Deep Learning to model Infectious diseases without loosing temporal components.

  • •

    One of the early studies to use LSTM networks to predict the COVID-19 transmission.

  • •

    We showed the trends of different countries and compared them with Canadian data to predict the future infections.

Keywords: Epidemic transmission, Time series forecasting, Machine learning, Corona virus, COVID-19, Long short term memory (LSTM) networks

Abstract

On March 11th 2020, World Health Organization (WHO) declared the 2019 novel corona virus as global pandemic. Corona virus, also known as COVID-19 was first originated in Wuhan, Hubei province in China around December 2019 and spread out all over the world within few weeks. Based on the public datasets provided by John Hopkins university and Canadian health authority, we have developed a forecasting model of COVID-19 outbreak in Canada using state-of-the-art Deep Learning (DL) models. In this novel research, we evaluated the key features to predict the trends and possible stopping time of the current COVID-19 outbreak in Canada and around the world. In this paper we presented the Long short-term memory (LSTM) networks, a deep learning approach to forecast the future COVID-19 cases. Based on the results of our Long short-term memory (LSTM) network, we predicted the possible ending point of this outbreak will be around June 2020. In addition to that, we compared transmission rates of Canada with Italy and USA. Here we also presented the 2, 4, 6, 8, 10, 12 and 14th day predictions for 2 successive days. Our forecasts in this paper is based on the available data until March 31, 2020. To the best of our knowledge, this of the few studies to use LSTM networks to forecast the infectious diseases.

1. Introduction

Every infectious disease outbreak exhibits certain patterns and such patterns needed to be identified based on transmission dynamics of such outbreaks. Intervening measures to eradicate such infectious diseases rely on the methods used to evaluate the outbreak when it occurs. Any outbreak in a country or province usually occurs at different levels of magnitude with respect to time i.e. seasonal changes, adaptation of virus over time. Usually patterns exhibited in such scenarios are non-linear in nature and this motivates us to design the system that can capture such non-linear dynamic changes. With the help of these non-linear systems, we can describe the transmission of such infectious diseases. In [1], [2] a transmission model for malaria and in [3] a mathematical model for analysing dynamics of tuberculosis has been developed to study the transmission using mathematical models. In [4] a laplacian based decomposition is used to solve the non-linear parameters in a Pine Witt disease. A modified SIRS model in [5] successfully helped to control the syncytial virus in infants. Similarly mathematical models presented in [6], [7] helped clinicians to better understand the characteristics of human liver and transmission of dengue outbreak.

Most of the Data driven approaches used in previous studies [8] are linear methods and often neglects the temporal components in the data. They depend upon regression without non-linear functions and failed to capture the dynamics of transmission of infectious diseases like novel corona virus. Statistical models such as Auto Regressive Moving Average (ARIMA), Moving Average (MA), Auto Regressive (AR) methods overwhelmingly depends on assumptions and such models are difficult for forecasting real-time transmission rates. Wide range of statistical and mathematical models [9], [10] have been proposed to model the transmission dynamics of current COVID-19 epidemic. In many cases, these models are not able to fit the given data perfectly and accuracy is also low while predicting the growth of COVID-19 transmission.

R0 is a popular statistical method specifically used to model an infectious disease. Often referred as âreproduction numberâ because, the infections reproduce itself with respect to time. R0 forecasts the number of people can get the infection from the infected person. In this model, an extra weight is applied to the person who never infected the current disease nor vaccinated. If the value of R0 of a disease is 10, then the infected person will spread the disease to 10 other people surrounding him. In [11] authors used R0 method to find the infection rate of novel virus on diamond princes cruise ship [11]. However, in such method it is difficult to find the starting point of the infectious disease by identifying patient zero and the people he interacted with during his incubation period. It is worth noting that mathematical models presented in [12], [13], [14] can be used to solve the complex non-linear patterns of infectious diseases.

Even though these epidemiological models are good at capturing vital components of an infectious disease, parameters of these models required several assumptions. Such hypothesized parameters would not fit the data perfectly and precision of such models will be low. Meanwhile, in engineering applications [15], model parameters are calculated with the help of real-time data. Similar approach was used in this research to find the model parameters instead of assumptions.

In order to overcome the barriers of statistical approaches, we developed the Deep Learning based network to predict the real-time transmission. Our model could help public health care providers, policy makers to make necessary arrangements to tackle the rush of potential COVID-19 patients. This experiment is based on the data sets of confirmed COVID-19 cases available until March 31, 2020.

Artificial Intelligence and mobile computing are one of the key factors for the success of technology in health care systems [16]. In the world of smart devices, data is being generated in the unprecedented way than ever before and promoted the role of machine learning in healthcare [16]. The world today is more connected than ever before this helped to share the real time infectious data between the countries. The distinctive feature of artificial intelligence is its flexibility, domain adaptation and economical to integrate with existing systems. Over the last few weeks, many researchers came up with several mathematical models to predict the transmission of novel corona virus [17], [18]. The major drawbacks of the existing models are linear, non-temporal and several assumptions while modelling the network. First of all, the covid-19 is a time series data set and it is highly recommended to use the sequential networks to extract the patterns from it. Second of all, the data we are dealing with is dynamic in nature so by using statistical and epidemiological models, results are often vague [19], [20]. In [21], [22], [23], [24] researchers used deep learning based LSTM networks to forecast COVID-19 infections. The LSTM models used in the above networks could not able to represent the spatio-temporal components simultaneously. In this paper we addressed the above problem by modifying the internal connections. In our modified LSTM cells, We have established the alternative connections between the input and output cells. This type of connections not only helps the networks to preserve spatio-temporal components, but also to transfer the historical information to the next units.

In this paper, we made an effort to predict the outbreak of COVID-19 based on past transmission data. First of all, coherence of input data needs to be analyzed in order to find the key feature i.e. number of new cases reported with respect to the previous day infections. After selecting the key parameters of the network, several experiments was conducted to find the optimal model that can predict future infections with minimum error. Previous studies on COVID-19 predictions, did not considered the recovery rate while developing the model. In this research, we considered the recovery rate as one of the features while building our model. From the design point of view, when a crisis occurs, algorithms tend to assign high probability and completely neglects the previous information which leads to biased predictions. We addressed this issue in our literature and solved this by using LSTM networks.

Our results are expected to alert the public health care providers of Canada to prepare themselves for the crisis against COVID-19. With the help of this real-time forecasting tool, front-line clinical staff will be alerted before the crisis.

The rest of this paper is structured as follows: section II describes methods, datasets and LSTM models used in this paper. In Section III, we have discussed our findings and in Section IV, concussion and future work was discussed

2. Methods and models

2.1. Dataset

The COVID-19 data used in this research is collected from Johns Hopkins University and Canadian Health authority, provided with number of confirmed cases until March 31, 2020. The data set also includes number of fatalities and recovered patients by the end of each day. The dataset is available in the time series format with date, month and year so that the temporal components are not neglected. A wavelet transformation [25] is applied to preserve the time-frequency components and it also mitigates the random noise in the dataset. The fundamental point to represent and forecast the trends of current is to select conventional functions to fit the data. The COVID-19 dataset is divided into training set (80%) on which our models are trained and testing set (20%) to test the performance of the model.

2.2. LSTM Network for modelling time series

A large part of real-world datasets are temporal in nature. Due to its distinctive properties, there are numerous unsolved problems with wide range of applications. Data collected over regular intervals of time is called time-series (TS) data and each data point is equally spaced over time. TS prediction is the method of forecasting upcoming trends/patterns of the given historical dataset with temporal features. In order to forecast COVID-19 transmission, it would be effective if input data has temporal components and it is different from traditional regression approaches. A time series (TS) data can be break downed into trend, seasonality and error. A trend in TS can be observed when a certain pattern repeats on regular intervals of time due to external factors like lockdown of country, mandatory social distancing, quarantines etc. In many real-world scenarios, either of trend or seasonality are absent. After finding the nature of TS, various forecasting methods have to be applied on given TS

Given the TS, it is broadly classified into 2 categories i.e. stationary and non-stationary. A series is said to be stationary, if it does not depend on the time components like trend, seasonality effects. Mean and variances of such series are constant with respect to time. Stationary TS is easier to analyze and results skilful forecasting. A TS data is said to non-stationary if it has trend, seasonality effects in it and changes with respect to time. Statistical properties like mean, variance, sand standard deviation also changes with respect to time.

In order to check the nature (stationarity and non-stationarity) of the given COVID-19 dataset, we have performed Augmented Dickey Fuller (ADF) test [26] on the input data. ADF is the standard unit root test to find the impact of trends on the data and its results are interpreted by observing p-values of the test. If P is between 5-1%, it rejects the null hypothesis i.e. it does not have a unit root and it is called stationary series. If P is greater than 5% or 0.05 the input data has unit root so it is regarded as non-stationary series.

Before diving into the model architecture, it is crucial to explain the internal mechanisms of LSTM networks and reasons behind using it instead of traditional Recurrent Neural Networks. Recurrent LSTM networks has capability to address the limitations of traditional time series forecasting techniques by adapting nonlinearities of given COVID-19 dataset and can result state of the art results on temporal data. Each block of LSTM operates at different time step and passes its output to next block until the final LSTM block generates the sequential output.

As of this writing, RNNs with blocks (LSTM) are the efficient algorithms to build a time series sequential model. The fundamental component of LSTM networks is memory blocks, which was invented to tackle vanishing gradients by memorizing network parameters for long durations. Memory block in LSTM architecture are similar to the differential storage systems of a digital systems. Gates in LSTM helps in processing the information with the help of activation function (sigmoid) and output is in between 0 or 1. Reason behind using sigmoid activation function is because, we need to pass only positive values to the next gates for getting a clear output. The 3 gates of LSTM network are represented with the following equations below:

Jt=sigmoid(wJ[ht−1,kt]+bJ) (1)
Gt=sigmoid(wG[ht−1,kt]+bG) (2)
Pt=sigmoid(wP[ht−1,kt]+bP) (3)

Where: Jt = function of input gate

Gt = function of forget gate

Pt = function of output gate

Wx = coefficients of neurons at gate (x)

Ht−1 = result from previous time step

kt = input to the current function at time-step t

bx = bias of neurons at gate (x)

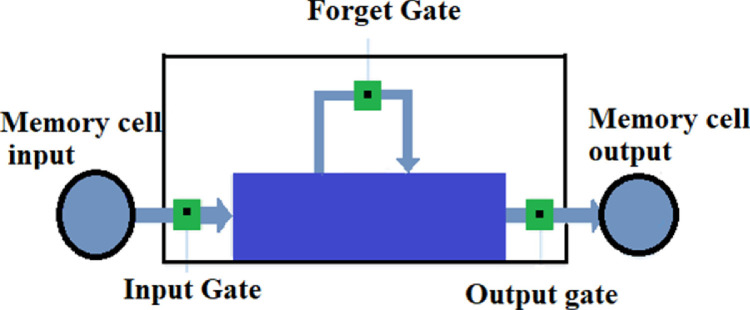
Input gate in the first equation gives the information that needs to be stored in the cell state. Second equation throws the information based on the forget gate activation output. The third equation for output gate combines the information from the cell state and the output of forget gate at time step âtâ for generating the output. The internal block diagram of LSTM block used in this study is shown in 1

Fig. 1.

Fig. 1

Open in a new tab

LSTM internal architecture.

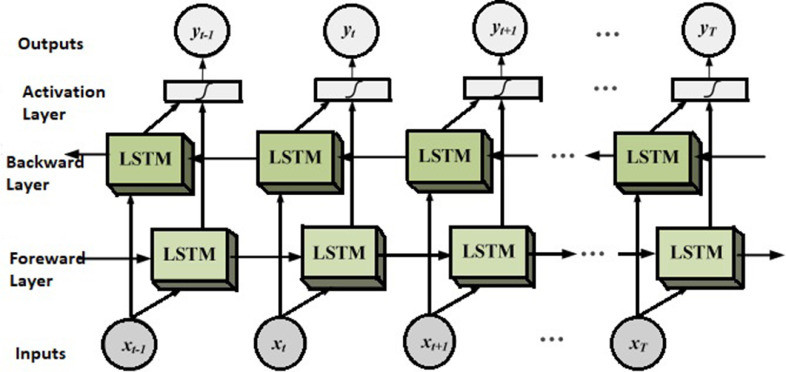
The motivation behind initiating self-loops is to create a path so that gradients or weights can be shared for long durations. Especially, this is useful while modelling deep networks where vanishing gradient is a frequent issue to deal with. By adjusting weights as self-looped gates, we can adjust the time scale to detect the dynamically changing parameters. Using the above techniques, LSTMs are able to produce the state-of-the-art results in [27]. The network architecture used in this study is shown in 2

Fig. 2.

Fig. 2

Open in a new tab

LSTM Architecture.

3. Results and discussion

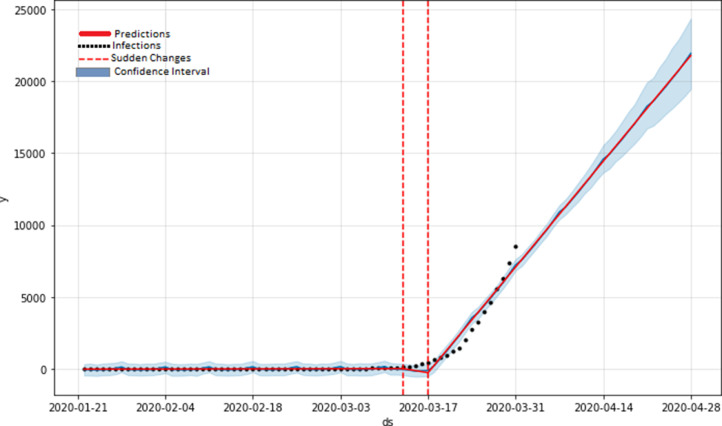
The methods used in this study are based on data guided approaches and are completely different from previous studies. Our approaches and predictive outcomes will provide assistance for restricting the infections and possible elimination of current COVID-19 pandemic. We trained our network with data until March 31, 2020 reported by Canadian health authority. In this study we found that policies or decisions taken by government will greatly affect the current outbreak.Several studies on forecasting of COID-19 transmission are based on the R0 method however, they didn’t include the sensitivity analysis to find the important features. We examined our model predictions using mean square error (MSE). In Fig. 4 we plotted the total number of confirmed cases and forecasted COVID-19 cases in Canada as a function of time. From the figure we can observe that, Canada didnât witness its peak yet and it is expected number of cases will soon increase exponentially despite the social distancing.

Fig. 4.

Fig. 4

Open in a new tab

Predictions of the LSTM model on current exposed and infectious cases (Red solid line). The red dotted lines represents the sudden changes from where number of infections started following exponential trend. The black dotted lines in the figure represents the training data or available confirmed cases. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

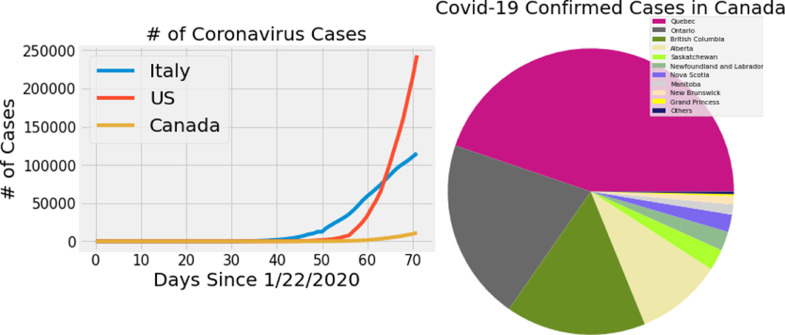
Although our model achieved better performance when compared with other forecasting models, it is unfortunate that transmissions are following increasing trend. The rate of infections in USA, Italy and Spain are growing exponentially meanwhile, the number of infections in Canada are increasing linearly in Fig. 3 . If Canadians follow the regulations strictly, the number of confirmed cases will soon decline.

Fig. 3.

Fig. 3

Open in a new tab

a) Number of infections in Canada vs USA vs Italy as of March 31, 2020. b) Distribution of confirmed cases in Canada as of March 31, 2020.

In our LSTM model-1 we trained and tested our network on Canadian dataset; the RMSE error is 34.83 with an accuracy of 93.4% for short term predictions in Canada. Meanwhile, based on our testing/validation dataset the RMSE error is about 45.70 with an accuracy of 92.67% for long term predictions. The predictions of LSTM model are shown in 4 with solid red line. It shows that our model was able to capture the dynamics of the transmission with minimum loss. From the Fig. 4 we can say that Canada witnessed linear growth in cases until March 16, 2020 after its first confirmed case. The current epidemic in Canada is predicted to continue until June 2020. Our second LSTM model-2 is trained on Italian dataset to predict short-term and long-term infections in Canada. For short term predictions, the RMSE error is about 51.46 which is higher than previous model. According to this second model within 10 days, Canada is expected to see exponential growth of confirmed cases.

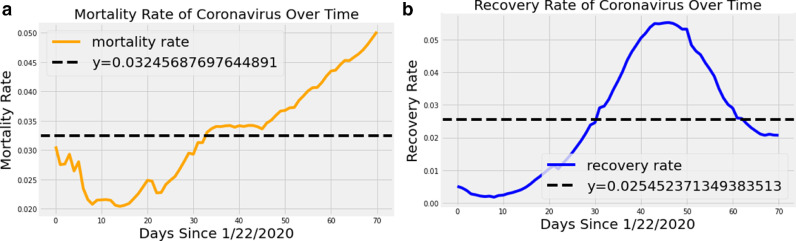
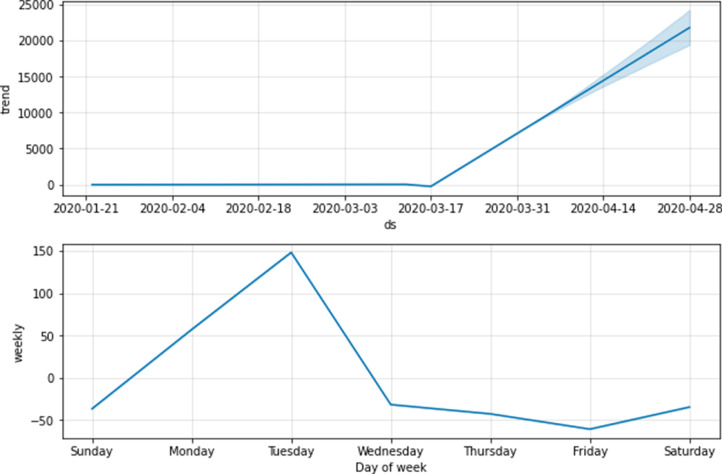
It was a challenging task to forecast the dynamics of transmission based on small dataset. Even though COVID-19 outbreak started in Canada around early January, the consistent epidemiological data wasn’t released until early February. Because of small dataset several statistical models struggled to select the optimal parameters and several unknown variables led to uncertainty in their predictions. LSTM model is different from statistical methods in many ways for instance, the proposed LSTM network fits the real-time data and without any assumptions while selecting hyperparameters. It was able to overcome the parameter assumptions using cross validation and achieved better performance by reducing the uncertainty. After reaching the inflection point, the recovery rate will start decrease rapidly and death rate may increase at the same time as shown in Fig. 5 . In order to find the trend of the infections we decomposed the given series and the trend of infections is increasing with respect to time. Further, number of infections followed increasing trend from Sunday to Tuesday and followed decreasing trend until Saturday as shown in Fig. 6 .

Fig. 5.

Fig. 5

Open in a new tab

a) Mortality rate of COVID-19 in Canada and the average mortality stands around 3.2% b) Recovery rate of COVID-19 patients shows that it is decreasing with respect to time because of rise in number of infections.

Fig. 6.

Fig. 6

Open in a new tab

Trend of infections in Canada.

As we are still under the stage of dilemma about the current situation of COVID-19 because, the accuracy of our estimates is bounded with a lot of external factors. So, it is recommended to conduct the follow-up study after this experiment to be more precise about the dynamics of this novel infectious disease. The actual number of cases might be higher than the cases reported by the government because, of the backlog of test results and some people will be immune before even testing. All the above factors may lead to discrepancy of our model estimations. Even though we addressed data imbalance by using statistical methods like interpolation and re-sampling yet we couldnât represent patients who are on incubation period or not tested. Other problem while modelling current pandemic is that, people travelling between the provinces. Based on our sensitivity analysis our projections may go down if current trials on potential vaccines achieves fruitful results. Finally, in order to minimize the bias on our training algorithm we introduced regularization.

Further, by training our network inversely, we found that outbreak in Canada started around early January but, it was not reported until January last week. Even without the knowledge of 1st case, our inverse training will help governments to better understand the outbreak of COVID-19 and helps then to prevent such outbreaks in future.

4. Conclusion and future work

The patterns from the data reveals that prompt and effective approaches taken by Canadian public health authorities to minimize the human exposure is showing a positive impact when compared with other countries like USA and Italy 3. Rate of transmission in Canada is following linear trend while in USA is witnessing an exponential growth of transmissions. However, it is too early to draw the conclusions about the current epidemic.

After simulations and data fitting, our model predicted Canada would reach peak within 2 weeks from now. However, the current outbreak resembles early 20th century Spanish flu [28], which killed millions of people and lasted for 2 years. Based on our model simulations, the current COVID-19 pandemic is expected to end within 3 months from now. Due to some unreported cases, a small number infection clusters may appear until December 2020. However, recent technological improvements and international cooperation between countries may even reduce the duration current pandemic.

To sum up, this is the first study to model the infections disease transmission model to predict the gravity of COVID-19 in Canada using deep learning approaches. Based on our current findings, provinces that have implemented social distancing guidelines before the pandemic has less confirmed cases than other provinces 3. For instance, Saskatchewan issued social distancing guidelines 2 weeks ahead than Quebec which has half of the confirmed cases in Canada. Our results could help Canadian government to monitor the current situation and use our forecasts to prevent further transmissions.

CRediT authorship contribution statement

Vinay Kumar Reddy Chimmula: Conceptualization, Methodology, Software, Writing - original draft, Writing - review & editing. Lei Zhang: Supervision, Writing - review & editing, Data curation.

Declaration of Competing Interest

1. Conflict of Interest

Potential conflict of interest exists:

We wish to draw the attention of the Editor to the following facts, which may be considered as potential conflicts of interest, and to significant financial contributions to this work: The nature of potential conflict of interest is described below:

No conflict of interest exists.

We wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.

2. Funding Funding was received for this work.

All of the sources of funding for the work described in this publication are acknowledged below: This research is funded by Saskatchewan Center for Patient Oriented research (SCPOR)

We confirm that we have given due consideration to the protection of intellectual property associated with this work and that there are no impediments to publication, including the timing of publication, with respect to intellectual property. In so doing we confirm that we have followed the regulations of our institutions concerning intellectual property.

Research Ethics

We further confirm that any aspect of the work covered in this manuscript that has involved human patients has been conducted with the ethical approval of all relevant bodies and that such approvals are acknowledged within the manuscript.

We confirm that the manuscript has been read and approved by all named authors.

We confirm that the order of authors listed in the manuscript has been approved by all named authors.

Footnotes

☆

This document is the results of the research project funded by the Saskatchewan Centre for Patient Oriented Research (SCPOR), Saskatchewan, Canada

Contributor Information

Vinay Kumar Reddy Chimmula, Email: vcw015@uregina.ca.

Lei Zhang, Email: lei.zhang@uregina.ca.

References

  • 1.Basing A., Tay S. Malaria transmission dynamics of the anopheles mosquito in kumasi, ghana. Int J Infect Dis. 2014;21:22. [Google Scholar]
  • 2.Chitnis N., Cushing J.M., Hyman J. Bifurcation analysis of a mathematical model for malaria transmission. SIAM J Appl Math. 2006;67(1):24–45. [Google Scholar]
  • 3.Sharomi O., Podder C.N., Gumel A.B., Song B. Mathematical analysis of the transmission dynamics of hiv/tb coinfection in the presence of treatment. Math Biosci Eng. 2008;5(1):145. doi: 10.3934/mbe.2008.5.145. [DOI] [PubMed] [Google Scholar]
  • 4.Shah K., Alqudah M.A., Jarad F., Abdeljawad T. Semi-analytical study of pine wilt disease model with convex rate under caputo–febrizio fractional order derivative. Chaos Solitons Fractals. 2020;135:109754. [Google Scholar]
  • 5.Jajarmi A., Yusuf A., Baleanu D., Inc M. A new fractional hrsv model and its optimal control: a non-singular operator approach. Physica A. 2019:123860. [Google Scholar]
  • 6.Baleanu D., Jajarmi A., Mohammadi H., Rezapour S. A new study on the mathematical modelling of human liver with caputo–fabrizio fractional derivative. Chaos Solitons Fractals. 2020;134:109705. [Google Scholar]
  • 7.Jajarmi A., Arshad S., Baleanu D. A new fractional modelling and control strategy for the outbreak of dengue fever. Physica A. 2019;535:122524. [Google Scholar]
  • 8.Knight G.M., Dharan N.J., Fox G.J., Stennis N., Zwerling A., Khurana R. Bridging the gap between evidence and policy for infectious diseases: how models can aid public health decision-making. Int J Infect Dis. 2016;42:17–23. doi: 10.1016/j.ijid.2015.10.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Benvenuto D., Giovanetti M., Vassallo L., Angeletti S., Ciccozzi M. Application of the arima model on the Covid-2019 epidemic dataset. Data Brief. 2020:105340. doi: 10.1016/j.dib.2020.105340. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Dehesh T., Mardani-Fard H., Dehesh P. Forecasting of covid-19 confirmed cases in different countries with arima models. medRxiv. 2020 [Google Scholar]
  • 11.Zhang S., Diao M., Yu W., Pei L., Lin Z., Chen D. Estimation of the reproductive number of novel coronavirus (Covid-19) and the probable outbreak size on the diamond princess cruise ship: a data-driven analysis. Int J Infect Dis. 2020;93:201–204. doi: 10.1016/j.ijid.2020.02.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Baleanu D., Jajarmi A., Sajjadi S.S., Asad J.H. The fractional features of a harmonic oscillator with position-dependent mass. Commun Theor Phys. 2020;72(5):55002. [Google Scholar]
  • 13.Yıldız T.A., Jajarmi A., Yıldız B., Baleanu D. New aspects of time fractional optimal control problems within operators with nonsingular kernel. Discret Cont Dyn Syst-S. 2020;13(3):407. [Google Scholar]
  • 14.Jajarmi A., Baleanu D., Sajjadi S.S., Asad J.H. A new feature of the fractional euler-lagrange equations for a coupled oscillator using a nonsingular operator approach. Front Phys. 2019;7:196. [Google Scholar]
  • 15.George D., Huerta E. Deep learning for real-time gravitational wave detection and parameter estimation: results with advanced ligo data. Phys Lett B. 2018;778:64–70. [Google Scholar]
  • 16.Panch T., Mattie H., Celi L.A. The ǣinconvenient truthǥ about ai in healthcare. Npj Digital Med. 2019;2(1):1–3. doi: 10.1038/s41746-019-0155-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Zhao S., Lin Q., Ran J., Musa S.S., Yang G., Wang W. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-ncov) in china, from 2019 to 2020: adata-driven analysis in the early phase of the outbreak. Int J Infect Diseas. 2020;92:214–217. doi: 10.1016/j.ijid.2020.01.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Shim E., Tariq A., Choi W., Lee Y., Chowell G. Transmission potential and severity of Covid-19 in south korea. Int J Infect Diseas. 2020 doi: 10.1016/j.ijid.2020.03.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Liestøl K., Andersen P.K. Updating of covariates and choice of time origin in survival analysis: problems with vaguely defined disease states. Stat Med. 2002;21(23):3701–3714. doi: 10.1002/sim.1322. [DOI] [PubMed] [Google Scholar]
  • 20.Krätschmer V. Strong consistency of least-squares estimation in linear regression models with vague concepts. J Multivar Anal. 2006;97(3):633–654. [Google Scholar]
  • 21.Bandyopadhyay S.K., Dutta S. Machine learning approach for confirmation of Covid-19 cases: positive, negative, death and release. medRxiv. 2020 [Google Scholar]
  • 22.Huang C.-J., Chen Y.-H., Ma Y., Kuo P.-H. Multiple-input deep convolutional neural network model for covid-19 forecasting in china. medRxiv. 2020 [Google Scholar]
  • 23.Tomar A., Gupta N. Prediction for the spread of Covid-19 in india and effectiveness of preventive measures. Sci Total Environ. 2020:138762. doi: 10.1016/j.scitotenv.2020.138762. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Pal R., Sekh A.A., Kar S., Prasad D.K. Neural network based country wise risk prediction of covid-19. arXiv preprint arXiv:200400959. 2020 [Google Scholar]
  • 25.Xu Y., Weaver J.B., Healy D.M., Lu J. Wavelet transform domain filters: a spatially selective noise filtration technique. IEEE Trans Image Process. 1994;3(6):747–758. doi: 10.1109/83.336245. [DOI] [PubMed] [Google Scholar]
  • 26.Cheung Y.-W., Lai K.S. Lag order and critical values of the augmented dickey–fuller test. J Bus Econ Stat. 1995;13(3):277–280. [Google Scholar]
  • 27.Karim F., Majumdar S., Darabi H. Insights into lstm fully convolutional networks for time series classification. IEEE Access. 2019;7:67718–67725. [Google Scholar]
  • 28.de Jong J.d., Claas E., Osterhaus A.D., Webster R.G., Lim W. A pandemic warning? Nature. 1997;389(6651):554. doi: 10.1038/39218. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Chaos, Solitons, and Fractals are provided here courtesy of Elsevier

RESOURCES