A bi-objective home healthcare routing and scheduling problem considering patients’ satisfaction in a fuzzy environment

Abstract

Home care services are an alternative answer to hospitalization, and play an important role in reducing the healthcare costs for governments and healthcare practitioners. To find a valid plan for these services, an optimization problem called the home healthcare routing and scheduling problem is motivated to perform the logistics of the home care services. Although most studies mainly focus on minimizing the total cost of logistics activities, no study, as far as we know, has treated the patients’ satisfaction as an objective function under uncertainty. To make this problem more practical, this study proposes a bi-objective optimization methodology to model a multi-period and multi-depot home healthcare routing and scheduling problem in a fuzzy environment. With regards to a group of uncertain parameters such as the time of travel and services as well as patients’ satisfaction, a fuzzy approach named as the Jimenez’s method, is also utilized. To address the proposed home healthcare problem, new and well-established metaheuristics are obtained. Although the social engineering optimizer (SEO) has been applied to several optimization problems, it has not yet been applied in the healthcare routing and scheduling area. Another innovation is to develop a new modified multi-objective version of SEO by using an adaptive memory strategy, so-called AMSEO. Finally, a comprehensive discussion is provided by comparing the algorithms based on multi-objective metrics and sensitivity analyses. The practicality and efficiency of the AMSEO in this context lends weight to the development and application of the approach more broadly.

Highlights

• •An extension to the home healthcare optimization considering the patients’ satisfaction is developed.
• •A fuzzy environment by applying the Jimenez’s method is utilized to handle the uncertain parameters.
• •A modified multi-objective metaheuristic as an extension to the social engineering optimizer is introduced.

1. Introduction

The advancement of medical and healthcare concepts in recent years as well as the economic and life expectancy growth, care of the ageing population is of particular concern in developed countries, particularly Europe and North America [1]. Home care services are an alternative answer to help the elderly people, defined by both healthcare practitioners and academics. These services, including nursing, wound-care, housekeeping, injection, cleaning and physiotherapy, are less expensive and more efficient than regular services delivered in hospitals or retirement homes [2], [3]. In addition, the ageing population prefer to receive their care at home. Based on official reports, the European population over 60 years old will grow to 54% by the year 2060 [4], which could lead to a rapid increase in home healthcare operations.

Caregivers provide several cares for elderly people at home [5], [6]. Moreover, old people may need a combination of different caregivers such as a nurse, physiotherapist or nutritionist [7]. The planning of caregivers including patient assignment, routing and scheduling decisions, is very difficult and requires a great deal of time and effort to find a valid plan [8]. The daily activities of caregivers start at the pharmacy [9]. After meeting the patients, the biological samples or the treatments taken from the patients are analyzed and their electronic health records are updated in a laboratory [5]. From the perspective of home healthcare managers, there are two important challenges. The first one is the transportation cost associated with the logistics activities of caregivers [10]. Another concern is the availability of patients and caregivers [11]. However, the availability of patients is considered as an uncertain issue rather than exact [8]. Thus, fuzzy logic by using triangular fuzzy numbers can help decision-makers to estimate the time windows of availability. The uncertain factors can be estimated by three possible scenarios including optimistic, realistic and pessimistic ones based on the triangular fuzzy numbers. Additionally, the patients’ satisfaction is another important factor characterizing the quality of home healthcare from the perspective of the patients. Although most of the studies focus on the total cost of home care services, the patients’ satisfaction is still scarce. These reasons motivate us to develop a bi-objective optimization decision-making model called the home healthcare routing and scheduling problem under fuzzy conditions. To this end, we use a fuzzy approach to cope with the uncertainty of travel parameters and patients’ satisfaction.

This type of optimization model is classically known as a variation of the vehicle routing problem [5], [6]. Due to the daily decision-making of this problem and the complexity of this combinatorial optimization model, the applications of heuristics and metaheuristics are popular in the literature [12], [13]. According to a well-known theory for optimization called “no free lunch”, no optimization algorithm is able to be efficient for all complicated optimization problems [14]. Since the proposed home healthcare routing and scheduling problem is more complex as compared with the previous ones, it is difficult to get a robust answer using current metaheuristics in the literature. This motivates our attempts to employ a recent metaheuristic, namely, social engineering optimizer (SEO) [15]. Therefore, a new modification on this metaheuristic based on an adaptive memory is designed to better address the proposed problem in comparison with itself and two other well-known metaheuristics.

In conclusion, an extension to the home healthcare optimization problem is proposed which is bi-objective, multi-period and multi-depot in a fuzzy environment. In addition to the cost, the patients’ satisfaction is also optimized. To address the proposed problem, a new modified SEO is developed. The main contributions are as follows:

• •An extension to the home healthcare optimization considering the patients’ satisfaction under uncertainty, is developed.
• •A fuzzy environment by applying the Jimenez’s method is utilized to handle the uncertain parameters.
• •A new modified SEO, as a new multi-objective metaheuristic algorithm, is introduced.

The rest of the paper is structured as follows. Section 2 collects a comprehensive review on the relevant studies. Section 3 addresses the problem description and the respective fuzzy model. Section 4, presents the encoding plan and the steps of the proposed metaheuristic. Section 5 addresses the computational and validation results of the proposed model. The paper concludes with the main findings and the future research directions in Section 6.

2. Background and literature

The roles of the optimization models and algorithms to the home healthcare logistics have been mainly highlighted during the last two decades [5], [6]. One of first papers addressing the problem was (Begur et al. in 1997 [16]). The authors applied a decision-making tool called as SDSS to model a simplified home healthcare routing problem through a case in the United States. Nine years later, the first vehicle routing optimization approach applied to the home healthcare was addressed by Bertels and Fahle [17]. They solved it by using a heuristic algorithm combining the linear and constraint programming methods and local search strategies. In 2007, a particle swarm optimization (PSO) was applied successfully by Akjiratikarl et al. [18] to address a home healthcare scheduling problem in Ukraine. A heuristic for the scheduling was also implemented. In 2009, Eveborn et al. [19] developed two mathematical models to improve both routing and scheduling problems of the home healthcare. Later in 2011, Trautsamwieser et al. [20] addressed a scheduling problem for the home healthcare under uncertainty. They considered a case of natural disaster based on Austrian flood in 2002 to validate their proposed stochastic model. Another contribution in the area of home healthcare scheduling was introduced by Rasmussen et al. [21]. They proposed a branch-and-price solution planning to solve it.

In recent years, the home healthcare routing optimization has gained a high attention rather than the home healthcare scheduling. The reason is that the home care logistic costs are the main concern for the organization of the home healthcare. In 2013, Liu et al. [22] proposed a home healthcare routing problem considering the supposition of time windows. They assumed both pickup and delivery operations, simultaneously, for drugs and biological samples, respectively. Their innovation was also the development of heuristics formulated by the tabu search (TS) and the genetic algorithm (GA). In 2014, Mankowska et al. [23] proposed a new home healthcare routing problem as a multi-period and multi-service. In their proposed problem, each caregiver can support at least two services regarding the required medications and time availability. In another research, Liu et al. [24] introduced a hybrid metaheuristic by an improvement on TS with infeasible and feasible local searches to tackle a home healthcare logistic problem. In 2015, Fikar and Hirsch [11] offered another routing and scheduling problem for the application of the home healthcare with the possibility of caregivers’ walking to visit the patients as well as the time window limitations. A case study in Austria was suggested to generate the test problems and to address the proposed problem, two hybrid metaheuristics based on TS and simulated annealing (SA) were introduced. In 2016, a bi-objective optimization model for the home care scheduling problem was firstly developed by Braekers et al. [25]. Their goal was to find an interaction between two minimization objectives, namely, the total cost and the patients’ inconvenience. They also used some simplified metaheuristics combined by dynamic programming. In 2017, Shi et al. [26] proposed a single objective and single depot routing and scheduling problem for the application of home healthcare with the suppositions of time windows and fuzzy demand function.

Regarding the recent advances in the home healthcare studies, novel optimization models with multiple objectives and complex constraints have been studied. In 2018, Lin et al. [27] offered a new coordinated home healthcare routing and scheduling problem by using a hybrid metaheuristic based on harmony search algorithm (HSA) and GA. They also added immigrant schemes and inheritance to this problem to consider the synchronization of the caregivers. Liu et al. [28] introduced another formulation of the bi-objective optimization to consider the medical team working in home care services. In addition to the transportation costs, they minimized the unemployment of caregivers through a group of medical operations. In another paper concerning metaheuristic algorithms, a memetic algorithm (MA) for the first time was applied by Decerle et al. [1] to a single objective multi-period routing and scheduling problem of the home healthcare. A Lagrangian relaxation-based algorithm was firstly contributed by Fathollahi-Fard et al. [3]. They also considered a penalty function to better optimize the routes of caregivers known as travel balancing. In another study, Cappanera et al. [29] proposed a robust optimization of the routing and scheduling problem for a home healthcare under uncertainty. As another multi-objective optimization, Fathollahi-Fard et al. [9] contributed the environmental pollution to the home healthcare by considering the operational routing and scheduling decisions. They developed four heuristics based on two decision rules to find an interaction between the transportation costs and green emissions. They also utilized salp swarm algorithm (SSA) and its hybridization with SA for the first time.

More recently in 2019, a dynamic accepting rule for the patients scheduling to support the home care services based on the total cost and the availability of caregivers, was proposed firstly by Demirbilek et al. [30]. Their main new supposition was that the patients arrived dynamically in each time period. Fathollahi-Fard et al. [12] developed three fast heuristics and a lower bound as well as a hybrid of SA and variable neighborhood search (VNS) to address a new variant of routing and scheduling problem for the home healthcare application. Lastly, Shi et al. [31] proposed a new robust optimization for the mentioned problem considering uncertain travel and service times. They applied two simplified metaheuristics based on SA and VNS to solve the proposed problem.

The literature review is summarized in Table 1 and the research gaps are identified. We classify the papers with respect to six criteria including the objective(s), depot(s), period(s), model’s output(s) and properties as well as the solution method(s). The outputs of model from the literature are the assignment of patients to pharmacies as well as the routing and scheduling of the caregivers. The main properties of models have been classified as the uncertainty approaches, synchronization, time windows, working time balancing, travel balancing, delivery time, green emissions and patients’ satisfaction. At last, the solution methods are a variety of exact, heuristic and metaheuristic algorithms as indicated in the literature.

Table 1.

Literature review.

Reference	Number of objectives		Number of depots		Number of periods		Outputs of the model			Suppositions of the model								Solution algorithm
	Single objective	Multi-objective	Single depot	Multi-depot	Single period	Multi-period	Assignment of patients	Routing of caregivers	Scheduling of caregivers	Time windows	Delivery time	Synchronization	Travel balancing	Working time balancing	Uncertainty	Patients’ satisfaction	Green emissions
[16]	✓	–	✓	–	✓	–	–	✓	–	–	–	–	–	–	–	–	–	SDSS
[17]	✓	–	✓	–	✓	–	–	✓	–	–	–	–	–	–	–	–	–	Hyper heuristic
[18]	✓	–	✓	–	✓	–	–	–	✓	–	–	–	–	–	–	–	–	PSO
[19]	✓	–	✓	–	✓	–	✓			✓	–	–	–	–	–	–	–	Exact
[20]	✓	–	✓	–	✓	–	–		✓	–	✓	–	–	–	✓	–	–	VNS
[21]	✓	–	✓	–	✓	–	–				✓	–	–	–	–	–	–	Exact
[33]	✓	–	✓	–	✓	–	✓				✓	–	–	–	✓	–	–	Heuristic
[22]	✓	–	✓	–	✓	–	–				✓	–	–	–	–	–	–	GA and TS
[24]	✓	–	✓	–	✓	–	–				✓	–	–	–	–	–	–	Feasible rules for TS
[23]	✓	–	✓	–	✓	–	–				✓	–	–	✓	–	–	–	Exact
[11]	✓	–	✓	–	–	✓	–	✓			✓	–	–	✓	–	–	–	TS
[25]	–	✓	✓	–	–	✓	–	✓			✓	–	–	–	–	–	–	Dynamic metaheuristic
[26]	✓	–	✓	–	✓	–	–				✓	–	✓	–	✓	–	–	Hybrid of GA and SA
[32]	✓	–	✓	–	✓	–	–				✓	–	✓	–	✓	–	–	GA, SA, BA and FA
[29]	✓	–	✓	–	–	✓	–	✓			✓	–	–	–	✓	–	–	Exact
[27]	✓	–	–	✓	–	✓						✓	–	–	–	–	–	Hybrid of HSA and GA
[28]	✓	–	–	✓	–	✓						✓	–	–	–	–	–	TS and GA
[9]	–	✓	✓	–	✓	–	–				✓	–	✓	–	–	–	✓	Heuristics, SA and SSA
[1]	✓	–	✓	–	–	✓	–	✓			✓	–	✓	–	–	–	–	MA
[3]	✓	–	✓	–	✓	–	–				✓	–	✓	–	–	–	–	Lagrangian relaxation
[34]	✓	–	–		✓	–	✓				✓	–	✓	–	–	–	–	Heuristics
[30]	✓	–	✓	–	–	✓	–	–	✓	–	✓	–	–		✓	–	–	Exact
[35]	✓	–	–	✓	–	✓	✓	–	✓	–	✓	–	–	–	–	–	–	Heuristics
[4]	–	✓	✓	–	✓	–	–					✓	–	✓	–	–	–	Hybrid of MA and ACO
[12]	✓	–	✓	–	✓	–	–				✓	–	✓	–	–	–	–	Heuristics and hybrid of VNS and SA
[31]	✓	–	✓	–	✓	–	–				✓	–	✓	–	✓	–	–	SA and TS
[13]	–	✓	–	✓	–	✓					✓	–	✓	–	–	–	✓	multi-objective of SA
[7]	✓	–	✓	–	–		✓	–	✓	✓	–	✓	–	✓	–	–	–	Matheuristic
[10]	✓	–	–		✓	–	–				✓	–	✓	–	✓	–	–	Heuristic
This study	–	✓	–	✓	–	✓					✓	–	✓	–	✓	✓	–	NSGA-II, multi-objective of SA, SEO and modified SEO

In general, according to the literature review and the summary of the aforementioned papers in Table 1, following findings can be concluded:

• •The routing optimization is considered rather than caregivers’ scheduling.
• •Most of the studies did formulation of the home healthcare optimization as a single objective, depot and time period optimization problem.
• •Considering the properties of the multi-depot, multi-period and multi-objective home healthcare optimization, is still scarce.
• •There are some multi-objective home healthcare models in the literature [4], [7], [9], [10], [13].
• •The use of uncertain models, is still scarce in the literature and there is only one paper considered fuzzy logic [26].
• •The simultaneous consideration of the delivery time, time window, travel balancing, and uncertainty of parameters and patients’ satisfaction is new and introduced in this study.
• •There is no similar work where the total cost is minimized and the patients’ satisfaction is maximized, simultaneously.
• •Having been applied to several home healthcare optimizations successfully, this study also utilizes SA and GA in their multi-objective forms.
• •Although there are many metaheuristics existing in the literature, there is no similar study using SEO that provides better solution for this NP-hard problem.

In our work, a bi-objective home healthcare routing and scheduling problem considering the patients’ satisfaction under uncertainty, is firstly proposed. The proposed model is a multi-period, multi-depot, and multi-objective optimization of the home healthcare operations. In addition, to the delivery time and time window suppositions, there are also different transportation systems and travel balancing limitations similar to many recent studies [3], [9], [12], [13], [26], [32]. Due to the uncertainty of some parameters, a fuzzy approach based on Jimenez’s method is applied for the first time. Lastly, a multi-objective version of SEO is modified by an adaptive strategy to improve its performance and computational cost. This algorithm is not only compared with itself but also SA and GA (non-dominated sorting GA abbreviated as NSGA-II) as the well-known algorithms in the literature.

3. Proposed problem

This study presents a multi-depot, multi-period and multi-objective home healthcare optimization model. As can be reported by the health records of the patients per period, home care services given by some expert caregivers are planned. The nurses as the caregivers and several patients are scheduled to route from the pharmacies to the laboratories. In each time period, a caregiver starts from their pharmacy before visiting the patient. After the visit, they should check the biological tests at the laboratory. Based on this analysis, the home service for each patient may be changed in each period regarding the updated health records of the patients.

The main optimization decisions for the proposed model are as follows. We firstly need to generate the cluster of each pharmacy and laboratory. In this regard, each patient is allocated to a pharmacy. As such, each laboratory is allocated to one pharmacy. At the end, the caregivers are routed and a plan to schedule the patients is generated for each time period. The transportation sector is the main activity in the application of the home healthcare. From each time period, the caregivers analyze the biological samples and read the tests of patients to update their health records.

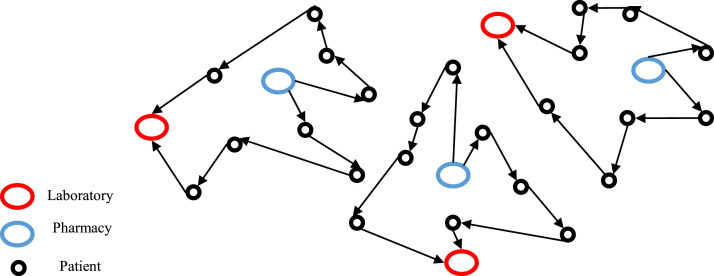
Generally, the main contribution of the proposed problem is to evaluate the patients’ satisfaction considering the privilege from patients to the caregivers for their provided home care service. This would be identified from previous data from the company. According to the explanation of the proposed problem, Fig. 1 provides an instance for the proposed problem with respect to the allocation and routing activities.

Fig. 1.

Proposed multi-depot home healthcare [13].

3.1. Problem description

Description of the proposed problem is inspired by the recent published papers in this area [3], [9], [12], [26], [31], [32]. This development is a new multi-period, multi-depot and multi-objective routing and scheduling problem for the application of the home healthcare. In this regard, let us assume that there are $M$ patients and a home healthcare company wants to provide the care. As such, there are $P$ pharmacies, each one has a capacity of $CAP{P}_p$ and $L$ laboratories, each one has a capacity of $CAP{L}_l$. In each period, the patients require a medication ($A_{it}$). After visiting the patient, the caregiver, should transport a biological sample ($B_{it}$). Each pharmacy employs $N_p$ caregivers. As such, $D_{ij}^M,D_{ip}^P$ and $D_{pl}^L$ are the distances among patients, pharmacy and laboratory, respectively. To assign the patients to pharmacies and the pharmacies to laboratories, an allocation cost is considered ($CS$).

Regarding the routing decisions, each caregiver is assigned to only one vehicle. The developed model supports different vehicles including cars and publics and so on. The transportation cost of $T{C}_k$ and capacity of $CA{P}_k$ have been considered according to the vehicles. The time window is also existed in our model. For each time period, the latest time (${\tilde{L}}_{it}$) and the earliest time (${\tilde{E}}_{it}$) of the availability of the patients are uncertain. With regards to home healthcare services, each nurse or caregiver has an estimated time to achieve the planned activities (${\tilde{W}}_{it}$). In this regard, the visit of patients i toj as the traveling time is ${\tilde{T}}_{ijt}$. The main contribution of the model is the supposition of privilege from patients to the caregivers for their provided services of the home care to increase the patients’ satisfaction (${\tilde{\lambda }}_{int}$). Notably, it is difficult to estimate this parameter and other parameters related to the time services. Due to the uncertainty of these parameters (i.e., ${\tilde{E}}_{it},{\tilde{L}}_{it},{\tilde{W}}_{it},{\tilde{T}}_{ijt},{\tilde{\lambda }}_{int}$), the tilde sign ($\mathrm{\sim }$) is considered and the fuzzy set theory will be utilized to estimate them. Furthermore, the first objective in addition to the transportation cost and allocation costs, includes the penalty of the overall distance for caregivers in order to manage the routes of caregivers and to do the travel balancing of the caregivers in each period. Accordingly, if the total number of the caregivers’ routes is higher than a value ($MDI{S}_{nkt}$), a penalty value is then considered ($PEN$).

3.2. Assumptions

This new development in the home healthcare optimization model supports the following assumptions:

• •The proposed bi-objective optimization model is a multi-period and multi-depot home healthcare optimization.
• •There is a set of time periods as the planning horizons during the activities of the proposed problem.
• •The patients’ satisfaction is considered to be optimized in addition to the total cost.
• •There is an allocation cost to assign the patients to pharmacies.
• •The vehicles have a unique cost and capacity.
• •Each patient must be assigned to one pharmacy and its demand must be satisfied as well.
• •No flow exits between the same pharmacies and laboratories.
• •Each caregiver starts from his/her pharmacy and backs to his/her laboratory at the end of each period.
• •It is assumed that the amount of medications for each patient is much higher than his/her collected biological samples.
• •The working time is uncertain and considered by the fuzzy logic.
• •The availability of patients and time windows are uncertain and estimated by the fuzzy logic.
• •The privilege from patients to the caregivers based on the provided home care services is estimated by the fuzzy numbers.
• •There is a limitation for distances traveled by the caregivers as a penalty function to do the travel balancing in the first objective.

3.3. Notations

To define the notations of the model, following indices, parameters and variables are listed:

Indices:
$k$	Index of vehicles, $k\in \{1,2,\dots ,K\}$
$i,j$	Index of patients, $i,j\in \{1,2,\dots ,M\}$
$l$	Index of laboratories, $l\in \{1,2,\dots ,L\}$
$p$	Index of pharmacies, $p\in \{1,2,\dots ,P\}$
$t$	Index of time periods, $t\in \{1,2,\dots ,T\}$
$n$	Index of caregivers for each pharmacy, $n\in \{1,2,\dots ,N_p\}$
Parameters:
$D_{ij}^M$	Distance of patientsi and j
$D_{ip}^P$	Distance of patient i and pharmacy p
$D_{pl}^L$	Distance of pharmacy p and laboratory l
$CAP{P}_p$	The capacity of pharmacy p
$CAP{L}_l$	The capacity of laboratory l
$CS$	The allocation cost per unit distance
$T{C}_k$	The transportation cost for the vehicle k
$CA{P}_k$	The capacity of vehicle k
${\tilde{W}}_{it}$	The working time of the patient i in time period t
${\tilde{\lambda }}_{int}$	The privilege from patient i to the caregiver n in time period t
${\tilde{E}}_{it}$	The earliest time of servicing to the patient i in time period t
${\tilde{L}}_{it}$	The latest time of servicing to the patient i in time period t
${\tilde{T}}_{ijt}$	The traveling time of patients i to j in time period t
$PEN$	Penalty for overall distance ($1<PEN<5$ )
$BIG$	A positive large number
$MDI{S}_{nkt}$	Maximum length of the route for each caregiver n by employing vehicle k in time period t
$A_{it}$	Demands of patient i in time period t
$B_{it}$	Biological samples from patient i in time period t
Decision variables:
$X_{ijnpl}^{kt}$	If the caregiver n started from pharmacy p to laboratory l by using vehicle k visits the patients i before j in time period t; 1; otherwise 0.
$Z_{ip}^P$	If patient i assigned to pharmacy p, 1; otherwise 0.
$Z_{pl}^L$	If pharmacy p assigned to laboratory l, 1; otherwise 0.
$S_{inpl}^t$	The time in which the caregiver n started from pharmacy p to laboratory l begins to service the patient i in time period t.
$O_{nkpl}^t$	The overall traveleddistance for the caregiver n from pharmacy p to laboratory l using vehicle k in time period t.

3.4. Formulation

The proposed mixed integer linear programming (MILP) model is established as follows:

$$\begin{array}{c}{Z}_1=min\text{(}\sum _{i=1}^M\sum _{p=1}^{P}CS\times \underset{ip}{\overset{P}{D}}\times \underset{ip}{\overset{P}{Z}}+\sum _{p=1}^P\sum _{l=1}^{L}CS\times \underset{pl}{\overset{L}{D}}\times \underset{pl}{\overset{L}{Z}}\hfill \\ +\sum _{k=1}^K\sum _{n=1}^{N_p}\sum _{i=1}^M\sum _{j=1}^M\sum _{p=1}^P\sum _{l=1}^L\sum _{t=1}^T{D}_{ij}^M\times T{C}_k\times X_{ijnpl}^{kt}\hfill \\ +\sum _{n=1}^{N_p}\sum _{k=1}^K\sum _{p=1}^P\sum _{l=1}^L\sum _{t=1}^T{O}_{nkpl}^t\times T{C}_k\times PEN\text{)}\hfill \end{array}$$ (1)

$$Z_2=max(\sum _{k=1}^K\sum _{n=1}^{N_p}\sum _{i=1}^M\sum _{p=1}^P\sum _{l=1}^L\sum _{t=1}^T{\tilde{\lambda }}_{int}\times \sum _{j=1}^M\underset{ijnpl}{\overset{kt}{X}})$$ (2)

$$s.t.\sum _{p=1}^P{Z}_{ip}^P=1,\forall i\in M$$ (3)

$$\sum _{i=1}^M{A}_i\times Z_{ip}^P\le CAP{P}_p,\forall i\in M$$ (4)

$$\sum _{p=1}^P{Z}_{pl}^L=1,\forall l\in L$$ (5)

$$\sum _{l=1}^L{Z}_{pl}^L=1,\forall p\in P$$ (6)

$$\sum _{i=1}^M\sum _{j=1}^M\sum _{n=1}^{N_p}\sum _{k=1}^K\sum _{p=1}^P{B}_{it}\times X_{ijnpl}^{kt}\le \sum _{p=1}^{P}CAP{L}_l\times Z_{pl}^L,\forall l\in L,t\in T$$ (7)

$$\sum _{n=1}^N\sum _{k=1}^K\sum _{j=1}^M\sum _{p=1}^P\sum _{l=1}^L{X}_{ijnpl}^{kt}=1,\forall i\in M,t\in T$$ (8)

$$\sum _{i=1}^M{A}_i\times \sum _{j=1}^M{X}_{ijnpl}^{kt}\le CA{P}_k,\forall k\in K,n\in N_p,p\in P,l\in L,t\in T$$ (9)

$$\begin{array}{c}\sum _{i=1}^M{X}_{ihnpl}^{kt}-\sum _{j=1}^M{X}_{hjnpl}^{kt}\hfill \\ =0,\forall h\in M,k\in K,n\in N_p,p\in P,l\in L,t\in T\hfill \end{array}$$ (10)

$$\begin{array}{c}{S}_{inpl}^t+{\tilde{T}}_{ijt}+{\tilde{W}}_{it}-BIG\times (1-X_{ijnpl}^{kt})\hfill \\ \le S_{jnpl}^t,\forall i,j\in M,k\in K,n\in N_p,p\in P,l\in L\hfill \end{array}$$ (11)

$${\tilde{E}}_{it}\le S_{inpl}^t\le {\tilde{L}}_{it},\forall i\in M,n\in N_p,p\in P,l\in L,t\in T$$ (12)

$$\begin{array}{c}{O}_{nkpl}^t\ge (\sum _{i=1}^M\sum _{j=1}^M{D}_{ij}^M\times X_{ijnpl}^{kt})\hfill \\ -MDI{S}_{nkt},\forall p\in P,l\in L,n\in N_p,k\in K,t\in T\hfill \end{array}$$ (13)

$$X_{ijnpl}^{kt}\le Z_{pl}^L,\forall i,j\in M,t\in T,l\in L,p,n\in N_p$$ (14)

$$S_{inpl}^t,O_{nkpl}^t\in R^{+}$$ (15)

$$X_{ijnpl}^{kt},Z_{ip}^P,Z_{pl}^L\in \{0,1\}$$ (16)

Eq. (1) gives the first objective ($Z_1$) indicating the total cost. The allocation of patients and pharmacies is done in the first two terms respectively. In the last two terms, the routing costs are optimized. The transportation cost is computed in the third term. Finally, the overall traveling distances of the caregivers is calculated.

Eq. (2) gives the second objective ($Z_2$) to maximize the patients’ satisfaction. Hence, the privilege adopted from patients to caregivers for their presented home care services are summed to be maximized.

Eq. (3) indicates that only one pharmacy is considered for each patient. Eq. (4) ensures that this pharmacy must satisfy the demand of the patients. Eqs. (5), (6) confirm the allocation of the pharmacy and laboratory in the case of one by one. Eq. (7) ensures that the capacity of the laboratory must be enough for allocated patients for their biological tests. Eq. (8) limits that each patient is met once only. Eq. (9) ensures that the capacity of the selected vehicle must be enough for the demand of the patients. Eq. (10) presents that after each visit, the caregiver must starts a new visit. Regarding the limitations of the time window, Eq. (11) confirms the arriving of patient j before $S_{inpl}^t+{\tilde{T}}_{ijt}+{\tilde{W}}_{it}$. Accordingly, BIG is a large scalar number. Eq. (12) reveals the time window of the patients in each time period. Eq. (13) computes the extra distance of caregivers if it is more than a maximum desired value. Eq. (14) shows that the allocation and routing decisions have a correlation with each other. At the end, Eqs. (15), (16) ensure the feasibility of decision variables for the proposed model.

Having a conclusion about the proposed model, this paper firstly contributes a bi-objective, multi-period and multi-depot and home healthcare considering the patients’ satisfaction as well as a penalty for overall distance to this research area.

3.5. Proposed fuzzy model

The proposed model has some uncertain parameters (i.e., ${\tilde{E}}_{it},{\tilde{L}}_{it},{\tilde{W}}_{it},{\tilde{T}}_{ijt},{\tilde{\lambda }}_{int}$). This study uses the fuzzy logic by using triangular fuzzy numbers which can help decision-makers to estimate the time windows of availability for caregivers and patients in addition to their satisfaction measurement. All these uncertain factors can be estimated by three possible scenarios including optimistic, realistic and pessimistic ones based on the fact of the triangular fuzzy numbers. We have defined the fuzzy logic to transform the optimization model in Section 3.4 into a definite equivalent model and then solve it by standard optimization methods to find the optimal solution.

Here, the developed problem considering fuzzy parameters is first assessed by a certain auxiliary model as introduced by Jimenez et al. [36] called the Jimenez’s method. Then, the model is transform to a multi-objective deterministic model based on the approach of Torabi–Hassini method [37] due to the proposed bi-objective a routing and scheduling problem for the application of the home healthcare.

3.5.1. Jimenez’s method

Jimenez et al. [36] presented a methodology to rank fuzzy numbers. In this method, triangular fuzzy numbers are considered to represent the fuzzy parameters [38], $\tilde{c}=\left(c^r,c^q,c^s\right)$. These three numbers for each fuzzy number can be estimated by optimistic, realistic and pessimistic scenarios [39], [40], [41]. As given in Eqs. (17), (18), we compute the expected value (EV) for a triangular fuzzy number $\left(\tilde{c}\right)$.

$$EV\left(\tilde{c}\right)=\left[E_1^c,E_1^c\right]=\left[{\int }_0^1{f}_c^{-1}\left(x\right)d_x,{\int }_0^1{g}_c^{-1}\left(x\right)d_x\right]=\left[{\int }_0^1\left(x\left(c^q-c^r\right)+c^r\right)d_x\right]=\left[{\int }_0^1\left(x\left(c^s-c^q\right)+c^s\right)d_x\right]=\left[\frac{1}{2}\left(c^r+c^q\right),\frac{1}{2}\left(c^q+c^s\right)\right]$$ (17)

$$EV\left(\tilde{c}\right)=\frac{E_1^c+E_1^c}{2}=\frac{c^r+2c^q+c^s}{4}$$ (18)

In this regard, the following transformation is also used for the constraints related to fuzzy parameters i.e., $({\tilde{a}}_{i}X\ge {\tilde{b}}_i,i=1,2,\dots ,I)$ and note that $\tilde{a}=\left(a^r,a^q,a^s\right)$ and $\tilde{b}=\left(b^r,b^q,b^s\right)$ and $\left(\alpha \right)$ is the feasibility level.

$$\begin{array}{c}\left(\alpha \frac{a_i^s+a_i^q}{2}+\left(1-\alpha \right)\times \frac{a_i^r+a_i^q}{2}\right)X\hfill \\ \ge \left(\alpha \frac{b_i^s+b_i^m}{2}+\left(1-\alpha \right)\times \frac{b_i^r+b_i^q}{2}\right)\hfill \end{array}$$ (19)

To have an equal constraint such as (${\tilde{a}}_{i}X={\tilde{b}}_i,i=1,2,\dots ,I$), the following equations are used to convert this constraint into the certain equivalent constraints as reported in Eqs. (20), (21):

$$\begin{array}{c}\left(\frac{\alpha }{2}\times \frac{a_i^s+a_i^q}{2}+\left(1-\frac{\alpha }{2}\right)\times \frac{a_i^r+a_i^q}{2}\right)X\hfill \\ \ge \left(\frac{\alpha }{2}\times \frac{b_i^s+b_i^q}{2}+\left(1-\frac{\alpha }{2}\right)\times \frac{b_i^r+b_i^q}{2}\right)\hfill \end{array}$$ (20)

$$\begin{array}{c}\left(\left(1-\frac{\alpha }{2}\right)\times \frac{a_i^s+a_i^q}{2}+\frac{\alpha }{2}\times \frac{a_i^r+a_i^q}{2}\right)X\hfill \\ \ge \left(\left(1-\frac{\alpha }{2}\right)\times \frac{b_i^s+b_i^q}{2}+\frac{\alpha }{2}\times \frac{b_i^r+b_i^q}{2}\right)\hfill \end{array}$$ (21)

After defuzzifying the constraints, the membership function is employed by applying Torabi–Hassini method proposed in 2008 [37] as given in Eq. (22).

$${\mu }_F=\left\{\begin{array}{cc}1\hfill & ifZ<Z^{\alpha -PIS}\hfill \\ \frac{Z^{\alpha -NIS}-Z}{Z^{\alpha -NIS}-Z^{\alpha -PIS}}\hfill & if{Z}^{\alpha -PIS}\le Z\le Z^{\alpha -NIS}\hfill \\ 0\hfill & ifZ>Z^{\alpha -NIS}\hfill \end{array}\right)$$ (22)

As such, for a maximization objective function, the following membership is utilized as given in Eq. (23).

$${\mu }_F=\left\{\begin{array}{cc}1\hfill & ifZ>Z^{\alpha -PIS}\hfill \\ \frac{Z^{\alpha -NIS}-Z}{Z^{\alpha -PIS}-Z^{\alpha -NIS}}\hfill & if{Z}^{\alpha -NIS}\le Z\le Z^{\alpha -PIS}\hfill \\ 0\hfill & ifZ>Z^{\alpha -NIS}\hfill \end{array}\right)$$ (23)

where the positive $\left(\alpha -PIS\right)$ and the negative $\left(\alpha -NIS\right)$ ideal solutions of the objective functions at the feasibility level $\left(\alpha \right)$ should be calculated by optimizing each objective function separately [9], [13], [42], [43], [44].

In conclusion, the formulation of the fuzzy model are the same as the deterministic one except for the uncertain parameters (i.e., ${\tilde{E}}_{it},{\tilde{L}}_{it},{\tilde{W}}_{it},{\tilde{T}}_{ijt},{\tilde{\lambda }}_{int}$). The following notations are defined and used:

${\mathrm{W}}_{it}^r$	Optimistic scenario for the working time of the patient i in time period t
${\mathrm{W}}_{it}^q$	Realistic scenario for the working time of the patient i in time period t
${\mathrm{W}}_{it}^s$	Pessimistic scenario for the working time of the patient i in time period t
${\lambda }_{int}^r$	Optimistic scenario for the privilege from patient i to the caregiver n in time period t
${\lambda }_{int}^q$	Realistic scenario for the privilege from patient i to the caregiver n in time period t
${\lambda }_{int}^s$	Pessimistic scenario for the privilege from patient i to the caregiver n in time period t
${\mathrm{E}}_{it}^r$	Optimistic scenario for the earliest time of servicing to the patient i in time period t
${\mathrm{E}}_{it}^q$	Realistic scenario for the earliest time of servicing to the patient i in time period t
${\mathrm{E}}_{it}^s$	Pessimistic scenario for the earliest time of servicing to the patient i in time period t
${\mathrm{L}}_{it}^r$	Optimistic scenario for the latest time of servicing to the patient i in time period t
${\mathrm{L}}_{it}^q$	Realistic scenario for the latest time of servicing to the patient i in time period t
${\mathrm{L}}_{it}^s$	Pessimistic scenario for the latest time of servicing to the patient i in time period t
${\mathrm{T}}_{ijt}^r$	Optimistic scenario for the traveling time of patients i to j in time period t
${\mathrm{T}}_{ijt}^q$	Realistic scenario for the traveling time of patients i to j in time period t
${\mathrm{T}}_{ijt}^s$	Pessimistic scenario for the traveling time of patients i to j in time period t

With regards to above definitions, the following certain auxiliary model is the equivalent to the main model in Section 3.4 as given in Eqs. (24) to (29).

$$\text{Eq. }\text{(1)}$$ (24)

$$\begin{array}{c}{Z}_2=\max \text{(}\sum _{k=1}^K\sum _{n=1}^{N_p}\sum _{i=1}^M\sum _{p=1}^P\sum _{l=1}^L\sum _{t=1}^T\left(\frac{{\lambda }_{\mathrm{int}}^r+2{\lambda }_{\mathrm{int}}^q+{\lambda }_{\mathrm{int}}^s}{4}\right)\hfill \\ \times \sum _{j=1}^M{X}_{ijnpl}^{kt}\text{)}\hfill \end{array}$$ (25)

$$s.t.$$

$$\text{Eqs. }\text{(3)}\text{ to }\text{(10)}$$ (26)

$$\begin{array}{c}{S}_{inpl}^t+(\frac{\alpha }{2}\times \frac{{\mathrm{T}}_{ijt}^s+{\mathrm{T}}_{ijt}^q}{2}+\left(1-\frac{\alpha }{2}\right)\times \frac{{\mathrm{T}}_{ijt}^r+{\mathrm{T}}_{ijt}^q}{2})\hfill \\ +(\frac{\alpha }{2}\times \frac{{\mathrm{W}}_{it}^s+{\mathrm{W}}_{it}^q}{2}+\left(1-\frac{\alpha }{2}\right)\times \frac{{\mathrm{W}}_{it}^r+{\mathrm{W}}_{it}^q}{2})\hfill \\ -BIG\times (1-X_{ijnpl}^{kt})\le S_{jnpl}^t;\hfill \\ \forall i,j\in M,k\in K,n\in N_p,p\in P,l\in L\hfill \end{array}$$ (27)

$$\begin{array}{c}\frac{\alpha }{2}\times \frac{{\mathrm{E}}_{it}^s+{\mathrm{E}}_{it}^q}{2}+\left(1-\frac{\alpha }{2}\right)\times \frac{{\mathrm{E}}_{it}^r+{\mathrm{E}}_{it}^q}{2}\hfill \\ \le S_{inpl}^t\le \frac{\alpha }{2}\times \frac{{\mathrm{L}}_{it}^s+{\mathrm{L}}_{it}^q}{2}+\left(1-\frac{\alpha }{2}\right)\times \frac{{\mathrm{L}}_{it}^r+{\mathrm{L}}_{it}^q}{2}\hfill \\ \forall i\in M,n\in N_p,p\in P,l\in L,t\in T\hfill \end{array}$$ (28)

$$\text{Eqs. }\text{(13)}\text{ to }\text{(16)}$$ (29)

4. Solution algorithm

As it is obvious, the routing problems are complex and NP-hard [2], [33]. Based on this feature, many new heuristics and metaheuristics are existed in the literature [4]. To solve the proposed problem, not only non-dominated sorting GA (NSGA-II) and multi-objective of SEO and SA are utilized, but also an adaptive memory SEO (AMSEO) is developed to better address the proposed routing and scheduling problem for the application of the home healthcare. In this section, an encoding representation is provided to show that how the metaheuristics can handle the problem and constraints. Then, the general idea of the multi-objective SEO is introduced. Finally, one of the main contributions is discussed to introduce an efficient modification of SEO using adaptive memory strategy. Note that since NSGA-II and SA are very popular in the literature, the description of its multi-objective version is not provided and can be referred to [13], [39], [45], [46], [47], [48].

4.1. Encoding representation

Since metaheuristics use the continuous search space, an encoding representation is needed to generate the feasible solutions to cover the constraints of model [10], [49]. This encoding representation also connects the optimization algorithms to the proposed optimization problem [50]. One of the well-known techniques for the solution scheme is the random key [51], [52], [53]. This strategy uses two stages and saves the time to search. It needs no repair to generate a feasible solution as well [50], [51], [52]. Here, this tool is considered to address the proposed home healthcare routing and scheduling problem.

At first, the patients to pharmacies ($Z_{ip}^P$) and to laboratories ($Z_{pl}^L$) assignments are calculated by Fig. 2, Fig. 3, respectively. As indicated in Fig. 2, by using the randomization of the metaheuristics, for three pharmacies, ten patients are allocated. For example, the patients $m_1$, $m_9$ and $m_{10}$ are considered for pharmacy $P_2$.

Fig. 2.

The patients to pharmacies assignment [12].

Fig. 3.

The assignment of pharmacies and laboratories [13].

As such, Fig. 3 shows the assignment of pharmacies and laboratories. Accordingly, an encoding scheme of the priority-based adopted by Samanlioglu et al. [53] is used. The assignment is planed one by one. For example, the first pharmacy is allocated to the second laboratory.

To start the planning of caregivers, first of all, the used vehicles for each caregiver is chosen. A matrix with the length of N is considered. $U(0,K)$ as a uniform distribution where K is the number of vehicles provided in the first phase. These numbers are rounded to clarify the vehicle of each caregiver. An example of this procedure is revealed by Fig. 4. Accordingly, for caregiver $n_1,n_2$ and $n_4$, the second vehicle type is used. For caregivers $n_3$ and $n_5$, the first and third types of vehicles are selected.

Fig. 4.

The allocation type of vehicles to caregivers [13].

At the end, to choose the patients’ route, $U(0,1)$ is considered to generate the sequence of 12 patients for this example. Fig. 5 shows an example accordingly. We need to sort and to specify the routes based on the adopted technique to satisfy the total desired traveling distance ($MDI{S}_{nkt}$), the vehicle capacity ($CA{P}_k$) and the time window’s limitation [32], [41]. Note that this encoding plan is repeated for each time period. Overall, the following route as an example for the second caregiver is generated regarding the example of Fig. 5:

$$n_2=\{m_5\to m_{11}\to m_3\}$$

Fig. 5.

Assignment of patients to each caregivers’ route [12].

4.2. Multi-objective SEO

This is the first research to apply a multi-objective of SEO and its new extension to the area of the home healthcare optimization. As a metaheuristic, the SEO has several advantages and a few disadvantages. In comparison with many swarm- and population-based metaheuristics, this algorithm is a new single point and local search metaheuristic. It has only three parameters to tune and the operators can mathematically change the position of solutions in the feasible search space.

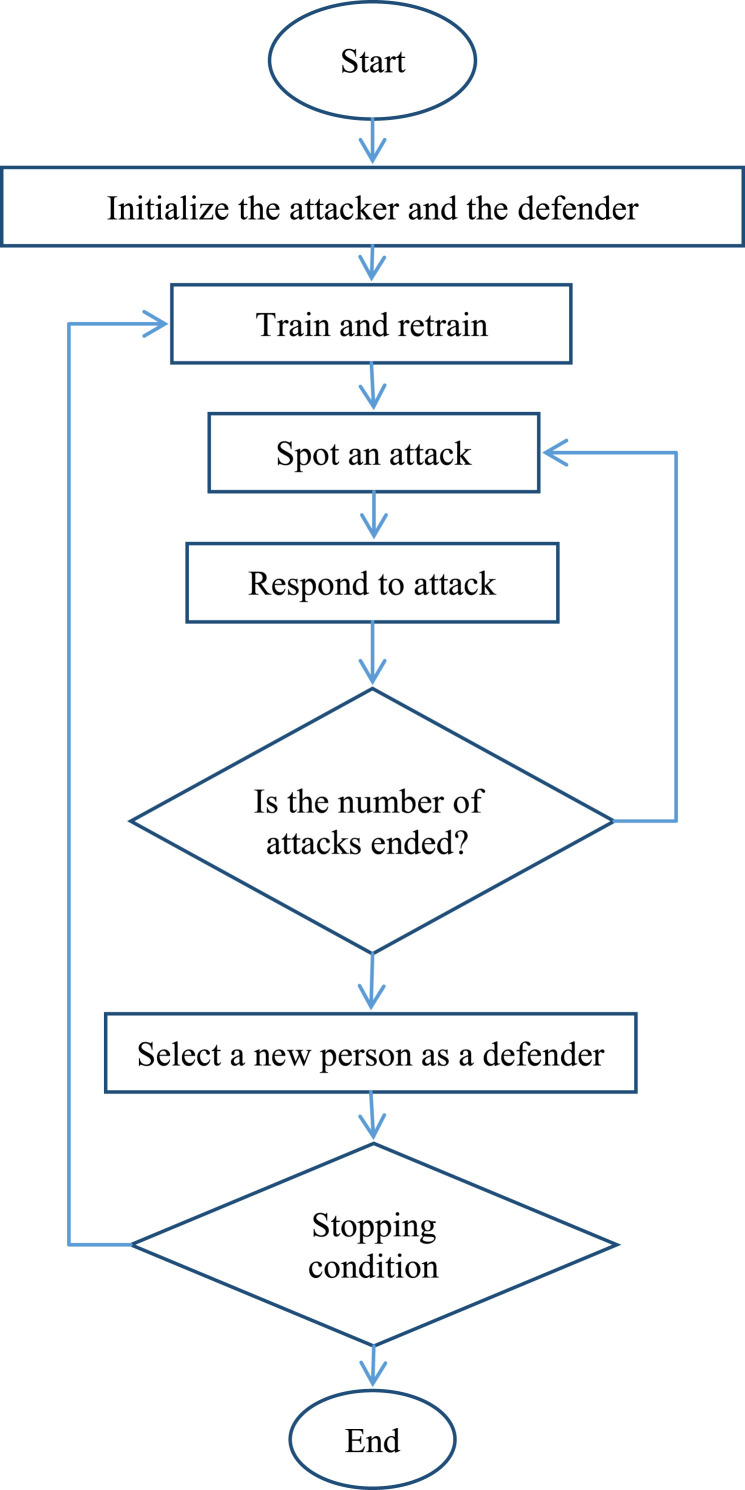
With regards to the randomization of SEO, two random solutions are firstly generated. The better performing solution of the two is then nominated as the attacker, and another one is the defender. Following Fathollahi-Fard et al. [15], and as shown in Fig. 6, the SEO randomly applies four techniques as the main search engine of the algorithm. As each technique is applied, and the defender values are modified in response to the attack, the fitness for the purpose of the changed defender position is compared with the previous values. The better position is adopted. If the defender fitness become stronger than the attacker, we will face an exchanging of the attacker and defender. The process is repeated until the attacks end, at which point the current defender is deleted and a new random solution is generated to replace it. In the following, its multi-objective version is illustrated.

Fig. 6.

Flowchart of the SEO algorithm [15].

The proposed home healthcare optimization for the routing and scheduling framework confirms a bi-objective optimization problem. The objectives are to minimize the total cost and to maximize the patients’ satisfaction. A Pareto-based algorithm is required to find the interaction between these objective functions [9], [13], and a multi-objective version of SEO is applied below.

Generally, the solution of any multi-objective model is a set of candidate solutions in the form of a Pareto optimal frontier [54], [55]. The best set of candidate solutions are those non-dominated solutions when compared to other candidates [56]. One solution will dominate another during the comparison if it has better fitness in at least one of the objective functions [38]. In this manner, a non-dominated solution set is generated. Fig. 7 provides a pseudo-code description of this process in SEO.

Fig. 7.

Pseudo code for a multi-objective version of SEO [15].

4.3. Adaptive memory of SEO (AMSEO)

Further to this first attempt to apply SEO to the home healthcare area, a new extension of the SEO is also proposed and considered using an adaptive memory approach (AMSEO). For SEO, the training and retraining steps and how to determine an attack are generally the main operators of the search engine. The proposed AMSEO is a comprehensive improvement in these phases, especially in real cases. Most notably, the proposed AMSEO is clearly different from other variants of SEO in its literature [57], [58].

In the clear majority of metaheuristic approaches, the general goal is to provide a better interaction between the exploration and exploitation search phases [4], [57]. Exploitation is typically the most demanding of the two. Given that the training and retraining phase is key to the exploitation phase, the proposed extension is to make that process more efficient. For the existing SEO training and retraining of the attacker, a percentage of defender traits as $\alpha$ is selected randomly. Rather than employing an arbitrary selection process, the AMSEO extension identifies if any specific trait is having a generally successful impact on the defender over the course of different iterations (whereupon the new defender can dominate the old one). Whenever any such trait is identified, the selection process is modified so that this trait can increase the chance of selection. The selection process adapts to reflect the more successful patterns of selection, learned over time. For example, consider that there are four traits and the initial rate of $\alpha$ is to weight each probability of selection equally, at 0.25 for each, $\mathrm{\{}$0.25, 0.25, 0.25, 0.25$\mathrm{\}}$. Over time the rates of success for each trait is recorded, and the relative probabilities adjusted accordingly. Thus, for a rate of success across the four traits of $\mathrm{\{}$3, 4, 2, 2$\mathrm{\}}$, the selection probabilities are adjusted to $\mathrm{\{}$0.27, 0.36, 0.18, 0.18$\mathrm{\}}$, respectively.

5. Computational experiments

In this section, extensive comparison and analyses are performed to evaluate the proposed model and the solution algorithm. First, the benchmark test problems are utilized to define instances with different complexities. Then, the algorithms are calibrated to enhance their capability to solve the problem fairly. The validation of the algorithms and results are checked. Next, a comparative study is done to evaluate the algorithms and show the superiority of the proposed one. Consequently, some sensitivities have been performed to evaluate the key parameters of the model. Eventually, to highlight the main findings, a discussion to show the managerial insights is provided.

5.1. Instances

To examine the model by different solution algorithms, some benchmark tests from recent papers [9], [12] are taken into consideration. The twelve instances with respect to the small, medium and large classifications as reported in Table 2. The computational time of metaheuristics is also controlled by the complexity of test problem by using equal time to search the solutions. In this regard, the metaheuristics are run for 30, 60 and 100 s for small, medium and large sizes, respectively. Regarding the parameters of the model, the details about their distribution are given in Table 3. Notably, each day is two periods i.e., morning and evening. Each period is eight hours as well. The planning horizon for our generated test problems are varied from one day to maximum three weeks.

Table 2.

The size of instances.

Level	Instance	Laboratories ($L$) and pharmacies ($P$)	Caregivers ($N_p$)	Vehicles ($K$)	Patients ($M$)	Periods ($T$)
Small	SP1	2	2	2	10	2
	SP2	2	3	2	25	4
	SP3	4	4	3	40	6
	SP4	6	6	3	65	8
Medium	MP5	8	8	3	80	14
	MP6	9	8	4	85	18
	MP7	9	9	5	95	24
	MP8	10	10	5	100	28
Large	LP9	12	12	6	120	32
	LP10	14	15	6	150	36
	LP11	16	16	7	160	40
	LP12	18	20	8	200	42

Table 3.

The details about the computation of model’s parameters.

Parameters	Distribution
$(x_i,y_i)$	$1000\times (U(0,1),U(0,1))$
$(x_j,y_j)$	$1000\times (U(0,1),U(0,1))$
$(x_p,y_p)$	$1000\times (U(0,1),U(0,1))$
$(x_L,y_L)$	$1000\times (U(0,1),U(0,1))$
$D_{ij}^M$	$\sqrt{{(x_i-x_j)}^2+{(y_i-y_j)}^2}$
$D_{ip}^P$	$\sqrt{{(x_i-x_p)}^2+{(y_i-y_p)}^2}$
$D_{pl}^L$	$\sqrt{{(x_p-x_L)}^2+{(y_p-y_L)}^2}$
$A_{it}$	$rand\{5,10,\dots ,100\}$
$CAP{P}_p$	$rand\{800,900,\dots ,2000\}$
$B_{it}$	$rand\{1,2,\dots ,30\}$
$CAP{L}_L$	$rand\{50,60,\dots ,100\}$
$BIG$	10000
$PEN$	For small sizes: 1.5, medium sizes: 3, large sizes: 4.5
$T{C}_k$	$rand\{10,11,\dots ,1000\}$
$CA{P}_k$	$rand\{200,300,\dots ,10000\}$
${\tilde{W}}_{it}$	${\mathrm{W}}_{it}^r=rand\{5,10,\dots ,20\}$
	${\mathrm{W}}_{it}^q=rand\{20,25,\dots ,40\}$
	${\mathrm{W}}_{it}^s=rand\{40,45,\dots ,60\}$
${\tilde{E}}_{it}$	${\mathrm{E}}_{it}^r=rand\{0,1,\dots ,3\}$
	${\mathrm{E}}_{it}^q=rand\{3,4,\dots ,7\}$
	${\mathrm{E}}_{it}^s=rand\{7,8,\dots ,10\}$
${\tilde{L}}_{it}$	${\mathrm{L}}_{it}^r=rand\{500,1000,\dots ,2000\}$
	${\mathrm{L}}_{it}^q=rand\{1000,1500,\dots ,3000\}$
	${\mathrm{L}}_{it}^s=rand\{2500,3000,\dots ,5000\}$
${\tilde{T}}_{ijt}$	${\mathrm{T}}_{ijt}^r=\frac{D_{ij}^M}{{\sum }_{i=1}^M{\sum }_{j=1}^M{D}_{ij}^M}\times 120\times S$a
	${\mathrm{T}}_{ijt}^q=\frac{D_{ij}^M}{{\sum }_{i=1}^M{\sum }_{j=1}^M{D}_{ij}^M}\times 90\times S$a
	${\mathrm{T}}_{ijt}^s=\frac{D_{ij}^M}{{\sum }_{i=1}^M{\sum }_{j=1}^M{D}_{ij}^M}\times 70\times S$a
${\tilde{\lambda }}_{int}$	${\lambda }_{int}^r=rand\{1,2,\dots ,5\}$
	${\lambda }_{int}^q=rand\{5,6,\dots ,10\}$
	${\lambda }_{int}^s=rand\{11,12,\dots ,15\}$
$MDI{S}_{nkt}$	$rand\{25000,30000,\dots ,50000\}$
$CS$	2

^aSpeed transfer coefficient based on the vehicles for transferring between patient i and j.

5.2. Calibration

Since the proposed home healthcare optimization problem has two objectives as a multi-objective optimization problem, the evaluation of algorithms in a multi-objective optimization uses Pareto-based assessment metrics [38]. This paper uses four popular evaluation metrics: the number of Pareto solutions (NPS) [9], the spread of non-dominance solutions (SNS) [48], mean ideal distance (MID) [13], and hyper volume (HV) [49]. In all of these metrics except MID, a higher value brings a better capability of algorithm to solve the problem. Since these metrics are well-known, more details about their definition and formulation can be referred to other similar studies.

Before starting the problem solving, it is required to tune the algorithms’ parameters. For calibration, various methods have been proposed, including Response Surface Method (RSM), Taguchi experimental design method, and F-Race methods. This study employs the RSM, first introduced by Box and Wilson [59]. In the RSM, based on the range of each factor as the input parameter of metaheuristics, the response value is computed as a measure for the overall desirability of the optimizer. Each factor ($x_i$) is coded as −1 to 1, relative to the low ($x_l$) and high ($x_h$) levels given by the selected range. Hence, the independent variables ($z_i$) related to each factor is generated by:

$$z_i=(\left(\frac{x_i-(x_h+x_l)}{(x_h-x_l)}\right)÷1∕2),i=\{1,2,\dots ,K\}$$ (30)

The variables’ number is shown by K. Then, a regression model to analyze the responses for each factor is considered [49]. To start the RSM, the employed optimizers are given in Table 4, along with their factors based on their range. More details about this methodology can be referred to [7], [15], [48].

Table 4.

Calibration of the algorithms.

Algorithm	Factors and their surface value			Total number of treatments$=$ ($n_f$, $n_{ax}$, $n_{cp}$)
SA	SubIt	T0	$R_{\propto }$	20=(23, 6, 6)
	(20, 50)	(500, 1000)	(0.99, 0.999)
NSGA-II	nPop	Pc	Pm	20=(23, 6, 6)
	(100, 150)	(0.65, 0.8)	(0.05, 0.2)
SEO and AMSEO	$N_{att}$	$\alpha$	$\beta$	20=(23, 6, 6)
	(10, 70)	(0.1, 0.4)	(0.05, 0.25)

A utility function proposed by Derringer and Suich [60] is applied to assess the metrics of each Pareto-optimal set, and optimize the multiple responses of the RSM, as computed by:

$$d_i\left(y_i\right)={\left(\frac{h_i-y_i}{h_i-l_i}\right)}^s,l_i<y_i<h_i$$ (31)

where the multiple response $y_i$ is transformed into the measurement of the utility function ($d_i$). $l_i$ and $h_i$ are the lower and upper bounds of response variables, respectively. The utility function is emphasized by $s$. Accordingly, the relative importance of the metrics is taken from the literature [9], [13], [48], [49]. The desirability of the algorithm in terms of the number of utility functions is computed by:

$$D=\sqrt[m]{d_1\left(y_1\right)\times d_2\left(y_2\right)\times \dots \times d_m\left(y_m\right)}$$ (32)

Notably, the evaluation metrics number are m. As such, D is the total desirability of the algorithm. It is evident that the higher the value of D, the more favorable is the algorithm.

Table 5 presents the approximate values of the tuned parameters, the R-squared (R ${}^2$) of assessment metrics, and the total desirability (D). Notably, R ${}^2$ measures statistically how closely the outputs fit the line of regression. The range of R ${}^2$ is always between 0 and 100%. Similar to the desirability, the higher the value of R ${}^2$, the more favorable is the algorithm.

Table 5.

Calibrated parameters of each algorithm, their respective R-squared (R²) and desirability (D).

Algorithm	Calibrated parameters	R2 (%)				D
		NPS	MID	SNS	HV
SA	Sb-It$=$32; T0$=$700; $R_{\propto }=0.9396$	54	72	60	58	0.6634
NSGA-II	nPop$=$125; Pc$=$0.75; Pm$=$0.15;	56	82	62	64	0.6893
SEO	$N_{att}=38$; $\alpha =0.15$; $\beta =0.15$	58	86	62	66	0.7238
AMSEO	$N_{att}=45$; $\alpha =0.25$; $\beta =0.1$	52	78	72	78	0.7581

5.3. Validation

The validation is needed to check the reliability of algorithms’ results. An epsilon constraint (EC) method firstly offered by Haimes et al. [61] is employed to solve the small instances. In this method, the objective function bounds are modified to generate a Pareto set [9], [13]. The formulation of this methodology given in Eq. (33) is based on the structure of the developed bi-objective home healthcare problem.

$$\begin{array}{c}min{Z}_1\hfill \\ \mathit{s.t.}\hfill \\ \text{Eqs. }\text{(26)}-\text{(29)}\hfill \\ Z_2\ge \epsilon \hfill \\ Z_2^{min}\le \epsilon \le Z_2^{max}\hfill \end{array}$$ (33)

To run the EC for a test problem (e.g., SP1), the main objective function ($Z_1$) should be minimized. To reach the PIS and NIS, the second objective ($Z_2$) should be considered as the main objective to be maximized. To estimate the bound of the EC method ($\epsilon$), the average of the PIS and NIS, and the upper quarter between the average and both PIS and NIS, are calculated.

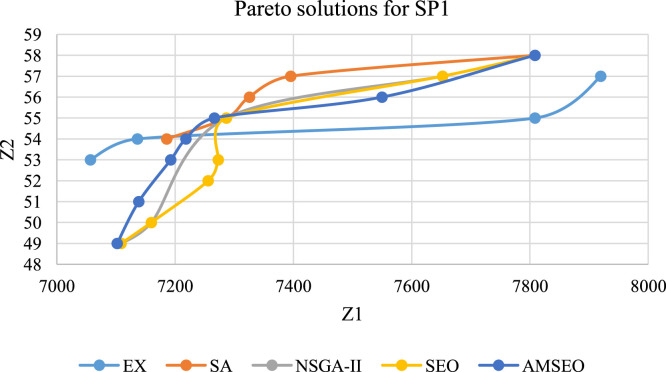
To ease the evaluation of solutions, the sorted ones for the three metaheuristics and the EC method are tabulated, as given for SP1 in Table 5. A graphical explanation of these solutions is given in Fig. 8. To validate the results of the metaheuristics, the non-dominated solutions are compared with the solutions of the EC. Based on this assessment, a modified NPS (MNPS) is the number of Pareto solutions as compared with the exact method that can be classified as the non-dominated solutions [25], [48]. Accordingly, the percentage of the MNPS from all generated Pareto solutions ($\frac{MNPS}{NPS}$) measures the performance of each metaheuristic. The higher the percentage, the more reliable the results. Table 7 provides a summary of results for each of the algorithms relative to the small problem levels.

Fig. 8.

Non-dominated solutions of all the algorithms in SP1.

Table 7.

Validation of each metaheuristic.

Test problem	SA		NSGA-II		SEO		AMSEO
	MNPS	MNPS/NPS	MNPS	MNPS/NPS	MNPS	MNPS/NPS	MNPS	MNPS/NPS
SP1	4	0.8	3	0.6	5	0.71	6	0.85
SP2	6	0.75	7	0.7	8	0.88	10	0.90
SP3	7	0.77	9	0.9	10	0.9	11	0.91
SP4	7	0.7	10	0.72	11	0.91	12	0.85
Average		0.75		0.73		0.85		0.88

The results of the validation, as noted in Table 6, show that all four metaheuristics generate good quality Pareto solutions, with AMSEO performing the best in each case. It can be observed in Fig. 8 that the solutions of AMSEO can outperform the other solutions. The strength of the AMSEO is demonstrated in the results provided in Table 7, where the average number of Pareto non-dominated solutions relative to the EC method is shown to be 0.88, and it is significantly higher than those of SA (0.75), NSGA-II (0.73) and the original version of SEO (0.85).

Table 6.

Pareto solutions for test problem SP1.

EC		SA		NSGA-II		SEO		AMSEO
$Z_1$	$Z_2$	$Z_1$	$Z_2$	$Z_1$	$Z_2$	$Z_1$	$Z_2$	$Z_1$	$Z_2$
7056.8	53	7185.7	54	7108.6	49	7108.6	49	7102	49
7136.2	54	7286.6	55	7159.7	50	7159.7	50	7138.5	51
7808.4	55	7325.7	56	7286.6	55	7255.8	52	7192.5	53
7919.5	57	7395.4	57	7652.1	57	7272.9	53	7218.2	54
–	–	7808.4	58	7808.4	58	7286.6	55	7266.4	55
–	–	–	–	–	–	7652.1	57	7549.7	56
–	–	–	–	–	–	7808.4	58	7808.4	58

5.4. Comparison

Here, the comparison among the algorithms is done. Regarding the metrics including NPS, MID, SNS and HV as introduced earlier, the performance of each metaheuristic is recorded for each test problem, and all results are given in Table 8. The best values in each metric for each problem are highlighted in bold. The comparison indicates that AMSEO outperforms the other algorithms by having the highest count of best cases in every evaluation metric (shown in the final row of Table 8), and overall by a factor of 27 (AMSEO) to 11 (SEO) to 6 (SA) to 5 (NSGA-II).

Table 8.

Results of the evaluation metrics for each metaheuristic.

Test problem	NPS				MID				SNS				HV
	SA	NSGA-II	SEO	AMSEO	SA	NSGA-II	SEO	AMSEO	SA	NSGA-II	SEO	AMSEO	SA	NSGA-II	SEO	AMSEO
SP1	5	5	7	7	2.7	2.3	1.45	1.6567	39053	39418.5	33613	42156	2.86E＋09	1.58E＋09	1.98E＋09	2.17E＋09
SP2	8	10	9	11	1.41	1.6	3.18	1.3832	71532	78760.5	72664	84093	2.91E＋09	5.83E＋09	2.85E＋09	3.81E＋09
SP3	9	10	11	12	1.88	2.12	3.41	2.5528	103674	104004	105584	104846	3.84E＋09	4.33E＋09	4.81E＋09	5.36E＋09
SP4	10	14	12	14	1.7	1.85	1.62	1.2058	116854	117621.5	113207	118923	5.18E＋09	4.58E＋09	3.97E＋09	6.48E＋09
MP5	11	12	14	12	3.53	2.85	2.19	1.1014	199064	204185.5	206584	209671	4.82E＋09	5.00E＋09	5.18E＋09	8.13E＋09
MP6	10	12	10	13	2.63	1.85	2.26	1.1175	298976	283356.5	225643	268749	6.49E＋09	9.46E＋09	5.92E＋09	8.92E＋09
MP7	11	12	13	15	1.41	1.054	2.62	1.1044	289074	306566.5	319065	326843	8.18E＋09	7.44E＋09	7.39E＋09	7.49E＋09
MP8	10	13	14	13	4.23	2.67	2.66	1.3081	375463	380037.5	382970	385034	9.22E＋09	8.63E＋09	8.14E＋09	9.11E＋09
LP9	14	12	13	13	1.97	1.86	3.71	2.8128	519065	546744	563271	573297	8.50E＋09	1.13E＋10	9.60E＋09	1.29E＋10
LP10	10	13	15	16	1.59	1.98	1.19	2.1869	40937	43501	45748	46743	2.18E＋10	2.34E＋10	1.82E＋10	2.85E＋10
LP11	12	13	14	14	1.96	1.654	1.17	1.5879	76134	72212	79267	70864	1.03E＋10	1.41E＋10	1.43E＋10	1.39E＋10
LP12	12	14	16	15	3.26	2.56	2.11	2.51	100689	100466.5	106429	101948	4.81E＋10	1.46E＋1	12.81E＋10	2.64E＋11
Best	1	1	4	7	1	2	3	6	1	0	3	8	3	2	1	6

To determine the best algorithm overall, the results reported in Table 8 are scaled using a transformation metric called the relative deviation index (RDI). Accordingly, the following formula is utilized by:

$$RDI=\frac{|I{D}_{sol}-A{L}_{sol}|}{MA{X}_{sol}-MI{N}_{sol}}$$ (34)

where $A{L}_{sol}$ is the value given by the assessment metric to assess the Pareto optimal sets. As such, $MA{X}_{sol}$ and $MI{N}_{sol}$ are the maximum and minimum possible values for the assessment metrics, respectively. Note that based on the nature of the assessment metric, $I{D}_{sol}$ would be one of $MA{X}_{sol}$ or $MI{N}_{sol}$. The lower the value of RDI, the better the performance of the algorithm.

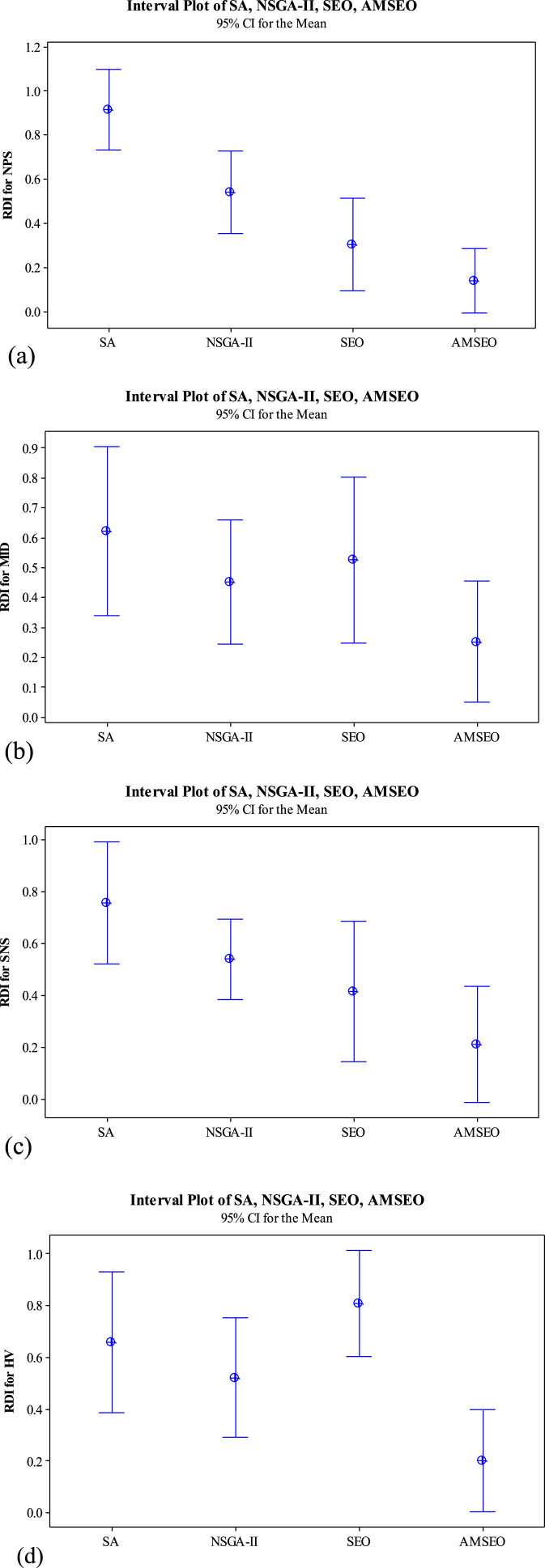
In order to determine the efficiency in this comparison, interval plots at the 95% statistical confidence level are provided in Fig. 9. These plots are based on the RDI metric. As is indicated in Fig. 9a, the performance of AMSEO is better than those of SEO, NSGA-II and SA in terms of the NPS. But, as is indicated in Fig. 9b, the performance of AMSEO is far superior as compared to those of other alternatives in terms of the MID metric. Moreover, the NSGA-II is slightly better than SEO and the SA shows the weakest point in this metric as well. As indicated in Fig. 9c, the performance of AMSEO is clearly better than those of other algorithms in terms of the SNS. As shown in Fig. 9d, the performance of AMSEO is once again far superior to other alternatives in terms of the HV metric.

Fig. 9.

Interval plots of the RDI metric for (a) NPS, (b) MID, (c) SNS, and (d) HV.

5.5. Sensitivity analysis

To validate the parameters of the model and their impacts on the total cost and satisfaction, some sensitivities are performed. A test problem is needed such as SP3 to do the analyses as its properties had been introduced in Table 2. To solve the model, the best metaheuristic in this study i.e., AMSEO is selected to do the sensitivities.

Since the model is multi-objective, to search the best solution among all non-dominated ones, the criterion of the lowest distance with the ideal solution in the best Pareto set, is selected by MID metric. To do the sensitivity analysis, some important parameters are chosen. We consider the penalty value ($PEN$), the number of caregivers ($N_p$) and patients (M) as well as the vehicle types (K) for underlying problem. Each sensitivity has four case studies. Finally, Table 9, Table 10, Table 11, Table 12 and Fig. 10, Fig. 11, Fig. 12, Fig. 13 provide the reports.

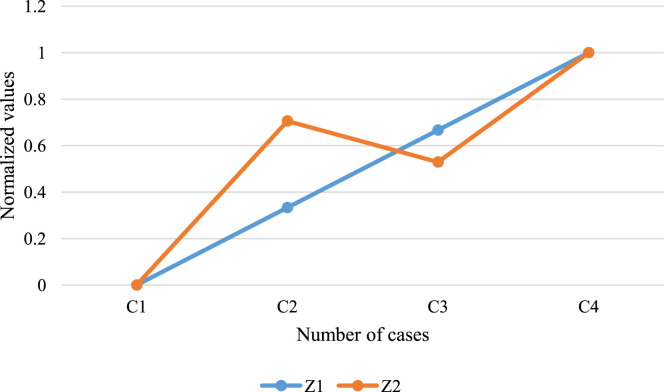
Table 9.

Sensitivity on the penalty value.

Number of cases	$PEN$	$Z_1$	$Z_2$
C1	1.5	65754	661
C2	2.5	73753.98	649
C3	3.5	81754.02	652
C4	4.5	89754	644

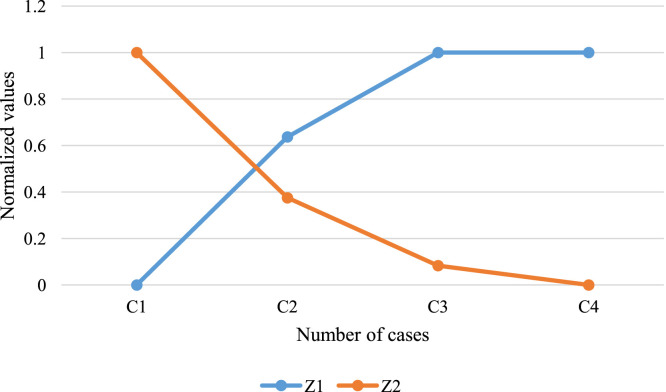
Table 10.

Sensitivity on the employed caregivers.

Number of cases	$N_p$	$Z_1$	$Z_2$
C1	3	59250	646
C2	4	65754	661
C3	5	69457.68	668
C4	6	69457.68	670

Table 11.

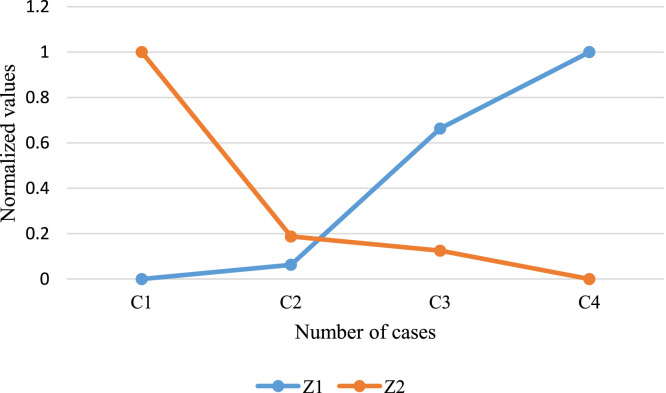
Sensitivity on the number of patients.

Number of cases	$M$	$Z_1$	$Z_2$
C1	30	63281.02	648
C2	40	65754	661
C3	50	89256	662
C4	60	102456	664

Fig. 10.

Sensitivity on the penalty of the extra traveling distance.

Fig. 11.

Sensitivity on the number of the caregivers.

Fig. 12.

Sensitivity on the number of patients.

Fig. 13.

Sensitivity on the vehicle’s types.

Regarding the penalty value ($PEN$), by altering this parameter from low to high, the sensitivity is given and summarized by Table 9. The objective functions are also noted in the table for each treatment. To have an analysis, the values have been normalized and revealed in Fig. 10. By increasing this parameter, the amount of both objectives is not better. The total cost is increased uniformly. However, the extra total cost has been decreased by this factor. The second objective to maximize the patients’ satisfaction is not better except C3. Generally, this parameter can reduce the optimality of objective functions.

Additionally, the number of assumed caregivers ($N_p$) has been focused on some sensitivity analyses. The reports are given in Table 10 and Fig. 11. Although the caregivers’ number is increased, the total cost and patients’ satisfaction reveal a different growth in analyzed scenarios. Accordingly, the changes are low. The total cost is firstly increased and then is fixed. The patients’ satisfaction is also better by incentives incensement. The patients may have more choices with better privileges to caregivers. With regards to the objective functions’ behavior, although an additional caregiver can increase the total cost, it is useful to satisfy the patients by providing a full range of the services.

In addition, the patients’ number (M) can change the complexity of the model. Accordingly, Table 11 and Fig. 12 provide the reports. It is evident that the total cost is increased by the growth of this parameter. However, the patients’ satisfaction is also better. It should be noted that after the second scenario, the rate of growth for objectives in the total cost is increased, while the patients’ satisfaction is not increased in the same rate. It means that by increasing the demand of home care services, the number of caregivers and vehicles are not increased, and the patients’ satisfaction reduces.

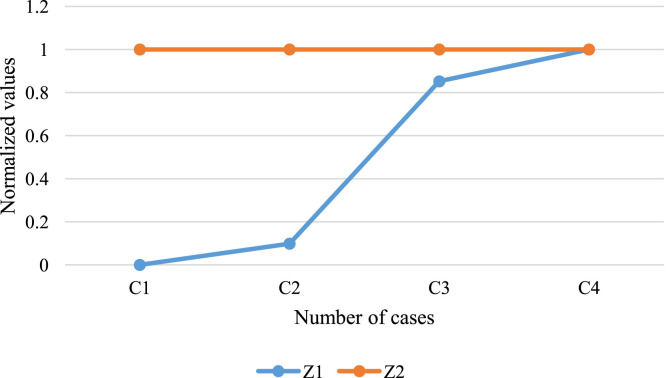
Typically, the transportation and logistics cost of the services of the home healthcare are the main challenge for the providers of these services. With regard to the number of vehicles (K), an incensement can be seen. Table 12 and Fig. 13 provide the reports. An increase in this parameter has no effect on the patients’ satisfaction. However, the total cost of system clearly increases due to different vehicles.

Table 12.

Sensitivity on the vehicle’s types.

Number of cases	$K$	$Z_1$	$Z_2$
C1	3	65754	661
C2	4	70554	661
C3	5	107256	661
C4	6	114456	661

5.6. Managerial insights

Academically, operational home healthcare optimization aims to define a plan for the caregivers’ routing and scheduling. From the majority of cases, specifically and perhaps in European and North American countries, the ageing population care is a challengeable concern. More broadly, in a case of an epidemic disease like COVID-19 in 2020 [62], the best and efficient way to do the care, is staying at home along with considering the healthcare instruments. Therefore, a simplified model to the home healthcare is not suitable to fully deliver all the real aspects of this important optimization problem. This paper aims to introduce an extension to the home healthcare optimization which is performance and practical. No doubt a multi-objective optimization is needed to accommodate the total cost of a structured logistics network with a set of pharmacies and laboratories as well as the patients’ satisfaction to provide better home care services. As some parameters of the model are uncertain, this study uses a fuzzy Jimenez’s method to control the uncertainty of service times, the privilege from patients to caregivers based on their performance from previous data and other key parameters of model. This estimation is done by using the triangular fuzzy numbers to consider the optimistic, realistic and pessimistic scenarios for these parameters. At last but not least, an algorithm allows this complex problem to be efficiently solved in a way which is strong and manageable computationally.

This paper confirms the viability of a home healthcare optimization with multiple objectives and real-life constraints. An MILP with two objectives, is applied to the proposed problem in a fuzzy environment firstly and a new adaptive extension of SEO (AMSEO) is also introduced. This study proposes four capable metaheuristics: SA, NSGA-II, SEO and AMSEO, to find a performance solution in an acceptable computational time. The AMSEO does the solving of the proposed problem very well. The proposed problem has some new contributions to the field. But, it shows more complexity than the previous home healthcare definitions. In addition, the patients’ satisfaction is considered in the problem in order to ensure better home care services. At the last but not least, the efficiency of the AMSEO for the field of the optimization lends a new application for other problem domains of equivalent complexity.

The testing of AMSEO to the proposed home healthcare optimization shows new managerial insights. This method provides a better performance in comparison with well-established algorithms from the literature to solve a practical home healthcare under uncertainty has been optimized efficiently. The fuzzy logic of the Jimenez’s method is used for the first time in the literature to tackle the uncertainty and can be applied to similar problems. As such, further investigation and development of AMSEO applied to this research area is warranted.

As mentioned earlier, the purpose of this work is to introduce a novel practical home healthcare optimization, some managerial implications with regards to the dynamics of routing and scheduling of the home care services in practice are highlighted. This study introduces multi-depot and multi-period home care operations by using different vehicles’ types and caregivers to support the patients’ satisfaction. Based on the real domain of the healthcare management, the caregivers who started from a pharmacy and provided the medications and tests after the patients’ meeting, go back to their laboratory to check the biological samples and tests to update the health records of the patients. Moreover, caregivers can provide this choice to patients to be more satisfied regarding the provided home care services. However, it can increase the total cost of the home care services.

The rest of managerial implications are generated by some sensitivities of the total cost and satisfaction objectives as given in Fig. 10, Fig. 11, Fig. 12, Fig. 13. Other managerial insight refers to the dynamic sensitivity of the algorithms to find a well-tuned level of controlling parameters as illustrated in Table 4, Table 5. Finally, the AMSEO, in which its performance is clarified and justified by four evaluation metrics of Pareto solutions including NPS, SNS, MID and HV during a comparison with SA, NSGA-II and the original version of SEO as reported in Fig. 9, can apply to other complex optimization problems.

6. Conclusion and future works

This paper demonstrates the viability of a home healthcare optimization problem definition by the total cost and patients’ satisfaction as the objectives and complex constraints such as the patients to pharmacies’ assignments, scheduling and routing constraints, delivery time, time windows and balancing of travels limitations using a bi-objective optimization linear approach. Due to the uncertainty of some parameters such as the service time and privilege from patients to caregivers based on their previous performance in home care services, the Jimenez’s approach is applied for the first time to the problem to tackle the fuzzy parameters in the objectives and constraints. A new adaptive extension of SEO in its multi-objective version (AMSEO) is well given the particular two objective functions of the problem definition. Based on the analyses, AMSEO performs significantly better than SEO, NSGA-II and SA, when all methods were tuned by response surface methodology (RSM) and compared across four popular evaluation metrics: the number of Pareto solutions (NPS), the spread of non-dominance solutions (SNS), mean ideal distance (MID), and hyper volume (HV). The epsilon constraint algorithm is obtained to check the model results at a small scale, and a more extensive sensitivity comparison is used to confirm the efficiency of AMSEO to solve the proposed problem more generally.

The home healthcare definition in this study reveals a new order of complexity for patients’ allocation, and caregivers’ routing and scheduling studies, however the possibility to introduce further financial and social factors is necessary to reflect the full scope of home healthcare optimization in practice. For example, sustainability factors such as patients’ risks and green emissions associated with the logistics services would offer interesting additions. Further sensitivity analysis using other assessment metrics of Pareto-based algorithms could also be applied to the current model, and the introduction of stochastic or robust optimization approaches to represent the uncertainty of parameters would also extend the study in important ways. More broadly, and ultimately more significantly perhaps, the application and development of AMSEO to other practical optimization problems, such as humanitarian logistics or closed-loop supply chains, offers exciting new directions for future researches.

CRediT authorship contribution statement

Amir Mohammad Fathollahi-Fard: Conceptualization, Formal analysis, Investigation, Methodology, Software, Validation, Original draft, Review & Editing. Abbas Ahmadi: Supervision, Project Admiration, Review & Editing. Fariba Goodarzian: Methodology, Visualization. Naoufel Cheikhrouhou: Supervision, Review & Editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.