A Hybrid Recommendation for Music Based on Reinforcement Learning

Abstract

The key to personalized recommendation system is the prediction of users’ preferences. However, almost all existing music recommendation approaches only learn listeners’ preferences based on their historical records or explicit feedback, without considering the simulation of interaction process which can capture the minor changes of listeners’ preferences sensitively. In this paper, we propose a personalized hybrid recommendation algorithm for music based on reinforcement learning (PHRR) to recommend song sequences that match listeners’ preferences better. We firstly use weighted matrix factorization (WMF) and convolutional neural network (CNN) to learn and extract the song feature vectors. In order to capture the changes of listeners’ preferences sensitively, we innovatively enhance simulating interaction process of listeners and update the model continuously based on their preferences both for songs and song transitions. The extensive experiments on real-world datasets validate the effectiveness of the proposed PHRR on song sequence recommendation compared with the state-of-the-art recommendation approaches.

Introduction

Recommendation systems have become indispensable for our daily life to help users navigate through the abundant data in the Internet. As the rapid expansion of the scale of music database, traditional music recommendation technology is difficult to help listeners to choose songs from such huge digital music resources. How to manage and recommend music effectively in the massive music library has become the main task of music recommendation system [1].

The mainstream recommendation algorithms can be classified as content-based [2, 3], collaborative filtering [5, 25], knowledge-based [6] and hybrid ones [7]. The collaborative filtering methods recommend items to users by exploiting the taste of other similar users. However, the cold-start and data sparse problem is very common in collaborative filtering. In knowledge-based approaches, users directly express their requirements and the recommendation system tries to retrieve items that are analogous to the users’ specified requirements. The content-based recommendation approaches are to find items similar to the ones that the users once liked, and the content information or expert label of items is also needed, but it does not require a large number of user-item rating records [4]. In order to improve performance, above methods can be combined into a hybrid recommendation system. The hybrid approach we use is feature augmentation, which takes the feature output from one method as input to another.

Nowadays, reinforcement learning [8] becomes one of the most important research hotspots. It mainly focuses on how to learn interactively, obtain feedback information in the action-evaluation environment, and then improve the choices of actions to adapt to the environment. In this paper, we propose a personalized hybrid recommendation algorithm for music based on reinforcement learning (PHRR). Based on the idea of hybrid recommendation, we utilize WMF-CNN model which uses content and collaborative filtering to learn and predict music features, and simulate listeners’ decision-making behaviors by model-based reinforcement learning process. What’s more, we establish a novel personalized music recommendation model to recommend song sequences which match listeners’ preferences better. Our contributions are as follows:

• Our proposed PHRR algorithm combines the method of extracting music features based on WMF-CNN process with reinforcement learning model to recommend personalized song sequences to listeners.

• We make innovative improvements to the method of learning listeners’ decision-making behaviors. And we promote the accuracy of model-learning by enhancing the simulation of interaction process in the reinforcement learning model.

• We conduct experiments in the real-world datasets. The experimental results show that the proposed PHRR algorithm has a better recommendation performance than other comparison algorithms in the experiments.

The rest of this paper is organized as follows. Section 2 reviews the related work. Section 3 presents details about the proposed PHRR algorithm. Section 4 introduces experimental results and analyses. In Sect. 5, we conclude our work.

Related Work

The recommendation system for music service differs from that for other service (such as movies or e-books), because the implicit user preferences on music are more difficult to track than the explicit rating of items in other applications. Besides, users are more likely to listen a song several times. In recent years, music recommendations have been widely studied in both academia and industry. Since music contains an appreciable amount of textual and acoustic information, several recommendation algorithms model users’ preferences based on extracted textual and acoustic features [24].

What’s more, the advanced recommendation approaches start to apply reinforcement learning [8] to the recommendation process, and consider the recommendation task as a decision problem to provide more accurate recommendations. Wang et al. [11] proposed a reinforcement learning framework based on Bayesian model to balance the exploration and exploitation of users’ preferences for recommendation. To learn user preferences, it uses a Bayesian model that accounts for both audio content and the novelty of recommendations. Chen et al. [12] combined interest forgetting mechanism with Markov models because people’s interest in earlier items will be lost from time to time. They believed that discrete random state was represented by random variables in Markov chain. Zhang et al. [15] took the social network and Markov chain into account, and proposed a PRCM recommendation algorithm based on collaborative filtering. Taking the influence of song transitions into account, Liebman et al. [13] added the listeners’ preferences for the transitions between songs to the recommendation process and proposed a reinforcement learning model named DJ-MC. Hu et al. [14] integrated users’ feedback into the recommendation model and proposed a Q-Learning based window list recommendation model called RLWRec based on greedy strategy, which traded off between the precision and recall of recommendation. It is a model-free reinforcement learning framework, and it has the data-inefficient problem without model.

Different from the previous research, we focus more on simulating interaction process of listeners based on their implicit preferences for songs and song transitions. Our main aim is to capture the changes of listeners’ preferences sensitively in the recommendation process and promote the recommendation quality of music.

Our Approach

Music Feature Extraction

As the song transition dataset is not large enough to train a good model, we can do “transfer learning”, i.e. the WMF-CNN process, from the larger Million Song Dataset [22]. To extract the music features, we use WMF [9, 17] to compute the feature vectors of some songs, which is an improved matrix factorization approach for implicit feedback datasets. The feature vectors calculated by WMF are used to train the CNN model [18] to learn the feature vectors of all other songs. Each song’s feature vector only needs to be trained once, so it doesn’t take a long time to train. Suppose that the play count for listener 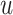listening to song 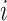is 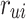, for each listener-song pair, we define a preference variable 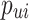and a confidence variable 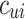( and 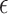are hyper-parameters, and are set as 2.0 and 1e-6 respectively):

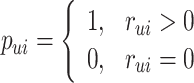1

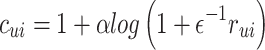2

The preference variable 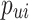indicates whether listener 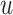has ever listened to song 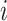or not. if it is 1, we assume that listener 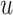may like song . The confidence variable measures the extent to which listener likes song 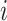. The song with a higher play count is more likely to be preferred. The objective function of WMF contains a confidence weighted mean squared error term and an L2-regularization term, given by Eq. 3.

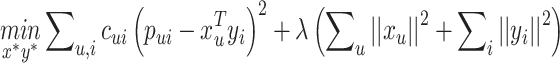3

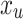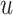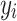where λ is the regularization parameter set as 1e-5, is the latent feature vector of listener and is the latent feature vector of song .

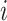In this paper, we use ResNet [26] as our CNN model, the input of the CNN model is mel-frequency cepstral coefficient spectrum (MFCC) [19] of songs, including 500 frames in the time dimension and 12 frequency-bins in the frequency dimension. The output vectors are the 20-dimensional predicted latent feature vector of songs. The objective function of CNN is to minimize the mean squared error (MSE) and weighted predict error (WPE), given by Eq. 4 (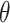 representing the model parameters).

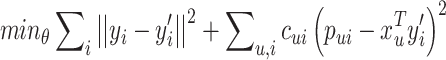4

where 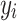is the feature vector of song 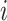calculated by WMF, and 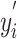is the predicted vector of song 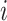by the CNN model.

Problem Description

We model the reinforcement learning based music recommendation problem as an improved Markov decision process (MDP) [10], which is denoted as a five-tuple . And the framework is shown in Fig. 1. Given the song set , the length of song sequences to recommend is defined as and the mathematical description of the MDP model for music recommendation is as follows.

Fig. 1.

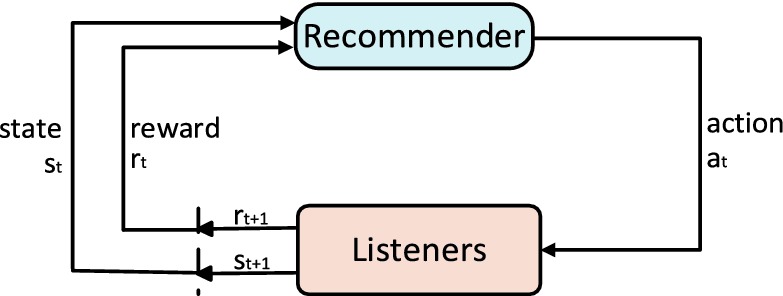
Reinforcement learning framework for music recommendation.

State set S. The state set denoted as } is the set of recommended song sequences including all intermediate states. A state is a song sequence in the recommendation process.

Action set A. The action set 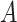is the actions of listening to songs in M, denoted as 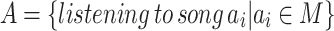. An action 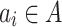means listening to song .

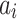State transition probability function P. We use abbreviated symbols 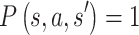to indicate that when we take action 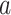in state , the probability of transition to 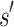is 1, and 0 otherwise, i.e.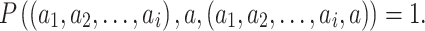

Reward function R. The reward function 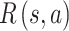obtains the reward value when listener takes action 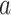in state 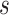, and each listener has a unique reward function. One of our key problems is how to calculate the reward function of new listeners effectively.

Final state T. The final state denoted as is the final recommended song sequence of length .

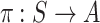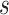Solving the MDP problem means to find a strategy , so that we can get an action for a given state . With the optimal strategy 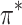, the highest expected total reward can be generated. However, the listener’s reward function is unknown, so the basic challenge of song sequence recommendation is how to model 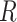effectively.

Listener Reward Function Model

Towards our recommendation problem, the probability function is already known, so the only unknown element is the reward function 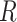. Most literatures about music recommendation only consider the listeners’ preferences for songs, without considering their preferences for song transitions. The reward function 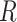should consider the listeners’ preferences both for songs and song transitions, as shown in Eq. 5.

5

where is the listener’s preference reward for song , and is the listener’s preference reward for the song transition from song sequence to song .

Listener Reward for Songs.

After extracting the features in Sect. 3.1, we obtain a 20-dimensional song feature vector. Then we use the binarized feature vector by sparse coding of the feature vector to represent the song’s features. As the feature vector is 20-dimensional, it has 20 descriptors. Each descriptor can be represented as m-bit binarized feature factors, so the binarized feature vector of song 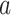denoted as 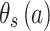is a 20 m-dimensional vector. What’s more, each listener has preference factors corresponding to binarized song feature factors respectively. For a 20 m-dimensional binarized feature vector 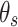, listener has a 20 m-dimensional preference vector 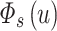. Therefore,

6

Listener Reward for Song Transitions.

When the listener listens to song 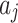after song 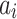, we note the reward function as 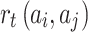. The song transition reward 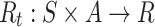is based on a certain song sequence 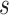and the next-song 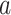to listen, as shown below.

7

In Eq. 7, the probability of the i-th song having influence on transition reward is 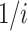. And its influence is attenuated over time, so the i-th song’s influence is reduced to times the original. As a result, the coefficient is the product of these two 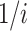[13].

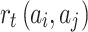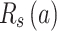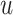The calculation equation of is similar to , as shown in Eq. 8. We use the sparse coding of song transition feature vector to generate the binarized feature vector . Each descriptor can be represented as -bit binarized feature factors. Similar to , listener has a 20 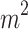-dimensional preference vector 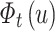for the 20 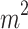-dimensional binarized feature vector .

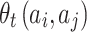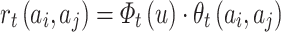8

Listener Preference for Songs.

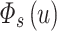We keep the listener’s historical song sequence whose length is longer than . In order to make tend to be uniform, we initialize each factor of the vector 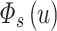to , where 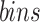indicates the discretization granularity of song feature and the value is same as m above. For each song 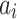in the listener’s historical song sequence, adds iteratively so the feature of song 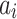can be learned. After is calculated, we normalize 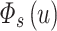so that the weights of m-bit factors corresponding to each descriptor sum to 1 respectively.

Listener Preference for Song Transitions.

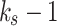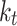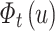Similar to the process of , the length of song transition sequence is noted as . In order to make tend to be uniform, we also initialize each factor of the vector to 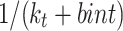, and the value of 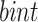is . Obviously, the song transition pattern of historical song sequence is the best transition pattern that listener prefers. For each transition from 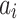to 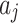in historical song sequence, 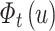adds 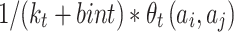iteratively. After 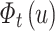is calculated, we normalize 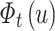in the same way as .

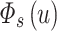Next-Song Recommendation Model

In order to reduce the time and space complexity of processing, we utilize the hierarchical searching heuristic method [20] to recommend next-song. And search is only performed from the search space where is relatively high (line 1). Besides, we take the horizon problem similar to the Go algorithm into account, which chooses the first step of the path with highest total reward as the next step (lines 9-14).

Since the song space is too large, it is not feasible to select songs from the complete song dataset . To alleviate this problem, we cluster songs by song type to reduce the complexity of searching (line 6). Clustering by song type is achieved by applying 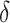-medoids algorithm [21], which is a method for representative selection.

Song Sequence Recommendation and Update Model

To recommend song sequence, we define 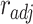as 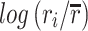, which determines the direction and size of update (lines 2-5). If is a positive value, it means that the listener likes the recommended song and the update direction is positive, and vice versa. And the relative contributions of the song reward and the song transition reward 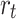to their total reward are calculated as 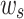and 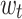respectively, as shown in Eq. 9 and Eq. 10.

9

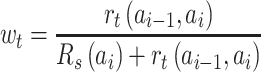10

11

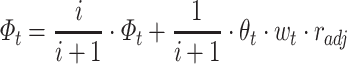12

Besides, the preference vector 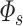and 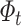are updated based on , 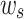and 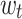, and need to be normalized. This update process considers the changes of listener’s interest over time and balances the degree of trusting history with new rewards (line 6-7).

Experiment

Datasets

Million Song Dataset.

Million Song Dataset (MSD) [22] is a dataset of audio feature for 1 million songs, providing powerful support for the CNN model to learn and extract music features. The dataset is available at http://labrosa.ee.columbia.edu/millionsong/.

Taste Profile Subset Dataset.

Taste Profile Subset Dataset [22] as shown in Table 1 is in the form of listener-song-play count triple, providing a sufficient amount of dataset for WMF. The dataset is available at https://labrosa.ee.columbia.edu/millionsong/.

Table 1.

A dataset of listener-song-playcount

#Listeners	#Songs	#Triplets
1000000	380000	48712660

Historical Song Playlist Dataset.

The dataset is collected from the music website Yes.com [23], which is available at http://lme.joachims.org/. As shown in Table 2, it contains 51,260 historical song sequences.

Table 2.

Listeners’ historical song playlist dataset

#Playlists	#Songs	#Song Transitions
51260	85262	2840554

Comparison Algorithms and Evaluation Methods

Comparison Algorithms.

We compare PHRR with baselines as below. For historical song playlist dataset, we use 90% of the dataset for training and the rest 10% for testing.

PHRR-S: PHRR-S algorithm is just the PHRR recommendation algorithm without taking song transitions into account.

DJ-MC [13]: DJ-MC algorithm is a reinforcement learning model added the listeners’ preferences for the transitions between songs to the recommendation process.

PRCM [15]: PRCM algorithm is a collaborative filtering recommendation algorithm taking the social network and Markov chain into account.

PopRec [16]: PopRec algorithm recommends the most popular songs.

RandRec: RandRec algorithm recommends songs randomly.

Evaluation Methods.

Our evaluation metrics include hit ratio of the recommended next-songs and F1-score of the recommended song sequences.

Hit Ratio (HR). We calculate hit ratio of the recommended next-songs for evaluation. In the historical song sequence dataset, the first songs of each song sequence are used to recommend the n+1th songs. We compare the recommended n+1th song with the true n+1th song in the actual song sequence. If it is same, it is hit, otherwise it’s not hit.

F1-Score (F1). The second evaluation indicator we use is F1-score. F1-score combines precision and recall of recommendation, and the Score calculated by Eq. 13 – Eq. 15 is used to evaluate the effect of song sequence recommendation.

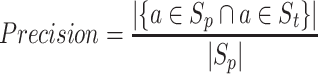13

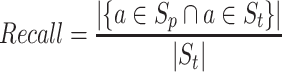14

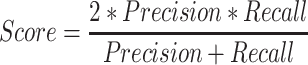15

where 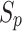represents the recommended song sequences, represents the song sequences presented in the historical song sequence dataset and indicates a song.

Experimental Results on Hit Ratio

The proposed PHRR algorithm is a recommendation algorithm to recommend song sequences. In this comparison experiment, the recommendation effects are measured by calculating the hit ratio of the recommended next-songs.

Performance Comparison on Hit Ratio.

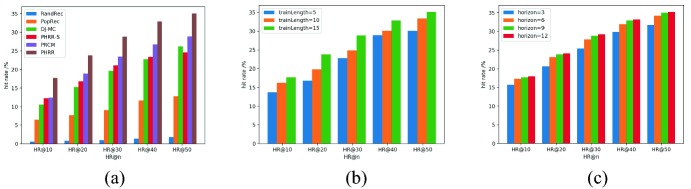
HR@k is the hit rate of the most probable k songs of the recommended next-songs. The results of hit ratio of above recommendation algorithms are shown in Table 3, and the best results are boldfaced.

Table 3.

Performance comparison on hit ratio

Algorithm	HR@10	HR@20	HR@30	HR@40	HR@50
PHRR	0.1787	0.2394	0.2896	0.3302	0.3520
PRCM	0.1255	0.1892	0.2356	0.2681	0.2897
DJ-MC	0.1232	0.1685	0.2110	0.2341	0.2462
PHRR-S	0.1016	0.1534	0.1965	0.2278	0.2619
PopRec	0.0651	0.0773	0.0916	0.1174	0.1289
RandRec	0.0060	0.0083	0.0101	0.0142	0.0186

Effect of Training Length of Song Sequence on Hit Ratio.

Reinforcement learning process is based on the feedback of interactive information and simulates the decision behavior of listeners. The longer the length of training song sequence is, the more simulated interactions are in reinforcement learning process. The experimental results of the effect of training length on hit ratio are shown in Fig. 2(b).

Fig. 2.

Experimental results on hit ratio. (a) Comparison experimental results on hit ratio. (b) Effect of training length of song sequence on hit ratio. (c) Effect of horizon length on hit ratio.

Effect of Horizon Length on Hit Ratio.

We consider the horizon problem similar to the Go algorithm when recommending next-song, that is, we choose the first song of the song sequence with highest total reward as the next-song (Algorithm 1). The experimental results of effect of horizon length on hit ratio are shown in Fig. 2(c).

Experimental Results and Analyses.

The result of Fig. 2(a) shows that hit ratio of PHRR is 7% higher than PRCM, 10% higher than DJ-MC, 11% higher than PHRR-S, 20% higher than PopRec, and the hit ratio of RandRec is as low as 1%. The results of Fig. 2(b) indicates that when the training sequence length n is 15, the hit ratio is higher than when n is 10 or 5. The longer the training sequence length is, the higher the hit ratio of the recommended next-songs is, and the recommendation result will be more accurate. Figure 2(c) shows that, as the horizon length increasing, the hit ratio of the recommended next-songs also tends to be higher.

Experimental Results on F1-Score

In this section, we use F1-score as an evaluation indicator to measure the effect of above algorithms on song sequence recommendation.

Performance Comparison on F1-Score.

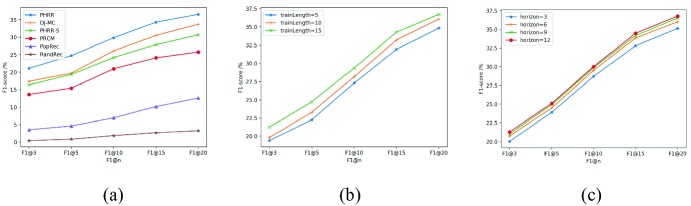
The results of F1-score of above recommendation algorithms are shown in Table 4. F1@k represents the F1-score of the recommended song sequence whose length is k, and the best results are boldfaced.

Table 4.

Performance comparison on F1-score

Algorithm	F1@3	F1@5	F1@10	F1@15	F1@20
PHRR	0.2113	0.2472	0.2986	0.3432	0.3657
DJ-MC	0.1738	0.1974	0.2610	0.3052	0.3374
PHRR-S	0.1640	0.1935	0.2421	0.2787	0.3068
PRCM	0.1365	0.1542	0.2098	0.2411	0.2576
PopRec	0.0354	0.0461	0.0697	0.1016	0.1262
RandRec	0.0042	0.0083	0.0186	0.0269	0.0325

Effect of Training Length of Song Sequence on F1-Score.

Compared with other reinforcement learning based algorithms, the proposed PHRR promotes the precision by enhancing the simulation of interaction process. The experimental results of the effect of song sequence training length on F1-score are shown in Fig. 3(b).

Fig. 3.

Experimental results on F1-score. (a) Comparison experimental results on F1-score. (b) Effect of training length of song sequence on F1-score. (c) Effect of horizon length on F1-score.

Effect of Horizon Length on F1-Score.

In the next-song recommendation stage (Algorithm 1), we only recommend the first song of the song sequence with highest total reward, instead of recommending this entire song sequence. Because as noise accumulating during the self-updating process, the variation of the model would be larger. The experimental results of the effect of horizon on F1-score are shown in Fig. 3(c).

Experimental Results and Analyses.

As shown in Fig. 3(a), F1-score of PHRR is 4% higher than DJ-MC, 6% higher than PHRR-S, 11% higher than PRCM and 20% higher than PopRec on average. PHRR enhances simulating listener’s interaction in the reinforcement learning process, while other algorithms don’t consider it. Figure 3(b) presents that, when the song sequence training length n is 15, F1-score is higher than when n is 10 or 5. The longer training length can bring more chances to enhance the simulation of interaction. Figure 3(c) indicates that as the horizon length increasing, F1-score shows a slight higher. The horizon length shouldn’t be too long, because too long horizon length is not significantly useful for improving the effect but increases the complexity.

Conclusion

In this paper, we propose a hybrid recommendation algorithm for music based on reinforcement learning (PHRR) to recommend higher quality song sequences. WMF and CNN are trained to learn song feature vectors from the songs’ audio signals. Besides, we present a model-based reinforcement learning framework to simulate the decision-making behavior of listeners, and model the reinforcement learning problem as a Markov decision process based on listeners’ preferences both for songs and song transitions. To capture the minor changes of listeners’ preferences sensitively, we innovatively enhance the simulation of interaction process to update the model more data-efficiently. Experiments conducted on real-world datasets demonstrate that PHRR has a better effect of music recommendation than other comparison algorithms.

In the future, we will incorporate more human behavioral characteristics into the model. We also want to analyze the role of these characteristics for recommendation.