LoPAD: A Local Prediction Approach to Anomaly Detection

Abstract

Dependency-based anomaly detection methods detect anomalies by looking at the deviations from the normal probabilistic dependency among variables and are able to discover more subtle and meaningful anomalies. However, with high dimensional data, they face two key challenges. One is how to find the right set of relevant variables for a given variable from the large search space to assess dependency deviation. The other is how to use the dependency to estimate the expected value of a variable accurately. In this paper, we propose the Local Prediction approach to Anomaly Detection (LoPAD) framework to deal with the two challenges simultaneously. Through introducing Markov Blanket into dependency-based anomaly detection, LoPAD decomposes the high dimensional unsupervised anomaly detection problem into local feature selection and prediction problems while achieving better performance and interpretability. The framework enables instantiations with off-the-shelf predictive models for anomaly detection. Comprehensive experiments have been done on both synthetic and real-world data. The results show that LoPAD outperforms state-of-the-art anomaly detection methods.

Introduction

According to [7], anomalies are patterns in data that do not conform to a well-defined notion of normal behavior. The mainstream methods for anomaly detection, e.g. LOF [5], are based on proximity between objects. These methods evaluate the anomalousness of an object through its distance or density within its neighborhood. If an object stays far away from other objects or in a sparse neighborhood, it is more likely to be an anomaly [1].

Another research direction in anomaly detection is to exploit the dependency among variables, which has shown successful applications in various fields [1]. Dependency-based methods firstly discover variable dependency possessed by the majority of objects, then the anomalousness of objects is evaluated through how well they follow the dependency. The objects whose variable dependency significantly deviate from the normal dependency are flagged as anomalies. These methods can detect certain anomalies that cannot be discovered through proximity because though these anomalies violate the dependency, they may still locate in a dense neighborhood.

A way to measure dependency deviation is to examine the difference between the observed value and the expected value of an object, where the expected value is estimated based on the underlying dependency [1]. Specifically, for an object, the expected value of a given variable is estimated using the values of a set of other variables of the object. Here, we call the given variable the target variable, and the set of other variables relevant variables.

Relevant variable selection and expected value estimation are the two critical steps of dependency-based anomaly detection, as they play a decisive role in the performance of the detection. However, they have not been well addressed by existing methods. Relevant variable selection faces a dilemma in high dimensional data. On the one hand, it is expected that the complete dependency, i.e., the dependency between a target variable and all the other variables, is utilized to discover anomalies accurately. On the other hand, it is common that in real-world data, only some variables are relevant to the data generation mechanism for the target variable. Irrelevant variables have no or very little contribution to the anomaly score, and even have a negative impact on the effectiveness [18]. How to find the set of most relevant variables that can capture the complete dependency around a target variable is a challenge, especially in high dimensional data given the large number of possible subsets of variables.

A naive approach is to use all other variables as the relevant variables for a target variable, as the ALSO algorithm [12] does. However, doing so leads to two major problems. Firstly, it is computationally expensive to build prediction models in high dimensional data. Secondly, conditioning on all other variables means irrelevant variables can affect the detection accuracy. Another approach is to select a small set of relevant variables. COMBN [2] is a typical method falling in this category. COMBN uses the set of all direct cause variables of a target in a Bayesian network as the relevant variables. However, only selecting a small subset of variables may miss some important dependencies, resulting in poor detection performance too.

To deal with these problems, we propose an optimal attribute-wise method, LoPAD (Local Prediction approach to Anomaly Detection), which innovatively introduces Markov Blanket (MB) and predictive models to anomaly detection to enable the use off-the-shelf classification methods to solve high dimensional unsupervised anomaly detection problem.

MB is a fundamental concept in the Bayesian network (BN) theory [13]. For any variable X in a BN, the MB of X, denoted as MB(X), comprises its parents (direct causes), children (direct effects) and spouses (the other parents of X’s children). Given MB(X), X is conditionally independent of all the other variables, which means MB(X) encodes the complete dependency of X. So for LoPAD, we propose to use MB(X) as the relevant variables of X. As in high dimensional data, MB(X) usually has much lower dimensionality than that of the dataset, which enables LoPAD to deal with high dimensional data.

Moreover, using MB(X) LoPAD can achieve a more accurate estimation of the expected value of X. The study in [9] has shown that MB(X) is the optimal feature set for a prediction model of X in the sense of minimizing the amount of predictive information loss. Therefore, we propose to predict the expected value of X with a prediction model using MB(X) as the predictors. It is noted that LoPAD is not limited to a specific prediction algorithm, which means a variety of off-the-shelf prediction methods can be utilized and thus relax the restrictions on data distributions and data types.

In summary, by using MB of a variable, LoPAD simultaneously solves the two challenges in dependency-based anomaly detection, relevant variable selection and expected value estimation. The main contributions of this work are as below:

• Through introducing Markov Blanket into dependency-based anomaly detection, we decompose the high dimensional unsupervised anomaly detection problem into local feature selection and prediction problems, which also provide better interpretation of detected anomalies.

• We develop an anomaly detection framework, LoPAD, to efficiently and effectively discover anomalies in high dimensional data of different types.

• We present an instantiated algorithm based on the LoPAD framework and conduct extensive experiments on a range of synthetic and real-world datasets to demonstrate the effectiveness and efficiency of LoPAD.

The LoPAD Framework and Algorithm

Notation and Definitions

In this paper, we use an upper case letter, e.g. X to denote a variable; a lower case letter, e.g. x for a value of a variable; a boldfaced upper case letter, e.g. 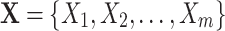for a set of variables; and a boldfaced lower case letters, e.g. 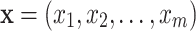, for a value vector of a set of variables. We have reserved the letter 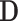for a data matrix of n objects and m variables, 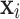for the i-th row vector (data point or object) of 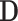, and 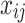for the j-th element in .

In LoPAD, the anomalousness of an object is evaluated based on the deviation of its observed value from the expected value. There are two types of deviations, value-wise deviation and vector-wise deviation as defined below.

Definition 1

(Value-wise Deviation). Given an object 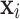, its value-wise deviation with respect to variable 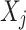is defined as:

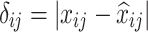1

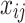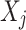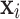where is the observed value of in , and

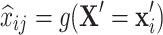2

is the expected value of 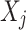estimated using the function g() based on the values on other variables .

Definition 2

(Vector-wise Deviation). The vector-wise deviation of object 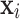is the aggregation of all its value-wise deviations calculated using a combination function as follows:

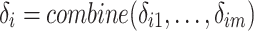3

From the above definitions, we see that value-wise deviation evaluates how well an object follows the dependency around a specific variable, and vector-wise deviation evaluates how an object collectively follows the dependencies. Based on the definitions, we can now define the research problem of this paper.

Definition 3

(Problem Definition). Given a dataset 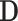with n objects and a user specified parameter k, our goal is to detect the top-k ranked objects according to the descending order of vector-wise deviations as anomalies.

The LoPAD Framework

To obtain value-wise deviation of an object, two problems need to be addressed. One is how to find the right set of relevant variables of a target variable, i.e. 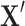in Eq. 2, which should completely and accurately represent the dependency of 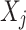on other variables. For high dimensional data, it is more challenging as the number of subsets of 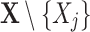increases exponentially with the number of variables in a dataset. The other problem is how to use the selected relevant variables to make an accurate estimation of the expected value.

The LoPAD framework adapts optimal feature selection technique and supervised machine learning technique to detect anomalies in three phases: (1) Relevant variable selection for each variable 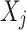using the optimal feature select technique; (2) Estimation of the expected value of 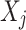using the selected variables with a predictive model; (3) Anomaly score generation.

Phase 1: Relevant Variable Selection. In this phase, the goal is to select the optimal relevant variables for a target variable. We firstly introduce the concept of MB, then explain why MB is the set of optimal relevant variables.

Markov Blankets are defined in the context of a Bayesian network (BN) [13]. A BN is a type of probabilistic graphical model used to represent and infer the dependency among variables. A BN is denoted as a pair of 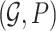, where 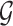is a Directed Acyclic Graph (DAG) showing the structure of the BN and P is the joint probability of the nodes in G. Specifically, 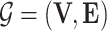, where 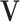is the set of nodes representing the random variables in the domain under consideration, and 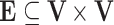is the set of arcs representing the dependency among the nodes. 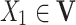is known as a parent of 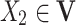(or 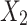is a child of ) if there exists an arc 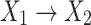. In a BN, given all its parents, a node X is conditionally independent of all its non-descendant nodes, known as the Markov condition for a BN, based on which the joint probability distribution of can be decomposed to the product of the conditional probabilities as follows:

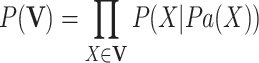4

where Pa(X) is the set of all parents of X.

For any variable 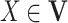in a BN, its MB contains all the children, parents, and spouses of X, denoted as MB(X). Given MB(X), X is conditionally independent of all other variables in 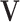, i.e.,

5

where .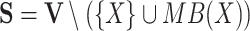

According to Eq. 5, MB(X) represents the information needed to estimate the probability of X by making X irrelevant to the remaining variables, which makes MB(X) is the minimal set of relevant variables to obtain the complete dependency of X.

Phase 2: Expected Value Estimation. This phase aims to estimate the expected value of a variable in an object (defined in Eq. 2) using the selected variables. The function g() in Eq. 2 is implemented with a prediction model. Specifically, for each variable, a prediction model is built to predict the expected value on the variable using the selected relevant variables as predictors. A large number of off-the-shelf prediction models can be chosen to suit the requirement of the data. By doing so, we decompose the anomaly detection problem into individual prediction/classification problems.

Phase 3: Anomaly Score Generation. In this phase, the vector-wise deviation, i.e., anomaly score, is obtained by applying a combination function over value-wise deviations. Various combination functions can be used in the LoPAD framework, such as maximum function, averaging function, weighted summation. A detailed study on the impact of different combination functions on the performance of anomaly detection can be found in [10].

The LoPAD Algorithm

As shown in Algorithm 1, we present an instantiation of the LoPAD framework, i.e. the LoPAD algorithm. Given an input dataset 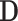, for each variable, its relevant variable selection is done at Line 3, then a prediction model is built at Line 4. From Lines 5 to 8, value-wise deviations are computed for all the objects. In Line 10, value-wised deviation is normalized. With Lines 11 to 13, vector-wise deviations are obtained by combining value-wise deviations. At Line 14, top-k scored objects are output as identified anomalies. As anomalies are rare in a dataset, although LoPAD uses the dataset with anomalies to discover MBs and train the prediction models, the impact of anomalies on MB learning and model training is limited.

For the LoPAD algorithm, we use the fast-IAMB method [16] to learn MBs. For estimating expected values, we adopt CART regression tree [4] to enable the LoPAD algorithm to cope with both linear and non-linear dependency. It is noted that regression models are notorious for being affected by the outliers in the training set. We adopt Bootstrap aggregating (also known as bagging) [3] to mitigate this problem to achieve better prediction accuracy.

Before computing vector-wise deviations, the obtained value-wised deviations need to be normalized. Specifically, for each object 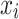on each target variable 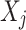, 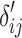is normalized as the Z-score using the mean and standard deviation of 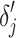. After normalization, negative values represent the small deviations. As we are only interested in large deviations, the vector-wise deviation is obtained by summing up the positive normalized value-wise deviations as follows:

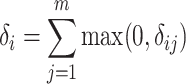6

The time complexity of the LoPAD algorithm mainly comes from two sources, learning MB and building the prediction model. For a dataset with n objects and m variables, the complexity of the MB discovering using fast-IAMB is 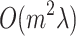[15], where is the average size of MBs. The complexity of building m prediction models is [4]. Therefore, the overall complexity of the LoPAD algorithm is .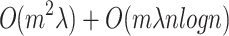

Experiments

Data Generation. For synthetic data, 4 benchmark BNs from bnlearn repository [14] are used to generate linear Gaussian distributed datasets. For each BN, 20 datasets with 5000 objects are generated. Then the following process is followed to inject anomalies. Firstly, objects and variables are randomly selected. Then anomalous values are injected to the selected objects on these selected variables. The injected anomalous values are uniformly distributed values in the range of the minimum and maximum values of the selected variables. In this way, the values of anomalies are still in the original range of the selected variables, but their dependency with other variables is violated. For each BN, the average ROC AUC (area under the ROC curve) of the 20 datasets is reported.

For real-world data, we choose 13 datasets (Table 1) that cover diverse domains, e.g., spam detection, molecular bioactivity detection, and image object recognition. AID362, backdoor, mnist and caltech16 are obtained from Kaggle dataset repository, and the others are retrieved from the UCI repository [8]. These datasets are often used in anomaly detection literature. We follow the common process to obtain the ground truth anomaly labels, i.e. using samples in a majority class as normal objects, and a small class, or down-sampling objects in a class as anomalies. Categorical features are converted into numeric ones by 1-of- encoding [6]. If the number of objects in the anomaly class is more than 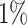of the number of normal objects, we randomly sample the latter number of objects from the anomaly class as anomalies. Experiments are repeated 20 times, and the average AUC is reported. If the ratio of anomalies is less than 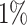, the experiment is conducted once, which is the case for the wine, AID362 and arrhythmia datasets.

Table 1.

The summary of 4 synthetic and 13 real-world datasets

Dataset	#Sample	#Variable	Normal class	Anomaly class
MAGIC-NAB	5000	44	NA	NA
ECOLI70	5000	46	NA	NA
MAGIC-IRRI	5000	64	NA	NA
ARTH150	5000	107	NA	NA
Breast cancer	448	9	Benign	Malignant
Wine	4898	11	4−8	3,9
Biodegradation	359	41	RB	CRB
Bank	4040	51	No	Yes
Spambase	2815	57	Non-spam	Spam
AID362	4279	144	Inactive	Active
Backdoor	56560	190	Normal	Backdoor
calTech16	806	253	1	53
Census	45155	409	Low	High
Secom	1478	590	−1	1
Arrhythmia	343	680	1,2,10	14
Mnist	1038	784	7	0
Ads	2848	1446	non-AD	Ad

Note: Normal and anomaly class labels are not applicable to synthetic datasets.

Comparison Methods. The comparison methods include dependency-based methods, ALSO [12] and COMBN [2]; and proximity-based methods, MBOM [17], iForest [11] and LOF [5]. The major difference in LoPAD, ALSO and COMBN is the choice of relevant variables. ALSO uses all remaining variables, and COMBN uses parent variables, while LoPAD utilizes MBs. The effectiveness of using MB in LoPAD is validated by comparing LoPAD with ALSO. MBOM and iForest are proximity-based methods, which detect anomalies based on density in subspaces. LOF is a classic density-based method, which is used as the baseline method.

In the experiments (including sensitivity tests), we adopt the commonly used or recommended parameters that are used in the original papers. For a fair comparison, both LoPAD and ALSO adopt CART regression tree [4] with bagging. In CART, the number of minimum objects to split is set to 20, and the minimum number of objects in a bucket is 7, the complexity parameter is set to 0.03. The number of CART trees in bagging is set to 25. In MBOM and LOF, the number of the nearest neighbor is set to 10. For iForest, the number of trees is set to 100 without subsampling.

All algorithms are implemented in R 3.5.3 on a computer with 3.5 GHz (12 cores) CPU and 32 G memory.

Performance Evaluation. The experimental results are shown in Table 2. If a method could not produce a result within 2 hour, we terminate the experiment. Such cases occur to COMBN and are shown as ‘-’ in Table 2. LoPAD yields 13 best results (out of 17) and LoPAD achieves the best average AUC of 0.859 with the smallest standard deviation of 0.027. Overall, dependency-based methods (LoPAD, ALSO and COMBN) perform better than proximity-based methods (MBOM, iForest and LOF). Compared with ALSO, LoPAD improves 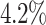on AUC, which is attributed to the use of MB. COMBN yields two best results, but its high time complexity makes it unable to produce results for several datasets. Comparing LoPAD with MBOM, LoPAD performs significantly better with a AUC improvement. Although iForest has the best result among the proximity-based methods, LoPAD has a AUC improvement over it. As to LOF, LoPAD has a 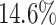AUC improvement over it. The average size of the MB is much smaller than the original dimensionality on all datasets, which means that comparing to ALSO, LoPAD works based on much smaller dimensionality but still achieves the best results in most cases.

Table 2.

Experimental results (ROC AUC)

Dataset	Average size of MBs	LoPAD	ALSO	MBOM	COMBN	iForest	LOF
MAGIC-NIAB	8.0	0.826 ± 0.033	0.775 ± 0.106	0.817 ± 0.052	0.719 ± 0.099	0.780 ± 0.035	0.819 ± 0.028
ECOLI70	6.5	0.987 ± 0.013	0.994 ± 0.008	0.992 ± 0.008	0.988 ± 0.013	0.799 ± 0.027	0.972 ± 0.014
MAGIC-IRRI	8.1	0.917 ± 0.051	0.861 ± 0.123	0.899 ± 0.041	0.876 ± 0.079	0.817 ± 0.037	0.891 ± 0.029
ARTH150	7.9	0.986 ± 0.011	0.986 ± 0.017	0.959 ± 0.022	0.984 ± 0.011	0.853 ± 0.028	0.962 ± 0.009
Breast cancer	3.5	0.996 ± 0.004	0.984 ± 0.011	0.961 ± 0.013	0.989 ± 0.006	0.991 ± 0.005	0.891 ± 0.031
Wine	8.9	0.812	0.782	0.800	0.722	0.754	0.782
Biodegradation	14.8	0.883±0.063	0.855 ± 0.084	0.808 ± 0.105	0.856 ± 0.082	0.883 ± 0.069	0.868 ± 0.083
Bank	17.7	0.750 ± 0.038	0.682 ± 0.045	0.661 ± 0.043	0.706 ± 0.051	0.679 ± 0.048	0.566 ± 0.043
Spambase	10.0	0.821 ± 0.038	0.653 ± 0.045	0.718 ± 0.034	0.808 ± 0.053	0.773 ± 0.041	0.801 ± 0.03
AID362	51.9	0.604	0.594	0.550	0.674	0.634	0.570
Backdoor	92.4	0.941 ± 0.005	0.922 ± 0.009	0.765 ± 0.027	–	0.794 ± 0.035	0.748 ± 0.018
calTech16	48.8	0.98 ±0.006	0.979±0.006	0.766±0.039	0.981±0.006	0.983±0.004	0.491±0.086
Census	69.3	0.663 ± 0.011	0.642 ± 0.012	0.608 ± 0.013	–	0.575 ± 0.02	0.502 ± 0.013
Secom	35	0.596 ± 0.067	0.594 ± 0.074	0.551 ± 0.066	0.610 ± 0.081	0.533 ± 0.074	0.538 ± 0.086
Arrhythmia	61.7	0.914	0.892	0.563	–	0.844	0.906
Mnist	65.3	0.997 ± 0.002	0.991 ± 0.004	0.606 ± 0.099	–	0.996 ± 0.003	0.958 ± 0.044
Ads	68.7	0.932 ± 0.032	0.894 ± 0.032	0.864 ± 0.033	–	0.754 ± 0.06	0.851 ± 0.036
Average AUC		0.859 ± 0.027	0.828 ± 0.041	0.758 ± 0.043	0.826 ± 0.048	0.791 ± 0.035	0.772 ± 0.039
AUC improvement		–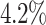
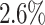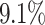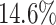Wilcoxon rank sum test p-value		–	0.0005	0.0001	0.0599	0.0007	0.0002

We apply the Wilcoxon rank sum test to the results of the 17 datasets (4 synthetic and 13 real-world datasets) by pairing LoPAD with each of the other methods. The null hypothesis is that the result of LoPAD is generated from the distribution whose mean is greater than the compared method. The p-values are 0.0005 with ALSO, 0.0001 with MBOM, 0.0599 with COMBN, 0.0007 with iForest and 0.0002 with LOF. The p-value with COMBN is not reliable because of the small number of results (COMBN is unable to produce results for 5 out of 21 datasets). Except for COMBN, all the p-values are far less than 0.05, indicating that LoPAD performs significantly better than the other methods.

The running time of these datasets is shown in Table 3. Overall, dependency-based methods are slower because they need extra time to learn MBs or the BN and prediction models. COMBN is unable to produce results in 2 h on 5 datasets. Comparing with ALSO, although LoPAD needs extra time to learn MBs, it is still significantly faster than ALSO. On average, LoPAD only requires 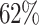of ALSO’s running time. It is noted that LoPAD could work as a model-based method, in which most of LoPAD’s running time occurs in the training stage. Once the model has been built, the testing stage is very fast.

Table 3.

Average running time (in seconds)

Dataset	LoPAD	ALSO	MBOM	COMBN	iForest	LOF
MAGIC-NIAB	12.8	35.5	28.4	2.5	1.2	1.7
ECOLI70	12.7	33.6	23.8	2.3	1.2	1.5
MAGIC-IRRI	14.7	61.4	41.4	5.5	1.5	2.0
ARTH150	20.0	164.8	68.9	10.0	2.1	2.7
Breast cancer	0.7	1.3	0.3	0.01	0.37	0.04
Wine	9.2	14.0	5.3	0.3	0.6	0.5
Biodegradation	4.8	7.6	1.6	0.6	0.39	0.04
Bank	14.3	23.4	18.6	7.9	1.0	0.8
Spambase	11.9	24.5	13.9	3.2	0.8	0.4
AID362	116.6	123.3	160.3	591.9	2.1	1.7
Backdoor	907.0	1148.8	1136.8	-	167.3	11.1
calTech16	53.4	52.7	54.9	558.0	0.8	0.1
Census	2582.1	6041	4810.5	-	382.3	313.8
Secom	75.1	454.8	133.8	1679.3	2.3	0.9
Arrhythmia	375.6	150.0	370.9	-	0.84	0.09
Mnist	366.4	267.4	389.1	-	1.9	0.4
Ads	2265.0	2437.4	2486.3	-	53.7	4.7
Average	402.5	649.5	573.2	238.4	36.5	20.1

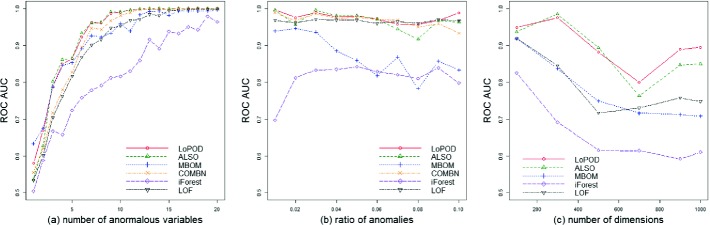
Evaluation of Sensitivity. In the evaluation of sensitivity, we consider three factors: (1) the number of variables with anomalous values injected; (2) the ratio of anomalies; (3) the dimensionality of the data. For the first two factors, The BN ARTH150 is used to generate test datasets. For the third one, datasets are generated using the CCD R package as follows. Given dimensions m, we randomly generate a DAG with m nodes and m edges. The parameters of the DAG are randomly selected to generate linear Gaussian multivariate distributed datasets. For each sensitivity experiment, 20 datasets with 5000 objects are generated, and the average ROC AUC is reported.

The sensitivity experimental results are shown in Fig. 1. In Fig. 1(a), the number of variables with injected anomalous values ranges from 1 to 20, while the ratio of anomalies is fixed to 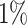. In Fig. 1(b), the ratio of anomalies ranges from to 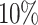, while the number of anomalous variables is fixed to 10. In Fig. 1(c), the dimension ranges from 100 to 1000, while the number of variables with injected anomalous values is 10 and the ratio of anomalies fixes to 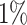. Overall, all methods follow similar trends in terms of their sensitivity to these parameters, and LoPAD shows consistent results which are better than comparison methods in most cases.

Fig. 1.

The results of sensitivity experiments

Anomaly Interpretation. One advantage of LoPAD is the interpretability of detected anomalies. For a detected anomaly, the variables with high deviations can be utilized to explain detected anomalies. The difference between the expected and the observed values of these variables indicate the strength and direction of the deviation. We use the result of the mnist dataset as an example to show how to interpret an anomaly detected by LoPAD. In mnist, each object is a 28 * 28 grey-scaled image of a hand-writing digit. Each pixel is a variable, whose value ranges from 0 to 255. Zero corresponds to white, and 255 is black. In our experiment, 7 is the normal class, and 0 is the anomaly class.

Figure 2(a) shows the average values of all the 1038 images in the dataset, which can be seen as a representation of the normal class (digit 7 here). Figure 2(b) is the top-ranked anomaly by LoPAD (a digit 0) and Fig. 2(c) is its expected values. In Fig. 2(d) (which also shows the top-ranked anomaly as in Fig. 2(b)), the pixels indicated with a red dot or a green cross are the top-100 deviated pixels (variables). The green pixels have negative deviations, i.e. their observed values are much smaller than their expected values, which means according to the underlying dependency, these pixels are expected to be darker. The red pixels have positive deviations, i.e. their observed values are much bigger than their expected values, which means they are expected to be much lighter.

Fig. 2.

The example of the interpretation of a detected anomaly

We can use these pixels or variables with high derivations to understand why this image is an anomaly as explained in the following. In Fig. 2(d), the highly deviated pixels concentrate in the 3 areas in the blue ellipses. These areas visually are indeed the areas where the observed object (Fig. 2(b)) and its expected value (Fig. 2(c)) differ the most. Comparing Fig. 2(d) with Fig. 2(a), we can see the anomalousness mainly locates in the 3 areas: (1) in area 1, the stroke is not supposed to be totally closed; (2) the little ‘tail’ in area 2 is not expected; (3) the stroke in area 3 should move a little to the left.

In summary, this example shows that the deviations from the normal dependency among variables can be used to explain the causes of anomalies.

Related Work

Dependency-based anomaly detection approach works under the assumption that normal objects follow the dependency among variables, while anomalies do not. The key challenge for applying approach is how to decide the predictors of a target variable, especially in high dimensional data. However, existing research has not paid attention to how to choose an optimal set of relevant variables. They either use all the other variables, such as ALSO [12], or a small subset of variables, such as COMBN [2]. The inappropriate choice of predictors has a negative impact on the effectiveness and efficiency of anomaly detection, as indicated by the experiments in Sect. 3. In this paper, we innovatively tackle this issue by introducing MBs as relevant variables.

Apart from dependency-based approach, the mainstream of anomaly detection methods is proximity-based, such as LOF [5]. These methods work under the assumption that normal objects are in a dense neighborhood, while anomalies stay far away from other objects or in a sparse neighborhood [7]. Building upon the different assumptions, the key difference between dependency-based and proximity-based approaches is that the former considers the relationship among variables, while the latter relies on the relationship among objects.

A branch of proximity-based approach, subspace-based methods, partially utilizes dependency in anomaly detection. In high dimensional data, the distances among objects vanish with the increase of dimensionality (known as the curse of dimensionality). To address this problem, some subspace-based methods are proposed [18] to detect anomalies based on the proximity with respect to subsets of variables, i.e., subspaces. However, although subspace-based anomaly detection methods make use of variable dependency, they use the dependency to determine subspaces, instead of measuring anomalousness. Often these methods find a subset of correlated variables as a subspace, then still use proximity-based methods to detect outlier in each subspace. For example, with MBOM [17], a subspace contains a variable and its MB, and LOF is used to evaluate anomalousness in each such a subspace. Another novel subspace-based anomaly detection method, iForest [11], randomly selects subsets of variables as subspaces, which shows good performance in both effectiveness and efficiency.

Conclusion

In this paper, we have proposed an anomaly detection method, LoPAD, which divides and conquers high dimensional anomaly detection problem with Markov Blanket learning and off-the-shelf prediction methods. Through using MB as the relevant variables of a target variable, LoPAD ensures that complete dependency is captured and utilized. Moreover, as MBs are the optimal feature selection sets for prediction tasks, LoPAD also ensures more accurate estimation of the expected values of variables. Introducing MB into dependency-based anomaly detection methods provides the sound theoretical support to the most critical steps of dependency-based methods. Additionally, the results of the comprehensive experiments conducted in this paper have demonstrated the superior performance and efficiency of LoPAD comparing to the state-of-the-art anomaly detection methods.