Deep Multivariate Time Series Embedding Clustering via Attentive-Gated Autoencoder

Abstract

Nowadays, great quantities of data are produced by a large and diverse family of sensors (e.g., remote sensors, biochemical sensors, wearable devices), which typically measure multiple variables over time, resulting in data streams that can be profitably organized as multivariate time-series. In practical scenarios, the speed at which such information is collected often makes the data labeling task uneasy and too expensive, so that limit the use of supervised approaches. For this reason, unsupervised and exploratory methods represent a fundamental tool to deal with the analysis of multivariate time series. In this paper we propose a deep-learning based framework for clustering multivariate time series data with varying lengths. Our framework, namely DeTSEC (Deep Time Series Embedding Clustering), includes two stages: firstly a recurrent autoencoder exploits attention and gating mechanisms to produce a preliminary embedding representation; then, a clustering refinement stage is introduced to stretch the embedding manifold towards the corresponding clusters. Experimental assessment on six real-world benchmarks coming from different domains has highlighted the effectiveness of our proposal.

Introduction

Nowadays, huge amount of data is produced by a large and diverse family of sensors (e.g., remote sensors, biochemical sensors, wearable devices). Modern sensors typically measure multiple variables over time, resulting in streams of data that can be profitably organized as multivariate time-series. While a major part of recent literature about multivariate time-series focuses on tasks such as forecasting [14, 19, 20] and classification [11, 26] of such data objects, the study of multivariate time-series clustering has often been neglected. The development of effective unsupervised clustering techniques is crucial in practical scenarios, where labeling enough data to deploy a supervised process may be too expensive (i.e., in terms of both time and money). Moreover, clustering allows to discover characteristics of multivariate time series data that go beyond the apriori knowledge on a specific domain, serving as tool to support subsequent exploration and analysis processes.

While several methods exist for the clustering of univariate time series [13], the clustering of multivariate time series remains a challenging task. Early approaches have been proposed which were generally based on adaptations of standard clustering techniques to such data, e.g., density based methods [3], methods based on independent component analysis [25] and fuzzy approaches [5, 8]. Recently, Hallac et al. [9] proposed a method, namely TICC (Toeplitz inverse covariance-based clustering), that segments multivariate time series and, successively, clusters subsequences through a Markov Random fields based approach. The algorithm leverages an (EM)-like strategy, based on alternating minimization, that iteratively clusters the data and then updates the cluster parameters. Unfortunately, this method does not produce a clustering solution considering the original time series but a data partition where the unit of analysis is the subsequence.

As regards deep learning based clustering, such methods have recent become popular in the context of image and relational data [17, 24], but their potential has not yet been fully exploited in the context of the unsupervised analysis of time series data. Tzirakis et al. [24] recently proposed a segmentation/clustering framework based on agglomerative clustering which works on video data (time series of RGB images). The approach firstly extracts a clustering assignment via hierarchical clustering, then performs temporal segmentation and, finally, extracts representation via Convolutional Neural Network (CNN). The clustering assignment is used as pseudo-label information to extract the new representation (training the CNN network) and to perform video segmentation. The proposed approach is specific to RGB video segmentation/clustering and it is not well suited for varying length information. All these factors limit its use to standard multivariate time-series analysis. A method based on Recurrent Neural Networks (RNNs) has also been recently proposed in [23]. The representation provided by the RNN is clustered using a divergence-based clustering loss function in an end-to-end manner. The loss function is designed to consider cluster separability and compactness, cluster orthogonality and closeness of cluster memberships to a simplex corner. The approach requires training and validation data to learn parameters and choose hyperparameter setting, respectively. Finally, the framework is evaluated on a test set indicating that the approach seems not completely unsupervised and, for this reason, not directly exploitable in our scenario.

In this work, we propose a new deep-learning based framework, namely DeTSEC (Deep Time Series Embedding Clustering), to cope with multivariate time-series clustering. Differently from previous approaches, our framework is enough general to deal with time-series coming from different domains, providing a partition at the time-series level as well as manage varying length information. The DeTSEC has two stages: firstly a recurrent autoencoder exploits attention and gating mechanisms to produce a preliminary embedding representation. Then, a clustering refinement stage is introduced to stretch the embedding manifold towards the corresponding clusters. We provide an experimental analysis which includes comparison with five state of the art methods and ablations analysis of the proposed framework on six real-world benchmarks from different domains. The results of this analysis highlight the effectiveness of the proposed framework as well as the added value of the new learnt representation.

The rest of the paper is structured as follows: in Sect. 2 we introduce the DeTSEC framework, in Sect. 3 we present our experimental evaluation, and Sect. 4 concludes the work.

DeTSEC: Deep Time Series Embedding Clustering

In this section we introduce DeTSEC (Deep Time Series Embedding Clustering via Attentive-Gated Autoencoder). Let be a multivariate time-series dataset. Each 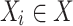is a time-series where 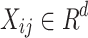is the multi-dimensional vector of the time-series 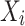at timestamp j, with , d being the dimensionality of 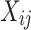and T the maximum time-series length. We underline that X can contain time-series with different lengths. The goal of DeTSEC is to partition X in a given number of clusters, provided as an input parameter. To this purpose, we propose to deal with the multivariate time-series clustering task by means of recurrent neural networks [1] (RNN), in order to manage at the same time (i) the sequential information exhibited by time-series data and (ii) the multivariate (multi-dimensional) information that characterizes time-series acquired by real-world sensors. Our approach exploits a Gated Recurrent Unit (GRU) [4], a type of RNN, to model the time-series behavior and to encode the original time-series in a new vector embedding representation. DeTSEC has two different stages. In the first one, the GRU based autoencoder is exploited to summarize the time-series information and to produce the new vector embedding representation, obtained by forcing the network to reconstruct the original signal, that integrates the temporal behavior and the multi-dimensional information. Once the autoencoder network has been pretrained, the second stage of our framework refines such representation by taking into account a twofold task, i.e., the reconstruction one and another one devoted to stretch the embedding manifold towards clustering centroids. Such centroids can be derived by applying any centroid-based clustering algorithm (i.e. K-means) on the new data representation. The final clustering assignment is derived by applying the K-means clustering algorithm on the embeddings produced by DeTSEC.

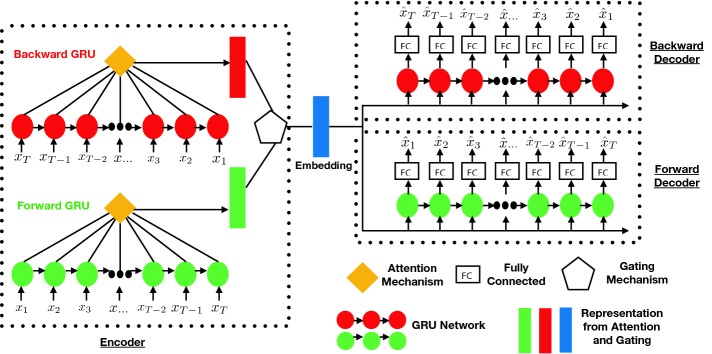
Figure 1 visually depicts the encoder/decoder structure of DeTSEC, consisting of three different components in our network architecture: i) an encoder, ii) a backward decoder and iii) a forward decoder. The encoder is composed by two GRU units that process the multivariate time series: the first one (in red) processes the time-series in reverse order (backward) while the second one (in green) processes the input time-series in the original order (forward). Successively, for each GRU unit, an attention mechanism [2] is applied to combine together the information coming from different timestamps. Attention mechanisms are widely used in automatic signal processing [2] (1D signal or Natural Language Processing) as they allow to merge together the information extracted by the RNN model at different timestamps via a convex combination of the input sources. The attention formulation we used is the following one:

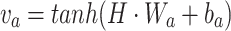1

2

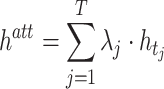3

where 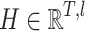is a matrix obtained by vertically stacking all feature vectors 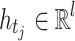learned at T different timestamps by the GRU and l is the hidden state size of the GRU network. Matrix 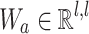and vectors 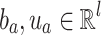are parameters learned during the process. The 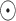symbol indicates element-wise multiplication. The purpose of this procedure is to learn a set of weights (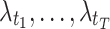) that allows to combine the contribution of each timestamp 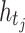. The SoftMax function is used to normalize weights so that their sum is equal to 1. The results of the attention mechanism for the backward (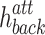) and for the forward () GRU units are depicted with red and green boxes, respectively, in Fig. 1. Finally, the two sets of features are combined by means of a gating mechanism [18] as follows:

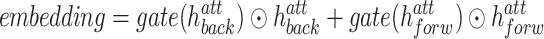4

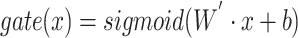5

where the gating function 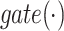performs a non linear transformation of the input via a sigmoid activation function and a set of parameters ( and b) that are learnt at training time. The result of the 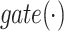function is a vector of elements ranging in the interval [0, 1] that is successively used to modulate the information derived by the attention operation. The gating mechanism adds a further decision level in the fusion between the 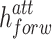and 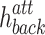information since it has the ability to select (or retain a part of) the helpful features to support the task at hand [27].

Fig. 1.

Encoder/Decoder structure of DeTSEC. The network has three main components: i) an encoder, ii) a forward decoder and iii) a backward decoder. The encoder includes forward/backward GRU networks. For each network an attention mechanism is employed to combine the sequential information. Subsequently, the gating mechanism combines the forward/backward information to produce the embedding representation. The two decoder networks have similar structure: the forward decoder reconstructs the original signal considering its original order (forward - green color) while the backward decoder reconstructs the same signal but in inverse order (backward - red color). (Color figure online)

The forward and backward decoder networks are fed with the representation (embedding) generated by the encoder. They deal with the reconstruction of the original signal considering the same order (resp. the reverse order) for the forward (resp. backward) decoder. This means that the autoencoder copes with the sum of two reconstruction tasks (i.e., forward and backward) where each reconstruction task tries to minimize the Mean Squared Error between the original data and the reconstructed one. Formally, the loss function implemented by the autoencoder network is defined as follows:

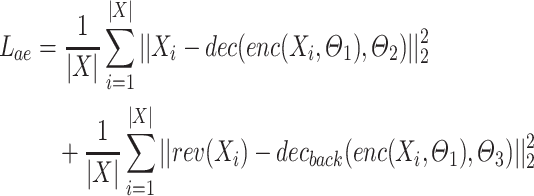6

where 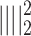is the squared L 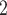distance, dec (resp. 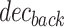) is the forward (resp. backward) decoder network, enc is the encoder network and 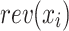is the time-series 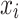in reverse order. 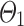are the parameters associated to the encoder while 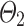(resp. 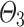) are the parameters associated to the forward (resp. backward) decoder.

Algorithm 1 depicts the whole procedure implemented by DeTSEC. It takes as input the dataset X, the number of epochs and the number of expected clusters nClust. The output of the algorithm is the new representation derived by the GRU based attentive-gated autoencoder, named embeddings. The first stage of the framework (lines 2–6) trains the autoencoder reported in Fig. 1 for a total of 50 epochs. Successively, the second stage of the framework (lines 8–14) performs a loop considering the remaining number of epochs in which, at each epoch, the current representation is extracted, a K-Means algorithm is executed to obtain the current cluster assignment and the corresponding centroids. Successively, the autoencoder parameters are optimized considering the reconstruction loss L plus a third term that has the objective to stretch the data embeddings closer to the corresponding cluster centroids:

7

where is a function that is equal to 1 if the data embedding of the time-series 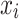belongs to cluster l and 0 elsewhere. 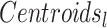is the centroid of cluster l. Finally, the new data representation (embeddings) is extracted (line 15) and returned by the procedure. The final partition is obtained by applying the K-Means clustering algorithm on the new data representation.

Experimental Evaluation

In this section we assess the behavior of DeTSEC considering six real world multivariate time series benchmarks. To evaluate the performance of our proposal, we compare it with several competing and baselines approaches by means of standard clustering evaluation metrics. In addition, we perform a qualitative analysis based on a visual inspection of the embedding representations learnt by our framework and by competing approaches.

Competitors and Method Ablations

For the comparative study, we consider the following competitors:

• The classic K-means algorithm [21] based on euclidean distance.

• The spectral clustering algorithm [15] (SC). This approach leverages spectral graph theory to extract a new representation of the original data. K-means method is then applied to obtain the final data partition.

• The Deep Embedding Clustering algorithm [28] (DEC) that performs partitional clustering through deep learning. Similarly to K-means, also this approach is suited for data with fixed length. Also in this case we perform zero padding to fit all the time-series lengths to the size of the longest one.

• The Dynamic Time Warping measures [7] (DTW) coupled with K-means algorithm. Such distance measure is especially tailored for time-series data with variable length-size.

• The Soft Dynamic Time Warping measures introduced in [6] (SOFTDTW). This measure is a differentiable distance measure recently introduced to manage dissimilarity evaluation between multivariate time-series of variable length. We couple such measure with the K-means algorithm.

Note that when using K-means and SC, due to the fact that multivariate time series can have different lengths, we perform zero padding to fit all the time-series lengths to the longest one. For the DEC method, we use the KERAS implementation1. For the DTW and SOFTDTW measures we use their publicly available implementations [22]. With the aim to understand the interplay among the different components of DeTSEC, we also propose an ablation study by taking into account the following variants of our framework:

• A variant of our approach that does not involve the gating mechanism. The information coming from the forward and backward encoder are summed directly without any weighting schema. We name such ablation DeTSEC.

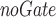• A variant of our approach that only involves the forward encoder/decoder GRU networks disregarding the use of the multivariate time series in reverse order. We name such ablation DeTSEC.

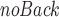Data and Experimental Settings

Our comparative evaluation has been carried out by performing experiments on six benchmarks characterized by different characteristics in terms of number of samples, number of attributes (dimensions) and time length: AUSLAN, JapVowel, ArabicDigits, RemSensing, BasicM and ECG. All datasets, except RemSensing – which was obtained contacting the authors of [10] – are available online2. The characteristics of the six datasets are reported in Table 1.

Table 1.

Dataset characteristics

Dataset	# Samples	# Dims	Min/Max length	Avg. length	# Classes
AUSLAN	2 565	22	45/136	57	95
JapVowel	640	12	7/29	15	9
ArabicDigits	8 800	13	4/93	39	10
RemSensing	1 673	16	37/37	37	7
BasicM	80	6	100/100	100	4
ECG	200	2	39/152	89	2

Clustering performances were evaluated by using two evaluation measures: the Normalized Mutual Information (NMI) and Adjusted Rand Index (ARI) [21]. The NMI measure varies in the range [0, 1] while the ARI measure varies in the range [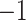, 1]. These measures take their maximum value when the clustering partition completely matches the original one, i.e., the partition induced by the available class labels. Due to the non deterministic nature of all the clustering algorithms involved in the evaluation, we run the clustering process 30 times for each configuration, and we report average and standard deviation for each method, benchmark and measure.

DeTSEC is implemented via the Tensorflow python library. For the comparison, we set the size of the hidden units in each of the GRU networks (forward/backward - encoder/decoder) to 64 for BasicM, ECG benchmarks and 512 for AUSLAN, JapVowel, ArabicDigits, RemSensing benchmarks. This difference is due to the fact that the former group includes datasets with limited number of samples that cannot be employed to efficiently learn recurrent neural networks with too many parameters. To train the model, we set the batch size equal to 16, the learning rate to 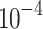and we use the ADAM optimizer [12] to learn the parameters of the model. The model are trained for 300 epochs: in the first 50 epochs the autoencoder is pre-trained while in the remaining 250 epochs the model is refined via clustering loss. Experiments are carried out on a workstation equipped with an Intel(R) Xeon(R) E5-2667 v4@3.20 GHz CPU, with 256 GB of RAM and one TITAN X GPU.

Quantitative Results

Table 2 reports on the performances of DeTSEC and the competing methods in terms of NMI and ARI. We can observe that DeTSEC outperforms all the other methods on five datasets over six. The highest gains in performance are achieved on speech and activity recognition datasetes (i.e., JapVowel, ArabicDigits, AUSLAN and BasicM). On such benchmarks, DeTSEC outperforms the best competitors of at least 8 points (AUSLAN) with a maximum gap of 45 points on ArabicDigits. Regarding the EGC dataset, we can note that best performances are obtained by K-Means and DEC. However, it should be noted that also in this case DeTSEC outperforms the competitors specifically tailored to manage multivariate time-series data (i.e., DTW and SOFTDTW).

Table 2.

Results in terms of Normalized Mutual Information and Adjusted Rand Index of the different competing methods on the six considered multivariate time series benchmarks.

	AUSLAN		JapVowel		ArabDigits		RemSens		BasicM		ECG
	NMI	ARI	NMI	ARI	NMI	ARI	NMI	ARI	NMI	ARI	NMI	ARI
K-means	0.35	0.23	0.16	0.11	0.14	0.06	0.39	0.43	0.25	0.11	0.16	0.25
SC	0.29	0.00	0.31	0.08	0.09	0.03	0.51	0.34	0.76	0.59	0.23	0.08
DEC	0.47	0.07	0.23	0.11	0.19	0.09	0.48	0.33	0.38	0.20	0.16	0.25
DTW	0.71	0.33	0.81	0.71	0.17	0.03	0.60	0.47	0.67	0.43	0.06	0.06
SOFTDTW	0.72	0.34	0.75	0.62	0.13	0.05	0.56	0.41	0.14	0.18	0.10	0.05
DeTSEC	0.80	0.47	0.96	0.89	0.64	0.53	0.61	0.45	0.80	0.62	0.12	0.19

Table 3 reports on the comparison between DeTSEC and its ablations. It can be noted how there is not a clear winner resulting from this analysis. DeTSEC obtains the best performance (in terms of NMI and ARI) on two benchmarks (ArabicDigits and BasicM), while DeTSEC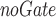 and DeTSEC appear to be more suitable for other benchmarks (even if the performances of DeTSEC remain always comparable to the best ones). For instance, we can observe that DeTSEC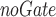 achieves the best performances on ECG. This is probably due to the fact that this ablation requires a lower number of parameters to learn, and this can be beneficial for processing datasets with a limited number of samples, timestamps and dimensions.

Table 3.

Results in terms of Normalized Mutual Information and Adjusted Rand Index of the different ablations of the proposed method on the six considered multivariate time series benchmarks.

	AUSLAN		JapVowel		ArabDigits		RemSens		BasicM		ECG
	NMI	ARI	NMI	ARI	NMI	ARI	NMI	ARI	NMI	ARI	NMI	ARI
DeTSEC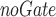	0.83	0.52	0.96	0.95	0.63	0.52	0.61	0.46	0.79	0.61	0.16	0.25
DeTSEC	0.79	0.46	0.96	0.96	0.60	0.49	0.61	0.50	0.79	0.61	0.05	0.1
DeTSEC	0.80	0.47	0.96	0.89	0.64	0.53	0.61	0.45	0.80	0.62	0.12	0.19

Visual Inspection

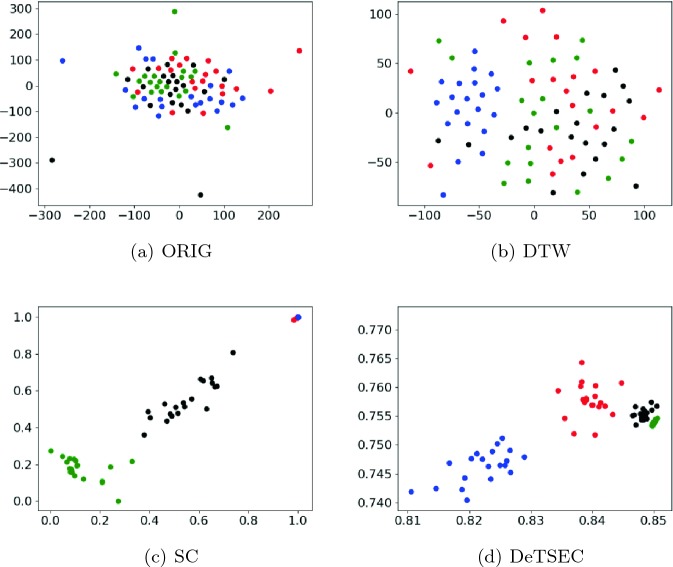
To proceed further in the analysis, we visually inspect the new data representation produced by DeTSEC and the best two competing methods (i.e., SC and DTW) by using BasicM as illustrative example. We choose this benchmark since it includes a limited number of samples (i.e., to ease the visualization and avoid possible visual cluttering) and it is characterized by timeseries of fixed length that avoid zero padding transformation. The BasicM benchmark includes examples belonging to four different classes that, in Fig. 2, are depicted with four different colors: red, blue, green and black. Figure 2(a), (b), (c) and (d) show the two-dimensional projections of the original data versus the DTW and SC approaches on such dataset. The two dimensional representation is obtained via the t-distributed stochastic neighbor embedding (TSNE) approach [16].

Fig. 2.

Visual projection of the original data (a), the distance matrix induced by Dynamic Time Warping measure (b), the representation generated via the Spectral Clustering method (c) and the embeddings learnt by DeTSEC (d) on the BasicM benchmark. (Color figure online)

In this evaluation, we clearly observe that DeTSEC recovers the underlying data structure better than the competing approaches. The original data representation (Fig. 2(a)) drastically fails to capture data separability. The DTW method (Fig. 2(b)) retrieves the cluster involving the blue points, on the left side of the figure, but it can be noted how all the other classes still remain mixed up. SC produces a better representation than the previous two cases but it still exhibits some issue to recover the four cluster structure: the green and black examples are slightly separated but some confusion is still present while the red and blue examples lie in a very close region (a fact that negatively impacts the discrimination between these two classes). Conversely, DeTSEC is able to stretch the data manifold producing embeddings that visually fit the underlying data distribution better than the competing approaches, and distinctly organize the samples according to their inner cluster structure.

To sum up, we can underline that explicitly managing the temporal auto-correlation leads to better performances regarding the clustering of multivariate time-series of variable length. Considering the benchmarks involved in this work, DeTSEC exhibits a general better behavior with respect to the competitors when the benchmark contains enough data to learn the model parameters. This is particularly evident when speech or activity recognition tasks are considered. In addition, the visual inspection of the generated embedding representation is in line with the quantitative results and it underlines the quality of the proposed framework.

Conclusions

In this paper we have presented DeTSEC, a deep learning based approach to cluster multivariate time series data of variable length. DeTSEC is a two stages framework in which firstly an attentive-gated RNN-based autoencoder is learnt with the aim to reconstruct the original data and, successively, the reconstruction task is complemented with a clustering refinement loss devoted to further stretching the embedding representations towards the corresponding cluster structure.

The evaluation on six real-world time-series benchmarks has demonstrated the effectiveness of DeTSEC and its flexibility on data coming from different application domains. We also showed, through a visual inspection, how the embedding representations generated by DeTSEC highly improve data separability. As future work, we plan to extend the proposed framework considering a semi-supervised and/or constrained clustering setting.