Abstract
High utility itemset mining consists of identifying all the sets of items that appear together and yield a high profit in a customer transaction database. Recently, this problem was extended to discover trending high utility itemsets (itemsets that yield an increasing or decreasing profit over time). However, an important limitation of that problem is that it is assumed that trends remain stable over time. But in real-life, trends may change in different time intervals due to specific events. To identify time intervals where itemsets have increasing/decreasing trends in terms of utility, this paper proposes the problem of mining Locally Trending High Utility Itemsets (LTHUIs) and their Trending High Utility Periods (THUPs). Properties of the problem are studied and an efficient algorithm named LTHUI-Miner is proposed to enumerate all the LTHUIs and their THUPs. An experimental evaluation shows that the algorithm is efficient and can discover insightful patterns not found by previous algorithms.
Keywords: High utility mining, Trending itemset, Local trends
Introduction
Frequent itemset mining (FIM) is a popular data mining task, which consists of enumerating all sets of values (items) that have a support (occurrence frequency) that is no less than a minimum threshold in a transaction database [5]. FIM has recently been generalized as high utility itemset mining (HUIM) to consider items having non binary purchase quantities in transactions and weights indicating their relative importance [2, 4, 10, 13–15]. The goal of HUIM is to find all itemsets that have a high utility (e.g. yield a high profit). Though, HUIM is useful to understand customer behavior, a key problem of HUIM is that the time dimension is ignored. But in real-life, the utility of itemsets vary over time. For example, the sales of some products in a retail store may increase or decrease over a few weeks as it loses or gains in popularity.
To discover high utility itemsets that have an increasing or decreasing utility over time, the problem of mining trending HUIs was proposed [9]. However, this problem only focuses on discovering itemsets that have trends spanning over the whole database (e.g. a set of products having sales that always follows an upward or downward trend). But that assumption is often unrealistic as an itemset may have upward or downward trends only during some time periods rather than in the whole database. For instance, the utility (profit) generated by the sale of sunscreen in a store may have an upward trend from May to July but not during the whole year. It is thus an important challenge to design algorithms to identify trends in non predefined time intervals. This is also challenging as it requires to not only consider a large search space of itemsets but also of time intervals.
This paper addresses this issue by proposing a novel problem of mining locally trending high utility itemsets (LTHUIs), that is to find all time intervals where itemsets have a high utility and show an upward or downward trend. To efficiently discover these patterns, this paper proposes a novel algorithm named Locally Trending High Utility Itemset Miner (LTHUI-Miner). It relies on novel upper-bounds and pruning techniques. An experimental evaluation on real transaction data shows that the proposed algorithm has excellent performance and can discover insightful patterns not found by previous algorithms.
The rest of this paper is organized as follows. Section 2 reviews related work. Section 3 defines the proposed problem of LTHUI mining. Then, Sect. 4 describes the designed algorithm, Sect. 5 presents the experimental evaluation. Lastly, Sect. 6 draws a conclusion and discusses future work.
Related Work
HUIM extends FIM [1, 5] and thus algorithms for these problems have similarities. However, there is also a key difference. FIM algorithms discover frequent itemsets by relying on the anti-monotonicity property of the support measure, which states that the support of an itemset cannot be greater than that of its subsets [1, 5]. This is a very powerful property to reduce the search space, but it does not hold for the utility measure in HUIM. To mine high utility itemsets efficiently, state-of-the-art HUIM algorithms such as Two-Phase [14], HUI-Miner [15], d2hup [13] and HU-FIMi [10] introduced various upper-bounds on the utility measure that respect the anti-monotonicity property to reduce the search space, and novel data structures to perform utility computation efficiently.
Though HUIM is useful to reveal profitable customer behavior, few HUIM algorithms consider the time dimension. The PHM algorithm [3] finds patterns that periodically appear and yield a high profit (e.g. a customer buys wine every week). The RUP algorithm [8] finds itemsets that recently had a high utility by applying a decay function to the utility measure (recent events are considered more important in utility calculations). And recently, to discover itemsets that follow some trends such as an increase or decrease in utility, the TPHUI-Miner algorithm [9] was designed. However, a major limitation of the three above algorithms is that they find patterns that shows some periodic behavior, recent behavior or trends valid for the whole database rather than for specific time intervals. But in real-life, the utility of itemsets vary over time, and some of these behaviors may only appear in some time intervals.
To find itemsets that have a high utility in some specific time periods, on-shelf high utility itemset mining was proposed [11]. However, the time periods need to be fixed by the user beforehand. To find high utility itemsets in non predefined time intervals, it was proposed to mine local high utility itemsets with the LHUI-Miner algorithm [7]. Though this algorithm can find insightful patterns, it is unable to discover trends such as an increase or decrease of utility in specific time periods. To address these limitations, the next section proposes the novel problem of discovering locally trending high utility itemsets.
Problem Definition
This section introduces HUIM, and then defines the proposed problem of mining locally trending high utility itemsets. The input of HUIM is a transaction database. Consider a set of items (products) 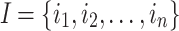 . A subset
. A subset 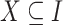 is called an itemset. An itemset
is called an itemset. An itemset  containing a single item i can be denoted without brackets as i, when the context is clear. A transaction T is an itemset, purchased by a customer. A transactional database is a multiset of transactions
containing a single item i can be denoted without brackets as i, when the context is clear. A transaction T is an itemset, purchased by a customer. A transactional database is a multiset of transactions  , where each transaction
, where each transaction  has a unique identifier tid and a timestamp
has a unique identifier tid and a timestamp  , which may not be unique. Each item i appearing in a transaction T is associated with a number
, which may not be unique. Each item i appearing in a transaction T is associated with a number 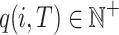 called its internal utility (purchase quantity). Moreover, each item
called its internal utility (purchase quantity). Moreover, each item 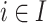 is associated with an external utility value
is associated with an external utility value 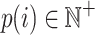 representing its relative importance (e.g. unit profit). For instance, Table 1 shows a database containing five items (a, b, c, d, e) and nine transactions (
representing its relative importance (e.g. unit profit). For instance, Table 1 shows a database containing five items (a, b, c, d, e) and nine transactions (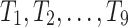 ), which will be used as running example. Timestamps are denoted as
), which will be used as running example. Timestamps are denoted as 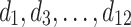 . The internal utility of an item in a transaction is shown as a number besides the item, while the external utility of items is given in Table 2. Transaction
. The internal utility of an item in a transaction is shown as a number besides the item, while the external utility of items is given in Table 2. Transaction 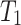 indicates that a customer purchased the items b, c, and e with purchase quantities (internal utility) of 2, 2 and 1, respectively. Their external utility (unit profit) are 2, 1 and 3, respectively.
indicates that a customer purchased the items b, c, and e with purchase quantities (internal utility) of 2, 2 and 1, respectively. Their external utility (unit profit) are 2, 1 and 3, respectively.
Table 1.
A transaction database
| Trans | Items | Timestamp |
|---|---|---|
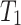 |
(b, 2), (c, 2), (e, 1) |  |
 |
(b, 4), (c, 3), (d, 2), (e, 1) | 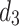 |
 |
(b, 5), (c, 1), (e, 1) |  |
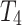 |
(a, 2), (b, 10), (c, 2) | 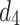 |
 |
(a, 2), (c, 6), (e, 2) |  |
 |
(b, 4), (c, 3) |  |
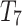 |
(b, 16), (c, 2) |  |
 |
(a, 2), (c, 6), (e, 2) |  |
 |
(b, 5), (c, 2), (e, 1) | 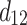 |
Table 2.
External utilities of items
| Item | Unit profit |
|---|---|
| a | 5 |
| b | 2 |
| c | 1 |
| d | 2 |
| e | 3 |
The task of HUIM consists of enumerating all high utility itemsets, i.e. itemsets having a utility that is no less than a positive minimum utility threshold (minutil) set by the user [14]. The utility of an item i in a transaction T is defined as 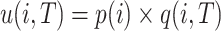 . The utility of an itemset X in T is defined as
. The utility of an itemset X in T is defined as 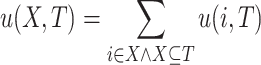 if
if  , and otherwise
, and otherwise 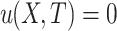 . The utility of an itemset X in a database D is defined as
. The utility of an itemset X in a database D is defined as  . For example, the utility of itemset
. For example, the utility of itemset  in the database is
in the database is 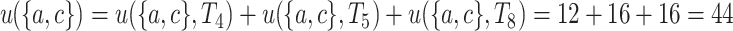 .
.
To find HUIs having increasing/decreasing trends in terms of utility in a database, Hackman et al. [9] proposed to mine trending high utility itemsets, i.e. HUIs having a positive/negative slope for a whole database. The slope of a HUI is defined as follows. The utility of an itemset X at a timestamp d in a database D is defined as:  . Let there be a HUI X and TS be the set of timestamps in a database D. The utility set of X in D is defined as the multiset
. Let there be a HUI X and TS be the set of timestamps in a database D. The utility set of X in D is defined as the multiset  . The slope of X in D is:
. The slope of X in D is: 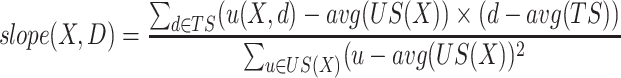 where avg is the average.
where avg is the average.
There are two important issues with the problem of mining trending HUIs [9]. First, in the above slope calculation, it can be argued that time should be used as denominator instead of the utility because the user is typically interested in how utility varies over time rather than the opposite. Second, the slope of a HUI is calculated for the whole database. Hence, the algorithm of Hackman et al. [9] is unable to find local trends such as a HUI that follows a trend only in a sub-time interval. To address these issues, this paper proposes to mine itemsets that have a high utility and follow an increasing/decreasing trend in some non predefined time intervals. This paper redefines the concepts of utility and slope such that the time is divided into non-overlapping consecutive bins to reduce the influence of small fluctuations in the utility of items. The user must set a bin length binlen
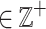 . Then, the average timestamp and average utility of each bin is used as basis for slope calculations.
. Then, the average timestamp and average utility of each bin is used as basis for slope calculations.
Definition 1
(Bin). Let there be a database D of m transactions, and two timestamps i, j such that  . The bin from time i to j is defined as
. The bin from time i to j is defined as  . The length of a bin
. The length of a bin  is length(
is length( ) = j − i + 1. The average timestamp of a bin
) = j − i + 1. The average timestamp of a bin 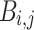 is defined as
is defined as 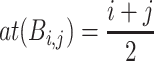 . The utility of an itemset X in a bin
. The utility of an itemset X in a bin  is defined as:
is defined as:  . The average utility of X in
. The average utility of X in  is defined as
is defined as 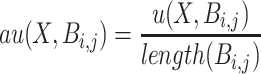 .
.
Definition 2
(Binned database). Let there be a database  and a fixed bin length binlen. The time interval
and a fixed bin length binlen. The time interval 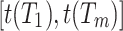 is divided into consecutive non-overlapping bins of length binlen. For the sake of simplicity, the last bin is ignored if its length is less than binlen. The number of bins in D is
is divided into consecutive non-overlapping bins of length binlen. For the sake of simplicity, the last bin is ignored if its length is less than binlen. The number of bins in D is  . The sequence of bins in D, ordered by time, is defined as:
. The sequence of bins in D, ordered by time, is defined as:  . Moreover, let BS[k] denotes the k-th element of BS.
. Moreover, let BS[k] denotes the k-th element of BS.
To detect non predefined time intervals containing trends, a sliding window of length winlen is slided over the sequence of bins BS.
Definition 3
(Window). Let there be a database D and a user-defined sliding window length winlen, such that  where
where  and
and  . Each window contains winlen/binlen bins. Let
. Each window contains winlen/binlen bins. Let  denotes the window containing the i-th bin until the j-th bin of the sequence BS, that is
denotes the window containing the i-th bin until the j-th bin of the sequence BS, that is  . A window
. A window 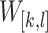 is a subset of
is a subset of  iff
iff 
 , i.e. all bins included in
, i.e. all bins included in 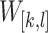 are also included in
are also included in  . A window
. A window 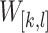 is a strict subset of
is a strict subset of  iff
iff  . The length of a window
. The length of a window 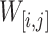 is length
is length . Let
. Let 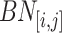 be the sequence of bins that are contained in
be the sequence of bins that are contained in 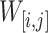 , ordered by time, that is
, ordered by time, that is  . Let
. Let 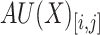 denotes the sequence of average utilities of an itemset X for the bins of
denotes the sequence of average utilities of an itemset X for the bins of  , that is
, that is  . Let
. Let  denotes the sequence of average timestamps corresponding to bins in
denotes the sequence of average timestamps corresponding to bins in 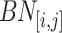 , that is
, that is  . In the following, indices [i, j] of W, BN, AU, and AT (which refer to sequence BS) are omitted when the context is clear. The utility of an itemset X in a window W is defined as:
. In the following, indices [i, j] of W, BN, AU, and AT (which refer to sequence BS) are omitted when the context is clear. The utility of an itemset X in a window W is defined as:  .
.
We then define the slope of an itemset in a sliding window as follows:
Definition 4
(Slope of an itemset in a sliding window). Let A[k] be the k-th element of a sequence of values A. The slope of an itemset X in a sliding window W is: 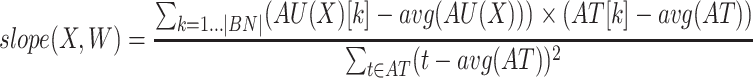 iff the itemset X appears in each bin of the sliding window W, i.e.,
iff the itemset X appears in each bin of the sliding window W, i.e.,  . A sliding window W meeting that latter condition is called a no-empty-bin sliding window of X. Otherwise, the slope is undefined. Besides, in the case where the denominator is 0, the slope is defined as 0.
. A sliding window W meeting that latter condition is called a no-empty-bin sliding window of X. Otherwise, the slope is undefined. Besides, in the case where the denominator is 0, the slope is defined as 0.
For example, if  ,
,  ,
,  , and
, and  . The utility of itemset
. The utility of itemset 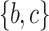 in
in  is
is 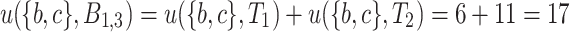 , the utility of itemset
, the utility of itemset 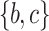 in
in  is
is 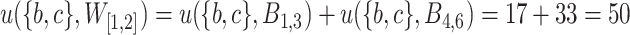 . The slope of itemset
. The slope of itemset 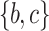 in
in  is
is  .
.
If binlen is set to a reasonably large value, the requirement that an itemset X appears in each bin of a sliding window to have a slope is reasonable, and ensures that the slope is not influenced by missing values. Based on the above definitions, the problem of mining locally trending HUIs is defined.
Definition 5
(Problem definition). Let there be some parameters 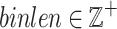 ,
, 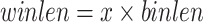 for an integer
for an integer 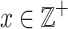 such that
such that  ,
, 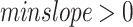 (or
(or  ) set by the user. A window
) set by the user. A window  is a Trending High Utility Period (THUP) of an itemset X if for any sliding window
is a Trending High Utility Period (THUP) of an itemset X if for any sliding window  where length
where length  , indicating an increasing trend (or
, indicating an increasing trend (or  , indicating a decreasing trend). Furthermore, a THUP
, indicating a decreasing trend). Furthermore, a THUP  is said to be a maximum THUP if there is no THUP
is said to be a maximum THUP if there is no THUP  such that
such that  . The problem of Locally Trending High Utility Itemset Mining (LTHUIM) is to find all Locally Trending High Utility Itemsets (LTHUIs), and their maximum Trending High Utility Periods (THUPs). An itemset is a LTHUI if it has at least one THUP.
. The problem of Locally Trending High Utility Itemset Mining (LTHUIM) is to find all Locally Trending High Utility Itemsets (LTHUIs), and their maximum Trending High Utility Periods (THUPs). An itemset is a LTHUI if it has at least one THUP.
For example, for  and
and 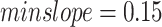 , three LTHUIs are found.
, three LTHUIs are found.  has a maximum THUP
has a maximum THUP 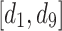 (utility = 82, slope = 0.52),
(utility = 82, slope = 0.52),  has a maximum THUP
has a maximum THUP  (utility = 95, slope = 0.52), and
(utility = 95, slope = 0.52), and  has a maximum THUP
has a maximum THUP  (utility = 27, slope = 0.19).
(utility = 27, slope = 0.19).
The LTHUI-Miner Algorithm
The search space in traditional HUIM consists of  itemsets. For the proposed problem, if there are w sliding windows, then there are
itemsets. For the proposed problem, if there are w sliding windows, then there are  potential THUPs to be considered. To efficiently find LTHUIs, the proposed LTHUI-Miner uses three properties that reduce the search space by eliminating items or itemsets w.r.t. the whole database or a sliding window.
potential THUPs to be considered. To efficiently find LTHUIs, the proposed LTHUI-Miner uses three properties that reduce the search space by eliminating items or itemsets w.r.t. the whole database or a sliding window.
Property 1
(Pruning a Low-TWU Item in a Database). For an item i and a database D, let there be a measure  . If
. If  , then any itemset
, then any itemset  is not a LTHUI.
is not a LTHUI.
This property was proven for HUIs in the traditional HUIM problem [14]. But it also holds for LTHUIM since every LTHUI must be a HUI.
For example, if  ,
,  and
and  ,
,  . Thus, d is a low TWU item in the database, and any itemset
. Thus, d is a low TWU item in the database, and any itemset  is not a LTHUI.
is not a LTHUI.
The second and third pruning properties require a total order  on the set of items I, which is used by LTHUI-Miner to explore the search space of itemsets. LTHUI-Miner performs a depth-first search starting from itemsets containing single items, and recursively extends each itemset by appending single items according to that order. Formally, an itemset
on the set of items I, which is used by LTHUI-Miner to explore the search space of itemsets. LTHUI-Miner performs a depth-first search starting from itemsets containing single items, and recursively extends each itemset by appending single items according to that order. Formally, an itemset 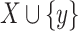 obtained by appending an item y to an itemset X is said to be an extension of X if
obtained by appending an item y to an itemset X is said to be an extension of X if  .
.
Property 2
(Pruning an Unpromising itemset using its Remaining Utility in a Database). The remaining utility of an itemset X in a transaction T is defined as  if
if  . The remaining utility of an itemset
X
in a database is defined as
. The remaining utility of an itemset
X
in a database is defined as  . If
. If  , then X and its transitive extensions are not LTHUIs.
, then X and its transitive extensions are not LTHUIs.
For example, if  ,
,  and
and  . The TWU ascending order on items is
. The TWU ascending order on items is 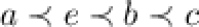 . Note that item d has been pruned using Property 1.
. Note that item d has been pruned using Property 1.  . Then, itemset
. Then, itemset 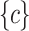 and its transitive extensions are not LTHUIs.
and its transitive extensions are not LTHUIs.
Property 3
(Pruning an Unpromising itemset using its Remaining Utility in a sliding window). The remaining utility of an itemset
X
in a sliding Window W is defined as  . If
. If  , then X and its transitive extensions have no THUP in W.
, then X and its transitive extensions have no THUP in W.
This property can be proved by observing that such itemsets cannot have a utility greater than or equal to minutil in the sliding window W, and thus these itemsets cannot have a THUP in W. For example, if  ,
,  and
and  ,
, 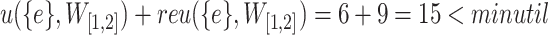 . Thus, the window
. Thus, the window  is not a THUP for itemset
is not a THUP for itemset  and its transitive extensions.
and its transitive extensions.
To efficiently calculate the utility of any itemset during the depth-first search and check the pruning conditions of Properties 2 and 3, the proposed algorithm utilizes a novel structure called Trending Utility-list (TU-list), which extends the utility-list structure used in traditional HUIM [4] with information about bins and time periods. The first part of a TU-list of an itemset X stores information about the utility of the itemset X in transactions where it appears, and about the utilities of items that could extend X in these transactions. Formally, the first part of a TU-list is a set of tuples called elements such that there is a tuple (tid, iutil, rutil) for each transaction  containing X where
containing X where  and
and  . The second part of a TU-list contains four lists named binUtils, binRutils, trendPeriods and promisingPeriods. They store the utility of X for each bin, the remaining utility of X for each bin, the maximum trending high utility periods of X and the promising periods of X, respectively. A promising period of an itemset X is a time period where X and its transitive extensions may have a utility greater than or equal to minutil based on Property 3. Formally, let there be some parameters
. The second part of a TU-list contains four lists named binUtils, binRutils, trendPeriods and promisingPeriods. They store the utility of X for each bin, the remaining utility of X for each bin, the maximum trending high utility periods of X and the promising periods of X, respectively. A promising period of an itemset X is a time period where X and its transitive extensions may have a utility greater than or equal to minutil based on Property 3. Formally, let there be some parameters  and
and 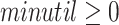 set by the user. A window
set by the user. A window  is a promising period of an itemset X if for any sliding window
is a promising period of an itemset X if for any sliding window  where length
where length  .
.
The TU-list structure of an itemset X has two interesting properties. First, it allows to directly calculate the utility u(X) of X without scanning the database, as the sum of the iutil values in the TU-list of X. Second, reu(X) can be calculated as the sum of rutil values. Moreover, the utility and remaining utility of an itemset X in a bin B and a window W can also be calculated from its TU-list by considering only transactions in B and W, respectively.
For example, the TU-list of itemset  is
is  and
and  . Then, the utility of itemset
. Then, the utility of itemset  in a database or window can be calculated without scanning the database again, e.g.,
in a database or window can be calculated without scanning the database again, e.g., 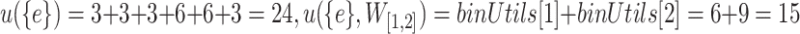 . The remaining utility of itemset
. The remaining utility of itemset  in a window can also be calculated directly using binRutils:
in a window can also be calculated directly using binRutils: 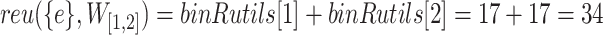 .
.
Another property of TU-lists is that those of two itemsets of the form  and
and  can be joined to obtain the TU-list of an itemset
can be joined to obtain the TU-list of an itemset 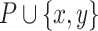 . This is done by first applying the construct procedure of HUI-Miner [15]. Then, the binUtils, binRutils, trendPeriods and promisingPeriods lists can be calculated by applying the findTrend procedure, presented in the next section.
. This is done by first applying the construct procedure of HUI-Miner [15]. Then, the binUtils, binRutils, trendPeriods and promisingPeriods lists can be calculated by applying the findTrend procedure, presented in the next section.
The Algorithm. We next present the proposed LTHUI-Miner algorithm by explaining how it finds increasing trends. Decreasing trends are found in a similar way. The algorithm takes as input a transaction database D and the binlen, winlen, minutil and minslope parameters. The algorithm outputs all LTHUIs and their maximum THUPs. The algorithm first scans the database to calculate the bins, sliding windows and TWU(i) of each item i. Then, each item i such that  is ignored from further processing as it cannot be part of a LTHUI by Property 1. Then, the processing order
is ignored from further processing as it cannot be part of a LTHUI by Property 1. Then, the processing order  on remaining items is defined as the increasing order of TWU, as in previous work [4]. Then, the algorithm scans the database again to create the TU-list of each remaining item. Thereafter, LTHUI-Miner recursively extends each of those items by appending items following the
on remaining items is defined as the increasing order of TWU, as in previous work [4]. Then, the algorithm scans the database again to create the TU-list of each remaining item. Thereafter, LTHUI-Miner recursively extends each of those items by appending items following the  order. This is done by calling the LTHUISearch procedure (Algorithm 1) with six parameters: (1) an itemset P (initially
order. This is done by calling the LTHUISearch procedure (Algorithm 1) with six parameters: (1) an itemset P (initially 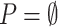 ), (2) a set exP of one-item extensions of P of the form
), (2) a set exP of one-item extensions of P of the form  where
where 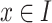 (initially, the remaining items), (3) binlen, (4) winlen, (5) minutil, and (6) minslope. The procedure first checks if the trendPeriods list of each itemset Px in the set exP is empty. If not, the itemset Px is output as a LTHUI with Px.TUlist.trendPeriods as its maximum THUPs. Moreover, if promisingPeriods of Px is not empty and Px is promising in the database according to Property 2, the algorithm will try to extend Px. This is done by joining Px with each itemset
(initially, the remaining items), (3) binlen, (4) winlen, (5) minutil, and (6) minslope. The procedure first checks if the trendPeriods list of each itemset Px in the set exP is empty. If not, the itemset Px is output as a LTHUI with Px.TUlist.trendPeriods as its maximum THUPs. Moreover, if promisingPeriods of Px is not empty and Px is promising in the database according to Property 2, the algorithm will try to extend Px. This is done by joining Px with each itemset 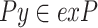 such that
such that  , to obtain itemsets of the form Pxy. The TU-list of Pxy is constructed by calling the construct procedure. Then, the procedure FindTrend is called to construct the binUtils, binRutils, trendPeriods and promisingPeriods of that TU-list, and Pxy is added to a set exPx. Then, the procedure LTHUI-Search is called with Px and exPx to check if itemsets in exPx are LTHUIs and explore their extensions.
, to obtain itemsets of the form Pxy. The TU-list of Pxy is constructed by calling the construct procedure. Then, the procedure FindTrend is called to construct the binUtils, binRutils, trendPeriods and promisingPeriods of that TU-list, and Pxy is added to a set exPx. Then, the procedure LTHUI-Search is called with Px and exPx to check if itemsets in exPx are LTHUIs and explore their extensions.
The FindTrend procedure takes as input (1) an itemset P, (2) a one item extension of P, (3) binlen, (4) winlen, (5) minutil and (6) minslope. First, the procedure scans the elements of the TU-list of Px to calculate binUtils and binRutils. Then, the procedure moves a sliding window over the sequence of bins BS to calculate the utility and slope of windows using two variables, namely winStart (the index in BS of the first bin of a sliding window, initialized to 0) and winEnd (the index in BS of the last bin of a sliding window, initialized to winlen/binlen). However, the process of sliding a window while calculating the slope and utility may be interrupted because some sliding windows in BS may have empty bins, and the slope cannot be calculated in that case. Thus, a loop is performed to find the next sliding window without empty bins, and then continue the sliding process until an empty bin is encountered or winEnd reaches the last bin of the sequence BS. In more details, this is done by first finding the first no-empty-bin sliding window starting from winStart, updating winStart, winEnd and calculating utils (utility of the itemset Px in that window), rutils (remaining utility of Px in that window) . Then, the following step is repeated until (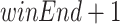 ) reaches the last bin of BS or the utility of Px in the bin of index (
) reaches the last bin of BS or the utility of Px in the bin of index ( ) is 0 or itemset P is unpromising in the sliding window
) is 0 or itemset P is unpromising in the sliding window 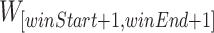 : (1) increase the index of the first and last bin of the sliding window, then update utils and rutils, (2) compare the value of utils,
: (1) increase the index of the first and last bin of the sliding window, then update utils and rutils, (2) compare the value of utils,  with minutil to determine whether to merge the sliding window with the previous period or add that window to Px.TUlist.trendPeriods and Px.TUlist.promisingPeriods. These latter are used to store maximum THUPs and promising periods.
with minutil to determine whether to merge the sliding window with the previous period or add that window to Px.TUlist.trendPeriods and Px.TUlist.promisingPeriods. These latter are used to store maximum THUPs and promising periods.
LTHUI-Miner is correct and complete, as it explores itemsets by recursively performing extensions of single items, and the algorithm only prunes extensions based on the pruning properties.

Experiment
To test the performance of LTHUI-Miner, experiments were done on a computer having an Intel Xeon E3-1270 v5 processor with 64 GB RAM, on Windows 10. LTHUI-Miner was implemented in Java. Two real-life datasets with timestamps were used: retail and foodmart. Let |I|, |D| and A represents the number of distinct items, the number of transactions and the average transaction length. retail contains transactions from an anonymous Belgian retail store (|I| = 16,470, |D| = 88,162, A = 10.30). foodmart is transactional data obtained and transformed from the SQL-Server 2000 distribution (|I| = 1559, |D| = 4141, A = 4.40). The timestamps of retail and foodmart were generated by adopting a distribution used in prior work for retail data [7].
Because LTHUIM is a new problem, the performance of LTHUI-Miner cannot be compared with prior work. Thus, we compared three versions of LTHUI-Miner: (1) LTHUI-Miner (with all pruning techniques), denoted as lthui, (2) LTHUI-Miner without Property 3, denoted as lthui-no-prop3, and (3) a version of LTHUI-Miner without Property 2 and 3. However, that latter ran out of memory for all the experiments, and thus its results are not reported in the following. Experiments were done by varying the minutil and minslope parameters to see the influence on runtime and pattern count, respectively. No results are shown for an algorithm if it ran out of memory, or the runtime exceeded one hour.
Influence of
minutil
on Runtime and Memory. In the first experiment, the parameter minutil was varied to evaluate the performance of LTHUI-Miner in terms of runtime. LTHUI-Miner was run with  (about 5.5 h),
(about 5.5 h), 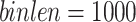 and
and  on the retail dataset, and run with
on the retail dataset, and run with  ,
,  and
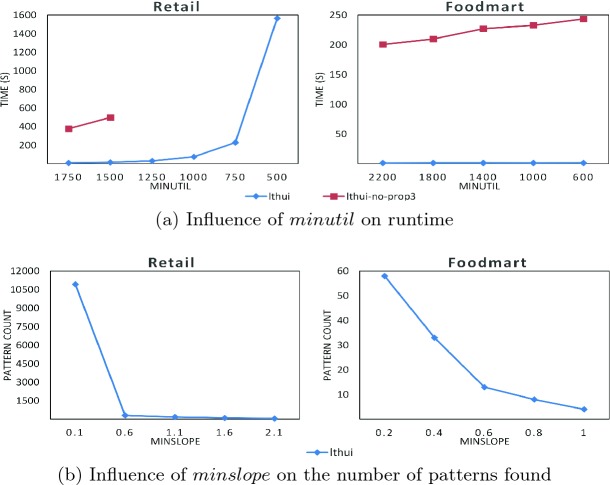
and  on the foodmart dataset. Fig. 1 (a) compares the runtimes of lthui and lthui-no-prop3 for the two datasets. It is observed that as minutil is decreased, runtime increases, which is reasonable since more patterns may be found. It is also observed that pruning an unpromising itemset in a sliding window using the remaining utility (Property 3) greatly reduces the runtime. For example, on the retail dataset, when
on the foodmart dataset. Fig. 1 (a) compares the runtimes of lthui and lthui-no-prop3 for the two datasets. It is observed that as minutil is decreased, runtime increases, which is reasonable since more patterns may be found. It is also observed that pruning an unpromising itemset in a sliding window using the remaining utility (Property 3) greatly reduces the runtime. For example, on the retail dataset, when  , the execution time of lthui-no-prop3 is 498 s, which is more than 32 times that of lthui, and on the foodmart dataset, when
, the execution time of lthui-no-prop3 is 498 s, which is more than 32 times that of lthui, and on the foodmart dataset, when  , lthui is up to 176 times faster than lthui-no-prop3. Memory consumption was also measured to compare the two algorithm versions. It was found that in most cases, the memory usage of lthui is less than lthui-no-prop3, which shows that Property 3 reduces memory consumption. Details are not shown due to the page limitation.
, lthui is up to 176 times faster than lthui-no-prop3. Memory consumption was also measured to compare the two algorithm versions. It was found that in most cases, the memory usage of lthui is less than lthui-no-prop3, which shows that Property 3 reduces memory consumption. Details are not shown due to the page limitation.
Fig. 1.
Experiment results
Influence of
minslope
on the Number of Patterns Found. In the second experiment, the minslope parameter was varied to evaluate its influence on the number of patterns found. Algorithms were run with  ,
,  and
and  on the retail dataset and
on the retail dataset and  ,
,  and
and 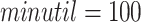 on the foodmart dataset. Results for the number of patterns are shown in Fig. 1 (b) for the two datasets. It is observed that as minslope increases, the number of patterns decreases, which was expected.
on the foodmart dataset. Results for the number of patterns are shown in Fig. 1 (b) for the two datasets. It is observed that as minslope increases, the number of patterns decreases, which was expected.
Pattern Analysis. On the two datasets, some patterns having a strong trend were found, which means that the utility of these itemsets was high and increased rapidly in their THUPs. For example, on retail and foodmart dataset, 179 and 13 patterns have slope values greater than 1.1 and 0.6 respectively. Discovering such strong trends can be very helpful for a retail store manager to understand customer behavior and take decisions, since products in LTHUIs generate high profits and the profits is growing quickly during their THUPs.
Conclusion
This paper has defined a novel problem of mining Locally Trending High Utility Itemsets having increasing/decreasing trend(s) in some non-predefined time periods. The properties of LTHUI mining were studied and a novel algorithm named LTHUI-Miner was proposed to efficiently mine all LTHUIs and their maximum THUPs. Besides, three pruning strategies were designed to improve the performance of LTHUI-Miner. The experimental evaluation has shown that the algorithm is efficient and can find useful patterns. In future work, techniques to automatically adjust parameters will be considered, as well as extensions for high utility episode mining [6], incremental pattern mining [12], [?] and using swarm optimization [16].
Contributor Information
Hady W. Lauw, Email: hadywlauw@smu.edu.sg
Raymond Chi-Wing Wong, Email: raywong@cse.ust.hk.
Alexandros Ntoulas, Email: antoulas@di.uoa.gr.
Ee-Peng Lim, Email: eplim@smu.edu.sg.
See-Kiong Ng, Email: seekiong@nus.edu.sg.
Sinno Jialin Pan, Email: sinnopan@ntu.edu.sg.
Philippe Fournier-Viger, Email: philfv@hit.edu.cn.
Yanjun Yang, Email: juneyoung9724@gmail.com.
Jerry Chun-Wei Lin, Email: jerrylin@ieee.org.
Jaroslav Frnda, Email: jfrnda@gmail.com.
References
- 1.Agrawal, R., Srikant, R., et al.: Fast algorithms for mining association rules. In: Proceedings of the 20th International Conference on Very Large Data Bases, VLDB, vol. 1215, pp. 487–499 (1994)
- 2.Dawar, S., Goyal, V.: Up-Hist Tree: an efficient data structure for mining high utility patterns from transaction databases. In: Proceedings of 19th International Conference on Database Engineering & Applications Symposium, pp. 56–61 (2015)
- 3.Fournier-Viger P, Lin JC-W, Duong Q-H, Dam T-L. PHM: mining periodic high-utility itemsets. In: Perner P, editor. Advances in Data Mining. Applications and Theoretical Aspects; Cham: Springer; 2016. pp. 64–79. [Google Scholar]
- 4.Fournier-Viger P, Chun-Wei Lin J, Truong-Chi T, Nkambou R. A survey of high utility itemset mining. In: Fournier-Viger P, Lin JC-W, Nkambou R, Vo B, Tseng VS, editors. High-Utility Pattern Mining; Cham: Springer; 2019. pp. 1–45. [Google Scholar]
- 5.Fournier-Viger, P., Lin, J.C.W., Vo, B., Chi, T.T., Zhang, J., Le, B.: A survey of itemset mining. WIREs Data Min. Knowl. Discov. (2017)
- 6.Fournier-Viger P, Yang P, Lin JC-W, Yun U. HUE-Span: fast high utility episode mining. In: Li J, Wang S, Qin S, Li X, Wang S, editors. Advanced Data Mining and Applications; Cham: Springer; 2019. pp. 169–184. [Google Scholar]
- 7.Fournier-Viger P, Zhang Y, Lin CW, Fujita H, Koh YS. Mining local and peak high utility itemsets. Inf. Sci. 2019;481:344–367. doi: 10.1016/j.ins.2018.12.070. [DOI] [Google Scholar]
- 8.Gan W, Lin JC-W, Fournier-Viger P, Chao H-C. Mining recent high-utility patterns from temporal databases with time-sensitive constraint. In: Madria S, Hara T, editors. Big Data Analytics and Knowledge Discovery; Cham: Springer; 2016. pp. 3–18. [Google Scholar]
- 9.Hackman A, Huang Y, Tseng VS. Mining trending high utility itemsets from temporal transaction databases. In: Hartmann S, Ma H, Hameurlain A, Pernul G, Wagner RR, editors. Database and Expert Systems Applications; Cham: Springer; 2018. pp. 461–470. [Google Scholar]
- 10.Uday Kiran R, Yashwanth Reddy T, Fournier-Viger P, Toyoda M, Krishna Reddy P, Kitsuregawa M. Efficiently finding high utility-frequent itemsets using cutoff and suffix utility. In: Yang Q, Zhou Z-H, Gong Z, Zhang M-L, Huang S-J, editors. Advances in Knowledge Discovery and Data Mining; Cham: Springer; 2019. pp. 191–203. [Google Scholar]
- 11.Lan G, Hong T, Tseng VS. Discovery of high utility itemsets from on-shelf time periods of products. Expert Syst. Appl. 2011;38(5):5851–5857. doi: 10.1016/j.eswa.2010.11.040. [DOI] [Google Scholar]
- 12.Lee J, Yun U, Lee G, Yoon E. Efficient incremental high utility pattern mining based on pre-large concept. Eng. Appl. AI. 2018;72:111–123. doi: 10.1016/j.engappai.2018.03.020. [DOI] [Google Scholar]
- 13.Liu, J., Wang, K., Fung, B.C.: Direct discovery of high utility itemsets without candidate generation. In: Proceedings of the 12th IEEE International Conference on Data Mining, pp. 984–989. IEEE (2012)
- 14.Liu Y, Liao W, Choudhary A. A two-phase algorithm for fast discovery of high utility itemsets. In: Ho TB, Cheung D, Liu H, editors. Advances in Knowledge Discovery and Data Mining; Heidelberg: Springer; 2005. pp. 689–695. [Google Scholar]
- 15.Qu J-F, Liu M, Fournier-Viger P. Efficient algorithms for high utility itemset mining without candidate generation. In: Fournier-Viger P, Lin JC-W, Nkambou R, Vo B, Tseng VS, editors. High-Utility Pattern Mining; Cham: Springer; 2019. pp. 131–160. [Google Scholar]
- 16.Song W, Huang C. Discovering high utility itemsets based on the artificial bee colony algorithm. In: Phung D, Tseng VS, Webb GI, Ho B, Ganji M, Rashidi L, editors. Advances in Knowledge Discovery and Data Mining; Cham: Springer; 2018. pp. 3–14. [Google Scholar]