Modeling multipartite virus evolution: the genome formula facilitates rapid adaptation to heterogeneous environments^†

Abstract

Multipartite viruses have two or more genome segments, and package different segments into different particle types. Although multipartition is thought to have a cost for virus transmission, its benefits are not clear. Recent experimental work has shown that the equilibrium frequency of viral genome segments, the setpoint genome formula (SGF), can be unbalanced and host-species dependent. These observations have reinvigorated the hypothesis that changes in genome-segment frequencies can lead to changes in virus-gene expression that might be adaptive. Here we explore this hypothesis by developing models of bipartite virus infection, leading to a threefold contribution. First, we show that the SGF depends on the cellular multiplicity of infection (MOI), when the requirements for infection clash with optimizing the SGF for virus-particle yield per cell. Second, we find that convergence on the SGF is very rapid, often occurring within a few cellular rounds of infection. Low and intermediate MOIs lead to faster convergence on the SGF. For low MOIs, this effect occurs because of the requirements for infection, whereas for intermediate MOIs this effect is also due to the high levels of variation generated in the genome formula (GF). Third, we explored the conditions under which a bipartite virus could outcompete a monopartite one. As the heterogeneity between environments and specificity of gene-expression requirements for each environment increased, the bipartite virus was more likely to outcompete the monopartite virus. Under some conditions, changes in the GF helped to exclude the monopartite competitor, highlighting the versatility of the GF. Our results show the inextricable relationship between MOI and the SGF, and suggest that under some conditions, the cost of multipartition can be outweighed by its benefits for the rapid tuning of viral gene expression.

1. Introduction

Many viruses have segmented genomes, dividing their hereditary material into what are effectively chromosomes (Sicard et al. 2016; Lucía-Sanz and Manrubia 2017). Whereas many segmented viruses package all of these genome segments into a single virus particle, multipartite (or multicomponent) viruses package genome segments into different virus particles (Fulton 1962). It has been generally thought that all or most segments must be transmitted between hosts to cause new infections. As a consequence, there would be a high cost for multipartite virus transmission because the probability of infection per virus particle is low and one or more segments might be lost during transmission (Fulton 1962; Iranzo and Manrubia 2012; Sánchez-Navarro, Zwart, and Elena 2013; Sicard et al. 2013, 2016). Nevertheless, many plant viruses have a multipartite genome organization (Sicard et al. 2016; Lucía-Sanz and Manrubia 2017). The first multipartite animal viruses were identified recently (Hu et al. 2016; Ladner et al. 2016), and their number is likely to grow (Male et al. 2016; Kraberger et al. 2019). An open key question is why multipartite genome organization evolved and is common among plant viruses, despite its obvious drawbacks. Are there benefits to multipartition that outweigh its cost to infection?

Since their discovery, many ideas have been proposed to explain the existence of multipartite viruses. One shortcoming of many of these proposals—including the evolutionary benefits of reassortment and faster nucleic-acid replication—is that they concern advantages of genome segmentation, and are therefore not neccessarily linked to multipartition as discussed elsewhere (Sicard et al. 2016). One proposal with empirical support is that smaller genome segments can lead to smaller and more stable foot-and-mouth disease virus particles (Ojosnegros et al. 2011), although the experimental conditions under which this virus was evolved are not very representative for infection in a multicellular host. Moreover, there does not seem to be an association between multipartition and genome size for plant viruses, precluding a general relationship (Sicard et al. 2016). Recent observations suggest that viruses can have distributed replication: gene products are shared between cells, ameliorating the cost of multipartition at the within-host level (Sicard et al. 2019). However, to what extent these hitherto unknown mechanisms apply to other viruses is unclear, and there will still be costs at the between-host level due to population bottlenecks (Gallet et al. 2018). Although some of these hypotheses are helpful and may explain a part of the story, it remains unclear why multipartition exists.

For all multipartite viruses examined to date, different genome segments are not present at equal frequencies (French and Ahlquist 1988; Hajimorad et al. 1991; Feng et al. 2006; Sicard et al. 2013; Hu et al. 2016; Wu et al. 2017), and these frequencies can change over time (Hajimorad et al. 1991; Sicard et al. 2013; Wu et al. 2017). These dynamics were tracked quantitatively for a nanovirus: for this dsDNA plant virus, when perturbed the genome-segment frequencies converged on a host-species-dependent equilibrium (Sicard et al. 2013). The set of genome-segment frequencies for all genome segments is known as the genome formula (GF), and its equilibrium value for a given environment is the setpoint genome formula (SGF) (Sicard et al. 2013). Later, we showed that frequency-dependent selection establishes a host-species-dependent SGF for alfalfa mosaic virus, a plant RNA virus, and that virus populations converged on this equilibrium within one week after perturbation (Wu et al. 2017). These observations and ongoing work on multipartite viruses have reinvigorated the hypothesis that multipartition serves to regulate viral gene-expression levels in different environments (Lucía-Sanz, Aguirre, and Manrubia 2018). Gene-expression levels probably depend on the GF, and different environments might require different levels of virus gene expression. These differences might occur because viral proteins might not function equally well in all environments, or some functions might need to be up- or down-regulated in certain environments. Under these assumptions, a particular SGF might result from the selection pressures acting on a virus population, and differences in SGF might be adaptive and therefore rapidly arise in different environments (Sicard et al. 2013, 2016; Wu et al. 2017; Gutiérrez and Zwart 2018). Note that we use the term ‘selection’ when describing directional changes in the GF. However, its meaning here is not equivalent to its standard use in evolutionary genetics, as here we define selection as adaptation by optimization of the GF. Genetic variability is not considered in the models.

The hypothesis that multipartition might have arisen to rapidly tune gene expression in different environments is tantalizing, but several aspects remain obscure. First, the role of the cellular multiplicity of infection (MOI), the number of virus particles invading a cell, is unclear. Empirical estimates of MOI typically are low for plant viruses (Gutiérrez et al. 2010; Miyashita and Kishino 2010; Tromas et al. 2014; Zwart and Elena 2015), although they appear to be considerably higher during unfettered cell-to-cell movement (Gutiérrez et al. 2015). It has been suggested that MOI imposes limits on the SGF if each segment must invade a cell to have infection (Gutiérrez and Zwart 2018), but these effects have not been explored systematically. Second, population bottlenecks will occur not only at the cell level, but also during between-host transmission (Zwart and Elena 2015; Gallet et al. 2018), making them an integral part of viral infection. Population bottlenecks can hamper the transmission of multipartite viruses and impose a cost, because all segments need to be transmitted (Fulton 1962; Sánchez-Navarro, Zwart, and Elena 2013). In a simple model of infection, multipartite viruses therefore require a high MOI to be able to compete with monopartite viruses (Iranzo and Manrubia 2012). Conversely, bottlenecks during transmission between cells or hosts will generate not only stochastic changes in allele frequency, i.e. genetic drift (Gallet et al. 2018), they will also generate stochastic changes in gene frequency, i.e. GF drift (Gutiérrez and Zwart 2018). For natural selection to change the SGF, it is indispensable to have variation in the GF (Gutiérrez and Zwart 2018). The effect of bottlenecks in general, and MOI as a specific case, on the costs and benefits of multipartition are therefore unclear. Third, empirical observations have inspired the hypothesis that multipartition might facilitate adaptation to different environments (Sicard et al. 2013), although strong evidence of this hypothesis is still lacking. Can the benefits introduced by this mechanism outweigh its inherent costs, and if so, under which conditions? How much environmental heterogeneity is needed to offset the cost of multipartition, and is this hypothesis biologically plausible? Here we set out to explore these three questions using computational models.

2. Model description

We developed parsimonious models to allow us to study the evolution of the GF of a multipartite virus population. We were particularly interested in modeling direct competition between a monopartite and a multipartite virus, when these two viruses are otherwise isogenic. We developed two different models of competition between monopartite and bipartite viruses. Model 1 has no co-infection exclusion, whereas Model 2 includes inter-specific co-infection exclusion. Although some of the model results focus on the evolution of the bipartite virus in isolation (i.e. without a monopartite virus being present), in the model description we present only the complete model for conciseness.

2.1 Model 1: basic model of multipartite virus infection

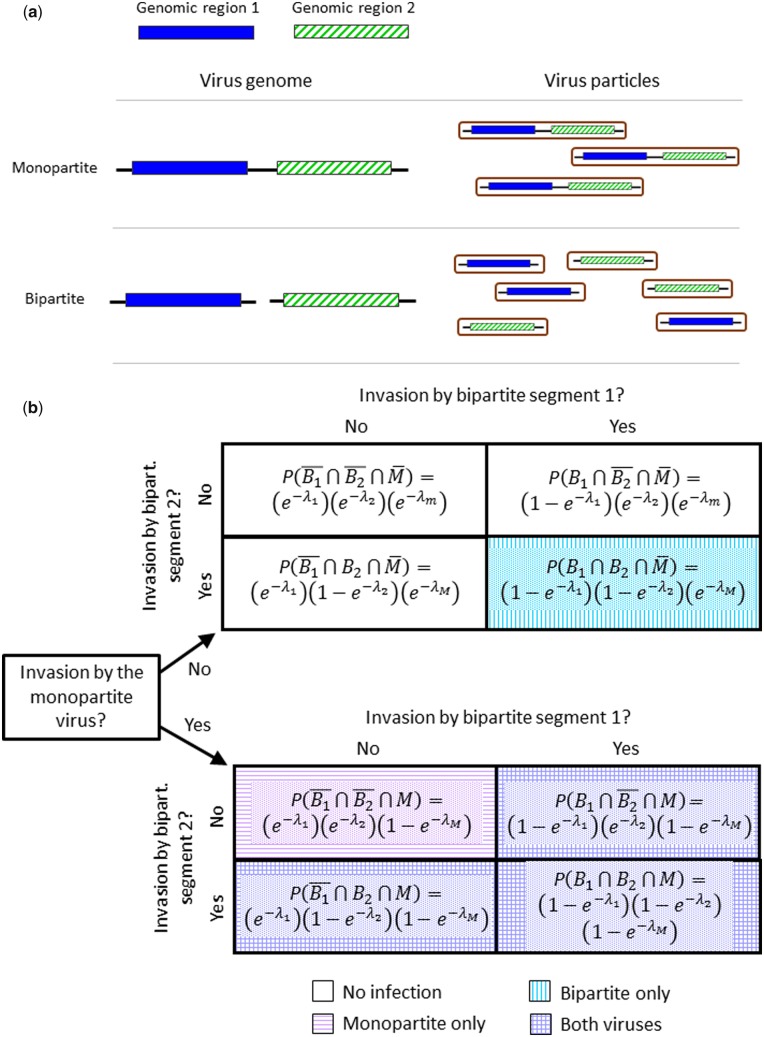
For simplicity, we consider a multipartite virus genome that is always composed of two genome segments. For both the monopartite and multipartite viruses, the virus genome is comprised of two genomic regions with a frequency g in a virus population (i.e. comprising this region as represented in both the monopartite and multipartite viruses in the inoculum or within a cell) and a ratio of genomic regions $r=\mathrm{ }{g}_1/g_2$. Subscripts of g refer to the genomic regions 1 and 2. For the monopartite, these two regions are on a single genome segment that is packaged into each virus particle, whereas for the multipartite virus, these two regions are on separate genome segments that are always packaged individually into virus particles (Fig. 1a). Virus particles containing one genome segment are present in the complete virus population at a frequency f. Hereafter, subscripts of f denote whether we are considering a virus type, m for monopartite and 1 and 2 for two types of bipartite virus particles. Note that therefore, $g_i=\left(f_i+f_m\right)/\left(f_1+f_2+{2f}_m\right)$ with i ∈ {1, 2}.

Figure 1.

(a) Schematic overview of the monopartite and bipartite viruses we are modeling. Both viruses contain two genomic regions, and are assumed to be isogenic except for their organization into one or two segments. Virus particles are assumed to always package only a single genome segment. (b) Overview of the infection status of cells according to which segments of the monopartite and bipartite viruses have invaded a cell. The formulae give the expected frequencies of these events. Lines in the compartments indicated the infection status of the cell, according to the legend at the bottom of the figure. Note that there can be co-infection between the monopartite and only a single segment of the bipartite virus. For Model 1, the frequencies of the invading virus particles will determine the relative frequency of the virus genome segments in the virus yield. For Model 2, co-infection of cells will follow the scheme above but the final infection status of the cell (i.e. which virus will generate progeny in that cell) is determined stochastically.

We consider the exposure of c cells to a virus inoculum in such a manner that we precisely control the cellular MOI, which we define as the λ virus particles of any type invading a cell. We allow only a single round of infection for each passage of the virus through these cells. We assume that each virus particle acts independently (e.g. Zwart et al. 2009) in the process of invasion, i.e. physically entering a host cell. For the monopartite virus, invasion by a single virus particle will always lead to infection. For the multipartite virus, there will only be infection following invasion by both types. As the probability of infection per virus particle is low and the number of virus particles will be large, the total number of virus particles invading a cell, K, will follow a Poisson distribution over cells such that: $P\left(K=k|\lambda \right)={\lambda }^k{e}^{-\lambda }/k!$, where k is a single realization of this random variable. As each virus particle acts independently in the invasion process—as opposed to the infection process in the case of the bipartite virus—for the monopartite virus ${\lambda }_m=f_m\lambda$ and for each bipartite virus segment ${\lambda }_i=f_i\lambda$ with i ∈ {1, 2}.

Two processes will determine the virus yield produced in each cell. First, to be infected both virus genome regions must be present in a cell. Hence, the cell must have been invaded by at least (1) a virus particle containing the monopartite virus, (2) two or more bipartite virus particles representing both genome segments (Fig. 1b). As the coding regions of the viruses are assumed to be isogenic, gene products can be freely shared between viruses when they co-infect a cell and combinations between the monopartite virus and one genome segment of the multipartite virus are also allowed (Fig. 1b). We assume neither virus has a competitive advantage at the within-cell level. Hence, the frequency of each invading virus particle in successfully infected cells, i.e. $f_i=\mathrm{ }{k}_i/\left(k_1+k_2+k_m\right)$ where i ∈ {m, 1, 2}, will be its frequency in the final pool of virus particles produced by that cell.

Second, a recent study has suggested that the GF may affect virus fitness, by tuning the expression of virus genes on different segments (Sicard et al. 2013). Therefore, the total virus yield produced in a cell will depend on the frequency of the genome segments, while we also assume there is sharing of virus proteins between the monopartite and bipartite virus in co-infected cells. We assume virus yield generated by an infected single cell (φ) follows the probability density function (PDF) of the Normal distribution as a function of the decimal logarithm of the ratio of the genomic regions r, such that $\phi \left(r\right)=\frac{1}{\sqrt{2\pi {\sigma }^2}}\mathrm{e}\mathrm{xp}\left[-{\left({\log }_{10}r-\mu \right)}^2/2{\sigma }^2\right]$ where μ is the mean of the distribution and σ² is its variance. We chose to decimal log-transform r so that we do not have to truncate the Normal distribution. We had also explored an alternative approach that uses a Beta distribution linking f₁ and virus-particle yield per cell, which renders similar results (Supplementary Appendix S1). At the end of one round of cellular infection, all virus particles produced in all cells are pooled and their relative frequencies are determined.

When considering competition between bipartite and monopartite viruses, we allow the environmental conditions (parameters influencing the total virus-particle yield per cell) to vary over time. When we run competitions in variable environments, there is a 0.2 probability that new values for this distribution will be drawn each passage. We then draw μ from a uniform distribution with range ±ψ, whilst σ² is fixed. When averaging over environments, the highest yield will be obtained for r = 1. The virus-particle yield function is therefore parametrized such that the monopartite virus has gene-expression levels optimized for the mean of all environments. This is a key point, as it is not possible for the monopartite virus to change its expression patterns in the simulations due to linkage between the two genomic regions.

2.2 Model 2: co-infection exclusion model

Many viruses show co- or superinfection exclusion, blocking the ability of closely related viruses to infect the same cells or host. To add interactions between the viruses to the model, we assume that the locus encoding a co-infection exclusion function is on the second genomic region. We make the simplifying assumption that co-infection exclusion only occurs between the monopartite and bipartite virus types, and that the frequency of the second genomic region in the invading virus particles will determine which virus excludes the other. The probability that the monopartite virus will successfully infect a cell co-invaded by both the monopartite virus and at least segment 2 of the bipartite virus is $\rho =k_m/\left(k_m+k_2\right)$, which is assumed to follow a Bernoulli distribution, and likewise for the multipartite virus. Note that under these assumptions, the second segment of the multipartite virus can block infection of the monopartite virus in a particular cell, without itself causing infection when the first bipartite segment has not invaded that cell.

2.3 Model predictions

We considered model predictions with numerical and simulation-based approaches. A numerical approach can in principle be used in all cases. Given MOI, f₁, f₂, and f_m the probability of a cell being invaded by any combination of the three genome segments (k₁, k₂, and k_m) is the product of the probabilities for each individual outcome as predicted by the Poisson distribution for invasion of that segment. From r and the virus-particle yield function, we can determine virus yield, $\phi \left(r\right)$, for all these combinations. The total yield (y) for the ith segment is then given by the expression:

$$y_i=e^{-3\lambda }\sum _{u=0}^{k_1}\sum _{v=0}^{k_2}\sum _{w=0}^{k_m}\frac{{\lambda }^{u+v+w}}{u!v!w!}{f}_i\phi \left(r\right),\mathrm{ }\left(1\right)$$

where i ∈ {1, 2, m} and we set k₁ + k₂ + k_m to a large value (200) so that all plausible numbers of invaders are represented. When considering the bipartite virus in isolation we can consider only invaded cells:

$$y_i=e^{-2\lambda }\sum _{u=1}^{k_1}\sum _{v=1}^{k_2}\frac{{\lambda }^{u+v}}{u!v!}{f}_i\phi \left(r\right).\mathrm{ }\left(2\right)$$

For the bipartite virus alone, if total virus yield is known we can use the f₁ value that maximizes viral yield as an estimate of the SGF, because we have assumed no within-cell competition between segments. For competition between monopartite and bipartite viruses a numerical approach could also be used. However, in the model we have incorporated stochastic changes in the environment, and we therefore used a simulation approach to make a large number of independent replicates more computationally tractable, as an individual simulation requires less computational resources than calculating a single numerical solution.

All model predictions were also considered using a simulation-based approach. We ran simulations of competitions over a range of MOI, ψ and σ² values to determine which conditions would favor the bipartite virus, with N = 1,000 independent simulations for each condition. We ran these competitions until either 1, one of the two viruses had gone to fixation, or 2, up to 1,000 passages (equivalent to 1,000 viral generations). As a metric of bipartite virus success, we consider the relative frequency of the bipartite virus in the pool of virus particles generated after the final passage, over all simulations:

$$\frac{1}{N}\sum _{i=1}^N\frac{f_{1,i}+f_{2,i}}{f_{1,i}+f_{2,i}+2f_{m,i}}.\mathrm{ }\left(3\right)$$

We are interested in choosing a total number of cells (c_tot) for our simulations such that for each passage the total number of infected cells infected by the whole virus population (c_inf) at any value of MOI is approximately c_inf. If we are randomly drawing the number of invaders from a Poisson distribution, for each passage $c_{\mathit{tot}}=c_{\mathit{inf}}/I$, where we can predict the fraction of infected cells as: $I=1-P\left(\overline{B_1}\bigcap \overline{B_2}\bigcap \stackrel{-}{M}\right)-P\left(\overline{B_1}\bigcap B_2\bigcap \overline{M}\right)-P\left(B_1\bigcap \overline{{\mathrm{B}}_2}\bigcap \overline{M}\right)=1-e^{-{\lambda }_m}\left(e^{-{\lambda }_1}+e^{-{\lambda }_2}-e^{-{\lambda }_1-{\lambda }_2}\right)$ (see Fig. 1b for details). Here B₁ and B₂ refer to the two segments of the bipartite virus and M to the monopartite virus and the bars means ‘absence of’. To speed up the simulations, however, we only modeled invaded cells and therefore randomly drew values from the zero-truncated Poisson distribution, using the rztpois() function from R library actuar v2.3-3 (Dutang, Goulet, and Pigeon 2008). The expected number of invaded cells, c_inv, must then be predicted as c_inv = c_infQ/I, where the fraction of invaded cells is $Q=1-P\left(\overline{B_1}\bigcap \overline{B_2}\bigcap \overline{M}\right)$. This similarity in the number of infected or invaded cells ensures that comparisons between different MOI values are not biased by large differences in the number of infected cells. This estimate was also used for Model 2, although in this case it is an approximation as multipartite segment 2 can exclude infection by the monopartite virus without actually infecting a cell. For all simulations we used c_inf = 10³, unless otherwise noted.

All models were implemented in R version 3.4.2 (R Core Team 2017). Model code, simulation results and numerical results are available in the Dryad Digital Repository (https://datadryad.org/stash/dataset/doi:10.5061/dryad.18931zcsw).

3. Results

We developed a model of competition between monopartite and bipartite viruses that allows selection to shape the GF of a multipartite virus. We were particularly interested in linking the frequency of virus genomic regions in infected cells to virus-particle yield per cell, to explore the relationship between the GF and virus fitness. We developed two models of competition between monopartite and bipartite viruses: Model 1 has no co-infection exclusion, whereas Model 2 allows for inter-specific co-infection exclusion. We used the log-normal PDF as the function linking the presence of virus genomic regions and yield, allowing the optimum (μ) and breadth (σ²) of the yield function to be tuned independently.

3.1 Effects of GF drift on virus-particle yield

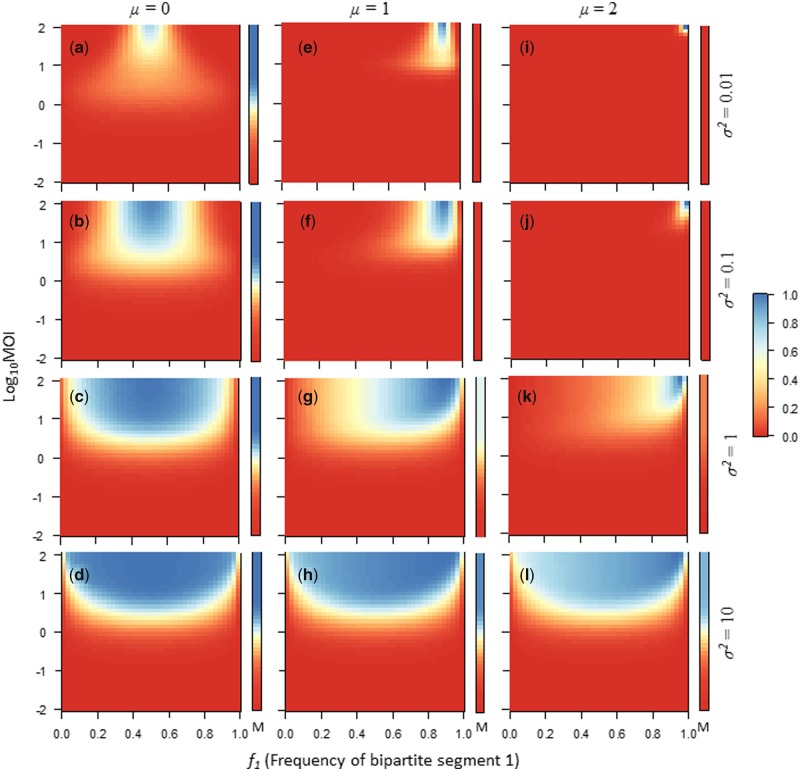
We first considered model predictions of virus-particle yield for the monopartite and bipartite viruses in isolation, for a range of values for the MOI (λ) and different values for the functions that determine the relationship between the GF and virus-particle yield. As we have defined co-infection exclusion to be a process that acts interspecifically, it will not affect model predictions here and therefore we only consider Model 1. We varied μ (the mean of the log-Normal distribution for the yield function, here in effect the value of r that renders optimal yield) and σ² (the variance of the log-Normal distribution, here in effect the sensitivity of virus-particle yield to changes in r) (Fig. 2). For this comparison, we considered the yield per cell exposed to the virus (as opposed to the yield per infected cell). Virus-particle yield of the bipartite virus is always equal to or less than that of the monopartite virus for a given MOI if the environment demands the two genome segments be present at equal frequencies (Fig. 2a–d). These effects occur because 1, multipartite viruses will infect fewer cells at a low MOI and 2, in infected cells there will be variation in the GF when MOI is intermediate (i.e. GF drift) and therefore deviations from the optimal $\log \mathrm{ }r=0$ for yield, μ. Both of these mechanisms result in a MOI-dependent cost of multipartition, one acting at the between-cell level and the other at the within-cell level.

Figure 2.

Virus-particle yield as predicted for Model 1 is shown with heat plots. For each square plot, the bipartite virus GF (as indicated by f₁, the frequency of genome segment 1 in the virus inoculum) is the abscissa, and the decimal logarithm of the cellular MOI is the ordinate. The bars to the right of each plot labeled with an M indicate virus-particle yield for the monopartite virus, in which the GF is fixed (g₁ = ½) and only MOI is varied. The heat colors indicate the virus-particle yield per cell, normalized by the maximum possible yield (legend is at the right-hand side). In this case, the yield is calculated over the whole population of exposed cells, and not for a fixed number of infected cells, to illustrate the combined effect of virus infectivity and virus-particle yield. The GF value for which highest yield is obtained per cell is shifted from f₁ = ½ (i.e. μ  =  0), to f₁ = 1/11 (i.e. μ  =  1), to f₁ = 1/101 (i.e. μ  =  2). The sensitivity of virus-particle yield to changes in the GF decreases as σ² increases from 10 to 0.01. Note that when the environment demands a balanced GF (μ  =  0, a–d), the yield for the monopartite virus is greater than or equal to that of the bipartite virus. The situation is reversed when an unbalanced GF is required (e–l), although when the sensitivity of virus-particle yield to changes in the GF is low (i.e. σ² = 10 in h and l), the monopartite virus again has a higher yield than the bipartite virus.

However, when the environment does not demand balanced gene expression (μ ≠ 0) and as the yield function becomes narrower (σ² is small), the bipartite virus has a higher yield than the monopartite virus (Fig. 2e–g and i–k). Hence, for our model multipartite viruses can have a yield advantage when the environment demands differences in the frequencies at which genomic regions are present. These figures reveal an interesting property of multipartite viruses. When the GF is displaced from the optimum for a given environment, at intermediate MOIs the virus-particle yield can be higher than at high MOIs (e.g. Fig. 2a and b). This effect occurs because at intermediate MOIs there is more GF drift, as the number of virus particles invading a cell is smaller. Whilst this ‘noise’ is costly when the inoculum frequency of virus genome segments is equivalent to the optimum of the environment, it can have immediate benefits when the virus is displaced from the optimum. Moreover, from an evolutionary perspective, variation in the GF is the raw material that selection requires to directionally change it toward the optimum (i.e. the SGF) for a given environment (Gutiérrez and Zwart 2018). Therefore, these virus-particle yield plots suggest there can be benefits associated with intermediate MOIs for multipartite viruses, as variation in the GF is required for adaptation by changes in the GF.

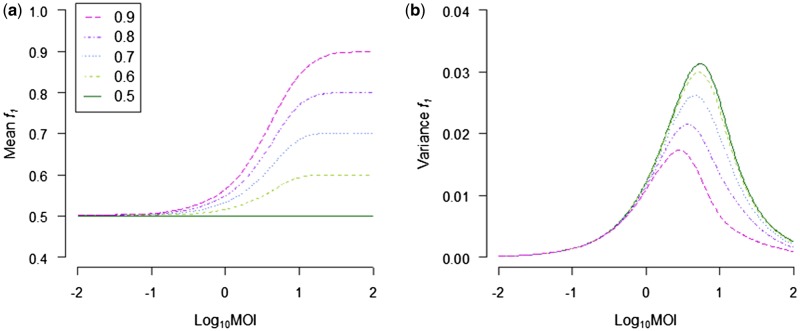
If we consider very low MOIs, then eventually the GF in infected cells is determined solely by the requirement for both segments to be present. In the extreme, only cells invaded by one virus particle of each genome segment will be present, and as f₁ = 0.5 for all infected cells there will be no variation in the GF. An overview of these predictions for how MOI will affect the mean and variance of the GF in infected cells as a function of MOI is given in Fig. 3. Based on these initial observations, we might expect the GF to change most rapidly at low to intermediate values. At intermediate values, the GF might change to maximize virus-particle yield per cell, whereas at low MOIs the requirement to have both segments present will be the main driver of GF changes.

Figure 3.

The effects of MOI on the mean and variance of the GF in infected cells (GF, as indicated by the frequency of segment 1, f₁) are demonstrated. On the abscissae the log-transformed MOI is given, and on the ordinate the mean f₁ (a) or variance (b) in infected cells. Different values of f₁ are used in the viral inoculum to which the cells are exposed, as indicated in the inset in (a). (a) At very low MOIs, f₁ always converges on 0.5 in infected cells, irrespective of its value in the inoculum. (b) The variance of f₁ is maximized at intermediate MOIs, and approaches zero at very low MOI values. Low MOI cause these effects on the mean and variance of f₁ because at low MOI, very few cells are infected, and almost all infected cells will only be invaded by one virus particle of each type.

3.2 MOI can affect the SGF

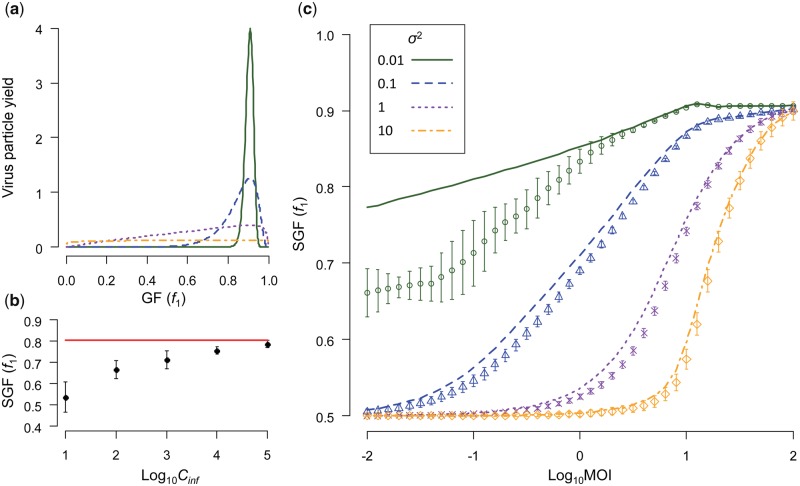
When the yield function is imbalanced (i.e. $\mu \mathrm{ }\ne 0$) and the probability of invasion is the same for all virus-particle types, at low MOIs there will be conflicting forces acting on the GF. On the one hand, the requirements for infection (i.e. presence of both viral genome segments) will drive a balanced GF when invasion probabilities for the different virus-particle types are equal (Fig. 3). One could intuitively expect that any genome-segment frequency at the SGF equilibrium would not be far below the reciprocal of MOI, as otherwise that genome segment would not be represented in many cells and infection levels would be low. On the other hand, when μ  ≠  0 selection for virus-particle yield per cell will pull the GF away from this 1:1 balance, irrespective of the MOI. We therefore considered whether the SGF can be MOI-dependent for a range of σ² values, with range representing very narrow (σ² = 0.01) to very broad (σ² = 10) yield functions (Fig. 4a). As we had anticipated, the SGF can indeed depend on the MOI, with the largest deviations from the optimum for cellular yield occurring at low MOIs (Fig. 4c). We found discrepancies between numerical and simulation-based predictions of the SGF (Fig. 4c). As we increased the number of infected cells in the simulations (c_inf), these predictions converged on the numerical prediction (Fig. 4b). The numerical prediction is in effect for an infinite population of infected cells. As the number of infected cells becomes larger, rare f₁ frequencies leading to higher yields are more regularly sampled and their contribution to determining the SGF becomes more prominent. Interestingly, this result also shows how sensitive the SGF can be to the exact conditions under which the virus is replicating.

Figure 4.

The effects of the cellular MOI on the SGF are illustrated. Note that for all panels μ  =  1, and that the legend for σ² shown in (d) also applies to (a) and (b). (a) Relationship between the GF and virus-particle yield per cell is shown. As σ² increases, the yield function becomes less sensitive to the GF with that cell (i.e. a broader function). When σ² = 10, the function is almost uniform. (b) For some conditions, there was a discrepancy between the numerical and simulation predictions. The abscissa is the number of effectively infected cells (c_inf), and the ordinate is the SGF as indicated by the frequency of segment 1 (f₁). For MOI = 0.1 and σ² = 0.01, we show the numerical prediction (red line) and mean ± SD for simulation results black circles with error bars. As the number of infected cells is increased in the simulations, the predictions converge on the numerical prediction. (c) Relationship between MOI and the SGF predicted by Model 1 is given. Decimal log-transformed MOI is the abscissa and the SGF the ordinate. Lines represent the prediction for the numerical model. Simulation results (±SD) are shown by the symbols, with colors corresponding to σ² values as indicated in the inset. For the simulations, we ran Model 1 until an equilibrium was reached (i.e. up to 500 generations depending on the MOI) for a large number of replicate experiments (1,000), with the highest yield per cell obtained when f₁ = 10/11 (i.e. μ  =  1). We ran the model including only the bipartite virus, with the starting virus inoculum set to f₁ = 0.91, f₂ = 0.09, and f_m = 0. Our results clearly indicate that MOI can affect the SGF, which arise because of the interplay between virus-particle yield per cell and the requirement for both types of virus particles to invade a cell (as illustrated in Fig. 3). For some conditions, there is a discrepancy between the numerical and simulation results, which can be accounted for by the number of infected cells used in the simulation (see (c)).

In real-world systems MOI is known to vary during the course of infection and be relatively low (González-Jara et al. 2009; Gutiérrez et al. 2010, 2015; Miyashita and Kishino 2010; Tromas et al. 2014; Zwart and Elena 2015; ). Our model suggests that SGF depends on MOI, especially at low MOI values. We therefore predict that the SGF can change over time during infection of a single host, as MOI changes during infection. These changes in SGF could depend solely on MOI dynamics, though there are clearly other processes such as host immune responses or the number of infected cells in which the virus is replicating that could come into play.

3.3 Low and intermediate MOIs lead to faster convergence on the SGF

Next, we set out to explore whether low and intermediate MOIs can lead to faster convergence on the SGF. As for determination of the SGF, we expect two effects to come into play: 1, the constraints upon SGF variation imposed by very low MOIs (Fig. 3a), and 2, the high GF variation generated by intermediate MOIs (Fig. 3b), which generates the variation on which selection for higher virus-particle yield can act. In this section, we consider the evolution of the bipartite virus in isolation for simplicity. To estimate how MOI affects the rate at which the GF changes without MOI-induced differences in the SGF, we studied how the GF evolves toward a balanced equilibrium after being displaced. When μ = 0, MOI does not affect the SGF, because there is not a clash between the requirements for infectivity and optimal virus-particle yield per cell.

We found very clear and consistent effects of MOI on the time to convergence on the SGF: populations at low MOIs converged more rapidly than those at high MOIs (Fig. 5). At very high MOIs and for broad yield functions (i.e. MOI = 100 and σ² = 10), it takes thousands of passages for the population to converge on the SGF. At low MOIs, between-cell GF variation approaches zero, but hard selection for infectivity (having both genome segments present in a cell) nonetheless drives rapid change. At high MOIs, little between-cell GF variation is generated (Fig. 3b) and cellular infection rates will be high irrespective of the GF, therefore limiting both variation and selection and hereby the rate at which the GF can evolve. Others have previously shown how low MOI 1, enhances selection for traits that act in trans (Miyashita and Kishino 2010) and 2, allows viruses to reach an equilibrium frequency more rapidly because of a lack of cooperative benefits when there are no co-infections (Leeks et al. 2018).

Figure 5.

The time until convergence on the SGF is shown. The decimal log-transformed MOI is the abscissa and the decimal log-transformed number of passages until convergence on the SGF is the ordinate. In all cases, μ  =  0 and the GF was displaced to f₁ = 0.1, and we then considered how many passages it took for the population to converge on an equilibrium when we varied the breadth of the yield function by manipulating σ². We considered that the population had reached the equilibrium of f₁ = 0.5 ± 0.01. Lines represent the prediction for the numerical model. Simulation model results (±SD) are shown by the symbols, with colors corresponding to σ² values as indicated in the legend. We again ran 1,000 replicates for the simulations.

The time to convergence on the SGF is sensitive to changes in MOI for different ranges of MOI values, which in turn depend on σ² (Fig. 5). The range of empirical MOI estimates is between 1 and 13 (González-Jara et al. 2009; Gutiérrez et al. 2010, 2015; Miyashita and Kishino 2010; Tromas et al. 2014; Zwart and Elena 2015; ), a range in which the model predicts the SGF and time to convergence on the SGF can depend on MOI. Overall, these results suggest that MOI might play an important role in determining both SGF and how long it takes for multipartite viruses to converge on the SGF in the real world. Many studies have found that MOI increases during the course of infection (González-Jara et al. 2009; Gutiérrez et al. 2010; Tromas et al. 2014). An increasing MOI during infection could help to bolster the benefits of multipartition while also mitigating its cost: during early infection, low MOI would foster rapid changes in the GF, whilst at late infection high MOIs would allow the virus to infect a higher number of cells, thereby increasing yield and the probability of transmission.

One striking aspect of our results is how quickly the GF converges on the equilibrium: for low and intermediate MOIs this often takes only one or two passages, each consisting only of a single round of replication. Our model therefore also underscores that adaptation by changes in the GF can be very rapid, requiring only a few generations of replication. As MOIs are generally low, especially during early infection (Zwart and Elena 2015), we therefore predict that GF changes can be extremely rapid. We have found convergence on the SGF after one week of infection (Wu et al. 2017), but our model suggests this adaptation may, indeed, be much faster.

3.4 Bipartite viruses can outcompete monopartite viruses in variable environments

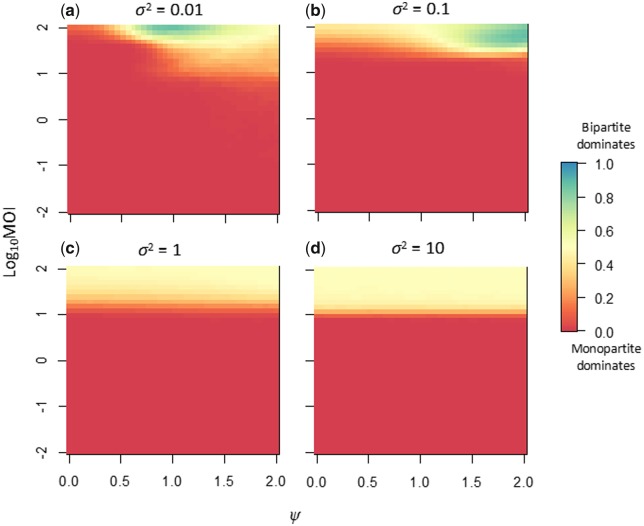
Our model illustrates that adaptation by changes in the GF occurs fastest for low MOIs, whilst the cost of multipartition is also highest at low MOIs. Moreover, a key question remains under what conditions—if any—the putative benefits related to rapidly changing genome-segment frequencies can outweigh the costs of multipartition. We therefore considered direct competitions between monopartite and bipartite viruses, by tuning the MOI (λ), the sensitivity of virus-particle yield to changes in the GF (σ²), and the magnitude of environmental heterogeneity (ψ). For Model 1, we found that for the majority of conditions the monopartite virus dominates (Fig. 6 and Supplementary Fig. S2). Only for a limited parameter space in which MOI was high (MOI > 30), virus-particle yield was sensitive to changes in r (σ² ≤ 0.1), and there was considerable environmental heterogeneity (ψ  >  0.5) did the multipartite dominate the competitions (Fig. 6). When virus-particle yield was insensitive to r (σ² ≥ 1), both viruses coexisted at high MOI irrespective of environmental heterogeneity (Supplementary Fig. S2). This result is not surprising however, as for Model 1 there is no co-infection exclusion and neither virus has a replicative advantage.

Figure 6.

The results of direct competitions between a monopartite and bipartite virus under Model 1, with no co-infection exclusion. For all panels, the magnitude of environmental heterogeneity is the abscissa, and the decimal log-transformed MOI is the ordinate. One thousand independent replicates of 1,000 generations of competition were performed for parameter combination, and the weighted frequency at which the bipartite predominates (see Equation (3)) is indicated by the heat colors (legend is on the far right). In all simulations, the initial frequencies of the two complete viruses were equal, such that $f_1=f_2=f_m=\mathrm{ }1/3$ as both segments of the bipartite need to be present to have a complete genome. Different panels represent different values of σ², the sensitivity of virus-particle yield to changes in the GF. Under most conditions, the monopartite virus predominates. For an overview of the frequency at which the monopartite and bipartite viruses were fixed, see Supplementary Fig. S2.

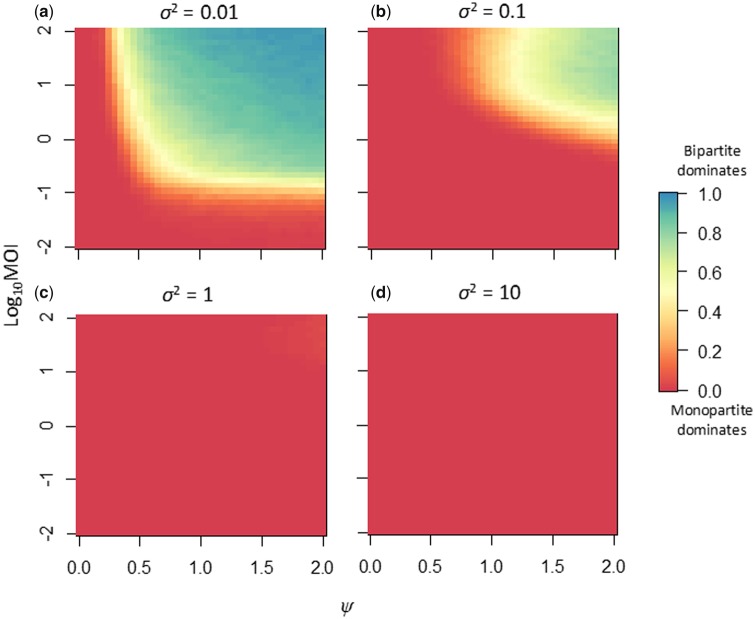
When we considered direct competitions for Model 2, which introduces inter-specific co-infection exclusion, we found that there was a much larger parameter space in which the multipartite virus could outcompete the monopartite virus (Fig. 7 and Supplementary Fig. S3). When virus-particle yield was very sensitive to changes in r (σ² = 0.01), the multipartite virus dominated when there was environmental heterogeneity (ψ  >  0.5) and nearly all MOI values considered (MOI > 0.25) (Fig. 7). For σ² = 0.1, the parameter space in which the multipartite dominates becomes smaller (ψ  >  1.25, MOI > 3). In contrast, for σ² ≥ 1 the monopartite virus always dominates. Either the monopartite or bipartite virus went to fixation in virtually all simulations (Supplementary Fig. S3), even when the success metric indicates an even probability of survival for each virus (Fig. 7). This result is not surprising as Model 2 includes co-infection exclusion.

Figure 7.

The results of direct competitions between a monopartite and bipartite virus under Model 2, with inter-specific co-infection exclusion. For all panels, the magnitude of environmental heterogeneity is the abscissa, and the decimal log-transformed MOI is the ordinate. One thousand independent replicates of 1,000 generations of competition were performed for parameter combination, and the weighted frequency at which the bipartite predominates (see Equation (3)) is indicated by the heat colors (legend is on the far right). In all simulations, the initial frequencies of the two complete viruses were equal, such that $f_1=f_2=f_m=\mathrm{ }1/3$. Different panels represent different values of σ², the sensitivity of virus-particle yield to changes in the GF. Compared with Model 1 (no co-infection exclusion; Fig. 5), when σ² is high the monopartite dominates competition completely. At low σ² values, there is a much larger parameter space in which the bipartite virus dominates. For an overview of the frequency at which the monopartite and bipartite viruses were fixed, see Supplementary Fig. S3.

These results therefore suggest that a bipartite virus can outcompete a monopartite virus when three conditions are met: 1, virus-particle yield is sensitive to changes in the frequency of genome segments, 2, the virus regularly encounters environments which demand different frequencies of genome segments, and 3, there is replicative isolation, that is, some mechanism that prevents monopartite viruses from taking advantage of multipartite viruses rapidly changing their gene expression. We have explored the role of co-infection exclusion, but other mechanisms could also bring about replicative isolation. Only when competitions were performed at very high MOI (>100), did we see that MOI could disadvantage the bipartite virus (Supplementary Fig. S4). Therefore, the cost of infection at low MOI appears to have a stronger impact on the competitive ability of multipartite viruses than limited GF variation at high MOI.

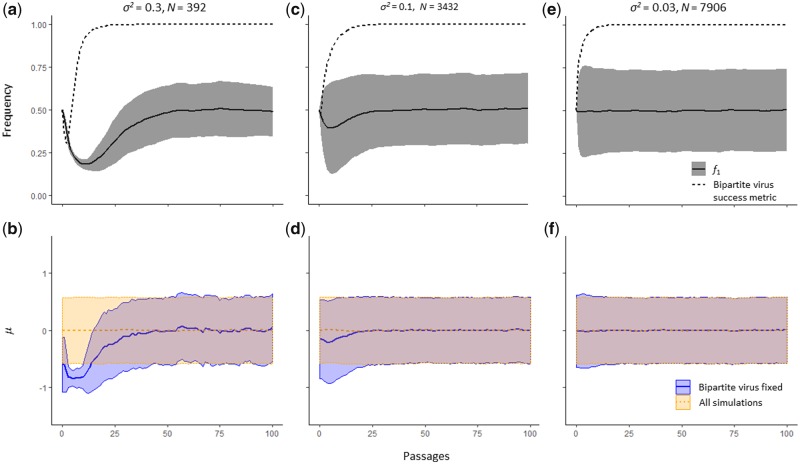
Changes in the GF could conceivably occur to a variety of selection pressures, as we have already shown the SGF can depend on MOI. We assigned a co-infection exclusion function on the second genome segment, and we therefore considered whether a higher frequency of this segment could be beneficial for displacing the monopartite competitor. Indeed, we found such an effect when neither virus dominated the competitions (Fig. 8). For those simulations in which the bipartite virus eventually won, the frequency of segment 2 was on average higher until the monopartite virus was displaced from the population. However, in these simulations the average σ² was also below 1 in early passages, suggesting that these GF changes were driven mainly by selection for virus-particle yield and not for an increased strength of inter-specific co-infection exclusion. Nevertheless, this up-regulation of segment 2 highlights how GF changes can affect multiple virus characteristics simultaneously in a manner that impacts viral fitness. Although changes in the GF probably can occur as a response to a wide variety of selection pressures, we speculate that selection for increased infectivity or virus-particle yield will predominate changes in the GF.

Figure 8.

Our simulations show the GF can play a role in direct competition between viruses. For all panels, the abscissa is passage number. In (a), (c), and (e), the ordinate is frequency, whereas in (b), (d), and (f), the ordinate is the average value of μ, the optimal yield value for the virus-particle yield function. For 10⁴ simulations, we performed 100 passages with MOI = 30 and ψ  =  1, and varied σ². In the upper panels, we consider only those populations in which the bipartite virus went to fixation, and plotted the GF for the bipartite virus alone ($f_1/\left(f_1+f_2\right)$, (solid line) with its standard deviation (gray shading). We also plotted the bipartite success metric (Equation (2), see Section 2), again only for those populations in which the bipartite virus went to fixation. In the lower panels, μ is given with its standard deviation, either for only those populations that fixed the bipartite virus (blue color) or all populations (orange). Above each column of panels, we indicate σ² and the number of simulated populations on which fixed the bipartite virus and were therefore plotted (N). When σ² = 1, the monopartite virus was fixed in all populations. (a) When σ² = 0.3, the monopartite virus is fixed in the majority of populations. Those populations that fix the bipartite virus (only 392 out of 10⁴) strongly downregulate f₁ and up-regulate f₂. Genome segment 2 contains the locus coding for co-infection exclusion, suggesting that up-regulation of this locus has helped the bipartite virus to displace the monopartite. Once the monopartite virus has been displaced, the mean GF returns to levels that maximize virus-particle yield in the absence of the monopartite competitor (f₁ = 0.5 as the mean μ  =  0). (b) In those populations that fixed the bipartite virus when σ² = 0.3, μ  <  0 on average in early passages. This result suggests that selection for increased virus-particle yield was the main driver of changes in the GF, rather than direct selection on the ability to exclude co-infection with the monopartite virus. In contrast, these changes in the GF did contribute to the maintenance and fixation of the bipartite virus. (c) When σ² = 0.1, the bipartite virus fixes in a third of populations. The downregulation of f₁ in early passages is still apparent, but less pronounced. (d) Similar to (b), for populations that fixed the bipartite virus μ  <  0, suggesting that selection for virus-particle yield as the main driver of changes in the GF. (e) When σ² = 0.03, the bipartite virus fixes in the majority of lineages, but there is no longer a downregulation of f₁ in early passages. Lower values of σ² gave results highly similar to (c). These results suggest that the GF can play a role in competition between viruses, up-regulating functions that are beneficial for excluding a competitor. However, in the parameter space were multipartite viruses predominate, these effects are weak and selection for virus yield appears to be more important in determining the GF. (f) For populations in which the bipartite virus was fixed when σ² = 0.03, the mean of μ does not appear to change over passages.

4. Discussion

We have developed a simple model of the evolution of a multipartite virus GF that offers some new perspectives on GF dynamics. First, this model illustrates that the GF equilibrium—i.e. SGF—is sensitive to the exact conditions under which a multipartite virus population is replicating, similar to results on the equilibrium frequency between cooperating viruses (Leeks et al. 2018). Changes in MOI—a parameter that is known to change markedly during virus infection of multicellular hosts—can affect the SGF, illustrating that the SGF can be highly sensitive to the exact conditions under which a virus population is replicating. It has been previously shown that the SGF is host-species dependent (Sicard et al. 2013; Wu et al. 2017). We speculate that many other factors besides host species and MOI can affect the SGF, including the virus genotype, host environment, and their interaction. Second, our model illustrates how intermediate MOIs can generate the variation in the GF that allows directional selection to change the GF. GF drift is however clearly a double-edged sword, since it also continually displaces the GF in some cells away from an optimum value, imposing a cost and resulting in selection to maintain the SGF. Third, this model strongly suggests that directional changes in the GF are very rapid, with virus populations reaching the SGF within one to a few generations at low MOIs. This result is compatible with empirical results, which suggest populations converge on the SGF rapidly (Sicard et al. 2013; Wu et al. 2017).

One interesting property of the model we have developed is that both the costs and benefits of multipartition are properties that emerge from the model. The cost of multipartition arises from lower rates of cellular infection when MOI is not high, whilst the benefits arise from rapid changes in the GF that increase competitive fitness. In our model, there appear to be two routes by which bipartite viruses increase their fitness: 1, by increasing the virus-particle yield, which appears to be the most prevalent manner in which the GF is adapting, and 2, by increasing copy number of loci coding for inter-specific co-infection exclusion to exclude the competing monopartite virus, which only occurs under some conditions. We view up-regulation of co-infection exclusion as an emerging property of the system, since we had not foreseen this behavior and had included co-infection exclusion so that the monopartite virus would benefit less strongly from GF adaptation by the bipartite virus. Our modeling results suggest that the GF could play a role in adaptation to a wide range of environmental changes, including competing viruses, highlighting the versatility that multipartite genomes possibly confer. It has been demonstrated that the GF of cucumber mosaic virus changes in the presence of satellites (Feng et al. 2012), suggesting the GF might then be optimizing expression in the presence of such parasitic genetic elements. We have modeled co-infection exclusion as an inter-specific process here, although for plant viruses co-infection exclusion is often an intra-specific process. However, a wide range of interactions between viruses is possible (Bennett 1953) and different mechanisms can act on different spatial scales (Bergua et al. 2014; Bergua, Kang, and Folimonova 2016). Co-infection exclusion has ramifications for the occurrence of coexistence and cooperation within virus populations (Leeks et al. 2018), whilst its possible effects on multipartite viruses infection kinetics and GF dynamics have not been considered fully to date.

When we performed direct competitions between otherwise identical monopartite and bipartite viruses, the bipartite virus could regularly outcompete the monopartite virus when 1, there was inter-specific co-infection exclusion, 2, virus-particle yield was sensitive to changes in the GF, and 3, there was environmental heterogeneity (the optimum for the virus-particle yield function is drawn from a broader range). Multipartite viruses were also more likely to outcompete monopartite viruses at higher MOIs, including the biologically relevant range of 1–10 (Zwart and Elena 2015) but only when there is co-infection exclusion. Our results therefore support the hypothesis that a possible benefit of multipartite viruses is the capacity to rapidly regulate gene expression in highly variable environments that demand changes in gene expression. We therefore favor a scenario in which having a broad host-range fosters the evolution of multipartite viruses, and therefore suggest that multipartition may facilitate host-range expansion. Intriguingly, a recent theoretical study found that easy transmission and homogeneous contact networks favor the transmission of multipartite viruses, and that multipartite viruses can often be maintained when multipartition does not have actual benefits (Valdano et al. 2019). These two views are compatible, since our modeling highlights benefits at the within-host level, whilst Valdano et al. (2019) explore mechanisms that would operate at the epidemiological level.

The rapid evolution of the GF could be an important benefit conferred by multipartition. We expect that changes in the GF will typically occur on shorter time scales than the fixation of beneficial mutations, due to the large and continuous supply of GF variation at low to medium MOIs. However, it has been argued that rapid rates of evolution can lead to shortsighted adaptation in viruses, leading to enhanced within-host replication at the detriment of between-host transmission (Lythgoe et al. 2017). Given the rapid rate at which we expect GF evolution to proceed, this problem could be exacerbated in GF evolution. For example, consider a situation in which 1, a highly unbalanced SGF is reached within a plant, and 2, the invasion probabilities for virus particles carrying different genome segments are similar and hence a balanced SGF would be optimal for between-host transmission. In this case the GF changes that are beneficial within the plant will impose a cost on transmission. The fast evolution of the GF suggested by our modeling results underscores the importance of considering how different levels of selection affect GF evolution.

These model results also suggest a number of ways to test the relevance of these ideas to real-world multipartite viruses. First, it has not been studied how quickly populations converge on the SGF, although experimental results suggest this convergence is rapid. One interesting approach to study these dynamics is measuring the GF in local lesions or primary infection foci (e.g. Miyashita and Kishino 2010), so that the GF can be measured in viral populations that have experience only a few generations. Second, the outcome of competition between monopartite and bipartite viruses depends heavily on the breadth of the function for virus-particle yield. The more sensitive virus-particle yield is to changes in the GF, the more relevant our framework will be. This relationship could be investigated empirically by measuring the GF and virus-particle yield in individual cells, for example by single-cell transcriptomics for RNA viruses. However, accumulation and competitive fitness appear to be largely independent properties for another plant virus (Zwart et al. 2014), and measuring the virus-particle yield of a cell might not elucidate its potential for between-cell transmission of infection. Third, the respective roles of the GF and mutations in adaptation have not been investigated. We speculate that whereas the GF will be important as an initial adaptive response, mutations will be more important during long-term adaptation of a multipartite virus to a constant environment, a pattern that occurs with copy number variants in other viruses (Elde et al. 2012; Cone et al. 2017) and in bacteria (Sandegren and Andersson 2009). We therefore predict that the GF will change rapidly in a new environment, but on longer time scales when point mutations are fixed, changes in the GF may be reversed. Both modeling approaches and experimental evolution could be used to tackle these interesting and hitherto unaddressed questions.

Santa Fe Institute Workshop on Integrating Critical Phenomena and Multi-Scale Selection in Virus Evolution, supported by the NSF Rules of Life Program grant DEB-1830688