Understanding Chemoselectivity in Proton-Coupled Electron Transfer: A Kinetic Study of Amide and Thiol Activation

Abstract

While the mechanistic understanding of proton-coupled electron transfer (PCET) has advanced significantly, few reports have sought to elucidate the factors that control chemoselectivity in these reactions. Here we present a kinetic study that provides a quantitative basis for understanding the chemoselectivity in competitive PCET activations of amides and thiols relevant to catalytic olefin hydroamidation reactions. These results demonstrate how the interplay between PCET rate constants, H-bonding equilibria, and rate-driving force relationships jointly determine PCET chemoselectivity under a given set of conditions. In turn, these findings predict reactivity trends in a model hydroamidation reaction, rationalize the selective activation of amide N−H bonds in the presence of much weaker thiol S−H bonds, and deliver strategies to improve the efficiencies of PCET reactions employing thiol co-catalysts.

Graphical Abstract

Useful synthetic methods exhibit reliable selectivities, enabling users to confidently predict reaction outcomes in complex settings. To this end, we have recently become interested in trying to understand the features governing chemoselectivity in multi-site proton-coupled electron transfer (MS-PCET) reactions. Oxidative MS-PCET reactions are redox processes wherein protons and electrons are exchanged between a substrate and two independent molecular acceptors – a Brønsted base and one electron oxidant – in a concerted elementary step. Similar to related hydrogen-atom transfer (HAT) reactions,¹ prior kinetic studies have shown that MS-PCET processes generally exhibit linear rate-driving force relationships,² suggesting that abstraction selectivity should track with bond strength differential with weaker bonds to hydrogen reacting preferentially. These quantitative insights reinforce a common intuition that homolytic activation of very strong bonds (BDFEs ≥ 100 kcal/mol) is generally not practical when much weaker bonds to hydrogen (BDFEs ≤ 80 kcal/mol) are also present.

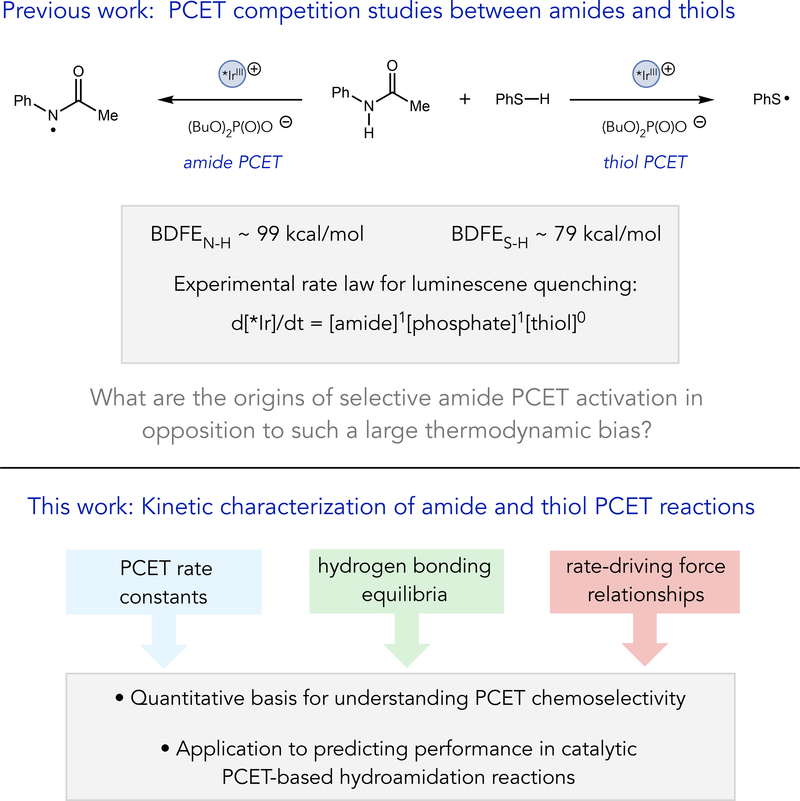
We recently observed a curious exception to this principle in the development of a catalytic method for alkene hydroamidation.^{3a, 3b} In these reactions, which were subsequently studied in detail by Nocera and coworkers,^3c a substrate amide N–H bond engages in a concerted MS-PCET reaction with an excited-state Ir(III) oxidant and a dialkyl phosphate base to furnish a reactive amidyl radical. Subsequent addition of the amidyl to a pendant olefin creates a new C–N bond and a vicinal carbon-centered radical that is then reduced by HAT from a thiophenol co-catalyst to form the closed-shell product. A surprising aspect of this reaction relates to the selectivity of the initial MS-PCET step. Both amides³ and thiols⁴ were demonstrated to be competent substrates for MS-PCET activation under the reaction conditions, and the thiophenol S–H bond (BDFE ~ 79 kcal/mol)⁵ is significantly weaker than the substrate amide N–H bond (BDFE ~ 99 kcal/mol).⁶ Accordingly, one might expect that the thiophenol would inhibit the desired N–H oxidation reaction by sequestering the Ir/phosphate catalysts in a highly favorable, but unproductive, PCET process. However, competitive luminescence quenching studies in a model system revealed a rate law for deactivation of the Ir excited state that exhibited a first-order concentration dependence on the amide and phosphate and a zero-order dependence on the concentration of thiol (Scheme 1).^3a Efficient and selective amide activation in opposition to such a large thermodynamic bias raises intriguing questions about the physical origins of MS-PCET selectivity in these systems.

Scheme 1.

MS-PCET chemoselectivity relevant to catalytic hydroamidation reactions

Here we present a kinetic study of both amide and thiol PCET activations that sheds light on this surprising selectivity. These experiments demonstrate that both pre-equilibrium hydrogen bonding and the sensitivity of the rate-driving force relationship for each substrate class plays a key role in determining PCET selectivity under a given set of conditions. In turn these findings provide insights into potential pitfalls associated with PCET-based catalysis with thiol H-atom donors, as well as actionable strategies to overcome them. The details of these investigations and their applications to predicting reactivity trends in a catalytic hydroamidation reaction are described herein.

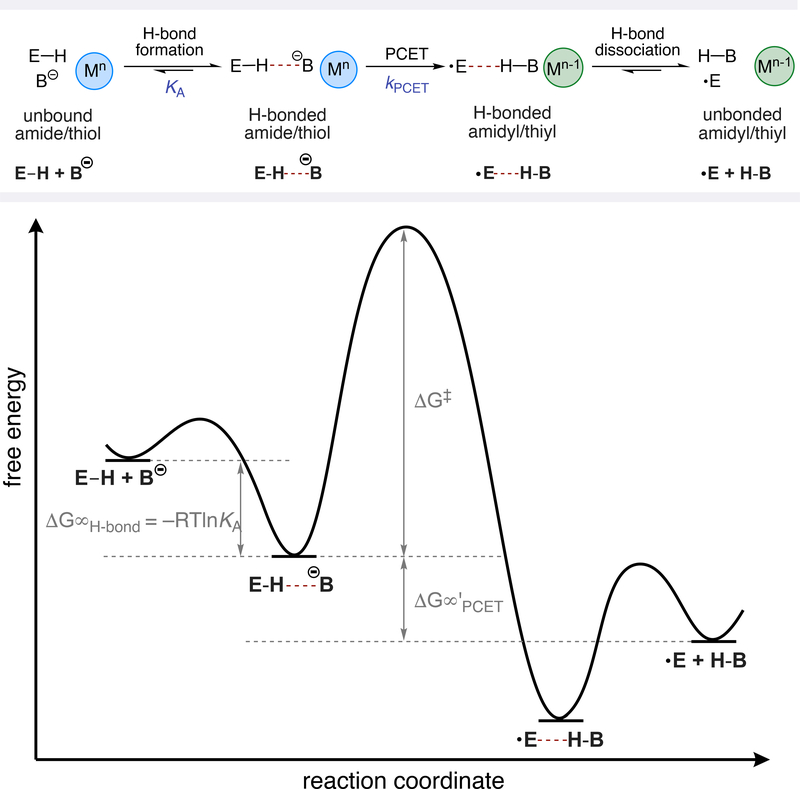
Oxidative MS-PCET reactions typically occur through hydrogen-bonded complexes between the substrate E–H bond and the Brønsted base.⁷ As such, the free energy profiles of these reactions are determined by both the kinetic barrier for the PCET event and the favorability of forming the reactive hydrogen-bonding complex, as illustrated in Figure 1. Based on this understanding, we studied the PCET reactions of four N-aryl amides (A1 – A4) and four aryl thiols (T1 – T4), mediated by two distinct Ir(III)-based photooxidants (Ir-1 and Ir-2) and a dibutyl phosphate base (NBu₄OP(O)(OBu)₂) in 1,2-dichloroethane (DCE) at room temperature (Table 1). The hydrogen bonding equilibrium constant (K_A) for association with the phosphate base and the PCET rate constant for oxidation of this H-bonded complex (k_PCET) were determined simultaneously for both the amide and the thiol series via a simple luminescence quenching method we recently described in a study of ketone PCET activation.^2c This method enabled us to evaluate the sensitivity of the reaction rates to changes in driving force associated with varying either the substrate or the potential of the excited state oxidant. The PCET rate constants and H-bonding equilibrium constants for both the amide and thiol series are presented in Table 1 and the corresponding rate-driving force correlations are shown in Figure 2.⁹

Figure 1.

Free energy surface for the MS-PCET activation of amides and thiols.

Table 1.

Kinetic and H-bonding equilibrium data

entry	amide/thiol	*Ir(III)	BDFEN-H/S-H (kcal/mol)6,8	KA(M−1)	ΔG°’PCET (kcal/mol)	kPCET (M−1s−1)
1	A1	Ir-1	98.9	1050	8.4	8.4×109
2	A1	Ir-2	98.9	1050	10.9	1.1×109
3	A2	Ir-1	101.1	3550	11.3	9.3×108
4	A2	Ir-2	101.1	3550	13.8	6.8×107
5	A3	Ir-1	101.6	1390	11.2	9.3×108
6	A3	Ir-2	101.6	1390	13.7	7.5×107
7	A4	Ir-1	100.0	1500	9.7	3.0×109
8	A4	Ir-2	100.0	1500	12.2	1.8×108
9	T1	Ir-1	79.1	200	−12.4	9.5×109
10	T1	Ir-2	79.1	200	−9.8	3.6×109
11	T2	Ir-1	76.9	44	−15.6	1.0×1010
12	T2	Ir-2	76.9	44	−13.0	7.0×109
13	T3	Ir-1	84.0	5600	−5.5	4.0×109
14	T3	Ir-2	84.0	5600	−3.0	1.0×109
15	T4	Ir-1	81.3	2150	−8.8	8.3×109
16	T4	Ir-2	81.3	2150	−6.3	2.2×109

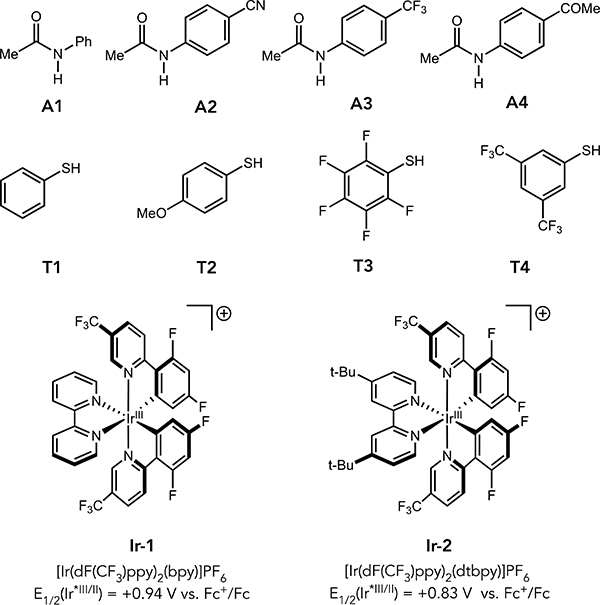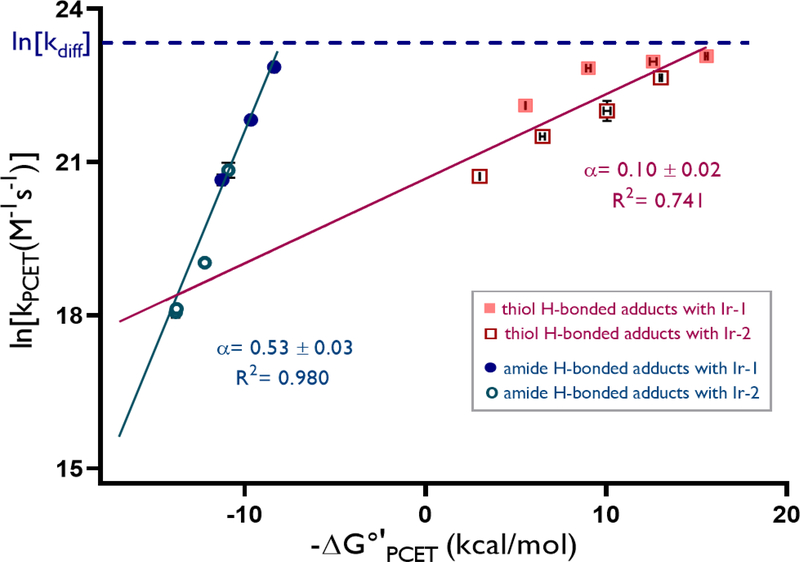
Figure 2.

Rate-driving force relationships

These results provide a compelling explanation for selective amide activation in the competitive luminescence quenching studies discussed above, as seen through comparison of the data for PCET activation of (A1) and (T1) by Ir-1 and the phosphate base. Surprisingly, the rate constants for PCET with both A1 (8.4 × 10⁹ M⁻¹s⁻¹) and T1 (9.5 × 10⁹ M⁻¹s⁻¹) approached the diffusion limit in DCE (~1 × 10¹⁰ M⁻¹s⁻¹).¹⁰ However, the K_A values indicated that the amide forms a more favorable hydrogen-bonded complex (K_{A =} 1050 M⁻¹) with the phosphate base than the thiol does (K_{A =} 200 M⁻¹), ensuring that the concentration of the reactive amide-phosphate H-bond complex in solution is significantly higher than that of the competing thiol-phosphate complex. As both elementary steps occur with similar rate constants, the thiol reaction is unable to take advantage of the additional 20 kcal/mol of driving force, and the resulting selectivity is gated by the relative concentration of the reactive H-bonded complexes in solution. Based on the K_A and k_PCET values obtained, the relative rates for amide and thiol activation at the concentrations of the synthetic hydroamidation reactions is ~ 50:1, consistent with the previously determined rate law for luminescence quenching.^3a

Evaluating a series of amide and thiol substrates with less favorable driving forces enabled us quantify the rate-driving force relationship for each substrate class outside of the diffusion-limited regime. Linear rate-driving force correlations were observed for both reactant classes. The amide series exhibited rate constants comparable to those obtained previously by Nocera,^3c and a Brønsted slope (α) of 0.53, similar to the value expected from Marcus theory.¹¹ However, the thiol series exhibits a much shallower dependence (α = 0.10), indicating a difference in intrinsic barriers for the two sets of substrates.^12,13 This value is similar in magnitude to the small Brønsted slope observed in our previous study of PCET activations of ketones that was attributed to non-perfect synchronization (NPS),^2c wherein factors that serve to stabilize the product are only partially realized at the transition state.¹⁴ Mayer and coworkers recently proposed a similar NPS-based explanation for modest Bronsted slopes in the MS-PCET oxidations of C–H bonds, and we anticipate that similar explanations may be operative here. ¹⁵

Importantly, MS-PCET chemoselectivity between competing substrates is determined by differences in both K_A and k_PCET. The differing slopes of the plots in Figure 2 highlights that changes in driving force effect k_PCET-amide and k_PCET-thiol with different sensitivities. Therefore, the selectivity between N–H and S–H activation pathways can be modified by changing the overall driving force for the reaction, which is jointly determined by the identity of the oxidant and the base catalysts. Similarly, differences in K_A values modulate the concentrations of the reactive H-bonded adducts, whose relative abundance also factors into the observed chemoselectivity.

To demonstrate how the interplay of these factors can influence the chemoselectivity of the PCET step, we define a selectivity factor Q, which is taken as □—the ratio of the PCET rate constant for oxidation of the amide-phosphate H-bond adduct times its concentration, to that of the thiol adduct counterpart (equation 1).

$$\mathrm{Q}=\frac{{\mathrm{k}}_{\mathrm{PCET}\mathrm{amide}}[\mathrm{amide}•\mathrm{phosphate}]}{{\mathrm{k}}_{\mathrm{PCET}\mathrm{thiol}}[\mathrm{thiol}•\mathrm{phosphate}]}$$ (1)

Q reflects the competition between the two H-bonded adducts to serve as the electron donor for a limiting concentration of the excited-state oxidant. As such, we hypothesized that the PCET selectivity reflected in Q may correlate with efficiency in a catalytic hydroamidation reaction, and that variation of the factors comprising Q could provide useful insight into the ways in which reaction outcomes can be rationally modulated (and complex reactivity trends understood) through careful choice of reaction conditions. Therefore, we evaluated a series of hydroamidation reactions where the value of Q and its component factors were systematically varied (Table 2). Importantly, during these catalytic reactions the amide substrate is consumed while the concentration of the thiol catalyst remains relatively constant.^3c This will cause the initial value of Q (Q₀ in Table 2) to decrease as the reaction proceeds, and below a certain threshold of Q the thiol is expected to compete kinetically with the amide substrate in the PCET event, effectively halting reaction progress.

Table 2.

Correlation of Selectivity Factor Q₀ with Catalytic Reaction Outcomes

entry	thiol	amide X=	*Ir(lll)	kPCET amide(M−1s−1)	KA amide(M−1)	kPCET thiol(M−1s−1)	KA thiol(M−1)	Q0	% yieldb	% recoveryb
1	PhSH	H	Ir-1	8.4×109	1050	9.5×109	200	96 : 4	100	0
2	PhSH	COMe	Ir-1	3.0×109	1500	9.5×109	200	91 : 9	100	0
3	PhSH	CN	Ir-1	9.3×108	3550	9.5×109	200	87 : 13	100	0
4	PhSH	H	Ir-2	1.1×109	1050	3.6×109	200	86 : 12	100	0
5	PhSH	COMe	Ir-2	1.8×108	1500	3.6×109	200	62 : 38	80	9
6	PhSH	CN	Ir-2	6.8×107	3550	3.6×109	200	57 : 43	8	85
7	3,5-(CF3)2C6H3SH	H	Ir-1	8.4×109	1050	8.3×109	2100	78 : 22	95	0
8	3,5-(CF3)2C6H3SH	H	Ir-2	1.1×109	1050	2.2×109	2100	64 : 36	85	0
9	3,5-(CF3)2C6H3SH	COMe	Ir-1	3.0×109	1500	8.3×109	2100	56 : 44	60	30
10	3,5-(CF3)2C6H3SH	CN	Ir-1	9.3×108	3550	8.3×109	2100	47 : 53	13	62
11	3,5-(CF3)2C6H3SH	COMe	Ir-2	1.8×108	1500	2.2×109	2100	23 : 77	10	47
12	3,5-(CF3)zC6H3SH	CN	Ir-2	6.8×107	3550	2.2×109	2100	18 : 82	0	84
13	C6F5SH	H	Ir-1	8.4×109	1050	4.0×109	5600	75 : 25	91	0
14	C6F5SH	H	Ir-2	1.1×109	1050	1.0×109	5600	61 : 39	61	23
15	C6F5SH	COMe	Ir-1	3.0×109	1500	4.0×109	5600	56 : 44	17	70
16	C6F6SH	CN	Ir-1	9.3×108	3550	4.0×109	5600	44 : 56	3	54
17	C6F5SH	COMe	Ir-2	1.8×108	1500	1.0×109	5600	24 : 76	trace	54
18	C6F5SH	CN	Ir-2	6.8×107	3550	1.0×109	5600	18 : 82	0	88
			In the following two entries, [thiol] = 0.04 M, [base] = 0.005 M
19	PhSH	H	Ir-2	1.1×109	1050	3.6×109	200	81 : 19	100	0
20	C6F6SH	H	Ir-2	1.1×109	1050	1.0×109	5600	35 : 65	15	50

^aReactions performed on 0.05 mmol scale.

^bYield and recovery assessed after 12h by ¹H-NMR relative to an internal standard.

The reactions in the upper portion of Table 2 are divided into three groups. Within each group, a single thiol is employed, while the identities of the amide and oxidant are varied. Notably, in all cases the reaction yields were found to trend together with the Q₀ values. The mass balance for reactions that did not reach full conversion was comprised predominantly of recovered starting material. Further evidence that PCET chemoselectivity had a direct impact on reaction outcomes could be found in entry 9, which reached a reaction endpoint of 60% yield and 30% recovery after 12 hours. However, adding a second equivalent of starting material after 12 hours (and thus re-raising the Q value above the critical threshold) resulted in restored hydroamidation reactivity and an additional 36% yield of product formation. This indicates that while the productive reaction had stalled, the catalyst system was still active and that the lack of reactivity was principally a function of a kinetically dominant but non-productive PCET activation of the thiol.

Evaluating the results in Table 2 more broadly, we can distinguish several general reactivity trends. First, amide substrates bearing electron-withdrawing groups (EWGs) are more favorable H-bonding partners for the anionic phosphate, resulting in an increased value of K_A-amide and a higher equilibrium concentration of the amide phosphate adduct. However, k_PCET-amide decreases for the same substrates as EWGs increase the strength of the N–H bond. Since the Brønsted α value for amides is comparatively large (~0.53), the change in driving force dominates and the overall rate of N–H PCET is suppressed. Accordingly, Q₀ also decreases, and the hydroamidation reactions of these substrates are less efficient than the parent compound (e.g. comparing entries 4, 5, 6; 8, 11, 12).

Incorporating EWGs into the aryl thiol also increases K_A-thiol and the equilibrium concentration of the thiol-phosphate complex, while simultaneously diminishing k_PCET-thiol as the S–H BDFE increases. However, the Brønsted slope for the thiol is comparatively small (α =0.10), indicating that changes in the driving force have comparatively little impact on k_PCET-thiol. As such, the increase in adduct concentration is the dominant factor, and serves to increase the overall rate of S–H PCET activation. This in turn decreases Q₀ and makes the hydroamidation reaction less efficient (e.g. comparing entries 5, 11, 17; 19, 20).

Finally, as the reduction potential of the Ir photocatalyst becomes more positive the driving force for both PCET reactions becomes more favorable. This causes both k_PCET-amide and k_PCET-thiol to increase while both K_A values remain constant. However, since k_PCET-amide is more sensitive to changes in the driving force than k_PCET-thiol, Q₀ increases when a stronger oxidant is employed, resulting in a more efficient hydroamidation reaction (e.g. comparing entries 3, 6; 9, 11). These results demonstrate how chemoselectivity in MS-PCET reactions and their attendant effects on reaction efficiency can be modulated simply by varying the driving force associated with the one-electron oxidant. Considered altogether, we note that every oxidant and thiol can effectively facilitate the hydroamidation reaction of at least one amide substrate; moreover, every amide substrate can be effectively cyclized with at least one combination of oxidant and thiol. These studies provide quantitative framework for interpreting reactivity trends and suggest general strategies for increasing selectivity for amide activation in marginal reactions. We anticipate that the framework presented here will provides a road map for studying chemoselectivity in other PCET reactions, where the interplay of hydrogen bonding affinities, differential PCET kinetics, and the sensitivities of the rate driving force relationships can be rationally exploited to improve the selectivity of a given process.