Measuring the Accessible Surface Area within the Nanoparticle Corona using Molecular Probe Adsorption

Abstract

The corona phase—the adsorbed layer of polymer, surfactant or stabilizer molecules around a nanoparticle—is typically utilized to disperse nanoparticles into a solution or solid phase. However, this phase also controls molecular access to the nanoparticle surface, a property important for catalytic activity and sensor applications. Unfortunately, few methods can directly probe the structure of this corona phase, which is subcategorized as either a hard, immobile corona or a soft, transient corona in exchange with components in the bulk solution. In this work, we introduce a Molecular Probe Adsorption (MPA) method for measuring the accessible nanoparticle surface area using a titration of a quenchable fluorescent molecule. For example, riboflavin is utilized to measure the surface area of gold nanoparticle standards, as well as corona phases on dispersed single walled carbon nanotubes and graphene sheets. A material balance on the titration yields certain surface coverage parameters, including the ratio of the surface area to dissociation constant of the fluorophore, $\frac{q}{K_D}$ as well as K_D itself. Uncertainty, precision, and the correlation of these parameters across different experimental systems, preparations, and modalities are all discussed. Using MPA across a series of corona phases, we find that the Gibbs free energy of probe binding scales inversely with the cube root of surface area, q. In this way, MPA is the only technique to date capable of discerning critical structure-property relationships for such nanoparticle surface phases. Hence, MPA is a rapid quantitative technique that should prove useful for elucidating corona structure for nanoparticles across different systems.

Graphical Abstract

Introduction

Nanoparticle dispersions represent a significant processing route for nanomaterials. Examples include the exfoliation of 2D materials from their bulk counterparts¹, dispersion of nanowires from as produced bulk solids^2–4, solvothermal synthesis of inorganic nanocrystals^{5, 6} and carbon dot^{7, 8}, and newly emergent covalent organic framework (COF) materials produced by organic synthesis^{9, 10}. In the solution phase, these materials invariably form a layer of adsorbed molecules called a corona around the particle. When covalently bound, as in the case of an inorganic nanocrystal, this phase is called capping chemistry. The surface coverage of these phases generally ranges from sparse, as in the case of poly ethylene oxide stabilized particles to nearly impenetrable, as in the case of some tightly bound polymer wrapping around carbon nanotubes¹¹. There is currently an absence of techniques to probe the corona phase and its surface area coverage directly despite its importance for catalytic activity at the nanoparticle surface^{12, 13}, nanosensor responses^14–17, and optoelectronic properties^{18, 19}. In this work, we introduce a new Molecular Probe Adsorption (MPA) method capable of measuring the nanoparticle surface area underlying the corona phase by titration with a quenchable fluorescent molecule. Using MPA, we measure the surface areas of a wide range of complex nanoparticle samples and discuss correlations with the properties of the corona phase.

Poly-disperse materials, including single-walled carbon nanotubes (SWNT)^{20, 21} and exfoliated 2D materials such as graphene^{22, 23} and graphene oxide²⁴ present several challenges for corona phase characterization. As an example, SWNTs have been the subject of several studies investigating dispersion methods, including those using surfactants and single stranded DNAs.^25–27 SWNT corona phases are utilized to produce molecular recognition sites in a technique called Corona Phase Molecular Recognition (CoPhMoRe), yielding molecular sensors with high selectivity.^{15, 28–32} The specific structure of the corona phase has been shown to control molecular interactions among other colloidal properties. However, there exist few techniques to characterize the structure of the nanoparticle corona phase in general. In previous work, our group introduced an approximate model of surface specific for SWNT only using nIR solvatochromism to yield an estimated surface area.³³ However, it is limited in accuracy as it requires a dielectric model of the corona, and does not extend to nanoparticle broadly.

Several characterization methods that estimate the surface area unique to metallic nanoparticles have been developed. DNA-functionalized gold nanoparticles are routinely characterized by fluorescence and UV absorption spectroscopy.^{34, 35} The numbers of fluorophores attached to DNA and gold nanoparticles (AuNPs) are measured, yielding a surface density in terms of molecules of DNA/cm².³⁴ In addition to DNA immobilized nanoparticles, enzyme-metallic nanoparticle conjugates have been investigated.^36–39 Kozlowski et al. reported the molar ratio of bound protein to the AuNPs and relative surface coverage through fluorescence measurements combined with UV-vis spectrophotometry, dynamic light scattering (DLS), and circular dichroism spectroscopy (CD).³⁹ Characterization studies of non-metallic nanoparticles coated with capping molecules have also been reported using a wider variety of techniques.^40–43 Cedervall et al. applied isothermal titration calorimetry (ITC) to measure the surface coverage of proteins on the copolymer nanoparticles due to physical adsorption.⁴⁰ Most nanoparticle surface characterization methods focus on a spherical assumption, which simplifies the analysis compared to other geometrical forms. Such methods only apply to particles with defined capping ligands, and necessarily require additional chemical steps for sample preparation, hindering high efficiency throughput.

In the present work, we address these limitations and introduce a MPA technique to determine the accessible surface area of the nanoparticle corona without altering the chemical nature of the encapsulating phase. Characterization of nanoparticles with various geometries—spanning spherical (AuNPs), cylindrical (SWNT), and 2-dimensional nano-sheets (graphene)—are reported using MPA. This method focuses on the adsorption of probe to accessible areas of the corona, which induces a quenching of the probe fluorescence in a manner proportional to the exposed surface area.⁴⁴ A probe adsorption site balance is employed in which the accessible surface area of the nanoparticle depends explicitly on the surface coverage, q, along with the dissociation constant of riboflavin to the accessible sites of nanoparticles, K_D. These two key parameters, q and K_D, represent the extent of how much dispersant molecules are covered on the nanoparticle surface and the equilibrium constant of riboflavin unbinding from the accessible sites on the corona, respectively. High ratios of $\frac{q}{K_D}$ predict greater availability of adsorption sites for riboflavin to adsorb within the corona phase, implying a loosely packed layer of polymers in the corona. This simple, quantitative technique provides a way of understanding the structure-property relationships of the nanoparticle corona.

Results and Discussion

Development of the site balance of probe adsorption on the nanoparticle surface

For the general case of a water soluble probe molecule in solution with a nanoparticle dispersion, there are three phases in which the probe can exist assuming that it has an affinity for the underlying particle. In addition to free, unbound probe in solution, there can exist probe molecules adsorbed to the regions of the nanoparticle uncovered by the corona. In cases where the system has free surfactant or polymer unbound to the nanoparticle surface, the probe can also partition into or onto such phases.

We have selected the molecule riboflavin for demonstration of the technique, although any fluorescent molecule can work in theory (Supplementary Figure 1). Riboflavin as a probe has particular affinity for nanocarbon based surfaces via π- π stacking, and it has a visible fluorescence that make it useful as a tracer or label. In the development below, we refer to riboflavin as the probe, understanding that it can be substituted for another.

Assuming a type 1, Langmuir isotherm, the amount of quenched probe due to the nanoparticle corona, C_probe,NP, is calculated using three parameters: the probe dissociation constant K_D, the surface coverage of adsorbed probe q, and the concentration of nanoparticles in solution C_NP. The resulting mass balance for the probe yields:

$$C_{probe,NP}=q{C}_{NP}\frac{C_{probe}}{C_{probe}+K_D}$$ (1)

Here, C_probe is the unbound concentration of probe in solution. Similarly, the amount of probe adsorbed to any free polymer or surfactant phases, C_probe,pol, is also calculated as:

$$C_{probe,pol}=q_{pol}{C}_{pol}\frac{C_{probe}}{C_{probe}+K_{D,pol}},$$ (2)

where q_pol is the number of vacant site per number of polymers; K_D,pol is the dissociation constant of probe interacting with polymers; C_pol is the concentration of polymers. Combining all three cases yields the total adsorption site balance:

$$C_{probe}+q_{pol}{C}_{pol}\frac{C_{probe}}{C_{probe}+K_{D,pol}}+q{C}_{NP}\frac{C_{probe}}{C_{probe}+K_D}=C_{total}$$ (3)

The value of C_probe can be measured using a calibration curve of fluorescence and probe concentration. For riboflavin, C_total was set between 0 μM and 5 μM.⁴⁵ It is reasonable to assume that K_D is roughly independent of the corona, an assumption that can be re-examined later. Additionally, the value of C_NP can be calculated indirectly using Beer’s law or directly via single particle tracking.^{46, 47} The other parameters, q_pol, C_pol and K_D,pol, are lumped into a parameter $\frac{q_{pol}{C}_{pol}}{K_{D,pol}}$ assuming that K_D,pol are an order of magnitude higher than C_probe. Equation (3) can be simplified as:

$$q{C}_{NP}\frac{C_{probe}}{C_{probe}+K_D}=C_{total}-C_{probe}-\frac{q_{pol}{C}_{pol}}{K_{D,pol}}{C}_{probe}=\Delta ,$$ (4)

where the left-hand side represents the Langmuir adsorption of riboflavin to nanoparticles and the terms of the right-hand side are set equal to some constant ∆. Inverting Equation (4) demonstrates a linear relationship between the reciprocal of C_probe and $\frac{C_{NP}}{\Delta }$:

$$\frac{C_{NP}}{\Delta }=\frac{K_D}{q}\frac{1}{C_{probe}}+\frac{1}{q}\hspace{1em}\hspace{1em}\hspace{1em}\Delta =C_{total}-C_{probe}-\frac{q_{pol}{C}_{pol}}{K_{D,pol}}{C}_{probe}.$$ (5)

This allows for linear regression of riboflavin titration data, with the linearity confirming the accuracy of the adsorption model. The parameters $\frac{K_D}{q}$ and $\frac{1}{q}$ exactly represent the slope and y-intercept respectively.

In the site balance, it was assumed that K_D was independent of the corona. Riboflavin binding may be dominated by its interactions with the nanoparticle surface, yielding a K_D value that is constant across different corona for the same nanoparticle. In reality, the corona itself can affect the probe through steric or other molecular forces and may subsequently influence K_D. It will therefore be of interest to examine $\frac{q}{K_D}$ for a given system, and, when possible, examine K_D for the given probe. Variation in the latter can reveal additional information about the binding site via its affinity for the probe.

Demonstrating the MPA technique for various nanoparticle systems

To test the efficacy of MPA on nanoparticle systems with different geometries, we examined AuNPs, SWNTs, and graphene with a fluorophore probe. The same amount of riboflavin was added to different concentrations of nanoparticles, and fluorescence spectra of riboflavin were collected (Figure 1a–c). When the probe is adequately selected, riboflavin intensity quenching is evident. The results prove there is an interaction between the probe and the nanoparticle system. In the case of AuNPs, the results are in agreement with previous studies of fluorescence resonance energy transfer (FRET).⁴⁸ In the case of SWNTs, the results are also in agreement with previous studies showing that riboflavin quenches the nIR fluorescence of SWNT in a variety of corona phases.⁴⁹ Figure 1a–c verify that the riboflavin probe adsorbs and is quenched by the three types of nanoparticle surfaces examined in this work. In contrast, polystyrene demonstrated no quenching of the riboflavin (Supplementary Figure 2).

Figure 1. Riboflavin emission spectra as a function of added nanoparticle concentration for various nanoparticles.

a. 10nm gold nanospheres. b. SWNTs dispersed by (AT)₁₅. c. graphene dispersed by polyvinylpyrrolidone (PVP). d. Probe fluorescence at different concentrations in three different systems: reference, free polymer solution (single strand DNA), and free polymer + SWNT solution. In case of ss(GT)₁₅, a NaCl buffered solution was chosen as the solvent background.

A calibration curve of riboflavin concentration vs. fluorescence intensity was used to calculate the concentration of the free probe for the three different nanoparticle systems in three different environments: reference solution, free polymer solution, and free polymer containing nanoparticle solution. In the case of corona phases composed of small molecule (anionic or cationic) surfactants, the concentration of surfactant is often above the critical micelle concentration (CMC), preventing removal of the free corona-forming molecules. The strategy of subtracting the ‘free polymer’ probe effect illustrated above appears to work. Figure 1d shows the fluorescence change of riboflavin in case of single strand (GT)₁₅ DNA wrapped SWNT corona phases as an example. The fluorescence intensity of the riboflavin probe decreases when the reference is compared to the ‘free polymer’ solution and further with the SWNT-containing solution throughout the range of riboflavin concentration. One observes that riboflavin adsorbs to quenching surfaces found from both the SWNT and polymer phases, amenable to quantitative calculation. Similar plots for SWNT with different corona phases were generated (see Supplementary Figure 3) with varying extents of quenching for each (analyzed in more detail below.) In the case of SWNT, one can observe the molecular interaction between nanoparticle and probe in two different ways: in addition to the riboflavin quenching, the corresponding nIR fluorescence quenching of the SWNT (Supplementary Figure 4) can be observed and compared, as we analyze below.

MPA applied to spherical gold nanoparticles (AuNPs)

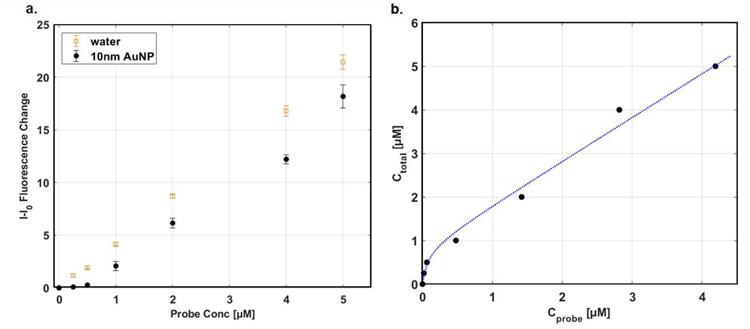
The surface area of spherical nanoparticles was first measured using MPA method and the results were discussed in details. The AuNPs have advantages of their uniform spherical structures whereas the conformations of SWNTs or graphene are dependent on either sonication or centrifugation process. 10nm citrate-capped AuNPs were chosen and the surface area obtained from MPA method was compared with the known geometric surface area. Varied concentrations of probe, which is riboflavin in this study, were added to the nanoparticle solution and the fluorescence of riboflavin corresponding to each concentration was collected (Figure 2a). Fluorescence quenching was observed for all concentrations of riboflavin, and the MPA site balance model in Equation (6) was fitted to the data (Figure 2b). It is well-studied that quenching by AuNPs is caused by both dynamic and static quenching⁵⁰ and it was assumed that the static quenching is dominant. In other words, probe quenching occurs due to contact interaction between the riboflavin and the AuNPs, rather than nonradiative energy transfer.

$$C_{probe}+q_{AuNP}{C}_{AuNP}\frac{C_{probe}}{C_{probe}+K_D}=C_{total}$$ (6)

Both q_AuNP and K_D were obtained from the fitting and the q_AuNP was then used to calculate the surface area as shown in Equation (7).

$$\frac{\text{Surface area}}{\text{AuNP particle}}=q_{AuNP}\times C_{AuNP}\times \frac{L}{\text{AuNP particle}}\times \frac{\text{Surface area}}{\text{Riboflavin}}\times N_{AV}$$ (7)

Here, it is assumed that the riboflavin adsorbs in a lateral direction and that its areal size is 0.623nm², which is estimated using its molecular weight and density. The calculated surface area from q_AuNP is 323nm² whereas the calculated spherical surface area is 314nm², demonstrating good agreement. We note that the citrate capping molecules surrounding the nanoparticles may result in small deviations from the geometric area. Nevertheless, the result from the MPA technique represents a rapid calculation that differs in this case by only 2.9%. The agreement of calculated area and geometric area of 10nm AuNPs validates that the technique can yield quantitative information about the surface area of nanoparticles.

Figure 2. Demonstration of MPA on various sizes of AuNPs.

a. Fluorescence of the riboflavin at maximum peak of spectra after varied concentrations of riboflavin were added in AuNPs solution. b. Fitted graph to the adsorption site balance of AuNPs.

Characterization of surface coverage of SWNT corona phases

Similar to other nanoparticles, the size distribution of SWNT corona phases has been conventionally characterized by AFM and cryo-TEM. In parallel, their conformation has been studied mainly by molecular dynamics simulation, but there has been lack of experimental method to determine it. Unlike AuNPs which was possible to validate it by comparing the calculated surface area and geometrical surface area, it is challenging for SWNT nanoparticles to demonstrate it. Instead, we explored different SWNT corona phases to validate the method and explore the connection between the surface coverage parameters and structure of wrapping molecules surrounding SWNT surfaces.

Total eleven corona phases were selected (Table 1), which are mainly categorized into three groups: surfactants, high molecular weight (MW) polymers, and single strand DNAs (ssDNAs). The surfactants include sodium dodecyl sulfate (SDS)²⁵, sodium cholate (SC)²⁷, and sodium dodecyl benzenesulfonate (SDBS)²⁵, which have been widely studied in the context of SWNTs and are known to form micelles. A mixture of SDS and SC was also tested to compare how much the surface coverage parameter changes compared to the pure surfactants. The second group consists of polystyrene sulfonate (PS) of which molecular weights are 70,000g/mol (PS 70k) and 200,000g/mol (PS 200k), chitosan⁵¹ and dextran^{31, 52.} Discussion of PS corona phases with different molecular weights addresses the polymer length as one of parameters affecting the surface coverage of SWNT corona phase. The ssDNA group includes (GT)₁₅, (AT)₁₅, and (GTTT)₇, which are well known to hybridize on the surface of SWNTs.^{53, 54} These three sequences were chosen to elucidate the extent to which the order of oligonucleotides affects the adsorption to the SWNTs. All SWNT corona phases were characterized by UV absorption spectra (Supplementary Figure 5) and nIR fluorescence spectra (Supplementary Figure 6).

Table 1.

List of SWNT corona phases explored in this study. They are categorized into three groups; high molecular weight polymer group (two top rows of table), surfactant group (three bottom left of table), single strand DNA group (three bottom right of table). Mixture of SDS and SC (SDS+SC) is not shown in the table.

Nomenclature	Structure	Note	Nomenclature	Structure	Note
Poly(sodium 4-styrenesulfonate)		MW 70,000g/mol	Poly(sodium 4-styrenesulfonate)		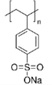MW 200,000g/mol
Chitosan		Medium weight, deacetylated	Dextran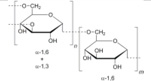
Sodium dodecyl benzenesulfonate (SDBS)		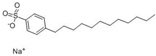Surfactant	(GT)15		DNA single strand
Sodium dodecylsulfate (SDS)		Surfactant	(AT)15		DNA single strand
Sodium cholate (SC)		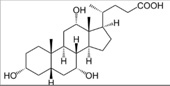Surfactant	(GTTT)7		DNA single strand

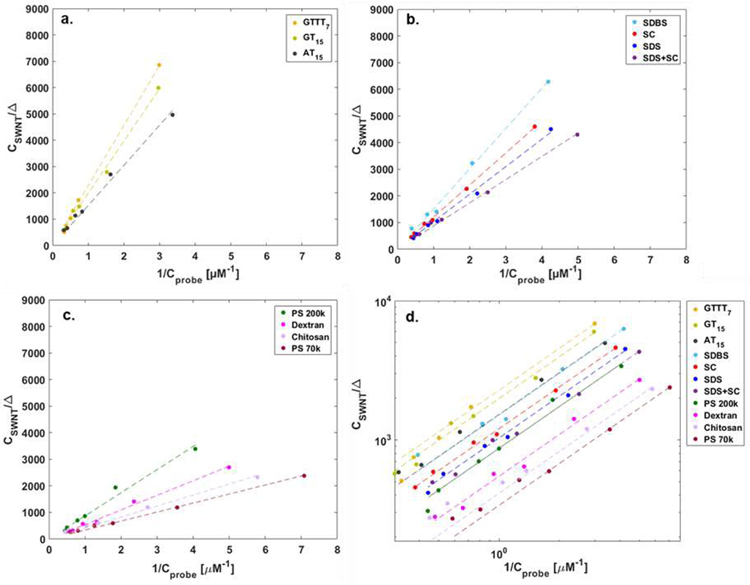
All corona phases showed linear fitting with R² value (> 0.98) to the adsorption site balance (Figure 3). The linearity of the fit implies that the probe adsorption conforms to the Langmuir isotherm from which the adsorption site balance equation was derived. The slope (inverse of $\frac{q}{K_D}$) is apparently constant throughout all concentrations of riboflavin added. This necessarily excludes possibility of corona rearrangement or displacement due to the probe adsorption and available interaction sites for the probe are conserved for the cases considered in this work. A wide range of $\frac{q}{K_D}$ values approximately from 440 [M⁻¹] to 2950 [M⁻¹] demonstrates that surface coverages of corona phases are diverse. The higher value of q indicates that the corona phase is covered by the polymers in a loose way and has more available sites for the riboflavin to adsorb. It can be interpreted to $\frac{q}{K_D}$ in the same manner by our assumption that K_D is same regardless of corona phases.

Figure 3. Linear fitting of SWNT corona phases data to adsorption site balance.

a. Fitted graph of corona phases with ssDNA group showing the high values of slope, inverse of $\frac{q}{K_D}$. b. Fitted graph of corona phases with surfactant group. c. Fitted graph of corona phases with high MW polymer group showing the low values of slope. d. log-log plot of fitting of eleven corona phases which shows the inverse of $\frac{q}{K_D}$ as y-intercept in the plot.

The corona phases categorized into three groups can be clearly distinguished based on the values of slope (Figure 3a–c). The ssDNA group among eleven corona phases exhibits a higher slope (i.e., smaller values of $\frac{q}{K_D}$) compared to the other two groups (Figure 3a). In fact, (GTTT)₇ hybridization showed the highest corona adsorption among ssDNA cases, followed by (GT)₁₅ and (AT)₁₅ hybridization. Considering the chemical structures of adenine (A), guanine (G) and thymine (T), increased hydrogen bonding between A and T may disrupt the uniform wrapping of (AT)₁₅ sequences on SWNT surface, resulting in less corona coverage compared to (GT)₁₅ and(GTTT)₇. We previously estimated the relative surface coverage of HiPCO SWNT wrapped by 9 different ssDNA sequences using a method based on the nIR fluorescent solvatochromic shift, as outlined in Bisker et al. This previous work estimated a reverse order where DNA surface coverage descends in the order of (GT)₁₅, (AT)₁₅, and (GTTT)₇.³² The solvatochromic shift method relies on a precise estimate of the effective dielectric constant of the DNA sections in contact with the SWNT. Without more precise estimates, this was assumed to be constant for all DNA and SWNT chiralities, and sequence independent. It also assumes that there is one surface coverage parameter for all SWNT diameters, lumping subtle changes in coverage into one estimate. The MPA method introduced in this work, in contrast, necessarily yields a more accurate measure of the surface coverage, independent of estimates of corona phase properties. It will be possible to explore corona phases that differ by chirality due to curvature and lattice alignment, as we have recently observed for the adsorption of ssDNA.⁵⁴

The surfactant group of corona phases showed the second highest slopes following ssDNA group (Figure 3b) and the high MW polymer group had the lowest slopes (Figure 3c). SDBS had the highest surface coverage among the surfactant group possibly due to the hydrophobic interaction between its benzene rings and the SWNT surface. The PS 200k-wrapped corona and PS 70k wrapped corona ranked the highest and lowest surface covered corona phases among the high MW polymer group.

From Figure 3, it is notable that the fitting results of each group are clustered together in a distinct way. This evident clustering can be attributed to their respective dispersion mechanisms. Historically, a number of studies have discussed the dispersion mechanism of surfactants. In surfactant groups, all three anionic surfactants discussed in this study, SDS, SDBS and SC, have been known to form micelles consisting roughly 55, 61, and 4–16 molecules, respectively.^55–57 Although the sizes of micelles differ, these surfactants share a common dispersion mechanism, leading to the medium interaction with SWNTs.

On the other hand, DNA can be characterized as having a high degree of interaction with SWNTs. DNA molecule consists of phosphate backbone, sugar rings and nucleobases. Since the bases are located relatively far from the phosphate backbones, there is a low steric hindrance between the SWNT and the DNA backbone. The higher accessibility of bases to the SWNT surface leads to its higher DNA surface coverage. These corona make up the most densely packed of those studied in this work (Figure 3a).

In contrast, the high MW polymers considered in this work appear to have more rigid backbones compared with DNA, and are therefore constrained in their ability to conform to the carbon nanotube surface. This seems to result in a lower polymer coverage and higher measured MPA surface area, q. Unlike DNA oligonucleotides, the more rigid backbones of the high MW polymers considered in this work are the site of interaction with the SWNT. Consequently, the distance between the hydrophobic domains along a backbone is necessarily shorter. It appears consistent that the high MW polymers in this work resulted in the highest exposed surface areas, q, on SWNT.

We also find that high MW polymers exhibit a wide range of SWNT coverage values, as indicated by the spread of slope values exhibited in Figure 3c. The chemical nature of the polymer backbone can either impede or promote efficient adsorption and packing on the surface. The persistence length or flexibility of the polymer is a significant consideration, with stiffer polymers having persistence lengths⁵⁸ larger than the tube diameter and leading to less polymer surface coverage (higher q ). However, in the cases of PS 200k and chitosan have similar chain lengths, but the polymer coverage of PS 200k is much higher (smaller q ) than that of chitosan. It is noteworthy that the backbone displays pendant aromatic rings capable of π- π stacking with the SWNT surface, while chitosan does not explain the difference. While persistence length of the adsorbed polymer on the nanoparticle surface is difficult to measure directly, the surface area measurement may provide an indirect measure for comparison with mechanical models of the polymer.^{59, 60}

Comparing the data on a log-log plot provides an aid to visualize the span of surface coverage values, q, (Figure 3d) as well as conformity to the Langmuir isotherm. The y-intercept corresponds to the inverse of $\frac{q}{K_D}$, which is the measured surface coverage exposed to the probe on the particle. A smaller value of $\frac{q}{K_D}$ corresponds with high corona phase coverage, so that the magnitude of y-intercept is directly proportional to the degree of this coverage, assuming equivalent probe binding strength (K_D). The (GTTT)₇ corona phase has the highest y-intercept and therefore the highest corona (DNA) surface coverage of the set among the eleven corona phases. In contrast, the PS 70k corona phase exhibits the lowest y-intercept and sparse polymer surface coverage, for the reasons discussed above.

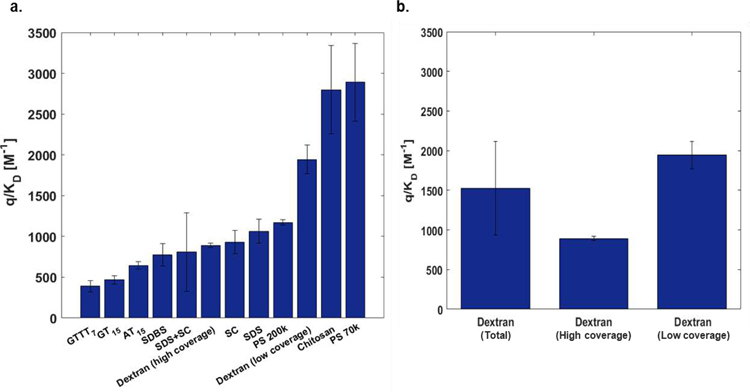
In order to test the robustness of the method, we prepared several independent batches of each corona phase and the $\frac{q}{K_D}$ parameters were statistically examined. Average values ranged from 390 [M⁻¹] to 2890 [M⁻¹] (Figure 4a). Consistent with the result from Figure 3d, the ssDNA corona phases have lowest values compared to other two groups where the high MW polymers had the highest values. Neither order nor parameter values of eleven corona phases were affected by the batch to batch variability, indicated by error bars (Figure 4a). Most of the corona phases showed batch-to-batch consistency indicated by small standard deviations. Notably, however, the corona phases wrapped by a mixture of SDS and SC (SDS+SC) exhibited a relatively high standard error. It is known that the two surfactants compete to adsorb to the SWNT surface in the system where the SDS is mixed with the bile salts⁶¹. This variability in the probe surface area may reflect that the corona is only meta-stable, changing slowly over time as the SDS and SC surface concentrations vary.

Figure 4. Summary of $\frac{q}{K_D}$ parameters of eleven corona phases.

a. Batch variation of probe surface coverage parameters of SWNT corona phases. b. $\frac{q}{K_D}$ values of dextran corona phases (Left: Total 5 batches included. Middle: 2 batches included. Right: 3 batches included)

The MPA technique allows us to examine the effect of polymer chain length on the surface coverage of the resulting corona phase. Two different lengths of polystyrene sulfonate chains, 70kDa (PS 70k) and 200kDa (PS 200k), were explored and the results indicate that the short polymer (PS 70k) wraps SWNTs more loosely than the longer polymer (PS 200k), since the former has much greater probe surface area, q. Long polymer chains can adsorb with more mass per unit length than their smaller counterparts if they are not restricted to monolayer coverage. The polystyrene sulfonate backbone is negatively charged, and at low to moderate ionic strength should be rigid, but a longer polymer may be able to attach at a greater number of points given this. O’Connell et al. studied the effect of polymer length by polyvinylpyrrolidone (PVP), and concluded that longer polymers were likely to entangle on the surface of SWNT, and this appears to be consistent with our findings.⁶² O’Connell et al. also assert that charged polymers like PS utilize a distinctly different wrapping mechanism from PVP, but we observe that the effect of polymer length applies for charged and neutral polymers. The comparison between PS 70k and PS 200k corona is instructive in that length has just as great an influence as polymer composition when it comes to the extent of surface coverage of the resulting corona phase.

Using MPA to probe surfactant exchange methods

Surfactant exchange using dialysis is a widely used technique for forming a corona phase when the sample cannot be ultra-sonicated or ultra-centrifuged directly. Here, the sample is first suspended in a sacrificial corona such as SC or SDS and placed in a dialysis bag along with the component of the final wrapping, such as a protein or polymer.³¹ Successive exchanges of the external buffer phase outside of the dialysis bag lowers the surfactant concentration in the interior as the molecules slowly leach out. This allows for the final, desired wrapping to finally adsorb to produce the target product. The technique is useful but the time required to reach the final endpoint of exchange is often variable and ambiguous, given the slow time constants involved for exchange. We explore the products of this process using MPA, showing that the resulting probe surface area can be a clear quality control metric for the final phase.

Several batches of dextran/SWNT corona phases were prepared by dialysis and we see a high degree of variability in the resulting MPA surface area parameters, reflected in a large standard deviation (Figure 4b). Indeed, MPA shows that two surface area limits are produced from the dialysis method for dextran corona: high and low polymer surface coverage. When dialysis results in complete removal of the sacrificial phase, the corona surface area show sparse coverage of dextran, consistent with other polymers. The high polymer surface coverage limit results when residual surfactant occupies otherwise free surface for probe adsorption. This interpretation is supported by very narrow confidence intervals for either case. We conclude that MPA may be useful tool for quality control for suspension methods in this way.

Comparison of MPA with intrinsic fluorescence-based measures of probe adsorption

MPA does not require one to monitor the optical response of the underlying nanoparticle, but a fluorescent substrate that quenches in response to the probe offers an opportunity to compare the adsorption isotherms. Semiconducting SWNT fluoresce in the nIR and provide just such an opportunity to independently compare the dissociation constant for probe binding, since fluorescence quenching can also be used to determine the surface coverage of the probe independently. As an example, one can then compare the K_D,SWNT from nIR fluorescence versus the MPA result. The Langmuir adsorption model in Equation (8) can be related to SWNT fluorescence intensity to yield another measurement of K_D,SWNT for the same probe (Table 2)

$$\frac{I_0-I}{I_0}=A\frac{C_{riboflavin}}{C_{riboflavin}+K_{D,\text{SWNT}}}$$ (8)

Table 2.

Comparison of Langmuir isotherm parameters from SWNT nIR fluorescence and $\frac{q}{K_D}$ from MPA with confidence intervals.

Method	MPA	SWNT nIR Fluorescence
SWNT corona phase	q/KD [M−1] [Confidence Interval]	KD,SWNT [μM] [Confidence Interval]	A [Confidence Interval]
(GTTT)7	438.5 [412.8 464.3]	1.13 [0.89 1.38]	0.46 [0.43 0.49]
(GT)15	503.7 [476.8 530.6]	1.00 [0.67 1.34]	0.49 [0.43 0.54]
(AT)15	764.6 [710.8 818.4]	1.53 [0.72 2.33]	0.17 [0.14 0.20]
SDS+SC	1149.0 [1091 1207]	0.50 [0.28 0.72]	0.59 [0.53 0.66]
SDS	991.8 [912 1072]	0.42 [0.32 0.52]	0.93 [0.88 0.98]
PS 200k	1193 [1037 1350]	1.50 [1.23 1.78]	0.60 [0.56 0.64]
Dextran	1825 [1714 1936]	2.44 [0.82 4.06]	0.84 [0.59 1.09]
Chitosan	2972 [2527 3417]	5.20 [3.23 7.18]	0.72 [0.56 0.89]

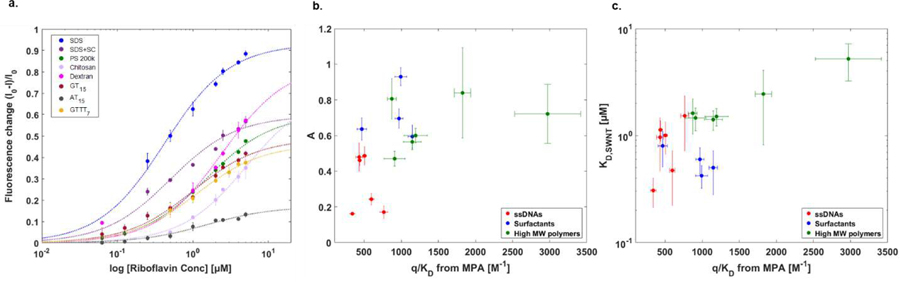
We find that the nIR fluorescence quenching of SWNT in response to the riboflavin probe (Figure 5a) appears well described by the same Langmuir adsorption model used for MPA. The resulting K_D,SWNT values as determined from this quenching appear in Table 2 and should be distinct from those measured from MPA. The former experiment monitors only semiconducting SWNT that are individually dispersed and non-defective or fragmented. On the other hand, MPA measures the adsorbed surface area of the entire sample, including aggregates, carbon fragments, metallic nanotubes and bundles. Never-the-less, one can compare the estimated parameters from Equation (8) (K_D,SWNT and A ) with the surface coverage parameter ($\frac{q}{K_D}$) for the same corona phase as measured by MPA. This correlation was investigated using these two types of experiments on identical batches of the colloidal dispersions. In Figure 5b, we find that the value of A versus the corresponding MPA value of $\frac{q}{K_D}$ for the same sample shows no correlation (R² value = 0.25). Again, the latter necessarily measures all of the probe adsorption sites and should provide a useful measure of sample quality. There does appear to be a correlation (R² =0.77) between $\frac{q}{K_D}$ from MPA and the K_D,SWNT as measured by nIR quenching (Figure 5c). This is analyzed in more detail in the next section.

Figure 5. nIR fluorescence study of SWNT corona phases.

a. Titration curve of probe adsorption as traced using SWNT nIR fluorescence. b. Scatter plot of $\frac{q}{K_D}$ as measured by MPA and proportionality constant A from Equation (8). c. Scatter plot of $\frac{q}{K_D}$ and K_D,SWNT from Equation (8) demonstrating an apparent trend for non-surfactant corona.

It is also noteworthy that there was no observable nIR fluorescence change on SC, SDBS, and PS 70k corona phases upon addition of riboflavin. This is another indication that the MPA measurement provides orthogonal information about the corona structure. The disparity suggests that riboflavin adsorbs in a configuration on these coronas such that it has negligible interaction with the SWNT exciton. This would be the case for a binding domain that involved more of the adsorbed corona and less of the underlying graphene lattice.

Structure-Property Relationships for Nanoparticle Corona

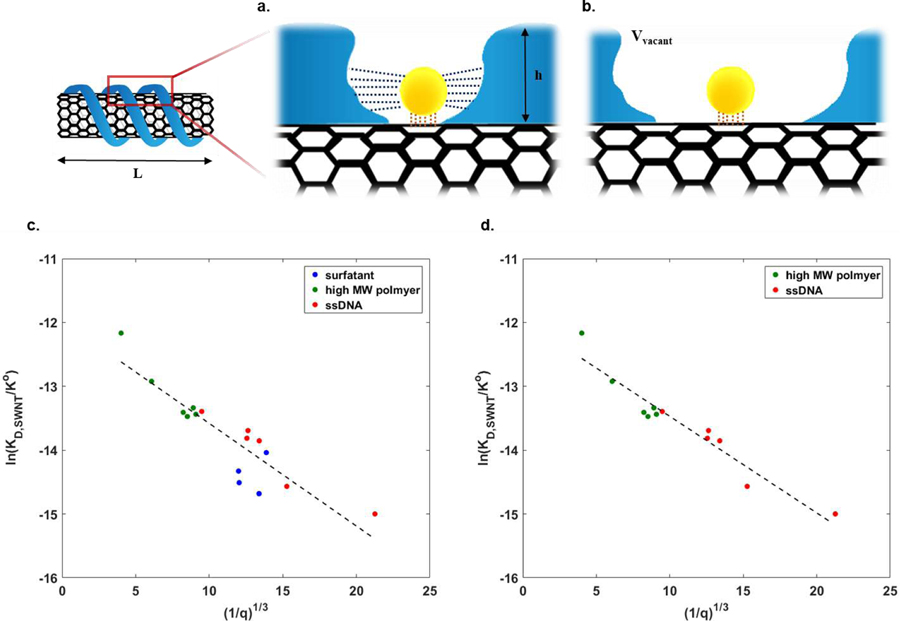
The results of MPA can be combined with other nanoparticle data to deduce important structure-property relationships for corona for the first time. As an example, we posit that a relationship between the available surface for probe adsorption, q, and the strength of probe binding, as measured by the dissociation constant should exist across a range of similar corona phases for a common nanoparticle substrate. Figure 6a–b illustrates this mechanistically. At high values of q, the probe adsorbs via a surface interaction dominated by the nanoparticle substrate alone (Figure 6b). Conversely, at low (probe) coverage (Figure 6a), the corona provides an additive attraction via Van der Waals bonding with the encroaching corona, potentially decreasing the observed K_D. Alternative scenarios may inhibit adsorption through steric interactions, changing the sign of the energetic contribution below.

Figure 6. Probe adsorption influenced by an attractive interaction within the corona.

a. The probe adsorbed within the loosely packed corona (at high q) interacts primarily with the nanoparticle surface (orange dotted line). b. Conversely, a tightly packed corona (at low q) exerts van der Waals attraction from both the corona itself (blue dotted line) along with the nanoparticle surface (orange dotted line). c. Linear fitting of MPA parameters from all SWNT corona phases (surfactant, high MW polymer, ssDNA) to the thermodynamic adsorption model of Equation (13), showing agreement with the predicted −1/3 exponent. d. Linear fitting of all data collected for SWNT corona phase types (high MW polymer and ssDNA) excluding small molecule surfactants, which adsorb differently, again demonstrating the −1/3 scaling.

As suggested in Fig 6, we can deconvolute the free energy of adsorption of the probe to surface and corona phase contributions: ΔG_surface and ΔG_corona. The former refers to the energy change upon probe adsorption to the nanoparticle surface. The latter is the adsorption energy decrease due to the Van der Waals attraction between probe and corona. The total free energy change of the system defines an equilibrium state, which can be related to the probe adsorption dissociation constant, K_D:

$$RT\hspace{0.17em}ln\left(K_D\right)=\Delta G_{surface}+\Delta G_{corona}$$ (9)

where R and T refer to the ideal gas constant and system temperature, respectively. As the distance between the probe and the enclosing corona closes, the magnitude of ΔG_corona becomes comparable to ΔG_surface, contributing to a lower equilibrium dissociation constant. We approximate the former as a sphere-surface interaction, with energy defined by the Hamaker constant and a characteristic distance, D:

$$\Delta G_{corona}=-\frac{A{r}_{probe}}{6D},A={\pi }^{2}C{\rho }_1{\rho }_2$$ (10)

where A, r_probe and D refer to the Hamaker constant, radius of the probe approximated as a sphere, and distance between sphere and surface, respectively.⁶³ The Hamaker constant, A, is determined by ρ₁ and ρ₂ which are the number of atoms per unit volume in two bodies, and C, a coefficient in the atom-atom pair potential. In 3 dimensional space where the nanoparticle is not covered by the corona, the volume of the vacant adsorption site, V_vacant, can be expressed as a function of q:

$$V_{vacant}=qLh{S}_{probe}{\rho }_C$$ (11)

Here, L and h refer to characteristic length of a cylindrical nanoparticle and height of corona phase with S_probe and ρ_C the adsorbed area of the probe and number density of carbon atom on one nanoparticle, respectively. The volumetric space responsible for the interaction between the two bodies is V_vacant – V_probe and the distance, D, can be derived as ${\left(V_{vacant}-V_{probe}\right)}^{1/3}$. In the SWNT example, q can be calculated by multiplying MPA parameter ($\frac{q}{K_D}$) and dissociation constant from the SWNT PL isotherm (K_D,SWNT) assuming the approximation that K_D is nearly equal to K_D,SWNT The resulting relationship emerges as:

$$RTln\left(K_D\right)=\Delta G_{surface}-\frac{A{r}_{probe}}{6{\left(qLh{S}_{probe}{\rho }_C-V_{probe}\right)}^{1/3}}$$ (12)

We further assume that V_probe is small compared to V_vacant and simplify to:

$$ln\left(K_D\right)=\frac{\Delta G_{surface}}{RT}-\frac{A{r}_{probe}}{6RT{\left(Lh{S}_{probe}{\rho }_C\right)}^{1/3}}\frac{1}{q^{1/3}}$$ (13)

Figure 6c–d shows that this inverse $q^{1/3}$ scaling describes the observed trend of ln(K_D,SWNT) for a series of SWNT corona phases explored in this study remarkably well. Figure 6c applies this thermodynamic equilibrium model to all SWNT corona phases with a linear correlation (R²=0.81). The slope should scale as $\frac{A{r}_{probe}}{6RT{\left(Lh{S}_{probe}{\rho }_C\right)}^{1/3}}$, with a value of −0.16 according to the correlation (Table 3). Calculations outlined in the supporting information estimate this slope from system parameters as −0.15 in remarkable agreement with observation. We conclude that this structure-function relationship is remarkably robust, and that others like it should exist for all nanoparticle systems. The Y-intercept, $\frac{\Delta G_{surface}}{RT}$, is observed to be −11.97, such that the ΔG_surface is approximately −29 kJ/mol at 20°C. Yao et al. explored the adsorption of methylene blue on the SWNT surface and the standard free energy at 20°C from the thermodynamic analysis with experimental data was found to be −11 kJ/mol, approximately 1/3 of the observed value.⁶⁴ However, this experimental value is well within the range of physical adsorption, providing a consistency check. It is also noted that the attraction between the probe and the corona (ΔG_corona) contribute to an energy stabilization by an additional 23 % of ΔG_surface at maximum. Specifically, the adsorption is energetically dominated by the nanoparticle surface as expected. On the other hand, in the case of surfactant and ssDNA-SWNT corona phases, the free energy of the system is further reduced by the attraction of the probe with tightly packed corona as well as with the SWNT surface.

Table 3.

Linear regression parameters from two data sets: all three groups and two groups including high MW polymer and ssDNA groups.

SWNT corona phase (group)	Slope	Y-intercept	R2
All groups (surfactant, ssDNA, high MW polymer)	−0.16 [−0.21 −0.12]	−11.97 [−12.51 −11.44]	0.81
High MW polymer & ssDNA groups	−0.15 [−0.18 −0.12]	−11.96 [−12.31 −11.60]	0.92

There are compelling reasons to exclude corona formed by small molecule surfactants. The adsorbed surfactant phase, like the corresponding bulk micelle, is a transient structure necessarily composed of a hydrophobic core and hydrophilic outer shell in an aqueous phase. Adsorbed surfactant corona can form hemimicellar structures, cylindrical geometries, or randomly adsorbed structures.^{65, 66} Regardless of structure, surfactant molecules form a dynamic equilibrium on the nanoparticle surface, in exchange with the bulk phase. Hence, the surfactant formed corona phase does not adhere to the pocket-shaped binding model characterized by V_vacant. Indeed, this appears supported by a notable increase in linearity, and corresponding R² value, when the analysis excludes surfactants (Figure 6d and Table 3). Overall, this analysis shows that the MPA technique outlined in this work provides information of high enough quality for formulating and evaluating structure-property relationships for nanoparticle corona, a longstanding goal of the field.

Extension to other probe molecules: fluorescein sodium

We examined the extension of MPA to another probe. Fluorescein sodium (NaFl) was chosen and we explored the response to the PS 70k-SWNT corona phase. Both probes show excellent linear regression with R² (>0.99) to the adsorption site balance (Supplementary Figure 1). This yields 2458.2 [M⁻¹] and 2849.2 [M⁻¹] as surface area values, in case of riboflavin and NaFl, respectively (Table 4). The difference in the MPA parameters between two probes is anticipated from the relative size of riboflavin to NaFl. The surface area is determined in units of probe number adsorbed to the nanoparticle surface, implying that smaller probe should adsorb a larger population with a higher MPA parameter value. As a first approximation, we can assume that the MPA surface area should be proportional to the inverse of molecular weight of the probe. The ratios of q/KD between the two probes is 0.86 for riboflavin to NaFl, which is consistent with the inverse of molecular weight ratio of two probes (0.88). We conclude that the MPA method works properly with other probes such as NaFl.

Table 4.

Comparison of $\frac{q}{K_D}$ from MPA with confidence intervals between riboflavin and fluorescein sodium.

Probe	q/KD [M−1] [Confidence Interval]	Ratio of q/KD	Molecular weight (MW) of probe	Ratio of MW
Riboflavin	2458.2 [2228.4 2687.9]	0.86	376.4	1
Fluorescein sodium (NaFl)	2849.2 [2629.9 3068.4]	1	330.3	0.88

Characterization of MPA surface area of graphene

We applied the MPA technique to colloidally dispersed 2D graphene platelets as an example of a challenging sample for corona phase measurement. Graphene samples dispersed using SC (SC-graphene) and PVP (PVP-graphene) were prepared for comparison. They were characterized by UV absorption spectra (Supplementary Figure 7).

We find, as shown in Figure 7, that MPA can distinguish significant differences between corona, which may reflect differences in surface coverage for each graphene corona phase. The surface coverage parameters were 215.6 [M⁻¹] and 909.9 [M⁻¹], from SC-graphene and from PVP-graphene respectively. SC-graphene clearly shows higher coverage of the surfactant phase than PVP-graphene for its polymer coverage, which match the trend from the SWNT analogs. This difference is also expected given that polymer adsorption of such a large molecular weight species has a reduced ability to pack tightly to block the probe.

Figure 7. Linear fitting of graphene corona phase data to adsorption site balance.

a. Probe fluorescence spectra in three different solutions: water, SC solution, and SC-graphene solution. b. Linear fitting of graphene corona phases data to adsorption site balance. SC-graphene and PVP-graphene samples were chosen.

Next, we compared two different nanoparticles covered by the same wrapping molecules. The MPA surface coverage values from SC-graphene (215.6 [M⁻¹]) and from SC-SWNT (937.6 [M⁻¹]) indicate that the wrapping molecules pack themselves more tightly on graphene than SWNT. The difference in coverage can be attributed to the presence of curvature of the nanoparticle surface. Specifically, the adsorption of the wrapping molecules to the surface of cylindrical shaped SWNT appears to be hindered compared to the planar graphene.

Conclusion

In the past decade, simulation tools have been applied to understand the adsorbed corona phases on nanoparticle surfaces, identifying various mechanisms of wrapping and structuring. These results strongly suggest that each nanoparticle/corona system has a distinct surface coverage, or area of exposed nanoparticle surface capable of measurement. It has been challenging to characterize the corona phase structure at the nanoparticle surface due to issues with dilution, molecular mobility, and total radiation cross section. However, in this work we introduce a Molecular Probe Adsorption technique based on fluorophore quenching of a calibrated probe as a tool to study the bound surface area of the corona phases at the nanoparticle surface. Our analysis does not rely on the photophysical response of the particle itself, and rapidly allows one to estimate the surface coverage normalized by the dissociation constant of probe adsorption, $\frac{q}{K_D}$. As an example, the concentration dependence of riboflavin fluorescence quenching was measured on a total of 14 different nanoparticle corona phases, on AuNP, SWNT and graphene, in order to validate our method. The results appear promising for the use of MPA as a rapid tool to understand one critical aspect of corona phase structure in solution: the adsorbed area. Because of this, MPA may have a significant impact on the basic science and technical applications of nanoparticles.