Abstract
External assistance in the form of strings called advice is given to an automaton in order to make it a non-uniform model of computation. Automata with advice are then examined to better understand the limitations imposed by uniformity, which is a typical property shared by all feasible computational models. The main contribution of this paper is to introduce and investigate an extension of the model introduced by Küçük et al. [6]. The model is called circular deterministic finite automaton with advice tape (cdfat). In this model the input head is allowed to pass over input multiple times. The number of allowed passes over the input, which is typically a function of input length, is considered as a resource besides the advice amount. The results proved for the model include a hierarchy for cdfat with real-time heads, simulation of 1w/1w cdfat by 1w/rt cdfat, lower bounds of resources provided to a cdfat in order to make it powerful enough to recognize any language, utilizable advice limit regardless of the allowed pass limit, a relation between utilizable pass limit and advice limit, and some closure properties.
Keywords: Formal languages, Automata theory, Advised computation
Introduction
Advised computation, where external trusted assistance is provided to a machine to help it for computational tasks, was introduced by Karp and Lipton [4] in 1982. Damm and Holzer [1] considered giving advice to restricted versions of Turing machines. Recent work on finite automata with advice include the papers of Yamakami [8–11], Tadaki et al. [7], Freivalds et al. [3], Küçük et al. [6] and Ďuriš et al. [2]. Today, there are many different models in literature, partly because of the several options available for a machine to access its advice. However, all such models share some common properties. There is an advice function, which maps input lengths to advice strings and not needed to be computable. Advice strings are composed of characters from an advice alphabet. The machine has to use the same advice string when operating on inputs of the same length. We investigate the class of languages recognized by a machine when it consults some advice function having some bounded growing rate. We then play with that upper bound to see what happens to the aforementioned class. An advised automaton takes advantage of an advice string by reading the character under the advice head and choosing appropriate transition from its transition function accordingly. So the same machine may recognize different languages using different advice functions.
We focus on the advice tape model introduced by Küçük et al. in [6]. Since that model becomes extremely powerful (able to recognize all languages) when allowed to use a 2-way input head, and is remarkably limited for the 1-way head case, [2, Theorem 2], [6, Theorem 13], we examine a limited version of two-way input access.
Some common terminology to be used in this paper are as follows: n denotes input length, M denotes an automaton, L denotes a language, h denotes an advice function, w denotes a string, 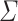 denotes input alphabet,
denotes input alphabet, 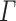 denotes advice alphabet,
denotes advice alphabet, 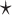 means any, ALL denotes the set of all languages, and
means any, ALL denotes the set of all languages, and 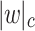 denotes the number of occurrences of character c in string w.
denotes the number of occurrences of character c in string w.
Here are some definitions of concepts that will be used in our discussion,
Definition 1
[6].
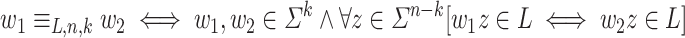 .
.
Definition 2
[2, Definition 5]. Let 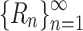 be a family of relations
be a family of relations 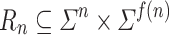 for some
for some  such that
such that 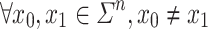 , there is a
, there is a 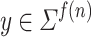 such that
such that 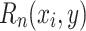 and
and 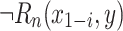 for some
for some 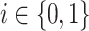 . Let
. Let 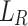 be the language
be the language 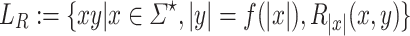 . We call
. We call 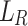 a prefix-sensitive language for relation family R.
a prefix-sensitive language for relation family R.
Definition 3
We call L a prefix-sensitive language iff there exists a relation family R such that 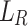 is a prefix-sensitive language for relation family R.
is a prefix-sensitive language for relation family R.
Our Model
We defined this model and decided to work on it because the model seems to provide a smooth passage from one-way input head to two-way input head. The name of the new model is circular deterministic finite automaton with advice tape (cdfat) which may have real-time or 1-way input and advice heads (4 possible versions). Circular machines read their input circularly, that is, when the input endmarker has seen and the next transition dictates machine to move its input head to right, the input head immediately returns to the beginning position. Advice head is not allowed to perform such a move.
Note that when restricted to a single pass on input, this model is exactly the same with the standard deterministic finite automaton with advice tapes model (except the two-way input head version) introduced by Küçük et al. [6].
Definition
A circular deterministic finite automaton is a 9-tuple 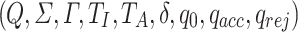 where
where
-
(i)
Q is a finite set of internal states,
-
(ii)
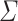 is a finite set of symbols called the input alphabet that does not contain the endmarker symbol,
is a finite set of symbols called the input alphabet that does not contain the endmarker symbol,  , such that
, such that  and
and  ,
, -
(iii)
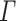 is a finite set of symbols called advice alphabet that does not contain the endmarker symbol,
is a finite set of symbols called advice alphabet that does not contain the endmarker symbol, 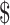 , such that
, such that 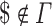 and
and  ,
, -
(iv)
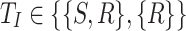 represents the set of allowed input head movements where S and R means stay-put and right respectively,
represents the set of allowed input head movements where S and R means stay-put and right respectively, -
(v)
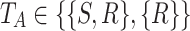 represents the set of allowed advice head movements where S and R means stay-put and right respectively,
represents the set of allowed advice head movements where S and R means stay-put and right respectively, -
(vi)
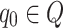 is the initial state on which the execution begins,
is the initial state on which the execution begins, -
(vii)
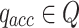 is the accept state on which the execution halts and accepts,
is the accept state on which the execution halts and accepts, -
(viii)
 is the reject state on which the execution halts and rejects,
is the reject state on which the execution halts and rejects, -
(ix)
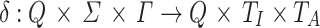 is the transition function such that,
is the transition function such that,  implies that when the automaton is in state
implies that when the automaton is in state 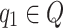 and it scans
and it scans 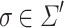 on its input tape and
on its input tape and 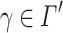 on its advice tape, a transition occurs which changes the state of the automaton to
on its advice tape, a transition occurs which changes the state of the automaton to 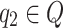 , meanwhile moving the input and advice tape heads in the directions specified respectively by
, meanwhile moving the input and advice tape heads in the directions specified respectively by 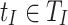 and
and  ,
,
A cdfat  is said to accept (reject) a string
is said to accept (reject) a string 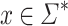 with the help of an advice string
with the help of an advice string 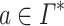 if and only if M, when started at its initial state
if and only if M, when started at its initial state 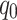 with
with 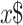 on the input tape and
on the input tape and 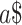 on the advice tape and while the tape heads scan the first symbols, reaches the accepting (rejecting) state,
on the advice tape and while the tape heads scan the first symbols, reaches the accepting (rejecting) state, 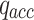 (
(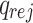 ), by changing states and moving the input and advice tape heads as specified by its transition function,
), by changing states and moving the input and advice tape heads as specified by its transition function, 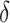 .
.
A language L defined on the alphabet 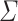 , is said to be recognized by such a cdfat M with the help of an advice function
, is said to be recognized by such a cdfat M with the help of an advice function 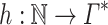 if and only if
if and only if
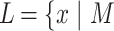 accepts x with the help of
accepts x with the help of 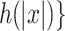 , and
, and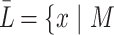 rejects x with the help of
rejects x with the help of 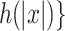 .
.
A language L is said to be recognized by a cdfat, M, using O(g(n))-length advice if there exists an advice function h with the following properties:
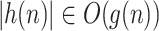 , and
, andM recognizes L with the help of h(n).
A language L is said to be recognized by a cdfat, M, using f(n) passes over the input if and only if during the execution of any input of length n, transitions of the form 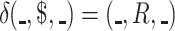 are used at most f(n) times in total.
are used at most f(n) times in total.
Note that it is not allowed for a cdfat to have a transition of the form 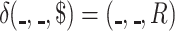 , however, there can be transitions
, however, there can be transitions 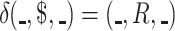 . The endmarker of the input is for informing the machine. It may be a different model if we omit it, for the sake of backward compatibility we continue to use it.
. The endmarker of the input is for informing the machine. It may be a different model if we omit it, for the sake of backward compatibility we continue to use it.
For the notational purposes, 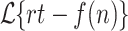 denotes the set of languages recognized by cdfat with real-time heads,
denotes the set of languages recognized by cdfat with real-time heads, 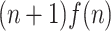 length advice and f(n) passes. When a head is allowed to stay-put on its tape, we use a different notation. For instance
length advice and f(n) passes. When a head is allowed to stay-put on its tape, we use a different notation. For instance  denotes the set of languages recognized by cdfat with 1-way input head and real-time advice head, using g(n) length advice and f(n) passes.
denotes the set of languages recognized by cdfat with 1-way input head and real-time advice head, using g(n) length advice and f(n) passes.
Results
Theorem 1
A language L is prefix-sensitive if and only if for all 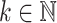 , there exists
, there exists 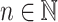 such that
such that 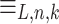 has
has 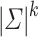 equivalence classes.
equivalence classes.
Proof
Assume that for some language L it holds that for all 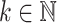 , there exists
, there exists 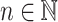 such that
such that 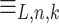 has
has 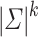 equivalence classes. Let f be a function which maps any
equivalence classes. Let f be a function which maps any 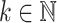 to an n so that
to an n so that 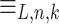 has
has  equivalence classes. Define an infinite family of relations
equivalence classes. Define an infinite family of relations 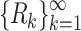 such that
such that 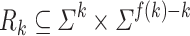 and for all
and for all 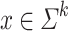 and all
and all 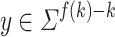 ,
,  . It holds that
. It holds that 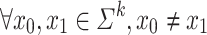 , there is a
, there is a 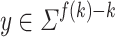 such that
such that 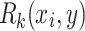 and
and  for some
for some 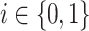 . Because if there were no such y for some
. Because if there were no such y for some 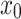 and
and  , then
, then 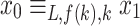 would be true and the number of equivalence classes would not be
would be true and the number of equivalence classes would not be 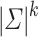 . According to the Definition 2, we concluded that L is prefix-sensitive.
. According to the Definition 2, we concluded that L is prefix-sensitive.
For the other direction, let L be a prefix-sensitive language. According to the Definition 2,  where
where 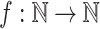 is a function and
is a function and 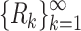 is an infinite sequence of relations such that
is an infinite sequence of relations such that 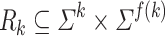 and
and  , there is a
, there is a 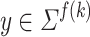 such that
such that 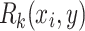 and
and 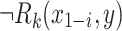 for some
for some 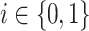 . It holds that for all
. It holds that for all  ,
,  has
has 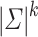 equivalence classes. Because if the number of equivalence classes of
equivalence classes. Because if the number of equivalence classes of 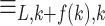 is less than
is less than 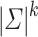 for some k, then there would be two strings
for some k, then there would be two strings 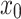 and
and 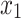 such that
such that 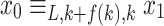 and that would imply that there is no y of length f(k) such that
and that would imply that there is no y of length f(k) such that 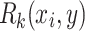 and
and 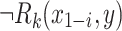 for some
for some 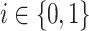 .
. 
Theorem 2
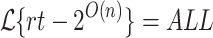 .
.
Proof
Let 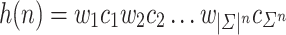 where each
where each 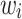 is a distinct input word of length n and each
is a distinct input word of length n and each 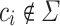 is either the accept or the reject symbol. Devise a machine M such that, it tries to match the input word and advice character by character in real-time execution. If a mismatch occurs while trying to match the input word, machine M will advance its input head until it is at the beginning position again. Note that the advice head will be at the first character of the next word on advice at the end of this process. Then it tries to match the next word and so on. At some point matching ends with success, that is, machine M will see the endmarker of input while trying to match the characters. At that point it will accept or reject the string depending on which
is either the accept or the reject symbol. Devise a machine M such that, it tries to match the input word and advice character by character in real-time execution. If a mismatch occurs while trying to match the input word, machine M will advance its input head until it is at the beginning position again. Note that the advice head will be at the first character of the next word on advice at the end of this process. Then it tries to match the next word and so on. At some point matching ends with success, that is, machine M will see the endmarker of input while trying to match the characters. At that point it will accept or reject the string depending on which 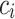 character it is seeing on the advice.
character it is seeing on the advice. 
Theorem 3
For any function 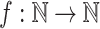 ,
, 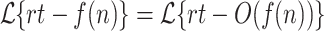 .
.
Proof
The idea is that for any given machine M, one can devise a new machine  such that
such that 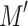 uses k times less passes than M for all n and for an arbitrary
uses k times less passes than M for all n and for an arbitrary 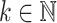 , and still recognizes the same language with the help of some other advice function. Let us group the passes of machine M so that
, and still recognizes the same language with the help of some other advice function. Let us group the passes of machine M so that 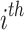 group consists of passes from
group consists of passes from 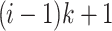 to ik. With a single pass, machine
to ik. With a single pass, machine 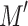 simulates a group of k passes of M. First pass simulates the first group and second pass simulates the second group and so on. Since
simulates a group of k passes of M. First pass simulates the first group and second pass simulates the second group and so on. Since  does not know which state to begin with a pass without knowing the result of the previous one, it simulates all possibilities and remembers the final state of the previous group of passes using again its states. Therefore the size of the state set of
does not know which state to begin with a pass without knowing the result of the previous one, it simulates all possibilities and remembers the final state of the previous group of passes using again its states. Therefore the size of the state set of 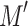 is
is 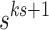 where s is the number of states of M.
where s is the number of states of M.
The new advice function 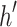 is a compressed version of the old one. Let
is a compressed version of the old one. Let 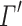 be the new advice alphabet whose symbols represent the k permutations of the symbols of
be the new advice alphabet whose symbols represent the k permutations of the symbols of  .
. 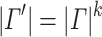 holds. Let
holds. Let 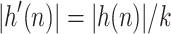 for all
for all  . Note that without loss of generality we assume that |h(n)| is an integer multiple of k. We prepare the new advice strings so that
. Note that without loss of generality we assume that |h(n)| is an integer multiple of k. We prepare the new advice strings so that 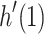 represents all strings from h(1) to h(k),
represents all strings from h(1) to h(k), 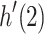 represents all strings from
represents all strings from 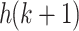 to h(2k) and so on.
to h(2k) and so on. 
Theorem 4
For any function 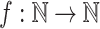 ,
,  .
.
Proof
Let 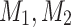 be machines recognizing
be machines recognizing 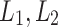 with the help of advice functions
with the help of advice functions  respectively. Let
respectively. Let 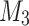 be the machine which is claimed to recognize the concatenation language
be the machine which is claimed to recognize the concatenation language 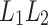 with the help of advice function
with the help of advice function 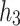 . The idea is to predict the words
. The idea is to predict the words  and
and  such that
such that  is the input word. Machine
is the input word. Machine 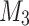 doesn’t know from where to divide the input, so it just tries all the possibilities. We replace the advice characters whose locations correspond to the last character of the first portion of the input with their marked versions in order to inform the machine
doesn’t know from where to divide the input, so it just tries all the possibilities. We replace the advice characters whose locations correspond to the last character of the first portion of the input with their marked versions in order to inform the machine  .
.
In the first pass over the input, machine 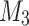 first simulates
first simulates  on the first portion of the input and stores the last internal state of that execution. Then it simulates
on the first portion of the input and stores the last internal state of that execution. Then it simulates 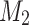 on the rest of the input and stores the last state of that execution too. Then it begins the second pass simulating
on the rest of the input and stores the last state of that execution too. Then it begins the second pass simulating 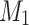 again but this time starting from the last saved state of that thread and when it completes,
again but this time starting from the last saved state of that thread and when it completes, 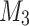 will update the last state of the thread and so on. Throughout the execution of
will update the last state of the thread and so on. Throughout the execution of 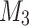 , two separate threads of execution are simulated at the same time. At the end of at most f(n) passes, if both threads end with accepting their respective sub-inputs,
, two separate threads of execution are simulated at the same time. At the end of at most f(n) passes, if both threads end with accepting their respective sub-inputs, 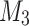 accepts the input. Otherwise,
accepts the input. Otherwise, 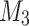 continues the computation with a different division of the input. Note that, given an input word of length n, there are
continues the computation with a different division of the input. Note that, given an input word of length n, there are 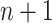 different pairs of words such that their concatenation is the input word. At the end of at most
different pairs of words such that their concatenation is the input word. At the end of at most 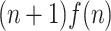 passes, if no division works,
passes, if no division works,  rejects the input. According to the Theorem 3, asymptotic rate of the passes is the important part so nf(n) passes can do the same job.
rejects the input. According to the Theorem 3, asymptotic rate of the passes is the important part so nf(n) passes can do the same job.
Note that we should double the old advice alphabet size and introduce marked versions of the old symbols in order to mark the position of input separation on the advice  . Also note that advice string
. Also note that advice string 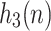 will be an interleaved version of the
will be an interleaved version of the 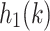 and
and 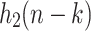 concatenated for all
concatenated for all 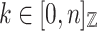 .
. 
Corollary 1
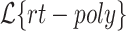 is closed under concatenation.
is closed under concatenation.
Lemma 1
Let  . Then for all n and for all k smaller than n,
. Then for all n and for all k smaller than n, 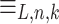 has
has 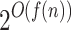 equivalence classes.
equivalence classes.
Proof
Let 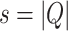 and let
and let 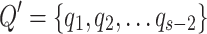 be the set of all states except the accept and reject states. Let
be the set of all states except the accept and reject states. Let 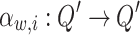 be a mapping which maps the internal state of machine when input head is for the first time on the first character of w and advice head is at the
be a mapping which maps the internal state of machine when input head is for the first time on the first character of w and advice head is at the 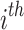 position to the internal state of machine when input head is for the first time on the first character right after the w. Besides its parameters w and i, this mapping depends on the content of the advice and transition function of the machine. Here we consider a single machine working on inputs of the same length n therefore the mapping depends only on its parameters.
position to the internal state of machine when input head is for the first time on the first character right after the w. Besides its parameters w and i, this mapping depends on the content of the advice and transition function of the machine. Here we consider a single machine working on inputs of the same length n therefore the mapping depends only on its parameters.
Consider execution of a real-time circular machine on two different inputs of length n, namely 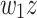 and
and 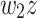 . If we can find two words
. If we can find two words 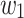 and
and 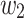 such that
such that  for all
for all  then the two inputs must have the same fate for all z.
then the two inputs must have the same fate for all z.
Given a single i, there are less than  distinct functions
distinct functions 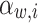 . Considering all f(n) functions mentioned above for a word w, there are less than
. Considering all f(n) functions mentioned above for a word w, there are less than 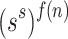 different permutations. Assuming that the number of equivalence classes of relation
different permutations. Assuming that the number of equivalence classes of relation 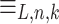 is greater than
is greater than  for some k and n, there would be two words
for some k and n, there would be two words 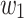 and
and 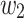 such that they are in different equivalence classes and have all the same mappings. This is a contradiction.
such that they are in different equivalence classes and have all the same mappings. This is a contradiction. 
Theorem 5
Let 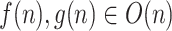 and
and 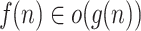 . Then
. Then  .
.
Proof
Consider the language family 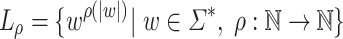 . Note that
. Note that 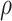 is assumed to be a non-decreasing function and the input length
is assumed to be a non-decreasing function and the input length 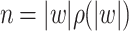 . Inputs consist of repetitions of a substring w. Define
. Inputs consist of repetitions of a substring w. Define  for all
for all 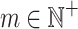 . Depending on the choice of
. Depending on the choice of 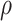 ,
, 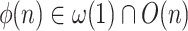 . We will give three lemmas. Two of them show a hierarchy for the range
. We will give three lemmas. Two of them show a hierarchy for the range 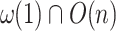 and the last one is to put the
and the last one is to put the 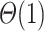 in.
in.
Lemma 2
 .
.
Since given the input length n and the function 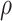 we can deduct the period of input, we can check a position of the repeating substring w for each pass. Therefore our machine will need
we can deduct the period of input, we can check a position of the repeating substring w for each pass. Therefore our machine will need 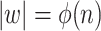 many passes.
many passes.
The advice strings are of the form (parentheses are meta-characters),
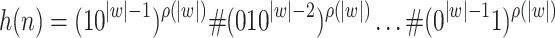 |
Our machine will first search for the first 1 on advice tape and when it has been found, the machine saves the corresponding input character in its states and continue searching for the next 1. When it sees the next 1 it checks the corresponding input character with the one it saved before. If they mismatch input is rejected. The machine then continue searching for 1s and do the same checking till the end of the first pass. It then start with the second pass and do the same procedure again, checking the equality of next character position in substring w. If the endmarker of advice is reached, input is accepted.
Lemma 3
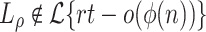 .
.
Observe that any  is prefix-sensitive. Thinking each word as concatenation of first period w and the rest, in other words selecting k to be
is prefix-sensitive. Thinking each word as concatenation of first period w and the rest, in other words selecting k to be 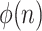 for all n,
for all n, 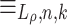 has
has 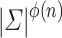 equivalence classes. According to the Lemma 1,
equivalence classes. According to the Lemma 1, 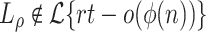 .
.
Lemma 4
No prefix-sensitive language is in 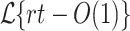 .
.
According to the Lemma 1, for any language 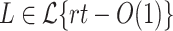 ,
, 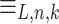 has
has 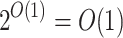 equivalence classes. Therefore according to Theorem 1, L is not prefix sensitive.
equivalence classes. Therefore according to Theorem 1, L is not prefix sensitive. 
Theorem 6
Let  and
and 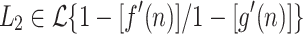 . Then
. Then 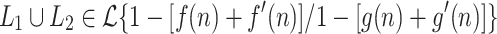 .
.
Proof
Let 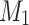 ,
, 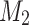 be machines recognizing languages
be machines recognizing languages  ,
,  with the help of advice functions
with the help of advice functions  and
and  respectively. Devise a new advice function,
respectively. Devise a new advice function,
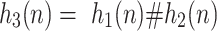 |
for all n where  is a brand new advice character that occurs nowhere else. Let
is a brand new advice character that occurs nowhere else. Let 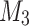 be the machine recognizing the union language with the help of
be the machine recognizing the union language with the help of 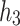 . Machine
. Machine 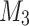 first simulates the
first simulates the  and during this simulation it treats the
and during this simulation it treats the 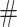 character in advice as an endmarker. When this simulation ends, which may take at most f(n) passes over the input,
character in advice as an endmarker. When this simulation ends, which may take at most f(n) passes over the input,  stores the result in its states and start simulating
stores the result in its states and start simulating 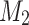 after adjusting its heads to proper positions, that is input head to the beginning and advice head to the next character after
after adjusting its heads to proper positions, that is input head to the beginning and advice head to the next character after 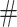 . After at most
. After at most 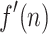 passes over the input, it completes the execution and store the result in its states. In this way it may end up in 4 different states for 4 possible acceptance status of
passes over the input, it completes the execution and store the result in its states. In this way it may end up in 4 different states for 4 possible acceptance status of 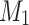 and
and 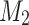 . Via combining some of those states into the accept state and the rest into the reject state; union, intersection or difference of
. Via combining some of those states into the accept state and the rest into the reject state; union, intersection or difference of 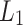 and
and 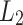 are all recognizable.
are all recognizable. 
Corollary 2
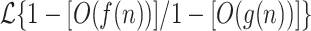 is closed under union and intersection.
is closed under union and intersection.
Theorem 7
For any function 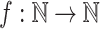 ,
, 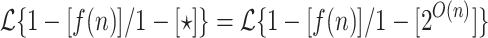 .
.
Proof
The proof is an easy modification of the proof given by Ďuriš et al. for [2, Theorem 3]. 
Theorem 8
For any function 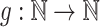 ,
, 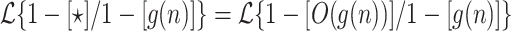 .
.
Proof
Consider the execution of an s-state cdfat with one-way heads. Pausing the advice head, passing on the input more than s times forces the machine to enter an infinite loop. Thus, a machine must advance its advice head before that threshold. Therefore at most sg(n) passes are possible for an execution which eventually halts. 
Theorem 9
For any functions  ,
, 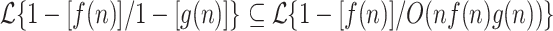 .
.
Proof
It is possible to simulate the one-way advice head with real-time advice head using additional advice. The idea is to replicate each advice character 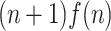 times and use separator characters
times and use separator characters 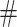 to mark the transition locations. That is, for all n,
to mark the transition locations. That is, for all n,
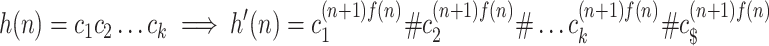 |
where 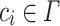 for all
for all 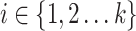 and the
and the 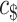 is a new advice character which is for repeating the endmarker (it is not allowed to have more than one real endmarker character). When the new machine reads
is a new advice character which is for repeating the endmarker (it is not allowed to have more than one real endmarker character). When the new machine reads 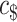 on
on 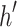 , it behaves exactly like the old machine seeing endmarker on h.
, it behaves exactly like the old machine seeing endmarker on h.
Instead of stay-putting advice head in old machine, let it move right one step in new machine. Instead of moving advice head one step in old machine, enter a subprogram which takes advice head to the next  character in new machine.
character in new machine.
This trick works because a cdfat with one-way heads must forward its advice head within 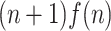 computational steps. This is because without loss of generality we can assume at least one head is moving in each step and of course input head can move at most
computational steps. This is because without loss of generality we can assume at least one head is moving in each step and of course input head can move at most  times in an execution.
times in an execution. 
Corollary 3
For any function 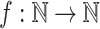 ,
, 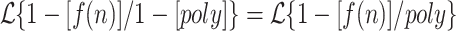 .
.
It is already known that dfat with 2-way input head is equal in power with the prefix advice model when provided with constant advice [5, Theorem 3.8]. Since our model is sandwiched in between the 2-way input model and advice prefix model when it comes to power, we deduce that 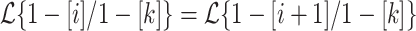 for all
for all  . Therefore an interesting question to ask is what is the minimum advice for which more passes over input enlarges the class of languages recognized. Küçük and others showed that when provided with polynomial advice, 2-way input head is more powerful than 1-way head [6, Theorem 14]. We proved a stronger result and gave an ultimate answer to the aforementioned question. It turns out that even 2 passes over input is more powerful than a single pass when the machine is provided with an increasing advice.
. Therefore an interesting question to ask is what is the minimum advice for which more passes over input enlarges the class of languages recognized. Küçük and others showed that when provided with polynomial advice, 2-way input head is more powerful than 1-way head [6, Theorem 14]. We proved a stronger result and gave an ultimate answer to the aforementioned question. It turns out that even 2 passes over input is more powerful than a single pass when the machine is provided with an increasing advice.
Theorem 10
Let 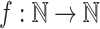 be any function in
be any function in 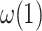 . Then
. Then  .
.
Proof
Consider the language family 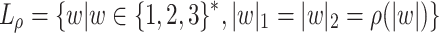 . The following two lemmas establish the proof.
. The following two lemmas establish the proof.
Lemma 5
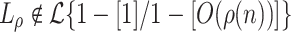 .
.
Proof
Küçük et al. proved that for any advice length function f, if 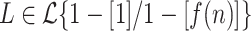 , then for all n and all
, then for all n and all 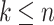 ,
, 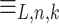 has O(f(n)) equivalence classes, [6, Lemma 6]. It can be shown that for all n, there exists
has O(f(n)) equivalence classes, [6, Lemma 6]. It can be shown that for all n, there exists 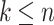 such that
such that 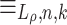 has
has 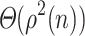 equivalence classes. Since
equivalence classes. Since 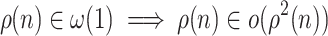 , we conclude that
, we conclude that  .
.
Lemma 6
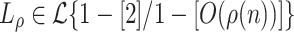 .
.
Proof
The idea is to devise a machine which in first pass counts the character 1 and in second pass counts the character 2. Let 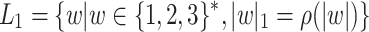 and
and 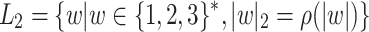 . Observe that
. Observe that 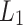 or
or 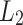 can easily be recognized by a cdfat with a single pass. In order to recognize
can easily be recognized by a cdfat with a single pass. In order to recognize 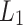 for instance, let
for instance, let 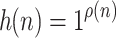 be the advice function, then consider a machine which stay-puts its advice head when it sees a character other than 1 on its input and advances its advice head when it sees 1 on input. It will accept a string iff both endmarkers are read at the same time.
be the advice function, then consider a machine which stay-puts its advice head when it sees a character other than 1 on its input and advances its advice head when it sees 1 on input. It will accept a string iff both endmarkers are read at the same time. 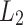 can be recognized similarly. Since
can be recognized similarly. Since 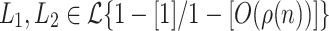 , according to Theorem 6,
, according to Theorem 6, 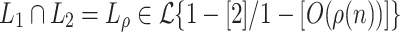 .
. 
Lemma 7
Let  . Then for all n and for all k smaller than n,
. Then for all n and for all k smaller than n, 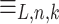 has
has  equivalence classes.
equivalence classes.
Proof
Define a configuration 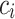 of a machine to be the pair of internal state and advice position. Define a non-stopping configuration
of a machine to be the pair of internal state and advice position. Define a non-stopping configuration 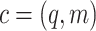 of a machine to be any configuration where q is a state other than accept and reject states. Let
of a machine to be any configuration where q is a state other than accept and reject states. Let 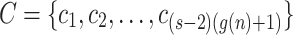 be the set of all non-stopping configurations for a machine and for input length n (
be the set of all non-stopping configurations for a machine and for input length n (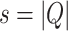 ). Without loss of generality assume our machines always end their execution when input head is on the endmarker. Let w be a substring of input (not containing the endmarker) and let
). Without loss of generality assume our machines always end their execution when input head is on the endmarker. Let w be a substring of input (not containing the endmarker) and let 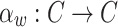 be a mapping which maps the configuration of machine when the first character of word w is read first time on input tape to the configuration of machine when the character right after the word w is read first time on input tape. Function
be a mapping which maps the configuration of machine when the first character of word w is read first time on input tape to the configuration of machine when the character right after the word w is read first time on input tape. Function 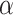 depends on transition function of the machine, the specific word w being processed and the advice content. We focus on a single machine and inputs of the same length n, therefore in our case
depends on transition function of the machine, the specific word w being processed and the advice content. We focus on a single machine and inputs of the same length n, therefore in our case 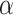 depends only on w.
depends only on w.
Consider execution of a circular machine on two different inputs of length n, namely  and
and 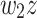 . Both inputs start execution at the initial configuration and after each pass they start with a new configuration. If we can find two words
. Both inputs start execution at the initial configuration and after each pass they start with a new configuration. If we can find two words 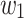 and
and 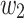 such that
such that 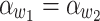 then the two inputs
then the two inputs  and
and 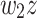 must have the same fate for all z.
must have the same fate for all z.
There are less than 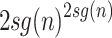 distinct functions
distinct functions 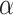 . Assuming that the number of equivalence classes of
. Assuming that the number of equivalence classes of 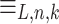 is greater than
is greater than 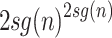 for some k and n, there would be two words
for some k and n, there would be two words 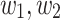 in two different equivalence classes such that they have the same mapping. This is a contradiction.
in two different equivalence classes such that they have the same mapping. This is a contradiction. 
Theorem 11
Let  . Then the classes
. Then the classes 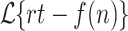 and
and 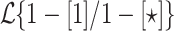 are incomparable.
are incomparable.
Proof
Recall that 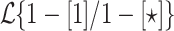 is nothing but our way of notating the class of languages recognized by the model introduced by Küçük et al. in [6] given access to unlimited advice. According to Theorem 5, a prefix-sensitive language is in
is nothing but our way of notating the class of languages recognized by the model introduced by Küçük et al. in [6] given access to unlimited advice. According to Theorem 5, a prefix-sensitive language is in 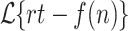 no matter how slow f(n) grows. However we know from Ďuriš et al. [2, Theorem 2] that no prefix-sensitive language is in
no matter how slow f(n) grows. However we know from Ďuriš et al. [2, Theorem 2] that no prefix-sensitive language is in 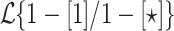 . Therefore
. Therefore 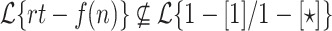 .
.
On the other hand, as stated in proof of Lemma 6, the language 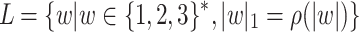 can be easily recognized by a machine with one-way heads, given access to
can be easily recognized by a machine with one-way heads, given access to  length advice. It is easy to see that for all n, there exists k such that
length advice. It is easy to see that for all n, there exists k such that  has
has 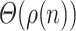 equivalence classes. When the
equivalence classes. When the 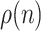 is selected to be linear in n, according to Lemma 1,
is selected to be linear in n, according to Lemma 1, 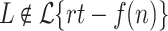 . Therefore
. Therefore 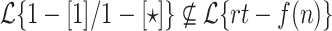 .
. 
An interesting question to ask is what is the minimum advice or pass needed in order for a model to recognize any language. We can show some lower bounds using Lemmas 1 and 7. PAL is the language of even palindromes.
Corollary 4
 .
.
Corollary 5
 .
.
Conclusions and Open Questions
We showed that cdfat with real-time heads can utilize up to linearly many passes over input. We showed that with exponential pass, the real-time machine can recognize any language. However we do not know if the machine can utilize more than linear passes. There may be a clever algorithm for recognizing any language with linear passes.
We showed that even the most powerful version of the cdfat, that is the one having one-way input and advice heads, cannot recognize some languages when there is not enough advice (a nearly linear bound). However we are not aware of an algorithm for this machine which uses less than exponential resources to recognize any language. It would be nice to know the minimum amount of resources needed to recognize any language.
We compared the class of languages recognized by single pass deterministic finite automaton with one-way heads and unlimited advice with the growing class of languages recognized by a real-time cdfat as we allow more passes over input. Since we know that the former class is bigger than the latter when we allow only constant amount of pass over input and the reverse is true when we allow exponential passes over input, we wonder how that growing takes place and is there any pass limit for which the two classes are equal. It turned out that this is not the case. As long as the allowed pass limit is not constant and sub-logarithmic, two classes are not subsets of each other. However we do not know exactly when the latter class encompasses the former one.
Acknowledgements
Thanks to Prof. Cem Say who have helped editing the paper and correcting my mistakes and to my family for their constant support and love.
Contributor Information
Alberto Leporati, Email: alberto.leporati@unimib.it.
Carlos Martín-Vide, Email: carlos.martin@urv.cat.
Dana Shapira, Email: shapird@g.ariel.ac.il.
Claudio Zandron, Email: zandron@disco.unimib.it.
Ahmet Bilal Uçan, Email: ahmet.ucan@boun.edu.tr.
References
- 1.Damm C, Holzer M. Automata that take advice. In: Wiedermann J, Hájek P, editors. Mathematical Foundations of Computer Science 1995; Heidelberg: Springer; 1995. pp. 149–158. [Google Scholar]
- 2.Ďuriš P, Korbaš R, Královič R, Královič R. Determinism and nondeterminism in finite automata with advice. In: Böckenhauer H-J, Komm D, Unger W, editors. Adventures Between Lower Bounds and Higher Altitudes: Essays Dedicated to Juraj Hromkovič on the Occasion of His 60th Birthday. Cham: Springer; 2018. pp. 3–16. [Google Scholar]
- 3.Freivalds R. Amount of nonconstructivity in deterministic finite automata. Theoret. Comput. Sci. 2010;411(38–39):3436–3443. doi: 10.1016/j.tcs.2010.05.038. [DOI] [Google Scholar]
- 4.Karp R, Lipton R. Turing machines that take advice. Enseign. Math. 1982;28:191–209. [Google Scholar]
- 5.Küçük, U.: Finite and small-space automata with advice. Ph.D. thesis, Boğaziçi University (2018)
- 6.Küçük U, Say ACC, Yakaryılmaz A. Finite automata with advice tapes. In: Béal M-P, Carton O, editors. Developments in Language Theory; Heidelberg: Springer; 2013. pp. 301–312. [Google Scholar]
- 7.Tadaki K, Yamakami T, Lin JCH. Theory of one-tape linear-time turing machines. Theoret. Comput. Sci. 2010;411(1):22–43. doi: 10.1016/j.tcs.2009.08.031. [DOI] [Google Scholar]
- 8.Yamakami, T.: Swapping lemmas for regular and context-free languages with advice. CoRR abs/0808.4122 (2008). http://arxiv.org/abs/0808.4122
- 9.Yamakami T. The roles of advice to one-tape linear-time turing machines and finite automata. Int. J. Found. Comput. Sci. 2010;21(6):941–962. doi: 10.1142/S0129054110007659. [DOI] [Google Scholar]
- 10.Yamakami T. Immunity and pseudorandomness of context-free languages. Theoret. Comput. Sci. 2011;412(45):6432–6450. doi: 10.1016/j.tcs.2011.07.013. [DOI] [Google Scholar]
- 11.Yamakami T. One-way reversible and quantum finite automata with advice. In: Dediu A-H, Martín-Vide C, editors. Language and Automata Theory and Applications; Heidelberg: Springer; 2012. pp. 526–537. [Google Scholar]


