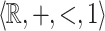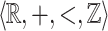Abstract
We show that it is decidable whether or not a relation on the reals definable in the structure 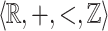 can be defined in the structure
can be defined in the structure 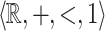 . This result is achieved by obtaining a topological characterization of
. This result is achieved by obtaining a topological characterization of 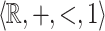 -definable relations in the family of
-definable relations in the family of 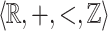 -definable relations and then by following Muchnik’s approach of showing that this characterization can be expressed in the logic of
-definable relations and then by following Muchnik’s approach of showing that this characterization can be expressed in the logic of 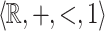 .
.
Introduction
Consider the structure 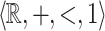 of the additive ordered group of reals along with the constant 1. It is well-known that the subgroup
of the additive ordered group of reals along with the constant 1. It is well-known that the subgroup 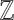 of integers is not first-order-definable. Add the predicate
of integers is not first-order-definable. Add the predicate 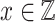 resulting in the structure
resulting in the structure 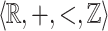 . Our main result shows that given a
. Our main result shows that given a 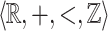 -definable relation it is decidable whether or not it is
-definable relation it is decidable whether or not it is 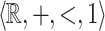 -definable.
-definable.
The structure 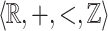 is a privileged area of application of algorithmic verification of properties of reactive and hybrid systems, where logical formalisms involving reals and arithmetic naturally appear, see e.g [1, 4, 13]. It admits quantifier elimination and is decidable as proved independently by Miller [16] and Weisfpfenning [20]. The latter’s proof uses reduction to the theories of
is a privileged area of application of algorithmic verification of properties of reactive and hybrid systems, where logical formalisms involving reals and arithmetic naturally appear, see e.g [1, 4, 13]. It admits quantifier elimination and is decidable as proved independently by Miller [16] and Weisfpfenning [20]. The latter’s proof uses reduction to the theories of 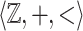 and
and 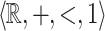 .
.
There are many ways to come across the structure 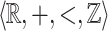 , which highlights its significance. One approach is through automata. Cobham considers a fixed base r and represents integers as finite strings of r digits. A subset X of integers is
, which highlights its significance. One approach is through automata. Cobham considers a fixed base r and represents integers as finite strings of r digits. A subset X of integers is 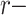 recognizable if there exists a finite automaton accepting precisely the representations in base r of its elements. Cobham’s theorem says that if X is r- and s-recognizable for two multiplicatively independent values r and s (i.e., for all
recognizable if there exists a finite automaton accepting precisely the representations in base r of its elements. Cobham’s theorem says that if X is r- and s-recognizable for two multiplicatively independent values r and s (i.e., for all 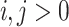 it holds
it holds  ) then X is definable in Presburger arithmetic, i.e., in
) then X is definable in Presburger arithmetic, i.e., in 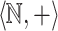 [11, 18]. Conversely, each Presburger-definable subset of
[11, 18]. Conversely, each Presburger-definable subset of 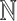 is r-recognizable for every r. This result was extended to integer relations of arbitrary arity by Semënov [19].
is r-recognizable for every r. This result was extended to integer relations of arbitrary arity by Semënov [19].
Consider now recognizability of sets of reals. As early as in 1962 Büchi interprets subsets of integers as characteric functions of reals in their binary representations and shows the decidability of a structure which is essentially an extension of 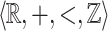 , namely
, namely 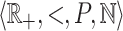 where P if the set of positive powers of 2 and
where P if the set of positive powers of 2 and 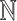 the set of natural numbers [9, Thm 4]. Going one step further Boigelot et al. [7] consider reals as infinite strings of digits and use Muller automata to speak of r-recognizable subsets and more generally of r-recognizable relations of reals. In the papers [3, 5, 6] the equivalence was proved between (1)
the set of natural numbers [9, Thm 4]. Going one step further Boigelot et al. [7] consider reals as infinite strings of digits and use Muller automata to speak of r-recognizable subsets and more generally of r-recognizable relations of reals. In the papers [3, 5, 6] the equivalence was proved between (1) 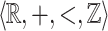 -definability, (2) r- and s-recognizability where the two bases have distinct primes in their factorization [6, Thm 5] and (3) r- and s-weakly recognizability for two independently multiplicative bases, [6, Thm 6] (a relation is r-weakly recognizable if it is recognized by some deterministic Muller automaton in which all states in the same strongly connected component are either final or nonfinal). Consequently, as far as reals are concerned, definability in
-definability, (2) r- and s-recognizability where the two bases have distinct primes in their factorization [6, Thm 5] and (3) r- and s-weakly recognizability for two independently multiplicative bases, [6, Thm 6] (a relation is r-weakly recognizable if it is recognized by some deterministic Muller automaton in which all states in the same strongly connected component are either final or nonfinal). Consequently, as far as reals are concerned, definability in 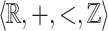 compared to recognizability or weak recognizability by automata on infinite strings can be seen as the analog of Presburger arithmetic for integers compared to recognizability by automata on finite strings.
compared to recognizability or weak recognizability by automata on infinite strings can be seen as the analog of Presburger arithmetic for integers compared to recognizability by automata on finite strings.
A natural issue is to find effective characterizations of subclasses of  recognizable relations. In the case of relations over integers, Muchnik proved that for every base
recognizable relations. In the case of relations over integers, Muchnik proved that for every base  and arity
and arity 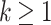 , it is decidable whether a r-recognizable relation
, it is decidable whether a r-recognizable relation 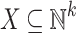 is Presburger-definable [17] (see a different approach in [14] which provides a polynomial time algorithm). For relations over reals, up to our knowledge, the only known result is due to Milchior who proved that it is decidable (in linear time) whether a weakly
is Presburger-definable [17] (see a different approach in [14] which provides a polynomial time algorithm). For relations over reals, up to our knowledge, the only known result is due to Milchior who proved that it is decidable (in linear time) whether a weakly 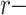 recognizable subset of
recognizable subset of 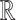 is definable in
is definable in 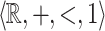 [15]. Our result provides an effective characterization of
[15]. Our result provides an effective characterization of 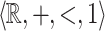 -definable relations within
-definable relations within 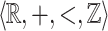 -definable relations. Our approach is inspired by Muchnik’s one, which consists of giving a combinatorical characterization of
-definable relations. Our approach is inspired by Muchnik’s one, which consists of giving a combinatorical characterization of 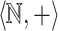 -definable relations that can be expressed in
-definable relations that can be expressed in 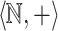 itself.
itself.
Now we give a short outline of our paper. Section 2 gathers all the basic on the two specific structures 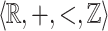 and
and 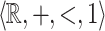 , taking advantage of the existence of quantifier elimination which allows us to work with simpler formulas. Section 3 introduces topological notions. In particular we say that the neighborhood of a point
, taking advantage of the existence of quantifier elimination which allows us to work with simpler formulas. Section 3 introduces topological notions. In particular we say that the neighborhood of a point 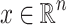 relative to a relation
relative to a relation 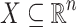 has strata if there exists a direction such that the intersection of all sufficiently small neighborhoods around x with X is the trace of a union of lines parallel to the given direction. This reflects the fact that the relations we work with are defined by finite unions of regions of the spaces delimited by hyperplanes of arbitrary dimension. In Sect. 5 we show that when X is
has strata if there exists a direction such that the intersection of all sufficiently small neighborhoods around x with X is the trace of a union of lines parallel to the given direction. This reflects the fact that the relations we work with are defined by finite unions of regions of the spaces delimited by hyperplanes of arbitrary dimension. In Sect. 5 we show that when X is 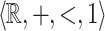 -definable all points (except finitely many which we call singular) have at least one direction which is a stratum. In Sect. 6 we give a necessary and sufficient condition for a
-definable all points (except finitely many which we call singular) have at least one direction which is a stratum. In Sect. 6 we give a necessary and sufficient condition for a 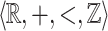 -definable relation to be
-definable relation to be 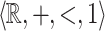 -definable, namely (1) it has finitely many singular points and (2) all intersections of X with arbitrary hyperplanes parallel to
-definable, namely (1) it has finitely many singular points and (2) all intersections of X with arbitrary hyperplanes parallel to 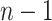 axes and having rational components on the remaining axis are
axes and having rational components on the remaining axis are 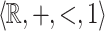 -definable. Then we show that these properties are expressible in
-definable. Then we show that these properties are expressible in 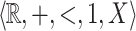 .
.
Preliminaries
Throughout this work we assume the vector space 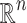 is provided with the metric
is provided with the metric 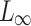 (i.e.,
(i.e., 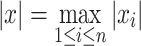 ). The open ball centered at
). The open ball centered at 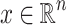 and of radius
and of radius 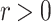 is denoted by B(x, r). Given
is denoted by B(x, r). Given 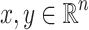 we denote by [x, y] (resp. (x, y)) the closed segment (resp. open segment) with extremities x, y. We use also notations such as [x, y) or (x, y] for half-open segments.
we denote by [x, y] (resp. (x, y)) the closed segment (resp. open segment) with extremities x, y. We use also notations such as [x, y) or (x, y] for half-open segments.
Let us specify our logical conventions and notations. We work within first-order predicate calculus with equality. We confuse formal symbols and their interpretations, except in Sect. 6.2 where the distinction is needed. We are mainly concerned with the structures 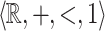 and
and 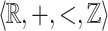 . In the latter structure,
. In the latter structure, 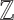 should be understood as a unary predicate which is satisfied only by elements of
should be understood as a unary predicate which is satisfied only by elements of 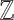 - in other words, we deal only with one-sorted structures. Given a structure
- in other words, we deal only with one-sorted structures. Given a structure 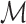 with domain D and
with domain D and 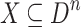 , we say that X is
, we say that X is 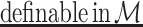 , or
, or 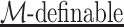 , if there exists a formula
, if there exists a formula 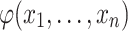 in the signature of
in the signature of 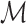 such that
such that 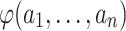 holds in
holds in 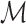 if and only if
if and only if 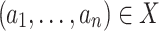 .
.
The 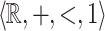 -theory admits quantifier elimination in the following way, which can be interpreted geometrically as saying that a
-theory admits quantifier elimination in the following way, which can be interpreted geometrically as saying that a 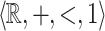 -definable relation is a finite union of closed and open polyhedra.
-definable relation is a finite union of closed and open polyhedra.
Theorem 1
[12, Thm 1]. Every formula in 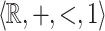 is equivalent to a Boolean combination of inequalities between linear combinations of variables with coefficients in
is equivalent to a Boolean combination of inequalities between linear combinations of variables with coefficients in 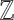 (or, equivalently, in
(or, equivalently, in 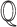 ).
).
In particular in the unary case, the definable subsets are finite unions of intervals whose endpoints are rational numbers, which shows that 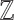 is not
is not 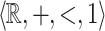 -definable.
-definable.
In the larger structure 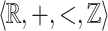 it is possible to separate the integer (superscript ‘I’) and fractional (superscript ‘F’) parts of the reals as follows.
it is possible to separate the integer (superscript ‘I’) and fractional (superscript ‘F’) parts of the reals as follows.
Theorem 2
[8, 6, p. 7]. Let 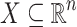 be definable in
be definable in 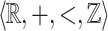 . Then there exists a unique finite union
. Then there exists a unique finite union
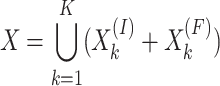 |
1 |
where
the relations
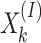 are pairwise disjoint subsets of
are pairwise disjoint subsets of 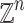 and are
and are  -definable
-definablethe relations
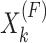 are distinct subsets of
are distinct subsets of 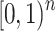 and are
and are 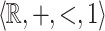 -definable
-definable
There is again a geometric interpretation of 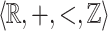 -definable relations as a regular (in a precise technical way) tiling of the space by a finite number of tiles which are themselves finite unions of polyhedra. As a consequence, the restriction of a
-definable relations as a regular (in a precise technical way) tiling of the space by a finite number of tiles which are themselves finite unions of polyhedra. As a consequence, the restriction of a 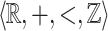 -definable relation to a bounded subset is
-definable relation to a bounded subset is 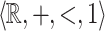 -definable as stated in the following lemma.
-definable as stated in the following lemma.
Lemma 1
For every 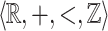 -definable relation
-definable relation  , its restriction to a bounded domain
, its restriction to a bounded domain 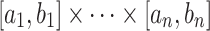 where the
where the 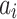 ’s and the
’s and the 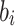 ’s are rationals, is
’s are rationals, is 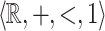 -definable.
-definable.
By considering the restriction of the 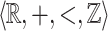 -relation to a ball containing all possible tiles with their closest neighbors, we get that the neighborhoods of
-relation to a ball containing all possible tiles with their closest neighbors, we get that the neighborhoods of 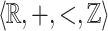 - and
- and 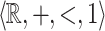 -definable relations are indistinguishable.
-definable relations are indistinguishable.
Lemma 2
For every 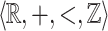 -definable relation
-definable relation 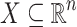 there exists a
there exists a 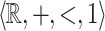 -definable relation
-definable relation 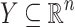 such that for all
such that for all 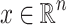 there exists
there exists 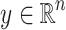 and a real
and a real 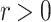 such that the translation
such that the translation 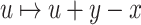 is a one-to-one mapping between
is a one-to-one mapping between 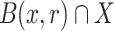 and
and 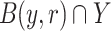 .
.
Strata
The aim is to decide, given 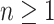 and a
and a 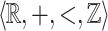 -definable relation
-definable relation 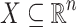 , whether X is
, whether X is 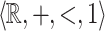 -definable. Though the relations defined in the two structures have very specific properties we define properties that make sense in a setting as general as possible. The following clearly defines an equivalence relation.
-definable. Though the relations defined in the two structures have very specific properties we define properties that make sense in a setting as general as possible. The following clearly defines an equivalence relation.
Definition 1
Given 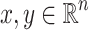 we write
we write  or simply
or simply 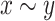 when X is understood, if there exists a real
when X is understood, if there exists a real 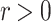 such that the translation
such that the translation 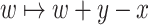 is a one-to-one mapping from
is a one-to-one mapping from 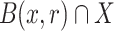 onto
onto 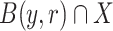 .
.
Example 1
Consider a closed subset of the plane delimited by a square. There are 10 equivalence classes: the set of points interior to the square, the set of points interior to its complement, the four vertices and the four open edges.
Definition 2
Given a non-zero vector
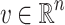 and a point
and a point 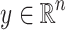 we denote by
we denote by 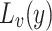 the line passing through y in the direction v. More generally, if
the line passing through y in the direction v. More generally, if 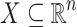 we denote by
we denote by 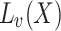 the set
the set 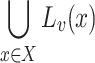 .
.- A non-zero vector
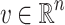 is an X-stratum at x (or simply a stratum when X is understood) if there exists a real
is an X-stratum at x (or simply a stratum when X is understood) if there exists a real 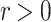 such that
such that
This can be seen as saying that inside the ball B(x, r), the relation X is a union of lines parallel to v.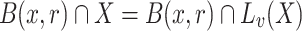
2 The set of X-strata at x is denoted by
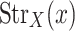 , or simply
, or simply 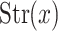 .
.
Proposition 1
For all 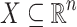 and
and 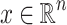 the set Str(x) is either empty or a (vector) subspace of
the set Str(x) is either empty or a (vector) subspace of 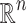 .
.
Definition 3
The dimension dim(x) of a point 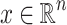 is the dimension of the subspace
is the dimension of the subspace 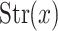 if
if 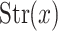 is nonempty or 0 otherwise.
is nonempty or 0 otherwise.
Definition 4
Given a relation 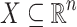 , a point
, a point 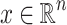 is X-singular, or simply singular, if
is X-singular, or simply singular, if 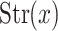 is empty, otherwise it is nonsingular.
is empty, otherwise it is nonsingular.
Note that non-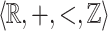 -definable relations may have no singular points: consider in the plane the collection of vertical lines at abscissa
-definable relations may have no singular points: consider in the plane the collection of vertical lines at abscissa  for all positive integers n. In this case any vertical vector is a stratum.
for all positive integers n. In this case any vertical vector is a stratum.
Now it can be shown that all strata at x can be defined by a common value r in expression (2).
Proposition 2
If Str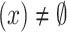 then there exists a real
then there exists a real 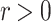 such that for every
such that for every 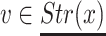 we have
we have
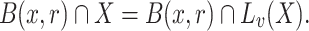 |
Definition 5
A safe radius (for x) is a real 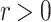 satisfying the condition of Proposition 2. Clearly if r is safe then so are all
satisfying the condition of Proposition 2. Clearly if r is safe then so are all 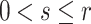 . By convention every real is a safe radius if
. By convention every real is a safe radius if 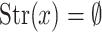 .
.
Example 2
(Example 1 continued). For an element x of the interior of the square or the interior of its complement, let r be the (minimal) distance from x to the edges of the square. Then r is safe for x. If x is a vertex then 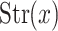 is empty and every
is empty and every 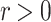 is safe for x. In all other cases r is the minimal distance of x to a vertex.
is safe for x. In all other cases r is the minimal distance of x to a vertex.
Lemma 3
If 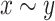 then Str(x) = Str(y).
then Str(x) = Str(y).
The converse of Lemma 3 is false in general. Indeed consider e.g. 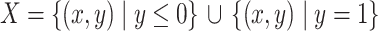 in
in 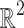 . The points (0, 0) and (0, 1) have the same subspace of strata, namely that generated by (1, 0), but
. The points (0, 0) and (0, 1) have the same subspace of strata, namely that generated by (1, 0), but 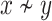 .
.
Now we combine the notions of strata and of safe radius.
Lemma 4
Let 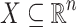 ,
, 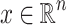 and r be a safe radius for x. Then for all
and r be a safe radius for x. Then for all 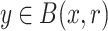 we have
we have 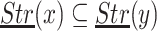 .
.
Example 3
(Example 1 continued). Consider a point x on an (open) edge of the square and a safe radius r. For every point y in B(x, r) which is not on the edge we have 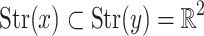 . For all other points we have
. For all other points we have 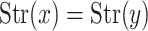 .
.
We relativize the notion of singularity and strata to an affine subspace 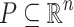 . The next definition should come as no surprise.
. The next definition should come as no surprise.
Definition 6
Given an affine subspace 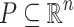 , a subset
, a subset 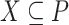 and a point
and a point 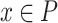 , we say that a vector v parallel to P is an (X, P)-stratum for the point
x if for all sufficiently small
, we say that a vector v parallel to P is an (X, P)-stratum for the point
x if for all sufficiently small 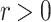 it holds
it holds
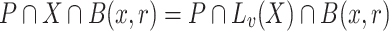 |
A point 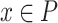 is (X, P)-singular if it has no (X, P)-stratum. For simplicity when P is the space
is (X, P)-singular if it has no (X, P)-stratum. For simplicity when P is the space 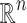 we will still stick to the previous terminology and speak of X-strata and X-singular points.
we will still stick to the previous terminology and speak of X-strata and X-singular points.
Singularity and nonsingularity do not go through restriction to affine subpaces.
Example 4
In the real plane, let 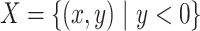 and P be the line
and P be the line 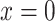 . Then the origin is not
. Then the origin is not 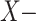 singular but it is
singular but it is 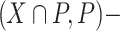 singular. All other elements of P admit (0, 1) as an
singular. All other elements of P admit (0, 1) as an 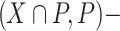 stratum thus they are not
stratum thus they are not 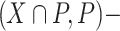 singular. The opposite situation may occur. In the real plane, let
singular. The opposite situation may occur. In the real plane, let  where
where 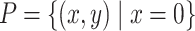 . Then the origin is
. Then the origin is 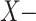 singular but it is not
singular but it is not 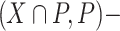 singular.
singular.
Local Properties
Local Neighborhoods
In this section we recall that if 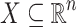 is
is 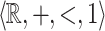 -definable then the equivalence relation
-definable then the equivalence relation 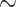 (introduced in Definition 1) has finite index. This extends easily to the case where X is
(introduced in Definition 1) has finite index. This extends easily to the case where X is 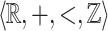 -definable.
-definable.
We modify the usual notion of cones so that it suits better our purposes.
Definition 7
A cone is an intersection of finitely many halfspaces defined by a condition of the form 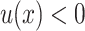 or
or 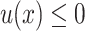 where u is a linear expression having rational coefficients. The origin of the space is thus an apex of the cone.
where u is a linear expression having rational coefficients. The origin of the space is thus an apex of the cone.
In particular a point, the empty set and the whole space are specific cones in our sense (on the real line they can be described respectively by  ,
, 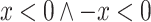 and
and 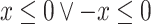 ). By convention, the origin is an apex of the empty set.
). By convention, the origin is an apex of the empty set.
By paraphrasing [2, Thm 1] where “face” means “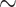 -equivalence class” in our terminology we have.
-equivalence class” in our terminology we have.
Proposition 3
Consider an 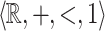 -definable relation X. There exists a finite collection
-definable relation X. There exists a finite collection 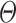 of
of  -formulas defining finite unions of cones such that for all
-formulas defining finite unions of cones such that for all 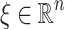 there exist some
there exist some 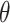 in
in 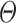 and some real
and some real 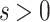 such that for all
such that for all 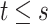 we have
we have
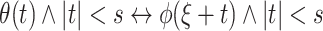 |
3 |
Corollary 1
Let 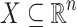 be
be 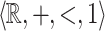 -definable.
-definable.
The equivalence relation
 has finite index.
has finite index.The set
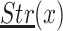 is finite when x runs over
is finite when x runs over 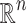 .
.- There exists a fixed finite collection
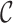 of cones (in the sense of Definition 7) such that for each
of cones (in the sense of Definition 7) such that for each 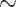 -class E there exists a subset
-class E there exists a subset 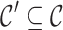 such that for every
such that for every 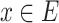 there exists
there exists 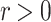 such that
such that 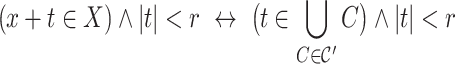
Because of Lemma 2 we have
Corollary 2
The statements of Corollary 1 extend to the case where X is 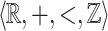 -definable.
-definable.
Combining Corollaries 1 and 2 allows us to specify properties of singular points for 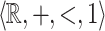 - and
- and 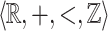 -definable relations.
-definable relations.
Proposition 4
Let 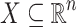 . If X is
. If X is 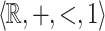 -definable then it has finitely many singular points and their components are rational numbers. If X is
-definable then it has finitely many singular points and their components are rational numbers. If X is 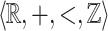 -definable then it has a countable number of singular points and their components are rational numbers.
-definable then it has a countable number of singular points and their components are rational numbers.
Application: Expressing the Singularity of a Point in a 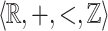 -Definable Relation
-Definable Relation
The singularity of a point x is defined as the property that no intersection of X with a ball centered at x is a union of lines parallel with a given direction. This property is not directly expressible within 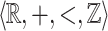 since the natural way would be to use multiplication on reals, which is not
since the natural way would be to use multiplication on reals, which is not 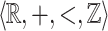 -definable. In order to be able to express the property, we give an alternative characterization of singularity which relies on the assumption that X is
-definable. In order to be able to express the property, we give an alternative characterization of singularity which relies on the assumption that X is 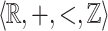 -definable.
-definable.
Lemma 5
Given an 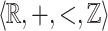 -definable relation
-definable relation  and
and 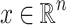 the following two conditions are equivalent:
the following two conditions are equivalent:
x is singular.
for all
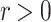 , there exists
, there exists 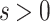 such that for all vectors v of norm less than s, there exist two points
such that for all vectors v of norm less than s, there exist two points 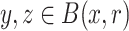 such that
such that 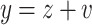 and
and 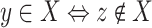 .
.
Observe that when X is not 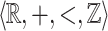 -definable, then the two assertions are no longer equivalent. E.g.,
-definable, then the two assertions are no longer equivalent. E.g.,  has only singular points but condition 2 holds for no point in
has only singular points but condition 2 holds for no point in 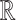 .
.
Relations Between Neighborhoods
We illustrate the purpose of this section with a very simple example. We start with a cube sitting in the horizontal plane with only one face visible. The rules of the game is that we are given a finite collection of vectors such that for all 6 faces and all 12 edges it is possible to choose vectors that generate the vectorial subspace of the smallest affine subspace in which they live. Let the point at the center of the upper face move towards the observer (assuming that this direction belongs to the initial collection). It will eventually hit the upper edge of the visible face. Now let the point move to the left along the edge (this direction necessarily exists because of the assumption on the collection). The point will hit the upper left vertex. Consequently, in the trajectory the point visits three different 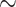 -classes: that of the points on the open upper face, that of the points on the open edge and that of the upper left vertex. Here we investigate the adjacency of such equivalence classes having decreasing dimensions. Observe that another finite collection of vectors may have moved the point from the center of the upper face directly to the upper left vertex.
-classes: that of the points on the open upper face, that of the points on the open edge and that of the upper left vertex. Here we investigate the adjacency of such equivalence classes having decreasing dimensions. Observe that another finite collection of vectors may have moved the point from the center of the upper face directly to the upper left vertex.
Since two 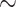 -equivalent points either have no stratum or the same subspace of strata, given a
-equivalent points either have no stratum or the same subspace of strata, given a 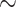 -class E it makes sense to denote by
-class E it makes sense to denote by 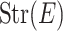 the empty set in the first case and the common subspace of all points in E in the latter case. Similarly, dim(E) is the common dimension of the points in E.
the empty set in the first case and the common subspace of all points in E in the latter case. Similarly, dim(E) is the common dimension of the points in E.
Compatibility
The above explanation should help the reader understand the following definition by considering the backwards trajectory: the point passes from an 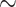 -equivalence class of low dimension into an
-equivalence class of low dimension into an 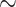 -equivalence class of higher dimension along a direction that is proper to this latter class. This leads to the notion of compatibility. For technical reasons we allow a class to be compatible with itself.
-equivalence class of higher dimension along a direction that is proper to this latter class. This leads to the notion of compatibility. For technical reasons we allow a class to be compatible with itself.
Definition 8
Let E be a nonsingular 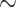 -class and let v be one of its strata. Given a
-class and let v be one of its strata. Given a 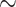 -class F, a point
-class F, a point 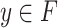 is compatible with
E if there exists
is compatible with
E if there exists 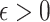 such that for all
such that for all 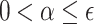 we have
we have 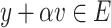 .
.
A 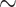 -class F is v-compatible with
E if there exists a point
-class F is v-compatible with
E if there exists a point 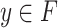 which is v-compatible with E.
which is v-compatible with E.
Lemma 6
Given a 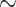 -class F and a vector
-class F and a vector 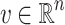 there exists at most one
there exists at most one 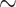 -class E such that F is v-compatible with E. If F is v-compatible with E, all elements of F are v-compatible with E.
-class E such that F is v-compatible with E. If F is v-compatible with E, all elements of F are v-compatible with E.
Observe that for any nonsingular 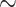 -class E and one of its strata v there always exists a
-class E and one of its strata v there always exists a 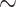 -class v-compatible with E, namely E itself, but also that conversely there might be different classes v-compatible with E.
-class v-compatible with E, namely E itself, but also that conversely there might be different classes v-compatible with E.
Example 5
Let X be the union of the two axes of the 2-dimensional plane and 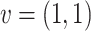 . The different classes are: the complement of X, the origin
. The different classes are: the complement of X, the origin 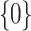 which is a singular point, the horizontal axis deprived of the origin, and the vertical axis deprived of the origin. The two latter
which is a singular point, the horizontal axis deprived of the origin, and the vertical axis deprived of the origin. The two latter 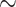 -classes are both
-classes are both 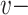 compatible with the class
compatible with the class 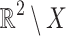 .
.
Intersection of a Line and Equivalence Classes
In this section we describe the intersection of a 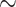 -class E with a line parallel to some
-class E with a line parallel to some 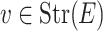 .
.
With the above example of the cube, a line passing through a point x on the upper face along any of the directions of 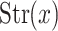 of dimension 2 intersects an open edge or a vertex at point y. In the former case dim
of dimension 2 intersects an open edge or a vertex at point y. In the former case dim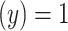 and in the latter dim
and in the latter dim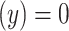 , and in both cases
, and in both cases 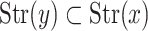 .
.
Lemma 7
Let 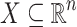 , F, G be two
, F, G be two 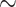 -classes, and
-classes, and 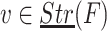 . Let y be an element of G which is adherent to
. Let y be an element of G which is adherent to 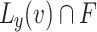 . Then
. Then 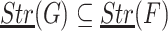 .
.
If F, G are different, then 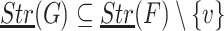 and therefore
and therefore 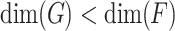 .
.
With the above example of the cube, every point x of a face (which is an open subset on the delimiting affine space supporting the face) is interior to some open segment passing through x, parallel to any direction of the subspace 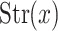 and included in the face. The same observation holds for a point on an open edge of the cube.
and included in the face. The same observation holds for a point on an open edge of the cube.
Lemma 8
Let 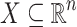 ,
, 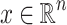 a nonsingular point and
a nonsingular point and 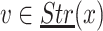 . There exist
. There exist 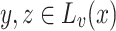 such that
such that 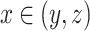 and every element w of (y, z) satisfies
and every element w of (y, z) satisfies 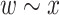 .
.
Corollary 3
Let 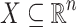 ,
, 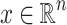 , E its
, E its 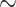 -class and let
-class and let 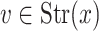 . The set
. The set 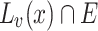 is a union of disjoint open segments (possibly infinite in one or two directions) of
is a union of disjoint open segments (possibly infinite in one or two directions) of 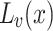 , i.e., of the form
, i.e., of the form 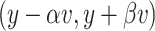 with
with 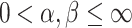 and
and 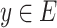 .
.
If 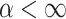 (resp.
(resp. 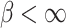 ) then the point
) then the point 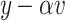 (resp.
(resp. 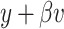 ) belongs to a
) belongs to a 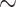 -class
-class 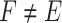 where F is v-compatible (resp.
where F is v-compatible (resp. 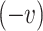 -compatible ) with E, and
-compatible ) with E, and 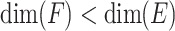 .
.
Corollary 4
Given a nonsingular 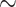 -class E, a point
-class E, a point 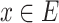 and
and 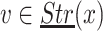 , the intersection of E with the line
, the intersection of E with the line 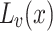 is a union of open segments whose endpoints have dimension (cf. Definition 3) less than that of E.
is a union of open segments whose endpoints have dimension (cf. Definition 3) less than that of E.
Characterization and Effectivity
Characterization of 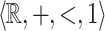 in
in 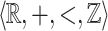
In this section we give the characterization of 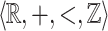 -definable relations which are
-definable relations which are 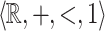 -definable. A rational section of a relation
-definable. A rational section of a relation 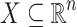 is a relation of the form
is a relation of the form
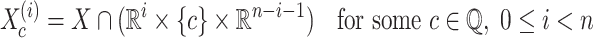 |
Theorem 3
Let 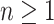 and let
and let 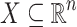 be
be 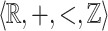 -definable. Then X is
-definable. Then X is 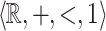 -definable if and only if the following two conditions hold
-definable if and only if the following two conditions hold
There exist finitely many
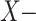 singular points.
singular points.Every rational section of X is
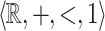 -definable.
-definable.
Observe that both conditions (1) and (2) are needed. Indeed, the relation 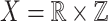 is
is 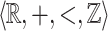 -definable. It has no singular point thus it satisfies condition (1), but does not satisfy (2) since, e.g., the rational section
-definable. It has no singular point thus it satisfies condition (1), but does not satisfy (2) since, e.g., the rational section 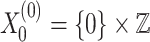 is not
is not 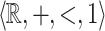 -definable. Now, consider the relation
-definable. Now, consider the relation 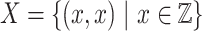 which is
which is 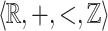 -definable. It does not satisfy condition (1) since every element of X is singular, but it satisfies (2) because every rational section of X is either empty or equal to the singleton
-definable. It does not satisfy condition (1) since every element of X is singular, but it satisfies (2) because every rational section of X is either empty or equal to the singleton 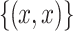 for some
for some 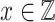 , thus is
, thus is 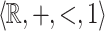 -definable.
-definable.
Now we give an idea of the proof since it cannot fit in the space allowed. The necessity of point 1 follows from Proposition 4. That of point 2 results from the fact that all rational constants are 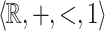 -definable by Theorem 1, and moreover that
-definable by Theorem 1, and moreover that 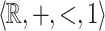 -definable relations are closed under direct product and intersection.
-definable relations are closed under direct product and intersection.
Now the sufficiency. Corollary 4 suggests that we proceed by induction on the dimension of the 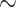 -classes. There are finitely many classes of dimension 0 since there are finitely many singular points so the base of the induction is guaranteed. Now the intersection of a nonsingular class E with a line passing through a point x in the class and parallel to a direction of the class is a finite union of open segments, see Lemma 6. If the segment containing x is closed or half-closed then one of its adherent point belongs to a class F of lower dimension and we can define E relatively to F via the notion of compatibility. However the line may not intersect any other equivalence class. So we consider the canonical subspaces, see below, since every line has an intersection with one of these.
-classes. There are finitely many classes of dimension 0 since there are finitely many singular points so the base of the induction is guaranteed. Now the intersection of a nonsingular class E with a line passing through a point x in the class and parallel to a direction of the class is a finite union of open segments, see Lemma 6. If the segment containing x is closed or half-closed then one of its adherent point belongs to a class F of lower dimension and we can define E relatively to F via the notion of compatibility. However the line may not intersect any other equivalence class. So we consider the canonical subspaces, see below, since every line has an intersection with one of these.
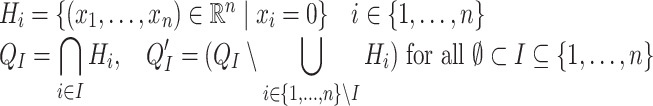 |
4 |
In particular 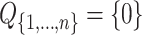 and by convention
and by convention 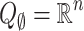 . The
. The 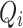 ’s are the canonical subspaces. The
’s are the canonical subspaces. The 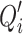 ’s are not vectorial subspaces but with some abuse of language we will write
’s are not vectorial subspaces but with some abuse of language we will write 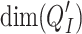 to mean
to mean 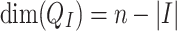 . Observe that point 2 of the theorem implies that for every I the intersection
. Observe that point 2 of the theorem implies that for every I the intersection 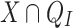 (resp.
(resp. 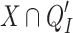 ) is
) is 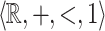 -definable.
-definable.
We consider the finite decomposition of the space consisting of all subsets 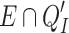 where E is a
where E is a  class and
class and 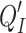 is as in 4. We associate to each subset
is as in 4. We associate to each subset 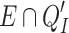 the pair of integers
the pair of integers 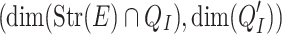 equipped with the product ordering, and we proceed by induction. The result follows from the fact that X is a union of finitely many
equipped with the product ordering, and we proceed by induction. The result follows from the fact that X is a union of finitely many  -classes, since if
-classes, since if 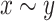 then both x and y belong to X or both belong to its complement.
then both x and y belong to X or both belong to its complement.
The proof can be seen as describing a trajectory starting from a point x in a 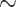 -class E, traveling along a stratum of E until it reaches a class of lower dimension F (by Corollary 4) or some canonical subspace. In the first case it resumes the journey from the new class F on. In the second case it is trapped in the canonical subspace: it resumes the journey by choosing one direction of the subspace until it reaches a new
-class E, traveling along a stratum of E until it reaches a class of lower dimension F (by Corollary 4) or some canonical subspace. In the first case it resumes the journey from the new class F on. In the second case it is trapped in the canonical subspace: it resumes the journey by choosing one direction of the subspace until it reaches a new 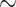 -class or a point belonging to a proper canonical subspace. Along the journey, either the dimension of the new class or the dimension of the canonical subspace decreases. The journey stops when the point reaches a
-class or a point belonging to a proper canonical subspace. Along the journey, either the dimension of the new class or the dimension of the canonical subspace decreases. The journey stops when the point reaches a 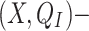 singular point, or the origin which is the least canonical subspace.
singular point, or the origin which is the least canonical subspace.
Decidability
So far we did not distinguish between formal symbols and their interpretations but here we must do it if we want to avoid any confusion. Let 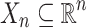 be a relation defined by a
be a relation defined by a 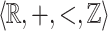 -formula
-formula 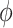 . In order to express that
. In order to express that  is actually
is actually 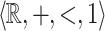 -definable we proceed as follows. Let
-definable we proceed as follows. Let 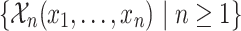 be a collection of relational symbols. We construct a
be a collection of relational symbols. We construct a 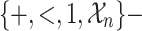 sentence
sentence 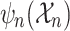 such that
such that 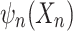 holds if and only
holds if and only 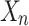 is
is 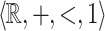 -definable.
-definable.
Proposition 5
Let 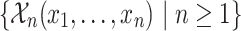 denote a set of relational symbols. For every
denote a set of relational symbols. For every 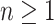 there exists a
there exists a 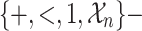 sentence
sentence 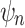 such that for every
such that for every 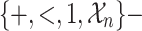 structure
structure 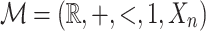 , if
, if 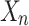 is
is 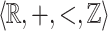 -definable then we have
-definable then we have  if and only if
if and only if 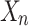 is
is 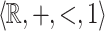 -definable.
-definable.
Sketch. The formula is of the form
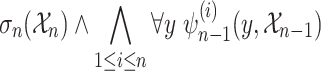 |
5 |
where each  is obtained from
is obtained from 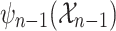 by inserting y at position i in the sequence of variables of the interpretation
by inserting y at position i in the sequence of variables of the interpretation 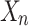 . The conjunct
. The conjunct 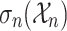 expresses the fact that
expresses the fact that 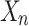 has finitely many singular points (point 1 of Theorem 3) and each conjunct
has finitely many singular points (point 1 of Theorem 3) and each conjunct 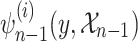 expresses the fact that, interpreting y as a parameter, the section is
expresses the fact that, interpreting y as a parameter, the section is 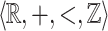 -definable (point 2 of Theorem 3). As an example
-definable (point 2 of Theorem 3). As an example 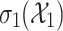 is as follows (the formula is correct only when
is as follows (the formula is correct only when 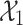 is interpreted as a
is interpreted as a 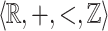 -definable relation)
-definable relation)
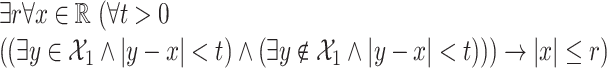 |
Theorem 4
For every 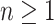 and every
and every 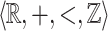 -definable relation
-definable relation 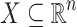 , it is decidable whether X is
, it is decidable whether X is 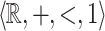 -definable.
-definable.
Proof
In Proposition 5, if we substitute the predicate 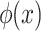 for every occurrence of
for every occurrence of 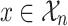 in
in 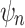 , then
, then 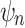 can be interpreted in the structure
can be interpreted in the structure 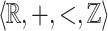 and the decidability of its truth value results from the decidability of
and the decidability of its truth value results from the decidability of 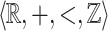 [20].
[20].
Conclusion
We discuss some extensions and open problems. Is it possible to remove our assumption that X is 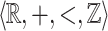 -definable in Theorem 3? We believe that the answer is positive and it can be formally proven in dimension 2. Note that even if one proves such a result, the question of providing an effective characterization is more complex. Indeed the sentence
-definable in Theorem 3? We believe that the answer is positive and it can be formally proven in dimension 2. Note that even if one proves such a result, the question of providing an effective characterization is more complex. Indeed the sentence 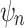 of Proposition 5 expresses a variant of the criterion of Theorem 3, and we use heavily the fact that we work within
of Proposition 5 expresses a variant of the criterion of Theorem 3, and we use heavily the fact that we work within 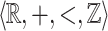 to ensure that this variant is actually equivalent to the criterion. In particular the construction of
to ensure that this variant is actually equivalent to the criterion. In particular the construction of 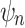 relies on Lemma 5 to express that a point is
relies on Lemma 5 to express that a point is 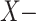 singular. However if we consider e.g.
singular. However if we consider e.g. 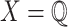 then every element x of X is singular while no element x of X satisfies the condition stated in Lemma 5.
then every element x of X is singular while no element x of X satisfies the condition stated in Lemma 5.
Another question is the following. In Presburger arithmetic it is decidable whether or not a formula is equivalent to a formula in the structure without <, cf. [10]. What about the case where the structure is 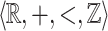 ?
?
Contributor Information
Alberto Leporati, Email: alberto.leporati@unimib.it.
Carlos Martín-Vide, Email: carlos.martin@urv.cat.
Dana Shapira, Email: shapird@g.ariel.ac.il.
Claudio Zandron, Email: zandron@disco.unimib.it.
Alexis Bès, Email: bes@u-pec.fr.
References
- 1.Becker B, Dax C, Eisinger J, Klaedtke F. LIRA: handling constraints of linear arithmetics over the integers and the reals. In: Damm W, Hermanns H, editors. Computer Aided Verification; Heidelberg: Springer; 2007. pp. 307–310. [Google Scholar]
- 2.Bieri H, Nef W. Elementary set operations with d-dimensional polyhedra. In: Noltemeier H, editor. Computational Geometry and its Applications; Heidelberg: Springer; 1988. pp. 97–112. [Google Scholar]
- 3.Boigelot, B., Brusten, J., Bruyère., V.: On the sets of real numbers recognized by finite automata in multiple bases. LMCS 6(1), 1–17 (2010)
- 4.Boigelot, B.: The Liege automata-based symbolic handler (LASH). http://www.montefiore.ulg.ac.be/ boigelot/research/lash/
- 5.Boigelot B, Brusten J. A generalization of Cobham’s theorem to automata over real numbers. Theor. Comput. Sci. 2009;410(18):1694–1703. doi: 10.1016/j.tcs.2008.12.051. [DOI] [Google Scholar]
- 6.Boigelot B, Brusten J, Leroux J. A generalization of Semenov’s theorem to automata over real numbers. In: Schmidt RA, editor. Automated Deduction – CADE-22; Heidelberg: Springer; 2009. pp. 469–484. [Google Scholar]
- 7.Boigelot B, Rassart S, Wolper P. On the expressiveness of real and integer arithmetic automata. In: Larsen KG, Skyum S, Winskel G, editors. Automata, Languages and Programming; Heidelberg: Springer; 1998. pp. 152–163. [Google Scholar]
- 8.Bouchy, F., Finkel, A., Leroux, J.: Decomposition of decidable first-order logics over integers and reals. In: 2008 15th International Symposium on Temporal Representation and Reasoning, pp. 147–155. IEEE (2008)
- 9.Büchi, J.R.: On a decision method in the restricted second-order arithmetic. In: Proceedings International Congress Logic, Methodology and Philosophy of Science, Berkeley 1960, pp. 1–11. Stanford University Press (1962)
- 10.Choffrut C, Frigeri A. Deciding whether the ordering is necessary in a Presburger formula. DMTCS. 2010;12(1):20–38. [Google Scholar]
- 11.Cobham A. On the base-dependence of sets of numbers recognizable by finite automata. Math. Syst. Theor. 1969;3(2):186–192. doi: 10.1007/BF01746527. [DOI] [Google Scholar]
- 12.Ferrante J, Rackoff C. A decision procedure for the first order theory of real addition with order. SIAM J. Comput. 1975;4(1):69–76. doi: 10.1137/0204006. [DOI] [Google Scholar]
- 13.Fränzle, M., Quaas, K., Shirmohammadi, M., Worrell, J.: Effective definability of the reachability relation in timed automata. Inf. Proc. Lett. 153, 105871 (2020)
- 14.Leroux, J.: A polynomial time Presburger criterion and synthesis for number decision diagrams. In: Proceedings of LICS 2005, pp. 147–156. IEEE (2005)
- 15.Milchior A. Büchi automata recognizing sets of reals definable in first-order logic with addition and order. In: Gopal TV, Jäger G, Steila S, editors. Theory and Applications of Models of Computation; Cham: Springer; 2017. pp. 440–454. [Google Scholar]
- 16.Miller C. Expansions of dense linear orders with the intermediate value property. J. Symb. Logic. 2001;66(4):1783–1790. doi: 10.2307/2694974. [DOI] [Google Scholar]
- 17.Muchnik AA. The definable criterion for definability in Presburger arithmetic and its applications. Theor. Comput. Sci. 2003;290(3):1433–1444. doi: 10.1016/S0304-3975(02)00047-6. [DOI] [Google Scholar]
- 18.Presburger, M.: Uber die vollstandigkeit eines gewissen systems der arithmetic ganzer zahlen, in welchem die addition als einzige operation hervortritt. In: du Premier Congrès des Mathématiciens des Pays Slaves, Warsaw, vol. 395, pp. 92–101 (1927)
- 19.Semenov AL. Presburgerness of predicates regular in two number systems. Siberian Math. J. 1977;18(2):289–300. doi: 10.1007/BF00967164. [DOI] [Google Scholar]
- 20.Weispfenning, V.: Mixed real-integer linear quantifier elimination. In: Proceedings of the 1999 International Symposium on Symbolic and Algebraic Computation, ISSAC 1999, pp. 129–136. ACM, New York (1999)