Abstract
The model of programs over (finite) monoids, introduced by Barrington and Thérien, gives an interesting way to characterise the circuit complexity class 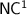 and its subclasses and showcases deep connections with algebraic automata theory. In this article, we investigate the computational power of programs over monoids in
and its subclasses and showcases deep connections with algebraic automata theory. In this article, we investigate the computational power of programs over monoids in  , a small variety of finite aperiodic monoids. First, we give a fine hierarchy within the class of languages recognised by programs over monoids from
, a small variety of finite aperiodic monoids. First, we give a fine hierarchy within the class of languages recognised by programs over monoids from 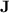 , based on the length of programs but also some parametrisation of
, based on the length of programs but also some parametrisation of  . Second, and most importantly, we make progress in understanding what regular languages can be recognised by programs over monoids in
. Second, and most importantly, we make progress in understanding what regular languages can be recognised by programs over monoids in 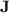 . We show that those programs actually can recognise all languages from a class of restricted dot-depth one languages, using a non-trivial trick, and conjecture that this class suffices to characterise the regular languages recognised by programs over monoids in
. We show that those programs actually can recognise all languages from a class of restricted dot-depth one languages, using a non-trivial trick, and conjecture that this class suffices to characterise the regular languages recognised by programs over monoids in  .
.
Introduction
In computational complexity theory, many hard still open questions concern relationships between complexity classes that are expected to be quite small in comparison to the mainstream complexity class  of tractable languages. One of the smallest such classes is
of tractable languages. One of the smallest such classes is  , the class of languages decided by Boolean circuits of polynomial length, logarithmic depth and bounded fan-in, a relevant and meaningful class, that has many characterisations but whose internal structure still mostly is a mystery. Indeed, among its most important subclasses, we count
, the class of languages decided by Boolean circuits of polynomial length, logarithmic depth and bounded fan-in, a relevant and meaningful class, that has many characterisations but whose internal structure still mostly is a mystery. Indeed, among its most important subclasses, we count 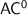 ,
, 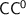 and
and 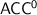 : all of them are conjectured to be different from each other and strictly within
: all of them are conjectured to be different from each other and strictly within 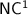 , but despite many efforts for several decades, this could only be proved for the first of those classes.
, but despite many efforts for several decades, this could only be proved for the first of those classes.
In the late eighties, Barrington and Thérien [3], building on Barrington’s celebrated theorem [2], gave an interesting viewpoint on those conjectures, relying on algebraic automata theory. They defined the notion of a program over a monoid M: a sequence of instructions (i, f), associating through function f some element of M to the letter at position i in the input of fixed length. In that way, the program outputs an element of M for every input word, by multiplying out the elements given by the instructions for that word; acceptance or rejection then depends on that outputted element. A language of words of arbitrary length is consequently recognised in a non-uniform fashion, by a sequence of programs over some fixed monoid, one for each possible input length; when that sequence is of polynomial length, it is said that the monoid p-recognises that language. Barrington and Thérien’s discovery is that  and almost all of its significant subclasses can each be exactly characterised by p-recognition over monoids taken from some suitably chosen variety of finite monoids (a class of finite monoids closed under basic operations on monoids). For instance,
and almost all of its significant subclasses can each be exactly characterised by p-recognition over monoids taken from some suitably chosen variety of finite monoids (a class of finite monoids closed under basic operations on monoids). For instance, 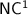 ,
,  ,
,  and
and 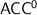 correspond exactly to p-recognition by, respectively, finite monoids, finite aperiodic monoids, finite solvable groups and finite solvable monoids. Understanding the internal structure of
correspond exactly to p-recognition by, respectively, finite monoids, finite aperiodic monoids, finite solvable groups and finite solvable monoids. Understanding the internal structure of  thus becomes a matter of understanding what finite monoids from some particular variety are able to p-recognise.
thus becomes a matter of understanding what finite monoids from some particular variety are able to p-recognise.
It soon became clear that regular languages play a central role in understanding p-recognition: McKenzie, Péladeau and Thérien indeed observed [12] that finite monoids from a variety  and a variety
and a variety  p-recognise the same languages if and only if they p-recognise the same regular languages. Otherwise stated, most conjectures about the internal structure of
p-recognise the same languages if and only if they p-recognise the same regular languages. Otherwise stated, most conjectures about the internal structure of  can be reformulated as a statement about where one or several regular languages lie within that structure. This is why a line of previous works got interested into various notions of tameness, capturing the fact that for a given variety of finite monoids, p-recognition does not offer much more power than classical morphism-recognition when it comes to regular languages (see [8, 10, 11, 13, 14, 20–22]).
can be reformulated as a statement about where one or several regular languages lie within that structure. This is why a line of previous works got interested into various notions of tameness, capturing the fact that for a given variety of finite monoids, p-recognition does not offer much more power than classical morphism-recognition when it comes to regular languages (see [8, 10, 11, 13, 14, 20–22]).
This paper is a contribution to an ongoing study of what regular languages can be p-recognised by monoids taken from “small” varieties, started with the author’s Ph.D. thesis [7]. In a previous paper by the author with McKenzie and Segoufin [8], a novel notion of tameness was introduced and shown for the “small” variety of finite aperiodic monoids 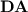 . This allowed them to characterise the class of regular languages p-recognised by monoids from
. This allowed them to characterise the class of regular languages p-recognised by monoids from  as those recognised by so called quasi-
as those recognised by so called quasi-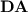 morphisms and represented a first small step towards a new proof that the variety
morphisms and represented a first small step towards a new proof that the variety  of finite aperiodic monoids is tame. This is a statement equivalent to Furst’s, Saxe’s, Sipser’s [6] and Ajtai’s [1] well-known lower bound result about
of finite aperiodic monoids is tame. This is a statement equivalent to Furst’s, Saxe’s, Sipser’s [6] and Ajtai’s [1] well-known lower bound result about  . In [8], the authors also observed that, while
. In [8], the authors also observed that, while 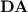 “behaves well” with respect to p-recognition of regular languages, the variety
“behaves well” with respect to p-recognition of regular languages, the variety  , a subclass of
, a subclass of 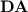 , does, in contrast, “behave badly” in the sense that monoids from
, does, in contrast, “behave badly” in the sense that monoids from 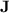 do p-recognise regular languages that are not recognised by quasi-
do p-recognise regular languages that are not recognised by quasi- morphisms.
morphisms.
Now, 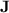 is a well-studied and fundamental variety in algebraic automata theory (see, e.g., [15, 16]), corresponding through classical morphism-recognition to the class of regular languages in which membership depends on the presence or absence of a finite set of words as subwords. This paper is a contribution to the understanding of the power of programs over monoids in
is a well-studied and fundamental variety in algebraic automata theory (see, e.g., [15, 16]), corresponding through classical morphism-recognition to the class of regular languages in which membership depends on the presence or absence of a finite set of words as subwords. This paper is a contribution to the understanding of the power of programs over monoids in 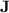 , a knowledge that certainly does not bring us closer to a new proof of the tameness of
, a knowledge that certainly does not bring us closer to a new proof of the tameness of  (as we are dealing with a strict subvariety of
(as we are dealing with a strict subvariety of 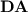 ), but that is motivated by the importance of
), but that is motivated by the importance of 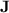 in algebraic automata theory and the unexpected power of programs over monoids in
in algebraic automata theory and the unexpected power of programs over monoids in 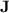 . The results we present in this article are twofold: first, we exhibit a fine hierarchy within the class of languages p-recognised by monoids from
. The results we present in this article are twofold: first, we exhibit a fine hierarchy within the class of languages p-recognised by monoids from  , depending on the length of those programs and on a parametrisation of
, depending on the length of those programs and on a parametrisation of 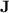 ; second, we show that a whole class of regular languages, that form a subclass of dot-depth one languages [15], are p-recognised by monoids from
; second, we show that a whole class of regular languages, that form a subclass of dot-depth one languages [15], are p-recognised by monoids from 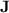 while, in general, they are not recognised by any quasi-
while, in general, they are not recognised by any quasi-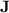 morphism. This class roughly corresponds to dot-depth one languages where detection of a given factor does work only when it does not appear too often as a subword. We actually even conjecture that this class of languages with additional positional modular counting (that is, letters can be differentiated according to their position modulo some fixed number) corresponds exactly to all those p-recognised by monoids in
morphism. This class roughly corresponds to dot-depth one languages where detection of a given factor does work only when it does not appear too often as a subword. We actually even conjecture that this class of languages with additional positional modular counting (that is, letters can be differentiated according to their position modulo some fixed number) corresponds exactly to all those p-recognised by monoids in 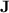 , a statement that is interesting in itself for algebraic automata theory.
, a statement that is interesting in itself for algebraic automata theory.
Organisation of the Paper. Following the present introduction, Sect. 2 is dedicated to the necessary preliminaries. In Sect. 3, we present the results about the fine hierarchy and in Sect. 4 we expose the results concerning the regular languages p-recognised by monoids from 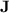 . Section 5 gives a short conclusion.
. Section 5 gives a short conclusion.
Note. This article is based on unpublished parts of the author’s Ph.D. thesis [7].
Preliminaries
Various Mathematical Materials
We assume the reader is familiar with the basics of formal language theory, semigroup theory and recognition by morphisms, that we might designate by classical recognition; for those, we only specify some things and refer the reader to the two classical references of the domain by Eilenberg [4, 5] and Pin [16].
General Notations and Conventions. Let 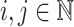 . We shall denote by
. We shall denote by 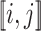 the set of all
the set of all 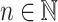 verifying
verifying 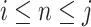 . We shall also denote by [i] the set
. We shall also denote by [i] the set  . Given some set E, we shall denote by
. Given some set E, we shall denote by 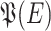 the powerset of E. All our alphabets and words will always be finite; the empty word will be denoted by
the powerset of E. All our alphabets and words will always be finite; the empty word will be denoted by  .
.
Varieties and Languages. A variety of monoids is a class of finite monoids closed under submonoids, Cartesian product and morphic images. A variety of semigroups is defined similarly. When dealing with varieties, we consider only finite monoids and semigroups, each having an idempotent power, a smallest 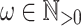 such that
such that  for any element x. To give an example, the variety of finite aperiodic monoids, denoted by
for any element x. To give an example, the variety of finite aperiodic monoids, denoted by  , contains all finite monoids M such that, given
, contains all finite monoids M such that, given  its idempotent power,
its idempotent power, 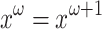 for all
for all  .
.
To each variety 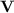 of monoids or semigroups we associate the class
of monoids or semigroups we associate the class  of languages such that, respectively, their syntactic monoid or semigroup belongs to
of languages such that, respectively, their syntactic monoid or semigroup belongs to 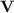 . For instance,
. For instance, 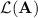 is well-known to be the class of star-free languages.
is well-known to be the class of star-free languages.
Quasi
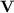 Languages. If S is a semigroup we denote by
Languages. If S is a semigroup we denote by 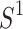 the monoid S if S is already a monoid and
the monoid S if S is already a monoid and  otherwise.
otherwise.
The following definitions are taken from [17]. Let 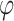 be a surjective morphism from
be a surjective morphism from 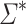 to a finite monoid M. For all k consider the subset
to a finite monoid M. For all k consider the subset  of M (where
of M (where 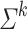 is the set of words over
is the set of words over  of length k). As M is finite there is a k such that
of length k). As M is finite there is a k such that  . This implies that
. This implies that 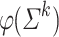 is a semigroup. The semigroup given by the smallest such k is called the stable semigroup of
is a semigroup. The semigroup given by the smallest such k is called the stable semigroup of
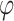 . If S is the stable semigroup of
. If S is the stable semigroup of 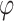 ,
,  is called the stable monoid of
is called the stable monoid of
 . If
. If 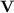 is a variety of monoids or semigroups, then we shall denote by
is a variety of monoids or semigroups, then we shall denote by 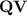 the class of such surjective morphisms whose stable monoid or semigroup, respectively, is in
the class of such surjective morphisms whose stable monoid or semigroup, respectively, is in 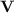 and by
and by 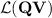 the class of languages whose syntactic morphism is in
the class of languages whose syntactic morphism is in  .
.
Programs over Monoids. Programs over monoids form a non-uniform model of computation, first defined by Barrington and Thérien [3], extending Barrington’s permutation branching program model [2]. Let M be a finite monoid and  an alphabet. A program
P
over
M
on
an alphabet. A program
P
over
M
on
 is a finite sequence of instructions of the form (i, f) where
is a finite sequence of instructions of the form (i, f) where 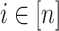 and
and  ; said otherwise, it is a word over
; said otherwise, it is a word over  . The length of P, denoted by
. The length of P, denoted by 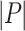 , is the number of its instructions. The program P defines a function from
, is the number of its instructions. The program P defines a function from 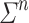 to M as follows. On input
to M as follows. On input  , each instruction (i, f) outputs the monoid element
, each instruction (i, f) outputs the monoid element 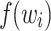 . A sequence of instructions then yields a sequence of elements of M and their product is the output P(w) of the program. A language
. A sequence of instructions then yields a sequence of elements of M and their product is the output P(w) of the program. A language  is consequently recognised by P whenever there exists
is consequently recognised by P whenever there exists 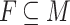 such that
such that  .
.
A language L over 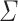 is recognised by a sequence of programs
is recognised by a sequence of programs 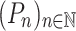 over some finite monoid M if for each n, the program
over some finite monoid M if for each n, the program  is on
is on 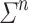 and recognises
and recognises  . We say
. We say  is of length s(n) for
is of length s(n) for  whenever
whenever 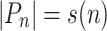 for all
for all 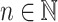 and that it is of length at most s(n) whenever there exists
and that it is of length at most s(n) whenever there exists  verifying
verifying 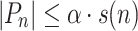 for all
for all 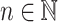 .
.
For 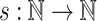 and
and 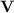 a variety of monoids, we denote by
a variety of monoids, we denote by  the class of languages recognised by sequences of programs over monoids in
the class of languages recognised by sequences of programs over monoids in 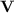 of length at most s(n). The class
of length at most s(n). The class 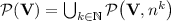 is then the class of languages p-recognised by a monoid in
is then the class of languages p-recognised by a monoid in  , i.e. recognised by sequences of programs over monoids in
, i.e. recognised by sequences of programs over monoids in 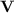 of polynomial length.
of polynomial length.
The following is an important property of  .
.
Proposition 1
([12, Corollary 3.5]). Let 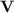 be a variety of monoids, then
be a variety of monoids, then 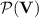 is closed under Boolean operations.
is closed under Boolean operations.
Given two alphabets 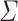 and
and 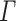 , a
, a 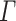 -program on
-program on 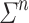 for
for 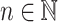 is defined just like a program over some finite monoid M on
is defined just like a program over some finite monoid M on  , except that instructions output letters from
, except that instructions output letters from  and thus that the program outputs words over
and thus that the program outputs words over 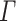 . Let now
. Let now  and
and  . We say that L
program-reduces to
K if and only if there exists a sequence
. We say that L
program-reduces to
K if and only if there exists a sequence 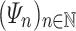 of
of 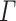 -programs (the program-reduction) such that
-programs (the program-reduction) such that  is on
is on  and
and 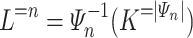 for each
for each 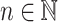 . The following proposition shows closure of
. The following proposition shows closure of 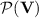 also under program-reductions.
also under program-reductions.
Proposition 2
([7, Proposition 3.3.12 and Corollary 3.4.3]). Let 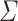 and
and 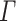 be two alphabets. Let
be two alphabets. Let 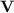 be a variety of monoids. Given
be a variety of monoids. Given 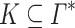 in
in  and
and 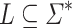 from which there exists a program-reduction to K of length t(n), for
from which there exists a program-reduction to K of length t(n), for  , we have that
, we have that  . In particular, when K is recognised (classically) by a monoid in
. In particular, when K is recognised (classically) by a monoid in  , we have that
, we have that 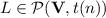 .
.
Tameness and the Variety 
We won’t introduce any of the proposed notions of tameness but will only state that the main consequence for a variety of monoids  to be tame in the sense of [8] is that
to be tame in the sense of [8] is that 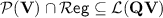 . This consequence has far-reaching implications from a computational-complexity-theoretic standpoint when
. This consequence has far-reaching implications from a computational-complexity-theoretic standpoint when 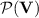 happens to be equal to a circuit complexity class. For instance, tameness for
happens to be equal to a circuit complexity class. For instance, tameness for  implies that
implies that 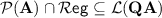 , which is equivalent to the fact that
, which is equivalent to the fact that  does not contain the language
does not contain the language  of words over
of words over  containing a number of 1s not divisible by m for any
containing a number of 1s not divisible by m for any  (a central result in complexity theory [1, 6]).
(a central result in complexity theory [1, 6]).
Let us now define the variety of monoids 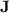 . A finite monoid M of idempotent power
. A finite monoid M of idempotent power  belongs to
belongs to 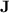 if and only if
if and only if  for all
for all  . It is a strict subvariety of the variety
. It is a strict subvariety of the variety 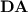 , containing all finite monoids M of idempotent power
, containing all finite monoids M of idempotent power  such that
such that  for all
for all 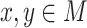 , itself a strict subvariety of
, itself a strict subvariety of  . The variety
. The variety 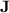 is a “small” one, well within
is a “small” one, well within 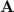 .
.
We now give some specific definitions and results about  that we will use, based essentially on [9], but also on [16, Chapter 4, Section 1].
that we will use, based essentially on [9], but also on [16, Chapter 4, Section 1].
For some alphabet 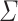 and each
and each  , let us define the equivalence relation
, let us define the equivalence relation 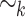 on
on 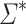 by
by  if and only if u and v have the same set of k-subwords (subwords of length at most k), for all
if and only if u and v have the same set of k-subwords (subwords of length at most k), for all 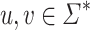 . The relation
. The relation 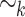 is a congruence of finite index on
is a congruence of finite index on 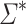 . For an alphabet
. For an alphabet 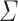 and a word
and a word  , we shall write
, we shall write  for the language of all words over
for the language of all words over  having u as a subword. In the following, we consider that
having u as a subword. In the following, we consider that  has precedence over
has precedence over 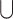 and
and 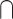 (but of course not over concatenation).
(but of course not over concatenation).
We define the class of piecewise testable languages
 as the class of regular languages such that for every alphabet
as the class of regular languages such that for every alphabet  , we associate to
, we associate to  the set
the set  of all languages over
of all languages over 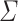 that are Boolean combinations of languages of the form
that are Boolean combinations of languages of the form  where
where 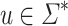 . In fact,
. In fact,  is the set of languages over
is the set of languages over  equal to a union of
equal to a union of 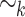 -classes for some
-classes for some  (see [18]). Simon showed [18] that a language is piecewise testable if and only if its syntactic monoid is in
(see [18]). Simon showed [18] that a language is piecewise testable if and only if its syntactic monoid is in  , i.e.
, i.e. 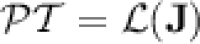 .
.
We can define a hierarchy of piecewise testable languages in a natural way. For  , let the class of
k-piecewise testable languages
, let the class of
k-piecewise testable languages
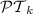 be the class of regular languages such that for every alphabet
be the class of regular languages such that for every alphabet 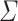 , we associate to
, we associate to 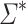 the set
the set 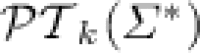 of all languages over
of all languages over  that are Boolean combinations of languages of the form
that are Boolean combinations of languages of the form  where
where 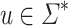 with
with  . We then have that
. We then have that  is the set of languages over
is the set of languages over  equal to a union of
equal to a union of  -classes. Let us define
-classes. Let us define 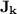 the inclusion-wise smallest variety of monoids containing the quotients of
the inclusion-wise smallest variety of monoids containing the quotients of 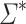 by
by 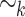 for any alphabet
for any alphabet 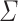 : we have that a language is k-piecewise testable if and only if its syntactic monoid belongs to
: we have that a language is k-piecewise testable if and only if its syntactic monoid belongs to 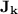 , i.e.
, i.e. 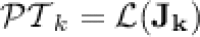 . (See [9, Section 3].)
. (See [9, Section 3].)
Fine Hierarchy
The first part of our investigation of the computational power of programs over monoids in 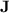 concerns the influence of the length of programs on their computational capabilities.
concerns the influence of the length of programs on their computational capabilities.
We say two programs over a same monoid on the same set of input words are equivalent if and only if they recognise the same languages. Tesson and Thérien proved in [23] that for any monoid M in 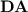 , there exists some
, there exists some 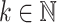 such that for any alphabet
such that for any alphabet  there is a constant
there is a constant 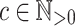 verifying that any program over M on
verifying that any program over M on 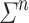 for
for 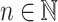 is equivalent to a program over M on
is equivalent to a program over M on  of length at most
of length at most  . Since
. Since 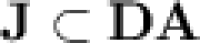 , any monoid in
, any monoid in 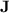 does also have this property. However, this does not imply that there exists some
does also have this property. However, this does not imply that there exists some 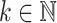 working for all monoids in
working for all monoids in 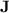 , i.e. that
, i.e. that 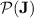 collapses to
collapses to  .
.
In this section, we show on the one hand that, as for 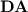 , while
, while 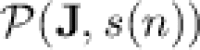 collapses to
collapses to  for any super-polynomial function
for any super-polynomial function 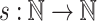 , there does not exist any
, there does not exist any  such that
such that  collapses to
collapses to 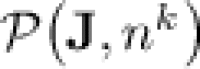 ; and on the other hand that
; and on the other hand that  does optimally collapse to
does optimally collapse to  for each
for each  .
.
Strict Hierarchy
Given  , we say that
, we say that  is a k-selector over
n if
is a k-selector over
n if 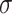 is a function of
is a function of 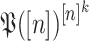 that associates a subset of [n] to each vector in
that associates a subset of [n] to each vector in 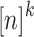 . For any sequence
. For any sequence  such that
such that 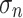 is a k-selector over n for each
is a k-selector over n for each 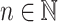 —a sequence we will call a sequence of
k-selectors—, we set
—a sequence we will call a sequence of
k-selectors—, we set  , where for each
, where for each  , the language
, the language  is the set of words over
is the set of words over 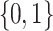 of length
of length 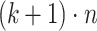 that can be decomposed into
that can be decomposed into 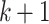 consecutive blocks
consecutive blocks  of n letters where the first k blocks each contain 1 exactly once and uniquely define a vector
of n letters where the first k blocks each contain 1 exactly once and uniquely define a vector  in
in  , where for all
, where for all  ,
,  is given by the position of the only 1 in
is given by the position of the only 1 in 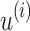 (i.e.
(i.e.  ) and v is such that there exists
) and v is such that there exists 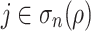 verifying that
verifying that  is 1. Observe that for any k-selector
is 1. Observe that for any k-selector 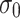 over 0, we have
over 0, we have  .
.
We now proceed similarly to what has been done in Subsection 5.1 in [8] to show, on one hand, that for all  , there is a monoid
, there is a monoid 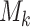 in
in  such that for any sequence of k-selectors
such that for any sequence of k-selectors  , the language
, the language 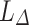 is recognised by a sequence of programs over
is recognised by a sequence of programs over  of length at most
of length at most  ; and, on the other hand, that for all
; and, on the other hand, that for all 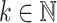 there is a sequence of k-selectors
there is a sequence of k-selectors  such that for any finite monoid M and any sequence of programs
such that for any finite monoid M and any sequence of programs  over M of length at most
over M of length at most  , the language
, the language  is not recognised by
is not recognised by 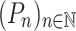 .
.
We obtain the following proposition.
Proposition 3
For all  , we have
, we have  . More precisely, for all
. More precisely, for all 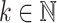 and
and 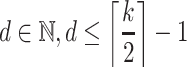 , we have
, we have 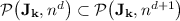 .
.
Collapse
Looking at Proposition 3, it looks at first glance rather strange that, for each 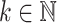 , we can only prove strictness of the hierarchy inside
, we can only prove strictness of the hierarchy inside  up to exponent
up to exponent  . We now show, in a way similar to Subsection 5.2 in [8], that in fact
. We now show, in a way similar to Subsection 5.2 in [8], that in fact 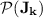 does collapse to
does collapse to  for all
for all  , showing Proposition 3 to be optimal in some sense.
, showing Proposition 3 to be optimal in some sense.
Proposition 4
Let 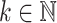 . Let
. Let  and
and 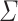 be an alphabet. Then there exists a constant
be an alphabet. Then there exists a constant  such that any program over M on
such that any program over M on 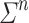 for
for  is equivalent to a program over M on
is equivalent to a program over M on  of length at most
of length at most  .
.
In particular,  for all
for all 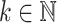 .
.
Regular Languages in 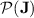
The second part of our investigation of the computational power of programs over monoids in 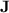 is dedicated to understanding exactly what regular languages can be p-recognised by monoids in
is dedicated to understanding exactly what regular languages can be p-recognised by monoids in 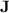 .
.
Non-tameness of 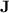
It is shown in [8] that  , thus giving an example of a well-known subvariety of
, thus giving an example of a well-known subvariety of  for which p-recognition allows to do unexpected things when recognising a regular language. How far does this unexpected power go?
for which p-recognition allows to do unexpected things when recognising a regular language. How far does this unexpected power go?
The first thing to notice is that, though none of them is in 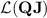 , all languages of the form
, all languages of the form 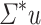 and
and  for
for 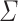 an alphabet and
an alphabet and  are in
are in  . Indeed, each of them can be recognised by a sequence of constant-length programs over the syntactic monoid of
. Indeed, each of them can be recognised by a sequence of constant-length programs over the syntactic monoid of 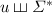 : for every input length, just output the image, through the syntactic morphism of
: for every input length, just output the image, through the syntactic morphism of  , of the word made of the
, of the word made of the  first or last letters. So, informally stated, programs over monoids in
first or last letters. So, informally stated, programs over monoids in  can check for some constant-length beginning or ending of their input words.
can check for some constant-length beginning or ending of their input words.
But they can do much more. Indeed, the language  does not belong to
does not belong to 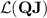 (compute the stable monoid), yet it is in
(compute the stable monoid), yet it is in 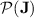 . The crucial insight is that it can be program-reduced in linear length to the piecewise testable language of all words over
. The crucial insight is that it can be program-reduced in linear length to the piecewise testable language of all words over 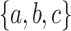 having ca as a subword but not the subwords cca, caa and cb by using the following trick (that we shall call “feedback-sweeping”) for input length
having ca as a subword but not the subwords cca, caa and cb by using the following trick (that we shall call “feedback-sweeping”) for input length 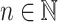 : read the input letters in the order
: read the input letters in the order 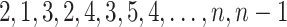 , output the letters read. This has already been observed in [8, Proposition 5].
, output the letters read. This has already been observed in [8, Proposition 5].
Lemma 1
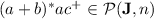 .
.
Using variants of the “feedback-sweeping” reading technique, we can prove that the phenomenon just described is not an isolated case.
Lemma 2
The languages 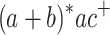 ,
,  ,
, 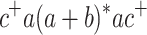 ,
, 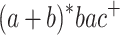 and
and  do all belong to
do all belong to 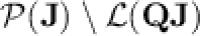 .
.
Hence, we are tempted to say that there are “much more” regular languages in 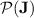 than just those in
than just those in  , even though it is not clear to us whether
, even though it is not clear to us whether  or not. But can we show any upper bound on
or not. But can we show any upper bound on  ? It turns out that we can, relying on two known results.
? It turns out that we can, relying on two known results.
First, since  , we have
, we have  , so Theorem 6 in [8], that states
, so Theorem 6 in [8], that states 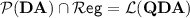 , implies that
, implies that  .
.
Second, let us define an important superclass of the class of piecewise testable languages. Let 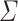 be an alphabet and
be an alphabet and 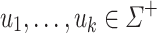 (
( ); we define
); we define  . The class of dot-depth one languages is the class of Boolean combinations of languages of the form
. The class of dot-depth one languages is the class of Boolean combinations of languages of the form  ,
, 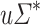 and
and  for
for 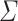 an alphabet,
an alphabet, 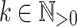 and
and  . The inclusion-wise smallest variety of semigroups containing all syntactic semigroups of dot-depth one languages is denoted by
. The inclusion-wise smallest variety of semigroups containing all syntactic semigroups of dot-depth one languages is denoted by 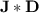 and verifies that
and verifies that  is exactly the class of dot-depth one languages. (See [11, 15, 19].) It has been shown in [11, Corollary 8] that
is exactly the class of dot-depth one languages. (See [11, 15, 19].) It has been shown in [11, Corollary 8] that 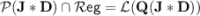 (if we extend the program-over-monoid formalism in the obvious way to finite semigroups). Now, we have
(if we extend the program-over-monoid formalism in the obvious way to finite semigroups). Now, we have  , so that
, so that 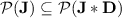 and hence
and hence 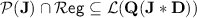 .
.
To summarise, we have the following.
Proposition 5
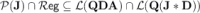 .
.
In fact, we conjecture that the inverse inclusion does also hold.
Conjecture 1
 .
.
Why do we think this should be true? Though, for a given alphabet  , we cannot decide whether some word
, we cannot decide whether some word 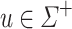 of length at least 2 appears as a factor of any given word w in
of length at least 2 appears as a factor of any given word w in 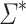 with programs over monoids in
with programs over monoids in 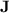 (because
(because  ), Lemma 2 and the possibilities offered by the “feedback-sweeping” technique give the impression that we can do it when we are guaranteed that u appears at most a fixed number of times in w, which seems somehow to be what dot-depth one languages become when restricted to belong to
), Lemma 2 and the possibilities offered by the “feedback-sweeping” technique give the impression that we can do it when we are guaranteed that u appears at most a fixed number of times in w, which seems somehow to be what dot-depth one languages become when restricted to belong to 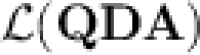 . This intuition motivates the definition of threshold dot-depth one languages.
. This intuition motivates the definition of threshold dot-depth one languages.
Threshold Dot-Depth One Languages
The idea behind the definition of threshold dot-depth one languages is that we take the basic building blocks of dot-depth one languages, of the form  for an alphabet
for an alphabet  , for
, for  and
and  , and restrict them so that, given
, and restrict them so that, given 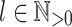 , membership of a word does really depend on the presence of a given word
, membership of a word does really depend on the presence of a given word 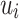 as a factor if and only if it appears less than l times as a subword.
as a factor if and only if it appears less than l times as a subword.
Definition 1
Let 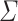 be an alphabet. For all
be an alphabet. For all  and
and  , we define
, we define 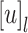 to be the language of words over
to be the language of words over  containing
containing  as a subword or u as a factor, i.e.
as a subword or u as a factor, i.e. 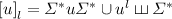 . Then, for all
. Then, for all  (
( ) and
) and  , we define
, we define  .
.
Obviously, for each  an alphabet,
an alphabet,  and
and 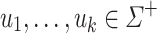 , the language
, the language 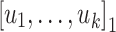 equals
equals 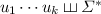 . Over
. Over 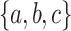 , the language
, the language  contains all words containing a letter c verifying that in the prefix up to that letter, ababab appears as a subword or ab appears as a factor. Finally, the language
contains all words containing a letter c verifying that in the prefix up to that letter, ababab appears as a subword or ab appears as a factor. Finally, the language  over
over  of Lemma 1 is equal to
of Lemma 1 is equal to  .
.
We then define a threshold dot-depth one language as any Boolean combination of languages of the form  ,
, 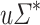 and
and 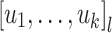 for
for 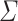 an alphabet, for
an alphabet, for  and
and  .
.
Confirming the intuition briefly given above, the technique of “feedback-sweeping” can indeed be pushed further to prove that the whole class of threshold dot-depth one languages is contained in  , and we dedicate the remainder of this section to prove it. Concerning Conjecture 1, our intuition leads us to believe that, in fact, the class of threshold dot-depth one languages with additional positional modular counting is exactly
, and we dedicate the remainder of this section to prove it. Concerning Conjecture 1, our intuition leads us to believe that, in fact, the class of threshold dot-depth one languages with additional positional modular counting is exactly  . We simply refer the interested reader to Section 5.4 of the author’s Ph.D. thesis [7], that contains a partial result supporting this belief, too technical and long to be presented here.
. We simply refer the interested reader to Section 5.4 of the author’s Ph.D. thesis [7], that contains a partial result supporting this belief, too technical and long to be presented here.
Let us now move on to the proof of the following theorem.
Theorem 1
Every threshold dot-depth one language belongs to 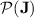 .
.
As 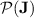 is closed under Boolean operations (Proposition 1), our goal is to prove, given an alphabet
is closed under Boolean operations (Proposition 1), our goal is to prove, given an alphabet 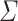 , given
, given 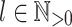 and
and  (
( ), that
), that 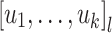 is in
is in 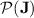 ; the case of
; the case of 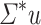 and
and  for
for  is easily handled (see the discussion at the beginning of Subsect. 4.1). To do this, we need to put
is easily handled (see the discussion at the beginning of Subsect. 4.1). To do this, we need to put 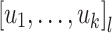 in some normal form. It is readily seen that
in some normal form. It is readily seen that  where the
where the 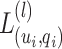 ’s are defined thereafter.
’s are defined thereafter.
Definition 2
Let  be an alphabet.
be an alphabet.
For all  ,
,  and
and 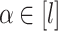 , set
, set 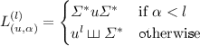 .
.
Building directly a sequence of programs over a monoid in  that decides
that decides  for some alphabet
for some alphabet  and
and 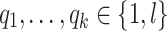 seems however tricky. We need to split things further by controlling precisely how many times each
seems however tricky. We need to split things further by controlling precisely how many times each  for
for 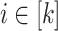 appears in the right place when it does less than l times. To do this, we consider, for each
appears in the right place when it does less than l times. To do this, we consider, for each 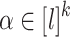 , the language
, the language 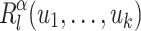 defined below.
defined below.
Definition 3
Let 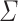 be an alphabet.
be an alphabet.
For all 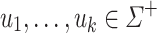 (
( ),
),  ,
, 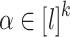 , we set
, we set
Now, for a given  , we are interested in the words of
, we are interested in the words of 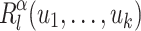 such that for each
such that for each  verifying
verifying 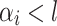 , the word
, the word  indeed appears as a factor in the right place. We thus introduce a last language
indeed appears as a factor in the right place. We thus introduce a last language 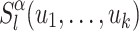 defined as follows.
defined as follows.
Definition 4
Let  be an alphabet.
be an alphabet.
For all  (
(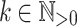 ),
),  ,
, 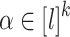 , we set
, we set
We now have the normal form we were looking for to prove Theorem 1: 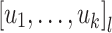 is equal to the union, over all
is equal to the union, over all  , of the intersection of
, of the intersection of 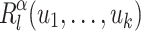 and
and 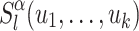 . Though rather intuitive, the correctness of this decomposition is not so straightforward to prove and, actually, we can only prove it when for each
. Though rather intuitive, the correctness of this decomposition is not so straightforward to prove and, actually, we can only prove it when for each 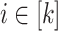 , the letters in
, the letters in 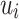 are all distinct.
are all distinct.
Lemma 3
Let  be an alphabet,
be an alphabet, 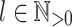 and
and 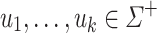 (
( ) such that for each
) such that for each  , the letters in
, the letters in  are all distinct. Then,
are all distinct. Then,
 |
Our goal now is to prove, given an alphabet  , given
, given 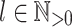 and
and  (
(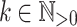 ) such that for each
) such that for each 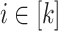 , the letters in
, the letters in 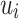 are all distinct, that for any
are all distinct, that for any 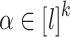 , the language
, the language 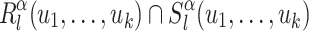 is in
is in  ; closure of
; closure of 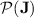 under union (Proposition 1) consequently entails that
under union (Proposition 1) consequently entails that  . The way
. The way 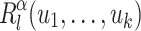 and
and 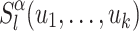 are defined allows us to reason as follows. For each
are defined allows us to reason as follows. For each 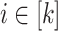 verifying
verifying 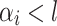 , let
, let 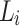 be the language of words w over
be the language of words w over  containing
containing 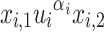 as a subword but not
as a subword but not 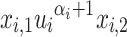 and such that
and such that  with
with 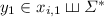 and
and 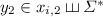 , where
, where 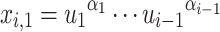 and
and  . If we manage to prove that for each
. If we manage to prove that for each  verifying
verifying 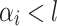 we have
we have  , we can conclude that
, we can conclude that  does belong to
does belong to 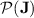 by closure of
by closure of 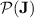 under intersection, Proposition 1. The lemma that follows, the main lemma in the proof of Theorem 1, exactly shows this. The proof crucially uses the “feedback sweeping” technique, but note that we actually don’t know how to prove it when we do not enforce that for each
under intersection, Proposition 1. The lemma that follows, the main lemma in the proof of Theorem 1, exactly shows this. The proof crucially uses the “feedback sweeping” technique, but note that we actually don’t know how to prove it when we do not enforce that for each  , the letters in
, the letters in 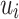 are all distinct.
are all distinct.
Lemma 4
Let 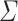 be an alphabet and
be an alphabet and 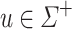 such that its letters are all distinct. For all
such that its letters are all distinct. For all  and
and  , we have
, we have
Proof (Sketch)
Let 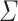 be an alphabet and
be an alphabet and 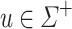 such that its letters are all distinct. Let
such that its letters are all distinct. Let 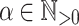 and
and  . We let
. We let
If 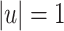 , the lemma follows trivially because L is piecewise testable and hence belongs to
, the lemma follows trivially because L is piecewise testable and hence belongs to  , so we assume
, so we assume  .
.
For each letter  , we shall use
, we shall use  distinct decorated letters of the form
distinct decorated letters of the form  for some
for some 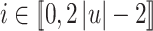 , using the convention that
, using the convention that 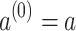 ; of course, for two distinct letters
; of course, for two distinct letters 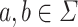 , we have that
, we have that  and
and 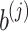 are distinct for all
are distinct for all 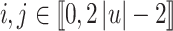 . We denote by A the alphabet of these decorated letters. The main idea of the proof is, for a given input length
. We denote by A the alphabet of these decorated letters. The main idea of the proof is, for a given input length  , to build an A-program
, to build an A-program  over
over 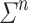 such that, given an input word
such that, given an input word 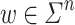 , it first ouputs the
, it first ouputs the 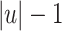 first letters of w and then, for each i going from
first letters of w and then, for each i going from 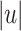 to n, outputs
to n, outputs  , followed by
, followed by 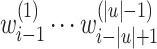 (a “sweep” of
(a “sweep” of 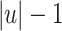 letters backwards down to position
letters backwards down to position  , decorating the letters incrementally) and finally by
, decorating the letters incrementally) and finally by 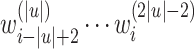 (a “sweep” forwards up to position i, continuing the incremental decoration of the letters). The idea behind this way of rearranging and decorating letters is that, given an input word
(a “sweep” forwards up to position i, continuing the incremental decoration of the letters). The idea behind this way of rearranging and decorating letters is that, given an input word 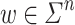 , as long as we make sure that w and thus
, as long as we make sure that w and thus 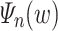 do contain
do contain  as a subword but not
as a subword but not  , then
, then  can be decomposed as
can be decomposed as 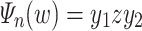 where
where 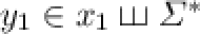 ,
,  , and
, and  are minimal, with z containing
are minimal, with z containing  as a subword for some
as a subword for some 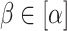 if and only if
if and only if 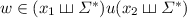 . This means we can check whether
. This means we can check whether 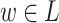 by testing whether w belongs to some fixed piecewise testable language over A.
by testing whether w belongs to some fixed piecewise testable language over A.
As explained before stating the previous lemma, we can now use it to prove the result we were aiming for.
Proposition 6
Let  be an alphabet,
be an alphabet, 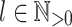 and
and 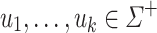 (
(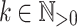 ) such that for each
) such that for each  , the letters in
, the letters in 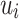 are all distinct. For all
are all distinct. For all 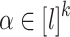 , we have
, we have 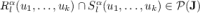 .
.
We thus derive the awaited corollary.
Corollary 1
Let 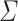 be an alphabet,
be an alphabet, 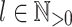 and
and 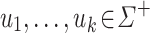 (
( ) such that for each
) such that for each 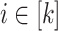 , the letters in
, the letters in  are all distinct. Then,
are all distinct. Then,  .
.
However, what we really want to obtain is that  without putting any restriction on the
without putting any restriction on the  ’s. But, in fact, to remove the constraint that the letters must be all distinct in each of the
’s. But, in fact, to remove the constraint that the letters must be all distinct in each of the 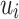 ’s, we simply have to decorate each of the input letters with its position minus 1 modulo a big enough
’s, we simply have to decorate each of the input letters with its position minus 1 modulo a big enough 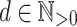 . This finally leads to the following proposition.
. This finally leads to the following proposition.
Proposition 7
Let 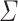 be an alphabet,
be an alphabet,  and
and 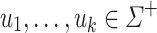 (
(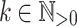 ). Then
). Then 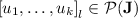 .
.
This finishes to prove Theorem 1 by closure of 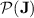 under Boolean combinations (Proposition 1) and by the discussion at the beginning of Subsect. 4.1.
under Boolean combinations (Proposition 1) and by the discussion at the beginning of Subsect. 4.1.
Conclusion
Although  is very small compared to
is very small compared to 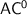 , we have shown that programs over monoids in
, we have shown that programs over monoids in 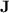 are an interesting subject of study in that they allow to do quite unexpected things. The “feedback-sweeping” technique allows one to detect presence of a factor thanks to such programs as long as this factor does not appear too often as a subword: this is the basic principle behind threshold dot-depth one languages, that our article shows to belong wholly to
are an interesting subject of study in that they allow to do quite unexpected things. The “feedback-sweeping” technique allows one to detect presence of a factor thanks to such programs as long as this factor does not appear too often as a subword: this is the basic principle behind threshold dot-depth one languages, that our article shows to belong wholly to 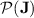 .
.
Whether threshold dot-depth one languages with additional positional modular counting do correspond exactly to the languages in  seems to be a challenging question, that we leave open. In his Ph.D. thesis [7], the author proved that all strongly unambiguous monomials (the basic building blocks in
seems to be a challenging question, that we leave open. In his Ph.D. thesis [7], the author proved that all strongly unambiguous monomials (the basic building blocks in 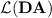 ) that are imposed to belong to
) that are imposed to belong to 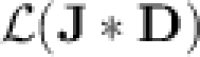 at the same time are in fact threshold dot-depth one languages. However, the proof looks much too complex and technical to be extended to, say, all languages in
at the same time are in fact threshold dot-depth one languages. However, the proof looks much too complex and technical to be extended to, say, all languages in  . New techniques are probably needed, and we might conclude by saying that proving (or disproving) this conjecture could be a nice research goal in algebraic automata theory.
. New techniques are probably needed, and we might conclude by saying that proving (or disproving) this conjecture could be a nice research goal in algebraic automata theory.
Acknowledgements
The author thanks the anonymous referees for their helpful comments and suggestions.
Contributor Information
Alberto Leporati, Email: alberto.leporati@unimib.it.
Carlos Martín-Vide, Email: carlos.martin@urv.cat.
Dana Shapira, Email: shapird@g.ariel.ac.il.
Claudio Zandron, Email: zandron@disco.unimib.it.
Nathan Grosshans, Email: nathan.grosshans@polytechnique.edu, https://www.di.ens.fr/~ngrosshans/.
References
-
1.Ajtai, M.:
 -formulae on finite structures. Ann. Pure Appl. Logic 24(1), 1–48 (1983)
-formulae on finite structures. Ann. Pure Appl. Logic 24(1), 1–48 (1983)
-
2.Barrington DAM. Bounded-width polynomial-size branching programs recognize exactly those languages in NC
 J. Comput. Syst. Sci. 1989;38(1):150–164. doi: 10.1016/0022-0000(89)90037-8. [DOI] [Google Scholar]
J. Comput. Syst. Sci. 1989;38(1):150–164. doi: 10.1016/0022-0000(89)90037-8. [DOI] [Google Scholar] -
3.Barrington DAM, Thérien D. Finite monoids and the fine structure of NC
 J. ACM. 1988;35(4):941–952. doi: 10.1145/48014.63138. [DOI] [Google Scholar]
J. ACM. 1988;35(4):941–952. doi: 10.1145/48014.63138. [DOI] [Google Scholar] - 4.Eilenberg S. Automata, Languages, and Machines. New York: Academic Press; 1974. [Google Scholar]
- 5.Eilenberg S. Automata, Languages, and Machines. New York: Academic Press; 1976. [Google Scholar]
- 6.Furst ML, Saxe JB, Sipser M. Parity, circuits, and the polynomial-time hierarchy. Math. Syst. Theory. 1984;17(1):13–27. doi: 10.1007/BF01744431. [DOI] [Google Scholar]
- 7.Grosshans, N.: The limits of Nečiporuk’s method and the power of programs over monoids taken from small varieties of finite monoids. Ph.D. thesis, University of Paris-Saclay, France (2018)
- 8.Grosshans, N., McKenzie, P., Segoufin, L.: The power of programs over monoids in DA. In: MFCS 2017, Aalborg, Denmark, 21–25 August 2017, pp. 2:1–2:20 (2017)
- 9.Klíma O, Polák L. Hierarchies of piecewise testable languages. Int. J. Found. Comput. Sci. 2010;21(4):517–533. doi: 10.1142/S0129054110007404. [DOI] [Google Scholar]
- 10.Lautemann C, Tesson P, Thérien D. An algebraic point of view on the Crane Beach property. In: Ésik Z, editor. Computer Science Logic; Heidelberg: Springer; 2006. pp. 426–440. [Google Scholar]
- 11.Maciel A, Péladeau P, Thérien D. Programs over semigroups of dot-depth one. Theor. Comput. Sci. 2000;245(1):135–148. doi: 10.1016/S0304-3975(99)00278-9. [DOI] [Google Scholar]
-
12.McKenzie P, Péladeau P, Thérien D. NC
 : the automata-theoretic viewpoint. Comput. Complex. 1991;1:330–359. doi: 10.1007/BF01212963. [DOI] [Google Scholar]
: the automata-theoretic viewpoint. Comput. Complex. 1991;1:330–359. doi: 10.1007/BF01212963. [DOI] [Google Scholar] - 13.Péladeau, P.: Classes de circuits booléens et variétés de monoïdes. Ph.D. thesis, Université Pierre-et-Marie-Curie (Paris-VI), Paris, France (1990)
- 14.Péladeau P, Straubing H, Thérien D. Finite semigroup varieties defined by programs. Theor. Comput. Sci. 1997;180(1–2):325–339. doi: 10.1016/S0304-3975(96)00297-6. [DOI] [Google Scholar]
- 15.Pin, J.: The dot-depth hierarchy, 45 years later. In: The Role of Theory in Computer Science - Essays Dedicated to Janusz Brzozowski, pp. 177–202 (2017)
- 16.Pin J. Varieties of Formal Languages. New York: Plenum Publishing Co.; 1986. [Google Scholar]
-
17.Pin J, Straubing H. Some results on
 -varieties. ITA. 2005;39(1):239–262. [Google Scholar]
-varieties. ITA. 2005;39(1):239–262. [Google Scholar] - 18.Simon I. Piecewise testable events. In: Brakhage H, editor. Automata Theory and Formal Languages; Heidelberg: Springer; 1975. pp. 214–222. [Google Scholar]
-
19.Straubing H. Finite semigroup varieties of the form
 J. Pure Appl. Algebra. 1985;36:53–94. doi: 10.1016/0022-4049(85)90062-3. [DOI] [Google Scholar]
J. Pure Appl. Algebra. 1985;36:53–94. doi: 10.1016/0022-4049(85)90062-3. [DOI] [Google Scholar] - 20.Straubing H. When can one finite monoid simulate another? In: Birget JC, Margolis S, Meakin J, Sapir M, editors. Algorithmic Problems in Groups and Semigroups. Boston: Springer; 2000. pp. 267–288. [Google Scholar]
- 21.Straubing H. Languages defined with modular counting quantifiers. Inf. Comput. 2001;166(2):112–132. doi: 10.1006/inco.2000.2923. [DOI] [Google Scholar]
- 22.Tesson, P.: Computational complexity questions related to finite monoids and semigroups. Ph.D. thesis, McGill University, Montreal (2003)
- 23.Tesson P, Thérien D. The computing power of programs over finite monoids. J. Autom. Lang. Comb. 2001;7(2):247–258. [Google Scholar]



