Abstract
Predicting evolution of expanding populations is critical to control biological threats such as invasive species and cancer metastasis. Expansion is primarily driven by reproduction and dispersal, but nature abounds with examples of evolution where organisms pay a reproductive cost to disperse faster. When does selection favor this ‘survival of the fastest?’ We searched for a simple rule, motivated by evolution experiments where swarming bacteria evolved into an hyperswarmer mutant which disperses ~ 100% faster but pays a growth cost of ~ 10% to make many copies of its flagellum. We analyzed a two-species model based on the Fisher equation to explain this observation: the population expansion rate (v) results from an interplay of growth (r) and dispersal (D) and is independent of the carrying capacity: . A mutant can take over the edge only if its expansion rate (v2) exceeds the expansion rate of the established species’ (v1); this simple condition (v2 > v1) determines the maximum cost in slower growth that a faster mutant can pay and still be able to take over. Numerical simulations and time-course experiments where we tracked evolution by imaging bacteria suggest that our findings are general: less favorable conditions delay but do not entirely prevent the success of the fastest. Thus, the expansion rate defines a traveling wave fitness, which could be combined with trade-offs to predict evolution of expanding populations.
Keywords: Range expansion, trade-off, dispersal, evolution, reaction-diffusion, Pseudomonas aeruginosa
Introduction
Biological threats often come in the form of expanding populations: A cancerous tumor spreads into a healthy tissue; bacteria colonize a clean surface and form a biofilm; exotic species occupy a new territory. Predicting the evolution of expanding populations, however, is a complex problem. Expansion can be a combination of many organismal traits, so evolutionary trajectories can occur in a multi-dimensional phenotypic space.
For the sake of simplicity, we can reduce phenotype into two traits: dispersal and growth. Individuals move and they consume local resources; resource availability is highest outside the population range, which creates an advantage to being at the population margin (Murray 2007). Therefore, there are two possible favorable evolutionary strategies: dispersing faster or growing faster. Fast-dispersing individuals take advantage of this spatial heterogeneity: they take over the edge, cutting-off competitors’ access to growth-limiting resources (Nadell et al. 2010; Phillips et al. 2010). In contrast, faster-growth individuals outcompete the rest of the population regardless of their location. Of course, simultaneously improving both traits—dispersal and growth—is even better. It is more delicate, and perhaps more interesting, to predict what could happen when one trait is improved at the expense of the other, which is often the case if organisms live with limited resources. For instance, if a mutant appears with better dispersal but has a lower growth rate because it spends too much energy on moving, will this mutant take over the population by reaching the edge, or will it be out-competed by the faster growing but slower dispersing wild-type?
There are many examples suggesting that population expansion selects for better dispersal, even at the cost of slower growth (Chuang and Peterson 2016). The invasion of the cane toads in Australia, a human-introduced species, is led by faster long-legged individuals with lower birth rates (Hudson et al. 2015); the South African mountain fynbos is threatened by invasive pine trees with lighter pine seeds that disperse better (Richardson et al. 1990) but produce weaker seedlings (Reich et al. 1994); metastatic cancer cells are more invasive due to a loss of contact inhibition of locomotion (Carmona-Fontaine et al. 2008) that also lowers their cellular proliferation rates (Biddle et al. 2011; Gerlee and Nelander 2012; Kim et al. 2017; Widmer et al. 2012). Additional field examples of invasive populations, where margin individuals acquired greater dispersal and slower growth, include other plants (Ganeshaiah and Shaanker 1991; Huang et al. 2015; Williams et al. 2016), fish (Agostinho et al. 2015), crickets (Simmons and Thomas 2004), butterflies (Hughes et al. 2003), and fungi (Garbelotto et al. 2015). Laboratory experiments with populations expanding towards a virgin territory with freshwater ciliates (Fronhofer and Altermatt 2015), beetles (Ochocki and Miller 2017; Weiss-Lehman et al. 2017), plants (Williams et al. 2016), and bacteria (Fraebel et al. 2017; Ni et al. 2017) led to similar results: population expansion can favor faster dispersal at the expense of slower growth.
Yet, previously proposed models suggest that faster growth is not always selected for. Growth can be traded off with competitive ability as in the r-K selection theory (Pianka 1970) and, in a spatially structured environment, the competition-colonization trade-off theory aims to explain the coexistence of interacting species (Tilman 1994). Nonetheless, these findings suggest that a better definition of fitness is required to understand evolution in expanding populations. Other questions ensue: Are there general conditions for favoring dispersal over growth? And how much cost can a fast-dispersing individual pay in terms of slower growth and still be favored by natural selection?
Here, we based our analysis on a well-established framework of spatial expansion in growing populations: the traveling wave derived from the Fisher-Kolmogorov-Petrovsky-Piscunov (F-KPP) equation. The F-KPP equation, in its original form, describes a 1-D monospecies population (Fisher 1937; Giometto et al. 2014; Kolmogorov et al. 1937). We expanded the F-KPP equation to investigate the conditions favoring faster dispersal or faster growth rate, and we solved the resulting two-species system to produce a simple rule governing the evolutionary outcome. Somewhat surprisingly, this rule had not been proposed before to the best of our knowledge, despite much theoretical and experimental work in this field. We then conducted simulations to delineate the conditions at which the rule is applicable, and the time-scales necessary for a full sweep of the population in biologically relevant situations. This rule allowed us to calculate the maximum cost in term of growth rate that a faster-dispersal mutant can pay and still win the competition. If the loss of growth rate is greater than this maximum cost, then better dispersal should no longer be favored. When a physiological trade-off between growth and dispersal is considered as well, then it is possible to predict the phenotype favored by natural selection.
It is often challenging to test the predictions of theoretical models with field studies, and experimental manipulation of natural ecosystems is often impractical. But we can use laboratory experiments with microbes to rigorously test our mathematical models (Dai et al. 2013; Gandhi et al. 2016; Hallatschek et al. 2007; Jessup et al. 2004; Mitri et al. 2016). Microbial model have the advantages of large populations sizes, short generation times, affordable DNA sequencing and—in many cases—tools for genetic engineering. We recently discovered that experimental evolution in swarming colonies of the bacterium Pseudomonas aeruginosa leads to the spontaneous evolution of hyperswarmers (van Ditmarsch et al. 2013). We used DNA sequencing and genetic engineering to show that hyperswarmer mutants have a single point mutation in a gene called fleN, which gives them multiple flagella and makes them more dispersive, and we confirmed that this evolution is reproducible in dozens of replicate experiments. Importantly, the many flagella always came at the cost of a slower growth (Table 1). P. aeruginosa wild-type individuals outcompete hyperswarmers in well-mixed liquid media where faster dispersal is useless; hyperswarmers, on the other hand, swarm faster on agar gel (Deforet et al. 2014) and outcompete the wild-type in this spatially structured environment where dispersal is key (van Ditmarsch et al. 2013). Thus, the hyperswarmer-wild-type dynamics can be used as a laboratory model to study the evolution in expanding populations where faster better dispersal comes with a growth cost.
Table 1:
Experimental swarming traits of P. aeruginosa and its hyperswarmer mutant
| Strain | Growth rate r (measured in Deforet et al. (2015)) | Expansion rate v (measured in Deforet et al. (2014)) | Diffusion rate D (calculated) | Decay length λ (calculated) |
|---|---|---|---|---|
| Wild-type | 1.1 ± 0.05h−1 | 3.0 ± 0.1mm/h | 2.0 ± 0.15mm2/h | 1.4 ± 0.07mm |
| Hyperswarmer | 1.0 ± 0.04h−1 | 4.0 ± 0.15mm/h | 4.0 ± 0.27mm2/h | 2.0 ± 0.11mm |
Note: Errors are standard deviations. Errors on calculated parameters are inferred from the formula of propagation of errors.
Here we exploited the differences in growth rate and dispersal between the wild-type P. aeruginosa and its hyperswarmer mutant to experimentally test our model using time-course experiments with bacteria engineered to express fluorescent labels. The quantitative experiments supported our model, suggesting that the theory—despite its simplicity—provides a general way to predict the evolution of expanding populations in a range of biological species and systems.
Methods
Theoretical model
One dimensional one species F-KPP
We modeled P. aeruginosa swarming population as a clonally reproducing population, expanding along a one-dimension axis towards an open habitat, according to the F-KPP equation:
| (1) |
where x is space, t is time, u is the local population density, K is the carrying capacity, r is the maximum per-capita growth rate and D quantifies dispersal. Growth and dispersal can obey different laws in nature; for generality, the F-KPP equation assumes logistic growth, where the per-capita growth rate decreases linearly as the population density increases, and assumes Fickian diffusion for dispersal. The F-KPP equation suits the common scenario where regions with excess of nutrients lie outside the population and determine the direction of expansion. Resource availability, proxied by 1 − u/K, is highest outside the population range; per capita growth, represented by r(1 − u/k), is maximal at the edge of the population. Eq. 1 has a traveling wave solution, u(x, t) = u0(x − vt), where the population front travels at a constant expansion rate , independent of the carrying capacity, and its density increases from the edge with a length-scale (Video 1 and Fig. S1) (Hallatschek and Nelson 2008; Murray 2007).
Edge of the population
The population density decays exponentially at the front. The range of the traveling wave is theoretically infinite. Therefore, in order to locate the front position, we arbitrarily defined the “edge” as the location where the density reaches 5% of the carrying capacity.
Two species F-KPP
The F-KPP equation is extended to a two-species system with coupled equations:
| (2) |
Species 1 has density function u1(x, t), disperses with coefficient D1 and grows with a rate r1; species 2 has u2(x, t), D2, and r2. Species 1 and 2 interact only by competing for the same resources, a feature implemented by the factor 1 − u1 − u2.
Competition
In competition situations, we define the winning species as the resident species at the edge, namely the species whose frequency exceeds 50% at the edge of the population (defined at the location where the total population becomes lower than 5% of the carrying capacity).
Numerical simulations
The deterministic numerical simulations (used for Fig. 1B, Fig. 2C, and Fig. 3A) were performed in MATLAB (The MathWorks) following Euler’s method, with dx = 0.1, dt = 0.001, D1 = 1, r1 = 1, and total spatial range of 400. For stochastic simulations (used in Fig. 2B), the model was expanded as explained in Appendix C: Stochastic Modeling.
Figure 1:
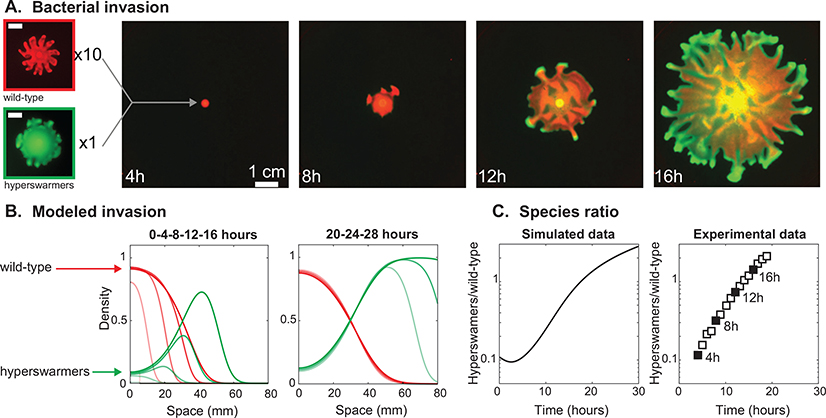
Evolutionary dynamics in an expanding population of swarming P. aeruginosa bacteria. A: Fluorescence time-lapse imaging shows a swarming competition in a mixed population of wild-type and hyperswarmers at 10:1 ratio and on a soft-agar gel. Leftmost panels: Monoclonal swarming colonies of wild-type (top) and hyperswarmer (bottom) imaged at T = 12h (scale bars 1 cm). B: Snapshots of numerical simulations of Eq. 2 modeling competition of P. aeruginosa (red lines) and the hyperswarmer mutant (green lines) with initial ratio 10:1, using parameters extracted from experiments (Table 1). Left panel shows time points represented in panel A. Right panel shows later time points, where the wild-type population stalls while the hyperswarmer population keeps expanding. C: Ratio of hyperswarmer biomass over wild-type biomass. The experimental data is extracted from fluorescence signals in panel A (black squares represent time points shown in A).
Figure 2:
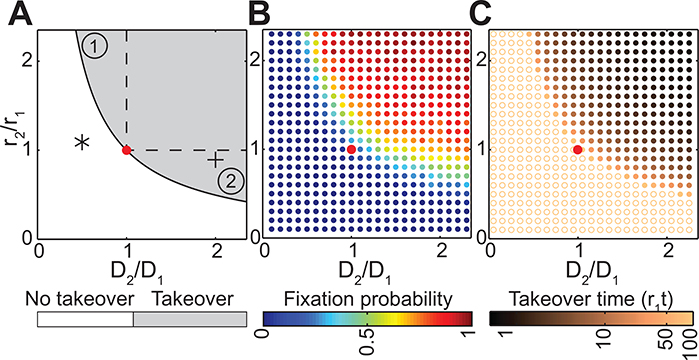
Faster-dispersing species take over expanding populations despite having a slower growth as long as v2 > v1. A: Phase diagram of evolutionary outcome in r2/r1,D2/D1 space, with 2 subdomains of interest in the success domain: (1) is the domain of success with higher growth rate and slower dispersal. (2) is the domain of success with faster dispersal but lower growth rate. The (+) symbol represents the hyperswarmer phenotype with respect to wild-type phenotype, as measured in the experimental conditions (Table 1). The (*) symbol represents the wild-type phenotype with respect to the hyperswarmer phenotype. B: Fixation probability obtained from the stochastic model with death rate (stochastic simulations performed with S = 1, K = 100, L = 2λ1). C: Takeover time obtained from the deterministic model (simulations performed with L = 2λ1 and S = 0.2). The empty orange circles represent the conditions where species 2 fails to takeover within the duration of the simulation (r1t = 180). In A-C, the red dot depicts the reference point (D2 = D1 and r2 = r1).
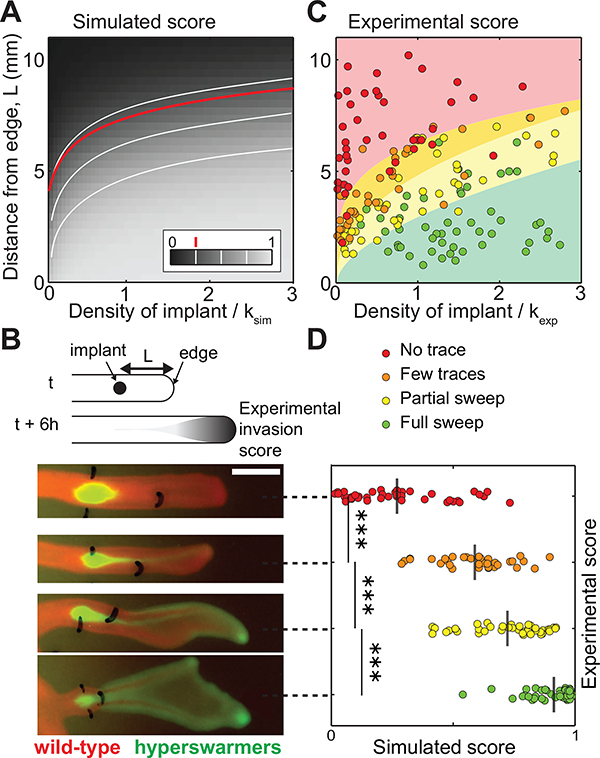
Figure 3:
Likelihood of fixation increases with the initial size of the introduced population and its proximity to the population edge. A: Simulation results of introducing species 2 into an expanding species 1. The color scale represents the simulated sweep score, i.e. the frequency f of the introduced species (species 2 with D2 = 2D1 and r2 = 0.9r1) at the population edge T = 6 h after introduction. White lines are iso-frequency lines for f = 0.25, 0.5, and 0.75. The red line is from Eq. 6 for f = 0.25. B: Laboratory experiments where the hyperswarmer (in green) was introduced at varying initial densities and distances to the edge of an expanding swarm of wild-type P. aeruginosa (in red). Scale bar is 5 mm. Leftmost marks depict the location of the hyperswarmer introduction; rightmost marks locate the position of the front of the P. aeruginosa population at the time of hyperswarmer implantation. The four snapshots represent four experimental replicates. C: Experimental sweep success evaluated visually at 6 hours after hyperswarmer introduction. Background colors represent results from multinomial logistic regression (see details in Appendix D: Statistical analysis). In agreement with the theory, sweep success is lower for large distances from the front and smaller initial densities. D: Comparison of simulated and experimental sweep scores for each experimental replicate. The grey vertical lines represent the average simulated sweep score and the p-values are < 10−3 (Kruskal-Wallis test). secrete molecules that are auto-fluorescent, and the long-term maturation kinetics of the fluorescent proteins used (GFP and DsRed) can vary. Therefore, the situation may start to differ from the idealized model. Once the edge has passed the dynamics can be quite different: in the resource-depleted region, the population is denser and covers the entire available area (Fig. S2). The spatial structure and dispersal are less relevant and the evolutionary fate of a new mutant is determined by high-density dynamics. The faster growing wild-type can catch up or new mutants carrying compensatory mutations that thrive in low resource environments may even appear (Yan et al. 2017). These successional dynamics may be a natural product of evolution, so long as there is someplace for the faster disperser to utilize.
Experimental Methods
We used swarming motility in P. aeruginosa as a laboratory model to study dynamics of expanding populations. Swarming plates (such as the one used for Fig. 1A) were made as previously described (Xavier et al. 2011). They consist of soft agar gel supplemented with casamino acids and salts.
Transplantation experiments
P. aeruginosa strain PA14 genetically modified to constitutively express DsRed proteins were grown in LB overnight, washed twice in Phosphate Buffered Saline (PBS), then diluted in PBS to OD600=0.01. Each plate is seeded with 2 μL of bacterial solution and kept at 37°C for 20h. An overnight culture of hyperswarmers (clone 4) (van Ditmarsch et al. 2013) genetically modified to constitutively express GFP proteins was washed twice in PBS and concentrated 100-fold by centrifugation. For each plate, the location of the tip of every branch of the colony was marked on the bottom side of the Petri dish. The implant sites were marked as well. A small volume of hyperswarmers culture (0.1–0.8 μL) was implanted at each implant site. From 6 to 11 branches were implanted per swarming colony. The entire procedure took less than 5 minutes per plate, which means the colony did not move significantly during the process. Immediately after implantation, each plate was placed inside a 37°C incubator containing a custom-made fluorescence imaging device. Two images were taken with the same light source (Blue LED equipped with a 500nm excitation filter): one with a 510nm emission filter (GFP channel), one without emission filter (brightfield channel). The camera dark noise and illumination unevenness were canceled out using this formula:
The size of each implant was manually evaluated from the total GFP signal within a region defined by thresholding. In order to make the experimental results comparable with simulations, this size was divided by the area of a circle of diameter of λWT. This gives the density of GFP as if the implant sites were λWT in diameter. Then we divided this density by the wild-type carrying capacity. To evaluate the local carrying capacity of the wild-type colony (Kexp), we grew a swarming colony with a wild-type mutant constitutively expressing GFP proteins, took an image using the same imaging device and performing the same post-acquisition treatment, and measured the average intensity of the branches. Six hours after implantation, plates were imaged with a plate scanner (GE Healthcare Typhoon) in DsRed and GFP channels. The distance between the implant site and the location of the tip of the branch at the time of implantation was measured with ImageJ. The outcome was estimated visually. The amount of hyperswarmers at the front of the branch was visually ranked in four levels: (i) ”No trace”: no visible trace of hyperswarmers at the edge of the colony (red dots in Fig. 3); (ii) ”A few traces”: a streak of hyperswarmers reached the edge (orange dots in Fig. 3); (iii) ”Partial sweep”: hyperswarmers settled at the tip and along the edge of the branch (yellow dots in Fig. 3); (iv) ”Full sweep”: hyperswarmers took over the ancestral population and disrupted the branch pattern (green dots in Fig. 3).
Growth curves
Overnight cultures of wild-type and hyperswarmer cells were washed in PBS and diluted in minimum media with casamino acids (it is the same recipe as the one used for swarming plates except agar is removed). Cells were grown in a 96-well plate in a plate scanner (Tecan) with 37°C incubation and agitation.
Competition experiments
Overnight cultures of wild-type DsRed and hyperswarmer GFP cells were washed in PBS and mixed to an approximate 1:1 ratio. To evaluate the pre-competition ratio, a sample of this mix solution was serially diluted in PBS and inoculated on a minimum media hard agar plate for CFU counting. 1 mL of the mix solution was poured on a fresh swarming plate. Once the plate was dry, it was incubated at 37°C for 4 hours. Finally, to evaluate the post-competition ratio, a small sample of the gel was scooped out using the wide end of a 1 mL sterile pipette tip to punch through the gel. The sample was placed in an Eppendorf tube with 0.5 mL of PBS, pipetted up and down 10 times to break the agar gel apart, vortexed for 10 seconds, then serially diluted in PBS and inoculated on a minimum media hard gar plate for CFU counting. CFU plates were scanned 24 hours later on a flatbed fluorescence scanner (Typhoon, GE Healthcare). Three competition plates per color combination were made per day (technical replicates). This experiment was performed three times (biological replicates).
Data Availability
All experimental data (shown in Fig. 1 and Fig. 3), and simulation results for Fig. 1 and Fig. 2 (as well as MATLAB scripts to generate them), are available in the Dryad Digital Repository (Deforet et al. 2019).
Results
Modeling swarming in P. aeruginosa with the F-KPP equation
P. aeruginosa populations swarm across agar gels containing nutrients and form branched colonies. Bacterial populations at the branch tips spread at a nearly constant rate (Table 1) by dividing and dispersing (Deforet et al. 2014). Knowing that cell sizes have a positive correlation with growth rates (Deforet et al. 2015) we compared the sizes of cells collected from the tip of a branch with the sizes of cells collected behind the tip; cells at the tip were longer, indicating faster growth at the edge of the population (Fig. S1). Each growing tip consumes resources in its vicinity and thus forms a nutrient gradient (Mitri et al. 2016) that drives a resource-limited growth similar to the F-KPP model.
A simple rule for the evolution of faster dispersal
Hyperswarmers grow ~ 10% slower in well-mixed liquid media due the cost of synthesizing and operating multiple flagella (Table 1), but, thanks to their ~ 100% faster dispersal on agar gel, they can outcompete the wild-type in spatially structured environments (Deforet et al. 2014; van Ditmarsch et al. 2013). On agar gel lacking spatial structure, hyperswarmers are outcompeted, as expected (Fig. S2). At the micrometer scale, an expanding population of hyperswarmers displays patterns of active turbulence typical of dense bacterial suspensions, which is different from the wild-type where cells remain nearly static even at the tips of swarming tendrils (Video 2).
To gain a better understanding of the competition dynamics in expanding swarming colonies we mixed wild-type bacteria (labeled with the red fluorescent protein DsRed Express) with hyperswarmers (labeled with the green fluorescent protein GFP) at 10:1 ratio. We then used time-lapsed florescence imaging to film the swarming competition (Fig. 1A). The time-lapse showed that hyperswarmers quickly reached the population edge, increasing their dominance as the colony expanded to win the competition (Video 3).
To determine the conditions favoring evolution of faster dispersal, we used an extension of the F-KPP equation for a two-species system, where u1 represents the wild type and u2 represents the hyperswarmer (See methods and models section). For simplicity, and according to data for the hyperswarmer system (van Ditmarsch et al. 2013) (Fig. S3), we assumed that both species have the same carrying capacity, which we normalized to 1. We assumed that their dispersal rates, determined by D1 and D2, are independent. This framework is well established and it has been used before to investigate competition in various contexts of range expansion (Lewis et al. 2002; Okubo et al. 1989; Pigolotti et al. 2013), including in a scenario with a linear trade-off between dispersal and growth (Reiter et al. 2014). It has been used also as a basis to elaborate more complex models (Bouin et al. 2012; Bénichou et al. 2012; Gandhi et al. 2016; Guo and Wu 2014; Holzer and Scheel 2014; King and McCabe 2003; Lehe et al. 2012; Perkins et al. 2016; Ramanantoanina et al. 2014). However, previous studies did not continue to derive a general rule for the evolutionary outcome of all possible values of dispersal and growth.
To derive a general rule, we first investigated the conditions that allow an introduced population to thrive and replace the resident population at the expansion front. We could determine analytically that, in the moving reference frame traveling at the speed v1, the frequency of species 2 at the edge grows at the rate
| (3) |
which defines the relative fitness of species 2 within a population of species 1 (see Appendix A: Analytical solution for the condition of success). Species 2 outcompetes species 1 at the edge only if the relative fitness of species 2 is positive, which corresponds to:
| (4) |
where and are the expansion rates of each species when grown alone.
Eq. 4 sets the conditions for success at the expansion edge. The intuition behind these evolutionary dynamics is well illustrated in a simulation of the competition between an established species (species 1) and a species with faster dispersal but slower growth (species 2), which we simulated (Fig. 1B) by numerically solving the system in Eq. 2 with parameters corresponding to the hyperswarmer system (r2/r1 = 0.9 and D2/D1 = 2, Table 1). Species 2, initially homogeneously mixed with species 1, outcompetes species 1 once it reaches the leading edge: its faster dispersal enables it to reach the low-density edge where it can take advantage of the resources available, despite a disadvantage in growth rate. Once species 2 dominates the edge, species 1 is left behind in the high-density region where growth has stopped. Over time, the global frequency of species 1—blocked by species 2 from reaching the edge and incapable of growing further—decreases whereas species 2 frequency keeps increasing thanks to its edge domination (Fig. 1C, left). These simulation results are consistent with experimental tests conducted here (Fig. 1C, right) and also with the original experiment that led to evolution of hyperswarmers (van Ditmarsch et al. 2013), which clearly showed that fleN mutants would outcompete the wild-type to extinction given sufficient competition time on swarming plates.
According to the condition for success (Eq. 4) the evolutionary outcome is entirely determined from the growth and dispersal rates. Importantly, and similar to the expansion rate obtained for a monospecies traveling wave, the evolutionary outcome is independent of the carrying capacity of each species (See Fig. S4 for confirmation with numerical simulations).
The success condition leads to a diagram that delineates a growth-dispersal space (Fig. 2A, where the condition is expressed as ). This diagram shows two trivial domains: when both growth and dispersal of species 2 are lower (D2 < D1 and r2 < r1), species 2 cannot outcompete species 1 because v2 is always lower than v1. Numerical simulations illustrate that for very low values of D2 and r2 species 1 continues to expand and travel at constant expansion rate whereas species 2 spreads out and stalls (Video 4, bottom left panel, and Fig. S5A). When growth and dispersal of species 2 are greater (D2 > D1 and r2 > r1), species 2 takes over because v2 is always higher than v1: species 2 grows rapidly, moves to the front where it reaches the active layer and outcompetes species 1 (Video 4, top right panel, and Fig. S5B).
The two domains where one trait is higher and the other is lower are less trivial, but arguably more relevant. Because of the trade-off between dispersal and growth commonly found in nature (Chuang and Peterson 2016), a higher growth does not necessarily yield to evolutionary success: If species 2 grows faster than species 1 but disperses much slower (r1 < r2 and D2 < D1r1/r2), then species 2 does not outcompete species 1. In other words, species 2 cannot take over the edge if its growth rate is not high enough to compensate a loss in dispersal (r1 < r2 < r1D1/D2). Domain 1 of Fig. 2A shows that takeover occurs when species 2 disperses slower than species 1 only if its growth rate is sufficiently higher (r2 > r1D1/D2, Video 4, top left panel, and Fig. S5C). Conversely, a slower growth does not mean takeover is impossible. If species 2 grows slower than species 1 but disperses sufficiently faster (r2 < r1 and D2 > D1r1/r2), then it outcompetes species 1. In other words, there is takeover by species 2 if its growth rate is not too low (r1D1/D2 < r2 < r1) so the gain in dispersal can compensate the loss in growth. (Video 4, bottom left panel, and Fig. S5D). Note that when species 2 replaces species 1 at the edge, the slope of the front changes accordingly (the length scale ranges from to , see Fig. S6).
In the model, the winning species takes over the front and replace the ancestor in the advancing front. However, the core of the population is not affected by the replacement that occurred at the edge. This results in the coexistence of two populations: the ancestor that remains in the initial spatial range and the competitor that occupies the newly extended range.
The simple condition for success, v2 > v1, makes quantitative predictions of evolutionary outcome; those predictions hold true in our experimental system despite intricacies such as the large-scale branching and small-scale turbulence. Hyperswarmers have a ~ 100% increase in dispersal (D2/D1 ~ 2) that comes at a ~ 10% growth rate cost (r2/r1 = 0.9) (Video 2 and Table 1). Therefore, the experimental system falls into domain 2 of the evolutionary outcome diagram (cross symbol in Fig. 2A).
We measured the frequency of hyperswarmers within the first millimeter of the colony from video frames; it increased exponentially with a rate of 0.39 ± 0.08h−1 (SD), which is in quantitative agreement with the theoretical expression of the relative fitness (Eq. 3 and Fig. S7). Hyperswarmers introduced into an expanding wild-type colony spread within a wild-type branch (Fig. S8), reach the tip of the branch, and take over the population (Video 5A) resembling our simulations (Fig. S5D).
Hyperswarmers evolved from a wild-type swarming colony (van Ditmarsch et al. 2013) and could take over the ancestral population thanks to a greater dispersal. To test our model, we asked whether this process was reversible: Could wild-type cells dominate the edge of an expanding hyperswarmer colony thanks to their greater growth rate? Our model predicted that wild-type cells would be unable to take over the hyperswarmer population edge since in this case v2 < v1 (D2/D1 = 0.5 and r2/r1 = 1.1, see star symbol in Fig. 2A). This was confirmed experimentally: wild-type cells introduced in a hyperswarmer colony simply spread out and were rapidly outpaced at the edge by the hyperswarmers (Video 5B). Note that if v2 < v1, species 2 cannot replace the species 1, not even by forming a block at the front. According to the model some individuals of species 1 will diffuse through and reach the edge to eventually take over (See simulations of this process in Fig. S9).
Success rule valid despite phenotypic variability
Even in mono-species systems, individuals with identical and defined genotypes can still display phenotypic variation, such as a varying number of flagella (Deforet et al. 2014; Waite et al. 2016). To study whether phenotypic variation had an effect on evolutionary outcome, we introduced non-heritable fluctuations in birth and death events as well as in the dispersal processes. These phenotypic variations were modeled as stochastic distributions around the mean population value, which is determined by the strain’s genotype (see Appendix C: Stochastic Modeling).
Our simulation results suggest that the success rule, v2 > v1, despite having been derived from deterministic assumptions, holds even in stochastic situations. The transition at v2 = v1 was, however, more gradual (Fig. 2B, Fig. S10, Fig. S11): the zone of transition broadened as stochasticity increased because, as expected from other stochastic studies (Gillespie 2010; Otto and Whitlock 1997), stochasticity allowed for a non-zero probability of deleterious mutants (v2 < v1) to take over and beneficial mutants (v2 > v1) had a non-zero probability of failing to take over. Larger carrying capacities lessened the stochastic effects and sharpened the transition zone, again as expected from previous stochastic analyses (Gillespie 2010; Otto and Whitlock 1997). Importantly, however, the rule v2 > v1 could still predict takeover of the population edge even with different carrying capacities (Fig. S11C).
We confirmed the generality of the success rule further by carrying out evolutionary simulations where mutations randomly arise at division. We considered two schemes: i) mutations that change growth and/or dispersal relative to the ancestor phenotype but do so in an uncorrelated way; ii) mutations that change growth and dispersal considering that the two traits are linearly correlated (linear trade-off) but independent of the ancestor phenotype. In the case of uncorrelated mutations, populations evolved—on average—towards a greater expansion rate (Fig. S12C). When the two traits were constrained by a trade-off, evolution converged to the value along the trade-off line that maximized the expansion rate (Fig. S12D–G). In summary, the several types of stochastic simulations conducted all supported that evolution of the population edge obeys the rule v2 > v1.
The role of spatial structure and founder effect
We then investigated whether our model would account for other factors that could affect competition in biologically relevant scenarios. For example, in most evolutionary scenarios where competition starts with a mutation, the size of the mutant population is initially very low (1 individual) whereas a competing species introduced by external processes (e.g. human intervention) can start at higher densities. Also, the initial location of the mutant species matters because resources are not evenly distributed in nature, and a mutant species may take over faster if it is introduced in the resource-rich leading edge than if it is introduced in deprived regions where it will take longer to grow to domination. In summary, species 2 should take longer to take over (i) when it is introduced further from the edge where resources are already limited or (ii) when its initial size is small. Our model sets the conditions for whether species 2 can successfully take over (Eq. 4, Fig. 2A) but does not give us the time necessary for establishing at the edge.
To investigate how the time to takeover depends on the location and initial size of the introduced population, we modeled the introduction of species 2 into a traveling wave formed by species 1. We assumed an initial density S across a small interval at a distance L from the edge for species 2 (Fig. B1), and we determined the time needed to outnumber (full sweep) species 1 at the front. Numerical simulations revealed that the general rule, v2 > v1, holds for all initial conditions given sufficient time (Fig. 2C). The time required, however, depends on the initial conditions, increasing approximately linearly with the distance L from the front and decreasing sub-linearly with the initial density S (Fig. S13 and S14).
To better distinguish the factors that influence the time required for takeover we considered two steps: first, we considered that species 2 disperses until it reaches the active layer. The time for species 2 to reach the edge depends on the distance from the introduction point to the front—a distance that increases constantly because species 1 is itself advancing—and also on the initial width of species 2. Second, once species 2 reaches the active layer it must grow to outnumber species 1. When the introduction is sufficiently far from the edge the time of takeover, tt, is:
| (5) |
where α and β depend on the parameters D1, D2, r1 and r2 (see Appendix B: Approximate predictions). This analysis confirmed simulation results that the time to takeover depends linearly on L but only sub-linearly on S (Fig. S13 and S14), highlighting that the distance to the edge is key to evolutionary success.
Experimental validation
We then tested these findings in our experimental system. We manipulated the distance to the edge (L) and the density (S) of a small population of hyperswarmers introduced into an expanding wild-type population, and we compared the experimental results to the corresponding simulations. In simulations, the evolutionary outcome was calculated as the frequency f of species 2 at the edge of the population 6 hours after implantation (Fig. 3A). In the experiments, we ranked the evolutionary outcome after 6 h of expansion as no trace, few traces, partial sweep and full sweep according to the amount of hyperswarmers visible at the edge (Fig. 3B, see details in Methods and Models section). The experiments confirmed the dominant role of L compared to S in determining the time of takeover (Eq. 5), which is evident from the concave shape of the evolutionary scores (Fig. 3C, see Appendix D: Statistical analysis).
The intuition behind the concave shape is that when the initial distance from the edge is too long then the mutant may not be able to take over within biologically relevant time, even if its initial size is large. The shape of the iso-frequency contour lines can be calculated from the simplified two-step model of takeover described above and is given by
| (6) |
where is the characteristic length of these lines. In the case of P. aeruginosa and its hyperswarmers, L0 = 1.1 ± 0.07 mm (SD). The results from our hyperswarmer experiments agree with the theoretical model (Fig. 3A and C; compare to lines of constant mutant frequency), indicating that the two-species F-KPP model, in spite of its simplifying assumptions and despite any intricacies of the experimental system (e.g. the swarming population is tri-dimensional; bacterial cells tend to lose motility as they lose access to resources inside the population, which freezes the spatial organization), is sufficiently general to describe evolutionary dynamics in swarming colonies.
Discussion
We showed that the multiple-species extension of the F-KPP equation (Lewis et al. 2002; Okubo et al. 1989; Pigolotti et al. 2013) produces a simple mathematical rule that predicts the evolutionary outcome in an expanding edge depending on the growth and dispersal rates of the competing species. The problem of evolution in an expanding population have been investigated before both theoretically (e.g Burton et al. (2010); Phillips (2015) and empirically (e.g. Phillips et al. (2006)), but its simple solution, the inequality v2 > v1, had not been—to the best of our knowledge—presented this way before.
Our model relies on the assumption that per-capita growth rate is maximal at the edge, where the population density is the lowest, and that dispersal ability is independent of population density. This assumption is valid within the first centimeters of our experimental swarming colony, where bacteria are quite motile and active. However, deep inside the colony, various processes at play hinder a quantitative analysis of population dynamics: the colony can progress from swarming colony into a biofilm-like mode that greatly lowers dispersal, starved bacteria
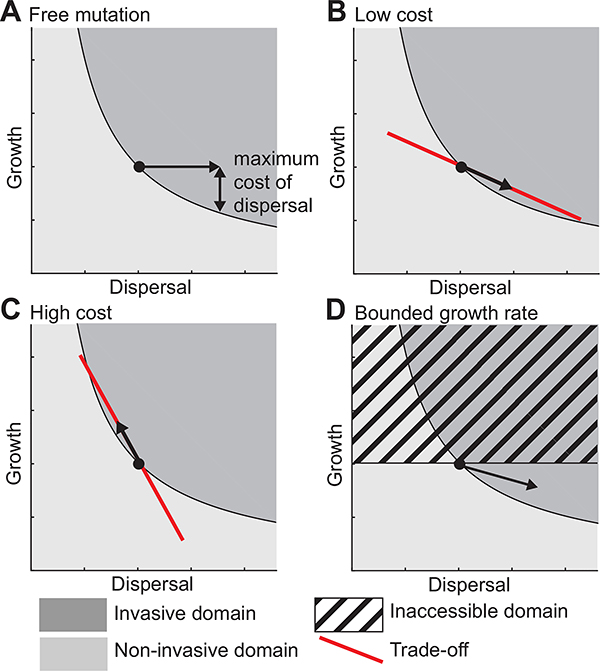
Our model makes a key conclusion: the outcome at the edge of expanding population can be independent of the system’s carrying capacity, because there the competition dynamics rely on the low-density of the population at the expanding edge. The success rule v2 > v1 allows determination of the maximal cost in growth |Δr|max that a mutant can afford to pay for faster dispersal and still be able to dominate the edge of the expanding population (Fig. 4A):
| (7) |
where ΔD is the difference between dispersal rate of the mutant and its ancestor. Eq. 7 quantifies exactly what the trade-off between r and D would need to be in order to evolve greater dispersal at the front. While this is not something that is easily confronted with data it is worth noting that there must be general mechanisms to sustain this in populations that have exhibited such evolutionary increases in dispersal. The evolutionary experiment that originally created the hyperswarmers always produced single point mutations in fleN, a gene that regulates flagella synthesis, and all had slower growth that the wild type (van Ditmarsch et al. 2013). We never observed mutants that evolved faster dispersal without a growth cost, even though we repeated the experiment dozens of times. Perhaps other mutants could increase dispersal even more, but were not favored because they either carried costs higher than |Δr|max or because they required evolution through more mutational steps.
Figure 4:
Evolutionary predictions from success rule in four scenarios. A: Illustration of the maximal cost of an increased dispersal. B and C: Linear trade-off between growth and dispersal that corresponds to a low cost of dispersal (B) and high cost of dispersal (C). D: The growth rate is bounded by physiology.
Hyperswarmer mutants paid a growth cost for synthesizing and operating their multiple flagella but—without affecting their competitive ability—dispersed faster than wild-type bacteria (domain 2 of Fig. 2A). It seems plausible that the supplemental flagella are functional, and their operation adds a cost, but we cannot provide evidence on this point. Extensive work showed that the mutation in fleN increases the number of flagella and slows down the growth rate (van Ditmarsch et al. 2013), but that growth cost could be due to the burden of synthesizing extra flagella or to the extra energetic burden of their operation. Untangling the two remains an interesting problem, but solving it requires molecular biology work beyond the scope of this paper.
The success rule v2 > v1 is the adaptive function that could be combined with a fitness set (de Mazancourt and Dieckmann 2004) to predict the co-evolution of growth and dispersal in expanding populations. For example, if the quantitative knowledge on the molecular, cellular, or physiological mechanisms of a trade-off between growth and dispersal can be represented by a line in (r, D) space the slope of that line, dr/dD, represents the cost of dispersal. When the trade-off is subtle, the slope is shallow and we predict that the population will evolve to disperse faster with a lower growth rate (Fig. 4B). Conversely, when the trade-off is strong, the slope is steep and we predict that the population will evolve a higher growth rate and slower dispersal (Fig. 4C). According to this model, the P. aeruginosa system has a subtle trade-off: the improved dispersal advantage of hyperswarmers is ~ 100% but costs only ~ 10% of their growth rate relatively to wild-type (van Ditmarsch et al. 2013).
Nature abounds with examples of trade-off between growth and dispersal (Chuang and Peterson 2016). Evolution in expanding populations often selects for better dispersal and slower growth (see examples cited in the introduction). Our model predicts that a species with faster growth but slower dispersal should be able to take over (domain 1 of Fig. 2A), but we never observed these cases in our experimental system. And, beyond observations by another group in laboratory experiments with Escherichia coli (Fraebel et al. 2017), we could not find examples in nature either. The reason for not finding evolution of rapid growers that disperse slower may be population history: Empirical and theoretical studies of range expansions suggest that only dispersal can be improved in expanding populations (Burton et al. 2010; Hallatschek and Fisher 2014; Perkins et al. 2013; Travis and Dytham 2002); invasion of new niches is possibly a rare event, whereas competition within a confined, but relatively homogenous environment is more common. In such situations, selection is not on dispersal but on growth, which means that—in most species—growth rates may already be close to their physiological maximum (Fig. 4D). Individuals challenged to overcome spatial structure may only have dispersal-related traits left to improve. Moreover, while the trade-off between growth and dispersal may be found and seem logical, a comparative analysis of dispersal in terrestrial and semi-terrestrial animals suggested that dispersal and fecundity may be positively correlated (Stevens et al. 2014).
Margins of an expansion front, with low population density and strong density gradient, are prone to dramatic evolutionary processes such as spatial sorting and expansion load, which can be generalized using the rule v2 > v1: (i) A mutant with a higher v will take over the population margin. This is a generalisation of the spatial sorting effect, where better dispersers (D2 > D1, with r2 = r1) accumulate at the population margins (Shine et al. 2011). (ii) Genetic drift in marginal populations can promote accumulation of deleterious mutations in the form of an expansion load (Hallatschek and Nelson 2008; Peischl et al. 2013). In our framework, this corresponds to the stochastic case where a mutant takes over the margin with a lower growth rate r2 < r1 and D2 = D1). We demonstrated that stochasticity can allow, more generally, a mutant with lower v to take over. This model suggests that the fitness (net balance between growth and death) can be replaced with a traveling wave fitness v, which combines growth rate and dispersal rate. An increase in v leads to spatial sorting, and stochastic effects can lead to accumulation of low v mutants at the edge (expansion load).
Our results produced a general and simple relationship that determines the maximum growth cost allowed for faster dispersal. This appealing simple rule is bound to our model assumptions, which apply more directly to microbial systems. Future work should address how more complex biological systems deviate, or not, from those assumptions. Possible expansions include situations where the growth rate is not maximal at the edge (Korolev 2015; Perkins et al. 2013), or where uncertainty about the quality of resources beyond the edge front factor in. The only interaction we considered here lies in the shared carrying capacity. Extension to more complex systems could also include explicit interactions between individuals, such as in competition-colonization models, introduced to address the question of coexistence in spatially structured environments (Tilman 1994).
In conclusion, our study provides theory to determine the evolutionary outcome of competition in an expanding population, which can be extended with trade-off constraints observed for each particular system. Every model requires simplifying assumptions, and ours is certainly not an exception. In systems that respect those assumptions, the success rule could be used to predict evolution in expanding populations. Systems in this category may include the growth of cancer tumors and invasion of non-native species in ecosystems.
Supplementary Material
Acknowledgments
The authors are grateful to Florence Débarre for her valuable comments on the manuscript. This work was supported by National Science Foundation award MCB-1517002/NSF 13-520 (to J.B.X) and by National Institutes of Health Grant R00CA191021 (to C.C.-F.). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Appendix A: Analytical solution for the condition of success
Formulation of the mathematical model
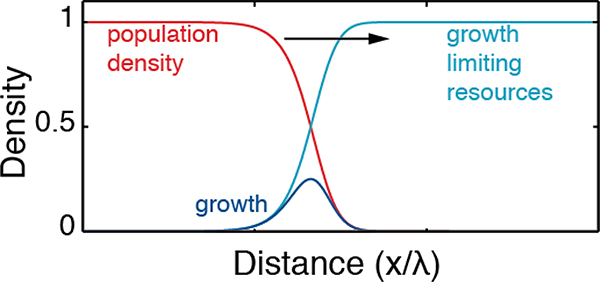
The traveling wave solution of the F-KPP equation is driven by growth at the edge of the population range. In the figure A1, the population density u is represented in red, the growth limiting resources (proxied by the difference between the carrying capacity and the population density) 1 − u in light blue, the growth ru(1 − u) in dark blue. The black arrow depicts the direction of expansion.
Figure A1:
Diagram of the traveling wave solution of the F-KPP equation.
We model the density of the two species (densities u1 and u2) by two coupled F-KPP equations with different growth rates (r1 and r2) and different diffusion rates (D1 and D2). The two species interact only by competing for common resources.
| (A1) |
We aim to define the range of parameters (D1, D2, r1, r2) that allows the takeover of an established traveling wave (species 1) by another species (species 2).
Eigenvalue problem
We reproduce the same arguments as in Korolev (2015) but with r1 ≠ r2. We introduce the functions u(t, x) = u1(t, x)+ u2(t, x), g1(t, x) = r1(1 − u(t, x)) and g2(t, x) = r2(1 − u(t, x)).
| (A2) |
To find the condition of takeover, we search for the condition of divergence of the fraction of secondary species:
| (A3) |
Korolev (2015) assumes f ≪ 1 and demonstrates that the condition of takeover can be found by solving an eigenvalue problem. Following the exact same steps, we find that in the moving reference frame (where the space variable is ) traveling at the velocity the eigenvalue problem is the following:
| (A4) |
where primes denote the derivative with respect to ξ, and is an eigenvalue. After another change of variables established by Korolev, equation A4 becomes
| (A5) |
Condition of takeover
Following Korolev’s reasoning (Korolev 2015), we find that the largest eigenvalue is found at large ξ, and its value is given by the maximal value of g2(c):
| (A6) |
If then the secondary species will never take over the primary species. If then the secondary species will eventually take over the primary species. Therefore, the condition of takeover corresponds to
| (A7) |
with and .
Appendix B: Approximate predictions
The equation A7 gives the condition of takeover, but not the time of takeover, which depends on the size S of the introduced population and the location of the introduction (distance L from the front).
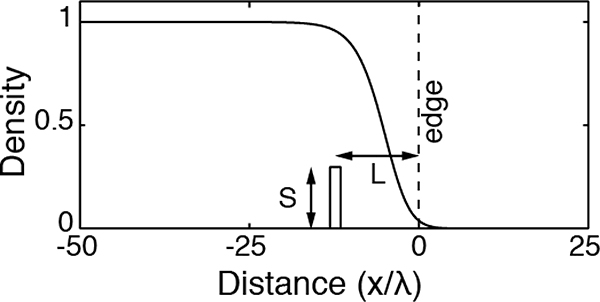
Definitions of S and L
We first consider a traveling wave formed by the species 1. Then the species 2 is introduced at a distance L from the population front, as depicted in the figure below.
Figure B1:
Diagram of the invasion scheme: the species 2 is implanted at a distance L from the edge, with a density S.
The front position is defined as the location where u1 is equal to 5% of the carrying capacity, without loss of generality. This threshold is arbitrarily selected but it is not essential for later conclusions. The position of the front at the time of introduction can be taken as the origin of the x-axis, and the time of the introduction sets the origin of time (i.e. u1(0, 0) = 0.05). The introduction imposes a density u2(x, 0) = S for −L −λ1 < x < −L + λ1, and u2(x, 0) everywhere else. Then we consider the F-KPP processes for both species simultaneously. We set r1 = 1 and D1 = 1 by rescaling space (x → x/λ1) and time (t → r1t): the remaining parameters are D2 and r2. The time ti at which the species 2 takes over the species 1 at the front is defined by:
| (B1) |
with the position of the front defined as
| (B2) |
An approximate time of takeover can be calculated by considering two consecutive steps. First, the introduced individuals of species 2 spread through spatial diffusion until the density f of species 2 at the edge reaches a maximum. During this step we assume that species 2 does not grow. Then, the individuals of species 2 that reached the edge follow the traveling wave. They have access to the resources and therefore they proliferate until they take over the species 1.
Diffusive spreading
The introduction is initially spatially limited, and performed at x = 0, at distance L from the edge. Then species 2 diffuses out, and its density is:
| (B3) |
where is the total size of the introduced population. To compare the theoretical and experimental results, we rescale the total size of the introduced population using its spatial extension:
| (B4) |
The density of species 2 at the edge of the traveling wave formed by species 1 is u2(x = v1t + L, t) and it reaches a maximum at
| (B5) |
At this time, the density of species 2 at the edge is
| (B6) |
Since the edge of the population range is defined as the location where the total density is 5% of the carrying capacity, the fraction of species 2 at the edge is
| (B7) |
Growth at the edge
At the edge, the densities of species 1 and species 2 are much smaller than the carrying capacity, so we consider that they grow exponentially. If species 1 and 2 grow exponentially with growth rates r1 and r2, respectively, then the evolution of the frequency f is given by the logistic equation with a growth rate r2 − r1. We study the early times of takeover, hence f remains much smaller than 1. Therefore, we simply write:
| (B8) |
Here, we study the dynamics of the frequency f in the moving reference frame (see Appendix A) at short times, so we can assume that f follows the dynamics given by the eigenvalue equation A4 and therefore grows at a rate corresponding to the maximal eigenvalue given in equation A6. Then we can replace r2 −r1 with in equation B8.
The dynamics of f is therefore:
| (B9) |
Frequency of species 2 at the edge
If the introduction is performed far enough from the edge (L > D2/v1), then equation B5 becomes simply tdiffusion ≃ L/v1 and equation B7 becomes:
| (B10) |
Since the evolves much more slowly then , we consider that L is constant in this term (we use for the experimental validation):
| (B11) |
The frequency of species 2 after a time t is given by equation B9 but using the shifted time t −tdiffusion that accounts for the time required for species 2 to reach the edge.
| (B12) |
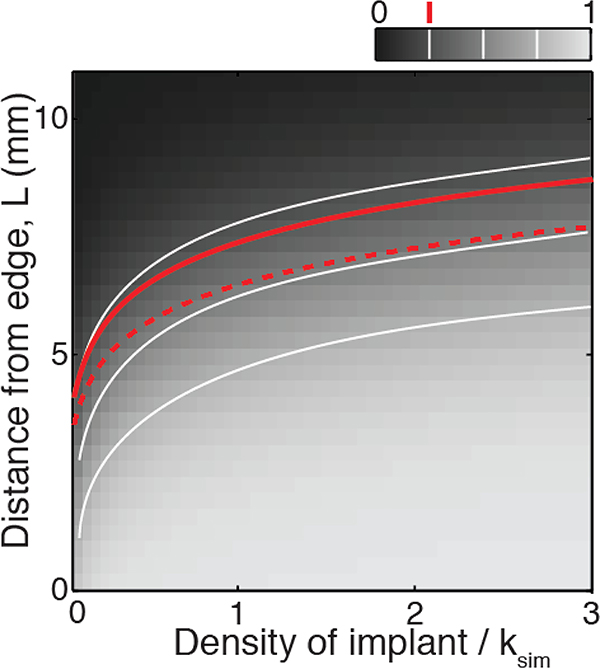
Hence the iso-frequency lines in Fig. 3A are given by S ~ eL/L0, with (equation 5 of the main text).
The iso-frequency for f = 0.25 is plotted in the figure below (red dashed line), together with the numerical results. The disagreement with the numerical results is mostly due to the simplicity of the model: first the species 2 diffuses out and reaches a maximum density at the edge, then it grows at the edge. In reality, species 2 starts growing as soon as it reaches the edge and gains access to resources. To account for this neglected growth term, we propose a simple correction: we replace the frequency at the edge fdiffusion with fdiffusion(1 + tdiffusionr2/2) in equation B9. The term fdiffusiontdiffusionr2/2 comes from the approximate integration of the growth of the frequency f at the edge from t = 0 (f = 0) to t = tdiffusion (f = fdiffusion). Including this growth term improves the agreement with the numerical simulations (red solid line of the figure below).
Time of takeover
If L > D2/v1, the time of diffusion from implantation to the edge is
| (B13) |
The time of growth tgrowth to reach a certain frequency f is:
| (B14) |
Overall, the time of takeover tt = tdiffusion + tgrowth scales as (equation 5 of the main text):
| (B15) |
Figure B2:
Comparison between numerical and theoretical results. The color scale represents the simulated score (the ratio f of species 2 density over total population density) at the front of the expansion range, at t = 6 hours after implantation. The secondary species is characterized by D2 = 2D1 and r2 = 0.9r1. The white lines are iso-frequency contour lines for simulated score f = 0.25, 0.5, and 0.75. The red dashed line is the f = 0.25 contour line from equation B12. The red solid line is the f = 0.25 contour line corrected for growth.
with
| (B16) |
Appendix C: Stochastic modeling
The model presented above is deterministic. We introduce stochasticity by updating species counts N1 and N2 using distribution functions based on equations A1.
Logistic Growth
At each time step, the counts of species 1 and 2 are updated to account for logistic growth:
| (C1) |
where Poisson(λ) is the Poisson distribution function, with parameter λ.
Exponential Growth + Death
To introduce a net death rate, we develop the expression of the deterministic logistic growth into a (positive) exponential growth term and a (negative) density dependent death term.
| (C2) |
Therefore, at each time step, species counts are updated in the following way:
| (C3) |
where Binomial(n, p) is the binomial distribution function, with parameters n (number of trials) and p (success probability in each trial).
Diffusion
At each time step, a random fraction of individuals of species 1 in deme x are randomly moved into demes x + dx and x − dx. All demes are processed sequentially in a random order with the following scheme:
draw B = Binomial(N1, p = D1 dt / dx2)
draw Bleft = Binomial(B, p = 0.5)
update N1(x, t + dt) → N1(x, t) − B
update N1(x − dx, t + dt) → N1(x − dx, t)+ Bleft
update N1(x + dx, t + dt) → N1(x + dx, t)+(B − Bleft)
Diffusion is performed in a similar way for species 2.
In practice, we set dt = 1 and dx = 1 without loss of generality. We also keep r1, r2, D1, and D2 small enough to ensure that the probabilities in binomial distributions remain smaller than one.
Evolutionary simulations without trade-off
At each time point, each division gives rise to a mutation, with a probability of 5%. Each new phenotype are randomly drawn from a normal distribution centered on the ancestor phenotype, with a standard deviation of 0.1 times the phenotype in each direction. To speed up the simulations, subpopulations that did not reach a certain size after a certain time since they appeared are cleared up and their counts are randomly distributed over the remaining populations.
Evolutionary simulations with trade-off
At each time point, each division gives rise to a mutation, with a probability of 1%. Each new phenotype randomly falls on the trade-off line (uniform distribution), which is splitted into 500 bins within the first quadrant of the space (r, D).
Appendix D: Statistical analysis
Figure 3C
To study the shape of the four classes of outcomes in the density-distance space (Figure 3C), we performed a classification with a multinomial logistic regression. Each boundary between two adjacent classes is tested independantly. In practice, we used the function mnrfit of MATLAB to fit the data with a power law model.
| (D1) |
where Class is 0 or 1 for each of the two tested classes.
The boundary between the two classes is defined by Class = 0.5:
| (D2) |
The exponent (−a1/a2) is lower than 1 (with statistical significance reported in the table below, the brackets represent 95% confidence intervals which are calculated from standard deviations calculated by the multinomial logistic regression and combined using Fieller’s theorem) in the three cases indicating that boundaries between classes have a concave shape, in agreement with the 2-species FKPP model.
| Boundary | exponent [95% confidence interval] |
|---|---|
| no trace - few traces | 0.24 [0.11, 0.38] |
| few traces - partial sweep | 0.43 [0.22, 0.63] |
| partial sweep - full sweep | 0.57 [0.27, 0.88] |
Figure S2
Figure S2 shows the results of the competition wildtype vs hyperswarmer on a plate when the spatial structure is suppressed. The wildtype outcompetes the hyperswarmer mutant. The significance of this result is estimated using a generalized linear model for binomial data (function fitglm.m in MATLAB). We used the formula c ~ 1 + f +(1|R)+(f|S), where c is the wildtype count, f is the categorical variable ‘before competition’ or ‘after competition’, R is the replicate index, and S is the color index (we performed the two types of experiments: wildtype GFP vs. hyperswarmer DsRed, and wildtype DsRed vs. hyperswarmers GFP). The fit gave a p-value = 5.8 × 10−5.
Literature Cited
- Agostinho AA, Suzuki HI, Fugi R, Alves DC, Tonella LH, and Espindola LA. 2015. Ecological and life history traits of hemiodus orthonops in the invasion process: looking for clues at home. Hydrobiologia 746:415–430. [Google Scholar]
- Biddle A, Liang X, Gammon L, Fazil B, Harper LJ, Emich H, Costea DE, and Mackenzie IC. 2011. Cancer stem cells in squamous cell carcinoma switch between two distinct phenotypes that are preferentially migratory or proliferative. Cancer research 71:5317–5326. [DOI] [PubMed] [Google Scholar]
- Bouin E, Calvez V, Meunier N, Mirrahimi S, Perthame B, Raoul G, and Voituriez R. 2012. Invasion fronts with variable motility: Phenotype selection, spatial sorting and wave acceleration. Comptes Rendus Mathematique 350:761–766. [Google Scholar]
- Burton OJ, Phillips BL, and Travis JMJ. 2010. Trade-offs and the evolution of life-histories during range expansion. Ecology letters 13:1210–1220. [DOI] [PubMed] [Google Scholar]
- Bénichou O, Calvez V, Meunier N, and Voituriez R. 2012. Front acceleration by dynamic selection in fisher population waves. Physical review. E, Statistical, nonlinear, and soft matter physics 86:041908. [DOI] [PubMed] [Google Scholar]
- Carmona-Fontaine C, Matthews HK, Kuriyama S, Moreno M, Dunn GA, Parsons M, Stern CD, and Mayor R. 2008. Contact inhibition of locomotion in vivo controls neural crest directional migration. Nature 456:957–961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chuang A, and Peterson CR. 2016. Expanding population edges: theories, traits, and trade-offs. Global change biology 22:494–512. [DOI] [PubMed] [Google Scholar]
- Dai L, Korolev KS, and Gore J. 2013. Slower recovery in space before collapse of connected populations. Nature 496:355–358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Mazancourt C, and Dieckmann U. 2004. Trade-off geometries and frequency-dependent selection. The American naturalist 164:765–778. [DOI] [PubMed] [Google Scholar]
- Deforet M, Carmona-Fontaine C, Korolev KS, and Xavier JB. 2019. Data from: Evolution at the edge of expanding populations. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deforet M, van Ditmarsch D, Carmona-Fontaine C, and Xavier JB. 2014. Hyperswarming adaptations in a bacterium improve collective motility without enhancing single cell motility. Soft matter 10:2405–2413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deforet M, van Ditmarsch D, and Xavier JB. 2015. Cell-size homeostasis and the incremental rule in a bacterial pathogen. Biophysical journal 109:521–528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher RA 1937. The wave of advance of advantageous genes. Annals of Eugenics 7:355–369. [Google Scholar]
- Fraebel DT, Mickalide H, Schnitkey D, Merritt J, Kuhlman TE, and Kuehn S. 2017. Environment determines evolutionary trajectory in a constrained phenotypic space. eLife 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fronhofer EA, and Altermatt F. 2015. Eco-evolutionary feedbacks during experimental range expansions. Nature communications 6:6844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gandhi SR, Yurtsev EA, Korolev KS, and Gore J. 2016. Range expansions transition from pulled to pushed waves as growth becomes more cooperative in an experimental microbial population. Proceedings of the National Academy of Sciences of the United States of America 113:6922–6927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ganeshaiah KN, and Shaanker RU. 1991. Seed size optimization in a wind dispersed tree butea monosperma: A trade-off between seedling establishment and pod dispersal efficiency. Oikos 60:3–6. [Google Scholar]
- Garbelotto M, Rocca GD, Osmundson T, di Lonardo V, and Danti R. 2015. An increase in transmission-related traits and in phenotypic plasticity is documented during a fungal invasion. Ecosphere 6. [Google Scholar]
- Gerlee P, and Nelander S. 2012. The impact of phenotypic switching on glioblastoma growth and invasion. PLoS computational biology 8:e1002556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillespie JH 2010. Population genetics: a concise guide. JHU Press. [Google Scholar]
- Giometto A, Rinaldo A, Carrara F, and Altermatt F. 2014. Emerging predictable features of replicated biological invasion fronts. Proceedings of the National Academy of Sciences of the United States of America 111:297–301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo J-S, and Wu C-H. 2014. Dynamics for a two-species competition–diffusion model with two free boundaries. Nonlinearity 28:1–27. [Google Scholar]
- Hallatschek O, and Fisher DS. 2014. Acceleration of evolutionary spread by long-range dispersal. Proceedings of the National Academy of Sciences of the United States of America 111:E4911–E4919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallatschek O, Hersen P, Ramanathan S, and Nelson DR. 2007. Genetic drift at expanding frontiers promotes gene segregation. Proceedings of the National Academy of Sciences of the United States of America 104:19926–19930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallatschek O, and Nelson DR. 2008. Gene surfing in expanding populations. Theoretical population biology 73:158–170. [DOI] [PubMed] [Google Scholar]
- Holzer M, and Scheel A. 2014. Accelerated fronts in a two-stage invasion process. SIAM Journal on Mathematical Analysis 46:397–427. [Google Scholar]
- Huang F, Peng S, Chen B, Liao H, Huang Q, Lin Z, and Liu G. 2015. Rapid evolution of dispersal-related traits during range expansion of an invasive vine mikania micrantha. Oikos 124:1023–1030. [Google Scholar]
- Hudson CM, Brown GP, Shine R, and Phillips BL. 2015. Virgins in the vanguard: low reproductive frequency in invasion-front cane toads. Biological Journal of the Linnean Society 116:743–747. [Google Scholar]
- Hughes CL, Hill JK, and Dytham C. 2003. Evolutionary trade-offs between reproduction and dispersal in populations at expanding range boundaries. Proceedings. Biological sciences 270 Suppl 2:S147–S150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jessup CM, Kassen R, Forde SE, Kerr B, Buckling A, Rainey PB, and Bohannan BJM. 2004. Big questions, small worlds: microbial model systems in ecology. Trends in ecology & evolution 19:189–197. [DOI] [PubMed] [Google Scholar]
- Kim IS, Heilmann S, Kansler ER, Zhang Y, Zimmer M, Ratnakumar K, Bowman RL, Simon-Vermot T, Fennell M, Garippa R, Lu L, Lee W, Hollmann T, Xavier JB, and White RM. 2017. Microenvironment-derived factors driving metastatic plasticity in melanoma. Nature communications 8:14343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King JR, and McCabe PM. 2003. On the fisher-kpp equation with fast nonlinear diffusion. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences 459:2529–2546. [Google Scholar]
- Kolmogorov A, Petrovskii I, and Piscunov N. 1937. A study of the equation of diffusion with increase in the quantity of matter, and its application to a biological problem. Byul. Moskovskogo Gos. Univ 1:1–25. [Google Scholar]
- Korolev KS 2015. Evolution arrests invasions of cooperative populations. Physical review letters 115:208104. [DOI] [PubMed] [Google Scholar]
- Lehe R, Hallatschek O, and Peliti L. 2012. The rate of beneficial mutations surfing on the wave of a range expansion. PLoS computational biology 8:e1002447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis MA, Li B, and Weinberger HF. 2002. Spreading speed and linear determinacy for two-species competition models. Journal of mathematical biology 45:219–233. [DOI] [PubMed] [Google Scholar]
- Mitri S, Clarke E, and Foster KR. 2016. Resource limitation drives spatial organization in microbial groups. The ISME journal 10:1471–1482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray J 2007. Mathematical Biology. Springer. [Google Scholar]
- Nadell CD, Foster KR, and Xavier JB. 2010. Emergence of spatial structure in cell groups and the evolution of cooperation. PLoS computational biology 6:e1000716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ni B, Ghosh B, Paldy FS, Colin R, Heimerl T, and Sourjik V. 2017. Evolutionary remodeling of bacterial motility checkpoint control. Cell reports 18:866–877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ochocki BM, and Miller TEX. 2017. Rapid evolution of dispersal ability makes biological invasions faster and more variable. Nature communications 8:14315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okubo A, Maini PK, Williamson MH, and Murray JD. 1989. On the spatial spread of the grey squirrel in britain. Proceedings of the Royal Society of London. Series B, Biological sciences 238:113–125. [DOI] [PubMed] [Google Scholar]
- Otto SP, and Whitlock MC. 1997. The probability of fixation in populations of changing size. Genetics 146:723–733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peischl S, Dupanloup I, Kirkpatrick M, and Excoffier L. 2013. On the accumulation of deleterious mutations during range expansions. Molecular ecology 22:5972–5982. [DOI] [PubMed] [Google Scholar]
- Perkins TA, Boettiger C, and Phillips BL. 2016. After the games are over: life-history trade-offs drive dispersal attenuation following range expansion. Ecology and evolution 6:6425–6434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perkins TA, Phillips BL, Baskett ML, and Hastings A. 2013. Evolution of dispersal and life history interact to drive accelerating spread of an invasive species. Ecology letters 16:1079–1087. [DOI] [PubMed] [Google Scholar]
- Phillips BL 2015. Evolutionary processes make invasion speed difficult to predict. Biological Invasions 17:1949–1960. [Google Scholar]
- Phillips BL, Brown GP, and Shine R. 2010. Life-history evolution in range-shifting populations. Ecology 91:1617–1627. [DOI] [PubMed] [Google Scholar]
- Phillips BL, Brown GP, Webb JK, and Shine R. 2006. Invasion and the evolution of speed in toads. Nature 439:803. [DOI] [PubMed] [Google Scholar]
- Pianka ER 1970. On r- and k-selection. The American Naturalist 104:592–597. [Google Scholar]
- Pigolotti S, Benzi R, Perlekar P, Jensen MH, Toschi F, and Nelson DR. 2013. Growth, competition and cooperation in spatial population genetics. Theoretical population biology 84:72–86. [DOI] [PubMed] [Google Scholar]
- Ramanantoanina A, Ouhinou A, and Hui C. 2014. Spatial assortment of mixed propagules explains the acceleration of range expansion. PloS one 9:e103409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reich P, Oleksyn J, and Tjoelker M. 1994. Seed mass effects on germination and growth of diverse european scots pine populations. Canadian Journal of Forest Research 24:306–320. [Google Scholar]
- Reiter M, Rulands S, and Frey E. 2014. Range expansion of heterogeneous populations. Physical review letters 112:148103. [DOI] [PubMed] [Google Scholar]
- Richardson D, Cowling RM, and Le Maitre DC. 1990. Assessing the risk of invasive success in pinus and banksia in south african mountain fynbos. Journal of Vegetation Science 1:629–642. [Google Scholar]
- Shine R, Brown GP, and Phillips BL. 2011. An evolutionary process that assembles phenotypes through space rather than through time. Proceedings of the National Academy of Sciences of the United States of America 108:5708–5711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simmons AD, and Thomas CD. 2004. Changes in dispersal during species’ range expansions. The American naturalist 164:378–395. [DOI] [PubMed] [Google Scholar]
- Stevens VM, Whitmee S, Le Galliard J-F, Clobert J, Böhning-Gaese K, Bonte D, Brändle M, Matthias Dehling D, Hof C, Trochet A, and Baguette M. 2014. A comparative analysis of dispersal syndromes in terrestrial and semi-terrestrial animals. Ecology letters 17:1039–1052. [DOI] [PubMed] [Google Scholar]
- Tilman D 1994. Competition and biodiversity in spatially structured habitats. Ecology 75:2–16. [Google Scholar]
- Travis J, and Dytham C. 2002. Dispersal evolution during invasions. Evol Ecol Res 4:1119–1129. [Google Scholar]
- van Ditmarsch D, Boyle KE, Sakhtah H, Oyler JE, Nadell CD, Déziel É, Dietrich LEP, and Xavier JB. 2013. Convergent evolution of hyperswarming leads to impaired biofilm formation in pathogenic bacteria. Cell reports 4:697–708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waite AJ, Frankel NW, Dufour YS, Johnston JF, Long J, and Emonet T. 2016. Non-genetic diversity modulates population performance. Molecular systems biology 12:895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiss-Lehman C, Hufbauer RA, and Melbourne BA. 2017. Rapid trait evolution drives increased speed and variance in experimental range expansions. Nature communications 8:14303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Widmer DS, Cheng PF, Eichhoff OM, Belloni BC, Zipser MC, Schlegel NC, Javelaud D, Mauviel A, Dummer R, and Hoek KS. 2012. Systematic classification of melanoma cells by phenotype-specific gene expression mapping. Pigment cell & melanoma research 25:343–353. [DOI] [PubMed] [Google Scholar]
- Williams JL, Kendall BE, and Levine JM. 2016. Rapid evolution accelerates plant population spread in fragmented experimental landscapes. Science (New York, N.Y.) 353:482–485. [DOI] [PubMed] [Google Scholar]
- Xavier JB, Kim W, and Foster KR. 2011. A molecular mechanism that stabilizes cooperative secretions in pseudomonas aeruginosa. Molecular microbiology 79:166–179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan J, Deforet M, Boyle KE, Rahman R, Liang R, Okegbe C, Dietrich LEP, Qiu W, and Xavier JB. 2017. Bow-tie signaling in c-di-gmp: Machine learning in a simple biochemical network. PLoS computational biology 13:e1005677. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All experimental data (shown in Fig. 1 and Fig. 3), and simulation results for Fig. 1 and Fig. 2 (as well as MATLAB scripts to generate them), are available in the Dryad Digital Repository (Deforet et al. 2019).