Earth's water reservoirs in a changing climate

Abstract

Progress towards achieving a quantitative understanding of the exchanges of water between Earth's main water reservoirs is reviewed with emphasis on advances accrued from the latest advances in Earth Observation from space. These exchanges of water between the reservoirs are a result of processes that are at the core of important physical Earth-system feedbacks, which fundamentally control the response of Earth's climate to the greenhouse gas forcing it is now experiencing, and are therefore vital to understanding the future evolution of Earth's climate. The changing nature of global mean sea level (GMSL) is the context for discussion of these exchanges. Different sources of satellite observations that are used to quantify ice mass loss and water storage over continents, how water can be tracked to its source using water isotope information and how the waters in different reservoirs influence the fluxes of water between reservoirs are described. The profound influence of Earth's hydrological cycle, including human influences on it, on the rate of GMSL rise is emphasized. The many intricate ways water cycle processes influence water exchanges between reservoirs and thus sea-level rise, including disproportionate influences by the tiniest water reservoirs, are emphasized.

1. Introduction

Earth is a watery place, hence its name—the blue planet. Its ability to support water in its three forms—vapour, liquid and solid—makes Earth a unique planet within the solar system. Through its properties as a greenhouse gas, water vapour determines the Earth's temperature, making the planet habitable, and allowing the oceans to exist in liquid form so that they can transport heat and nutrients around the Earth system. Precipitation sustains life on Earth, and the great ice sheets help to regulate Earth's weather and climate. At the same time, the hydrological cycle which describes the movement of water between these three phases of water—vapour, liquid and solid—is determined by the weather and climate. And the latent heat, which is released or taken up when water changes from one phase to another, is a fundamental driver of Earth's weather and climate systems. So, a symbiotic relationship exists between water, weather, climate and indeed all life on Earth.

Although there are different hypotheses about where Earth's water came from [1], we are certain that the amount of water currently on Earth is the same as it was billions of years ago. Throughout Earth's history, water has been distributed between four distinct reservoirs—the oceans, ice sheets and glaciers (the cryosphere), terrestrial storage and the atmosphere. Today, the oceans contain about 96.5% of all Earth's water with an average salinity of around 35 grams of salt per kilogram of seawater. About 1% of Earth's water is saline groundwater, and approximately 2.5% constitutes the fresh water of the planet. This fresh water can be further disaggregated into three main reservoirs. The first is the cryosphere which represents about 68.5% of all fresh water on Earth, primarily stored in ice sheets and glaciers. The remaining fresh water (approx. 31%) is mostly in land reservoirs in the form of surface water (lakes and rivers), and as soil moisture, but with the majority being in underground water in aquifers.

The atmosphere is the smallest reservoir of fresh water, being only 0.1% of all fresh water found on Earth. This water exists in three phases, with 99.9% of it in the form of vapour, and the remaining 0.1% of the water in the atmosphere being suspended liquid and solid water in clouds. However, these tiny amounts of water in the atmosphere have disproportionate influences on fluxes to and from all other reservoirs as we highlight below and indeed on the overall energy balance of the planet. Without water vapour in the atmosphere the Earth would be substantially colder and life as we know it would not exist.

In the past, as the Earth has gone through major climatic shifts, such as glacial-interglacial cycles associated with changes in solar forcing, there have been substantial movements of water between these reservoirs that can be expressed as changes in global mean sea level (GMSL). From as far back as 1700, GMSL was fairly constant [2] until the early twentieth century when it began to rise, and as figure 1 shows, it is now increasing at a rate of approximately 3 cm decade⁻¹ according to the satellite altimetry observational record that began in 1992 (e.g. [4]). Some of this can be attributed to thermal expansion (figure 1) because the planet has been warming due to human emissions of greenhouse gases. The oceans, with their high thermal capacity, take up over 90% of this additional warming [5,6]. However, the largest contribution to the increases in GMSL we observe today is due to an increase in the mass of the oceans (figure 1) associated with changes in the water cycle in response to anthropogenic forcing.

Figure 1.

Time series of global mean sea level (GMSL) recorded since 1992 from altimeter measurements on orbiting satellites [3]. This can be partitioned between changes in ocean mass derived from gravity fluctuation measurements from the space-borne gravity observing system (see box 1 and blue curve) and in ocean heat content derived from in situ measurements by ARGO floats (red). (Online version in colour.)

The mass of ocean water is determined fundamentally by three distinct processes, which involve water moving from one reservoir to another: (i) the balance between evaporation and precipitation (ocean-atmosphere exchange); (ii) the addition or extraction of fresh water by ice sheets and glaciers (ocean-cryosphere exchange); (iii) the run-off of fresh water into the oceans by rivers, whose flow rates are themselves determined by the land balance between precipitation and evapotranspiration (ocean-land-atmosphere exchange). In other words, the water cycle is fundamental to GMSL, and the observed increase in GMSL is a manifestation of profound changes in the water cycle as the planet warms.

The movement of water between reservoirs, fundamental to the problem of GMSL change, only involves freshwater and so the ocean salinity can also act as a signature of the integrated exchanges between water reservoirs. Beyond that, ocean salinity affects ocean density and hence can drive changes in ocean circulation, such as the overturning, thermohaline circulation. This, in turn, has profound consequences on the exchanges between the reservoirs and ultimately climate itself. Understanding the freshwater budget is, therefore, fundamental to understanding the evolution of the Earth system and its response to climate change.

Figure 1 shows that, beyond the overall trend in GMSL, large interannual variations in GMSL exist that exemplify the impacts of exchanges that occur between water reservoirs. Figure 2 is the de-trended time series of both sea-level rise (SLR) anomalies (SLRA) and ocean water mass anomalies (figure 2a), and between SLRA and latent heat flux anomalies (figure 2b). It is clear that fluctuations in the rate of SLR are significantly influenced by small fluctuations in the ocean water mass and thus in the fluxes of freshwater to and from the ocean, conveyed in part by the latent heat flux anomalies of figure 2b.

Figure 2.

(a) De-trended time series of sea-level rise to give sea-level anomalies (SLA_total), contribution to SLA of ocean water mass variations (SLA_mass) and sea surface salinity anomalies (SSSA) averaged between 50 N and 50S from the measurements of the SMOS satellite expressed in terms of practical salinity units (PSU). (b) Time series of SLA and latent heat flux anomalies (LH) averaged between 50 N and 50 S. The correlation between these two time series is −0.7 after 2012. (Online version in colour.)

Also shown in figure 2a is the time series of sea surface salinity (SSS) anomalies provided by satellite observations from the soil moisture and ocean salinity (SMOS) satellite [7] averaged between 50°N and 50°S. As discussed later, time series of SSS reflect the water exchanges between the oceans and atmosphere and offer a glimpse of how Earth's hydrological cycle varies and how this variation is intimately connected to many of Earth's responses to global warming.

Figures 1 and 2 convey a further important point, that it is the coupled interactions between the various elements of the water cycle which lie at the core of important physical feedbacks that influence the ultimate response of the entire Earth system to both internal and external forcings. While this particular view of Earth's water within the Earth system is not new, the latest advances in Earth Observation are enabling us to document the small shifts of water that are occurring between these reservoirs today; these small exchanges fundamentally control the response of Earth's climate to the greenhouse gas forcing it is now experiencing, and are therefore vital to understanding the future of our planet.

The purpose of this paper is to review progress toward understanding Earth's water reservoirs based on the latest technologies in Earth Observations. It focuses on the global perspectives, framed around GMSL, with an emphasis on the interactions between the various reservoirs. We start with an overview of the current understanding of water reservoirs and the fluxes between them. This is followed with a more in-depth review around individual reservoirs and exchanges that occur between them. A brief synopsis of different sources of data and types of satellite instrumentation used to construct this view is provided in the annex (box 1).

Box 1. Monitoring Earth's ancient waters.

Water locked deep in Earth's major ice sheets or stored in its aquifers is water that fell from the atmosphere as rain and snow over time and as long ago as hundreds of thousands to millions of years ago. Radioactive isotopes analysed from groundwater samples have been used to characterize the age of Earth's ground water as illustrated in the studies of Yokochi et al. [8] and Gleeson et al. [9]. Yokochi et al. [8] used radiokrypton ⁸¹Kr, a radioactive cosmogenic isotope, to determine the paleo-climatic sources of recharge of the subsurface water in the Nubian Sandstone Aquifer in the Negev Desert, Israel. They could identify two distinct moisture sources of the recharge: one less than 38 ka from the Mediterranean and the other approximately 361 ka from the tropical Atlantic. Gleeson et al. [9] use tritium (³H), a radioactive isotope of hydrogen, to quantify the more recent age of groundwater less than 100 years old (young groundwater) and the fraction that is modern (younger than 50 years old). That study concludes that less than 6% of the groundwater in the uppermost portion of Earth's landmass is modern. These reservoirs of ancient water, and modern water in particular, are now being disrupted by human activities as a result of ice melt as the planet warms, and by increased pumping of fossil water to the surface for irrigation and human water resources.

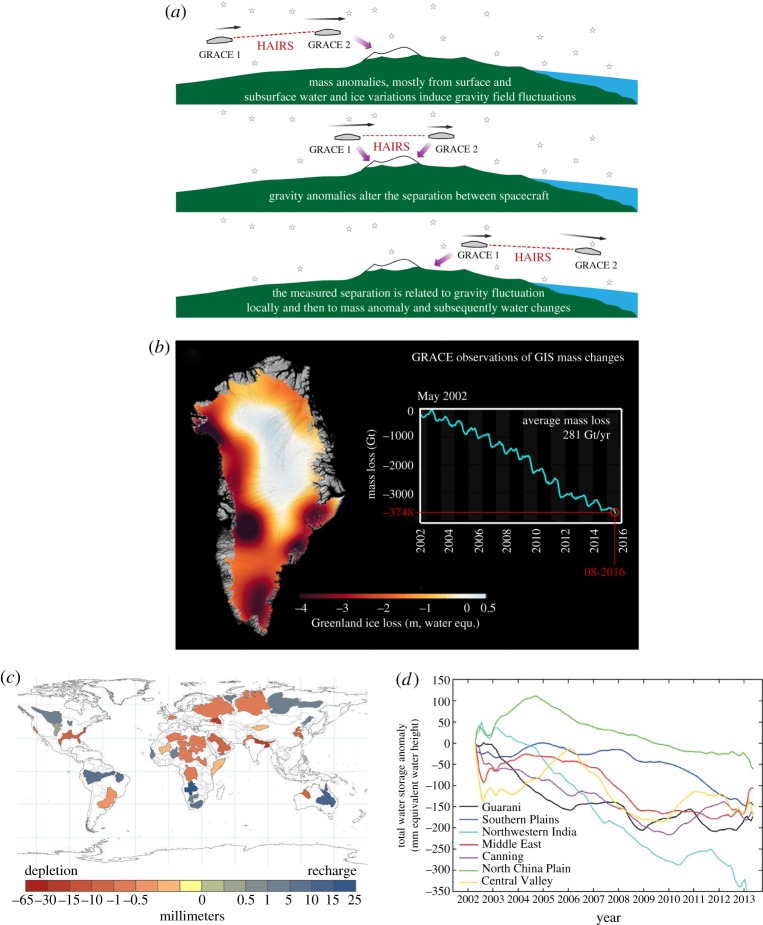
Figure B1.

(a) The GRACE measurement approach: gravity field fluctuations, a result of surface and subsurface mass variations, are used to estimate the changes to water mass within Earth water reservoirs. (b) The systematic ice mass loss from Greenland over the GRACE observing period from 2002 to 2016. (c) GRACE groundwater storage annual trends for Earth's 37 largest aquifers for period 2003–2013 (from [10]). (c,d) Water storage declines (millimetre equivalent water height) in several of the world's major aquifers in Earth's arid and semi-arid mid-latitudes, derived from the NASA GRACE satellite mission. The monthly storage changes are shown as anomalies for the period April 2002–May 2013, with 24-month smoothing. (Online version in colour.)

A series of mass change missions (MC), including the NASA Gravity Recovery and Climate Experiment (GRACE) satellite mission, the GRACE Follow-on (GRACE-FO) and the Gravity field steady-state Ocean Circulation Explorer (GOCE, [11]) provides a way of monitoring the changes to these ancient waters by observing monthly changes to the Earth's gravity field. After the removal of signals owing to changes in the solid Earth and atmosphere, the movements of water and ice through the Earth system at specific temporal and spatial scales can be identified.

The measurement technique of GRACE is highlighted in figure B1a. Gravity anomalies are derived from precise measurements of the changing distance between twin GRACE satellites in near-circular, polar orbits at 460 km altitude, that maintain along-track separation of ≈ 220 ± 50 km. GRACE has collected science data near continuously since the commissioning of the mission in April 2002 through to August 2016 with the mission ending primarily through the failure of spacecraft batteries. GRACE-FO was launched in May of 2018.

Gravity measurements have provided important insights on how mass loss from Earth's major ice sheets in Greenland and Antarctica that are a major contributor to rising sea levels (figure 1). GRACE measurements have shown that Greenland has lost on average 281 gigatonnes (Gt) of ice per year between 2002 and 2016, and that this loss is focused in particular regions (figure B1b). As discussed by Bevis et al. [12] and §4 below, the recent de-glaciation of Greenland is a response to both oceanic and atmospheric forcing, acting on different parts of the ice sheet.

Surface water is the principal freshwater supply that meets human water demand globally. However, our dependence on modern groundwater has increased over time as surface supplies become less reliable and predictable [13] and demands for freshwater from the growing populations increase. Groundwater is currently the primary source of freshwater for approximately two billion people while half or more of the irrigation water used to grow the world's food is supplied from underground sources [14]. Despite its importance, knowledge on the state of large groundwater systems is limited, compared to surface water [14,15], largely because the prohibitive cost and complexity of monitoring large aquifer systems. GRACE observations in part address this observing gap and now provide a measure of changes to groundwater storage (figure B1c). Analysis of GRACE data suggests that eight of the world's largest 37 aquifers are being stressed at critically unsustainable rates of depletion (figure B1c; [10]). Nearly, all of these aquifers underlie the word's great agricultural regions and are primarily responsible for their high productivity.

2. Exchanges between Earth's water reservoirs

The main reservoirs of water expressed as water volume shown in figure 3 is similar to and an update of previous depictions of Earth's water budget (e.g. Shiklomanov, and Sokolov, [16,20]). As noted, the oceans are the main reservoir for Earth's water, and the cryosphere is the main reservoir of Earth's freshwater. While estimates of the volume of water in the oceans can be linked to altimeter satellite observations [17], and the volumes of water in Earth's major ice sheets and the atmosphere can also be deduced from measurements, including those from Earth-orbiting satellites (e.g. figure 11 below), as noted the volume of water below the Earth's surface over land, the groundwater (GW), is less certain (e.g. [21]). Even estimates of water volumes of individual aquifer basins can vary by up to an order of magnitude [10]. The fraction of this groundwater that is fresh is even less known because there are no direct observations and few estimates of it exist. Shiklomanov & Sokolov [16] estimate this fraction to be approximately 48% of the total GW. More importantly, the fraction of this fresh water that is both accessible and can be sustainably extracted for human use, considered to be the modern GW fraction, is estimated to be only 1–5% of the total GW (e.g. [9,10,21]).

Figure 3.

Earth's main water reservoirs and the fluxes of water between them. Also shown are known estimates of the change in these fluxes. All fluxes and estimates of change correspond to the period of the beginning of Earth observations and this period varies depending on the fluxes and studies that produce them. Updated from [9,16–18] and other sources including [19]. The flux changes, largely unknown, are denoted by Δ and those highlighted in red have an observational or physical basis underlying them. (Online version in colour.)

Figure 11.

(a) The annual frequency of ice and (b) water clouds over Greenland from joint CloudSat, CALIPSO observations. (c) The average relationship between mean liquid and ice water paths of clouds and the mean annual effect of these clouds on the surface radiation balance. This effect is positive at each location, indicative of the greenhouse effect, and increases with thicker clouds as the cloud water paths increase. (d) Evolution of GrIS SMB indicates that the cloudy simulations with an associated greenhouse effect have a lower SMB as a result of greater melt. Shaded areas indicate uncertainties (adapted from [104]). (Online version in colour.)

More important than the volumes of the individual reservoirs are the fluxes of water between them. These fluxes are primarily associated with (i) precipitation and evaporation between the atmosphere and other reservoirs, (ii) water fluxing to the oceans from the cryosphere as ice melts, and (iii) run-off from the land. Many of the flux estimates provided in figure 3 are derived from the observational synthesis study of Rodell et al. [19], which integrated a large volume of satellite and in situ data and developed a water cycle budget both constrained by the uncertainties those authors attached to the individual observed fluxes and by the global energy balance described in a related study by L'Ecuyer et al. [22].

Quantifying the fluxes of water between the reservoirs continues to challenge the climate science community and deriving them from Earth Observations has been and continues to be an important goal of the World Climate Research Program's Global Energy and Water Exchanges (GEWEX) project (GEWEX, e.g. [23,24]). Estimating the even smaller changes to these fluxes over time as the planet warms is especially challenging. In reality, water is continually shifting in ways that significantly influence the Earth's climate, and these fluxes and their changes over time are highly relevant to understanding Earth system interactions and their response to climate change.

The depiction of water exchanges between reservoirs provided in figure 3, with only small fluxes between the reservoirs, might be misinterpreted as depicting a largely stagnant water cycle. For example, it would take about 3300 years to evaporate all of the water from the ocean at the current rate of evaporation. The fresh water within and on land would be lost after approximately 190 years using the same argument, and all the ice from Earth's major ice sheets would be removed after 640 years given current ice mass discharge estimates. By contrast, the tiny reservoir of water contained within the atmosphere is constantly being recycled at a rapid rate. The annual amount of precipitation accumulating at the Earth's surface is about 38 times the atmosphere's total capacity to hold water in the form of water vapour at current temperatures. This indicates that water cycles between the Earth's surface and the atmosphere notionally at a rate slightly less than 10 days, which is tiny compared to that for the ocean and land (box 2).

Box 2. Tracking the land-ocean exchanges of water vapour using water isotopes.

It is reasonable to suppose that a significant source of the water that precipitates over land derives from evaporation from the oceans, and is transported by the atmospheric circulation to remote regions. The Indian Summer Monsoon is a prime example where the gathering of moisture from the expanse of the Indian Ocean by the monsoon winds is the fundamental source of water for the monsoon rains. By contrast, for some continental areas, far removed from the influence of the oceans, a considerable fraction of rain water is re-cycled through evaporation from the land surface and transpiration from the vegetation that grows on it. Evidence for the local recycling of water has been difficult to obtain in the past, and climate models give very different estimates of how much water originates from the large-scale transports from the oceans versus local recycling (e.g. [25]).

Advances in the use of stable water isotopes to infer characteristic of re-cycling are transforming our understanding of the water cycle. By measuring concentrations of stable water isotopes in water vapour, soil water and rainwater, and in turn referencing these to ocean water, we are able to distinguish sources of water that define the fluxes of figure 3. For example, Benetti et al. [26] analysed in situ ocean water samples to combine measures of the stable isotopes of ocean water with SSS from which they could identify different ocean surface water masses and their horizontal advection, and about hydrological processes that influence ocean water such as whether evaporation or precipitation is a more dominant influence.

The use of stable water isotopes is made possible by the molecular differences among common water isotopes (referred to as isotopologues, such as H₂¹⁶O and HDO – ‘heavy water’). Fractionation of these isotopologues occurs when water changes phase. Heavier isotopes (HDO) preferentially condense, whereas lighter isotopes (H₂¹⁶O) preferentially evaporate [27]. This fractionation is commonly expressed in terms of a ratio (R) of concentrations of the heavier, rarer isotope to the more abundant, lighter isotope and then contrasted against the same ratio derived from the International Atomic Energy Agency (IAEA) Vienna Standard Mean Ocean Water (VSMOW). For example, the deuterium (D) composition of a given sample of water, R_samp, is expressed using the δ notation in units of per mil (‰)

$$\delta D=\frac{R_{\text{samp}}-R_{\text{VSMOW}}}{R_{\text{VSMOW}}}\times 1000.$$

Evaporation from the ocean surface and condensation during water vapour transport act to deplete the deuterium content relative to its source, resulting in typical isotopic composition values of δD of approximately −70 to −80‰ for tropical ocean waters. By contrast, little fractionation occurs during steady-state evapotranspiration over land, so that the mean isotopic composition of evapo-transpired vapour is close to that of soil water [28,29], and thus has characteristically smaller negative values of δD, typically in the range −20 to −40‰. Using δD, we can, therefore, separate ocean evaporation and terrestrial evapotranspiration (ET) as isotopically distinct moisture sources, with terrestrial ET relatively enriched in deuterium compared to water evaporated from the ocean.

Figure B2 is an example of analysis of satellite measurements from the Aura Tropospheric Emission Sounder (TES) of the specific humidity (q) and the deuterium content of water vapour (δD), for pressures in the free troposphere between 825 and 500 hPa, visualized in the form of a diagram expressing the joint distributions of these two measurements [30]. The data are for southern Amazonia corresponding to the transition from the dry season to the wet season (left two panels), and to the first 60 days of the wet season (right panel), for the years 2006–2010. Overlain on each figure are simple models describing the isotopic composition of water vapour from land (blue) or ocean (black) as it mixes with more isotopically depleted air in the upper troposphere. The isotopic composition of water vapour evaporated from tropical land generally has a value between 0 and −75‰, whereas water vapour originating from the tropical ocean generally has a range between −75 and −100‰ (e.g. [31,32] and refs therein). The dashed lines demonstrate what happens to that same water vapour if instead it undergoes repeated condensation.

Any values above the solid black (ocean model) line are, therefore, likely from a tropical land source. The value ‘Diff-Land’ describes the mean and RMS of the observations' isotopic composition relative to the ocean mixing model for a given humidity. The left panels show that the air above the Amazon during the dry season is a combination of transpired humidity and other air-parcels that are likely a combination of ocean and land-sources that have undergone mixing and condensation. Right before the rainy season the distribution shifts upwards to the right with many more air parcels now likely originating from evapotranspiration. After the rainy season begins, there is more frequent advection of air from the ocean as well as heavily depleted air-parcels that are due to more frequent deep convection (more distillation of heavy isotopes via convective precipitation) resulting in depleted HDO. These shifts in the q – δD distributions over the S. Amazon provide direct observational evidence that rainforest transpiration during the late dry season plays a central role in initiating the dry-to-wet season transition over the southern Amazon.

Figure B2.

Joint distributions of water vapour and its deuterium content (δD) in the lower troposphere (825–500 hPa) based on TES observations during the pre-transition stage (day −60 to −30, a), early transition (day 30–0, b), and the first 60 days of the Amazonian wet season (day 0–60, c). Simple models of evaporation and mixing from land and ocean (solid blue and black, respectively) as well as rainfall/Rayleigh models (dotted blue and black) are shown for comparison.

3. Ocean exchanges

(a). Sea surface salinity

When the ocean exchanges water with other reservoirs it does so via freshwater thus altering the salinity of ocean water. The bulk correlation between SSS anomalies and GRACE ocean mass anomalies, highlighted in figure 2, hints at this direct relationship. In fact, we have known since the earliest of oceanographic measurements, almost a century ago, that ocean salinity highly correlates with the net exchange of water between the ocean and atmosphere. This relation, adapted from the historical study of Wüst [33], is highlighted in figure 4 showing the ship-based measured difference between precipitation (P) and evaporation (E) as a function of SSS (‰).

Figure 4.

The relation between zonal values of E-P and surface salinity (units are in practical salinity scale 1978 [34], after Wüst [33]. The solid line is the relation S (all seas) = 34.5 + 0.0175(E-P) also from [33].

Today we think of ocean salinity measurements as a window into understanding the regional patterns of change in E-P. Changing patterns of salinity also imply changing patterns of moisture sources to the atmosphere with subsequent effects on precipitation. This point is highlighted in the studies by Li et al. [35,36] which demonstrate a link between SSS anomalies in one season to precipitation anomalies in a subsequent season thus implying SSS information offers some potential for seasonal precipitation prediction. Specifically, Li et al. [35,36] illustrate the connections between springtime changes in SSS and the subsequent summer time changes in precipitation in both the U.S. midwest and African Sahel.

Figure 5 presents multi-decadal patterns of SSS change from several studies using historical in situ ocean data (e.g. [41] for review). Although these SSS reconstructions are noisy, making it difficult to deduce the mean net E-P trends, they all reveal similar patterns of change. Regions of increasing salinities correspond to the evaporation-dominated sub-tropics and mid-latitudes, and regions of decreasing salinities correspond to the rainfall-dominated regions such as the tropical atmospheric convergence zones and higher latitude storm track regions. The strong and coherent relationship between the change and mean patterns, expressed through the high spatial pattern correlation coefficient of approximately 0.7 [42], illustrates the notion of the ‘wet wetter and dry drier’ regional responses of the hydrological cycle change [43,44], whereby salty ocean regions (compared to the global mean) are becoming saltier and fresh regions are becoming fresher [45] thus supporting the notion of an intensification of the hydrological cycle over the period of time the SSS data have been collected.

Figure 5.

(a) A 58-year mean climatology of global sea surface salinity (SSS) after Durack & Wijffels [37]). (b–e) Four long-term estimates of global sea surface salinity (SSS) change, (b) from Durack & Wiffels ([37] analysis period 1950–2008), (c) Boyer et al. ([38]; analysis period 1955–1998), (d) Hosoda et al. ([39]; analysis period 1975–2005) and (e) Good et al. ([40]; analysis period 1950–2012) all scaled to represent equivalent magnitude changes over a 50-year period (practical salinity scale 1978, 50 yr^–1) (adapted from [41], fig. 2). (Online version in colour.)

(b). The 2010–2011 drop in GMSL

During the approximately 2-year period between 2010 and 2011, the GMSL dropped almost 5 mm (highlighted in both figures 1 and 2) despite a long-term background rate of rise of 3 mm per year. Using a combination of satellite and in situ data, Boening et al. [46] show that the decline in ocean mass, which explains the sea-level drop, coincides with an equivalent increase in terrestrial water storage, primarily over Australia, northern South America, and Southeast Asia. This temporary shift of water from the ocean to land is closely related to the transition from El Niño conditions in 2009/10 to a strong 2010/11 La Niña, which affected the global atmospheric circulation and hence ocean evaporation and precipitation patterns worldwide.

The observed shifts in precipitation and terrestrial water storage associated with the specific period of falling GMSL during 2010–2011 are highlighted in figure 6 (from [47]). This figure is a summary of the evolution both of water storage overland from GRACE and precipitation from the NASA TRMM satellite observations, from early 2010 to late 2011. Six-month averages are shown to reduce noise inherent to GRACE retrievals and resolve large-scale structures. Precipitation averages are offset three months from mass averages in order to assist in inferring their relationship to mass tendencies through the accumulation of precipitation over time.

Figure 6.

Evolution of GRACE (left column) and TRMM anomalies (right column) for six-month intervals during 2010 and 2011 when the GMSL dropped by almost 5 mm. Intervals shown for TRMM anomalies are offset by three months in order to provide context for changes in mass (fig. 3 of [47]).

Analysis of more than a decade of GRACE observations by Reager et al. [48] illustrates how interannual to decadal variations in continental water storage, driven by changes in the delivery of atmospheric moisture to the continents, profoundly influences the background trend of SLR over short periods of time. Figure 6 exemplifies this point illustrating how interannual variations in continental water storage, can substantially influence and even overwhelm the background trend of SLR over short periods of time. The analysis of Fasullo et al. [47] suggests that the retention of water within Australia, due to water that flows inward to its inland and closed drainage basins that lie below sea level, contributes uniquely and substantially to the intensity and persistence of global land hydrologic mass increase and thus to the 2011 drop in GMSL. The bounce back of sea level to its expected rate of rise is delayed because this inland water is only able to return water back to the oceans via evaporation, transport and eventual rainout.

4. Cryospheric exchanges

The melting of Earth's ice sheets and glaciers, and the subsequent runoff and discharge of ice into the oceans, are a major sources of freshwater exchange between the cryosphere and oceans, and a significant factor in recent SLR (figure 1).

(a). The Antarctic and Greenland ice sheets

The Antarctic and Greenland ice sheets (AIS and GrIS, respectively) together hold 25 million cubic km of ice, representing enough water to raise global sea level by 70 m. To first order, the mass balance of these major ice sheets is a quasi-balance between the snow that accumulates annually on an ice sheet and the annual loss of ice by melt and discharge. Annual snowfall on the ice sheets alone is estimated to be equivalent to approximately 6.5 mm of sea level, so that only small annual imbalances between snowfall and discharge of ice and melt water into the ocean could influence present-day sea-level rise.

Although estimation of ice sheet mass balance has been a main goal of glaciological research for decades, reliable observations of how ice mass has changed over recent time has only been possible with the advent of space observations. These current Earth observations indicate that neither the AIS nor the GrIS are in strict balance today. Mounginot et al. [49], for example, find the entire GrIS to have been in approximate balance between 1979 and 1990 but is now out of mass balance since that time. Total annual discharge is now increasing over time exceeding the estimated annual accumulation, with the result that there is a net ice loss from Earth's main ice sheets.

The mass balance of an ice sheet is currently deduced from observations in three primarily different ways (e.g. [50]):

• (i)The mass budget method—this is an approach that quantifies the individual components of the ice sheet mass budget. Snowfall is an important driver of temporal and spatial variability of ice sheet mass balance [46,51–53] and the snow accumulation over both AIS and GrIS has been inferred from different sources, ranging from direct observations of snowfall (e.g. [54]), inferences of accumulation from ice core data, meteorological reanalysis (e.g. [55]) and regional atmospheric climate models constrained by re-analysis (e.g. [56]). These different sources more or less agree with annual accumulations ranging from about 2000–2400 Gt yr⁻¹ over AIS and 400–900 Gt yr⁻¹ over GrIS. Snow accumulation from regional atmospheric climate models, forced by reanalysis data, and downscaled at the kilometre scale to capture melt processes along low elevation areas are estimated to have uncertainties of order 5–10% [57–59] based on comparison to in situ data in Greenland and Antarctica. Ice discharge is measured at the grounding line using new techniques for measuring ice velocity over large areas from interferometric synthetic-aperture radar (InSAR) data combined with ice thickness derived from airborne radar soundings or deduced from surface elevation data assuming hydrostatic equilibrium of ice in ocean waters. The velocity mapping technique is now advanced enough that the calibration of continental-scale mosaic of ice velocity does not require precision in situ measurements.
• (ii)Measurements of elevation change over time, such as by the Ice, Cloud and Land Elevation Satellite (ICESat) spaceborne lidar or by the European Cryosat, with a small-footprint radar altimeter. These changes in elevation are translated into measurements of volume change associated with isostatic rebound or tectonics. Satellite radar altimeters (Seasat, Geosat and European Remote Sensing Satellites ERS-1 and -2) have been used to infer elevation change rates over Greenland and Antarctica since 1978 but estimates have been improved considerably with the advent of Cryosat and ICESat. The largest source of uncertainty in these estimates is the conversion of volume to mass, which implies that we know at which density the volume changes are taking place, which could in principle be anywhere between the density of fresh snow (300 kgm⁻³) and the density of solid ice (917 kgm⁻³).
• (iii)Weighing of the ice sheets—gravity-change measurements from NASA's GRACE satellite mission provide a direct estimate of the mass changes as highlighted in Figure B1b, albeit over coarse spatial resolutions of the order of 300 km (e.g. [60–62).

Shepherd et al. [63] and later Shepherd et al. [64] reconciled the mass balances derived from these different methods providing a best estimate of the GrIS and AIS mass balance as part of an ESA/NASA supported Ice sheet Mass Balance Intercomparison Experiment 2011–12 (IMBIE). One conclusion of the study was that the three space-based methods produce consistent results, when properly applied to common periods; and that combinations of all methods yield more reliable estimates, with overall mass change estimates closely mirroring GRACE-only estimations. More recently, Mouginot et al. [49] and Rignot et al. [56], using the mass budget method, extended the time series of GrIS and AIS ice mass loss back to 1972 and 1979, respectively. These studies benefit from updated information taken from various sources including more complete time series of ice velocity, improvements in ice thickness available from NASA's Operation IceBridge (OIB, e.g. [65]), bathymetric surveys from NASA's Ocean Melting Greenland (OMG), and airborne gravity surveys. The authors use these sources of data and apply the mass budget method described above with the derived mass balances falling within errors of the IMBIE-2 multi-sensor assessment, except for East Antarctica where GRACE is affected by residual uncertainties in the GIA correction and the mass budget method indicates a sustained and substantial mass loss.

The analyses of Mouginet et al. [49,56] confirm that ice losses from both GrIS and AIS have accelerated over the entire period observed (e.g. Table 1). This acceleration is also evident in figure 7 showing the time series of the surface mass balance (SMB), discharge (D) and mass change (M = SMB-D). The Mouginot et al. assessment of GrIS loss (figure 7a) indicates that the ice sheet was in near balance between 1972 and 1990 after which time the loss of ice mass accelerated, being dominated by a small number of glaciers. Antarctica experienced relatively positive SMB anomalies between the 1970s and 1990s followed by negative SMB anomalies between the 1990s and 2017 (figure 7b) while ice discharge increased markedly after 2000. The total mass loss from Antarctica increased by a factor 6 over the period observed, from 40 ± 9 Gt yr⁻¹ in the 11-y time period 1979–1990 to 50 ± 14 Gt yr⁻¹ in 1989–2000, 166 ± 18 Gt yr⁻¹ in 1999–2009 and finally 252 ± 26 Gt yr⁻¹ in 2009–2017 (table 1). The loss of ice from Antarctica, however, is very regionally dependent with West Antarctica losing the most mass, while East Antarctica having lost smaller amounts. The mass loss in West Antarctica is also associated with enhanced polar westerlies, probably driven by persistent La Nina conditions in the tropical Pacific and its related atmospheric circulation anomalies (teleconnections). These enhanced westerlies were concentrated in areas closest to warm, salty, subsurface circumpolar deep water (e.g. [67]), and acted to push this sub-surface, warm, salty water toward Antarctica to melt its floating ice shelves, destabilize the glaciers, and raise sea level. In East Antarctica, more observations will be needed to confirm the mass loss, but the impact of warm circumpolar deep water is also evident there in sectors such as Wilkes Land, through the high rates of ice-shelf melt [68] and especially through recent discovery of relatively warm waters near some of its ice shelves [69].

Table 1.

Ice mass loss trends in Gt yr⁻¹ (1 mm of sea-level rise = 360 Gt yr⁻¹).

region	trend (Gt yr−1)	period	source
Antarctica ice sheet (AIS)	−40 ± 9	1979–1990	[56]
		−50 ± 14	1989–2000
		−166 ± 18	1999–2009
		−252 ± 26	2009–2017
	(−109 ± 26)	(1992–2017)	[64]
Greenland (GrIS)	+47 ± 21	1972–1980	[49]
		−51 ± 17	1980–1990
		−41 ± 17	1990–2000
		−187 ± 17	2000–2010
		−286 ± 20	2010–2018
	(−142 ± 49)	(1992–2011)	[63]
glaciers	−259 ± 28	2003–2009	[66]
total land ice (glaciers + AIS + GrIS)	549 ± 57	2003–2009	[66]

Figure 7.

Time series of cumulative anomalies in SMB (blue), ice discharge (D, red) and total mass (M, purple = SMB-D) in Gt of (a) GIS and (b) AIS with uncertainties. Also shown are the equivalent sea-level rise contributions attached to this ice mass loss (recreated from both [56] and [49]). (Online version in colour.)

(b). Glaciers

Glacial retreat is a highly visible indicator of global warming today and has delayed impacts on other parts of the Earth system. In addition to raising seawater levels, widespread retreat of glaciers affects human society by changing seasonal stream runoff, and increasing geohazards [70]. Huss & Hock [71] indicate that approximately half of 56 glaciated watersheds globally have already passed peak glacier runoff. Rounce et al. [72] identify the widespread expansion of glacier lakes due to retreat in Nepal from 2000 to 2015, which pose a glacier lake outburst flood hazard.

Glacier retreat reflects of strongly negative mass balances over the last 30 years [73]. Global estimates of glacier mass changes have traditionally been based on the extrapolation of local glaciological measurements. These records indicate a greater mass loss than subsequently estimated from early analysis of using the GRACE data satellite. Gardner et al. [66] provided the first consensus estimate of glacial ice loss from a synthesis of the mass-budget estimates from both satellite gravimetry and altimetry, and from local glaciological records. All regions examined lost mass during the 2003–2009 period reviewed, with the largest losses from Arctic Canada, Alaska, coastal Greenland, the southern Andes and high-mountain Asia. Over the period of study, the change in the global mass budget for all other glaciers was –259 ± 28 Gt yr⁻¹ which is comparable to the ice mass loss from the Greenland and Antarctica ice sheets alone over the same period of time. Gardner et al. [66] estimate that the mass loss of total land ice (all glaciers + ice sheets) is −549 ± 57 Gt yr⁻¹, amounting to a sea-level rise contribution of 1.51 ± 0.16 mm of sea-level equivalent per year, which is approximately 61% of the observed total global sea-level rise.

(c). Sea Ice

Another important component of the cryosphere is sea ice and its change over time. The freezing and melting seasonal cycle in Arctic sea ice means that fresh water is removed from the Arctic Ocean in winter as ice forms and returned to it in summer as ice melts with minimal overall exchange of water between the reservoirs. However, one of the strongest signals of a warming climate has been the systematic loss of Arctic sea ice especially in summer, which leads to the amplification of human-induced warming in the Arctic region due to the albedo feedback, and also impacts the Earth system in other ways. For example, the loss of sea ice acts to freshen and warm the waters of the Arctic Ocean and its surrounding seas, which may have the potential to affect the deep-water formation that drives the Atlantic Thermohaline Circulation. It has also been argued that Arctic amplification may affect the behaviour of the North Atlantic jet stream and other aspects of the global circulation, potentially giving rise to more extreme weather and climate events (e.g. [74]). Hence, despite the zero-sum impact of sea ice on SLR, the evolution of sea ice remains a major control on polar climate, which in turn affects the evolution of glaciers and ice sheets and thus the cryospheric water reservoir.

5. Land exchanges

The 116 km³ per year of continental precipitation identified in figure 3, accumulates as snow in colder regions, or is routed through soils, plants and streams, on its way to returning to the oceans or the atmosphere. Over the long term, precipitation entering catchment areas is stored in soils and aquifers or exits as either runoff, ultimately to the oceans, or by evapotranspiration (ET) directly back to the atmosphere. These different partitions of water are intimately connected and feedback on one another. For example, water stored in soils plays an essential role in influencing precipitating weather systems and thus the precipitation that enters the land surface (e.g. [75]). Anderson & Shepherd [76] introduce the notion of ‘brown ocean’ concept whereby saturated soils from antecedent rainfall serve to provide a source of moisture and latent heating that sustains or even intensifies tropical cyclones after landfall. As we discuss below, some areas also experience significant human interference, through groundwater withdrawals for irrigation and human use, and through river water management and extraction, which alter the land water balance and the flow of freshwater to the oceans.

(a). Land/atmosphere exchanges—evapotranspiration

The terrestrial water cycle is controlled fundamentally by the difference between water gained from precipitation and lost by ET and water runoff to the oceans. ET is notoriously difficult to quantify; it is multifaceted and complicated, involving different processes that return water to the atmosphere. Water can be evaporated directly from soils, from surface waters and from interception by vegetation, and transpired by plants. ET is further controlled by a combination of radiative, atmospheric, and vegetation drivers. Thus, quantifying the contribution of ET as an exchange flux globally remains a challenge (e.g. [19,77]). Because of these challenges and the large uncertainty attached to any one technique, the values of Rodell et al. [19], cited in figure 3, are an average of three different ET sources, and the total uncertainty (bias and random errors) is estimated as the standard deviation of the three estimates for each region and time period.

Further partitioning ET into the fractions by interception, transpiration, soil evaporation and surface water evaporation is made possible by interpretation of stable isotope measurements of water vapour and liquid water, from both global satellite data and/or direct isotopic measurements of samples of precipitation and water runoff. Both approaches, however, leverage differences between the ratio of heavy to light isotopes of water in transpiration and evaporation (see box 2). From this combined approach, and as shown in figure 8, Good et al. [40] estimate a total ET flux of 85 ± 16 km³ per year. That this estimate is larger than the value of Rodell et al. [19] quoted in figure 3, underscores the degree of uncertainty inherent in this flux.

Figure 8.

Partitioned continental hydrologic fluxes according to [78], their figure 3. Terrestrial precipitation (annual mean± 1 s.d.) not intercepted by vegetation mixes into soils or flows into surface waters. Soil water is withdrawn by plant roots via transpiration, subjected to evaporation and leaks into the surface water. Of the flux entering the surface waters, 38% is derived from the soils, with the remainder being consistent with precipitation routed directly via preferential flow paths. Surface water that does not evaporate returns to the ocean as runoff. (Online version in colour.)

The transpired fraction determined by Good et al. [40] is consistent with previous studies and places an observational constraint on transpiration estimates from global Earth system models, which range between 38 and 80% of the observational estimates (e.g. [79–81]). Less than 10% of total ET is directly from evaporation of soil moisture and surface water, with around 3% from just surface water; this is consistent with estimates from global Earth system models, which range from 2 to 4% when reported [81]. Globally, tropical forests provide the bulk of continental transpiration, although these regions contribute modest amounts of soil and surface water evaporation as well. The runoff flux is smaller than the total runoff quoted in figure 3, because the snow-melt contribution to river runoff is not included.

(b). Land-ocean exchanges: terrestrial water storage

The interannual variations of GMSL rise, highlighted in figure 2, reveal periods of acceleration and deceleration associated with sustained variability in mass transport between land and ocean. In general, we are able to trace most episodic periods of falling sea levels to increasing water stored on land (figure 6). The periods of marked SLR for example during 2014–2016, when SLR accelerated rapidly, are also likely a result of internal variability of Earth's hydrological cycle associated with climate variability, such as the El Nino/Southern Oscillation (ENSO). This hypothesis is consistent with reduced evaporation from the ocean (figure 2b), associated with weaker than normal winds driven by atmospheric circulation changes.

We know, however, that climate-driven changes in water stores, such as global snow, surface water, soil moisture and groundwater stores, are important components of decadal sea-level budgets (e.g. [2]). This is exemplified by the magnitude of the amplitude of the annual cycle of land water storage, estimated to be 17 ± 4 mm of sea-level equivalent, moved through the seasonal distribution of water from ocean to land (e.g. [82]). Because of this large-amplitude oscillation, natural changes to land water storage can impose large influences on the apparent rate of SLR as highlighted in figure 2. To underscore this point, the altimeter-reported rate of SLR slowed to 2.4 mm year⁻¹ between 2003 and 2011, compared to the mean rate of 3.4 mm year⁻¹ for the entire altimeter record; this is despite the increased mass loss from glaciers [66] and ice sheets during that period.

The net effect on sea level from changes in land water mass storage comprises two major contributors—natural climate-driven storage variability as already discussed, and human-induced storage variability. Some human activities, such as the impoundment of water in reservoirs and artificial lakes, reduces the outflow of water to the sea, while on the other hand, river runoff is increased due to groundwater mining, wetland and endorheic lake storage losses, and deforestation. The contributions of these different negative and positive human drivers of land water storage on SLR, including the potential contributions from natural climate variability, are summarized in figure 9, taken from Reager et al. [48]. This figure displays the rates of different contributions to the observed rise in GMSL over the 2002–2014 GRACE study period. Of the observed ocean mass change of 1.58 mm year⁻¹, approximately 0.77 mm year⁻¹ arises from Greenland melt, 0.49 mm year⁻¹ from Antarctica melt, with a total change (including glaciers) of 0.32 ± 0.13 mm year⁻¹ from continental land water storage, being about 20% of the total mass change contribution.

Figure 9.

Global mass budget estimate (fig. 3 of [48]) expressed as sea-level rise equivalent. The net of the land water storage is disaggregated into the contributions of SLR by land glaciers, human-driven changes (see text) and climate-driven water storage (including soil moisture changes and water storage). (Online version in colour.)

Reager et al. [48] further isolated the hydrology-only ‘land water storage’ signal, by removing the global land glacier mass loss trends, estimated to be 0.65 ± 0.09 mm year⁻¹ of SLR, and taking the human-driven component of 0.38 ± 0.12 mm year⁻¹ from [2]. The residual of these terms represents the climate-driven land water storage change component, estimated over the study period to be –0.71 ± 0.20 mm year⁻¹ equivalent SLR, nearly equal and opposite to the contribution of the Greenland Ice Sheet. This study shows that natural variability in the global hydrological cycle and the partitioning between land and ocean, can act to offset the apparent rate of SLR by a substantial amount for periods up to a decade, further underscoring the need to account for water cycle processes in the interpretation of GMSL observations from altimetry.

(c). Land-ocean exchanges: river runoff

Continental freshwater runoff or discharge is an important part of the global water cycle [20] and an important flux of water from land to ocean. The majority of information about runoff comes aggregation of river streamflow data. While there are a large number of analyses of streamflow over individual river basins there are relatively few global syntheses of river outflow to quantify variations and changes in global freshwater discharge from land into the oceans. Dai [83] produce a dataset that contains time series of all available monthly river flow rates observed at the farthest downstream station for the world's largest 925 rivers, plus long-term mean river flow rates and continental discharge into the individual and global oceans. Analysis by Dai et al. [18] applied to an earlier version of these data reveal large variations in yearly streamflow for most of the world's large rivers and find that precipitation is a major source of discharge trends and interannual-to-decadal variations observed. Whether variations of continental runoff affect the interannual variability of SLR highlighted in figure 2, however, has not yet been studied. Furthermore, present global runoff estimates have to be considered to be highly uncertain and the uncertainty value cited in figure 3 is likely to be an underestimate. Recent studies suggest river streamflow-based estimates significantly underestimate the discharges of water to oceans from land owing in part to the neglect of neglect submarine groundwater flows. Using novel data assimilation methods, Wang & Polcher [84] estimate, a 40–60% increase in runoff into the Mediterranean sea than was previously calculated from river runoff data (box 3).

Box 3. The greening of Earth.

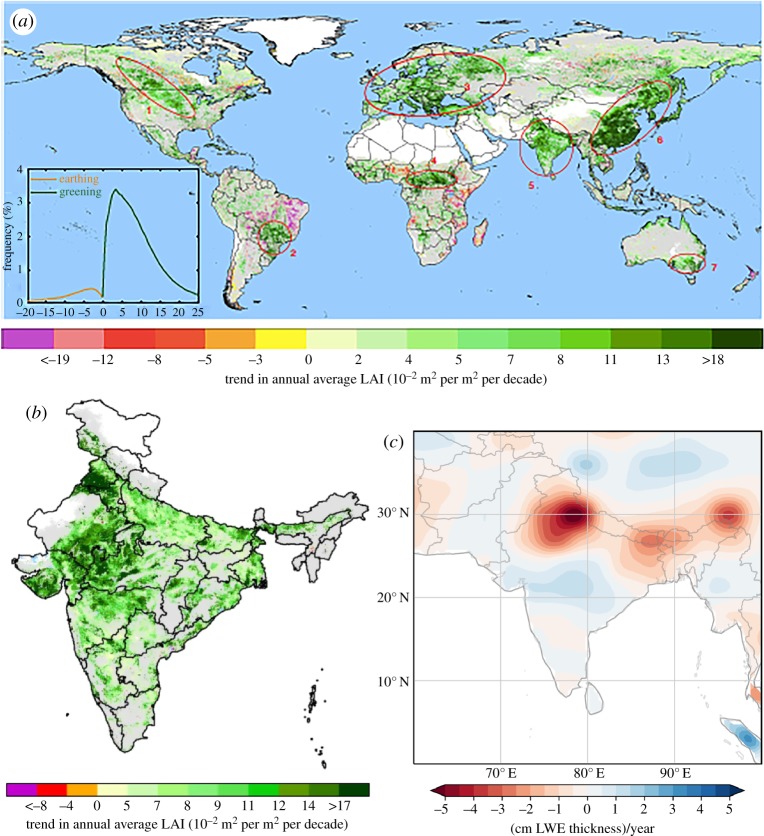
The greenness of Earth is monitored from satellite measurements of reflected sunlight differences between two spectral regions, one at wavelengths in the shortwave infrared region where plants appear bright and the second at visible wavelengths where plants appear much darker. The greener the plants, the larger are the differences in reflection between these two spectral bands. Conversely, the more stressed are plants, the smaller is the reflection difference. Satellite-based measures of greenness are expressed as leaf area index (LAI) which is a dimensionless ratio of area of leaves to area of underlying ground. An 18-year climatology (2000–2017) of LAI from the MODIS reflection data (figure B3a) reveals an increasing LAI due to both direct factors (such as human land-use management) and indirect factors (such as climate change, CO₂ fertilization, nitrogen deposition and recovery from natural disturbances).

Figure B3.

(a) Global Map of trends in annual average MODIS leaf area index (AI) for 2000–2017. Statistically significant trends (Mann–Kendall test, p ≤ 0.1) are colour-coded. Grey areas show vegetated land with statistically insignificant trends. White areas depict barren lands, permanent ice-covered areas, permanent wetlands and built-up areas. Blue areas represent water. The highlighted greening areas in red circles mostly overlap with croplands, with the exception of circle number 4 [85]. (b) Expanded view of the trend in annual average LAI in croplands in India [85]. (c) GRACE record length trends (2002–2016) over the Indian subcontinent (in liquid water equivalent (LWE) units in cm per year), showing extensive groundwater depletion in Northwest India, as first described by Rodell et al. [86]. (Online version in colour.)

These satellite data reveal a strikingly prominent greening of China and India, in particular, and a greening that overlaps the distribution of croplands worldwide. China alone accounts for 25% of the global net increase in leaf area with only 6.6% of global vegetated area. Chen et al. [85] find that the greening in China arises from forests (42%) and croplands (32%), whereas the greening in India is mostly from croplands (82%). Over India much of the cropland is irrigated from groundwater withdrawal, especially in the dry season. The area of greening in India (figure B3b) correlates to the map of groundwater changes (figure B3c) between 2002 and 2016 based on GRACE satellite observations. The estimated rate of depletion of groundwater in north-western India is as much as 4.0 cm of liquid water equivalent (LWE) per year in some locations, further emphasizing the strong impacts of human groundwater consumption for irrigation in this region.

6. The atmospheric reservoir, the greenhouse effect and climate change

As noted earlier, the atmosphere is the smallest reservoir of fresh water, being only 0.1% of all fresh water found on Earth, but its control on the Earth's climate is profound. This water exists in three phases, with 99.9% of it in the form of vapour, and the remaining 0.1% of the water in the atmosphere being suspended liquid and solid water in clouds. If we were to compress the entire water vapour content of the atmosphere into a layer of liquid at room temperature, it would form a thin layer of water that spreads over Earth only 25–30 mm deep. This is tiny compared to the 2.7 km deep layer of water that would form if we were also to wrap all the water in Earth's oceans into a single layer around the entire Earth.

(a). Water vapour and the greenhouse effect

Although tiny, the effect of atmospheric water vapour content on the fluxes between the different water reservoirs of Earth, outlined in figure 3, is profound. The ability of water vapour to absorb and emit infrared (IR) radiation across a wide portion of the IR spectrum, as was first measured by Tyndall [87] more than 150 years ago, establishes Earth's greenhouse effect. Water vapour is instrumental in setting the vertical profile of atmospheric temperatures in the troposphere, and its distribution in the vertical means that the troposphere is being cooled radiatively. In fact, the tropospheric energy budget is largely a balance between radiative cooling on the one hand due to IR emission by greenhouse gases (primarily water vapour) and clouds, and warming from latent heat release, as water vapour condenses to form clouds and precipitation.

The relationship between water vapour, temperature and the absorption/emission of IR radiation represents one of the most important physical feedbacks in the Earth's system and a primary influence on how much Earth warms in response to increases in carbon dioxide. The essential ingredients of this feedback were concisely noted in the 1905 correspondence to the astrophysicist C.G. Abbott by the American geologist T.C. Chamberlain. Chamberlain notes:

water vapor, confessedly the greatest thermal absorbent in the atmosphere, is dependent on temperature for its amount, and if another agent, as CO₂, not so dependent, raises the temperature of the surface, it calls into function a certain amount of water vapor which further absorbs heat, raises the temperature and calls forth for more vapor….

The central mechanism to this water vapour feedback is the link between water vapour and temperature defined by the Clausius–Clapeyron (C-C) thermodynamic relationship, connecting saturation vapour pressure to temperature. From this, we can expect that water vapour in a column of air, and thus the magnitude of the entire atmospheric reservoir, increases at approximately 7% for each degree Kelvin of warming. A number of important consequences then follow from this expected change. One is the positive water vapour feedback (e.g. [88]) that is responsible for more than 75% of the projected warming associated with carbon dioxide increases (e.g. [89]). Another often cited consequence is the potential acceleration of the atmospheric hydrological cycle because the atmosphere holds more water [90].

We now have an almost 30-year observational record of the column water vapour over oceans derived from satellite observations of microwave emissions. These data have been compiled into a 29-year climatology [91] which can now be used to test the degree to which water vapour follows the simple expectation of C-C theory. Figure 10 shows the distribution of the local gradients of the relationship between observed changes in column vapour and observed changes in sea surface temperature. The mean of these oceanic gradients is 7.7% K⁻¹, consistent with our broad expectation of the thermodynamic control on water vapour change. However, the regional patterns of the slopes give a spread of more than a factor of 2 over the oceans, showing significant structure that reflects the influence of other processes, notably the atmospheric circulation, which converges water vapour in some regions, and transports water vapour away from others.

Figure 10.

(a) The regionally distributed slopes of the correlations between column water vapour change and sea surface temperature (SST) change (in % K⁻¹) over a 29-year period of sustained satellite water vapour and SST observations. (b) The distributions of the slopes the mean of the distributions. (Online version in colour.)

(b). Cloud effects

Water vapour connects water at the Earth's surface to clouds and then precipitation, which in turn acts to return water back to the surface and is thus a central component of Earth's water cycle. It is the latent heat released in this conversion of vapour to liquid and ice that provides the main source of heating that balances the atmospheric radiative cooling by greenhouse gases and clouds (box 4).

Box 4. An integrated Earth observing system for clouds and precipitation.

Observing Earth system processes and related consequences of them has long been recognized as a major challenge. Making joint measurements of multiple parameters of the Earth system on one platform was the motivation of the Earth Observing Systems (EOS) Aqua,Terra and Aura platforms [92]. With the joint launch of the NASA CloudSat [93] and the NASA/CNES Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observations (CALIPSO) [94] satellites on 28 April 2006, a W-band cloud profiling radar (CPR) and a 530 and 1060 nm backscatter aerosol lidar were introduced to the A-train constellation (Figure B4a). The concept of an integrated observing constellation then flourished, demonstrating a new cross-disciplinary observing paradigm based on a distributed observing system. Figure B4b illustrates the potential of these observations, revealing the vertical structure of clouds, convection and precipitation through the center and eye wall of typhoon Yuta.

Figure B4.

(a) The A-Train constellation of satellites as in 2014. (b) An example of the profile of clouds and precipitation provided by the combination of lidar and radar through Typhoon Yuta on 10th of October 2018 clearly revealing the eye of the storm. The lidar provides a view of the upper thin clouds (orange) and the radar (yellows, reds and magenta) through deep clouds provide direct measure of cloud water, ice and rain. (c) The climatology of precipitation frequency of occurrence (expressed as a fraction) available from the CloudSat radar observations. Shown are the total occurrences from rain, drizzle and snow combined at 1 × 3 degree resolution derived from 10 years of space-borne radar observations.

These new observations are our most accurate global depiction of the clouds on Earth. They have revealed new insights on their Greenhouse effect (e.g. Figure 11); new measures of their ice contents (e.g. [95,96]); important insights on the formation of rain in clouds [97,98]; and definitive information about how often clouds precipitate (Figure B4c). These observations are now providing important constraints on climate model representations of the observed twentieth century warming. The model sensitivity study of Golaz et al. [99], for example, demonstrated that simple changes to the rain physics in models, which acts to alter the frequency of the lightest rains from the lowest and shallowest clouds, resulted in global model simulations that could either mimic the observed twentieth century warming of Earth or completely eliminate the warming. This example merely serves to highlight how small exchanges of water within the atmosphere can exert a profound influence on the degree of global warming, and in turn all the exchanges between the other larger reservoirs as a result of that warming.

The transport of atmospheric water vapour by the large-scale wind fields associated with weather systems, has a strong influence on where clouds form and how much precipitation falls. As with so many of the exchanges between water reservoirs, the dynamics of the global atmospheric and ocean circulations is central to understanding the Earth's water cycle.

Although the amount of water in clouds is two orders of magnitude smaller than the amount of vapour (figure 3), and the water content of precipitation is even smaller, these small amounts of water also profoundly influence our climate and the sustainability of life on Earth. The distribution of clouds globally, and the amount and type of water (ice or liquid) in them, is a fundamental element of the cloud-climate feedback problem [100], which remains one of the largest source of uncertainty in climate change projections (IPCC [101]). Not only is the amount of water in clouds central to these feedbacks, including how aerosols affect cloud radiative properties (e.g. [102]), but the vertical distribution of clouds also fundamentally determines their impact on the energy balance of Earth's atmosphere (e.g. [103]), and is thus an influential factor that determines how much precipitation falls globally from the atmosphere.

An example of how the effects of the minute amounts of water in clouds can affect the exchanges between the largest reservoirs of water—the cryosphere and the oceans—is given in figure 11 (also discussed by Bennartz et al. [105]). This figure is adapted from the study of van Tricht et al. [104]. The new cloud observations reveal significant occurrences of low cloud over Greenland (figure 11a,b) which were not previously identified. These clouds are composed of small amounts of water and ice in which the estimated total water content is about 6.5 × 10⁶ m³. Although minute compared to the main water reservoirs described in figure 3, these clouds have a significant influence on the surface energy balance of Greenland. This is illustrated in figure 11c in the form of the difference between the all-sky and clear-sky surface radiation fluxes. Clouds increase the net downward infrared radiation to the surface, through an enhanced greenhouse effect, which is more dominant than the associated reduction of the surface solar flux by reflection of sunlight at these higher latitudes. This increased downward IR radiative flux is strongly correlated to the vertically integrated cloud liquid and ice water contents (figure 11c). Averaged over Greenland, clouds reduce the annual mean surface radiative heat loss from the surface by 29.5 (±5.2)Wm⁻² which in turn acts to enhance ice melt.

Van Tricht et al. [104] estimated the impact of this enhanced greenhouse effect of low-lying clouds on Greenland ice melt using a snow model coupled to a regional climate model. The model is able to reproduce the evolution of the Greenland Ice sheet (GrIS) surface mass balance (SMB) from 2007 to 2010 (figure 11d). Sensitivity experiments performed with this model demonstrated that the greenhouse effect of clouds provides enough energy to enhance the GrIS melt water runoff by 56 ± 20 Gt yr⁻¹ (i.e. about 30% of the enhanced ice loss, and 10% of the total annual ice loss, table 2), with similar contributions from ice (25 Gt) and liquid (31 Gt) water clouds.

The study of Li et al. [106] is another example of the importance of the Greenhouse effect of polar clouds on sea ice. They find that the Greenhouse effect of snowfall from clouds, typically unaccounted for in models, contributes substantially to the discrepancy that commonly exists between modelled and observed Antarctic sea-ice concentration. From 50 to 70° S, the simulated sea-ice-area bias is reduced by 2.12 × 10⁶ km² (55%) in winter and by 1.17 × 10⁶ km² (39%) in summer, mainly because increased wintertime longwave heating restricts sea-ice growth and so reduces summer albedo.

(c). Precipitation

Precipitation is a basic flux of water that connects Earth's main reservoirs but we cannot yet adequately monitor the global changes in precipitation with our present-day observing systems to address comprehensively basic questions about how the character of preciaption is changing. There are, however, relatively tight physical constraints on the global changes of precipitation set by the C-C approximately 7% K⁻¹ change in global mean total water vapour content of the atmosphere (e.g. Figure 10). Furthermore, global annual mean precipitation changes scale at a rate set by the radiative balance of the Earth's atmosphere which in turn is controlled to a large extent by changes to water vapour. (e.g. [107]). This energy constraint on global-mean precipitation predicts a proportional change that is about half that the increase in atmospheric water vapour content [107]. On more regional and local scales, changes to precipitation are more widely held to increase proportionately to the increase in atmospheric water vapour content although other factors are also important to these local changes (e.g. [108]) as underscored in the amplitude of the patterns of change in E-P implied by salinity change (figure 5).

Precipitation is remarkably heterogeneous over both space and time and measuring precipitation from space to provide a global understanding of its properties, however, is a leading challenge confronting the Earth observational community. We have made important progress with global measurements of precipitation from satellite programs like the Tropical Rainfall Measurement Mission (TRMM, [109]) and now more recently the Global Precipitation Mission (GPM, [110]) and with efforts to blend surface rain gauge observations with satellite observations (such as Global precipitation Climatology Project, [111]; Integrated Multi-satellitE Retrievals for GPM, IMERG; https://pmm.nasa.gov/data-access/downloads/gpm.

Today, several different global satellite-based precipitation products exist with assessments of them being a topic of ongoing research (e.g. [112]). These products are based on two different methodologies applied to space-based measurements (e.g. [113]) or some blending of the two. One exploits space-borne radar measurements in which the returned echo (typically expressed in terms of a dB of reflectivity Z, e.g. dBZ) directly related to the presence of precipitation hydrometeors. Radars provide a number of clear advantages over the passive methods described next. Three space-borne radar systems have provided data on hydrometeors over the past two decades. The TRMM precipitation radar (PR) was the first atmospheric radar in space with a minimum detectable signal of about 17 dBZ [114] which translates to the heavier rain events typical of tropical storms. The NASA-JAXA Global Precipitation Mission (GPM, [110]) includes a dual-frequency precipitation radar (DPR) with minimum detectible signals of 12 and 18 dBZ again restricted to detecting heavier precipitation. The higher operating frequency of the ‘cloud profiling’ radar (CPR) of CloudSat with a minimum detectable signal of −28 dBZ, 4–5 orders of magnitude more sensitive than either TRMM or DPR. It is able to detect the presence of most forms of precipitation (Figure B4c), including lighter precipitation and light and moderate snowfall missed by these other spaceborne radars and even operational ground-based radar networks [115,116].

The second class of space-based precipitation measurements is less direct and is based on interpretation of ‘passive’ infrared (IR) or microwave (PMW) radiance measurements. The connection between observed radiances and to surface rain rates are ostensibly non-unique depending on hydrometeor profiles (e.g. [117]) among other factors. Most passive measurement systems are calibrated by or merged with surface rain gauge data and thus, over land, are not entirely independent of these surface measurements. While these passive methods have an advantage in the space–time coverage they offer, they tend to be heterogenous differing over land and ocean, and suffer from an imprecise understanding of the detectible range of observed precipitation the methods observe making interpretation of trends in precipitation and shifts in the distribution of precipitation problematic.

(d). Is precipitation becoming more intense?

Addressing the question as to how precipitation will change with climate change is not just a matter of understanding by how much the total accumulated water that falls is changed such as identified in figure 3 but it is critical to understand how the character of precipitation also changes (e.g. [90,118]). One aspect of this character is the most intense precipitation and the question as to how rain intensity will change in a future warming planet is not only one of the major challenges confronting Earth sciences today but also a pressing societal challenge. Analysis of surface rain gauge data (e.g. [119]) has revealed that the intensity of the heaviest precipitation amounts has been increasing over time. Evidence suggests that on a daily time-scale rain intensity of the 90th and 99th percentiles increase at rates consistent with that imposed on water vapour as implied by the C-C relationship whereas the shorter duration sub-daily intense rains increase a rates above the C-C expectation (e.g. [119–121]). The hydrological impacts of a shift in precipitation toward more intense daily/sub-daily rainfall extremes are profound and underscore the pressing need for observing precipitation frequency/intensity characteristics at a global scale and for differing climatic zones.

In a recent study, Roca et al. [122] explored the relationship between surface air temperature change and daily 1° × 1° scale extreme precipitation (90th and 99th percentiles) over tropical land regions confined between 30°S and 30°N. A set of 10 observational products ranging from satellite only to rain gauges only products and various blended intermediates were analysed. Figure 12a presents the rain intensity distribution of daily 1° × 1° accumulated precipitation over the tropical land regions considered for rain rates above 1 mm day⁻¹. Although these distributions vary between subset of datasets that rely on the GPM constellation satellites is only considered the spread is much smaller. The sensitivity of the rainfall extreme to the surface temperature is also very robust across these constellation-based products. This is highlighted in figure 12b which shows the daily 99.9th and 99th percentiles of precipitation as a function of the 2 m surface air temperature and indicates that the dependence on temperature is more complex that merely predicted by C-C behaviour. Three regimes of behaviour emerge. A cold regime between 287 and 293 K in which there is little to no variation with surface temperature, a warm regime (299–305 K) characterized by an overall decrease of the extreme precipitation with temperature attributed to the limited supply of moisture over the arid land regions this regime represents [123] and a C-C region (293–299 K) which accounts for approximately 73% of the total precipitation data analysed.

Figure 12.

(a) Distribution of occurrence of daily 1°×1° accumulated precipitation over the tropical (30° S–30° N) land for the period 2012–2016. The colours correspond to various precipitation datasets listed on the right and described further in [122]. (b) The value of the 99.9th and 99th percentiles of the 1 × 1 daily accumulated tropical precipitation function of the 2 m daily temperature for a sub-set of the ensemble the observational products of (a). Shading is the standard deviation of the ensemble. The dashed-dot grey lines correspond to the C-C 6.5% K⁻¹ rate of change. (Online version in colour.)

7. Summary

This paper reviews progress toward a quantitative understanding of the exchanges of water between Earth's main water reservoirs with emphasis placed on the progress accrued from the latest advances in Earth Observation from space. Figure 3 provides a synthesis of these observations expressed as the volume of water in Earth's four main reservoirs and the fluxes between them depending on the reservoir in question. Our level of understanding of the volume of water within the reservoirs varies significantly. The atmospheric reservoir volume, for example, is well-documented supported by global observations of water vapour, as is the ocean volume estimate supported by ocean altimeter observations. The volume of water in Earth's cryosphere has also significantly advanced by Earth observations of the cryosphere over the past few decades, but our understanding of the volume of groundwater storage is highly uncertain.

The main points to be derived from this review are:

• (1) The water exchanges between reservoirs are a result of processes that are at the core of important physical Earth-system feedbacks, which fundamentally control the response of Earth's climate to the greenhouse gas forcing it is now experiencing. These fluxes also control the rise of global mean sea level (SLR) which is the topic used to frame discussion throughout.

• (2) While significant progress has occurred, our ability to document the exchanges and their change over time is still a major to challenge facing the Earth science community. Most of the fluxes of water between the reservoirs presented in figure 3 result from the assimilation of many sources of data beyond the global space-based observations that are the principal focus of this paper and advancing the development of approaches for assimilating such heterogeneous data is a high priority (NRC, [124]).

• (3) The importance of maintaining sources of in situ data also cannot be overstated. For example our quantitative view of global precipitation relies on blending surface rain gauge data with satellite data, our ability to estimate ice melt from glacial retreat heavily leans on localized glaciological records collected in the field, our understanding of the properties of groundwater depends on individual samplings in selected aquifers, our understanding of ocean salinity changes relies on decades of ocean in situ sampling and our ability to estimate runoff is based on river flow data.

• (4) Earth's hydrological cycle, including human influences on it, is shown to significantly affect the apparent rate of GMSL rise by substantial amounts for extended periods of time. Examples of the intricate ways water cycle processes influence SLR are described, including disproportionate influences of by the tiniest water reservoirs, such as on the effects of clouds on the surface energy balance of Earth's major ice sheets, among other factors.

The Earth observations introduced in this review paper, although not coordinated, are an essential part of our global observing strategy of the hydrological cycle. Although there is no clear and comprehensive strategy for monitoring the fully integrative aspects of Earth's hydrological cycle, plans are underway to continue both a number of critical observations central to defining some aspects of the exchanges described in this paper as well as offering an augmentation of them in the coming decade. The Copernicus Program led and funded by the European Union, is supported by a family of satellites—the Sentinels—that is to provide continuous, consistent global monitoring of key hydrological variables, including SLR in the coming decade. The major space agencies of the world also continue to support new measurements of Earth water. The National Research Council of the U.S. academy recently outlined a roadmap for the Earth observation priorities of the 2017–2027 decade (NRC, [124]). That study specifically recommended that the graviometric observations of Earth's water reservoirs provided by GRACE and its follow on be maintained through the coming decade and beyond. The study also recommended observations important for monitoring ice loss via altimetric observations also be maintained. Of high priority for the coming decade are advanced observations of clouds and precipitation that can better characterize the dynamical nature of the water exchanges in the atmosphere and advanced observations of Earth's ecosystems that will better constrain the fluxes of water between the vegetated surface and the atmosphere.

Appendix A. Data resources

The approximate 25 year time-series of GMSL presented in figure 1 includes data from the satellite altimeter measurements of TOPEX/Poseidon and its successors Jason-1and Jason-2 [4]. These data were processed by the Sea Level Research Group of the University of Colorado (CU). The ocean mass change time series also shown are data from measurements provided by the GRACE satellite mission [125]. As with most Earth observational data records, slightly different forms of the data records exist according to which particular research group developed it. Estimates of the sea level trend from various groups, for example, differ slightly between them owing to the differences in treating the time-variable biases in the radiometer corrections, the sea-state bias models, the inter- and intra-mission biases, and the differing orbits [126]. We use the CU data as it has a small residual trend (−0.03 mm yr⁻¹) after subtracting both ocean mass from GRACE and the steric sea level component from the ARGO in situ ocean temperature measurements suggesting a consistency of the data record (e.g. [127]).

A variety of other Earth observational data records are also contained within figure 2. Changes to the mass of ice sheets (box 1), glaciers, and snow pack, regional groundwater storage, and surface water storage and ocean water mass (figure 1) are primarily deduced from the GRACE observations.

Surface latent and sensible heat fluxes are from the Woods Hole Oceanographic Institution Objectively Analyzed air-sea Fluxes (OAFlux) dataset (version 3, [128]), at 1° horizontal resolution. Many data sources have been integrated to produce the flux values cited in figure 3 and most of this integration is described in the Rodell et al. study. Precipitation data are largely extracted from the Global Precipitation Climatology Project (GPCP) data record [129]. These data are a hybrid of satellite observations and surface rain gauge data and biases that are thought to exist in these data are described in [54]. The evaporation from oceans are also largely satellite based being derived from near surface humidity and ocean surface winds as described by Clayeson et al. [130]. Land evaporation fluxes are an average of three different approaches that also involve large amounts of different satellite data sources (e.g. [19]

Radiances obtained from microwave radiometers on orbiting satellites have been complied into an approximate 30-year climatology [91,131] providing quantitative information on the atmospheric reservoir. These data provide measures of column water vapor and the water content of clouds and precipitation but limited to ocean regions. The water isotope data described in box 2 and used to infer the fractionation of the land fluxes into components are largely from the satellite observations of the Tropospheric Emission Sounder [132].

The ten different precipitation products analyzed in figure 12 range from hybrid of radar and PMW observations, IR-based methods to rain gauge-based products and products that blend different combinations of these observational types. The sources of these data are described in [133].

Data accessibility

This article has no additional data.

Authors' contributions

G.L.S. wrote most of the paper and coordinated all inputs. D.J.S. provided important inputs to the general theme of paper and inputs to §7. M.Z.H. provided a number of new figures and related analysis (notably figures 1 and 2 and figure 10). P.J.D provided general comments and important inputs to figure 3 and provided figure 5. J.T.R. provided inputs to box 1 and §6 and provided the new GRACE analysis shown in figure B3c. J.W. provided the new analysis to create figure B2. R.R. provided inputs to §7 and figure 12.

Competing interests

We declare we have no competing interests.