On the methods for reactivation and replay analysis

Abstract

A major task in the history of neurophysiology has been to relate patterns of neural activity to ongoing external stimuli. More recently, this approach has branched out to relating current neural activity patterns to external stimuli or experiences that occurred in the past or future. Here, we aim to review the large body of methodological approaches used towards this goal, and to assess the assumptions each makes with reference to the statistics of neural data that are commonly observed. These methods primarily fall into two categories, those that quantify zero-lag relationships without examining temporal evolution, termed reactivation, and those that quantify the temporal structure of changing activity patterns, termed replay. However, no two studies use the exact same approach, which prevents an unbiased comparison between findings. These observations should instead be validated by multiple and, if possible, previously established tests. This will help the community to speak a common language and will eventually provide tools to study, more generally, the organization of neuronal patterns in the brain.

This article is part of the Theo Murphy meeting issue ‘Memory reactivation: replaying events past, present and future’.

1. Introduction

Thirty years ago, while the relationship between sleep and memory had so far been investigated at the behavioural level, Pavlides and Winson in 1989 provided, for the first time, compelling evidence that neuronal activity in the hippocampus during sleep was affected by previous wake experiences. They were able to change the sleep firing rates, and burstiness, of individual place cells by exposing animals to the locations such cells were tuned to. As a control, place cells for locations the animals were blocked from traversing did not show these changes. The same year, György Buzsáki [1] suggested that hippocampal sharp-waves, transient bouts of increased spiking activity in the hippocampus observed during reward consumption, drowsiness and non-rapid eye movement (NREM) sleep, would be instrumental in the reactivation of activity patterns that formed during the previous behaviour. The two-stage model of memory [1], building upon previous theoretical work by Marr [2], states that reactivation of neuronal patterns during ‘offline’ periods is the physiological support of the long-established role of the hippocampus in memory formation [3]. These preliminary descriptions of cell-specific reactivation pointed towards a potential role of NREM sleep in memory consolidation at a time when the rapid eye movement (REM) memory–retention hypothesis was the prevailing view [4–7]. Although these studies marked a turning point in the study of sleep-dependent memory processes, they did not address the key question of how spiking activity is organized at the population level.

During sharp waves, hippocampal CA1 neurons fire synchronously, producing a ripple oscillation in the local field potential (LFP) [8], one of the fastest (100–200 Hz) oscillations in the healthy brain. Together, these two features of the CA1 LFP form sharp wave-ripple (SWR) events. The development of multi-channel recording techniques allowed Wilson & McNaughton [9] to demonstrate which reactivation was a population-wide phenomenon by showing that the pairwise correlations which formed with experience were preserved during subsequent sleep, especially at times of SWRs. SWRs entrain downstream targets of the hippocampus in the entorhinal cortex [10], confirming the original hypothesis that these physiological events may underlie a global phenomenon implied in memory formation.

Since these seminal studies, to assess reactivation, a simple within animal paradigm has become the standard protocol in the field. The typical experiment consists of a naive animal sleeping in its home cage for several hours, being exposed to a new environment or maze, and then returning to its home cage for several more hours. This paradigm then allows for the comparison of activity patterns between the behavioural epoch and the post-behaviour epoch, while using the pre-behaviour epoch as an internal control to determine if such activity patterns were pre-existing.

One key issue with the study of these phenomena is that the observation and quantification of such patterns depend intimately on the choice of methods used for detection and statistical assessment of their existence.

2. Reactivation methods

(a). Cell-pair correlation and explained variance

Using a technical tour-de-force, Wilson & McNaughton [9] used multiple tetrodes to simultaneously record from dozens of neurons in the hippocampus of freely moving rats during sleep and exploration [9]. They demonstrated that cell-pair correlations for place cells with overlapping firing fields were stronger during sleep after exploration (POST) than during preceding sleep (PRE). Overall, the ensemble correlations were highly similar during exploration and sleep POST, revealing that the pattern of co-firing between hippocampal neurons which formed with awake experience was reactivated during sleep.

Cell-pair correlations such as these are simply computed by binning spike trains in vectors of spike counts (typically in the range 10–100 ms) and by evaluating the Pearson's correlation between these vectors. Reactivation can be then evaluated as the difference in POST correlations between cell-pairs of overlapping or non-overlapping place fields [9]. However, this method has two main issues. First, it only indirectly reflects the relationship between the cell-pair correlations during wakefulness and sleep. Second, a proper measure of changes in correlation must account for the prior relationship between wake correlation and sleep PRE. The first issue can be solved by computing the correlation of cell-pair correlations, referred thereafter as cell-pair coherence, between any two states (e.g. wake and POST). The second issue is addressed by computing the partial correlation between wake-POST cell-pair coherence knowing the wake-PRE cell-pair coherence [11]. This measure is now usually referred to as explained variance (EV) [12]. In mathematical terms, this can be expressed as

$$\text{EV}={\left(\frac{r_{W,\mathrm{POST}}-r_{W,\mathrm{PRE}}{r}_{\mathrm{PRE},\mathrm{POST}}}{\sqrt{(1-r_{W,\mathrm{PRE}}^2)(1-r_{\mathrm{PRE},\mathrm{POST}}^2)}}\right)}^2,$$

with r_A,B, being the cell-pair coherence between epochs A and B. See the electronic supplementary material for a full mathematical formulation.

One caveat with EV is that it is not compared to a proper control but is simply expected to be stronger than wake-PRE coherence [12]. That is, EV by itself does not have any measure for the degree of variability (i.e. noise) across correlations. Additionally, it assumes a ‘forward’ flow of time, analysing the change in correlation structure from PRE to POST. To address these issues, Pennartz et al. [13] introduced the reverse explained variance (REV) in which the PRE and POST cell-pair coherence are swapped (i.e. the ‘flow’ of time is reversed). Reactivation can thus be assessed by a significant difference between EV and REV across recording sessions.

EV has three main limitations. First, it does not account for the possible change in firing rates (independent of correlations) that inevitably leads to changes in correlation [14]. It is possible to control for this by subsampling spike trains to equalize rates [15], or greatly increase the time bin size in order to estimate the contribution of slow time-scale rate fluctuations. Second, it does not allow for the resolution of reactivation in time as it evaluates only reactivation over an entire sleep epoch. Third, all cell-pair correlation values are considered, not controlling for the fact that data of limited duration inevitably generates non-zero correlations.

(b). Tracking reactivation over time

Methods have been developed to compare at a given time the instantaneous co-firing with a template of ensemble spiking ([16], see ‘template matching’ below). Using a template allows for the tracking of the time course of reactivation, and thus to correlate, for example, the instantaneous reactivation with some physiological events such as SWRs. However, the template is composed of only one instance or trial of spiking activity, and thus is prone to high level of noise.

An intermediate solution is to evaluate at any given time the similarity of pairwise co-firing at a given time with average correlation from another epoch. This basically decomposes in time the cell-pair coherence and gives a time series referred to as reactivation strength. Specifically, it consists of projecting the population vectors at a given time onto the correlation matrix (e.g. from wake).

Specifically, population vectors are the z-scored binned spike trains from the neuronal ensemble, so that the instantaneous co-firing (i.e. the products of spike counts) can be compared to the correlation values (note that a correlation value between any two variables is the average of the product of their z-scored values).

One issue with this measure is that it is strongly sensitive to the firing of individual neurons (i.e. neuron pairs with higher spike counts will have higher correlations; [14]). To make the measure independent of single-neuron rate fluctuation, the diagonal of the matrix can be set at 0.

In the general case, reactivation strength can be expressed as

$$R_{\mathrm{sleep}}(t)={\mathit{z}}_{\mathrm{sleep}}^{\mathit{T}}(t)P_{\mathrm{wake}}{\mathit{z}}_{\mathrm{sleep}}(\mathit{t}),$$

where P is a projector (in the simplest case, the correlation matrix) with diagonal elements equal to 0.

Using the correlation matrix for the projection does not address the possibility that noisy correlations can potentially overshadow the actual signal, or at least diminish dramatically the effect size. Other methods, described below, were developed to address this problem (figure 1).

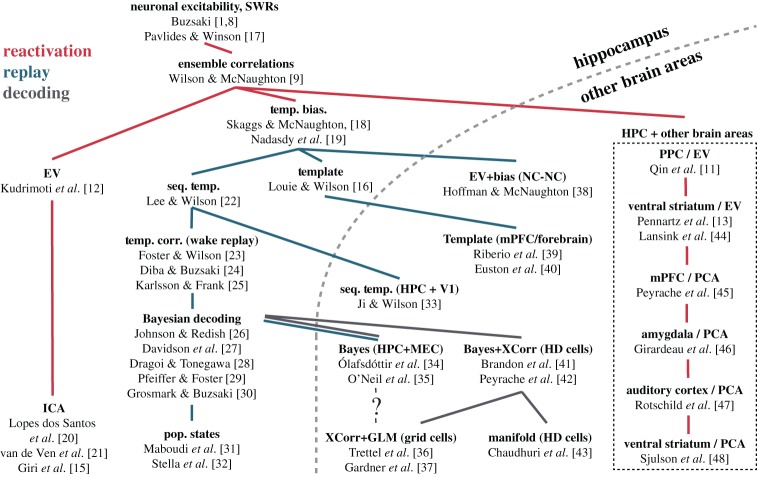
Figure 1.

Phylogeny of method development. We have attempted to trace out when new methods were developed, and what phenomenon (reactivation or replay) they quantify. Red traces indicate phylogenetic branches of reactivation method development. Blue traces indicate branches of replay method development. Grey traces indicate branches using ‘decoding’ methods. Abbreviations: Bayes, Bayesian decoding; EV/REV, explained variance/reverse explained variance; GLM, generalized linear models; HPC, hippocampus; mPFC, medial prefrontal cortex; NC, neocortex; PoP States, population states; PPC, posterior parietal cortex; Seq. Temp., sequence template; Temp. Bias, temporal bias; V1, primary visual cortex; XCorr, cross-correlation. (Online version in colour.)

(c). Principal component analysis

A useful strategy when it comes to focusing the analysis on the relevant intrinsic signals is to extract from the correlation matrix the components that account for more covariance than what is expected from random data of similar duration. Principal component analysis (PCA) is the method of choice to begin with as it is directly related to the correlation matrix.

PCA consists in finding in the original data the axis (that is, a linear combination of the inputs) that maximize the variance. Mathematically, each principal component (PC) corresponds to an eigenvector of the correlation matrix, which corresponds to the axis in n-dimensional space (n being the number of neurons) pointing in the direction of the maximal variance (or the maximal remaining variance in direction orthogonal to the previous PCs). Each PC is associated with an eigenvalue equal to the total variance explained by this combination of inputs. Numerous studies have used PCA to extract low-dimensional features of neuronal population activity (e.g. [49,50]). Replacing the correlation matrix by the PC projectors [51] yields a reactivation strength specific to one PC [45]. In this case, the projector is simply the outer product of the eigenvector (see the electronic supplementary material for more details and figure 2).

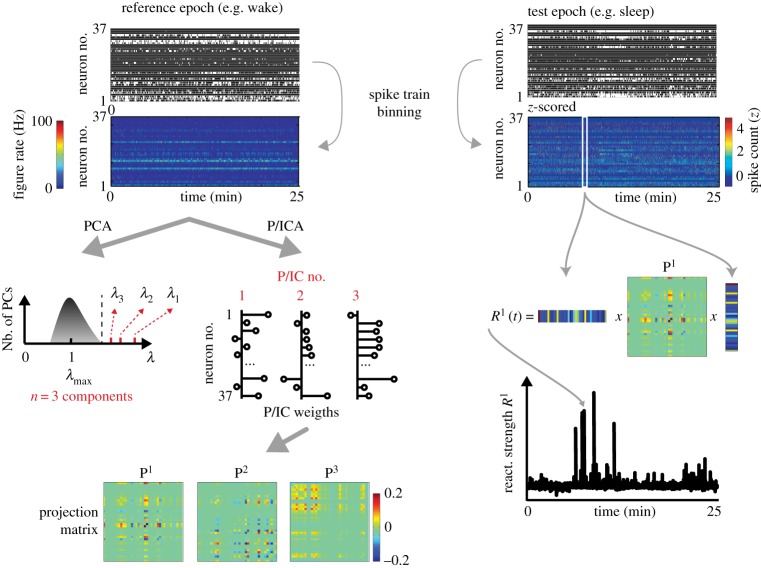
Figure 2.

Reactivation. The first step in reactivation methods is to determine the number of significant components (i.e. linear combination of the binned spike trains) that explain more variance than what is expected by chance in the reference epoch. This is done by decomposing the correlation matrix of the binned spike trains of the reference epoch into its eigenvectors (i.e. PCA) and determining the number of its eigenvalues (λ) that are greater than the theoretical upper bound of the eigenvalue spectrum (the Marchenko–Pastur bound, λ_max). Then, the binned spike trains are decomposed into their significant projection matrices (three in this example), which are equal to the outer product of the correlation matrix eigenvectors (or principal components, PCs) or of the independent components (ICs) (see text). Then, the data of the target epoch are binned, z-scored and projected onto the projection matrices, resulting in reaction strengths (R) that track the time-resolved reactivation of target neuronal ensembles relative to the reference epoch. The diagonal of the projection matrices is set to 0 to make the reactivation strength more robust to the fluctuation of single-neuron activity. (Online version in colour.)

(d). Determining the number of significant principal components

Usually, the number of PCs that are kept to describe the original dataset in a compressed form is determined by the desired amount of variance explained by the PCs (e.g. ‘the first n PCs explain X% of the variance’). The explained variance is, by definition, the sum of the eigenvalues associated with each PC (the total covariance of a correlation matrix is the number of variables). For an infinite-long recording of independently firing neurons, the correlation matrix should be the identity matrix and each PC should be associated with an eigenvalue of 1 (they cannot explain more variance than what is contained in a single spike train). However, recordings are all finite in duration and neurons covary in spiking activity. This results in a spectrum of eigenvalues that is distributed around 1, with a width depending on the number of variables (i.e. neurons) and time bins.

During active wakefulness (when cortical networks are in the so-called asynchronous state), cell-pair correlations remain low and distributed around 0 [52], resulting in correlation matrix eigenvalues narrowly distributed around 1. Thus, it is unlikely that a subset of PCs can explain a large percentage of the total variance. Instead, it is more useful to determine the PCs that explain variance exceeding what is expected from random data (i.e. independently firing neurons). Two equivalent approaches are possible. First, shuffling the data (bin-to-bin for each cell) results in a null distribution of eigenvalues from which one can determine the upper bound of the eigenvalues expected from random data. All PCs associated with eigenvalues exceeding this upper bound can be considered ‘significant’ and to convey the actual signal. Another way to determine this upper bound is to use results from random matrix theory, namely the Marchenko–Pastur distribution of eigenvalues expected for random datasets. One crucial aspect of the spectrum of eigenvalues of a correlation matrix is that it is sharply bounded, and thus, any PC whose eigenvalue exceeds the theoretical upper bound can be considered significant with almost absolute certainty (a small correction for finite data is possible but is generally negligible).

The main limitation of the PCA method is that it forces components to be orthogonal to each other (by construction). While it captures relevant aspects of covariance, it may not identify properly the assemblies of neurons that are coordinated [53].

(e). Other decomposition of neuronal data: independent component analysis and beyond

Independent component analysis (ICA) has proved very useful to extract meaningful information from large datasets, in many different fields [54]. When applied to artificially generated spike trains, it successfully separates assemblies of coordinated neurons, even when assemblies have overlapping member neurons [20], a situation in which PCA fails. In the case of determining specific patterns of co-activated units, the ICA is quite similar to the PCA method. ICA is performed on the data projected onto the subspace of the significant components (as determined from the spectrum of eigenvalues) to de-mix the PCs into independent components. The overall variance explained (i.e. average over a sleep epoch) by ICA can be less than with PCA, yet the ICA may be more suitable to track the activation time course of a given assembly (and be potentially more interpretable). This has proved successful in recent studies focusing on the reactivation of hippocampal ensembles [15,21].

PCA and ICA are only two (arguably popular) methods for dimensionality reduction, especially in the context of neuronal data [55]. A number of alternatives were developed similar to PCA, but with slightly different optimization constraints. For example, while standard PCA assumes normally distributed data, it has been generalized to the exponential family (including binary and Poisson distributed data) [56].

3. Replay methods

The methods described so far examine the instantaneous co-activation across populations of neurons. That is, they examine patterns of activity by binning neural data in time (10–200 ms) and examining only zero-lag relationships. As such, they are all methods of quantification for reactivation, however, there are strong temporal relations in all sensory experience and the accompanying neural population activity. Therefore, methods that examine the temporal evolution of neural population dynamics are necessary for the examination of replay.

(a). Cross-correlograms

The first method to posit that the temporal order of hippocampal sequences during behaviour are later ‘replayed’ during sleep used cross-correlograms (CCG) between pairs of neurons [18]. By iteratively shifting in time (±200 ms) and correlating pairs of spike trains, the cross-correlogram can be calculated. Skaggs and McNaughton then examined the asymmetry B for cells i and j, by subtracting parts of the CCG, centered on zero-lag:

$$B_{ij}={\int }_0^{200}{x}_{ij}(t)\text{d}t-{\int }_{-200}^0{x}_{ij}(t)\text{d}t.$$

For each epoch of a recording session, an asymmetry index (B_pre, B_behav and B_post) could be calculated and compared. A requisite supposition of identifying replay is that sequenced activation of ensembles during behaviour should also occur during POST-behaviour epochs more than expected when compared to either a random generative process or the previously existing internal dynamics of the network. If the temporal bias of spikes during a behaviour is maintained during a POST-behaviour sleep session, and it did not exist in a PRE-behaviour sleep session, the asymmetry indices B_behav and B_post should be more correlated than B_behav and B_pre. From such correlations between asymmetry indices, the authors concluded that the sequential neural activity during the experience was being replayed preferentially after the behaviour occurred [18].

While this method remains one of the simplest and most intuitive approaches to quantifying replayed sequences of activity, it suffers from several drawbacks. Aspects of this method are susceptible to issues arising from data processing, data inclusion, and firing rate distributions and are further described in the electronic supplementary material.

(b). Template-based approaches

The next class of approaches that were developed consist of a typical PRE/behaviour/POST recording session where the behavioural session is used to create a template (i.e. firing rate-maps), typically over spatial bins of a maze or environment. This template of firing rates over spatial positions is then compared with epochs of time during the PRE and POST sleep sessions. The explicit goal of these methods is to find epochs of time where the pattern of activity that occurred on a maze, reoccurs while the animal is asleep. Detected ‘similar’ events are then presumed to be replaying activity patterns induced during a prior experience.

A major hurdle with this approach has to do with temporal scaling. The timescale at which activity patterns change during a behaviour or maze traversal may be quite different than during sleep, where such sequences must be internally generated.

(i). Template-based approaches I: template correlation analysis

To overcome this, two early papers from the Wilson laboratory [16,22] implemented a scaling factor analysis. By warping the behavioural template with different temporal scales (0.5 to 20-fold), they could assess both the correlation between template and sleep activity and the scaling factor of the template with the highest correlation. Thus, if ‘replay’ exists at a faster or slower temporal scale than sequences during behaviour, both the temporal compression and similarity to behavioural sequences can be quantified. Their template correlation C_t was defined as

$$C_t=\frac{1}{{\sigma }_x{\sigma }_y}\hspace{0.17em}\frac{1}{N\cdot C}\sum _{c=1}^C\sum _{n=1}^N(\frac{x_{nc}}{X_c}-\overline{x})(\frac{y_{nc}}{Y_c}-\overline{y}),$$

where $x_{nc}$ and $y_{nc}$ are the binned smoothed spike counts for cell c at time n across two different epochs. n is the number of bins and C is the number of cells, $\overline{x}$ and $\overline{y}$ are the average bin values for the two epochs, X_c and Y_c the root mean square of the bin values. By varying the time bin size for one of the two spike trains X or Y relative to the other, the scaling factor can be adjusted. This method further demonstrated replay in the prefrontal cortex [40] and in distributed networks of the forebrain ([39]).

(ii). Template-based approaches II: rank-order correlations

A major assumption of the early template-based methods was that the mapping between template and candidate events was linear. That is, the rate of change through a behavioural sequence could be related to the rate of change through the replay sequence with a scalar multiplication (the scaling factor analysis described above assumes this). However, if replay sequences are flexible, dynamically adjusting the rate of change within a given event, this linearity assumption could severely impede our ability to detect and quantify such events.

Perhaps what is important is the ordering of spikes within candidate events, rather than the precise temporal relations between neurons? Lee & Wilson [22] were the first to report replay of multi-neuronal sequences (greater than three neurons) in the hippocampus during sleep. To this end, they used combinatorics to determine the ‘true’ probability to observe the sequence of a candidate replay event knowing the order of firing during exploration, independent of the relative timing between neurons. For some reasons, this method was then replaced by simpler approaches. A series of papers [23,24] have since used the rank-order correlation method that compares only the order in which place fields fire on a maze with the ordering of spikes within a given candidate replay event. The correlation between these two rank orders can then be used to quantify the similarity of sequences, while disregarding precise temporal structure that may be considered ‘noise’. While not strictly a ‘rank-order’ correlation, a recently developed weighted distance correlation is also capable of capturing similar ordinal relationships without relying on linear relationships between templates and candidate events [57]. Specifically, the method is far less susceptible to single ‘gaps’ in a replay trajectory than the rank-order correlation, or weighted correlation (described below) methods.

A major caveat of the rank order method is the ambiguity that is introduced by neurons with multiple place fields. Should a neuron be ordered by its more reliable field? The higher firing rate field? Should it be included twice? Typically, such neurons are excluded when using this approach. The probabilistic approach described below can be much more robust to such ambiguities.

(iii). Template-based approaches III: the Bayesian approach

Another method, initially used to estimate an animals position during behaviour [58], has also been used extensively for detecting and analysing replay [26–28,30,59,60]. By comparing several reconstruction methods, Zhang and colleagues found that the Bayesian framework was particularly amenable to spiking data. Given the average firing rate $f_i(x)$ for n neurons, we estimate the animal's location x given the number of spikes n of all the cells within a time window $\tau$,

$$P(x|n)=P(x)\left(\prod _{i=1}^N{f}_i{(x)}^{n_i}\right)\text{exp}\left(-\tau \sum _{i=i}^N{f}_i(x)\right)$$

where n is the number of neurons and $P(x)$ is the probability for the animal to be at position x (i.e. the normalized occupancy map).

This method uses an average firing ratemap for each recorded neuron (i.e. it also uses a template) to estimate the probability distribution of the animal's position given a spike count vector at time t. Typically, candidate replay events are discretized into 10–50 ms time bins (τ), and this method is applied to a series of time bins, generating a posterior probability matrix corresponding to approximately 50–500 ms. Once this matrix has been calculated, various algorithms can be used to estimate a goodness of fit, assuming that replay should consist of a continuous trajectory across time bins. The Radon transform [27] and the linear weighted correlation [60] are two common ways to quantify this posterior probability matrix. Another approach consists in fixing the number of spikes per bin, and thus to use bins of variable size [32]. While this technique should lead, by construction, to higher and more homogeneous posterior probability of decoding, it gives similar results to fixed-time bin methods.

(iv). Comparisons and general problems with template-based methods

Each of these methods attempts to quantify a single phenomenon, the degree of similarity between spatio-temporal patterns of neural activity occurring at different points in time. However, it remains unclear how well these methods would agree with one another. Given identical sets of data, do these methods provide similar quantifications of replay? In reviewing the literature of template-based methods, we were unable to find any two papers that used precisely the same data processing and analysis methods. Differences in time bin sizes, smoothing, event detection/inclusion, spike inclusion (first or all), place field definition and additional heuristics made direct comparison of the methods impossible. To overcome this, we used a single dataset (n = 39 recordings, n = 5 rats; figure 3a,b; [61]) where candidate events were detected using a single set of criteria (see the electronic supplementary material). Similar results were observed using simulated data and an alternative previously published dataset [30]. A total of 54 templates were constructed (all linear tracks) using a minimum of at least six place cells with only one field (see caveats of rank-order correlations).

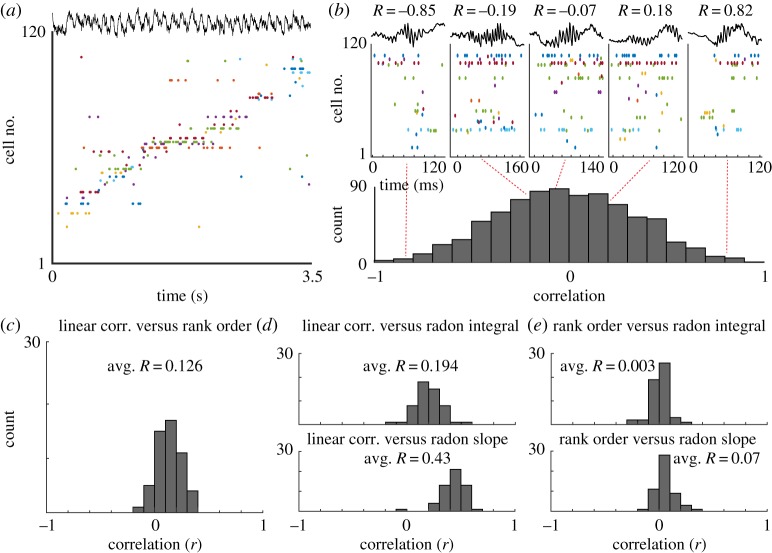
Figure 3.

Replay. (a) Example recordings of hippocampal neurons with place tuning, as an animal traverses a maze. (b) Upper: example candidate replay events. R-values are the linear weighted correlations between each event and the template generated from maze traversals. Cells are sorted and coloured to match figure 1a. Lower: histogram of weighted correlation values for all candidate replay events. (c) Histogram of correlation values when comparing linear weighted correlations with the rank-order correlation method for all candidate replay events. (d) Upper: histogram of correlation values when comparing linear weighted correlations with the integral of the line of best fit, using the radon transform method, for all candidate replay events. Lower: histogram of correlation values when comparing linear weighted correlations with the slope of the line of best fit, using the radon transform method, for all candidate replay events. (e) Upper: histogram of correlation values when comparing rank order correlations with the integral of the line of best fit, using the radon transform method, for all candidate replay events. Lower: histogram of correlation values when comparing rank-order correlations with the slope of the line of best fit, using the radon transform method, for all candidate replay events. (Online version in colour.)

We then provided these candidate events and rate-mapped templates to the rank order correlation method and the Bayesian method, using either the linear weighted correlation or the radon transform to assess goodness of fit. When comparing the rank-order correlation with the linear weighted correlation we found that the event-by-event correlation between these two methods was, on average, R = 0.126 across all sessions and templates (figure 3c). Making a similar comparison between the linear weighted correlation and the radon transform approach, we found a greater degree of agreement (R = 0.43; figure 3d). However, when comparing the rank-order correlation with the radon transform method we found that these metrics were not significantly correlated with one another (R = 0.07; figure 3e). Thus, the determination of which candidate replay events are significant ‘replays’ may depend on the method used, rather than the underlying neural activity pattern. This was confirmed in a set of simulations of candidate events under different signal-to-noise conditions. Given different signal-to-noise ratio, each replay and reactivation method was uniquely susceptible such that agreement across methods could be degraded (figure 4).

Figure 4.

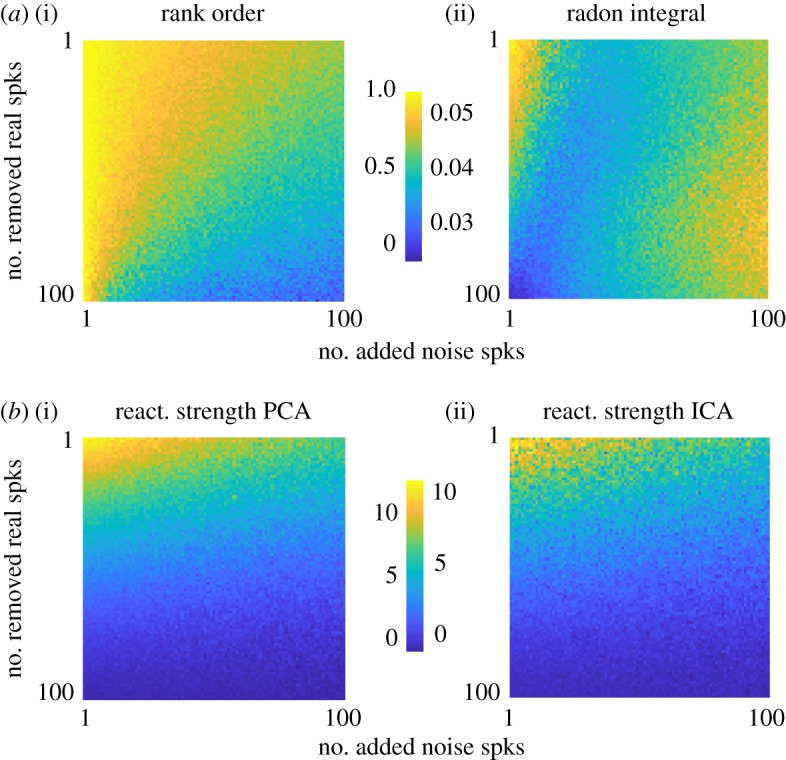
Simulations of candidate events. (a) Rank-order correlation (i) and radon integral (ii) for a set of simulated replay events (n = 100 cells, one spike each per event). x-axis is the number of randomly inserted ‘noise’ spikes. y-axis is the number of randomly removed ‘real’ spikes. These spikes are added and removed from a ‘perfect’ replay event where every cell fires one spike in the same order as a template. (b) Reactivation strength using PCA (i) and reactivation strength using ICA (ii) for the same set of events shown in (a). (Online version in colour.)

Another common issue with the above methods for replay detection has to do with the template itself. It is not clear how such methods could be generalized to non-spatial features of experience. How would one go about creating a template for internal state transitions as they relate to experience and memory? Without measuring every aspect of the experience for an organism (both external and internal sensations) one cannot conclude that a candidate replay event is not ‘replaying’ something the experimenter did not measure. Unsupervised methods for quantifying structure across neural populations have shown promising early results in tackling this problem [31,43,62].

Perhaps the greatest issue with this set of methods is the converse perspective. How do we conclude that a candidate replay event ‘replays’ something significantly? All current approaches have used a within-event shuffling approach. That is, each detected candidate event is evaluated relative to a distribution of shuffled events using data from only that event. Using the various within-event shuffling methods, consistently 5–20% of all candidate events are typically detected as significant replay events [23,25,27,30,60,63]. However, it is often unclear with these methods how many candidate events should be expected to appear as replays given chance (i.e. false positives across a null distribution). This estimation of false-positive rate is highly dependent on the number of cells recorded, their firing rates, and the quantification method used. As an example of this, a random sequence generator (length = 10) can provide significant rank-order correlations with any random template sequence approximately 5–12% of the time (n = 100 events), and when shorter sequences are examined (length = 5) the false positive rate can reach up to 20% (see the online simulations). Additionally, it is known that neural activity is constrained to a much smaller set of sequential patterns than pure randomness [64,65], thus making this a lower bound. This is especially true for event detection methods that rely on periods of silence or suppression (approx. 100 ms) followed by a population burst [24,27,29], a regime where faster firing rate neurons are more likely to fire first [66]. Of course, differences in excitability alone certainly do not result in all the sequences reported in the hippocampus [67], but controlling for these potential confounding factors seems crucial to assess the validity of replay analyses.

Therefore, by examining single events relative to a distribution of shuffles it is difficult to conclude that something is being replayed. Rather, examining the proportion of significant events, out of all candidate events, is necessary if we are to conclude that an experience has altered a neural network in such a way that it replicates previously occurring sequential activity more than would be expected by chance. It is important to note here that changes in excitability and firing rates across the PRE and POST session [17] may change the proportion of events expected by chance (i.e. the false positive rate) to be replays. Along the same lines, a recent example of this approach reported that replay trajectories, when the whole distribution of events is examined, do not necessarily reinstate previously experienced exploration paths but instead matches the statistics expected from a fluid undergoing Brownian diffusion [32]. This raises the question of what constitutes replay of actual memories versus spontaneous and random exploration during sleep of the attractor states of the network [36,37,42,43].

(v). General problems with reactivation and replay methods

One key limitation is thus how cell-pair correlation depends on intrinsic and non-specific factors. It is now well established, both experimentally and theoretically, that the correlation between two spike trains is a function of the firing rate of the two neurons, independent of the actual amount of shared inputs [14]. Hence, the change in intrinsic excitability initially reported in the hippocampus [17] could explain, at least in part, the change in cell-pair correlation [68]. A systematic review and analysis of this possibility is still missing in the field.

Another aspect directly related to changes in the excitability is the distribution of firing rates observed in typical electrophysiological recordings (approx. 0.001–100 Hz). This lognormally distributed range of firing rates is problematic in that most of the current methods can be heavily biased by a small subset of the fastest firing neurons. While some methods attempt to equalize this through normalization (z-scoring, ICA, etc.), it is less clear how the brain might weigh such vastly different scales of firing in reading out reactivation/replay activity. A related, and unexplored topic is the influence that time bin size has on the results of these methods. Typical time bin sizes are approximately 50–200 ms for many reactivation studies, and approximately 10–50 ms for many replay studies, however, a systemic variation of bin size and its impact on pattern detection is lacking. Preliminary simulations suggest bin size can greatly alter how some template-based replay detection methods perform (see the online simulations).

An intriguing, yet understudied, aspect of hippocampal physiology that may impact our interpretation of reactivation and replay is the time required to conduct these types of experiments. As this paradigm can take many hours (3–10) and often uses food or water rewards during the novel maze exposure, it is important to note that circadian and metabolic effects on activity patterns have not been thoroughly examined within this paradigm. It is worth noting that hippocampal ripple rate may be modulated over the circadian cycle, independent from circadian effects on sleep/wake, (D. Tingley 2019, unpublished) and hippocampal neurons express receptors for many hormones related to metabolic function [69].

4. Future directions

(a). Unifying current methods

Perhaps the unifying theme in reviewing the methods for reactivation and replay is the degree of variability in how they are applied, both at the level of data preprocessing and in the assumptions that each method makes with respect to the data. In some cases, these discrepancies in methodology appear to be contributing to differences in interpretation [34,35,70]. As additional methods are developed, it will be crucial for researchers to directly compare multiple methods to assess how similarly, or different, new methods are from those that have been previously published. Other possibilities include adopting a single community-developed code base and standardization [71], or further developing a taxonomy of methods [72] as have been done in some fields.

(b). Template-free approaches

A set of analytical approaches also exist that may be used to examine replay without the generation of a behavioural template. These methods quantify neural data in an unsupervised manner that allows the experimenter to capture reliable patterns during a period of exploration or behaviour. These patterns can then be compared with patterns observed during PRE or POST behaviour recording sessions and warped in time to assess compression or expansion of such patterns. While a clear benefit of these approaches is the ability to relate two sets of data to each other without the use of a precise template, this means the experimenter may not have a good idea what the observed patterns are best related to in terms of the animals' behaviour or state (i.e. we may be unable to ground such relations to anything meaningful). Nonetheless, promising new methods that decompose population time series [62], cluster neural patterns [73,74] or estimate neural states [31,75] have begun to be used for the unsupervised detection and quantification of neural sequences. Finally, the recent development of deep learning techniques that can capture the statistics of neuronal patterns, even in single trials [76] is an interesting direction that will probably attract a lot of attention in the coming years.

5. Generalized assembly detection: what is the ‘relevant’ pattern?

While much work has been done to detect and quantify activity patterns across ensembles of neurons (see [77] for review), it is often less clear how the statistics of neural data impact the interpretability of such methods. The study of reactivation and replay, as we have described it so far, present one advantage: these phenomena represent a sort of ‘ground-truth’, as the reinstatement of a neuronal pattern during sleep somehow validates the approach, unlike a pure statistical description of neuronal data independent of memory processes. Yet, many questions remain unanswered. Should two neurons with an order of magnitude difference in firing rate be treated the same? Can a post-synaptic neuron read-out (i.e. integrate) these spatio-temporal patterns which are often distributed across hundreds of milliseconds?

Such a generalized framework for ensemble detection, given such first-order statistics, could help to unify a field where no two papers use precisely the same method of quantification. We still do not know which, if any, mental state ‘replay’ corresponds to. To break through this impasse, we can no longer keep examining these phenomena relative to the external world. Perhaps the perspective we should be taking, is that of a downstream neuron or population. For example, a post-synaptic neuron learning the covariance between its inputs with Hebbian synapses and regularizing its total synaptic weights performs, at first approximation, a process identical to PCA [78]. Rather than asking what a particular methodological approach can extract from a population of neurons, designing methods that behave like post-synaptic neurons or populations would be a fruitful perspective when asking what the relevant information content is within a population of observed neurons.

Data accessibility

Replay and reactivation methods, as well as simulations, are available in the RnR_methods toolbox: https://github.com/DavidTingley/RnR_methods.

Authors' contributions

D.T. analysed the data, D.T. and A.P. wrote the manuscript.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by a Canadian Research Chair in Systems Neuroscience (grant no. 245716), a CIHR Project grant (no. 155957), an NSERC Discovery grant (no. RGPIN-2018-04600) and an IRDC grant (no. 108877-001) to A.P.