Abstract
Interaction between hippocampal sharp-wave ripples (SWRs) and UP states, possibly by coordinated reactivation of memory traces, is conjectured to play an important role in memory consolidation. Recently, it was reported that SWRs were differentiated into multiple subtypes. However, whether cortical UP states can also be classified into subtypes is not known. Here, we analysed neural ensemble activity from the medial prefrontal cortex from rats trained to run a spatial sequence-memory task. Application of the hidden Markov model (HMM) with three states to epochs of UP–DOWN oscillations identified DOWN states and two subtypes of UP state (UP-1 and UP-2). The two UP subtypes were distinguished by differences in duration, with UP-1 having a longer duration than UP-2, as well as differences in the speed of population vector (PV) decorrelation, with UP-1 decorrelating more slowly than UP-2. Reactivation of recent memory sequences predominantly occurred in UP-2. Short-duration reactivating UP states were dominated by UP-2 whereas long-duration ones exhibit transitions from UP-1 to UP-2. Thus, recent memory reactivation, if it occurred within long-duration UP states, typically was preceded by a period of slow PV evolution not related to recent experience, and which we speculate may be related to previously encoded information. If that is the case, then the transition from UP-1 to UP-2 subtypes may help gradual integration of recent experience with pre-existing cortical memories by interleaving the two in the same UP state.
This article is part of the Theo Murphy meeting issue ‘Memory reactivation: replaying events past, present and future'.
Keywords: memory reactivation, slow-wave sleep, UP–DOWN oscillation, hidden Markov model, principal component analysis
1. Introduction
According to standard consolidation theory, coordinated reactivation of recent memory traces in the hippocampus [1] and cortex [2,3] is part of the mechanism by which memories of recent experiences are consolidated into partially abstracted, long-term memory. The first supporting evidence for such coordination came from multi-electrode recordings from freely behaving rats that showed simultaneous reactivation of patterns corresponding to the same experience in the cortex and hippocampus during slow-wave sleep (SWS) [2,4]. In another multisite neuronal recording study, pyramidal cells in the deep layers of medial prefrontal cortex (mPFC), where most of the hippocampal fibres make contact, responded phasically to sharp-wave ripples (SWRs), but not during spindles [5]. These findings suggest that there is a window of information transfer between the hippocampus and the neocortex during SWS. Furthermore, a recent electrophysiological study of rat auditory cortex (AC) and hippocampus found closed-loop activity between AC and hippocampus during SWS; activity in AC preceded and predicted the subsequent hippocampal activity, while hippocampal patterns predicted subsequent AC activity [6].
In the past couple of decades, hippocampal memory reactivation has been studied extensively. First a selective increase in the firing rate of rat place cells that had been allowed to be active in their place field was found during subsequent sleep [7]. This finding showed that the elevated activity of a single neuron can be maintained during subsequent sleep. From Hebb's cell assembly perspective (neurons that fire together wire together) [8], it is also crucial to ask whether cell-pair correlations that were established during waking are maintained during subsequent sleep. Wilson & McNaughton [1] showed that increased correlations during task were maintained during subsequent SWS. Further studies showed that these correlations were more pronounced during SWRs and that they decayed to a statistically undetectable level in about 30 min, at least in hippocampus [9–11] (but also see a recent report [12]). It was also found that sequence-memory replay was temporally compressed [13,14] and that, during SWRs in quiet wakefulness, hippocampal sequences are sometimes replayed in reverse order [15]. Thus, SWRs are the prime neural states in which hippocampal memory reactivation occurs. Recently, simultaneous electrophysiological and imaging recording of rhesus monkeys revealed that SWRs were differentiated into four subtypes [16]. These subtypes triggered different brain-wide dynamical events, suggesting that they may serve different memory functions or, indeed, correspond to different memories.
Compared to hippocampal reactivation, less is known about cortical memory reactivation. Our previous analyses of neuronal ensembles of the rat mPFC showed that memory-trace sequences were reactivated about five to seven times faster than the sequence speed observed during behaviour and that reactivation was concentrated in UP states [17]. Despite efforts in characterizing UP states [18,19], it is not clear whether they are composed of multiple subtypes, similar to the findings for the hippocampus [16]. If they exist, it is important to understand how the UP subtypes are related to cortical memory reactivation.
To answer these questions, we analysed previously recorded multi-neuronal spiking activity in the mPFC from three rats that were trained to run a sequential task on a circular arena [17]. Briefly, the rats ran to a specific series of locations around the perimeter of a 1.3 m circular platform with electrical brain stimulation targeting the medial forebrain bundle (MFB) as a reward. Sequences, consisting of six or eight locations, were repeated throughout the course of a 50–60 min running session, alternating in blocks of three cued and three non-cued sequences throughout the task session. Rats ran the sequence task continuously during two task blocks (task 1 and task 2) each day. Neural activity was recorded for the entire recording session starting from a first rest period (rest 1) preceding the first task block and in two post-task sleep periods following each task block (rest 2 and rest 3). Each rest session was approximately 30–60 min in duration. In short, a daily recording session consisted of ‘rest 1' – ‘task 1' – ‘rest 2' – ‘task 2' – ‘rest 3' configuration. Rats were implanted with microdrives containing 12 independently manipulatable four-conductor electrodes (tetrodes) [20], allowing simultaneous recording of 55–122 neurons within the mPFC. In this study, we analysed 10 datasets (four datasets from rat 1, three datasets from rat 2 and three datasets from rat 3) that exhibit strong reactivation of ‘task 2' neural activity during the motionless periods in ‘rest 3' (table 1).
Table 1.
Neuron count in each dataset and the firing rates, durations and the exponential time constants τ for UP-1 and UP-2. Number of neurons recorded in mPFC in each dataset is shown in the column ‘neurons’. Firing rate and duration are shown in their respective columns for UP-1 and UP-2 separately (mean ± s.e.m.). The exponential time constant, τ (ms), from the state vector decorrelation exponential fit for UP-1 and UP-2, is shown under the columns ‘UP-1 decay constant (ms)’ and ‘UP-2 decay constant (ms)'.
| dataset | neurons | UP-1 firing rate (Hz) | UP-2 firing rate (Hz) | UP-1 duration (s) | UP-2 duration (s) | UP-1 decay constant (ms) | UP-2 decay constant (ms) |
|---|---|---|---|---|---|---|---|
| 1 (rat 1) | 72 | 2.21 ± 0.023 | 2.85 ± 0.047 | 0.63 ± 0.020 | 0.40 ± 0.014 | 218 | 50 |
| 2 (rat 1) | 119 | 1.99 ± 0.021 | 2.41 ± 0.033 | 0.78 ± 0.029 | 0.41 ± 0.018 | 107 | 40 |
| 3 (rat 1) | 122 | 1.91 ± 0.017 | 2.43 ± 0.027 | 0.68 ± 0.024 | 0.43 ± 0.017 | 141 | 108 |
| 4 (rat 1) | 120 | 1.29 ± 0.011 | 1.54 ± 0.021 | 0.99 ± 0.040 | 0.55 ± 0.022 | 113 | 91 |
| 5 (rat 2) | 74 | 2.16 ± 0.023 | 2.59 ± 0.024 | 0.82 ± 0.024 | 0.55 ± 0.020 | 141 | 105 |
| 6 (rat 2) | 78 | 2.64 ± 0.015 | 2.64 ± 0.026 | 0.70 ± 0.017 | 0.56 ± 0.016 | 148 | 97 |
| 7 (rat 2) | 69 | 2.23 ± 0.013 | 2.55 ± 0.023 | 0.93 ± 0.025 | 0.53 ± 0.018 | 114 | 100 |
| 8 (rat 3) | 55 | 3.28 ± 0.020 | 3.66 ± 0.029 | 0.56 ± 0.011 | 0.47 ± 0.011 | 126 | 73 |
| 9 (rat 3) | 62 | 2.97 ± 0.019 | 3.11 ± 0.025 | 0.56 ± 0.011 | 0.51 ± 0.013 | 222 | 101 |
| 10 (rat 3) | 57 | 3.00 ± 0.023 | 3.41 ± 0.027 | 0.59 ± 0.014 | 0.55 ± 0.015 | 204 | 114 |
Using the hidden Markov model (HMM) [21], we asked whether the UP state could be separated into subtypes. We also asked whether the subtypes of UP state were correlated with memory reactivation dynamics. To understand the current results, it is important to bear in mind that, in the datasets in question, the animals had run hundreds of laps on a stereotyped spatial sequence, and that the degree of replay and the high degree of temporal compression are likely to be at least partly related to this repeated stereotyped behaviour.
2. Results
Our previous study showed that neuronal ensemble activity during waking could be modelled by the HMM as a sequence of firing rate states with fast and coherent transitions [22]. Here, we extended the HMM approach to spontaneous neuronal activity during sleep.
(a). Three-state Hidden Markov model detected DOWN states and two subtypes of UP states
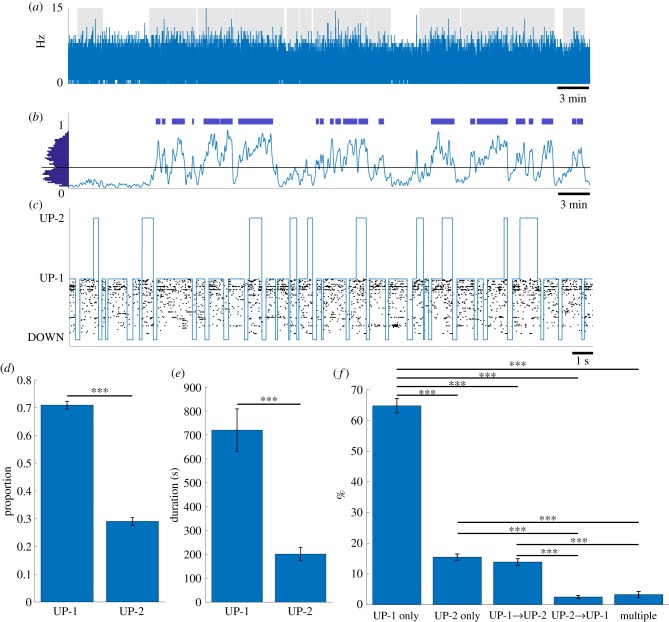
First, we calculated the time series of population firing rate of all recorded neurons, called multi-unit activity (MUA) (figure 1a). The bin size was set to 20 ms so that it was small enough to detect a single DOWN state and was also robust to fluctuation of population activity in the millisecond time scale owing to the relatively small number of recorded neurons. Next, to estimate the smoothed density of DOWN states, we convolved Gaussian kernels with the time points where the MUA value reaches zero. To obtain a robust result, we used three different kernels with standard deviations of 1.5, 2.0 and 3.0 s and averaged the densities (figure 1b; electronic supplementary material, figure S1). Detection of UP–DOWN oscillation periods was based on the distribution of the DOWN state density where the threshold was chosen at the position of a valley in this distribution (figure 1b, left). Periods that exceed the threshold during motionless periods (figure 1a, grey background) were considered periods of UP–DOWN oscillations (figure 1b, blue horizontal bars). In this study, the detected periods of UP–DOWN oscillations are called UP–DOWN epochs, and a total of 154 epochs were identified in 10 datasets.
Figure 1.
Detection of DOWN, UP-1 and UP-2 states using HMM. (a) An example of population firing rate during post-task rest using a 20 ms bin size. Grey patches depict motionless periods. (b) A binary vector was created from bins where the population firing rate equaled zero and convolved with three Gaussian kernels with standard deviations of 1.5, 2 and 3 s, normalized and then averaged together to get the density of down states. The average distribution of values from these 3 Gaussian kernels is shown on the left. A threshold was chosen based on the position of a valley in this distribution. The threshold was used to find epochs of potential UP–DOWN oscillations (blue bars). (c) Results of the HMM. Sequence of states shown in blue and a raster plot depicting the neuron firings for one epoch. (d) Proportion of the occurrences of each subtype (mean ± s.e.m.). (e) Total time spent within each subtype (mean ± s.e.m.) (f) UP-1 and UP-2 composition within UP states. The percentages of UP states containing UP-1 only, UP-2 only, a transition from UP-1 to UP-2, a transition from UP-2 to UP-1 and UP states containing multiple transitions were quantified and averaged over datasets (mean ± s.e.m.). (***p < 0.001).
For each detected UP–DOWN epoch, we applied the HMM with three states. We aimed at detecting not only the transitions between UP and DOWN states but also possible subtypes of UP state. Briefly, at every 1-ms bin, the ID of neurons that fired in that bin was detected. If multiple neurons fired, the neuron ID was selected randomly. If no neuron fired, that bin was set as 0. For the 10 datasets analysed in this study, the average percentage of bins with coincident firing was 1.68%. This is approximately 2.5 times higher than the percentage of coincident firing in our previous study (0.65%) [22]. The difference may depend on several factors such as that the number of simultaneously recorded neurons in the local brain area was different (the median of 5 in [22] and 73 in this study) and that animals used were different (monkey in [22] and rat in this study). Regardless of the difference, 1.68% is small and is unlikely to affect the overall results. The unidimensional sequence of these neuron IDs was given to the HMM. For each dataset, the HMM was trained using all detected UP–DOWN epochs in rest 3. Once it was trained, the most probable sequence of hidden states for each epoch was generated using the trained HMM. The HMM identified three states, one with low-firing activity and two with high-firing activity (figure 1c). We call the low activity state a DOWN state and both the high activity states UP states. The two subtypes in UP state is called UP-1 and UP-2 states. Definition of UP-1 and UP-2 is given in the next section. To assess how well DOWN and UP states are separated, we compared the firing rate distributions of DOWN and UP states in each epoch and ran the two-sample Wilcoxon rank-sum test. We found that the firing rate distributions were significantly different (p < 0.05) in 152 out of 154 epochs. The remaining two epochs were too short to run the test. These results showed that the HMM with three states identified DOWN and UP states successfully. We also found that UP-1 occurred significantly more frequently than UP-2 (71.0 ± 1.37% versus 29.0 ± 1.37% (mean ± s.e.m.) Lilliefors test for normality: for both UP-1 and UP-2, paired t-test: , figure 1d) and that the total duration of UP-1 was significantly longer than UP-2 (720.3 ± 88.9 s (78.1% ± 1.24%) versus 201.5 ± 28.2 s (21.9% ± 1.24%) (mean ± s.e.m.), Lilliefors test for normality: for both UP-1 and UP-2, paired t-test: , figure 1e).
Figure 1c indicates that a single UP state comprises UP-1 or UP-2 entirely or exhibits a transition between UP-1 and UP-2. To investigate the relative frequency of these compositions, we classified UP states into five composition types: ‘UP-1 only', ‘UP-2 only', ‘UP-1 to UP-2 transition', ‘UP-2 to UP-1 transition' and ‘multiple transitions'. The percentage plot of five types elucidated that a single UP state was dominated by ‘UP-1 only' (64.8%), followed by ‘UP-2 only' (15.5%), ‘UP-1 to UP-2’ (13.9%), ‘multiple transitions' (3.3%) and ‘UP-2 to UP-1' (2.5%) (figure 1f). Interestingly, asymmetry existed for ‘UP-1 only' and ‘UP-2 only' UP states; ‘UP-1 only’ was 4.2 times more frequent than ‘UP-2 only'. Similarly, transition between UP-1 and UP-2 was also asymmetric; ‘UP-1 to UP-2 transition' was 5.6 times more frequent than ‘UP-2 to UP-1 transition'. Note that 3.3% of ‘multiple transitions' indicates that a single UP state was rarely composed of more than 2 subtypes. Statistical tests confirmed that other than a ‘UP-2 only' and ‘UP-1 to UP-2 transition’ pair and an ‘UP-2 to UP-1 transition’ and ‘multiple transitions' pair, everything was statistically significant (Lilliefors test for normality: for all five types, one-way ANOVA: , follow-up multi-comparison test with Tukey-Kramer criterion: except for ‘UP-2 only' versus ‘UP-1 to UP-2 transition': and ‘UP-2 to UP-1 transition' versus ‘multiple transitions': , all pairs: ). In summary, the three-state HMM parsed neural activity into three states, one with low-firing rates (DOWN state) and two with high-firing rates (UP-1 and UP-2 subtypes). The relative compositions of a single UP state vary widely; ‘UP-1 only' and ‘UP-1 to UP-2 transition' was four to six times more frequent than ‘UP-2 only' and ‘UP-2 to UP-1 transition', respectively. The results suggest that UP states are dominated by UP-1 and that UP-2 tends to follow UP-1 if they occur in the same UP state.
(b). Two subtypes of UP state are characterized by different rates of population vector decorrelation
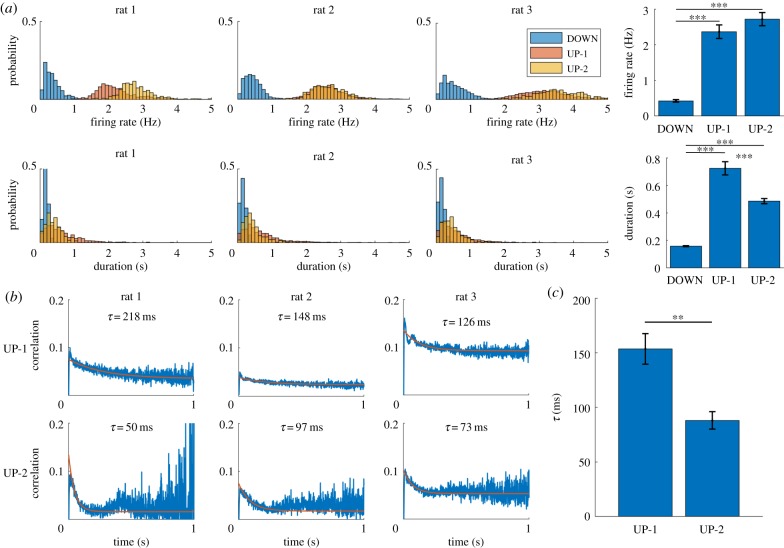
To characterize the three detected states (DOWN, UP-1 and UP-2), we first calculated the mean firing rate of three states. The histogram of firing rate, defined as total spikes from all cells divided by state duration, showed that DOWN state was strongly skewed toward lower firing rates and that the two UP subtypes have similar firing rates (figure 2a, top left; three representative examples from 1 day of recording of rat 1, rat 2 and rat 3; blue, orange and yellow bars represent DOWN state, UP-1 and UP-2, respectively). Individual values of the mean firing rate for all 10 datasets are available in table 1. Comparison of the medians of firing rates over 10 datasets confirmed that the firing rate distributions were significantly different between the DOWN state and two UP subtypes but there was no significant difference between the subtypes (one way ANOVA test: , follow-up multi-comparison test with Tukey-Kramer criterion: DOWN versus UP-1: , DOWN versus UP-2: , UP-1 versus UP-2: , figure 2a, top right). Next, we calculated the duration of the DOWN state and the two UP subtypes. The histogram showed that the DOWN state had a much shorter duration than the two UP subtypes (figure 2a, bottom left, three representative examples as figure 2a, top left). Individual values of the mean duration for all 10 datasets are available in table 1. Comparison of the medians of duration over 10 datasets revealed that the DOWN state was significantly shorter than two UP subtypes and that UP-1 was significantly longer than UP-2 (one way ANOVA test: , follow-up multi-comparison test with Tukey-Kramer criterion: DOWN versus UP-1: , DOWN versus UP-2: , UP-1 versus UP-2: , figure 2a, bottom right). This result is consistent with the representative example in figure 1c where UP-1 tended to be longer than UP-2.
Figure 2.
Firing rate, duration and state vector decorrelation of UP subtypes. (a) Distributions of different attributes for the three states detected using HMM. Firing rate (top) and duration (bottom) show the distribution for all occurrences of each state for three representative datasets. Mean firing rate and duration for each subtype were calculated and the bar plots over datasets are shown (mean ± s.e.m.) (right) (***p < 0.001). (b) State vector decorrelation for UP-1 (top) and UP-2 (bottom). An exponential function (orange) was fit to each of these decorrelations. (c) The decay constant τ from the exponential fit in (b) for UP-1 and UP-2 across datasets (mean ± s.e.m.) (**p < 0.01).
Although descriptive statistics such as the mean firing rate and duration summarized important features of the DOWN and two UP subtypes, they did not characterize the properties in temporal dynamics. To this end, we investigated how quickly the population vectors (PVs) decorrelate within each subtype. For each UP-1 and UP-2 event, we calculated the correlation coefficient (CC) between the PVs as a function of the temporal separation between the vectors. The PV was defined as a vector containing the number of spikes for each neuron within a bin. The bin size of the firing rate vectors was 1 ms. PV decorrelation was computed as follows. For a specific UP subtype event, CCs between the first PV(1) and the succeeding PVs, PV(2), PV(3), PV(4), … , PV(T), were calculated and the result was stored as CC(1, 2), CC(1, 3), CC(1, 4), … , CC(1, T), where T is the number of bins in the UP subtype event. Next, CCs between the second PV(2) and the succeeding PVs, PV(3), PV(4), PV(5), … , PV(T), were calculated and the result was stored as CC(2, 3), CC(2, 4), CC(2, 5), … , CC(2, T). Repeating this procedure filled an upper triangle of [T × T] matrix of CCs for the specific UP subtype event. We repeated this procedure for all UP subtype events. Averaging the CC matrices for UP-1 and UP-2 events separately resulted in one averaged CC matrix for UP-1 and one for UP-2. By taking diagonal averages on the upper triangle portion (e.g. for one-bin separation, the average was taken over C(1, 2), C(2, 3), C(3, 4), …, C(T – 1,T)), we obtained a series of CC values describing how PVs decorrelated as a function of the temporal separation between them. Finally, we fitted the curve by an exponential function with a bias . In the representative examples (figure 2b, the same three rats as figure 2a), the UP-1 decorrelated more slowly than the UP-2 for all three animals; the exponential time constants were , , , , and . To investigate whether the exponential time constants are significantly different between UP-1 and UP-2, we averaged the exponential time constants over 10 datasets (figure 2c; UP-1: 153.3 ± 14.8 ms, UP-2: 87.7 ± 8.1 ms (mean ± s.e.m.)). Individual values of the exponential time constant for all 10 datasets are available in table 1. Statistical test confirmed that the exponential time constant was significantly different between UP-1 and UP-2 (Lilliefors test for normality: for both distributions, paired t-test: ). Based on these results, we call the long-duration and slow-decaying subtype the ‘UP-1' state and the short-duration and fast-decaying subtype the ‘UP-2' state. In summary, the two subtypes of UP state were characterized by the differences in duration as well as in the PV decorrelation rate. These rates can be interpreted as a reflection of the speed of neural sequence readout [17,23].
(c). Memory reactivation occurred predominantly in the UP-2 state
To investigate possible functional differences between UP-1 and UP-2, we asked whether they were correlated with memory reactivation dynamics. Using template matching (TM) [17,23,24], we assessed the strength of memory reactivation and the best temporal compression rate during rest 3. Briefly, a template is the multi-neuronal spiking activity that was observed when an animal was engaged in a specific behaviour. In the sequential task, there were six or eight behaviour segments that correspond to the animal's departure from one reward point and arrival at the next one. Thus, we generated six or eight templates and they were represented by an N × M matrix, where N represents the number of recorded neurons and M represents the number of time bins. Following the previous study [17], bin size was set 100 ms. In order to measure memory reactivation signals, a target matrix with the same size as the template was selected from rest 3. Similarity between two matrices, template and target, was calculated using the Pearson correlation coefficient measure proposed by Louie & Wilson [24]. The TM comparison was performed from the beginning to the end of rest 3. After TM by the original template was completed, the template was shuffled by randomly permuting columns (column shuffle) and the TM procedure was performed again. This shuffling was repeated 500 times. The mean and standard deviation of the correlation values found for each time bin from these shuffled TM results were used to z-score the original TM correlation. In this study, we used the column shuffle because it typically produced the most conservative z-score compared to other shuffling (e.g. bin shuffle, swap shuffle and shift shuffle [24]). In order to investigate whether the reactivation happens faster than the speed of the patterns during behaviour, we modified the bin size of the target matrix between 10 and 100 ms; 10 ms corresponds to 10× compression and 100 ms corresponds to no compression (1× compression). The best compression rate was assessed by counting the number of significant z-score peaks of the TM results (e.g. the peaks > z-score = 5). The compression rate with the maximum number of the peaks was chosen as the best compression rate. This procedure was repeated for each template, and the template with the maximum number of the z-score peaks was selected as the best overall template and the corresponding compression rate was selected as the best overall compression rate. Note that the templates that we investigated in this study were highly similar to each other because of the similarity of sequences between different reward sites. Therefore, all templates reactivated in a similar manner.
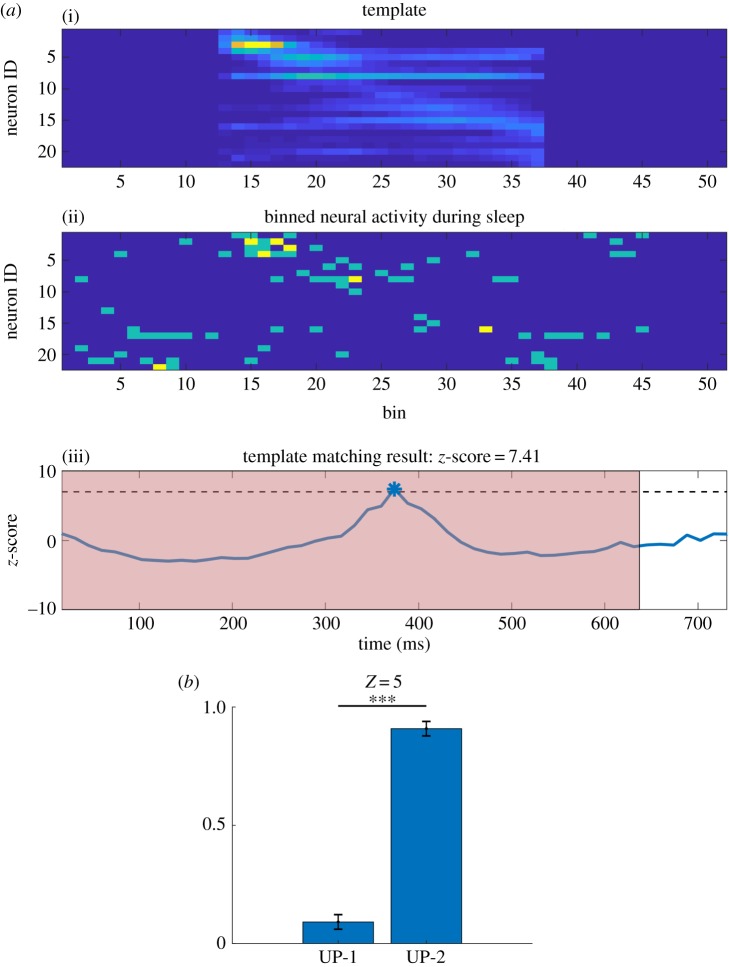
An example TM result is depicted in figure 3a. The template consisting of 22 neurons and 25 bins (figure 3a(i)) was moved over a segment of rest 3 (figure 3a(ii)). This procedure resulted in TM correlations that were z-scored by the shuffling procedure (figure 3a(iii)). The timing of memory reactivation occurrence was estimated at the centre of the TM result. This example shows that the best TM correlation, with z-score = 7.41, was detected at around 380 ms in which time was aligned with neural activity during rest 3 (figure 3a(ii)). As the red background represents UP-2, it indicates that reactivation occurred within UP-2. As was shown in previous studies, reactivation was never perfect; some neurons do not fire and the order of neurons' firing can be reversed. Even though the z-scored TM correlation reached 7.41, the raw correlation value was 0.396.
Figure 3.
Template matching. (a) Example of the template matching algorithm. (i) The template obtained by averaging neural activity of one segment of the sequence during task 2 of one recording session from an animal. (ii) A snapshot of neural activity during rest 3. The template was binned using a 100 ms bin. The neural activity during rest 3 was binned using a 14.3 ms (approx. 100/7 ms) bin, representing a match using a 7× compression rate in this example. Compression rates between 1× and 10× were explored and the one that had the most z-scored correlation peak values above 5 was selected as the best compression rate. The corresponding z-scored correlation values are shown in (iii). Dashed line depicts a threshold of 7 and the peak is used to mark the moment of best match, which is taken as the time when replay occurred. The red patch depicts UP-2. (b) Ratio of number of replay events found in UP-1 and UP-2. Replay events exceeding z-score value of 5 were used. (***p < 0.001).
To investigate the relationship between UP subtypes and the timing of memory reactivation, we combined the results of subtype detection by HMM and that of TM. We found that memory reactivation occurred predominantly in the UP-2 (figure 3b, 9.0 ± 3.3% in UP-1 and 91.0 ± 3.3% in UP-2 (mean ± s.e.m.), the threshold z-score = 5, Lilliefors test for normality: for both UP-1 and UP-2, paired t-test: ). If reactivation is distributed over UP-1 and UP-2 equally, the ratio is expected to be proportional to the subtype event ratio (71.0% in UP-1 and 29.0% in UP-2, figure 1d) or similarly to the subtype event duration (78.1% in UP-1 and 21.9% in UP-2). Both suggest that more reactivation should occur in UP-1. However, the opposite result was obtained, indicating that memory reactivation of recent experience preferred UP-2.
For the 10 datasets that we analysed in this study, the compression rates of the TM memory reactivation were 5–10 times with a mean of 7.4 times. This means that sequence reactivation during rest 3 occurred on average 7.4 times faster than the speed that was observed during the task period. We asked whether these compression rates were comparable to the ratios of the exponential time constants of PV decorrelation between the task and UP subtypes. The ratio between task and UP-2, was distributed between 4.1 and 12.7 with a mean of 7.5. This suggests that the PVs during UP-2 decorrelate on average 7.5 times faster than those during task. The ratio between task and UP-1, was distributed between 1.8 and 7.2 with a mean of 4.5, suggesting that the PVs during UP-1 decorrelate on average 4.5 times faster than those during task. Statistical test over the three variables, TM compression rate, and , confirmed that and TM compression rate were not significantly different, while and TM compression rate as well as and were significantly different (Lilliefors test for normality: for all distributions, one-way ANOVA: , follow-up multi-comparison test with Tukey-Kramer criterion: TM compression rate versus : , TM compression rate versus : , versus : ). These results confirmed that the compression rates by TM were comparable to the ratio of exponential time constants between the task and UP-2, but not with that between the task and UP-1. Taken together, these results show that memory sequence reactivation occurs predominantly in UP-2. We also confirmed that the decorrelation speed of the PVs during UP-2 was comparable to the TM compression rate.
(d). Sequence of UP subtypes is influenced by the duration of UP state and occurrence of memory reactivation
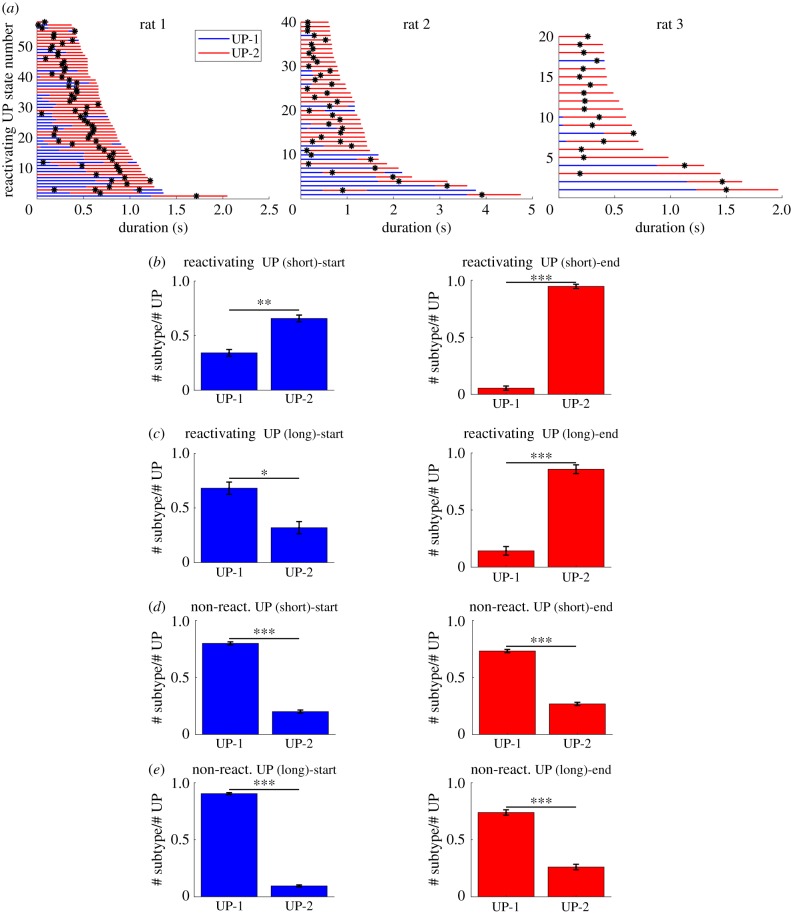
To investigate how the UP-1 and UP-2 are sequenced within a single UP state, especially in UP states that contained significant reactivation signals (reactivating UP states), we sorted the reactivating UP states by duration (figure 4a, the same three rats as figure 2a,b). We found that entire UP states were dominated by UP-2 when the duration of UP states was relatively short. When the duration got longer, UP states tended to start with UP-1 and transit to UP-2.
Figure 4.
Start and end analysis of UP states. (a) All reactivating UP states from three datasets from different animals were sorted by their duration. Blue and red portions represent UP-1 and UP-2 states, respectively. Shorter UP states tend to be dominated by the UP-2 whereas longer UP states tend to start with the UP-1 and end with the UP-2. The black ticks represent the time of the template matching peaks. (b) Quantification of the start and end of UP states over 10 datasets. UP states were divided into short and long ones using thresholds between 580 and 1250 ms (*p < 0.05, **p < 0.01, ***p < 0.001). (left) The start of short reactivating UP states. (right) The end of short reactivating UP states. (c) (left) The start of long reactivating UP states. (right) The end of long reactivating UP states. (d,e) The same measures as (b) and (c) but for UP states without reactivation. (Online version in colour.)
We quantified this tendency by dividing the reactivating UP states into two groups. With a duration threshold of 580–1250 ms, the two groups had almost the same number of samples. We then investigated in which UP subtypes (UP-1 or UP-2) the reactivating UP states started and ended. We found that reactivating UP states with short durations tended to start and end with the UP-2, supporting the observation that UP states were dominated by UP-2 (figure 4b, left: UP-1: 0.3321 ± 0.0369, UP-2: 0.6679 ± 0.0369 (mean ± s.e.m.): Lilliefors test for normality: for both distributions, two-sample t-test: ; figure 4b, right: UP-1: 0.0520 ± 0.0186, UP-2: 0.948 ± 0.0186 (mean ± s.e.m.): Lilliefors test for normality: for both distributions, two-sample t-test: ). By contrast, reactivating UP states with long durations tended to start with UP-1 and end with UP-2. (figure 4c, left: UP-1: 0.682 ± 0.0366, UP-2: 0.318 ± 0.0366 (mean ± s.e.m.): Lilliefors test for normality: for both distributions, two-sample t-test: ; figure 4c, right: UP-1: 0.143 ± 0.0381, UP-2: 0.857 ± 0.0381 (mean ± s.e.m.): Lilliefors test for normality: for both distributions, two-sample t-test: ).
To investigate whether the sequential structure of UP-1 and UP-2 described above is specific to reactivating UP states, we also analysed non-reactivating UP states by categorizing them into short- and long-duration ones, using the same duration threshold as above. We found that both short and long UP states started and ended with the UP-1 predominantly (figure 4d, left: UP-1: 0.798 ± 0.0134, UP-2: 0.202 ± 0.0134 (mean ± s.e.m.): Lilliefors test for normality: for both distributions, two-sample t-test: ; figure 4d, right: UP-1: 0.730 ± 0.0143, UP-2: 0.271 ± 0.0143 (mean ± s.e.m.): Lilliefors test for normality: for both distributions, two-sample t-test: ; figure 4e, left: UP-1: 0.904 ± 0.0096, UP-2: 0.096 ± 0.0096 (mean ± s.e.m.): Lilliefors test for normality: for both distributions, two-sample t-test: ; figure 4e, right: UP-1: 0.741 ± 0.0244, UP-2: 0.259 ± 0.0244 (mean ± s.e.m.): Lilliefors test for normality: for both distributions, two-sample t-test: ). These results suggest that a sequence of UP subtypes within a single UP state is influenced by occurrence of reactivation of recent experience. In summary, we showed that the short reactivating UP states were dominated by UP-2 and the long reactivating UP states exhibited transition from UP-1 to UP-2. We also showed that the sequential structure of subtypes within non-reactivating UP states was different from that of reactivating ones, indicating that the sequence of UP subtypes depended on the existence of memory reactivation of recent experience.
(e). Two UP subtypes are separated along the first principal component
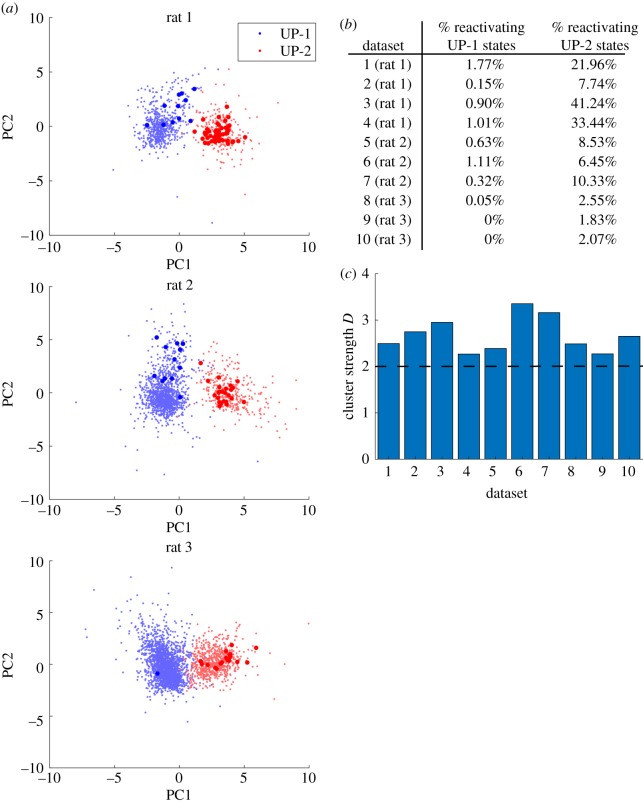
Finally, we asked whether UP-1 and UP-2 could be separated distinctively. To answer this question, we first converted an individual UP subtype event in rest 3 to a mean firing rate vector. That is, an UP subtype that was represented by a [N × T] matrix, where N is the number of neurons and T is the number of time bins, was converted to a [N × 1] mean firing rate vector. The mean firing rate vectors from both UP-1 and UP-2 were concatenated together to make one large matrix. Then, neuron-wise (row-wise) standardization was performed using the mean and the standard deviation of each neuron's firing activity. Principal component analysis (PCA) was performed on this set of vectors, and the result was projected onto two-dimensional space spanned by the first two principal components (figure 5a, the same three rats as figures 2a,b and 4a). Each dot represents a UP subtype event where UP-1 is plotted in blue and UP-2 in red. Larger dots denote the UP subtype events containing significant TM reactivations (z-score = 5 and above). Percentages of UP-1 and UP-2 events that had significant reactivation for each dataset are summarized in figure 5b. We found that the two subtypes were clearly separated along the first principal component but not in other principal components (electronic supplementary material, figure S2). We also confirmed that 7 other datasets exhibited a similar tendency. To assess how well UP-1 and UP-2 clusters were separated, we calculated the cluster strength measure D [25]. In short, D is a measure of the quality of clustering result where a higher D value indicates better cluster separation with small within-cluster distances and large inter-cluster distances. Generally, clustering is considered valid when clusters have D > 2. We found that D > 2 for all 10 datasets (figure 5c), suggesting that two UP subtype clusters were clearly separated. In conclusion, we found that UP-1 and UP-2 were distinct states and that they were separated along the direction of the first principal component.
Figure 5.
UP subtype clusters. (a) Principal component analysis was run on the set of standardized mean firing rate vectors of each subtype event. UP-1 and UP-2 events were projected onto two-dimensional space spanned by the first two principal components. Larger dots denote UP subtype events where replay was detected (z-score = 5). Three representative datasets were shown. (b) Percentage of UP-1 and UP-2 events that had significant reactivation (z-score = 5) for each dataset. (c) Cluster strength measure D was calculated for each dataset. Clustering is considered valid when clusters have D > 2. (Online version in colour.)
3. Discussion
Inspired by the recent finding that SWRs can sometimes be differentiated into multiple subtypes [16], we investigated whether the cortical UP state could be decomposed into subtypes. Using the HMM with three states, we showed that the UP–DOWN oscillations were separated into a DOWN state and two UP state subtypes. The two subtypes were characterized by different durations and different speed of PV decorrelation, where the long-duration and slow-decorrelating subtype is called UP-1 and the short-duration and fast-decorrelating subtype is called UP-2. We showed that a sequential reactivation of recent experience predominantly occurred in the UP-2 state. Furthermore, we found that a short-duration reactivating UP state was predominantly composed of UP-2 and a long-duration reactivating UP state exhibited a transition from UP-1 to UP-2. Finally, we showed that UP-1 and UP-2 were distinct states that were separated along the direction of the first principal component.
The finding that long reactivating UP states exhibited a transition from UP-1 to the UP-2 has several implications. We speculate that the long reactivating UP state may reactivate other experiences during UP-1, possibly remote experiences, and transit to reactivation of recent experience during UP-2. This mechanism may support gradual integration of recent experience with pre-existing cortical memories. It may have attractor dynamics that is similar to the transition from global to fine information in the macaque temporal cortex [26,27]. Although there is no evidence that remote memory is reactivated during UP-1 because neural activity templates for the remote experiences are not easily available, this UP-1 to UP-2 transition is in line with the hypothesis of inter-leaved reactivation of newer and older memories as a mechanism of preventing catastrophic interference [28].
According to a standard consolidation model [29], the hippocampus is thought to integrate information from the distributed cortical modules and rapidly fuse the information into a coherent memory trace. Reactivation of the hippocampal–cortical network during sleep leads to strengthening and/or rearrangement of cortico-cortical connections, which eventually allows new memories to become independent of the hippocampus. Although evidence suggests that the hippocampal–cortical interaction occurs around SWRs and UP states, the detailed interactions in the SWR subtype and UP subtype level are not clear. We speculate that SWRs interact with UP-2 more strongly than UP-1 because UP-2 contains reactivation of recent experience. However, it warrants future investigation.
In this study, we have detected two subtypes of UP states by the three-state HMM. It is possible that cortical UP states are further decomposed into more than 2 subtypes, just as SWRs were differentiated into four subtypes [16]. This question can be investigated using the HMM with 4 or more hidden states. However, it is out of the scope of this short paper and warrants future investigation.
4. Methods
(a). Recording procedures
Three male Brown Norway/Fisher 344 Hybrid rats 7–9 months old at the time of surgery, 350–400 g) were used for the recording, which consisted of two 50–60 min sequential task sessions and three 30–60 min rest sessions. The recording started with the first rest session (rest 1), followed by the first task session (task 1), the second rest session (rest 2), the second task session (task 2) and the third rest session (rest 3). Two rats were implanted with a hyperdrive (more details below) containing 12 independently movable tetrodes [21,30] in the mPFC and twisted-pair local field potential electrodes in the hippocampus. The third rat was implanted with a dual-bundle Hyperdrive in the mPFC and CA1 of the hippocampus. The numbers of recorded neurons in each dataset are summarized in table 1. Detailed surgical and recording procedures are explained in the experimental protocol of [17]. Here, we provide brief description.
(i). Apparatus
All behaviour took place on a 1.3 m diameter circular arena. Light-emitting diodes (LEDs) were positioned at eight equally spaced locations around the perimeter. The LEDs were located 2 cm above the table surface and flashed at 2 Hz when lit. The experiment was controlled by a microcontroller card and a standard PC computer. The computer also performed data acquisition. Custom software monitored the rat's position and turned on lights, tones and electrical brain stimulation as required.
(ii). Data acquisition
Neural recordings were obtained via a chronically implanted ‘hyperdrive' consisting of 12 independently movable tetrodes. Each tetrode consisted of four polyimide-coated nichrome wires (diameter 14 µm) twisted together [20]. Hyperdrive construction was as described in Gothard et al. [30]. During recording sessions, the hyperdrive was connected to a unity-gain headstage that enabled low-noise transmission of neural data to the recording system. The headstage also contained an array of LEDs that could be detected by an overhead camera, enabling tracking of the position of the rat on the maze at 60 frames per second (FPS). All data were recorded using a Neuralynx Cheetah recording system. Single unit data from each tetrode were amplified, filtered between 0.6 and 6 kHz and digitized at 32 kHz. Video spatial resolution was approximately 3 pixels cm−1.
(iii). Surgery and electrode placement
NIH guidelines and IACUC approved protocols were followed for all surgical and behavioural procedures. Each rat was anaesthetized with Isoflurane, placed in a stereotaxic holder and injected with Penicillin G. The skull was cleared of skin and fascia and craniotomies were opened for two stimulating electrodes targeting the MFB and a hyperdrive. The hyperdrive was centred over the left mPFC at 2.9–3.0 mm AP, 1.3 mm ML and angled at 9.5° towards the midline. Rats were returned to ad libitum feeding and allowed to recover for 3–4 days after surgery. Single units from mPFC were recorded with respect to a reference electrode positioned deep in the mPFC (5000 µm from brain surface). After all recordings were complete, the tips of the recording electrodes were marked by electrolytic lesions (5 µamp for 10 s, positive to electrode, negative to ground) to confirm the recording location.
(iv). Reward
MFB stimulation was used as reinforcing reward. All stimulation used two wires. The choice of electrodes was determined empirically based on the rat's response. A range of stimulation parameters was explored using an operant conditioning chamber equipped to deliver MFB stimulation when the rat performed a nose poke. The final selected MFB stimulation consisted of a train of 400 µs wide, 70–100 µA, biphasic current pulses, delivered at 150 Hz for 320–370 ms.
(v). Behavioural procedures
For pre-training purposes, all rats were food-deprived to 85% of their ad libitum weight. The rats were pre-trained to find reward at one of the eight, equally spaced zones on the edge of the circular arena. A training session lasted 50–60 min and comprised a randomly selected series of segments. The process of running each segment will subsequently be referred to as a ‘trial'. Each trial began with two, simultaneously presented cues: a non-directional 4 kHz tone that signalled the availability of reward somewhere in the arena, and the illumination of one blinking LED that marked the correct reward zone. Rats were trained to run to the vicinity of the correct reward zone (within 10 cm) whereupon the reward was delivered and the trial completed. The next trial began after a fixed delay from the onset of reward delivery (500 ms for stimulation-trained and 1000 ms for the food trained rat). This training continued until each rat made direct trajectories to reward locations. Sequence training occurred following surgery. Sequence tasks were presented to each rat by cueing reward zones in a predetermined order. The trial structure and delay period were the same as during pre-training except that MFB stimulation was substituted for food reward. After a rat completed a sequence three times with guidance from LED cues (a ‘cued’ block of sequences), a 5 s delay was inserted between the non-spatial, audio cue and the illumination of the cue light, providing time for the rat to move to the next reward location without the aid of the visual cue. Given the typical running speed of a rat, the vast majority of cue-delay trials in well learned sequences were completed without the LED and are hence referred to as ‘non-cued’ trials. After the rat completed the non-cued sequence three times, audio and visual cues were presented simultaneously, again, starting another cued block. Blocks of three, complete traversals of the sequence alternated between cued and non-cued throughout the duration of the recording session. Sequences that contained six or eight segments were used. For each sequence, rats were trained until they reached asymptotic performance. Asymptotic performance was usually reached within 3 days, using two training sessions per day. Electrodes were then pushed down to acquire new cells and a new sequence was initiated. The new sequence was created by flipping and rotating the original sequence so as to create a sequence novel to the rat. The flip ensured that the order of turns was reversed while the rotation ensured that a different configuration of places was rewarded. In this paper, we used the data from task 2 as the task session and rest 3 as the post-task rest session because memory reactivation signal was most clearly detected in this combination [17].
(b). Detection of UP–DOWN oscillation epochs
In order to assess the epochs that potentially contain clear UP and DOWN states within SWS, the firing rates of MUA using a 20 ms bin size were calculated. Subsequently, by finding all the bins where the multi-unit firing rate is equal to zero, indicating DOWN states, a binary vector was made that marks the position of these bins. Then, this binary vector was convolved with a Gaussian kernel. To obtain robust results, the binary vector was convolved separately with three kernels having different standard deviations of 1.5, 2 and 3 s (electronic supplementary material, figure S1). The convolved traces were then averaged together and resulted in a relatively clear bimodal distribution for each of the 10 datasets. The valley in this bimodal distribution was used as a threshold for the averaged convolved trace and periods above this threshold were used as epochs with potentially high density of UP and DOWN oscillations. Using video recording, it was verified whether or not the selected epochs occurred when the animal was motionless and we only selected the parts occurring while the animal was still
(c). Hidden Markov model
An HMM is a statistical Markov model in which the system being modelled is assumed to be a Markov process with unobserved (hidden) states [21]. In an HMM, the state is not directly visible but the output, dependent on the state, is visible. Each detectable hidden state by HMM has a probability distribution over the possible output tokens. In the HMM, each state is defined by a vector consisting of the average firing rates of the N recorded neurons. For each state, neurons are assumed to be independent of the events before and can be fully described by the immediate firing probability, similar to a stationary Poisson process. The HMM can be fully described by two matrices, E and A. Eij is an emission matrix that determines the probability of neuron j firing in state Si. is a transition matrix that gives the probability of transitioning from state Si to state Sj. The probability of a transition between two hidden states only depends on the identities of the states. As a result, is independent of time. The HMM model predicts a distinct hidden state at time t to represent all of the information preceding it. These matrices, E and A, are determined as a part of the training algorithm for HMMs. The HMM used in this study was a three-state model trained by binning the MUA with 1 ms bins. Each bin was set to the ID of the neuron that fired in that bin and if no neuron fired a value of 0 was given. In cases where multiple neurons fired within the same bin, which was on average 1.68% of the bins of our datasets, a randomly selected neuron ID among the IDs of firing neurons was used. Neuron IDs were provided in the recording procedure by Neuralynx cheetah recording system, and these IDs do not necessarily carry specific information.
In order to understand how HMM works, the key point is to calculate, which is the probability of the observation sequence O, given the model λ, where and [21]. In our case, is the ID of the neuron that fired within the bin, with 0 being used to indicate that no spikes occurred. The probability of the observation sequence O for the state sequence Q is
| 4.1 |
where is the state at time t and T is the number of all observations. By assuming the observations are statistically independent, we get the following expression:
| 4.2 |
in which we define as the probability distribution for the firing of neuron j in the state Si. For the state sequence Q:
| 4.3 |
where is the state transition probability distribution. Subsequently, the joint probability of O and Q can be defined as
| 4.4 |
Then, by calculating the sum of this joint probability across all possible state sequences q, the probability of O, given the model, can be calculated as follows:
| 4.5 |
| 4.6 |
Now the best approach to make the calculations computationally feasible is the forward–backward procedure. The forward probability, is defined as
| 4.7 |
which is the probability of the partial observation sequence up to time t, , with state Si at time t, given the model . The equation can be solved as follows:
-
(1)Initialization
By introducing the joint probability of state Si and initial observation , the forward probabilities are initialized.4.8 -
(2)Induction
4.9
By completing the computation for all states j, and subsequently, iterating all t, the probability of the complete history of the observation from which the likelihood can be obtained is defined by the forward probability as follows:
| 4.10 |
As a result, to find we just need to find the sum of s.
In the same manner, the backward probability can be defined as
| 4.11 |
which is the probability of partial observation sequence from time t + 1 to the end, given that the state at time t is and the model λ.
Again, for the backward probability we can solve it as follows:
-
(1)Initialization
4.12 Here for the initialization step we arbitrarily define to be 1 for all i.
-
(2)Induction
4.13
The probability of being in state at time t and state at time given the model and the observation can be defined as follows to explain how the HMM parameters re-estimate ξt(i, j):
| 4.14 |
Also, the variable, which is the probability of being in state Si at time t, given the observation sequence O and the model λ, is defined as follows:
| 4.15 |
This equation can be explained by using the forward and backward probabilities as follows:
| 4.16 |
Then the relation between and after summing over j is
| 4.17 |
Now by summing over the time index, the obtained quantity can be interpreted as the expected number of times that state Si is visited, or equally, the expected number of transitions from Si. Similarly, by summing over time index, the expected number of transitions from Si to Sj would be obtained. By using the above formulae, the method for re-estimation of HMM parameters can be achieved. Then, the re-estimation of the model parameters in the maximization step is defined as follows:
| 4.18 |
and
| 4.19 |
In equation (4.18), is the expected number of transitions from Si to Sj and is the expected number of transitions from Si to any state. Thus, the variable can be interpreted as the probability of transition from Si to Sj, which is exactly what it was supposed to be. For equation (4.19), is the expected number of times in which the system is in the state Si and with observation , which in this study indicates the probability distribution of firing for neuron j. The denominator again is the expected number of times the system is in state Si. Consequently, variable is the probability of observing neuron j firing while the system is in the state Si. It has been proven by Dempster et al. [31] that the re-estimated model is more likely than the initial model: As a result, we can find a new model by which the observation of sequence is more likely to be generated, as the model is led to a maximum-likelihood estimate.
Each detected UP–DOWN oscillation epoch was treated as a separate trial that was used to train the HMM for each dataset. The most probable sequence of hidden states was generated using this HMM for each epoch. In this study, similar to Ponce-Alvarez et al. [22], the re-estimation stops at the point the increase in the log of the likelihood is less than a tolerance factor (10−6) or it was not reached by the maximum number of iterations (500). We reran the re-estimation algorithm ten times, each time by using new initial parameters, to verify that the likelihood has reached the global maximum likelihood and not only a local maximum. For the emission matrix, the initial components were chosen randomly, while for the transition matrix components were randomly initialized as diagonal elements D in the range (0.99–0.999), and for non-diagonal elements equal to .
By using three-state HMM, the three states were identified as the DOWN state, the UP-1 state and the UP-2 state. The DOWN state was distinguished as a state with a very low mean firing rate. The UP-1 state was characterized by having a slower PV decorrelation time constant and longer duration than UP-2.
In order to check how much the result given by HMM is consistent, and as it is technically impossible to use cross-validation for our method, we used two methods to measure the stability of the HMM result instead. In the first method, after finding all DOWN states that were provided by the original HMM, the number of all DOWN states was divided into halves. First, an HMM was trained using only the data from the first half of the DOWN states and the corresponding UP state that followed each DOWN state. All the methods are the same except here we only used approximately half of the data to feed to the HMM. Similarly, another HMM was created using the second half of the DOWN states and associated subsequent UP states. For the second method, the DOWN states from the original HMM were split into even and odd subsets. Once again, two new models were trained using these two subsets and their subsequent UP states. Finally, these four (first half, second half, odd and even) models generated using these subsets of the original data were compared against the initial HMM to check the consistency of the results (electronic supplementary material, figure S3). The state sequence for each epoch was obtained for each of these models and each was compared to the original HMM. The state sequence gives us the most likely hidden state at each observation bin, using a 1 ms bin size. Using only UP states that contained a transition between UP-1 and UP-2, we found the percentage of bins that had the same value as the original HMM. This was then averaged over datasets. The average percentage agreement was similar for each of the four different subsets, with 96.0% agreement for the odd model, 95.8% for the even model, 96.0% for the first half model and 95.6% for the second half model.
To investigate how much the neuron dynamics affected the results of the states detected by the HMM, we performed two types of shuffling of the unidimensional input data: the data within each subtype found by the original HMM was shuffled (within subtypes) and the data within the entire UP state was shuffled (entire UP state). This was then compared to the results from the original model. Each shuffling method was performed 10 times. Additionally, neuron IDs were randomly shuffled (neuron IDs). The 10 shuffles were compared against the original HMM to determine how much the neuron IDs influenced the results (electronic supplementary material, figure S4a). Similar to the previous section, the percentage of bins from the state sequence that were the same between the shuffled HMM and the original HMM was calculated. This used data only from UP states that had a transition between UP-1 and UP-2 and their preceding DOWN state. These were averaged over the ten shuffles and the datasets. Per cent agreement was 70.4% for entire upstate shuffling, 96.5% for neuron ID shuffling and 94.5% for within subtype shuffling. The result that shuffling within each subtype and randomization of neuron IDs did not affect the performance indicated that each subtype can be characterized by the neurons that change their firing activity in each type. In fact, there are a small number of neurons that change their firing rate between subtypes significantly (electronic supplementary material, figure S4b). They tended to be high-firing rate neurons, presumably interneurons. We also confirmed that removing these high-firing rate neurons induced drastic change in the subtype detections (data not shown), suggesting that these highly active neurons, possibly interneurons, may play a key role in distinguishing the UP subtypes.
(d). Template matching analysis
As we typically had six or eight segments as parts of the sequence task, six or eight templates were generated for each session. Each template starts when the animal departs from one reward point and ends when the animal arrives at the next one. More precisely, a segment was defined as the time between arrival at one reward zone and arrival at the next reward zone, excluding times during which MFB stimulation was delivered. Each row of the template comprised the spike counts from one cell within a series of 100 ms bins covering one segment, averaged over all repetitions of the sequence. Repetitions were first screened for segments that took inordinately long (i.e. segments during which the rat was off-task). For each segment, any repetitions during which the traversal time exceeded four times the distance of the quartile from the median were excluded. For the remaining repetitions, each segment was scaled so that traversal time equalled the median time. The spikes from these scaled repetitions were then averaged in 100 ms bins [17]. In TM analysis, we used stable neurons that were active during all parts of experiment and showed task-related change in their firing rates. In order to measure the similarity of a target matrix that is selected with the same size and dimensions as a template, we used CC as defined in [24]. After TM was performed the template was shuffled by randomly permuting columns (column shuffle) and the TM procedure was performed again. We used the column shuffle because it typically produced the most conservative z-score compared to other shuffling (e.g. bin shuffle, swap shuffle and shift shuffle [24]). This shuffling was repeated 500 times. The mean and standard deviation of the correlation values found for each time bin from these shuffled TM results were used to z-score the original TM result. For the purpose of investigating whether the reactivation happens faster than the speed of the patterns during behaviour, we performed TM analysis with a different range of compression factors between 1 and 10× [17]. To assess which compression factor is the best for the specific dataset, we counted the number of significant peaks of the TM results (e.g. the peaks > z-score = 5) and selected the compression factor with the maximum number of the peaks. This procedure was repeated for each template and the template with the maximum number of the z-score peaks was selected as the best overall template, and the corresponding compression rate was selected as the best overall compression rate.
(e). Population vector decorrelation
Sequences of spike times for each neuron were binned using a bin size of 1 ms to obtain the number of spikes fired within each bin. A PV, defined as a vector containing the number of spikes fired for each neuron within a bin, was created and compared against all other PVs succeeding it within the specific subtype event by computing the Pearson CC. These CCs were then averaged at each lag across the different UP-1 and UP-2 states. An exponential function, , was fit using the data up to the point where the correlation slope, which was smoothed using a 25 ms moving average, changes from negative to positive after an initial delay. The decay constant, τ, was found from the fit exponential.
(f). Principal component analysis
To estimate how UP-1 and UP-2 can be distinguishably clustered, each subtype event was represented by a vector of the mean firing rate for each neuron within the subtype event and normalized using z-score. These vectors were then concatenated together to create a matrix on which the PCA was performed. The data were then projected onto each principal component and the resulting scores for the first two principal components were plotted against each other to produce two clusters for each subtype. The quality of these clusters was measured using cluster distance [25]. For each cluster, the centroid was found by computing
| 4.20 |
where is the two-dimensional projection for the ith subtype event in cluster k with a size of Nk. Cluster distance
| 4.21 |
was then calculated for each dataset, where
| 4.22 |
and is the set of all . This compares the distances from all points within cluster k to its centroid to the distance of all other points to centroid k.
Supplementary Material
Ethics
National Institutes of Health guidelines and the University of Arizona Institutional Animal Care and Use Committee-approved protocols (A-3248-01) were followed for all surgical and behavioural procedures.
Data accessibility
Data and analysis scripts are available by contacting the author or by download from: doi:10.5061/dryad.qv9s4mwbb.
Authors' contributions
B.L.M. and D.R.E. conceived the experimental project. D.R.E. and M.T. performed the experiment. A.P.-A. and S.G. performed the initial HMM analysis. S.M., L.K., K.A. and M.T. performed the subsequent HMM analysis and reactivation analysis. M.T., B.L.M., K.A. and S.M. wrote the paper. L.K., A.P.-A. and S.G. contributed to editing of the paper.
Competing interests
We declare we have no competing interests.
Funding
This work was supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) (grant nos 1631465 (B.L.M.) and 06109 (M.T.)); by the Canadian Institutes of Health Research (CIHR) (grant no. PJT 156040 (B.L.M.)) and by the USA Defence Advanced Research Projects Agency (DARPA) (grant no. HR0011-18-2-0021 (B.L.M.)).
References
- 1.Wilson MA, McNaughton BL. 1994. Reactivation of hippocampal ensemble memories during sleep. Science 265, 676–679. ( 10.1126/science.8036517) [DOI] [PubMed] [Google Scholar]
- 2.Qin YL, McNaughton BL, Skaggs WE, Barnes CA. 1997. Memory reprocessing in corticocortical and hippocampocortical neuronal ensembles. Phil. Trans. R. Soc. Lond. B 352, 1525–1533. ( 10.1098/rstb.1997.0139) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hoffman KL, McNaughton BL. 2002. Coordinated reactivation of distributed memory traces in primate neocortex. Science 297, 2070–2073. ( 10.1126/science.1073538) [DOI] [PubMed] [Google Scholar]
- 4.Ji D, Wilson MA. 2007. Coordinated memory replay in the visual cortex and hippocampus during sleep. Nat. Neurosci. 10, 100–107. ( 10.1038/nn1825) [DOI] [PubMed] [Google Scholar]
- 5.Peyrache A, Battaglia FP, Destexhe A. 2011. Inhibition recruitment in prefrontal cortex during sleep spindles and gating of hippocampal inputs. Proc. Natl Acad. Sci. USA 108, 17 207–17 212. ( 10.1073/pnas.1103612108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Rothschild G, Eban E, Frank LM. 2017. A cortical–hippocampal–cortical loop of information processing during memory consolidation. Nat. Neurosci. 20, 251–259. ( 10.1038/nn.4457) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Pavlides C, Winson J. 1989. Influences of hippocampal place cell firing in the awake state on the activity of these cells during subsequent sleep episodes. J. Neurosci. 9, 2907–2918. ( 10.1523/JNEUROSCI.09-08-02907.1989) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hebb D. 1949. The organization of behavior. New York, NY: Wiley. [Google Scholar]
- 9.Kudrimoti HS, Barnes CA, McNaughton BL. 1999. Reactivation of hippocampal cell assemblies: effects of behavioral state, experience, and EEG dynamics. J. Neurosci. 19, 4090–4101. ( 10.1523/JNEUROSCI.19-10-04090.1999) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Nadasdy Z, Hirase H, Czurko A, Csicsvari J, Buzsaki G. 1999. Replay and time compression of recurring spike sequences in the hippocampus. J. Neurosci. 19, 9497–9507. ( 10.1523/JNEUROSCI.19-21-09497.1999) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tatsuno M, Lipa P, McNaughton BL. 2006. Methodological considerations on the use of template matching to study long-lasting memory trace replay. J. Neurosci. 26, 10 727–10 742. ( 10.1523/JNEUROSCI.3317-06.2006) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Giri B, Miyawaki H, Mizuseki K, Cheng S, Diba K. 2019. Hippocampal reactivation extends for several hours following novel experience. J. Neurosci. 39, 866–875. ( 10.1523/JNEUROSCI.1950-18.2018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Skaggs WE, McNaughton BL. 1996. Replay of neuronal firing sequences in rat hippocampus during sleep following spatial experience. Science 271, 1870–1873. ( 10.1126/science.271.5257.1870) [DOI] [PubMed] [Google Scholar]
- 14.Lee AK, Wilson MA. 2002. Memory of sequential experience in the hippocampus during slow wave sleep. Neuron 36, 1183–1194. ( 10.1016/S0896-6273(02)01096-6) [DOI] [PubMed] [Google Scholar]
- 15.Foster DJ, Wilson MA. 2006. Reverse replay of behavioural sequences in hippocampal place cells during the awake state. Nature 440, 680–683. ( 10.1038/nature04587) [DOI] [PubMed] [Google Scholar]
- 16.Ramirez-Villegas JF, Logothetis NK, Besserve M. 2015. Diversity of sharp-wave–ripple LFP signatures reveals differentiated brain-wide dynamical events. Proc. Natl Acad. Sci. USA 112, E6379–E6387. ( 10.1073/pnas.1518257112) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Euston DR, Tatsuno M, McNaughton BL. 2007. Fast-forward playback of recent memory sequences in prefrontal cortex during sleep. Science 318, 1147–1150. ( 10.1126/science.1148979) [DOI] [PubMed] [Google Scholar]
- 18.McFarland JM, Hahn TT, Mehta MR. 2011. Explicit-duration hidden Markov model inference of UP-DOWN states from continuous signals. PLoS ONE 6, e21606 ( 10.1371/journal.pone.0021606) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ghorbani M, Mehta M, Bruinsma R, Levine AJ. 2012. Nonlinear-dynamics theory of up-down transitions in neocortical neural networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 85, 021908 ( 10.1103/PhysRevE.85.021908) [DOI] [PubMed] [Google Scholar]
- 20.McNaughton BL, O'Keefe J, Barnes CA. 1983. The stereotrode: a new technique for simultaneous isolation of several single units in the central nervous system from multiple unit records. J. Neurosci. Methods 8, 391–397. ( 10.1016/0165-0270(83)90097-3) [DOI] [PubMed] [Google Scholar]
- 21.Rabiner LR. 1989. A tutorial on hidden Markov-models and selected applications in speech recognition. Proc. IEEE 77, 257–286. ( 10.1109/5.18626) [DOI] [Google Scholar]
- 22.Ponce-Alvarez A, Nacher V, Luna R, Riehle A, Romo R. 2012. Dynamics of cortical neuronal ensembles transit from decision making to storage for later report. J. Neurosci. 32, 11 956–11 969. ( 10.1523/JNEUROSCI.6176-11.2012) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.McNaughton BL. 1998. The neurophysiology of reminiscence. Neurobiol. Learn. Mem. 70, 252–267. ( 10.1006/nlme.1998.3851) [DOI] [PubMed] [Google Scholar]
- 24.Louie K, Wilson MA. 2001. Temporally structured replay of awake hippocampal ensemble activity during rapid eye movement sleep. Neuron 29, 145–156. ( 10.1016/S0896-6273(01)00186-6) [DOI] [PubMed] [Google Scholar]
- 25.Fellous JM, Tiesinga PH, Thomas PJ, Sejnowski TJ. 2004. Discovering spike patterns in neuronal responses. J. Neurosci. 24, 2989–3001. ( 10.1523/JNEUROSCI.4649-03.2004) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sugase Y, Yamane S, Ueno S, Kawano K. 1999. Global and fine information coded by single neurons in the temporal visual cortex. Nature 400, 869–873. ( 10.1038/23703) [DOI] [PubMed] [Google Scholar]
- 27.Matsumoto N, Okada M, Sugase-Miyamoto Y, Yamane S. 2005. Neuronal mechanisms encoding global-to-fine information in inferior-temporal cortex. J. Comput. Neurosci. 18, 85–103. ( 10.1007/s10827-005-5476-4) [DOI] [PubMed] [Google Scholar]
- 28.McClelland JL, McNaughton BL, O'Reilly RC. 1995. Why there are complementary learning systems in the hippocampus and neocortex: insights from the successes and failures of connectionist models of learning and memory. Psychol. Rev. 102, 419–457. ( 10.1037/0033-295X.102.3.419) [DOI] [PubMed] [Google Scholar]
- 29.Frankland PW, Bontempi B. 2005. The organization of recent and remote memories. Nat. Rev. Neurosci. 6, 119–130. ( 10.1038/nrn1607) [DOI] [PubMed] [Google Scholar]
- 30.Gothard KM, Skaggs WE, Moore KM, McNaughton BL. 1996. Binding of hippocampal CA1 neural activity to multiple reference frames in a landmark-based navigation task. J. Neurosci. 16, 823–835. ( 10.1523/JNEUROSCI.16-02-00823.1996) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Dempster AP, Laird NM, Rubin DB. 1977. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. B 39, 1–38. ( 10.1111/j.2517-6161.1977.tb01600.x) [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data and analysis scripts are available by contacting the author or by download from: doi:10.5061/dryad.qv9s4mwbb.