Coordinated activities of retrosplenial ensembles during resting-state encode spatial landmarks

Abstract

The brain likely uses offline periods to consolidate recent memories. One hypothesis holds that the hippocampal output provides a unique, global linking or ‘index’ code for each memory, and that this code is stored in the cortex in association with locally encoded attributes of each memory. Activation of the index code is hypothesized to evoke coordinated memory trace reactivation thus facilitating consolidation. Retrosplenial cortex (RSC) is a major recipient of hippocampal outflow and we have described populations of neurons there with sparse and orthogonal coding characteristics that resemble hippocampal ‘place’ cells, and whose expression depends on an intact hippocampus. Using two-photon Ca²⁺ imaging, we recorded ensembles of neurons in the RSC during periods of immobility before and after active running on a familiar linear treadmill track. Synchronous bursting of distinct groups of neurons occurred during rest both prior to and after running. In the second rest epoch, these patterns were associated with the locations of tactile landmarks and reward. Complementing established views on the functions of the RSC, our findings indicate that the structure is involved with processing landmark information during rest.

This article is part of the Theo Murphy meeting issue ‘Memory reactivation: replaying events past, present and future’.

1. Introduction

The retrosplenial cortex (RSC) performs key functions in the processing and long-term storage of visuospatial information. The structure receives strong afferent projections from the dorsal hippocampus, both directly and indirectly through the subiculum [1–5]. In both humans and other animals, lesioning the RSC produces deficits in learning and retrieval of spatial information [6–10]. In particular, RSC has been shown to encode environmental landmarks, directional heading and conjunctive features of space in both egocentric and allocentric frames of reference [11–17]. The formation of unique spatial sequences in the RSC relies on an intact hippocampus [18]. These attributes make RSC a prime candidate for investigating the neocortical patterns of neural activity that support the encoding and consolidation of spatial memories.

Reactivation of behavioural memory patterns has been reported in multiple neocortical areas, including both associational and primary/secondary regions [19–26]. Similarly, direct optogenetic stimulation of c-fos tagged retrosplenial ensembles was successful in reproducing contextual fear-conditioned responses [27]. Yet, despite the overwhelming signs of its implication in memory functions, spontaneous reinstatement of task-related memory traces in the RSC during offline periods has so far not been reported. To investigate this possibility, we adapted standard experimental procedures used for studying reactivation in spatial tasks to two-photon calcium imaging. A secondary motivation for this study was to determine whether memory trace reactivation can be observed in neocortex using two-photon imaging, which has much lower temporal resolution than electrophysiological recording. Such a demonstration would open the door to future studies that could exploit the ability to record simultaneously from very large populations distributed widely over the cortex, a capability not currently available with electrophysiology. Accordingly, we recorded from large ensembles of neurons in the dysgranular RSC (dRSC) before, during and after virtual navigation over a linear treadmill populated with tactile landmarks.

2. Material and Methods

(a). Subjects and surgical procedures

All animal procedures were conducted in compliance with the guidelines established by the Canadian Council for Animal Care and were approved by the Animal Welfare Committee of the University of Lethbridge. Three Thy1-GCaMP6s transgenic mice, aged between two and eight months, were used. Following surgery, animals were single-housed in clear plastic cages under a 12 L/12 D cycle. Mice were administered dexamethasone (0.2 mg kg⁻¹, intramuscular) and 0.5 ml of a mixture of 5% dextrose and atropine (3 μg ml⁻¹, subcutaneous), before being anaesthetized with 1.5% isoflurane. Body temperature was maintained at 37°C using a regulated infrared heating pad. Lidocaine (7 mg kg⁻¹) was injected subcutaneously under the incision site. A 5 mm diameter craniotomy was performed over the dorsal cortex (+2 to −3 mm AP; ±2.5 mm ML) (figure 1b). A compound glass window, composed of a 7 mm diameter round coverslip stacked over two 5 mm diameter coverslips (held together with optical adhesive NOA71, Norland), was implanted over the craniotomy and retained using tissue adhesive (Vetbond, 3M). A custom titanium head-plate was fixed to the skull with Metabond (Parkell) and dental adhesive. A rubber ring was attached along the perimeter of the head-plate to retain distilled water during imaging and to insulate the recording site from light contamination. Mice recovered for a minimum of one week before the start of experiments.

Figure 1.

Imaging apparatus and experimental design. (a) Water-deprived mice were head-restrained over a 150 cm long treadmill belt on which were mounted several tactile cues. An LED light illuminated the portion of the belt in front of the mice, who were thus able to see the incoming landmarks. Cue positions and sizes are illustrated to scale with the belt over the x-axis. (b) Example of cranial window implant for one mouse. The windows inside of which imaging was conducted for this study are delineated by black boxes. (c) Each imaging session was divided into three 10 min blocks. Before and after running, animals rested quietly over the belt, while surrounded by a cardboard enclosure. The belt was clamped during rest and released during run. A 1 min segment from each imaging block is illustrated from one example session. The time-courses of deconvolved ΔF/F for all simultaneously imaged neurons were z-scored and temporally smoothed with a σ = 1 s Gaussian kernel. Traces for each neuron were normalized by the peak (range between 0 and 1). Neurons were sorted by the location with the highest average response during running. Animal position and linear velocity are shown below. (d) The average running speed as a function of location (n = 3 mice; n = 13 sessions). Shaded regions denote s.e.m.

(b). Behavioural task

Water-restricted mice were habituated to head-fixation and underwent daily training to run over a linear treadmill track for over two weeks, as previously described [15,18]. The duration of each training session began with 15 min and was gradually extended to 1 h over the course of 5 days. The treadmill consisted of two three-dimensional printed polyamide wheels with radii of 5 cm (figure 1a). The wheel centres were separated by 40 cm. Position was decoded from an optical encoder (Broadcom) attached to the front wheel. A 150 cm long belt made from the soft fabric of a Velcro strip (Country Brook) was looped around the wheels. A photo-reflective tape was applied to one spot underneath the belt. The tape triggered a photoelectric sensor (Omron) that opened an electromagnetic pinch valve (Bio-Chem Valve) to dispense sucrose water reward.

Once performance reached over 50 laps per hour, the duration of running was reduced to 20 min and animals were made to rest for 20 min before and after running by clamping the belt. The belt was lined with four distinct tactile cues (figure 1a), made up of hot glue (first and last cues), reflective tape (middle cue) and a strip of Velcro (second cue before reward). During navigation, a dim LED light illuminated the area in front of the animals, so that they could see approaching landmarks. During rest, a cardboard enclosure was placed around the mice to substitute for a flower pot used in previous paradigms [28]. Mice were trained under this new protocol for another two weeks or until movement was detected for less than 30% of the duration of rest. For imaging experiments, the durations of REST1, RUN and REST2 epochs were shortened to 10 min each (figure 1c). During rest, the belt was clamped to discourage movements. With the belt clamped, the treadmill encoder was still sensitive enough to detect any small movement made by the animals.

(c). Two-photon imaging

All imaging data were acquired using a Thorlabs Bergamo II multi-photon microscope. Ti : sapphire laser (Coherent) light tuned to an excitatory wavelength of 920 nm was passed to the tissue through a 16× water immersion objective (Nikon, NA 0.8, 80–120 mW output power measured at the sample). Rasterization was conducted by Galvo-Resonant scanners. The emitted GCaMP6 signals were amplified using a GaAsP photomultiplier tube (Hamamatsu) and digitized to a resolution of $800\times 800\hspace{0.17em}\text{pixels}$ at a sampling rate of 19 Hz. We imaged an 835 × 835 μm window over layers II–III of the agranular RSC at depths between 100 and 200 μm (imaging windows centred at −1.8 to −2.5 mm AP, 0.5 mm ML; figure 1b). A strip of Velcro wrapped around the body of the objective was lowered to the level of the rubber ring to block ambient light.

(d). Image preprocessing and place field analysis

Image preprocessing was performed as previously described [15,18]. Registration and identification of regions of interest (ROIs) were conducted automatically using Suite2p [29]. Neurons were manually selected based on the morphology of the ROIs and the presence of distinct calcium deflections in the fluorescence trace. The raw fluorescent-time-course for each neuron was extracted from the corresponding ROIs. Neuropil contamination, estimated from the surround of ROIs, was subtracted [30]. Baseline fluorescence was approximated and the ratio ΔF/F₀ was obtained. Firing rates were inferred by deconvolving the ratio time-courses using constrained non-negative matrix factorization [31]. All subsequent analyses were conducted using the deconvolved time-courses in MATLAB R2017a (MathWorks).

Two criteria were used to classify neurons that express spatial-selectivity (henceforth termed ‘place’ cells). Spatial information (I; bits) was given by [32] as

$$I=\sum _{i=1}^N{p}_i\frac{\hspace{0.17em}{f}_i}{f}{\log }_2\frac{\hspace{0.17em}{f}_i}{f},$$ 2.1

where for N spatial bins, p_i is the occupancy probability in bin i, f_i is the mean deconvolved fluorescence in bin i and f is the overall mean fluorescence. We generated a null distribution of spatial information by circularly shuffling the time-courses 1000 times. To be considered spatially receptive, neurons must contain spatial information higher than the 95th percentile of the null distribution. We obtained a continuous wavelet transform W over the spatial tuning curve of each neuron using a Mexican Hat mother wavelet Ψ:

$$W(\sigma ,\tau )=\frac{1}{\sqrt{\sigma }}\sum _{i=1}^N{f}_i\mathit{\Psi }\left(\frac{i-\tau }{\sigma }\right)$$ 2.2

and

$$\mathit{\Psi }(t)=\frac{2}{{\pi }^{1/4}\sqrt{3}}(1-t^2){\mathrm{e}}^{-t^2/2}$$ 2.3

where σ and τ are the scale and translation parameters, respectively. For initial detection, the local maxima in the transform indicated the locations (given by τ) and the widths (given by σ) of potential place fields [33,34]. To remove spurious peaks caused by noise, we obtained a threshold λ of 3 median absolute deviations from the median from the wavelet coefficients at the lowest scale (σ = 1). Only local maxima with values higher than λ in the transform were selected as potential place fields. Local maxima that were contained within the receptive field of a local maximum at a higher scale σ were removed. A place field must be wider than 5% of the length of the environment, but narrower than 80%. The mean activity within a place field must be 2.5 times higher than the mean activity outside of place fields. When comparing the activity inside a place field and outside any place field, the peak activity must occur within the place field in a third of the laps. Cells that, after passing all criteria, still contained at least one place field were classified as spatially receptive neurons.

(e). Identification of neuronal ensembles

To identify and group neurons that expressed spontaneous co-activity during rest, we applied agglomerative clustering to the correlation matrices of rate vectors (figure 2b; for a comprehensive review on hierarchical clustering, see Murtagh & Contreras [35]). First, we removed movement epochs by identifying any region of time in which the instantaneous velocity deviated from 0. Rate vectors were smoothed using a σ = 1 s Gaussian kernel to reduce temporal jitter and to increase temporal correlation. Then, we computed the Pearson correlation matrix of rate vectors between each neuron pair. Correlation coefficients r were converted to a distance metric d = 1 − r. Finally, we performed agglomerative clustering on the upper triangle of the distance matrix using unweighted average distance linkage criterion. We set a cut-off threshold of d < 0.75, which corresponds to an average correlation coefficient of r > 0.25 within a cluster. Clusters containing fewer than 10 members were rejected.

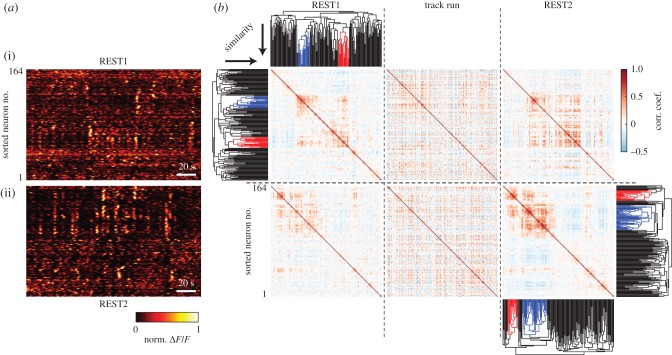
Figure 2.

Sub-populations of retrosplenial neurons repeatedly co-activate during rest. (a) 200 s segments of the deconvolved time-courses of REST1 and REST2 were taken from the same session as in figure 1. Sorting the neurons by firing rate vector similarity (see b) reveals groups of neurons that were spontaneously and repeatedly co-active (in this article, we term these synchronous groups ‘ensembles’). (b) Pearson correlation matrices were computed between the rate vectors of all cell-pairs for each imaging block. Hierarchical clustering was conducted independently on the correlation matrices of REST1 and REST2 to group neurons expressing synchronous patterns of activity (clustered neurons are grouped by colour in the dendrogram; see Material and Methods). From the root of the dendrogram, clusters are sorted by ascending order of similarity. Neurons are sorted so as to maximize the similarities between adjacent neurons. Neurons in row (i) (including neurons in (a)) are sorted according to the REST1 clustering results, while neurons in row (ii) are sorted by REST2 cluster linkages. In other words, direct comparisons by eye is possible between plots over the same row. In this example recording, two ensembles were detected in both REST1 and REST2. Note that, in general, REST1 and REST2 may not necessarily contain the same number of ensembles. The red and blue colours identify ensembles that were independently detected in REST1 and REST2. The colours were randomly chosen and do not imply any relationships between the two epochs.

For each ensemble, synchronous calcium events (SCEs) were identified by calculating the multi-unit activity (MUA) from the z-scored deconvolved ΔF/F of all neurons that were part of the ensemble. Any continuous segment of time in which the MUA exceeded 3 s.d. above the mean were classified as SCEs (electronic supplementary material, figure S1). SCEs that occurred less than 250 ms apart were identified as part of the same SCE. Inter-event intervals were measured between the onset of each SCE, within the same ensemble.

(f). Bayesian reconstruction

Methods for Bayesian reconstruction were as previously described [18,36]. Briefly, we obtained the probability for the animal to be at a position x given the population firing vector n:

$$\text{Pr}(x|n)=\frac{\text{Pr}(n|x)\text{Pr}(x)}{\text{Pr}(n)}=C\left(\prod _{i=1}^N{f}_i{(x)}^{n_i}\right)\exp (-\tau \sum _{i=1}^N{f}_i(x)),$$ 2.4

where f_i(x) is the mean deconvolved fluorescence of neuron i as a function of position derived from training data, and n_i is the time-course vector, a mean activity within time bins of length τ obtained from testing data. The resulting matrix Pr(x|n) contains the probability for the animal to be at any position x for every time point in n_i (figure 5a; electronic supplementary material, figure S1). The decoded position over time is given by argmax_xPr(x|n). Sessions in which the animal covered less than 10 laps were rejected from analysis (electronic supplementary material, table S1).

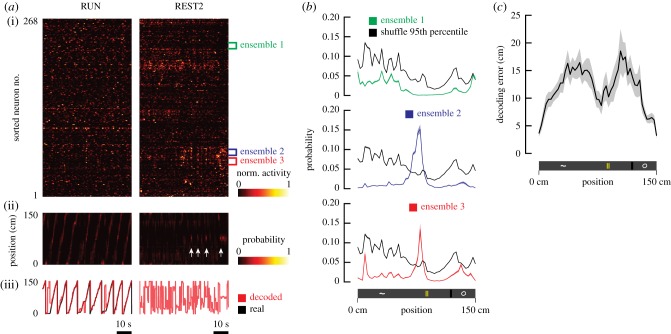
Figure 5.

Bayesian reconstruction of location from resting neural activity. (a) 1 minute segments of the time-courses of neural activity during RUN and REST2 were taken from an example recording session (i). Neurons were sorted by similarity between the rate vectors of cell-pairs during REST2. Three ensembles were simultaneously identified in these data and are highlighted in this plot. The outputs from Bayesian reconstruction of position are represented as a matrix of probability that the animal is at a given location for any given point in time (ii). The parameters of the Bayesian model were estimated using all running laps and were tested on the resting-state activity. White arrows denote the time points where SCEs were detected from ensemble 2. The decoded positions, defined as the location of highest probability, are plotted in conjunction with real positions (iii). (b) The mean decoded probability as a function of location, during all frames in which an SCE occurred, was plotted for all three ensembles (shaded regions: s.e.m.). Black plots represent the 95th percentiles obtained from shuffled data. For ensembles 2 and 3, the decoded probability at the location right in front of the middle landmark was higher than the probability obtained from shuffled data. (c) The mean decoding error as a function of position (shaded regions: s.e.m.; n = 13 sessions). The Bayesian model was trained on even trials, and errors were evaluated with odd trials.

To validate the quality of decoding, fluorescence time-courses from odd laps were used as training sets and decoding errors were obtained as the absolute value of the difference between decoded position and real position on even laps (figure 5c). For rest epochs, the model was trained on all trials during running periods, and decoding was conducted on the resting-state population vectors that corresponded with SCEs. To evaluate the likelihood that positions were decoded by chance, we shuffled the identities of neurons and performed the decoding procedure 1000 times (figure 5b; electronic supplementary material, figure S1). This method ensures that the temporal structure of the time-courses is preserved. A p-value was obtained at each position for each SCE-associated time frame by counting the instances where Pr(x|n), decoded from rest, was higher than the randomly permuted data.

As a secondary shuffling criterium, we used a ‘time bins shuffle’. We randomly permuted the time bins in the posterior probability matrix Pr(x|n) 1000 times and obtained p-values by counting the number of instances in which the probabilities during SCE-associated time frames were higher than the shuffled probabilities. This method was included to account for the mismatch created between the place fields’ tuning profiles f_i(x) and the resting state population firing vectors n_i from ‘cell identity shuffling’ [37]. However, this method is susceptible to a different source of noise by considering time frames that were outside of SCEs, hence creating a mismatch between temporal structures. We included the results obtained from this shuffling method in the electronic supplementary material, figure S3 and table S2B.

3. Results

(a). Sub-populations of retrosplenial neurons are spontaneously and recurrently co-activated during rest

We began by investigating the population dynamics in the retrosplenial network during quiet-wakeful periods. We only considered regions of the recording in which animals were immobile. We observed spontaneous and concerted activity among groups of neurons, during resting periods both before (REST1) and after (REST2) exposure to task (figure 2a). For the remainder of this article, we shall refer to these groups of synchronous neurons as ‘ensembles’. Ensembles were identified based on the similarity between the rate vectors across pairs of neurons (figure 2b; see Material and Methods). Ensemble neurons formed a small subset of the population. On average, 13.5% of neurons expressed co-activity during REST1 (±2.6% s.e.m.), while 20.2% (±3% s.e.m.; n = 13 sessions; n = 3 mice) were synchronous during REST2 (figure 3a). Per imaging session, an average of 2.1 ensembles were simultaneously active in REST1 (±0.4 s.e.m.; n = 13 sessions; n = 3 mice), and 2.6 ensembles in REST2 (±0.3 s.e.m.; n = 13 sessions; n = 3 mice) (figure 3b). Though there was an overall tendency for REST2 neuronal populations to express a higher degree of synchrony, the effect was not significant with the current sample size.

Figure 3.

During the resting state, sparse subsets of neurons engage in synchronous activation. (a) The fraction of neurons that were co-active during REST1 and REST2 (white dot, median; box, first and last quartiles; whiskers, minimum and maximum values; Wilcoxon signed-rank test n.s.). These fractions include all neurons that were classified as part of an ensemble in a recording, for all 13 imaging sessions conducted. (b) Distribution of the number of ensembles simultaneously detected during rest. For each of the 13 imaging sessions, we count the number of ensembles that co-existed in REST1 and in REST2. (c) Distributions of the time interval between successive SCEs over linear (i) and logarithmic scales (ii) (n = 102 REST1 SCEs; n = 147 REST2 SCEs). We took the difference between the onset time-stamp of each adjacent SCE that was part of the same ensemble.

Neurons grouped into ensembles exhibited synchronous activity, termed SCEs [38]. These events occurred at a mean rate of 0.66 events per minute (±0.06 s.e.m.; n = 27 ensembles) during REST1 and 0.53 events per minute (±0.05 s.e.m.; n = 34 ensembles) during REST2. The time interval between events appeared to be lognormally distributed (figure 3c), with a mean interval of 70 s during REST1 (+1.13/− 0.88 s s.e.m.) and 55 s in REST2 (+1.1/− 0.91 s s.e.m.). Together, the results suggest that SCEs occur in close succession to each other (at a rate of approx. 1 SCE per minute) over sparse regions of time.

(b). Resting-state ensembles are stable following active virtual navigation

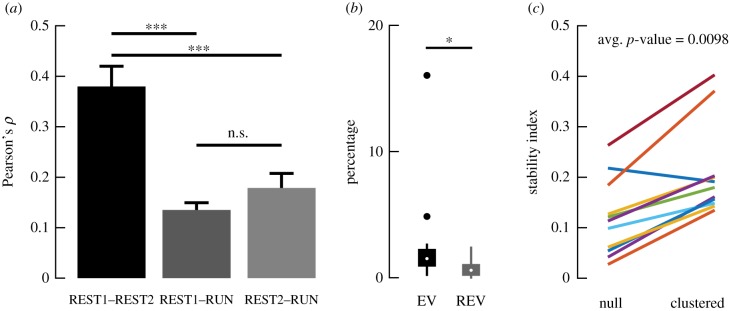
Next, we examined whether neuronal ensembles remained stable following virtual navigation. We began by comparing the correlation structure of the entire neuronal population across the three behavioural epochs. A Pearson correlation matrix was calculated for the rate vectors across each epoch (figure 2b). The correlation coefficients between cell-pairs in the upper matrix were in turn correlated across all three epochs. The population activity between resting periods exhibited a greater degree of similarity than between rest and run epochs (figure 4a). Explained variance (EV) was used to quantify the percentage of the variance in the pairwise correlations of the neuronal population in RUN that could be explained by the REST2 correlations, given the correlations that existed between REST1 and RUN (figure 4b) [39,40]. A higher fraction of the variance in the RUN correlations was predicted by the REST2 correlations, compared with REST1. Therefore, although the REST epochs were more similar in correlation structures, REST2 correlations exhibited a higher degree of resemblance with the RUN structures than REST1. This result provided the first evidence for reactivation. Looking into ensembles, the likelihood of obtaining a given degree of overlap between REST1 and REST2 co-active neurons was modelled after a hypergeometric distribution. The latter is a probability density function which, in the present scenario, can be used to describe the probability of redrawing k neurons out of n draws from a population of N neurons, given that K neurons were already drawn previously. The degree of overlap between resting-state synchronous neurons was significantly above chance, with an average p-value <0.01 (figure 4c). However, a sizeable fraction of neurons was also substituted following exposure to task; the stability index averaged at 0.21 (±0.03 s.e.m.). In the next section, we explore the contributions of these reorganizations to the encoding of space.

Figure 4.

Population and ensemble activities are stable following task exposure. (a) For each session, we took the upper triangle of the correlation matrices for the firing rate vectors of all cells for each individual imaging block (n = 3 mice; n = 13 sessions). We computed the Pearson correlation between the correlation coefficients of the cell-pairs as a measure of similarity between the population activity structure across the three imaging blocks. The mean and standard errors of the resulting Pearson correlation coefficients are shown (one-way ANOVA; ***p < 0.001). The lack of significant difference between REST1–RUN and REST2–RUN possibly reflected the fact that the animals were already highly experienced on the task. (b) Explained variance was calculated as $\text{EV}={((R_{\mathrm{RUN},\mathrm{REST}2}-R_{\mathrm{RUN},\mathrm{REST}2}{R}_{\mathrm{REST}1,\mathrm{REST}2})/\sqrt{(1-R_{\mathrm{RUN},\mathrm{REST}1}^2)(1-R_{\mathrm{REST}1,\mathrm{REST}2}^2)})}^2$, where the R-values correspond to Pearson correlation coefficients in (a) [39,40]. These values were controlled against the reverse explained variance (REV). REV was obtained using the same equation, but by substituting REST2 with REST1 epochs and vice versa. EV was significantly higher than REV, suggesting that reactivation had occurred (p = 0.0183; Wilcoxon rank sum test; n = 13 sessions; n = 3 mice; white dot, median; box, first and last quartiles; whiskers, minimum and maximum values; solid dots, outliers). (c) To assess the fraction of neurons that remained co-active after RUN, we calculated a stability index O/(N₁ + N₂ − O), where N₁ is the number of co-active neurons detected in REST1, N₂ is the number of co-active neurons detected in REST2 and O is the number of neurons that were co-active during both resting blocks. To determine how likely it was that the resulting values were obtained by chance, we estimated the expected number of overlapping neurons between the two blocks as the expected value of the corresponding hypergeometric distribution (shown as ‘null’). The average p-value from the hypergeometric distribution, indicating how likely it is that the proportion of overlap O was due to chance, is reported.

(c). Resting-state co-activity encodes the location of landmarks following navigation

We employed a Bayesian approach to determine whether SCEs contained information relevant to previously explored space. We first confirmed that a Bayesian model can accurately decode animal position from neural activity acquired during running. We estimated the model parameters using the activity during even lap runs and measured the difference between decoded position and actual position on odd trials (figure 5c). The mean decoding error was 11.8 cm (±0.3 s.e.m.), confirming the accuracy of the model. For resting data, we derived the model parameters from all running laps, and decoded position over the time frames during which SCEs occurred (figure 5a). The generated output gave the probability for the animal to be at any given position over the linear track at any given frame of time. To control for spurious results, the same analysis was conducted 1000 times with the identity of the neurons randomly shuffled (figure 5b). A p-value could therefore be obtained by accumulating the number of instances in which a position contained a higher probability of being decoded than the shuffled distribution (figure 6a).

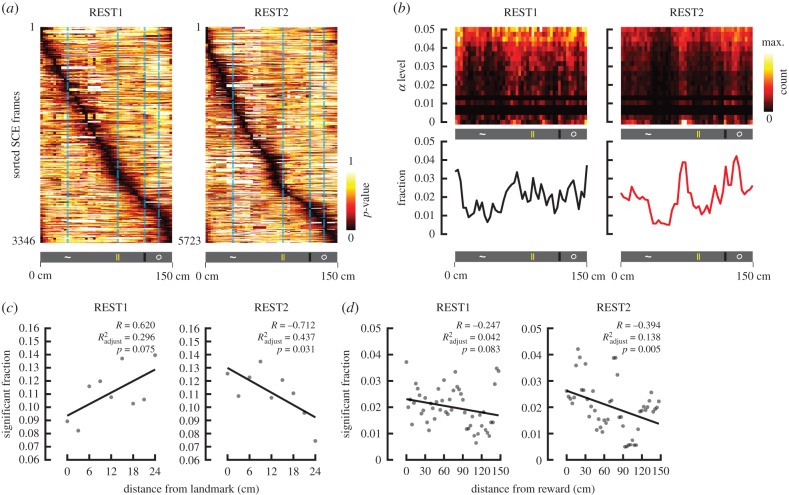
Figure 6.

REST2 ensemble co-activation decodes positions near landmarks and reward. (a) For each time frame associated with an SCE, p-values were obtained as the fraction of probabilities obtained from shuffling that were greater than the probabilities obtained from the true data, at every given position. In other words, we evaluated the degree to which a decoded position during an SCE is likely due to chance (the lower the p-value, the less likely the decoding was obtained by chance). These time frames were sorted according to the location of most significant decoding. Results from all SCE-associated time frames (obtained from all three animals, all 13 sessions) are shown for REST1 and REST2. (b) Joint density distributions of the fraction of significantly decoded positions at different α levels (p-values). α levels were binned over a logarithmic scale. The fractions of significant decoding (p < 0.05; analogous to summing over the columns) as a function of position is shown below. Notice in REST1, the fractions are more uniformly distributed, while in REST2, the fractions are more concentrated near the locations of landmarks. (c) The fraction of frames that significantly decoded position (p < 0.05) is compared with the distance from the closest landmark over a scatter plot. Since the landmarks were not separated uniformly over the same distance, the fractions were normalized by the occupancy over each spatial bin. Linear regression fit line depicted in black. (d) Same as (c), but evaluating the distance needed to be travelled before receiving reward.

For REST2 SCEs, the fraction of significantly decoded positions was anti-correlated with the distance from local landmarks (figure 6c; electronic supplementary material, table S2). This trend indicates that synchronous activity patterns during post-task rest decode more frequently locations in proximity to landmarks. By contrast, pre-exposure activities were not significantly related to landmark locations. The decoding fractions were anti-correlated with the distance from the reward in REST2, suggesting that higher precedence was gradually assigned to locations leading up to the reward. These results were consistently observed in all three animals tested (electronic supplementary material, figures S3–S5).

(d). Reorganization of ensemble members is tied to environmental features

Lastly, we looked for the presence of any discernible features in the spatial coding characteristics of synchronous neurons. Both prior and subsequent to task exposure, ensembles did not selectively recruit highly spatially receptive neurons. In REST1, 59% (±7% s.e.m.) of co-active neurons were classified as ‘place cells’, while 58% (±4% s.e.m.) was the average for REST2. Over the entire population, 57% (±4% s.e.m.) of neurons were spatially receptive. Surprisingly, the spatial information content of the portion of co-active neurons that were lost subsequent to task was significantly higher than that of neurons that were gained (figure 7a). To explain this intriguing result, we eliminated the summation step in equation (2.1), which computes the spatial information content of neurons. This in turn yielded a vector of the relative contribution of each location to the total spatial information of a neuron (figure 7b). We found that a large fraction of spatial information in REST1 ensembles was contributed by the very beginning of the track, right after animals received a reward. In comparison, REST2 ensembles expressed higher spatial information over the first 30 cm and last 10 cm, corresponding with the first and last landmarks. This observation concurs with the results obtained from Bayesian analysis, where a large fraction of decoded positions in REST1 corresponded with the beginning of the track (figure 6b). The spatial distribution of the locations of place field centres also became more compact for REST2 co-active neurons (figure 7c). A higher fraction of place fields were expressed by REST2 and ‘gained’ neurons at locations of landmarks compared with REST1 and ‘lost’ as well (figure 7d).

Figure 7.

Rearrangements of ensemble neurons subsequent to behaviour are tied to features in the environment. (a) Cumulative densities of the spatial information content of co-active neurons in REST1 and REST2 (n = 3 mice; n = 13 sessions; n = 413 REST1 neurons; n = 617 REST2 neurons). Spatial information was calculated for each neuron from the RUN data, and is a measure of the amount of information conveyed by individual neurons about the animal’s position during RUN. The densities were further separated by neurons that were no longer co-active following exposure (lost) and those that became co-active (gained) (n = 169 stable/overlapping neurons). The spatial information content of ‘lost’ neurons was unexpectedly higher than that of ‘gained’ neurons (one-tailed two-sample Kolmogorov–Smirnov test p < 0.05). To clarify the reasons behind this discrepancy, we skipped the summation step in equation (2.1). In doing so, we obtained the relative contribution of each position to the total spatial information for a given neuron. (b) The relative contribution to spatial information of co-active neurons as a function of position for all neurons in (a). Lines denote mean, and shaded areas depict s.e.m. Black dots denote positions where the spatial information content was higher for REST1 neurons than REST2 and vice versa for red dots (Wilcoxon signed-rank test; p < 0.05). For the ‘lost’ neurons, the majority of spatial information came from the beginning of the track, immediately after a reward was received. This over-representation accounts for the overall higher spatial information reported in (a). The spatial distribution of information was more uniform for ‘gained’ neurons with significantly less sensitivity towards the receiving of reward. ‘Gained’ neurons also contained higher spatial information in the first 30 cm leading to the first cue, and in the last 10 cm leading to the reward. (c) Histograms for the spatial distribution of place field centres for REST1 and REST2 neurons that were classified as ‘place cells’. Place field centres were identified for individual neurons from the RUN data (see Material and Methods). Curves plotted over the histograms were obtained by smoothing the fractions with a 5 cm Gaussian kernel. The distribution for ‘lost’ and REST1 neurons expressed high variance over successive locations. In comparison, ‘gained’ and REST2 neurons showed less dispersion (coefficient of variation c_v = σ/μ; c_v = 0.506 REST1; c_v = 0.474 REST2; c_v = 0.564 ‘lost’; c_v = 0.477 ‘gained’; n = 50 spatial bins). (d) The difference was taken between the curves in (c) to reflect the difference in the fractions of place fields between REST2 and REST1 (i), and ‘gained’ and ‘lost’ (ii), as a function of position. REST2 and ‘gained’ neurons contained more place fields near the locations of landmarks than REST1 and ‘lost’ neurons. Conversely, REST1 and ‘lost’ neurons expressed more place fields at the beginning of the track, right after the location where rewards were delivered. These results are consistent with the results in panel (b).

4. Discussion

In this study, we investigated the resting-state neural dynamics of the RSC, and identified neural patterns of activity associated with prior spatial experiences. We found that the structure of resting-state activities in retrosplenial neuronal populations is distinctly stable following ‘virtual’ spatial navigation. This feature impacts traditional techniques used for analysing reactivation, such as explained variance, template matching and principal components analysis, which all require strong correlations between task-related and resting-state population vectors [23,40]. By contrast, only a sparse subset of RSC neurons formed ensembles that expressed task-relevant activities during resting epochs. With population sparseness comes the necessity to record simultaneously from large numbers of neurons in order to extract statistical effects. This is made especially difficult for microelectrode recordings that target superficial layers of the neocortex, where stable large-scale recordings are often impaired by tissue damage. In the RSC, the bulk of hippocampal back-projections terminate in layers II/III, which are rich in NMDA-receptors [41]. Widely held theories postulate that the presence of rapid plasticity mechanisms in the neocortex supports the gradual consolidation of new and unique experiences through outflow of information encoded by the hippocampus [42–47]. Support for the existence of such a model in the RSC has been provided by our recent works: first, the generation of spatial sequences encoded by the RSC requires an intact hippocampus [18]; second, a greater fraction of spatially receptive neurons reside in superficial RSC layers rather than deep layers [15]. The advantage of the two-photon technique in imaging large populations of superficial layer neurons may therefore have contributed to our observation of experience-related activity patterns during resting periods. It remains to be determined whether superficial and deep layers participate equally in reinstatement.

The presence of offline activities associated with landmark location comes as no surprise when considering the large body of studies that are consistent with such a function. Lesioning the RSC impaired the ability of the head-direction system to sustain stable representations using landmarks [48]. Correspondingly, head-direction cells in the dysgranular RSC are reoriented by local landmarks within a global environment [14]. In humans, patients with lesions to the RSC were able to identify familiar landmarks, but experienced substantial impairments in remembering the spatial relationships between landmarks [49,50]. Functional magnetic resonance imaging (fMRI) studies revealed that the RSC was most engaged during presentation of stable landmarks [51]. Together, the combination of rodent and human evidence indicates that the RSC performs an active role in landmark encoding during both online and offline periods. Rather perplexing is the seemingly undervalued role of the RSC when considering the amount of information available to the structure. Indeed, during online periods, spatial coding in the RSC emerges as continuous representations over the environment [12,15]. Further studies are required to resolve whether offline RSC activities imply spatial cognitive functions beyond landmark encoding.

One major outstanding question generated from our results is the time-course of memory trace events in the RSC in relation to the rest of the brain. According to prevalent theories of consolidation, novel experiences first encoded by the hippocampus are gradually merged with existing representations in the neocortex [42,52,53]. As one of the main output structures of the hippocampus, we expect the RSC to reinstate experience-associated memory traces during early stages of consolidation. Answering this question is beyond the scope of the current article, as the animals used in this study had been previously exposed to the behavioural task. Meta-analytically, reactivation observed in other brain regions, including the prefrontal cortex [19], the posterior parietal cortex [26] and the visual cortex [22], did not employ naive animals either. Therefore, it can be hypothesized that consolidation occurs over a shorter time scale in the RSC; perhaps stronger reactivation would be observed during the early stages of task acquisition. Further investigation is required to uncover the time-course of memory consolidation in the RSC in relation to other regions. Altogether, our results demonstrate the involvement of the RSC in spontaneous retrieval of spatial landmark information during offline periods.

Ethics

All animal procedures were conducted in compliance with the guidelines established by the Canadian Council for Animal Care and were approved by the Animal Welfare Committee of the University of Lethbridge.

Data accessibility

All data reported in this article are available in Dryad (doi:10.5061/dryad.hhmgqnkd4) [54].

Authors' contributions

HR.C., A.R.N. and I.M.E. conceptualized and developed the experiments. I.M.E. conducted the behavioural recordings. J.S. performed all animal surgeries. HR.C. conducted all data analyses. HR.C. and B.L.M. wrote the article, which all authors commented on and edited. B.L.M. and M.H.M. supervised the study.

Competing interests

We declare we have no competing interest.

Funding

This work was supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) (grant no. 1631465 (B.L.M.)), by the Canadian Institutes of Health Research (CIHR) (no. PJT 156040 (B.L.M.)) and by the USA Defense Advanced Research Projects Agency (DARPA) (grant no. HR0011-18-2-0021 (B.L.M.)).