Leveraging elastic instabilities for amplified performance: Spine-inspired high-speed and high-force soft robots

Bistable spined soft robots enable high-speed cheetah-like galloping and fast-speed swimming, as well as high-force manipulation.

Abstract

Soft machines typically exhibit slow locomotion speed and low manipulation strength because of intrinsic limitations of soft materials. Here, we present a generic design principle that harnesses mechanical instability for a variety of spine-inspired fast and strong soft machines. Unlike most current soft robots that are designed as inherently and unimodally stable, our design leverages tunable snap-through bistability to fully explore the ability of soft robots to rapidly store and release energy within tens of milliseconds. We demonstrate this generic design principle with three high-performance soft machines: High-speed cheetah-like galloping crawlers with locomotion speeds of 2.68 body length/s, high-speed underwater swimmers (0.78 body length/s), and tunable low-to-high-force soft grippers with over 1 to 10³ stiffness modulation (maximum load capacity is 11.4 kg). Our study establishes a new generic design paradigm of next-generation high-performance soft robots that are applicable for multifunctionality, different actuation methods, and materials at multiscales.

INTRODUCTION

Recently, soft robotics have attracted tremendous research interest because of their safe and adaptive interaction with humans and harsh environments, enabling a wide range of new functionalities that can rarely be achieved by conventional rigid robots (1), including manipulation of delicate objects (2, 3), navigation through a confined space (4, 5), and actuation with multiple degrees of freedom (6, 7). Despite these advances, it remains challenging to achieve high performance in soft robots, e.g., high-speed locomotion and high-strength manipulation, because of the intrinsic limitations of their soft bodies (8). Normally, high-speed locomotion requires fast response, large force output, high strain energy storage, and high-precision motion of the actuators. Soft-bodied robots have typically shown small force exertion, large deformation, and slow response time, resulting from their materials softness and structural compliance. Soft materials make it difficult to rapidly store and release large amounts of mechanical energy, limiting their applications in high-speed locomotion and high-strength object manipulation (9). Most studied soft robots to date demonstrate a relatively slow locomotion speed in the range of 0.02 to 0.8 body length per second (BL/s) both on land and underwater, as well as limited payload capability of grasping (10) in soft manipulators, which are far below the locomotion speed (1 to 100 BL/s) and high-strength object manipulation (>10 kg) in animals and rigid robots. In addition, soft machines are often designed for single-purpose functionality in either locomotion or manipulation; a generic soft machine that serves multiple purposes under different working scenarios could largely simplify the design, as well as improve the working efficiency and its versatility.

In nature, a number of quadrupeds exhibit exceptionally high-speed locomotion that has evolved through millions of years of evolution. Locomotion principles have been garnered from their study and embedded into bioinspired terrestrial robots (11). Among the locomotor gaits, galloping is typically used at the highest running speeds, e.g., the fastest galloping cheetah demonstrates a record speed of 29 m/s on land. Galloping has also been suggested as the most energy-efficient mode of locomotion in quadrupedal mammals (12). The roles and benefits of spine flexion and extension for high-speed locomotion are investigated for vertebrate animals in terms of self-stabilization and elastic energy storage (13). Recently, active spine mechanisms (14) were studied in legged robots for high-speed and energetically economic locomotion (15, 16). It was found that active spine actuation can increase speed and enhance stability. However, the potential benefit of the active spine mechanism in soft locomotive robotics remains unexplored.

Most current soft-bodied robots are designed to be inherently stable and usually unimodally stable. Relaxing this design constraint allows exploration of the principle of elastic instability for rapid energy storage and release in a soft robot. Very recently, bistability has been studied in soft robotics for untethered directional propulsion (17), autonomous control of airflow in soft bistable valves (18), and soft fluidic actuators with amplified responses (19). Although bistable soft actuators have been applied to high–power density design for hydrodynamic interaction (20), exploration and analysis of rigid and soft materials (21), and multilinkage and multiple spring mechanisms (22), they have primarily been tailored for high-speed jumping locomotion.

To address these challenges, we present a generic design principle that harnesses mechanical instability for both high-performance and versatile soft robots ranging from high-speed terrestrial and aquatic locomotion to high-force manipulation. Inspired by the spine flexion and extension in high-speed yet energy-efficient quadrupedal mammals such as galloping cheetahs, we propose here a soft actuator with a tunable bistable spine mechanism for rapid energy storage/release, as schematically shown in Fig. 1A. Bistability enables both amplified actuation speed and forces for high-speed locomotion and wide-range stiffness modulation for high-force manipulation in soft actuators. Our design leverages high nonlinearity phenomena of instability to fully explore the ability of soft machines to rapidly store and release energy. Our work represents a new family of versatile actuators that are soft but strong with high-speed or high-force output and a wide-range of tunable stiffness, notably expanding the spectrum of conventional ones made of rigid bodies and elastic joints (e.g., series elastic actuators) (23).

Fig. 1. Spine-inspired bistable soft actuators.

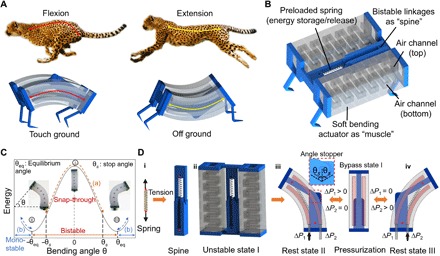
(A) Bioinspired by the active spine mechanism during cheetahs’ high-speed galloping, a bistable spine-based hybrid soft actuator is proposed to realize the similar spine flexion and extension through reversible snap-through bistability for design of high-speed locomotive soft robots. (B) Schematic design of a bistable hybrid soft bending actuator (BH-SBA). It consists of three components: two soft pneumatic two-way bending actuators as skeletal muscle, a three-dimensionally (3D) printed flexible mechanism composed of two rigid hinged links as a spine, and a pretensioned spring that connects two ends of the mechanism for potential mechanical energy storage and release. (C) Schematics of energy landscape of the bistable actuator, showing one peak (unstable state I) and two localized minimum energy states (stable states II and III). It provides two operating regimes: one is the bistable switch in path a, and the other is the monostable state in path b. Insets show the corresponding Ecoflex-based bistable actuator prototypes at each state. (D) Schematic illustration of the bistable working mechanism under both nonactuated (spring pretension release at resting states in i to iii) and actuated states (reversible snapping-through under pneumatic actuation in iii and iv). The inset shows the set of an angular stopper to constrain the maximum bending angle at the preset stopping angle of θ_s.

The bistable hybrid soft actuator presented here is constructed by combining spring-based bistable linkages as a “skeletal spine” and soft pneumatic bending actuators as “skeletal muscle” (Fig. 1B). It harnesses a rapid, switchable snap-through instability between two stable states that are actuated by soft pneumatic bending actuators. The mechanical energy of our actuator is stored in a linear spring connected to the linkage-based spine, which can be tuned from low to high energy storage capacity through simple spring pretension or springs with different stiffness. This spring in soft actuators acts as a force amplifier. It substantially enlarges not only the actuation speed and force but also the design space for stiffness modulation through tunable snap-through instabilities. We first study the design principle of a bistable hybrid soft actuator and characterize its actuation response. We develop an energy-based theoretical model to understand its nonlinear behavior, including the relationship among design parameters (e.g., spring stiffness and pretension length), control inputs (pneumatic actuation pressure), and outputs (including force, bending angle, and energy barrier). We then examine its amplified mechanical performance in both response time and force output through bistability. Last, we explore the simplicity of using the tunable bistable mechanism for applications ranging from high-speed terrestrial and aquatic locomotion to high-force grasping.

RESULTS

Design principles of a bistable hybrid soft actuator

We leverage the physical principle of elastic instability to guide the design of fast and strong soft machines, where energy competition and synergy relationship between springs and soft pneumatic actuators determine the bistability of the hybrid soft actuator. Bistability provides two distinct dynamic operating regimes: (i) bistable mode switching between two stable states (path a in Fig. 1C) [upon activation, highly nonlinear, reversible, snap-through bistability triggers instantaneous and notable changes in speed and position through rapid energy storage and release (Fig. 1C), which guides the design of high-speed soft crawler and swimmer] and (ii) monostable mode bending beyond the equilibrium configuration (path b in Fig. 1C) (the tunable pretension in the spring provides high-force output with a wide range of stiffness modulation for the design of high-force soft grippers).

To understand the design methodology and relationship between design parameters and performance, we first studied the design principle for the bistable hybrid soft bending actuator (BH-SBA) of the cheetah-inspired high-speed crawlers. Figure 1B shows the schematic design of the BH-SBA. It consists of a bistable flexible spine mechanism with a pretensioned linear spring and two identical soft bidirectional bending actuators as “skeletal muscle.” Each soft actuator has two layers of embedded pneumatic channels (fig. S1A) for actuating reversible bistability to generate switchable two-way bending upon pressurization control in dual channels (fig. S1B). The three-dimensionally (3D) printed bistable spine mechanism is composed of two rigid hinged linkages to guide the bending motion of soft actuators (fig. S1C). The pretensioned spring that connects two ends of the bistable mechanism can store and release potential mechanical energy. The geometrical and materials property parameters of a BH-SBA prototype are listed in table S1. As schematically illustrated in Fig. 1D, the working principle follows four steps. First, the spring is pretensioned (Fig. 1D, i) and attached to both ends of the straight linkages (Fig. 1D, ii) to enable a BH-SBA. The linkage-based spine with attached stress-free soft bending actuators and embedded pretensioned spring results in an unstable state (Fig. 1D, ii), which have the maximum energy as shown in the schematic energy profile of Fig. 1C (state I) and a zero bending angle θ (θ is defined in the inset of Fig. 1C). Second, after releasing the pretension in the spring, the BH-SBA bends and eventually rests in one equilibrium [i.e., the stable state shown in Fig. 1D (iii)], which has local minimum energy with θ = −θ_eq (state II in Fig. 1C). Third, upon pneumatic actuation, i.e., inflating the exterior layered pneumatic channel of the bending actuator at rest states [ΔP₁ > 0 in Fig. 1D (iii)], the BH-SBA bends toward the unstable state, where the spring stores the most energy. Fourth, when it bypasses the unstable state, it rapidly snaps to the other stable state with θ = θ_eq [Fig. 1D (iv) and state III in Fig. 1C]. This bistable mode can be reversibly switched by following path a in Fig. 1C through actuating the other side of the channeled layer in the bending actuators. Thus, the actuator can generate a swing motion under dual-channel actuation between two stable states. In the working regime of path b with the monostable mode, in step 3, the interior layered pneumatic channel [ΔP₂ > 0 in Fig. 1D (iii)] is pressurized instead to further bend away from both unstable and equilibrium states for potential applications in soft manipulator discussed later; thus, in this case, bistability is not activated, and only single-channel actuation is needed. In the following, we will explore the mechanical behavior of the BH-SBA under both nonactuated and actuated states.

The competition between energy release and storage during bending of the soft pneumatic actuators and stretching of the spring determines the bistability of the system. Figure 2A shows the analytical energy landscape of the bistable actuator without pressurization as a function of the bending angle θ. The total potential energy U_total (blue curve) is the sum of the strain energy in the soft bending actuator U_actuator (mainly dominated by its bending energy; red curve) and the stretching energy in the spring U_spring (yellow curve; see details in the Supplementary Materials), i.e.

$$U_{\text{total}}=U_{\text{actuator}}+U_{\text{spring}}$$ (1)

Fig. 2. Design principle of energy competition and synergy relationship between springs and soft pneumatic actuators.

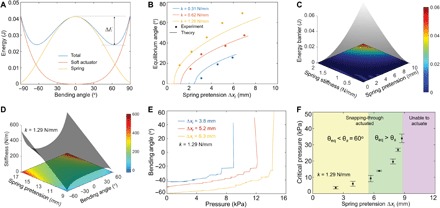
(A) The total energy of the bistable system (blue curve) as sum of strain energy in the soft bending actuator (red curve) and stretching energy in the spring (yellow curve). The energy difference between the peak and valley defines the energy barrier ΔE. (B) Comparison between theory and experiments on equilibrium bending angle versus spring pretension length at state I (∆x_I). (C) Energy barrier ΔE as a function of Δx_I and k in the spring. (D) Actuator stiffness as a function of spring pretention length and bending angle. (E) The measured actuated bended angle change with the increase of pressure p during the snapping-through bistability switching from state II to state III for the bistable actuators with different pretension. (F) Critical pressure for pneumatically actuating the bistable switch between two stable states as a function of pretention length Δx_I. There exists a threshold value of Δx_I, below which the bistable switch can be activated (yellow and green zone) while beyond which it fails to be activated (purple zone) because of the large energy barrier. The resting position after pretension release is at the equilibrium angle θ_eq with θ_eq < θ_s = 60° in the yellow zone and at the stopping angle of θ_s = 60° in the green zone.

U_actuator shows a convex parabolic shape with respect to the bending angle with a minimum value of 0 J at θ = 0°, whereas U_spring exhibits a concave parabolic relationship with respect to the bending angle with a maximum energy of $U_I=k\mathrm{\Delta }{x}_I^2/2$ at θ = 0°, where k is the spring stiffness and ∆x_I is the spring pretension length. The competition between U_actuator and U_spring leads to a symmetric profile of the total potential energy with one peak (unstable state I) at θ = 0° and two minimum points at two equilibrium and stable states II and III at θ = ±θ_eq. The value of θ_eq can be obtained by minimizing the total potential energy (see details in the Supplementary Materials), i.e.

$$\frac{{dU}_{\text{total}}}{d\mathrm{\theta }}=0$$ (2)

Figure 2B shows the analytical equilibrium bending angle θ_eq from Eq. 2 as a function of spring stiffness k and pretension length ∆x_I. It shows that for all springs, θ_eq increases monotonically and nonlinearly with both ∆x_I and k, i.e., the more energy it stores in the pretensioned spring, the larger angle it bends after pretension release, which is consistent with the experimental data. However, note that the BH-SBA does not bend (i.e., θ_eq = 0) upon release of the pretension until the spring is extended beyond a threshold value. It implies that the initial potential energy U_I stored in the pretensioned spring should be large enough to overcome the strain energy in the soft actuator to trigger the onset of instability. The energy difference between maximum and minimum in Fig. 2A defines the energy barrier ΔE of the bistable system. It requires ΔE > 0 to enable the bistability. Figure 2C shows that the energy barrier ΔE can be tuned by either ∆x_I or k in the spring (see details in the Supplementary Materials), where ΔE increases nonlinearly and monotonically with both ∆x_I and k. Similarly, Fig. 2D shows that at a given spring constant k (e.g., k = 1. 29 N/mm), the stiffness K of end effector of the bistable hybrid bending actuator varies with the bending angle θ and increases markedly with ∆x_I. Here, K is defined as (see details in the Supplementary Materials)

$$K=\frac{{df}_b}{d\mathrm{\delta }}, f_b=\frac{T}{0.5L \text{cos} \mathrm{\theta }},T=\frac{{dU}_{\text{total}}}{d\mathrm{\theta }}$$ (3)

where f_b is the static blocking force or reaction force at a given deflection of δ, T is the joint torque, and L is the length of the hinged linkages. Figure 2D shows that its stiffness can be manipulated over a large range from about 10 N/m to over 500 N/m by simply tuning ∆x_I from about 9 to 17 mm. The wide-range stiffness modulation provides the bistable actuator as a potential manipulator with tunable strength from low to high force as discussed later.

The switch between two equilibrium states in the BH-SBA can be actuated through pneumatic pressurization of the soft bending actuator to overcome the energy barrier. Figure 2E shows the measured bending angle θ as a function of the pneumatic pressure p for different spring pretension length ∆x_I when actuated from one stable state with a negative bending angle. For all springs, it shows a similar nonlinear J-shaped curve, where θ first increases gradually and monotonically with p (the actuator unbends), followed by an instantaneous and steep rise when approaching to the unstable state (the actuator snaps to the other stable state instantaneously), indicating the onset of snap-through bistability. The steep increase of the bending angle in Fig. 2E also defines the critical pressure P_c for actuating the bistability.

The highly nonlinear relationship between p and θ shown in Fig. 2E poses challenges to control the bending angle of the BH-SBA with pneumatic pressure. However, it is feasible to constrain its maximum bending angle during cyclic motion, which is of important implications in locomotion when bistable actuators are integrated for the design of mobile robots discussed later. Here, we set the angular position limit of the bistable mechanism to stop its rotational movement at preset stopping angles θ_s [inset of Fig. 1D (iii)]. By setting the value of stopping angles to be smaller than the equilibrium bending angle θ_eq predicted by Eq. 2, i.e., θ_s < θ_eq (Fig. 1C), the maximum bending angle during swing motion can be constrained and is equal to the preset stopping angle even when it is overpressurized.

Next, we examine the critical actuation pressure P_c to enable the bistability of the BH-SBA with a preset stopping angle θ_s. Here, we focus on how the energy barrier, determined by the initially stored energy in the spring, affects P_c by manipulating the pretension length ∆x_I (k = 1.29 N/mm and θ_s = 60° are fixed). It shows that P_c increases nonlinearly with ∆x_I. When ∆x_I is small (i.e., ∆x_I < ~5.5 mm, highlighted by yellow color), P_c increases linearly with ∆x_I at a small slope, and the actuator rests at the equilibrium position after pretension release without arriving at the preset stop angle due to θ_s > θ_eq (Fig. 2F). As ∆x_I further increases (~5.5 mm < ∆x_I < ~8.8 mm, highlighted by green color), P_c increases markedly and nonlinearly with ∆x_I, and the actuator rests at the preset angle stopper after pretension release due to θ_s < θ_eq (Fig. 2F). Consequently, it requires much higher pressure to actuate the BH-SBA. For example, for the actuator with ∆x_I ≈ 5.6 mm, it only requires ~10-kPa pressure to induce the snap through. However, when ∆x_I is increased to ∆x_I ≈ 8.6 mm, a 1.5 times increase in ∆x_I leads to over 3.4 times increase in the actuation pressure (~34 kPa) for the BH-SBA to snap. When ∆x_I further increases to be larger than 8.8 mm (highlighted by purple color), we observe that it fails to trigger the onset of snap-through bistability since the pneumatic actuation cannot overcome the high energy barrier even when we increase the input pressure to be as high as 100 kPa. There are several factors attributed to the high nonlinearity and the absence of snap-through bistability: (i) Large input pressure always leads to the overinflation of the air channel along the out-of-plane direction, which does not contribute to the in-plane expansion-induced bilayer bending. (ii) The soft bending actuators in the bistable hybrid actuator always have a nonuniform curvature, especially when preloaded with large spring pretension (i.e., with large initial bending angles). In this way, the middle section in the soft actuators always has a much larger curvature than sections at two ends. This large curvature may collapse or even close the air channel in the middle, making it difficult to be actuated even when the input pressure is substantially increased, which explains the region of no snap-through bistability shown in Fig. 2F.

Bistability for force amplification and rapid response

To understand the force amplification and rapid response effects enabled by bistability, we further study the actuation performances of the bistable hybrid actuator (BH-SBA), including motion (Fig. 3A and movie S1), dynamic blocking force (Fig. 3, B and C), and response time (Fig. 3D), in comparison with its two counterparts with the same geometry after removing the spring to disable the bistability. One is the hybrid soft bending actuator (H-SBA) without spring (left inset of Fig. 3B, denoted as “hybrid”), and the other one is the soft bending actuator with neither linkages nor springs (middle inset of Fig. 3B, denoted as “soft”). In the bistable actuator, the spring stiffness k is 1.29 N/mm, and the pretension in the spring ∆x_I is 6 mm, which corresponds to an analytical equilibrium bending angle of θ_eq = 63° (Fig. 2B). To constrain its actuated swing angle right at the preset stopping angle, we set θ_s = 60° < θ_eq in the spine mechanism guided by the design principle discussed above. To enable the occurrence of snap-through bistability, we set the actuation pressure to be 20 kPa, which is moderately higher than the critical actuation pressure (Fig. 2F). The three actuators with their base structure fixed are pneumatically actuated at the same pressure of 20 kPa and the same frequency of 3.2 Hz during the swing motion (the timing control parameters are shown in fig. S2 and table S2, and the experimental setup for measurement is shown in fig. S3).

Fig. 3. Bistability for amplified force and fast response.

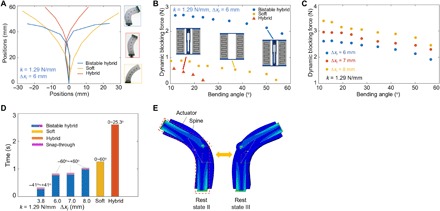
Comparison of mechanical performances between the bistable hybrid actuator (blue color) and its two bistability-disabled counterparts: a soft actuator without both linkages and springs (yellow color) and a hybrid actuator without springs (red color). (A) Tracking of the bended shapes at two stable states. (B) Dynamic blocking forces at different blocked bending angles. Insets are schematics of front views of the three actuators. (C) Dynamic blocking force as a function of spring pretension. All the actuators in (A) to (C) are pressurized at 20 kPa. (D) The response time of achieving the largest bending angle for three bistable, hybrid, and soft actuators with different spring pretensions under the same actuation. All actuators are pressurized at 30 kPa with the same flow rate of 3 liters/min. For bistable ones, the response time is composed of two parts including before (highlighted by blue color) and after snapping-through (highlighted by pink color). (E) Finite element simulation results on the actuated switch between two stable states of the bistable hybrid actuator through pressurization.

Figure 3A shows the trajectories of deformed bodies and the maximum bending angles θ_max of the three bending actuators at rest states. Compared to its soft (θ_max ~ 55°; bottom right of Fig. 3A) and hybrid (θ_max ~ 25°; middle right of Fig. 3A) counterparts, the BH-SBA exhibits the largest θ_max (top right of Fig. 3A) and rests right at the preset stopping angle 60° as designed (movie S2). The SBA has the largest deflection, resulting from both axial elongation and bending deformation. However, the axial elongation in both hybrid bending actuators is largely constrained by the rigid spine mechanism with a dominated bending deformation, which facilitates activating the bistability. In addition, the soft bending actuators in both hybrid actuators exhibit similar deformation motion, which follows the rigid rotation of the upper linkage around the joint in the spine mechanism. Thus, our model is able to analyze the bending angle and curvature of the hybrid bending actuators. In contrast, it is more challenging to analyze the curvature and bending angle of the SBA because of the axial elongation discussed above.

Figure 3B shows the corresponding measured dynamic blocking force F_b as a function of the bending angle during the swing motion of the three actuators, where the dynamic blocking force is much higher than the measured static blocking force by quasi-static indentation of the hybrid soft prototype (fig. S4) and the bistable flexible linkages alone (fig. S5). The dynamic blocking force F_b is defined as the dynamic impact force measured from the tip of the actuator when its swing motion actuated from its rest position is blocked by a rigid plate at a certain angle. The dynamic blocking force is studied because it represents the ground reaction force of legged robots to characterize the propulsion capability for high-speed locomotion. The experiment shows that as the actuator bends away from the center with θ = 0° to θ = θ_max with the largest deflection at rest states, F_b drops monotonically with the increase of the bending angle for all the three actuators, and the BH-SBA demonstrates the highest blocking force. As expected, the SBA generates a smaller dynamic blocking force of less than 1 N because of its materials compliance. Unexpectedly, despite its substantially enhanced stiffness with a hybrid design, the measured dynamic blocking force in the H-SBA is slightly lower than the SBA because of its much smaller swing angle θ_max, where θ_max ~ 25° in the hybrid one is less than half of the swing angle θ_max ~ 55° in the soft one. In distinct contrast, the peak dynamic blocking force near the center with θ ~ 10° is substantially enhanced to ~2.7 N in the BH-SBA, which is approximately three times larger than the soft one and seven times larger than the hybrid one. In addition, at the rest states with θ = θ_max, F_b drops to approximately zero for both nonbistable actuators, whereas the reduced F_b at the stopping angle is still close to 2 N for the BH-SBA, demonstrating the benefit of bistability in amplifying the output force capability. We further examine how the input pressure influences the dynamic blocking force F_b of the BH-SBA at a given certain bending angle. The results in fig. S6 show that F_b increases monotonically first with the pressure input and then approaches a plateau, exhibiting a highly nonlinear behavior.

With the understanding of force amplification through bistability mechanism, we further exploit the enhancement of the dynamic blocking force by manipulating the initial mechanical energy storage in the spring, i.e., $U_I=k\mathrm{\Delta }{x}_I^2/2$ through tuning pretension length ∆x_I. We test three prototypes of the BH-SBAs with the same geometry but different spring pretension (∆x_I = 6, 7, and 8 mm). All actuators are pressurized at 20 kPa to enable the bistability, and the spring stiffness is kept as the same k = 1.29 N/mm. Figure 3C shows the comparison of the measured dynamic blocking forces versus bending angle at different spring pretension lengths. As expected, the larger spring potential energy it stores, the higher dynamic blocking force it generates. The actuator with ∆x_I = 8 mm demonstrates the largest dynamic blocking force with a range of 2.5 to 3.4 N, which is about 30% higher than that with ∆x_I = 6 mm. Meanwhile, as discussed above, an increased ∆x_I leads to a marked increased critical actuation pressure to trigger the occurrence of bistability; thus, a relatively high pneumatic pressure is normally required to achieve a high blocking force.

In addition to maximum bending angle constraint and output force amplification, the proposed bistable hybrid system also contributes to rapid response during the swing motion. Upon the same actuation pressure of 30 kPa and the same air flow rate of ~ 3 liters/min, we compare the response time of six prototypes with bistability being disabled or enabled in Fig. 3D and table S3. It shows that the H-SBA exhibits the longest response time 2.60 s to bend from 0° to its maximum bending angle 25.3° at 30 kPa, which is over twice of the time of 1.26 s for the SBA bent from 0° to its maximum bending angle ~60°. On the contrary, the BH-SBAs take the least response time of less than 1 s to switch from the far left (negative θ) to the far right (positive θ). Their response time is composed of two parts including before (Δt_II-I; highlighted by blue color in Fig. 3D) and after snapping-through (Δt_I-III; highlighted by pink color in Fig. 3D), i.e., bending from state II (negative resting angle) to state I (zero bending angle) and from state I to state III (positive resting angle), respectively. We find that as the spring pretension ∆x_I increases, Δt_II-I increases markedly from 0.26 to 0.98 s to overcome the increased energy barrier. However, when beyond the unstable state, the snapping-through time Δt_I-III decreases with increased spring pretension ∆x_I to release the increased stored energy more quickly. It is observed that for the studied prototypes, Δt_I-III is less than 60 ms to snap to its resting state and the normalized snapping-through time, i.e., Δt_I-III/Δt_II-I, decreases markedly from 0.24 to 0.05 when ∆x_I increases from 3.1 to 8.0 mm.

It is observed that the snap-through bistability in the BH-SBAs is well captured by the corresponding finite element method (FEM) simulations using ABAQUS (SIMULIA, Dassault Systèmes; 6.14; Fig. 3E and movie S3; see details in the Supplementary Materials), where all actuators are actuated under a 40-kPa pressure and their transient dynamic responses with respect to time are recorded by the simulations. Despite the discrepancy between the absolute value of actuation and snap-through time in simulations with respect to experiments due to failing to model the pneumatic flow rate in experiments, the FEM results capture the trend of increased actuation time and decreased snapping-through time with the increase of spring pretension (table S4 and fig. S7). Figure S7 shows that for BH-SBAs with different spring pretension length, the relationship between simulated bending angle and actuation time exhibits J-shaped–like high nonlinearity, where the slope increases markedly after the unstable state.

Bistability for high-speed crawler

Bioinspired by the flexion and extension motion of the spine in mammals such as the cheetah during high-speed galloping (Fig. 4A), we explore harnessing the bistable spine mechanism–enabled power amplification and fast response for its application in high-speed locomotive soft robots. As schematically illustrated in Fig. 4A, simply attaching four claws to the BH-SBA constitutes the proposed high-speed bistable hybrid soft robot. Similar to the active spine of the cheetah, the bistable linkage–based spine in the crawler bend downward to store energy and shorten the length of stride and then bend upward, bypassing the unstable straight configuration to quickly release the stored energy to increase its stride length. The active flexion and extension motion is driven by the soft pneumatic bending actuator as “muscles.” The prototype is 7 cm long and 6 cm wide with a mass of 45 g. The spring stiffness k is 1.29 N/mm, and the pretension length is 6 mm at state I. The stopping angle of the spine is θ_s = 60°. Small elastomer pads are attached on the claws, as shown in Fig. 4B, to break the deformation symmetry through the passive switchable friction for front and rear claws (24). At the rest state, its soft body is initially bent downward (top of Fig. 4B) and the forefeet have much larger static friction force (because the Ecoflex elastomer is in contact with the surface) than the rear ones (right of Fig. 4B). This generates a forward motion when the soft body is actuated and bent upward; when the crawler is in a convex shape, i.e., bent up (bottom of Fig. 4B), the rear legs have larger friction force than the front ones. This also results in forwarding locomotion when the body is actuated and bent downward.

Fig. 4. Bistability for high-speed crawler.

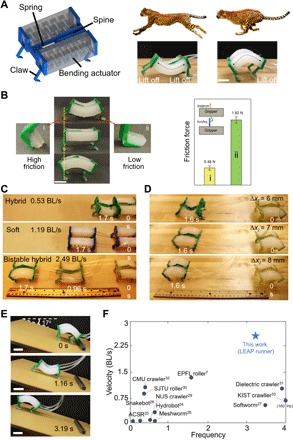
(A) Locomotion gaits of the proposed bio-inspired crawler by the spine actuation in the fastest galloping cheetahs. The spine bends upward to store energy when touching ground and bends downward to release energy and extend its stride length with legs lifting off the ground during the high-speed locomotion. (B) Left: Mechanism of directional locomotion. The Ecoflex elastomer pads attached to the claws provide tunable friction force (i, high friction; ii, low friction) and transit the symmetric bending of the bistable actuator into directional locomotion. Right: Static friction forces of claws with and without Ecoflex pad–substrate contact. The claw shows ~280% increase in the friction force (1.82 N) when the attached Ecoflex pad contacts the substrate. The inset shows the schematic of friction force measurement. (C) Demonstration of locomotion in the high-speed bistable crawler and its two counterparts with disabled bistability at different actuation time: soft crawler based on the soft actuator and hybrid soft crawler based on the hybrid one. All actuators are pressurized at the same pressure of 20 kPa and the same frequency of 3.2 Hz. The bistable hybrid soft crawler shows the fastest speed (~2.49 BL/s). (D) Demonstration of locomotion in the high-speed bistable crawler with different values of spring’s stored energy in the bistable actuator. All actuators are pressurized at the same pressure of 30 kPa and the same frequency of 2.63 Hz. The one with largest spring pretension shows the fastest speed (~2.68 BL/s). (E) Demonstration of the proposed bistable hybrid soft crawler’s capability in climbing slightly titled surfaces (tilting angle of 17°). The other two counterparts fail to climb. Scale bars, 25 mm. (F) Comparison of locomotion velocity measured in BL/s between our proposed bistable hybrid soft crawler (denoted as star-shaped symbol) and reported locomotive soft robots in literatures. LEAP, Leveraging Elastic instabilities for Amplified Performance. Photo credit: Yichao Tang, Temple University.

Despite the simplicity of the design, the proposed bistable hybrid soft crawler exhibits a superior high locomotion speed (experimental setup in fig. S8). It can achieve a linear locomotion speed of 174.4 mm/s, or 2.49 BL/s, when pressurized at 20 kPa (average actuation frequency is 3.2 Hz; fig. S2 and table S1) on a wooden surface (bottom of Fig. 4C). Such a high locomotion speed is 2.1 times the speed of its counterpart soft crawler based on the SBA (middle of Fig. 4C) and 4.7 times the speed of the hybrid soft crawler based on the H-SBA (top of Fig. 4C). The comparison of real-time locomotion videos can be found in movie S4. The slow motion of the bistable hybrid soft crawler (movie S5) shows that its locomotion gait is similar to that of high-speed cheetahs during their energy-economic galloping (Fig. 4A). The forefeet touch the land bending up its back to store energy before they lift off and then straightened and bent downward to lengthen the stride by extending the forefeet with all feet off the ground. In contrast, for the other two soft and hybrid counterparts, all the feet always remain in contact with the ground and thus consume more energy to overcome the friction (movie S4). Note that different from the power supply from muscles and tendons in legs and spines of animals, the energy storage and quick release in the bistable hybrid soft crawler are triggered by the snap-through bistability in the sole spine mechanism, which saves energy cost and enables large force exertion and fast response for high-speed locomotion.

One of the advantages of this proposed technique is that we can change the speed of locomotion by tuning the energy barrier of the BH-SBA through spring pretension or spring stiffness. Next, we explore how the spring’s stored energy due to spring pretensions affects the locomotion speed of the proposed crawler. According to Fig. 3C, a larger pretension in the spring, i.e., larger energy barrier, leads to a higher dynamic blocking force and thus higher reaction force in the bistable actuator. This improved force output contributes to a higher ground reaction force of the crawler’s feet that provide the crawler with larger friction force to move forward. Thus, larger spring pretension length results in faster locomotion, which is verified by the experimental test shown in Fig. 4D and movie S6. We compare the locomotion speed of three identical bistable crawlers but only with different ∆x_I = 6, 7, and 8 mm in the spring, respectively. All crawlers are pressurized at 30 kPa with an average actuation frequency of 2.63 Hz (fig. S2 and table S1). The result shows that the crawler with the largest spring pretension length (∆x_I = 8 mm) demonstrates the highest locomotion velocity by leveraging high energy storage and rapid energy release. It can achieve a linear locomotion speed of 187.5 mm/s, or 2.68 BL/s, which is 18.7% faster than the crawler with ∆x_I = 7 mm and 38.8% faster than the crawler with ∆x_I = 6 mm. We further test its locomotion capability on a tilted surface. We find that when the surface is tilted to 17°, the bistable hybrid soft crawler can still achieve a fast location speed of 0.56 BL/s (Fig. 4E). However, the other two counterparts are not capable of climbing up the tilted surface (movie S7).

In Fig. 4F, we compare the locomotion velocity of the proposed bistable hybrid soft crawler with a few representative locomotive soft and hybrid soft robotics (7, 24–33) and categorize them in the chart of body length speed versus actuation frequency. These soft robot–based crawlers, mostly having continuous compliant bodies and stable structures, demonstrate a relatively slow speed in the range of 0.02 to 0.5 BL/s because of either slow actuation speed or small force exertion of the composed soft actuator, where the speed approximately increases with the actuation frequency for the reported crawlers. Disparate from its counterparts, despite the similar key component of soft material–based soft actuator, the proposed bistable hybrid soft crawler is much faster, which is over 2.5 times of the high energy density–based dielectric crawler. Meanwhile, it requires less input pressure (it only requires 20-kPa pressurization for operation) because of the benefit of rigid skeleton and force amplifier, which is even comparable, in velocity, with some rigid robots and terrestrial animals (1 to 100 BL/s) (24) . Note that despite the hybrid design, the motion of the proposed crawler is actively and directly driven by the continuous deformation of the soft bending actuators under pneumatic actuation, while the passive deformation in the spine is driven by the soft actuators, playing the role as a passive force and speed amplifier. The stored energy in spring, which can be tuned by changing spring stiffness or pretension, plays a dominant role in its energy barrier, thus affecting its force output, velocity, and energy efficiency. Ideally, a larger energy–stored spring generates a larger energy gap, thus corresponding to a larger force exertion from the bistable hybrid system. However, meanwhile, the high-energy spring increases the energy consumption of the bistable hybrid system because it requires more energy input to overcome the high energy barriers. It may lead to a drop in the frequency and velocity of the bistable hybrid system unless external energy is increased (e.g., increase the airflow rate). Therefore, a trade-off should be considered for selecting the stiffness and pretension of the spring for the design of high-speed locomotive robots. Design optimization will be studied in the future to further improve the performance of the proposed high-speed crawler.

Bistability for high-speed underwater swimmer

In addition to a terrestrial high-speed locomotive soft robot, the swing motion of soft body in fishes inspires us to explore the multifunctionality of bistable hybrid soft actuators as a high-speed underwater robot. The structure of this fish-inspired swimming robot is depicted in Fig. 5A. It is composed of an encapsulated bistable hybrid actuator and an attached thin plastic sheet–based fin (thickness, 0.25 mm) at its rear for enhancing the propulsion force. Compared to terrestrial locomotion, underwater locomotion requires a relatively higher output force to overcome the water resistance for propulsion due to the fluid-structure interaction. Therefore, for the pneumatic bending actuator–based swimmer, it needs more energy input through a high actuation pressure of 150 kPa, which could lead to the structural failure of its soft body if not strengthened. To enhance the force output and structural reliability, we encapsulate the soft bending actuators with conformable, stretchable, and bendable polymeric wrinkling–based envelope by following the method by Cianchetti et al. (34), as highlighted in the red color of wrinkled skin in Fig. 5A. When protected with braided sheath, the bending actuator can sustain higher pressure and survive longer fatigue life (34); therefore, here, we use the encapsulated soft bending actuator for underwater locomotion. The bending actuator is 45 mm in length and 25 mm in diameter. The whole prototype is ~150 mm long with a mass of 51 g. The preset stopping angle of the linkages is θ_s = 45°. The spring stiffness is 1.09 N/mm with 10-mm pretension length.

Fig. 5. Bistability for high-speed underwater fish-like soft robot.

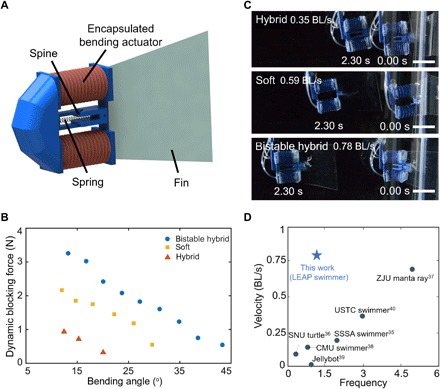
(A) Schematic of the proposed fish-like robot, which is composed of the bistable actuator attached with a polymeric fin. The schematic head is for decoration purpose only. (B) Comparison between the bistable actuator and its two counterparts of hybrid and soft actuators in dynamic blocking force versus blocked bending angle. All actuators are pressurized at 160 kPa and an average frequency of 1.3 Hz. (C) Demonstration of underwater locomotion in bistable hybrid soft swimmer and its two counterparts at different actuation time: soft swimmer based on encapsulated soft actuator and hybrid soft swimmer based on encapsulated hybrid actuator. The bistable hybrid soft swimmer shows the fastest speed. Scale bars, 50 mm. (D) Comparison of swimming velocity between the proposed bistable hybrid soft fish-like robot (denoted as star-shaped symbol) and various reported underwater soft swimmers (denoted as round symbols). Photo credit: Yichao Tang, Temple University.

Similarly, we measure the dynamic blocking force and deformation of the encapsulated bistable hybrid actuator and compare with its two counterparts without bistability under the same pneumatic pressure of 160 kPa. As expected, the bistable hybrid one generates the largest maximum dynamic blocking force over 4 N and maximum bending angle θ_max of 45°, which is equal to θ_s = 45°. In contrast, its two hybrid and soft counterparts show smaller force exertion and smaller maximum bending angle (Fig. 5B).

Figure 5C shows the comparison of swimming speed between the proposed bistable hybrid soft swimming robot and its two counterparts under the same pneumatic pressure of 160 kPa and average frequency of 1.3 Hz (fig. S2 and table S1; experimental setup in fig. S8): soft swimmer based on the encapsulated soft actuator and hybrid swimmer based on the encapsulated springless hybrid actuator. It shows that the bistable hybrid soft swimming robot can achieve a maximum average locomotion speed of ~117 mm/s (bottom of Fig. 5C), or 0.78 BL/s, which is 32 and 122% faster than its two counterparts: soft swimmer (middle of Fig. 5C) and hybrid swimmer (top of Fig. 5C), respectively. The comparison of real-time underwater locomotion between the three swimmers can be found in movie S8.

We further compare the speed performance of our bistable hybrid soft swimmer with other reported soft swimming robots, which use different actuation methods (e.g., shape memory alloy and ionic polymer-metal composite actuators) and frequencies (Fig. 5D) (35–40). It shows that regardless of different actuation methods, the swimming velocities approximately follow a monotonically increasing trend with the actuation frequency, arriving at 0.7 BL/s at 5 Hz in the system of a manta ray–inspired electronic fish (37). In contrast, despite a relatively low average actuation frequency of 1.3 Hz, the proposed bistable hybrid soft swimmer achieves 0.78 BL/s high speed (star-shaped symbol), outperforming most of the reported soft swimmers (round symbols). Although the bistable hybrid soft swimmer is still slower than biological fishes that typically exhibit a swimming capability of 2 to 10 BL/s (41), future work on optimization of the bistable structure, actuators, springs, and the morphology of the robot hold great potential to fill this gap.

High-force bistable soft gripper with tunable stiffness

So far, we have demonstrated the versatility of bistability for force amplification and rapid response in enabling high-speed terrestrial and aquatic locomotive soft robots in the bistable operating regime. As schematically illustrated in Fig. 1C, bistability also provides another monostable operating regime in the actuator. Next, we explore leveraging the monostable regime for the design of high-force bistable soft grippers with wide-range stiffness modulation. The spring-based hybrid mechanism alone without activating bistability has the capability to produce high force for soft robots. The key of high-force output lies in the spring that supports a wide range of tunable stiffness, as demonstrated in Fig. 2D.

Stiffening/softening is an important feature of soft robots in maintaining their shape changes and realizing adaptable force exertion to different working environments. Research efforts have been dedicated to building soft robots with variable stiffness by harnessing granular jamming (7), phase changes (42), or tendon-driven stiffening (43), but these robots have limited ranges of stiffness and limited force outputs. We use a strategy similar to tendon-driven stiffening to our hybrid soft-rigid system. Despite the simplicity in implementation, we demonstrate its effectiveness in manipulating the stiffness as below.

Figure 6A shows the schematic of the bistable hybrid soft gripper, which is similar to the encapsulated bistable hybrid actuator in Fig. 5A but operating in the monostable regime. The dual-actuation design allows independent operation of the pneumatic actuator (e.g., to handle delicate objects as Fig. 6D) or motor-driven tendon actuator (e.g., to handle stiff and heavy objects as Fig. 6E). A dc electric motor–driven tendon is attached to the end of the extension spring. When the dc motor is actuated, it pulls the tendon and thus extends the spring (Fig. 6C), bending the actuator to close the “fingers” toward the stopping angle. Further extension of the spring beyond the stopping angle substantially stiffens the actuator. For this tendon spring–driven system, the spring stiffness plays a dominant role in determining the stiffening modulation. Thus, using a spring with higher stiffness ensures a larger amplification in stiffness. To understand this effect, we characterize its variable stiffness with static blocking force (N) as a function of the spring extension. The pincer-grasping posture is shown in the inset of Fig. 6B. In the test, the actuator is bent at 80° (the stopping angle in the linkages is θ_s = 85°) with its free end blocked by a force sensor. Simultaneously, the motor pulls the spring (the spring stiffness is 9.67 N/mm), and the bending actuators are pressurized at 120 kPa. The experiment results (Fig. 6B) show that its static blocking force can be manipulated between 0.1 to 103 N by tuning the length of the spring, which agrees well with the simple theoretical model (see the Supplementary Materials for details). As a soft variable actuator, it demonstrates a 1 to 10³ range in stiffness modulation by harnessing the spring tendon–stiffening system, which is difficult to achieve with most previously reported stiffening methods used for pneumatic actuators (42, 44). In addition, unlike stiffening mechanisms that only allow for binary (or limited) stiffness control (45, 46), the proposed stiffening strategy provides continuous tunability via tensioning of the spring, thus providing the potential to construct soft machines by harnessing a wide range of stiffness modulation.

Fig. 6. Bistable hybrid soft grippers with wide-range variable stiffness modulation.

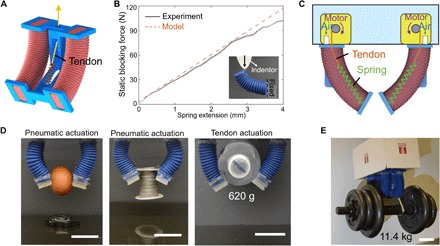
(A) Schematic of the encapsulated bistable hybrid actuator driven by tendon. (B) Stiffness test of the encapsulated actuator (bent at 75°; insets). We characterize the force as a function of spring extension. The solid line is the mean of three experiments (with shaded error bar), and the dashed line presents the theoretical model result. The stiffness is calculated as the slope of the force versus indentation depth. (C) Schematic illustration of the proposed gripper by assembling two actuators. The manipulation can be controlled by both motors, through pulling the spring, and pneumatic signals. (D) Demonstrations of its capability in grasping various objects in different shapes and weight. (E) Demonstration of high-load manipulation. Scale bars, 50 mm. Photo credit: Yichao Tang, Temple University.

Taking advantage of this wide-range modulation and programmable stiffness, we design and fabricate a strength-adjustable hybrid soft gripper, which allows for manipulating a variety of objects ranging from fragile lightweight to high-load objects. As schematically shown in Fig. 6C, the gripper is composed of two encapsulated bistable hybrid actuators, each one is driven by the independently controlled pneumatics and dc motors (fig. S9). Pneumatic actuation is used for gripping lightweight and fragile objects by using the intrinsic compliance of soft materials/structures. This soft gripper requires the tendon in slack, and thus, the spring remains inactive, while motor-driven actuation is used for grasping heavy objects through pulling the spring to amplify the bending stiffness. On the basis of this simple working mechanism, we successfully demonstrate that the proposed hybrid soft gripper is versatile to grasp objects in a variety of shapes, sizes, and weights. For example, when pressured at 90 kPa without activating the tendon (i.e., the tendon and spring remain relaxed), the gripper is capable of grasping a fragile egg, a small-size reagent bottle, a steel wrap, and tape rolls in regular spheroidal or cylindrical shapes as shown in Fig. 6D and movie S9. When driven by motors, the gripper is capable of directly grasping much heavier objects such as a bottle of water (620 g; right of Fig. 6D) and a 3.6-kg payload of dumbbells by wrapping around the objects (movie S9). The grasping payload is further enhanced by pulling across the gripper’s “finger” tips, for example, a 9.2-kg payload of dumbbells (movie S9). Currently, the largest payload that our gripper can grasp is 11.4 kg (25.3 lb), as demonstrated in Fig. 6E and movie S9, which is ~180 times the weight of a single actuator. For all the tests, we use the same high-stiffness spring (k = 9.67 N/mm), and it is stretched by 3 mm at the stopping angle position for grasping the maximum payload. Note that the grasping force of our gripper is mainly determined by the spring. Therefore, its grasping capacity can be further improved by using springs with higher stiffness. More details and grasping videos can be found in the Supplementary Materials.

DISCUSSION

We demonstrate that by harnessing the rapid response of snap-through bistability, bistable hybrid soft machines can be customized for different applications with substantially improved mechanical performance, including high speed, high force, tunable bistability, and programmable stiffness. Compared to conventional stable soft bending actuators, bistability enables not only 20 times faster response time (tens of milliseconds) but also over three times higher exertion force. We develop an energy-based theoretical model to guide the design of bistable soft actuators, including the relationship among design parameters, control inputs, and outputs. This paper investigates two operating regimes of bistability for multifunctional high-performance soft robot design: bistable mode through the competition-synergy relationship between springs and pneumatic actuators and monostable mode through tunable spring pretension and spring stiffness. It serves as a design guideline for building these soft actuators/robots. Although we only demonstrate the integration of our actuator in building high-speed locomotive robots and high-strength manipulators, the high-speed and high-force output without sacrificing the advantages of soft robots could find potential applications in surgical robots, wearable devices, etc. The proposed bistable hybrid system opens a new avenue for constructing next-generation high-performance soft robots across multiscales with multifunctionalities, and we envision that it could also inspire further exploration into building large-scale (≥10¹ cm) soft machines.

Despite the use of PneuNets-type conventional pneumatic soft actuators in our demonstrated hybrid systems, the proposed bistable strategy could be expanded to a broad range of soft robots and soft actuators (e.g., fluidic elastomer actuators, shape memory actuators, electroactive polymers, and stimuli-responsive materials) in response to different actuation inputs, including pressure, heat, electricity, light, and magnetic field. We believe that the proposed bistability strategy could also substantially improve their performance in force exertion, velocity, stiffness, and energy efficiency.

Inducing bistability in soft bending actuators potentially makes it more difficult to control the bending motion. In this work, we intentionally avoid controlling the bending angle after the onset of snap-through (Fig. 2E) to realize rapid motion. It might be challenging to control the bending angle to a desired value in a short time period because soft pneumatic actuator has low bandwidth. However, the controllability of the angle positions can still be enhanced by properly activating the antagonist pneumatic actuator, similar to how a conventional soft bending actuators is controlled (5), but considering the additional force generated by the spring. Another issue of the proposed hybrid system is that its overall degree of freedom is reduced since a rigid linkage with a revolute joint is used. This can be addressed by replacing the rigid linkage with a single-piece and compliant mechanism [e.g., the carbon fiber reinforced prepreg design of the flytrap-inspired bistable robot (47)] or prestrained soft elastomers for energy storage (32). Thus, bistable soft robots made of entirely soft materials could be realized.

Future improvement of our hybrid soft machines includes the following: (i) increasing the energy storage density and peak power [the maximum stored energy in the spring is limited by the pneumatic actuation to overcome the high energy barrier; the current stored energy density of the bistable hybrid soft actuator is about 1.2 J/kg, and the peak power is about 8 W (table S1), which is far below the combustion-based jumping soft actuators (36); improvements could be achieved through reinforcing the soft actuator or hydraulic actuation]; (ii) achieving active control of the spring pretension length during the motion of the bistable actuator, e.g., driven by dc motor or using shape memory spring (this active control will enable programmability in force, velocity, energy barrier, and stiffness of the bistable actuator, therefore allowing the soft robotic crawler or swimmer to change speed and achieve new locomotion modes such as jumping or escaping); (iii) optimizing the proposed crawler and swimmer for faster locomotion [this could be achieved through structural optimization of the bistable actuator, replacing the rigid legs with energy-stored legs or replacing the PneuNets with modified fast pneumatic networks for a higher actuation frequency (48)]; (iv) constructing a modular hybrid robot (with the bistable actuator as a single module) that enables multiple degree of freedom (for example, by positioning multiple modules in orthogonal directions) and multistability for various applications; and (v) improving sensing and control. Current robot prototypes use simple sensors (e.g., pressure sensors) to perform low-level control for the pneumatic actuator, and the Arduino microcontroller controls the timing of coordination between the pneumatic actuation and the bistable mechanism (table S2). In our future work, we will investigate sensing and control (e.g., how to use inertial measurement unit to measure joint angles to control the speed of locomotion of our robotic crawler) for improved performance and intelligence.

MATERIALS AND METHODS

Motion characterization

The motions of studied bending actuators (Fig. 3A) were captured by a high-speed camera (model MQ022CG-CM, USB 3.0, Ximea GmbH) with a 60-Hz external synchronization signal. The recording time was 10 s, generating 600 frames. The tracking method was based on using the simple linear iterative clustering algorithm to generate trackable, meaningful superpixels, followed by a 2D Kalman filter to predict the positions of actuators (49).

Fabrication of bending actuators

The pneumatic soft bending actuators without encapsulation were fabricated following the conventional molding-demolding manufacturing technique for fluid-driven soft actuators reported in (1). Encapsulated pneumatic bending actuators were fabricated following (34). The braided structure (denoted by red color in Fig. 5A) was prepared by compressing the polyester sleeve (McMaster-Carr, 9284K4) through a steel rod and then curing in the oven at 60° for 20 min. All rigid skeletons, mostly made of polylactic acid, were 3D printed using Ultimaker 2+ and were bonded with the soft actuators using both Ecoflex 00-50 (Smooth-On Inc.) and Insta-Cure glue (Bob Smith).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/19/eaaz6912/DC1